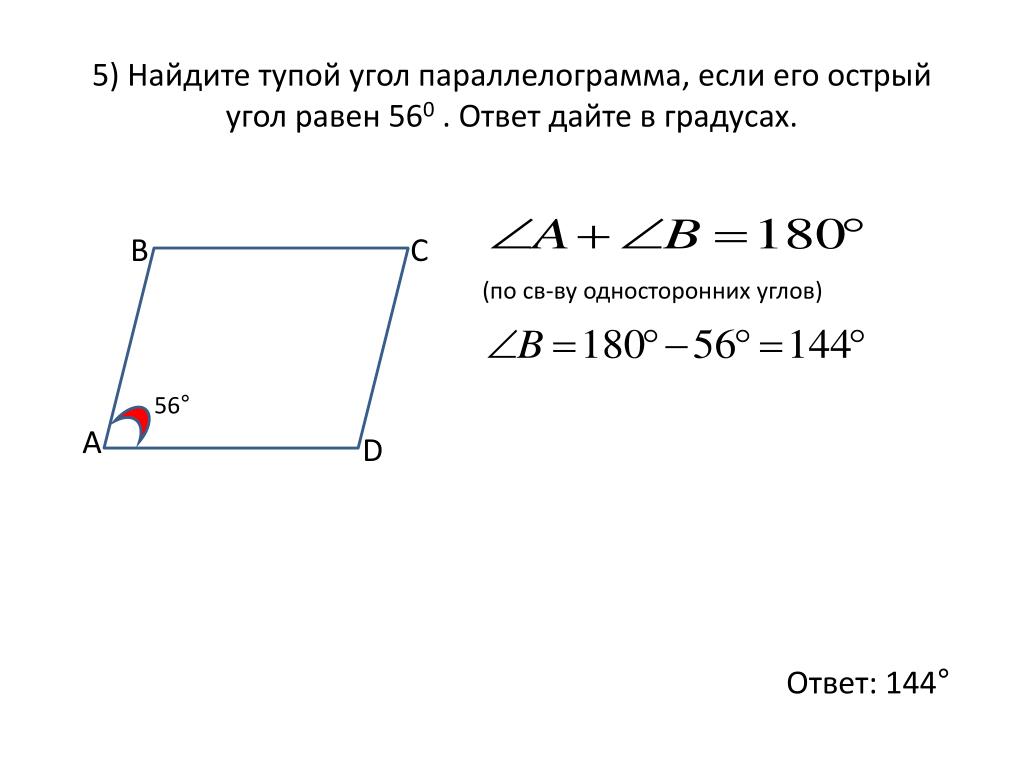
Параллелограмм. Свойства параллелограмма. Cумма углов параллелограмма.
- Альфашкола
- Статьи
- Параллелограмм
Что такое Параллелограмм?
Если четырехугольник имеет две пары противоположных сторон, параллельных и равных по величине, то он называется параллелограммом в геометрии.
Параллелограмм имеет четыре стороны, четыре вершины, четыре угла.
- Если мы сложим четыре угла параллелограмма, мы получим 360°
- В параллелограмме, если какой-либо из углов является прямым углом, то он называется прямоугольником.
- В параллелограмме , если один из углов является прямым углом и все стороны равны, то он называется квадратом.

- Если в параллелограмме все стороны равны, то он называется ромбом.
Поскольку трапеция имеет только одну пару противоположной параллели, трапеция не является параллелограммом.
Геометрические свойства параллелограмма
Нарисуйте параллелограмм на листе бумаги и вырежьте его из бумаги. Нарисуйте пунктирную линию вдоль одной из диагоналей и прорежьте ее поперек. Теперь мы получим два треугольника.
Положите один треугольник на другой. При необходимости мы могли бы перевернуть треугольники, и мы могли бы видеть, что два треугольника являются равными.
\(ABD_{тр}=BCD_{тр}\)
Свойства параллелограмма
- Противоположные друг другу стороны совпадают.
Доказательство:
Поскольку Диагональ параллелограмма разрезает параллелограмм на два равных треугольника, можно сказать, что соответствующие стороны треугольника являются равными.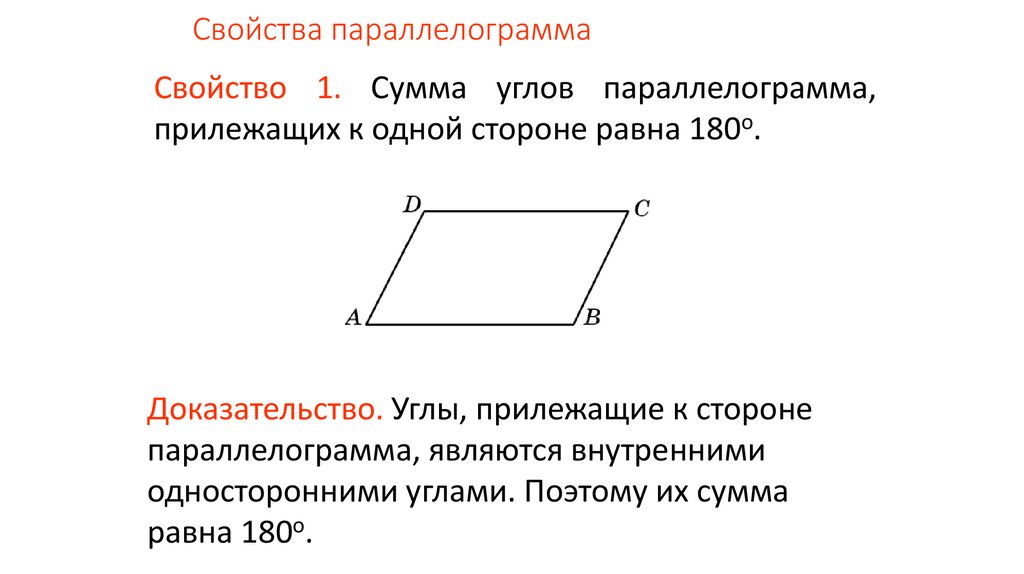
- Противоположные углы параллелограмма друг другу равны.
- Диагонали параллелограмма разделяют друг друга пополам.
Важным условием, которое мы используем, чтобы проверить, является ли данный четырехугольник параллелограммом, является то, что пара противоположных сторон равна и параллельна.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Ирина Анатольевна Фокина
Репетитор по математике
Стаж (лет)
Образование:
Гомельский государственный университет им Ф. Скорины
Скорины
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-9 классов. Доступно и позитивно познакомимся с удивительным миром цифр и формул. Индивидуальный подход к каждому ученику. Помогу Вашему ребенку стать настоящим волшебником, которому будет под силу не только элементарная магия цифр, но и умопомрачительные превращения математических формул.
Александр Ринатович Набиуллин
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии для 7-11 классов. Подготовка к ОГЭ, ЕГЭ. «Химик — он не бог, но всё умеет». Старый полушутливый девиз из студенчества.
Химия — это практически всё, что нас окружает. Понимание её сути позволяет очень многое: различать полезные добавки в пище, бесполезные и небезопасные, понимать роль удобрений для растений и роль лекарств для человека. Кроме того, это ещё и очень интересно. :)
Понимание химии — универсальный ключ к знаниям в этой области. Это позволяет решать любые практические и теоретические задачи, от школьного до олимпиадного уровня.
Подготовка к ОГЭ, ЕГЭ. «Химик — он не бог, но всё умеет». Старый полушутливый девиз из студенчества.
Химия — это практически всё, что нас окружает. Понимание её сути позволяет очень многое: различать полезные добавки в пище, бесполезные и небезопасные, понимать роль удобрений для растений и роль лекарств для человека. Кроме того, это ещё и очень интересно. :)
Понимание химии — универсальный ключ к знаниям в этой области. Это позволяет решать любые практические и теоретические задачи, от школьного до олимпиадного уровня.
Жанна Александровна Бояркина
Репетитор по математике
Стаж (лет)
Образование:
Благовещенский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Всегда готова поделиться знаниями! Считаю, что учить наизусть скучные правила необязательно. Главное — понимать что и как, тогда ученик и без скучных заучиваний сможет свободно сформулировать любое правило, а полученные знания будут прочными и навсегда.
Готовлю к ОГЭ и ЕГЭ, мои ученики показывают хорошие и отличные результаты на экзаменах.
На уроках придерживаюсь трех единств: наглядно, понятно, просто.
Всегда готова поделиться знаниями! Считаю, что учить наизусть скучные правила необязательно. Главное — понимать что и как, тогда ученик и без скучных заучиваний сможет свободно сформулировать любое правило, а полученные знания будут прочными и навсегда.
Готовлю к ОГЭ и ЕГЭ, мои ученики показывают хорошие и отличные результаты на экзаменах.
На уроках придерживаюсь трех единств: наглядно, понятно, просто.
Похожие статьи
- Важность образования в XXI веке
- Производная
- Как перевести квадратные метры в квадратные километры
- Рациональные числа
- Укусы насекомых: об опасности, способах защиты и первой помощи
- Спасение от жары: рецепты домашнего мороженого и лимонада для детей и взрослых
- Как правильно общаться с ребенком об успеваемости?
- Вымершие животные, которые могли существовать, если бы не деятельность человека
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
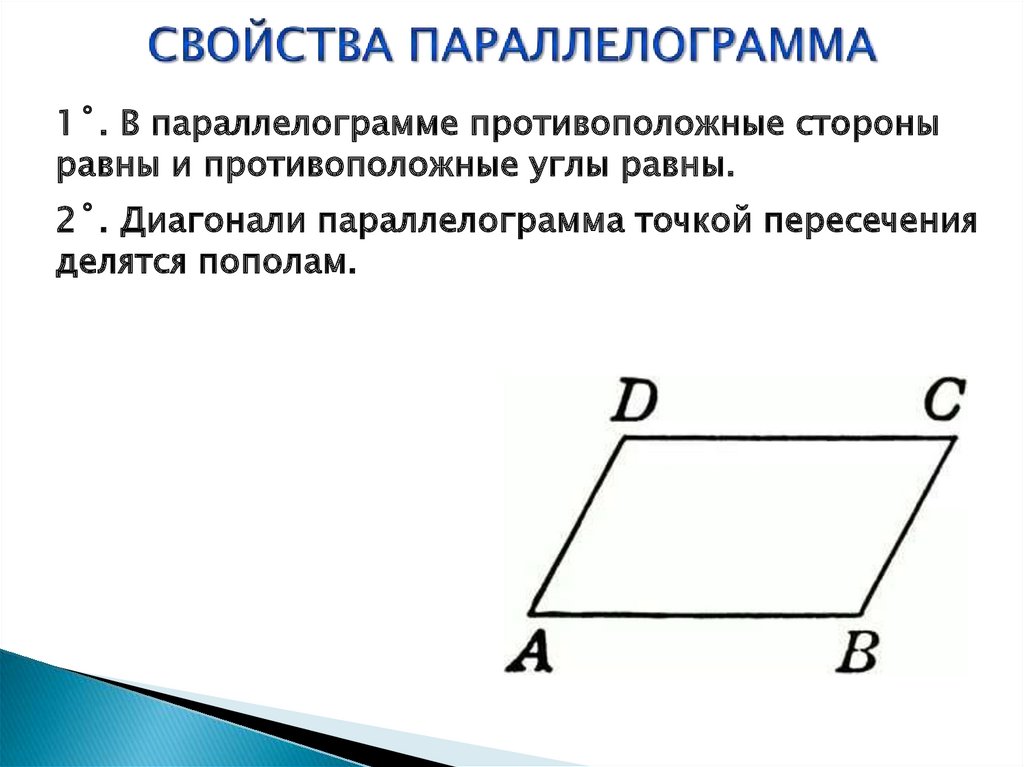
Параллелограмм, его свойства.
 Признаки параллелограмма.
Признаки параллелограмма.Параллелограмм.
Приступаем к изучению разных видов четырёхугольников.
Определение. Параллелограммом называется выпуклый четырёхугольник, у которого стороны попарно параллельны.
– параллелограмм. У него .
Рассмотрим свойства параллелограмма.
ТЕОРЕМА. У параллелограмма противолежащие стороны и углы равны.
Дано: – параллелограмм
Доказать:
Доказательство.
1. Проведём диагональ . Рассмотрим и .
2. и ; и – внутренние односторонние при параллельных прямых, значит,
.
3. Итак, , ч.т.д.
ТЕОРЕМА. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Дано: – параллелограмм
и – диагонали
Доказать:
Доказательство.
1. Т.к. параллелограмм является выпуклым четырёхугольником, то, по свойству выпуклых многоугольников, его диагонали пересекаются, т.е. .
2. Рассмотрим и .
по II признаку равенства треугольников , ч.т.д.
Итак, параллелограмм обладает двумя свойствами:
Противолежащие стороны и углы параллелограмма равны.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Признаки параллелограмма.
Часто бывает ситуация, когда известны какие-то свойства четырёхугольника, а какой вид имеет этот четырёхугольник неизвестно. В этом случае помогут признаки параллелограмма.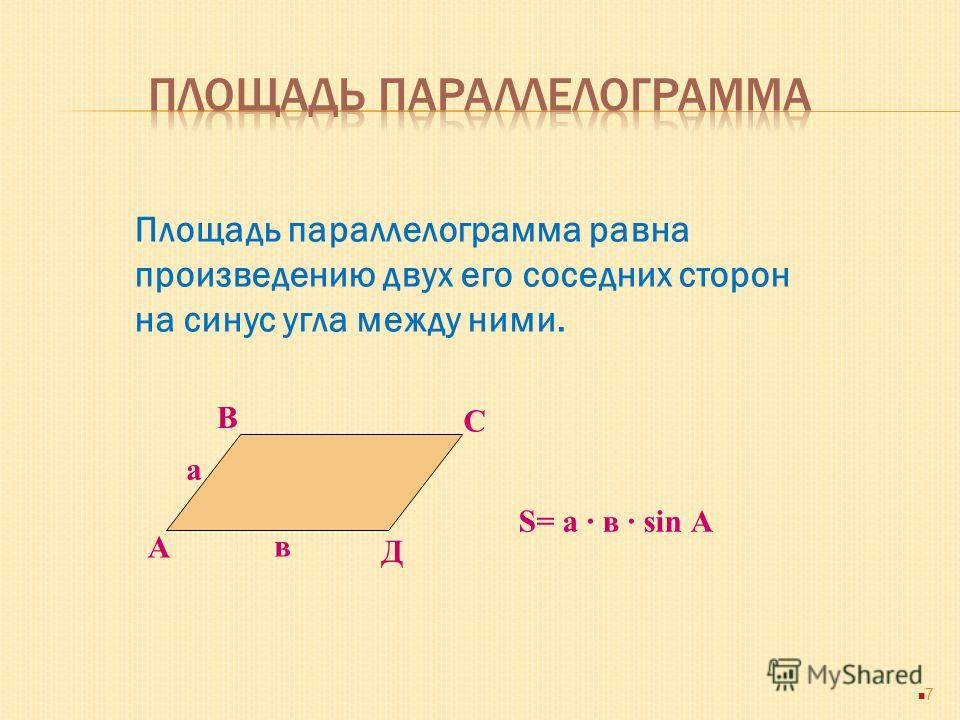
ТЕОРЕМА (I признак параллелограмма).
Если в четырёхугольнике две стороны равны и параллельны, то такой четырёхугольник является параллелограммом.
Дано: – четырёхугольник
Доказать: – параллелограмм.
Доказательство.
Проведём диагональ и рассмотрим и .
. Эти углы являются внутренними накрест лежащими при прямых и , значит, по признаку параллельности прямых, .
Итак, в четырёхугольнике , т.е. стороны попарно параллельны, значит, – параллелограмм (по определению), ч.т.д.
ТЕОРЕМА (II признак параллелограмма).
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник является параллелограммом.
Дано: – четырёхугольник
Доказать: – параллелограмм.
Доказательство.
Проведём диагональ и рассмотрим и .
и . А эти пары углов являются внутренними накрест лежащими. По признаку параллельных прямых: «если внутренние накрест лежащие углы равны, то прямые параллельны», делаем вывод, что , а . По определению параллелограмма, данный четырёхугольник является параллелограммом, ч.т.д.
ТЕОРЕМА (III признак параллелограмма).
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то такой четырёхугольник является параллелограммом.
Дано: – четырёхугольник,
и – диагонали, ,
Доказать: – параллелограмм.
Доказательство.
Рассмотрим и .
по I признаку равенства треугольников и . А эти углы являются внутренними накрест лежащими при прямых и , значит, .
Мы доказали, что в четырёхугольнике две стороны параллельны и равны (), значит, по I признаку, этот четырёхугольник является параллелограммом, ч.т.д.
Начертите параллелограмм . Проведите в нём диагонали и . Обозначьте их точку пересечения буквой .
Найдите длину отрезка , если известно, что диагональ см.
Чему равна диагональ , если известно, что отрезок см?
Найдите периметр треугольника , если сторона равна см, а диагонали и равны см и см соответственно.
Две стороны параллелограмма равны см и см. Найдите периметр параллелограмма.
Сумма двух противолежащих углов параллелограмма равна . Чему равны эти углы?
Периметр параллелограмма равен см. Одна из его сторон равна см. Определите остальные стороны параллелограмма.
Найдите углы параллелограмма, если известно, что один из них равен сумме двух других углов параллелограмма.
Одна из сторон параллелограмма равна см, а другая – в раза меньше. Найдите периметр параллелограмма.
Высоты параллелограмма равны см и см. Найдите расстояние от точки пересечения диагоналей параллелограмма до одной из меньших сторон.
В параллелограмме сторона см, диагонали равны см и см, точка – точка пересечения диагоналей. Чему равен периметр треугольника ?
В параллелограмме один угол равен . Найдите остальные углы параллелограмма.
В треугольнике . Из точки, взятой на стороне , проведены две прямые, параллельные сторонам и . Определите вид получившегося четырёхугольника и все его углы.
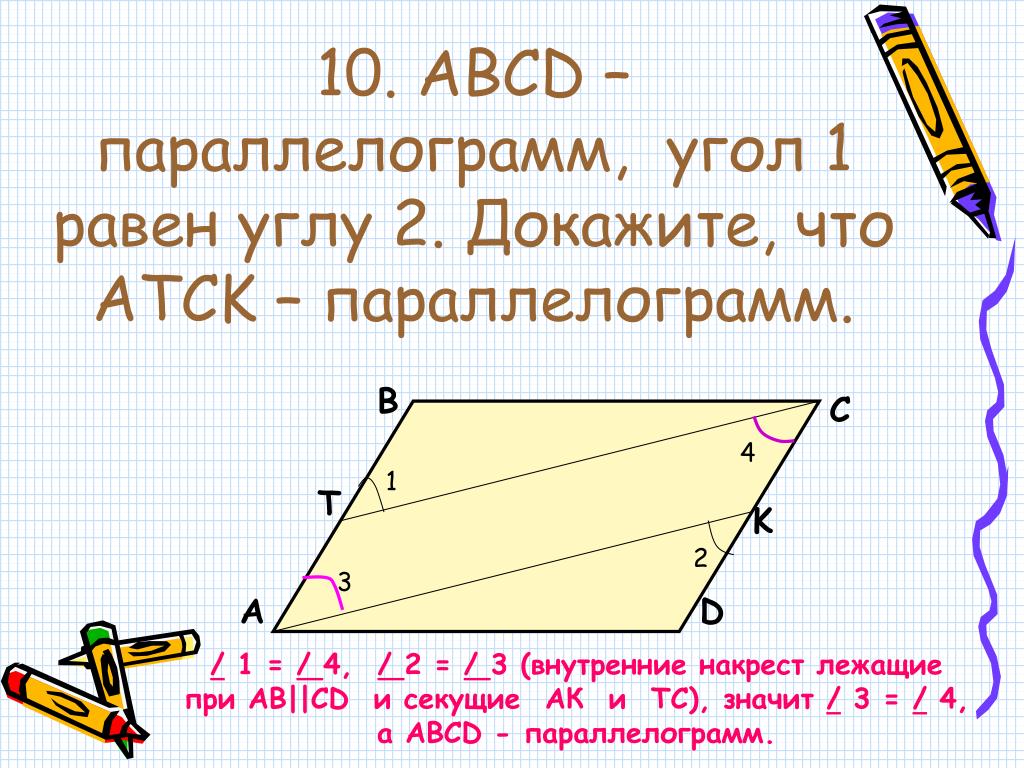
Четырёхугольник – параллелограмм, отрезки равны. Докажите, что также является параллелограммом.
Диагональ параллелограмма продолжена на равные отрезки и . Докажите, что также является параллелограммом.
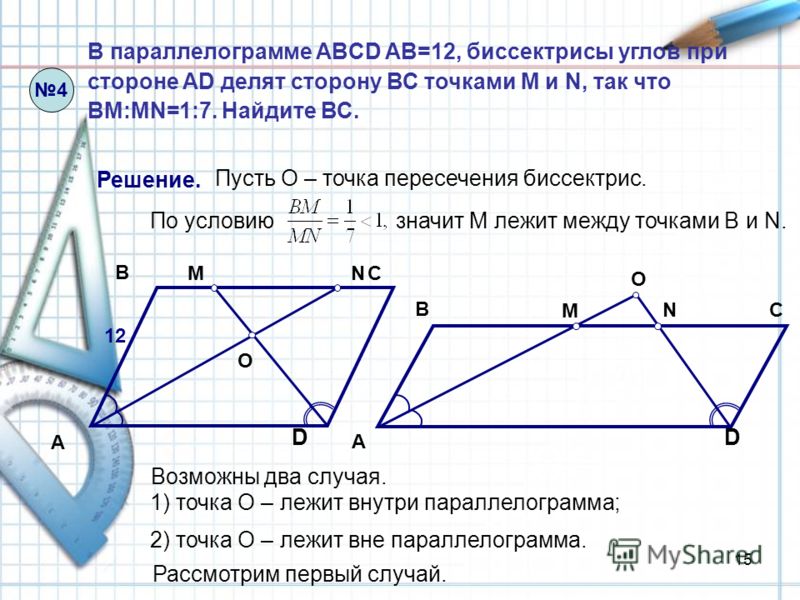
В параллелограмме биссектриса угла пересекает сторону в точке , причём, . Найдите периметр параллелограмма.
Диагональ параллелограмма составляет со сторонами параллелограмма углы в и . Найдите углы параллелограмма.
Стороны параллелограмма относятся как , а его периметр равен см. Найдите стороны параллелограмма.
В четырёхугольнике . Диагонали четырёхугольника пересекаются в точке . Найдите периметр .
Из вершины параллелограмма с острым углом проведён перпендикуляр к прямой . Найдите и .
В выпуклом четырёхугольнике . Докажите, что .
Середина отрезка является центром окружности с диаметром , причём, точки не лежат на одной прямой. Докажите, что .
Докажите, что .
Постройте параллелограмм по большей стороне, меньшей диагонали и углу между ними.
В четырёхугольнике – точка пересечения диагоналей. Периметр треугольника равен см, см, см. Найдите .
Дан параллелограмм с острым углом . Из вершины опущен перпендикуляр к прямой . Найдите и .
В выпуклом шестиугольнике все стороны равны, . Докажите, что .
Дан параллелограмм . На продолжении диагонали за вершины и отмечены точки и соответственно так, что . Докажите, что .
Постройте параллелограмм по меньшей стороне, острому углу и углу между этой стороной и меньшей диагональю.
Одна сторона параллелограмма втрое больше другой стороны. Найдите стороны параллелограмма, если его периметр равен см.
В параллелограмме с острым углом из вершины проведён перпендикуляр к прямой . Найдите углы параллелограмма, если .
Найдите углы параллелограмма, если .
Один из углов параллелограмма на меньше другого. Найдите углы параллелограмма.
В параллелограмме с острым углом из вершины проведён перпендикуляр к прямой . Найдите углы параллелограмма, если .
Докажите, что четырёхугольник, имеющий центр симметрии, является параллелограммом.
На диагонали параллелограмма отмечены две точки и так, что . Докажите, что четырёхугольник – параллелограмм.
На сторонах и параллелограмма вне его построены правильные треугольники и . Докажите, что треугольник равносторонний.
Докажите, что выпуклый четырёхугольник является параллелограммом, если .
Угол параллелограмма меньше угла . Докажите, что .
В параллелограмме проведена биссектриса угла , которая пересекает сторону в точке .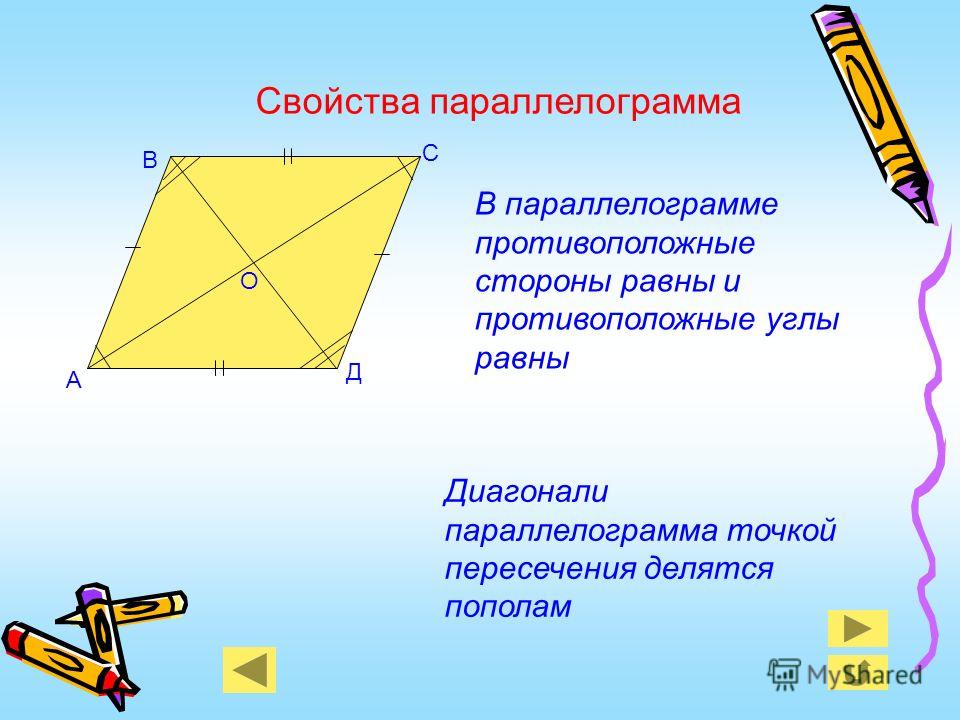
Докажите, что треугольник равнобедренный.
Найдите сторону , если см, а периметр параллелограмма равен см.
На стороне параллелограмма взята точка так, что .
Докажите, что – биссектриса угла .
Найдите периметр параллелограмма, если см, см.
В выпуклом четырёхугольнике диагонали и пересекаются в точке . – медиана треугольника , – медиана треугольника . Докажите, что – параллелограмм.
Прямая параллельна стороне параллелограмма и пересекает стороны и в точках и соответственно. Докажите, что – параллелограмм.
В проведена медиана . На её продолжении за точку отложен отрезок , равный . Докажите, что четырёхугольник является параллелограммом.
С тороны и треугольника продолжены на точку так, что . Докажите, что четырёхугольник – параллелограмм.
Докажите, что четырёхугольник – параллелограмм.
– параллелограмм, . Найдите .
Одна из сторон параллелограмма на см больше другой. Периметр параллелограмма равен см. Найдите стороны параллелограмма.
В параллелограмме диагональ перпендикулярна стороне и равна ей. Найдите углы параллелограмма.
Периметр параллелограмма равен см. Найдите длины сторон, если известно, что диагональ параллелограмма делит угол на части и .
В параллелограмме из вершины тупого угла проведена высота к стороне так, что . Найдите углы параллелограмма.
Найдите длины высот параллелограмма, если известно, что стороны см и см, а углы относятся как .
Найдите углы параллелограмма, если известно, что один из них в раз меньше суммы всех остальных углов параллелограмма.
В треугольнике проведена медиана и продолжена на свою длину за точку .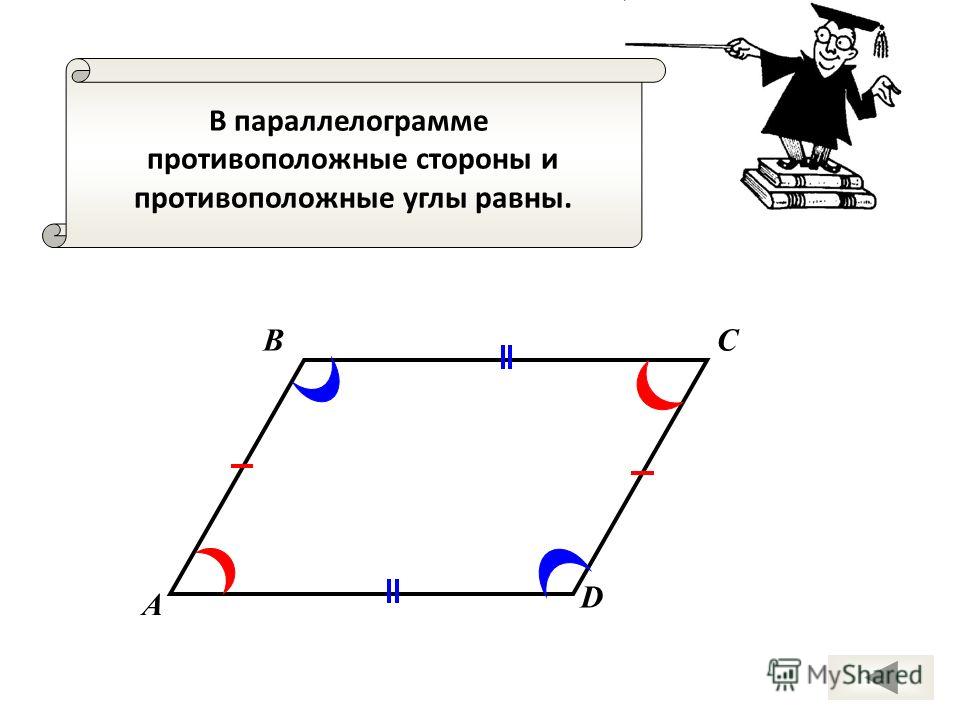 Найдите периметр четырёхугольника , если периметр треугольника равен см, см.
Найдите периметр четырёхугольника , если периметр треугольника равен см, см.
Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол . Найдите углы параллелограмма.
Биссектриса угла параллелограмма пересекает сторону в точке . Найдите периметр параллелограмма, если см, см.
Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол . Найдите углы параллелограмма.
Периметр параллелограмма равен см. Биссектрисы углов и пересекаются на стороне . Найдите длины сторон параллелограмма.
Биссектриса угла параллелограмма пересекает сторону в точке . Найдите углы параллелограмма, если известно, что .
Периметр параллелограмма равен см. Биссектриса угла и биссектриса угла делят сторону на три равные части так, что точка лежит между точками и . Найдите длины сторон параллелограмма.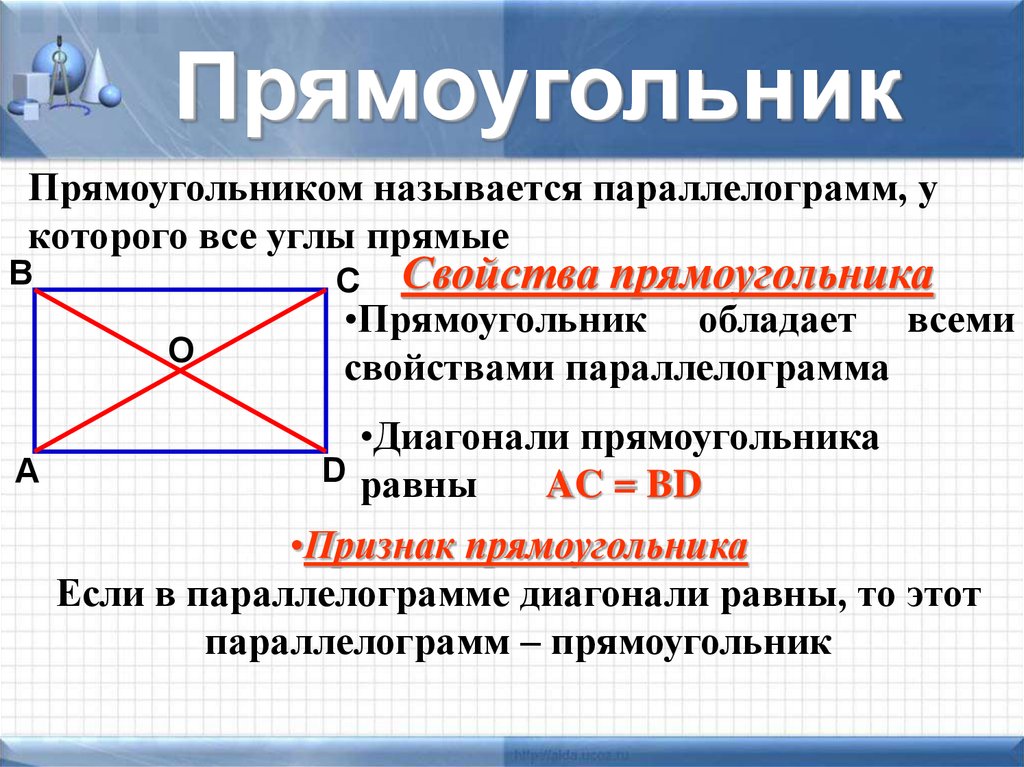
Биссектриса угла параллелограмма пересекает сторону в точке . Найдите углы параллелограмма, если известно, что .
Биссектриса угла параллелограмма пересекает сторону в её середине . Периметр треугольника равен см, а длина отрезка больше стороны на см. Найдите периметр параллелограмма.
5
Соотношение углов в параллелограмме. Н.Никитин Геометрия
Параллелограммом называют четырехугольник противолежащие стороны которого попарно параллельны. Также параллелограмм владеет такими свойствами, как противоположные стороны равны, противоположные углы равны, сумма всех углов равна 360 градусов.
Вам понадобится
- Знания по геометрии.
Инструкция
1. Представим дан один из углов параллелограмма и равен A. Обнаружим значения остальных 3. По свойству параллелограмма противоположные углы равны. Значит угол, лежащий наоборот данного равен данному и его значение равно А.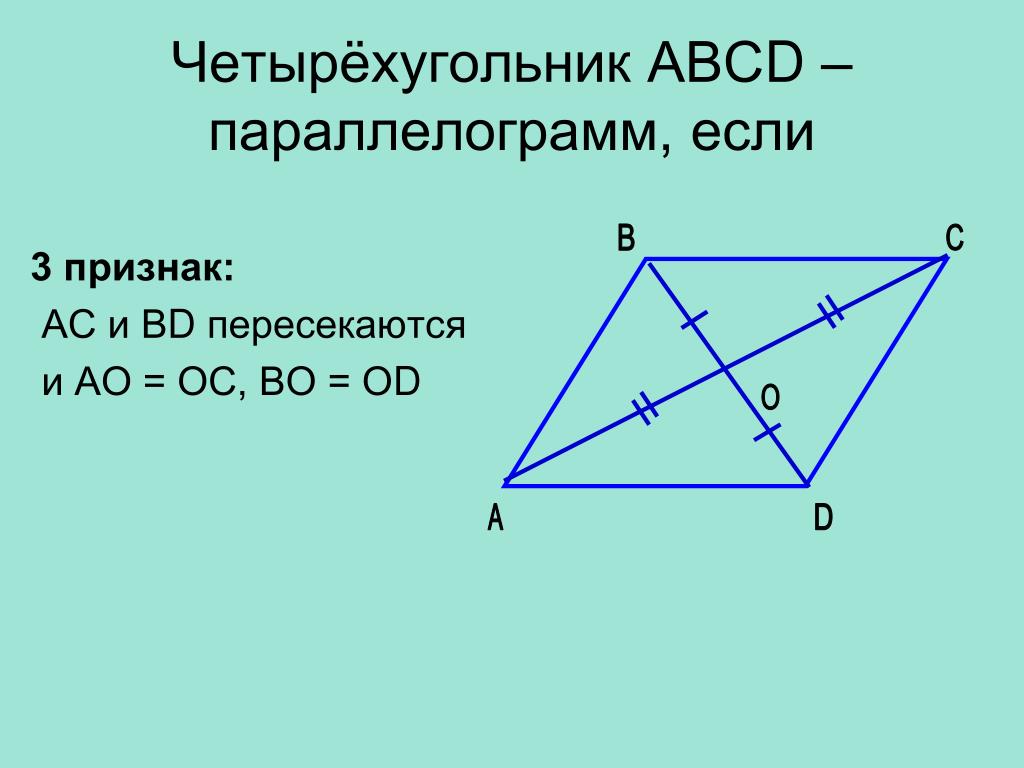
2. Обнаружим оставшиеся два угла. Потому что сумма всех углов в параллелограмме равна 360 градусов, а противоположные углы между собой равны, то получается, что угол, принадлежащий одной стороне с данным, равен (360 — 2А)/2. Ну либо позже реформирования получим 180 — А. Таким образом в параллелограмме два угла равны А, а два других угла равны 180 — А.
Обратите внимание!
Значение одного угла не может превышать 180 градусов. Полученные значения углов дозволено легко проверить. Для этого сложите их и, если сумма равна 360, все посчитано правильно.
Полезный совет
Прямоугольник и ромб являются частным случаем параллелограмма, следственно все свойства и способы вычисления углов применимы и к ним.
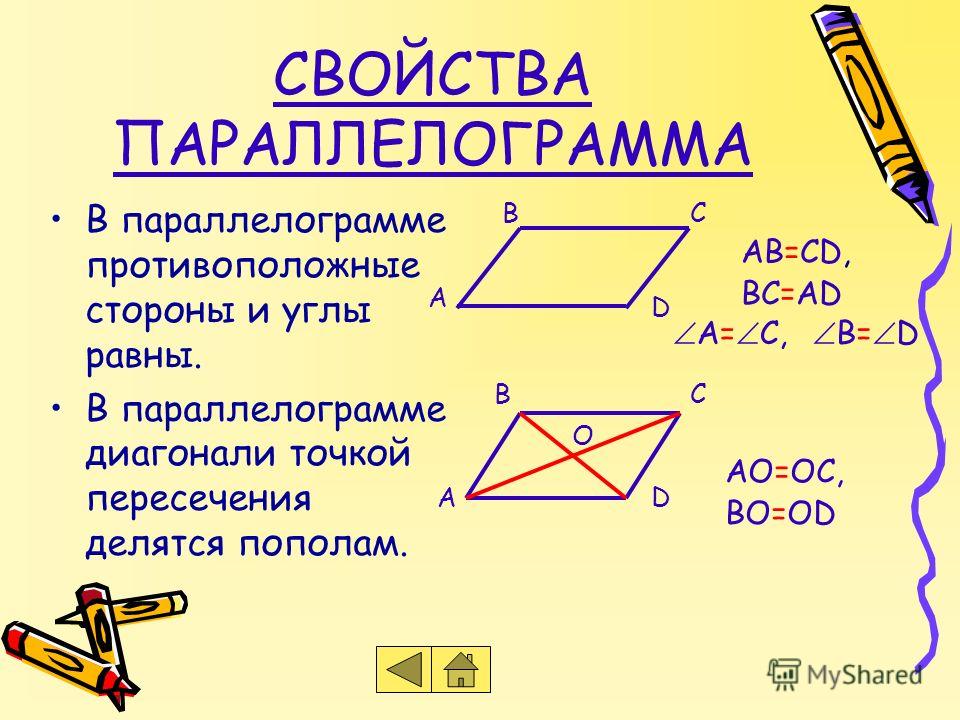
Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны, т. е. лежат на параллельных прямых (рис.1).
Теорема 1. О свойстве сторон и углов параллелограмма. В параллелограмме противоположные стороны равны, противоположные углы равны и сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.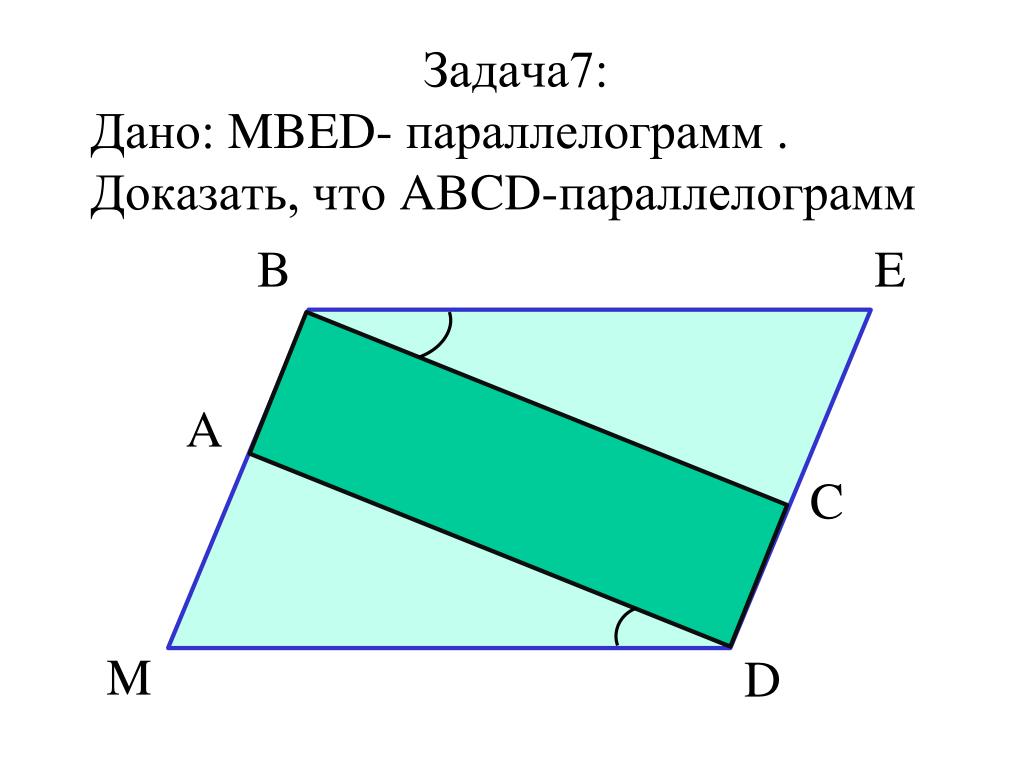
Доказательство. В данном параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC (рис.2).
Эти треугольники равны, так как ∠ 1 = ∠ 4, ∠ 2 = ∠ 3 (накрест лежащие углы при параллельных прямых), а сторона АС общая. Из равенства Δ ABC = Δ ADC следует, что АВ = CD, ВС = AD, ∠ B = ∠ D. Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых. Теорема доказана.
Замечание. Равенство противоположных сторон параллелограмма означает, что отрезки параллельных, отсекаемых параллельными, равны.
Следствие 1. Если две прямые параллельны, то все точки одной прямой находятся на одном и том же расстоянии от другой прямой.
Доказательство. В самом деле, пусть а || b (рис.3).
Проведем из каких-нибудь двух точек В и С прямой b перпендикуляры ВА и CD к прямой а. Так как АВ || CD, то фигура ABCD — параллелограмм, и следовательно, АВ = CD.
Расстоянием между двумя параллельными прямыми называется расстояние от произвольной точки одной из прямых до другой прямой.
По доказанному оно равно длине перпендикуляра, проведенного из какой-нибудь точки одной из параллельных прямых к другой прямой.
Пример 1. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.
Решение. По теореме 1 противоположные стороны параллелограмма равны. Обозначим одну сторону параллелограмма через х, другую через у. Тогда по условию $$\left\{\begin{matrix} 2x + 2y = 122 \\x — y = 25 \end{matrix}\right.$$ Решая эту систему, получим х = 43, у = 18. Таким образом, стороны параллелограмма равны 18, 43, 18 и 43 см.
Пример 2.
Решение. Пусть условию задачи отвечает рисунок 4.
Обозначим АВ через х, а ВС через у. По условию периметр параллелограмма равен 10 см, т. е. 2(x + у) = 10, или х + у = 5. Периметр треугольника ABD равен 8 см. А так как АВ + AD = х + у = 5 то BD = 8 — 5 = 3 . Итак, BD = 3 см.
Пример 3. Найти углы параллелограмма, зная, что один из них больше другого на 50°.
Решение. Пусть условию задачи отвечает рисунок 5.
Обозначим градусную меру угла А через х. Тогда градусная мера угла D равна х + 50°.
Углы BAD и ADC внутренние односторонние при параллельных прямых АВ и DC и секущей AD. Тогда сумма этих названных углов составит 180°, т. е.
х + х + 50° = 180°, или х = 65°. Таким образом, ∠ A = ∠ C = 65°, a ∠ B = ∠ D = 115°.
Пример 4. Стороны параллелограмма равны 4,5 дм и 1,2 дм. Из вершины острого угла проведена биссектриса. На какие части делит она большую сторону параллелограмма?
Решение. Пусть условию задачи отвечает рисунок 6.
АЕ — биссектриса острого угла параллелограмма. Следовательно, ∠ 1 = ∠ 2.
Задача 1 . Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.
∠C =∠A = 65° как противоположные углы параллелограмма.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.
∠В = 180° — ∠А = 180° — 65° = 115°.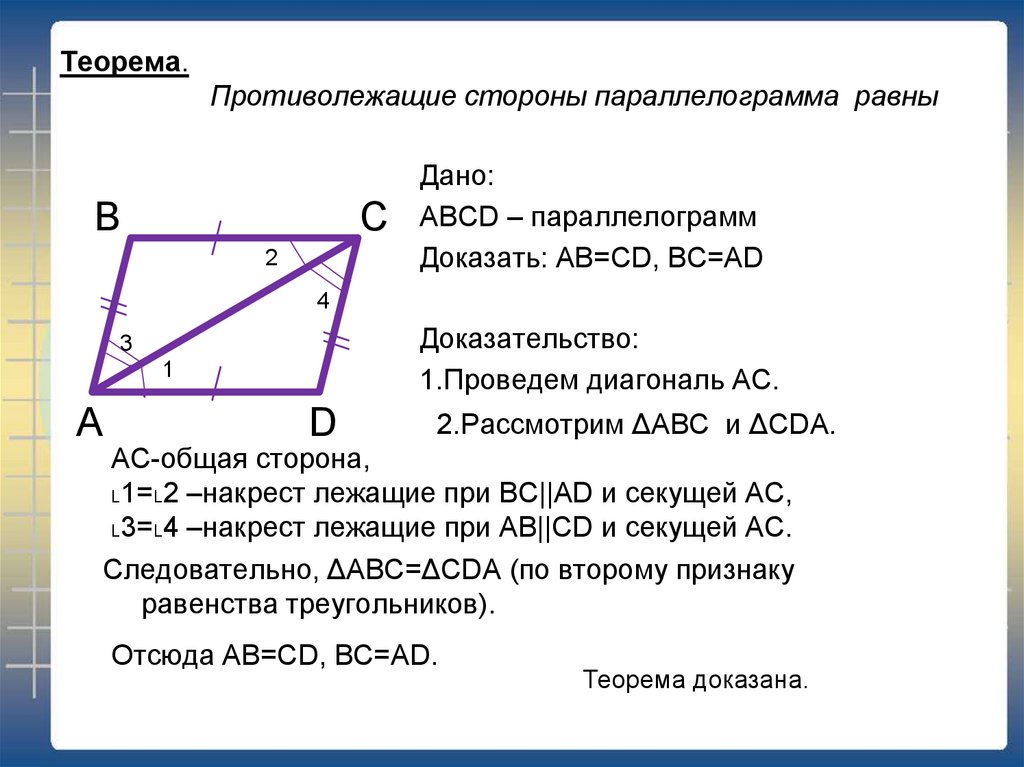
∠D =∠B = 115° как противолежащие углы параллелограмма.
Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.
Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.
Так как у параллелограмма имеется 2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°: 2 = 110°.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.
Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.
Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.
Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.
х = 180 : 4;
Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.
Противолежащие углы параллелограмма равны, следовательно,
∠А =∠С = 45°; ∠В =∠D = 135°.
Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.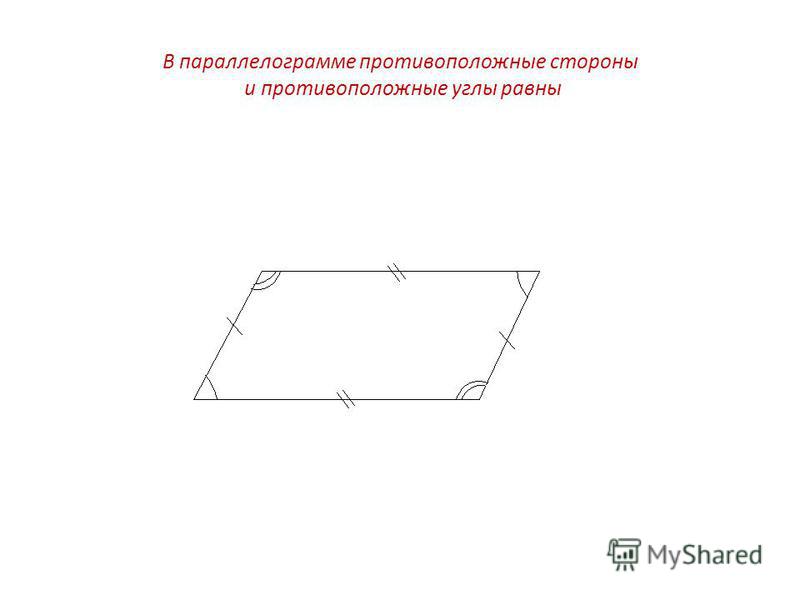
Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.
Доказательство.
Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.
AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.
Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.
∙ (AB + AD).
Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:
тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:
2 ∙ (2x + 5x) = 3,5;
2 ∙ 7x = 3,5;
x = 3,5 : 14;
Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.
Проверка.
Периметр параллелограмма P ABCD = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).
Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.
Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.
Параллелограммом называется такой четырехугольник, в котором противоположные стороны попарно параллельны.
Параллелограмм обладает всеми свойствами четырехугольников, но кроме этого имеет и свои отличительные особенности. Зная их, мы можем с легкостью находить как стороны, так и углы параллелограмма.
Свойства параллелограмма
- Сумма углов в любом параллелограмме, как и в любом четырехугольнике, равна 360°.

- Средние линии параллелограмма и его диагонали пересекаются в одной точке и делятся ею пополам. Эту точку принято называть центром симметрии параллелограмма.
- Противоположные стороны у параллелограмма всегда равны.
- Также у этой фигуры всегда равны противоположные углы.
- Сумма углов, которые прилегают к любой из сторон параллелограмма, всегда составляет 180°.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон. Это выражается формулой:
- d 1 2 + d 2 2 = 2 (a 2 +b 2), где d 1 и d 2 — диагонали, a и b — смежные стороны.
- Косинус тупого угла всегда меньше нуля.
Как найти углы заданного параллелограмма, применяя эти свойства на практике? И какие еще формулы могут нам в этом помочь? Рассмотрим конкретные задания, в которых требуют: найдите величины углов параллелограмма.
Нахождение углов параллелограмма
Случай 1. Известна мера тупого угла, требуется найти острый угол.
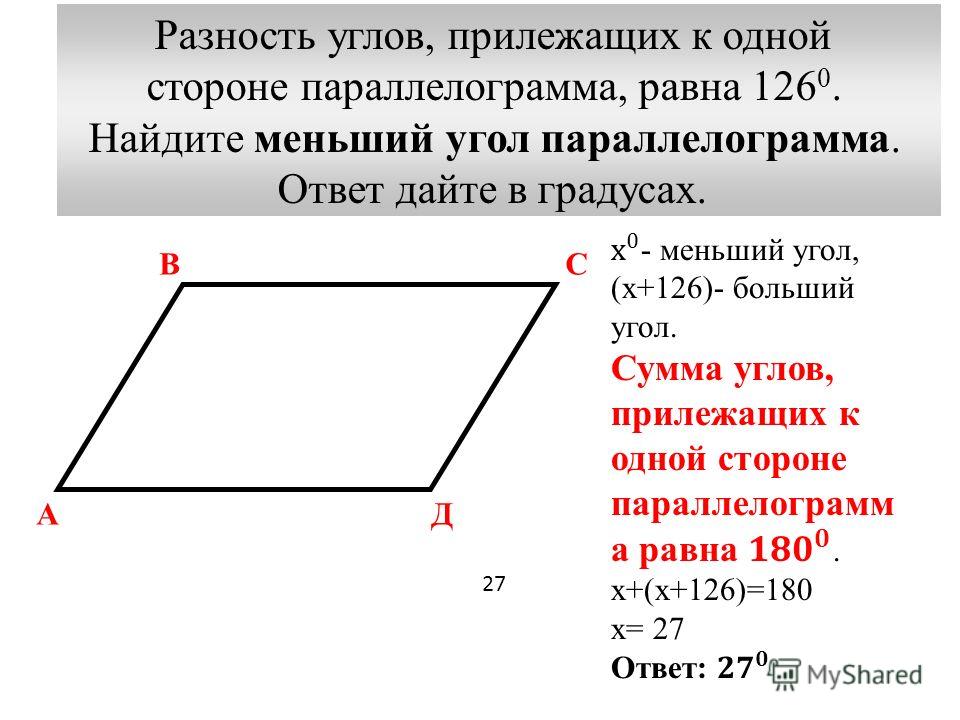
Пример: В параллелограмме ABCD угол A равен 120°. Найдите меру остальных углов.
Решение: Пользуясь свойством № 5, мы можем найти меру угла B, смежного с тем углом, который дан в задании. Он будет равен:
- 180°-120°= 60°
А теперь, пользуясь свойством №4, мы определяем, что два оставшихся угла C и D противоположны тем углам, которые мы уже нашли. Угол C противоположен углу A, угол D — углу B. А следовательно они попарно им равны.
- Ответ: B = 60°, C = 120°, D=60°
Случай 2. Известны длины сторон и диагонали
В таком случае нам необходимо воспользоваться теоремой косинусов.
Мы можем сначала по формуле вычислить косинус нужного нам угла, а потом по специальной таблице найти, чему равен сам угол.
Для острого угла формула такая:
- cosa = (А² + В² — d²) / (2 * А * В), где
- а — это искомый острый угол,
- А и В — стороны параллелограмма,
- d — меньшая диагональ
Для тупого угла формула немного меняется:
- cosß = (А² + В² — D²) / (2 * А * В), где
- ß — это тупой угол,
- А и В — стороны,
- D — большая диагональ
Пример: необходимо найти острый угол параллелограмма, стороны которого равны 6 см и 3 см, а меньшая диагональ равна 5. 2 см
2 см
Подставляем значения в формулу для нахождения острого угла:
- cosa = (6 2 + 3 2 — 5.2 2) / (2 * 6 * 3) = (36 + 9 — 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2
- cosa = 1/2. По таблице выясняем, что искомый угол равен 60°.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Углы параллелограмма. Теоремы, доказательства, свойства
В параллелограмме четыре внутренних угла, а сумма внутренних углов параллелограмма всегда равна 360°. Противолежащие углы параллелограмма равны, а смежные углы параллелограмма попарно смежны. Познакомимся подробнее со свойствами углов параллелограмма.
| 1. | Свойства углов параллелограмма |
2. | Теоремы, относящиеся к углам параллелограмма |
| 3. | Часто задаваемые вопросы об углах параллелограмма |
Свойства углов параллелограмма
Параллелограмм – это четырехугольник с равными и параллельными противоположными сторонами. Есть некоторые особые свойства параллелограмма, которые отличают его от других четырехугольников. Обратите внимание на следующий параллелограмм, чтобы соотнести его свойства, приведенные ниже:
- Противоположные углы параллелограмма конгруэнтны (равны). Здесь ∠А = ∠С; ∠Д = ∠В.
- Сумма всех углов параллелограмма равна 360°. Здесь ∠A + ∠B + ∠C + ∠D = 360°.
- Все соответствующие последовательные углы являются дополнительными. Здесь ∠A + ∠B = 180°; ∠В + ∠С = 180°; ∠С + ∠D = 180°; ∠D + ∠А = 180°
Теоремы, относящиеся к углам параллелограмма
Теоремы, относящиеся к углам параллелограмма, помогают решать задачи, связанные с параллелограммом. Две важные теоремы приведены ниже:
Две важные теоремы приведены ниже:
- Противоположные углы параллелограмма равны.
- Смежные углы параллелограмма являются дополнительными.
Давайте узнаем об этих двух специальных теоремах параллелограмма подробно.
Противоположные углы параллелограмма равны
Теорема: В параллелограмме противоположные углы равны.
Дано: ABCD — параллелограмм с четырьмя углами ∠A, ∠B, ∠C, ∠D соответственно.
К Докажите: ∠A =∠C и ∠B=∠D
Доказательство: В параллелограмме ABCD диагональ AC делит параллелограмм на два треугольника. О сравнении треугольников ABC и ADC. Здесь у нас есть:
AC = AC (общие стороны)
∠1 = ∠4 (чередующиеся внутренние углы)
∠2 = ∠3 (чередующиеся внутренние углы)
Таким образом, два треугольника конгруэнтны, △ABC ≅ △ADC
.
Это дает ∠B = ∠D по CPCT (соответствующие части конгруэнтных треугольников).
Точно так же мы можем показать, что ∠A = ∠C.
Отсюда доказано, что противоположные углы в любом параллелограмме равны.
Обратная теорема гласит, что если противоположные углы четырехугольника равны, то это параллелограмм. Докажем то же самое.
Дано: ∠A =∠C и ∠B=∠D в четырехугольнике ABCD.
Доказать: ABCD — параллелограмм.
Доказательство:
Сумма всех четырех углов этого четырехугольника равна 360°.
= [∠A + ∠B + ∠C + ∠D = 360º]
= 2(∠A + ∠B) = 360º (Мы можем заменить ∠C на ∠A и ∠D на ∠B, так как известно, что ∠A =∠C и ∠B =∠D)
= ∠А + ∠В = 180º. Это показывает, что соседние углы являются дополнительными. Следовательно, это означает, что AD || ДО Н.Э. Аналогично можно показать, что AB || CD.
Следовательно, АД || до н.э. и АВ || CD.
Следовательно, ABCD — параллелограмм.
Смежные углы параллелограмма являются дополнительными
Смежные углы параллелограмма являются дополнительными.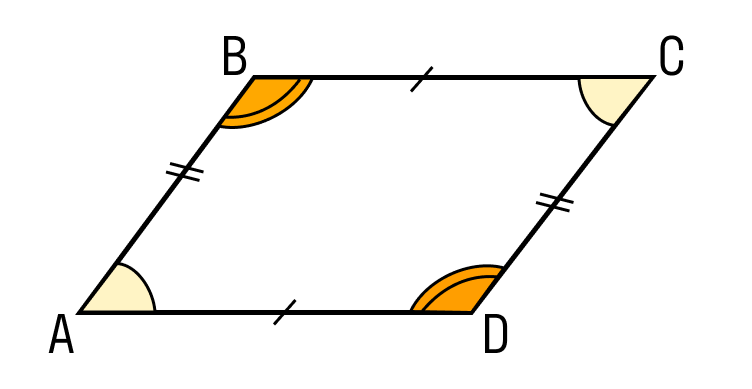 Докажем это свойство, учитывая следующий факт и используя тот же рисунок.
Докажем это свойство, учитывая следующий факт и используя тот же рисунок.
Дано: ABCD — параллелограмм с четырьмя углами ∠A, ∠B, ∠C, ∠D соответственно.
Чтобы доказать: ∠A + ∠B = 180°, ∠C + ∠D = 180°.
Доказательство: Если AD считается секущей и AB || CD.
По свойству секущей мы знаем, что внутренние углы, лежащие по одну сторону от секущей, являются дополнительными.
Следовательно, ∠A + ∠D = 180°.
Аналогично,
∠В + ∠С = 180°
∠С + ∠D = 180°
∠А + ∠В = 180°
Следовательно, сумма соответствующих двух смежных углов параллелограмма равна 180°.
Таким образом, доказано, что смежные углы параллелограмма являются дополнительными.
Связанные статьи об углах параллелограмма
Ознакомьтесь с интересными статьями, приведенными ниже, которые связаны с углами параллелограмма.
- Периметр параллелограмма
- Рабочие листы с параллелограммами
- Формула параллелограмма
- Свойства параллелограммов
Решенные примеры на углы параллелограмма
Пример 1: Один угол параллелограмма равен 75°.
 Найдите величину прилежащего к нему угла и меры всех остальных углов параллелограмма.
Найдите величину прилежащего к нему угла и меры всех остальных углов параллелограмма. Решение:
Учитывая, что один угол параллелограмма = 75°
Пусть прилежащий угол равен х
Мы знаем, что последовательные (прилежащие) углы параллелограмма являются дополнительными.
Следовательно, 75° + x° = 180°
х = 180 ° — 75 ° = 105°
Чтобы найти величину всех четырех углов параллелограмма, мы знаем, что противоположные углы параллелограмма равны.
Отсюда ∠1 = 75°, ∠2 = 105°, ∠3 = 75°, ∠4 = 105°Пример 2: Значения противоположных углов параллелограмма даны следующим образом: ∠1 = 75°, ∠3 = (x + 30)°, найти значение x.
Дано: ∠1 и ∠3 — противоположные углы параллелограмма.Решение:
Дано: ∠1 = 75° и ∠3 = (x + 30)°
Мы знаем, что противоположные углы параллелограмма равны.
Следовательно,
(х + 30)° = 75°
х = 75° — 30°
х = 45°
Следовательно, значение x равно 45°.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по углам параллелограмма
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об углах параллелограмма
Сумма углов параллелограмма равна 360°?
Да, все внутренние углы параллелограмма в сумме составляют 360°. Например, в параллелограмме ABCD ∠A + ∠B + ∠C + ∠D = 360°. Согласно свойству суммы углов многоугольников, сумма внутренних углов в многоугольнике может быть рассчитана с помощью количества треугольников, которые могут быть сформированы внутри него. В данном случае параллелограмм состоит из 2-х треугольников, значит, сумма внутренних углов равна 360°. Это также можно рассчитать по формуле S = (n — 2) × 180 °, где «n» представляет количество сторон в многоугольнике. Здесь «n» = 4. Следовательно, сумма внутренних углов параллелограмма = S = (4 — 2) × 180 ° = (4 — 2) × 180 ° = 2 × 180 ° = 360 °.
Здесь «n» = 4. Следовательно, сумма внутренних углов параллелограмма = S = (4 — 2) × 180 ° = (4 — 2) × 180 ° = 2 × 180 ° = 360 °.
Какая связь между смежными углами параллелограмма?
Смежные углы параллелограмма также известны как последовательные углы, и они всегда являются дополнительными (180°).
Как связаны противоположные углы параллелограмма?
Противоположные углы параллелограмма всегда равны, тогда как смежные углы параллелограмма всегда являются дополнительными.
Как найти недостающие углы параллелограмма?
Мы можем легко найти недостающие углы параллелограмма с помощью трех специальных свойств:
- Противоположные углы параллелограмма конгруэнтны.
- Последовательные углы параллелограмма являются дополнительными.
- Сумма всех углов параллелограмма равна 360°.
Что такое внутренние углы параллелограмма?
Углы, образуемые внутри параллелограмма и образуемые каждой парой смежных сторон, являются его внутренними углами. Сумма внутренних углов параллелограмма равна 360°, а любые два соседних (последовательных) угла параллелограмма являются дополнительными.
Сумма внутренних углов параллелограмма равна 360°, а любые два соседних (последовательных) угла параллелограмма являются дополнительными.
Все ли углы параллелограмма равны?
Нет, у параллелограмма не все углы равны. Существуют две основные теоремы, касающиеся углов параллелограмма, которые утверждают, что противоположные углы параллелограмма равны, а последовательные (смежные) углы являются дополнительными.
Чему равна сумма внутренних углов параллелограмма?
Сумма внутренних углов параллелограмма всегда равна 360°. Согласно свойству суммы углов многоугольников, сумма внутренних углов многоугольника может быть найдена по формуле S = (n — 2) × 180 °, где «n» показывает количество сторон в многоугольнике. В этом случае ‘n’ = 4. Следовательно, сумма внутренних углов параллелограмма = S = (4 — 2) × 180 ° = (4 — 2) × 180 ° = 2 × 180 ° = 360 °.
Углы параллелограмма равны 90 градусов?
В некоторых параллелограммах, таких как прямоугольники и квадраты, все углы равны 90°. Однако углы других параллелограммов не обязательно могут быть равны 90°.
Однако углы других параллелограммов не обязательно могут быть равны 90°.
Конгруэнтны ли противоположные углы параллелограмма?
Да, противоположные углы параллелограмма равны. Однако смежные углы параллелограмма всегда являются дополнительными.
Конгруэнтны ли последовательные углы параллелограмма?
Нет, последовательные (прилежащие) углы параллелограмма не равны, они дополнительные.
Смежны ли противоположные углы параллелограмма?
Нет, по теоремам, основанным на углах параллелограмма, противолежащие углы не являются дополнительными, они равны.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по параллелограмму
Как найти угол в параллелограмме
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
ACT Math Help » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы » Как найти угол в параллелограмме
В параллелограмме , и высота равна . Что такое ?
Что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы можем начать эту задачу, нарисовав высоту и пометив длины заданными значениями.
Когда мы это делаем, мы видим, что мы нарисовали треугольник внутри паралеллограммы, включая . Поскольку мы знаем длины двух сторон этого треугольника, мы можем использовать тригонометрию, чтобы найти .
Что касается , мы знаем значения противоположной стороны и гипотенузы треугольника. Таким образом, мы можем использовать функцию синуса для решения .
Сообщить об ошибке
В параллелограмме , и . Находить .
Возможные ответы:
Правильный ответ:
Пояснение:
В параллелограмме последовательные углы являются дополнительными. Таким образом,
Таким образом,
Сообщить об ошибке
является параллелограммом. Находить .
Возможные ответы:
Правильный ответ:
Объяснение:
В параллелограмме последовательные углы являются дополнительными (т. е. складываются), а противоположные углы конгруэнтны (т. е. равны). Используя эти свойства, мы можем написать систему уравнений.
1.
2.
Начиная с уравнения 1.,
9000 Подставляя в уравнение0003
Наконец, поскольку противоположные углы равны, мы это знаем.
Сообщить об ошибке
является параллелограммом. Находить .
Возможные ответы:
Правильный ответ:
Пояснение:
В параллелограмме смежные углы смежные, а противоположные углы равны. Используя эти свойства, мы можем написать систему уравнений.
Используя эти свойства, мы можем написать систему уравнений.
1.
2.
3.
Starting with equation 1.,
Substituting into equation 2.,
Используя уравнение 3.,
Сообщить об ошибке
Параллелограмм , . Что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
В пареллелограмме последовательные углы являются дополнительными.
Сообщить об ошибке
Параллелограмм , . Что такое ?
Возможные ответы:
Правильный ответ:
Пояснение:
В параллелограмме противоположные углы равны.
Сообщить об ошибке
является параллелограммом. Находить .
Возможные ответы:
Правильный ответ:
Объяснение:
В параллелограмме смежные углы являются дополнительными, а противоположные углы равны.
3
0 Сообщить об ошибке 30002 В параллелограмме , . Что такое
Возможные ответы:
Правильный ответ:
Объяснение:
В приведенном выше параллелограмме и являются последовательными углами (т. е. рядом друг с другом). В параллелограмме последовательные углы являются дополнительными, то есть они складываются.
Сообщить об ошибке
Параллелограмм , . Что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
В параллелограмме , и противоположные углы. В параллелограмме противоположные углы равны. Это означает, что эти два угла равны.
Сообщить об ошибке
Какая сумма в параллелограмме и ?
Возможные ответы:
Правильный ответ:
Пояснение:
В параллелограмме последовательные углы являются дополнительными. и последовательны, поэтому их сумма равна .
Сообщить об ошибке
← Назад 1 2 Далее →
Уведомление об авторских правах
Все ресурсы ACT Math
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
Четырехугольники — Параллелограммы | Шмуп
Параллелограммы повсюду.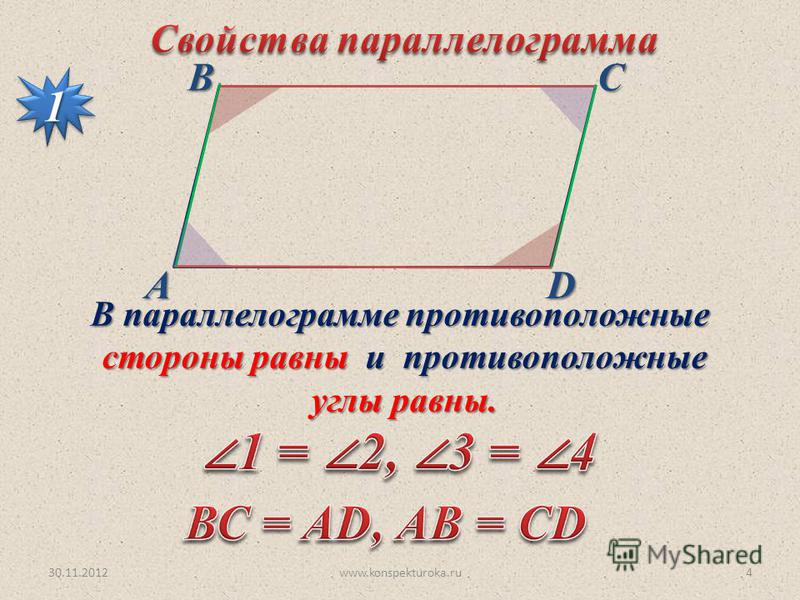 Они прячутся у всех на виду, глядя нам прямо в лицо. Как вешалки для полотенец и туалеты, мы используем их каждый день и никогда не задумываемся о них. Прямо сейчас, когда вы читаете это, вы смотрите на параллелограмм. Да, это верно. Экран вашего компьютера представляет собой параллелограмм. Если только у вас не особенно шаткий экран.
Они прячутся у всех на виду, глядя нам прямо в лицо. Как вешалки для полотенец и туалеты, мы используем их каждый день и никогда не задумываемся о них. Прямо сейчас, когда вы читаете это, вы смотрите на параллелограмм. Да, это верно. Экран вашего компьютера представляет собой параллелограмм. Если только у вас не особенно шаткий экран.
Параллелограмм — это любой четырехугольник с двумя наборами параллельных сторон. Когда мы думаем о параллелограммах, мы обычно думаем о чем-то подобном.
Если вы не серьезно повредили экран своего компьютера, это, вероятно, не выглядит так. Ради вашего банковского счета, мы искренне надеемся, что это не так. Он должен быть прямоугольным. Так что дает?
У прямоугольника два набора параллельных сторон, не так ли? Так что это такой же параллелограмм, как и выше. На самом деле квадраты, ромбы и прямоугольники являются частными случаями параллелограммов.
Пока не забивайте себе голову этими параллелограммами. Мы рассмотрим их более подробно позже.
Мы рассмотрим их более подробно позже.
Поскольку параллелограммы так же распространены, как заморозки мозга в магазине мороженого, давайте приступим к ним. Только не в магазине мороженого. Это просто антисанитарно.
Поскольку параллелограмм представляет собой особый тип четырехугольника, он обладает всеми достоинствами четырехугольников, такими как 360° внутренних углов, противоположные углы, стороны и вершины, а также две почетные и широкие диагонали.
Да, мы только что назвали эти диагонали «благородными и щедрыми», и это не потому, что они жертвуют на благотворительность или работают волонтерами в бесплатных столовых. Дело в том, что диагонали параллелограмма делят его на два равных треугольника.
Не верите нам? Мы можем доказать это. Не могли бы вы?
Пример задачи
Учитывая, что ABCD является параллелограммом, докажите, что Δ ABC и Δ CDA конгруэнтны.
| Заявления | Причины |
1. ABCD — параллелограмм ABCD — параллелограмм | , данный | 2. 7343434343434343434343434343434343434343434343434343434343434343434343434343434343434344. CD и BC || DA | Definition of a parallelogram (1) |
| 3. ∠ BAC ≅ ∠ DCA , ∠ BCA ≅ ∠ DAC | Alternate interior angles theorem (3) |
| 4. AC ≅ AC | Reflexive property |
| 5. Δ ABC ≅ Δ CDA | ASA Postulate (3, 4) |
Bam! Конгруэнтные треугольники. Мы не хотим говорить, что сказали вам об этом, поэтому мы выберем «Мы сообщили вам об этом».
А знаете, что еще лучше? Благодаря CPCTC (Corresponding Parts of Congruent Triangles are Congruent) мы можем сразу доказать еще три теоремы:
- Обе пары противоположных сторон параллелограмма конгруэнтны.
 Таким образом, для ABCD , AB ≅ CD и BC ≅ DA .
Таким образом, для ABCD , AB ≅ CD и BC ≅ DA . - Обе пары противоположных углов равны Итак, для ABCD , ∠ B ≅ ∠ D и ∠ A ≅ ∠ C .
- Два последовательных угла являются дополнительными. Таким образом, ∠ A и ∠ B являются дополнительными, как и ∠ C и ∠ D .
Со всеми этими теоремами о параллелограммах мы словно нашли математическое золото. Но подождите, есть еще! Закажите в течение следующих десяти минут, и мы добавим еще одну теорему абсолютно бесплатно! Просто заплатите 4,95 доллара за доставку и обработку. Или, если вы не хотите, вы можете получить теорему бесплатно! Просто справляйтесь с этим сами.
Пример задачи
Учитывая, что ABCD — параллелограмм, докажите, что его диагонали AC и BD делят друг друга пополам.
| Statements | Reasons | |||||
1. ABCD is a parallelogram ABCD is a parallelogram | Given | |||||
| 2. ∠ BAE ≅ ∠ DCE and ∠ ABE ≅ ∠ CDE | Теорема об альтернативных внутренних углах (1) | |||||
| 3. AB ≅ CD | Противоположные стороны параллелограммы — конгруэнтные (1) | |||||
| 4. Δ ABE ≅ CDE9 | 77.ALOULAT77.ALOULE | 77.ALED | 77.ALED | 77.ALED | 77.ALED | 7 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 700077 7000777. |
| 5. AE ≅ CE and BE ≅ DE | CPCTC (4) | |||||
| 6. E is the midpoint of AC and BD | Definition of середина (5) | |||||
| 7. AC и BD делят друг друга пополам | Определение биссектрисы отрезка (6) |
О, вы думали, что с ними покончено, не так ли? Что ж, нам не хочется лопать твой пузырь, приятель, но мы узнали об этих треугольниках не просто так. И не только для того, чтобы порадовать учителя математики.
И не только для того, чтобы порадовать учителя математики.
Мы установили пять различных теорем о параллелограммах. Так что вполне разумно, что мы задаем наши любимые вопросы о математике. «Почему мы заботимся?» «Какое это имеет значение?» «Как это вообще относится к моей жизни?» «Почему так важны эти маленькие золотые крупицы мудрости?»
Что ж, мы могли бы продолжить собирать эти самородки и, в конечном счете, дать Форт-Ноксу шанс заработать деньги. С другой стороны, мы накопили бы кучу бесполезных фактов, когда могли бы использовать их в качестве учебников для параллелограмма.
Допустим, вы обвинили четырехугольник в том, что он является параллелограммом. Теперь вам нужно изложить свое дело. Вот несколько способов убедить присяжных, что четырехугольник является параллелограммом:
- Две пары противоположных сторон параллельны. (Это определение параллелограмма.)
- Обе пары противоположных сторон конгруэнтны.
- Одна пара противоположных сторон конгруэнтна и параллельна.

- Обе пары противоположных углов равны.
- Диагонали делят друг друга пополам.
Многие из этих утверждений являются обратными утверждениями доказательств, которые мы уже придумали. Ранее мы предполагали, что фигура является параллелограммом, и показали, что эта фигура обладает некоторыми особыми свойствами. Теперь мы говорим, что если фигура обладает этими свойствами, она должно быть параллелограммом. Помимо определения, мы должны показать, что каждое из этих утверждений верно. К счастью для нас, нам просто нужно применить факты, которые мы уже знаем.
Пример задачи
Дано: Четырехугольник ABCD имеет две пары противоположных сторон, которые конгруэнтны.
Докажите: ABCD — параллелограмм.
| Заявления | Причины |
| 1. AB ≅ CD and BC ≅ DA | Given |
2. Diagonal AC creates Δ ABC and Δ CDA Diagonal AC creates Δ ABC and Δ CDA | Definition of a triangle |
| 3. AC ≅ AC | Рефлексивное свойство |
| 4. Δ ABC Δ CDA | SSS Postulate (1, 3) | CPCTC (4) |
| 6. AB || CD и до н.э. || DA | Конвер -альтернативные внутренние углы Теорема (5) |
| 7. ABCD — параллелограмма | Определение параллелограмма (6) |
We Cay The Preseor in the Preseer in the Preseer in the stay in the stay in the arterem способы, но мы не собираемся прямо сейчас.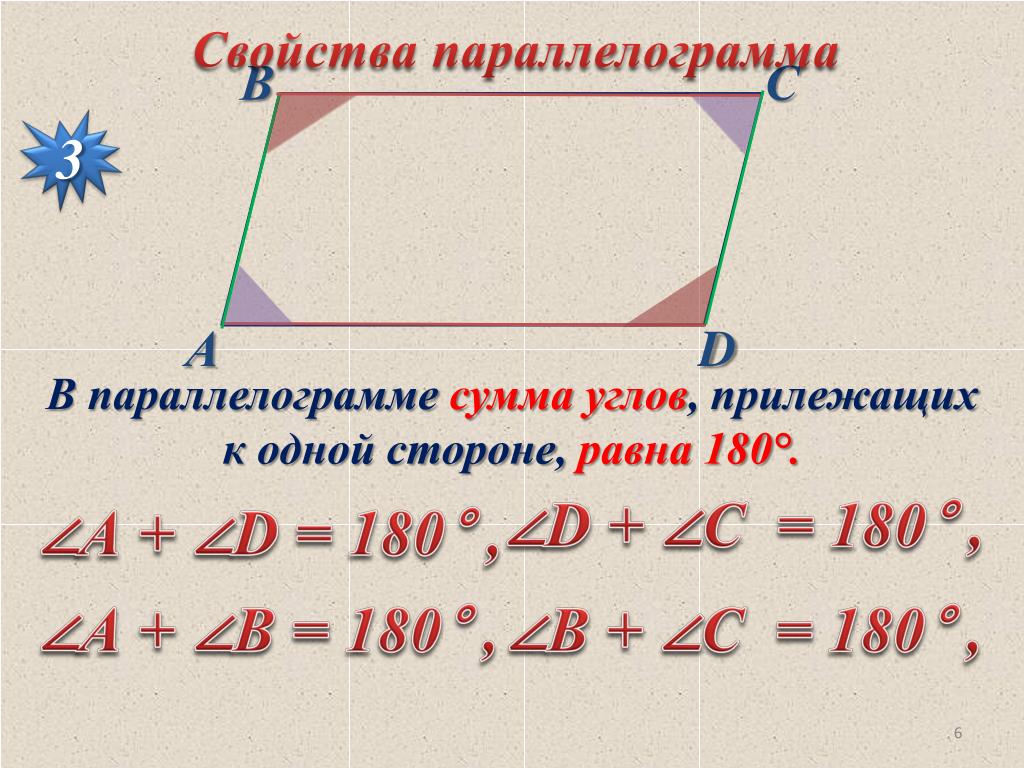



 Найдите величину прилежащего к нему угла и меры всех остальных углов параллелограмма.
Найдите величину прилежащего к нему угла и меры всех остальных углов параллелограмма. 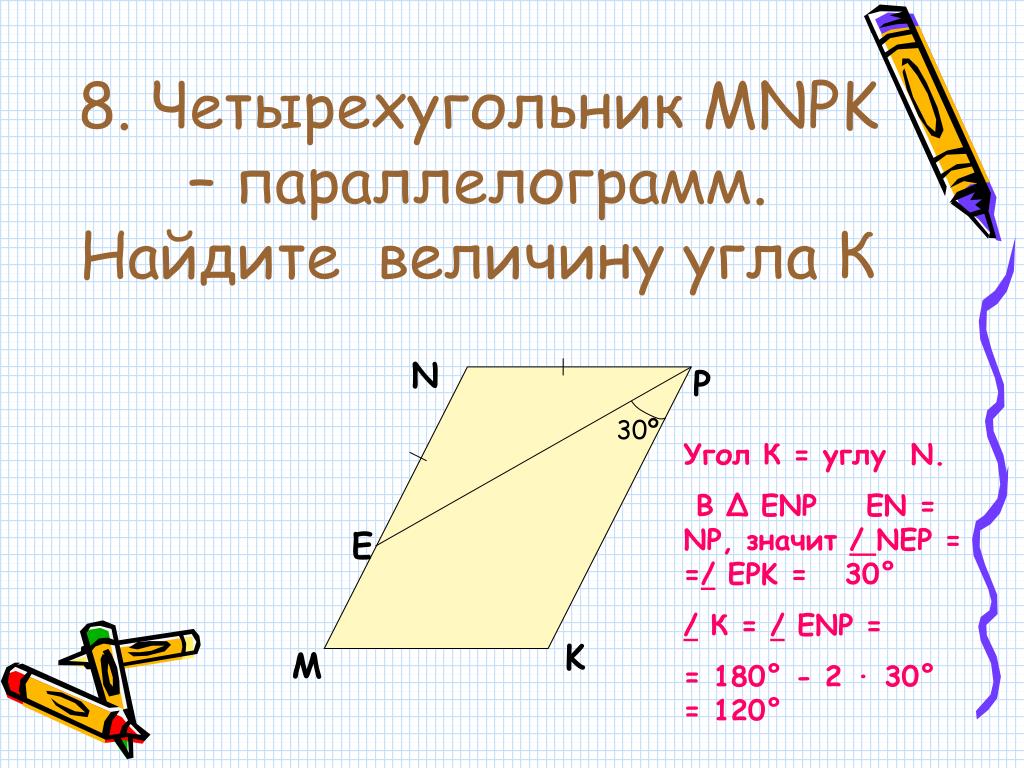
 Таким образом, для ABCD , AB ≅ CD и BC ≅ DA .
Таким образом, для ABCD , AB ≅ CD и BC ≅ DA .