Примеры с отрицательными числами и положительными числами: fkn+antitotal | студентам & программистам

Содержание

В каких случаях отрицательное число больше положительного. Применение положительных и отрицательных чисел в жизни человека

Можно ли из меньшего числа вычесть большее? Рассмотрение этого вопроса мы начали .

Для того чтобы прояснить ситуацию, нарисуем вертикальную линию и отметим на ней точкой положение города. Эту точку мы будем считать точкой отсчета или нулем. Теперь нанесем на прямую по несколько равных делений выше и ниже нулевой точки. Пусть каждое деление соответствует одному километру.

Числа выше точки отсчета (то есть к северу от города) будем называть обычными (или положительными) , а числа ниже точки отсчета (то есть к югу от города) будем называть числами, меньшими нуля, или отрицательными .

Теперь нам понадобится специальный символ, который поможет различить положительные и отрицательные числа. Обычно для этого используют систему обозначений, основанную на способе, которым можно получить это число. Любое положительное число получается в результате сложения других положительных чисел. Символом сложения является

знак «+» , поэтому положительные числа обозначаются +1, +2, +3 и так далее. Само название «положительное число» говорит о том, что это число реально существует.

Отрицательные числа получаются как результат вычитания, скажем, при вычитании (2-3) мы получаем число на единицу меньше нуля. Его обозначают -1. Таким образом, отрицательные числа обозначают — -1, -2, -3, и так далее.

То, что числа, меньшие нуля, получили название отрицательных, не случайно. Даже когда математики освоили операции с числами , меньшими нуля, надо было подчеркнуть, что эти числа не существуют в действительности.

Обратите внимание, ноль не является ни положительным, ни отрицательным числом .

Теперь у нас вертикальная размеченная линия, то есть шкала, и мы можем использовать ее для операций сложения и вычитания. Поскольку положительные числа увеличиваются вверх по шкале, а операции сложения положительных чисел приводят к увеличению чисел, будем считать, что сложение – это движение вверх по шкале.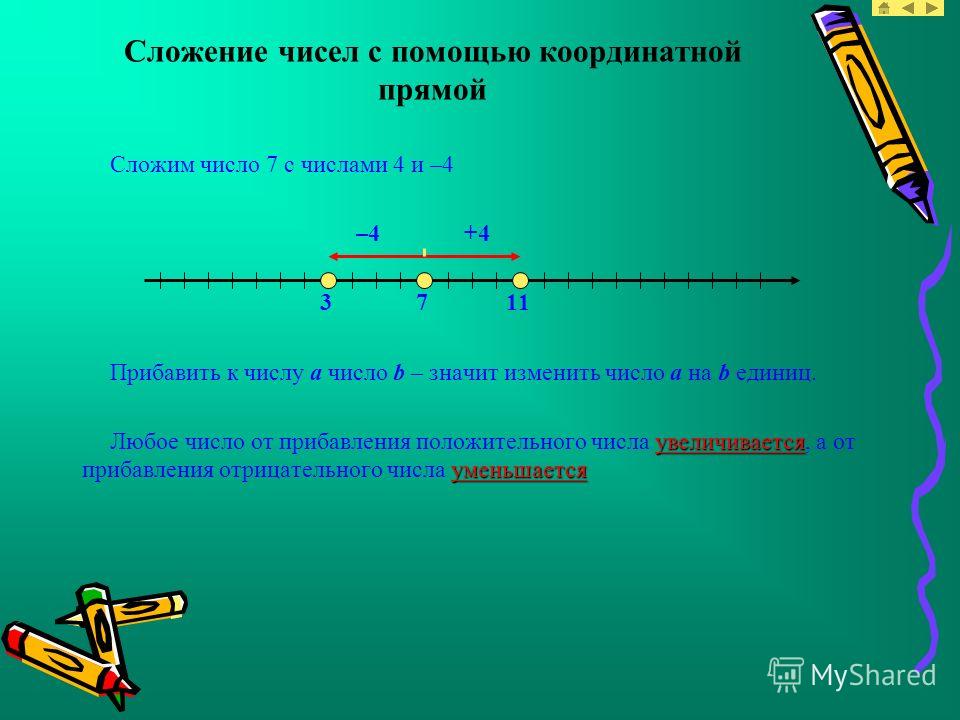

Вычитание – это операция, противоположная сложению, поэтому вычитание – это движение вниз по шкале.

Предположим, надо сложить +2 и +5. Записать это выражение можно следующим образом: (+2) + (+5). Скобки нам понадобились по той причине, что необходимо отделить плюс как знак от плюсов, обозначающих положительные числа. Но поскольку мы привыкли к тому, что обычно имеем дело с положительными числами, то часто знаки «+» перед положительными числами просто опускают. Тогда получаем: 2+5. Необходимо ставить знаки «+» перед положительными числами только в тех случаях, когда надо привлечь особое внимание к знаку числа.

Теперь отложим на нашей шкале два деления вверх. Это число 2. Прибавим еще 5 делений и остановимся на делении 7, то есть 2+5=7. Мы можем начать с 5 и прибавить два деления. Мы опять получим 7. Тут я еще раз хочу обратить ваше внимание на тот факт, что от перемены мест слагаемых сумма не меняется.

Теперь займемся вычитанием. Предположим, надо вычесть 2 из 5. От точки 5 на шкале мы откладываем вниз два деления и оказываемся в точке 3. Таким образом, получаем 5-2=3.

Теперь нам надо выяснить, как обращаться с отрицательными числами. Можно ли производить с ними такие же действия, как и с положительными числами? Если да, то они окажутся очень полезными, несмотря на то что не являются «настоящими» числами. И действительно, отрицательные числа нашли широчайшее применение не только в науке и инженерной практике, но и в повседневной деятельности. Они применяются, например, в бухгалтерии, где запасы и доходы обозначаются положительными числами, а расходы – отрицательными.

Вельмякина Кристина и Николаева Евгения

Данная исслеловательская работа направлена на изучение применения положительных и отрицательных чисел в жизни человека.

Скачать:

Предварительный просмотр:

МБОУ «Гимназия №1» Ковылкинского муниципального района

Применение положительных и отрицательных чисел в жизни человека

Исследовательская работа

Выполнили:

ученицы 6В класса

Вельмякина Кристина и Николаева Евгения

Руководитель: учитель математики и информатики

Соколова Наталья Сергеевна

Ковылкино 2015

Введение 2

1. История возникновения положительных и отрицательных чисел 4

2.Применение положительных и отрицательных чисел 6

Заключение 13

Список используемой литературы 14

Введение

Введение положительных и отрицательных чисел было связано с необходимостью развития математики как науки, дающей общие способы решения арифметических задач, независимо от конкретного содержания и исходных числовых данных.

Изучив положительные и отрицательные числа на уроках математики, мы решили узнать, а где еще кроме математики используются данные числа. И оказалось, что положительные и отрицательные числа имеют довольно широкое применение.

Данная исследовательская работа направлена на изучение применения положительных и отрицательных чисел в жизни человека.

Актуальность данной темы заключается в изучении применения положительных и отрицательных чисел.

Цель работы: Изучить применение положительных и отрицательных чисел в жизни человека.

Объект исследования: Области применения положительных и отрицательных чисел в жизни человека.

Предмет исследования: Положительные и отрицательные числа.

Метод исследования: чтение и анализ используемой литературы и наблюдения.

Для достижения цели исследования были поставлены следующие задачи:

1. Изучить литературу по данной теме.

2. Понять суть положительных и отрицательных чисел в жизни человека.

3. Исследовать применение положительных и отрицательных чисел в различных областях.

4. Сделать выводы.

История возникновения положительных и отрицательных чисел

Впервые положительные и отрицательные числа появились в Древнем Китае уже примерно 2100 лет тому назад.

Во II в. до н. э. китайский ученый Чжан Цань написал книгу «Арифметика в девяти главах». Из содержания книги видно, что это не вполне самостоятельный труд, а переработка других книг, написанных задолго до Чжан Цаня. В этой книге впервые в науке встречаются отрицательные количества. Они понимаются им не так, как понимаем и применяем их мы. Полного и ясного понимания природы отрицательных и положительных величин и правил действия с ними у него нет. Каждое отрицательное число он понимал как долг, а положительное – как имущество. Действия с отрицательными числами он производил не так, как мы, а используя рассуждения о долге. Например, если к одному долгу прибавить другой долг, то в результате получиться долг, а не имущество (т, е. по нашему (- а) + (- а) = — 2а. Знака минус тогда не знали, поэтому, чтобы отличить числа, выражавшие долг, Чжань Цань писал их другими чернилами, чем числа, выражавшие имущество (положительные). Положительные количества в китайской математике называли «чен» и изображали красным цветом, а отрицательные – «фу» и изображали черным. Такой способ изображения использовался в Китае до середины XII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел – цифры, которые изображали отрицательные числа, перечеркивали черточкой наискось справа налево. Хотя китайские ученые и объяснили отрицательные количества как долг, а положительные — как имущество, всё же они избегали широкого употребления их, так как числа эти казались непонятными, действия с ними были неясны.

Если же задача приводила к отрицательному решению, то старались заменить условие (как греки), чтобы в итоге получалось решение положительно. В V-VI столетиях отрицательные числа появляются и очень широко распространяются в индийской математике. В отличие от Китая в Индии были уже известны и правила умножения, деления. В Индии отрицательные числа систематически использовали в основном так, как это мы делаем сейчас. Уже в произведении выдающегося индийского математика и астронома Брахмагупты (598 – около 660 гг.) мы читаем: «имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму».

Знаки «+» и «-» широко использовались в торговле. Виноделы на пустых бочках ставили знак «-», означавший убыль. Если бочку наполняли, то знак перечеркивали и получали знак «+», означавший прибыль.

Эти знаки как математические ввел Ян Видман в XV.

В европейской науке отрицательные и положительные числа окончательно вошли в употребление лишь со времени Французского математика Р.Декарта(1596 – 1650), давшего геометрическое истолкование положительным и отрицательным числам как направленных отрезков. В 1637 году он ввел «координатную прямую».

В 1831 году Гаусс полно обосновал, что отрицательные числа абсолютно равнозначны по правам с положительными, а то что их можно применить не во всех случаях значения не имеет.

История возникновения отрицательных и положительных чисел заканчивается в XIX веке когда Уильям Гамильтон и Герман Грассман создали полную теорию положительных и отрицательных чисел. С этого момента начинается история развития данного математического понятия.

Применение положительных и отрицательных чисел

Медицина

Близорукость и дальнозоркость

Отрицательные числа выражают патологию глаза. Близорукость (миопия) проявляется снижением остроты зрения. Для того чтобы при близорукости глаз мог ясно видеть отдаленные предметы применяют рассеивающие (отрицательные) линзы. Близорукость (-), дальнозоркость (+).

Дальнозоркость (гиперметропия) — вид рефракции глаза, при котором изображение предмета фокусируется не на определенной области сетчатки, а в плоскости за ней. Такое состояние зрительной системы приводит к нечеткости изображения, которое воспринимает сетчатка.

Причиной дальнозоркости может быть укороченное глазное яблоко, либо слабая преломляющая сила оптических сред глаза. Увеличив ее, можно добиться того, что лучи будут фокусироваться там, где они фокусируются при нормальном зрении.

С возрастом, зрение особенно вблизи все больше ухудшается из-за уменьшения аккомодативной способности глаза вследствие возрастных изменений в хрусталике — снижается эластичность хрусталика, ослабевают мышцы, удерживающие его, и как следствие снижается зрение. Именно поэтому возрастная дальнозоркость (пресбиопия ) наличествует практически у всех людей после 40–50 лет.

При малых степенях дальнозоркости обычно сохраняется высокое зрение и вдаль, и вблизи, но могут быть жалобы на быструю утомляемость, головную боль, головокружение. При средней степени гиперметропии — зрение вдаль остается хорошим, а вблизи затруднено. При высокой дальнозоркости — плохое зрение и вдаль, и вблизи, так как исчерпаны все возможности глаза фокусировать на сетчатке изображение даже далеко расположенных предметов.

Дальнозоркость, в том числе и возрастная, может быть выявлена только при проведении тщательного диагностического обследования (при медикаментозном расширении зрачка хрусталик расслабляется и проявляется истинная рефракция глаза).

Близорукость – это болезнь глаз, при которой человек плохо видит предметы, расположенные вдалеке, но хорошо видит те предметы, которые находятся близко. Близорукость также называется миопией.

Считается, что около восьмисот миллионов людей болеют близорукостью. Близорукостью могут страдать все: и взрослые, и дети.

В наших глазах существуют роговица и хрусталик. Эти составляющие глаза способны пропускать лучи, преломляя их. А на сетчатке возникает изображение. Потом это изображение становится нервными импульсами и по зрительному нерву передается в мозг.

Если роговица и хрусталик преломляют лучи так, что фокус находится на сетчатке, то изображение будет четким. Поэтому люди без каких-либо болезней глаз будут хорошо видеть.

При близорукости изображение получается размытым и нечетким. Это может происходить по следующим причинам:

– если глаз сильно удлиняется, то сетчатка отходит от стабильного расположения фокуса. При близорукости у людей глаз достигает тридцати миллиметров. А у нормального здорового человека величина глаза равна двадцать три – двадцать четыре миллиметра;– если хрусталик и роговица преломляют лучи света слишком сильно.

По данным статистики, на земле каждый третий человек страдает миопией, то есть близорукостью. Таким людям сложно увидеть предметы, которые находятся вдалеке от них. Но при этом если книга или тетрадь будут близко расположены от глаз человека, который болеет близорукостью, то он будет хорошо видеть данные предметы .

2) Термометры

Посмотрим на шкалу обычного уличного термометра.

Она имеет вид, изображенный на шкале 1. На ней нанесены только положительные числа, и поэтому при указании численного значения температуры приходится дополнительно пояснять 20 градусов тепла (выше нуля). Это для физиков неудобно – ведь слова в формулу не подставишь! Поэтому в физике применяется шкала с отрицательными числами (шкала 2).

3) Баланс на телефоне

Проверяя баланс на своем телефоне или планшете можно увидеть число со знаком (-), это означает что данный абонент, имеет задолжность и не может осуществить звонок, пока не пополнит свой счет, число же без знака (-) означает что можно звонить или осуществлять какую-либо другую функцию.

Уровень моря

Посмотрим на физическую карту мира. Участки суши на ней раскрашены различными оттенками зеленого и коричневого цветов, а моря и океаны раскрашены голубым и синим. Каждому цвету соответствует своя высота (для суши) или глубина (для морей и океанов). На карте нарисована шкала глубин и высот, которая показывает, какую высоту (глубину) означает тот или иной цвет, например, такая:

Шкала глубин и высот в метрах

Глубже 5000 2000 200 0 200 1000 2000 4000 выше

На этой шкале мы видим только положительные числа и нуль. За нуль принимается высота (и глубина тоже), на которой находится поверхность воды в Мировом океане. Использование в этой шкале только неотрицательных чисел неудобно для математика или физика. У физика получается такая шкала.

Шкала высот в метрах

Меньше -5000 -2000 -200 0 200 1000 2000 4000 больше

Используя такую шкалу, достаточно указать число без всяких дополнительных слов: положительные числа отвечают различным местам на суше, находящимся над поверхностью моря; отрицательные числа соответствуют точкам, находящимся под поверхностью моря.

В рассмотренной нами шкале высот за нулевую принимается высота поверхности воды в Мировом океане. Эта шкала используется в геодезии и картографии.

В отличие от этого, в быту мы обычно за нулевую высоту принимаем высоту поверхности земли (в том месте, в котором мы находимся).

5) Качества человека

Каждый человек индивидуален и неповторим! Однако мы не всегда задумываемся над тем, какие же черты характера определяют нас как личность, что в нас привлекает людей, а что отталкивает. Выделяют положительные и отрицательные качества человека. Например, положительные качества активность, благородность, динамичность, отважность, предприимчивость, решительность, самостоятельность, смелость, честность, энергичность, отрицательные, агрессивность, вспыльчивость, конкурентоспособная, критичность, упрямство, эгоистичность.

6) Физика и расческа

Положите на стол несколько маленьких кусочков тонкой бумаги. Возьмите чистую сухую пластмассовую расческу и 2-3 раза проведите ею по своим волосам. Расчесывая волосы, вы должны услышать легкое потрескивание. Затем медленно поднесите расческу к клочкам бумаги. Вы увидите, что они сначала притягиваются к расческе, а потом отталкиваются от нее.

Этой же расческой можно притягивать воду. Такое притяжение легко наблюдать, если поднести расческу к тонкой струйке воды, спокойно вытекающей из крана. Вы увидите, что струйка заметно искривляется.

Теперь сверните из тонкой бумаги (лучше всего папиросной) две трубочки длиной 2-3см. и диаметром 0,5см. Подвесьте их рядом (так, чтобы они слегка касались друг друга) на шелковых нитках. Расчесав волосы, прикоснитесь расческой к бумажным трубочкам – они сразу разойдутся в стороны и останутся в таком положении (то есть нитки будут отклонены). Мы видим, что трубочки отталкиваются друг от друга.

Если у вас есть стеклянная палочка (или трубочка, или пробирка) и кусочек шелковой ткани, то опыты можно продолжить.

Потрите палочку о шелк и поднесите к обрывкам бумаги – они начнут «прыгать» на палочку точно так же, как и на расческу, и затем соскальзывать с нее. Струйка воды тоже отклоняется стеклянной палочкой, а бумажные трубочки, к которым вы палочкой прикоснулись, отталкиваются друг от друга.

А теперь возьмите одну палочку, к которой вы прикасались расческой, и вторую трубочку, — и поднесите друг к другу. Вы увидите, что они притягиваются друг к другу. Итак, в этих опытах проявляются силы притяжения и силы отталкивания. В опытах мы видели, что заряженные предметы (физики говорят – заряженные тела) могут притягиваться друг к другу, а могут и отталкиваться друг от друга. Это объясняется тем, что существует два вида, два сорта электрических зарядов, причем заряды одного и того же вида отталкиваются друг от друга, а заряды разных видов притягиваются.

7) Счет времени

В разных странах по-разному. Например, в Древнем Египте каждый раз, когда начинал править новый царь, счёт лет начинался заново. Первый год правления царя считался первым годом, второй – вторым и так далее. Когда этот царь умирал и к власти приходил новый, вновь наступал первый год, затем второй, третий. Иным был счет лет, применявшийся жителями одного из древнейших городов мира-Рима. Год основания своего города римляне считали первым, следующий — вторым и так далее.

Счет лет, которым мы пользуемся, возник давно и связан с почитанием Иисуса Христа – основателя христианской религии. Счёт лет от рождения Иисуса Христа постепенно был принят в разных странах.В нашей стране он введён царём Петром Первым триста лет назад. Время, исчисляемое от Рождества Христова, мы называем НАША ЭРА (а пишем сокращённо Н.Э.). Продолжается наша эра две тысячи лет. Рассмотрим «линию времени» на рисунке.

Основание Начало Первое упоминание о Москве Рождение А. С. Пушкина

Рима восстания

Спартака

Заключение

Работая с различными источниками и исследуя различные явления и процессы, мы выяснили, что отрицательные и положительные используются в медицине, физике, географии, истории, в современных средствах связи, при изучении качеств человека и других сферах деятельности человека. Данная тема является актуальной и находит широкое применение и активно используются человеком.

Эту работу можно использовать на уроках математики, мотивируя учащихся к изучению положительных и отрицательных чисел.

Список используемой литературы

Вигасин А.А,.Годер Г.И., «История древнего мира», учебник 5 кл.,2001.
Выговская В.В. « Поурочные разработки по Математике:6 класс» — М.:ВАКО, 2008г.
Газета «Математика» №4, 2010г.
Гельфман Э.Г. «Положительные и отрицательные числа», учебное пособие по математике для 6-го класса, 2001.

Правила отрицательных. Сложение отрицательных чисел, правило, примеры

На действиях с положительными и отрицательными числами основан практически весь курс математики. Ведь как только мы приступаем к изучению координатной прямой, числа со знаками «плюс» и «минус» начинают встречаться нам повсеместно, в каждой новой теме. Нет ничего проще, чем сложить между собой обычные положительные числа, нетрудно и вычесть одно из другого. Даже арифметические действия с двумя отрицательными числами редко становятся проблемой.

Однако многие путаются в сложении и вычитании чисел с разными знаками. Напомним правила, по которым происходят эти действия.

Сложение чисел с разными знаками

Если для решения задачи нам требуется прибавить к некоторому числу «а» отрицательное число «-b», то действовать нужно следующим образом.

Возьмем модули обоих чисел — |a| и |b| — и сравним эти абсолютные значения между собой.
Отметим, какой из модулей больше, а какой меньше, и вычтем из большего значения меньшее.
Поставим перед получившимся числом знак того числа, модуль которого больше.

Это и будет ответом. Можно выразиться проще: если в выражении a + (-b) модуль числа «b» больше, чем модуль «а», то мы отнимаем «а» из «b» и ставим «минус» перед результатом. Если больше модуль «а», то «b» вычитается из «а» — а решение получается со знаком «плюс».

Бывает и так, что модули оказываются равны. Если так, то на этом месте можно остановиться — речь идет о противоположных числах, и их сумма всегда будет равна нулю.

Вычитание чисел с разными знаками

Со сложением мы разобрались, теперь рассмотрим правило для вычитания.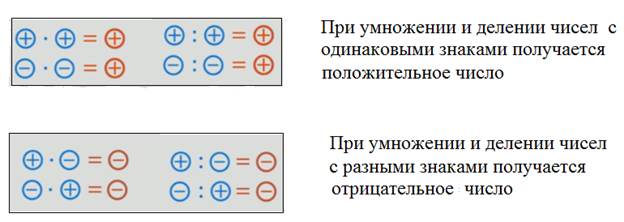 Оно тоже довольно простое — и кроме того, полностью повторяет аналогичное правило для вычитания двух отрицательных чисел.

Для того, чтобы вычесть из некоего числа «а» — произвольного, то есть с любым знаком — отрицательное число «с», нужно прибавить к нашему произвольному числу «а» число, противоположное «с». Например:

Если «а» — положительное число, а «с» — отрицательное, и из «а» нужно вычесть «с», то записываем так: а – (-с) = а + с.
Если «а» — отрицательное число, а «с» — положительное, и из «а» нужно вычесть «с», то записываем следующим образом: (- а)– с = — а+ (-с).

Таким образом, при вычитании чисел с разными знаками в итоге мы возвращаемся к правилам сложения, а при сложении чисел с разными знаками — к правилам вычитания. Запоминание данных правил позволяет решать задачи быстро и без труда.

Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три.

Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды. В зимнее время, когда на улице очень холодно, температура бывает отрицательной (или как говорят в народе «минусовой»).

Например, −10 градусов холода:

Обычные же числа, которые мы рассматривали ранее, такие как 1, 2, 3 называют положительными. Положительные числа — это числа со знаком плюс (+).

При записи положительных чисел знак + не записывают, поэтому мы и видим привычные для нас числа 1, 2, 3. Но следует иметь ввиду, что эти положительные числа выглядят так: +1, +2, +3.

Содержание урока

Это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:

Здесь показаны числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.

Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.

Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом ∞. Отрицательное направление будет обозначаться символом −∞, а положительное символом +∞. Тогда можно сказать, что на координатной прямой располагаются все числа от минус бесконечности до плюс бесконечности:

Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.

Например, точка А(2) читается как «точка А с координатой 2» и будет обозначаться на координатной прямой следующим образом:

Здесь A — это имя точки, 2 — координата точки A.

Пример 2. Точка B(4) читается как «точка B с координатой 4»

Здесь B — это имя точки, 4 — координата точки B.

Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:

Здесь M — это имя точки, −3 — координата точки M.

Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O

Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.

Существуют такие словосочетания, как «чем левее, тем меньше» и «чем правее, тем больше» . Наверное, вы уже догадались о чём идёт речь. При каждом шаге влево, число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.

Сравнение отрицательных и положительных чисел

Правило 1. Любое отрицательное число меньше любого положительного числа.

Например, сравним два числа: −5 и 3. Минус пять меньше , чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.

Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3

Видно, что −5 лежит левее, а 3 правее. А мы говорили, что «чем левее, тем меньше» . И правило говорит, что любое отрицательное число меньше любого положительного числа. Отсюда следует, что

−5

«Минус пять меньше, чем три»

Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.

Например, сравним числа −4 и −1. Минус четыре меньше , чем минус единица.

Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1

Видно, что −4 лежит левее, а −1 правее. А мы говорили, что «чем левее, тем меньше» . И правило говорит, что из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Отсюда следует, что

Минус четыре меньше, чем минус единица

Правило 3. Ноль больше любого отрицательного числа.

Например, сравним 0 и −3. Ноль больше , чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3

Видно, что 0 лежит правее, а −3 левее. А мы говорили, что «чем правее, тем больше» . И правило говорит, что ноль больше любого отрицательного числа. Отсюда следует, что

Ноль больше, чем минус три

Правило 4. Ноль меньше любого положительного числа.

Например, сравним 0 и 4. Ноль меньше , чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:

Видно, что на координатной прямой 0 располагается левее, а 4 правее. А мы говорили, что «чем левее, тем меньше» . И правило говорит, что ноль меньше любого положительного числа. Отсюда следует, что

Ноль меньше, чем четыре

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Правило сложения отрицательных чисел

Если вспомнить урок математики и тему «Сложение и вычитание чисел с разными знаками», то для сложения двух отрицательных чисел необходимо:

выполнить сложение их модулей;
дописать к полученной сумме знак «–».

Согласно правилу сложения можно записать:

$(−a)+(−b)=−(a+b)$.

Правило сложения отрицательных чисел применяется к отрицательным целым, рациональным и действительным числам.

Пример 1

Сложить отрицательные числа $−185$ и $−23 \ 789.$

Решение .

Воспользуемся правилом сложения отрицательных чисел.

Найдем модули данных чисел:

$|-23 \ 789|=23 \ 789$.

Выполним сложение полученных чисел:

$185+23 \ 789=23 \ 974$.

Поставим знак $«–»$ перед найденным числом и получим $−23 \ 974$.

Краткая запись решения: $(−185)+(−23 \ 789)=−(185+23 \ 789)=−23 \ 974$.

Ответ : $−23 \ 974$.

При сложении отрицательных рациональных чисел их необходимо преобразовать к виду натуральных чисел, обыкновенных или десятичных дробей.

Пример 2

Сложить отрицательные числа $-\frac{1}{4}$ и $−7,15$.

Решение.

Согласно правилу сложения отрицательных чисел, сначала необходимо найти сумму модулей:

$|-\frac{1}{4}|=\frac{1}{4}$;

Полученные значения удобно свести к десятичным дробям и выполнить их сложение:

$\frac{1}{4}=0,25$;

$0,25+7,15=7,40$.

Поставим перед полученным значением знак $«–»$ и получим $–7,4$.

Краткая запись решения:

$(-\frac{1}{4})+(−7,15)=−(\frac{1}{4}+7,15)=–(0,25+7,15)=−7,4$.

Для сложения положительного и отрицательного числа необходимо:

вычислить модули чисел;

выполнить сравнение полученных чисел:

если они равны, то исходные числа являются противоположными и их сумма равна нулю;
если они не равны, то нужно запомнить знак числа, у которого модуль больше;

из большего модуля вычесть меньший;

перед полученным значением поставить знак того числа, у которого модуль больше.

Сложение чисел с противоположными знаками сводится к вычитанию из большего положительного числа меньшего отрицательного числа.

Правило сложения чисел с противоположными знаками выполняется для целых, рациональных и действительных чисел.

Пример 3

Сложить числа $4$ и $−8$.

Решение.

Требуется выполнить сложение чисел с противоположными знаками. Воспользуемся соответствующим правилом сложения.

Найдем модули данных чисел:

Модуль числа $−8$ больше модуля числа $4$, т.е. запомним знак $«–»$.

Поставим знак $«–»$, который запоминали, перед полученным числом, и получим $−4.$

Краткая запись решения:

$4+(–8) = –(8–4) = –4$.

Ответ : $4+(−8)=−4$.

Для сложения рациональных чисел с противоположными знаками их удобно представить в виде обыкновенных или десятичных дробей.

Вычитание чисел с разными и отрицательными знаками

Правило вычитания отрицательных чисел:

Для вычитания из числа $a$ отрицательного числа $b$ необходимо к уменьшаемому $a$ добавить число $−b$, которое является противоположным вычитаемому $b$.

Согласно правилу вычитания можно записать:

$a−b=a+(−b)$.

Данное правило справедливо для целых, рациональных и действительных чисел. Правило можно использовать при вычитании отрицательного числа из положительного числа, из отрицательного числа и из нуля.

Пример 4

Вычесть из отрицательного числа $−28$ отрицательное число $−5$.

Решение.

Противоположное число для числа $–5$ – это число $5$.

Согласно правилу вычитания отрицательных чисел получим:

$(−28)−(−5)=(−28)+5$.

Выполним сложение чисел с противоположными знаками:

$(−28)+5=−(28−5)=−23$.

Ответ : $(−28)−(−5)=−23$.

При вычитании отрицательных дробных чисел необходимо выполнить преобразование чисел к виду обыкновенных дробей, смешанных чисел или десятичных дробей.

Сложение и вычитание чисел с разными знаками

Правило вычитания чисел с противоположными знаками совпадает с правилом вычитания отрицательных чисел.

Пример 5

Вычесть положительное число $7$ из отрицательного числа $−11$.

Решение.

Противоположное число для числа $7$ – это число $–7$.

Согласно правилу вычитания чисел с противоположными знаками получим:

$(−11)−7=(–11)+(−7)$.

Выполним сложение отрицательных чисел:

$(−11)+(–7)=−(11+7)=−18$.

Краткая запись решения: $(−28)−(−5)=(−28)+5=−(28−5)=−23$.

Ответ : $(−11)−7=−18$.

При вычитании дробных чисел с разными знаками необходимо выполнить преобразование чисел к виду обыкновенных или десятичных дробей.

В рамках этого материала мы затронем такую важную тему, как сложение отрицательных чисел. В первом параграфе мы расскажем основное правило для этого действия, а во втором – разберем конкретные примеры решения подобных задач.

Yandex.RTB R-A-339285-1

Основное правило сложения натуральных чисел

Перед тем, как вывести правило, вспомним, что мы вообще знаем о положительных и отрицательных числах. Ранее мы условились, что отрицательные числа нужно воспринимать как долг, убыток. Модуль отрицательного числа выражает точные размеры этого убытка. Тогда сложение отрицательных чисел можно представить как сложение двух убытков.

Воспользовавшись этим рассуждением, сформулируем основное правило сложения отрицательных чисел.

Определение 1

Для того чтобы выполнить сложение отрицательных чисел , нужно сложить значения их модулей и поставить минус перед полученным результатом. В буквенном виде формула выглядит как (− a) + (− b) = − (a + b) .

Исходя из этого правила, можно сделать вывод, что сложение отрицательных чисел аналогично сложению положительных, только в итоге у нас обязательно должно получиться отрицательное число, ведь перед суммой модулей надо ставить знак минус.

Какие можно привести доказательства этого правила? Для этого нам потребуется вспомнить основные свойства действий с действительными числами (или с целыми, или с рациональными –они одинаковы для всех этих типов чисел). Для доказательства нам нужно всего лишь продемонстрировать, что разность левой и правой части равенства (− a) + (− b) = − (a + b) будет равна 0 .

Вычесть одно число из другого – это то же самое, что и прибавить к нему такое же противоположное число. Следовательно, (− a) + (− b) − (− (a + b)) = (− a) + (− b) + (a + b) . Вспомним, что числовые выражения со сложением обладают двумя основными свойствами – сочетательным и переместительным. Тогда мы можем сделать вывод, что (− a) + (− b) + (a + b) = (− a + a) + (− b + b) . Поскольку, сложив противоположные числа, мы всегда получаем 0 , то (− a + a) + (− b + b) = 0 + 0 , а 0 + 0 = 0 .Наше равенство можно считать доказанным, значит, и правило сложения отрицательных чисел мы тоже доказали.

Во втором параграфе мы возьмем конкретные задачи, где нужно складывать отрицательные числа, и попробуем применить в них изученное правило.

Пример 1

Найдите сумму двух отрицательных чисел — 304 и — 18 007 .

Решение

Выполним действия пошагово. Сначала нам надо найти модули складываемых чисел: — 304 = 304 , — 180007 = 180007 . Далее нам нужно выполнить действие сложения, для чего мы используем метод подсчета столбиком:

Все, что нам осталось, – это поставить минус перед результатом и получить — 18 311 .

Ответ: — — 18 311 .

От того, какие у нас числа, зависит, к чему мы можем свести действие сложения: к нахождению суммы натуральных чисел, к сложению обыкновенных или десятичных дробей. Разберем задачу с такими числами.

Пример N

Найдите сумму двух отрицательных чисел — 2 5 и − 4 , (12) .

Решение

Находим модули искомых чисел и получаем 2 5 и 4 , (12) . У нас получились две разные дроби. Сведем задачу к сложению двух обыкновенных дробей, для чего представим периодическую дробь в виде обыкновенной:

4 , (12) = 4 + (0 , 12 + 0 , 0012 + . . .) = 4 + 0 , 12 1 — 0 , 01 = 4 + 0 , 12 0 , 99 = 4 + 12 99 = 4 + 4 33 = 136 33

В итоге мы получили дробь, которую будет легко сложить с первым исходным слагаемым (если вы забыли, как правильно складывать дроби с разными знаменателями, повторите соответствующий материал).

2 5 + 136 33 = 2 · 33 5 · 33 + 136 · 5 33 · 5 = 66 165 + 680 165 = 764 165 = 4 86 105

В итоге мы получили смешанное число, перед которым нам осталось только поставить минус. На этом расчеты завершены.

Ответ: — 4 86 105 .

Действительные отрицательные числа складываются аналогичным образом. Результат такого действия принято записывать числовым выражением. Его значение можно и не вычислять или ограничиться примерными расчетами. Так, к примеру, если нам надо найти сумму — 3 + (− 5) , то ответ мы записываем как — 3 − 5 . Сложению действительных чисел мы посвятили отдельный материал, в котором можно найти и другие примеры.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Сложить два отрицательных числа. Сложение отрицательных чисел: правило, примеры

В этой статье мы поговорим про сложение отрицательных чисел . Сначала дадим правило сложения отрицательных чисел и докажем его. После этого разберем характерные примеры сложения отрицательных чисел.

Навигация по странице.

Правило сложения отрицательных чисел

Прежде чем дать формулировку правила сложения отрицательных чисел, обратимся к материалу статьи положительные и отрицательные числа . Там мы упоминали, что отрицательные числа можно воспринимать как долг, а в этом случае определяет величину этого долга. Следовательно, сложение двух отрицательных чисел – это есть сложение двух долгов.

Этот вывод позволяет осознать правило сложения отрицательных чисел . Чтобы сложить два отрицательных числа, нужно:

сложить их модули;
поставить перед полученной суммой знак минус.

Запишем правило сложения отрицательных чисел −a и −b в буквенном виде: (−a)+(−b)=−(a+b) .

Понятно, что озвученное правило сводит сложение отрицательных чисел к сложению положительных чисел (модуль отрицательного числа является числом положительным). Также понятно, что результатом сложения двух отрицательных чисел является отрицательное число, о чем свидетельствует знак минус, который ставится перед суммой модулей.

Правило сложения отрицательных чисел можно доказать, основываясь на свойствах действий с действительными числами (или таких же свойствах действий с рациональными или целыми числами). Для этого достаточно показать, что разность левой и правой частей равенства (−a)+(−b)=−(a+b) равна нулю.

Так как вычитание числа – это все равно, что прибавление противоположного числа (смотрите правило вычитания целых чисел), то (−a)+(−b)−(−(a+b))=(−a)+(−b)+(a+b) . В силу переместительного и сочетательного свойств сложения имеем (−a)+(−b)+(a+b)=(−a+a)+(−b+b) . Так как сумма противоположных чисел равна нулю, то (−a+a)+(−b+b)=0+0 , а 0+0=0 в силу свойства сложения числа с нулем. Этим доказано равенство (−a)+(−b)=−(a+b) , а значит, и правило сложения отрицательных чисел.

Осталось лишь научиться применять правило сложения отрицательных чисел на практике, что мы и сделаем в следующем пункте.

Примеры сложения отрицательных чисел

Разберем примеры сложения отрицательных чисел . Начнем с самого простого случая – сложения отрицательных целых чисел, сложение будем проводить по правилу, рассмотренному в предыдущем пункте.

Пример.

Выполните сложение отрицательных чисел −304 и −18 007 .

Решение.

Выполним все шаги правила сложения отрицательных чисел.

Сначала находим модули складываемых чисел: и . Теперь нужно сложить полученные числа, здесь удобно выполнить сложение столбиком :

Теперь ставим знак минус перед полученным числом, в результате имеем −18 311 .

Запишем все решение в краткой форме: (−304)+(−18 007)= −(304+18 007)=−18 311 .

Ответ:

−18 311 .

Сложение отрицательных рациональных чисел в зависимости от самих чисел можно свести либо к сложению натуральных чисел , либо к сложению обыкновенных дробей , либо к сложению десятичных дробей .

Пример.

Сложите отрицательное число и отрицательное число −4,(12) .

Решение.

По правилу сложения отрицательных чисел сначала нужно вычислить сумму модулей. Модули складываемых отрицательных чисел равны соответственно 2/5 и 4,(12) . Сложение полученных чисел можно свести к сложению обыкновенных дробей. Для этого переведем периодическую десятичную дробь в обыкновенную дробь : . Таким образом, 2/5+4,(12)=2/5+136/33 . Теперь выполним

Например, −10 градусов холода:

Содержание урока

Здесь A — это имя точки, 2 — координата точки A.

Пример 2. Точка B(4) читается как «точка B с координатой 4»

Здесь B — это имя точки, 4 — координата точки B.

Здесь M — это имя точки, −3 — координата точки M.

Сравнение отрицательных и положительных чисел

Правило 1. Любое отрицательное число меньше любого положительного числа.

−5

«Минус пять меньше, чем три»

Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.

Например, сравним числа −4 и −1. Минус четыре меньше , чем минус единица.

Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1

Минус четыре меньше, чем минус единица

Правило 3. Ноль больше любого отрицательного числа.

Ноль больше, чем минус три

Правило 4. Ноль меньше любого положительного числа.

Ноль меньше, чем четыре

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Сложение отрицательных чисел.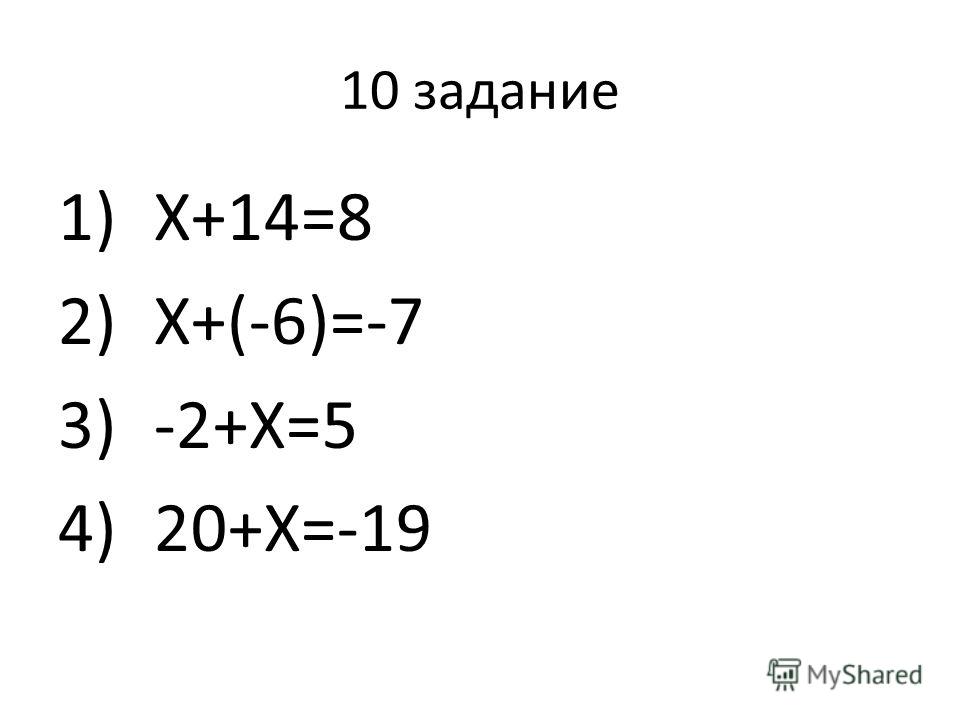

Сумма отрицательных чисел есть число отрицательное. Модуль суммы равен сумме модулей слагаемых .

Давайте разберемся, почему же сумма отрицательных чисел будет тоже отрицательным числом. Поможет нам в этом координатная прямая, на которой мы выполним сложение чисел -3 и -5. Отметим на координатной прямой точку, соответствующее числу -3.

К числу -3 нам нужно прибавить число -5. Куда мы пойдем от точки, соответствующей числу -3? Правильно, влево! На 5 единичных отрезков. Отмечаем точку и пишем число ей соответствующее. Это число -8.

Итак, при выполнении сложения отрицательных чисел с помощью координатной прямой мы все время находимся слева от начала отсчета, поэтому, понятно, что результат сложения отрицательных чисел есть число тоже отрицательное.

Примечание. Мы складывали числа -3 и -5, т.е. находили значение выражения -3+(-5). Обычно при сложении рациональных чисел просто записывают эти числа с их знаками, как бы перечисляют все числа, которые нужно сложить. Такую запись называют алгебраической суммой. Применяют (в нашем примере) запись: -3-5=-8.

Пример. Найти сумму отрицательных чисел: -23-42-54. (Согласитесь, что эта запись короче и удобнее вот такой: -23+(-42)+(-54))?

Решаем по правилу сложения отрицательных чисел: складываем модули слагаемых: 23+42+54=119. Результат будет со знаком «минус».

Записывают обычно так: -23-42-54=-119.

Сложение чисел с разными знаками.

Сумма двух чисел с разными знаками имеет знак слагаемого с большим модулем. Чтобы найти модуль суммы, нужно из большего модуля вычесть меньший .

Выполним сложение чисел с разными знаками с помощью координатной прямой.

1) -4+6. Требуется к числу -4 прибавить число 6. Отметим число -4 точкой на координатной прямой. Число 6 — положительное, значит от точки с координатой -4 нам нужно идти вправо на 6 единичных отрезков. Мы оказались справа от начала отсчета (от нуля) на 2 единичных отрезка.

Результат суммы чисел -4 и 6 — это положительное число 2:

— 4+6=2. Как можно было получить число 2? Из 6 вычесть 4, т.е. из большего модуля вычесть меньший. У результата тот же знак, что и у слагаемого с большим модулем.

2) Вычислим: -7+3 с помощью координатной прямой. Отмечаем точку, соответствующую числу -7. Идем вправо на 3 единичных отрезка и получаем точку с координатой -4. Мы были и остались слева от начала отсчета: ответ — отрицательное число.

— 7+3=-4. Этот результат мы могли получить так: из большего модуля вычли меньший, т.е. 7-3=4. В результате поставили знак слагаемого, имеющего больший модуль: |-7|>|3|.

Примеры. Вычислить: а) -4+5-9+2-6-3; б) -10-20+15-25.

Правило сложения отрицательных чисел

выполнить сложение их модулей;
дописать к полученной сумме знак «–».

Согласно правилу сложения можно записать:

$(−a)+(−b)=−(a+b)$.

Пример 1

Сложить отрицательные числа $−185$ и $−23 \ 789.$

Решение .

Воспользуемся правилом сложения отрицательных чисел.

Найдем модули данных чисел:

$|-23 \ 789|=23 \ 789$.

Выполним сложение полученных чисел:

$185+23 \ 789=23 \ 974$.

Поставим знак $«–»$ перед найденным числом и получим $−23 \ 974$.

Краткая запись решения: $(−185)+(−23 \ 789)=−(185+23 \ 789)=−23 \ 974$.

Ответ : $−23 \ 974$.

Пример 2

Сложить отрицательные числа $-\frac{1}{4}$ и $−7,15$.

Решение.

Согласно правилу сложения отрицательных чисел, сначала необходимо найти сумму модулей:

$|-\frac{1}{4}|=\frac{1}{4}$;

Полученные значения удобно свести к десятичным дробям и выполнить их сложение:

$\frac{1}{4}=0,25$;

$0,25+7,15=7,40$.

Поставим перед полученным значением знак $«–»$ и получим $–7,4$.

Краткая запись решения:

$(-\frac{1}{4})+(−7,15)=−(\frac{1}{4}+7,15)=–(0,25+7,15)=−7,4$.

Для сложения положительного и отрицательного числа необходимо:

вычислить модули чисел;

выполнить сравнение полученных чисел:

если они равны, то исходные числа являются противоположными и их сумма равна нулю;
если они не равны, то нужно запомнить знак числа, у которого модуль больше;

из большего модуля вычесть меньший;

перед полученным значением поставить знак того числа, у которого модуль больше.

Пример 3

Сложить числа $4$ и $−8$.

Решение.

Найдем модули данных чисел:

Модуль числа $−8$ больше модуля числа $4$, т.е. запомним знак $«–»$.

Поставим знак $«–»$, который запоминали, перед полученным числом, и получим $−4.$

Краткая запись решения:

$4+(–8) = –(8–4) = –4$.

Ответ : $4+(−8)=−4$.

Вычитание чисел с разными и отрицательными знаками

Правило вычитания отрицательных чисел:

Согласно правилу вычитания можно записать:

$a−b=a+(−b)$.

Пример 4

Вычесть из отрицательного числа $−28$ отрицательное число $−5$.

Решение.

Противоположное число для числа $–5$ – это число $5$.

Согласно правилу вычитания отрицательных чисел получим:

$(−28)−(−5)=(−28)+5$.

Выполним сложение чисел с противоположными знаками:

$(−28)+5=−(28−5)=−23$.

Ответ : $(−28)−(−5)=−23$.

Сложение и вычитание чисел с разными знаками

Правило вычитания чисел с противоположными знаками совпадает с правилом вычитания отрицательных чисел.

Пример 5

Вычесть положительное число $7$ из отрицательного числа $−11$.

Решение.

Противоположное число для числа $7$ – это число $–7$.

Согласно правилу вычитания чисел с противоположными знаками получим:

$(−11)−7=(–11)+(−7)$.

Выполним сложение отрицательных чисел:

$(−11)+(–7)=−(11+7)=−18$.

Краткая запись решения: $(−28)−(−5)=(−28)+5=−(28−5)=−23$.

Ответ : $(−11)−7=−18$.

Теперь давайте разберемся с умножением и делением .

Предположим, нам нужно умножить +3 на -4. Как это сделать?

Давайте рассмотрим такой случай. Три человека залезли в долги, и у каждого по 4 доллара долга. Чему равен общий долг? Для того чтобы его найти, надо сложить все три долга: 4 доллара + 4 доллара + 4 доллара = 12 долларов. Мы с вами решили, что сложение трех чисел 4 обозначается как 3×4. Поскольку в данном случае мы говорим о долге, перед 4 стоит знак «-». Мы знаем, что общий долг равен 12 долларам, так что теперь наша задача имеет вид 3х(-4)=-12.

Мы получим тот же результат, если по условию задачи каждый из четырех человек имеет долг по 3 доллара. Другими словами, (+4)х(-3)=-12. А поскольку порядок сомножителей значения не имеет, получаем (-4)х(+3)=-12 и (+4)х(-3)=-12.

Давайте обобщим результаты. При перемножении одного положительного и одного отрицательного числа результат всегда будет отрицательным числом . Численная величина ответа будет той же самой, как и в случае положительных чисел. Произведение (+4)х(+3)=+12. Присутствие знака «-» влияет только на знак, но не влияет на численную величину.

А как перемножить два отрицательных числа?

К сожалению, на эту тему очень трудно придумать подходящий пример из жизни. Легко себе представить долг в сумме 3 или 4 доллара, но совершенно невозможно вообразить -4 или -3 человека, которые залезли в долги.

Пожалуй, мы пойдем другим путем. В умножении при изменении знака одного из множителей меняется знак произведения. Если мы меняем знаки у обоих множителей, мы должны дважды сменить знак произведения , сначала с положительного на отрицательный, а затем наоборот, с отрицательного на положительный, то есть у произведения будет первоначальный знак.

Следовательно, вполне логично, хотя немного странно, что (-3)х(-4)=+12.

Положение знака при умножении изменяется таким образом:

положительное число х положительное число = положительное число;
отрицательное число х положительное число = отрицательное число;
положительное число х отрицательное число = отрицательное число;
отрицательное число х отрицательное число = положительное число.

Иначе говоря, перемножая два числа с одинаковыми знаками, мы получаем положительное число . Перемножая два числа с разными знаками, мы получаем отрицательное число .

Такое же правило справедливо и для действия противоположного умножению – для .

Вы легко можете в этом убедиться, проведя обратные операции умножения . Если в каждом из примеров, приведенных выше, вы умножите частное на делитель, то получите делимое, и убедитесь, что оно имеет тот же самый знак, например (-3)х(-4)=(+12).

Поскольку скоро зима, то пора уже подумать о том, в что переобуть своего железного коня, что бы не скользить по льду и чувствовать себя уверено на зимних дорогах. Можно, например, взять шины йокогама на сайте: mvo.ru или какие-то другие, главное, что бы качественный, больше информации и цены вы можете узнать на сайте Mvo.ru.

10 важных примеров положительных и отрицательных чисел в реальной жизни

Положительный или отрицательный знак перед числом имеет огромное значение. В то время как положительный подразумевает добавление, отрицательный подразумевает уменьшение. Эта идея упрощает выводы в ряде областей, таких как количество и направления. Эти примеры из реальной жизни заслуживают внимания.

Иногда полезно учиться на примерах из реальной жизни, так как ученики лучше обращают внимание на детали. Чтобы помочь ученикам в изучении положительных и отрицательных чисел, мы перечислили десять реальных приложений, которые вы, возможно, тщательно изучили, но не заметили значения этих чисел.

Зачем нужно знать положительные и отрицательные числа?

Каждый день мы используем несколько приложений с положительными и отрицательными числами. Понимание знака часто имеет решающее значение в таких ключевых областях, как авиация, судоходство, акции, транспорт и понимание статистики. Небольшая ошибка в знаке может создать грубую ошибку, которая может оказать существенное влияние. Соответственно, учащимся может понадобиться узнать причину «почему существуют эти числа?» и «Каковы применения этих положительных и отрицательных чисел?

Каково представление о положительных и отрицательных числах?

Цифры указывают количество или стоимость. Положительные и отрицательные значения могут указывать на сложение или вычитание. Если количество увеличивается, мы говорим, что определенное количество вещи прибавилось к предыдущему количеству, или наоборот, если оно уменьшается. Отрицательное число просто показывает снижение по сравнению с предыдущим состоянием или значением, а положительное число показывает приращение в предыдущем состоянии или значении. Например, годовой процент роста ВВП страны может быть отрицательным, что указывает на рецессию.

Вот несколько преимуществ положительных-отрицательных чисел:

Мы можем определить более широкий диапазон температур даже ниже нуля градусов, что помогает нам проводить многие химические реакции, требующие отрицательных температур.
Точное измерение высоты помогает выполнять полеты на более безопасном расстоянии в небе. (1000 футов друг от друга)
Часовые пояса по всему миру определяются путем добавления или вычитания часов из GMT.
Определение фокусных расстояний оптических линз для четкого зрения.
Положительная-отрицательная поляризация способствует прохождению заряда, что приводит к возникновению электрического тока.

Помимо теоретической части, мы сталкиваемся с некоторыми примерами из реальной жизни, где мы ежедневно используем концепцию положительных и отрицательных чисел, даже не осознавая этого. Вот 10 реальных дискуссий о значении положительных и отрицательных чисел.

Где мы используем положительные и отрицательные числа в реальной жизни?

Числа, как положительные, так и отрицательные, видны почти повсюду вокруг нас. Мы можем их не замечать, но их значение в этих немногих областях очень важно. Вот несколько примеров из реальной жизни, которые могут помочь вам в идентификации:

1. Фондовая биржа

Фондовый рынок — это биржа, на которой можно купить или продать акции зарегистрированных на бирже компаний. Это центр финансовой деятельности в экономике. Оценки и изображения здесь охватывают как положительные, так и отрицательные числа.

Каждую секунду значение индекса колеблется, указывая на положительную или отрицательную тенденцию. Целое положительное число указывает на рост цен на акции, а знак минус означает снижение цен на акции.

Ваша прибыль и убытки также рассчитываются в виде положительных и отрицательных знаков. Например, если цена акции составляет 100 долларов, а на следующий день она поднимается до 110 долларов, акция считается положительной с 10-процентным увеличением.

2. Измерение температуры

Измерение температуры может быть примечательным примером в повседневной жизни, где мы используем положительные и отрицательные числа. Отчеты о погоде показывают, является ли температура места высокой или низкой с точки зрения положительных и отрицательных знаков, прежде чем указывать числовое значение температуры.

В странах у экватора температура выше, а у близлежащих полюсов температура выше нуля. Отрицательная температура является четким индикатором температуры ниже точки замерзания. Например, температура в ОАЭ составляет 45°C, что указывает на то, что там будет жаркий климат. С другой стороны, температура арктического региона составляет -25°C, а значит, будет холодно.

3. Высота

Высота указывает расстояние от уровня моря. Проще говоря, это означает, насколько высоко или низко находится объект от верхней части морского дна. Считайте уровень моря началом линии числа высоты, точно так же, как 0 является началом линии числа счета.

По мере увеличения высоты над уровнем моря к небу числа становятся положительными. Когда высота падает ниже уровня моря, числа становятся отрицательными. Хотя высота может быть отрицательной, она записывается как «X футов ниже уровня моря» вместо -x футов над уровнем моря.

4. Широта и долгота

Широта и долгота являются важными географическими ориентирами. Широта говорит, как далеко к северу или югу от экватора места, а долгота говорит, как далеко к востоку или западу от нулевого меридиана. Он основан на системе сетки широты и долготы Земли, которая делит земной шар с севера на юг на две зоны и с востока на запад на четыре зоны. Система сетки позволяет путешественникам найти дорогу из точки А в точку Б.

Воображаемые линии широты и долготы были проведены вокруг земной поверхности для определения точного местоположения. Середина земли определялась как экватор или 0 градусов. Северный полюс обозначается как 90°, а Южный полюс обозначается как -90°. Следовательно, широта, показанная в северном полушарии, имеет положительные значения, а значения широты в южном полушарии отрицательны. Долготы колеблются от 0° на нулевом меридиане, который проходит через Лондон, Великобритания, до ±180° на антимеридиане в Тихом океане.

5. Лифты (лифты)

Мы пользуемся лифтами каждый день. Это вертикальная транспортная среда, которая помогает нам перемещаться между несколькими этажами/этажами здания. Здесь первый этаж обозначен как нулевой. В то время как верхние этажи отмечены как 1,2,3, подвал и парковка обычно отмечены как -1, -2 и -3 и так далее.

Наблюдая за этим в большинстве общественных мест и зданий, мы часто сталкиваемся с повседневным примером использования положительных и отрицательных чисел.

6. Банковские выписки

Когда вы проверяете свои банковские выписки или транзакции, перед некоторыми транзакциями стоит знак +, а перед другими — знак. Положительный знак указывает на то, что деньги депонированы или зачислены на счет. С другой стороны, отрицательный знак указывает на дебет, то есть деньги были отправлены кому-то другому.

Для простоты понимания зачисленные деньги или проценты обозначаются знаком плюс, а знак минус/минус обозначает дебет и начисления. Просматривая банковскую выписку, можно легко наблюдать эти цифры.

7. Понимание статистики

Нам нужно изучить положительные и отрицательные целые числа, чтобы сделать определенный результат из статистических данных. Например, расчет общей численности населения в конкретной стране потребует оценки иммигрантов, эмигрантов и постоянного населения. Затем нам нужно сложить иммигрантов и постоянное население и вычесть из него эмигрантов. Должностным лицам может потребоваться сложить отрицательное и положительное население, чтобы выполнить расчеты населения и разработать политику для вашей страны.

8. Спорт

Многие индикаторы спортивных событий требуют отображения отрицательных значений.

В бейсболе дифференциал ранов отрицателен, если команда отдает больше ранов, чем они забили сами.
Прирост ярдов в футболе может быть положительным или отрицательным.

Гонщикам Формулы-1 может быть дано время прохождения круга или сектора, например, рекордного круга или только что пройденного круга. Число положительное, если водитель проехал круг в более медленном темпе, и отрицательное, если в более быстром темпе.

9. Экзаменационные баллы MCQ (с отрицательной оценкой)

Экзамены MCQ обычно являются способом оценки знаний по предмету. Некоторые из этих тестов также могут снижать оценку за каждый неправильный ответ. Следовательно, учащиеся также могут получить отрицательное число. Таким образом, сумма отрицательных оценок превышает положительные оценки, и тогда чистый прирост баллов становится отрицательным. Это может быть неприятным событием для студента.

10. Рейтинг музыкальных чартов — рейтинг Billboard/Spotify

Музыкальные чарты или рейтинги видео публикуются на Billboard каждую неделю. Повышение ранга обозначается знаком плюс перед песней. Целочисленное значение указывает, на сколько рангов поднялась песня. Если песня опускается в рейтинге, вы можете увидеть отрицательный знак рядом с песней с целым числом, которое показывает, что рейтинг песни снизился.

Подведение итогов,

Растет потребность в понимании положительных и отрицательных чисел, поскольку они необходимы в математике, технике, бизнесе, авиации и других смежных областях. Кроме того, положительные и отрицательные числа важны, потому что они позволяют сравнивать и диверсифицировать числовые данные. Отрицательные числа часто дополняют описание различных величин.

Несмотря на то, что существует множество реальных приложений, мы перечислили наиболее распространенные варианты, свидетелями которых могли быть многие люди. Ознакомьтесь с ними, чтобы привить вашему малышу важность положительных и отрицательных чисел.

Что отличает отрицательные числа от положительных кроме того, что они (почти) противоположны?

До сих пор ни один из ответов не касался основного вопроса, поэтому кажется, что умножение асимметрично и удовлетворяет «положительное время положительное положительное», в то время как «отрицательное время отрицательное положительное». Причина в том, что умножение не так просто, как кажется. $\def\nn{\mathbb{N}}$ $\def\zz{\mathbb{Z}}$ $\def\rr{\mathbb{R}}$

Этот ответ обязательно будет длинным, чтобы объяснить в разумных подробностях, как можно построить реальную арифметику интуитивно с нуля, а не просто путем аксиоматизации. Это неизбежно, поскольку аксиомы поля могут показать, что $-1 \times -1 = 1$, но не дают никакого понимания того, почему это должно быть именно так.

Точка зрения 1 является более фундаментальной и требует меньше интуиции, но вам нужно будет следовать медленно и внимательно, чтобы полностью понять и оценить ее, поэтому, если вы хотите получить быстрый ответ, перейдите к точке зрения 2 и остановитесь, как только я начну чтобы связать его с точкой зрения 1.

Точка зрения 1

Сначала мы можем начать с натуральных чисел $\nn$, которые вы понимаете интуитивно, независимо от того, используете ли вы блоки или строки символов или рассматриваете каждое натуральное число как способ представления числа повторений какая-то процедура.

Реальные числа $\rr$ представляют смещение, как вы упомянули в своем вопросе. Но что представляет собой $a \times b$? Вы не можете умножить смещение на другое смещение! Значит, здесь имеется в виду другое. Давайте посмотрим, что мы можем определить интуитивно. Определите $k \times x$ как «$k$ раз больше, чем $x$» для любых $k \in \nn$ и $x \in \rr$. Конечно, $0_\nn \times x = 0_\rr$ и $1_\nn \times x = x$ для любого $x \in \rr$. Обратите внимание, что я четко различаю $0_\nn$ ($0$ раз) и $0_\rr$ (нулевое количество). Также обратите внимание, что $x \times k$ не имеет никакого значения (пока), поскольку нет смысла говорить о «$x$ столько же, сколько $k$ раз».

Обратите внимание, что $\nn$ встраивается в $\rr$ следующим образом. Вы можете трактовать $k_\rr$ как $k \times 1_\rr$, что по нашему определению означает «$k$ умножить на $1_\rr$». В физическом мире это соответствует количеству «$k$ единиц».

Теперь вы можете интуитивно проверить выполнение двух важных свойств:

$( a +_{_\nn} b ) \times x = a \times x + b \times x$ для любых $a,b \in \nn$ и $x \in \rr$.
$( а \times_{_\nn} b ) \times x = a \times ( b \times x )$.

Здесь я использовал «$+_{_\nn}$» и «$\times_{_\nn}$» для сложения и умножения в $\nn$, чтобы отличить его от «$+$» и » $\times$» в $\rr$. На основании этих двух свойств мы говорим, что $\nn$ действует на $\rr$ через $\times$. Это понятие действия вездесуще, даже если вы этого не осознаете. Например, $\nn$ действует на физические сущности через $\def\of{\text{ times }}$$\of$ следующим образом: «$k \of X = \text{$k$ экземпляров $X$ }$». Мы говорим «$2$ яблок», подразумевая под этим «$2 \яблок$» = «2 экземпляра яблок». Мы интуитивно понимаем, что можем оперировать абстрактными числами для подсчета физических объектов, поэтому у нас есть:

$( 2 + 3 ) \яблок = 2 \яблок + 3 \яблок$.
$( 2 \cdot 3 ) \яблок = 2 \из ( 3 \яблок )$.
[аналогично для всех других физических объектов, что является ключевым пониманием; работает не только для яблок!]

Аналогично, $\nn$ действует на (реальные) действия через $\of$ следующим образом: «$k \of A = \text{$A$ повторяется $k$ раз}$».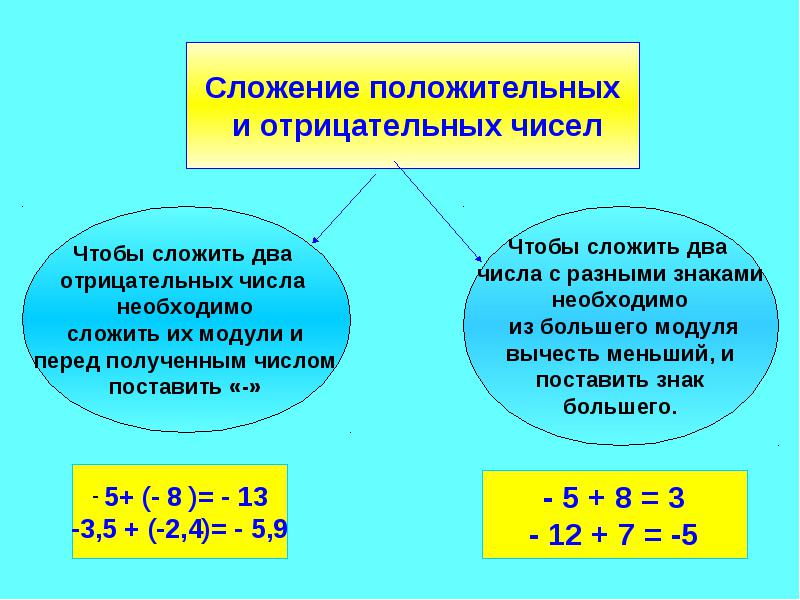 Опять же, мы можем проверить, что оба свойства выполняются.

Все это примеры действия $\nn$ на некотором наборе. Некоторые из них могут быть осмысленно расширены до действия $\zz$ над одним и тем же набором, но не над другими. Нам бы хотелось, чтобы $(-_{_\zz}k) \times x = -( k \times x )$ для любых $k \in \zz$ и $x \in \rr$. Для смещения это будет означать, что «$(-1_\zz) \times x$» — это просто «смещение, противоположное $x$».

Уже здесь мы видим асимметрию, потому что $(-1_\zz) \times (-1_\rr) = 1_\rr$ и $1_\zz \times 1_\rr = 1_\rr$. Первое означает «$-1$, умноженное на противоположное единице смещения», а второе просто означает «единичное смещение», и оба они одинаковы. Таким образом, ответ на ваш вопрос с этой точки зрения заключается в том, что асимметрия исходит из концепции итерации, которая присуща действию $\zz$ на $\rr$.

Просто для полноты картины: $\zz$ не действует на физические объекты, потому что нет прямых противоположностей физическим объектам, которые в сочетании с оригиналом ничего не дают. Использование понятия «недостаток» или «долг» просто меняет коллекцию; изначально это коллекция из физически существующих объектов, впоследствии это коллекция записей относительных количеств физических объектов. По сути, это тот же самый способ, которым мы математически строим $\zz$ из $\nn$. Также $\zz$ действует только на обратимые действия.

Точка зрения 2

Действительные числа — это коэффициенты масштабирования или, еще лучше, сами масштабы с центром в начале координат. $2$ — это увеличение исходной точки в $2$. $1$ — это масштабирование идентичности, которое вообще ничего не делает. $0$ — это масштабирование, которое сворачивает все в исходное положение. $-1$ — это масштабирование, которое переводит каждую точку в точку, противоположную началу координат. Умножение действительных чисел — это то же самое, что составление двух масштабирований вместе (выполнение одного за другим). Обратите внимание, что интуитивно порядок масштабирования не имеет значения, что дает нам коммутативность умножения в $\rr$.

Очевидно $-1 \times -1 = 1$, отвечая на вопрос об асимметрии . Основная причина на самом деле та же, что и в другой точке зрения, потому что здесь положительное значение является особенным просто потому, что $1$ является масштабированием идентичности (оставьте его как есть), в то время как положительное значение является особенным, потому что $1$ является единицей измерения (точно так же, как оно является). Обратите внимание на основное сходство!

Вышеизложенное объясняет только мультипликативную структуру вещественных чисел, так при чем здесь аддитивная структура? На самом деле мы можем объединить его с Точка зрения 1 путем рассмотрения самих действительных чисел как позиций на линии, проходящей через начало координат (эквивалентно смещениям от начала координат), а затем определить , что масштабирование $r$ — это точно масштабирование с центром в $0$ на линии, которая приводит точку $1$ на прямой до точки $r$. Здесь мы воспользовались интуицией о том, что такой масштаб существует и что он уникален, поэтому между масштабами и точками на прямой существует взаимно однозначное соответствие. Чтобы сохранить совместимость с предыдущим абзацем, мы по-прежнему определяем композиционное масштабирование $r \times s$ как композиционное масштабирование сначала на $r$, а затем на $s$.

Так как скейлинг $( r \times s )$ переводит точку $x$ в ту же точку, если бы мы сделали сначала скейлинг $s$, а затем $r$, мы имеем второе свойство для действия скейлингов $\rr $ по точкам $\rr$. Это более ясно в символах, где мы пишем $\def\on{\text{ on }}$»$r \on x$» для обозначения «результата масштабирования $r$, примененного к $x$»:

$( r \times s ) \on x = r \on ( s \on x )$.

Из определения скейлинга и коммутативности скейлинга получаем:

$r \times x = ( r \times x ) \on 1 = r \on ( x \on 1 ) = r \on x$.
$r \on s = r \times s = s \times r = s \on r$.

Теперь мы определяем добавление точек $x,y$ на линии как векторное добавление (добавляем смещения от начала координат), а затем определяем добавление масштабов $r,s$, чтобы они были точно такими же в соответствии с на соответствие между шкалами и точками! Обратите внимание, что интуитивно (или «определение» масштабирования/масштабирования) мы можем видеть, что результат сложения векторов один и тот же независимо от того, в каком масштабе мы его наблюдаем, и поэтому масштабирование перед добавлением должно давать то же самое, что и добавление перед масштабированием. Символически:

$r \on x + r \on y = r \on ( x + y )$.

Из приведенных выше результатов мы наконец можем получить первое свойство действия $\rr$ на $\rr$:

$( r + s ) \on x = x \on ( r + s ) = x \on r + x \on s = r \on x + s \on x$.

Эти свойства соответствуют свойствам умножения действительных чисел (коммутативность, ассоциативность и дистрибутивность над сложением), которые труднее всего обосновать интуитивно. Остальные оставлены в качестве упражнения.

Таким образом, мы установили, что арифметика $\rr$ отражает факты масштабирования (или масштабирования) в реальном мире, по крайней мере, согласно нашей интуиции. Даже если окажется, что это не совсем так, это, безусловно, служит хорошим приближением, и, следовательно, исследование теорем о $\rr$ дает нам приблизительные факты о реальном мире.

Сноски

Конечно, приведенные выше точки зрения не могут быть использованы для доказательства существования реальных чисел, но, по крайней мере, дают разумное обоснование того, почему мы считаем, что $\rr$ полезен для описания реального мира.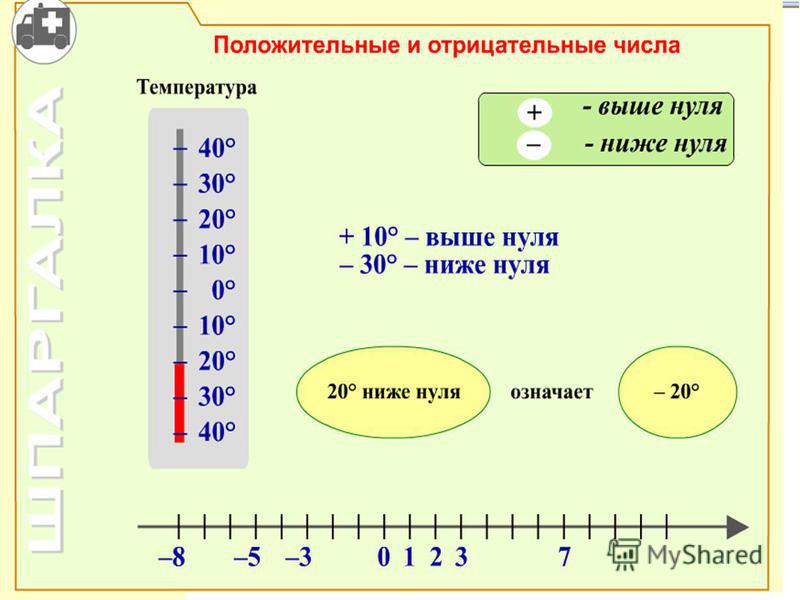 Тем не менее объяснение может быть преобразовано в строгое построение действительных чисел в любой формальной системе, достаточно мощной, чтобы позволить построение простых наборов, функций от $\nn$ до $\nn$, отношений эквивалентности и классов эквивалентности.

Сложение и вычитание / Абсолютное значение ｜ Hatsudy

Когда вы изучаете математику, вы должны понимать отрицательные числа. В отличие от того, когда вы изучали только положительные целые числа, изучение концепции нуля, сложения и вычитания позволит вам выполнять сложные вычисления.

Вам может показаться странным, что есть числа меньше нуля. Однако мы используем отрицательные числа во многих аспектах нашей повседневной жизни. Поэтому очень важно использовать для расчетов как отрицательные, так и положительные целые числа.

Так что же такое концепция 0 и отрицательных чисел? Как мы можем думать и вычислять положительные и отрицательные числа?

Изучая математику, мы все должны понимать положительные и отрицательные числа. Мы объясним, как вычислять положительные и отрицательные целые числа, с некоторыми упражнениями.

Содержание

1 0 (Ноль) используется для обозначения критерия
1.1 Положительные целые числа (натуральные числа) и отрицательные целые числа указывают на увеличение или уменьшение эталона
1.2 Как различать большие и малые числа, и абсолютное значение
2 Сложение и вычитание положительных чисел
2.1 Использование скобок при сложении положительных чисел
2.2 Правила вычитания положительных чисел
3 Сложение и вычитание отрицательных чисел
3.1 Узнайте, как складывать отрицательные числа, заменяя
3.2 Почему отрицательное вычитание является положительным?
4 Упражнения: сложение и вычитание положительных и отрицательных чисел
5 Использование положительных и отрицательных чисел для сложения и вычитания

0 (ноль) используется для обозначения критерия

что нет ничего. Например, если у вас есть 1 доллар, и если вы его потратите, у вас будет 0 долларов.

Если небытие означает ноль, понятие негатива не имеет смысла. Узнавая об отрицательных целых числах, многие люди путаются, потому что могут подумать, что есть числа, которые меньше, чем несуществующие.

Однако 0 не просто означает, что его не существует. У него есть и другие значения. Это критерий. Используя ноль в качестве стандарта, мы используем положительные и отрицательные числа, в зависимости от того, больше или меньше это число нуля.

Например, мы используем температуру в нашей повседневной жизни. Стандартная температура составляет 0°C (32°F). Если температура ниже 0°C, число отрицательное. В городе, где идет снег, многие люди будут испытывать отрицательные температуры.

Учитывая этот факт, мы можем понять, что нет ничего странного в использовании отрицательных чисел, а также положительных чисел; поскольку ноль означает стандарт, многие люди используют отрицательные числа в своей повседневной жизни.

Положительные целые числа (натуральные числа) и отрицательные целые числа указывают на увеличение или уменьшение от эталона

Как только вы узнаете, что ноль имеет понятие стандарта, вы поймете, что означают положительные и отрицательные целые числа. Положительные целые числа (натуральные числа) и отрицательные целые числа указывают, насколько далеко они находятся от контрольной точки (0).

На следующем рисунке с нулем в качестве точки отсчета числа справа представляют собой положительные целые числа (натуральные числа).

С другой стороны, числа слева от нуля являются отрицательными целыми числами. Используя плюс и минус, мы можем выразить увеличение или уменьшение стандарта.

Например, давайте похудеем, сев на диету. В этом случае большинство людей используют свой текущий вес в качестве точки отсчета (ноль). Если вы похудели на 3 кг, то можно сказать, что вы успешно набрали -3 кг веса.

-Можно заменить плюс и минус

Следовательно количество плюсов и минусов можно заменить. Например, следующее имеет такое же значение.

Я похудела на 3 кг.
Я прибавил в весе -3 кг.

Кроме того, следующее имеет такое же значение:

Температура падает на 5°C.
Температура повышается на -5°C.

Важно понимать, что эти перефразирования возможны при изучении положительных и отрицательных чисел.

Как отличить большие и маленькие числа и абсолютные значения

Как мы можем различать большие и маленькие числа с положительными и отрицательными числами? Чтобы понять это, нам нужно понять концепцию абсолютной стоимости.

Мы поняли, что можем проверять положительные и отрицательные числа, основываясь на нуле. Для больших и малых чисел проверьте, насколько они далеки от нуля. Независимо от того, положительное оно или отрицательное, абсолютное значение показывает, насколько оно далеко от нуля.

Например, абсолютное значение 4 равно 4. С другой стороны, абсолютное значение -3 равно 3. Если мы продвинемся на три влево от 0, мы получим -3. Поскольку расстояние от 0 равно 3, абсолютное значение -3 равно 3.

Как только мы изучим эту концепцию, мы сможем различать большие и маленькие числа. Например, с помощью 5 и 3 мы видим, что 5 больше, чем 3. Следовательно, мы можем выразить 5>3. С другой стороны, какое число больше, -3 или -5?

Абсолютное значение -3 равно 3. Кроме того, абсолютное значение -5 равно 5. Важным фактом является то, что чем больше число (абсолютное значение) отрицательного числа, тем меньше становится число. Абсолютное значение -5 больше -3. Следовательно, -3 является большим числом и может быть выражено как $-3>-5$.

Может показаться странным, что хотя число большое, знак минус делает его маленьким. Тем не менее, мы также используем это в нашей повседневной жизни.

Например, между -3°C (26,6°F) и -20°C (-4°F), -20°C холоднее. Это потому, что -20°C является большим отрицательным числом. Поймите, что хотя число (абсолютное значение) велико, оно будет маленьким числом в отрицательном числе.

Сложение и вычитание положительных чисел

Понимание понятий ноль и отрицательные числа поможет вам понять сложение и вычитание положительных и отрицательных чисел.

Положительные и отрицательные числа легко понять, если узнать о них из сложения и вычитания положительных чисел. При работе с положительными числами существует два типа.

Сложение положительных чисел
Вычитание положительных чисел

Мы объясним каждое из них.

Использование скобок при сложении положительных чисел

Вы уже узнали о сложении положительных чисел в начальной школе по математике. Поэтому вы сможете без труда понять сложение положительных чисел с положительными числами. Например, следующий расчет несложный.

$3+1=4$

В этом случае $3+1$ также можно выразить следующим образом.

$3+(+1)$
$(+3)+(+1)$

Все они имеют одинаковое значение. Кроме того, вы можете использовать два + подряд. Однако вместо того, чтобы писать ++, мы используем круглые скобки.

— Добавить положительное число к отрицательному

Как мы можем добавить положительное число к отрицательному числу? Например, следующий расчет.

$-5+3$

Его также можно выразить как $-5+(+3)$ или $(-5)+(+3)$. В любом случае, этот расчет требует добавления 3 к -5. Другими словами, вы должны ответить на число, которое на 3 больше, чем -5.

Абсолютное значение -5 равно 5. Делая от +3 до -5, мы можем пройти три шага вправо и получить -2. Следовательно, ответ -2.

Правила вычитания положительных чисел

В отличие от этого, как мы можем думать о вычитании положительных чисел? Например, предположим, что у нас есть следующий расчет

$3-2=1$

Мы уже изучали этот расчет в начальной школе. Важно то, что его можно заменить следующими уравнениями.

$3-(+2)=1$
$(+3)-(+2)=1$

Во всех положительных числах скрыт +.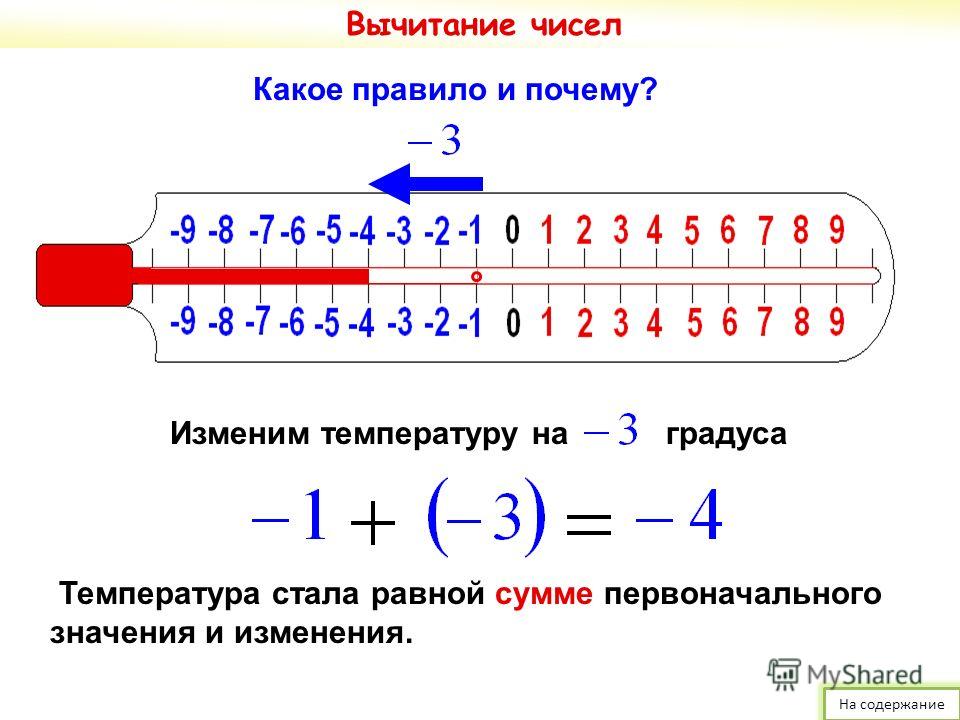 Например, когда мы используем число 2 или 3, мы можем представить его как +2 или +3. Для положительных целых чисел (натуральные числа) + можно опустить. Чтобы описать это подробно, $3-2$ можно представить как $3-(+2)$.

-Вычитание положительного числа из отрицательного числа

Конечно, положительные числа (натуральные числа) вычитаются из отрицательных чисел. Например, каков ответ на следующий расчет?

$-1-3$

Это уравнение также можно заменить на $-1-(+3)$ или $(-1)-(+3)$. Чтобы из -1 вычесть +3, ответ должен быть числом, которое на 3 меньше -1.

Следовательно, ответ равен -4.

$-1-3=-4$
$-1-(+3)=-4$
$(-1)-(+3)=-4$

Вычисляется так .

Сложение и вычитание отрицательных чисел

Мы обсудили положительные числа, и нетрудно понять сложение и вычитание положительных чисел. Сложность заключается в сложении и вычитании отрицательных чисел.

Сложение отрицательных чисел
Вычитание отрицательных чисел

Что это значит? Например, когда мы вычисляем $1 – (-3)$, мы получаем следующее.

$1-(-3)=1+3=4$

Многие люди пытаются научиться считать, не понимая зачем. Тем не менее, вы должны понять причину. Итак, мы объясним в том числе причины.

Узнайте, как складывать отрицательные числа, заменяя

Часто выполняются вычисления, включающие сложение отрицательных чисел. Например, что мы думаем о следующем вычислении?

$2+(-4)$

Как упоминалось выше, цифры можно перефразировать. Например, если вы похудели на 2 кг, вы можете перефразировать это так: «Я набрал -2 кг веса». Несмотря на то, что это выражается как прибавка в весе, это плюс -2 кг, значит, вы похудели.

Таким образом, вы можете заменить положительный на отрицательный. Другими словами, мы можем перефразировать это следующим образом.

$2-4$: на 4 меньше.
$2+(-4)$: -4 выше

Вычесть 4 из 2 равно -2. Число на 4 меньше 2 равно -2. Поймите, что добавление отрицательного числа, по сути, то же самое, что и вычитание положительного числа.

Почему отрицательное вычитание положительное?

Когда дело доходит до понимания отрицательных чисел, многих людей смущает вычитание отрицательных чисел. До сих пор мы объясняли следующее.

Сложение положительных чисел (целые положительные числа)
Вычитание положительных чисел (целые положительные числа)
Сложение отрицательных чисел (целые отрицательные числа)

Сложение и вычитание положительных чисел уже изучают в начальной школе. Кроме того, сложение отрицательных чисел можно перефразировать как вычитание положительных чисел (натуральных чисел). С другой стороны, как мы можем вычислить, например, следующее?

$2-(-3)$

Мы также можем перефразировать этот расчет. Знак минус имеет противоположное значение. Как было сказано выше, выражение «Я похудел на 2 кг» можно перефразировать как «Я набрал -2 кг».

Итак, как понимать выражение «Я похудел на -3 кг»? Так как минус имеет обратное свойство, то уменьшение на -3 кг означает увеличение на 3 кг. Минус минуса есть плюс.

Вот почему, когда вы вычитаете отрицательное число, вы можете превратить его в положительное число.

$2-(-3)=2+3=5$

Важно отметить, что минус имеет противоположное значение. Многие люди не понимают в математике, почему вычитание отрицательного значения дает положительное значение. Как только вы поймете, что отрицание имеет противоположное значение и может быть перефразировано, вы поймете эту причину.

Упражнения: сложение и вычитание положительных и отрицательных чисел

Q1: Выразите размер следующих чисел, используя знак неравенства.

$-2、4、-3$
$-0.3、-3、0$

A1: Ответы.

Для отрицательных чисел, чем выше число (абсолютное значение), тем меньше число. Поскольку это понятие противоположно положительным числам, порядок неравенства следующий.

$4>-2>-3$
$0>-0,3>-3$

Например, в (b) при сравнении 0, 0,3 и 3 порядок старших чисел $3>0,3>0$. Для отрицательного числа верно обратное: чем выше число (абсолютное значение), тем оно меньше, поэтому $0>-0,3>-3$.

Q2: Выполните следующие вычисления.

$7-(+3)$
$-0,5+(-0,2)$
$-3-(-6)$
$\displaystyle\frac{1}{2}-\left(- \displaystyle\frac{1}{3}\right)$
$-3 +(-2)-(-6)-5$

A2: Ответы.

При вычислении положительных и отрицательных чисел давайте перефразируем их. Как в математике младших классов средней школы, так и в математике старших классов все считают после замены знаков. Суть замены заключается в следующем.

$+$ и $+$ становятся $+$
$+$ и $-$ становятся $-$
$-$ и $+$ становятся $-$
$-$ и $-$ становятся $+$

Таким образом можно перефразировать все операции сложения и вычитания, включая десятичные дроби и дроби. Следовательно, мы можем рассчитать следующим образом.

(а)

$7-(+3)=7-3=4$

(б)

$-0,5+(-0,2)=-0,5-0,2=-0,7$

3 (c)

$-3-(-6)=-3+6=3$

(d)

$\displaystyle\frac{1}{2}-\left(-\displaystyle \frac{1}{3}\right)$

$=\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}$

$=\displaystyle\frac{3}{ 6}+\displaystyle\frac{2}{6}=\displaystyle\frac{5}{6}$

(e)

$-3+(-2)-(-6)-5$

$=-3-2+6-5=-4$

Нельзя решить проблему, не перефразируя плюсы и минусы. Убедитесь, что вы знаете, добавляете вы или вычитаете. Если вы меняете знаки, это арифметика начальной школы, поэтому все, что вам нужно сделать, это сложить и вычесть.

С дробями немного сложнее, потому что вам нужно перефразировать знаки, а затем настроить знаменатель. Однако счет дробей нужно учить еще в начальной школе, так что это несложно.

Q3: Выполните следующие расчеты.

В приведенной ниже таблице показано, на сколько сантиметров выше четыре человека от A до D ростом от 160 см.

	A	B	C	D
Difference from 160 cm (cm)	12	-4	7	-9

How many centimeters выше будет самый высокий человек, чем самый низкий человек?
Найдите средний рост четырех человек.

A3: Ответы.

а. На сколько сантиметров выше самого высокого человека будет самый низкий?

Самый высокий человек А.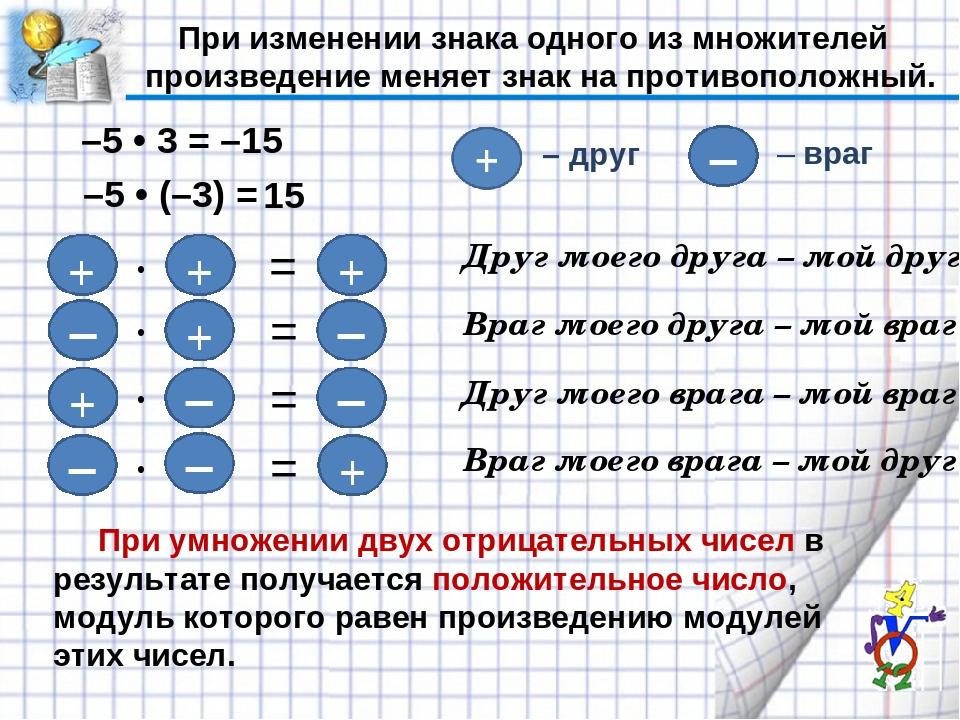 Самый низкий человек D. A выше на +12 см, а D на 9 см ниже.

При расчете разницы между числами нужно вычесть. Например, согласно приведенной выше диаграмме рост A +12 см, а рост C +7 см; разница в росте между A и C составляет $12см-(+7см)=12см-7см=5см$. Точно так же мы используем вычитание при сравнении чисел.

Разница высот между A и D рассчитывается следующим образом.

$12-(-9)=12+9=21см$

Следовательно, самый высокий человек на 21 см выше самого маленького.

б. Найдите средний рост четырех человек.

При вычислении среднего роста одним из способов расчета среднего роста является вычисление соответствующих высот от A до D. Если вы вычислите высоту каждой из них, вы получите следующее

	A	B	C	D
Height (cm)	172 cm	156 cm	167 cm	151 cm

After adding the heights from A до D, вы можете разделить высоту на четыре, чтобы получить среднее значение высоты. Но нельзя ли найти среднее более простым способом?

В связи с этим попробуем подсчитать, насколько оно отличается от среднего значения. Как показано ниже, рост четырех человек разный.

A: +12 см
B: -4 см
C: 7 см
D: -9 см

Какова средняя разница в росте между четырьмя людьми? Если сложить разницу в росте между четырьмя людьми, получится следующее.

$12+(-4)+7+(-9)$

$=12-4+7-9=6см$

Общая разница в росте между 4 людьми составляет 6 см. Если разделить общую сумму на количество человек, то можно вычислить среднее значение. Другими словами, мы можем получить среднее значение того, на сколько см выше (или ниже) каждый человек из 160 см.

Если разделить 6 см (общее значение) на 4 человек, получится 6÷4$=1,5см$. Это означает, что средний рост 4 человек на +1,5 см выше 160 см. Следовательно, средний рост 4 человек составляет 161,5 см.

$160+1,5=161,5$

Использование положительных и отрицательных чисел для сложения и вычитания

При изучении отрицательных чисел многие люди путаются; они не понимают, почему существуют значения ниже 0 (ноль).

В каких случаях отрицательное число больше положительного. Применение положительных и отрицательных чисел в жизни человека

Скачать:

Предварительный просмотр:

Правила отрицательных. Сложение отрицательных чисел, правило, примеры

Сложение чисел с разными знаками

Вычитание чисел с разными знаками

Сравнение отрицательных и положительных чисел

Вычитание чисел с разными и отрицательными знаками

Сложение и вычитание чисел с разными знаками

Основное правило сложения натуральных чисел

Сложить два отрицательных числа. Сложение отрицательных чисел: правило, примеры

Правило сложения отрицательных чисел

Примеры сложения отрицательных чисел

Сравнение отрицательных и положительных чисел

Вычитание чисел с разными и отрицательными знаками

Сложение и вычитание чисел с разными знаками

10 важных примеров положительных и отрицательных чисел в реальной жизни

Что отличает отрицательные числа от положительных кроме того, что они (почти) противоположны?

Точка зрения 1

Точка зрения 2

Сноски

Сложение и вычитание / Абсолютное значение ｜ Hatsudy

0 (ноль) используется для обозначения критерия

Положительные целые числа (натуральные числа) и отрицательные целые числа указывают на увеличение или уменьшение от эталона

Как отличить большие и маленькие числа и абсолютные значения

Сложение и вычитание положительных чисел

Использование скобок при сложении положительных чисел

Правила вычитания положительных чисел

Сложение и вычитание отрицательных чисел

Узнайте, как складывать отрицательные числа, заменяя

Почему отрицательное вычитание положительное?

Упражнения: сложение и вычитание положительных и отрицательных чисел

Использование положительных и отрицательных чисел для сложения и вычитания

Добавить комментарий Отменить ответ