Преобразование схем электрических цепей в электротехнике (ТОЭ)
Содержание:
Преобразование схем электрических цепей:
При расчете электрических цепей часто возникает целесообразность преобразования схем этих цепей в более простые и удобные для расчета. Так, при одном или нескольких источниках электрической энергии в ряде случаев удается преобразовать электрическую схему в одноконтурную или в схему с двумя узлами, что весьма упрощает последующий расчет.
Описываемые ниже приемы преобразования схем электрических цепей применимы для цепей постоянного и переменного тока-, ради общности изложения они приводятся в комплексной записи.
Одним из основных видов преобразования электрических схем, часто применяемых на практике, является преобразование схемы со смешанным соединением элементов. Смешанное соединение элементов представляет собой сочетание более простых соединений — последовательного и параллельного, рассмотрению которых и посвящен данный параграф.
На рис. 4-1 изображена ветвь электрической цепи, в которой последовательно включены комплексные сопротивления
Напряжения на отдельных участках цепи обозначены через
По второму закону Кирхгофа
или, что то же,
Сумма комплексных сопротивлений всех последовательно соединенных участков цепи
называется эквивалентным комплексным сопротивлением.
Если мнимые части комплексов
представляют собой сопротивления одинакового характера— индуктивного или емкостного (рис. 4-2), то эквивалентное комплексное сопротивление Z находится в результате
арифметического сложения в отдельности сопротивлений индуктивностей или величин обратных емкостям:
или
где
Ток в цепи равен:
Напряжения на участках цепи, соединенных последовательно, относятся как комплексные сопротивления этих участков: напряжение на k-м участке равно произведению суммарного напряжения на отношение комплексного сопротивления участка к эквивалентному комплексному сопротивлению цепи:
Приведенные выше формулы справедливы при любых значениях
На рис.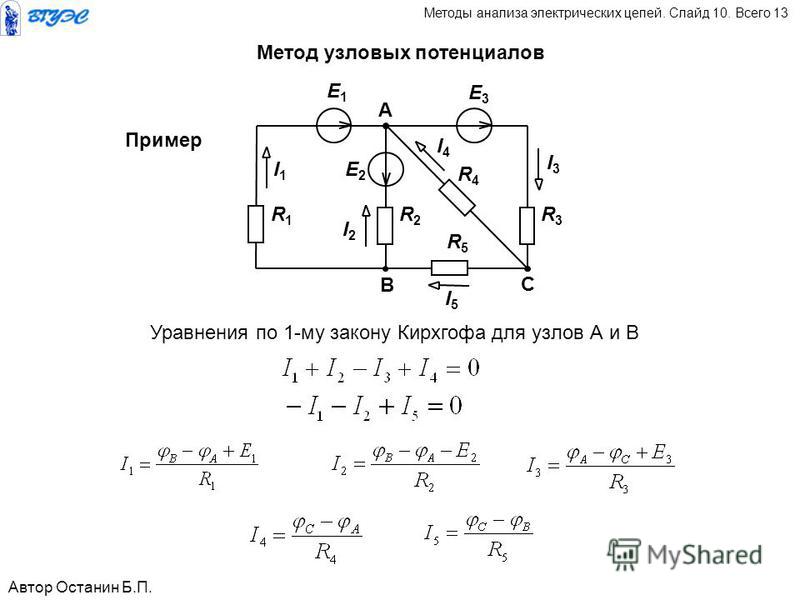 4-3 изображена схема электрической цепи с двумя узлами. Между этими узлами параллельно соединены ветви с комплексными проводимостями Напряжение на всех ветвях одинаковое, равное
4-3 изображена схема электрической цепи с двумя узлами. Между этими узлами параллельно соединены ветви с комплексными проводимостями Напряжение на всех ветвях одинаковое, равное
Токи в ветвях обозначены через
По первому закону Кирхгофа
или, что то же,
Сумма комплексных проводимостей всех ветвей, соединенных параллельно,
называется эквивалентной комплексной проводимостью.
Если мнимые части комплексов представляют собой проводимости одинакового характера — емкостного или индуктивного (рис. 4-4), то эквивалентная
комплексная проводимость Y находится в результате арифметического сложения отдельных активных проводимостей , емкостей или величин обратных индуктивностям:
или
где
Суммарный ток в цепи равен:
Токи в ветвях относятся, как их комплексные проводимости: ток в ветви равен произведению суммарного тока всех ветвей на отношение комплексной проводимости ветви к эквивалентной комплексной проводимости:
Данным выражением особенно удобно пользоваться при n > 2. При этом значения могут быть любыми.
При этом значения могут быть любыми.
В случае параллельного соединения двух ветвей (n = 2) обычно пользуются выражениями, в которые входят сопротивления ветвей; эквивалентное комплексное сопротивление равно: v 1 1 Z,Z2
Токи в параллельных ветвях:
t. e. ток одной из двух параллельных ветвей равен суммарному току, умноженному на сопротивление другой ветви и деленному на сумму сопротивлений обеих ветвей.
Электрические схемы, имеющие смешанное соединение, могут быть преобразованы в более простую электрическую схему путем замены параллельных ветвей одной ветвью и соответственно последовательно соединенных участков цепи — одним участком.
На рис. 4-5 показан пример электрической цепи со смешанным соединением. Эта схема легко приводится к одноконтурной. Первоначально вычисляется эквивалентная комплексная проводимость параллельных ветвей; затем находится величина, обратная проводимости, т.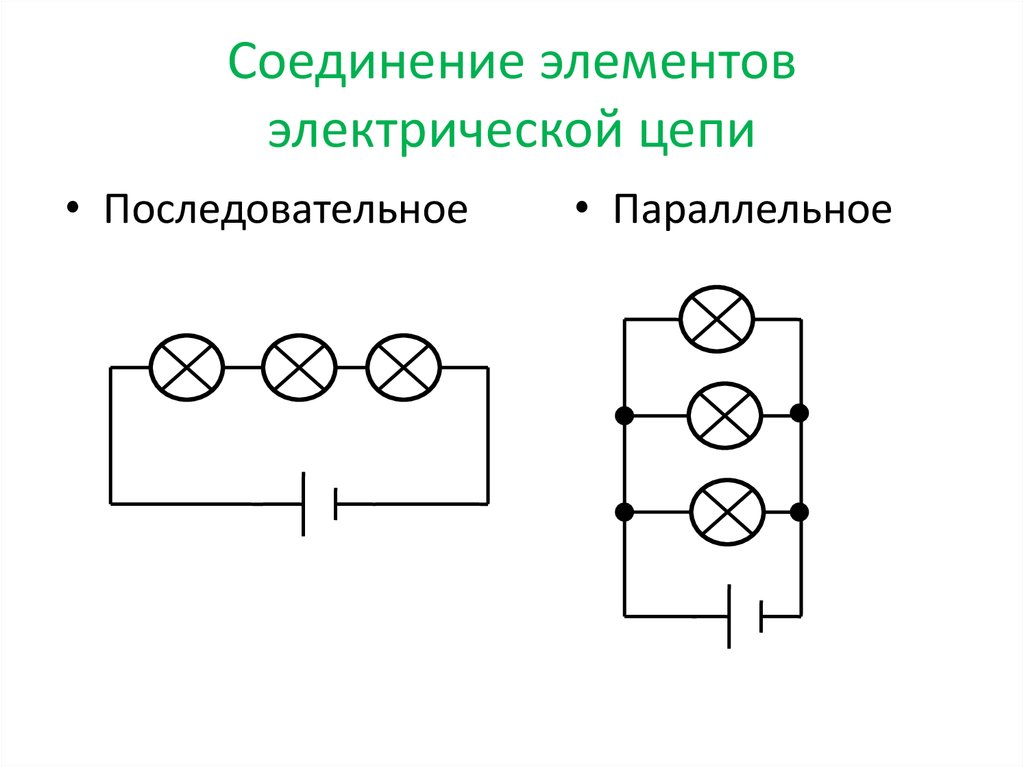 е. общее комплексное сопротивление параллельных ветвей; найденное комплексное сопротивление суммируется с комплексным сопротивлением последовательно включенного участка. Полученное суммарное
е. общее комплексное сопротивление параллельных ветвей; найденное комплексное сопротивление суммируется с комплексным сопротивлением последовательно включенного участка. Полученное суммарное
комплексное сопротивление эквивалентно сопротивлению исходной цепи со смешанным соединением.
Расчетные выражения для рассматриваемого случая будут следующие:
Суммарное комплексное сопротивление всей цепи равно:
а суммарный ток
Токи в ветвях относятся, как комплексные проводимости ветвей:
Таким юбразом, многоконтурная электрическая схема со смешанным соединением приводится к одноконтурной,
имеющей суммарное комплексное сопротивление Z или соответственно суммарную комплексную проводимость Y. Распределение токов и напряжений в смешанной цепи подчиняется правилам, указанным в предыдущем параграфе.
Описанный выше порядок преобразования схемы и нахождения распределения токов принципиально применим и для так называемой цепной схемы, показанной на рис.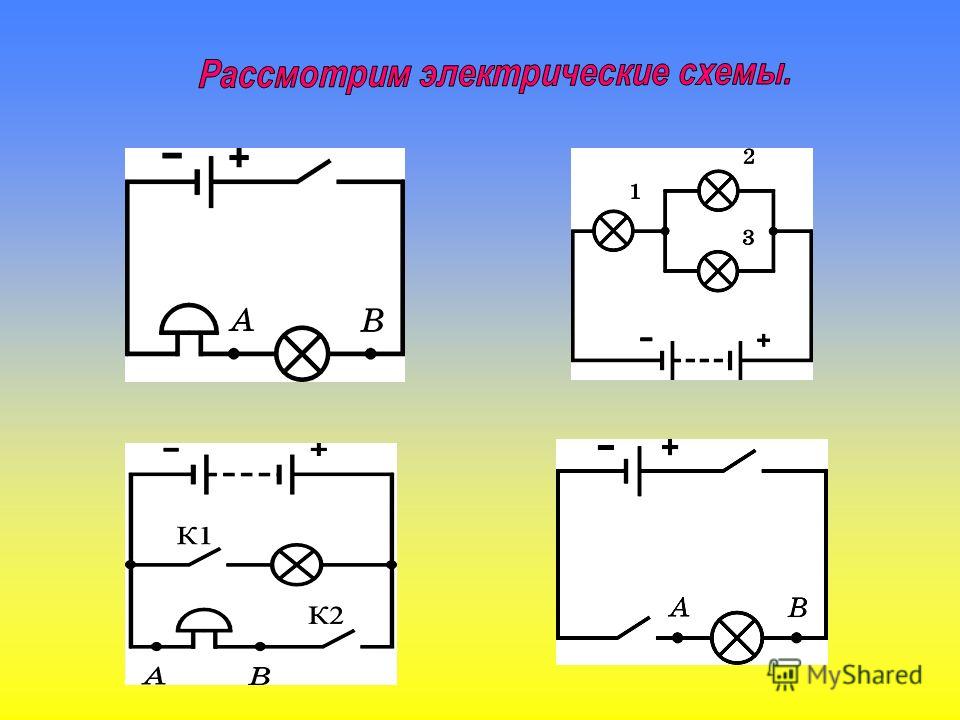 4-6. Просуммировав комплексные сопротивления в последней ветви, найдем комплексную проводимость ветви, которую алгебраически сложим с и получим суммарную комплексную проводимость двух последних ветвей; вычислив обратную величину, т. е. комплексное сопротивление, прибавим к ней Продолжая
4-6. Просуммировав комплексные сопротивления в последней ветви, найдем комплексную проводимость ветви, которую алгебраически сложим с и получим суммарную комплексную проводимость двух последних ветвей; вычислив обратную величину, т. е. комплексное сопротивление, прибавим к ней Продолжая
таким образом дальше, получим в итоге результирующее комплексное сопротивление цепи и соответственно суммарный ток который может быть путем последовательных вычислений распределен между всеми ветвями сложной цепи.
Однако такой способ расчета цепной схемы является достаточно трудоемким и утомительным. Более целесообразно в этом случае воспользоваться другим методом, который известен под названием метода подобия или единичного тока.
Задавшись током в последней ветви, равным единице находим напряжение на комплексном сопротивлении равное При этом ток .
Следовательно,
Прибавив к напряжению на падение напряжения от тока в комплексном сопротивлении получим напряжение на Продолжая таким образом дальше, найдем в конечном итоге ток и напряжение Ввиду того что ток был произвольно выбран равным единице, полученное напряжение не будет равно заданному напряжению на выводах цепи.
Эквивалентные участки цепи с последовательным и параллельным соединениями
Обозначим комплексное сопротивление участка цепи, состоящего из двух последовательно соединенных элементов, через Комплексная проводимость данного участка цепи равна причем активная и реактивная проводимости:
Если два элемента с проводимостями g и b, вычисленными по этим формулам, соединить параллельно, то суммарная комплексная проводимость будет равна Y и соответственно комплексное сопротивление будет равно Z,
Такие две цепи с последовательным и параллельным соединениями, имеющие одинаковые сопротивления на выводах, называются эквивалентными.
Ввиду того что реактивное сопротивление х, входящее в расчетные формулы, в общем случае зависит от частоты, условие эквивалентности этих цепей выполняется только при той частоте, для которой вычислено х.
Пусть, например, задана схема с последовательным соединением сопротивления и индуктивности (рис. 4-7, а). Преобразуем ее в схему с параллельным соединением элементов (рис. 4-7, б).
Активная и реактивная проводимости исходной цепи:
Из условия эквивалентности цепей следует, что параметры новой цепи будут:
Вычислив по этим формулам получим схему цепи, эквивалентной исходной при данной частоте При других значениях частоты параметры будут иметь другие значения, следовательно эквивалентность цепей нарушится.
При например, при достаточно высокой частоте:
Если исходной является схема рис. 4-7, б и заданными параметрами являются то параметры эквивалентной цепи (рис. 4-7, а) определятся из выражений:
Из полученных выражений видно, что числовые значения эквивалентной цепи зависят от частоты.
Условия эквивалентности для цепей с последовательным и параллельным соединением сопротивления и емкости имеют вид:
При достаточно высокой частоте и тогда
Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи
сохраняются неизменными.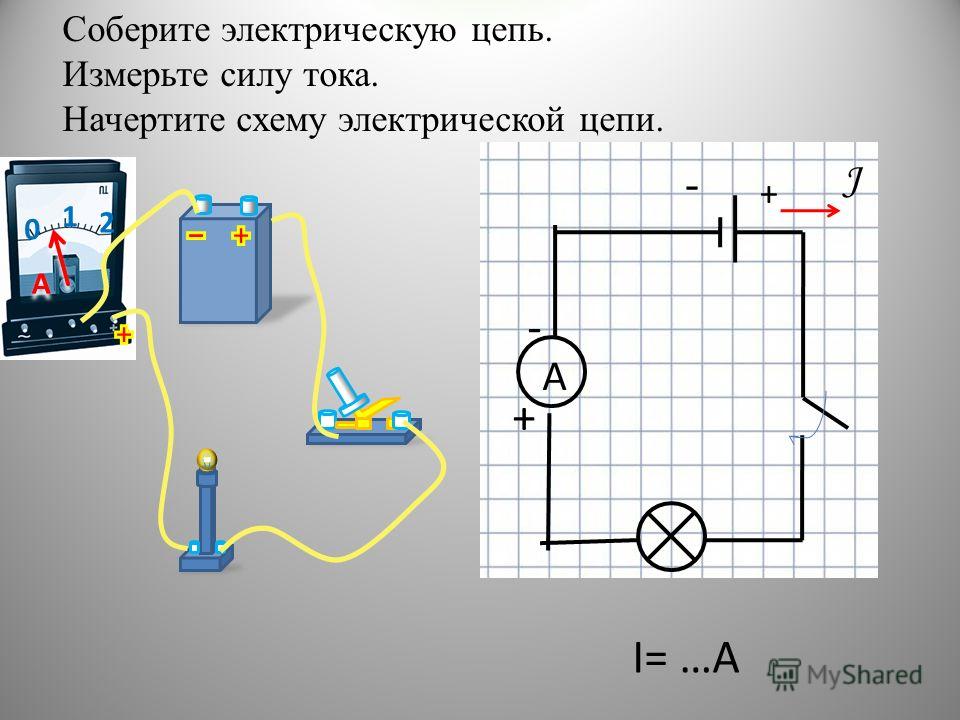 Иначе говоря, эквивалентность треугольника и звезды понимается в том смысле, что при одинаковых напряжениях между одноименными выводами токи, входящие в одноименные выводы, одинаковы. Это равносильно тому, что мощности в этих цепях одинаковы.
Иначе говоря, эквивалентность треугольника и звезды понимается в том смысле, что при одинаковых напряжениях между одноименными выводами токи, входящие в одноименные выводы, одинаковы. Это равносильно тому, что мощности в этих цепях одинаковы.
На рис. 4-8 показан случай, когда преобразование треугольника в эквивалентную звезду дает возможность преобразовать многоконтурную схему в одноконтурную.
Для вывода расчетных выражений, служащих для преобразования треугольника в эквивалентную звезду, ниже приняты следующие обозначения (рис. 4-9):
- — сопротивления сторон треугольника;
- — сопротивления лучей звезды;
- — токи, подходящие к выводам 1, 2, 3\
- — Токи в ветвях треугольника.
Выразим токи в ветвях треугольника через приходящие токи.
По второму закону Кирхгофа сумма напряжений в контуре треугольника равна нулю:
По первому закону Кирхгофа для узлов 2 и 1
Решение этих уравнений относительно Дает:
Напряжение между выводами 1 и 2 схемы рис. 4-9, а будет:
4-9, а будет:
a в схеме рис. 4-9, б оно равно:
Для эквивалентности необходимо равенство напряжений при всяких токах
Это возможно при условии:
Третье выражение получается в результате круговой замены индексов.
Итак, комплексное сопротивление луча звезды равно произведению комплексных сопротивлений прилегающих сторон треугольника, деленному на сумму комплексных сопротивлений трех сторон треугольника.
Выше было получено выражение для тока в стороне 1—2 треугольника в зависимости от токов Круговой заменой индексов можно получить токи в двух других сторонах треугольника:
В расчетах также возникает необходимость замены звезды эквивалентным треугольником. На рис. 4-10 показан, например, случай, когда такая замена позволяет
преобразовать сложную электрическую схему в одноконтурную.
При переходе от звезды к треугольнику заданными являются сопротивления звезды Выражения для искомых сопротивлений треугольника находятся в результате совместного решения трех уравнений (4-1).
Деление третьего уравнения на первое, а затем на второе дает:
Выражая отсюда и подставляя их в первое уравнение (4-1), получим:
откуда
Аналогично круговой заменой индексов получим:
И
Отедовательно, комплексное сопротивление стороны треугольника равно сумме комплексных сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.
Токи в лучах звезды легко выражаются через токи в сторонах треугольника. С учетом положительных направлений на рис. 4-9 имеем:
Два разнородных источника электрической энергии — источник э. д. с. и источник тока — считаются эквивалентными,, если при замене одного источника другим токи и напряжения во внешней электрической цепи, с которой эти источники соединяются, остаются неизменными. На рис. 4-11 изображены эквивалентные источники тока, посылающие во внешнюю цепь ток и поддерживающие на своих выводах одинаковое напряжение
Условием эквивалентности источников, именуемым в дальнейшем правилом об эквивалентных источниках э. д.с. и тока, служит следующее соотношение между э. д. с. Ё источника э. д. с. и током
д.с. и тока, служит следующее соотношение между э. д. с. Ё источника э. д. с. и током
источника тока:
где Z — внутреннее комплексное сопротивление как источника э. д. с., так и источника тока.
Действительно, напряжение на источнике э. д. с. получается в результате вычитания из э. д. с. падения напряжения от тока в комплексном сопротивлении Z источника (рис. 4-11, а).
Соответственно напряжение на источнике тока при том же токе посылаемом во внешнюю цепь, равно падению напряжения от тока в комплексном сопротивлении Z источника (рис. 4-11,6).
В обоих случаях напряжения на выводах обоих источников одинаковы:
т. е. получается условие (4-3), не зависящее от тока нагрузки.
При отсоединении эквивалентных источников э. д. с.
и тока от внешней цепи напряжение на выводах обоих источников равно Ё. Именно это обстоятельство и равенство внутренних комплексных сопротивлений обоих источников и обеспечивают их эквивалентность при любом режиме работы.
Следует заметить, что мощности, расходуемые во внутренних сопротивлениях эквивалентных источников э. д. с. и тока, неодинаковы. В первом случае полная мощность, расходуемая в источнике, равна во втором случае
Например, при отсоединении источников от внешней цепи в первом случае мощность в источнике не расходуется, а во втором случае она составляет
Поэтому эквивалентность источников следует понимать только в смысле неизменности токов, напряжений и мощностей во внешней электрической цепи, присоединенной к источникам.
Если внутреннее сопротивление источника э. д. с. равно нулю, то непосредственное применение формулы (4-3) для нахождения эквивалентного источника тока по, заданной э. д. с. источника не представляется возможным. В таких случаях сопротивление внешней цепи, включенной последовательно с э. д. с., можно рассматривать в качестве внутреннего сопротивления источника, что позволит применить формулу (4-3).
В случае сложной электрической цепи замена источника э.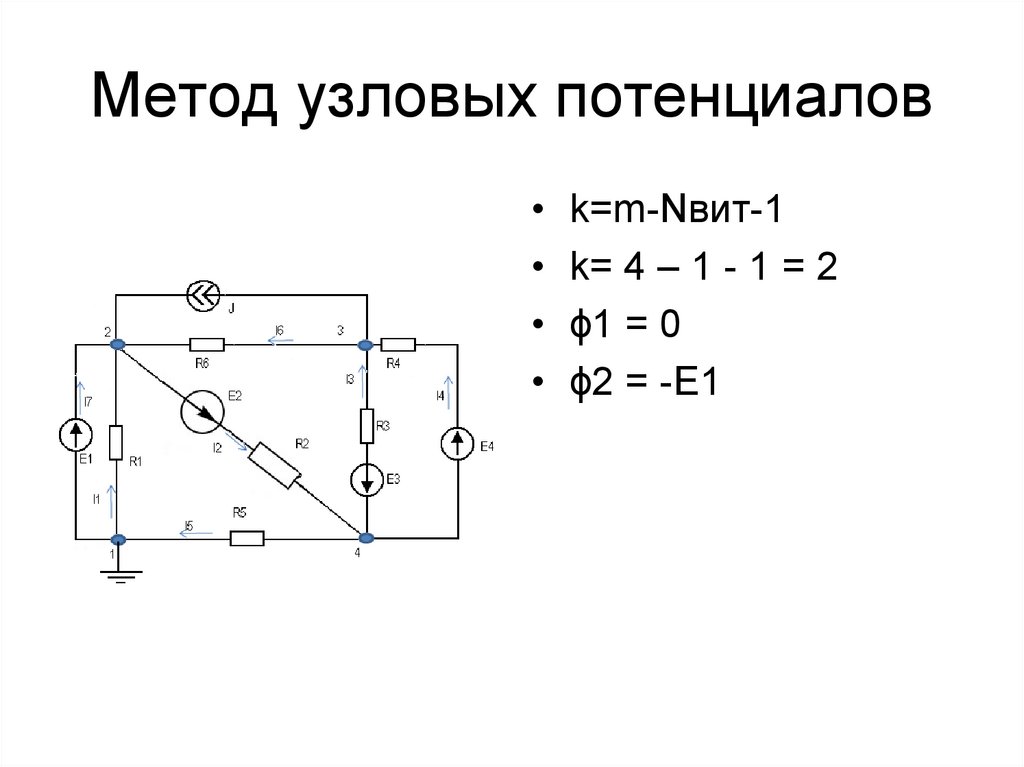 д. с. эквивалентным источником тока или обратно может иногда упростить расчет.
д. с. эквивалентным источником тока или обратно может иногда упростить расчет.
Целесообразность такой замены проиллюстрирована, в частности, в следующем параграфе.
Применим правило об эквивалентных источниках э. д. с. и тока к преобразованию схемы с параллельным соединением n ветвей, содержащих источники э. д. с. (рис. 4-12, а).
Заменяя заданные источники э. д. с. источниками тока, получаем схему рис. 4-12, б. Источники тока в совокупности образуют эквивалентный источник тока (рис. 4-12, в), причем
и
Пользуясь этим соотношением, можно в конечном итоге перейти от схемы рис. 4-12, в к схеме рис. 4-12, s, являющейся эквивалентом исходной схемы рис. 4-21, а. Здесь
Таким образом, n параллельных ветвей с источниками э. д. с. между двумя узлами могут быть заменены одним источником тока (рис. 4-12, в) или источником э. д. с. (рис. 4-12, s).
Ток во внешней цепи (в ветви с сопротивлением равен:
Напряжение между двумя узлами находится по формуле
Выведенные здесь выражения широко используются для расчета электрических цепей с двумя узлами, а также более сложных цепей, приводящихся к двум узлам.
Расчет электрической цепи облегчается в ряде случаев в результате переноса в схеме источников э. д. с. или тока. Как это видно из уравнений Кирхгофа, токи в схеме определяются заданными величинами суммарных э. д. с. в контурах независимо от того, из каких отдельных слагающих они состоят. Поэтому изменение расположения в схеме источников э. д. с., при котором суммарные э. д. с. во всех контурах сохраняются неизменными, не влияет на токи в ветвях. Аналогично напряжения на ветвях определяются заданными суммарными токами источников тока в узлах, и поэтому изменение расположения в схеме источников тока, при котором их суммарные токи во всех узлах сохраняются неизменными, не влияет на напряжения в схеме.
Если, например, требуется исключить источник э. д. с. из какой-либо ветви, то в данную ветвь вводится компенсирующая э. д. с., причем точно такая же э. д. с. вводится одновременно во все остальные ветви, сходящиеся
в одном из узлов данной ветви.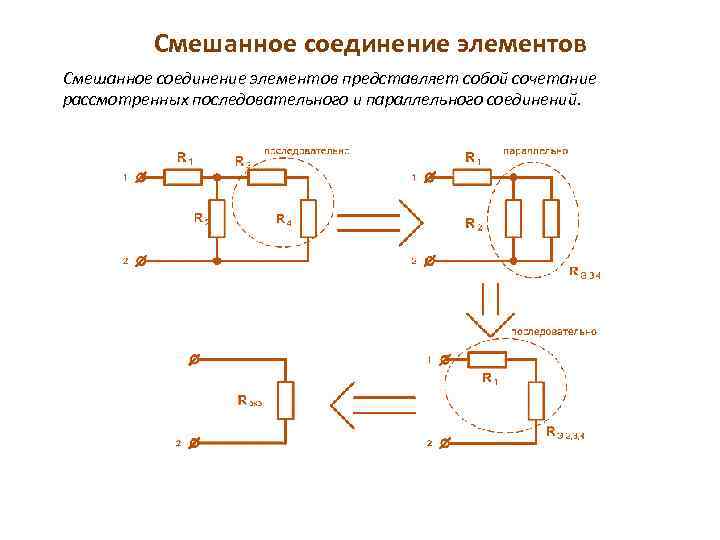 Компенсирующая и дополнительные э. д. с. имеют одинаковое направление по отношению к рассматриваемому узлу. В результате этого источник э. д. с. из ветви исключается и появляются источники э. д. с. в других ветвях схемы. Суммарные э. д. с. во всех контурах и соответственно токи в ветвях остаются прежними.
Компенсирующая и дополнительные э. д. с. имеют одинаковое направление по отношению к рассматриваемому узлу. В результате этого источник э. д. с. из ветви исключается и появляются источники э. д. с. в других ветвях схемы. Суммарные э. д. с. во всех контурах и соответственно токи в ветвях остаются прежними.
Итак, источник э. д. с. может быть перенесен из какой-либо ветви схемы во все другие ветви, присоединенные к узлу данной ветви, без изменения токов в схеме.
Справедливо и обратное положение: если во всех ветвях, кроме одной, сходящихся в узле, имеются одинаковые источники э. д. с. (рис. 4-13, а), направленные все к одному узлу или все от узла, то они могут быть заменены одним источником э. д. с. в ветви, в которой источник отсутствовал (рис. 4-13, б).
Это положение подтверждается тем, что суммарные э. д. с. в контурах схем на рис. 4-13, а и б одинаковы.
Имеется и другое доказательство данного положения: ввиду равенства э. д. с. всех источников вторые выводы
их могут быть объединены, как имеющие одинаковый потенциал.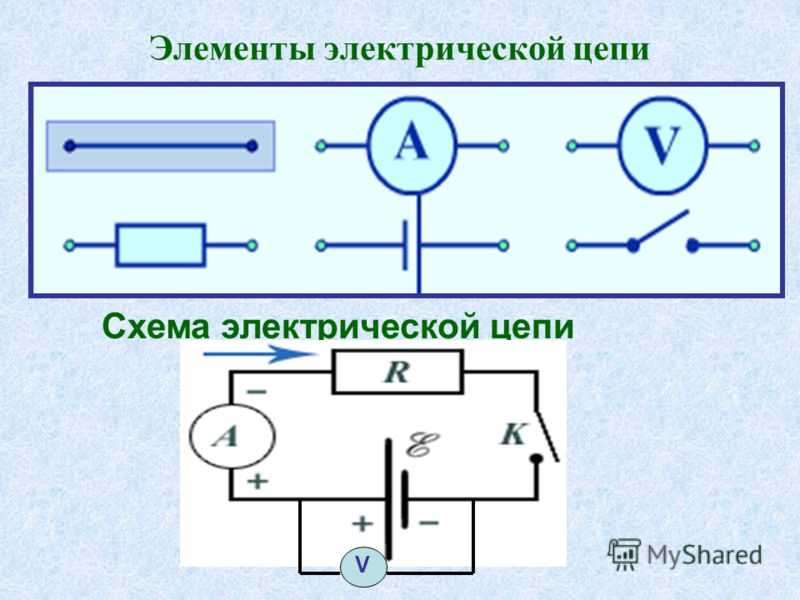 В результате такого объединения, показанного на рис. 4-13, а пунктиром, получается схема рис. 4-13, б.
В результате такого объединения, показанного на рис. 4-13, а пунктиром, получается схема рис. 4-13, б.
В случае переноса источников тока они присоединяются к узлам схемы так, чтобы оставались неизменными их суммарные токи в узлах.
Так, например, несмотря на то, что источники тока размещены в схемах рис.
4-14, а и б различно, суммарные токи источников в узлах обеих схем одинаковы. Поэтому и напряжения между узлами не изменились.
Итак, источник тока может быть заменен источниками тока, подключенными. параллельно всем
ветвям, которые составляли контур с рассматриваемым источником.
• Перенос источников в схеме успешно сочетается на практике с различными методами преобразований и расчетов (см. пример 4-1).
Пример 4-1.
Вычислить ток в диагональной ветви мостовой схемы рис. 4-15, а.
Дано:
Заданный источник тока может быть заменен двумя источниками, подключенными параллельно сопротивлениям (рис. 4-15, б). Пользуясь условием эквивалентности источников э, д, с, и тока, получаем схему рис, 4-15, в с двумя узлами. По формуле (4-4) напряжение на ветви равно
Пользуясь условием эквивалентности источников э, д, с, и тока, получаем схему рис, 4-15, в с двумя узлами. По формуле (4-4) напряжение на ветви равно
В. Искомый ток
Преобразование симметричных схемСхема электрической цепи, в которой имеется ось симметрии, называется симметричной. Например, схема рис. 4-16, а симметрична относительно вертикальной оси. В симметричных схемах легко выявляются точки или узлы с одинаковым потенциалом. В ветвях, присоединенных к таким узлам, токи равны нулю. Поэтому эти ветви
можно разрезать, не нарушая распределения токов и напряжений в схеме. Точки, имеющие одинаковый потенциал, могут быть объединены. Рассечение ветвей, по которым не проходит ток, и объединение точек равного потенциала упрощают схему и облегчают расчет.
Так, в симметричной схеме рис. 4-16, б токи в соединениях, пересекающих ось симметрии, отсутствуют. Разрезав схему по оси симметрии, получим с обеих сторон одноконтурную схему рис. 4-16, в, которая легко рассчитывается.
4-16, в, которая легко рассчитывается.
Допустим теперь, что полярность источников в симметричной схеме неодинакова (рис. 4-17, а). В этом случае (равенство э. д. с. источников и различие их полярности) токи в симметричных ветвях (например, и напряжения между соответствующими парами выводов, симметрично расположенными относительно оси, равны и противоположны по знаку. Отсюда следует, что напряжения между всеми точками, лежащими на оси симметрии, равны нулю Поэтому все точки схемы на оси симметрии могут быть замкнуты накоротко (рис. 4-17, б).
Таким образом, расчет сложных симметричных схем приводится к расчету более простых схем.
На рис. 4-18, а и б показана симметричная мостовая схема, имеющая две оси симметрии — вертикальную и
горизонтальную. В продольных ветвях ток отсутствует; потенциалы средних точек поперечных (перекрещенных) ветвей одинаковы.
Поэтому продольные ветви могут быть рассечены, а средние точки поперечных ветвей — объединены. В результате с обеих сторон получится одноконтурная схема (рис. 4-18, в), расчет которой крайне прост.
В результате с обеих сторон получится одноконтурная схема (рис. 4-18, в), расчет которой крайне прост.
Если изменить полярность одного из источников (рис. 4-19, а), то роли продольных и поперечных ветвей поменяются и преобразованная часть схемы примет вид, показанный на рис. 4-19, б.
В разобранных выше примерах э. д. с. источников были равны. В случае неравенства э. д. с. источников преобразование симметричной схемы удобно сочетается с методом наложения (см. пример 7-5).
Помогаю с учёбой — Преподаватель Анна Евкова
Рада видеть вас на моем сайте. Если вы здесь – значит, вам необходима помощь с учебой. |
Я, Анна Евкова, бывший преподаватель Самарского института информатики и вычислительной техники и моя команда преподавателей поможем вам справиться с трудностями в заданиях. Мы поможем с любым заданием от простого заказа в одну формулу, или если у вас будет заказ на написание большой работы примерно на 198 страниц — мы это тоже умеем!
Я всегда в вашем смартфоне, заказывайте где удобно и когда удобно — просто прислав файлы в Telegram!
Все заказы выполняются качественно, профессионально и высылаются раньше срока. Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Подготовимся онлайн совместно со мной или с преподавателем из моей команды, проработаем базовые темы, освоим сложные разделы, отработаем экзаменационные задания и подойдём к сдаче любого предмета максимально подготовленным и расскажем все секреты.
Лучшие университеты мира: МГУ и MIT
Моя видео презентация:
Пять простых шагов и всё будет на ❝отлично❞
Шаг 1. Сфотографируйте задание так, чтобы изображение было максимально четким. В чат прикрепите необходимые для выполнения вашей работы, лекции, учебники, методички и т.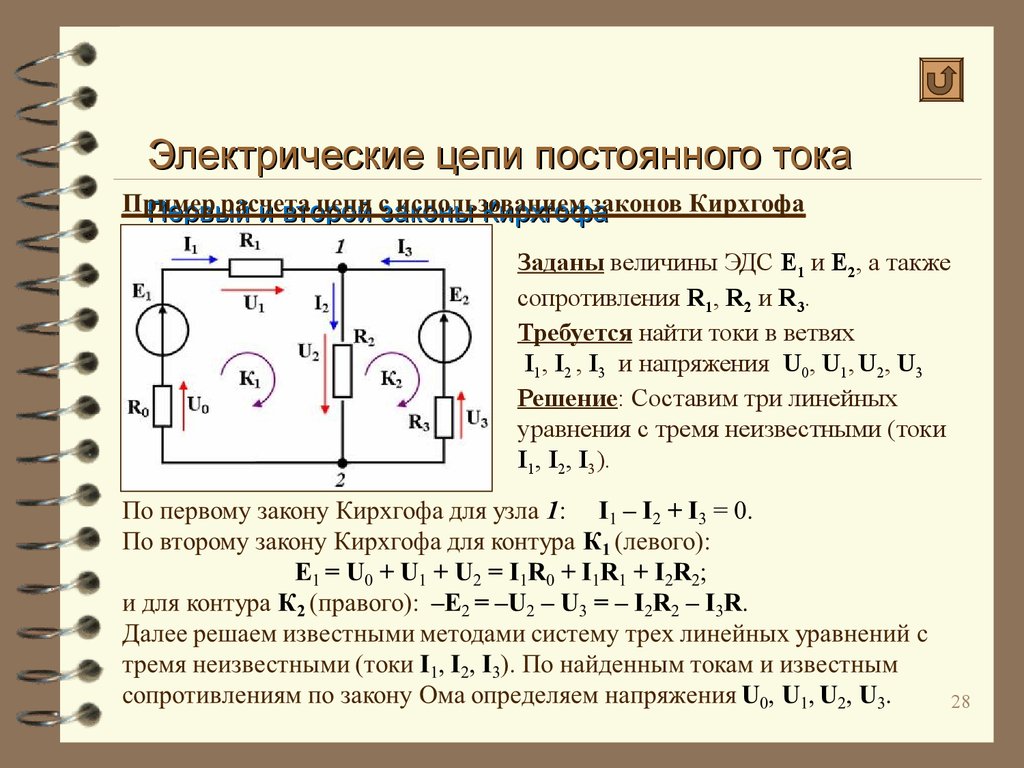 д. (если имеются). При необходимости напишите дополнительные пояснения.
д. (если имеются). При необходимости напишите дополнительные пояснения.
Шаг 2. Все файлы пришлите мне в чат в Telegram.
После этого я изучу и оценю. (Не забывайте чем больше времени, тем меньше цена!)
Шаг 3. Если всё понравится — оплатите. Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Шаг 4. Приступаю к работе. Все необходимые требования и сроки будут соблюдены. Более 78% заказов отправляются в чат раньше указанного времени.
Шаг 5. Получаете заказ в чат. Если у вас возникнут вопросы, я подробно отвечу. Гарантия на заказ действует 1 год. В течение этого времени ошибки в заказе будут исправлены.
ТОП 5 ответов на ваши вопросы
Как вы работаете?
Для того, чтобы разобраться с этим вопросом, предлагаю ознакомиться с простым алгоритмом:
- Вы присылаете необходимые файлы с описанием в Telegram.

- Я знакомлюсь с файлами, и оцениваю заказ.
- Вы оплачиваете заказ.
- Я, или преподаватель, начинаем работу над заказом.
- В согласованный срок, или раньше, Вы получаете свою работу файлом в чат.
Какая будет цена?
Невозможно ответить на этот вопрос не изучив файлы. Стоимость определяется исходя из нескольких важных факторов: уровень сложности задания, определенные требования к оформлению.
Для точной оценки стоимости присылайте файлы в чат в Telegram. Например: лекции, методички, учебники (если такие имеются).
Какой срок выполнения?
Минимальный срок выполнения заказа варьируется от 2 до 4 дней. Главное помнить, что для срочных заказов цена будет увеличиваться, а срок выполнения сокращаться.
Как происходит оплата?
Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Какие гарантии?
Любые ошибки, допущенные мной или преподавателем в заказе, исправим в течении 1 года.
Что обо мне говорят студенты и школьники
Разместила отзывы с Ютуба и чуть ниже с Вконтакте, остальные отзывы на моём ютуб канале и социальных сетях.
youtube.com/embed/vtUKcvDOhBs»> youtube.com/embed/cBeKupGTino»>
Правовые документы:
Условия использования
Политика конфиденциальности
Помогаю с учёбой — Преподаватель Анна Евкова
Рада видеть вас на моем сайте. Если вы здесь – значит, вам необходима помощь с учебой. |
Я, Анна Евкова, бывший преподаватель Самарского института информатики и вычислительной техники и моя команда преподавателей поможем вам справиться с трудностями в заданиях. Мы поможем с любым заданием от простого заказа в одну формулу, или если у вас будет заказ на написание большой работы примерно на 198 страниц — мы это тоже умеем!
Я всегда в вашем смартфоне, заказывайте где удобно и когда удобно — просто прислав файлы в Telegram!
Все заказы выполняются качественно, профессионально и высылаются раньше срока. Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Подготовимся онлайн совместно со мной или с преподавателем из моей команды, проработаем базовые темы, освоим сложные разделы, отработаем экзаменационные задания и подойдём к сдаче любого предмета максимально подготовленным и расскажем все секреты.
Лучшие университеты мира: МГУ и MIT
Моя видео презентация:
Пять простых шагов и всё будет на ❝отлично❞
Шаг 1. Сфотографируйте задание так, чтобы изображение было максимально четким. В чат прикрепите необходимые для выполнения вашей работы, лекции, учебники, методички и т. д. (если имеются). При необходимости напишите дополнительные пояснения.
д. (если имеются). При необходимости напишите дополнительные пояснения.
Шаг 2. Все файлы пришлите мне в чат в Telegram.
После этого я изучу и оценю. (Не забывайте чем больше времени, тем меньше цена!)
Шаг 3. Если всё понравится — оплатите. Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Шаг 4. Приступаю к работе. Все необходимые требования и сроки будут соблюдены. Более 78% заказов отправляются в чат раньше указанного времени.
Шаг 5. Получаете заказ в чат. Если у вас возникнут вопросы, я подробно отвечу. Гарантия на заказ действует 1 год. В течение этого времени ошибки в заказе будут исправлены.
ТОП 5 ответов на ваши вопросы
Как вы работаете?
Для того, чтобы разобраться с этим вопросом, предлагаю ознакомиться с простым алгоритмом:
- Вы присылаете необходимые файлы с описанием в Telegram.

- Я знакомлюсь с файлами, и оцениваю заказ.
- Вы оплачиваете заказ.
- Я, или преподаватель, начинаем работу над заказом.
- В согласованный срок, или раньше, Вы получаете свою работу файлом в чат.
Какая будет цена?
Невозможно ответить на этот вопрос не изучив файлы. Стоимость определяется исходя из нескольких важных факторов: уровень сложности задания, определенные требования к оформлению.
Для точной оценки стоимости присылайте файлы в чат в Telegram. Например: лекции, методички, учебники (если такие имеются).
Какой срок выполнения?
Минимальный срок выполнения заказа варьируется от 2 до 4 дней. Главное помнить, что для срочных заказов цена будет увеличиваться, а срок выполнения сокращаться.
Как происходит оплата?
Оплатить можно с помощью баланса мобильного телефона, картой Visa и MasterCard, а также через Apple Pay и Google Pay.
Какие гарантии?
Любые ошибки, допущенные мной или преподавателем в заказе, исправим в течении 1 года.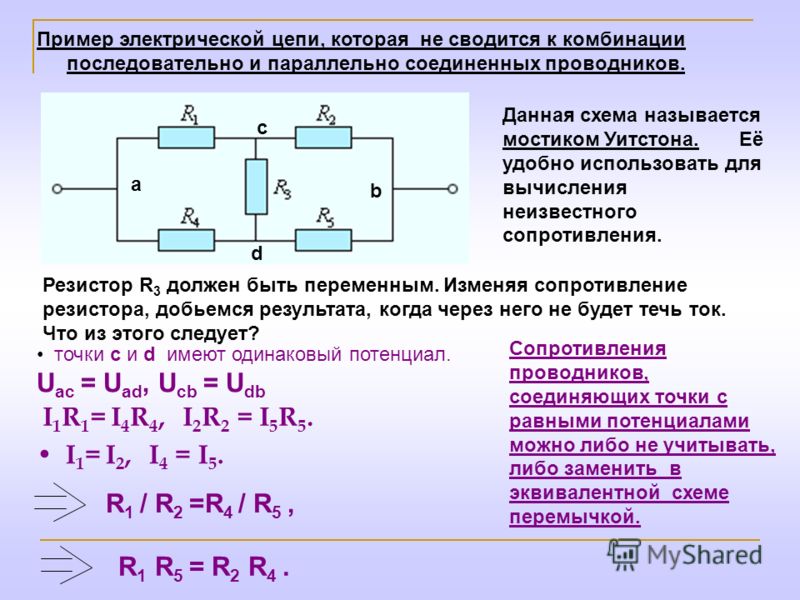
Что обо мне говорят студенты и школьники
Разместила отзывы с Ютуба и чуть ниже с Вконтакте, остальные отзывы на моём ютуб канале и социальных сетях.
youtube.com/embed/vtUKcvDOhBs»> youtube.com/embed/cBeKupGTino»>
Правовые документы:
Условия использования
Политика конфиденциальности
Символы электрических цепей и принципиальные схемы
До сих пор в этом разделе учебника «Класс физики» основное внимание уделялось ключевым компонентам электрической цепи, а также понятиям разности электрических потенциалов, тока и сопротивления. Концептуальное значение терминов было введено и применено к простым схемам. Были обсуждены математические отношения между электрическими величинами и смоделировано их использование при решении задач. Урок 4 будет посвящен способам соединения двух или более электрических устройств в электрическую цепь. Наше обсуждение будет развиваться от простых схем к относительно сложным схемам.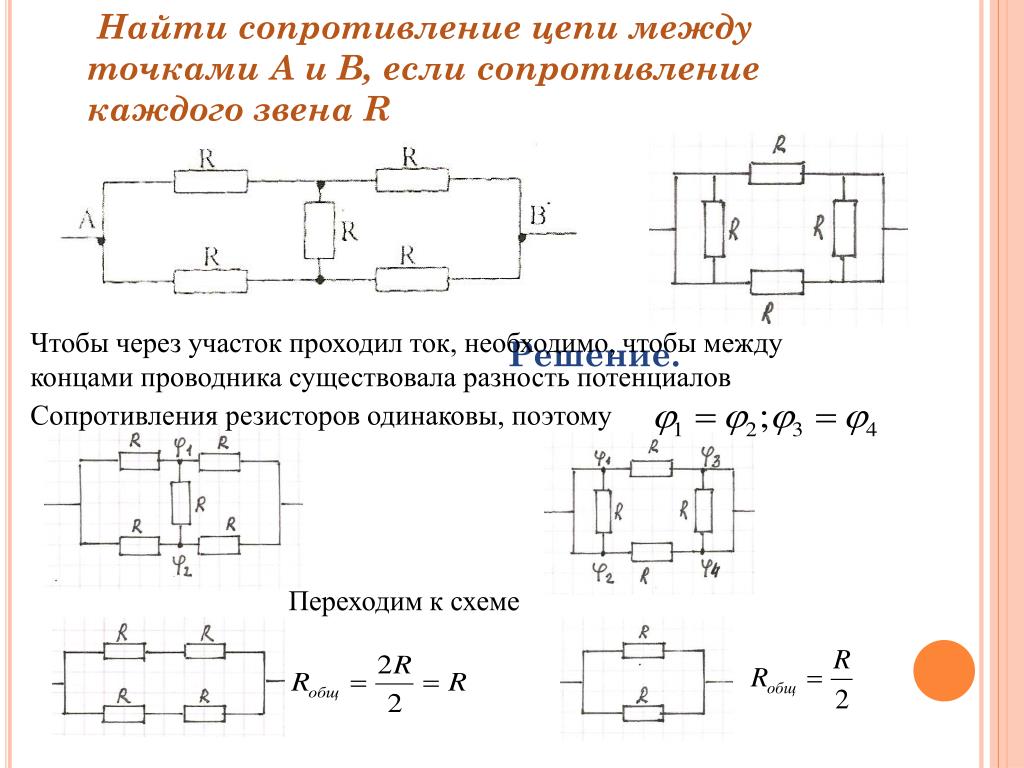 К этим сложным цепям будут применяться прежние принципы разности электрических потенциалов, тока и сопротивления, и для их анализа будут использоваться те же математические формулы.
К этим сложным цепям будут применяться прежние принципы разности электрических потенциалов, тока и сопротивления, и для их анализа будут использоваться те же математические формулы.
Электрические цепи, простые или сложные, могут быть описаны различными способами. Электрическая цепь обычно описывается простыми словами. Сказать что-то вроде «Лампочка подключена к D-элементу» — достаточное количество слов, чтобы описать простую схему. Во многих случаях в уроках с 1 по 3 слова использовались для описания простых схем. Услышав (или прочитав) слова, человек привыкает быстро представлять схему в уме. Но еще один способ описать схему — просто нарисовать ее. Такие рисунки обеспечивают более быстрое мысленное представление фактической схемы. Чертежи электрических цепей, подобные приведенному ниже, многократно использовались в уроках с 1 по 3.
«Схема содержит лампочку и 1,5-вольтовый D-элемент. |
Последним средством описания электрической цепи является использование обычных символов цепи для создания принципиальной схемы цепи и ее компонентов. Некоторые символы цепей, используемые на принципиальных схемах, показаны ниже.
Отдельный элемент или другой источник питания представлен длинной и короткой параллельными линиями. Набор элементов или аккумуляторов представлен набором длинных и коротких параллельных линий. В обоих случаях длинная линия представляет собой положительный вывод источника энергии, а короткая линия представляет собой отрицательный вывод. Прямая линия используется для обозначения соединительного провода между любыми двумя компонентами цепи. Электрическое устройство, оказывающее сопротивление потоку заряда, обычно называется резистором и изображается зигзагообразной линией.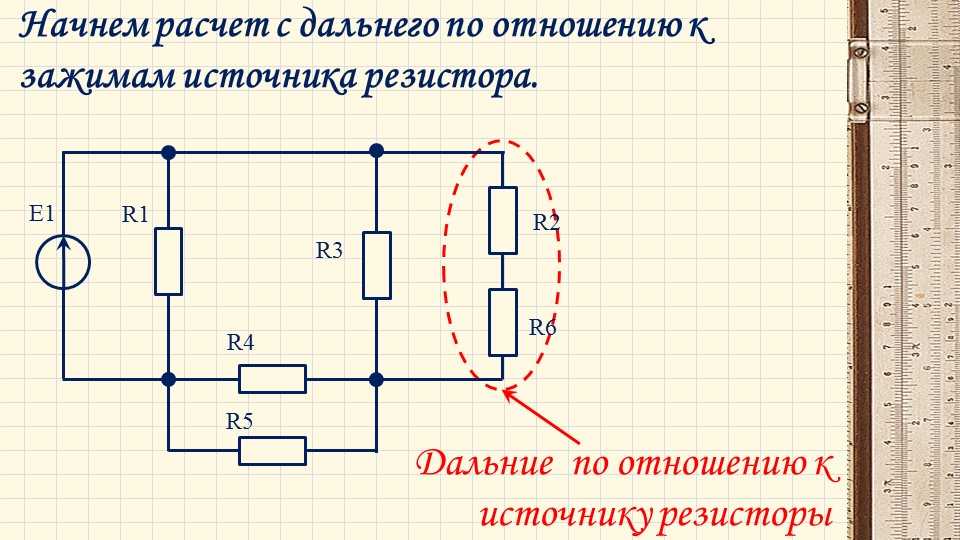 Открытый переключатель обычно представляет собой разрыв прямой линии на подъем части линии вверх по диагонали. Эти символы цепей будут часто использоваться в оставшейся части урока 4, поскольку электрические цепи представлены схематическими диаграммами. Важно либо запомнить эти символы, либо часто обращаться к этому короткому списку, пока вы не привыкнете к их использованию.
Открытый переключатель обычно представляет собой разрыв прямой линии на подъем части линии вверх по диагонали. Эти символы цепей будут часто использоваться в оставшейся части урока 4, поскольку электрические цепи представлены схематическими диаграммами. Важно либо запомнить эти символы, либо часто обращаться к этому короткому списку, пока вы не привыкнете к их использованию.
В качестве иллюстрации использования электрических символов на принципиальных схемах рассмотрим следующие два примера.
Пример 1:
Описание со словами: Три D-элемента помещены в батарейный блок для питания цепи, содержащей три лампочки.
Используя словесное описание, можно получить ментальную картину описываемой цепи. Это словесное описание может быть затем представлено рисунком трех ячеек и трех лампочек, соединенных проводами. Наконец, символы схемы, представленные выше, могут использоваться для представления одной и той же схемы.Обратите внимание, что три набора длинных и коротких параллельных линий использовались для представления аккумуляторной батареи с тремя D-ячейками. И обратите внимание, что каждая лампочка представлена своим индивидуальным символом резистора. Прямые линии использовались для соединения двух клемм батареи с резисторами и резисторов друг с другом.
Приведенные выше схемы предполагали, что три лампочки были соединены таким образом, что заряд, протекающий по цепи, последовательно проходил через каждую из трех лампочек. Путь положительного пробного заряда, покидающего положительный полюс батареи и пересекающего внешнюю цепь, должен проходить через каждую из трех подключенных лампочек, прежде чем вернуться к отрицательному полюсу батареи. Но разве только так можно соединить три лампочки? Должны ли они быть подключены последовательно, как показано выше? Точно нет! Фактически приведенный ниже пример 2 содержит одно и то же словесное описание, но рисунок и принципиальные схемы выполнены по-разному.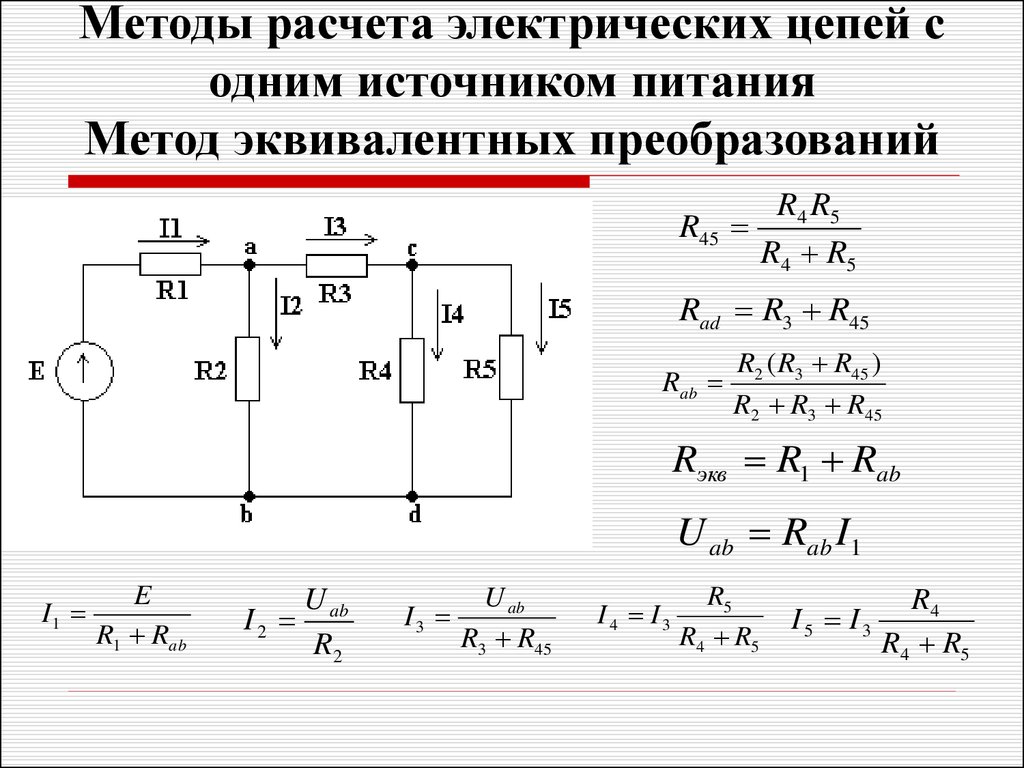
Пример 2:
Описание со словами: Три D-элемента помещены в батарейный блок для питания цепи, содержащей три лампочки.
Используя словесное описание, можно получить ментальную картину описываемой цепи. Но на этот раз соединения лампочек выполняются таким образом, чтобы на схеме была точка, где провода ответвляются друг от друга. Место разветвления упоминается как узел . Каждая лампочка помещается в свою отдельную ветку. Эти ответвления в конечном итоге соединяются друг с другом, образуя второй узел. Один провод используется для подключения этого второго узла к отрицательной клемме аккумулятора.
Эти два примера иллюстрируют два распространенных типа соединений в электрических цепях. Когда в цепи присутствует два или более резистора, их можно соединить последовательно или параллельно . Оставшаяся часть урока 4 будет посвящена изучению этих двух типов соединений и их влиянию на электрические величины, такие как ток, сопротивление и электрический потенциал.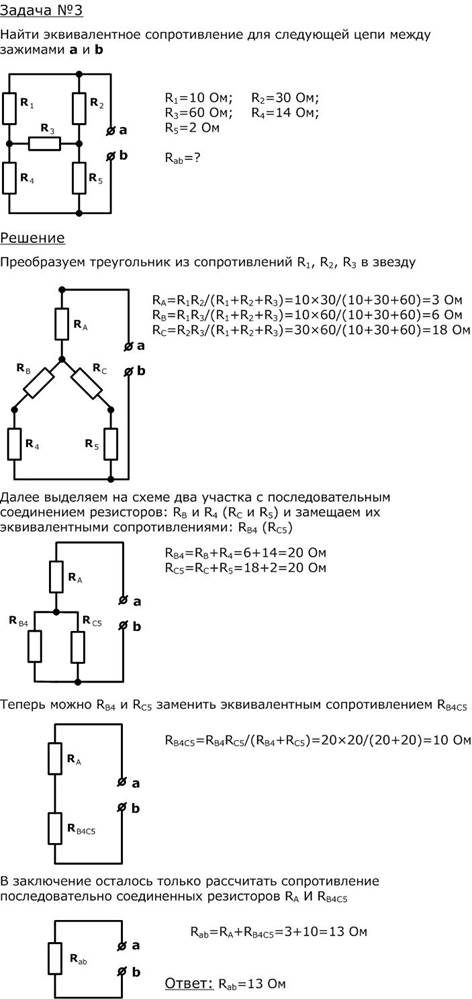 Следующая часть урока 4 познакомит вас с различием между последовательными и параллельными соединениями.
Следующая часть урока 4 познакомит вас с различием между последовательными и параллельными соединениями.
1. Используйте символы цепей для построения принципиальных схем следующих цепей:
a. Отдельный элемент, лампочка и выключатель соединены вместе в цепи, так что выключатель можно размыкать и замыкать, чтобы включить лампочку.
б. Пакет из трех D-ячеек включен в цепь для питания лампочки фонарика.
в. | д. |
2. Используя понятие условного тока, нарисуйте на схеме справа сплошную линию, указывающую направление условного тока. Поместите наконечник стрелки на непрерывную линию.
Следующий раздел:
Понимание принципиальных схем — AP Physics 1
Все ресурсы AP Physics 1
7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
AP Physics 1 Справка » Электричество и волны » Электричество » Схемы » Понимание принципиальных схем
Каково эквивалентное сопротивление показанной выше цепи?
Возможные ответы:
Правильный ответ:
Объяснение:
Когда резисторы соединены последовательно, они складываются нормально, например,
когда они соединены последовательно, они складываются в обратном порядке
Используя эти правила, мы можем сначала объединить все резисторы последовательно ( ), который можно изобразить следующим образом:
Используя правило параллельности, найдите полное эквивалентное сопротивление.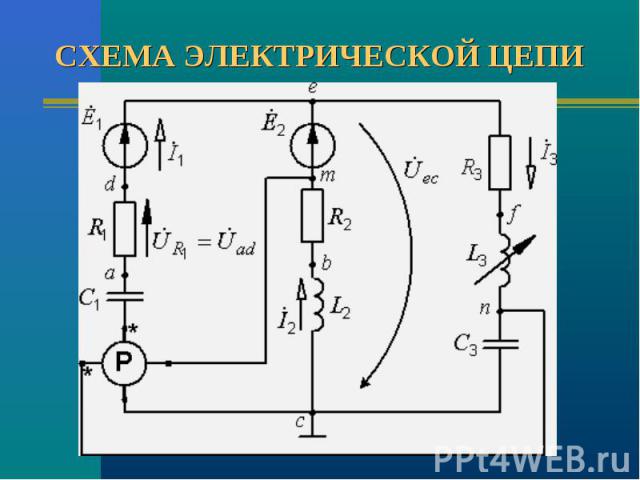
Сообщить об ошибке
Каков заряд конденсатора на данной электрической схеме?
Возможные ответы:
Правильный ответ:
Объяснение:
Соотношение между зарядом конденсатора и падением напряжения на нем:
Поскольку падение напряжения на обоих и одинаковое, нам просто нужно побеспокоиться о правильной части цепи. Конденсаторы противоположны резисторам, когда дело доходит до нахождения эквивалентной емкости, поэтому для последовательно соединенных конденсаторов два конденсатора справа добавят как таковые
Подстановка в первое уравнение.
Поскольку два конденсатора соединены последовательно, они должны иметь тот же заряд, что и эквивалентный конденсатор.
Сообщить об ошибке
Сколько тока проходит на данной схеме?
Возможные ответы:
Правильный ответ:
Пояснение:
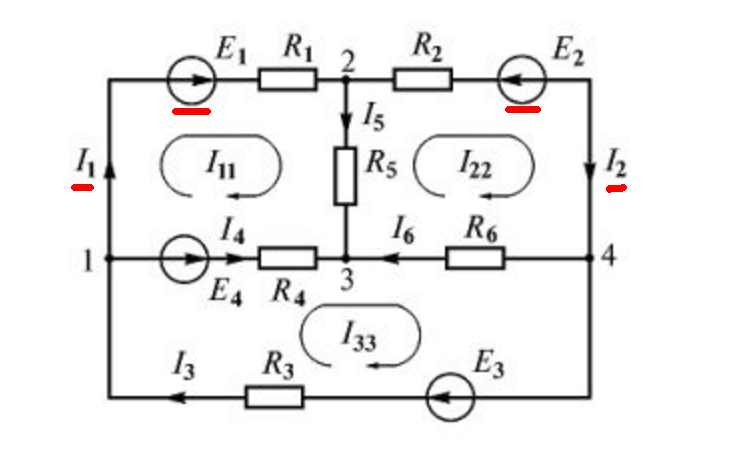
Первым шагом к решению этой задачи является использование правил Кирхгофа для написания набора уравнений для нахождения неизвестных. Ниже изображены две петли, и мы назначаем цепи 3 тока. Первый и второй ток проходят вверх через батареи 1 и 2 соответственно, а третий ток проходит вниз через .
Ниже изображены две петли, и мы назначаем цепи 3 тока. Первый и второй ток проходят вверх через батареи 1 и 2 соответственно, а третий ток проходит вниз через .
Эти начальные условия дают нам наше первое уравнение:
Теперь, используя правило контура и установив все изменения напряжения в контуре равными нулю, мы получим эти два уравнения для двух контуров. Петля слева дает нам:
Петля справа дает нам:
Поскольку мы хотим найти ток, который протекает через , нам нужно найти для . Самый простой способ сделать это — взять первое уравнение и заменить либо или в одном из двух других уравнений. Следующее решение заменит первое уравнение, чтобы выполнить это.
Переставить.
Упростите второе уравнение.
Наконец, решите и приравняйте два уравнения.
Сообщить об ошибке
Какова эквивалентная емкость данной электрической схемы?
Возможные ответы:
Правильный ответ:
Объяснение:
Конденсаторы складываются противоположно тому, как резисторы складываются в цепи.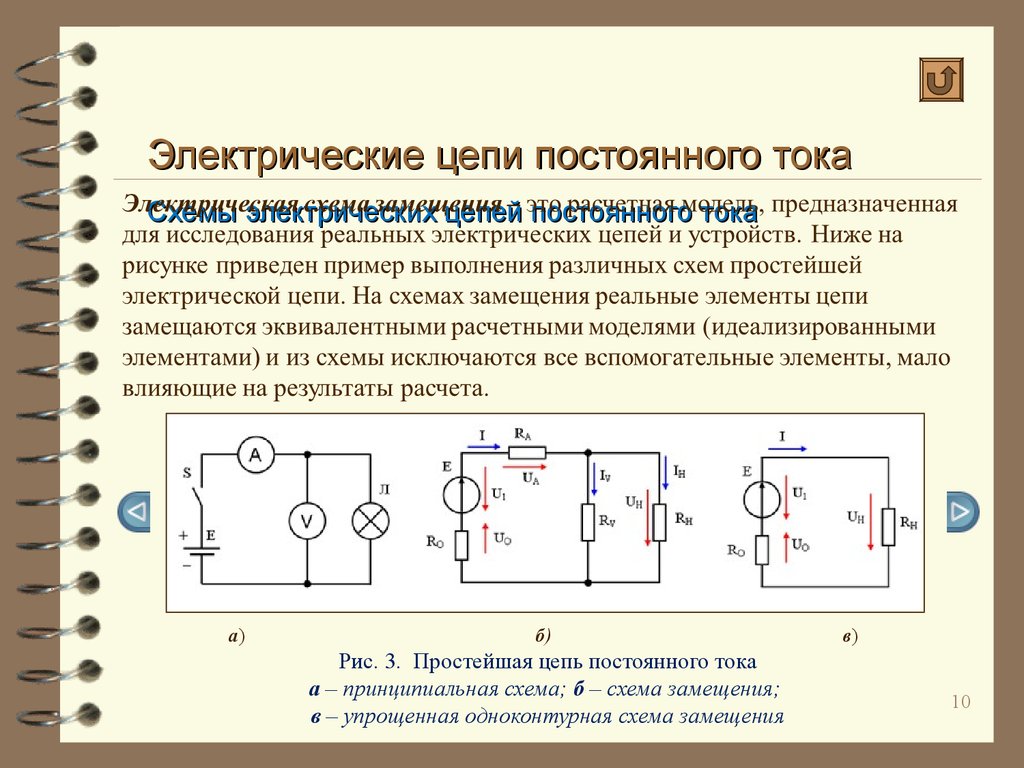 То есть для конденсаторов последовательно добавляют так:
То есть для конденсаторов последовательно добавляют так:
Конденсаторы, подключенные параллельно, добавляются следующим образом:
Используйте эту информацию, чтобы сложить все последовательно подключенные конденсаторы. Единственная ветвь, к которой это относится, — это правая ветвь.
Эквивалентная схема показана ниже:
Подключите конденсаторы параллельно.
Сообщить об ошибке
Какая мощность рассеивается в приведенной выше схеме?
Возможные ответы:
Правильный ответ:
Объяснение:
Первым шагом к решению проблемы со схемой будет определение и расчет всех неизвестных токов с использованием законов Кирхгофа. Нарисовав петли в цепи и установив падение напряжения на петле равным нулю, мы можем рассчитать неизвестные токи и найти мощность.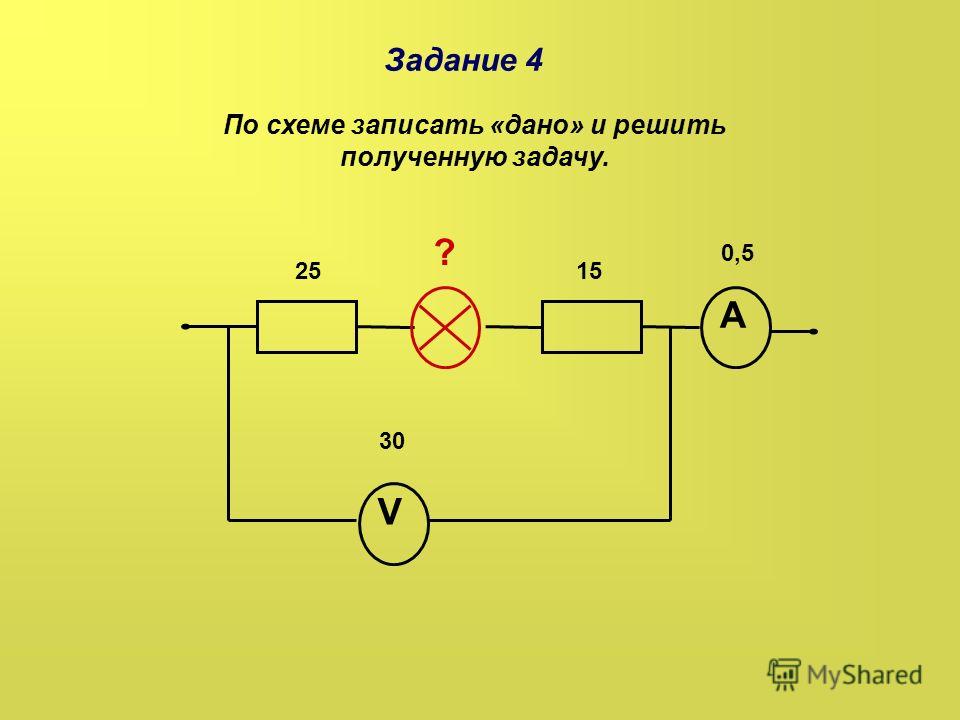 Две петли указаны здесь на этой диаграмме.
Две петли указаны здесь на этой диаграмме.
Обозначьте ток, протекающий через батарею, как , ток, протекающий через и , как , а ток, протекающий через , как . Первая петля слева при записи по правилу петли дает:
Решите для тока.
Второй контур дает нам:
Подставьте значение для
Найдите мощность, рассеянную через
Каков общий ток в приведенной выше цепи, сообщите об ошибке
2?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти силу тока, сначала найдите суммарное сопротивление параллельно включенных резисторов:
После этого рассчитайте ток по закону Ома:
Сообщить об ошибке
Какое общее напряжение выше в цепи?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти напряжение, сначала найдите суммарные сопротивления параллельно включенных резисторов:
Используйте закон Ома, чтобы найти напряжение.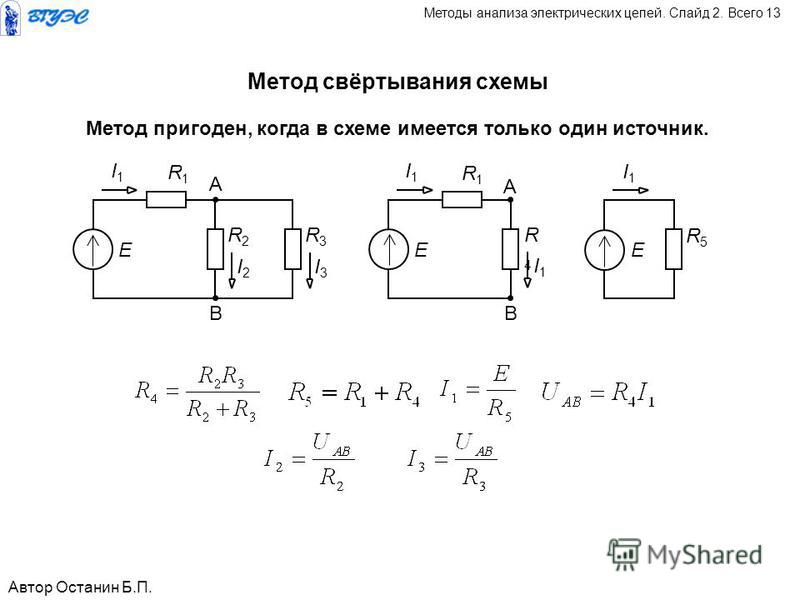
Сообщить об ошибке
Какое сопротивление в приведенной выше схеме?
Возможные ответы:
Правильный ответ:
Пояснение:
Найдите полное сопротивление цепи, которое можно определить по закону Ома.
Теперь можно найти сопротивление второго резистора. Поскольку два резистора включены параллельно, их общее сопротивление зависит от следующего:
Переставьте и решите
Сообщить об ошибке
Каково общее сопротивление в приведенной выше схеме?
Возможные ответы:
Правильный ответ:
Объяснение:
Найдите объединенные сопротивления резисторов, включенных параллельно:
Объедините эти два объединенных последовательных резистора, чтобы найти общее сопротивление:
Сообщить об ошибке
Каково падение напряжения в приведенной выше схеме?
Возможные ответы:
Правильный ответ:
Объяснение:
Найдите полное сопротивление цепи.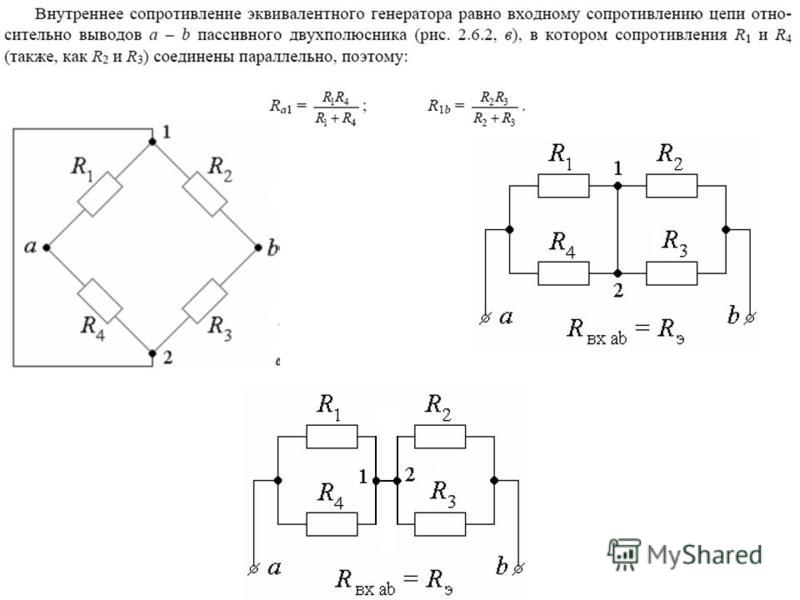 Сначала вычислите значения объединенных сопротивлений резисторов, включенных параллельно:0002 Таким образом, общее сопротивление равно:
Сначала вычислите значения объединенных сопротивлений резисторов, включенных параллельно:0002 Таким образом, общее сопротивление равно:
Теперь обратите внимание, что, поскольку и параллельны, падение напряжения на них одинаково. Используйте закон Ома, чтобы связать ток с точки зрения напряжения и сопротивления.
Заменить Закон Ом для сопротивления через:
Отчет о ошибке
← Предыдущий 1 2 Следующий →
Уведомление о авторском праве
Все AP Physics 1 Ресурсы
9000.0002 7 диагностических тестов 170 практических тестов Вопрос дня Карточки Learn by Concept
Упростите свою работу в области силовой электроники с помощью инструмента для построения схем
Инструменты моделирования помогают инженерам проектировать и улучшать электрические системы. Такие решения способны решать сложные проблемы за меньшее время.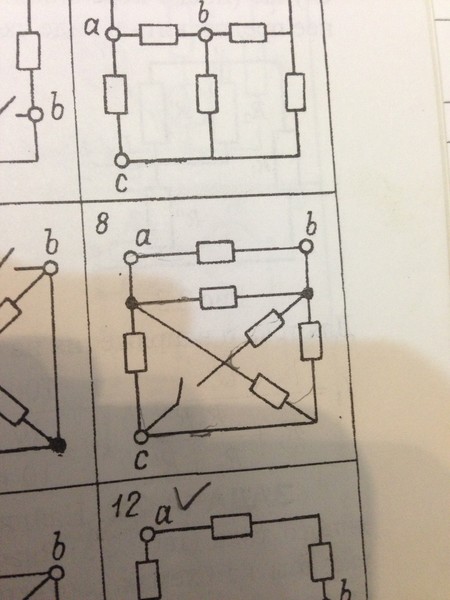 Однако перед моделированием какой-либо электрической системы ее необходимо смоделировать. Это то, что мы позволяем пользователям делать с помощью Schematic Editor — приложения для построения схем, которое мы разрабатываем вместе с нашим клиентом. Позвольте показать вам, как это упрощает и оптимизирует рабочие процессы инженеров в области силовой электроники.
Однако перед моделированием какой-либо электрической системы ее необходимо смоделировать. Это то, что мы позволяем пользователям делать с помощью Schematic Editor — приложения для построения схем, которое мы разрабатываем вместе с нашим клиентом. Позвольте показать вам, как это упрощает и оптимизирует рабочие процессы инженеров в области силовой электроники.
Основная идея промышленного моделирования заключается в создании копии системы и последующем всестороннем тестировании этой системы, как если бы она была реальной. Поскольку многие системы уже существуют или основаны на своих аналоговых предшественниках, их необходимо перепроектировать или изобразить на диаграмме, чтобы можно было протестировать. Многие инженерные интерфейсы, используемые для построения диаграмм или моделирования, созданы с учетом ограничительных спецификаций, или, возможно, вообще не уделяется должного внимания их интерфейсам и взаимодействию с пользователем.
Редактор схем OPAL-RT позволяет пользователям разрабатывать силовую электронную модель реальной системы. Затем симулятор клиента позволяет ему протестировать эту модель на реальном оборудовании, подключенном к эмулируемому миру. Пользователи могут опробовать свое решение без необходимости иметь реальную производственную систему. Например, инженер может смоделировать контроллер электромобиля с помощью редактора схем. Затем она или он может смоделировать это с помощью симулятора OPAL-RT, подключенного к реальному контроллеру. Таким образом, инженер может изменить условия работы и выполнить некоторые маневры на автомобиле, чтобы увидеть реакцию контроллера и проверить, хорошо ли работает логика, реализованная в контроллере.
Затем симулятор клиента позволяет ему протестировать эту модель на реальном оборудовании, подключенном к эмулируемому миру. Пользователи могут опробовать свое решение без необходимости иметь реальную производственную систему. Например, инженер может смоделировать контроллер электромобиля с помощью редактора схем. Затем она или он может смоделировать это с помощью симулятора OPAL-RT, подключенного к реальному контроллеру. Таким образом, инженер может изменить условия работы и выполнить некоторые маневры на автомобиле, чтобы увидеть реакцию контроллера и проверить, хорошо ли работает логика, реализованная в контроллере.
Компания OPAL-RT, владеющая редактором схем, предлагает полную среду для моделирования электрических цепей. Они продавали его вместе с дорогим программным обеспечением сторонних компаний, но решили создать собственное конкурентное решение. Так начался наш проект.
OPAL-RT работает в области силовой электроники, которая является требовательной и сложной областью. Он охватывает широкий диапазон от промышленной передачи и распределения электроэнергии до микропроектирования и тестирования микросхем и схем, например, для электрических самолетов и лодок. Очень важно тестировать каждое решение перед его выпуском, чтобы избежать ненужного риска и потерь.
Он охватывает широкий диапазон от промышленной передачи и распределения электроэнергии до микропроектирования и тестирования микросхем и схем, например, для электрических самолетов и лодок. Очень важно тестировать каждое решение перед его выпуском, чтобы избежать ненужного риска и потерь.
С самого начала мы знали, что тема этого проекта сложная, но это нас не обескуражило. Такие задачи всегда мотивируют нас на работу!
Мы засучили рукава и начали изучать отрасль силовой электроники, чтобы мы могли легко понять потребности клиента и ценность приложения для бизнеса.
Мы тесно сотрудничали с представителями OPAL-RT, проводили встречи и семинары как в Польше, так и в Канаде.
СОЗДАНИЕ КОНТРОЛЬНОЙ СХЕМЫ. ЗАДАЧИ Мы начали работу над этим приложением с подготовки прототипа для клиента. Тогда мы разработали первую функциональную версию приложения, позволяющую пользователю создавать простейшие электрические схемы. Проанализировав дальнейшие требования, мы официально запустили проект.
В начале нам нужно было выяснить, какой формат и структура данных лучше всего использовать в диаграммной модели. Когда этот шаг будет завершен, мы сможем использовать установленную структуру для создания серверной части, включая веб-API и базу данных PostgreSQL. WebAPI был связан только с уровнем доступа к данным, однако он включал сложную бизнес-логику, для выполнения которой требовалось несколько спринтов. Когда вся фундаментальная основа системы была на месте, все, что у нас было во внешнем интерфейсе, можно было маршрутизировать через API и базу данных. Результатом стала возможность как сохранять версии моделей, так и считывать их обратно в контексте.
С самого начала проекта мы использовали GoJS — библиотеку JavaScript для визуализации данных — для создания инструмента для разработки расширенных схем электрических цепей.
Часто, когда мы добавляем новую сложную функциональность, мы тратим время на изучение того, как лучше всего вписать ее в общую архитектуру. Хорошо организованные все функции и основанные на надежном обмене данными между уровнями приложений значительно упрощают разработку и обслуживание приложений. Многие новые функции требуют от нас разработки решений, для которых GoJS изначально не предназначалась.- Многие из наших задач нестандартны, например, динамическое добавление портов или объединение линий. Затем нам нужно мыслить нестандартно — , — говорит Пшемек, разработчик и технический архитектор, работающий над этим проектом.
Хорошо организованные все функции и основанные на надежном обмене данными между уровнями приложений значительно упрощают разработку и обслуживание приложений. Многие новые функции требуют от нас разработки решений, для которых GoJS изначально не предназначалась.- Многие из наших задач нестандартны, например, динамическое добавление портов или объединение линий. Затем нам нужно мыслить нестандартно — , — говорит Пшемек, разработчик и технический архитектор, работающий над этим проектом.
Пользователь — инженер, работающий с приложением Schematic Editor, теперь может легко создавать сложные электрические цепи. Это возможно благодаря:
- интуитивно понятному интерфейсу приложения,
- блоки на палитре, точно отражающие элементы электрической схемы, и
- интуитивно понятный и удобный способ рисования линий.
Одним из основных преимуществ этого приложения являются механизмы проверки с обратной связью в режиме реального времени. Линии визуально меняются каждый раз, когда изменяется состояние электрической цепи, и это визуально сообщается пользователю. Такая проверка в реальном времени не позволяет пользователю, например, нарисовать неправильное соединение — действие приостанавливается и отображается уведомление. Реализация этой функции в режиме реального времени означает, что система является интеллектуальной и получает входные данные, а также обеспечивает обратную связь. Многие инструменты на рынке имеют функции проверки, но в этом случае пользователь получает уведомление по мере продвижения диаграммы для рассмотрения и корректировки пользователем.
Линии визуально меняются каждый раз, когда изменяется состояние электрической цепи, и это визуально сообщается пользователю. Такая проверка в реальном времени не позволяет пользователю, например, нарисовать неправильное соединение — действие приостанавливается и отображается уведомление. Реализация этой функции в режиме реального времени означает, что система является интеллектуальной и получает входные данные, а также обеспечивает обратную связь. Многие инструменты на рынке имеют функции проверки, но в этом случае пользователь получает уведомление по мере продвижения диаграммы для рассмотрения и корректировки пользователем.
Пользовательский симулятор или решатель OPAL-RT позволяет им тестировать модель силовой электроники с помощью физического или виртуального оборудования и оборудования, подключенного к моделируемому миру. Пользователи вносят изменения, пробуют конфигурации и возвращаются к чертежной доске по своему желанию, не покидая смоделированного пространства.

 »
» Обратите внимание, что три набора длинных и коротких параллельных линий использовались для представления аккумуляторной батареи с тремя D-ячейками. И обратите внимание, что каждая лампочка представлена своим индивидуальным символом резистора. Прямые линии использовались для соединения двух клемм батареи с резисторами и резисторов друг с другом.
Обратите внимание, что три набора длинных и коротких параллельных линий использовались для представления аккумуляторной батареи с тремя D-ячейками. И обратите внимание, что каждая лампочка представлена своим индивидуальным символом резистора. Прямые линии использовались для соединения двух клемм батареи с резисторами и резисторов друг с другом.