Оценка параметров уравнения регреcсии
Проверить значимость параметров уравнения регрессии можно, используя t-статистику.Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α xβ;
y = α βx;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.
Требуется:
1. Построить уравнения парной регрессии y от x:
- линейное;
- степенное;
- показательное;
- равносторонней гиперболы.
3. Оценить статистическую значимость уравнения регрессии в целом.
4. Оценить статистическую значимость параметров регрессии и корреляции.
5.
Выполнить прогноз затрат на производство при прогнозном выпуске продукции, составляющем 195 % от среднего уровня.
7. Оценить модель через среднюю ошибку аппроксимации.
Посмотрите, как легко было найдено уравнение степенной регрессии с помощью сервиса.
Решение:
1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент корреляции
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Коэффициент детерминации
R2=0.942 = 0.89, т.е. в 88.9774 % случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая
| x | y | x2 | y2 | x ∙ y | y(x) | (y-y)2 | (y-y(x))2 | (x-xp)2 |
| 78 | 133 | 6084 | 17689 | 10374 | 142. 16 |
115.98 | 83.83 | 1 |
| 82 | 148 | 6724 | 21904 | 12136 | 148.61 | 17.9 | 0.37 | 9 |
| 87 | 134 | 7569 | 17956 | 11658 | 156.68 | 95.44 | 514.26 | |
| 79 | 154 | 6241 | 23716 | 12166 | 143.77 | 104.67 | 104.67 | 0 |
| 89 | 162 | 7921 | 26244 | 14418 | 159.9 | 332.36 | 4.39 | 100 |
| 106 | 195 | 11236 | 38025 | 20670 | 187. 33 |
2624.59 | 58.76 | 729 |
| 67 | 139 | 4489 | 19321 | 9313 | 124.41 | 22.75 | 212.95 | 144 |
| 88 | 158 | 7744 | 24964 | 13904 | 158.29 | 202.51 | 0.08 | 81 |
| 73 | 152 | 5329 | 23104 | 11096 | 134.09 | 67.75 | 320.84 | 36 |
| 87 | 162 | 7569 | 26244 | 14094 | 156.68 | 332.36 | 28.33 | 64 |
| 76 | 159 | 5776 | 25281 | 12084 | 138. 93 |
231.98 | 402.86 | 9 |
| 115 | 173 | 13225 | 19895 | 201.86 | 854.44 | 832.66 | 1296 | |
| 0 | 0 | 0 | 16.3 | 20669.59 | 265.73 | 6241 | ||
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 25672.31 | 2829.74 | 8774 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(1) = 4.01*1 + 99.18 = 103.19
y(2) = 4.01*2 + 99.18 = 107.2
... ... ...
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
T табл (n-m-1;α/2) = (11;0.
05/2) = 1.796
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
Sa = 0.1712
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Статистическая значимость коэффициента регрессии b не подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
796):
(a — tтабл·Sa; a + tтабл·Sa)
(1.306;1.921)
(b — tтабл·Sb; b + tтабл·Sb)
(-9.2733;41.876)
где t = 1.796
2) F-статистики
Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим
Перейти к онлайн решению своей задачи
Уравнения, параметры, неравенства: что нужно знать, чтобы точно сдать профильную математику
На что обращать внимание при подготовке к профильной математике, как подступиться к сложным задачам и какими пособиями пользоваться при подготовке. Об этом на онлайн-консультации в официальной группе ЕГЭ во «ВКонтакте» рассказал Алексей Доронин — учитель математики и лауреат конкурса «Учитель года России- 2011».
ЕГЭ-2018 по профильной математике (будут сдавать 1 июня) состоит из двух частей:
- Часть первая — восемь заданий (1–8) базового уровня сложности с кратким ответом.
- Часть вторая — четыре задания (9–12) повышенного уровня сложности с кратким ответом и семь заданий (13–19) высокого уровня сложности с развёрнутым ответом.
Во время подготовки к экзамену важно не только научиться решать задачи, но и правильно рассчитать время, за которое вы эти задания выполняете. Как это сделать? Попробуйте в спокойной обстановке решить 12 первых задач из демоверсии ЕГЭ по профильной математике и посмотрите, сколько времени на это тратите. Хорошо, если у вас получается решать эти задания за 40 минут и ещё оставить 10 минут на проверку (всего на экзамен даётся 235 минут). Старайтесь придерживаться этой планки, иначе не будете успевать и рискуете сделать нелепые ошибки из-за невнимательности. Например, видите геометрическую задачу: тут же рисуете треугольник на клетчатой бумаге и на автомате начинаете вычислять площадь. А задание вообще может быть связано с нахождением средней линии, высоты, биссектрисы или медианы.
И ни в коем случае не превращайте подготовку к экзамены в нарешивание огромного количества вариантов.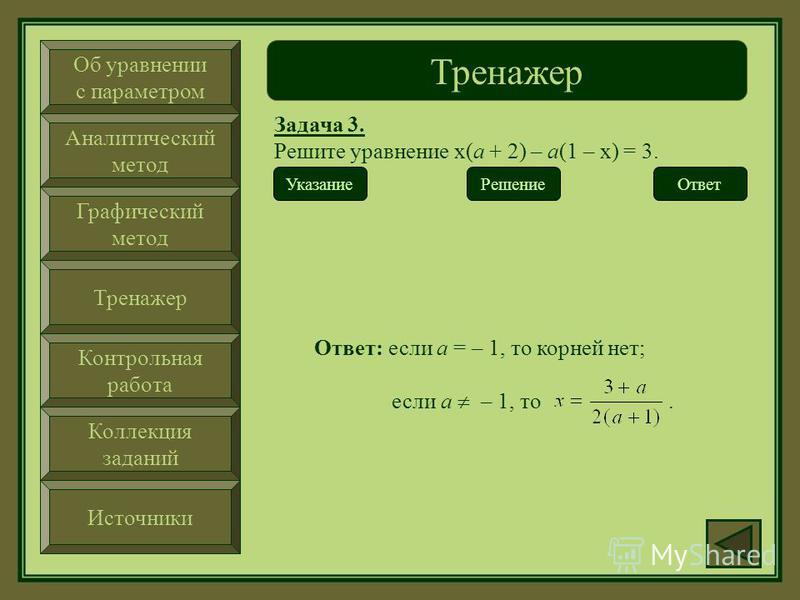
Надеяться на то, что вы прорешаете сто вариантов и великолепно справитесь с экзаменом — не совсем правильно. Лучше сначала сосредоточиться на решении первых 12 задач, и только после того, как поймёте, что вы без проблем решаете задания повышенной сложности, можно приступать к отработке решения самых сложных.
О том, как их выполнять и на что обращать внимание, расскажу подробнее.
Задания № 13 и 15 — проверяют, как вы решаете уравнения и неравенстваЕсть много ресурсов с типовыми заданиями, где мы в разных примерах видим одно и то же неравенство. Поменяют три на пять основание логарифма, и выпускники снова и снова их решают. Но в этом году будет другое содержание части С и другое неравенство, поэтому лучше изучить разные методы решения неравенств. Тут вам поможет методический курс Шарыгина «Решение задач» — в нём очень много неравенств. Можно найти страницу, где есть показательные решения логарифмических неравенств — около тридцати вариантов. Попробуйте их все решить.
Если у вас получится, то проблем на экзамене, думаю, не будет.
Ещё важно следить за вычислительной частью. Потому что арифметическая ошибка, которая повлияла на ход решения, — сразу плохо, и вряд ли задание будет вообще как-то оцениваться. Поэтому когда вы выполняете соответствующие преобразования, всё-таки смотрите, как вы находите дискриминант, как раскладываете на множитель квадратный трёхчлен. Следите за коэффициентом, за тем, как умножаете на отрицательное или положительно число, потому что именно такие нелепые ошибки приводят к неправильному ответу.
Задания № 14 и 16 — проверяют, как вы решаете задачи с геометрическими фигурами, координатами и векторами
В задачах № 14 и 16 есть пункты «а» и «б». Обычно в пункте «а» нужно доказать, в пункте «б» — вычислить. Часто ученики пытаются доказать пункт «а», вязнут в доказательстве и бросают задачу. При этом они не читают пункт «б», хотя его можно было бы решить, используя пункт «а», и получить один балл. Так было в прошлом году: те ребята, которые не смогли справиться с доказательством пункта «а», но вычислили пункт «б», получили один балл.
Часто спрашивают, нужно ли помнить названия теорем, которые используются при доказательстве. Сами названия использовать не нужно, но если вы доказываете взаимную перпендикулярность двух плоскостей, то, конечно, должны прописать условия, при которых признак перпендикулярности плоскостей срабатывает.
Формулировки вроде «прямая теорема Пифагора» или «обратная теорема Пифагора» прописывать не обязательно, потому что проверять будут именно содержание: смогли ли вы заметить те моменты, которые помогают выполнить доказательство пункта «а».
Как правильно решать стереометрическую задачу № 14? Расскажу на примере одного из своих любимых учебников «Математика: алгебра и начала математического анализа. Геометрия.10 класс» (авторы Е. В. Потоскуев и Л. И. Звавич). В конце учебника можно найти список основных теоретических фактов и посмотреть, что вы по ним знаете. Например, как доказывать перпендикулярность прямой и плоскости, как найти расстояние между скрещивающимися прямыми. На все факты, которые есть в учебниках, на экзамене можно ссылаться без доказательств.
Даже если в одном учебнике описан какой-то интересный приём решения задач, а в другом — нет. Главное, чтобы учебники входили в федеральный перечень.
Задача № 17 — проверяет, как вы применяете знания на практике (тут может быть разное)
При решении задачи № 17 нужно составить математическую модель. Обычно это или уравнение, или неравенство. Иногда бывает функция, которую нужно исследовать. Здесь, скорее всего, функция будет не сложнее, чем квадратичная (из первых 12 заданий ЕГЭ). Но есть важный момент: чтобы получить один балл за решение экономической задачи, нужно прописать, что является переменной x, переменной p и переменной s. Не нужно сразу записывать в бланк само уравнение без этой преамбулы — один балл как раз и ставится за то, как вы сумели правильно составить математическую модель. На этот момент обратите особенное внимание. Даже если у вас получилось очень сложное уравнение, которое, возможно, вы не сможете решить, но составлено оно было правильно, — вы законно получите один балл.
Во всех практикоориентированных задачах, хоть в профильном экзамене, хоть в базовом, числа и значения реальные. Если у вас появляется какая-то нереальная скорость, нереальные размеры объекта, то стоит ещё раз посмотреть на решение — может быть, что-то здесь не так.
Задание № 18 — проверяет, как вы решаете уравнения и неравенства (задача с параметром)
Решение задач с параметром — вопрос сложный. Готовиться к такой задаче есть смысл, только если вы блестяще решаете все другие задачи (в том числе задание № 19). При подготовке стоит посмотреть, какие есть способы решения задачи с параметром, потому что вы можете решить 100 задач одним и тем же способом, а на экзамене будет совсем другой.
В принципе либо это аналитический способ, где задачу с параметром нужно разбить на несколько задач, либо это графический или геометрический способ, когда у вас есть некая геометрическая конструкция, и вы её анализируете. Для подготовки можно использовать замечательную книгу «Задачи с параметрами» Горнштейна.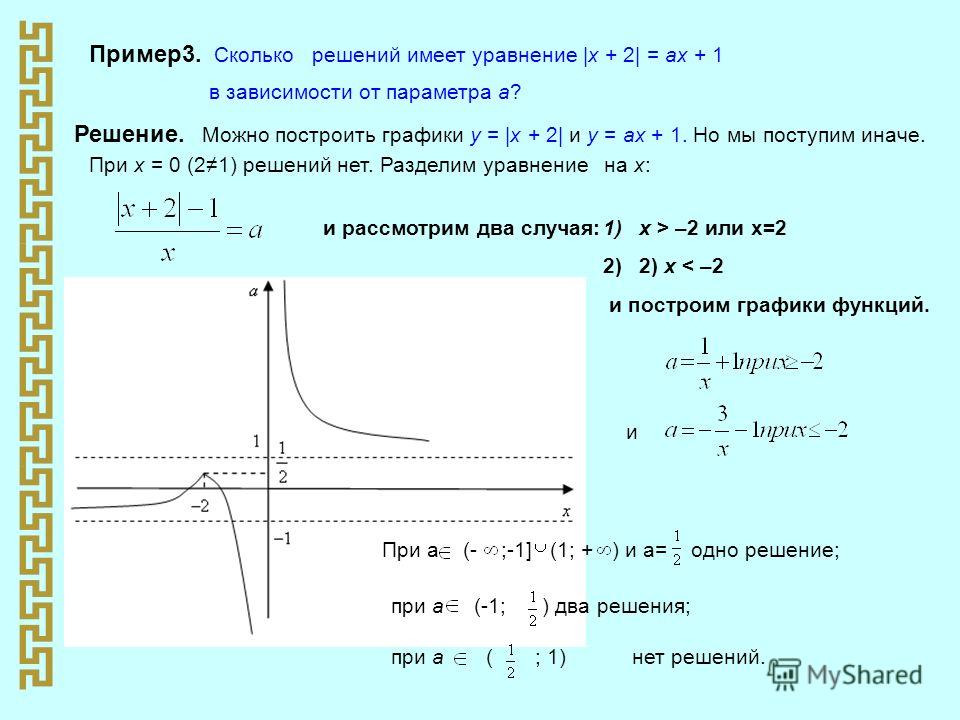
И есть совсем новый сборник «Я сдам ЕГЭ! Математика. Практикум и диагностика. Профильный уровень» И. В. Ященко.
Задание № 19 — проверяет, как вы строите и исследуете простейшие математические модели
Есть мнение, что задача № 19 — олимпиадная, но это не так. Я бы сказал, что это сложная задача школьного учебника по математике. Никаких знаний, никаких утверждений, которые касаются олимпиадной математики, вам не потребуется. В задаче есть три пункта — «а», «б», «в». В пункте «а» вам нужно будет построить пример, в пункте «б» — доказать утверждение, в пункте «в» — не только найти пример и дать ответ (например, 25), но и доказать, что больше 25 в ответе получиться не может. И не забывайте обращать внимание на формулировки «найдите натуральные числа» или «найдите целые числа» — это правда частая ошибка.
Чем пользоваться при подготовке ЕГЭ
- Открытый банк заданий ФИПИ
- Mathege.ru
- Статград
- 5 полезных блогов, которые расскажут (и покажут), как готовиться к ЕГЭ
списков — Как написать идеальное описание параметров уравнения? — TeX
Это старый пост, но все решения требуют, чтобы уравнение и объяснения были даны отдельно.
Я предпочитаю иметь единую среду, которая сочетает в себе уравнение и объяснение его переменных.
Приведенный ниже код определяет новую среду формула , в которой вы указываете формулу в качестве первого аргумента и даете объяснение переменных в виде списка, разделенного запятыми, в теле среды. Например, код
\begin{формула}{P+N=S_{d}}
P : условный коэффициент проницаемости,
N : количество волн,
S_{d}: уровень урона
\end{формула}
производит
Вдохновленный хорошим ответом эгрега, есть дополнительные аргументы. Вы можете использовать восклицательный знак, если вам нужен разрыв строки после , где: , и вы можете изменить , где: на что угодно, используя (второй) необязательный аргумент. Итак,
\begin{formula}![где используемая нами замечательная запись:]{P+N=S_{d}}
P : условный коэффициент проницаемости,
N : количество волн,
S_{d}: уровень урона
\end{формула}
9P~ \sqrt{\cot \alpha}
}
H_s: {значительная высота волны, равная среднему значению 1/3 самой высокой волны},
\Delta: {относительная плавучая плотность, равная $\rho_r / \rho_w - 1$, где
$\rho_w$ — плотность воды},
D_{n50}: номинальный диаметр, определяемый уравнением (2),
P: условный коэффициент проницаемости,
S_d: уровень урона,
N: количество волн,
\xi_m: параметр брейкера на основе среднего периода волны $T_m$,
\alpha: угол наклона,
\конец{формула*}
производит:
Обратите внимание, что пояснения переменных, содержащие запятые, необходимо заключать в фигурные скобки.
Вот полный код:
\documentclass{article}
\usepackage{аммат}
\usepackage{etoolbox}
\usepackage{xparse}
% добавить одну строку объяснения - #3 поглощает весь лишний мусор
\def\ExplainVariable#1:#2:#3!!!{$#1$ &$\;\;=$ #2 \\}
\NewDocumentEnvironment{формула}{ т! O {где:} м б }{%
\begin{уравнение}#3\end{уравнение}
#2 \IfBooleanT{#1}{\\[1ex]}
\renewcommand*\do[1]{\ExplainVariable##1::!!!}%
\tabular[t]{r@{}l}\docsvlist{#4}\endtabular
{}
\NewDocumentEnvironment{формула*}{ т! O {где:} м б }{%
\begin{уравнение*}#3\end{уравнение*}
#2 \IfBooleanT{#1}{\\[1ex]}
\renewcommand*\do[1]{\ExplainVariable##1::!!!}%
\tabular[t]{r@{}l}\docsvlist{#4}\endtabular
{}
\начать{документ}
\begin{формула}{P+N=S_{d}}
P : условный коэффициент проницаемости,
N : количество волн,
S_{d}: уровень урона
\end{формула}
\bigskip
\begin{формула}![где замечательное обозначение, которое мы используем:]{P+N=S_{d}}
P : условный коэффициент проницаемости,
N : количество волн,
S_{d}: уровень урона
\end{формула}
\bigskip
\begin{формула*}{
\frac{H_s}{\Delta D_{n50} } = 1,0~ P^{0,13}~ \left(\frac{S_d}{N} \right)^{0,2}
\xi_m^P~ \sqrt{\cot \alpha}
}
H_s: {значительная высота волны, равная среднему значению 1/3 самой высокой волны},
\Delta: {относительная плавучая плотность, равная $\rho_r / \rho_w - 1$, где
$\rho_w$ — плотность воды},
D_{n50}: номинальный диаметр, определяемый уравнением (2),
P: условный коэффициент проницаемости,
S_d: уровень урона,
N: количество волн,
\xi_m: параметр брейкера на основе среднего периода волны $T_m$,
\alpha: угол наклона,
\конец{формула*}
\конец{документ}
Основная идея — проанализировать тело среды Formula с помощью \docsvlist из пакета etoolbox.
списки — Выравнивание параметров уравнения — TeX
Вы должны , а не оставлять пустую строку между \end{equation} и \begin{conditions} , иначе описание может быть отделено от уравнения.
Также у вас не должно быть пустой строки перед \begin{equation} ни при каких обстоятельствах.
С другой стороны, такое длинное описание переменных, скорее всего, приведет к плохим разрывам страниц, независимо от того, отделены они от уравнения или нет.
Вероятно, для таких случаев лучше использовать простую списочную среду: знаки равенства не обязательны и могут быть заменены глаголом is .
Вот исправленная версия вашего кода; Я сделал несколько небольших исправлений, и вы можете сравнить их со своей версией. После = заглавной буквы нет: они тяжелые и не сочетаются с запятыми; с должно быть $i$th и по x должно быть всегда должно быть по $x$ (даже лучше, по ~$x$ ).
Окончание с \endtabularx\\[\baselineskip] вызовет предупреждение.
\usepackage{массив,таблицаx,вычисление}
\newlength{\conditionwd}
\newenvironment{условия}[1][где:]
{%
# 1 \ tablex {\ textwidth- \ width {# 1}} [t] {
>{$}l<{$} @{${}={}$} X@{}
}%
}
{\endtabularx\\[\belowdisplayskip]}
\начать{документ}
\citet{hernandez19{n} \left[\left(\frac{M_x m_x}{E_c I_i}+\frac{kV_xv_x}{A_iG_i}\right) \times \Delta_x \right]
\label{eqn:PROLAM отклонение}
\end{уравнение}
\begin{условия}
$\Delta$ & Полный прогиб клееной балки в точке $x$,\\
$M_x$ & Изгибающий момент в точке $x$, вызванный фактической нагрузкой,\\
$m_x$ & Изгибающий момент в точке $x$, вызванный единичной нагрузкой в середине пролета балки,\\
$V_x$ & Сдвиг в точке $x$, вызванный фактической нагрузкой,\\
$v_x$ & Сдвиг в точке $x$, вызванный единичной нагрузкой в середине пролета балки,\\
$k$ & Форм-фактор (1,2 для прямоугольного сечения),\\
$E_c$ & Постоянное значение MOE, используемое в преобразованном поперечном сечении,\\
$I_i$ & Момент инерции i-го преобразованного сечения в точке x,\\
$A_i$ & Преобразованная площадь в i-м преобразованном сечении в точке x,\\
$G_i$ & Модуль сдвига i-го преобразованного сечения в точке x,\\
$\Delta_x$ & Шаг, с которым выполняются вычисления,\\
$n$ & Общее количество приращений по длине балки. {n} \left[
\left(\frac{M_x m_x}{E_c I_i}+\frac{kV_xv_x}{A_iG_i}\right) \times \Delta_x
\Правильно]
\label{eqn:PROLAM отклонение}
\end{уравнение}
куда
\begin{itemize}[labelindent=0pt,leftmargin=*,широкий=$M_x$,align=left,itemsep=0pt]
\item[$\Delta$] - полный прогиб клееной балки в точке $x$,
\item[$M_x$] — изгибающий момент в точке $x$, вызванный фактической нагрузкой,
\item[$m_x$] — изгибающий момент в точке $x$, вызванный единичной нагрузкой в середине пролета балки,
\item[$V_x$] - сдвиг в точке $x$, вызванный фактической нагрузкой,
\item[$v_x$] — сдвиг в точке $x$, вызванный единичной нагрузкой в середине пролета балки,
\item[$k$] — форм-фактор ($1.2$ для прямоугольного сечения),
\item[$E_c$] - постоянное значение MOE, используемое в преобразованном поперечном сечении,
\item[$I_i$] — момент инерции $i$-го преобразованного сечения в точке $x$,
\item[$A_i$] - преобразованная площадь в $i$м преобразованном сечении в точке $x$,
\item[$G_i$] — модуль сдвига $i$-го преобразованного сечения в точке $x$,
\item[$\Delta_x$] — приращение, с которым выполняются вычисления,
\item[$n$] - общее количество приращений по длине балки.
{n} \left[
\left(\frac{M_x m_x}{E_c I_i}+\frac{kV_xv_x}{A_iG_i}\right) \times \Delta_x
\Правильно]
\label{eqn:PROLAM отклонение}
\end{уравнение}
куда
\begin{itemize}[labelindent=0pt,leftmargin=*,широкий=$M_x$,align=left,itemsep=0pt]
\item[$\Delta$] - полный прогиб клееной балки в точке $x$,
\item[$M_x$] — изгибающий момент в точке $x$, вызванный фактической нагрузкой,
\item[$m_x$] — изгибающий момент в точке $x$, вызванный единичной нагрузкой в середине пролета балки,
\item[$V_x$] - сдвиг в точке $x$, вызванный фактической нагрузкой,
\item[$v_x$] — сдвиг в точке $x$, вызванный единичной нагрузкой в середине пролета балки,
\item[$k$] — форм-фактор ($1.2$ для прямоугольного сечения),
\item[$E_c$] - постоянное значение MOE, используемое в преобразованном поперечном сечении,
\item[$I_i$] — момент инерции $i$-го преобразованного сечения в точке $x$,
\item[$A_i$] - преобразованная площадь в $i$м преобразованном сечении в точке $x$,
\item[$G_i$] — модуль сдвига $i$-го преобразованного сечения в точке $x$,
\item[$\Delta_x$] — приращение, с которым выполняются вычисления,
\item[$n$] - общее количество приращений по длине балки.