10 класс. Алгебра. Контрольные работы. Колягин Ю.М. | Учебно-методический материал по алгебре (10 класс):
Контрольная работа по алгебре и началам анализа №1
«Делимость чисел» (профильный уровень)
1 вариант
- Найти остаток от деления 485638 на 5, не выполняя деления.
- Найти последнюю цифру числа .
- Доказать, что число делится на 26.
- Натуральные числа и делятся на натуральное число . Найти .
- Доказать, что уравнение не имеет целочисленных решений.
- Доказать, что уравнение не имеет целочисленных решений.
Контрольная работа по алгебре и началам анализа №1
«Делимость чисел» (профильный уровень)
2 вариант
- Найти остаток от деления 728362 на 4, не выполняя деления.
- Найти последнюю цифру числа .
- Доказать, что число делится на 17.
- Натуральные числа и делятся на натуральное число . Найти .
- Доказать, что уравнение не имеет целочисленных решений.

- Доказать, что число делится на 4 при любых целых х и у.
……………………………………………………………………………………………………
Контрольная работа по алгебре и началам анализа №2
«Алгебраические уравнения» (базовый уровень)
1 вариант
- Выполнить деление многочлена на многочлен .
- Решить уравнение .
- Возвести в степень .
- Решить систему уравнений: а) б)
в)
Контрольная работа по алгебре и началам анализа №2
«Алгебраические уравнения» (базовый уровень)
2 вариант
- Выполнить деление многочлена на многочлен .
- Решить уравнение .
- Возвести в степень .
- Решить систему уравнений : а) б)
в)
…………………………………………………………………………………………………
Контрольная работа по алгебре и началам анализа №2
«Алгебраические уравнения» (профильный уровень)
1 вариант
- Выполнить деление многочлена на многочлен .

- Не выполняя деления, найти остаток от деления многочлена на двучлен .
- Решить уравнение .
- Возвести в степень .
- Решить уравнение .
- Решить систему уравнений
Контрольная работа по алгебре и началам анализа №2
«Алгебраические уравнения» (профильный уровень)
2 вариант
- Выполнить деление многочлена на многочлен .
- Не выполняя деления, найти остаток от деления многочлена на двучлен .
- Решить уравнение .
- Возвести в степень .
- Решить уравнение .
- Решить систему уравнений
…………………………………………………………………………………………………
Контрольная работа по алгебре и началам анализа №3 А-10
«Степень с действительным показателем» (базовый уровень)
1 вариант
1) Вычислить: а) , б) .
2) Упростить выражение при , :
а) , б) .
3) Сократить дробь .
4) Сравнить числа: а) и , б) и .
5) Найти сумму бесконечно убывающей геометрической прогрессии, если , .
Контрольная работа по алгебре и началам анализа №3 А-10
«Степень с действительным показателем» (базовый уровень)
2 вариант
1) Вычислить: а) , б) .
2) Упростить выражение при , :
а) , б) .
3) Сократить дробь .
4) Сравнить числа: а) и , б) и .
5) Найти второй член бесконечно убывающей геометрической прогрессии, если сумма её членов равна , а знаменатель равен .
………………………………………………………………………………………………………
Контрольная работа по алгебре и началам анализа №3 А-10
«Степень с действительным показателем» (профильный уровень)
1 вариант
1) Вычислить: а) , б) .
2) Упростить выражение при , :
а) , б) .
3) Сократить дробь при .
4) Избавиться от иррациональности в знаменателе дроби .
5) Упростить выражение .
6) В бесконечно убывающей геометрической прогрессии первый член на 9 больше второго. Сумма прогрессии, составленной из членов данной прогрессии с нечетными номерами, на 12 больше суммы прогрессии, составленной из членов данной прогрессии с четными номерами. Найти эту прогрессию.
Контрольная работа по алгебре и началам анализа №3 А-10
«Степень с действительным показателем» (профильный уровень)
2 вариант
1) Вычислить: а) , б) .
2) Упростить выражение при , :
а) , б) .
3) Сократить дробь при .
4) Избавиться от иррациональности в знаменателе дроби .
5) Упростить выражение .
6) Найти сумму бесконечно убывающей геометрической прогрессии, если сумма всех её членов, стоящих на нечетных местах, в 4 раза больше суммы всех её членов, стоящих на четных местах, а сумма первых трех членов прогрессии равна 63.
…………………………………………………………………………………………………….
Контрольная работа по алгебре и началам анализа №4
«Степенная функция» (базовый уровень)
1 вариант
- Найти область определения функции .
- Изобразить эскиз графика функции и перечислить её основные свойства. Пользуясь свойствами этой функции:
а) сравнить с единицей ; б) сравнить и .
- Решить уравнение:
а) ; б) ; в) .
- Установить, равносильны ли неравенства и .
- Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
Контрольная работа по алгебре и началам анализа №4
«Степенная функция» (базовый уровень)
2 вариант
- Найти область определения функции .
- Изобразить эскиз графика функции и перечислить её основные свойства. Пользуясь свойствами этой функции:
а) сравнить с единицей ; б) сравнить и .
- Решить уравнение:
а); б); в).
- Установить, равносильны ли неравенства и.
- Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
……………………………………………………………………………………………………….
Контрольная работа по алгебре и началам анализа №4
«Степенная функция» (профильный уровень)
1 вариант
- Найти область определения функции .
- Изобразить эскиз графика функции и перечислить её основные свойства.
- Решить уравнение:
1) , 2) ,
3) , 4) .
- Решить систему уравнений
- Решить неравенство .
Контрольная работа по алгебре и началам анализа №4
«Степенная функция» (профильный уровень)
2 вариант
- Найти область определения функции .
- Изобразить эскиз графика функции и перечислить её основные свойства.

- Решить уравнение:
1) , 2) ,
3) , 4) .
- Решить систему уравнений
- Решить неравенство .
………………………………………………………………………………………………..
Контрольная работа по алгебре и началам анализа №5
«Показательная функция» (базовый уровень)
1 вариант
- Сравнить числа: 1) и , 2) и .
- Решить уравнение: 1) , 2) .
- Решить неравенство .
- Решить неравенство: 1) , 2) .
- Решить систему уравнений
- (дополнительно) Решить уравнение .
Контрольная работа по алгебре и началам анализа №5
«Показательная функция» (базовый уровень)
2 вариант
- Сравнить числа: 1) и , 2) и .
- Решить уравнение: 1) , 2) .
- Решить неравенство .
- Решить неравенство: 1) , 2) .
- Решить систему уравнений
- (дополнительно) Решить уравнение .
……………………………………………………………………………………………. .
.
Контрольная работа по алгебре и началам анализа №5
«Показательная функция» (профильный уровень)
1 вариант
- Сравнить числа и .
- Решить уравнение: а) , б) .
- Решить неравенство: а) , б) .
- Решить уравнение .
- Решить графически неравенство .
- (доп.) Решить неравенство .
Контрольная работа по алгебре и началам анализа №5
«Показательная функция» (профильный уровень)
2 вариант
- Сравнить числа и .
- Решить уравнение: а) , б) .
- Решить неравенство: а) , б) .
- Решить уравнение .
- Решить графически неравенство .
- (доп.) Решить неравенство .
………………………………………………………………………………………………….
Контрольная работа по алгебре и началам анализа № 6
«Логарифмическая функция»
1 вариант
- Вычислить: 1) , 2) , 3) .
- Сравнить числа и .
- Решить уравнение .

- Решить неравенство .
- Решить графически уравнение .
- Решить уравнение .
- Решить неравенство: 1)
2) .
- (Дополнительно) Решить уравнение .
Контрольная работа по алгебре и началам анализа № 6
«Логарифмическая функция»
2 вариант
- Вычислить: 1) , 2) , 3) .
- Сравнить числа и .
- Решить уравнение .
- Решить неравенство .
- Решить графически уравнение .
- Решить уравнение .
- Решить неравенство: 1) ,
2).
- (Дополнительно) Решить уравнение.
………………………………………………………………………………………………..
Контрольная работа по алгебре и началам анализа №7
«Тригонометрические формулы»
1 вариант
- Найти значение выражения: 1) , 2) , 3) .
- Вычислить ,, если и .

- Упростить выражение .
- Доказать тождество .
- Решить уравнение .
Контрольная работа по алгебре и началам анализа №7
«Тригонометрические формулы»
2 вариант
- Найти значение выражения: 1), 2) , 3) .
- Вычислить , , если и .
- Упростить выражение.
- Доказать тождество.
- Решить уравнение.
……………………………………………………………………………………………..
Контрольная работа по алгебре и началам анализа №8
«Тригонометрические уравнения»
1 вариант
- Решить уравнение: 1) , 2) .
- Найти все корни уравнения на отрезке.
- Решить уравнение:
1) ,
2) ,
3) ,
4) ,
5) ,
6) .
Контрольная работа по алгебре и началам анализа №8
«Тригонометрические уравнения»
2 вариант
- Решить уравнение: 1) , 2) .

- Найти все корни уравнения на отрезке.
- Решить уравнение:
1) ,
2),
3) ,
4),
5) ,
6) .
………………………………………………………………………………………………..
Контрольная работа № 1 | |
1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а).у = – х + 5 б).у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: | 2 вариант 1). 2). Найти D(у), если: 3). Построить график функции: а).у = х – 7 б).у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
Контрольная работа № 2 по теме: «Тригонометрические функции числового и углового аргумента» | |
1 вариант 1). Вычислите: 2). Упростите: 3).Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . | 2 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . |
Контрольная работа № 3 по теме: «Тригонометрические функции» | |
1 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке. 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . | 2 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке. 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
Контрольная работа № 4 по теме: «Тригонометрические уравнения» | |
1 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения, принадлежащие отрезку . | 2 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения, принадлежащие отрезку . |
Контрольная работа № 5 по теме: «Преобразование тригонометрических выражений» | |
1 вариант 1). 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . | 2 вариант 1). Вычислите: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . |
Контрольная работа № 6 по теме: «Производная. Уравнение касательной к графику функции» | |
1 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . | 2 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с. 4). Дана функция . Найдите: а). б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
Контрольная работа № 8 (итоговая) | |
1 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить, в каких точках промежутка касательная к графику данной функции составляет с осьюОхугол 600. 2). Решите уравнение: 3). Упростите выражение: а).; б). . 4). Постройте график функции с полным исследованием функции . | 2 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке . 2). Решите уравнение: 3). Упростите выражение: а).; б). . 4). Постройте график функции с полным исследованием функции . |
Упростить в алгебре
Упрощение: сделать проще!
Одна из больших задач, которые мы делаем в алгебре, — это упрощение .
Вас часто будут просить изложить что-то «в простейшей форме»
Какая самая простая форма?
Вообще проще когда проще пользоваться .
| Начните с: | 5х + х — 3 | |
| Объединить похожие термины: | 6x − 3 |
Теперь им немного проще пользоваться.
А:
| Начните с: | 3 6 | |
| Упростите дробь, разделив верх и низ на 3: | 1 2 |
«Половина» однозначно проще, чем «три шестых», если только не важно знать, что что-то разрезали на шестые.
А:
| Начните с: | 2w(5wy) | |
| Перемножить константы и переменные: | 10 Вт 2 г |
Теперь им немного проще пользоваться.
А:
| Начните с: | 2x 2 − 6x + 2 х — 3 | |
| Полиномиальное длинное деление: | 2x + 2 х — 3 |
А:
| Начните с: | x 2 — 2x — 3 | |
| Факторинг: | (х-3)(х+1) |
С последним примером можно поспорить! Некоторые люди говорят, что в нужно удалить скобки , чтобы сделать его «проще», но (x−3)(x+1) обычно намного проще в использовании.
Мораль истории:
«Упрощенный» иногда очевиден, но также может зависеть от того, что вы хотите сделать.
Как упростить
Есть много способов упростить!
Когда мы упрощаем, мы используем те же навыки, что и для решения уравнений, и на этой странице есть несколько полезных советов.
Некоторые из этих вещей могут помочь:
- Объединить похожие термины
- Фактор
- Расширение (противоположное факторингу)
- Очистить дроби, умножив
- Найдите закономерность, которую вы видели раньше, например, разницу квадратов.
А что здесь проще?
Вот еще один интересный случай:
| Это: | кажется достаточно простым | |||
| Но это: | имеет рационализированный знаменатель (обычно считается более простым и предпочтительным для учителей!) |
Что проще? Вам решать!
Упростите выражение (10.
 11.22) × z
11.22) × zАлгебра — это изучение и обработка математических символов. Выражения алгебры состоят из известных чисел и неизвестных значений. Эти неизвестные величины определяются некоторыми основными алгебраическими операциями. Некоторые основные стандартные формулы выведены для проведения этих расчетов.
Алгебраические выражения
Алгебраические выражения — это математические выражения, включающие целочисленные константы, переменные, коэффициенты переменных и степень в начале переменных. Эти выражения связаны между собой различными алгебраическими операциями.
Типы алгебраических операций на основе количества термов.
- Мономиальные выражения: Мономиальные выражения — это алгебраические выражения, которые имеют только один член. Например: 5x, 2y, +1 — некоторые одночленные выражения.
- Биномиальные выражения: Биномиальные выражения — это алгебраические выражения, состоящие из двух членов.
 Например: 2x + 3, x+ y и т. д. — некоторые биномиальные выражения.
Например: 2x + 3, x+ y и т. д. — некоторые биномиальные выражения. - Полиномиальные выражения: Полиномиальные выражения — это алгебраические выражения, содержащие несколько членов. Например: ab + bc + ca, x + xy + 1 и т. д. — некоторые полиномиальные выражения.
Основные алгебраические формулы
Основные алгебраические формулы используются в математических расчетах. Формулы для определения неизвестных величин или выполнения алгебраических операций приведены ниже.
- a² – b² = (a – b)(a + b)
- (a + b)² = a² + 2ab + b²
- (a – b)² = a² – 2ab + b²
- а² + b² = (а – b)² + 2аб.
- (a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc.
- (a – b – c)² = a² + b² + c² – 2ab – 2ac + 2bc.
- a³ – b³ = (a – b) (a² + ab + b²)
- a³ + b³ = (a + b) (a² – ab + b²)
Упростите выражение
Решение:
Следующие шаги могут быть использованы для решения задачи,
- Упрощение данного алгебраического выражения
= 11/10/22 z
- Нарушение деления чисел
= 11/10 × 1/22 .







 Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5).
Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5).

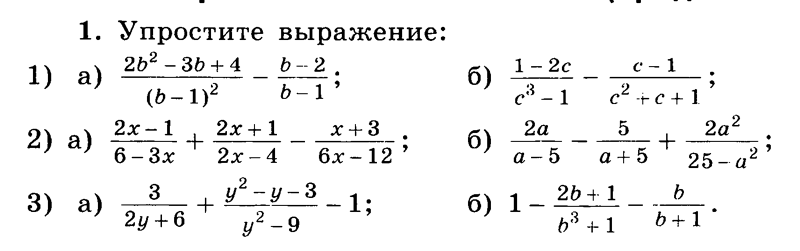 Вычислить:
Вычислить:
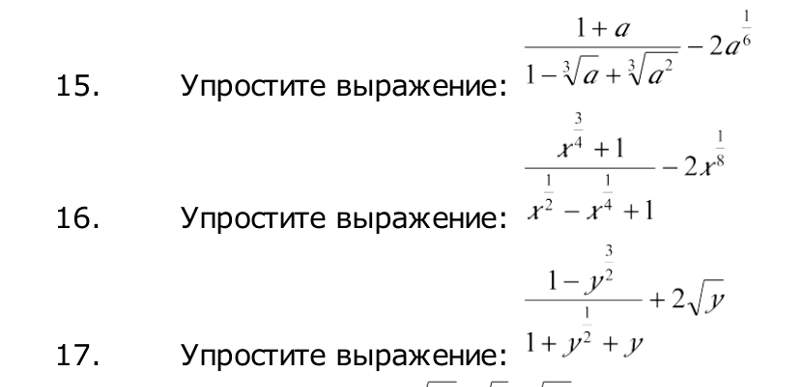 Промежутки возрастания и убывания функции;
Промежутки возрастания и убывания функции;
 Например: 2x + 3, x+ y и т. д. — некоторые биномиальные выражения.
Например: 2x + 3, x+ y и т. д. — некоторые биномиальные выражения.