lim как решать
Вы искали lim как решать? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра лимит, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «lim как решать».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как lim как решать,алгебра лимит,алгебра пределы,все о пределах,высшая математика для чайников пределы,высшая математика лимиты,высшая математика пределы,высшая математика пределы для чайников,вычислить пределы функций пошаговое решение,задания пределы,задачи на пределы,задачи на пределы с решениями,задачи пределы,задачи с решениями на пределы,лимит как решать,лимит математика,лимиты как решать,матанализ для тупых,матанализ для чайников пределы,матанализ пределы,матанализ пределы для чайников,математика предел,математика пределы,математика пределы для чайников,математический анализ для чайников пределы,математический анализ пределы,математический анализ пределы для чайников,математический предел,матпрофи пределы,методы решения пределов,нахождение пределов с подробным решением,предел 0,предел алгебра,предел в математике,предел в математике это,предел математика,предел математический,предел функции для чайников,предел это в математике,пределы алгебра,пределы в математике,пределы высшая математика,пределы для чайников,пределы как решать,пределы как решаются,пределы матан,пределы матанализ для чайников,пределы математика,пределы математика для чайников,пределы математический анализ,пределы математический анализ для чайников,пределы примеры решений,пределы примеры решения,пределы решений примеры,пределы решения,пределы с бесконечностью как решать,пределы теория с примерами,примеры на пределы,примеры решений пределов,примеры решения пределов,решение пределов онлайн с подробным решением для чайников,решение пределов примеры,решение пределов примеры с решением,решение пределов с подробным решением,решения пределов пример,способы нахождения пределов,способы решения пределов,теория пределов для чайников,формулы лимитов,что такое в математике предел,что такое в математике пределы,что такое предел в математике.
Решить задачу lim как решать вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Свойства пределов функции
Предел функции является в математическом анализе одним из основных понятий. Функция f(x) в точке х0 предел имеет L. Если все значения х достаточно близки к х0, то близко к L и значение f(x).
На бесконечности предел функции описывает поведение значения самой функции, когда аргумент ее становится бесконечно большим.
Предел функции обозначается в виде f(x) → L в случае, если х→а
К основным свойствам пределов функции относят:
- предел постоянной величины, который равен самой постоянной величины;
- предел суммы, который равен сумме пределов самих функций. Также по аналогии и предел разности функций равен разности пределов данных функций;
- предел суммы множества функций равен также сумме пределов таких функций. По аналогии рассчитывает и предел нескольких функций, который равен разности пределов данных функций;
- повышение предела произведения функции (постоянного коэффициента) на знак предела;
- произведению пределов функций равен предел произведения двух функций;
- расширенное свойство предела произведения, которое в том заключается, что предел произведения функций равен и произведению пределов данных функций;
- предел частного функций равен отношению пределов данных функций, но только в том случае, если предел знаменателя нулю не равен;
- предел функции степенной, где действительным числом является степень р;
- предел функции показательной, при которой основание b больше 0;
- предел функции логарифмической, в которой основание b больше 0;
- теорема «двух милиционеров», при которой «зажатой» остается функция f(x)между другими двумя функции, которые также стремятся к пределу А.
Все перечисленные свойства пределов позволяют исходный предел функции свести к уже известному, чтобы получить ответ.
| Число b называется пределом функции f(x) при x → a, если для любого ε > 0 сущестувует δ > 0 такое, что для любого x из δ-окрестности a (|x — a| | ||||||||||||||
| Запись: ∀ ε > 0 ∃ δ > 0 : |x — a| |f(x) — f(a)| | ||||||||||||||
Обозначение | ||||||||||||||
| ||||||||||||||
Свойства пределов | ||||||||||||||
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
Замечательные пределы | ||||||||||||||
| ||||||||||||||
| ||||||||||||||
e = 2,718281828459045235360287471352662497757. .. | ||||||||||||||
Связь между десятичными и натуральными логарифмами | ||||||||||||||
| lg(x) = M ln(x), | ||||||||||||||
| где M = lg(e) = 0,43429448190325182765112891891666… |
Что такое предел в исчислении? Предел — это просто…
Вспомните
Обе части исчисления основаны на пределах!
Предел функции — это значение, к которому $$f(x)$$ приближается по мере того, как $$x$$ приближается к некоторому числу.
Примеры
Пример 1
Давайте посмотрим на график $$f(x) = \frac 4 3 x -4$$ и исследуем точки, в которых $$x$$ «близок» к $$x = 6$$. Мы начнем с точек, где $$x$$ меньше 6.
Обратите внимание, что по мере того, как значения $$x$$ приближаются к 6, значения функции приближаются к $$y = 4$$. Теперь давайте посмотрим на точки функции, где $$x$$ больше 6.
Таблица нанесенных точек
$$
\начать{массив}{л|с}
х & f(x)\\\hline
\hline
7 и 5.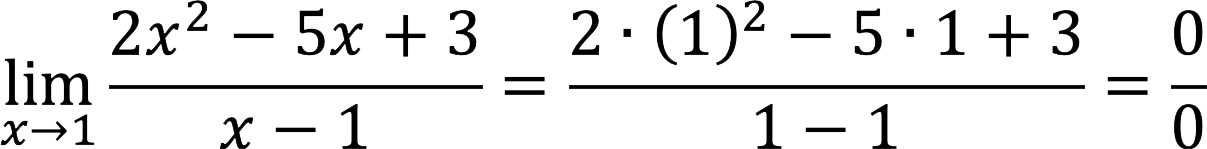
33333\\\hлиния
6,5 и 4,66667\\\hлиния
6,25 и 4,33333\\\hлиния
6.1 и 4.13333\\\hлиния
6.01 и 4.01333\\\hлиния
\конец{массив}
$$
Как и раньше, чем ближе мы подходили к $$x = 6$$, тем ближе подходила функция к $$y = 4$$.
Конечно, поскольку $$f(6) = 4$$, это может показаться неудивительным. Тем не менее, это идея предела, и ее можно резюмировать следующим образом:
Когда $$x$$ приближается к определенному числу, к чему приближается функция?
Обозначение предела
У математиков есть специальные обозначения, указывающие на то, что они работают с предельными значениями. Например, ответ на Пример 1 будет записан так:
Пример 2
Предположим, что $$f(x) = \frac{\sin x}{x }$$.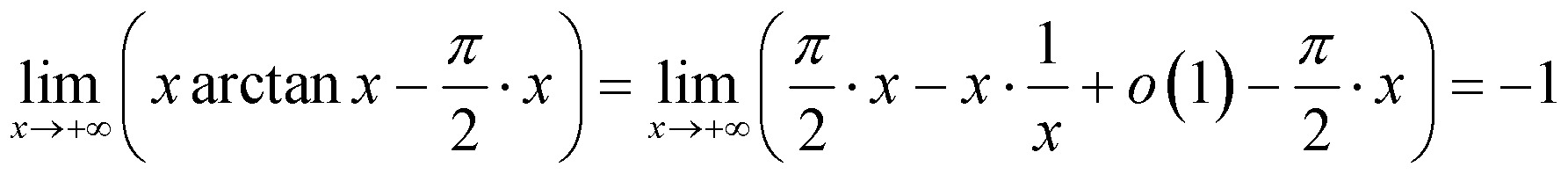
Что такое $$\displaystyle \lim_{x\to0} f(x)=$$?
Заманчиво просто подставить $$x$$ = 0, чтобы попытаться получить ответ, но если мы попробуем
$$f(0) = \frac{\sin 0} {\color{red}{0}} \mbox{не определено! (Деление на ноль)}$$
Несмотря на то, что функция не определена, когда $$x$$ = 0, мы все равно можем ответить на вопрос. вопрос с использованием лимита.
Следующие две таблицы помогут нам понять, что происходит вблизи $$x$$ = 0.
При приближении $$x$$ к 0…
$$ \начать{массив}{л|с} х & f(x)\\\hline \hline -1 & 0,84143\\\hлиния -0,5 и 0,9588\\\hline -0,1 и 0,99808\\\hлиния -0,01 и 0,99945\\\hлиния -0,001 и 0,9999998\\\hлиния \конец{массив} $$
$$f(x)$$ приближается к 1.
ИЛИ
При приближении $$x$$ к 0…
$$ \начать{массив}{л|с} х & f(x)\\\hline \hline 1 & 0,84143\\\hлиния 0,5 и 0,9588\\\hline 0,1 и 0,99808\\\hлиния 0,01 и 0,99945\\\hлиния 0,001 и 0,9999998\\\hлиния \конец{массив} $$
$$f(x)$$ приближается к 1.
В обеих таблицах чем ближе x приближается к 0, тем ближе функция приближается к 1. Теперь давайте взглянем на график функции, просто для визуальной проверки.
Как и в таблицах, график показывает, что по мере приближения к $$x$$ = 0, Значение $$y$$ приближается к 1 !
Или, если использовать математические обозначения:
$$\displaystyle\lim_{x\to0}\frac{\sin x} x = 1$$.
Важно
$$\displaystyle \lim_{x\to0} \frac{\sin x} x = 1$$ НЕ говорит $$f(x) = 1$$, когда $$x=0$$ $$\displaystyle \lim_{x\to0} \frac{\sin x} x = 1$$ говорит, что $$f(x)$$ получает $$\textit{close}$$ до 1, если $$x$ $ приближается к 0 .
Проблема с нашей точностью
Давайте еще раз взглянем на эти таблицы из второго примера.
При приближении $$x$$ к 0…
$$ \начать{массив}{л|с} х & f(x)\\\hline \hline -1 & 0,84143\\\hлиния -0,5 и 0,9588\\\hлиния -0,1 и 0,99808\\\hline -0,01 и 0,99945\\\hлиния -0,001 и 0,9999998\\\hлиния \конец{массив} $$
$$f(x)$$ приближается к 1.
ИЛИ
При приближении $$x$$ к 0…
$$ \начать{массив}{л|с} х & f(x)\\\hline \hline 1 & 0,84143\\\hлиния 0,5 и 0,9588\\\hline 0,1 и 0,99808\\\hлиния 0,01 и 0,99945\\\hлиния 0,001 и 0,9999998\\\hлиния \конец{массив} $$
$$f(x)$$ приближается к 1.
Во втором примере мы сказали, что $$f(x)$$ приближается к 1. Но разве они не приближаются к 0,9999999? Так что же верно?
$$ \displaystyle\lim_{x\to0} \frac{\sin x} x = 1? $$
ИЛИ
$$ \displaystyle\lim_{x\to0}\frac{\sin x} x = 0,9999999? $$
Это проблема с использованием таблиц значений (такая же проблема с графиками).
Они недостаточно точны, чтобы получить точный ответ!
Существуют способы точного определения предельных значений, но эти методы рассматриваются в последующих уроках. На данный момент важно помнить, что при использовании таблиц или графиков лучшее, что мы можем сделать, — это оценить.
Следовательно, по таблицам и графики, ответы на два примера выше должны быть
Пример 1: $$\displaystyle \lim_{x\to6} \left(\frac 4 3 x — 4\right) \приблизительно 4$$
и
Пример 2: $$\displaystyle \lim_{x\to0} \frac{\sin x} x \приблизительно 1$$
Реклама
ac.kr 
)
)
)
)
)
)
)
)