📐 Калькулятор синуса, косинуса, тангенса онлайн
Интернет-магазин детских книг » Калькуляторы онлайн для решения математических задач »
В форме онлайн-калькулятора тригонометрических функций укажите величину угла: число градусов (°), минут (‘), секунд (»). Зная синус, можно найти косинус и тангенс. Если дано дробное значение функции тригонометрии, например, sin=4/5, укажите в поле «числитель» число 4, в поле «знаменатель» число 5. Если tg = -0,5, то число «-0,5» указывается в поле «числитель».
Заполните поле «Текст с картинки». Нажмите кнопку «Решить».
Онлайн калькулятор тригонометрических функций предназначен для того, чтобы быстро найти ответ на задачу, в которой нужно рассчитать, чему равен синус, косинус, тангенс онлайн.
Здесь также выполняется расчет котангенса, секанса, косеканса, версинуса, коверсинуса, гаверсинуса, экссеканса и экскосеканса. Единицы измерения – градусы, минуты, секунды. Ответ вычисляется после нажатия на кнопку «Решить».
Пример задачи. Используем онлайн калькулятор синуса, косинуса, тангенса для того, чтобы найти синус и тангенс, зная косинус угла А в виде дроби Cos A = 1/3. В поле «тригонометрическая функция» указывается «cos», «числитель» — число «1», «знаменатель» — число «3».
Решение синусов и тангенсов:
По таблице «Косинусы» находим значение угла A с градусами и минутами = 70,528779° = 70°32′.
Так как Sin2 + Cos2 = 1, то, используя тригонометрический калькулятор синусов онлайн:
1) значение синуса Sin A = √1 — (1/3) 2 = √9/9 — 1/9 = √(9 — 1)/9 = √8/9 = 2,828427 / 3 = 0,942809;
2) значение тангенса tg A = Sin A / Cos A = (2,828427 / 3) • (3/1) = 8,485281/3 = 2,828427.
Пример задачи. Найти синус, тангенс через косинус угла А = Cos A = -0,5 с помощью онлайн калькулятора синусов, косинусов, тангенсов, котангенсов. В поле «тригонометрическая функция» указывается «cos», «числитель» — число «- 0,5».
Решение синусов и тангенсов:
По таблице «Косинусы» находим угол A в градусах = 120° = 120°0′.
Используем формулу основного тригонометрического тождества
Sin2 + Cos2 = 1. Далее требуется вычислить синус.
1) значение синуса Sin A = √1 — (-0,5)2 = √1 — 0,25 = √0,75 = 0,866025;
2) значение тангенса tg A = Sin A / Cos A = 0,866025 / -0,5 = -1,732051.
Пример задачи.
Используем калькулятор синусов и косинусов градусов, минут, секунд онлайн, чтобы найти значение синуса, косинуса, тангенса, котангенса угла A = 12°34’56» = 12 градусов 34 минуты 56 секунд.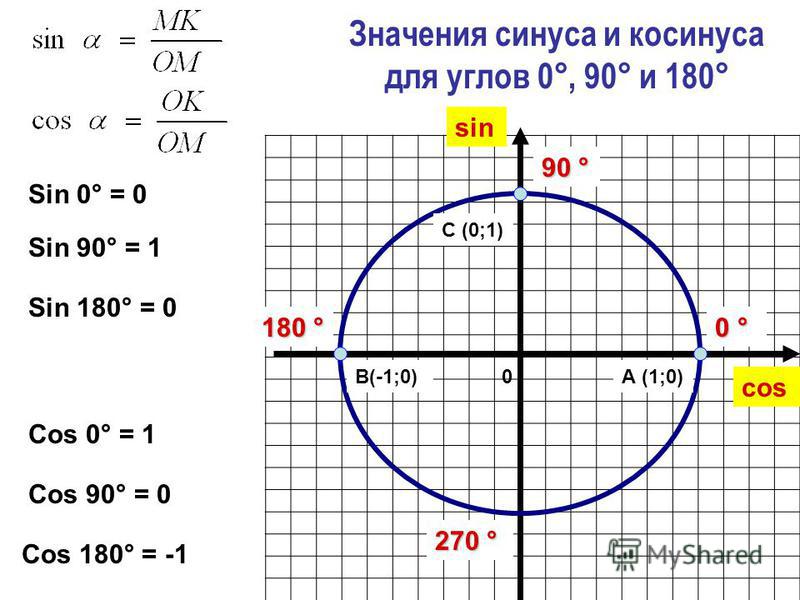
Решение:
A = 12°34’56» = 12,582222°
Синус угла sin 12°34’56» = 0,2178404227.
Косинус угла cos 12°34’56» = 0,9759844015.
Тангенс угла tg 12°34’56» = sin 12°34’56» / cos 12°34’56» = 0,2232007218.
Котангенс угла ctg 12°34’56» = cos 12°34’56» / sin 12°34’56» = 4,4802722491.
Секанс sec 12°34’56» = 1 / cos 12°34’56» = 1,0246065402.
Косеканс cosec 12°34’56» = 1 / sin 12°34’56» = 4,5905162484.
Версинус versin 12°34’56» = 1 — cos 12°34’56» = 0,0240155994.
Гаверсинус haversin 12°34’56» = 0,0240155994 / 2 = 0,0120077997.
Экссеканс exsec 12°34’56» = 1,0246065402 — 1 = 0,0246065402.
Экскосеканс excsc 12°34’56» = 4,5905162484 — 1 = 3,5905162484.
Дано:
ΔABC – прямоугольный треугольник,
гипотенуза AB = c,
катет BC = a,
катет AC = b,
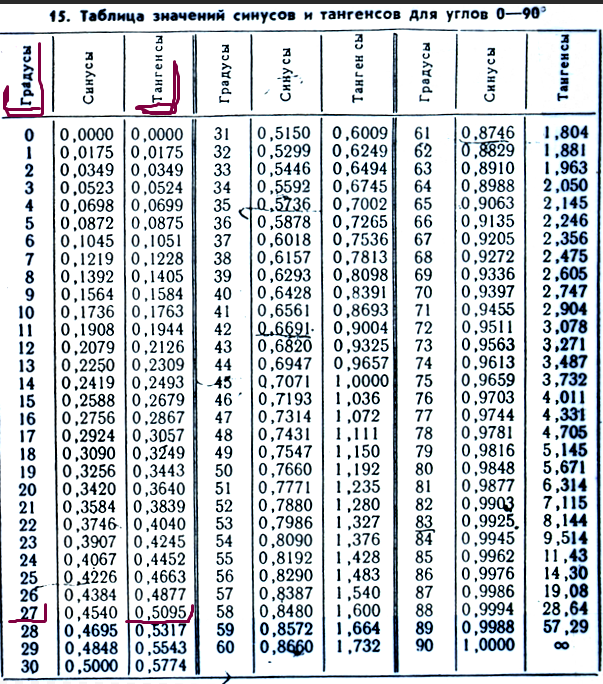
Таблица значений синуса угла
В геометрии синус угла A – отношение противолежащего катета «a» к гипотенузе «c».
Математическая формула синуса. sin A = a/c
Синус угла 0 градусов: sin 0° = sin 0 = 0
Синус угла 30 градусов: sin 30° = sin (π/6) = 1/2
Синус угла 45 градусов: sin 45° = sin (π/4) = √2/2
Синус угла 60 градусов: sin 60° = sin (π/3) = √3/2
Синус угла 90 градусов: sin 90° = sin (π/2) = 1
Синус угла 180 градусов: sin 180° = 0
Таблица косинуса угла
Косинус угла A – отношение прилежащего катета «b» к гипотенузе «c».
Формула косинуса. cos A = b/c
Косинус угла 0 градусов: cos 0° = cos 0 = 1
Косинус угла 30 градусов: cos 30° = cos (π/6) = √3/2
Косинус угла 45 градусов: cos 45° = cos (π/4) = √2/2
Косинус угла 60 градусов: cos 60° = cos (π/3) = 1/2
Косинус угла 90 градусов: cos 90° = cos (π/2) = 0
Косинус угла 180 градусов: cos 180° = –1
Таблица тангенса угла
В тригонометрии тангенс угла A – отношение противолежащего катета «a» к прилежащему катету «b».
Геометрическая формула тангенса.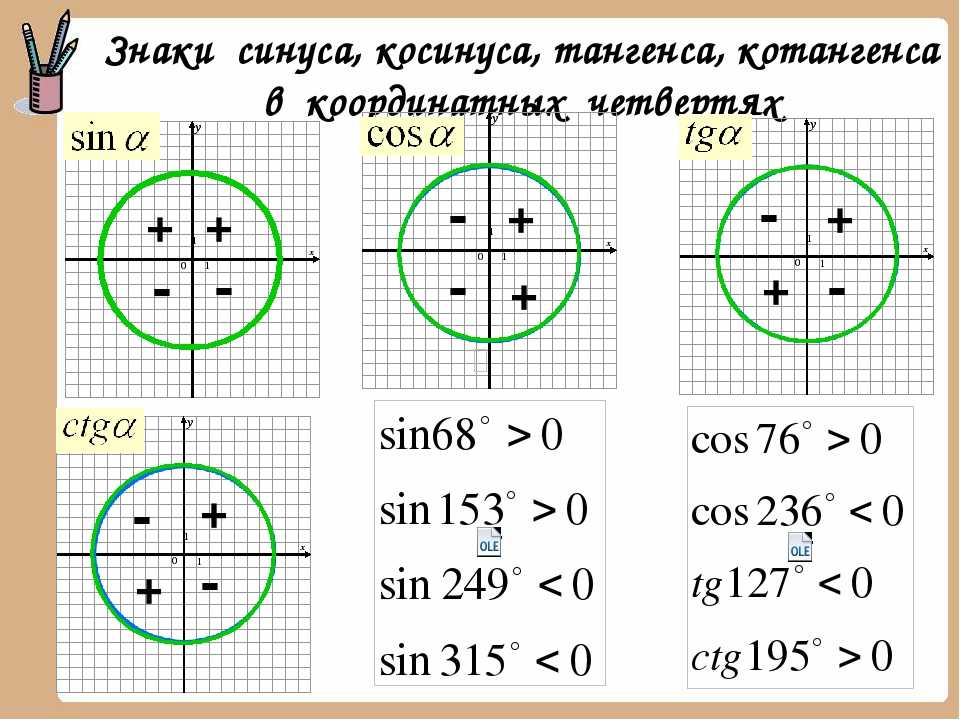
tg A = a/b
Тангенс угла 0 градусов: tg 0° = tg 0 = 0
Тангенс угла 30 градусов: tg 30° = tg (π/6) = √3/3
Тангенс угла 45 градусов: tg 45° = tg (π/4) = 1
Тангенс угла 60 градусов: tg 60° = tg (π/3) = √3
Тангенс угла 90 градусов: tg 90° = tg (π/2) = не определяется
Тангенс угла 180 градусов: tg 180° = 0
Котангенс угла
Котангенс угла A – отношение длины прилежащего катета «b» к противолежащему катету «a».
Формула котангенса. ctg A = b/a
Секанс
Секанс угла A равен отношению гипотенузы «c» к длине прилежащего катета «b».
Формула секанса. sec A = c/b
Косеканс
Косеканс угла A – отношение гипотенузы «c» к противолежащему катету «a».
Формула косеканса. cosec A = c/a
Версинус
Формула версинуса. versin A = 1 — cos A.
Коверсинус
Коверсинус рассчитывается как coversin A = 1 — sin A.
Гаверсинус
Формула гаверсинуса. haversin A = (versin A)/2.
Экссеканс
Экссеканс вычисляется по формуле: exsec A = sec A — 1.
Экскосеканс
Формула экскосеканса. excsc A = cosec A — 1.
Тангенс онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор вычислит синус, косинус, тангенс, котангенс, секанс, косеканс угла как в градусной, так и в радианной мере.
Введите число
синус (sin)косинус (cos)тангенс (tg)котангенс (ctg)секанс (sec)косеканс (cosec)градусырадианы
Что такое тангенс угла
Пусть задан прямоугольный треугольник ABC с острым углом α, тогда тангенсом угла α будет отношение противолежащего катета к прилежащему tg α = BC/AB.
Тангенс угла можно определить как отношение синуса угла к косинусу данного угла
tg α = sin α / cos α
Так же для определения тангенса угла можно воспользоваться окружностью, построенной в декартовой системе координат, радиуса R и центром в начале координат O.
На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
Для вычисления тангенса угла, можно также воспользоваться осью тангенсов. Определим окружность радиуса R как единичную с центром в начале координат O. Параллельно оси y, на расстоянии равном радиусу окружности расположим прямую x=1. На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α и продолжим луч OP до пересечения с прямой x=1. Тангенсу угла α будет соответствовать значение в точке B.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
тригонометрия — Как получить значение синуса/косинуса из тангенса
спросил
Изменено 5 лет, 3 месяца назад
Просмотрено 76 тысяч раз
$\begingroup$
Я знаю, что: $\tan(\alpha) = 1/2$.
Как получить чистые значения синуса/косинуса 9\circ$) углы $\alpha$.
2) Вы знаете, что тангенс $\alpha$ равен ${1\over2}$. Поскольку $\tan={\text{противоположный}\over \text{прилегающий}}$, вы можете обозначить сторону треугольника, примыкающую к $\alpha$, «1», а противоположную сторону — «2».
3) По теореме Пифагора можно найти длину гипотенузы треугольника.
4) Теперь вы можете прочитать $\sin(\alpha)$ из завершенного треугольника. И помните, что грех от угла противоположен/гипотенуза — 1/радикал 5 92 \alpha = \frac{4}{5}.$$
Таким образом, возможно $$\sin \alpha = \pm \frac{1}{\sqrt{5}}, \quad \cos \alpha = \pm \frac{2}{\sqrt{5}}.$$
Нам еще нужно показать, что эти возможности возможны. Мы знаем, что существует $\alpha$, такое что $\tan \alpha = \frac{1}{2}$. т.е. исходное уравнение имеет решение. Теперь, если $\alpha$ — решение, то $\alpha + \pi$ — тоже. Отсюда мы можем сделать вывод, что и $\sin \alpha = \frac{1}{\sqrt{5}}$, и $\sin \alpha = -\frac{1}{\sqrt{5}}$ достижимы и так и $\cos \alpha = \pm \frac{1}{\sqrt{5}}$.
Причем знаки должны быть одинаковыми для обоих. Таким образом, решения
$$(\cos\alpha,\sin\alpha)\in\{(\frac{1}{\sqrt{5}}, \frac{1}{\sqrt{5}}), (-\frac{ 1}{\sqrt{5}}, -\frac{1}{\sqrt{5}})\}.$$
$\endgroup$
Калькулятор тригонометрии для преобразования значений в sin, cos, tan и т. д.
Тригонометрические функции определены с помощью единичной окружности.
| Введите значение: |
| Грех | |
| Кос | |
| Желто-коричневый | |
| Детская кроватка | |
| сек | |
| Косек |
| Дуговой грех | |
| Arc Cos | |
| Загар | |
| Дуговая кроватка | |
| Арк сек | |
| Арк Косек |
градусов
| Грех | |
| Кос | |
| Желто-коричневый | |
| Детская кроватка | |
| сек | |
| Косек |
| Дуговой грех | |
| Arc Cos | |
| Загар дуги | |
| Дуговая кроватка | |
| Арк сек | |
| Арк Косек |
Sin(θ) — вертикальная составляющая, cos(θ) — горизонтальная координата конечной точки дуги.
где
Sin(q) = противоположность / гипотенуза
Cos(q) = смежная / гипотенуза
Tan(q) = противоположная
Таблица основных тригонометрических чисел наиболее распространенных углов выглядит следующим образом:
| Угол | грех | потому что | желто-коричневый | детская кроватка | сек | косек |
| 0 или | 0 | 1 | 0 | Не определено | 1 | Не определено |
| 30 или | 1 / 2 | √3 / 2 | 1 / √3 | √3 | 2 / √3 | 2 |
| 45 или | 1 / √2 | 1 / √2 | 1 | 1 | √2 | √2 |
| 60 или | √3 / 2 | 1 / 2 | √3 | 1 / √3 | 2 | 2 / √3 |
| 90 или | 1 | 0 | Не определено | 0 | Не определено | 1 |
Разница между радианом (RED) и градусами (DEG)
Радиан равен 180 градусам, потому что весь круг равен 360 градусам и равен двум пи радианам.