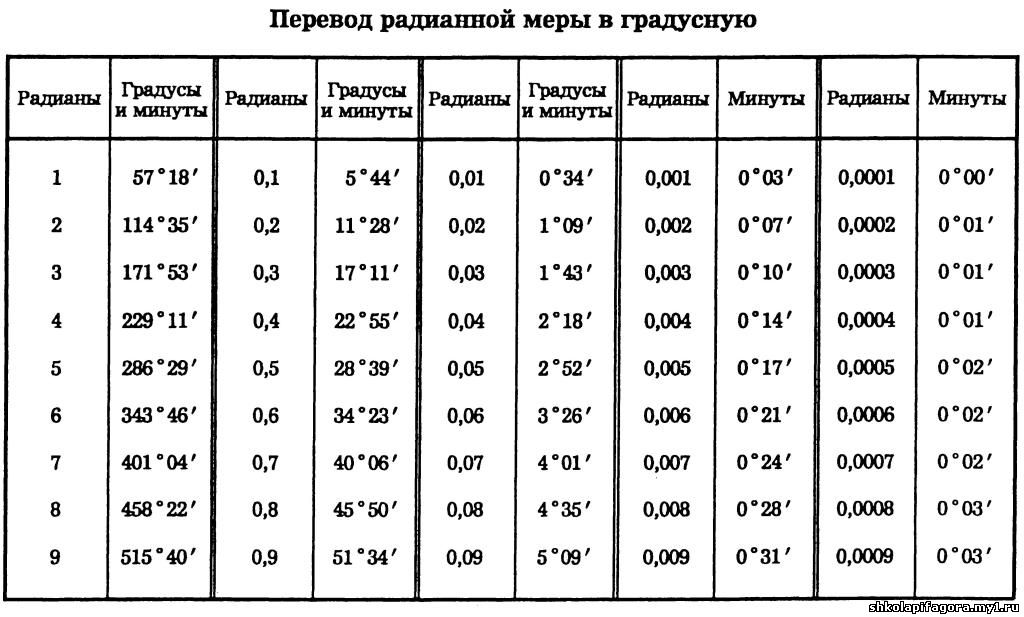
| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Проценты на знаках крутого уклона » АвтоНоватор
Каждый автоводитель хотя бы раз за свой стаж вождения проезжал по холмистой местности. Перед крутыми спусками и подъемами стоят знаки с черным треугольником процентным обозначением. Что эти проценты означают и для чего указываются?
Перед крутыми спусками и подъемами стоят знаки с черным треугольником процентным обозначением. Что эти проценты означают и для чего указываются?
Что означают проценты
На знаках крутых спусков и подъемов в процентах обозначают тангенс угла наклона. Если посмотреть на дорогу сбоку и представить ее в виде прямоугольного треугольника — сама дорога это гипотенуза, линия горизонта это прилежащий катет, а высота спуска это противолежащий катет, то тангенс — отношение высоты подъема или спуска к линии горизонта. Другими словами, проценты показывают изменение вертикального уровня дороги в метрах на сто метровом участке.
Почему используются проценты
В процессе дорожного движения угол наклона в градусах водителю ни о чем не скажет. А количество процентов обозначает на сколько машина спустится или поднимется через каждые 100 метром, то есть если на знаке стоит 12%, это означает подъем или спуск на 12 метров через каждые 100 метров.
Второй момент удобства указания угла наклона в процентах заключается в том, что его тангенс равен коэффициенту сцепления колеса автомобиля с дорожным покрытием. Благодаря этому можно рассчитать скорость движения, с которой можно подняться в гору или спуститься по склону, не вылетев с трассы.
Благодаря этому можно рассчитать скорость движения, с которой можно подняться в гору или спуститься по склону, не вылетев с трассы.
Как перевести проценты в градусы
Перевести угол наклона из процентов в градусы можно на калькуляторе в телефоне, переключив его в «инженерный режим». Количеством градусов будет считаться значение арктангенса процента, изображённого на дорожном знаке.
Зачем водителю знать точное значение крутизны подъема или спуска
В зависимости от погодных условий сцепление колёс с дорожным покрытием будет разным. Наверняка каждый водитель ездил и в гололёд, и в дождь, и в снег, ощущая эту разницу. Указатели со спуском или подъемом уставаливают в том месте, где угловой коэффициент приближается к 10%. Если в дождливую погоду на подъеме затормозить, то как минимум машина не поднимется.
К тому же в старых приморских городах существуют улицы, в которых угол наклона превышает всевозможные нормативы. То есть при движении по склону мокрого асфальта с угловым коэффициентом 20% эффективность торможения падает в два раза.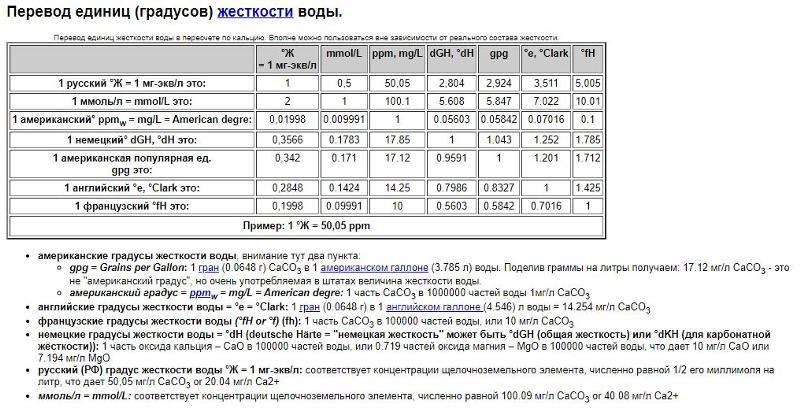
Поэтому важно обращать внимание на знаки подъемов и спусков, особенно в плохую погоду. Знание коэффициента сцепления колес с дорогой в зависимости от погодных условий и угла наклона может даже спасти жизнь в некоторых ситуациях.
- Автор: iarriba
- Распечатать
Оцените статью:
(42 голоса, среднее: 4.4 из 5)
Поделитесь с друзьями!
Adblock
detector
Z — Таблица преобразования % в отношение к градусам
Читать 47696 раз
| Преобразование процентного уклона/градиента/тангажа в отношение или градусы | ||||||
| % | Соотношение | Градусов | ||||
| 0 | 0,0 | 0,000 | ||||
| 1 | 100,0 | 0,571 | ||||
| 2 | 50,0 | 1,142 | ||||
| 3 | 33,3 | 1,713 | ||||
| 4 | 25,0 | 2,284 | ||||
| 5 | 20,0 | 2,855 | ||||
| 6 | 16,7 | 3,426 | ||||
| 7 | 14,3 | 3,997 | ||||
| 8 | 12,5 | 4,568 | ||||
| 9 | 11.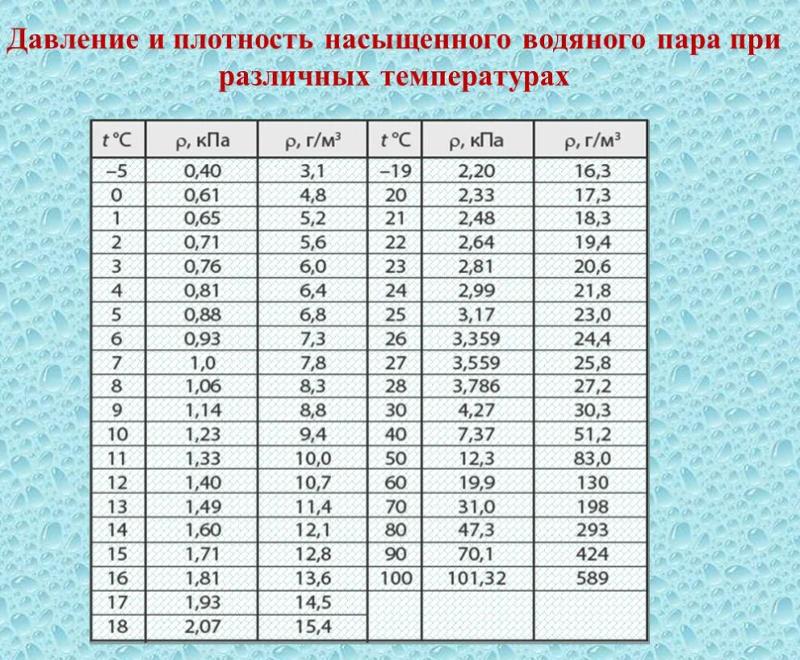 1 1 | 5.139 | ||||
| 10 | 10,0 | 5.710 | ||||
| 11 | 9.1 | 6.281 | ||||
| 12 | 8,3 | 6.852 | ||||
| 13 | 7,7 | 7,423 | ||||
| 14 | 7.1 | 7,994 | ||||
| 15 | 6,7 | 8,565 | ||||
| 16 | 6,3 | 9. 136 136 | ||||
| 17 | 5,9 | 9.707 | ||||
| 18 | 5,6 | 10,278 | ||||
| 19 | 5,3 | 10.849 | ||||
| 20 | 5,0 | 11.310 | ||||
| 21 | 4,8 | 11.881 | ||||
| 22 | 4,5 | 12.452 | ||||
| 23 | 4,3 | 13. 023 023 | ||||
| 24 | 4,2 | 13.594 | ||||
| 25 | 4,0 | 14.165 | ||||
| 26 | 3,8 | 14.736 | ||||
| 27 | 3,7 | 15.307 | ||||
| 28 | 3,6 | 15.878 | ||||
| 29 | 3,4 | 16.170 | ||||
| 30 | 3,3 | 16.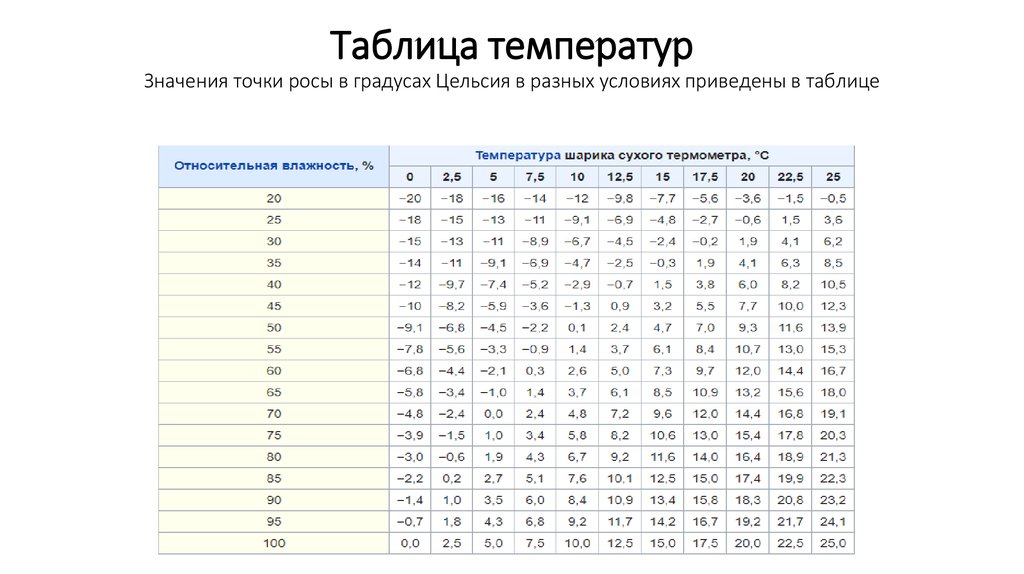 700 700 | ||||
| 31 | 3,2 | 17.267 | ||||
| 32 | 3.1 | 17.833 | ||||
| 33 | 3,0 | 18.400 | ||||
| 34 | 2,9 | 18,967 | ||||
| 35 | 2,9 | 19.533 | ||||
| 36 | 2,8 | 20.100 | ||||
| 37 | 2,7 | 20. 667 667 | ||||
| 38 | 2,6 | 21.233 | ||||
| 39 | 2,6 | 21.310 | ||||
| 40 | 2,5 | 21.800 | ||||
| 41 | 2,4 | 22.277 | ||||
| 42 | 2,4 | 22.754 | ||||
| 43 | 2,3 | 23.231 | ||||
| 44 | 2,3 | 23. 708 708 | ||||
| 45 | 2,2 | 24.185 | ||||
| 46 | 2,2 | 24.662 | ||||
| 47 | 2.1 | 25.139 | ||||
| 48 | 2.1 | 25.616 | ||||
| 49 | 2,0 | 26.093 | ||||
| 50 | 2,0 | 26.570 | ||||
| 51 | 2,0 | 27. 009 009 | ||||
| 52 | 1,9 | 27.448 | ||||
| 53 | 1,9 | 27.887 | ||||
| 54 | 1,9 | 28.326 | ||||
| 55 | 1,8 | 28.765 | ||||
| 56 | 1,8 | 29.204 | ||||
| 57 | 1,8 | 29.643 | ||||
| 58 | 1,7 | 30. 082 082 | ||||
| 59 | 1,7 | 30.521 | ||||
| 60 | 1,7 | 30,960 | ||||
| 61 | 1,6 | 31.363 | ||||
| 62 | 1,6 | 31.766 | ||||
| 63 | 1,6 | 32.169 | ||||
| 64 | 1,6 | 32.572 | ||||
| 65 | 1,5 | 32,975 | ||||
| 66 | 1,5 | 33. 378 378 | ||||
| 67 | 1,5 | 33.781 | ||||
| 68 | 1,5 | 34.184 | ||||
| 69 | 1,4 | 34.587 | ||||
| 70 | 1,4 | 34,990 | ||||
| 71 | 1,4 | 35.660 | ||||
| 72 | 1,4 | 36.330 | ||||
| 73 | 1,4 | 37. 000 000 | ||||
| 74 | 1,4 | 37.670 | ||||
| 75 | 1,3 | 38.340 | ||||
| 76 | 1,3 | 39.010 | ||||
| 77 | 1,3 | 39.680 | ||||
| 78 | 1,3 | 40.350 | ||||
| 79 | 1,3 | 41.020 | ||||
| 80 | 1,3 | 38. 660 660 | ||||
| 81 | 1,2 | 38,993 | ||||
| 82 | 1,2 | 39.326 | ||||
| 83 | 1,2 | 39.659 | ||||
| 84 | 1,2 | 39,992 | ||||
| 85 | 1,2 | 40.325 | ||||
| 86 | 1,2 | 40.658 | ||||
| 87 | 1,1 | 40,991 | ||||
| 88 | 1,1 | 41. 324 324 | ||||
| 89 | 1,1 | 41.657 | ||||
| 90 | 1,1 | 41.990 | ||||
| 91 | 1,1 | 42.291 | ||||
| 92 | 1,1 | 42.592 | ||||
| 93 | 1,1 | 42.893 | ||||
| 94 | 1,1 | 43.194 | ||||
| 95 | 1,1 | 43. 495 495 | ||||
| 96 | 1,0 | 43.796 | ||||
| 97 | 1,0 | 44.097 | ||||
| 98 | 1,0 | 44.398 | ||||
| 99 | 1,0 | 44.699 | ||||
| 100 | 1,0 | 45.000 | ||||
Еще в этой категории: « Контакты Горные перевалы Южная Африка Стена Facebook »
вернуться к началу
Почему велосипедисты используют %, а лыжники — градусы для склонов?
Вопрос в наш почтовый ящик. «Мой друг увлекается внетрассовым катанием и всегда говорит о градиентах в градусах, скажем, 30 градусов. Однако для велосипедистов чаще используются проценты. Почему такая разница и как перевести одно в другое?»
«Мой друг увлекается внетрассовым катанием и всегда говорит о градиентах в градусах, скажем, 30 градусов. Однако для велосипедистов чаще используются проценты. Почему такая разница и как перевести одно в другое?»
Градусы и проценты
Лыжники действительно используют градусы, чтобы указать, насколько крутой склон. Количество градусов рассчитывается от горизонтальной оси или оси X.
Процент наклона можно рассчитать двумя способами. Первоначальный способ заключается в том, чтобы посмотреть, насколько поднимается дорога (а) на определенном расстоянии, измеренном по горизонтали (б). Однако большинство профильных веб-сайтов (таких как Cyclingcols и Climbfinder) используют пройденное расстояние (c) вместо горизонтального расстояния, так что (фиктивный) подъем, который идет прямо вверх, является 100% крутым, а не бесконечным. Между прочим, для дорог до 40 % практически не имеет значения, какую из этих двух формул использовать. Для очень экстремальных подъемов разница становится больше.
Насколько крут Мортироло?
Для этого расстояния используются разные значения (B или C). Например, в большинстве профилей высот используется один километр или 500 метров. Но ваш велокомпьютер использует гораздо меньшее значение, иногда всего 5 или 10 метров. Вот почему вы иногда можете видеть на экране чрезвычайно высокие значения (иногда до 30%), когда вы лезете, в то время как среднее значение для этого километра во много раз ниже. Это часто приводит к приятным разговорам за выпивкой: насколько крутым был Мортироло на самом деле? Все зависит от измеряемого расстояния. Кроме того, велокомпьютер с его барометрическим альтиметром всегда отстает от реальности. Если вы въезжаете в крутую часть Коль-де-ла-Редут со скоростью 40 км/ч, вы увидите страшные 20% на экране намного позже.
Почему проценты?
В дорожном строительстве проценты распространены, потому что они понятнее, чем градусы. Это потому, что процент растет быстрее, чем количество градусов. Используя оригинальный способ расчета процентов, угол в 45 градусов означает наклон в 100%. Используя проценты, небольшие различия намного легче прояснить. Если наклон более 45 градусов, то измерять в процентах уже нет особого смысла, потому что число быстро становится все больше и больше. Процент 9Наклон 0 градусов даже бесконечен.
Используя оригинальный способ расчета процентов, угол в 45 градусов означает наклон в 100%. Используя проценты, небольшие различия намного легче прояснить. Если наклон более 45 градусов, то измерять в процентах уже нет особого смысла, потому что число быстро становится все больше и больше. Процент 9Наклон 0 градусов даже бесконечен.
Преобразование
Преобразование не так просто, если вы хотите узнать точный расчет, вы можете прочитать его здесь. На рисунке ниже (источник: Википедия) четко показаны отношения между числами.
Едете по горнолыжному склону? Забудьте об этом (в большинстве случаев)
Изображение также сразу дает понять, насколько крутые горнолыжные склоны на самом деле по сравнению с подъемами. Самый простой склон (в большинстве альпийских стран) синий. Обычно это максимум 20 градусов, что составляет более 30%! Любой, кто поднимался на Коль-де-ла-Лоз и немного катался по голубой трассе, знает, насколько это сложно, так что это неудивительно.