Периметр прямоугольника с заданной площадью и длиной Калькулятор
✖Площадь прямоугольника — это общее количество плоскостей, ограниченных границей прямоугольника.ⓘ Площадь прямоугольника [A] | акрАкко (служба США)НаходятсяАрпентамбарКарроКруговая дюймаКруговая MilCuerdaарамДунамРаздел электрон КрестаГаусадьбаMuпингплощадьPyongклочок землиСабинРазделКвадратный АнгстремПлощадь СантиметрПлощадь цепи Площадь декаметровойквадратный дециметрКвадратный футКвадратный фут (служба США)Площадь гектометровыеКвадратный дюймквадратный километрКвадратный метрПлощадь микрометраПлощадь MilКвадратная миляКвадратная миля (римская)Квадратная миля (Статут)Квадратная миля (служба США)Площадь МиллиметрПлощадь NanometreМера площадиПлощадь полюсаПлощадь РодКвадратный Rod (служба США)Квадратный дворрастяжениегородокВарас Castellanas CuadВарас Conuqueras Cuad | +10% -10% | |
✖Длина прямоугольника — это любая из пары параллельных сторон, которая длиннее оставшейся пары параллельных сторон. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Периметр прямоугольника — это общая длина всех граничных линий прямоугольника. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Периметр прямоугольника с заданной площадью и длиной Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Площадь прямоугольника: 48 Квадратный метр —> 48 Квадратный метр Конверсия не требуется
Длина прямоугольника: 8 метр —> 8 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
28 метр —> Конверсия не требуется
< 25 Периметр прямоугольника Калькуляторы
Периметр прямоугольника по площади и тупому углу между диагоналями
Идти Периметр прямоугольника = 2*sqrt(Площадь прямоугольника*cosec((pi-Тупой угол между диагоналями прямоугольника)/2)*sec((pi-Тупой угол между диагоналями прямоугольника)/2)+(2*Площадь прямоугольника))
Периметр прямоугольника по радиусу окружности и углу между диагональю и шириной
Идти Периметр прямоугольника = 4*Окружность прямоугольника*sqrt(1+(2*sin((pi/2)-Угол между диагональю и шириной прямоугольника)*cos((pi/2)-Угол между диагональю и шириной прямоугольника)))
Периметр прямоугольника по диагонали и углу между диагональю и шириной
Идти Периметр прямоугольника = 2*Диагональ прямоугольника*sqrt(1+(2*sin((pi/2)-Угол между диагональю и шириной прямоугольника)*cos((pi/2)-Угол между диагональю и шириной прямоугольника)))
Периметр прямоугольника по радиусу окружности и тупому углу между диагоналями
Идти Периметр прямоугольника = 4*Окружность прямоугольника*sqrt(1+(2*sin((pi-Тупой угол между диагоналями прямоугольника)/2)*cos((pi-Тупой угол между диагоналями прямоугольника)/2)))
Периметр прямоугольника по диагонали и тупому углу между диагоналями
Идти Периметр прямоугольника = 2*Диагональ прямоугольника*sqrt(1+(2*sin((pi-Тупой угол между диагоналями прямоугольника)/2)*cos((pi-Тупой угол между диагоналями прямоугольника)/2)))
Периметр прямоугольника по площади и углу между диагональю и шириной
Идти Периметр прямоугольника = 2*sqrt((Площадь прямоугольника*sec(Угол между диагональю и шириной прямоугольника)*cosec(Угол между диагональю и шириной прямоугольника))+(2*Площадь прямоугольника))
Периметр прямоугольника с заданной площадью и углом между диагональю и длиной
Идти Периметр прямоугольника = 2*sqrt((Площадь прямоугольника*sec(Угол между диагональю и длиной прямоугольника)*cosec(Угол между диагональю и длиной прямоугольника))+(2*Площадь прямоугольника))
Периметр прямоугольника по площади и острому углу между диагоналями
Идти Периметр прямоугольника = 2*sqrt(Площадь прямоугольника*cosec(Острый угол между диагоналями прямоугольника/2)*sec(Острый угол между диагоналями прямоугольника/2)+(2*Площадь прямоугольника))
Периметр прямоугольника с учетом диаметра окружности и угла между диагональю и длиной
Идти Периметр прямоугольника = 2*Диаметр окружности прямоугольника*sqrt(1+(2*sin(Угол между диагональю и длиной прямоугольника)*cos(Угол между диагональю и длиной прямоугольника)))
Периметр прямоугольника по радиусу окружности и острому углу между диагоналями
Идти Периметр прямоугольника = 4*Окружность прямоугольника*sqrt(1+(2*sin(Острый угол между диагоналями прямоугольника/2)*cos(Острый угол между диагоналями прямоугольника/2)))
Периметр прямоугольника по диагонали и острому углу между диагоналями
Идти Периметр прямоугольника = 2*Диагональ прямоугольника*sqrt(1+(2*sin(Острый угол между диагоналями прямоугольника/2)*cos(Острый угол между диагоналями прямоугольника/2)))
Периметр прямоугольника по радиусу окружности и углу между диагональю и длиной
Идти Периметр прямоугольника = 4*Окружность прямоугольника*sqrt(1+(2*sin(Угол между диагональю и длиной прямоугольника)*cos(Угол между диагональю и длиной прямоугольника)))
Периметр прямоугольника по диагонали и углу между диагональю и длиной
Идти Периметр прямоугольника = 2*Диагональ прямоугольника*sqrt(1+(2*sin(Угол между диагональю и длиной прямоугольника)*cos(Угол между диагональю и длиной прямоугольника)))
Периметр прямоугольника по ширине и диаметру окружности
Идти Периметр прямоугольника = 2*(Ширина прямоугольника+sqrt(Диаметр окружности прямоугольника^2-Ширина прямоугольника^2))
Периметр прямоугольника по длине и диаметру окружности
Идти Периметр прямоугольника = 2*(Длина прямоугольника+sqrt(Диаметр окружности прямоугольника^2-Длина прямоугольника^2))
Периметр прямоугольника по ширине и радиусу окружности
Идти Периметр прямоугольника = 2*(Ширина прямоугольника+sqrt((4*Окружность прямоугольника^2)-Ширина прямоугольника^2))
Периметр прямоугольника по длине и радиусу окружности
Идти Периметр прямоугольника = 2*(Длина прямоугольника+sqrt((4*Окружность прямоугольника^2)-Длина прямоугольника^2))
Периметр прямоугольника по диагонали и ширине
Идти Периметр прямоугольника = 2*(sqrt(Диагональ прямоугольника^2-Ширина прямоугольника^2)+Ширина прямоугольника)
Периметр прямоугольника по диагонали и длине
Идти Периметр прямоугольника = 2*(Длина прямоугольника+sqrt(Диагональ прямоугольника^2-Длина прямоугольника^2))
Периметр прямоугольника с заданной площадью и длиной
Идти Периметр прямоугольника = (2*(Площадь прямоугольника+Длина прямоугольника^2))/Длина прямоугольника
Периметр прямоугольника по площади и ширине
Идти Периметр прямоугольника = 2*((Площадь прямоугольника/Ширина прямоугольника)+Ширина прямоугольника)
Периметр прямоугольника по площади и диаметру окружности
Идти Периметр прямоугольника = 2*sqrt(Диаметр окружности прямоугольника^2+(2*Площадь прямоугольника))
Периметр прямоугольника по площади и радиусу окружности
Идти Периметр прямоугольника = 2*sqrt((2*Площадь прямоугольника)+(4*Окружность прямоугольника^2))
Периметр прямоугольника по площади и диагонали
Идти Периметр прямоугольника = 2*sqrt(Диагональ прямоугольника^2+(2*Площадь прямоугольника))
Периметр прямоугольника
Идти Периметр прямоугольника = 2*(Длина прямоугольника+Ширина прямоугольника)
< 6 Периметр прямоугольника Калькуляторы
Периметр прямоугольника с заданной площадью и длиной формула
Периметр прямоугольника = (2*(Площадь прямоугольника+Длина прямоугольника^2))/Длина прямоугольника
P = (2*(A+l^2))/l
Что такое прямоугольник?
Прямоугольник — это двумерная геометрическая фигура, имеющая четыре стороны и четыре угла. Четыре стороны разделены на две пары, в которых каждая пара линий равна по длине и параллельна друг другу. А соседние стороны перпендикулярны друг другу. Обычно двумерные фигуры с четырьмя граничными ребрами называются четырехугольниками. Итак, прямоугольник — это четырехугольник, у которого все углы прямые.
Четыре стороны разделены на две пары, в которых каждая пара линий равна по длине и параллельна друг другу. А соседние стороны перпендикулярны друг другу. Обычно двумерные фигуры с четырьмя граничными ребрами называются четырехугольниками. Итак, прямоугольник — это четырехугольник, у которого все углы прямые.
Share
Copied!
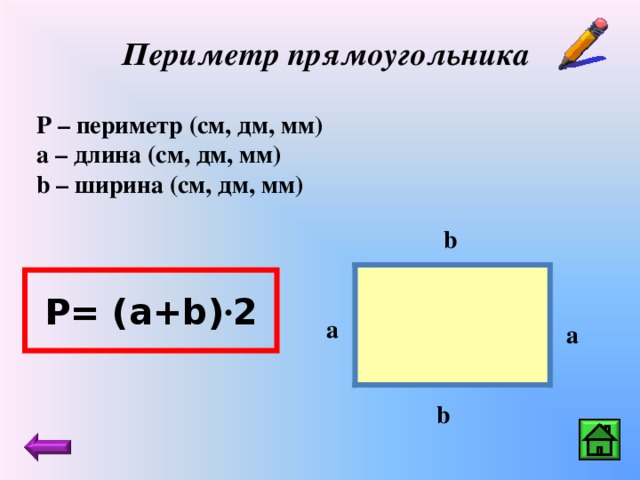
Периметр прямоугольника 2 класс
Тема урока: «Периметр прямоугольника»
Цели урока: познакомить с понятием «периметр прямоугольника», совершенствовать вычислительные навыки и умения решать задачи, развивать умение рассуждать, сопоставлять, сравнивать.
Планируемые результаты:
— Предметные: учить находить периметр прямоугольника разными способами, развивать геометрические представления, совершенствовать умение решать текстовые задачи.
— Личностные: определять личностный смысл изучения темы, применять новые знания на практике.
Тип урока: изучение нового материала.
Оборудование: учебник по Математике 2 класс 2 часть 2015 год; Программа «Школа России»; М.И. Моро, М.А.Бантова.
№ | Этап урока Метод и приемы | Хро-нометраж | Содержание урока. Деятельность учителя. | Деятельность ученика | УУД |
1. | Включение в учебную деятельность Словес.: слово учителя. | ≈ 3 | Приветствие. (слайд 1 ) Давайте, ребята. Учиться считать, Делить, умножать, Прибавлять, вычитать. Запомните все, Что без точного счета Не сдвинется с места Любая работа. Чтение слов Меркушевича (слайд 2) | Приветствовать учителя, настраиваться на работу. | Р.: принимают и сохраняют уч. задачу. К.: участвуют в учебном диалоге; формулируют ответы и выводы; обмениваются мнениями; строят реч.
|
2. 3. 4 5. 6. 7. 8. 9. 10. | Актуализация знаний Практич: устный счет. Практич.: логическая разминка Практич.: работа с фигурами. Самоопределение к деятельности Словес.: ответы на вопросы. Словес.: определение темы и цели урока. Практич: писм. задание.
Практич.: нахождение периметра. Практич.: анализ и решение задачи. Практич: сам. Работа. Первичное усвоение новых знаний. Физминутка Включение нового в систему знаний. Сравнение с эталоном. Реализация построенного проекта Закрепление с проговариванием во внешней речи. Самостоятельная работа по повторению. Рефлексия | 5 5 6 1 1 5 6 10 1 | Устный счёт Запишите число, классная работа. — Прочитайте слова , расположив ответы в порядке возрастания 15-(6+5) (У) 17-(18-9) (Н) 4+8-7 (М) (90+5)-(43-40) (А) (46-40)+(58-8) (Ц) (3+8)+(12-6) (И) — Какие выражения можно заменить умножением? Почему? 3+3+3+3 а+а+а 5+5+4+4 а+в+а+в 7+5+3 — Расставьте вместо звездочек знаки + и – та, чтобы получилось верное равенство. 2*6*3*4*5*8=12 (2+6-3+4-5+8) Сегодня мы совершим ещё одно путешествие в страну Геометрия. Что означает это слово? Посмотрите на этот замок(слайд3) — Из каких геометрических фигур состоит замок? — На какие 2 группы можно разделить все эти фигуры?(многоугольники и круг) -Если круг убрать? — Как теперь можно разделить фигуры на 2 группы?(треугольники и четырехугольники) Если треугольники убрать. — Как назвать одним словом оставшиеся фигуры?(четырехугольники) — На какие 2 группы их можно разделить?(фигуры с прямыми и без прямых углов) — Какие фигуры остались?(прямоугольники) — Докажите, что оставшиеся фигуры-прямоугольники. — Сколько пар одинаковых сторон у прямоугольника?(2) — Что можно узнать, зная длину сторон прямоугольника? (периметр) -Давайте измерим стороны этого прямоугольника и найдём его периметр. ( Р= 5+11+5+11 (см)) -Можно ли эту сумму заменить произведением? — Как вы это определили? (если слагаемые одинаковые, то сложение можно заменить умножением) — Сколько произведений по ним можно составить?(2) — Тогда скажите, о чем мы с вами сегодня поговорим на уроке? — Какие цели поставим на уроке?(учиться находить периметр прямоугольника разными способами) (слайд 4) — Хорошо. — А теперь постройте у себя в тетрадях прямоугольник со сторонами 3 см и 6 см и подпишите длину его сторон. — Что такое периметр?(сумма длин всех сторон) -А сейчас мы в этом потренируемся. — Найдите периметр прямоугольника.(3+6+3+6=18(см)) — Это первый способ нахождения периметра прямоугольника. (слайд 5) — Сумму каких слагаемых можно заменить умножение?(3+3 и 6+6) — Замените. (3*2+6*2=18 (см)) — Это 2 способ нахождения периметра прямоугольника. Но можно по-другому записать это решение. — Посмотрите на свой прямоугольник. Сколько разных сторон у него?(2:длина и ширина) — Как эти стороны называются?(длина и ширина) — Запишите их сумму?(3+6) — Сколько раз в прямоугольнике повторяются эти стороны?(2) Учитель делает запись на доске, а учащиеся в тетрадях. (3+6)*2=18 (см) — Это 3 способ нахождения периметра. — Обозначим длину прямоугольника латинской буквой а, а ширину – буквой в. Поставим в наши решения. — Мы получили три формулы нахождения периметра прямоугольника. Р=а+в+а+в Р=а*2+в*2 Р=(а+в)*2 (слайд6) №1(стр.52)(слайд7) — Посмотрите, как находили периметр прямоугольника. — Совпадает ли решение с теми формулами, которые мы с вами только что вывели? №2(стр.52)(слайд 6) — Сколько способов нахождения периметра вы знаете? — Прочитайте условие. — Найдите самостоятельно периметр этого прямоугольника разными способами. 1)Нахождение периметра прямоугольника ( по эталону) Работа в тетради по вариантам. Найдите периметр прямоугольника по формуле: 1 вариант – Р=а+в+а+в 2 вариант – Р=а*2+в*2 2)Проверка по эталону. -Как найти периметр прямоугольника? -Для чего нужно находить периметр прямоугольника? -Людям каких профессий это необходимо? -Пользуются ли ваши родители нахождением периметра? №3 — Прочитайте условие задачи. — Что нужно узнать? №7 (Самостоятельное выполнение 1 группа -1 и 2 примеры, 2 группа – 3 и 4 примеры. (работа в группах) (слайд7) 82-46=36 37+58=95 49-38=11 65+35=100 Ребята, как вы думаете, пригодится ли нам в жизни знание формул периметра прямоугольника? Давайте мы ещё раз их запишем на доске и в тетрадях. | Вычислять. Отвечать на вопросы. Доказывать. Определять тему, ставить цели. Отвечать на вопросы. Находить 2 способ нахождения периметра. Записывать решение в тетрадь. Находить 3 способ вычисления периметра. Находить периметр, записывать решение. Записывать решение задачи. Производить вычисления. Делать выводы, отвечать на вопросы. | Р.: принимают и сохраняют уч. задачу при выполнении заданий; действуют с уче-том выделенных учителем ориентиров; применяют освоенные способы действия. К. : участвуют в учебном диалоге; формулируют ответы и выводы; обмениваются мнениями; строят реч. высказывания. К. : участвуют в учебном диалоге; формулируют ответы и выводы; обмениваются мнениями; строят реч. высказывания.
. Р.: принимают и сохраняют уч. задачу при выполнении заданий; действуют с уче-том выделенных учителем ориентиров; применяют освоенные способы действия. К. : участвуют в учебном диалоге; формулируют ответы и выводы; обмениваются мнениями; строят реч. высказывания. П: извлекать необходимую информацию из текста учителя, ориентировать в системе знаний. Р.: осмысляют уч. материал; действуют с учетом выделенных учителем ориентиров |
11. 12. | Итог урока. (предметная). Словес.: ответы на вопросы, самоанализ Домашнее задание
| ≈1 1 | — Чем мы с вами занимались на уроке? — Какие поставили в начале урока цели? — Достигли их? — Какое открытие мы сделали на уроке? — Оцените свою работу на уроке. (слайд 8) Домашнее задание с. 52 №4, 8 Повторить формулы нахождение периметра прямоугольника. (Слайд 9) | Делать вывод, отвечать на вопросы. Записывать домашнее задание | Р.: осмысляют уч. материал; действуют с учетом выделенных учителем ориентиров; адекватно воспринимают оценку учителя. |
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/251217-perimetr-prjamougolnika-2-klass
| 1 | Найти том | сфера (5) | | |
| 2 | Найти площадь | круг (5) | | |
| 3 | Найдите площадь поверхности | сфера (5) | | |
| 4 | Найти площадь | круг (7) | | |
| 5 | Найти площадь | круг (2) | | |
| 6 | Найти площадь | круг (4) | | |
| 7 | Найти площадь | круг (6) | | |
| 8 | Найти том | сфера (4) | | |
| 9 | Найти площадь | круг (3) | | |
| 10 9(1/2) | ||||
| 11 | Найти простую факторизацию | 741 | ||
| 12 | Найти том | сфера (3) | | |
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | ||
| 14 | Найти площадь | круг (10) | | |
| 15 | Найти площадь | круг (8) | | |
| 16 | Найдите площадь поверхности | сфера (6) | | |
| 17 | Найти простую факторизацию | 1162 | ||
| 18 | Найти площадь | круг (1) | | |
| 19 | Найдите окружность | круг (5) | | |
| 20 | Найти том | сфера (2) | | |
| 21 | Найти том | сфера (6) | | |
| 22 | Найдите площадь поверхности | сфера (4) | | |
| 23 | Найти том | сфера (7) | | |
| 24 | Оценить | квадратный корень из -121 | ||
| 25 | Найти простую факторизацию | 513 | ||
| 26 | Оценка | квадратный корень из 3/16* квадратный корень из 3/9 | ||
| 27 | Найти том | коробка (2)(2)(2) | | |
| 28 | Найдите окружность | круг (6) | | |
| 29 | Найдите окружность | круг (3) | | |
| 30 | Найдите площадь поверхности | сфера (2) | | |
| 31 | Оценить | 2 1/2÷22000000 | ||
| 32 | Найдите Том | коробка (5)(5)(5) | | |
| 33 | Найти том | коробка (10)(10)(10) | | |
| 34 | Найдите окружность | круг (4) | | |
| 35 | Преобразование в проценты | 1,7 | ||
| 36 | Оценить | (5/6)÷(4/1) | ||
| 37 | Оценить | 3/5+3/5 | ||
| 38 | Оценить | ф(-2) | 92 | |
| 40 | Найти площадь | круг (12) | | |
| 41 | Найти том | коробка (3)(3)(3) | | |
| 42 | Найти том | коробка (4)(4)(4) | 92-4*-1+2||
| 45 | Найти простую факторизацию | 228 | ||
| 46 | Оценить | 0+0 | ||
| 47 | Найти площадь | круг (9) | | |
| 48 | Найдите окружность | круг (8) | | |
| 49 | Найдите окружность | круг (7) | | |
| 50 | Найти том | сфера (10) | | |
| 51 | Найдите площадь поверхности | сфера (10) | | |
| 52 | Найдите площадь поверхности | сфера (7) | | |
| 53 | Определить, является простым или составным | 5 | ||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | ||
| 61 | Найдите площадь поверхности | сфера (12) | | |
| 62 | Найти том | сфера (1) | | |
| 63 | Найдите окружность | круг (2) | | |
| 64 | Найти том | коробка (12)(12)(12) | | |
| 65 | Добавить | 2+2= | ||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | |
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | ||
| 68 | Оценить | 7/40+17/50 | ||
| 69 | Найти простую факторизацию | 1617 | ||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | ||
| 71 | Оценить | 9÷4 | ||
| 72 | Оценка 92 | |||
| 74 | Оценить | 1-(1-15/16) | ||
| 75 | Преобразование в упрощенную дробь | 8 | ||
| 76 | Оценка | 656-521 | 9-2 | |
| 79 | Оценить | 4-(6)/-5 | ||
| 80 | Оценить | 3-3*6+2 | ||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | |
| 82 | Найдите площадь поверхности | сфера (8) | | |
| 83 | Найти площадь | круг (14) | | |
| 84 | Преобразование в десятичное число | 5 ноября | ||
| 85 9-2 | ||||
| 88 | Оценить | 1/2*3*9 | ||
| 89 | Оценить | 4/4-17/-4 | ||
| 90 | Оценить | 11. 02+17.19 02+17.19 | ||
| 91 | Оценить | 3/5+3/10 | ||
| 92 | Оценить | 4/5*3/8 | ||
| 93 | Оценить | 6/(2(2+1)) | ||
| 94 | Упростить | квадратный корень из 144 | ||
| 95 | Преобразование в упрощенную дробь | 725% | ||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | ||
| 97 | Оценить | 7/10-2/5 | ||
| 98 | Оценить | 6÷3 | ||
| 99 | Оценить | 5+4 | ||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 |
периметр прямоугольника равен 30 футов.
 Ширина на 5 футов больше, чем длина. Какая ширина и длина?
Ширина на 5 футов больше, чем длина. Какая ширина и длина?Геометрия
Джесслин М.
спросил 28.08.19Подписаться
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Уиз С. ответил 28.08.19
Репетитор
Новое в Византе
Опытный и терпеливый репетитор по математике
Смотрите таких репетиторов
Смотрите таких репетиторов
Периметр прямоугольника равен 30 футов. Ширина на 5 футов больше, чем длина. Какая ширина и длина?
=>
ширина = w
длина = l = w+5
2(l+w) =p
2(w+5+w) = 30
2(2w+5)=30
2w +5 =15
2w =10
w =5
ширина = w= 5 футов
длина = l = w+5 =5+5 =10 футов
Голосовать за 1 Понизить
Подробнее
Отчет
Захари В. ответил 28.08.19
ответил 28.08.19
Репетитор
5,0 (134)
Я физик, который хочет, чтобы все знали физику!
Об этом репетиторе ›
Об этом репетиторе ›
Мы знаем, что периметр прямоугольника равен сумме всех сторон. У прямоугольника четыре стороны, но два набора одинаковых размеров. Таким образом, мы можем записать периметр (P) как сумму длин (L) и ширин (W), или:
П = Д + Д + Ш + Ш = 2Л + 2Ш.
Нам дали две части информации: 1. что периметр (P) прямоугольника составляет 30 футов, и 2. что ширина (W) на 5 футов больше, чем длина (L). Мы можем выразить эту информацию с помощью следующих двух уравнений:
P = 2L + 2W = 30 футов
W = L + 5 футов
Теперь у нас есть два неизвестных. Мы не знаем ни длины (L), ни ширины (W) прямоугольника, но у нас есть два линейно независимых уравнения, то есть такое же количество неизвестных, что и у нас, поэтому мы можем найти ширину (W) и длина (L) прямоугольника.
W = L + 5 футов
2L + 2W = 30 футов
Используя уравнение W = L + 5 футов, мы можем подставить его в уравнение периметра и получить:
2L + 2(L + 5 футов) = 30 футов
Теперь разделите обе части уравнения на 2:
L + (L + 5 футов) = 15 футов
Группировка общих терминов:
2L + 5 футов = 15 футов
Вычитание 5 футов из обеих частей уравнения:
2L + 5 футов — 5 футов = 15 футов — 5 футов
2L = 10 футов
И разделив обе стороны на 2, получим:
L = 5 футов .
Теперь, используя новое найденное значение L и соотношение W = L + 5 футов, мы можем найти ширину (W):
W = (5 футов) + 5 футов
W = 10 футов .
Итак, мы нашли длину (L) и ширину (W) прямоугольника, и они равны:
L = 5 футов
W = 10 футов
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.



 ⓘ Периметр прямоугольника с заданной площадью и длиной [P]
ⓘ Периметр прямоугольника с заданной площадью и длиной [P]
 высказывания.
высказывания. 
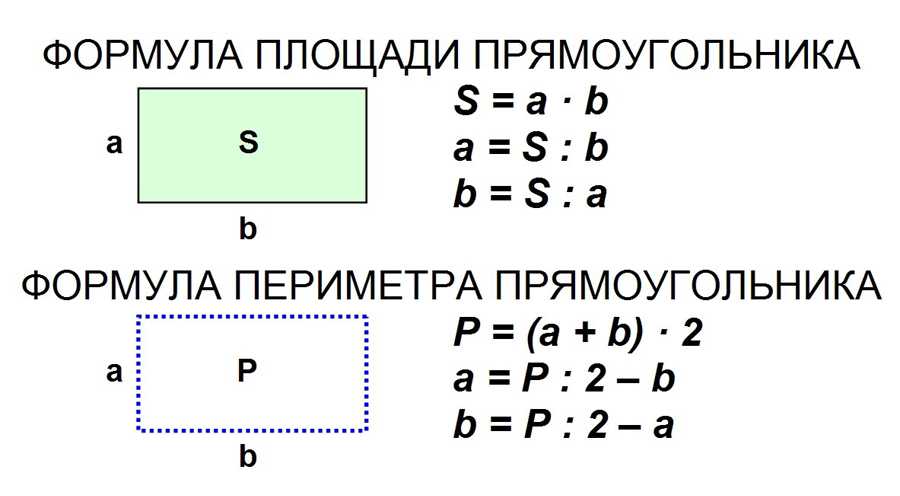 (4 стороны, 4 угла, все углы прямые, противоположные стороны равны)
(4 стороны, 4 угла, все углы прямые, противоположные стороны равны)