Периметр треугольника — Стоматология в Химках
Математика периметр треугольника
Периметром треугольника, как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Формула периметра треугольника выглядит так:
| Сторона a= | Сторона b= | Сторона c= |
| Ответ: Периметр треугольника = 12.000 |
Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a = 4см, b = 6 см, c = 7 см. подставим данные в формулу: см
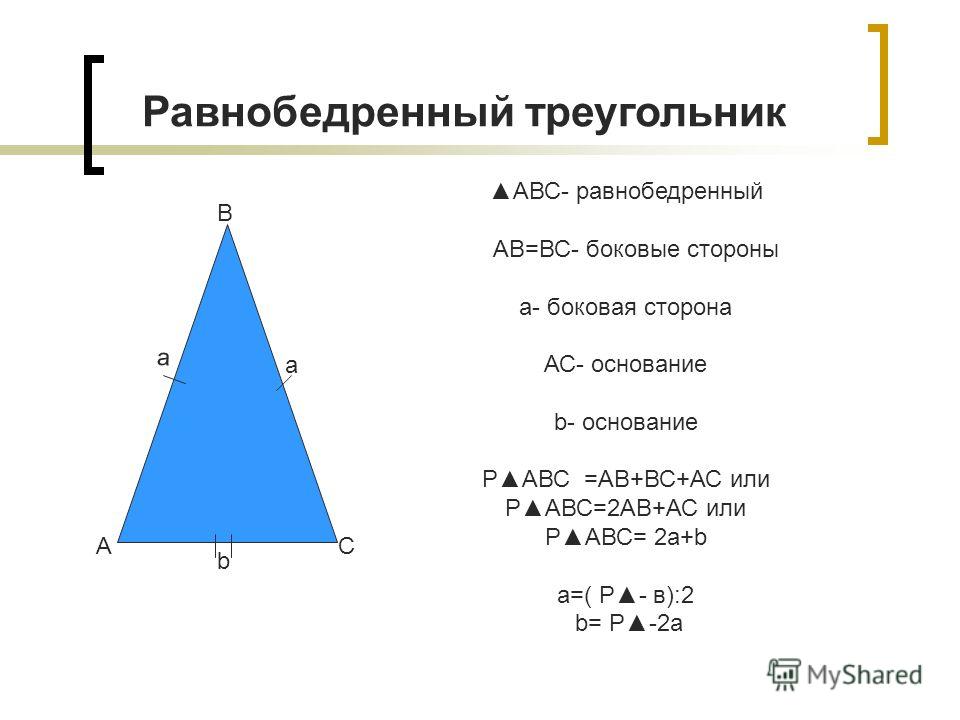
Формула расчета периметра Равнобедренного треугольника будет выглядеть так:
Формула расчета периметра Равностороннего треугольника:
Пример расчета периметра равностороннего треугольника. Когда все стороны фигуры равны, то их можно просто умножить на три.
В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по Теореме Пифагора. К примеру, если известны длины катетов, то можно найти гипотенузу по формуле: » />
Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.
Дан треугольник с катетами a = b =5 см. Найти периметр. Для начала найдем недостающую сторону с. =sqrt=sqrt=7″ />см
Теперь посчитаем периметр: см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.
В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле: » />
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле:
Если эти выражения подставить в формулу периметра, можно получить:
+ c*cos+c=c*(sin+cos+1)» />
Задача: Дан прямоугольный треугольник с гипотенузой с = 7 см и острым углом α = 30°. Найти периметр треугольника. Подставляем значения в формулу.
Найти периметр треугольника. Подставляем значения в формулу.
+>/2+1)=7(/2+1)=16,45″ />см
Периметр треугольника равен 16,45 см
Зная одну сторону и противолежащий ей катет можно вычислить две недостающие.
К примеру, дан треугольник, в котором сторона a = 5 см, а противолежащий ей угол α =45°. Тогда сторону b можно найти через формулу:>» />
Сторону с найдем так: >» />
Периметр, с применением таких формул, будет рассчитываться следующим образом: > +a/> =a(1+1/> +1/>)» />
Теперь произведем расчеты по уже известной формуле: см
Задача: Дан прямоугольный треугольник с гипотенузой с = 7 см и острым углом α = 30°. Найти периметр треугольника. Подставляем значения в формулу.
Периметр треугольника равен 16,45 см
В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле: » />
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле:
Для начала найдем недостающую сторону с.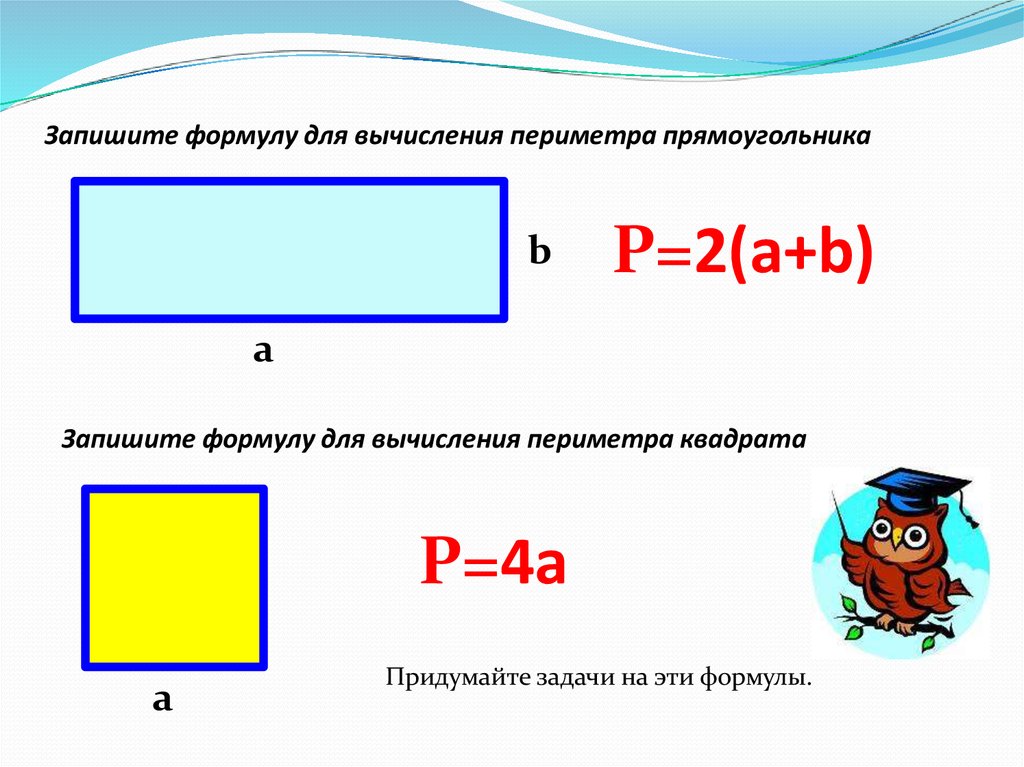
2mb. ru
29.07.2020 6:49:47
2020-07-29 06:49:47
Источники:
Https://2mb. ru/matematika/geometriya/perimetr-treugolnika/
Периметр ⚠️ треугольника: как найти, формула, в чем измеряется » /> » /> .keyword { color: red; }
Математика периметр треугольника
Учимся находить периметр треугольника разными способами, а также тренируем полученные знания на примерах задач.
Периметр треугольника
Периметр треугольника — это сумма длин всех его сторон.
Треугольник — это геометрическая фигура, которая состоит из трех точек (вершин), не лежащих на одной прямой. Эти точки попарно соединены тремя отрезками, которые называются сторонами (ребрами) многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Рассмотрим несколько способов нахождения периметра рассматриваемой фигуры.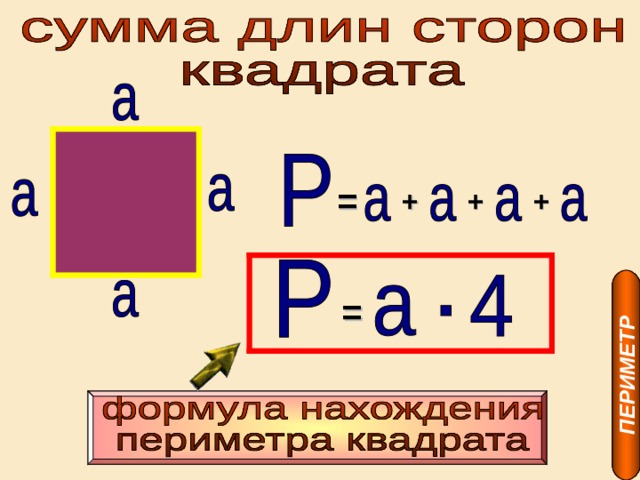 Каждая из предложенных формул опирается на те величины, которые нам уже известны.
Каждая из предложенных формул опирается на те величины, которые нам уже известны.
Способы нахождения
По трем сторонам
Если мы уже знаем длину каждого ребра фигуры, расчет периметра будет проходить так:
Где a, b и с — это стороны треугольника.
В случае, если нам известны стороны равнобедренного треугольника (у которого два ребра равны), формула для расчета периметра выглядит следующим образом:
Где a — основание фигуры, а b и с — равные ребра.
Треугольник может также быть равносторонним (когда все стороны равны). Тогда P будем находить в соответствии с расчетами:
Где a — это любая сторона фигуры.
По площади и радиусу вписанной окружности
Когда нам известна площадь данного многоугольника и радиус вписанной в него окружности, расчет P выглядит так:
Где S — площадь фигуры, r — радиус вписанной в нее окружности.
По двум сторонам и углу между ними
Так как нам известен угол и две стороны, которыми он образован, мы можем найти третью сторону треугольника по теореме косинусов. И потом уже вычислить сумму длин всех ребер фигуры.
И потом уже вычислить сумму длин всех ребер фигуры.
Теорема косинусов выглядит так:
Где α — известный угол.
Тогда формула для расчета периметра всей фигуры в этом случае:
По боковой стороне и высоте (для равнобедренного)
Возвращаясь к свойствам равнобедренного треугольника, вспоминаем, что высота, проведенная к основанию треугольника из противоположной вершины, является одновременно высотой, биссектрисой и медианой. Это значит, что оба прямоугольных треугольника, которые она образует, равны между собой.
Формула для поиска периметра нашего равнобедренного будет опираться на теорему Пифагора. Пусть 1/2 основания (с) = d. Тогда:
Где a — сторона равнобедренного треугольника и гипотенуза прямоугольного, h — высота равнобедренного и катет прямоугольного.
Не забываем, что d — это лишь половина основания равнобедренного треугольника, поэтому для поиска периметра результат нужно будет умножить на 2.
По двум катетам (для прямоугольного)
Еще раз вспомним теорему Пифагора для нахождения гипотенузы (обозначим ее буквой с).
Где a и b — катеты треугольника.
Подставляем значение c в формулу для нахождения периметра и получаем:
Примеры решения задач
Для тренировки полученных знаний, рассмотрим несколько примеров решения задач на поиск периметра треугольника.
Задача №1
Какой P треугольника, если его стороны равны 6 см, 7 см и 3 см.
Решение:
Подставляем в формулу P = a+b+c известные величины и получаем: P = 6+7+3=16 см.
Задача №2
Известно, что основание равнобедренного треугольника равно 6 см, а его боковая сторона — 4 см. Найти P фигуры.
Решение:
Для данного случая подходит формула P=a+2b, подствляем значения: \(P=6+4\times2 = 14\) см.
Задача №3
Нам известно, что площадь треугольника — 24 см 2 , а радиус вписанной в него окружности — 8 см. Найти P.
Решение:
В данном случае рассчитывать P будем следующим образом: \(P=\fracr\) . С уже известными нам величинами получаем: \(P=\frac8 = 6\) см.
Задача №4
Дан равнобедренный треугольник. Нам известна его боковая сторона (4 см) и высота, опущенная к основанию (2 см). Нужно вычислить периметр фигуры.
Решение:
Мы знаем, что в этом случае P вычисляется, как \(P=2\sqrt+2a\) . С имеющимися значениями получается: \(P=2\sqrt+2\times2 = 4\sqrt3+4\) см.
Ответ: P=4\sqrt3+4 см.
Задача №5
Дан прямоугольный треугольник с катетами 5 см и 7 см. Определить периметр фигуры.
Решение:
В формулу \(P=\sqrt+a+b\) подставляем известные значения: \(P=\sqrt+5+7 = \sqrt+12\) см.
Треугольник может также быть равносторонним когда все стороны равны.
Wiki. fenix. help
03.03.2018 4:44:12
2018-03-03 04:44:12
Источники:
Https://wiki. fenix. help/matematika/perimetr-treugolnika
Как найти периметр треугольника: формула через длины сторон » /> » /> .keyword { color: red; }
Математика периметр треугольника
В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.
- Формула вычисления периметра Примеры задач
Формула вычисления периметра
Периметр ( P) любого треугольника равняется сумме длин всех его сторон.
P = a + b + c
Периметр равнобедренного треугольника
Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за B). Сторона A, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:
P = a + 2b
Периметр равностороннего треугольника
Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за A). Периметр такой фигуры вычисляется так:
P = 3a
Примеры задач
Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.
Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.
Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона — 8 см.
Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.
Примеры задач.
Microexcel. ru
28.10.2017 10:44:20
2017-10-28 10:44:20
Источники:
Https://microexcel. ru/perimetr-treugolnika/
Урок математики в 5-м классе по теме «Периметр прямоугольника»
- Араджиони Елена Николаевна
Разделы: Математика
Цель урока:
Закрепить умения и навыки в вычислении периметра многоугольника, познакомить с формулой вычисления периметра прямоугольника, научить пользоваться этой формулой.
1. Постановка цели урока
Тема урока «Периметр прямоугольника». Наша задача повторить, что называется периметром, как вычисляется периметр многоугольника, вывести формулу вычисления периметра прямоугольника, научиться пользоваться формулой.
2. Математическая разминка. Вычислить:
1) 4% от 300;
2) 6% от 200:
3) 3/8 от 24;
4) 0,18:2*100;
5) 6,4*0,1 + 0,6*5
6) число 63000 уменьшить в 100 раз, число 77000 увеличить в 10 раз.
Объяснение учителя.
В каждом доме есть измерительные приборы: это сантиметровая лента, линейка, счетчики электрической энергии и другие. Измерение-это важнейшее дело в современной жизни. И, конечно, не могли обойтись без измерений древние строители пирамид, храмов и дворцов.
Миля – семи верстам = 7 км 47 метрам.
Верста =500 саженей =1 км 7 м.
Сажень =3 аршинам семи футам и 2 метрам 13 см.
Аршин=16 вершкам =28 дюймам=71 см 2мм
Фут = 12 дюймов = 30 см. 5 мм.
Дюйм = 10 линиям = 2 см 5 мм.
Линия = 10 точкам = 2,5 мм (просмотр презентации Приложение 1).
Некоторые из этих единиц используются и сейчас. Например, в Англии: фут и дюйм; у нас в России дюйм. Вы знаете сказку Андерсена «Дюймовочка» и теперь можете объяснить, откуда девочка получила свое имя. Сегодня мы с вами повторим единицы длины, которые нам понадобятся при решении по теме урока (Рисунок 1)
Сегодня мы с вами повторим единицы длины, которые нам понадобятся при решении по теме урока (Рисунок 1)
3. Повторение.
1. Вспомним, что называется периметром многоугольника.
2. Выполним упражнения на вычисление периметра (работа по карточкам).
а)Ртреуг =19+16+24=59 (см.)
б)Р квадрата =15*4 = 60 см.
в) Р многоугольника = 8+11+10+15+17=61 см.
Как вычислить Р треугольника, что надо сделать сначала (измерить стороны) А затем? (сложить полученные числа)
Учитель : как называется треугольник, у которого все стороны равны?
Чему равен Р треугольника со сторонами по 25 см.? Как можно вычислить его периметр?
25+25+25=75 см.
25*3= 75 см.
Находим периметр квадрата двумя способами , длину квадрата выразим в миллиметрах. Записать на доске а=14 см. 5 мм.= 145 мм.
5 мм.= 145 мм.
145+145+145+ 145=580 (мм)
145*4=580 (мм)
Переходим к вычислению периметра прямоугольника. Что вы знаете о сторонах прямоугольника (противоположные стороны равны)
Сколькими способами можно вычислить периметр прямоугольника?
- способ:40+40+25+25=130 см.
- способ: 40*2+25*2= 130 см.
- способ (40 + 25)* 2 =130 см.
4. Самостоятельная работа.
Начертите прямоугольник, у которого длина 8 см., ширина на 2 см. короче. Вычислите периметр прямоугольника тремя способами.
Проверка: Учитель записывает на доске:
1) 8+8+6+6=28 см. а + а + в +в;
2) 8*2+6*2=28 см. 2*а+2*в;
3) (8+6)*2=28 см. (а + в)*2.
5. Новый материал
Запишем периметры для наших фигур:
Рравностор.треуг =3а, Рквадрата =4а
Периметр прямоугольника Р = (а+в)*2
6. Закрепление нового материала:
Закрепление нового материала:
1) Заполните таблицу
| а | 23 см | 35 см. | 7 см. | 12 см | 50 мм. |
| в | 11 см | 70 мм | 5 дм. | 4 см. | 6 дм |
| Р | ? | ? | ? | ? | ? |
2) Решение и оформление задачи:
Вычислите длину стороны квадрата, периметр которого равен 84 см
Ркв = 84 см. Р=4* а
а -? а=Р:4 = 84:4 = 21 (см.)
Ответ 21 см.
3) Решение практических задач
а) найти периметр класса (а = 6м.; в = 4 м., Р = (6 + 4)*2 = 20 м). Ответ 20 м.
б) Сколько штук штакетника необходимо для забора на дачном участке, если его длина а=45м., ширина в =25 м. и на каждый метр длины идет 10 штук.
а=45 м. Р = (а + в) *2 = ( 45+25)*2= 140 (м)
в = 25 м. N = 140 *10 = 1400 (штук)
n= 10 шт.
Ответ: 1400 штук.
N — ?
В заключение урока проведем самостоятельную работу по вариантам.
1 Вариант
- Длина прямоугольника 9 см., ширина 5 см. Найти периметр
- Длина прямоугольника 69 см., ширина в 3 раза короче. Найти периметр.
- Сторона треугольника 14 см., 3 дм, 20 см. Найти периметр.
- Найти сторону треугольника, у которого все они равны, а периметр равен 51 см.

2. Вариант
- Сторона квадрата16 см. Найти периметр.
- Периметр квадрата 64 см. Найти сторону квадрата.
- Ширина прямоугольника15 см, длина в 3 раза короче. Найти периметр.
- Периметр прямоугольника 44 см., длина его 3 дм. Найти ширину.
7. Итог урока. Повторить формулы периметров. Выставление оценок за урок.
8.Задание на дом параграф 2 п.6; № 207; 208; 209; №210.
В чем выражается периметр. Что такое периметр
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
- Найти периметр прямоугольника, если его полупериметр — 21 дм.

Знания о том, как найти периметр, учащиеся получают еще в начальной школе. Потом эта информация постоянно используется на протяжении всего курса математики и геометрии.
Общая для всех фигур теория
Стороны принято обозначать латинскими буквами. Причем их можно обозначать как отрезки. Тогда букв потребуется по две для каждой стороны и записанные большими. Или ввести обозначение одной буквой, которая обязательно будет маленькой.
Буквы всегда выбирают по алфавиту. Для треугольника они будут первыми тремя. У шестиугольника их будет 6 — от а до f. Это удобно для введения формул.
Теперь о том, как найти периметр. Он является суммой длин всех сторон фигуры. Количество слагаемых зависит от ее вида. Обозначается периметр латинской буквой Р. Единицы измерения совпадают с теми, которые даны для сторон.
Формулы периметров разных фигур
Для треугольника: Р=а+в+с. Если он равнобедренный, то формула преобразуется: Р=2а+в. Как найти периметр треугольника, если он равносторонний? Поможет такая: Р=3а.
Для произвольного четырехугольника: Р=а+в+с+d. Его частным случаем является квадрат, формула периметра: Р=4а. Есть еще прямоугольник, тогда требуется такое равенство: Р=2(а+в).
Как быть, если неизвестна длина одной или нескольких сторон треугольника?
Воспользоваться теоремой косинусов, если среди данных есть две стороны и угол между ними, который обозначается буквой А. Тогда до того, как найти периметр, придется посчитать третью сторону. Для этого пригодится такая формула: с² = а² + в² — 2 ав cos(А).
Частным случаем указанной теоремы является сформулированная Пифагором для прямоугольного треугольника. В ней значение косинуса прямого угла становится равным нулю, а значит, последнее слагаемое просто исчезает.
Бывают ситуации, когда узнать, как найти периметр треугольника, можно по одной стороне. Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.
В ситуации, когда периметр фигуры нужно узнать по площади, пригодятся другие формулы. Например, если известен радиус вписанной окружности, то в вопросе о том, как находить периметр треугольника, пригодится следующая формула: S=р*r, здесь р — полупериметр. Его нужно вывести из данной формулы и умножить на два.
Примеры задач
Условие первой. Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.
Решение. Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см.
Ответ. Периметр треугольника равен 12 см.
Условие второй. Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.
Решение . Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Ответ. Периметр равняется 37 см.
Условие третьей. Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Решение. Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см.
Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.
Ответ. Сторона квадрата 4 см.
Достаточно узнать длину всех ее сторон и найти их сумму. Периметром называется совокупная длина границ плоской фигуры. Иными словами, это сумма длин ее сторон. Единица измерения периметра должна соответствовать единице измерения его сторон. Формула периметра многоугольника имеет вид Р = a + b + c…+ n, где Р — периметр, а вот а, b, с и n — длина каждой из сторон. Иначе вычисляется (или периметр круга): используется формула р = 2 * π * r, где r — радиус, а π — постоянное число, приблизительно равное 3,14. Рассмотрим несколько простых примеров, наглядно демонстрирующих, как найти периметр. В качестве образца возьмем такие фигуры как квадрат, параллелограмм и окружность.
Иначе вычисляется (или периметр круга): используется формула р = 2 * π * r, где r — радиус, а π — постоянное число, приблизительно равное 3,14. Рассмотрим несколько простых примеров, наглядно демонстрирующих, как найти периметр. В качестве образца возьмем такие фигуры как квадрат, параллелограмм и окружность.
Как найти периметр квадрата
Квадратом называется правильный четырехугольник, у которого равны все стороны и углы. Так как все стороны квадрата равны, сумму длин его сторон можно вычислить по формуле Р = 4 * a, где а — длина одной из сторон. Таким образом, со стороной 16,5 см равен Р = 4 * 16,5 = 66 см. Так же можно вычислить периметр равностороннего ромба.
Как найти периметр прямоугольника
Прямоугольник — это четырехугольник, все углы которого равны 90 градусам. Известно, что в такой фигуре, как прямоугольник, длины сторон равны попарно. Если ширина и высота прямоугольника имеют одинаковую длину, то он называется квадратом. Обычно длиной прямоугольника называют наибольшую из сторон, а шириной — наименьшую. Таким образом, чтобы получить периметр прямоугольника, необходимо удвоить сумму его ширины и высоты: P = 2 * (а + b), где а — высота, а b — ширина. Имея в наличии прямоугольник, одна сторона которого является длиной и равна 15 см, а другая шириной с установленным значением в 5 см, мы получим периметр, равный Р = 2 * (15 + 5) = 40 см.
Таким образом, чтобы получить периметр прямоугольника, необходимо удвоить сумму его ширины и высоты: P = 2 * (а + b), где а — высота, а b — ширина. Имея в наличии прямоугольник, одна сторона которого является длиной и равна 15 см, а другая шириной с установленным значением в 5 см, мы получим периметр, равный Р = 2 * (15 + 5) = 40 см.
Как найти периметр треугольника
Треугольник образован тремя отрезками, которые соединяются в точках (вершинах треугольника), не лежащих на одной и той же прямой. Треугольник называется равносторонним, если равны все три его стороны, и равнобедренным, если равных сторон две. Чтобы узнать периметр необходимо длину его стороны умножить на 3: Р = 3 * a, где а — одна из его сторон. Если стороны треугольника не равны между собой, необходимо провести операцию сложения: Р = а + b + с. Периметр равнобедренного треугольника со сторонами 33, 33 и 44 соответственно будет равен: P = 33 + 33 + 44 = 110 см.
Как найти периметр параллелограмма
Параллелограмм — это четырехугольник с попарно параллельными противоположными сторонами. Квадрат, ромб и прямоугольник являются частными случаями фигуры. Противоположные стороны любого параллелограмма равны, поэтому для вычисления его периметра воспользуемся формулой P = 2 (а + b). В параллелограмме со сторонами 16 см и 17 см сумма сторон, или периметр, равна Р = 2 * (16 + 17) = 66 см.
Квадрат, ромб и прямоугольник являются частными случаями фигуры. Противоположные стороны любого параллелограмма равны, поэтому для вычисления его периметра воспользуемся формулой P = 2 (а + b). В параллелограмме со сторонами 16 см и 17 см сумма сторон, или периметр, равна Р = 2 * (16 + 17) = 66 см.
Как найти длину окружности
Окружность является замкнутой прямой, все точки которой расположены на равном удалении от центра. Длина окружности и ее диаметр всегда имеют одинаковое отношение. Это отношение выражено константой, записывается при помощи буквы π и равняется примерно 3,14159. Узнать периметр круга можно по произведению радиуса на 2 и на π. Получается, что длина окружности с радиусом в 15 см будет равна Р = 2 * 3,14159 * 15 = 94,2477
Сегодня у нас речь пойдет о том, как вычислить периметр многоугольника . Но сначала поговорим о многообразии фигур. Посмотрите на рисунок. Какие фигуры мы здесь видим? Это прямоугольник и квадрат – многоугольники, которые имеют по четыре стороны, а также треугольник, имеющий три стороны, и пятиугольник с пятью сторонами.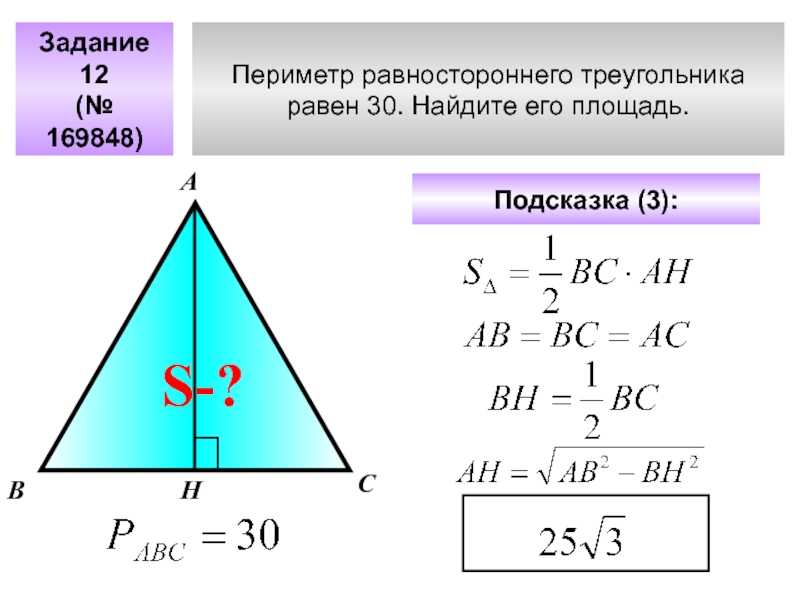
И как же найти периметр этих фигур?
Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .
Периметр обозначается заглавной латинской буквой Р .
Давайте рассмотрим несколько примеров.
Вычислим периметр многоугольника О. Как мы говорили ранее, периметр многоугольника – это сумма длин всех его сторон. Сложим все стороны нашего многоугольника:
Р = 15 + 17 + 10 + 10 + 20 + 15 = 87
Но можно вычислить периметр и другим способом, используя умножение. Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:
Р = 15 × 2 + 10 × 2 + 17 + 20 = 87
Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.
Прямоугольник – это такой четырехугольник, у которого противоположные стороны равны. Например, чтобы вычислить А со сторонами а и б , надо сложить эти стороны и умножить полученный результат на 2 :
Р(прямоугольника) = (а + б) × 2
То есть, если сторона прямоугольника а = 5 см , а сторона прямоугольника б = 3 см , то периметр прямоугольника будет:
Р = (5 + 3) × 2 = 16 см
А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?
Р(прямоугольника) = 2 × а + 2 × б
а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2
Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?
Чему равны остальные стороны прямоугольника?
Если мы знаем одну сторону прямоугольника, значит длины двух, из четырех сторон нам известны. Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.
сторона б = (16 – 2 × 5) ÷ 2 = 3 см
Ответ: у прямоугольника две стороны по 5 см и две по 3 см.
Квадрат – это прямоугольник, у которого все стороны равны. Чтобы вычислить надо длину одной стороны умножить на 4:
Р(квадрата) = а × 4
Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:
Р(В) = 5 × 4 = 20 см
А если известен периметр квадрата, как найти длины его сторон? Очень просто, надо его периметр разделить на четыре:
а = Р ÷ 4
Пример: Периметр квадрата 24 см. Чему равны его стороны?
а = 24 ÷ 4 = 6
Ответ: Стороны квадрата равны 6 см.
По подобию вычисления периметра квадрата вычисляется периметр всех равносторонних многоугольников
. То есть равен длине одной его стороны умноженной на количество сторон.
Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:
Р(равностороннего многоугольника) = а × n
Например, у пятиугольника Д сторона а = 6 см . Найдем его периметр:
Р(Д) = 6 × 5 = 30 см
Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.
Как вычислять периметр?
Нам частенько приходилось слышать от учителей: «Занимайтесь прилежно, знания очень пригодятся вам в жизни», и, действительно, такое случается. Например, когда мы беремся за ремонт, нам совершенно необходимо знать, как рассчитать периметр той или иной фигуры, чтобы определить требуемое количество строительного материала. В этой статье для тех, кто забыл школьный курс, расскажем о том, как вычислять периметр различных фигур.
Что такое периметр?
Периметр — это длина линии, очерчивающей геометрическую фигуру; длина всех сторон плоской фигуры. Таким образом, чтобы найти периметр фигуры, достаточно измерить длину каждой стороны и сложить все результаты. Однако иногда можно сделать расчет более простым способом с помощью специальных формул. Далее разберем способы нахождения периметра различных фигур с помощью обоих методов.
Таким образом, чтобы найти периметр фигуры, достаточно измерить длину каждой стороны и сложить все результаты. Однако иногда можно сделать расчет более простым способом с помощью специальных формул. Далее разберем способы нахождения периметра различных фигур с помощью обоих методов.
Периметр треугольника
Перед тем как вычислить периметр треугольника, необходимо измерить длину каждой стороны. После этого просто сложите их — это и будет периметр.
Однако если мы имеем дело с равнобедренным треугольником, можно измерить одну из равных сторон и умножить полученное значение на два, а затем прибавить к нему длину основания.
Для вычисления периметра равностороннего треугольника, достаточно и вовсе померить только одну сторону и умножить полученное значение на три.
Периметр четырехугольника
Разберем в данном разделе, как вычислить периметр квадрата, ромба, прямоугольника, параллелепипеда и трапеции.
Квадрат и ромб
Как известно, у квадрата четыре стороны и все они равны, а значит, для вычисления периметра квадрата необходимо померить одну из его сторон, а затем умножить полученное значение на 4. Собственно говоря, точно так же находится периметр ромба, потому как у ромба все стороны равны.
Собственно говоря, точно так же находится периметр ромба, потому как у ромба все стороны равны.
Прямоугольник и параллелограмм
У прямоугольника стороны равны попарно, таким образом, для вычисления периметра, потребуется померить большую и меньшую сторону, каждое из полученных значений умножить на два и сложить получившиеся значения. Аналогично находится периметр параллелограмма.
Трапеция
Еще один тип четырехугольника — трапеция. У этой фигуры, как правило, все стороны разной длины, а потому для нахождения периметра придется измерить каждую сторону и сложить их. Однако трапеция может быть равнобедренной. В таком случае для расчета периметра можно воспользоваться следующей формулой: P = a+b+2c, где c — длина одной из равных сторон.
Существует, кстати, еще один способ определения периметра равнобедренной трапеции — так называемый «метод средней линии». Сначала нужно провести эту самую среднюю линию (она проводится через две точки — середины равных сторон), затем надо измерить ее, умножить полученное значение на два и прибавить две длины равных сторон.
Периметр многоугольника
Для нахождения периметра многоугольника, как правило, действует правило — измерь все стороны и сложи их. Однако некоторые частные случаи позволяют более просто справиться с задачей. Например, если перед вами так называемый правильный шестиугольник, его периметр можно посчитать, умножив длину стороны на 6.
Для расчета периметра круга или, как говорят чаще, длины окружности, существует специальная формула: P=2πr, где π — постоянное значение, равное 3,14; r — радиус окружности. Формула также может выглядеть так: P=πd, где d- диаметр окружности.
Кстати, фактически π — это отношение длины окружности к ее диаметру. Доказано, что это значение для всех окружностей одинаково и равно 3,14.
Формулы пути, площади, периметра 5 класс презентация, доклад, проект
Формулы
Пути
площади
периметра
МОУ «Лицей № 62» г. Саратова
Учитель математики ВОЕВОДИНА Ольга Анатольевна
Что же такое формула?
Запись какого-нибудь правила с помощью букв называют формулой.
Задача № 1.
Велосипедист едет со скоростью 15 км/ч. Какое расстояние он проедет за 4 ч?
Решение.
Запишем правило нахождения пути по скорости и времени движения в буквенном виде.
Найдите по формуле пути :
Значение скорости, если:
2) Значение времени t, если:
№ 683
№ 681
600 км
V=60 км/ч
V=40 км/ч
Чему равно расстояние между машинами через t часов после выезда?
100 -скорость сближения
№ 680
V=50 км/ч
V= 70 км/ч
S км ? через t часов
S= (50+70)t
S= 120t
120 – скорость удаления
Решение.
Сделаем вывод:
1) При движении навстречу друг другу СКОРОСТЬ СБЛИЖЕНИЯ равна сумме скоростей.
2) При движении в стороны друг от друга СКОРОСТЬ УДАЛЕНИЯ равна сумме скоростей.
№ 682
198 см
V=130 cм/мин
V=97 см/мин
Чему будет равно расстояние между черепахами через t минут?
S=(130-97)t
S= 33 t
33 – скорость сближения
Через сколько минут первая черепаха догонит вторую?
t=198 : 33 = 6 (мин)
Сделаем вывод:
При движении в одном направлении скорость сближения (или удаления)
равна разности скоростей.
Формула для периметра
Назовите какие геометрические фигуры здесь изображены?
квадрат
шестиугольник
треугольник
прямоугольник
круг
Что такое периметр многоугольника?
Периметр многоугольника –
это сумма длин всех его сторон.
Обозначение периметра P
№ 677
Запишите формулу для вычисления периметра прямоугольника и вычислите его.
1) a= 4 дм, b= 3 дм
P=2(a+b)
P= 2(4+3)=14 дм
2) Р=30 см, а=7 см, b?
2(7+b)=30
(7+b)=15
b=15-7
b=8
Ответ: 8 см
№ 678
Запишите формулу для вычисления периметра Р квадрата, сторона которого а. Вычислите по этой формуле:
1) Периметр квадрата, со стороной 9 см.
2) Сторону квадрата, периметр которого 64 см.
P= 4a, P=4 ×9=36 (см)
a=P : 4, a= 64 : 4=16 (см)
Самостоятельная работа
1 вариант
2 вариант
1). Периметр квадрата 84 м.
Найдите его сторону.
2). Найдите по формуле пути:
Значение S, если v=12 км/ч,
t=3 ч.
3). Найдите по формуле периметра
прямоугольника:
cторону a, если Р=122 м,
b=34 м.
1). Периметр квадрата 144 м.
Найдите его сторону.
2). Найдите по формуле пути:
Значение t, если s=180 м,
v=15 м/с.
3). Найдите по формуле периметра
прямоугольника:
периметр P, если,
a= 15 см, b=25 см.
Формула для площади
Фигура на рисунке состоит из 6 квадратов, со стороной 1 см каждый.
Площадь одного такого квадрата называют квадратным сантиметром.
Пишут: 1
Чтобы найти площадь прямоугольника, надо умножить его длину на ширину.
S=ab – формула площади прямоугольника
Две фигуры называются равными, если одну из них можно так наложить на вторую, что эти фигуры совпадут.
Площади и периметры равных фигур равны.
№ 713
A
B
C
D
E
P
Треугольники ABC и DEP равны. Чему равен периметр треугольника DEP, если AB=3 см, BC=4 см, CA=5 см.
Чему равен периметр треугольника DEP, если AB=3 см, BC=4 см, CA=5 см.
Решение.
P(ABC)= AB+BC+AC,
P(ABC)= 3+4+5=12 cм,
P(ABC)=P(DEP)=12 см.
Ответ: 12 см.
Задача 1
В некотором царстве, в некотором государстве была такая единица длины – бумбамс. Двор вокруг дворца имел форму прямоугольника со сторонами 50 и 80 бумбамсов. Найти площадь двора в квадратных бумбамсах.
Решение.
S= 50×80
S= 4000 (кв. бумб.)
Ответ. 4000 кв. бумб.
Задание на дом:
п.17-18, № 740, 741(б), 742 (а), 744
Спасибо за урок
Скачать презентацию
Мерзляк 5 класс — § 15. Прямоугольник. Ось симметрии фигуры
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1.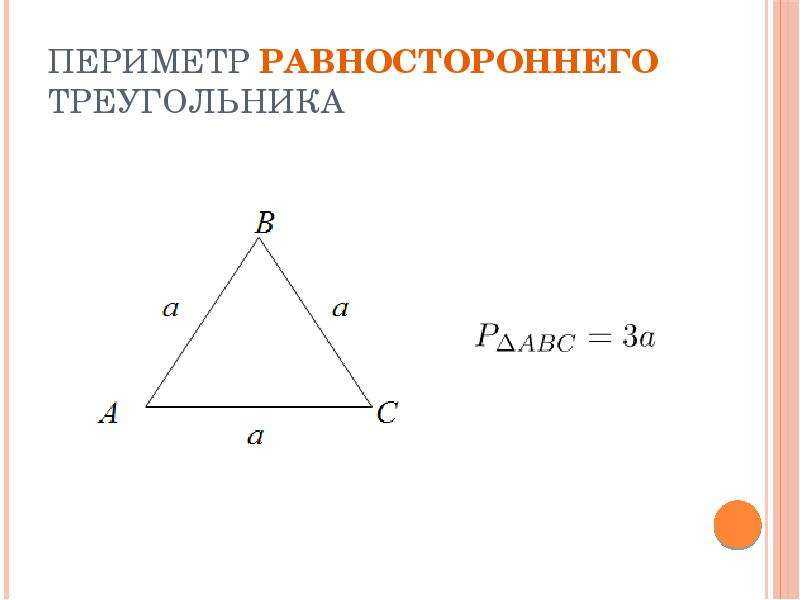 Какой четырёхугольник называют прямоугольником?
Какой четырёхугольник называют прямоугольником?
Прямоугольник — это четырёхугольник, у которого все углы прямые.
2. Какие стороны прямоугольника называют соседними? Противолежащими?
- соседние стороны прямоугольника — это стороны, которые имеют общую вершину
- противолежащие стороны прямоугольника — это стороны, которые не имеют общих вершин
3. Что называют длиной и шириной прямоугольника?
Длиной и шириной прямоугольника называют соседние стороны прямоугольника.
4. Каким свойством обладают противолежащие стороны прямоугольника?
Противолежащие стороны прямоугольника равны.
5. Какую фигуру называют квадратом?
Квадрат — это прямоугольник, у которого все стороны равны.
6. Объясните, какие фигуры называют симметричными относительно прямой.
Фигуру называют симметричной, относительно прямой, если при сгибе по этой прямой противоположные части фигуры совпадают друг с другом.
7. Как называют прямую, относительно которой симметрична фигура?
Ось симметрии.
8. Какие вы знаете фигуры, имеющие ось симметрии?
Круг, равнобедренный и равносторонний треугольник, квадрат, прямоугольник.
9. Сколько осей симметрии имеет прямоугольник, отличный от квадрата? Квадрат? Равносторонний треугольник?
- Прямоугольник, отличный от квадрата, имеет 2 оси симметрии.
- Квадрат имеет 4 оси симметрии.
- Равносторонний треугольник имеет 3 оси симметрии.
Решаем устно
1. Каждая сторона треугольника равна 12 см. Как называют такой треугольник? Чему равен его периметр?
Такой треугольник называют равносторонним. Его периметр равен P = 3a = 3 • 12 = 36 см.
Ответ: равносторонний, 36 см.
2. Периметр равнобедренного треугольника равен 32 см, а одна из его сторон — 12 см. Найдите длины двух других сторон треугольника. Сколько решений имеет задача?
Задача может иметь 2 решения.
Решение 1.
Пусть 12 см — это длина основания равнобедренного треугольника. Тогда, при периметре 32 см, боковые стороны этого треугольника будут равны:
(32 — 12) : 2 = 20 : 2 = 10 (см) — длина каждой из боковых сторон треугольника.
Ответ: двумя другими сторонами будут две боковые стороны: 10 см и 10 см.
Решение 2:
Пусть 12 см — это длина одной из боковых сторон равнобедренного треугольника. Тогда вторая боковая сторона этого треугольника также равна 12 см, а основание, при периметре треугольника 32 см, будет равно:
32 — 12 • 2 = 32 — 24 = 8 (см) — длина основания треугольника.
Ответ: двумя другими сторонами будут: основание — 8 см и вторая боковая сторона — 12 см.
3. Найдите сторону равностороннего треугольника, если она меньше его периметра на 10 см.
У равностороннего треугольника все три стороны равны, а периметр — это сумма все сторон треугольника.
Если одна сторона равностороннего треугольника меньше периметра на 10 см, значит сумма двух оставшихся сторон равна 10 см.
10 : 2 = 5 (см) — длина стороны равностороннего треугольника.
Ответ: 5 см.
4. Вычислите значение у по формуле у = х • х + 12, если:
1) х = 1
у = 1 • 1 + 12 = 1 + 12 = 13
Ответ: у = 13
2) х= 10
у = 10 • 10 + 12 = 100 + 12 = 112
Ответ: у = 112
Упражнения
359. Постройте:
1) прямоугольник, соседние стороны которого равны 4 см и 2 см
AB = DC = 4 см
AD = BC = 2 см
2) квадрат со стороной 3 см
AB = BC = CD = DA = 3 см
360. Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.
AB = DC = 35 мм
AD = BC = 5 мм
361. Вычислите периметр:
1) прямоугольника, соседние стороны которого равны 42 см и 23 см
P = 2a + 2b = 2 • 42 + 2 • 23 = 84 + 46 = 130 (см)
Ответ: P = 130 см.
2) квадрата со стороной 8 дм
P = 4a = 4 • 8 = 32 (дм)
Ответ: P = 32 дм.
362. Найдите периметр прямоугольника, соседние стороны которого равны 13 мм и 17 мм.
P = 2a + 2b = 2 • 13 + 2 • 17 = 26 + 34 = 60 (мм)
60 мм = 6 см
Ответ: P = 6 см.
363. Какие из букв, изображённых на рисунке 135, имеют ось симметрии?
Ось симметрии имеют в данном случае буквы А, В, Е, Т.
364. Сколько осей симметрии имеет многоугольник, изображённый на рисунке 136?
- а) робм — 2 оси симметрии
- б) правильный пятиугольник — 5 осей симметрии
- в) правильный шестиугольник — 6 осей симметрии
365. 1) Длина одной из сторон прямоугольника равна 14 см, что на 5 см больше длины соседней стороны. Найдите периметр прямоугольника.
1) 14 — 5 = 9 (см) — длина соседней стороны прямоугольника
P = 2a + 2b
2) 2 • 14 + 2 • 9 = 28 + 18 = 46 (см)
Ответ: P = 46 см.
2) Периметр прямоугольника равен 34 см, а одна из его сторон — 12 см. Найдите длину соседней стороны прямоугольника.
Найдите длину соседней стороны прямоугольника.
1) 12 • 2 = 24 (см) — сумма длин двух противоположных сторон прямоугольника
2) 34 — 24 = 10 (см) — сумма длин двух других, соседних им, противоположных сторон треугольника.
3) 10 : 2 = 5 (см) — длина соседней стороны прямоугольника.
Ответ: 5 см.
366. Одна сторона прямоугольника равна 8 см, а соседняя — в 4 раза больше. Найдите периметр прямоугольника.
1) 8 • 4 = 32 (см) — длина соседней стороны прямоугольника.
P = 2a + 2b
2) 2 • 8 + 2 • 32 = 16 + 64 = 80 (см)
Ответ: P = 80 см.
367. Квадрат со стороной 12 см и прямоугольник, одна из сторон которого равна 8 см, имеют равные периметры. Найдите неизвестную сторону прямоугольника.
1) 12 • 4 = 48 (см) — периметр квадрата.
2) 8 • 2 = 16 (см) — сумма двух противоположных сторон прямоугольника.
3) 48 — 16 = 32 (см) — сумма длин двух других, соседних им, противоположных сторон треугольника.
4) 32 : 2 = 16 см (см) — длина соседней стороны прямоугольника.
Ответ: 16 см.
368. Прямоугольник, соседние стороны которого равны 42 см и 14 см, и квадрат имеют равные периметры. Найдите длину стороны квадрата.
1) 2 • 42 + 2 • 14 = 84 + 28 = 112 (см) — периметр прямоугольника.
2) 112 : 4 = 28 (см) — длина стороны квадрата.
Ответ: 28 см.
369. Сколько квадратов изображено на рисунке 137?
- а) На рисунке изображено 14 квадратов (9 маленьких + 4 средних + 1 большой).
- б) На рисунке изображено 13 квадратов (4 очень маленьких + 4 маленьких + 4 средних + 1 большой).
370. Из куска проволоки сделали модель пятиугольника (рис. 138).
Какие из моделей перечисленных фигур, длины сторон которых выражаются натуральным числом сантиметров, можно сделать из этого куска проволоки: 1) квадрат; 2) пятиугольник, все стороны которого равны; 3) равносторонний треугольник?
1) 5 + 3 + 2 + 4 + 6 = 20 (см) — проволоки потребовалось для изготовления первоначальной модели.
2) 20 : 4 = 5 (см) — длина стороны квадрата, сделанного из этого куска проволоки.
3) 20 : 5 = 4 (см) — длина стороны пятиугольника, сделанного из этого куска проволоки.
4) 20 : 3 ≠ натуральному числу. Значит из этого куска проволоки нельзя изготовить равносторонний треугольник, длины сторон которого выражаются натуральным числом.
Ответ: квадрат и пятиугольник.
371. Прямоугольник ABCD разрезали на квадраты так, как показано на рисунке 139. Сторона наименьшего из квадратов равна 4 см. Найдите длины сторон прямоугольника ABCD.
- На рисунки мы видим три вида квадратов: большие, средние и маленькие.
- По условию, сторона маленького квадрата равна 4 см. По рисунку видно, что сторона большого квадрата соответствует трём длинам сторон маленьких квадратов:
1) 4 • 3 = 12 (см) — длина стороны большого квадрата.
- Вдоль стороны AD прямоугольника ABCD расположено два больших квадрата и один маленький. Значит:
2) AD = 12 + 12 + 2 = 24 + 4 = 28 (см) — длина нижней стороны прямоугольника ABCD.
- У прямоугольника противоположные стороны равны. Значит:
3) AD = BC = 28 (см) — длина верхней стороны прямоугольника ABCD.
- Вдоль верхней стороны прямоугольника ABCD расположено 4 средних квадрата. Значит:
4) 28 : 4 = 7 (см) — длина стороны среднего квадрата.
- Вдоль боковой стороны AB прямоугольника ABCD расположен один большой квадрат и один средний квадрат. Значит:
5) AB = 12 + 7 = 19 (см) — длина боковой стороны прямоугольника ABCD
- У прямоугольника противоположные стороны равны. Значит:
6) AB = CD = 19 (см) — длина противоположной боковой стороны прямоугольника ABCD
Ответ: у прямоугольника ABCD две стороны по 19 см и дву стороны по 28 см.
372. Начертите прямоугольник, соседние стороны которого равны 3 см и 6 см. Разделите его на три равных прямоугольника. Вычислите периметр каждого из полученных прямоугольников. Сколько решений имеет задача?
Задача имеет 2 решения.
Решение 1.
ABGE = EGHF = FHCD
a = AB = EG = FH = DC = 6 (см) — длина стороны малого прямоугольника.
b = AE = EF = FD = BG = GH = HC = 3 : 3 = 1 (см) — длина соседней стороны малого прямоугольника.
P = 2a + 2b = 2 • 6 + 2 • 1 = 12 + 2 = 14 (см) — периметр малого прямоугольника.
Ответ: P = 14 см.
Решение 2.
AKMD = KLNM = LBCN
a = AD = KM = LN = BC = 3 (см) — длина стороны малого прямоугольника.
b = AK = KL = LB = DM = MN = NC = 6 : 3 = 2 (см) — длина соседней стороны малого прямоугольника.
P = 2a + 2b = 2 • 3 + 2 • 2 = 6 + 4 = 10 (см) — периметр малого прямоугольника.
Ответ: P = 10 см.
373. Существует ли среди прямоугольников с периметром 12 см такой, который можно разделить на два равных квадрата? В случае положительного ответа выполните рисунок и вычислите периметр каждого из полученных квадратов.
Да, такой прямоугольник существует. Например, прямоугольник ABCD со сторонами AB = DC= 4 см и AD = BC = 2 см. Его периметр P = 12 см (2 • 4 + 2 • 2 = 8 + 4 = 12) и его можно разделить на 2 равных квадрата со сторонами 2 см. Это квадраты AMLD и MBCL.
Например, прямоугольник ABCD со сторонами AB = DC= 4 см и AD = BC = 2 см. Его периметр P = 12 см (2 • 4 + 2 • 2 = 8 + 4 = 12) и его можно разделить на 2 равных квадрата со сторонами 2 см. Это квадраты AMLD и MBCL.
Вычислим периметр полученных квадратов (так как квадраты равные, то и их периметры тоже равны):
P = 4а = 4 • 2 = 8 (см).
Ответ: Да, возможно. Периметр каждого из образованных квадратов AMLD и MBCL равен 8 см.
374. Как надо разрезать квадрат на четыре равные части, чтобы из них можно было сложить два квадрата?
375. Как надо разрезать равнобедренный прямоугольный треугольник на четыре равные части, чтобы из них можно было сложить квадрат?
376. Как надо разрезать прямоугольник со сторонами 8 см и 4 см на четыре части, чтобы из них можно было сложить квадрат?
377. Как надо разрезать квадрат на треугольник и четырёхугольник, чтобы из них можно было сложить треугольник?
378. Как надо разрезать квадрат со стороной 6 см на две части по ломаной, состоящей из трёх звеньев, чтобы из полученных частей можно было сложить прямоугольник?
Как надо разрезать квадрат со стороной 6 см на две части по ломаной, состоящей из трёх звеньев, чтобы из полученных частей можно было сложить прямоугольник?
Упражнения для повторения
379. Проведите прямую МК, луч PS и отрезок АВ так, чтобы луч PS пересекал отрезок АВ и прямую МК, а прямая МК не пересекала отрезок АВ.
380. В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 55 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?
- Предположим, что в магазине продали 55 кг лимонов 36 кг апельсинов и 34 кг мандаринов. Тогда можно найти массу фруктов оставшихся в магазине:
1) 740 — (55 + 36 + 34) = 740 — (55 + 70) = 740 — 125 = 615 (кг) — фруктов осталось в магазине после продажи.
- По условию задачи в магазине остались равные массы лимонов, апельсинов и мандарины.
 Узнаем сколько килограммов каждого вида фруктов осталось:
Узнаем сколько килограммов каждого вида фруктов осталось:
2) 615 : 3 = 205 (кг) — масса каждого вида фруктов осталось в магазине.
- Теперь найдём какова масса фруктов изначально:
3) 205 + 55 = 260 (кг) — лимонов было в магазине изначально.
4) 205 + 36 = 241 (кг) — апельсинов было в магазине изначально.
5) 205 + 34 = 239 (кг) — мандаринов было в магазине изначально.
Ответ: лимонов — 260 кг, апельсинов — 241 кг, мандаринов — 239 кг.
381. От дома до дачи можно доехать на автобусе, или на электропоезде, или на маршрутном такси. В таблице указано время, которое надо затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Каким видом транспорта при этом надо воспользоваться?
1) 10 мин + 1 ч 15 мин + 5 мин = 1 ч 30 мин — потребуется для поездки на автобусе.
2) 8 мин + 56 мин + 10 мин = 74 мин = 1 ч 14 мин — потребуется для поездки на электропоезде.
3) 7 мин + 1 ч 5 мин + 8 мин = 1 ч 20 мин — потребуется для поездки на маршрутном такси.
Ответ: наименьшее время на дорогу — 1 ч 14 мин, для этого надо воспользоваться электропоездом.
382. Найдите сумму корней уравнений:
Задача от мудрой совы
383. Как с помощью пятилитрового бидона и трёхлитровой банки набрать на берегу реки 4 л воды?
- Наливаем из реки полный 5-литровый бидон.
- Переливаем 3 литра в 3-х литровую банку. В 5-ти литровом бидоне останется 2 литра воды.
- Выливаем из 3-х литровой банки воду обратно в реку.
- Переливаем остаток воды из 5-литрового бидона (2 литра) в 3-литровую банку.
- Наливаем из реки полный 5-литровый бидон.
- Переливаем воду из 5-литрового бидона в 3-литровую банку.
При последнем действии мы сможем вылить в банку только 1 литр воды, так как в ней уже есть 2 литра воды. То есть в 5-литровом бидоне останется искомые 4 литра воды (5 — 1 = 4).
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Формулы 5 класс онлайн-подготовка на Ростелеком Лицей
Введение.
 Формула чисел Фибоначчи
Формула чисел Фибоначчи
Упражнение. Необходимо посмотреть на экран и запомнить следующий ряд чисел в течение следующих 5–7 секунд:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
Затем, не смотря на экран, попробуйте записать их на бумаге.
Не стоит переживать, если не вышло, так как существует формула, которая позволяет построить этот ряд.
Формула имеет следующий вид:
Каждый член последовательности равен сумме двух предыдущих.
Выпишем две единицы. Третий член получим как их сумму:
Четвертый является суммой 1 и 2:
Следующий уже как сумму 2 и 3:
Затем:
И так далее 21, 34, 55, 89, 144, 233 …ряд можно продолжать до бесконечности.
Такой ряд называется рядом чисел Фибоначчи, по имени средневекового математика, который изучал эти числа.
Теперь, зная формулу чисел Фибоначчи, каждый может взять бумагу и написать любое количество этих чисел. Формула позволяет освободить память, автоматизировать вычисления.
Сами числа Фибоначчи играют очень важную роль в физике и биологии. Если интересно, по этой ссылке можно посмотреть видео, рассказывающее о роли чисел Фибоначчи в растительном мире.
Формулы
В математике и других науках используются разные формулы. Все они упрощают работу, экономят время и силы. Формулу создают один раз, а потом постоянно ими пользуются.
Есть 4 типа формул, с которыми человек обычно сталкивается. Все эти 4 типа и будут рассмотрены на уроке.
Формула-определение
Часто формула является определением новой величины.
Рассмотрим два примера:
1) Формула скорости
Задача. Машина ехала 6 часов, проехала 480 км. Какова была скорость машины?
На самом деле, сначала надо ответить на другой вопрос: что такое скорость?
Время и расстояние понятны. Они наблюдаемые величины. 6 часов мы отмерили с помощью часов, расстояние измерили с помощью километровых столбиков на дороге.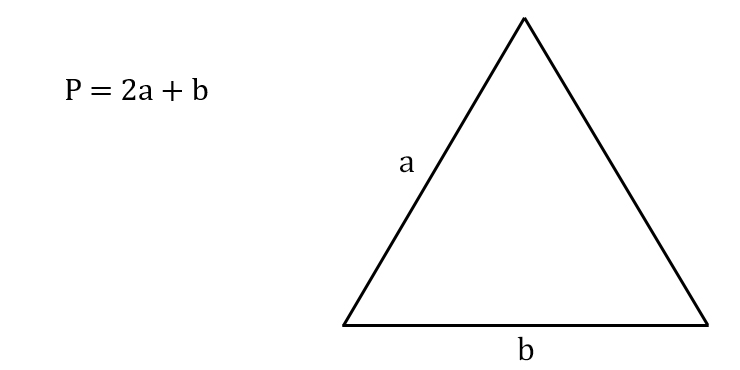
А вот на вопрос «что такое скорость автомобиля» мы как раз и отвечаем формулой.
Определение.
Скорость, а вернее средняя скорость, – это расстояние, деленное на время.
Данная формула и есть ее определение. То есть это уже величина не наблюдаемая, а вычисляемая.
Теперь можно вычислить решение задачи:
2) Длина окружности
Люди давно заметили, что соотношение длины окружности и ее диаметра постоянно.
То есть если длину окружности делить на длину диаметра, то всегда получается одна и та же величина, какого бы размера ни была окружность.
Эту величину, это число, назвали (пи).
Данная формула является определением числа .
Чаще ее можно увидеть в другой эквивалентной форме:
Задача. Найти длину окружности, радиус которой равен 20 см. (Рис. 1.)
Рис. 1. Окружность с радиусом 20 см
Решение:
Формула чисел Фибоначчи тоже является формулой-определением чисел Фибоначчи.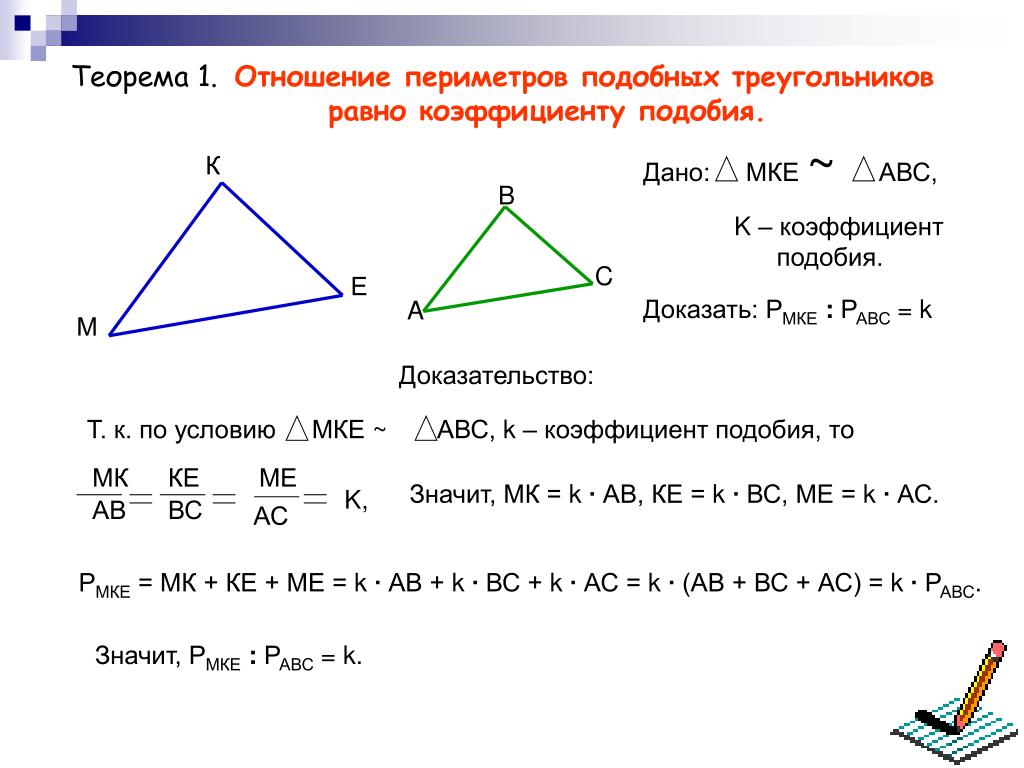
Формула-теорема
На рисунке можно увидеть прямоугольник с высотой и шириной . Внутри прямоугольника вписан треугольник. Вопрос: какую часть прямоугольника он занимает (рис. 2)?
Рис. 2. Прямоугольник с вписанным треугольником
Ответить сразу на этот вопрос не получится. Проведем отрезок из верхней точки треугольника вниз (рис. 3), то есть высоту треугольника. Эта высота тоже будет равна .
Левая часть треугольника занимает половину левого прямоугольника, правая – половину правого. Очевидно, весь треугольник занимает половину всего прямоугольника.
Рис. 3. Прямоугольник с вписанным треугольником с высотой
Значит, его площадь равна половине прямоугольника.
Так как площадь прямоугольника равна произведению одной стороны на другую (), то площадь треугольника:
где – основание треугольника, – его высота.
Эта формула была выведена, доказана, а не использована в качестве определения. Обычно такие формулы называют еще теоремами.
Обычно такие формулы называют еще теоремами.
Для чего нужна эта формула? Понятно, если известны основание треугольника и его высота, то возможно найти площадь.
Но эта формула сообщает еще один удивительный факт.
Как бы ни была передвинута вершина треугольника, основание и высота у него не меняются, а значит, и площадь не меняется тоже (рис. 4).
Рис. 4. Передвижение вершины треугольника
Экспериментальная формула
Часто люди видят, что одно явление зависит от других. Но сделать математическую запись этой зависимости обычно очень непросто.
Так, например, давно было понятно, что если тело толкать или тащить с разной силой, то результат будет разный. Но как описать эту зависимость, долго было не понятно.
Ньютон сформулировал это в виде формулы, которая называется вторым законом Ньютона:
где – сила, которая действует на тело; – масса тела.
Она описывает такое свойство: во сколько раз больше сила, которая действует на тело, во столько раз быстрее тело разгоняется. Эту величину – скорость разгона – называют ускорением.
Эту величину – скорость разгона – называют ускорением.
Формула-тождество
Формула квадрата суммы
Пусть есть два числа и . Что означает запись ?
Это значит, что умножается само на себя.
Известно, что это произведение равно площади квадрата с такой стороной. Потому вторая степень и называется квадратом. Проведены две вспомогательные линии. Большой квадрат разбивается на 4 части (рис. 5).
Тогда площадь большого квадрата равна сумме всех четырех фигур:
Эта формула позволяет упрощать вычисления. Она так и называется, формулой сокращенного умножения.
Рис. 5. Большой квадрат, разбитый на 4 части
Пример:
Задание. Задан прямоугольник со сторонами и и квадрат со стороной . Напишите самостоятельно формулы периметров для каждой фигуры и формулу площади квадрата.
Вспомним, что периметр многоугольника – это сумма длин всех его сторон. Обозначается большой латинской буквой .
Обозначается большой латинской буквой .
Проверка.
Периметр прямоугольника равен сумме его четырех сторон. Так как противоположные стороны равны, то получаем:
У квадрата все стороны равны, поэтому его периметр:
Квадрат является прямоугольником, его площадь равна произведению двух соседних сторон, но они равны друг другу:
Полученные формулы периметров и площади настолько просты, что нет никакой нужды их запоминать. Каждый раз, когда понадобится найти периметр или площадь таких фигур, можно будет опираться на смысл этих понятий.
Что на самом деле является полезным умением – это переписывать формулу в том виде, который нам более удобен в данный момент.
Задача 1
Нужно в компьютер ввести формулу для расчета времени движения автобуса. Расстояние и средняя скорость будут меняться (разные маршруты, разное состояние дорог).
Мы знаем, что средняя скорость задается своей формулой:
Но нам нужна формула для расчета времени. Перенесем в левую часть формулы, скорость, наоборот, в правую:
Перенесем в левую часть формулы, скорость, наоборот, в правую:
Получили формулу для расчета времени в пути. Это та же самая формула, но записанная в другом, эквивалентном, виде.
Что изменится, если расстояние меняться не будет (маршрут всегда один) и составит 350 км? Меняется только средняя скорость из-за погодных условий. Так как расстояние не меняется, то подставим его в формулу:
Новая формула пригодна для расчета времени только для этого конкретного маршрута, но зато требует ввода только одного значения, а не двух.
Найдем с помощью нее необходимое время на дорогу, если средняя скорость составляет 40 км/ч, 50 км/ч, 60 км/ч:
Ответ: , ,
Задача 2
Банки краски хватает на покраску 15 кв. метров забора. Какой длины часть забора можно покрасить, если у нас одна банка?
Решение
Понятно, что до тех пор, пока мы не знаем высоту забора, мы не сможем ответить на эти вопросы. Но мы можем подготовиться, составить формулы для вычисления этой длины. Как только высота забора будет известна, мы подставим ее в формулу и найдем длину.
Но мы можем подготовиться, составить формулы для вычисления этой длины. Как только высота забора будет известна, мы подставим ее в формулу и найдем длину.
Итак, покрашенная часть забора – это прямоугольник. Высоту забора обозначим , а длину покрашенной части – (рис. 6).
Рис. 6. Закрашенный участок стены
Площадь, закрашенная с помощью одной банки, – , но она же .
Выразим длину :
Если банка была одна, то покрашенная площадь равна .
Мы получили формулу для расчета.
Если теперь мы узнаем высоту забору, то легко найдем длину окрашенной части забора (; ; ):
Ответ: ; ; .
Вывод
На этом уроке было изучено, что формула – это алгоритм («Подумали один раз, вывели формулу, а пользуемся всю жизнь»).
Кроме того, было выделено 4 типа формул: формула-определение, формула-теорема, экспериментальная формула, математическое тождество.
Также следует запомнить, что формулу можно записывать в разных эквивалентных видах, в зависимости от того, какую величину мы хотим вычислять.
Список литературы
- Виленкин Н.Я. Математика: учеб. для 5 кл. общеобр. учр. 17-е изд. – М.: Мнемозина, 2005.
- Шевкин А.В. Текстовые задачи по математике: 5–6. – М.: Илекса, 2011.
- Ершова А.П., Голобородько В.В. Вся школьная математика в самостоятельных и контрольных работах. Математика 5–6. – М.: Илекса, 2006.
- Хлевнюк Н.Н., Иванова М.В.. Формирование вычислительных навыков на уроках математики. 5–9 классы. – М.: Илекса, 2011.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет портал «Фестиваль педагогических идей» (Источник)
- Интернет портал «Математика онлайн» (Источник)
- Интернет портал «Гипермаркет знаний» (Источник)
Домашнее задание
- Какова была средняя скорость автомобиля, если расстояние в 432 км он проехал за 6 часов?
- Чему равна площадь треугольника с высотой 5 см и основанием 7 см?
- Найдите длину окружности, если она в три раза больше той окружности, радиус которой равен 15 см.

Периметр треугольника — определение, формулы, примеры
Периметр треугольника — это общая длина всех трех его сторон. Треугольник – это многоугольник, который имеет три стороны, для нахождения периметра треугольника используются различные методы. В этой статье рассмотрены все формулы нахождения периметра различных типов треугольников.
Реальный пример использования периметра треугольника: Периметр треугольника используется для расчета длины проволоки, используемой для ограждения любого треугольного поля. Он также используется для создания треугольной мебели, стола и других предметов.
Каков периметр треугольника?
Периметр треугольника — это общее расстояние, пройденное вдоль границы любого треугольника. Периметр можно рассматривать как общую длину границ любой плоской фигуры. Поскольку периметр является мерой длины, он измеряется в м, см, км и т. д.
Формула периметра треугольника
Для нахождения периметра треугольника берется сумма длин всех его сторон. Формула, необходимая для нахождения периметра треугольника:
Формула, необходимая для нахождения периметра треугольника:
Периметр = сумма трех сторон треугольника
Давайте разберемся в этой формуле с различными типами треугольников.
Периметр разностороннего треугольникаПериметр треугольника равен сумме всех сторон треугольника. Если длины сторон треугольника равны a, b и c, то
Периметр = a + b + c
, где
a , b , c длины сторон
Периметр равнобедренного треугольника Неравная сторона равна ‘
C ‘, затемПериметр Isockeles Triangle = B + B + C
= 2B + Cгде
b длина двух равных сторон
c третья сторона
периметр равностороннего треугольника A = B = C, следовательно,
Периметр равностороннего треугольника = B + B + B = 3B
, где,
B — длина боковой длины
ПЕРИМЕтр правого трианга
0027
Для прямоугольного треугольника, т. е. треугольника с одним углом 90°. Периметр вычисляется путем сложения длин всех данных сторон. Формула для нахождения периметра прямоугольного треугольника:
е. треугольника с одним углом 90°. Периметр вычисляется путем сложения длин всех данных сторон. Формула для нахождения периметра прямоугольного треугольника:
Формула периметра прямоугольного треугольника, P = a + b + c
длины сторон
Как найти периметр треугольника
Периметр треугольника вычисляется с использованием шагов, описанных ниже:
Шаг 1: Отметьте размер каждой стороны треугольника и убедитесь, что все размеры указаны в одних и тех же единицах измерения.
Шаг 2: Сложите значения всех сторон, чтобы найти периметр.
Шаг 3: Сумма, полученная на шаге 2, является требуемым периметром (используйте единицы измерения, равные длине сторон).
Решение:
Даны стороны треугольника 4см, 5см и 6см.
Таким образом, это разносторонний треугольник .
Таким образом, периметр треугольника = сумма сторон = 4 + 5 + 6 = 15 см
Пример 2. В равнобедренном треугольнике две стороны равны 5 см и 6 см. Чему может быть равен периметр треугольника?
Решение:
Учитывая, треугольник равнобедренный треугольник. Таким образом, любые две стороны треугольника равны.
Итак, третья сторона может быть как 5см, так и 6см.
Если третья сторона 5 см, то
Периметр = 5 + 5 + 6 = 16 см
Если третья сторона 6 см, то
Периметр = 5 + 6 + 6 = 17 см
Итак, периметр может быть 16см или 17см.
Пример 3: Чему равен периметр равностороннего треугольника, длина одной стороны которого равна 5 см?
Решение:
Учитывая, что треугольник является равносторонним треугольником, таким образом, все три стороны равны по длине.
Поскольку одна сторона равна 5 см, две другие стороны также будут равны 5 см.
Итак, периметр = 5 + 5 + 5 = 15см.
Пример 4. Если периметр равностороннего треугольника равен 21 см, найдите длины его трех сторон.
Решение:
Поскольку в равностороннем треугольнике все три стороны равны по длине, периметр равен трем длинам сторон.
Пусть длина любой стороны будет равна ‘a’ единиц. Таким образом, периметр равен ‘3a’ единиц.
Итак, мы можем написать,
3a = 21
a = 7 см
Таким образом, длина каждой стороны равна 7 см.
Пример 5: Найдите длину двух равных сторон равнобедренного треугольника, если длина неравной стороны 5 см, а периметр 17 см.
Решение:
Часто задаваемые вопросы о периметре треугольникаДана длина неравной стороны 5см, периметр 17см.
Так как это равнобедренный треугольник , длины двух других сторон равны. Пусть длина каждой равной стороны равна a единиц.
Таким образом, периметр = а + а + 5
Поскольку периметр = 17 см, мы можем написать,
17 = а + а + 5
2а + 5 = 17
2а = 12
а0 = 60002 а0Таким образом, длина равных сторон равнобедренного треугольника равна 6см.
Вопрос 1: Какова формула периметра равностороннего треугольника?
Ответ:
У равностороннего треугольника все стороны равны. Таким образом, периметр равностороннего треугольника равен 3а единицам, где а — длина стороны треугольника.
Вопрос 2: Что понимается под периметром треугольника?
Ответ:
Периметр треугольника – это сумма длин сторон треугольника.
Если a, b и c — стороны треугольника, то периметр = a + b + c.
Вопрос 3: Каков периметр равностороннего треугольника?
Ответ:
Периметр треугольника — это длина всех его сторон. В равностороннем треугольнике со стороной а. Периметр = 3×a
Вопрос 4: Как найти площадь треугольника?
Ответ:
Для вычисления периметра треугольника складывается сумма всех трех его сторон.
Вопрос 5: Сколько треугольников с периметром 8 единиц?
Ответ:
Возможен только один треугольник с периметром 8 и длинами сторон 8/3, 8/3 и 8/3 единиц.
Связанный артикул
- Периметр прямоугольника
- Окружность круга
Как найти периметр треугольника (формула и видео) // Tutors.
 com
comПериметр треугольника (формула и примеры)
видео Определения Формула Примеры Вызов
Возможно, один из самых простых способов работы с многоугольниками — это определение их периметра или расстояния вокруг их сторон. Треугольник — простейший многоугольник, поэтому найти его периметр несложно!
Чему вы научитесь:
Проработав этот урок и видео, вы сможете:
- Определить периметр
- Распознавать типы треугольников
- Вспомнить и объяснить метод нахождения периметра треугольников
- Найдите длины сторон треугольника с помощью алгебры, если известен периметр
Что такое периметр?
Периметр — это расстояние вокруг сторон многоугольника или другой формы. Периметр всегда является той же линейной единицей измерения, что и единица измерения сторон.
В приведенном ниже равностороннем треугольнике △WUT имеет стороны WU, UT и TW.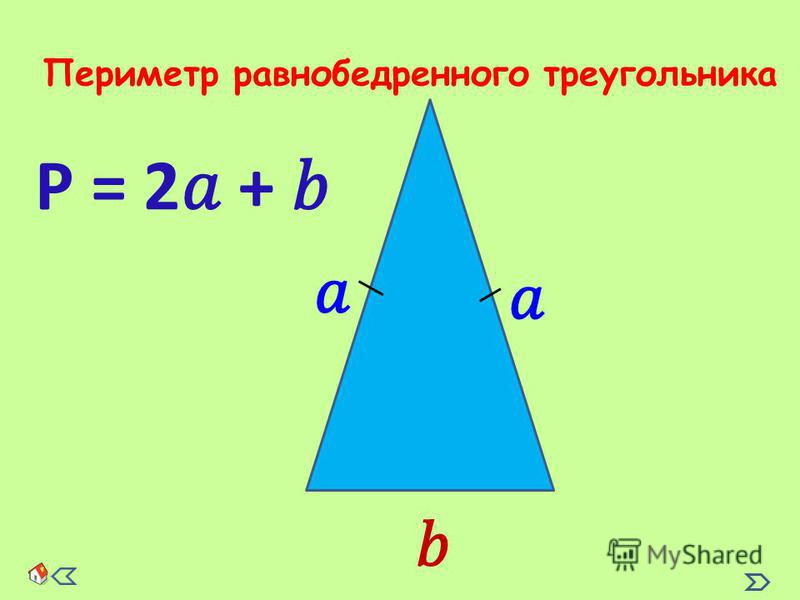 Маленькие галочки по бокам указывают на то, что все три стороны одинаковы, поэтому измерение для WU, 27 метров, верно и для двух других сторон.
Маленькие галочки по бокам указывают на то, что все три стороны одинаковы, поэтому измерение для WU, 27 метров, верно и для двух других сторон.
[вставьте равносторонний △WUT, как описано]
Чтобы найти периметр треугольника, сложите длины трех сторон: Классификация треугольников
Треугольник представляет собой трехстороннюю плоскую фигуру, замыкающуюся в пространстве. Три стороны образуют три внутренних угла. Треугольники бывают разных конфигураций, в зависимости от вашего выбора, чтобы сосредоточиться на их сторонах или углах:
По сторонам
- Равносторонний — Три стороны одинаковой длины
- Равнобедренный — Две стороны одинаковой длины, называемые ногами
- Неравносторонний — Нет сторон одинаковой длины
По углам
- Острые — Три внутренних угла < 90°
- Тупой — Один внутренний угол > 90°
- Вправо — Один внутренний угол = 90°
Остроугольные и тупоугольные треугольники относятся к категории косоугольных треугольников s, что означает, что у них нет прямых углов.
Формула периметра треугольника
Вы можете найти периметр каждого из этих треугольников, используя эту формулу:
P = a + b + c
Это всегда верно, где P — периметр, а a, b и с — длины сторон.
Периметр равносторонних треугольников
Только с равносторонними треугольниками можно заменить сложение умножением. Поскольку у равносторонних треугольников три равные стороны, P = 3 × a или P = 3a, где P – периметр, а – длина любой стороны.
P = 3a
Как найти периметр треугольника
Вот разносторонний треугольник DOT с измеренными сторонами 9 ярдов, 11 ярдов и 13 ярдов:
[вставить △DOT как описано]3
Сложите три длины:
P = 9 + 11 + 13
P = 33 ярда
Вот равнобедренных треугольников LEG с основанием EG, равным 175 мм. Измеряется только одна нога, LE = 200 мм.
[вставьте △LEG как описано]
Какова длина стороны GL? Вам не сказали, какой длины был GL!
Подумай.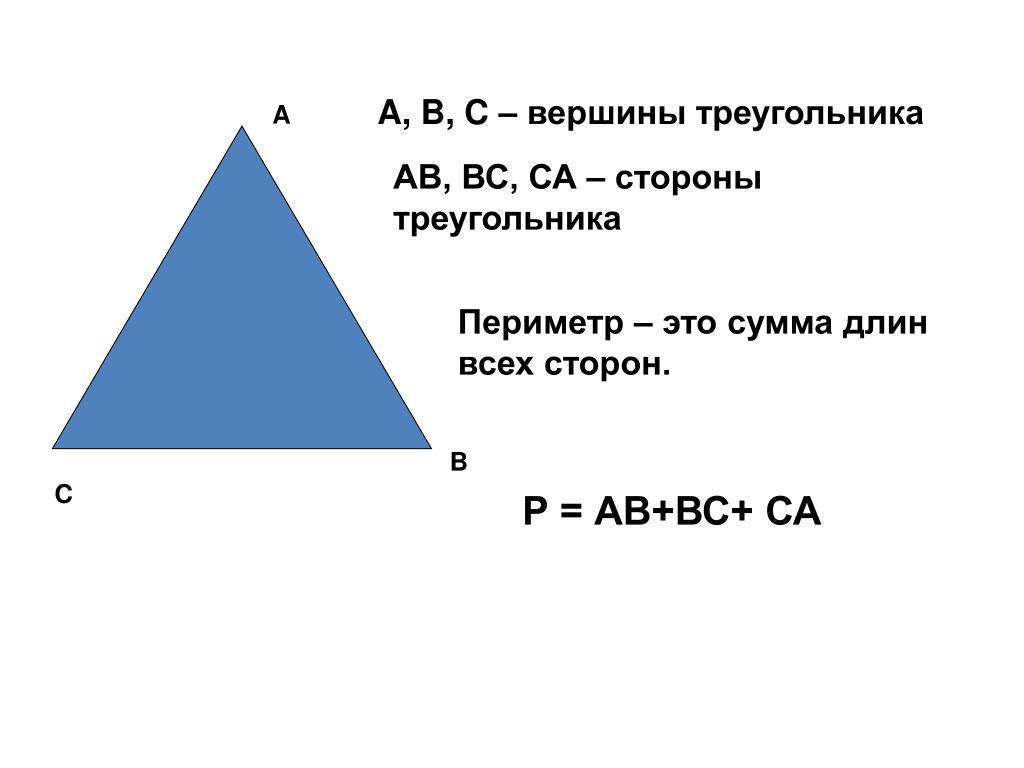 Все будет хорошо.
Все будет хорошо.
В равнобедренном треугольнике другой катет равен идентифицированному катету, так что вы также знаете, что GL = 200 мм! Сложите стороны:
P = 175 + 200 + 200
P = 575 мм
Задача по алгебре периметра
Некоторые учебники и учителя математики могут взять простую концепцию, такую как периметр треугольника, и превратить ее в задачу. Вот △ЯК с заданным периметром 118 км (да, это большой треугольник), но стороны обозначены необычным образом.
[вставьте △YAK, как описано]
У нас есть сторона YA как «5 больше, чем в два раза», и YK как «10 меньше, чем в шесть раз больше того же числа», а сторона AK как «на 15 больше». чем в четыре раза больше таинственного числа». Что нам со всем этим делать?
Превратите каждое предложение в алгебраическое выражение. Пусть x будет неизвестным числом:
«5 больше, чем удвоенное число» становится:
2x + 5 = YA
«10 меньше, чем шесть раз равное число» становится:
6x — 10 = YK
«15 больше, чем в четыре раза больше загадочного числа» становится:
4x + 15 = AK
Периметр – это сумма сторон, поэтому, если сложить эти выражения вместе, вы GET:
2x+5+6x-10+4x+15 = 118 км
Условия комбинации:
12x+10 = 118 км
Выброска 10 с обеих сторон. = 108 км
= 108 км
Разделите обе стороны на 12:
x = 9 км
Вернитесь к каждому выражению и замените x на 9 км:
2x+5 = YA
2 (9)+5 = YA
23 = YA
. ..
6x-10 = YK
6 (9)-10 = YK
44 = YK
…
4x+15 = AK
4 (9)+15 = AK
51 = AK
Чтобы подтвердить наши стороны, добавьте, чтобы увидеть, равны ли они заданному периметру:
23 + 44 + 51 = 118 км
Молодец! Вы использовали алгебру, чтобы решить задачу периметра!
Итоги урока
Теперь, когда вы прошли весь урок, вы можете определять периметр, распознавать типы треугольников, вспоминать и объяснять метод нахождения периметра треугольников путем сложения длин их сторон и , учитывая периметр, найдите длины сторон треугольника с помощью алгебры.
Следующий урок:
Как найти периметр прямоугольника
Как найти площадь и периметр треугольника (видео)
vimeo.com/video/398535722?app_id=122963″ frameborder=»0″ allow=»autoplay; fullscreen» allowfullscreen=»»>TranscriptFAQsPractice
Привет и добро пожаловать на это видео о периметре и площади треугольника!
Для начала давайте быстро рассмотрим, что измеряют периметр и площадь . Представьте, что у нас есть двор треугольной формы.
Если бы мы хотели построить забор вокруг нашего двора, нам нужно было бы знать расстояние вокруг двора. Это периметр . Если бы мы хотели купить дерн для нашего двора, нам нужно было бы знать площадь двора, чтобы мы могли купить правильное количество.
И хотя может быть немного необычно иметь двор в форме треугольника, у вас может быть часть двора, которую вы хотите оградить или дерн в форме треугольника.
Как найти периметр треугольника
Итак, теперь, когда мы знаем, что такое периметр и площадь, давайте выясним, как найти периметр . Нам не нужна причудливая формула или что-то в этом роде. Все, что нам нужно сделать, это сложить длины сторон вместе. Итак, если мы знаем все стороны нашего двора, мы можем легко найти периметр:
Нам не нужна причудливая формула или что-то в этом роде. Все, что нам нужно сделать, это сложить длины сторон вместе. Итак, если мы знаем все стороны нашего двора, мы можем легко найти периметр:
\(20м+20м+12м=52м\) забора. Не так много для этого. Обратите внимание, что ответ дан в метрах. Потому что периметр — это расстояние. Пройтись по двору означало бы пройти 52 метра.
Вот и все, независимо от того, какой у вас тип треугольника. Просто сложите длины сторон, и у вас будет периметр.
Как найти площадь треугольника
Теперь займемся площадью. Существует формула для нахождения площади треугольника: \(A= \frac{1}{2}bh\)
Давайте быстро объясним, откуда взялось это \(\frac{1}{2}\). Формула площади параллелограмма \(A=bh\). Если мы сравним две фигуры, то увидим, что параллелограмм можно составить из двух треугольников одинакового размера:
Таким образом, мы можем сказать, что треугольник — это половина параллелограмма, откуда в формуле берется одна половина.
Для треугольников формула площади работает немного по-разному в зависимости от типа треугольника. Начнем с прямоугольных треугольников.
У нас есть формула, но нам нужно ответить на вопрос, какая сторона \(b\), а какая \(h\)?
Для прямоугольного треугольника, подобного этому, \(b\) и \(h\) — это две стороны, примыкающие к прямому углу или следующие за ним. Неважно, что есть что, поэтому допустим, что \(b=6\) см и \(h=8\) см.
Теперь мы можем подставить их в нашу формулу:
\(A=\frac{1}{2}(6 \text{см})(8 \text{см})\)
Это всегда хорошая идея заменить скобки, чтобы помочь держать вещи организованными. Мы даже оставили юниты, чтобы посмотреть, что с ними будет. На данный момент нам осталось сделать только умножение, так что в соответствии с 92\).
В задачах на площади ответ всегда будет в квадратных единицах. Это потому, что мы пытаемся определить, сколько квадратных сантиметров поместится в нашем треугольнике. Мы можем ясно увидеть это, взглянув на равнобедренный прямоугольный треугольник, длина катетов которого равна 5 единицам, на миллиметровке:
Мы можем ясно увидеть это, взглянув на равнобедренный прямоугольный треугольник, длина катетов которого равна 5 единицам, на миллиметровке:
Сколько квадратов внутри треугольника? Мы можем их сосчитать. Сначала мы посчитаем целые квадраты, которые помещаются внутрь, затем добавим половинки квадратов:
Есть 10 полных квадратов плюс 5 полуквадратов, всего 12\(\frac{1}{2}\) квадраты.
Если мы воспользуемся нашей формулой, мы найдем то же самое:
\(A=\frac{1}{2}(5)(5)\)
\(A=\frac{1}{2 }(25)\)
\(A=12,5\)
Теперь мы увидели, как работает формула, и лучше поняли, почему единицы возводятся в квадрат. Осталось только найти площади острого и тупоугольного треугольников.
Начнем с остроугольного треугольника:
Обратите внимание, что высота всегда перпендикулярна основанию. Отсюда мы можем найти площадь: 92\)
Q
Как найти периметр треугольника?
A
Найдите периметр треугольника, сложив вместе длины всех трех сторон.
Пример. Чему равен периметр этого треугольника?
P = 7 + 8 + 16 = 31 см
Q
Как найти площадь прямоугольного треугольника?
A
Найдите площадь прямоугольного треугольника, умножив его основание на высоту и разделив на 2. 92\)
Q
Как найти периметр прямоугольного треугольника?
A
Найдите периметр прямоугольного треугольника, сложив вместе меры всех трех сторон.
Практические вопросы
Вопрос №1:
Каков периметр этого треугольника?
25 см
14 см
23 см
17 см
Показать ответ
Ответ:
см. Правильный ответ: Чтобы найти периметр многоугольника, сложите длины всех сторон.
\(P=3+11+9=23\text{ см}\)
Скрыть ответ
Вопрос №2:
Какова площадь этого треугольника?
6 ft 2
12 ft 2
3 ft 2
9 ft 2
Show Answer
Answer:
The correct answer is 6 ft 2 .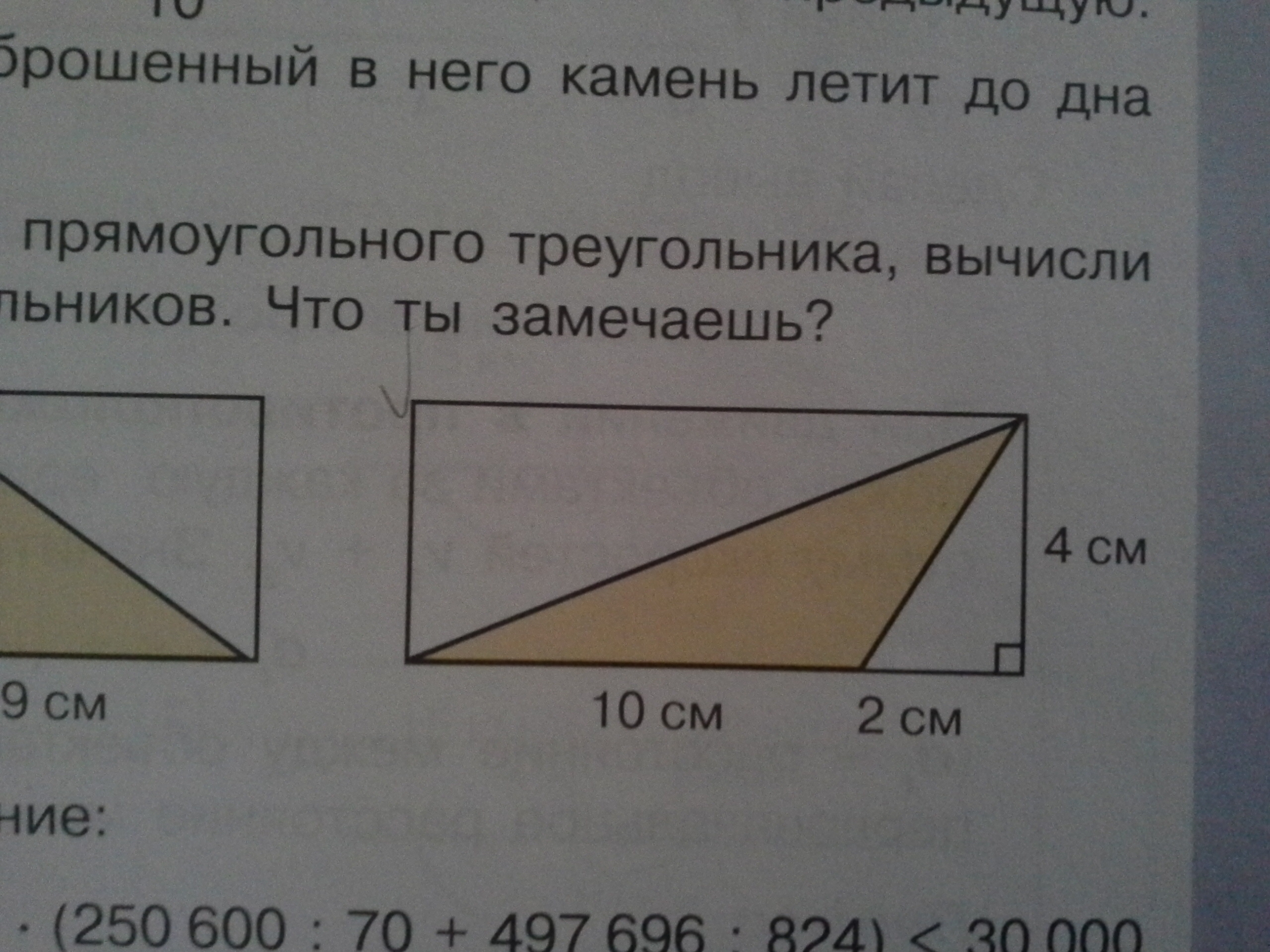 Чтобы найти площадь треугольника, используйте эту формулу:
Чтобы найти площадь треугольника, используйте эту формулу:
\(A=\frac{1}{2}bh\)
Основание ( 92\)
Скрыть ответ
Вопрос №3:
По какой формуле находится периметр любого треугольника?
\(P=3s\)
\(P=a+b+c\)
\(P=a+b+c+d\)
\(P=2a+b\)
Показать ответ
Ответ:
Правильный ответ \(P=a+b+c\). Чтобы найти периметр многоугольника, сложите длины каждой стороны \(P=a+b+c\). \(P=3s\) можно использовать только для равносторонних треугольников, а не для всех треугольников. И \(P=2a+b\) можно использовать только для равнобедренных треугольников.
Скрыть ответ
Вопрос №4:
Какова площадь этого треугольника?
81 in 2
63 in 2
74 in 2
126 in 2
Show Answer
Answer:
The correct answer is 63 in 2 .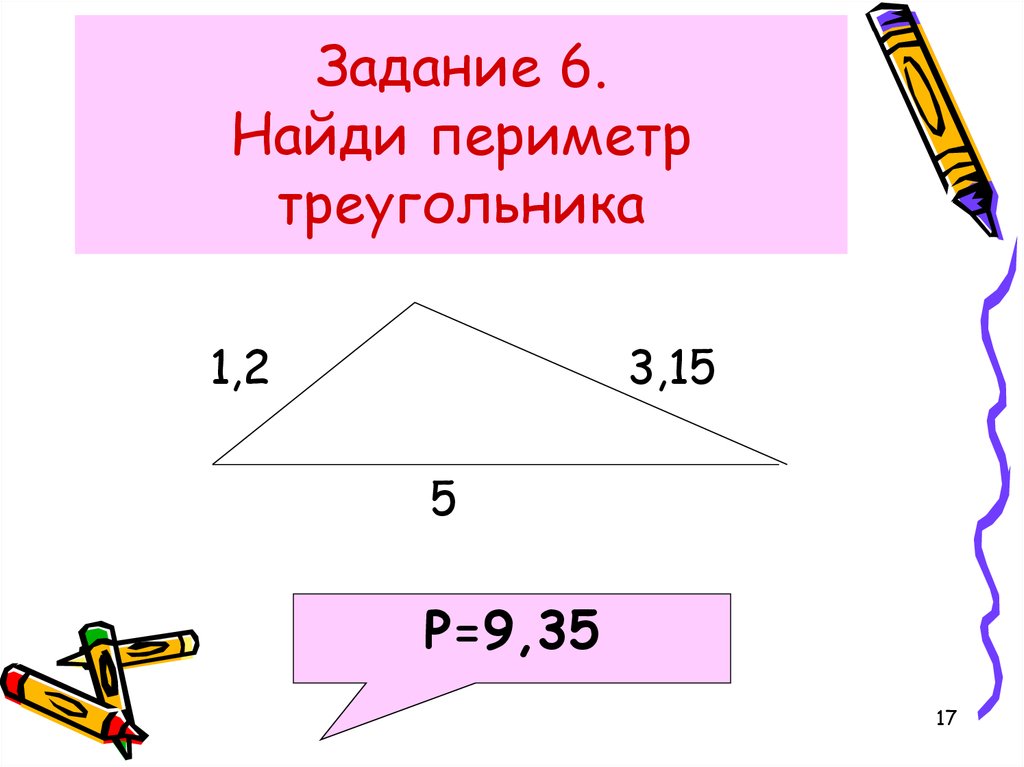 Формула площади треугольника:
Формула площади треугольника:
\(A=\frac{1}{2}bh\)
Основание ( b ) равно 18 дюймам, а высота (92\)
Скрыть ответ
Вопрос №5:
Каков периметр этого равнобедренного треугольника?
32 см
29 см
21 см
34 см
Показать ответ
Ответ:
см. Правильный ответ: Чтобы найти периметр многоугольника, сложите длины всех сторон. Поскольку это равнобедренный треугольник, две его стороны равны 13 см.
\(P=13+13+8=34\text{см}\)
Скрыть ответ
Вернуться к видео по геометрии
853779
Q7 Найдите периметр треугольника со сторонами 10 см 14 см и 15 см Перейти
Упражнение 10.1
 2
2- Зная наши цифры
- Целые числа
- Игра с числами
- Основные геометрические идеи
- Понимание элементарных форм
- Целые числа
- Фракции
- Десятичные
- Обработка данных
- Измерение
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 10 — Измерение
>
Упражнение 10. 1
>
Вопрос 15
1
>
Вопрос 15
Вопрос 15 Упражнение 10.1
В7) Найдите периметр треугольника со сторонами 10 см, 14 см и 15 см.
Ответ:
Решение:
Периметр треугольника = сумма всех сторон
= 10 + 14 + 15
= 39 см.
Периметр треугольника 39 см.
Стенограмма видео
«Привет, ребята, добро пожаловать на элитную домашнюю работу сегодня мы делаем вопрос номер семь то есть найти периметр треугольник со стороной 10 сантиметр 14 сантиметр и 15 сантиметров, так что давайте прежде всего нарисуйте грубый набросок этого треугольника так что это твой треугольник тебе не нужен ты знаешь нарисуйте его точно в масштабе, который независимо от длина дает вам нарисовать это так нет необходимости так это либо 10, либо 14, а затем 50. Итак, что вам нужно сделать, чтобы найти ответ просто добавьте их, чтобы ваш ответ 10 плюс 14 плюс 15 так что ответ на ваш вопрос 15 плюс 14 будет 2929 плюс 10 39 лет так что ваш ответ на этот вопрос 39 сантиметр большое спасибо ребята за посмотри видео если есть еще сомнения, пожалуйста, напишите это в комментарии раздел так же ставьте лайк под видео и подписывайтесь наш канал большое спасибо »
Связанные вопросы
Q1) Найдите периметр каждой из следующих фигур: (a) (b) (c) (d) (e) (f)
Найдите периметр каждой из следующих фигур:
Крышка прямоугольной коробки со сторонами 40 см на 10 см заклеена скотчем по всему периметру. Что такое лен…
Что такое лен…
Q2) Крышка прямоугольной коробки со сторонами 40 см на 10 см заклеена по всему периметру скотчем. Что это …
Q3) Размеры столешницы 2 м 25 см на 1 м 50 см. Каков периметр столешницы?
Размеры столешницы 2 м 25 см на 1 м 50 см. Каков периметр столешницы?
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Exercise 10.1
Exercise 10.2
Exercise 10.3
Chapters
Knowing Our Numbers
Whole Numbers
Playing With Numbers
Basic Geometrical Ideas
Understanding Elementary Shapes
Integers
Fractions
Decimals
Обработка данных
Измерение
Алгебра
Отношение и пропорция
Симметрия
Практическая геометрия
Курсы
Быстрые ссылки
Термины и политики
Термины и политики
2022 © Качественные учебные пособия Pvt Ltd Все права защищены
Область и периметр Треугольников: Значение, Форма, примеры
- Записанные платты.

- Последнее изменение 25 августа 2022 г.
- Автор ШВЕТА Б.Р.
- Последнее изменение 25 августа 2022 г.
Площадь и периметр треугольников : Периметр – это общая длина трех сторон любого треугольника. Площадь треугольника — это область или поверхность, ограниченная формой треугольника. Мы находим Периметр, когда зажигаем рождественские гирлянды вокруг дома или ограждаем сад на заднем дворе. Точно так же находим площадь пола комнаты, чтобы определить размер приобретаемого ковра.
В этой статье вы узнаете, что такое периметр и как вычислить периметр различных типов треугольников, когда известны длины всех сторон. Кроме того, решенные кейсы помогут вам получить другие точки зрения на предмет. Давайте посмотрим на статью, чтобы лучше понять концепцию.
Что такое периметр?
Определение : Слово «периметр» происходит от греческого слова « пери », означающего вокруг , и « метрон » означает меру . Периметр – это сумма длин границ любой формы.
Периметр – это сумма длин границ любой формы.
Периметр треугольника
Треугольник – это многоугольник, имеющий три стороны и три угла. Периметр треугольника можно получить, просто сложив длины всех трех сторон. Периметр любого многоугольника равен сумме длин сторон.
Формула периметра фигуры замкнутой формы обычно равна длине внешней линии фигуры.
Если треугольник имеет \(3\) сторон \(a, b\) и \(c\), то периметр треугольника \((P) = (a + b + c)\,\rm{единицы} \).
Формулы периметра треугольника
Формулы для периметра различных типов треугольников объясняются ниже:
Периметр равностороннего треугольника
Периметр равностороннего треугольника определяется выражением \(= a + a + a = 3a\,\rm{единицы}\)Периметр равнобедренного треугольника
Если \(a\) и \(a\) две равные стороны, а \(b\) — основание равнобедренного треугольника, то его периметр равен \(= a + a + b = (2a + b )\,\rm{единицы}\)Периметр разностороннего треугольника
Периметр разностороннего треугольника определяется выражением \(= (a + b + c)\,\rm{единицы}\)Что такое площадь?
Площадь — это область или поверхность, окруженная формой объекта. Пространство, занимаемое фигурой или любой другой геометрической фигурой, называется площадью этой фигуры. Площадь фигур зависит от их размеров и свойств. Площади различны для разных форм. Площадь круга отличается от площади квадрата. 92)\).
Пространство, занимаемое фигурой или любой другой геометрической фигурой, называется площадью этой фигуры. Площадь фигур зависит от их размеров и свойств. Площади различны для разных форм. Площадь круга отличается от площади квадрата. 92)\).
Формулы площади треугольника
Формула площади треугольника определяется выражением \( = \frac{1}{2} \times {\text{основание}} \times {\text{высота}}\)\(A = \frac{1}{2} } \times b \times h\) квадратных единиц
Доказательство формулы площади треугольника
Площадь прямоугольника определяется выражением \(A = \rm{длина} × \rm{ширина} = l × b\). Диагонали прямоугольника делят его площадь на две равные половины. Итак, здесь диагональ \(AC\) разделила прямоугольник на две равные половины \(ABC\) и \(ADC\). В треугольнике \(ABC\) длина \(BC\) теперь считается основанием, а ширина \(AB\) теперь считается высотой треугольника. Итак, площадь треугольника \(ABC = \frac{1}{2} \times {\text{площадь}}\, {\text{из}}\, {\text{the}}\, {\ текст{прямоугольник}}\)
\(ABCD = \frac{1}{2} \times BC \times AB = {\text{Площадь}}\,{\text{из}}\,{\text{}}\,{\text {Треугольник}}\)
\(ABC = \frac{1}{2} \times BC \times AB\)
\(A = \frac{1}{2} \times {\text{base}} \ раз {\text{высота}}\)
\(A = \frac{1}{2} \times b \times h\)
Следовательно, доказано. 2}\,{\text{квадрат}} \, {\ текст {единицы}} \)
2}\,{\text{квадрат}} \, {\ текст {единицы}} \)
Площадь разностороннего треугольника (формула Герона)
Площадь треугольника с тремя сторонами разной меры можно рассчитать по формуле Герона.
Формула Герона включает два шага,
1. Вычислить «\(s\)» (половина периметра треугольника):
\(s = \frac{ {a + b + c}}{2}\)
2. Затем вычислить площадь:
\(A = \sqrt {s\left({s – a} \right)\left({s – b} \right)\left({s – c} \right)} \)
Площадь равностороннего треугольника: частный случай формулы Герона
Таким образом, формула Герона или формула Герона могут быть использованы для получения специальной формулы, применимой только для вычисления площади равностороннего треугольника.
В равностороннем треугольнике длины всех сторон равны. Итак, \(а = b = с\).
Итак, \(s = \frac{ {a + b + c}}{2} = \frac{ {a + a + a}}{2} = \frac{ {3a}}{2}\)
Итак, площадь \( = \sqrt {s(s – a)(s – b)(s – c)} = \sqrt {\ frac {{3a}} {2} \times \left( {\ frac{ {3a}}{2} – a} \right) \times \left( {\frac{{3a}}{2} – a} \right) \times \left( {\frac{{3a}}{2 } – а} \справа)} \) 92}}}{4}} \)
Формулы площади треугольника с использованием тригонометрии
В \(\Delta ABC\) \(a, b\) и \(c\) — стороны треугольника.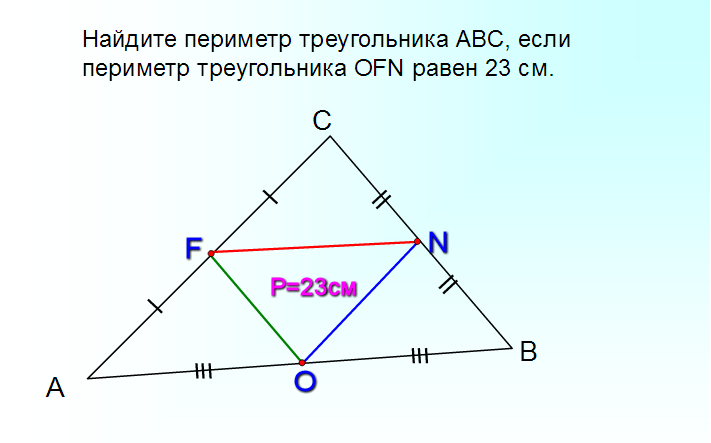 (Условно \(a\) считается стороной, противоположной \(\угол A\). Аналогично, \(b\) и \(c\) рассматриваются как стороны, противоположные углам \(\угол B \) и \(\угол C\) соответственно.
(Условно \(a\) считается стороной, противоположной \(\угол A\). Аналогично, \(b\) и \(c\) рассматриваются как стороны, противоположные углам \(\угол B \) и \(\угол C\) соответственно.
В этом случае формула площади треугольника задается следующим образом:
,\sin \,\sin C\)
\( {\text{Площадь}} = \frac{1}{2}bc\,\sin\,\sin A\)
\( {\text{Площадь}} = \frac{1}{2}ca\,\sin \,\sin B\)
Следовательно, площадь \( = \frac{1}{2} \times { \text{произведение любых двух сторон}} \times {\text{сторона угла, включая эти две стороны}}{\text{.}}\)
Площадь треугольника с координатами вершин
Площадь треугольника можно получить, если заданы координаты трех вершин треугольника на декартовой плоскости.
В треугольнике \(ABC\), показанном выше, \(A(x_1, y_1 )\), \(B(x_2, y_2 )\) и \(C(x_3, y_3 )\) являются координатами вершины.
Используйте следующую формулу:
\({\text{Площадь}} = \frac{1}{2}\left[ {{x_1}\left( {{y_2} – {y_3}} \right) + {x_2 }\left( {{y_3} – {y_1}} \right) + {x_3}\left( {{y_1} – {y_2}} \right)} \right]\)
Решенные примеры — площадь и периметр треугольников
Q.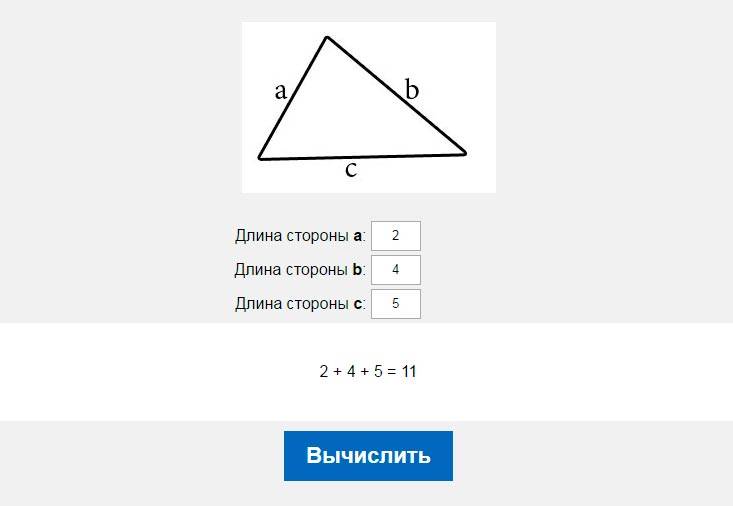 1. Найдите периметр нижеприведенного треугольника .
1. Найдите периметр нижеприведенного треугольника .
Ответ: Три стороны треугольника: \(5\,\rm{см}\), \(5\,\rm{см}\) и \(4\,\rm{ см}\).
Мы знаем, что периметр \(=\) сумма всех сторон.
Теперь периметр треугольника \(= 5\,\rm{см} + 5\,\rm{см} + 4\,\rm{см} = 14\,\rm{см}\)
Отсюда , периметр данного треугольника \(ABC\) равен \(14\,\rm{см}\).
Q.2. Найдите площадь прямоугольного треугольника, длины сторон которого кроме гипотенузы равны \(12\,\rm{см}\) и \(5\,\rm{см}\)
Ответ : Если длины сторон, кроме гипотенузы, равны \(5\,\rm{см}\) и \(12\,\rm{см}\), то одна из длин должна быть высотой, а другая длина будет высотой. 92}.\)
Q.3. Найдите площадь треугольника, длины сторон которого равны \(5\,\rm{см}\), \(6\,\rm{см}\) и \(7\,\rm{см}\)
Ответ: Даны длины трех сторон треугольника.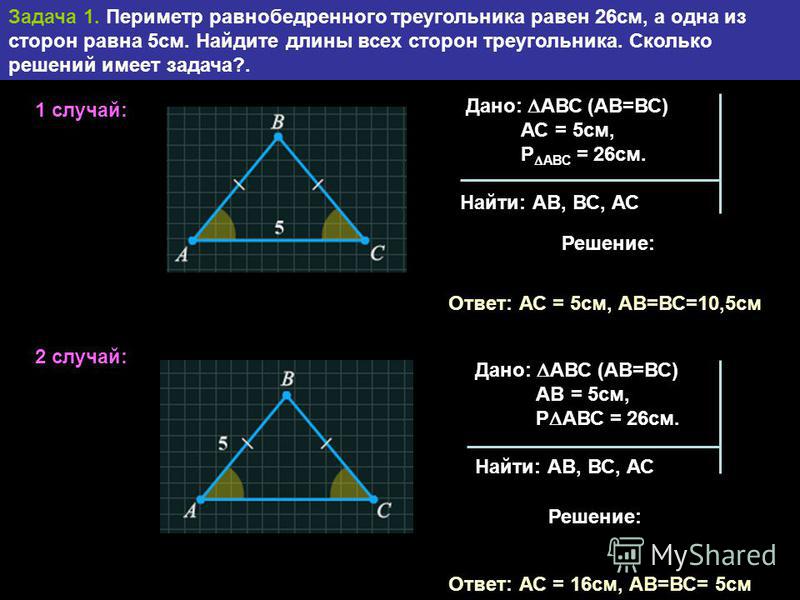 Итак, мы можем использовать формулу Герона для вычисления площади треугольника.
Итак, мы можем использовать формулу Герона для вычисления площади треугольника.
Здесь \(a = 5\,\rm{см}\), \(b = 6\,\rm{см}\) и \(c = 7\,\rm{см}\)
Согласно этой формуле, площадь треугольника определяется как
\( {\text{площадь}} = \sqrt {s(s – a)(s – b)(s – c)} \) 92}\) Сводка
Эта статья поможет вам узнать, как рассчитать периметр и площадь различных видов треугольников в зависимости от имеющейся информации о треугольнике. Зная это, можно рассчитать периметр и площадь любой земли треугольной формы или любого другого предмета треугольной формы.
Это также помогает рассчитать периметр и площадь любой земли правильной или неправильной многоугольной формы или любого другого объекта, разделив многоугольник на треугольники по диагоналям, а затем получив площадь каждого треугольника и сложив их.
Изучение концепции периметра
Часто задаваемые вопросы (FAQ) — Площадь и периметр треугольников
Q.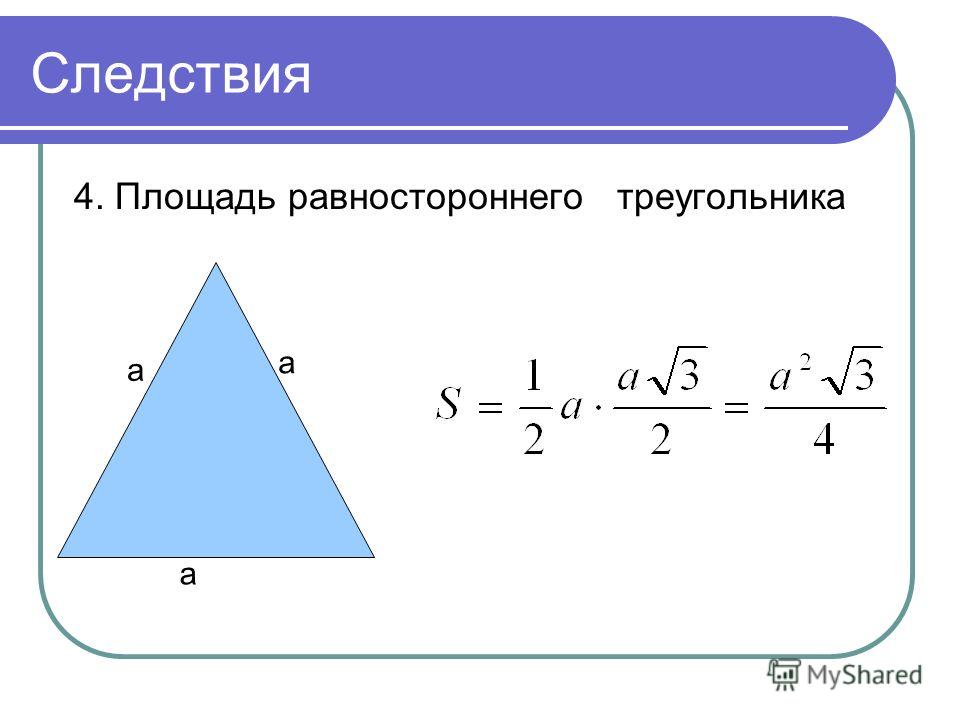 1. Какая формула периметра треугольника?
1. Какая формула периметра треугольника?
Ответ: Треугольник — двумерная замкнутая фигура, имеющая три стороны и три угла. Периметр треугольника вычисляется простым сложением длин всех трех сторон.
Периметр треугольника \(=\) Сумма длин трех сторон 92}\,{\text{квадрат}}\,{\text{единицы}}\)
И периметр равностороннего треугольника определяется выражением,
\(P = a + a + a = 3a\, {\ текст{единицы}}\)
Q.3. Какова площадь треугольника?
Ответ: Площадь треугольника определяется как общее пространство или площадь, занимаемая тремя сторонами любого треугольника.
Общая формула для нахождения площади треугольника:
Формула площади треугольника определяется как текст {высота}}} \справа){\текст{квадрат}}\,{\текст{единицы}}\)
Q.4. Каков периметр \(\Delta ABC\)?
Ответ: Периметр треугольника \(\Delta ABC\) равен сумме длин всех трех сторон.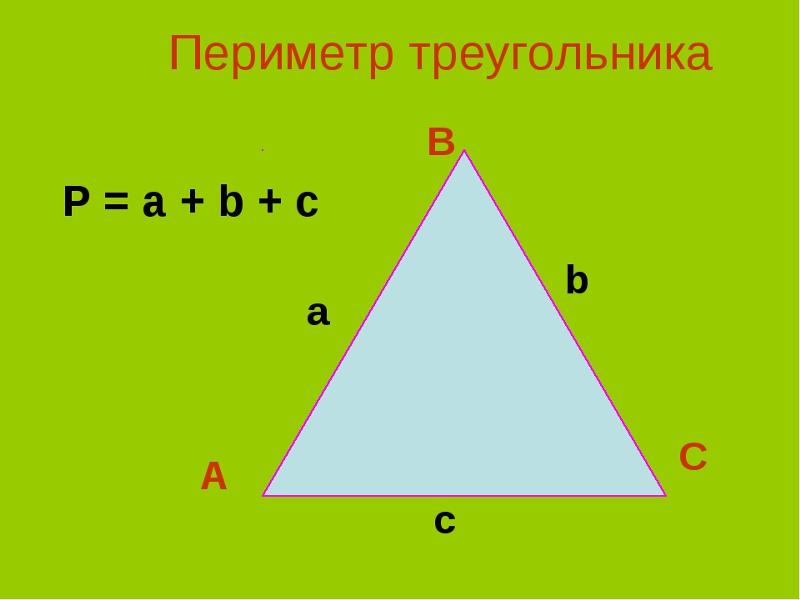
\(P = (AB + BC + CA)\, {\text{единицы}}\)
Q.5. Как вычислить периметр?
Ответ: Периметр любой фигуры можно вычислить, просто сложив длины всех сторон данной фигуры.
Сокращение глупых ошибок; Пройдите бесплатные пробные тесты, связанные с треугольниками
Открытые учебники | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.

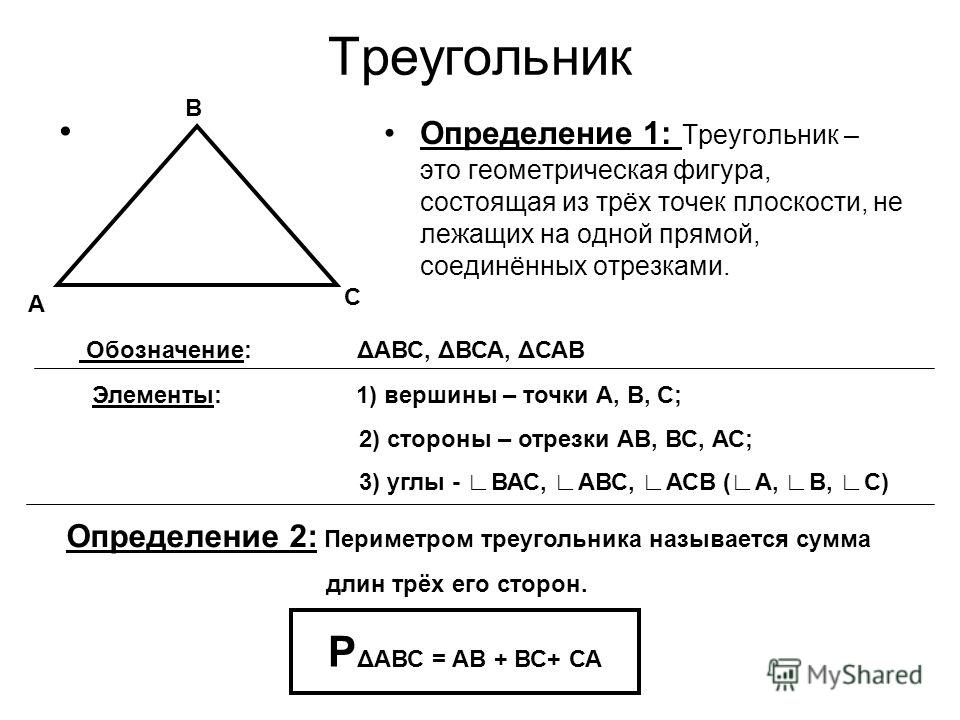

 Узнаем сколько килограммов каждого вида фруктов осталось:
Узнаем сколько килограммов каждого вида фруктов осталось:
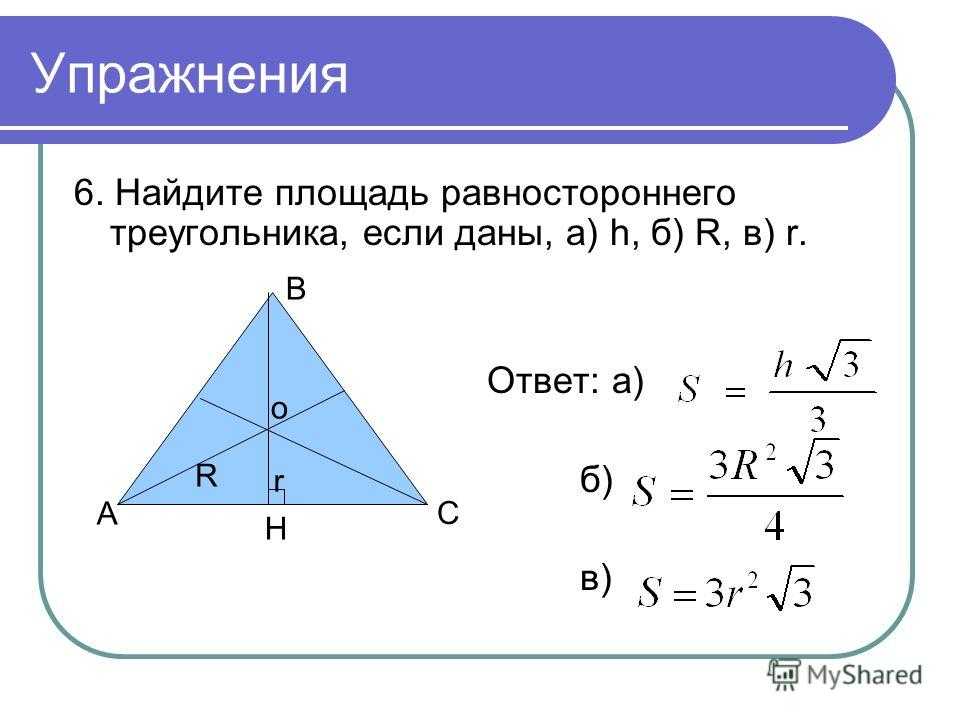 Таким образом, это разносторонний треугольник .
Таким образом, это разносторонний треугольник .

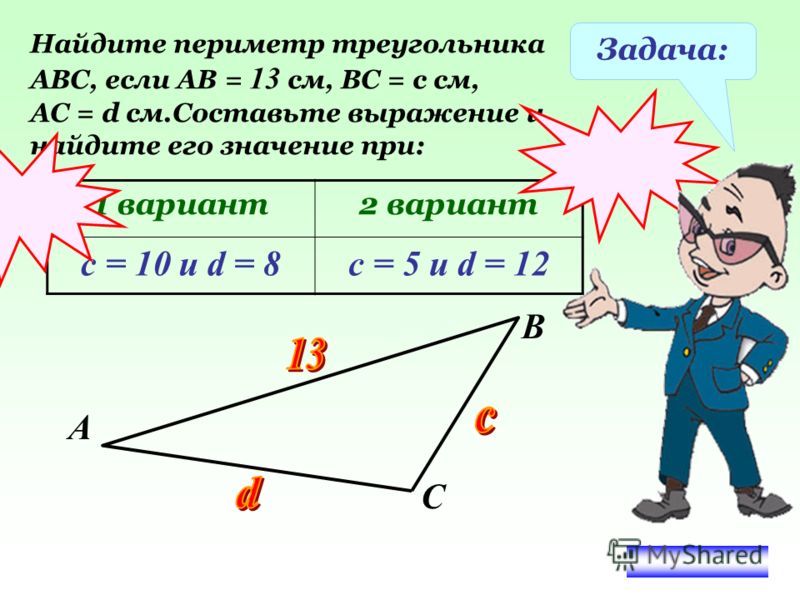 Если a, b и c — стороны треугольника, то периметр = a + b + c.
Если a, b и c — стороны треугольника, то периметр = a + b + c.