Как вычислить предел в маткаде
Как вычислить предел в маткаде
Для нахождения пределов в Mathcad введем несколько понятий, которые будут необходимы нам в дальнейшем. Число m является пределом числовой последовательности , если для любого положительного числа alt=»Пределы в Mathcad» width=»15″ height=»15″ />найдется зависящее от него натуральное число, N такое, что при всех n > N выполняется неравенство | an –m | < alt=»Пределы в Mathcad» width=»15″ height=»15″ />. При этом пишут:
Число m является пределом функции f(x) в конечной или бесконечной точке х0, если для любой последовательности хn, n = 1,2,…, стремящейся к х0, последовательность f(xn) , n = 1,2,… стремится к точке m. В этом случае пишут
. Если , то говорят о пределе функции y = f(x) справа. Если , то говорят о пределе функции слева.
Если , то говорят о пределе функции слева.
Аналогичная символика принята в Mathсad. При этом для вычисления предела последовательности и функции, предела функции слева и справа приняты следующие обозначения:
При в вычислении пределов в Mathcad используется только знак символьного равенства. В процессе проведения вычислений, кроме результатов, могут выдаваться различные сообщения. Если ошибочно введено выражение, для которого предстоит вычислить предел, то Mathсad выводит сообщение: “ No symbolic result was found -> Символический результат не был найден”. Если Mathсad не может вычислить выражение, то в качестве ответа повторяется само условие задачи. Если предел не существует, то результатом вычислений будет выражение: “Undefined – Не определен”. Пример вычисления пределов приведен на листинге.
Вычисление пределов, производных и интегралов в Mathcad
Для осуществления операций дифференциального и интегрального исчисления в Mathcad предусмотрен ряд операторов, вызываемый при помощи панели инструментов «Исчисление», которая, в свою очередь, вызывается кнопкой панели инструментов «Математика». Операторы данной панели перечислены в табл. 14.2.
Операторы данной панели перечислены в табл. 14.2.
| Оператор | Кнопка | Сочетание клавиш |
| Производная | Shift+/ (на основной клавиатуре) | |
| Производная n-го порядка (n≤5) | Ctrl+Shift+/ (на основной клавиатуре) | |
| Определенный интеграл | Shift+7 | |
| Неопределенный интеграл | Ctrl+I | |
| Суммирование | Ctrl+Shift+4 | |
| Суммирование по дискретной переменной | Ctrl+4 | |
| Вычисление произведения | Ctrl+Shift+3 | |
| Вычисление произведения по дискретной переменной | Ctrl+3 | |
| Вычисление предела | Ctrl+L | |
| Вычисление предела слева | Ctrl+A | |
| Вычисление предела справа | Ctrl+B |
В силу математического определения неопределенный интеграл не может быть вычислен численно, поэтому данный оператор применяется только в символьных вычислениях (см. следующую лаб. работу).
следующую лаб. работу).
Операторы суммирования вставляет в рабочий лист шаблон вида
,
где знакоместо справа от знака суммы предназначено для выражения, подлежащего суммированию, знакоместо внизу слева – для ввода переменной суммирования (от нее должно зависеть суммируемое выражение), а знакоместа внизу справа и вверху служат для ввода границ интервала суммирования. При этом переменная суммирования последовательно получает все значения из заданного интервала. Оператор суммирования по дискретной переменной вставляет в рабочий лист шаблон вида
,
не имеющий знакомест для границ интервала. В знакоместо внизу необходимо вставить переменную суммирования, которая предварительно должна быть определена как дискретная переменная. Интервалы суммирования, таким образом, задаются на этапе определения дискретной переменной. Вышеперечисленное относится и к вычислению произведения.
После ввода оператора вычисления производной при щелчке правой кнопкой мыши по его шаблону в контекстном меню появляется пункт Показать производную как, позволяющий выбрать, будет ли производная отображаться как общая или частная (буква d меняется на ∂ и наоборот).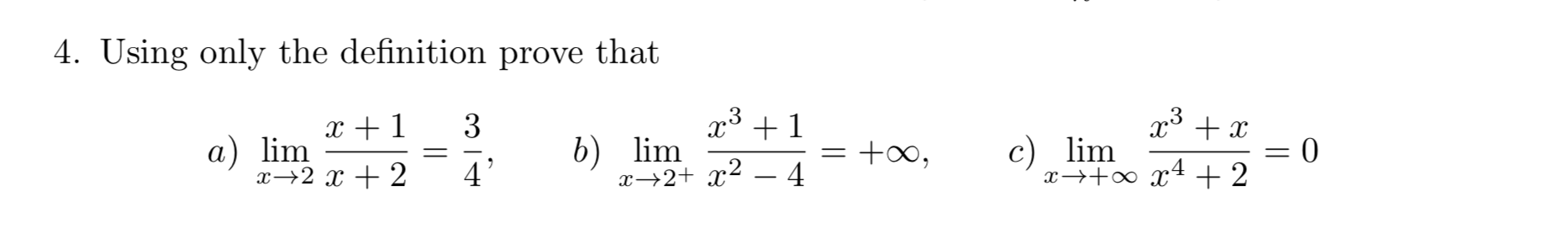
Часто при вычислении сумм, произведений, пределов, определенных интегралов одной из границ интервала выступает бесконечность. Для ввода соответствующего символа служит кнопка на панели инструментов «Исчисление» или комбинация клавиш Ctrl+Shift+Z.
Операторы дифференциального и интегрального счисления можно комбинировать друг с другом. Таким образом, в частности, можно задавать вычисления двойных и тройных интегралов. Эти операторы также можно использовать при определении переменных и функций – это точно такие же математические операторы, как сложение или умножение. Примером может служить выражение (для его вычисления должны быть определены функция f(x,y) и значение переменной r):
Урок 18. Символьные вычисления в Mathcad
Mathcad представляет из себя WYSIWYG-редактор, в котором можно размещать математические и текстовые области. До этого урока в математических областях мы проводили только численные расчеты. Однако расчеты в Mathcad могут быть и символьными (аналитическими) – это позволяет совершать операции дифференцирования, интегрирования, вычисления пределов, разложение в ряд и т. д. и записать результат вычисления в привычном виде.
д. и записать результат вычисления в привычном виде.
Если Вы только начинаете работу с символьными вычислениями, лучше проводите их в отдельных файлах. Если Вы используете одинаковые имена переменных для символьных и численных вычислений, то они могут взаимодействовать и мешать друг другу. Вы можете вставлять результаты из одного файла в другой.
В этом уроке мы будем в основном использовать те инструменты, которые уже изучили, но с той большой разницей, что вычисления будут символьными.
Оператор «Аналитическое преобразование»
Мы уже знаем пять различных знаков «равно» в Mathcad:
Добавим в этот список еще один знак – аналитическое преобразование:
Этот оператор достаточно важен, поэтому будет полезным запомнить его сочетание клавиш.
Там, где это возможно, аналитическое преобразование дает точный результат, без округления. Примеры:
Если параметры известны, аналитическое преобразование вставит их в результат:
Интегрирование
В качестве первого примера возьмем интеграл: вкладка Математика –> Операторы и символы –> Операторы –> Математический анализ –> Интеграл:
Введите в местозаполнители следующее:
Аналитическое преобразование даст:
Это вычисление динамично – если Вы меняете функцию, результат также меняется. Чтобы найти определенный интеграл, введите в местозаполнители пределы интегрирования:
Чтобы найти определенный интеграл, введите в местозаполнители пределы интегрирования:
Таким же образом можно вычислить результат численно:
Mathcad может брать достаточно сложные интегралы, где численное вычисление не работает:
Mathcad может брать двойные и тройные интегралы:
Дифференцирование
Введите оператор дифференцирования, затем переменную, затем функцию:
Чтобы найти производную более высокого порядка, введите в дополнительный местозаполнитель за переменной в знаменателе (щелкните по оператору, чтобы увидеть этот местозаполнитель):
Таким же образом можно найти частную производную:
Пределы
Для вычисления предела введите оператор со вкладки Математика –> Операторы и символы –> Операторы –> Математический анализ, введите в местозаполнители точку и функцию и вычислите символьно:
Оператор предела содержит четвертый местозаполнитель (щелкните по оператору, чтобы увидеть его). Используйте этот местозаполнитель, чтобы вычислять предел слева (с [-]) или предел (с [+]). Мы проиллюстрируем все три предела на примере функции тангенса:
Используйте этот местозаполнитель, чтобы вычислять предел слева (с [-]) или предел (с [+]). Мы проиллюстрируем все три предела на примере функции тангенса:
Пределы последовательностей и функций.
Вычисление пределов является одной из основных задач математического анализа. Система MathCAD позволяет с высокой эффективностью находить любые пределы.
Операторы MathCAD для вычисления пределов расположены на панели Calculus. Данная панель содержит три кнопки:
Two-sided Limit (двухсторонний предел), Left-sided Limit (левосторонний предел) и Right-sided (правосторонний предел), при нажатии на которые появляются соответственно
Необходимо помнить, что пределы, в отличие от большинства математических операций в MathCAD, можно вычислить только в символьном виде, а при попытке вычислить предел численно (с помощью знака “=”) будет выдано сообщение об ошибке.
Предел последовательности. Фактически предел последовательности, если он существует, — это число, к которому приближаются элементы последовательности при значении индекса n, стремящегося к . Для вычисления предела последовательности надо ввести шаблон для двухстороннего предела, заполнить его, затем ввести соответствующую команду из символьного меню или знак символьного вывода .
Для вычисления предела последовательности надо ввести шаблон для двухстороннего предела, заполнить его, затем ввести соответствующую команду из символьного меню или знак символьного вывода .
Если последовательность не имеет предела, то будет выдано слово undefined (не определено).
Знак символьного вывода позволяет использовать функцию пользователя.
Предел функции в точке. Необходимость вычисления пределов функции возникает в задачах даже чаще, чем пределов последовательностей. В точках, где функция непрерывна, все три предела будут иметь одинаковое значение — значение функции в этой точке.
Но во многих задачах можно столкнуться с функциями, значение которых в тех или иных точках с формальной математической точки зрения не определено (особые точки типа 0/0 или /, точки разрыва функции). Для того, чтобы получить правильное значение функции в особой точке, следует вычислить ее предел в этой точке. При вычислении пределов в особых точках также используется двухсторонний предел.
Как видно из вышеприведенного примера, значения функций f(x) и g(x) в точке x равно 0. Это происходит потому, что MathCAD вычисляет вначале числитель, и если он равен 0, то и всей дроби присваивается значение 0, знаменатель даже не вычисляется.
Если возникает необходимость построить график функции, которая содержит особую точку, то из-за упомянутой выше особенности MathCAD при вычислении дробей график будет содержать дефект. Исправить эту ошибку и получить правильный график на всем интервале можно, если при вычислении функции в особой точке заменить значение функции на значение предела. Это можно сделать с помощью встроенной функции If.
Для анализа точек разрыва служат односторонние пределы. В точках разрыва не определено не только значение самой функции, но и значение ее двухстороннего предела. Поэтому для исследования точек разрыва функции вычисляют левый и правый пределы в этой точке.
Как вычислить предел в mathcad
Как посчитать предел функции
Как посчитать максимум функции в цикле?
Добрый день! Уже во многих темах побывала, а всё не получается. Есть функция J(t,t0) Я хочу.
Есть функция J(t,t0) Я хочу.
Предел функции
Решите, пожалуйста! Найдите предел функции f(x) при стремлении аргумента к нулю
Найти предел кусочной функции
Прошу помощи в поиску предела кусочной функции в MathCad.
Посчитать предел функции двух переменных
Здравствуйте! Никак не могу посчитать предел \frac при x\rightarrow 0.
Пределы последовательностей и функций.
Вычисление пределов является одной из основных задач математического анализа. Система MathCAD позволяет с высокой эффективностью находить любые пределы.
Операторы MathCAD для вычисления пределов расположены на панели Calculus. Данная панель содержит три кнопки:
Two-sided Limit (двухсторонний предел), Left-sided Limit (левосторонний предел) и Right-sided (правосторонний предел), при нажатии на которые появляются соответственно
Необходимо помнить, что пределы, в отличие от большинства математических операций в MathCAD, можно вычислить только в символьном виде, а при попытке вычислить предел численно (с помощью знака “=”) будет выдано сообщение об ошибке.
Предел последовательности. Фактически предел последовательности, если он существует, — это число, к которому приближаются элементы последовательности при значении индекса n, стремящегося к . Для вычисления предела последовательности надо ввести шаблон для двухстороннего предела, заполнить его, затем ввести соответствующую команду из символьного меню или знак символьного вывода .
Если последовательность не имеет предела, то будет выдано слово undefined (не определено).
Знак символьного вывода позволяет использовать функцию пользователя.
Предел функции в точке. Необходимость вычисления пределов функции возникает в задачах даже чаще, чем пределов последовательностей. В точках, где функция непрерывна, все три предела будут иметь одинаковое значение — значение функции в этой точке.
Но во многих задачах можно столкнуться с функциями, значение которых в тех или иных точках с формальной математической точки зрения не определено (особые точки типа 0/0 или /, точки разрыва функции). Для того, чтобы получить правильное значение функции в особой точке, следует вычислить ее предел в этой точке. При вычислении пределов в особых точках также используется двухсторонний предел.
Для того, чтобы получить правильное значение функции в особой точке, следует вычислить ее предел в этой точке. При вычислении пределов в особых точках также используется двухсторонний предел.
Как видно из вышеприведенного примера, значения функций f(x) и g(x) в точке x равно 0. Это происходит потому, что MathCAD вычисляет вначале числитель, и если он равен 0, то и всей дроби присваивается значение 0, знаменатель даже не вычисляется.
Если возникает необходимость построить график функции, которая содержит особую точку, то из-за упомянутой выше особенности MathCAD при вычислении дробей график будет содержать дефект. Исправить эту ошибку и получить правильный график на всем интервале можно, если при вычислении функции в особой точке заменить значение функции на значение предела. Это можно сделать с помощью встроенной функции If.
Для анализа точек разрыва служат односторонние пределы. В точках разрыва не определено не только значение самой функции, но и значение ее двухстороннего предела. Поэтому для исследования точек разрыва функции вычисляют левый и правый пределы в этой точке.
Поэтому для исследования точек разрыва функции вычисляют левый и правый пределы в этой точке.
Как вычислить предел в mathcad
Вы здесь: Всё о Mathcad Всё о Mathcad Математический анализ Пределы в Mathcad
Пределы в Mathcad
Для нахождения пределов в Mathcad введем несколько понятий, которые будут необходимы нам в дальнейшем. Число m является пределом числовой последовательности , если для любого положительного числа alt=»Пределы в Mathcad» />найдется зависящее от него натуральное число, N такое, что при всех n > N выполняется неравенство | an –m | < alt=»Пределы в Mathcad» />. При этом пишут:
Число m является пределом функции f(x) в конечной или бесконечной точке х0, если для любой последовательности хn, n = 1,2,…, стремящейся к х0, последовательность f(xn) , n = 1,2,… стремится к точке m. В этом случае пишут
В этом случае пишут
. Если , то говорят о пределе функции y = f(x) справа. Если , то говорят о пределе функции слева.
Аналогичная символика принята в Mathсad. При этом для вычисления предела последовательности и функции, предела функции слева и справа приняты следующие обозначения:
При в вычислении пределов в Mathcad используется только знак символьного равенства. В процессе проведения вычислений, кроме результатов, могут выдаваться различные сообщения. Если ошибочно введено выражение, для которого предстоит вычислить предел, то Mathсad выводит сообщение: “ No symbolic result was found -> Символический результат не был найден”. Если Mathсad не может вычислить выражение, то в качестве ответа повторяется само условие задачи. Если предел не существует, то результатом вычислений будет выражение: “Undefined – Не определен”. Пример вычисления пределов приведен на листинге.
Вычислить пределы. решение задачи Математический анализ с ответом
Пример 1
Вычислить пределы:
Пример 2
Найти пределы:
Пример 3
Пример 4
Пример 5
Найти предел:
Пример 6
Найти предел:
Пример 7
Найти предел:
Пример 8
Вычислить предел:
Пример 9
Вычислить предел:
Пример 10
Вычислите предел функции:
Пример 11
Вычислите предел функции, не используя правило Лопиталя:
Пример 12
Вычислите предел или покажите, что он не существует
Пример 13
Вычислить предел:
Пример 14
Вычислить предел:
Пример 15
Вычислить предел:
Пример 16
Вычислить предел:
при x0 = 2
Пример 17
Вычислить предел:
при x0 = 3
Пример 18
Вычислить предел:
при x0 = ∞
Пример 19
Найти предел:
Пример 20
Вычислить предел:
Пример 21
Вычислить предел:
Пример 22
Вычислить предел:
Пример 23
Вычислить предел:
Пример 24
Вычислить предел:
Пример 25
Вычислить предел:
Пример 26
Вычислить предел:
Пример 27
Вычислить предел:
Пример 28
Вычислить предел:
Пример 29
Вычислить предел:
Пример 30
Вычислить предел:
Пример 31
Вычислить предел:
Пример 32
Вычислить предел:
Пример 33
Вычислить пределы:
Пример 34
Вычислить пределы:
Пример 35
Вычислить пределы:
Пример 36
Вычислить предел:
Пример 37
Найти предел:
Пример 38
Найти предел функции:
Пример 39
Найти предел функции:
Пример 40
Вычислить предел функции:
Пример 41
Вычислить предел:
Пример 42
Вычислить предел:
Пример 43
Вычислить предел:
Пример 44
Вычислить предел:
Пример 45
Вычислить предел:
Пример 46
Вычислить предел функции
Пример 47
Вычислить предел функции
Пример 48
Найти предел:
Пример 49
Вычислить предел:
Пример 50
Вычислить предел:
Пример 51
Вычислить предел:
Пример 52
Вычислить предел:
Пример 53
Вычислить предел:
Пример 54
Вычислить предел:
Пример 55
Вычислить предел:
Пример 56
Вычислить пределы числовых последовательностей:
Пример 57
Вычислить пределы числовых последовательностей:
Пример 58
Вычислить предел функции:
Пример 59
Вычислить предел функции:
Пример 60
Вычислить предел функции:
Пример 61
Вычислить предел функции:
Пример 62
Вычислить предел функции:
Пример 63
Вычислить предел:
m = 1, n = 5
Пример 64
Вычислить предел:
m = 1, n = 5
Пример 65
Вычислить предел:
m = 1, n = 5
Пример 66
Вычислить предел:
m = 1, n = 5
Пример 67
Вычислите предел:
Пример 68
Вычислите предел:
Пример 69
Вычислить предел:
Пример 70
Вычислить предел:
Пример 71
Найти предел:
Пример 72
Вычислить предел функции:
Пример 73
Вычислить предел функции:
Пример 74
Вычислить предел функции:
Пример 75
Вычислить предел функции:
Пример 76
Вычислить предел функции:
Пример 77
Вычислить предел функции:
Пример 78
Найти предел:
Пример 79
Найти предел:
Пример 80
Вычислить предел.
Пример 81
Вычислить предел.
Пример 82
Вычислить предел.
Пример 83
Вычислить предел:
Пример 84
Вычислить предел:
Пример 85
Вычислить предел:
Пример 86
Найти указанный предел:
Пример 87
Найти указанный предел:
Пример 88
Найти указанный предел:
Пример 89
Найти указанный предел:
Пример 90
Найти указанный предел:
Пример 91
Найти указанный предел:
Пример 92
Найти указанный предел:
Пример 93
Найти указанный предел:
Пример 94
Найти указанный предел:
Пример 95
Найти предел функции:
Пример 96
Найти производную функции:
Пример 97
Вычислить пределы с помощью правила Лопиталя:
Пример 98
Вычислить предел с помощью правила Лопиталя:
Пример 99
Вычислить предел:
Пример 100
Вычислить предел. 2
2
Вычислить предел, используя правило Лопиталя
Вычислить предел, используя правило Лопиталя
|
 | Метод замены переменной в пределе | Бесконечно малые функции. Сравнение бесконечно малых | Может ли функция быть бесконечно малой на бесконечности? | Сравнение бесконечно малых функций | Что принципиально важно во всех рассмотренных примерах? | Замечательные эквивалентности в пределах | Первое правило Лопиталя | Второе правило Лопиталя |
| Метод замены переменной в пределе | Бесконечно малые функции. Сравнение бесконечно малых | Может ли функция быть бесконечно малой на бесконечности? | Сравнение бесконечно малых функций | Что принципиально важно во всех рассмотренных примерах? | Замечательные эквивалентности в пределах | Первое правило Лопиталя | Второе правило Лопиталя | Читайте также:
|
Для разминки разберёмся с парой небольших воробушков:
Пример 3
Вычислить предел по правилу Лопиталя
Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:
В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения .
Рассмотренный пример разруливается и через замечательные пределы, похожий случай разобран в конце статьи Сложные пределы.
Пример 4
Вычислить предел по правилу Лопиталя
Это пример для самостоятельного решения.
Типична ситуация, когда после дифференцирования получаются трех- или четырёхэтажные дроби:
Пример 5
Вычислить предел, используя правило Лопиталя
Напрашивается применение замечательной эквивалентности, но путь жёстко предопределён по условию:
После дифференцирования настоятельно рекомендуюизбавляться от многоэтажности дробии проводить максимальные упрощения. Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: , но в некоторых пределах запутаются даже отличники.
Пример 6
Вычислить предел, используя правило Лопиталя
Пример 7
Вычислить предел, используя правило Лопиталя
Это примеры для самостоятельного решения. В Примере 7 можно ничего не упрощать, слишком уж простой получается после дифференцирования дробь. А вот в Примере 8 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными.
И, упрощения совершенно необходимы, когда после дифференцирования неопределённостьне устранена.
Пример 8
Вычислить предел, используя правило Лопиталя
Поехали:
Интересно, что первоначальная неопределённость после первого дифференцирования превратилась в неопределённость , и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при , а , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.
На днях мне попалось любопытное задание:
Пример 9
Вычислить предел функции, используя правило Лопиталя
Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.
Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.
Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….
В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида .
Расправа с неопределённостью подробно разобрана в Примерах №№9-13 урокаМетоды решения пределов. Давайте для проформы ещё один:
Пример 10
Вычислить предел функции, используя правило Лопиталя
На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость в неопределённость . А затем заряжаем правило Лопиталя:
Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.
Неопределённость тоже не сопротивляется превращению в или :
Пример 11
Вычислить предел функции с помощью правила Лопиталя
Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций.
Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью . На первом шаге делаем дробь трёхэтажной, получая неопределённость , далее решение идёт по шаблонной схеме:
После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости применяем правило Лопиталя ещё раз:
Готово.
Исходный предел можно было попытаться свести к двум бубликам:
Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.
Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести – к «нулю на ноль» или к «бесконечности на бесконечность».
В свою очередь на огонёк подтягиваются собутыльники и более экзотические товарищи . Метод трансформации прост и стандартен:
Пример 12
Вычислить предел функции с помощью правила Лопиталя
Для устранения неопределённости используем основное логарифмическое тождество: . В данном случае :
На предпоследнем шаге, согласно известному школьному свойству, «сносим» синус из степени за пределы логарифма, получая произведение . На последнем шаге перемещаем значок предела в показатель (поскольку экспоненциальная функция непрерывна, да и предел относится, прежде всего, к верхнему этажу).
Чтобы не мельчить, вычислим предел показателя отдельно:
С неопределённостью разбираемся уже знакомым способом – делаем дробь трёхэтажной, получая долгожданную неопределённость , к которой применимо правило Лопиталя:
Метаморфозы продолжаются, теперь вылезла неопределённость «ноль на ноль». В принципе, можно избавиться от косинуса, указав, что он стремится к единице. Но мудрая стратегия заключается в том, чтобы никто ни до чего не докопался. Поэтому сразу применим правило Лопиталя, как этого требует условие задачи:
В принципе, можно избавиться от косинуса, указав, что он стремится к единице. Но мудрая стратегия заключается в том, чтобы никто ни до чего не докопался. Поэтому сразу применим правило Лопиталя, как этого требует условие задачи:
Не торопитесь, предел не равен нулю! Мы вычислили только предел показателя. В конце решения главное не забыть про экспоненту, я сейчас сам чуть про неё не забыл =) Окончательно:
В ряде случаев после использование основного логарифмического тождества удаётся миновать неопределённость :
Пример 13
Очередной папуас тоже сдаётся перед формулой . В данном случае :
В результате сразу получена неопределённость , что облегчает задачу. Предел показателя для удобства вычислим отдельно:
В итоге:
Аналогичное задание для самостоятельного решения:
Пример 14
Вычислить предел по правилу Лопиталя
Полное решение и ответ в конце урока.
Предел с неопределённостью по правилу Лопиталя, если честно, у себя не нашёл, но для полноты картины решим многострадальный шестой пример урока Замечательные пределы:
Пример 15
Вычислить с помощью правила Лопиталя
Решайте =)
В заключение хочу успокоить гринписовцев – ни один воробей от оружия серьёзно не пострадал, пределы – птицы юркие, да и ядра формы обтекаемой. Вспоминаем обычное требование: «…не пользуясь правилом Лопиталя». С беспощадной действительностью соприкоснёмся в статье Сложные пределы.
Желаю успехов!
Решения и ответы:
Пример 4
Пример 6
Пример 7
Пример 9
Пример 14
Используем основное логарифмическое тождество и преобразование :
Вычислим предел показателя:
Таким образом:
Пример 15
Используем основное логарифмическое тождество:
Вычислим предел показателя:
Таким образом:
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Сложные пределы
В данной статье будут рассмотрены пределы повышенной сложности, и заключительный практикум по теме предназначен, прежде всего, для читателей со средним и высоким уровнем подготовки. Если ваши навыки вычисления пределов невелики или вовсе отсутствуют, пожалуйста, начните с вводного урока Пределы функций. Примеры решений. Многие методы решения пределов, о которых пойдёт речь, уже знакомы и сложность будет состоять преимущественно в технике вычислений. Кроме того, мы рассмотрим примеры с более редкими замечательными пределами, которые до сей поры были обделены моим вниманием.
Если ваши навыки вычисления пределов невелики или вовсе отсутствуют, пожалуйста, начните с вводного урока Пределы функций. Примеры решений. Многие методы решения пределов, о которых пойдёт речь, уже знакомы и сложность будет состоять преимущественно в технике вычислений. Кроме того, мы рассмотрим примеры с более редкими замечательными пределами, которые до сей поры были обделены моим вниманием.
Пока не знаю, сколько будет примеров, 15-ть, 20-ть или больше, но в любом случае программа предстоит насыщенная, поэтому сразу приступим к зачистке территории:
Пример 1
Найти предел, не пользуясь правилом Лопиталя
При подстановке «единицы» в выражение под знаком предела, получается неопределённость , которая устраняется стандартным методом: числитель и знаменатель необходимо разложить на множители, а затем что-нибудь сократить. Разложить на множители…. Были бы у нас многочлены второй степени – без проблем. Но как раскладывать кубические многочлены? Познакомимся с новым приёмом, который основан на одной из теорем алгебры. Сначала кратко передам теоретическую суть:
Но как раскладывать кубические многочлены? Познакомимся с новым приёмом, который основан на одной из теорем алгебры. Сначала кратко передам теоретическую суть:
Рассмотрим многочлен положительной степени. Если число является корнем уравнения , то многочлен делится на многочлен без остатка. В результате деления получается многочлен , при этом: .
Да, многочлены, как и числа, можно делить друг на друга. Термины те же:
– делимое;
– делитель;
– частное.
Начнём оформлять решение и детально разберём техническую сторону вопроса:
Разложим числитель и знаменатель на множители.
Числитель: поскольку число является корнем уравнения , то многочлен делится на многочлен без остатка. Деление выполняется столбиком. В школе столбиком мы делили числа, и принцип деления многочленов весьма похож. Записываем начальный шаблон: Обратите внимание на очень важную вещь: в многочлене в явном виде отсутствует «икс» в первой степени. При делении ОБЯЗАТЕЛЬНО прописываем все недостающие слагаемые, прикрепляя к ним нулевые коэффициенты.
При делении ОБЯЗАТЕЛЬНО прописываем все недостающие слагаемые, прикрепляя к ним нулевые коэффициенты.
Теперь в углу нужно разоблачить незнакомца :
Каким он должен быть? Девчонки, признавайтесь =) …Нет-нет-нет, он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :
Очевидно, что данному критерию удовлетворяет . Действительно, . Записываем первый трофей:
Далее нашего героя необходимо умножить на делитель :
, а результат записать во второй строке слева:
Проводим отчёркивание и из первой строки почленно вычитаем вторую строку:
Если подробно, (ноль под чертой не пишем),
Сносим сверху следующее слагаемое:
Алгоритм идёт на следующий круг. Снова ищем одночлен , он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :
В данном случае . Рисуем его справа под чертой:
и умножаем на делитель :
, результат записываем в 4-ую строку:
Ещё раз отчёркиваем и проводим почленное вычитание: (ноль под чертой не пишем), :
Сносим сверху последнее слагаемое:
Организуем завершающий цикл. Необходимо подобрать третье слагаемое , которое при умножении на «икс» даёт :
Необходимо подобрать третье слагаемое , которое при умножении на «икс» даёт :
Уравнению соответствует корень , который записываем справа под чертой:
Умножаем на делитель :
, результат записываем в 6-ую строку:
Выполняем завершающее отчёркивание и почленное вычитание:
В итоге получился ноль, и это значит, что все вычисления выполнены правильно. Иными словами, многочлен поделился на без остатка. Таким образом:
Желающие могут раскрыть скобки в правой части и убедиться, что получится исходный многочлен .
Рассмотренный алгоритм на самом деле не сложен, и рука набивается довольно быстро.
Знаменатель. Разборки аналогичны. Так как число является корнем уравнения , то соответствующий многочлен делится на без остатка:
В итоге
Открываем решение и записываем всё, что нажито непосильным трудом:
Приключения продолжаются – после сокращения неопределённость не устранена. Но уже легче, квадратные трёхчлены можно разложить на множители тривиальным способом, рассмотренным на первом уроке про пределы функций. Тем не менее, в целях закрепления алгоритма продолжим деление. Да простит меня сервак =)
Но уже легче, квадратные трёхчлены можно разложить на множители тривиальным способом, рассмотренным на первом уроке про пределы функций. Тем не менее, в целях закрепления алгоритма продолжим деление. Да простит меня сервак =)
Числитель. Поскольку число является корнем уравнения , то соответствующий многочлен делится на без остатка. Поехали. На первом шаге подбираем ТАКИМ образом, чтобы при его умножении на «икс» получить :
Искомое значение :
Умножаем на делитель :
, результат записываем слева, отчёркиваем и проводим почленное вычитание:
Из первой строки сносим оставшееся слагаемое:
Второе значение при умножении на «икс» должно давать «икс»:
Очевидно, что :
Умножаем на делитель :
, результат записываем ниже, отчёркиваем и проводим почленное вычитание:
В остатке получился ноль, значит, деление выполнено верно. Таким образом:
Таким образом:
Аналогично расправляемся со знаменателем:
То есть
Снова открываем решение и получаем окончательный ответ:
Выполним проверку. Дважды используем правило Лопиталя:
Сравните трудоёмкость двух способов решения. Думаю, теперь вам понятно, почему запрещают применять правило Лопиталя =)
Времени и сил на первый пример совсем не жалко, так как необходимость делить многочлены время от времени возникает в других задачах, в частности, при нахождении нулей функции, в интегралах от дробно-рациональной функции. Поэтому с энтузиазмом отнесёмся к другим пределам… …они будут ещё длиннее =) Никто не знает, вдруг в жизни пригодится. Хах. Вспомнился заезженный анекдот в тему: если к вам на улице подошли Свидетели Иеговы, перехватите инициативу – начните им рассказывать про тройные интегралы.
Пример 2
Найти предел, не пользуясь правилом Лопиталя
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Полное решение и ответ в конце урока.
Вернёмся к другому известному способу решения пределов, повысив их сложность:
Пример 3
Найти предел, не пользуясь правилом Лопиталя
Неопределённость ликвидируется стандартным методом – умножением и делением на сопряженное выражение. Единственное отличие, приём используется два раза:
1) для устранения разности домножаем числитель и знаменатель на сопряженное выражение ;
2) для устранения разности домножаем числитель и знаменатель на сопряженное выражение .
Далее дважды используется формула . Сама техника решения подробно рассмотрена на уроке Пределы. Примеры решений.
Оформляем:
Оба вышеуказанных действия выгоднее выполнить «за один присест». Умножим числитель и знаменатель на сопряженные выражения:
Проверим решение по правилу Лопиталя:
Пример 4
Найти предел, не пользуясь правилом Лопиталя
Это более сложный пример для самостоятельного решения.
Иногда в пределах рассматриваемого типа приходится использовать не только формулу разности квадратов , но и формулу разности кубов:
Пример 5
Найти предел
Неопределённость устраняется умножением и делением на сопряженное выражение. Аналогичные, но более простые пределы мы рассмотрели в Примерах №№11-13 урокаМетоды решения пределов. Только здесь работает формула разности кубов:
В данном случае . И, согласно формуле, для разности сопряженным выражением будет вот этот вот страх:
Умножим и разделим на сопряженное выражение, чтобы использовать формулу :
Тоже знакомая картина….
Старшая степень числителя: 2
Старшая степень знаменателя: 2
Таким образом, числитель и знаменатель одного порядка роста, и сразу можно сказать, что предел равен конечному числу.
Разделим числитель и знаменатель на :
Готово.
Пример 6
Найти предел
Это пример для самостоятельного решения. После умножения/деления на сопряженное выражение и упрощений предел будет сведён к случаю Примеров №№1-3 статьи о бесконечно малых функциях. Полное решение и ответ в конце урока.
А сейчас обещанные на уроке Методы решения пределов плюшки на замену переменной. Повышенной сложности:
Пример 7
Найти предел, не пользуясь правилом Лопиталя
Аргумент стремится к не самому распространённому числу: , с ходу и не сообразишь, есть здесь вообще неопределённость или нет. Поэтому откроемтригонометрическую таблицу, и выпишем следующие значения:
Проверим предел на наличие неопределённости:
Да, действительно, два бублика.
Проведём предварительный анализ. В пределе находятся тригонометрические функции, и решение, скорее всего, сведётся к первому замечательному пределу. В этой связи напрашивается замена, после которой новая переменная будет стремиться к нулю.
В этой связи напрашивается замена, после которой новая переменная будет стремиться к нулю.
Но перед заменой целесообразно провести некоторое упрощение выражения. В пределе есть тангенс, а работать с этой функцией неудобно (как и с котангенсом тоже). Таким образом, сначала лучше свести всё дело к синусам и косинусам. Пример свирепый, поэтому я закомментирую каждый шаг:
(1) Используем формулу .
(2) Дробь числителя приводим к общему знаменателю.
(3) Избавляемся от трёхэтажности дроби, а также от косинуса, указывая, что .
(4) Выносим константу за значок предела.
Неопределённость никуда не делась, но от тангенса мы избавились, что уже является небольшим достижением
Проведем замену переменной:
Если , то
Ну и ещё – из замены нужно выразить: .
(5) Выполняем подстановку в соответствии с выполненной заменой.
(6) Используем тригонометрические формулы:
(7) Используя значения , упрощаем выражение.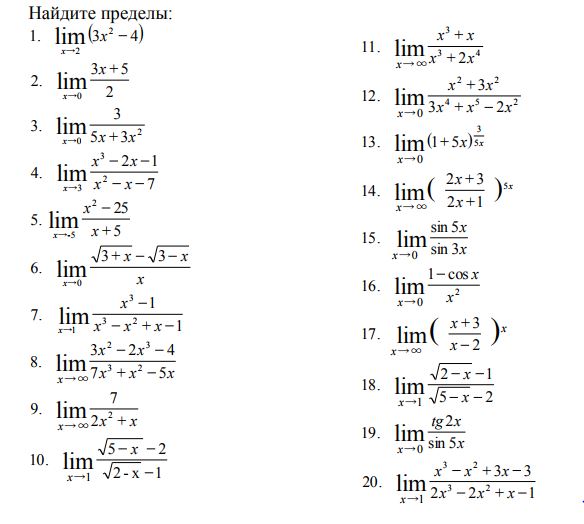
(8) Раскрываем скобки в числителе и знаменателе.
(9) Приводим подобные слагаемые в числителе.
(10) Константу –2 выносим за значок предела. В знаменателе переставляем слагаемые.
И снова два нуля, причём не видно как решать предел дальше…. Но если хорошенько пошуршать в тригонометрических формулах, то история закончится счастливым концом:
(11) Используем формулы половинного угла: . В числителе избавляемся от косинуса, указывая, что .
(12) В знаменателе выносим за скобки .
(13) Сокращаем числитель и знаменатель на .
Забавно, что всё обошлось даже без замечательного предела.
Не знаю, кто и на каком месте будет рвать себе волосы, но правило Лопиталя даёт ответ фантастически быстро:
Пример 8
Найти предел, не пользуясь правилом Лопиталя
Это пример для самостоятельного решения. В тригонометрической таблиценет информации об отрицательных значениях угла. Понятие ориентации угла дано в статьеПростейшие задачи с прямой на плоскости. Наглядная иллюстрация с конкретными примерами также фигурирует при нахождении аргумента комплексного числа. Чтобы воспользоваться таблицей, прибавляем один «оборот»: , то есть и – это один и тот же угол. Таким образом:
Понятие ориентации угла дано в статьеПростейшие задачи с прямой на плоскости. Наглядная иллюстрация с конкретными примерами также фигурирует при нахождении аргумента комплексного числа. Чтобы воспользоваться таблицей, прибавляем один «оборот»: , то есть и – это один и тот же угол. Таким образом:
Полное решение и ответ в конце урока
Как-то незаслуженно оказались забыты степени:
Пример 9
Найти предел
На повестке дня неопределённость , и решение, очевидно, нужно свести к замечательной формуле . Но в нашем пределе нет единицы, только одинокий косинус. Что делать? Организуем!
(1) Приводим основание степени к виду , для этого используем искусственный приём: прибавляем и вычитаем единицу. Таким образом:
(2) В целях применения 2-го замечательного предела возводим основание в степень , и, чтобы ничего не изменилось – в обратную степень .
(3) Используем замечательный предел .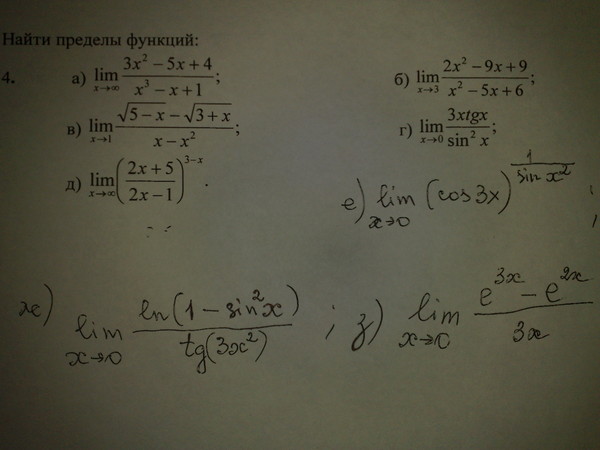
(4) Теперь в показателе необходимо устранить неопределённость 0:0. Сначала меняем знак в числителе: , минус выносим из предела.
(5) В числителе используем формулу .
(6) Искусственно преобразуем знаменатель, чтобы получить два первых замечательных предела.
Очень кстати в одном примере подвернулись сразу оба замечательных предела, и после их повторения во второй части статьи рассмотрим:
Дата добавления: 2015-07-25; просмотров: 670 | Нарушение авторских прав
| | | следующая страница ==> | |
| Показательная функция, с основанием, бОльшим единицы ( и т.д.) более высокого порядка роста, чем степенная функция с положительной степенью. | | | Замечательные пределы с экспонентой и логарифмом |
Пределы для чайников с примерами решения
Содержание:
- Сформулируем определение предела функции
Прежде чем перейти к определению предела, напомним, что в математике используются три вида бесконечностей
Бесконечность не является числом, она показывает, как меняется переменная величина, которая конечна в любой момент времени.
Теперь определим понятие последовательности и ее предела.
Последовательностью называется множество чисел, которое перенумеровано с помощью целых чисел и расположено в порядке возрастания номеров
Если задана последовательность то тем самым любому целому неотрицательному значению поставлено в соответствие значение
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Например, члены геометрической прогрессии являются последовательными значениями функции где
Может случиться так, что с увеличением значения будет неограниченно приближаться к какому-то числу В этом случае говорят, что число является пределом функции целочисленного аргумента или последовательности при и пишут или
Число является пределом последовательности если для можно найти такое что для всех с номерами справедливо неравенство [4, 32]
Возможно вам будут полезны данные страницы:
Признак Лейбница |
Как решать пределы: пример решения |
Как решать пределы с корнями: в числителе |
Уравнение прямой в пространстве |
Используя приведенное определение, докажем, что последовательность имеет предел, равный 1
Согласно определению имеем
Таким образом, мы доказали, что для любого наперед заданного можно найти такое что при всех будет выполняться (3. 1), а это означает, что 1 есть предел исходной последовательности.
1), а это означает, что 1 есть предел исходной последовательности.
Теперь рассмотрим функцию непрерывного аргумента и предположим, что неограниченно приближается к числу При этом может оказаться, что соответствующее значение неограниченно приближается к некоторому’ числу В этом случае говорят, что число есть предел функции при
Сформулируем определение предела функции
Число называется пределом функции при если для можно найти такое что для всех удовлетворяющих условию будет справедливо неравенство Заметим, что функция не обязательно должна быть определена в предельной точке она должна быть определена лишь в некоторой окрестности этой точки.
Тот факт, что — предел функции при записывается так:
Данное нами определение иллюстрируется рис. 3.3. Используя приведенное определение предела, докажем, что
На основании определения имеем
Таким образом, мы доказали, что исходная функция будет отличаться от 6 меньше чем на если будет выполняться неравенство (3.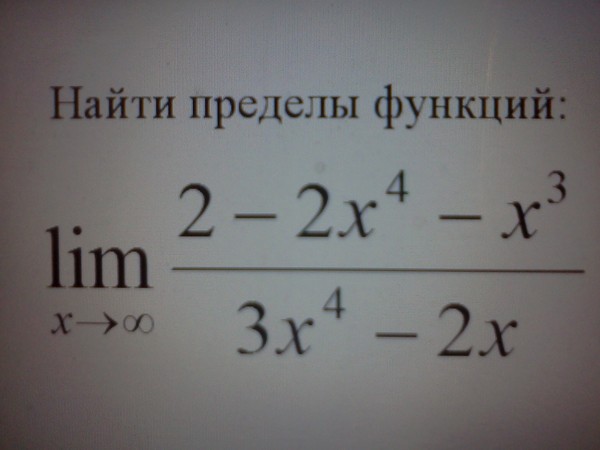 2). В данном случае
2). В данном случае
Приведенное определение не дает способа вычисления пределов. Ниже мы рассмотрим некоторые из таких методов.
Дадим понятие о левых и правых пределах функции и точках ее разрыва.
Если при так что принимает только значения меньшие то пишут и называют левым пределом.
Аналогично, если при так что принимает только значения большие то пишут и называют правым пределом [4, 30].
Геометрическая иллюстрация левого и правого пределов дана на рис. 3.4
Из рис. 3.4. следует, что в точке функция имеет разрыв. Он носит название разрыва первого рода (в точке разрыва первого рода левый и правый пределы не равны и конечны). Все остальные точки разрыва называются точками разрыва второго рода [4, 30]. Примерами разрывов второго рода являются бесконечные разрывы (рис. 3.5)
Предположим, что аргумент функции неограниченно возрастает т. е. является бесконечно большим аргументом. Может оказаться, что при этом функция стремится к некоторому пределу (рис. 3.6).
е. является бесконечно большим аргументом. Может оказаться, что при этом функция стремится к некоторому пределу (рис. 3.6).
Функция стремится к пределу при если для можно найти такое что для всех значений удовлетворяющих неравенству будет выполняться условие
Теперь рассмотрим случай стремления функции к бесконечности при
Функция стремится к бесконечности при если для можно найти такое что для всех значений удовлетворяющих условию выполняется неравенство
Это определение иллюстрируется рис. 3.7.
Напомним, что функция называется ограниченной в данной области изменения аргумента, если существует такое, что для всех значений принадлежащих рассматриваемой области, будет выполняться неравенство Если такого числа нет, то является неограниченной в данной области.
Например, функция является ограниченной на своей области определения (рис. 3.8).
Дадим определение бесконечно малой величины.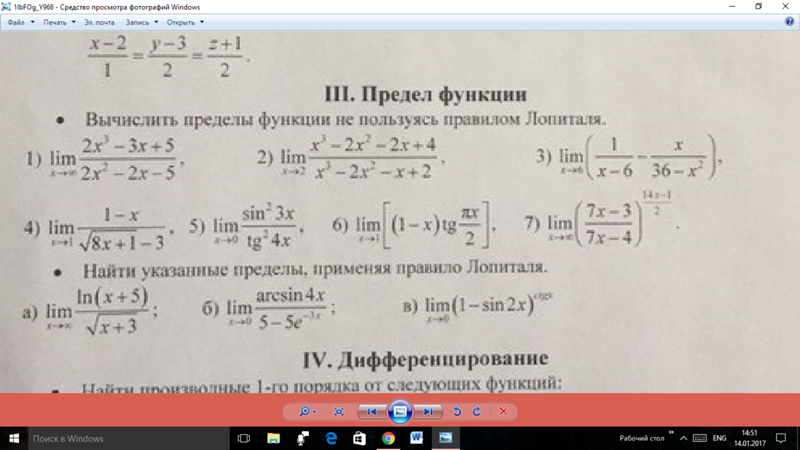 Функция называется бесконечно малой при или если или
Функция называется бесконечно малой при или если или
Например, функция при есть бесконечно малая величина, так как
Постоянное очень малое число не является бесконечно малой величиной. Единственное число, которое рассматривается в качестве бесконечно малой величины, это ноль. Связь бесконечно малых и бесконечно больших величин можно проследить из теоремы 3.1: если — бесконечно малая величина, то — бесконечно большая величина, и наоборот [4]
Пример с решениемПример 3.1
Пример 3.2
Пример 3.3
Если подставить предельное значение, то получим неопределенность Поэтому для решения подобных примеров используют следующий прием: делят числитель и знаменатель на в максимальной степени, в данном случае на Тогда получим
Пример 3.4
Пример 3.5
(Предел в квадратных скобках — это второй замечательный предел).
Пример 3.6
Пример 3.7
Так как логарифмичеешя функция непрерывна, то можно воспользоваться формулой (3.5).
Пример 3.8
Данный предел можно свести к первому замечательному пределу путем замены переменной, т.е.
при
тогда получим
Пример 3.9
Пример З.10
Пример 3.11
Пример 3.12
Как рассчитать пределы для различных функций
Ключевые термины
Цели
Применение пределов непрерывности функций
Введение в ограничения
Рассмотрим простую параболу ниже:
, если вы продолжаете следуйте за x 9003. также увеличивается с нарастающей скоростью. Вы могли бы (совершенно правильно) сказать, что функция f равна неограниченному при увеличении x — или, альтернативно, f не имеет ограничений по мере увеличения x .
также увеличивается с нарастающей скоростью. Вы могли бы (совершенно правильно) сказать, что функция f равна неограниченному при увеличении x — или, альтернативно, f не имеет ограничений по мере увеличения x .
Теперь рассмотрим другой пример: .
AS x становится очень большой в этом случае, функция F .
и так далее. Хотя нет значения x достаточно велико, чтобы сделать f равным нулю, f становится произвольно близким к нулю, когда x приближается к бесконечности (∞). Математически мы говорим, что предел f ( x ) при приближении x к ∞ равен 0. Или, символически,
Аналогично, если x приближается к -∞, функция f в этом случае также становится сколь угодно близкой к нулю. Но нам не нужно ограничивать пределы крайними значениями независимой переменной. А как насчет других интересных особенностей этой функции? Рассмотрим, как работать с пределами при приближении к x = 0. Во-первых, обратите внимание, что предел зависит от направления, с которого приближается значение x . В этом случае, если мы начнем с левой стороны и приблизимся к x = 0, функция f становится все меньше и меньше (в смысле большей величины, но с отрицательным знаком) без ограничений. Чтобы представить эту ситуацию символически, мы называем предел -∞, но это просто означает, что функция не имеет минимального действительного значения. Мы используем маленький верхний индекс «–» для обозначения приближения слева: Когда мы приближаемся к x = 0 справа (обозначено верхним индексом «+»), f становится сколь угодно большим, поэтому мы говорим, что предел равен ∞. Мы также можем посмотреть на предел любой произвольной точки, а не только на «особые» точки. Рассмотрим х = 1, Итак, давайте еще раз посмотрим на общее выражение для предела данной функции f ( x ) при приближении x к некоторой константе c. Учитывая все приведенные выше примеры, теперь мы можем сказать, что если функция f сколь угодно близко (но не обязательно достигает) к некоторому значению L , когда x приближается к c с любой стороны, то L является предел этой функции для x приближается к c. В этом случае мы говорим, что предел существует. Односторонние пределы — это когда функция приближается к определенному значению только с одной стороны (как в приведенной ниже функции). Хотите узнать больше? Почему бы не пройти онлайн-курс Precalculus? Часто мы можем определить предел, просто вычислив f ( c ), но очевидно, что это не всегда работает (особенно если c не входит в домен f ). Кроме того, нам может понадобиться рассмотреть направление, с которого мы приближаемся к c (для односторонних ограничений). Однако обычно вы можете легко рассчитать предел, если посмотрите на график или таблицу значений около x = c. Практическая задача: Рассчитайте следующие пределы. а. б. г. д. Решение: Полезно сначала построить график функции, чтобы увидеть эти ограничения. а. Для этого предела рассмотрим значение ln x , поскольку x все ближе и ближе к 0. Функция приближается к -∞, поэтому предел равен б. В этом случае мы можем просто подставить c в функцию. Обратите внимание, что предел равен 0 независимо от направления приближения. в. Здесь, как x становится произвольно большим, как и ln x (т. е. функция не имеет реального максимального значения). Таким образом, д. Опять же, в этом случае направление подхода не имеет значения. Мы можем просто подключить e к функции. Правила ограничений Некоторые ограничения могут включать сложные выражения. Эти правила для пределов позволяют нам разбивать сложные выражения на более простые для нахождения предела. Практическая задача: Объясните словами, почему для многочлена p ( x ) всегда верно следующее. Решение: Напомним, что многочлен p ( x ) имеет следующий вид, где значения c i (где i = 0, 1, 2, 3,. Поскольку x приближается к k, многочлен (в любой его форме) приближается к p ( k ), потому что областью определения многочлена являются все действительные числа. Таким образом, когда мы имеем дело с пределами для полиномов, мы можем просто подставить предельное значение для x непосредственно в функцию. Математическое доказательство этого факта не слишком сложное, но результат достаточно интуитивен. Практическая задача: Рассчитайте следующие пределы. а. б. г. Решение: В каждом конкретном случае можно использовать ряд подходов. Один из них — построить график функции и посмотреть на поведение функции вблизи предельного значения x (это часто бывает полезно независимо от выбранного вами подхода). а. Здесь замена возможна без проблем. Вы также можете использовать правила лимитов. б. В этом случае функция является многочленом степени 2. Можно просто подставить. в. Для этой функции нельзя напрямую применять правила лимитов и замещения. Посмотрите на график, обратите внимание, что значение x приближается справа. Применение пределов: непрерывность Рассмотрим более простое применение пределов: непрерывность функции. Посмотрите еще раз на функцию . Интуитивно мы можем сказать, что функция непрерывна (т. Обратите внимание, что функция непрерывна на открытом интервале ( a, b ), если она непрерывна во всех точках этого интервала. Практическая задача: Определить, является ли функция непрерывной в заданной точке. а. на х = 1 б. при x = 0 c. п. х на х = e Решение: Для задачи a обратите внимание, что функция равна прямой x + 2, за исключением того, что в ней отсутствует точка (1, 3). Однако функция не определена при x = 1. Следовательно, мы не можем использовать подстановку, чтобы найти предел. Поскольку функция нарушает одно (фактически два) условия непрерывности, она не является непрерывной в х = 1, Для части b обратите внимание, что ни одно из условий непрерывности не выполнено. Предела не существует (это ∞), и функция не определена при x = 0. Следовательно, функция не является непрерывной при x = 0, Для части c обратите внимание, что функция определена как x = e: п е = 1 Кроме того, предел определен и может быть рассчитан путем подстановки: Таким образом, ln x непрерывно при x = e. 

 В этом случае предела не существует; однако мы можем найти односторонние пределы, как мы это сделали выше.
В этом случае предела не существует; однако мы можем найти односторонние пределы, как мы это сделали выше.
 В этих и других случаях часто бывает полезно использовать правила, упрощающие вычисления. Ниже приведены основные свойства пределов для произвольных функций f ( x ) и g ( x ) и произвольная константа k.
В этих и других случаях часто бывает полезно использовать правила, упрощающие вычисления. Ниже приведены основные свойства пределов для произвольных функций f ( x ) и g ( x ) и произвольная константа k.  , n ) являются константами:
, n ) являются константами: В качестве альтернативы вы можете использовать правила ограничений и, при необходимости, просто заменить.
В качестве альтернативы вы можете использовать правила ограничений и, при необходимости, просто заменить. е. в ней нет «разрывов») слева от х = 0 и справа от х = 0, но не х = 0. А как насчет более математического определения? Мы можем использовать лимиты. Функция непрерывна в конкретной точке x = c , если выполняются все следующие условия:
е. в ней нет «разрывов») слева от х = 0 и справа от х = 0, но не х = 0. А как насчет более математического определения? Мы можем использовать лимиты. Функция непрерывна в конкретной точке x = c , если выполняются все следующие условия: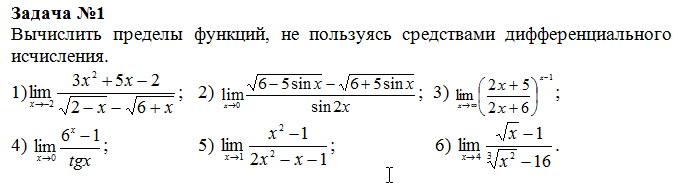 Интересно, что лимит здесь существует:
Интересно, что лимит здесь существует:
Нахождение пределов графически
Нахождение пределов графическиК концу этой лекции вы должны быть в состоянии использовать график функции, чтобы найти пределы для ряда различных функций, включая пределы на бесконечности, и определить, когда пределы не существуют (и когда они не существуют). существуют, чтобы объяснить, почему). Вы также должны уметь правильно использовать предельные обозначения.
Поскольку эта лекция посвящена ограничениям, давайте вернемся к нашему неформальному определению пределов из прошлой лекции:
Предел (неофициальное определение)
Если f(x) в конце концов становится все ближе и ближе к определенному значению L по мере того, как x приближается к выбранному значению c из правого , то мы говорим, что предел f(x) как x приближается к c справа L .
Если f(x) в конце концов получит все ближе и ближе к определенному значению L по мере того, как x приближается к выбранное значение c из остается , тогда мы говорим, что предел f(x) при приближении x к c слева есть L .
Если предел f(x) при приближении x к c одинаков справа и слева, то мы говорим, что предел f(x) при приближении x к c равен L .
(Если f(x) никогда не приближается к определенному конечному значению как x приближается к c , тогда мы говорим, что предела не существует . Если f(x) имеет разные правый и левый пределы, то двусторонний предел ( lim x → c f(x) ) не существует
.) Обозначение:Конкретно пишем:
lim x → c- f(x) = L для обозначения « предела f(x) при приближении x к c слева равен L »
LIM x → C+ F (x) = L , чтобы обозначить « Предел из F (X), когда x подходит к Справам из F (X).

lim x → c f(x) = L для обозначения « предела f(x) при приближении x к c равен L »
Будьте осторожны!: Знак плюс или минус, который появляется после C Обозначает Направление , из которого x приближается к C — Это не означает , что C, C. C. C, C. C. C. C, C, C. положительное или отрицательное (может быть и то, и другое)!
Например:
lim x → -2- f(x) = L означает, что предел f(x) при приближении x к -2 слева составляет 9042 L;
lim x → -2+ f(x) = L означает, что предел f(x) при приближении к x справа равен x ;
lim x → 2- f(x) = L означает, что предел f(x) , поскольку x 2 слева от L приближается к 9042 x ; и
lim x → 2+ f(x) = L означает, что предел f(x) при приближении к x справа равен x ;
Это определение является неформальным , потому что мы формально не определили, что мы подразумеваем под «подходами» или «в конечном итоге все ближе и ближе». Как только мы разработаем более интуитивное представление о том, что такое ограничения на самом деле, мы вернемся и формально определим эти термины.
Как только мы разработаем более интуитивное представление о том, что такое ограничения на самом деле, мы вернемся и формально определим эти термины.
Лучший способ для нас лучше понять, что такое предел, — это просто перейти и начать рассматривать различные функции и обсуждать, каким может быть предел для конкретных значений x для этой функции. Но прежде чем мы это сделаем, мы кратко введем определение, которое будем использовать в следующих примерах. На протяжении всей лекции мы будем часто использовать слово 9.0042 прерывистость , поэтому мы определяем его (по крайней мере пока неформально) здесь:
Непрерывная, Прерывистая (неофициальное определение)
Функция является непрерывной в интервале, если график этой функции на этом интервале можно нарисовать одним росчерком (не отрывая ручки от бумаги).
A разрыв на графике — это любая точка, в которой график НЕ является непрерывным (например, дыра, скачок, асимптота).
Существуют более формальные определения непрерывности, но мы пока используем это, потому что его легко понять интуитивно. Позже мы вернемся и определим это понятие более формально.
Ограничения конкретных функций
Лучший способ понять, что на самом деле представляют собой ограничения, — это посмотреть на множество различных примеров, демонстрирующих различные типы поведения около x=c для некоторого фиксированного значения c . Итак, давайте прыгать прямо в!
В этой лекции мы разрабатываем каждый пример, только глядя на график. Однако каждую из этих функций также можно выразить алгебраически (с помощью уравнения), и мы также можем найти пределы функций алгебраически, используя это уравнение для вычисления предела. О том, как это сделать, мы поговорим в следующей лекции.
Простой пример, где
lim x → c f(x) = f(c) : Для многих простых функций предел f(x) в c совпадает со значением f(x) в c . Например, для функции на графике ниже предел f(x) при 1 равен просто 2, что мы и получим, если вычислим функцию f при 2. Поскольку точка (1,2) находится на графике f(x) , предел равен 2, поэтому мы могли бы написать:
Например, для функции на графике ниже предел f(x) при 1 равен просто 2, что мы и получим, если вычислим функцию f при 2. Поскольку точка (1,2) находится на графике f(x) , предел равен 2, поэтому мы могли бы написать:
lim x → 1 ф(х) = 2
Этот пример был не очень интересен, потому что не совсем понятно, зачем нам здесь вообще нужно вычислять предел: поскольку эта функция полностью непрерывна около x = 1, значение функции равно 1 и значение, к которому функция приближается по мере приближения x к 1, — это одно и то же!
Определение предела, однако, особенно полезно для функций, где функция not defined exactly at x=c (but where it is defined all around c ), or where the value of f(x) at c отличается от значения, к которому f(x) приближается, когда x приближается к c .
Пример с отверстием в точке
x=c:Для функции на графике ниже f(x) не определяется, когда x = -2. Глядя на график, мы видим, что в этой точке есть дыра или разрыв. Однако в этом случае мы можем видеть, что по мере продвижения вдоль линии, представляющей функцию f(x) , от влево к x = -2 значение f(x) становится ближе и ближе к -4. Точно так же, когда мы движемся вдоль линии, представляющей функцию f(x) , от справа к x = -2, значение f(x) все ближе и ближе к -4. Таким образом, в этом случае мы можем сделать вывод, что:
lim x → -2 f(x) = -4
Пример функции с разрывом скачка в точке
x=c , состоящей из одной точки : Для функции на графике ниже f(x) определяется, когда x = -2, но значение f(x) при -2 совсем не похоже на значение, к которому будет приближаться f(x) по мере приближения x к -2 либо слева, либо справа. Глядя на график, мы видим, что в этой точке есть скачок, так что когда x = -2, f(x) = -1; однако, когда x равно около (но НЕ равно) -2, f(x) на самом деле близко к -4.
Глядя на график, мы видим, что в этой точке есть скачок, так что когда x = -2, f(x) = -1; однако, когда x равно около (но НЕ равно) -2, f(x) на самом деле близко к -4.
В этом случае мы можем видеть, что при движении по линии, представляющей функцию f(x) от слева к x = -2, значение f(x) все ближе и ближе к -4. Точно так же, когда мы движемся вдоль линии, представляющей функцию f(x) , от справа к x = -2, значение f(x) становится все ближе и ближе к -4. Таким образом, хотя функция на самом деле равна -1, когда мы на самом деле находимся в x = -2, в любой другой точке вокруг x = -2 функция вместо этого приближается к -4. Таким образом, в этом случае предел на самом деле отличается от значения функции в этой точке:
f( -2 ) = -1 ; но
lim x → -2 f(x) = -4
Пример с функцией, которая имеет разрыв скачка в точке
x=c и разные пределы справа и слева: Для функции на графике ниже f(x) определяется, когда x = 1, но значение, которое f(x) будет приближаться по мере приближения x к 1 слева, отличается от значения, к которому оно будет приближаться по мере приближения x к 1 справа. Глядя на график, мы видим, что по мере того, как x приближается к 1 слева, f(x) приближается к отрицательное два; однако, поскольку x приближается к 1 справа, f(x) приближается к положительный 2.
Глядя на график, мы видим, что по мере того, как x приближается к 1 слева, f(x) приближается к отрицательное два; однако, поскольку x приближается к 1 справа, f(x) приближается к положительный 2.
Еще раз обратите внимание, что фактическое значение функции в 1 не имеет отношения к нахождению предела: возможно, что иногда предел f(x) в c на самом деле будет f(c) (как это произошло в нашем первом примере в этой лекции), но большую часть времени предел f(x) при c будет отличаться от значения f(c) , особенно когда f(c) не определено, или когда имеется разрыв в точке x=c .
В этом случае, LIM x → 1+ F (x) = F (C) , но LIM X → 1+ . ) не равно f(c) . Кроме того, поскольку пределы слева и справа различны, двусторонний предел lim x → 1 f(x) не существует. В частности, мы можем написать:
) не равно f(c) . Кроме того, поскольку пределы слева и справа различны, двусторонний предел lim x → 1 f(x) не существует. В частности, мы можем написать:
лим x → 1- f(x) = -2
lim x → 1+ f(x) = 2
lim x → 1 f(x) не существует
Пример с функцией, имеющей бесконечный разрыв (или вертикальную асимптоту) в точке
x=c : Для функции на графике ниже f(x) не определяется, когда x = 0, потому что по мере того, как x становится все ближе и ближе к 0 с любой стороны, f(x) становится все больше и больше: чем ближе становится x до 0, тем больше становится f(x) . При x = 0, f(x) не имеет конкретного значения на графике.
При x = 0, f(x) не имеет конкретного значения на графике.
Когда это происходит, мы говорим, что f(x) неограниченно возрастает по мере того, как x приближается к с . Каждый раз, когда это происходит с пределом, мы можем просто написать, что предела не существует, потому что f(x) не приближается ни к какому фиксированному, конечному значению , поскольку x приближается к c . Однако писать это немного громоздко, поэтому вместо этого математики изобрели для этого небольшое сокращение:
.Обозначение пределов, которые увеличиваются (или уменьшаются) без ограничений, ±∞
Обозначение:
IF F (x) Увеличивается без ограничения по адресу x . или lim x → c- f(x) = +∞
Аналогично, если f(x) неограниченно возрастает по мере того, как x приближается к c справа, мы можем написать:
LIM x → C+ F (x) = ∞ или LIM x → C+ → C+ .
Если f(x) неограниченно возрастает по мере того, как x приближается к c как слева, так и справа, мы можем написать: = ∞ или lim x → c f(x) = +∞
Существует также вероятность того, что f(x) будет уменьшать без ограничений (становиться все меньше и меньше или все более и более отрицательным), когда x приближается к c . В этом случае мы можем использовать символ — ∞ .
Будьте осторожны!: Использование символа бесконечности ∞ — это просто сокращение для того, чтобы сказать, что лимит НЕ существует потому что он увеличивается или уменьшается без ограничения .
Но бесконечность, или символ ∞, НЕ является числом , и поэтому никакое уравнение или функция никогда не могут быть равны бесконечности !
Мы должны быть очень осторожны при использовании символа бесконечности: мы можем сказать, что предел равен бесконечности, чтобы показать, что поведение функции a s x приближается к c «взрывается» бесконечно, но мы можем НИКОГДА сказать, что f(x) само равно бесконечности, потому что никакая функция никогда не может достичь значения бесконечности: в каждой точке графика f(x), f(x) имеет конкретное значение, даже если это значение очень-очень велико (или очень-очень мало). (Даже если f не определено в определенной точке, это , а не равно бесконечности в этой точке — если оно не определено, то это не равно что угодно в этот момент.)
(Даже если f не определено в определенной точке, это , а не равно бесконечности в этой точке — если оно не определено, то это не равно что угодно в этот момент.)
Итак, возвращаясь к нашему примеру, мы можем написать:
lim x → 0- f(x) = + ∞
(или левосторонний предел не существует, потому что f(x) неограниченно возрастает)
lim x → 0+ f(x) = + ∞
(или правосторонний предел не существует, потому что f(x) неограниченно возрастает)
lim x → 0 f(x)= + ∞
(или двусторонний предел не существует, потому что f(x) неограниченно возрастает)
Пример с функцией, имеющей бесконечный разрыв (или вертикальную асимптоту) в точке
x=c, с различным поведением предела слева и справа: Для функции на графике ниже f(x) не определено, когда x = 1, потому что по мере того, как x становится все ближе и ближе к 1 от вправо , f(x) просто продолжает приближаться больше и больше: чем ближе x становится к 1 от справа , тем больше становится f(x) . И по мере того, как x становится все ближе и ближе к 1 из слева , f(x) становится все меньше и меньше (или все более и более отрицательным): чем ближе x приближается к 1 от слева , тем меньше (или более отрицательное) f(x) ) получается.
И по мере того, как x становится все ближе и ближе к 1 из слева , f(x) становится все меньше и меньше (или все более и более отрицательным): чем ближе x приближается к 1 от слева , тем меньше (или более отрицательное) f(x) ) получается.
Итак, при x = 1, f(x) не имеет на графике никакого конкретного значения.
Итак, в этом случае мы можем написать:
lim x → 1- f(x) = — ∞
(или левосторонний предел не существует, потому что f(x) неограниченно убывает)
lim x → 1+ f(x) = + ∞
(или правосторонний предел не существует, потому что f(x) неограниченно возрастает)
lim x → 1 f(x)= ∞
(или двусторонний предел не существует, потому что f(x) неограниченно уменьшается/увеличивается)
Теперь мы видели два примера, где f(x) неограниченно увеличивалось (или уменьшалось) по мере того, как x приближалось к определенному значению c , но может иметь место и противоположное поведение: поведение f(x) , когда x увеличивается (или уменьшается) без ограничений. В некоторых случаях может случиться так, что x становится все больше и больше, f(x) все ближе и ближе к определенному значению L , и в этих случаях мы могли бы написать что-то вроде этого:
В некоторых случаях может случиться так, что x становится все больше и больше, f(x) все ближе и ближе к определенному значению L , и в этих случаях мы могли бы написать что-то вроде этого:
lim x →+ ∞ f(x)= L
Точно так же мы могли бы рассмотреть, как ведет себя f(x) , когда x уменьшается без ограничений, и если бы f(x) приближалось к определенному значению L , мы могли бы написать что-то вроде этого:
lim x → — ∞ f(x)= L
Теперь мы переходим к некоторым примерам, где мы рассматриваем поведение f(x) при неограниченном увеличении или уменьшении x . Другими словами, мы пытаемся определить, приближается ли f(x) к определенному фиксированному конечному значению по мере того, как мы продвигаемся все дальше и дальше вправо или влево на графике f(x) .
Пример с функцией, предел которой равен нулю на бесконечности:
Для функции на графике ниже мы сначала рассматриваем поведение f(x) по мере того, как x увеличивает без ограничений, или, другими словами, мы рассматриваем то, что происходит с f(x) по мере того, как мы продвигаемся дальше. и правее на графике. В этом случае f(x) становится все ближе и ближе к нулю. Оно никогда не может достичь нуля, потому что у функции нет конца: x может продолжать увеличиваться бесконечно. Но поведение функции как x увеличивается в том, что оно становится все ближе к 0, даже если никогда не сможет достичь его.
Точно так же, когда x безгранично уменьшается на , или по мере того, как мы двигаемся все дальше и дальше влево по графику, f(x) становится все ближе и ближе к нулю. Опять же, здесь поведение f(x) по мере того, как x уменьшается (или становится все более и более отрицательным), заключается в том, что оно становится все ближе к 0, даже если оно никогда не может достичь его.
Итак, в этом случае мы можем написать:
lim x → +∞ f(x) = 0
lim x → — ∞ f(x) = 0
Пример с функцией, предел которой равен двум на бесконечности:
Для функции на графике ниже мы сначала рассматриваем поведение f(x) по мере того, как x увеличивает без ограничений, или, другими словами, мы рассматриваем то, что происходит с f(x) по мере того, как мы продвигаемся дальше. и правее на графике. В этом случае f(x) становится все ближе и ближе к двум. Он никогда не может достичь двух, потому что у функции нет конца: x может продолжать увеличиваться бесконечно. Но поведение функции по мере увеличения x заключается в том, что она становится все ближе к 2, даже если она никогда не может этого достичь.
Точно так же, когда x безгранично уменьшается на , или по мере того, как мы двигаемся все дальше и дальше влево по графику, f(x) становится все ближе и ближе к двум. Опять же, здесь поведение f(x) по мере того, как x уменьшается (или становится все более и более отрицательным), состоит в том, что оно становится все ближе к 2, даже если оно никогда не может достичь его.
Итак, в этом случае мы можем написать:
lim x → +∞ f(x) = 2
lim x → — ∞ f(x) = 2
Пример с функцией, предел которой не существует на бесконечности:
Для функции на графике ниже мы сначала рассматриваем поведение f(x) по мере того, как x увеличивает без ограничений, или, другими словами, мы рассматриваем то, что происходит с f(x) по мере того, как мы продвигаемся дальше. и правее на графике. В этом случае f(x) кажется неограниченно возрастающим: кажется, что оно становится все больше и больше по мере того, как мы двигаемся вправо по графику, никогда не приближаясь к конкретному значению y .
и правее на графике. В этом случае f(x) кажется неограниченно возрастающим: кажется, что оно становится все больше и больше по мере того, как мы двигаемся вправо по графику, никогда не приближаясь к конкретному значению y .
Точно так же, когда x безгранично уменьшается на , или по мере того, как мы двигаемся все дальше и дальше влево по графику, f(x) кажется неограниченно уменьшающимся: кажется, что оно становится все меньше и меньше (или больше). и более отрицательные) при движении влево по графику.
Итак, в этом случае мы можем написать:
lim x → +∞ f(x) = + ∞
(или предела не существует, потому что f(x) неограниченное увеличение)
lim x → — ∞ f(x) = — ∞
(или предела не существует, потому что f(x) неограниченно уменьшается)
Заметим, что не обязательно, чтобы f(x) неограниченно возрастало по мере неограниченного возрастания x и что f(x) неограниченно уменьшалось по мере неограниченного уменьшения x . Например, для функции на графике ниже у нас было бы обратное:
Например, для функции на графике ниже у нас было бы обратное:
lim x → +∞ f(x) = — ∞
(или предела не существует, потому что f(x) неограниченно уменьшается)
lim x → — ∞ f(x) = + ∞
(или предела не существует, потому что f(x) неограниченно возрастает)
Пример с функцией, имеющей разные пределы на положительной и отрицательной бесконечности:
Функция также может иметь разные пределы на положительной бесконечности и на отрицательной бесконечности (или даже существовать предел для одного из них, но не для другого). Все это утверждение на самом деле означает, что поведение f(x) может сильно отличаться в крайнем левом углу нашего графика, чем в крайнем правом. Например, на графике ниже мы видим, что предел существует как при неограниченном уменьшении x , так и при неограниченном увеличении x , и что этот предел в каждом случае разный:
Например, на графике ниже мы видим, что предел существует как при неограниченном уменьшении x , так и при неограниченном увеличении x , и что этот предел в каждом случае разный:
lim x → +∞ f(x) = 1
lim x → — ∞ f(x) = -1
Нет никаких причин, по которым наш предел должен быть отрицательным, поскольку x становится «более отрицательным» (т. » (то есть как x → + ∞). Например, у нас может быть противоположный случай, как в функции, представленной на следующем графике:
lim x → +∞ f(x) = -1
lim x → — ∞ f(x) = 1
Пример с функцией, имеющей осциллирующий разрыв:
Последняя возможность, когда мы ищем предел x приближается к c заключается в том, что f(x) никогда ни к чему не приближается, поскольку x становится все ближе и ближе к c : у нас может быть поведение, как на приведенном ниже графике, где f(x) просто колеблется все более и более дико по мере того, как x становится все ближе и ближе к c либо слева, либо справа.
Глядя на изображение графика выше, трудно точно сказать, что происходит, поскольку x все ближе и ближе к 1: похоже, что колебания становятся все более и более плотными, так что f(x) постоянно движется вперед и назад между -1 и 1, никогда не останавливаясь, но в этом нельзя быть уверенным. (Без фактического уравнения для рассмотрения, которое точно объяснило бы, каковы значения f(x) , когда мы приближаемся к 1, мы на самом деле не можем доказать, что это поведение этой конкретной функции, поэтому на данный момент, Я просто попрошу вас поверить мне на слово.) Но чтобы лучше понять, как на самом деле работает поведение f(x) при приближении x к 1, вы можете немного поэкспериментировать с интерактивной анимацией ниже. .
В интерактивной анимации ниже вы можете увидеть это поведение более четко, переместив ползунок вправо, который увеличивает значения x на графике примерно на единицу. Мы можем видеть, что по мере приближения к единице график просто колеблется все чаще и чаще, пока не станет настолько плотным, что мы больше не сможем видеть пробелы между графиком и пустым пространством вокруг него.
Мы можем видеть, что по мере приближения к единице график просто колеблется все чаще и чаще, пока не станет настолько плотным, что мы больше не сможем видеть пробелы между графиком и пустым пространством вокруг него.
зум
В данном конкретном случае единственный вывод, который мы можем сделать (предполагая, что вы убеждены в том, что эта функция ведет себя так, как я описал до сих пор на словах), состоит в том, что предел f(x) at x=c не существует. В этом случае единственное, что мы можем написать, это просто:
.lim x → 1 f(x) не существует
В этом случае мы можем НЕ написать, что предел равен бесконечности, потому что поведение f(x) по мере приближения x к 1 есть НЕ что оно неограниченно возрастает — скорее, поведение из f(x) по мере того, как x приближается к 1, будет бесконечно колебаться между -1, 1 и всеми числами, попадающими между .
Это важно, потому что нам важно понимать, что пределы могут не существовать по различным причинам . Мы можем написать lim x → c f(x) = ± ∞ в тех случаях, когда предел не существует3, потому что
2 f(x) неограниченно увеличивается или уменьшается , и НЕ в случаях, когда f(x) имеет различных значений слева и справа, ИЛИ в случаях, когда f(x) колеблется бесконечно среди набора значений, поскольку x приближается к c .
До сих пор мы обсудили все способы, которыми мы можем находить пределы графически, рассматривая график функции визуально. В следующей лекции мы дадим уравнения для каждой из функций, представленных в этой лекции, и мы исследуем, как мы можем найти пределы функций алгебраически (даже если мы не можем смотреть на график).
Но прежде чем мы закончим эту лекцию, давайте задумаемся об основных паттернах и структуре, которые мы наблюдали, рассматривая этот набор различных функций с очень разными типами поведения около x=c .
Одним из наиболее важных навыков в математике является способность распознавать закономерности и классифицировать выражения, уравнения или другие математические объекты на основе их свойств .
Математика — это поиск структуры (классификация уравнений, выражений или других объектов на основе общих свойств)!
Например, когда мы делаем домашнее задание, мы можем решить 30 разных задач, но обычно многие из них имеют одинаковую структуру , даже если они имеют разные числа или переменные. Часто эти 30 проблем действительно можно разделить на пять различных типов проблем. Если мы сможем это увидеть, то сможем сделать свою жизнь намного проще, потому что теперь вместо того, чтобы пытаться решить 30 задач, нам просто нужно понять подход, необходимый для решения задач каждого из пяти типов.
Вот пример проблемы, с которой сталкиваются многие студенты, изучающие алгебру, обычно потому, что они отвлекаются на детали и переменные и забывают искать основную структуру уравнения:
Решите для h: A = 2Π rh + 2Π r 2
При решении этой задачи многие ученики отвлекаются на то, что в уравнении много переменных, и квадрат, и иррациональное число пи.
.Однако ни одна из этих деталей не имеет отношения к структура уравнения. Это уравнение на самом деле имеет следующую структуру :
А = В ч + С
, где B и C просто заменяют «некоторое выражение, которое не содержит никаких h ». Другими словами, нам все равно, сколько странных или интересных алгебраических выражений записано на месте, где 2Π r появляется в исходном уравнении — вместо этого мы можем просто думать обо всем этом выражении как просто о коэффициенте ч . Все, о чем мы заботимся здесь, это то, что для того, чтобы найти h , нам нужно иметь возможность получить h отдельно с одной стороны , поэтому нам нужно вычесть любое выражение справа, которое не содержит h с обеих сторон, чтобы исключить его из правой части уравнения.
И затем, как только мы это сделали, нам нужно будет разделить обе части уравнения на любой коэффициент, равный 9.0042 ч .
Но все следующие примеры имеют ту же структуру , что и исходная задача выше:
Решите для h: A = 2Π rh + 2Π r 2
Решите для h: A = Bh + C
Найдите h: 42,6578 = 94 h + 0,55
Найти h: (Π r 2 A ) 2 = π R 6 A 7 + (2π R + 2π R + (2π R + 2π R 9291 2 2 ) ).
Найдите h: 1 = 2 h + 3
Найдите h: 1 = (3+4 r) + 2 h
В каждом из этих примеров говорится, что некоторое количество равно другому количеству, умноженному на ч плюс еще одно количество.
Таким образом, чтобы решить каждое из этих уравнений, нам просто нужно вычесть член, который не содержит ч из обеих частей уравнения (чтобы сократить его до нуля в правой части), а затем нам нужно будет разделить обе части на полный коэффициент ч (т.е. то, что умножается на h , каким бы запутанным и сложным он ни был).
Итак, как это помогает нам лучше понять, что происходит на занятиях по математическому анализу (или другим математическим дисциплинам, не являющимся алгеброй)? В этом случае имеет смысл вспомнить все предельные примеры, которые мы только что рассмотрели в этой лекции. Почему я выбрал именно те примеры, которые были рассмотрены в этой лекции? Я выбрал их не случайно. Я специально отобрал их, чтобы охватить все возможные виды поведения, которые мы можем наблюдать около 9 лет.0042 x=c , чтобы дать вам хорошее представление обо всем, что может произойти, когда мы пытаемся оценить предел. Итак, давайте вернемся к примерам, которые мы только что рассмотрели в этой лекции, и посмотрим, сможем ли мы найти базовую структуру и шаблоны .
- f(x) непрерывен в интервале около х=с. В этом случае односторонние пределы справа и слева одинаковы и оба равны f(c) . (Например, на графике ниже, когда c = 1.)
- Если f(x) не является непрерывным ни в каком интервале вокруг x=c , то может произойти одно из следующих событий:
- На x=c есть дыра, но вокруг x=c есть интервал, так что f(x) непрерывна везде в этом интервале, кроме точки x=c . В этом случае f(x) не определено при x=c , но односторонние пределы справа и слева одинаковы, и оба они равны f(c) . (Например, на графике ниже, когда c = -2.)
- Имеется скачок в единственной точке, где x=c , но есть интервал вокруг x=c , так что f(x) непрерывен везде в этом интервале, кроме x=c ; поэтому односторонние пределы справа и слева в этом случае одинаковы, но они не равны f(c) .
 (Например, на графике ниже, когда c = -2.)
(Например, на графике ниже, когда c = -2.) - Имеется скачок в точке, где x=c , , но есть интервал вокруг x=c , так что f(x) непрерывно всюду в этом интервале, кроме точки х=с ; однако в этом случае односторонние пределы справа и слева различны, и хотя бы один из них не равен f(c) . (Например, на графике ниже, когда c = 1.)
- Существует вертикальная асимптота при x=c , так что f(x) неограниченно увеличивается или уменьшается по мере того, как x приближается к c справа и/или слева. В этом случае не существует ни одностороннего правого, ни левого предела, а значит, не существует и двустороннего предела. (Например, на графике ниже, когда с =1.)
- Вокруг x=c наблюдается какое-то «действительно необычное» поведение, такое как все более плотные бесконечные колебания, так что f(x) никогда не приближается ни к какому конкретному значению, как x приближается к c (либо только с одной стороны или с обеих сторон).
 (Например, на графике ниже, когда c = 1.)
(Например, на графике ниже, когда c = 1.)
Еще одна вещь, которая может произойти (которая не рассматривается в примере в предыдущей лекции), состоит в том, что f(x) может быть прерывистым везде в некотором интервале вокруг x=c . Это трудно изобразить графически, но мы можем привести пример, в котором мы определяем функцию таким образом, чтобы она прыгала в каждой точке на прямой с действительными числами. Например, функция, называемая функцией Дирихле, имеет разрыв в каждой отдельной точке. Вот как это определяется: Если x — рациональное число, то f(x) = 1; но если х иррациональное число, ф(х) =0. Понимание того, почему эта функция везде разрывна, немного выходит за рамки этого курса, но если вам интересно понять, почему это так, вам просто нужно принять предположение, что вокруг любого заданного иррационального числа мы не можем найти достаточно маленький интервал. исключить все рациональные числа; и вокруг любого заданного рационального числа мы не можем найти достаточно маленький интервал, чтобы исключить все иррациональные числа. Это означает, что вокруг любого заданного значения x=c мы никогда не сможем найти интервал около c , где f(x) непрерывно (даже если мы допускаем, что f(x) является прерывистым при x=c ).
Это означает, что вокруг любого заданного значения x=c мы никогда не сможем найти интервал около c , где f(x) непрерывно (даже если мы допускаем, что f(x) является прерывистым при x=c ).
- На x=c есть дыра, но вокруг x=c есть интервал, так что f(x) непрерывна везде в этом интервале, кроме точки x=c . В этом случае f(x) не определено при x=c , но односторонние пределы справа и слева одинаковы, и оба они равны f(c) . (Например, на графике ниже, когда c = -2.)
Для пределов на бесконечности (т.е. когда x приближается к ±∞), ситуация менее сложная. По сути, возможны два случая:
- Когда x приближается к ±∞, f(x) приближается к определенному конечному значению L , и в этом случае предел равен L. (Это то же самое, что сказать, что f(x) имеет горизонтальную асимптоту в точке x=c .)
- Когда x приближается к ±∞, f(x) никогда не приближается к определенному конечному значению , а просто продолжает неограниченно увеличиваться или уменьшаться (т. е. f(x) неограниченно увеличивается или уменьшается, или приближается к ±∞).
 В этом случае предела не существует.
В этом случае предела не существует.
По мере продвижения к следующей лекции мы постараемся найти правила и процедуры алгебраического вычисления пределов (т. е. используя только уравнение для f(x) вместо графика), мы захотим запомнить этот список возможных типов предельного поведения! Это поможет нам выяснить, сколько различных типов алгебраических методов нам может понадобиться для оценки пределов — если две разные функции имеют разные типы поведения около x=c , то нам, возможно, придется использовать два разных метода. к нахождению предела для каждой функции алгебраически!
Расчет пределов с помощью алгебры — AP Calculus AB
Все ресурсы AP Calculus AB
3 диагностических теста 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
AP Calculus AB Помощь » Функции, графики и ограничения » Ограничения функций (включая односторонние ограничения) » Вычисление пределов с помощью алгебры
Вычислить
Возможные ответы:
Предел не существует
0
5
10
Правильный ответ:
10
Объяснение:
Во-первых, мы замечаем, что замена x на 5 даст нам 0 в знаменателе.
Итак, мы упростим уравнение, заметив, что числитель — это разность двух квадратов.
Теперь мы можем заменить x на 5, и мы получим ответ 10.
Сообщить об ошибке
Оцените следующий предел:
Возможные ответы:
Правильный ответ:
Объяснение:
Вынесите множитель x-4 из числителя и упростите:
Оцените предел для x=4:
Несмотря на разрыв при x=4, предел при x=4 равен 10, потому что функция приближается к десяти слева и справа.
Сообщить об ошибке
Оцените следующий предел:
Возможные ответы:
Правильный ответ:
Объяснение:
Умножьте числитель на множители и упростите выражение.
Оценить функцию при x=2.
Существует разрыв в точке x=2, но поскольку предел при приближении x к 2 справа равен пределу при приближении x к 2 слева, предел существует.
Отчет о ошибке
Оцените следующий предел:
Возможные ответы:
Не существует
. Правильный ответ:
. Объяснение:
Разложите числитель, чтобы оценить предел:
Оцените предел:
Имеется разрыв при x=0, но предел равен 8, потому что предел справа равен пределу слева.
Сообщить об ошибке
Оцените следующий предел:
Возможные ответы:
Правильный ответ:
82 Объяснение:
Когда x приближается к бесконечности, значения x, возведенные в наивысшую степень, доминируют над функцией, а все остальные значения становятся незначительными. В этом пределе x 3 имеет наивысший порядок в числителе, а 5x 2 имеет наивысшую степень из всех значений в знаменателе. Мы можем упростить ограничение до следующего:
В этом пределе x 3 имеет наивысший порядок в числителе, а 5x 2 имеет наивысшую степень из всех значений в знаменателе. Мы можем упростить ограничение до следующего:
После вынесения x 2 легко увидеть, что предел расходится в бесконечность.
Сообщить об ошибке
Возможные ответы:
Не определено.
Правильный ответ:
Объяснение:
Первым шагом к оценке пределов всегда является попытка прямой подстановки значения в функцию. В этом случае это все, что вам нужно сделать.
Отчет о ошибке
Возможные ответы:
Undefined
Правильный ответ:
. Объяснение:
Объяснение:
Чтобы начать эту задачу, нам нужно разложить квадратное уравнение на множители. Это приведет к дыре в , что позволит нам напрямую подставить предельное значение в результирующую функцию для определения предела.
Сообщить об ошибке
Возможные ответы:
Не определено.
Правильный ответ:
Объяснение:
Чтобы оценить этот предел, нам нужно напрямую подставить рассматриваемое значение в нашу функцию. Обратите внимание, что это значение находится в домене функции, поэтому прямая подстановка — единственный метод, который нам здесь нужен.
Сообщить об ошибке. Объяснение:
Этот предел нельзя вычислить простой подстановкой; не определен в , поэтому сначала нужно немного упростить.
. (Старт)
. (Умножить на числитель)
. (Отменить условия)
. (Замените в )
.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
← Назад 1 2 3 4 Далее →
Уведомление об авторских правах
Все ресурсы AP Calculus AB
3 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции
MathScene — Пределы — Урок 1
MathScene — Пределы — Урок 12008 Расмус Эф ог Джанн Сак |
Функции, определяемые пределами и интервалами
Что происходит со значением функции как x
становится бесконечно большим? Становится ли функция также бесконечно большой? Делает
он достигает максимума или минимума? Что происходит на самом деле? Это то, что мы собираемся
для размышления в следующем тексте.
Мы знаем, что не можем разделить на ноль, но что произойдет, если мы разделим на число, очень близкое к нулю? Мы увидим, что иногда график функция поднимается или опускается почти перпендикулярно возле этой точки, а иногда и граф не может пройти через точку, оставив бесконечно малую дыру.
Математика использует понятие пределов для рассмотрения задач такого рода.
Посмотрите на функцию
Калькулятор Casio, кажется, рисует стрит линии, когда его просят построить график этой функции (см. диаграмму). Если вы выбираете большой масштабе, таком как INIT в V-Window, вы можете заметить небольшой перерыв в графике, когда x = 1. Это потому, что когда x = 1, мы делим на ноль и функция в этом пункте не определено. Область определения функции D f = R\{1}.
Сейчас попробуем разобраться что происходит как х приближается к 1. Математически это записывается следующим образом:
Лим — это сокращение от латинского слова лаймы. что означает ограничение. Приведенное выше обозначение означает значение, до которого функция
стремится по мере приближения x к 1.
что означает ограничение. Приведенное выше обозначение означает значение, до которого функция
стремится по мере приближения x к 1.
Мы можем использовать алгебру, чтобы упростить функцию но нельзя упускать из виду исходную функцию и проблему деления на нуль.
Теперь у нас больше нет задача деления на ноль, поэтому мы можем подставить значение x = 1 в выражение ( вычислитьf(1)).
= 1 + 1 = 2
Это показывает нам, что функция стремится к значению 2, когда x стремится к 1.
Мы можем заполнить эту дыру, если определим непрерывная функция с тем же алгебраическим выражением, но с добавлением значения которую функция может принимать при x = 1. Эта новая функция g(x) определяется следующим образом: |
Таким образом, мы получаем
показан непрерывный график
. |
Функции, определенные таким образом, имеют более более одного выражения, в зависимости от значений, которые принимает x, называются функции, определяемые интервалом.
Пример 1
Найдите значение
В этом случае нет задача деления на ноль, чтобы мы могли подставить число 2 в выражение вместо х.
2 3 2 2 = 8 4 = 4
Функция f(x) = x 3 x 2 становится все ближе и ближе к 4 по мере того, как x становится все ближе и ближе до 2.
Пример 2
Находить Лимит
В этом случае мы не можем дать x значение 3, так как это означало бы деление на ноль. Однако мы можем факторизовать выражение в числителе и сократить множитель x 3
Положите значение 3 для x. |
Пример 3
Найдите предел
Теперь мы не можем упростить
выражение, поэтому мы пытаемся найти решение, подставляя значения x рядом с
1. Выбираем значения как чуть больше, так и чуть меньше 1.
Выбираем значения как чуть больше, так и чуть меньше 1.
См. следующую таблицу значений.
График состоит из двух частей с вертикальной асимптотой по x = 1,
Давайте рассмотрим, что происходит когда x приближается к значению 1. Из графика видно, что мы должны рассмотрим отдельно значения выше и ниже x = 1. Мы можем сделать это легко используя ПРЕВОСХОД. Мы помещаем числа чуть меньше 1 в столбец A и чуть больше, чем 1 в колонке D. 92/(Д11). Обе формулы скопировал вниз.
Мы видим, что когда x равно меньше 1, то есть когда x приближается к значению 1 слева (слева от номер 1 по оси X ), значения f(x) (столбец B) все ближе и ближе к ∞. Когда х больше чем 1, то есть приближается к 1 справа, функция f(x) приближается к +∞. Конечно, бесконечности не существует, какое бы большое число вы там ни представляли. всегда существует еще больший.
Рисуем следующее вывод:
Предел не существует.
Снидми 4
Учитывайте лимит.
Мы не можем вставить значения x
меньше нуля, потому что квадратный корень из отрицательного числа не
существует.
В этих условиях можно говорить только о пределе справа, т. е.
когда x больше 0,
Следующие обозначения б/у:
+
знак показывает, что x приближается к 0 справа ( x > 0 ).
Калькулятор CASIO показывает следующий график:
График спускается из
оси у, а затем идет вправо по оси х. Ни x, ни f(x) не принимают
отрицательные значения. Для малых значений x значения y большие
а для больших значений x значения y малы. Очевидно, что f(x) стремится к
бесконечность при стремлении x к нулю, поэтому
не существует.
Пример 5
Находить если он существует.
Не очевидно, как мы можем
отменить это выражение, но тот факт, что значение x = 1, делает оба
числитель и ноль знаменателя говорят нам, что факторизация возможна. Использование правила (a b)(a + b) = a 2 b 2 дает
следующий.
Использование правила (a b)(a + b) = a 2 b 2 дает
следующий.
Чтобы найти предел f(x), когда x стремится к a, есть три различные ситуации, которые могут возникнуть: 1. Вычисляем f(a) ( a подставляется в выражение вместо х). 2. Если числитель и Знаменатель f(x) равен нулю, когда x = a, тогда f(x) можно разложить на множители и упрощено путем отмены. Затем вычисляется f(a), если это возможно. 3. Если при х = а, знаменатель равен нулю, а числитель не ноль, тогда предел делает не существует. |
Пример 6
Рассмотрим следующий интервал
определенная функция: |
В этом примере предел f(x) поскольку x стремится к 1, не существует, поскольку это зависит от того, больше ли x или менее 1,
и
Говорят, что функция f(x) быть непрерывной в точке (a, f(a)), если она существует в интервале вокруг x = a и г. Обратно, если функция непрерывна, то она непрерывна во всех точка своего домена. |
Теперь мы рассмотрим пределы когда х стремится к + или бесконечность.
Это не проблема при рассмотрении полиномиальных функций. При стремлении x к бесконечности ( + или ) функция также стремится к бесконечности. Будет ли это + или бесконечность, зависит на срок с наибольшей силой. Ни логарифм функции, экспоненциальные функции или функции квадратного корня представляют любые проблема.
Другое дело однако с рациональными функциями (функции в виде f(x)/g(x)).
При рассмотрении нам нужно посмотреть, увеличивается ли числитель или знаменатель быстрее.
Если числитель f(x),
увеличивается быстрее, когда x стремится к бесконечности, то предела не существует, но
стремится к + или бесконечности.
Однако, если знаменатель g(x) увеличивается больше быстро, то предел, вероятно, будет стремиться к определенному значению.
Пример 7
Теперь давайте посмотрим на некоторые примеры, когда x стремится к бесконечности.
а)
Здесь знаменатель стремится к бесконечности, а числитель
не меняется. Когда мы делим на число, которое становится все больше и больше,
результат становится меньше и
меньшее стремится к нулю. Так что предел равен нулю.
б)
Здесь знаменатель
увеличивается быстрее, чем числитель, поэтому дробь становится меньше и
меньшее стремится к нулю.
в)
Это обратная сторона б).
Числитель увеличивается быстрее, и результат становится все больше и больше.
стремящуюся к бесконечности. Мы говорим, что предела не существует.
(Примечание. В некоторых текстах говорится, что пределом является бесконечность).
г)
В этом примере
знаменатель имеет большую степень, чем числитель, и поэтому увеличивается больше
быстро. Дробь стремится к нулю, поэтому
Равен 0, если g(x) увеличивается быстрее, чем f(x) . Это происходит, если для Например, мощность знаменателя g(x) больше мощности числителя f(x). |
Пример 8
Находить .
Что происходит, когда числитель и знаменатель — многочлены одной степени? Оба увеличивают одинаково быстро. Если мы разделим все на наивысшую степень x (в этот случай x 2 ) мы можем найти решение.
При стремлении x к бесконечности два
членов в числителе, x/x 2 и 2/x 2 стремятся к нулю при выходе
у нас 1 в числителе и 2 в знаменателе. Таким образом, результат:
Таким образом, результат:
Задачи с пределами рациональных функций, где числитель и знаменатель — полиномы одной степени, можно решается делением всего на наибольшую степень х. |
Попрактикуйтесь в этих методах, затем тест 1 на ограничения.
шт. не забудьте заполнить свой контрольный список.
Ограничения
Ограничения
Пример
Рассмотрим функцию
х 2 — 1
f(x) =
х 2 +2х — 3
Если мы подставим 1, мы получим 0/0 который не определен. Как выглядит эта функция около х = 1?
Мы можем построить следующую таблицу:
| х | . 9 9 | .99 | 1.1 | 1.01 | 1.001 |
| ф(х) | .487 | .499 | .512 | .501 | .5001 |
Мы можем видеть, что эта функция приближается к 0,5, когда x приближается к 1. Ниже приведен график этой функции.
Этот пример приводит нас к следующему определению
Определение предела Если f(x) становится сколь угодно близким к одному числу L по мере приближения x c с обеих сторон, затем |
Мы можем думать об определении предела как x -> c как о двух туристах, один идущий справа, а другой идущий слева. Если они будут идти к одному и тому же месту, тогда это место называется пределом.
Свойства пределов
Предположим, что
и что а является константой. затем
затем
А)
Б)
С)
Д)
Е)
Пример
Предположим, что
затем
Алгебра и пределы
При нахождении предела всегда сначала подставляйте число. Если вы получите определенное значение, то это и есть ответ. В противном случае вам, возможно, придется сделать алгебра, чтобы найти предел.
Пример:
lim как х -> 1 (х 2 — 1)/(х 2 +2x — 3)
= lim as x -> 1 (x — 1)(x + 1)/(x + 3)(x — 1)
= lim как х -> 1 (х + 1)/(х + 3) = 2/4 = 0,5
Найдите предел
Решение
Во-первых, обратите внимание: если мы подставим 1 вместо x, мы получим 0/0. Алгебра, которая будет работа факторинговая.
Теперь подключите 1, чтобы получить
2/4 = 1/2
Пример
Найдите предел
Решение
Опять же, если мы подключаемся, мы получаем 0/0. Какая алгебра подойдет для этого
проблема? Вспомните из основ алгебры, как рационализировать знаменатель.
Наша стратегия будет заключаться в рационализации числителя. Мы умножаем
числитель и знаменатель на сопряженный корень.
Какая алгебра подойдет для этого
проблема? Вспомните из основ алгебры, как рационализировать знаменатель.
Наша стратегия будет заключаться в рационализации числителя. Мы умножаем
числитель и знаменатель на сопряженный корень.
Теперь мы можем подставить 9 вместо х получить
1
1
=
4 +
4 8
Односторонние ограничители
Определим левый предел
как координата y кривой при движении точки слева.
Аналогично определим правый предел
как координата y кривой, когда точка движется слева.
Пример
Находить
Решение
График функции изображен ниже.
Прогуливаясь с левой стороны, значение y приближается к -1. Следовательно
предел -1. Обратите внимание, что без знака «-» предел
не существовало бы.
Мы говорим, что предел существует, если левый и правый пределы равны.
Неограниченные пределы
Пример
Находить
Решение
Подставив 2, мы получим 6/0, что не определено. Если мы подставим число слева от 2, например 1,99999, мы получаем очень большое отрицательное число. Мы говорят, что предел отрицательная бесконечность.
Назад на главную страницу исчисления
Назад к математике домашняя страница отдела
электронная почта Вопросы и предложения
Объяснение урока: Оценка пределов с использованием алгебраических методов
В этом пояснении мы узнаем, как использовать алгебраические методы, такие как факторизация, для оценки пределов.
Предел функции в точке описывает поведение функции вблизи заданной точки, а не значение функции в этой точке. Хотя это различие очень важно помнить, мы знаем, что во многих случаях предел функции фактически равен значению функции в точке. В таких случаях мы можем оценить предел, непосредственно подставив предельную точку в функцию.
Хотя это различие очень важно помнить, мы знаем, что во многих случаях предел функции фактически равен значению функции в точке. В таких случаях мы можем оценить предел, непосредственно подставив предельную точку в функцию.
Этот метод явно недействителен, если функция не определена в предельной точке. Другими словами, если предельная точка не принадлежит области определения функции, мы не можем вычислить предел прямой подстановкой. Мы по-прежнему можем использовать таблицу значений или график функции для оценки предела, но эти методы обычно требуют калькулятор для завершения и часто не дает нам полного представления о значении предела. В этом объяснении мы представим алгебраический метод вычисления некоторых пределы без использования калькуляторов.
Во всех пределах, которые мы будем рассматривать в этом объяснении, функции будут в виде частного, так что знаменатель равен нулю в предельной точке,
и, таким образом, предельная точка не будет лежать в области определения. Более конкретно, мы рассматриваем пределы вида
lim, где→𝑓(𝑥)𝑔(𝑥),𝑔(𝑎)=0.
Более конкретно, мы рассматриваем пределы вида
lim, где→𝑓(𝑥)𝑔(𝑥),𝑔(𝑎)=0.
Мы не можем найти такие пределы прямой подстановкой, так как подстановка предельной точки в частное приведет к тому, что в знаменателе будет ноль. Если числитель 𝑓(𝑥) не стремится к нулю вблизи предельной точки (т.е. lim→𝑓(𝑥)≠0), то можно сказать, что этого предела не существует. Это связано с тем, что частное будет становиться все больше и больше по размеру (абсолютное значение), если знаменатель приближается к нулю. а числитель — нет. Мы можем лучше понять это, рассмотрев частный случай, когда 𝑓(𝑥)=1𝑥 и 𝑎=0. Мы можем вычислить таблицу значений функции вблизи предельной точки 𝑥=0.
| 𝑥 | −1 | −0.5 | −0.1 | −0.01 | 0 | 0.01 | 0.1 | 0.5 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 𝑓(𝑥) | −1 | -2 | -10 | -100 | Не определено | 100 | 10 | 2 | 1 |
Из этой таблицы мы четко видим, что 𝑓 (𝑥) не приближается к значению. когда 𝑥 приближается к 0. Фактически, абсолютное значение 𝑓(𝑥) становится больше, когда 𝑥 приближается к 0. Таким образом, мы можем заключить, что
lim→1𝑥 не существует. Мы также можем наблюдать это на графике 𝑦=1𝑥.
когда 𝑥 приближается к 0. Фактически, абсолютное значение 𝑓(𝑥) становится больше, когда 𝑥 приближается к 0. Таким образом, мы можем заключить, что
lim→1𝑥 не существует. Мы также можем наблюдать это на графике 𝑦=1𝑥.
На приведенном выше графике видно, что абсолютное значение функции 1𝑥 неограниченно возрастает по мере приближения 𝑥 к 0. В общем, это то, что мы ожидаем от предела формы lim→𝑓(𝑥)𝑔( 𝑥) где знаменатель 𝑔(𝑥) приближается к 0, когда 𝑥 приближается к 𝑎, а числитель — нет.
Свойство: предел частного
Предел lim→𝑓(𝑥)𝑔(𝑥) не существует, если выполняются оба следующих условия:
Следовательно, при оценке предела частного мы должны сначала проверить, стремится ли знаменатель к нулю. Если это так, то мы должны проверить,
числитель также стремится к нулю. Если это не так, мы знаем, что предела не существует, обозначаемого DNE. Мы можем запомнить это, написав символически
10=.DNE
Мы можем запомнить это, написав символически
10=.DNE
Здесь числитель 1 символизирует любую ненулевую константу, и это не означает, что числитель должен быть равен 1.
Это оставляет нам другой случай, когда числитель также стремится к нулю. Формально это приводит к случаю 00, которая называется неопределенной формой.
Определение: неопределенная форма
Неопределенная форма — это алгебраическое выражение чисел или бесконечности, поведение которого невозможно определить в текущей форме. Например, выражение 00 — неопределенная форма.
Неопределенные формы часто встречаются при оценке пределов, но очень важно иметь в виду, что неопределенная форма никогда не является окончательным ответом . Вместо этого неопределенные формы означают, что мы не можем определить значение предела, используя этот конкретный метод. В частности, если 𝑓(𝑥)
и 𝑔(𝑥) оба стремятся к нулю, когда 𝑥 приближается к 𝑎, мы можем сказать, что предел
lim→𝑓(𝑥)𝑔(𝑥) принимает неопределенный вид 00. Но это неверно
заявить, что этот предел равен 00. Нельзя переоценить, что неопределенная форма равна , а не — ответ на проблему предела. Это также не означает, что предела не существует или что мы не можем его найти. Когда мы замечаем, что наш предел принимает неопределенный вид, нам нужно
найти другой метод, чтобы найти этот предел.
Но это неверно
заявить, что этот предел равен 00. Нельзя переоценить, что неопределенная форма равна , а не — ответ на проблему предела. Это также не означает, что предела не существует или что мы не можем его найти. Когда мы замечаем, что наш предел принимает неопределенный вид, нам нужно
найти другой метод, чтобы найти этот предел.
В нашем первом примере мы рассмотрим предел, который принимает неопределенную форму 00.
Пример 1. Нахождение предела рациональной функции в точке
Найти lim→3𝑥−18𝑥+24𝑥−16 .
Ответить
В этом примере нам нужно найти предел рациональной функции. Мы знаем, что можем найти предел рациональной функции прямой подстановкой только если знаменатель не равен нулю в предельной точке. Мы можем проверить это условие, подставив предельную точку 𝑥=4 в знаменатель 𝑥−16: 4−16=0.
Поскольку знаменатель равен нулю в предельной точке, мы не можем найти этот предел прямой подстановкой.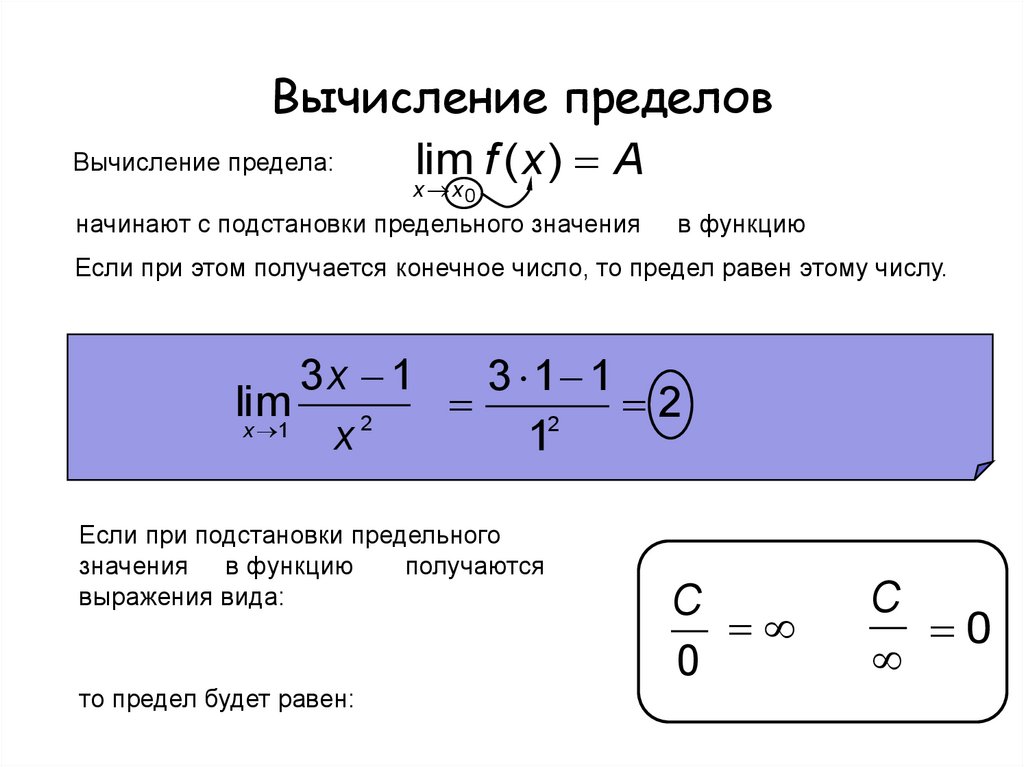 В таком случае мы знаем, что предела не существует
если числитель также не равен нулю. Мы можем проверить это условие, подставив 𝑥=4 в числитель:
3×4−18×4+24=48−72+24=0,
В таком случае мы знаем, что предела не существует
если числитель также не равен нулю. Мы можем проверить это условие, подставив 𝑥=4 в числитель:
3×4−18×4+24=48−72+24=0,
Это означает, что наше частное принимает форму 00, когда мы подставляем предельную точку. Напомним, что 00 является неопределенной формой, и это не является допустимым ответом на какую-либо предельную проблему. Это говорит нам о том, что мы должны использовать другой метод для оценки этого предела.
Мы отметили, что и числитель, и знаменатель равны нулю при 𝑥=4. Напомним теорему об остатках, которая утверждает, что если
𝑓 — многочлен с 𝑓(𝑎)=0, тогда (𝑥−𝑎) — множитель
𝑓(𝑥). В этом случае теорема об остатках говорит нам, что (𝑥−4) является фактором многочленов
в числителе и знаменателе частного. Это означает, что после факторизации обоих многочленов мы можем исключить этот множитель из частного. Отмена
этот множитель из двух многочленов означает, что если это не повторяющийся множитель одного из многочленов, результирующие многочлены больше не будут иметь 4
как их корень. Это означает, что подстановка 𝑥=4 в упрощенное частное не даст нуля в знаменателе, следовательно, подтверждается
метод прямой замены в пределе.
Это означает, что подстановка 𝑥=4 в упрощенное частное не даст нуля в знаменателе, следовательно, подтверждается
метод прямой замены в пределе.
Давайте разработаем это упрощение, сначала разложив числитель на множители. Заметив общий множитель 3 в числителе, можно написать 3𝑥−18𝑥+24=3𝑥−6𝑥+8=3(𝑥−4)(𝑥−2).
Чтобы разложить знаменатель, вспомним формулу разности квадратов, 𝑎−𝑏=(𝑎 −𝑏)(𝑎+𝑏). Используя эту формулу, мы можем написать 𝑥−16=𝑥−4=(𝑥−4)(𝑥+4).
Следовательно, мы можем записать частное как 3𝑥−18𝑥+24𝑥−16=3(𝑥−4)(𝑥−2)(𝑥−4)(𝑥+4).
Мы видим, что множитель (𝑥−4) является общим между обоими числителями и знаменатель этого частного. Отменив этот общий фактор, мы можем записать эту функцию как 3(𝑥−2)𝑥+4.
Обратите внимание, что эта новая функция имеет то же значение, что и исходная рациональная функция, за исключением точки 𝑥=4, где исходная функция не определена. Поскольку предел функции касается только значения функции вблизи предельной точки, мы знаем, что эта функция имеет тот же предел при 𝑥=4. как исходная рациональная функция. Другими словами,
limlim→→3𝑥−18𝑥+24𝑥−16=3(𝑥−2)𝑥+4.
как исходная рациональная функция. Другими словами,
limlim→→3𝑥−18𝑥+24𝑥−16=3(𝑥−2)𝑥+4.
Предел в правой части приведенного выше уравнения — это предел рациональной функции, знаменатель которой не равен нулю в предельной точке. Следовательно, мы можем решить этот предел прямой подстановкой: lim→3(𝑥−2)𝑥+4=3(4−2)4+4=68=34.
Отсюда имеем lim→3𝑥−18𝑥+24𝑥−16=34.
В предыдущем примере мы нашли предел функции в неопределенной форме 00. Хотя исходный предел был в неопределенной форме форму, мы смогли алгебраически упростить данную функцию, а затем использовать прямую замену, чтобы решить проблему. Основная идея алгебраического метода решить такой предел, чтобы упростить это частное с помощью алгебраических манипуляций с другим выражением, где мы сможем использовать метод прямой подстановки.
Когда мы упрощаем рациональную функцию, сокращая общий множитель в числителе и знаменателе, результирующая функция обычно не идентична исходной. В частности, область определения результирующего выражения часто больше на одно число, не принадлежащее области определения исходной функции. Увеличенный домен
в упрощенной функции это то, что позволяет использовать прямую замену для оценки предела.
В частности, область определения результирующего выражения часто больше на одно число, не принадлежащее области определения исходной функции. Увеличенный домен
в упрощенной функции это то, что позволяет использовать прямую замену для оценки предела.
На графике исходной функции эта предельная точка представлена незакрашенным кружком, что указывает на то, что функция в этой точке не определена. С другой стороны, график упрощенной функции идентичен графику исходной функции, за исключением того, что в нем нет пустого отверстия. Эту разницу мы можем увидеть на графиках. исходной и упрощенной функций из предыдущего примера.
Из графика видно, что исходная функция не определена при 𝑥=4, а упрощенная функция там определена. В противном случае,
два графика идентичны. Поскольку предел функции не касается значения функции в предельной точке, эта разница не влияет на предел. Следовательно, предел исходной функции можно получить, найдя предел упрощенной функции, которая может быть получена прямой подстановкой.
Свойство: пределы функций
Пусть 𝑓(𝑥) и 𝑔(𝑥) — функции, удовлетворяющие 𝑓(𝑥)=𝑔(𝑥) для любого 𝑥≠𝑎. Затем, limlim→→𝑓(𝑥)=𝑔(𝑥).
Это свойство может оправдать большинство алгебраических шагов для оценки пределов. Мы предполагаем это свойство, когда будем использовать алгебраические методы для оценки пределов.
Как вычислить пределы рациональных функций в неопределенной форме 0/0
Пусть 𝑝(𝑥) и 𝑞(𝑥) полиномиальные функции, удовлетворяющие 𝑝(𝑎)=0 и 𝑞(𝑎)=0. Тогда, чтобы вычислить предел формы lim→𝑝(𝑥)𝑞(𝑥), нам нужно
- разложить как 𝑝(𝑥), так и 𝑞(𝑥),
- отменить все общие множители,
- приравнять предел упрощенного частного к исходному пределу,
- вычислить предел.
Если два полинома 𝑝(𝑥) и 𝑞(𝑥) удовлетворяют условиям 𝑝(𝑎)=0
и 𝑞(𝑎)=0, они оба должны иметь множители (𝑥−𝑎) по теореме об остатках. Затем эти факторы нейтрализуются и приводят к
упрощенная рациональная функция. Если на этом шаге исключаются все (𝑥−𝑎) множители из знаменателя, упрощенное частное будет
больше не имеют нулевого знаменателя в предельной точке 𝑥=𝑎. В этом случае мы можем оценить предел, используя прямую замену. С другой стороны,
если на этом шаге исключаются все (𝑥−𝑎) множители из числителя, но не из знаменателя, результирующий предел будет в
форма 10, что означает, что предел не существовал бы.
Если на этом шаге исключаются все (𝑥−𝑎) множители из знаменателя, упрощенное частное будет
больше не имеют нулевого знаменателя в предельной точке 𝑥=𝑎. В этом случае мы можем оценить предел, используя прямую замену. С другой стороны,
если на этом шаге исключаются все (𝑥−𝑎) множители из числителя, но не из знаменателя, результирующий предел будет в
форма 10, что означает, что предел не существовал бы.
Рассмотрим еще один пример вычисления предела рациональной функции в неопределенной форме 00 алгебраическими методами.
Пример 2. Нахождение предела рациональной функции в точке с помощью факторизации
Найти lim→𝑥+642𝑥+6𝑥−8.
Ответ
В этом примере нам нужно найти предел рациональной функции. Мы знаем, что можем найти предел рациональной функции только прямой подстановкой
если знаменатель не равен нулю в предельной точке. Начнем с изучения того, что происходит с данным частным, когда мы подставляем предел
точка 𝑥=−4:
(−4)+642×(−4)+6×(−4)−8=−64+6432−24−8=00.
Выражение 00 называется неопределенной формой. Мы знаем, что неопределенная форма никогда не является правильным ответом на предельную проблему. Напомним, что мы можем попытаться найти предел рациональной функции в неопределенной форме, выполнив следующие шаги:
- Фактор числителя и знаменателя.
- Отменить все общие множители.
- Приравнять предел упрощенного частного к исходному пределу.
- Оценить предел.
Мы можем начать с того, что отметим общий множитель 2 в знаменателе, что приводит к 2𝑥+6𝑥−8=2𝑥+3𝑥−4.
Мы можем разложить квадратное выражение в скобках, чтобы записать знаменатель в виде 2(𝑥−1)(𝑥+4).
Далее мы факторизуем числитель, который представляет собой кубический многочлен. Заметив, что 64=4, мы можем написать 𝑥+64=𝑥+4.
Это сумма двух кубов, которую можно разложить по формуле 𝑎+𝑏=(𝑎+𝑏)𝑎−𝑎𝑏+𝑏.
Применяя эту формулу к числителю с 𝑎=𝑥 и 𝑏=4, получаем
𝑥+4=(𝑥+4)𝑥−4𝑥+16.
Это приводит к limlim→→→𝑥+642𝑥+6𝑥−8=(𝑥+4)𝑥−4𝑥+162(𝑥−1)(𝑥+4)=𝑥 −4𝑥+162(𝑥−1).
Отмена множителя (𝑥+4) на последнем шаге имеет важное значение, поскольку этот множитель отвечает за создание обоих числитель и знаменатель равны нулю в предельной точке. Мы видим, что знаменатель упрощенного частного не равен нулю при предельная точка 𝑥=−4. Следовательно, мы можем найти этот предел прямой подстановкой: lim→𝑥−4𝑥+162(𝑥−1)=(−4)−4×(−4)+162(−4−1)=16+16+16−10=48−10= −245.
Итак, имеем lim→𝑥+642𝑥+6𝑥−8=−245.
В следующем примере мы можем применить алгебраический метод, чтобы найти предел рациональной функции в неопределенном образуют 00 под квадратным корнем.
Пример 3. Нахождение предела композиции рациональных и корневых функций в точке
Найти lim→𝑥+18𝑥−19𝑥−𝑥.
Ответ
В этом примере нам нужно найти предел функции, которая является композицией функции извлечения квадратного корня и рациональной функции. Мы знаем, что можем найти
предел функции, являющейся композицией рациональной функции и функции квадратного корня прямой подстановкой, если предельная точка принадлежит области определения
функции. Чтобы число принадлежало области определения такой функции, мы должны убедиться, что знаменатель рациональной функции не равен нулю
в этом числе и что выражение под квадратным корнем неотрицательно в этом числе. Короче говоря, если мы можем вычислить значение функции в точке
заданный номер, то этот номер принадлежит домену.
Мы знаем, что можем найти
предел функции, являющейся композицией рациональной функции и функции квадратного корня прямой подстановкой, если предельная точка принадлежит области определения
функции. Чтобы число принадлежало области определения такой функции, мы должны убедиться, что знаменатель рациональной функции не равен нулю
в этом числе и что выражение под квадратным корнем неотрицательно в этом числе. Короче говоря, если мы можем вычислить значение функции в точке
заданный номер, то этот номер принадлежит домену.
Начнем с изучения того, что происходит с данной функцией, когда мы подставляем предельную точку 𝑥=1: 1+18×1−191−1=00.
Выражение 00 называется неопределенной формой. Мы знаем, что неопределенная форма никогда не является правильным ответом на предельную проблему. Напомним, что мы можем попытаться найти предел рациональной функции в неопределенной форме, выполнив следующие шаги:
- Фактор числителя и знаменателя.

- Отменить все общие множители.
- Приравнять предел упрощенного частного к исходному пределу.
- Оценить предел.
Хотя функция в нашем пределе не является строго рациональной функцией, такой же шаг упрощения в рациональной функции под квадратным корнем может быть используется для нахождения предела.
Факторизация числителя частного, 𝑥+18𝑥−19=(𝑥−1)(𝑥+19).
Знаменатель разлагается как 𝑥−𝑥=𝑥(𝑥−1).
Тогда мы можем упростить лимлим→→→𝑥+18𝑥−19𝑥−𝑥=(𝑥−1)(𝑥+19)𝑥(𝑥−1)=𝑥+19𝑥.
Отмена множителя (𝑥−1) на последнем шаге важна, потому что этот множитель отвечает за то, что числитель
а знаменатель равен нулю в предельной точке. Мы видим, что знаменатель упрощенной рациональной функции под квадратным корнем больше не равен
к нулю в предельной точке 𝑥=1. Кроме того, частное под квадратным корнем принимает положительное значение в предельной точке. Это означает, что
𝑥=1 находится в области определения этой функции, которая является композицией функции квадратного корня и рациональной функции. Мы знаем, что в таких случаях
мы можем вычислить предел прямой подстановкой. Это ведет к
лим→𝑥+19𝑥=1+191=√20=2√5.
Мы знаем, что в таких случаях
мы можем вычислить предел прямой подстановкой. Это ведет к
лим→𝑥+19𝑥=1+191=√20=2√5.
Следовательно, lim→𝑥+18𝑥−19𝑥−𝑥=2√5.
В предыдущих примерах мы нашли предел рациональной функции в неопределенной форме, разложив числитель и знаменатель функции на множители и упростив. Мы отметили, что когда предел рациональной функции при 𝑥=𝑎 приводит к неопределенной форме 00, всегда существует множитель (𝑥−𝑎) как в числителе, так и в знаменателе. Это означает, что мы всегда можем упростить эту рациональную функцию до тех пор, пока либо числитель или знаменатель (в большинстве случаев оба) отличен от нуля в предельной точке. В этот момент мы можем найти предел прямой подстановкой.
Однако этот процесс может быть более сложным, если мы сталкиваемся с функцией, которую трудно вычислить. Спасительной благодатью в таких ситуациях является знание того, что
быть множителем вида (𝑥−𝑎) как в числителе, так и в знаменателе. Зная это, мы можем найти факторизованную форму
многочлен как (𝑥−𝑎)𝑝(𝑥) для некоторого другого многочлена 𝑝(𝑥). Этот процесс выполняется с использованием полиномиального длинного деления,
как показано в следующем примере.
Зная это, мы можем найти факторизованную форму
многочлен как (𝑥−𝑎)𝑝(𝑥) для некоторого другого многочлена 𝑝(𝑥). Этот процесс выполняется с использованием полиномиального длинного деления,
как показано в следующем примере.
Пример 4. Нахождение предела рациональной функции в точке
Найти lim→𝑥−493𝑥+24𝑥+13𝑥−56.
Ответ
В этом примере нам нужно найти предел рациональной функции. Мы знаем, что можем найти предел рациональной функции только прямой подстановкой если знаменатель не равен нулю в предельной точке. Начнем с изучения того, что происходит с данным частным, когда мы подставляем предел точка 𝑥=−7: (−7)−493×(−7)+24×(−7)+13×(−7)−56=49−49−1029+1176−91−56=00.
Выражение 00 называется неопределенной формой. Мы знаем, что неопределенная форма никогда не является правильным ответом на предельную проблему. Напомним, что мы можем попытаться найти предел рациональной функции в неопределенной форме, выполнив следующие шаги:0008
- Разложить на множители числитель и знаменатель.

- Отменить все общие множители.
- Приравнять предел упрощенного частного к исходному пределу.
- Оценить предел.
В частности, мы знаем, что и числитель, и знаменатель содержат множитель (𝑥+7), так как эти полиномы равны к нулю при 𝑥=−7. Начнем с факторизации числителя. Мы знаем, что 49=7, поэтому мы можем использовать формулу разности квадратов, 𝑎−𝑏=(𝑎+𝑏)(𝑎−𝑏), чтобы разложить числитель на множители: 𝑥−49=(𝑥+7)(𝑥−7).
В то время как числитель разложить на множители просто, знаменатель сложнее. Чтобы найти факторизацию знаменателя в виде (𝑥+7)𝑝(𝑥), мы будем использовать полиномиальное длинное деление. Деление знаменателя на 𝑥+7,
Это приводит к факторизации знаменателя (𝑥+7)3𝑥+3𝑥−8.
Это приводит к limlim→→→𝑥−493𝑥+24𝑥+13𝑥−56=(𝑥+7)(𝑥−7)(𝑥+7)(3𝑥+3𝑥−8) =𝑥−73𝑥+3𝑥−8.
Отмена множителя (𝑥+7) на последнем шаге важна, потому что этот множитель отвечает за то, что числитель
а знаменатель равен нулю в предельной точке. Если знаменатель упрощенного частного не равен нулю в предельной точке 𝑥=−7,
мы можем найти этот предел прямой подстановкой:
lim→𝑥−73𝑥+3𝑥−8=−7−73(−7)+3×(−7)−8=−14147−21−8=−14118=−759.
Если знаменатель упрощенного частного не равен нулю в предельной точке 𝑥=−7,
мы можем найти этот предел прямой подстановкой:
lim→𝑥−73𝑥+3𝑥−8=−7−73(−7)+3×(−7)−8=−14147−21−8=−14118=−759.
Следовательно, lim→𝑥−493𝑥+24𝑥+13𝑥−56=−759.
До сих пор мы научились вычислять предел рациональной функции в неопределенной форме 00 с помощью алгебраических методов. Теперь обратим внимание на пределы в неопределенной форме, где числитель или знаменатель имеют квадратные корни. Для рациональных функций мы могли бы решить задачу неопределенной формы, разложив числитель и знаменатель на множители и удалив общий множитель. В общем случае это невозможно для частных, которые не рациональные функции, так как трудно разложить на множители выражения, не являющиеся полиномами.
В случае, когда частное содержит выражения квадратного корня, полезен трюк с использованием сопряженного выражения. Пара выражений
√𝑎+√𝑏 и √𝑎−√𝑏 называются сопряженной парой. Используя формулу разности квадратов, мы можем написать
√𝑎+√𝑏√𝑎−√𝑏=𝑎−𝑏.
Используя формулу разности квадратов, мы можем написать
√𝑎+√𝑏√𝑎−√𝑏=𝑎−𝑏.
Этот метод можно использовать для удаления квадратных корней из выражения. Таким образом, чтобы упростить частное с квадратными корнями, мы можем умножить числитель и знаменатель частного сопряженным выражением сначала удалить квадратные корни.
Практическое руководство. Вычисление пределов частных, содержащих квадратные корни
Пусть 𝑓(𝑥) — частное функций, содержащих квадратные корни. Чтобы оценить предел 𝑓(𝑥) в неопределенной форме 00 надо
- умножить числитель и знаменатель частного на сопряженное выражение,
- упростить и сократить все общие множители,
- приравнять предел упрощенного частного к исходному пределу,
- оценить предел.
В следующем примере мы будем использовать этот метод для оценки предела функции, содержащей квадратные корни.
Пример 5. Нахождение предела разности степеней с участием корней
Определить lim→√𝑥+12−4𝑥−4.
Ответ
В этом примере нам нужно найти предел функции, которая является результатом суммы, разности, частного и композиции функции квадратного корня и полиномиальные функции. Мы знаем, что можно найти предел таких функций прямой подстановкой, если предельная точка принадлежит области определения функции. Чтобы число принадлежало области определения такой функции, мы должны убедиться, что знаменатель функции не равен нулю у этого числа и что выражение под квадратным корнем неотрицательно при этом числе. Короче говоря, если мы можем вычислить значение функции по заданному числу, то номер принадлежит домену.
Начнем с изучения того, что происходит с данной функцией, когда мы подставляем предельную точку 𝑥=4: √4+12−44−4=√16−40=00.
Выражение 00 называется неопределенной формой. Мы знаем, что неопределенная форма никогда не является правильным ответом на предельную проблему. Напомним, что мы можем упростить частное выражение, включающее квадратные корни, сначала умножив числитель и знаменатель частного на сопряженное выражение. В данной функции квадратный корень стоит в числителе: √𝑥+12−4. Для выражения вида
√𝑎−√𝑏, сопряженное выражение равно √𝑎+√𝑏. Мы знаем, что умножение на сопряженные числа может
удалить квадратные корни с помощью
√𝑎+√𝑏√𝑎−√𝑏=𝑎−𝑏.
В данной функции квадратный корень стоит в числителе: √𝑥+12−4. Для выражения вида
√𝑎−√𝑏, сопряженное выражение равно √𝑎+√𝑏. Мы знаем, что умножение на сопряженные числа может
удалить квадратные корни с помощью
√𝑎+√𝑏√𝑎−√𝑏=𝑎−𝑏.
Мы можем написать √𝑥+12−4=√𝑥+12−√16, что приводит к сопряженному выражению √𝑥+12+√16. Мы можем умножить верх и низ этого частного на это выражение, чтобы получить √𝑥+12−4𝑥−4×√𝑥+12+√16√𝑥+12+√16=(𝑥+12)−16(𝑥−4)√𝑥+12+4=𝑥−4(𝑥 −4)√𝑥+12+4=1√𝑥+12+4.
Отмена множителя (𝑥−4) на последнем шаге важна, потому что этот множитель числитель и знаменатель равны нулю в предельной точке. Мы можем видеть, что знаменатель упрощенной рациональной функции под квадратным корнем перестает быть равным нулю в предельной точке 𝑥=4. Мы можем написать limlim→→√𝑥+12−4𝑥−4=1√𝑥+12+4.
Мы видим, что знаменатель полученной функции не равен нулю в предельной точке 𝑥=4, поэтому мы можем оценить это
ограничить прямой заменой:
lim→1√𝑥+12+4=1√4+12+4=18.
Это приводит к lim→√𝑥+12−4𝑥−4=18.
В следующем примере мы рассмотрим предел частного, где и числитель, и знаменатель содержат выражения квадратного корня.
Пример 6. Нахождение предела комбинации корневых функций в точке с использованием рационализации
Найти lim→√𝑥−1−2√𝑥−4−1.
Ответ
В этом примере нам нужно найти предел функции, которая является результатом разности, частного и композиции функции извлечения квадратного корня и полиномиальные функции. Мы знаем, что можем найти предел такой функции прямой подстановкой, если предельная точка принадлежит области определения функции. Чтобы число принадлежало области определения такой функции, мы должны убедиться, что знаменатель функции не равен нулю при этом числе и что выражение под квадратным корнем неотрицательно при этом числе. Короче говоря, если мы можем вычислить значение функции по заданному числу, то номер принадлежит домену.
Начнем с изучения того, что происходит с данной функцией, когда мы подставляем предельную точку 𝑥=5:
√5−1−2√5−4−1=√4−2√1−1=00.
Выражение 00 называется неопределенной формой. Мы знаем, что неопределенная форма никогда не является правильным ответом на предельную проблему. Напомним, что мы можем упростить частное выражение, включающее квадратные корни, сначала умножив числитель и знаменатель частного на сопряженное выражение. В данном частном и числитель, и знаменатель содержат два выражения квадратного корня. Для выражения вида √𝑎−√𝑏, сопряженное выражение √𝑎+√𝑏. Мы знаем, что умножение на сопряженные числа может удалить квадратные корни на √𝑎+√𝑏√𝑎−√𝑏=𝑎−𝑏.
Это означает, что сопряжение √𝑥−1−2 равно √𝑥−1+2 и что сопряжение √𝑥−4−1 равно √𝑥−4+1. Нам нужно умножить числитель и знаменатель этого частного на оба этих множителя: √𝑥−1−2√𝑥−4−1×√𝑥−1+2√𝑥−4+1√𝑥−1+2√𝑥−4+1=√𝑥− 1−2√𝑥−1+2√𝑥−4−1√𝑥−4+1×√𝑥−4+1√𝑥−1+2=(𝑥−1)−4( 𝑥−4)−1×√𝑥−4+1√𝑥−1+2=𝑥−5𝑥−5×√𝑥−4+1√𝑥−1+2=√𝑥−4+1√𝑥−1+ 2.
Отмена множителя (𝑥−5) на последнем шаге важна, потому что этот множитель отвечает за создание обоих
числитель и знаменатель равны нулю в предельной точке. Мы можем видеть, что знаменатель упрощенной рациональной функции под квадратным корнем
перестает быть равным нулю в предельной точке 𝑥=5. Мы можем написать
limlim→→√𝑥−1−2√𝑥−4−1=√𝑥−4+1√𝑥−1+2.
Мы можем видеть, что знаменатель упрощенной рациональной функции под квадратным корнем
перестает быть равным нулю в предельной точке 𝑥=5. Мы можем написать
limlim→→√𝑥−1−2√𝑥−4−1=√𝑥−4+1√𝑥−1+2.
Мы видим, что знаменатель полученной функции не равен нулю в предельной точке 𝑥=5, поэтому мы можем оценить этот предел прямой заменой: lim→√𝑥−4+1√𝑥−1+2=√5−4+1√5−1+2=√1+1√4+2=24=12.
Это приводит к lim→√𝑥−4+1√𝑥−1+2=12.
Другой вид частного в неопределенной форме содержит разность частных. Если предел в неопределенной форме содержит разность или сумму частных, то нам нужно сначала упростить выражение, найдя общий знаменатель.
Практическое руководство. Вычисление пределов с учетом разности частных
Пусть 𝑓(𝑥) — функция, выражение которой включает сумму или разность частных. Если предел 𝑓(𝑥) принимает неопределенный вид, нам нужно
- найти сумму или разность частных путем нахождения общего знаменателя,
- упростить и сократить все общие множители,
- приравнять предел упрощенного частного к исходному пределу,
- оценить предел.

В нашем последнем примере мы найдем предел функции, включающей разность частных, принимающую неопределенную форму.
Пример 7. Нахождение предела комбинации рациональных и полиномиальных функций в точке
Найти lim→−𝑥.
Ответ
В этом примере нам нужно найти предел частного, числитель которого представляет собой разность меньших частных. Функция, для которой мы берем предел, результат разности и частного рациональной функции, константы и многочлена. Мы знаем, что можем найти предел рациональной функции по формуле прямая подстановка только в том случае, если предельная точка принадлежит области определения функции. Мы знаем, что число принадлежит области определения функции, если мы можем вычислить значение функции по числу.
Начнем с изучения того, что происходит с данной функцией, когда мы подставляем предельную точку 𝑥=0: −0=00.
Выражение 00 называется неопределенной формой. Мы знаем, что неопределенная форма никогда не является правильным ответом на предельную проблему. Напомним, что мы можем оценить предел, включающий сумму или разность частных, найдя сумму или разность. Чтобы найти разность двух частных,
нам нужно найти общий знаменатель. Общий знаменатель между 𝑥+6 и 6 равен 6(𝑥+6). Следовательно, разница
частных в числителе данной функции есть
1𝑥+6−16=1𝑥+6×66−16×𝑥+6𝑥+6=66(𝑥+6)−𝑥+66(𝑥+6)=6−(𝑥+6)6(𝑥+6)= 6−𝑥−66(𝑥+6)=−𝑥6(𝑥+6).
Мы знаем, что неопределенная форма никогда не является правильным ответом на предельную проблему. Напомним, что мы можем оценить предел, включающий сумму или разность частных, найдя сумму или разность. Чтобы найти разность двух частных,
нам нужно найти общий знаменатель. Общий знаменатель между 𝑥+6 и 6 равен 6(𝑥+6). Следовательно, разница
частных в числителе данной функции есть
1𝑥+6−16=1𝑥+6×66−16×𝑥+6𝑥+6=66(𝑥+6)−𝑥+66(𝑥+6)=6−(𝑥+6)6(𝑥+6)= 6−𝑥−66(𝑥+6)=−𝑥6(𝑥+6).
Это упрощает числитель данного частного. Знаменатель данного частного равен 𝑥, что равносильно умножению числитель на 1𝑥. Следовательно, −𝑥=−𝑥6(𝑥+6)×1𝑥=−16(𝑥+6).
Отмена множителя 𝑥 на последнем шаге важна, потому что этот множитель отвечает за создание как числителя, так и
знаменатель равен нулю в предельной точке. Мы видим, что знаменатель упрощенной рациональной функции больше не равен
равен нулю в предельной точке 𝑥=0. Это означает
limlim→→−𝑥=−16(𝑥+6).
Поскольку знаменатель рациональной функции в пределе правой части этого уравнения не равен нулю, мы можем оценить это ограничить прямой заменой: lim→−16(𝑥+6)=−16(0+6)=−136.
Следовательно, lim→−𝑥=−136.
Давайте закончим повторением нескольких важных понятий из этого объяснения.
Ключевые моменты
- Говорят, что предел формы lim→𝑓(𝑥)𝑔(𝑥) находится в неопределенной форме 00, если и числитель, и знаменатель частного стремятся к нулю при 𝑥=𝑎. Неопределенная форма это никогда не является правильным ответом на проблему предела, но это означает, что нам нужно больше работать, чтобы оценить этот предел.
- Использование алгебраических методов для вычисления предела означает, что мы сначала упрощаем данное выражение до такой степени, что мы можем вычислить предел прямой подстановкой. Мы можем сделать это, используя свойство, что если 𝑓(𝑥)=𝑔(𝑥) для всех 𝑥≠𝑎, то
limlim→→𝑓(𝑥)=𝑔(𝑥).






 Однако ни одна из этих деталей не имеет отношения к структура уравнения. Это уравнение на самом деле имеет следующую структуру :
Однако ни одна из этих деталей не имеет отношения к структура уравнения. Это уравнение на самом деле имеет следующую структуру : И затем, как только мы это сделали, нам нужно будет разделить обе части уравнения на любой коэффициент, равный 9.0042 ч .
И затем, как только мы это сделали, нам нужно будет разделить обе части уравнения на любой коэффициент, равный 9.0042 ч .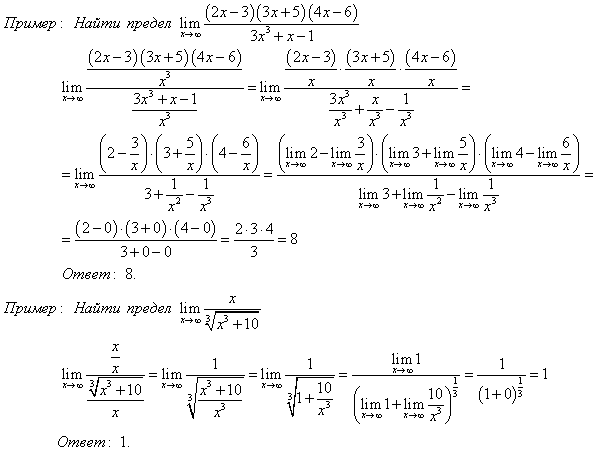 Таким образом, чтобы решить каждое из этих уравнений, нам просто нужно вычесть член, который не содержит ч из обеих частей уравнения (чтобы сократить его до нуля в правой части), а затем нам нужно будет разделить обе части на полный коэффициент ч (т.е. то, что умножается на h , каким бы запутанным и сложным он ни был).
Таким образом, чтобы решить каждое из этих уравнений, нам просто нужно вычесть член, который не содержит ч из обеих частей уравнения (чтобы сократить его до нуля в правой части), а затем нам нужно будет разделить обе части на полный коэффициент ч (т.е. то, что умножается на h , каким бы запутанным и сложным он ни был).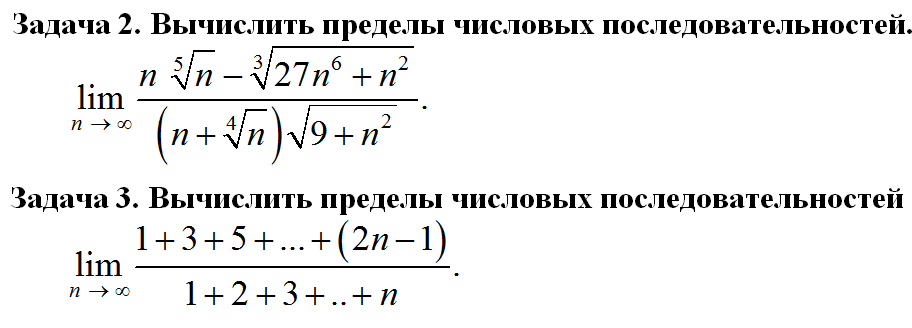 (Например, на графике ниже, когда c = -2.)
(Например, на графике ниже, когда c = -2.)  (Например, на графике ниже, когда c = 1.)
(Например, на графике ниже, когда c = 1.)  Это означает, что вокруг любого заданного значения x=c мы никогда не сможем найти интервал около c , где f(x) непрерывно (даже если мы допускаем, что f(x) является прерывистым при x=c ).
Это означает, что вокруг любого заданного значения x=c мы никогда не сможем найти интервал около c , где f(x) непрерывно (даже если мы допускаем, что f(x) является прерывистым при x=c ). В этом случае предела не существует.
В этом случае предела не существует.
 Если это верно для всех
значений x в области определения f(x), то мы говорим, что функция
непрерывный.
Если это верно для всех
значений x в области определения f(x), то мы говорим, что функция
непрерывный.


