Преобразуйте в многочлен:
(a-8)(a+8)-5a(6-a)=
(a-3)(a-2)-(a-4)²=
(b+2)(b-2)+(5b+4)²=
5(a+2)²-(5a²+29a)=
(5x-4)²-3x(5-x)=
(p+8)(p-3)+(p+7)²=
(a-x)²+(a+x)²=
(2ab-b²)+2(a-b)²=…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мирГеография
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Яне могу решить найти производную функции y=x^68cosx
Алгебра, 2020-10-06 20:24:49, Alenka341
Ответ
Ответ разместил: kuznecovamargo
Производная произведения
y = x^68 * cosx
y ‘ = (x^68)’ cosx + (cosx)’ x^68 =
= 68* x^67* cosx — x^68 * sinx =
= x^67* (68 cosx — x sinx)
Ответ
Ответ разместил: сел5
Ответ
Ответ разместил: romka1014
Используем формулу:
( u × v )’ = u’v + uv’ — производная произведения
У’ = ( х² × cosx ) ‘ = ( х² )’ × соsx + x² × ( cosx )’ = 2x × cosx — x² × sinx = x × ( 2cosx — xsinx )
y'( 0 ) = 0
ОТВЕТ: 0
Ответ
Ответ разместил: Trdfgg
. 2) =( sqrt(2)/2 + п/4*sqrt(2)/2)/(1\2) = 2* (sqrt(2)/2 + (п*sqrt(2)/2)/8) = 2(sqrt(2)/2 *(1+п)) = sqrt(2)/2 *(1+п)
2) =( sqrt(2)/2 + п/4*sqrt(2)/2)/(1\2) = 2* (sqrt(2)/2 + (п*sqrt(2)/2)/8) = 2(sqrt(2)/2 *(1+п)) = sqrt(2)/2 *(1+п)
Другие вопросы по: Алгебра
Відредагуйте речення: 1.мені подобаються фарби осіннього лісу. 2.такий вітер піднявся, що поступила пропозиція позакривати вікна й двері. 3.через пару днів їхні відношення покращат…
Опубликовано: 01.03.2019 04:10
Ответов: 1
Один из корней уравнения 5х в квадрате+bх+24=0 равен 8 .найдите другой корень и коэффициент b.(по теореме виета)…
Опубликовано: 02.03.2019 20:00
Ответов: 1
Звуко-буквеный разбор слова подхвачу…
Опубликовано: 03.03.2019 04:50
Ответов: 1
Разобрать слово по составу/ высокогорный/…
Опубликовано: 03.03.2019 10:50
Ответов: 2
4класс .на мельницу 58 меш. пшеницы и 38 меш. жита. пшеницы на 16 ц больше, чем жита. сколько отдельно килограммов жита и пшеницы завезено, если все мешки имели одинаковый вес?…
сколько отдельно килограммов жита и пшеницы завезено, если все мешки имели одинаковый вес?…
Опубликовано: 07.03.2019 16:30
Ответов: 1
Клиент банка внес 8000 р. на вклад с годовым доходом 5%. какая сумма окажется у него на счету через 2 года, если он никаких сумм со счета не снимал и дополнительных влажений не дел…
Опубликовано: 08.03.2019 02:30
Ответов: 1
Популярные вопросы
Надо сочинить стихотворение о зиме с рифм ….
Опубликовано: 01.03.2019 22:30
Ответов: 3
Собственная скорость лодки 6 км/ч. скорость течения реки 2 км/ч. какое расстояние проплывёт лодка за 2 часа, если будет плыть по течению? какое расстояние проплывёт лодка за 3 часа…
Опубликовано: 02.03.2019 01:10
Ответов: 3
Запишите основное уравнение мкт газа через абсолютную температуру…
Опубликовано: 03. 03.2019 01:50
03.2019 01:50
Ответов: 1
Методом электронного , определить коэффициенты в следующей схеме реакции: cuo+nh4=n2+cu+h3o…
Опубликовано: 03.03.2019 03:00
Ответов: 2
Определить длину звуковой волны с частотой 68 гц. скоростьзвука в воздухе 340 м/с. услышит ли человек этот звук?…
Опубликовано: 04.03.2019 06:00
Ответов: 3
На полке на 8 книг больше чем нга столе ,сколько всего книг на столе и на полке ? подчеркни предложение которым надо дополнить условие реши полученую на полке на 12 книг больше чем…
Опубликовано: 04.03.2019 09:00
Ответов: 3
1попытайтесь составить перечень предметов-символов, которые отражают культуру современных подростков. 2. проведите опрос среди одноклассников: «что нравится и не нравится в совреме…
Опубликовано: 04.03.2019 10:40
Ответов: 2
Напишите сочинение на тему»добрый человек в моём понимании» !. ..
..
Опубликовано: 04.03.2019 11:40
Ответов: 3
Примеры развивающихся стран. по какому признаку проводится их классификация, на какие группы они подразделяются…
Опубликовано: 07.03.2019 14:20
Ответов: 3
Вычислите количество вещества, которое составляют 42г. гидроксида бария. сколько ионов каждого вида будет содержать эта порция щелочи?…
Опубликовано: 07.03.2019 17:20
Ответов: 2
Больше вопросов по предмету: Алгебра Случайные вопросы
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | лог х | ||
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
КриссТал: Введение в математический анализ
КриссТал: Введение в математический анализ [Домашняя страница] [Введение в числа] [Отзывы читателей (математика)] [Язык] [Затмения] [Лондон] [Астрономия] [Математика] [Физика] [Химия] [Биология] [Футбол] [Телевидение] 11 [Телевидение] 11 1 [Другое] Рекламная ссылка Чтобы разместить здесь ссылку, свяжитесь с веб-мастером.  |
Введение
Исчисление — очень важный раздел математики. Это форма математики, применяемая к непрерывным графам (графам без пробелов). Исчисление имеет два аспекта:- Дифференцирование (нахождение производных функций)
- Интегрирование (нахождение неопределенных интегралов или вычисление определенных интегралов)
В этом эссе представлена Дифференциация .
Производная позволяет нам вычислить наклон или тангенс графика в любой точке P. Процесс, с помощью которого находится производная, называется дифференцированием 9. 0941 .
0941 .
График ниже представляет собой простую параболу, уравнение которой у = х 2 .
Производной присваивается символ
Это произносится как dy через d x или dy dx .
Производная — это функция, которая дает наклон (тангенс) графика в любой точке. Производная измеряет скорость изменения y по отношению к x . Он описывает в точных математических терминах, как меняется у при изменении х. Это понятие очень важно в науке.Можно показать, что если y = x 2 , то производная равна
Итак, для этой кривой, когда x = 1, наклон равен 2; наклон при x = 3 равен 6,
Производная y = x 3 равна dy/dx = 3x 2 .Для y = x 4 производная равна dy/dx = 4x 3 .
 Пример 1: Найдите наклон кривой y = x 3 в точках x = -1 и x = 2 при условии, что производная равна 3x 2 .
Пример 1: Найдите наклон кривой y = x 3 в точках x = -1 и x = 2 при условии, что производная равна 3x 2 . Производная этой кривой равна dy/dx = 3x 2 . Когда х = -1, dy/dx = 3; когда x = 2, dy/dx = 12.
В этом разделе я перечислю правила нахождения производных общих типов функций.
Константы и степени x
| Функция | Производная |
|---|---|
| у = а | dy/dx = 0 |
| y = ax n | dy/dx = anx n-1 |
| Эта формула работает для всех значений n (a и n — числа). | |
Производная числа равна нулю.
ax n — это функция, состоящая из числа (a), умноженного на x, возведенного в степень, n. Чтобы найти производную этой функции, умножьте число на степень (an) и уменьшите степень индекса на 1.
(i) у = 3 х 3 ; (ii) у = 1/х; (iii) у = 2√х.
Используя формулу для производной (dy/dx = anx n-1 ), мы можем показать, что (i) когда y = 3x 3 , dy/dx = 9x 2
(ii) когда y = 1/x , это можно записать как y = x -1 . Поэтому dy/dx = -x -2 = -1/(х 2 )
(iii) когда y = 2√x , это можно записать как y = 2x (1/2) .
Следовательно, dy/dx = x -(1/2) = 1/(√x)
Когда y = -2x 3 , dy/dx = -6x 2 . Для x = -2 dy/dx = -24.
 Покажите, что кривые y = 3x и y = 2 имеют постоянный наклон.
Покажите, что кривые y = 3x и y = 2 имеют постоянный наклон. y = 3x можно записать y = 3x 1 ; dy/dx = 3x 0 = 3 , что является константой. «Кривая», y = 3x, представляет собой прямую линию с наклоном 3. y = 2 можно записать как y = 2x 0 , dy/dx = 0 (еще одна константа). «Кривая» y = 2 представляет собой прямую линию, параллельную оси x (нулевой наклон).
Сложение и вычитание
Вот как различать функции, которые складываются или вычитаются.| Функция | Производная |
|---|---|
| y = u + v | dy/dx = du/dx + dv/dx |
| y = u — v | dy/dx = du/dx — dv/dx |
| В этих уравнениях u и v являются функциями от x. | |
Если две функции сложить вместе, их можно дифференцировать по отдельности и добавить производные. Если вычитаются две функции, их можно дифференцировать по отдельности и вычесть производные.
Если вычитаются две функции, их можно дифференцировать по отдельности и вычесть производные.
(i) Для функции y = 4x 2 + 2x + 3 производная равна dy/dx = 8x + 2 (ii) Для функции x 5 — 5/x производная равна dy/dx = 5x 4 + 5/x 2
Синус и косинус
Вот как найти производные синусов и косинусов.| Функция | Производная |
|---|---|
| y = aSin(u) | dy/dx = a(du/dx)Cos(u) |
| y = aCos(u) | dy/dx = -a(du/dx)Sin(u) |
| В этих уравнениях u является функцией x. (а — число). Значение u (или x) должно быть в радианах. | |
Производная синуса есть косинус. Умножьте полученный косинус на производную функции внутри исходного синуса. Производная косинуса минус синус. Умножьте полученный синус на производную функции внутри исходного косинуса.
Умножьте полученный косинус на производную функции внутри исходного синуса. Производная косинуса минус синус. Умножьте полученный синус на производную функции внутри исходного косинуса.
(i) y = Sin(x) ; dy/dx = Cos(x) (ii) y = 3Cos(2x) ; dy/dx = -6Sin(2x) (iii) y = Sin(x 2 ) ; dy/dx = 2xCos(x 2 ) (iv) y = x — Cos(x) ; у = 1 + Sin(x)
Товары
Продукты — это функции, перемноженные вместе.| Функция | Производная |
|---|---|
| y = uv | dy/dx = u (dv/dx) + v (du/dx) |
В этом уравнении u и v являются функциями x, умноженными вместе.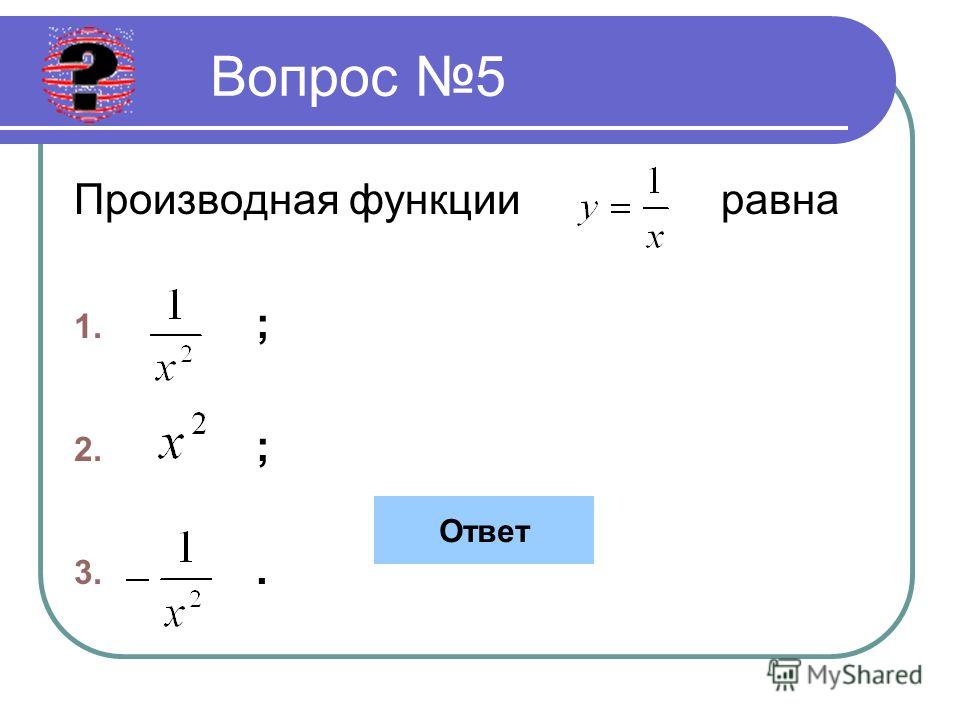 Это называется дифференциацией продуктов. | |
При перемножении двух функций производная находится следующим образом. Первая функция умножается на производную второй функции. Вторая функция умножается на производную первой функции. Эти два новых термина добавлены вместе.
Пример 7: Дифференцировать y = xSin(x) Это продукт (uv), поэтому мы используем приведенную выше формулу для дифференциации продуктов. dy/dx = xCos(x) + Sin(x) .
y = (x 2 + 1)√x 3 можно записать у = (х 2 + 1)х (3/2) Используя формулу дифференциации продуктов, dy/dx = (x 2 + 1)(3/2)x (1/2) + x (3/2) (2x)
= (3/2)(х 2 + 1)√х + 2х√х 3
Коэффициенты
Это пара разделенных функций.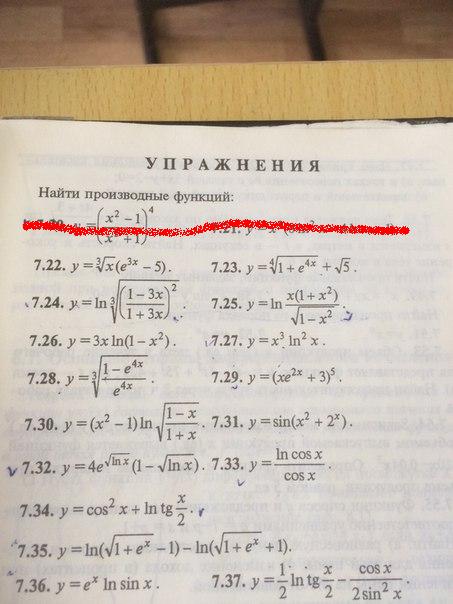
| Функция | Производная |
|---|---|
| y = u/v | (v(du/dx) — u(dv/dx)) / v 2 |
| В этом уравнении u и v являются функциями x в форме деления. Это называется дифференцированием частных. | |
Если разделить две функции, то производная находится следующим образом. Функция знаменателя (та, что под чертой) умножается на производную функции числителя (той, что над чертой). Функция числителя умножается на производную функции знаменателя. Эти два новых члена вычитаются вместе и делятся на квадрат исходного знаменателя.
Пример 9: Дифференцировать y = Tan(x). y = Tan(x) можно записать как y = Sin(x) / Cos(x) . Это частное. dy/dx = [Cos(x).Cos(x) — Sin(x).-Sin(x)] / Cos 2 (x) , (используя приведенную выше формулу частного) = [Cos(x). = 1 / Cos 2 (х)  Cos(x) + Sin(x).Sin(x)] / Cos 2 (x) =
[Cos 2 (x) + Sin 2 (x)] / Cos 2 (x)
Cos(x) + Sin(x).Sin(x)] / Cos 2 (x) =
[Cos 2 (x) + Sin 2 (x)] / Cos 2 (x)
Обратная величина косинуса называется секансом (Sec): 1 / Cos(x) = Sec(x). Следовательно, производная от y = Tan(x) равна
Используя формулу отношения к y = Sin(x) / (x 2 + 1) , dy/dx = [(x 2 + 1)Cos(x) — 2xSin(x)] / [(x 2 + 1) 2 ] Когда x = 0, dy/dx = (0 + 1 — 0) / (0 + 1) 2 = 1 / 1 = 1.
Неявное дифференцирование
Это позволяет нам различать функции, которые содержат y, смешанные с x.
| Функция | Производная |
|---|---|
| (Функция в y) | (Производная от y)(dy/dx) |
| Значение y в функции можно дифференцировать, если оно умножается на dy/dx. Это называется неявным дифференцированием. | |
Если в y есть функция, ее все равно можно дифференцировать. Дифференцируйте его, как и раньше, затем умножьте на dy/dx.
Пример 11: Найдите наклон окружности с помощью уравнения x 2 + у 2 = 4 в точке (0, -2). Это уравнение можно решить относительно y и затем продифференцировать. Но проще использовать неявное дифференцирование: 2x + 2y(dy/dx) = 0 . Перестановка дает: dy/dx = -2x/2y = — x/y В точке x = 0, y = -2, dy/dx = 0.

Неявное дифференцирование дает (dy/dx)Cos(y) = 2x . Преобразование в (dy/dx) = 2x/Cos(y) . Вспоминая, что Cos 2 (y) + Sin 2 (y) = 1, мы можем сказать, что Cos(y) = √[1 — Sin 2 (y)] . Замена дает (dy/dx) = 2x/√[1 — Sin 2 (y)]
= 2x/√[1 — x 4 ] .
Обратные тригонометрические функции
Выражение типа Sin(y) = x можно переписать как y = ArcSin(x) , где выражение ArcSin(x) называется обратным синусом от x. Обратные тригонометрические функции имеют свои правила дифференцирования.| Функция | Производная |
|---|---|
| y = ArcCos(x) | dy/dx = -1 / [1 — x 2 ] 1/2 |
| y = ArcSin(x) | dy/dx = 1 / [1 — x 2 ] 1/2 |
| y = ArcTan(x) | dy/dx = 1 / [1 + x 2 ] |
Углы (x) должны быть в радианах. | |
Производная определяется как dy/dx = -1/[1 — x 2 ] 1/2 . Помещение значения x = 0,5 дает dy/dx = -1/[1 — 0,5 2 ] 1/2 = -1,154.
Логарифмы
| Функция | Производное |
|---|---|
| Ln(u) | (1/u)(du/dx) |
| В этом уравнении u является функцией x. Ln — натуральный логарифм (по основанию e). | |
Производная натурального логарифма функции есть обратная величина функции, умноженная на производную функции.
Пример 14. Найдите dy/dx для уравнения y = Ln(x).Это просто определяется как dy/dx = 1/x .
Пример 15. Дифференцируем y = Ln(Cos(x)).
Использование приведенной выше формулы дает dy/dx = (1/Cos(x)).-Sin(x) = -Sin(x)/Cos(x) = -Tan(x)
Логарифмы можно использовать для дифференцирования более сложных функций:
Пример 16: Найдите dy/dx, когда 2 y = 3 Sin(x) . 2 y = 3 Sin(x) нельзя дифференцировать как есть. Мы можем взять логарифмы с обеих сторон: Ln(2 y ) = Ln(3 Sin(x) ) . Помня логарифмические правила индексов, мы можем переписать это как: yLn(2) = Sin(x)Ln(3) . Теперь это можно дифференцировать неявно: (dy/dx)Ln(2) = Ln(3)Cos(x) , что дает dy/dx = Ln(3)Cos(x)/Ln(2) .
Экспоненциальные функции
Эти функции содержат переменную в качестве индекса.| Функция | Производное |
|---|---|
| a u | (du/dx)a u Ln(a) |
| e u | (du/dx)e u |
В этом уравнении u — функция x, a — число. Число e является основанием натуральных логарифмов. | |
Производная числа, возведенная в степень функции, — это число, возведенное в степень функции, умноженное на производную функции, умноженную на логарифм числа. Если число равно e, производная функции просто умножается на e, возводимую в функцию.
Пример 17: Дифференцируйте следующую функцию: y = 2 3x . Использование приведенной выше формулы для y = 2 3x дает dy/dx = 3.Ln(2).2 3x . Пример 18: Дифференцируйте следующие функции: (i) y = e Sin(x) ,
(ii) у = е х . (i) Использование приведенной выше формулы для y = e Sin(x) дает dy/dx = Cos(x).e Sin(x) . (ii) Производная от y = e x равна dy/dx = e х .
Решение уравнений (метод приближений Ньютона)
Исчисление может быть использовано для получения приближенных решений уравнений. Это можно использовать для вычисления корней и для получения значений для уравнений, которые не могут быть легко решены алгебраически.Прежде чем дать формулу и метод, я определю следующие сокращенные термины:
| Символ | Значение | Примеры |
|---|---|---|
| Функция x | x 2 — 3x + 5 или Sin (3x) — 2x | |
| Значение функции x, f(x), когда x установлено равным | Если f(x) = x 2 — 3x + 5, f(0) = 5 (присвоить x значение 0 в f(x)), f(1) = 3 (присвоить x значение 1 в f(x) х)) | |
| Производная функции x, f(x) | Если f(x) = x 2 — 3x + 5, F(x) = 2x — 3 (производная) | |
| Значение производной функции x, F(x), при x = a | Если f(x) = x 2 — 3x + 5, F(x) = 2x — 3 и F(1) = -1 |
Формула Ньютона для приближений:
где f(x) — функция, которую нужно решить, а a — предположение о решении.
- Возьмите функцию и поставьте значение x = a. Это ф(а).
- Возьмите производную функции F(x) и поставьте значение x = a. Это Ф(а).
- Разделите два значения: f(a) / F(a).
- Вычтите это из предположения, a.
- Это даст приблизительное значение x для исходного уравнения, f(x) = 0.
Это значение x основано на значении, выбранном для a. Чем лучше исходное предположение для a, тем ближе будет x к правильному значению. Если догадка а не близка к правильному значению, эта формула может вообще не работать.
Затем новое значение x можно вставить в формулу, и процесс повторяется до тех пор, пока не будет достигнута желаемая точность. Чем ближе угаданное значение (а) к правильному значению, тем меньше раз нужно использовать формулу.
Подобный повторяющийся процесс называется итерацией .
Несколько примеров покажут, как работает формула.
Это означает решение уравнения x 2 = 10 , которое можно преобразовать в x 2 — 10 = 0 . Теперь это в желаемом формате, f(x) = 0 . Функция f(x) имеет значение: Таким образом, производная функции F(x): Глядя на уравнение («проверкой»), мы знаем, что решение этого уравнения близко к 3 (поскольку 3 2 = 9), поэтому мы устанавливаем значение первого предположения, a, равным 3. Мы можем затем запишите компоненты, необходимые для использования формулы Ньютона: Используя формулу Ньютона: x приблизительно = a — f(a) / F(a) = 3 — f(3) / F(3) = 3 — (-1/6) = 3 + 1/6 = 3,1666 Мы начали с того, что предположили, что x равно 3, и получили лучшее приближение (3,1666). Использование формулы Ньютона во второй раз дает: x приблизительно = a — f(a) / F(a) = 3,1666 — f(3,1666) / F(3,1666) = 3,1666 — (0,0273 / 6,3332) = 3,1622 Повторение процесса с новым значением дает третье значение x как 3,1623 с точностью до четырех знаков после запятой. После трехкратного использования формулы ответ выходит как x = 3,162 с точностью до трех знаков после запятой. Теперь мы можем использовать это новое значение в формуле, чтобы получить еще лучшее приближение.
Теперь мы можем использовать это новое значение в формуле, чтобы получить еще лучшее приближение.
Начнем с записи функции и ее производной: f(x) = x 3 — 5x + 3 и F(x) = 3x 2 — 5 Глядя на уравнение, мы видим, что f(1) = -1 и f(2) = 1, поэтому должно быть значение, близкое к 2, которое дает f(x) = 0. Используя формулу Ньютона: x приблизительно = a — f(a) / F(a) = 2 — f(2) / F(2) = 2 — (1/7) = 1,857 Это означает, что 1,857 является более близким приближением к значению x, чем 2. Теперь мы можем установить значение 1,857 и снова запустить процесс: Используя формулу Ньютона (второй раз): x приблизительно = a — f(a) / F(a) = 1,857 — f(1,857) / F(1,857) = 1,857 — (0,1187 / 5,3453) = 1,834 Используя это значение: Используя формулу Ньютона (третий раз): x приблизительно = a — f(a) / F(a) = 1,834 — f(1,834) / F(1,834) = 1,834 — (-0,0012 / 5,0906) = 1,834 Таким образом, к третьей итерации значение установилось (с точностью до трех знаков после запятой) до x = 1,834. Мы можем положить наше предполагаемое значение ( а) равно 2; фактическое значение x будет немного меньше.
Мы можем положить наше предполагаемое значение ( а) равно 2; фактическое значение x будет немного меньше.
Кубические уравнения обычно имеют три корня. Существует еще одно значение x, которое можно найти, установив для предположения (a) значение -2. Читателю будет приятно узнать, что я оставлю это в качестве упражнения.
Пример 20. Решите уравнение Cos(x) = x с точностью до трех знаков после запятой. Не существует простого метода алгебраического решения этого уравнения. Мы могли бы сделать это графически, построив графики y = Cos(x) и y = x на том же листе бумаги и найти значение x, где они пересекаются. Это показано на диаграмме ниже.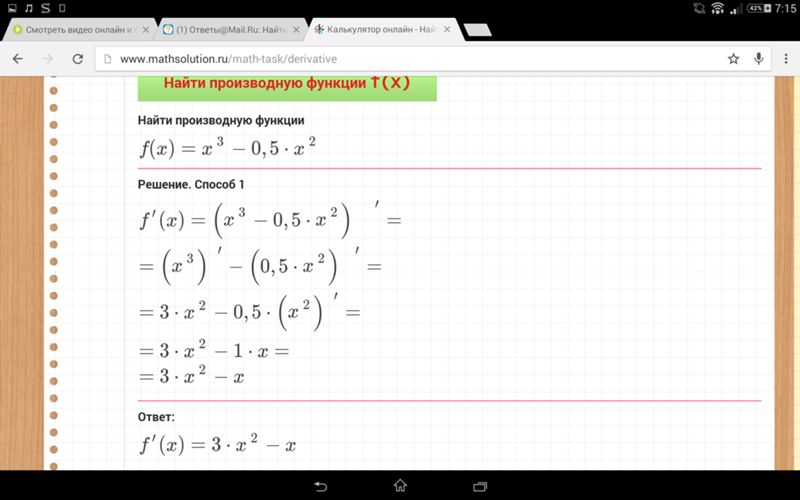 Из наших знаний о линейных графиках мы также знаем, что y = x — это прямая линия с положительным наклоном, проходящая через начало координат. Из этого анализа (и изучив приведенный выше график) мы можем сделать вывод, что две функции встретятся в одном месте вблизи значения x = 1. Следовательно, мы можем установить наше первое предположение (a) равным 1,9.0910 Напомним, что при дифференциации тригонометрических функций мы должны работать в радианах , а не в градусах. Итак, теперь мы можем оценить компоненты формулы Ньютона.
Из наших знаний о линейных графиках мы также знаем, что y = x — это прямая линия с положительным наклоном, проходящая через начало координат. Из этого анализа (и изучив приведенный выше график) мы можем сделать вывод, что две функции встретятся в одном месте вблизи значения x = 1. Следовательно, мы можем установить наше первое предположение (a) равным 1,9.0910 Напомним, что при дифференциации тригонометрических функций мы должны работать в радианах , а не в градусах. Итак, теперь мы можем оценить компоненты формулы Ньютона.
- а = 1
- f(a) = f(1) = Cos(1) — 1 = -0,4596
- F(a) = F(1) = -Sin(1) — 1 = -1,8414
Используя формулу Ньютона:
x приблизительно = a — f(a) / F(a) = 1 — f(1) / F(1) = 1 — (-0,4596 / -1,8414) = 0,7504
Используя это значение:
- а = 0,7504
- f(a) = f(0,7504) = Cos(0,7504) — 0,7504 = -0,0189
- F(a) = F(0,7504) = -Sin(0,7504) — 1 = -1,6819
Используя формулу Ньютона во второй раз:
x приблизительно = a — f(a) / F(a) = 0,7504 — f(0,7504) / F(0,7504) = 0,7504 — (-0,0189 / -1,6819) = 0,7391
Используя это новое значение:
- а = 0,7391
- f(a) = f(0,7391) = Cos(0,7391) — 0,7391 = -0,0000 (до четырех знаков после запятой)
- F(a) = F(0,7391) = -Sin(0,7391) — 1 = -1,6735
Из приведенного выше видно, что значение f(0,7391) составляет от нуля до четырех знаков после запятой, поэтому значение аппроксимации не изменится.
Следовательно, с точностью до трех знаков после запятой x = 0,739 после трех итераций.
Скорость изменения
Производная измеряет скорость изменения функций, которые являются непрерывными и переменными. Подобные функции широко используются в науке.Если существует связь между пройденным расстоянием (с) и временем (t), то производная расстояния по времени ds/dt дает скорость (v) в любой момент времени.
Пример 21: Частица движется так, что ее расстояние (в м) от фиксированной точки равноs = 2t 2 — 3t + 1, где t — время в секундах. Найдите его скорость через 4 с.
Скорость v определяется как ds/dt, поэтому мы дифференцируем приведенное выше уравнение относительно t: v = ds/dt = 4t — 3 . Когда t = 4 с, v = 13 м/с.
Если существует связь между скоростью частицы (v) и временем (t), то производная v по t dv/dt , дает ускорение (а) в любой момент времени.
Ускорение a определяется как dv/dt, поэтому мы дифференцируем приведенное выше уравнение относительно t: а = dv/dt = 4 . Ускорение постоянно и равно 4 м/с 2 .
Если есть связь между энергией (E) и во времени (t), тогда производная от E по t, dE/dt , дает в степени (P) в любое время.
Пример 23: Устройство использует энергию в зависимости от времени: E = t 3 , где E — энергия в джоулях, а t — время в секундах. Найдите мощность, потребляемую через 2 с. Мощность P определяется как dE/dt, поэтому мы дифференцируем приведенное выше уравнение относительно t: P = dE/dt = 3t 2 . Таким образом, мощность через 2 с составляет 12 Вт.
Таким образом, дифференцирование является одним из самых мощных инструментов в математике и физике.
© 2001, 2009 КрысТалВведение в алгебру и как решать простые уравнения. Графики — это способ показать, как выглядят алгебраические функции и отношения. Индекс и база. Определены логарифмы. Основание 10 и основание e. Использование логарифмов в вычислениях. Ряд для логарифмов. Прямоугольные треугольники, синусы, косинусы, тангенсы. Использование тригонометрических функций, рядов и формул. Больше алгебры. Определители и их использование при решении одновременных уравнений. Частичные дроби. Введение в ограничения, включая правило Лопиталя. 92, а также чему он равен. Это будет темой последнего раздела этого сообщения в блоге.
Но прежде чем мы углубимся в эту идею, давайте подытожим другое содержание лекций.
Лекция 4A Я начинаю лекцию 4A с решения задач с экспоненциальными уравнениями.
Общий смысл решения таких задач таков. Учитывая две точки данных
и , ищем числа и такие, что график показательной функции проходит через эти точки.
Это означает, что мы хотим, чтобы
и оба были правдой. Деление первого уравнения на второе дает , предполагая . Затем это уравнение решается путем извлечения корня из обеих частей. Затем вы можете использовать одно из исходных уравнений для решения .
Другим важным моментом в лекции 4А является идея моделирования данных. Рассматриваются реальные данные о валовом внутреннем продукте (ВВП) США. Затем я графически сравниваю, какая модель лучше «подходит» для данных — линейная или экспоненциальная. Считается, что экспоненциальная модель лучше, потому что ее остатки (ошибки) более случайны. Это очень важная перспектива, если вы хотите использовать математические модели в реальной жизни.
Затем я графически сравниваю, какая модель лучше «подходит» для данных — линейная или экспоненциальная. Считается, что экспоненциальная модель лучше, потому что ее остатки (ошибки) более случайны. Это очень важная перспектива, если вы хотите использовать математические модели в реальной жизни.
Последний пункт лекции 4А — композиция функций. Композиция функций означает, что мы применяем две функции в последовательности . Учитывая две функции
и соответствующие домены и кодомены, мы можем сформировать новую функцию. Эта функция определяется формулой . Другими словами, вывод подключается к . Это важная концепция как для более глубокого понимания функций, так и для идеи обратной функции.
Лекция 4BЭто приводит нас к лекции 4B, где я начинаю описывать обратные функции и их свойства.
Исчисление 1, лекция 4B: композиция функций, обратные функции, квадратичные функции Сначала более подробно дается идея композиции функций на примере.
Отсюда определяются обратные функции для взаимно однозначных функций. Для заданной взаимно однозначной (инъективной) функции
ее обратная функция определена так, чтобы удовлетворять двум свойствам относительно композиции. Оно должно удовлетворять всем в области . И оно должно удовлетворять всем в области (которая является диапазоном .
Еще один факт, который я подчеркиваю в этой лекции, заключается в том, что функции, которые не являются взаимно однозначными, иногда можно сделать таковыми путем соответствующего ограничения их доменов. В частности, области определения квадратичных функций можно соответствующим образом ограничить, используя метод завершения квадрата для записи их формул в вершинной форме.
Лекции 5A и 5BЯ начинаю лекцию 5A, используя систему компьютерной алгебры (CAS) Mathematica , чтобы построить график 92 в этом посте.
youtube.com/embed/4RxpcyLF9Ic?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en-US&autohide=2&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»> Вычисление 1, Упражнение 5A: График Mathematica, Обратный квадрат (завершение квадрата), Введение в производныеЯ также использую функцию под названием «Управление» в Mathematica , чтобы сделать анимацию графика
по мере увеличения . Это соответствует горизонтальному переносу (сдвигу) «родительской» функции.
Отсюда я решаю физическую задачу о высоте объекта под действием силы тяжести, используя функцию, обратную квадратичному. Как уже упоминалось, метод завершения квадрата используется для преобразования квадратного числа в вершинную форму. Затем область определения сужается и по квадратичной формуле находится соответствующая обратная функция. 92 при произвольном значении x для измерения (мгновенной) скорости изменения функции в этой точке. Это также описывается как наклон касательной к графику
Это также описывается как наклон касательной к графику
в этой точке.
Начните с выбора произвольного значения
. Тогда пусть будет ненулевым числом.
Это стандартное обозначение для изменения x . Мы действительно воображаем, что независимая переменная (вход) для функции
меняется с на . Если , то вход увеличивается и . Если , то вход убывает.
Для простоты предположим, что
. График не является линией, поэтому он не имеет постоянного наклона. Однако среднюю скорость изменения на закрытом интервале все же можно определить. Он определяется как наклон линии, соединяющей точки и .
Эта линия называется секущей к графику
. Его наклон равен . Для можно сделать следующее упрощение этого выражения.
.
Наглядное изображение секущей линии, приближающейся к касательной
Последнее равенство верно до тех пор, пока
, что мы и предполагаем. То, что мы только что сделали, можно визуализировать, как показано ниже.
То, что мы только что сделали, можно визуализировать, как показано ниже.
Так что же тогда является производной ? Это предел наклона этих секущих, поскольку
«уходят» в ноль. Этот предел, , если он существует , то определяется как наклон касательной к графику при заданном значении . Другими словами, в данной точке на графике касательной является линия, проходящая через эту точку с наклоном, равным только что описанному пределу .
Производная — это предел
Но что такое предел?
Мы уточним ограничения в следующем посте. На данный момент в данной ситуации просто подумайте об этом как о значениях
as становится все ближе и ближе к нулю, фактически не равняясь нулю (потому что тогда мы будем делить на ноль).
Начиная с
когда , этот предел можно найти, подумав о значениях когда близко к нулю.
Как происходит это мышление? Проще говоря, поскольку
является «хорошей» (непрерывной) функцией (понимаемой как «фиксированная»), мы можем просто подключиться, чтобы получить ответ.
Это производное от
! Условно мы пишем .
Сейчас вы вполне можете почесать затылок и сказать: , но подождите минутку! Я думал, мы говорим
! Но мы вставили ноль в конце! Как же так?!?!?
Это, мой друг, часть сбивающей с толку тонкости ограничений. Как я уже сказал, мы углубимся в это в другом посте.
Не расстраивайтесь, если вы не сразу это понимаете. В конце концов, даже гениальные Исаак Ньютон и Готфрид Вильгельм Лейбниц не до конца понимали это в 1600-х годах. Полного понимания пришлось ждать, пока в 1800-х годах не появились Огюстен-Луи Коши и Карл Вейерштрасс.
Но не волнуйтесь! Вы можете «стоять на плечах этих гигантов». Вы действительно можете «получить это» с достаточной помощью и временем на размышления!
4 Базовая дифференциация
4 Базовая дифференциация 4 Базовая дифференциация
Дифференциация заключается в вычислении наклона или градиент кривой y ( x ) в заданной точке, х .
Подумайте о дорожных знаках: холм 1 из 10 означает, что вы проезжаете 1 метр. вверх на каждые 10 метров, которые вы проезжаете.
Обозначение : Мы используем символ Δ дельта для обозначения
(большое) изменение значения переменной. Если, скажем, x меняется со значения x 1 на новое
значение, x 2 , затем
Таким образом, градиент кривой y ( x ) можно записать как:
Линейные уравнения
Для прямолинейного графика уравнения y ( x ) = m x + c , градиент задается просто значением м .
Примеры
- y = 3 x + 6, градиент = 3
- у = 5 х — 3, градиент = 5
- y = -2 x + 1, градиент = -2
- y = 6 — 3 x , градиент = -3
Измерение градиентов
Если мы не знаем уравнения прямой, мы можем работать
из градиента, сведя в таблицу значения г против x и построение графика.
Пример Значения y и x приведены ниже,
какой градиент?
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| у | -11 | -8 | -5 | -2 | 1 | 4 | 7 |
Графический метод
(i) График графика
(ii) Выберите любые 2 точки вдоль линии ( x 1 , y 1 ) и ( x 2 , у 2 )
(iii) Нарисуйте треугольники (как на диаграмме) или просто рассчитайте х и и .
(iv) Рассчитать градиент из: градиент =
Численный метод : выберите точки, для которых у нас есть значения,
скажем, (-2, -8) и (1,1). Теперь у нас есть:
Поскольку точка пересечения находится на y = -2, мы знаем, что уравнение.
этой строки должно быть
Нахождение градиента общей функции
Линейные кривые просты, но как нам найти наклон любого кривая, y ( x ) в точке x ?
Градиент кривой в точке A такой же, как и у касательной в точке A . Итак, все, что нам нужно сделать, это построить касательной и измерьте ее градиент, Δ y / Δ x .
Пример Чему равен градиент y ( x ) = x 2 — 4 x — 1, когда x = 4?
Решение Постройте кривую, затем постройте касательную
когда х = 4 на глаз, как умеешь. Измерьте градиент
Δ y / Δ x , завершив треугольник.
Измерьте градиент
Δ y / Δ x , завершив треугольник.
Графически находим, что = 4.
Аналитическая дифференциация
Рисование касательных — довольно громоздкий метод получения градиентов.
Существует ли аналитический метод?
Ответ: дифференцирование . Упрощенный вывод
об этом дано в раздаточном материале, но нам нужно только действительно узнать
«волшебная формула» (см. ниже) .
Обозначение : наклон или градиент , или дифференциал, или производная может быть записана многими эквивалентными способами:
Для других имен переменных и функций существует эквивалент
обозначение.
напр. для с ( т ), у нас есть,
для E(ν) имеем
для φ(λ) имеем
Дифференциация «волшебная формула» (для стандартных
полиномы)
Чтобы дифференцировать полиномиальную функцию, нужно умножить
ведущий множитель, a , и показатель степени (мощность).
