Николай Лобачевский: параллельные прямые все-таки пересекаются!
Комсомольская правда
НаукаВеликие ученые РоссииИнтересное
Ксения КОНЮХОВА
12 марта 2015 16:55
Геометрия Лобачевского дала базу для всей современной физики [видео]
Николай Лобачевский известен тем, что создал новую геометрию
Николай Лобачевский известен тем, что создал новую геометрию, в которой параллельные прямые запросто пересекаются. На самом деле все не совсем так. Он просто внимательно изучил имеющуюся на тот момент геометрию Евклида и внес в нее кое-какие коррективы. Учитывая, что этой науке к тому моменту уже исполнилось 2 с лишним тысячи лет, без обновлений было не обойтись…
Николай Иванович Лобачевский родился 20 ноября 1792 года в Нижнем Новгороде. Семья была из простых. Дедушка будущего ученого был поляком, о бабушке известно лишь то, что она была крепостной крестьянкой у князя Михаила Долгорукого. Отец ученого служил чиновником в геодезическом департаменте и умер, когда Николаю было 8 лет.
С деньгами в семье было совсем плохо, и мать отправила Николая и двух его братьев в казанскую гимназию, где они смогли учиться за госсчет. В 16 лет Николай окончил учебу и попробовал поступить в только что открывшийся Казанский университет. С первого раза не выходит, зато со второй попытки Николая зачисляют на первый курс.
Из-за того, что университет только-только открылся, в первые годы там царила неразбериха. Доходило до того, что преподавать математику приходилось самим студентам! Впрочем, Лобачевский к паинькам не относился. Его современники туманно намекают на «студенческие шалости», в которых он участвовал на 1 — 2-м курсах. Но смогли доказать его участие только в одной проделке, когда Николай с приятелями под видом пиротехнических опытов запустили ракету прямо в аудитории! В наказание ему пришлось несколько дней просидеть в карцере.
С тех пор будущий ученый взялся за ум. Засел за учебу, увлекся химией и математикой… Но совсем без приключений не обошлось. Например, в 1811 году Лобачевский чересчур увлекся празднованием Нового года — настолько, что администрация даже хотела его отчислить.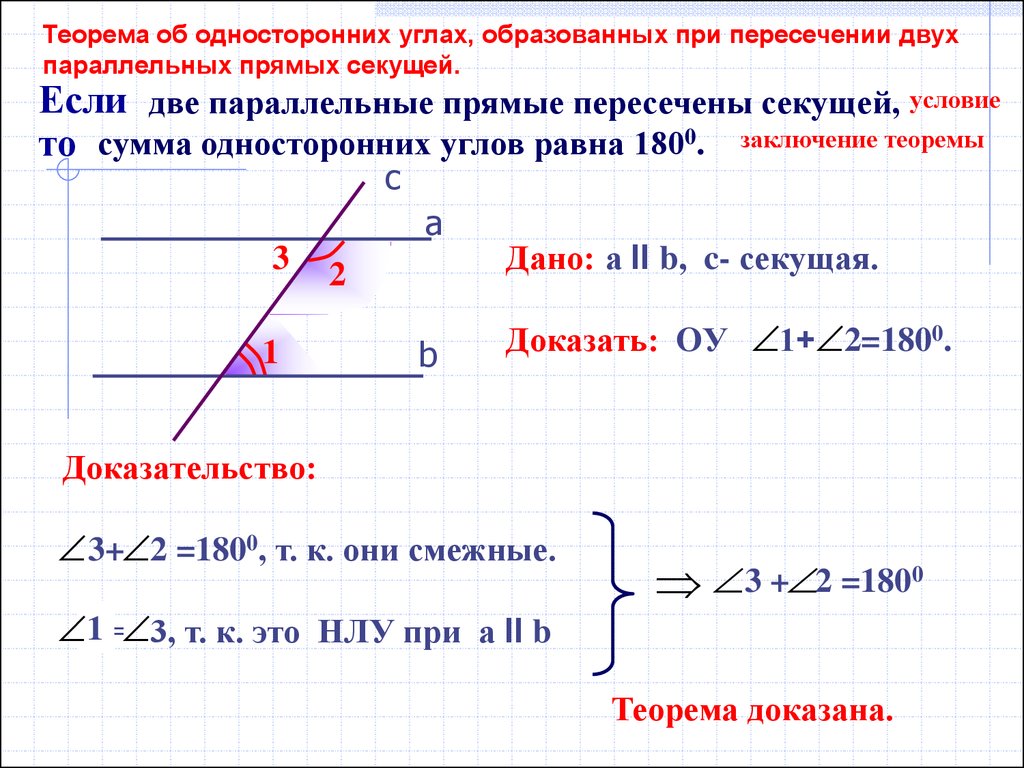 А это, как и сейчас, означало для юноши только одно — армию!
А это, как и сейчас, означало для юноши только одно — армию!
«В генваре месяце Лобачевский оказался самого худого поведения, — гласил рапорт, поданный университетскому начальству. — Несмотря на приказание начальства не отлучаться из университета, он в новый год, а потом еще раз ходил в маскарад и многократно в гости, за что опять наказан написанием имени на черной доске и выставлением оной в студентских комнатах на неделю. Несмотря на сие, он после того снова еще был в маскараде»…
Но благодаря заступничеству преподавателей, Лобачевского оставили в университете. Правда, лишили пособия на учебники, так что теперь ему приходилось покупать их за свой счет. Доучиться оставалось всего полгода, так что Лобачевский без особых проблем получил степень магистра по математике и физике с отличием.
Отправлять талантливого студента восвояси никому не хотелось. Поэтому с Лобачевского взяли обещание, что он будет вести себя хорошо, и заставили покаяться во всех прошлых проделках. На этих условиях его взяли преподавать арифметику и геометрию, а также заниматься научной работой.
На этих условиях его взяли преподавать арифметику и геометрию, а также заниматься научной работой.
Сперва карьера пошла вверх: в 1820 году Лобачевский стал деканом физико-математического факультета. Но потом в Казанский университет прислали проверку. Ревизор отчитался об «отсутствии благочестия» в вузе и взялся устанавливать новые порядки. В университете открылась кафедра богословия, все достойные ученые и профессора либо разъехались, либо были уволены.
В такой атмосфере первый труд Лобачевского остался незамеченным. Еще в студенческие годы он пытался доказать пятый постулат Евклида, который звучит так:
«Если на плоскости при пересечении двух прямых третьей сумма внутренних односторонних углов меньше 180, то эти прямые при достаточном продолжении пересекаются».
То есть о параллельных прямых тут речи нет вообще! Речь идет лишь о непересекающихся… Разница в том, что между параллелями должно быть одинаковое расстояние по всей их длине. А для непересекающихся прямых это необязательно!
Над этим постулатом математики бились не одну сотню лет. Дело в том, что доказать его математическими средствами невозможно! Поэтому ученые и пытались создать свою геометрию, которая была бы лишена этого недостатка.
Дело в том, что доказать его математическими средствами невозможно! Поэтому ученые и пытались создать свою геометрию, которая была бы лишена этого недостатка.
В первом своем учебнике, написанном в 1823 году, Лобачевский попытался это сделать и опровергнуть это утверждение. Но рецензентов возмутили такие вольности. Да и то, что ученый использовал метрическую систему, не добавило ему баллов. После такого разгрома Лобачевский еще долго не брался за написание учебников… Следующее пособие, по алгебре, он опубликовал только через 10 лет.
В 1826 году попечители Казанского университета осознали, что что-то идет не так, и ревизора отстранили «за злоупотребления властью». И в 1827 году новым ректором университета выбрали Николая Лобачевского.
Ученый получает карт-бланш. Он активно погружается во все хозяйственные дела, не забывая при этом и про научные изыскания. Ведет занятия по алгебре, физике, началам анализа, теории вероятностей. И параллельно с этим читает открытые лекции по неевклидовой геометрии.
Одной из главных обязанностей Лобачевский считал наведение порядка в университете. По воспоминаниям современников, профессора сперва жаловались на строгие правила и формализм математика. Но вскоре поняли, что Лобачевский не злоупотребляет властью. «Когда он видел, что члены совета начинали спорить и спору их не предвиделось конца, Лобачевский обыкновенно прерывал заседание, оставлял спорный вопрос открытым до следующего раза; затем он приглашал к себе на дом спорщиков и у себя в кабинете в мирной беседе за чашкой чаю приводил их к соглашению. Этот прием всегда имел хорошие последствия, и на другом совете дело обходилось уже без всяких споров», — отзывался о нем попечитель университета Мусин-Пушкин.
В 1829 году Лобачевский публикует серьезный научный труд «О началах геометрии». Именно он дал старт новому разделу науки — неевклидовой геометрии.
Если говорить просто, то Лобачевский считает неправильным, что непересекающихся прямых может быть только две. И предлагает свою аксиому:
«На плоскости через точку, не лежащую на данной прямой, проходит более, чем одна прямая, не пересекающая данную».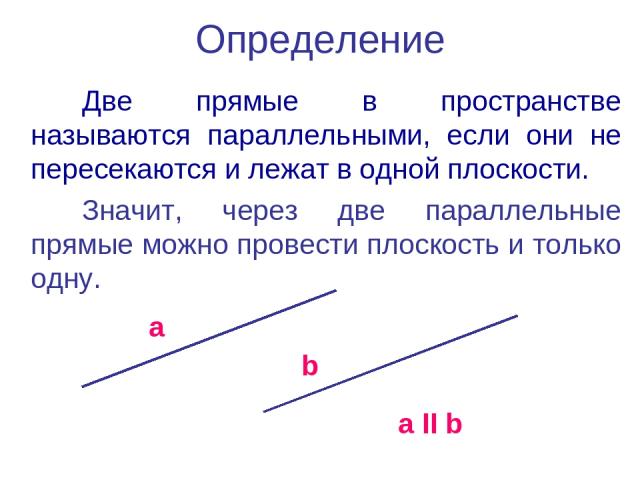
Дело в том, что Евклид в прямом смысле слова плоско мыслил! Свой постулат он сформулировал только для плоскости. Если нарисовать прямую А и точку на листе бумаги, то через эту точку и правда можно провести всего одну прямую В, не пересекающую предыдущую.
А вот на кривой поверхности таких прямых будет гораздо больше. То есть Евклид описал лишь один частный случай, а не все существующие варианты. Пространство может быть и в форме седла, и в форме воронки… И геометрия Лобачевского описывает лучше всего именно такие формы — «с отрицательной кривизной».
Лобачевский предположил, что в трехмерном пространстве параллельные прямые вполне могут иметь общие точки
Но современники Лобачевского понять этой логики не смогли. На него обрушился целый вал пасквилей и карикатур. Никто не мог поверить, что провинциальный педагог смог всерьез опровергнуть античную аксиому.
В 1832 году ученый женился на Варваре Моисеевой, которая была почти на 20 лет моложе его. В имении жены, недалеко от Казани, он развел большой сад. По преданию, Лобачевский сам посадил кедры и с грустью сказал, что не дождется их плодов. Предсказание сбылось — первые орехи были сняты в год смерти ученого. А кедровая роща на том месте сохранилась до сих пор…
По преданию, Лобачевский сам посадил кедры и с грустью сказал, что не дождется их плодов. Предсказание сбылось — первые орехи были сняты в год смерти ученого. А кедровая роща на том месте сохранилась до сих пор…
В 1846 году Николая Ивановича отстраняют от должности ректора и лишают профессорской кафедры. Семья лишается значительной части дохода, имение жены приходится продать за долги. Здоровье ученого начинает слабеть, зрение падает. Последний свой труд, «Пангеометрию», Лобачевский создал в 1855 году. Текст записывали под диктовку его ученики — сам Николай Иванович к тому моменту уже ослеп.
Николай Иванович Лобачевский скончался 12 февраля 1856 года, и был похоронен в Казани, на Арском кладбище. Сочинения ученого оценили по достоинству только после его смерти, во второй половине 1860-х годов.
Современная физика Вселенной пришла к выводу, что пространство, где мы с вами живем, обладает отрицательной кривизной. И именно геометрия Лобачевского описывает его лучше всего.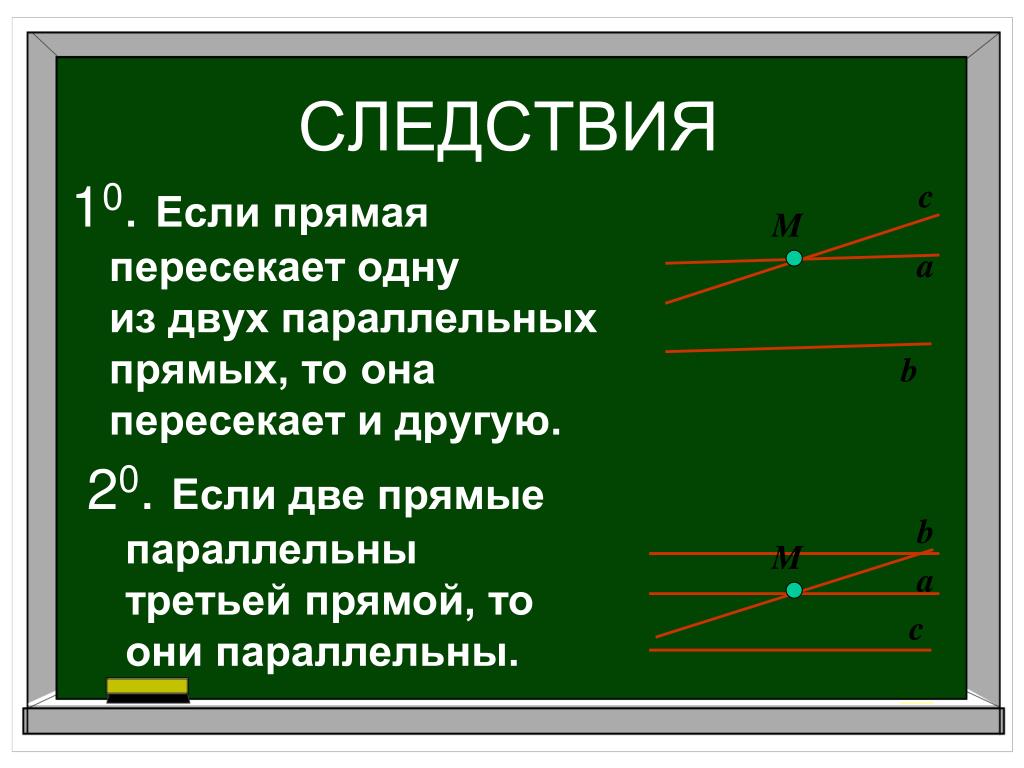
Без геометрии Лобачевского у нас не было бы теории относительности Эйнштейна, исследований Клейна и Пуанкаре. Его работы расширили наше представление о мире и дали возможность составить о нем более точное представление.
Великие ученые: Николай Лобачевский
Русский математик, создатель неевклидовой геометрии, деятель университетского образования и народного просвещения.
Читайте также
Возрастная категория сайта 18+
Сетевое издание (сайт) зарегистрировано Роскомнадзором, свидетельство Эл № ФС77-80505 от 15 марта 2021 г.
И.О. ГЛАВНОГО РЕДАКТОРА — НОСОВА ОЛЕСЯ ВЯЧЕСЛАВОВНА.
Сообщения и комментарии читателей сайта размещаются без предварительного редактирования. Редакция оставляет за собой право удалить их с сайта или отредактировать, если указанные сообщения и комментарии являются злоупотреблением свободой массовой информации или нарушением иных требований закона.
АО «ИД «Комсомольская правда». ИНН: 7714037217 ОГРН: 1027739295781
127015, Москва, Новодмитровская д. 2Б, Тел. +7 (495) 777-02-82.
ИНН: 7714037217 ОГРН: 1027739295781
127015, Москва, Новодмитровская д. 2Б, Тел. +7 (495) 777-02-82.
Исключительные права на материалы, размещённые на интернет-сайте www.kp.ru, в соответствии с законодательством Российской Федерации об охране результатов интеллектуальной деятельности принадлежат АО «Издательский дом «Комсомольская правда», и не подлежат использованию другими лицами в какой бы то ни было форме без письменного разрешения правообладателя.
Приобретение авторских прав и связь с редакцией: [email protected]
Пересекаются ли параллельные прямые ➕
Думаю, вы не раз встречались с детской наебкой деления на ноль. Когда учитель говорит, что вы еще маленькие, нихуя не знаете, а вот когда будете в ВУЗе, тогда и узнаете, что и как *там в Египте* с делением на ноль. Когда ты получил общее образование (9 классов) и переходишь в Среднюю школу (10—11 классы), более плотно изучив пределы и поняв, как все это работает, начинаешь посмеиваться над глупой шкилой, которая нихуя в этой жизни не выкупает. Тебе кажется, что при стремлении знаменателя к нулю, у тебя получается дробь все больше и больше, а экстраполировав это на реальную жизнь ты спокойно заменяешь знаменатель на ноль и получаешь бесконечность — то есть при делении чего-либо на 0 ты в ответе получишь бесконечность. И вот ты приходишь в ВУЗ на пару по МатАну, там, проходя пределы, ты вожделеешь, когда препод начнет вещать о делении на ноль, но вот он говорит, что все нихуя не так и на ноль делить все-таки нельзя, а можно лишь делить на бесконечно малую, получая при этом бесконечно большую, но не бесконечность. И на этом моменте ты можешь уже посмеиваться над пажилой средней шкилой, которая смеется над более младшими, что те не шарят, как работает эта жизнь.
Тебе кажется, что при стремлении знаменателя к нулю, у тебя получается дробь все больше и больше, а экстраполировав это на реальную жизнь ты спокойно заменяешь знаменатель на ноль и получаешь бесконечность — то есть при делении чего-либо на 0 ты в ответе получишь бесконечность. И вот ты приходишь в ВУЗ на пару по МатАну, там, проходя пределы, ты вожделеешь, когда препод начнет вещать о делении на ноль, но вот он говорит, что все нихуя не так и на ноль делить все-таки нельзя, а можно лишь делить на бесконечно малую, получая при этом бесконечно большую, но не бесконечность. И на этом моменте ты можешь уже посмеиваться над пажилой средней шкилой, которая смеется над более младшими, что те не шарят, как работает эта жизнь.
Эта долгая поучительная предыстория была не зря. Даже я помню, как мы пытались доказать нашей учительнице по математике и что делить на ноль можно, и что параллельные линии пересекаются. Просто у молодого и неокрепшего ума происходит разрыв шаблона, когда ему говорят, что параллельные линии не пересекаются.
На самом деле, это мы сейчас знаем, что параллельные линии не пересекаются, а вот в 19 веке люди просто не могли принять этот факт. Изначально он был описан в «Началах» Евклида и был 5 аксиомой, которая гласила: «И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых». У этого пункта есть другая страничка, которая называется постулатом Прошла (в Древней Греции разграничивали понятия «постулат» и «аксиома»), который гласит, что через точку, не лежащей на данной прямой, можно провести прямую, параллельную данной, и причем только одну. Это звучит полегче, но от Евклидовой формулировке у меня до сих пор не стоит.
Самым первым таким поцом, который смог не просто создать Абсолютную геометрию (геометрия без 5 аксиомы, но с непересекающимися параллельными прямыми), а создать абсолютно новую геометрию — Николай Иванович Лобачевский, который сформулировал одноименную геометрию. Не буду ее полностью сейчас разбирать, просто напомню, что эта геометрия (в частном и простом случае) на псеводосфере. Псевдосфера выглядит как воронка или как модель, которой изображается черная дыра. В этой геометрии параллельные прямые (именно прямые, те прямые, которые прямые в евклидовом геометрии, но об этом потом) пересекаются, и при том, они обязательно пересекутся.

Другим случаем может быть геометрия Римана, сформулированная Георгом Фридрихом Бернхардом Риманом. Эта геометрия является геометрией на эллипсоиде (есть отдельная геометрия, которая называется геометрией на сфере, которая совпадает с геометрией Римана в частном случае). Там прямые, параллельные в Евклидовой геометрии, могут преспокойно пересекаться и даже больше — они, как и в геометрии Лобачевского, обязательно пересекутся. Вот только опять же это нихуя не прямые в Романовой геометрии. Что в геометрии Лобачевского параллельные и ультрапараллельные прямые не очень похожи на прямые, так и геометрии Римана пересекающиеся «прямые» на самом деле нихуя не прямые. Дело в том, что в этой геометрии роль прямых на себя берут круги (хотя правильнее было бы говорить окружности, но почему-то их называют кругами). Два круга будут параллельны друг другу тогда, когда они не пересекаются (а не тогда, когда у них совпадают центры), то есть через точку, не лежащей на данном круге можно провести бесконечное количество кругов, параллельных данному.
На самом деле, довольно глупо было бы получить какой-то другой ответ, так как по определению параллельность — это отношение каких-то объектов друг к другу таким образом, чтобы они друг с другом не пересекались, сколько бы мы эти объекты ни продолжали.
#детский_вопрос@appi.retelling
Спасибо за то, что вы с нами.
С любовью, Рителлинг❤️
Спасибо за то, что вы с нами.
С любовью, Рителлинг favorite
Две прямые параллельные пересекаются –
Кто из великих математиков доказал что параллельные прямые могут пересекаться
Николай Лобачевский: параллельные прямые все-таки пересекаются!
Николай Лобачевский известен тем, что создал новую геометрию, в которой параллельные прямые запросто пересекаются.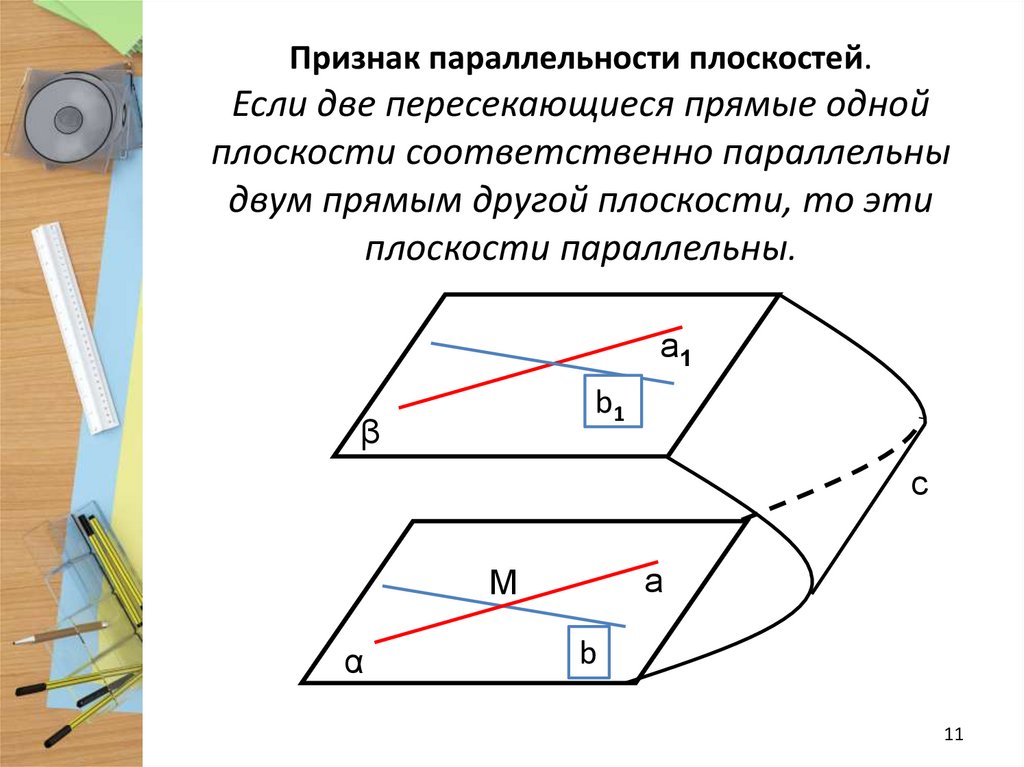 На самом деле все не совсем так. Он просто внимательно изучил имеющуюся на тот момент геометрию Евклида и внес в нее кое-какие коррективы. Учитывая, что этой науке к тому моменту уже исполнилось 2 с лишним тысячи лет, без обновлений было не обойтись…
На самом деле все не совсем так. Он просто внимательно изучил имеющуюся на тот момент геометрию Евклида и внес в нее кое-какие коррективы. Учитывая, что этой науке к тому моменту уже исполнилось 2 с лишним тысячи лет, без обновлений было не обойтись…
Николай Иванович Лобачевский родился 20 ноября 1792 года в Нижнем Новгороде. Семья была из простых. Дедушка будущего ученого был поляком, о бабушке известно лишь то, что она была крепостной крестьянкой у князя Михаила Долгорукого. Отец ученого служил чиновником в геодезическом департаменте и умер, когда Николаю было 8 лет.
С деньгами в семье было совсем плохо, и мать отправила Николая и двух его братьев в казанскую гимназию, где они смогли учиться за госсчет. В 16 лет Николай окончил учебу и попробовал поступить в только что открывшийся Казанский университет. С первого раза не выходит, зато со второй попытки Николая зачисляют на первый курс.
Из-за того, что университет только-только открылся, в первые годы там царила неразбериха.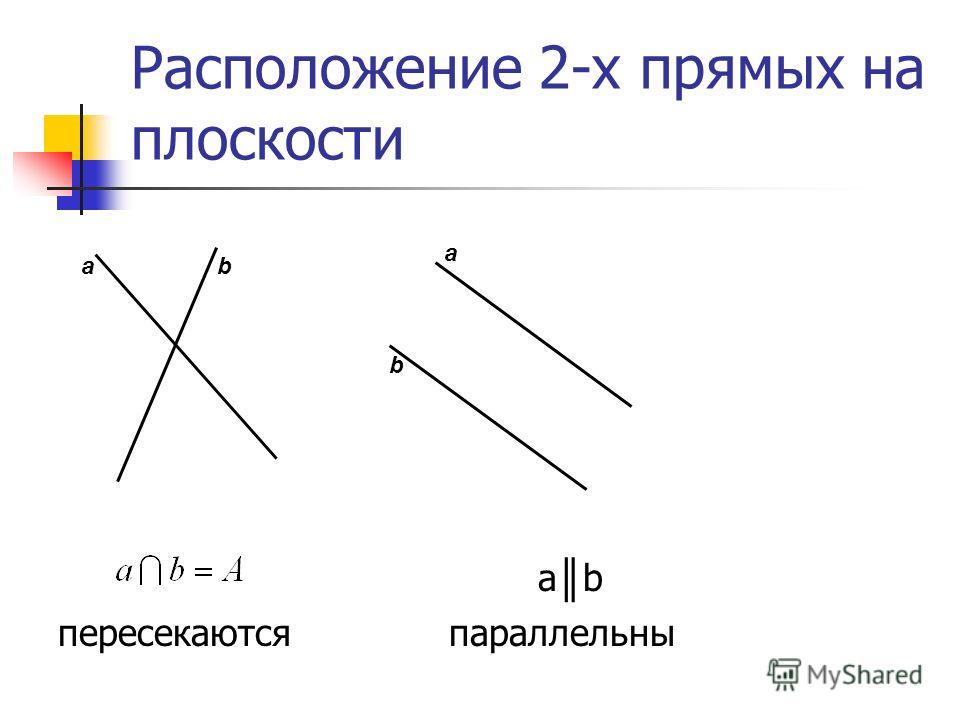 Доходило до того, что преподавать математику приходилось самим студентам! Впрочем, Лобачевский к паинькам не относился. Его современники туманно намекают на «студенческие шалости», в которых он участвовал на 1 — 2-м курсах. Но смогли доказать его участие только в одной проделке, когда Николай с приятелями под видом пиротехнических опытов запустили ракету прямо в аудитории! В наказание ему пришлось несколько дней просидеть в карцере.
Доходило до того, что преподавать математику приходилось самим студентам! Впрочем, Лобачевский к паинькам не относился. Его современники туманно намекают на «студенческие шалости», в которых он участвовал на 1 — 2-м курсах. Но смогли доказать его участие только в одной проделке, когда Николай с приятелями под видом пиротехнических опытов запустили ракету прямо в аудитории! В наказание ему пришлось несколько дней просидеть в карцере.
С тех пор будущий ученый взялся за ум. Засел за учебу, увлекся химией и математикой… Но совсем без приключений не обошлось. Например, в 1811 году Лобачевский чересчур увлекся празднованием Нового года — настолько, что администрация даже хотела его отчислить. А это, как и сейчас, означало для юноши только одно — армию!
«В генваре месяце Лобачевский оказался самого худого поведения, — гласил рапорт, поданный университетскому начальству. —
Несмотря на приказание начальства не отлучаться из университета, он в новый год, а потом еще раз ходил в маскарад и многократно в гости, за что опять наказан написанием имени на черной доске и выставлением оной в студентских комнатах на неделю. Несмотря на сие, он после того снова еще был в маскараде»…
Несмотря на сие, он после того снова еще был в маскараде»…
Но благодаря заступничеству преподавателей, Лобачевского оставили в университете. Правда, лишили пособия на учебники, так что теперь ему приходилось покупать их за свой счет. Доучиться оставалось всего полгода, так что Лобачевский без особых проблем получил степень магистра по математике и физике с отличием.
Отправлять талантливого студента восвояси никому не хотелось. Поэтому с Лобачевского взяли обещание, что он будет вести себя хорошо, и заставили покаяться во всех прошлых проделках. На этих условиях его взяли преподавать арифметику и геометрию, а также заниматься научной работой.
Сперва карьера пошла вверх: в 1820 году Лобачевский стал деканом физико-математического факультета. Но потом в Казанский университет прислали проверку. Ревизор отчитался об «отсутствии благочестия» в вузе и взялся устанавливать новые порядки. В университете открылась кафедра богословия, все достойные ученые и профессора либо разъехались, либо были уволены.
В такой атмосфере первый труд Лобачевского остался незамеченным. Еще в студенческие годы он пытался доказать пятый постулат Евклида, который звучит так:
«Если на плоскости при пересечении двух прямых третьей сумма внутренних односторонних углов меньше 180, то эти прямые при достаточном продолжении пересекаются».
То есть о параллельных прямых тут речи нет вообще! Речь идет лишь о непересекающихся… Разница в том, что между параллелями должно быть одинаковое расстояние по всей их длине. А для непересекающихся прямых это необязательно!
Над этим постулатом математики бились не одну сотню лет. Дело в том, что доказать его математическими средствами невозможно! Поэтому ученые и пытались создать свою геометрию, которая была бы лишена этого недостатка.
В первом своем учебнике, написанном в 1823 году, Лобачевский попытался это сделать и опровергнуть это утверждение. Но рецензентов возмутили такие вольности. Да и то, что ученый использовал метрическую систему, не добавило ему баллов. После такого разгрома Лобачевский еще долго не брался за написание учебников… Следующее пособие, по алгебре, он опубликовал только через 10 лет.
После такого разгрома Лобачевский еще долго не брался за написание учебников… Следующее пособие, по алгебре, он опубликовал только через 10 лет.
В 1826 году попечители Казанского университета осознали, что что-то идет не так, и ревизора отстранили «за злоупотребления властью». И в 1827 году новым ректором университета выбрали Николая Лобачевского.
Ученый получает карт-бланш. Он активно погружается во все хозяйственные дела, не забывая при этом и про научные изыскания. Ведет занятия по алгебре, физике, началам анализа, теории вероятностей. И параллельно с этим читает открытые лекции по неевклидовой геометрии.
Одной из главных обязанностей Лобачевский считал наведение порядка в университете. По воспоминаниям современников, профессора сперва жаловались на строгие правила и формализм математика. Но вскоре поняли, что Лобачевский не злоупотребляет властью. «Когда он видел, что члены совета начинали спорить и спору их не предвиделось конца, Лобачевский обыкновенно прерывал заседание, оставлял спорный вопрос открытым до следующего раза; затем он приглашал к себе на дом спорщиков и у себя в кабинете в мирной беседе за чашкой чаю приводил их к соглашению.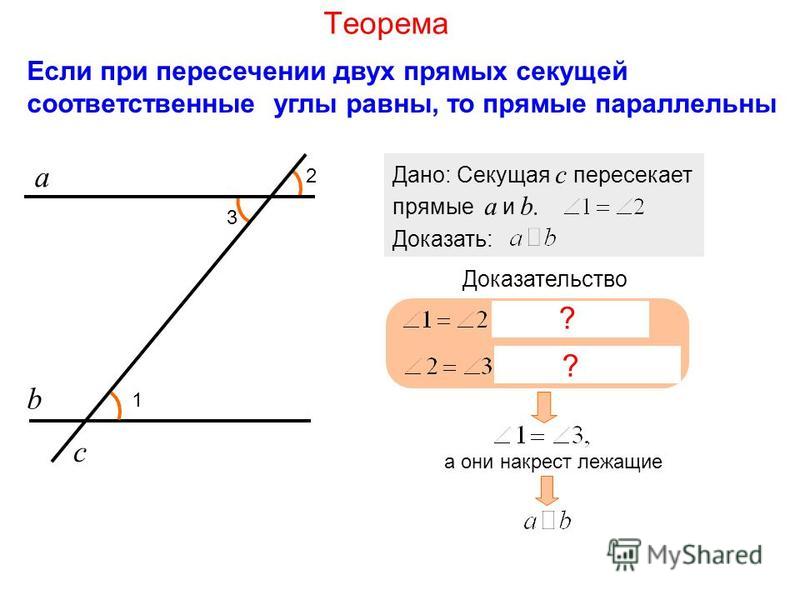 Этот прием всегда имел хорошие последствия, и на другом совете дело обходилось уже без всяких споров», — отзывался о нем попечитель университета Мусин-Пушкин.
Этот прием всегда имел хорошие последствия, и на другом совете дело обходилось уже без всяких споров», — отзывался о нем попечитель университета Мусин-Пушкин.
В 1829 году Лобачевский публикует серьезный научный труд «О началах геометрии». Именно он дал старт новому разделу науки — неевклидовой геометрии.
Если говорить просто, то Лобачевский считает неправильным, что непересекающихся прямых может быть только две. И предлагает свою аксиому:
«На плоскости через точку, не лежащую на данной прямой, проходит более, чем одна прямая, не пересекающая данную».
Дело в том, что Евклид в прямом смысле слова плоско мыслил! Свой постулат он сформулировал только для плоскости. Если нарисовать прямую А и точку на листе бумаги, то через эту точку и правда можно провести всего одну прямую В, не пересекающую предыдущую.
А вот на кривой поверхности таких прямых будет гораздо больше. То есть Евклид описал лишь один частный случай, а не все существующие варианты. Пространство может быть и в форме седла, и в форме воронки… И геометрия Лобачевского описывает лучше всего именно такие формы — «с отрицательной кривизной».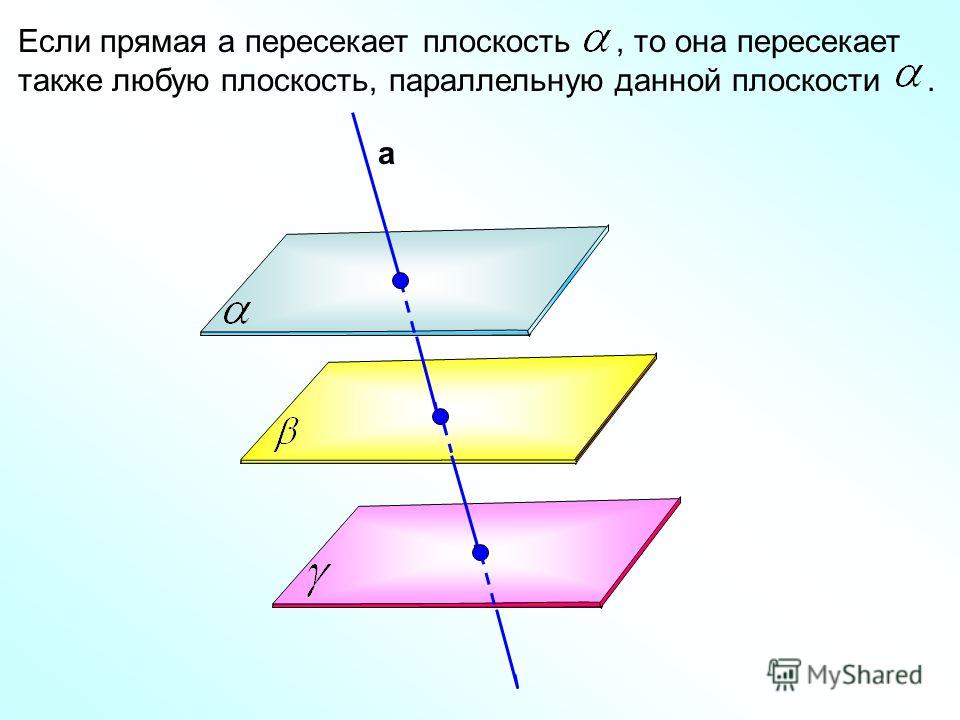
Лобачевский предположил, что в трехмерном пространстве параллельные прямые вполне могут иметь общие точки
Но современники Лобачевского понять этой логики не смогли. На него обрушился целый вал пасквилей и карикатур. Никто не мог поверить, что провинциальный педагог смог всерьез опровергнуть античную аксиому.
В 1832 году ученый женился на Варваре Моисеевой, которая была почти на 20 лет моложе его. В имении жены, недалеко от Казани, он развел большой сад. По преданию, Лобачевский сам посадил кедры и с грустью сказал, что не дождется их плодов. Предсказание сбылось — первые орехи были сняты в год смерти ученого. А кедровая роща на том месте сохранилась до сих пор…
В 1846 году Николая Ивановича отстраняют от должности ректора и лишают профессорской кафедры. Семья лишается значительной части дохода, имение жены приходится продать за долги. Здоровье ученого начинает слабеть, зрение падает. Последний свой труд, «Пангеометрию», Лобачевский создал в 1855 году. Текст записывали под диктовку его ученики — сам Николай Иванович к тому моменту уже ослеп.
Николай Иванович Лобачевский скончался 12 февраля 1856 года, и был похоронен в Казани, на Арском кладбище. Сочинения ученого оценили по достоинству только после его смерти, во второй половине 1860-х годов.
Современная физика Вселенной пришла к выводу, что пространство, где мы с вами живем, обладает отрицательной кривизной. И именно геометрия Лобачевского описывает его лучше всего.
Без геометрии Лобачевского у нас не было бы теории относительности Эйнштейна, исследований Клейна и Пуанкаре. Его работы расширили наше представление о мире и дали возможность составить о нем более точное представление.
Великие ученые: Николай Лобачевский.Русский математик, создатель неевклидовой геометрии, деятель университетского образования и народного просвещения.
Ответы@Mail. Ru: параллельные прямые пересекаются?
Параллельные прямые не пересекаются ни в какой геометрии. Просто, например, в евклидовой геометрии, через точку можно провести одну прямую, параллельную данной, в геометрии Лобачевского-Бояи — пучок прямых, параллельных данной, а в геометрии Римана параллельных прямых вообще нет, все прямые пересекаются.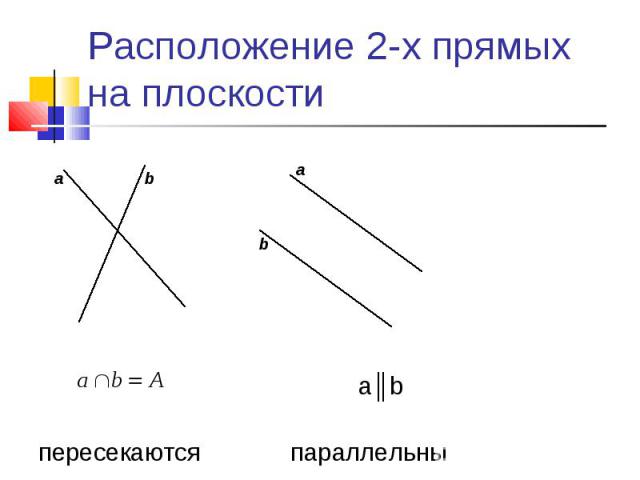 Про геометрии с непостоянной кривизной пространства, вроде сферической, распространятся не буду из экономии места. Главное — параллельные прямые не пересекаются, но не во всех геометриях вообще существуют параллельные прямые.
Про геометрии с непостоянной кривизной пространства, вроде сферической, распространятся не буду из экономии места. Главное — параллельные прямые не пересекаются, но не во всех геометриях вообще существуют параллельные прямые.
Нет, потомучто они паралельны и пересекаться ни как не могут
Нет не могут. Потому что они паралельны.
Геометрию учить надо было в школе.
Иногда и параллельные прямые пересекаются…
В Евклидовой геометрии нет. В сферической «прямые» — кратчайшее расстояние между точками, меридианы пересекаются. Риманова геометрия включает пространства с любой кривизной. Весь вопрос в том, какое наше пространство. Считается римановым. PS Правильнее сказать на сфере в бытовом, а не строго научном смысле этого слова, так как сфера в неевклидовой геометрии это такое, что и не снилось нашим мудрецам! А возникший ниже терминологический спор связан с тем, что именно Риман дополнил геометрию Лобачевского геометрией на сфере, развил и обобщил
Пересекаются! научно доказанный факт
В гиперболической геометрии возможно пересечение параллельных прямых сравним Евклид: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. гиперболическая геометрия: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
гиперболическая геометрия: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Да запросто пересекаются 🙂 Например, в искривленном пространстве, в близи черной дыры паралельные прямые вообще могут слится, пересечся и в узел завязаться :))))
Да, это доказано!
Практически абсолютно бесконечные параллельные прямые линии пересекаются друг с другом в точке абсолютной бесконечности, так как каждая из них имеет в реальном пространстве мира вселенной их абсолютно бесконечное конической его формы сужение и расширение, что позволяет обоим этим прямым быть не двумя а одной конически сужающейся и конически расширяющейся общей линией, которая пересекается своими произвольно взятыми коническими прямыми боками в точке абсолютной бесконечности.
Ало, они пересекутся, моему учителю и всем преподавателям обьсняли это, когда они ходили на учебу, в это трудно поверить, и можно ломать голову, но Евклид доказал, что они пересекутся — это факт
5.
 2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямыхВидеоурок: Параллельные прямые, перпендикулярные к плоскости
Лекция: Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
Пересекающиеся прямые
Если на плоскости имеются несколько прямых, то они либо рано или поздно пересекутся произвольно, либо под прямым углом, или же будут параллельными. Давайте же разберемся с каждым случаем.
Пересекающимися можно назвать те прямые, у которых будет хотя бы одна точка пересечения.
Вы спросите, почему хотя бы одна, не может же прямая пересечь другую прямую две или три раза. Вы правы! Но прямые могут полностью совпасть друг с другом. В таком случае общих точек будет бесконечное множество.
Параллельность
Параллельными можно назвать те прямые, которые никогда не пересекутся, даже на бесконечности.
Иными словами, параллельные – это те, у которых нет ни одной общей точки. Обратите внимание на то, что данное определение справедливо только в том случае, если прямые находятся в одной плоскости, если же они не имеют общих точек, находясь в разных плоскостях, то они считаются скрещивающимися.
Обратите внимание на то, что данное определение справедливо только в том случае, если прямые находятся в одной плоскости, если же они не имеют общих точек, находясь в разных плоскостях, то они считаются скрещивающимися.
Примеры параллельных прямых в жизни: два противоположных края экрана монитора, линии в тетрадях, а также многие другие части вещей, имеющих квадратную, прямоугольную и другие формы.
Когда хотят показать на письме, что одна прямая параллельная второй, то используют следующее обозначение a||b. Данная запись говорит, что прямая а параллельна прямой b.
При изучении данной темы важно понять еще одно утверждение: через некоторую точку на плоскости, которая не принадлежит данной прямой, можно провести единственную параллельную прямую. Но обратите внимание, снова поправка – на плоскости. Если рассматривать трехмерное пространство, то можно провести бесконечное множество прямых, которые не будут пересекаться, но будут скрещивающимися.
Утверждение, которое было описано выше, называется Аксиомой о параллельности прямых.
Перпендикулярность
Прямые можно назвать только в том случае Перпендикулярными, если они пересекаются под углом, равным 90 градусов.
В пространстве через некоторую точку на прямой можно провести бесконечное множество перпендикулярных прямых. Однако, если речь идет о плоскости, то через одну точку на прямой можно провести единственную перпендикулярную прямую.
Скрещенные прямые. Секущая
Если некоторые прямые пересекаются в некоторой точке под произвольным углом, их можно назвать Скрещивающимися.
У любых скрещивающихся прямых есть вертикальные углы и смежные.
Если у углов, которые образованы двумя скрещивающимися прямыми, одна сторона общая, то они называются смежными:
Смежные углы в сумме дают 180 градусов.
Если же углы, образованные двумя скрещивающимися прямыми, не имеют общей стороны, то они называются вертикальными:
Вертикальные углы всегда равны.
Если же некоторая прямая пересекает две других прямых, то она называется Секущей.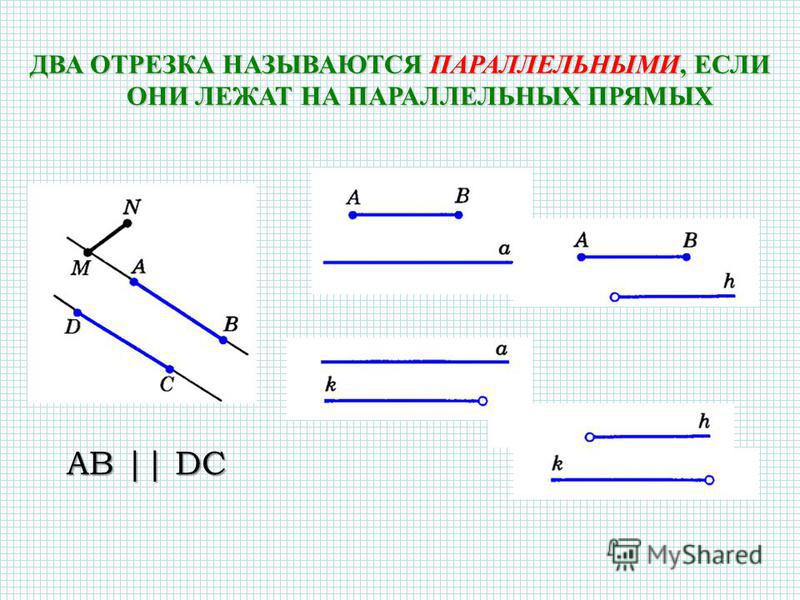
Частным случаем является секущая двух параллельных прямых:
Пять распространенных мифов о геометрии Лобачевского — Российская газета
7 февраля 1832 года Николай Лобачевский представил на суд коллег свой первый труд по неевклидовой геометрии. Этот день стал началом переворота в математике, а работа Лобачевского — первым шагом к теории относительности Эйнштейна. Сегодня «РГ» собрала пятерку самых распространенных заблуждений о теории Лобачевского, бытующих среди далеких от математической науки людей
Миф первый. Геометрия Лобачевского не имеет ничего общего с Евклидовой.
На самом деле геометрия Лобачевского не слишком сильно отличается от привычной нам Евклидовой. Дело в том, что из пяти постулатов Евклида четыре первых Лобачевский оставил без изменения. То есть он согласен с Евклидом в том, что между двумя любыми точками можно провести прямую, что ее всегда можно продолжить до бесконечности, что из любого центра можно провести окружность с любым радиусом, и что все прямые углы равны между собой. Не согласился Лобачевский только с пятым, наиболее сомнительным с его точки зрения постулатом Евклида. Звучит его формулировка чрезвычайно мудрено, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.
Не согласился Лобачевский только с пятым, наиболее сомнительным с его точки зрения постулатом Евклида. Звучит его формулировка чрезвычайно мудрено, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.
Миф второй. В теории Лобачевского параллельные прямые пересекаются
Это не так. На самом деле пятый постулат Лобачевского звучит так: «На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную». Иными словами, для одной прямой можно провести как минимум две прямые через одну точку, которые не будут ее пересекать. То есть в этом постулате Лобачевского речи о параллельных прямых вообще не идет! Говорится лишь о существовании нескольких непересекающихся прямых на одной плоскости. Таким образом, предположение о пересечении параллельных прямых родилось из-за банального незнания сути теории великого российского математика.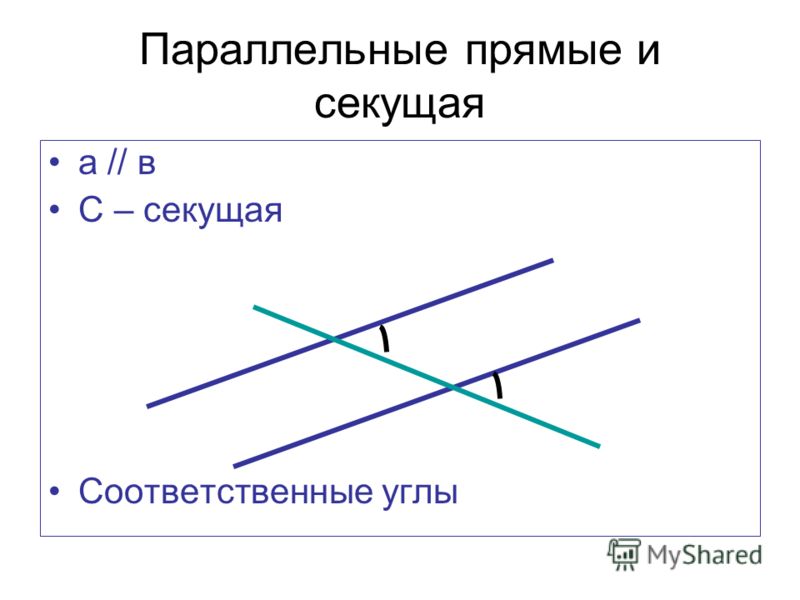
Миф третий. Геометрия Лобачевского — единственная неевклидова геометрия
Неевклидовы геометрии — это целый пласт теорий в математике, где основой является отличный от Евклидова пятый постулат. Лобачевский, в отличие от Евклида, к примеру, описывает гиперболическое пространство. Существует еще теория, описывающая сферическое пространство — это геометрия Римана. Вот в ней-то как раз параллельные прямые пересекаются. Классический тому пример из школьной программы — меридианы на глобусе. Если посмотреть на лекало глобуса, то окажется, что все меридианы параллельны. Меж тем, стоит нанести лекало на сферу, как мы видим, что все ранее параллельные меридианы сходятся в двух точках — у полюсов. Вместе теории Евклида, Лобачевского и Римана называют «три великих геометрии».
Миф четвертый. Геометрия Лобачевского не применима в реальной жизни
Напротив, современная наука приходит к пониманию, что Евклидова геометрия — лишь частный случай геометрии Лобачевского, и что в реальный мир точнее описывается именно формулами русского ученого.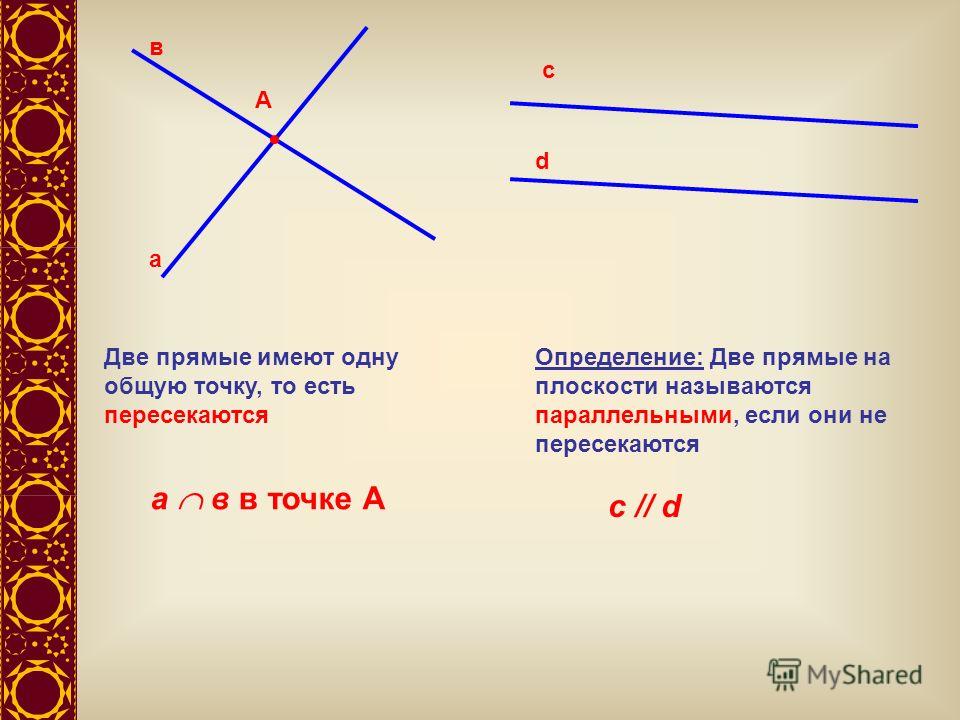 Сильнейшим толчком к дальнейшему развитию геометрии Лобачевского стала теория относительности Альберта Эйнштейна, которая показала, что само пространство нашей Вселенной не является линейным, а представляет собой гиперболическую сферу. Между тем, сам Лобачевский, несмотря на то, что всю жизнь работал над развитием своей теории, называл ее «воображаемой геометрией».
Сильнейшим толчком к дальнейшему развитию геометрии Лобачевского стала теория относительности Альберта Эйнштейна, которая показала, что само пространство нашей Вселенной не является линейным, а представляет собой гиперболическую сферу. Между тем, сам Лобачевский, несмотря на то, что всю жизнь работал над развитием своей теории, называл ее «воображаемой геометрией».
Миф пятый. Лобачевский первым создал неевклидову геометрию
Это не совсем так. Параллельно с ним и независимо от него к подобным выводам пришли венгерский математик Янош Бойяи и знаменитый немецкий ученый Карл Фридрих Гаусс. Однако труды Яноша не были замечены широкой публикой, а Карл Гаусс и вовсе предпочел не издаваться. Поэтому именно наш ученый считается первопроходцем в этой теории. Однако существует несколько парадоксальная точка зрения, что первым неевклидову геометрию придумал сам Евклид. Дело в том, что он самокритично считал свой пятый постулат не очевидным, поэтому большую часть из своих теорем он доказал, не прибегая к нему.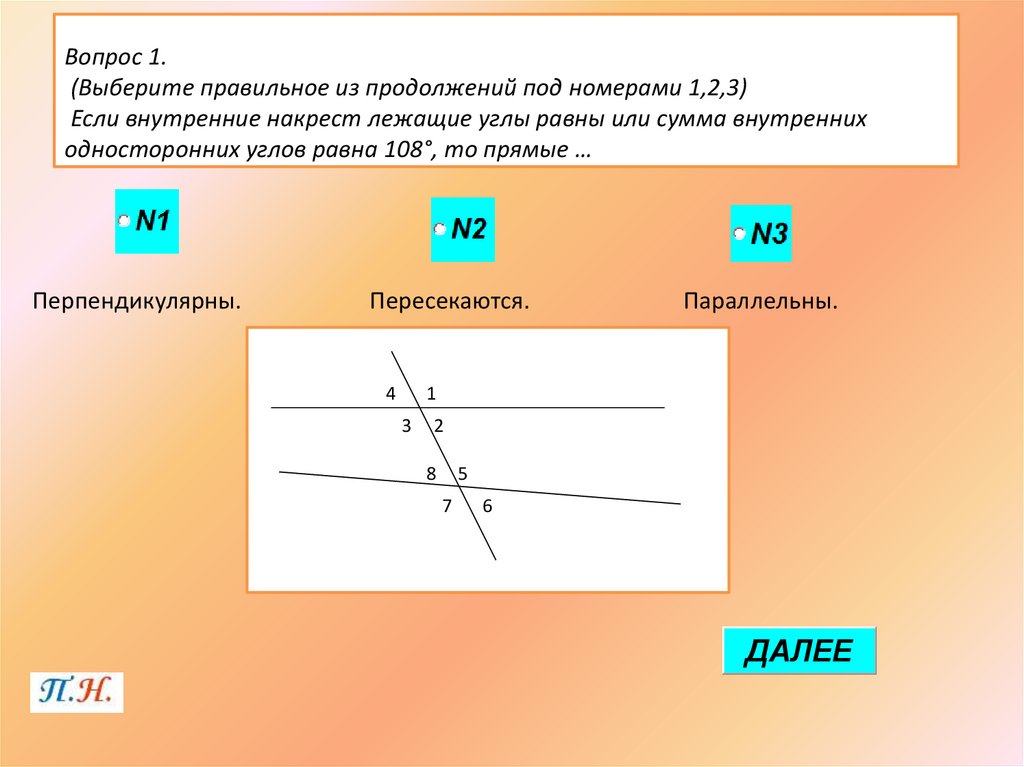
Как доказать что 2 параллельные прямые пересекаются в бесконечности?
Есть такая геометрия (математика) Лобачевского, где не так с параллельными прямыми как в классической Эвклидовой геометрии. Француз Понселе получил проективное пространство из обычного, постулировав существование «бесконечно удаленной плоскости» , содержащей «бесконечно удаленную прямую» для каждого пучка параллельных плоскостей, и «бесконечно удаленную точку» для каждого пучка параллельных прямых. Это позволило утверждать, что две параллельные прямые пересекаются в бесконечно удаленной точке.
А параллельные прямые в идеале вроде не пересекаются
Никак. Есть разные геометрии. В одной геометрии, например, через данную точку на плоскости можно провести прямую, параллельную данной, причем только одну. Это геометрия Евклида. В другой геометрии этого сделать нельзя, параллельных прямых на плоскости в ней вообще нет, все прямые на плоскости пересекаются, это геометрия Римана. В третьей через данную точку на плоскости можно провести бесконечное множество прямых параллельных данной (по крайней мере, две) , это геометрия Лобачевского. Это аксиомы в этих геометриях. Их принимают без доказательств, и на их основе строят свои дальнейшие рассуждения. Аксиомы не доказывают, это не теоремы. Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, то геометрия Римана — реализуется на поверхностях с постоянной положительной гауссовой кривизной. Есть и другие геометрии, например сферическая.
Это аксиомы в этих геометриях. Их принимают без доказательств, и на их основе строят свои дальнейшие рассуждения. Аксиомы не доказывают, это не теоремы. Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, то геометрия Римана — реализуется на поверхностях с постоянной положительной гауссовой кривизной. Есть и другие геометрии, например сферическая.
По свойствам паралельные никогда не пересекаются даже в бесконечности. Пребставь, что рельсы где-нибудь в каком-нибудь населеном пункте пересекутся. Что будет?
Вы не знаете определения параллельности прямых. Посмотрите определение: чтобы прямые можно было назвать параллельными — необходимым условием является их непересекаемость. Раз пересекаются — значит прямые непараллельны…
Сегодня я нашел доказательство пересечения двух параллельных прямых в бесконечности.
Теория параллельных прямых. Теория треугольника, страница 14
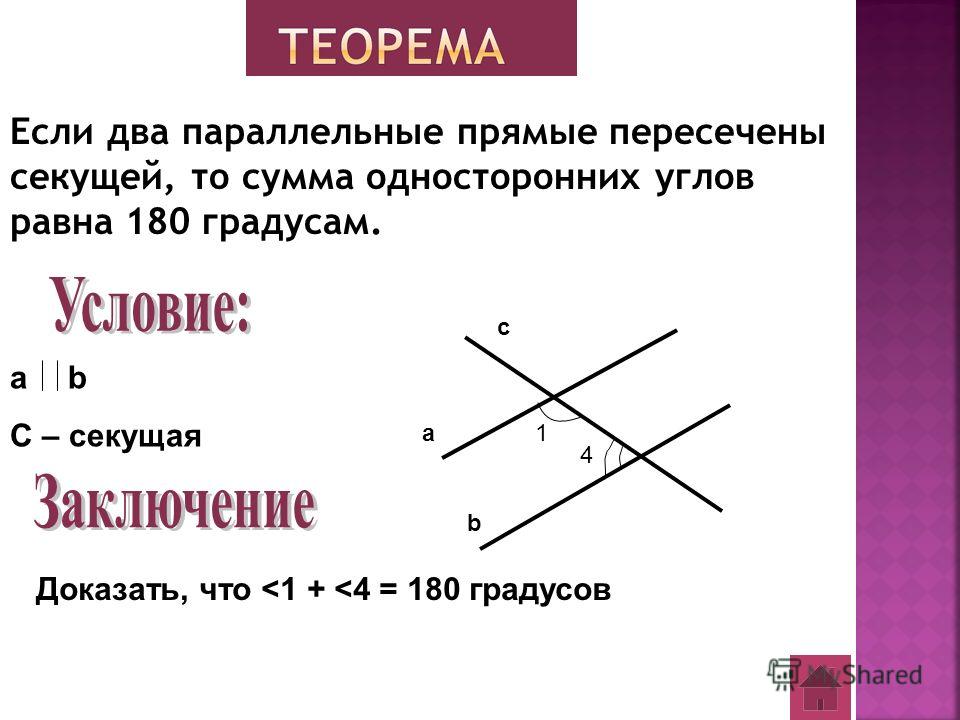
Если при пересечении двух прямых секущей сумма внутренних односторонних углов не равна 180°, то прямые не параллельны, то есть при достаточном продолжении пересекаются.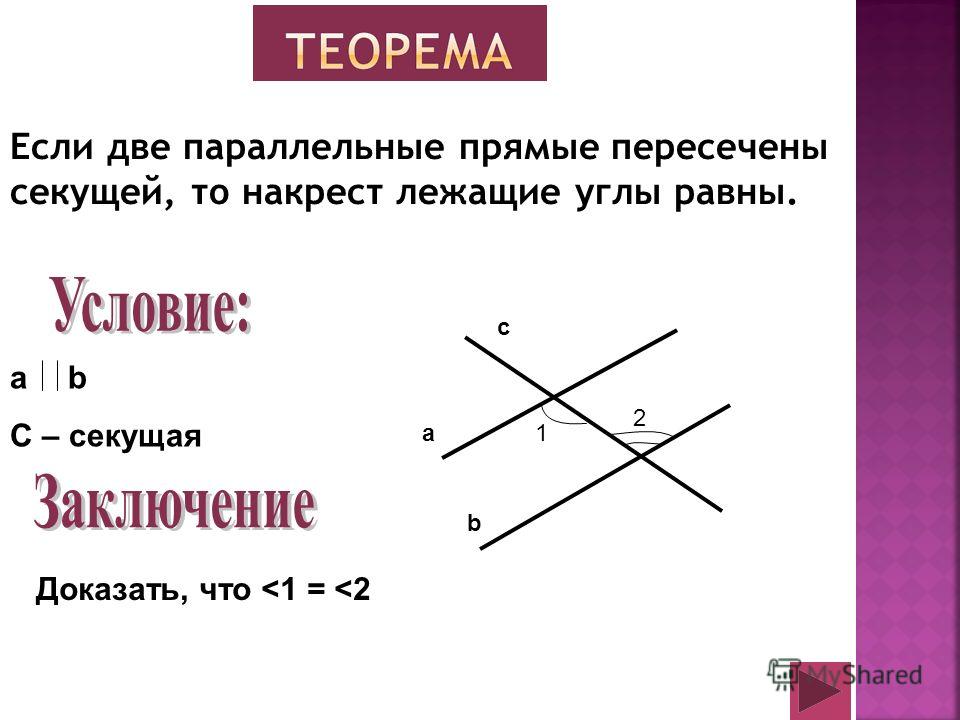
Доказательство. Если бы эти прямые не пересекались, то они были бы параллельны, и тогда сумма внутренних односторонних углов равнялась бы 180°, что противоречит условию. Теорема доказана.
Сформулируйте обратную теорему.
3.3. Взаимное расположение четырех прямых.
Мы изучили различные случаи взаимного расположения двух и трёх прямых на плоскости. Теперь изучим взаимное расположения четырёх прямых на плоскости. Изобразим разные случаи.
А) две пересекающиеся прямые пересекают две другие пересекающиеся прямые:
Б) каждая из двух пересекающиеся прямых пересекает две параллельные прямые:
В) две параллельные прямые пересечены двумя параллельными прямыми:
Г) три параллельные прямые пересечены третьей прямой:
Д) все четыре прямые параллельны:
Какие фигуры вы можете увидеть на этих рисунках? Например, на рис.3.23, слева, видна фигура, состоящая из четырех отрезков, два из которых параллельны. На рис.3.23 Видно, что при пересечении двух параллельных прямых двумя другими параллельными прямыми получилась фигура, у которой противоположные стороны попарно параллельны и равны.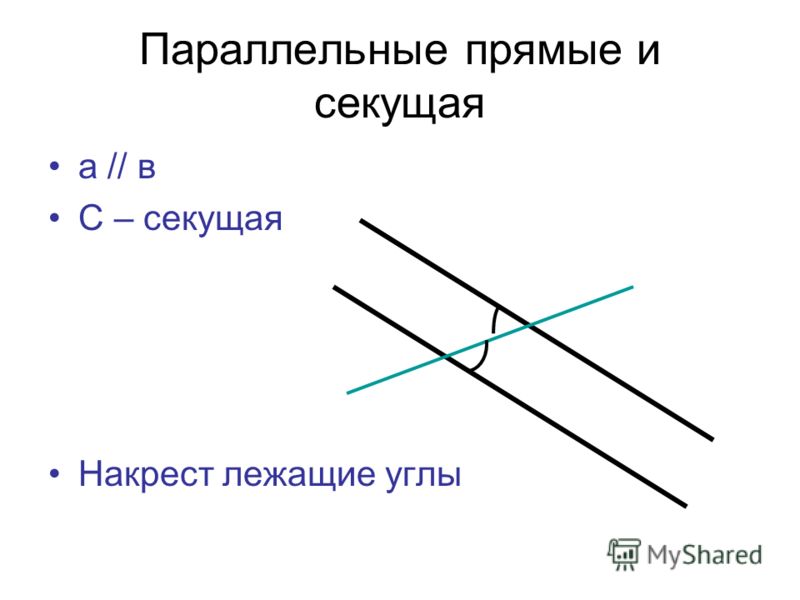 Докажем это.
Докажем это.
Лемма 1. При пересечении двух параллельных прямых двумя другими параллельными между собой прямыми получается фигура, у которой противоположные стороны параллельны.
Доказательство. Пусть параллельные между собой прямые A, B и параллельные между собой прямые C, D пересекаются в точках A, B, C, D (рис.3.26).
Докажем, что АВ=СD и АD=ВС. Проведём отрезок АС (рис.3.27, а). Для начала докажем, что АВ=СD.
Углы ÐACD иÐСAB равны как внутренние накрест лежащие при параллельных прямых A и B и секущей AC. Углы ÐDAC иÐACB равны как внутренние накрест лежащие при параллельных прямых C и D и секущей AC.
На луче АВ отложим отрезок АЕ, равный отрезку CD (рис.3.27, б). Углы ÐACD иÐСAE равны, значит, их соответственные поперечины AD и CE равны.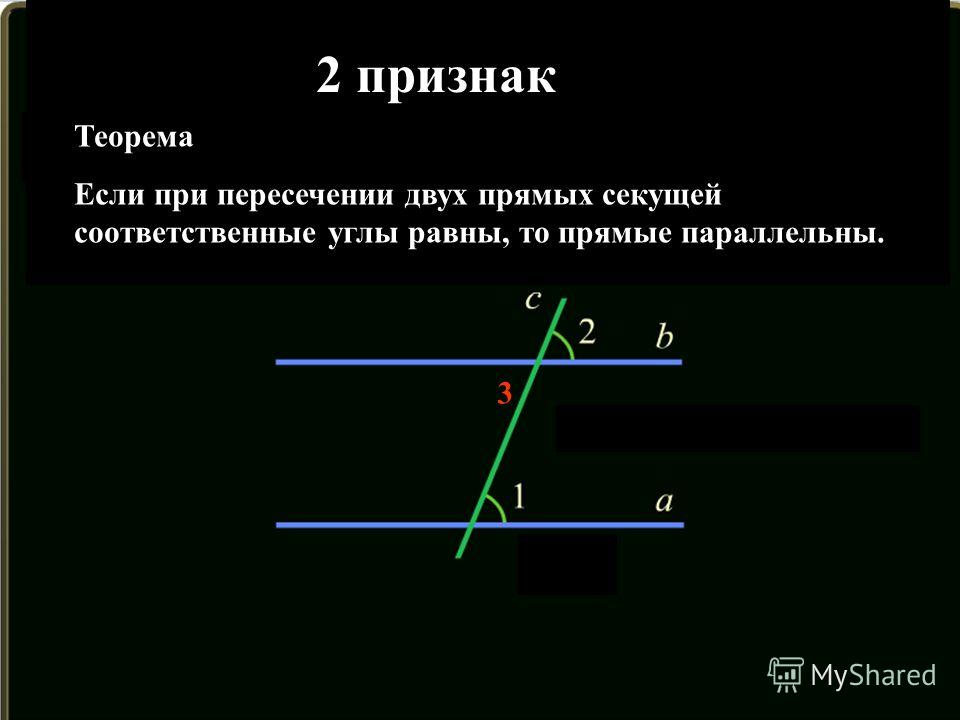 То есть АЕ и DC – соответственные поперечины углов ÐDAC иÐACB, но они равны по построению, а значит, угол ÐACЕ равен углу ÐDAC. Но угол ÐDAC равен углу ÐACB. Это означает, что равны углы ÐACЕ иÐACB, то есть точка Е лежит на луче СВ. По построению точка Е лежит на луче АВ. Но эти лучи пересекаются в точке В, то есть точки В и Е совпадают и АВ=АЕ=CD.
То есть АЕ и DC – соответственные поперечины углов ÐDAC иÐACB, но они равны по построению, а значит, угол ÐACЕ равен углу ÐDAC. Но угол ÐDAC равен углу ÐACB. Это означает, что равны углы ÐACЕ иÐACB, то есть точка Е лежит на луче СВ. По построению точка Е лежит на луче АВ. Но эти лучи пересекаются в точке В, то есть точки В и Е совпадают и АВ=АЕ=CD.
Итак мы доказали, что равны отрезки АВ и СD. Отрезки AD и CB равны как соответственные поперечины равных углов. Утверждение леммы 1 доказано.
Следствие 5: Противоположные углы фигуры ABCD равны (рис.3.27).
Параллельные прямые пересекаются: миф или реальность?
Автор: Панкратов Влад Научный руководитель: Попова Е. А. Параллельные прямые пересекаются: миф или реальность?
Актуальность: параллельные прямые не пересекаются в школьном курсе геометрии, но почему рельсы на горизонте сходятся? И есть предположение, что параллельные прямые пересекаются.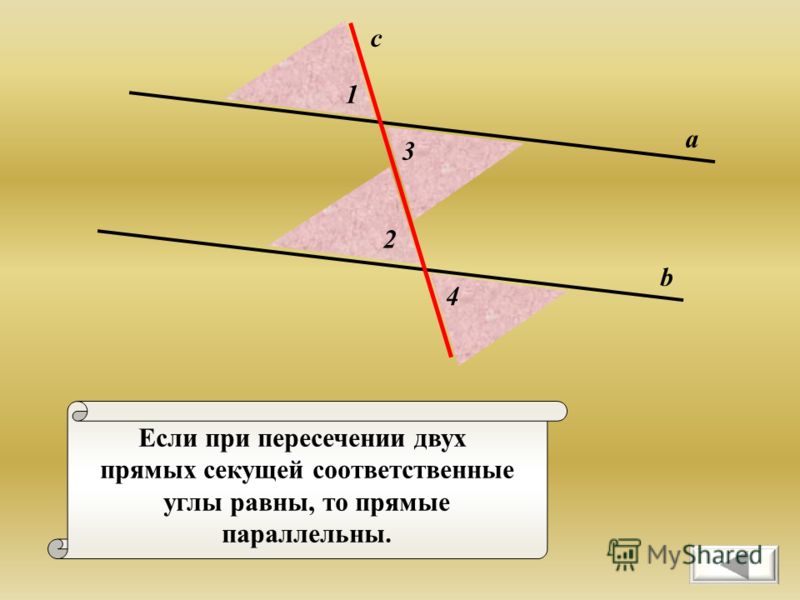 Так ли это? Я и решил выяснить.
Так ли это? Я и решил выяснить.
Происхождение понятия параллельных прямых. От Евклида Евкли́д ( 300 г. до н. э.) — древнегреческий математик, автор “Начал”. Начала Евклида — это сборник математических трудов, который состоит из 13 книг. В первой книге рассматриваются 5 важных постулатов.
Рассмотрим примечательные 5 постулатов “Начал” Евклида: 1. От всякой точки до всякой точки можно провести прямую. 2. Ограниченную прямую можно непрерывно продолжать по прямой. 3. Из всякого центра всяким раствором может быть описан круг. 4. Все прямые углы равны между собой. 5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых
Необычность 5 постулата Евклида В течение двух тысячелетий не прекращались попытки исключить 5 постулат из списка аксиом и вывести как теорему, как получилось с 4 постулатом. Все эти попытки окончились неудачей.
Источник понятия “ параллельные прямые ” Следствием 5 постулата является понятие параллельных прямых, не пересекающихся на всем их протяжении; и, далее, аксиома параллельности: через точку, не лежащую на заданной прямой, нельзя провести более одной прямой, параллельной этой заданной прямой.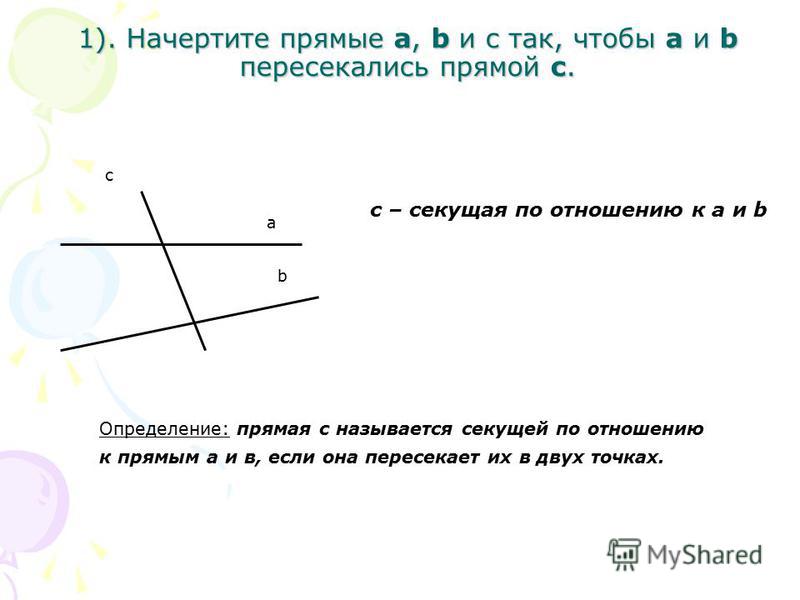
В результате безуспешных попыток доказать 5 постулат возникли неевклидовые геометрии. Рассмотрим их: Геометрия Николая Ивановича Лобачевского. Сферическая геометрия древних греков. Геометрия Георгия Римана.
Лобачевский Николай Иванович Годы жизни : 1792 – 1856 ( Нижний Новгород – Казань) Ректор Казанского университета “ Коперник геометрии ”
Геометрия Лобачевского Ответ с улицы: «Лобачевский доказал, что параллельные прямые пересекаются.» «Лобачевский открыл, что параллельные прямые могут и пересечься». «А что такое параллельные прямые?» «Параллельные — это такие прямые, которые лежат в одной плоскости и не пересекаются». Несовместимые ответы!
Ф ольклор ( folklore — народная мудрость): Однажды Лобачевский думал, кутаясь в пальто: Как мир прямолинеен, видно, что-то здесь не то! И он вгляделся пристальней в безоблачную высь, И там все параллельные его пересеклись.
Диалоги на “ Эхе Москвы ” В е н е д и к т о в. Вот вы скажите, параллельные прямые пересекаются? С л у ш а т е л ь. Нет. В е н е д и к т о в. А вот у Лобачевского пересекаются, там другая система отсчёта. Леонид Радзиховский : «Вот когда Лобачевский придумал свою неевклидову геометрию, что две параллельные прямые могут пересечься, — это был действительно переворот в области геометрии и физики».
Нет. В е н е д и к т о в. А вот у Лобачевского пересекаются, там другая система отсчёта. Леонид Радзиховский : «Вот когда Лобачевский придумал свою неевклидову геометрию, что две параллельные прямые могут пересечься, — это был действительно переворот в области геометрии и физики».
Аксиомы о параллельных Правильная формулировка : через точку, не лежащую на заданной прямой, нельзя провести более одной прямой, параллельной этой заданной прямой. В школьном курсе ( Атанасян Л. С.): через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. В версии Лобачевского: через точку, не лежащую на заданной прямой, можно провести более одной прямой, параллельной этой заданной прямой. Правда, как известно, у каждого своя, но истина одна. Истина состоит в том, что параллельные друг другу прямые не пересекаются даже у Лобачевского!
Важно: А ксиому о параллельных доказать нельзя. В третьем десятилетии XIX в. два великих геометра — российский математик Николай Иванович Лобачевский и венгерский математик Янош Б о йаи —независимо друг от друга построили геометрическую теорию, основанную на отрицании аксиомы о параллельных. Эту теорию за рубежом, как правило, называют геометрией Лобачевского– Бойаи, а в России — геометрией Лобачевского. У нее есть и «обезличенное» название — гиперболическая геометрия. Геометрия Лобачевского применима в космологии, если учесть, что наше пространство искривлено гиперболически.
Эту теорию за рубежом, как правило, называют геометрией Лобачевского– Бойаи, а в России — геометрией Лобачевского. У нее есть и «обезличенное» название — гиперболическая геометрия. Геометрия Лобачевского применима в космологии, если учесть, что наше пространство искривлено гиперболически.
“ Плоскость ” Лобачевского — “ седло ” , “ воронка ” Лобачевский Николай Иванович умер, не дожив до признания своей теории 10 лет, осмеянный, больной, в нищете, его уволили из университета. Янош Бойаи сошел с ума, не получив отклика и поддержки своих идей у математиков того времени (у Карла Гаусса – короля математиков)
Сферическая геометрия Древних Греков. Сферическая геометрия — раздел геометрии, изучающий геометрические фигуры на поверхности сферы. Сферическая геометрия возникла в древности в связи с потребностями географии и астрономии. Сферическая геометрия нужна не только астрономам, штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, а также при геодезических съемках больших территорий поверхности Земли, когда становится необходимым учитывать ее шарообразность.
I век нашей эры Древняя Греция Геометрический труд “ Сферика ” – аналогично “ Началам ” Евклида Менелай Александрийский
Особенности сферической геометрии Прямые – большие круги (меридианы, экватор, параллели – малые круги ) Есть двуугольник У сферического треугольника могут быть все три угла прямыми Сумма углов треугольника меньше 3П, но больше П Две прямые пересекаются дважды (например, на северном и южном полюсах) Нет понятия параллельности
Геометрия Римана Геометрия Римана (эллиптическая геометрия) — одна из трёх «великих геометрий» (Евклида, Лобачевского и Римана). Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, то геометрия Римана реализуется на поверхностях с постоянной положительной гауссовой кривизной, т. е. на сферах. Исторически геометрия Римана появилась позже двух других геометрий (в 1854 г.).
Годы жизни: 1826 – 1866 (Германия – Италия) Место работы: Гёттингенский университет Научная сфера: математика, механика, физика Основатель римановой геометрии Георг Фридрих Бернхард Риман
Геометрия Римана похожа на сферическую геометрию, но отличается тем, что любые две «прямые» имеют не две, как в сферической, а только одну точку пересечения.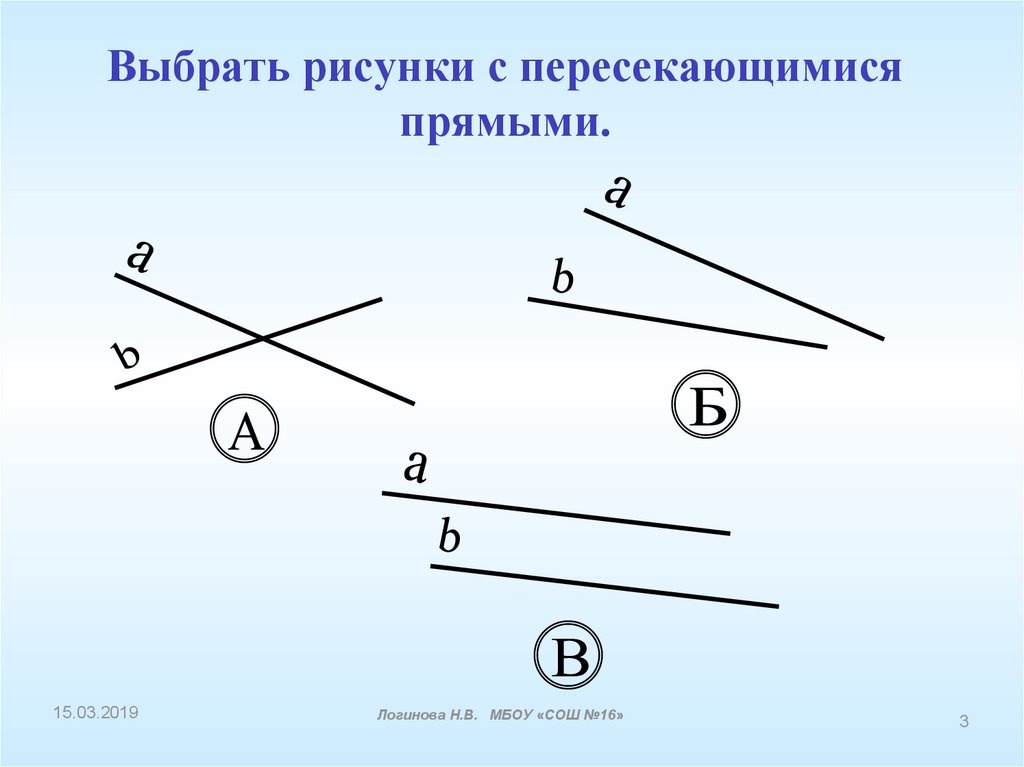 Поэтому иногда геометрией Римана называют геометрию на сфере, в которой противоположные точки отождествлены. В геометрии Римана любые прямые пересекаются, и таким образом, в ней нет параллельных прямых. Геометрия Римана не является абсолютной геометрией, ей нет практического применения.
Поэтому иногда геометрией Римана называют геометрию на сфере, в которой противоположные точки отождествлены. В геометрии Римана любые прямые пересекаются, и таким образом, в ней нет параллельных прямых. Геометрия Римана не является абсолютной геометрией, ей нет практического применения.
Заключение : Итак, подводя итоги, ответим на вопрос: “Параллельные прямые пересекаются”? Нет, в идеале они не пересекаются ни у Евклида (2 параллельные прямые), ни у Лобачевского (прямая и пучок прямых в незримо больших масштабах) – это миф. Но нет дыма без огня: параллельных прямых не существует в сферической геометрии древних греков и в геометрии Римана. А в реальности: нет прямых, как нет и других объектов геометрии, поэтому одна прямая или их несколько, параллельных данной.
Практически абсолютно бесконечные параллельные прямые линии пересекаются друг с другом в точке абсолютной бесконечности, так как каждая из них имеет в реальном пространстве мира вселенной их абсолютно бесконечное конической его формы сужение и расширение, что позволяет обоим этим прямым быть не двумя а одной конически сужающейся и конически расширяющейся общей линией, которая пересекается своими произвольно взятыми коническими прямыми боками в точке абсолютной бесконечности.
Николай Лобачевский известен тем, что создал новую геометрию, в которой параллельные прямые запросто пересекаются. На самом деле все не совсем так. Он просто внимательно изучил имеющуюся на тот момент геометрию Евклида и внес в нее кое-какие коррективы. Учитывая, что этой науке к тому моменту уже исполнилось 2 с лишним тысячи лет, без обновлений было не обойтись…
Николай Иванович Лобачевский родился 20 ноября 1792 года в Нижнем Новгороде. Семья была из простых. Дедушка будущего ученого был поляком, о бабушке известно лишь то, что она была крепостной крестьянкой у князя Михаила Долгорукого. Отец ученого служил чиновником в геодезическом департаменте и умер, когда Николаю было 8 лет.
С деньгами в семье было совсем плохо, и мать отправила Николая и двух его братьев в казанскую гимназию, где они смогли учиться за госсчет. В 16 лет Николай окончил учебу и попробовал поступить в только что открывшийся Казанский университет. С первого раза не выходит, зато со второй попытки Николая зачисляют на первый курс.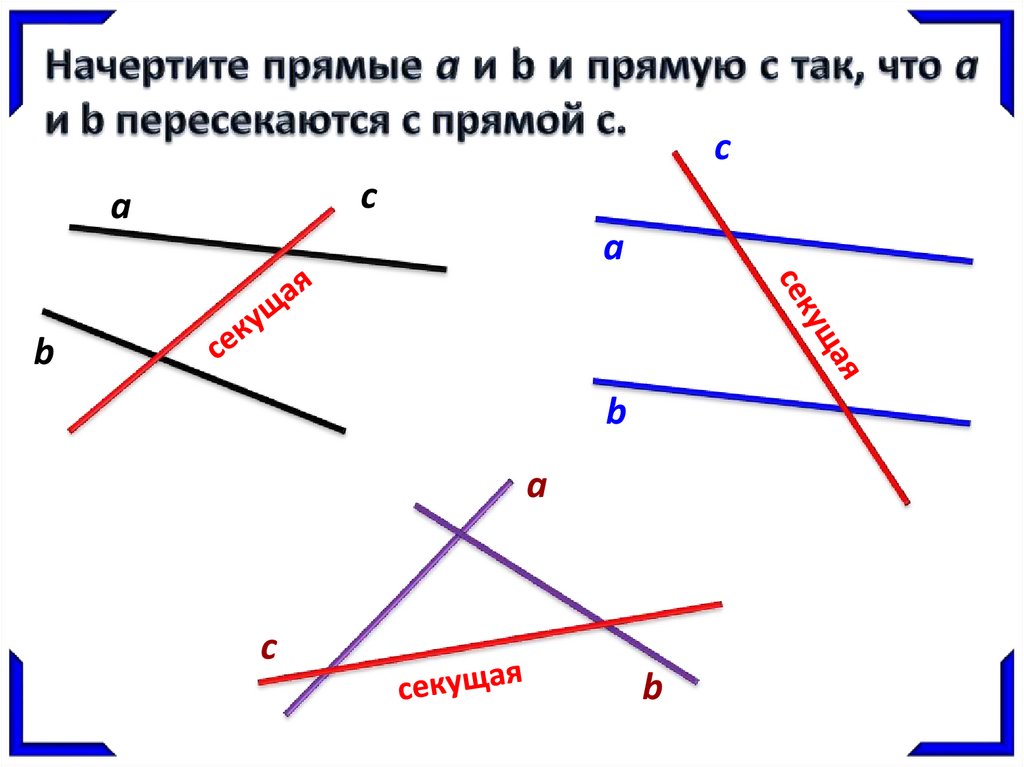
Из-за того, что университет только-только открылся, в первые годы там царила неразбериха. Доходило до того, что преподавать математику приходилось самим студентам! Впрочем, Лобачевский к паинькам не относился. Его современники туманно намекают на «студенческие шалости», в которых он участвовал на 1 — 2-м курсах. Но смогли доказать его участие только в одной проделке, когда Николай с приятелями под видом пиротехнических опытов запустили ракету прямо в аудитории! В наказание ему пришлось несколько дней просидеть в карцере.
С тех пор будущий ученый взялся за ум. Засел за учебу, увлекся химией и математикой… Но совсем без приключений не обошлось. Например, в 1811 году Лобачевский чересчур увлекся празднованием Нового года — настолько, что администрация даже хотела его отчислить. А это, как и сейчас, означало для юноши только одно — армию!
«В генваре месяце Лобачевский оказался самого худого поведения, — гласил рапорт, поданный университетскому начальству. —
Несмотря на приказание начальства не отлучаться из университета, он в новый год, а потом еще раз ходил в маскарад и многократно в гости, за что опять наказан написанием имени на черной доске и выставлением оной в студентских комнатах на неделю. Несмотря на сие, он после того снова еще был в маскараде»…
Несмотря на сие, он после того снова еще был в маскараде»…
Но благодаря заступничеству преподавателей, Лобачевского оставили в университете. Правда, лишили пособия на учебники, так что теперь ему приходилось покупать их за свой счет. Доучиться оставалось всего полгода, так что Лобачевский без особых проблем получил степень магистра по математике и физике с отличием.
Отправлять талантливого студента восвояси никому не хотелось. Поэтому с Лобачевского взяли обещание, что он будет вести себя хорошо, и заставили покаяться во всех прошлых проделках. На этих условиях его взяли преподавать арифметику и геометрию, а также заниматься научной работой.
Сперва карьера пошла вверх: в 1820 году Лобачевский стал деканом физико-математического факультета. Но потом в Казанский университет прислали проверку. Ревизор отчитался об «отсутствии благочестия» в вузе и взялся устанавливать новые порядки. В университете открылась кафедра богословия, все достойные ученые и профессора либо разъехались, либо были уволены.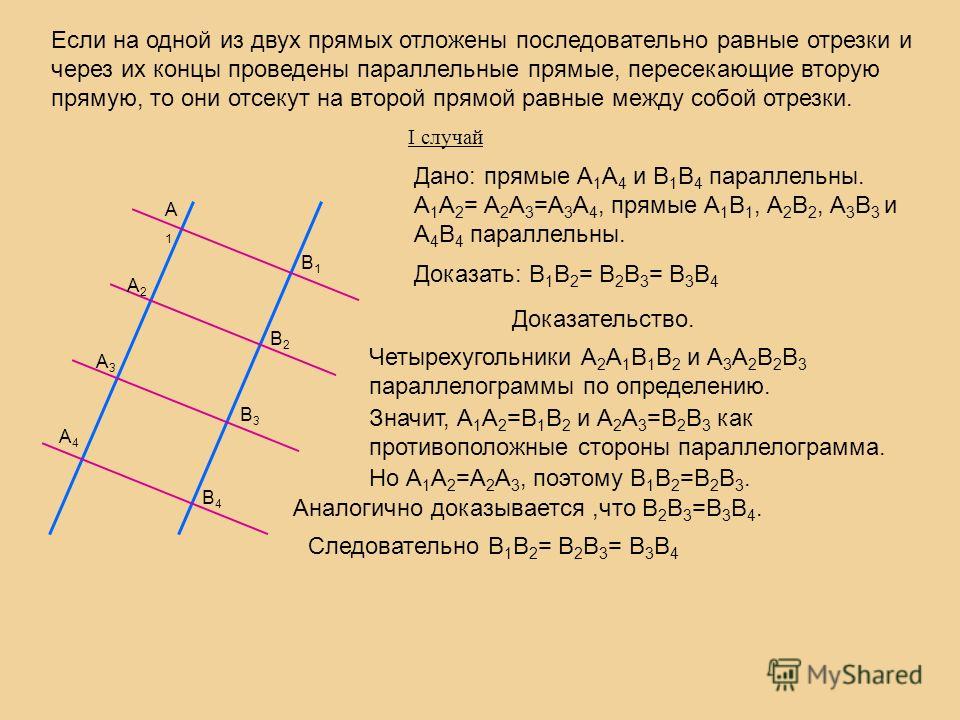
В такой атмосфере первый труд Лобачевского остался незамеченным. Еще в студенческие годы он пытался доказать пятый постулат Евклида, который звучит так:
«Если на плоскости при пересечении двух прямых третьей сумма внутренних односторонних углов меньше 180, то эти прямые при достаточном продолжении пересекаются».
То есть о параллельных прямых тут речи нет вообще! Речь идет лишь о непересекающихся… Разница в том, что между параллелями должно быть одинаковое расстояние по всей их длине. А для непересекающихся прямых это необязательно!
Над этим постулатом математики бились не одну сотню лет. Дело в том, что доказать его математическими средствами невозможно! Поэтому ученые и пытались создать свою геометрию, которая была бы лишена этого недостатка.
В первом своем учебнике, написанном в 1823 году, Лобачевский попытался это сделать и опровергнуть это утверждение. Но рецензентов возмутили такие вольности. Да и то, что ученый использовал метрическую систему, не добавило ему баллов. После такого разгрома Лобачевский еще долго не брался за написание учебников… Следующее пособие, по алгебре, он опубликовал только через 10 лет.
После такого разгрома Лобачевский еще долго не брался за написание учебников… Следующее пособие, по алгебре, он опубликовал только через 10 лет.
В 1826 году попечители Казанского университета осознали, что что-то идет не так, и ревизора отстранили «за злоупотребления властью». И в 1827 году новым ректором университета выбрали Николая Лобачевского.
Ученый получает карт-бланш. Он активно погружается во все хозяйственные дела, не забывая при этом и про научные изыскания. Ведет занятия по алгебре, физике, началам анализа, теории вероятностей. И параллельно с этим читает открытые лекции по неевклидовой геометрии.
Одной из главных обязанностей Лобачевский считал наведение порядка в университете. По воспоминаниям современников, профессора сперва жаловались на строгие правила и формализм математика. Но вскоре поняли, что Лобачевский не злоупотребляет властью. «Когда он видел, что члены совета начинали спорить и спору их не предвиделось конца, Лобачевский обыкновенно прерывал заседание, оставлял спорный вопрос открытым до следующего раза; затем он приглашал к себе на дом спорщиков и у себя в кабинете в мирной беседе за чашкой чаю приводил их к соглашению. Этот прием всегда имел хорошие последствия, и на другом совете дело обходилось уже без всяких споров», — отзывался о нем попечитель университета Мусин-Пушкин.
Этот прием всегда имел хорошие последствия, и на другом совете дело обходилось уже без всяких споров», — отзывался о нем попечитель университета Мусин-Пушкин.
В 1829 году Лобачевский публикует серьезный научный труд «О началах геометрии». Именно он дал старт новому разделу науки — неевклидовой геометрии.
Если говорить просто, то Лобачевский считает неправильным, что непересекающихся прямых может быть только две. И предлагает свою аксиому:
«На плоскости через точку, не лежащую на данной прямой, проходит более, чем одна прямая, не пересекающая данную».
Дело в том, что Евклид в прямом смысле слова плоско мыслил! Свой постулат он сформулировал только для плоскости. Если нарисовать прямую А и точку на листе бумаги, то через эту точку и правда можно провести всего одну прямую В, не пересекающую предыдущую.
А вот на кривой поверхности таких прямых будет гораздо больше. То есть Евклид описал лишь один частный случай, а не все существующие варианты. Пространство может быть и в форме седла, и в форме воронки… И геометрия Лобачевского описывает лучше всего именно такие формы — «с отрицательной кривизной».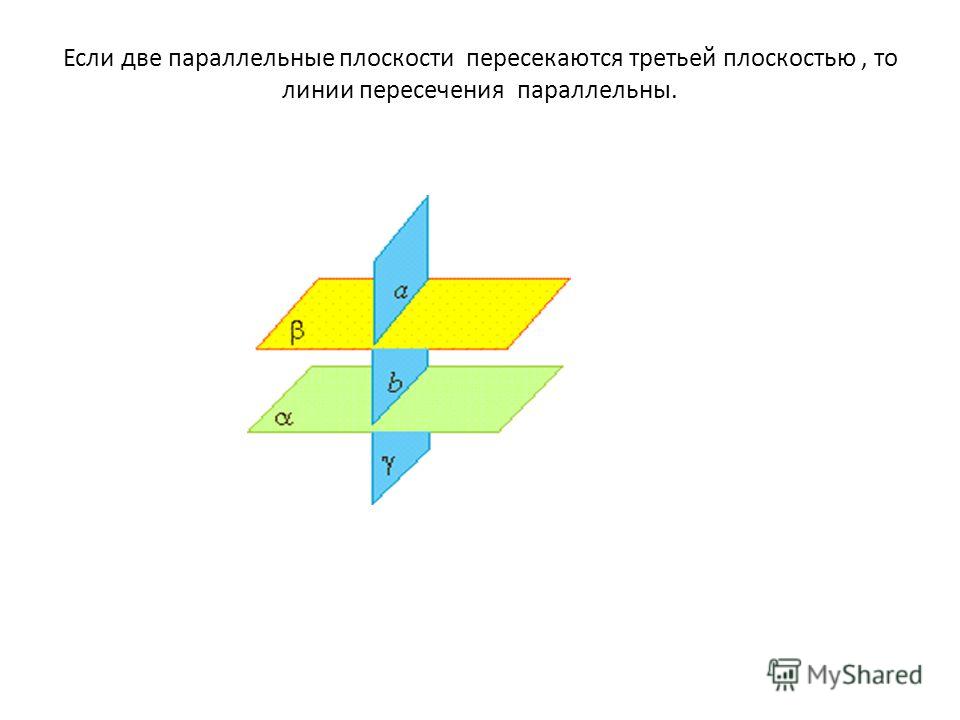
Лобачевский предположил, что в трехмерном пространстве параллельные прямые вполне могут иметь общие точки
Но современники Лобачевского понять этой логики не смогли. На него обрушился целый вал пасквилей и карикатур. Никто не мог поверить, что провинциальный педагог смог всерьез опровергнуть античную аксиому.
В 1832 году ученый женился на Варваре Моисеевой, которая была почти на 20 лет моложе его. В имении жены, недалеко от Казани, он развел большой сад. По преданию, Лобачевский сам посадил кедры и с грустью сказал, что не дождется их плодов. Предсказание сбылось — первые орехи были сняты в год смерти ученого. А кедровая роща на том месте сохранилась до сих пор…
В 1846 году Николая Ивановича отстраняют от должности ректора и лишают профессорской кафедры. Семья лишается значительной части дохода, имение жены приходится продать за долги. Здоровье ученого начинает слабеть, зрение падает. Последний свой труд, «Пангеометрию», Лобачевский создал в 1855 году. Текст записывали под диктовку его ученики — сам Николай Иванович к тому моменту уже ослеп.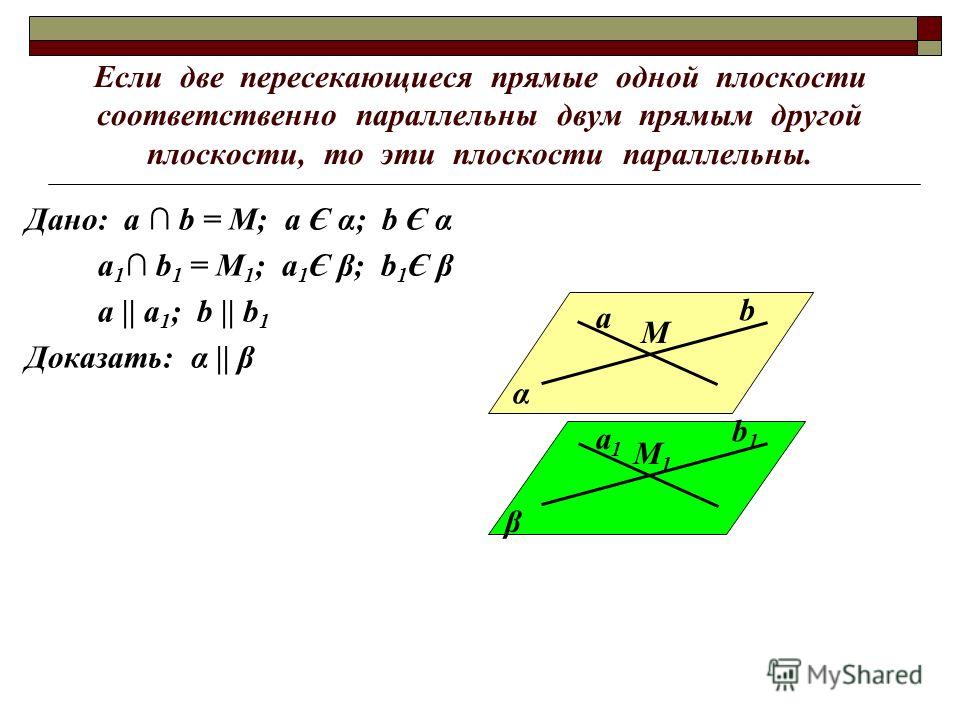
Николай Иванович Лобачевский скончался 12 февраля 1856 года, и был похоронен в Казани, на Арском кладбище. Сочинения ученого оценили по достоинству только после его смерти, во второй половине 1860-х годов.
Современная физика Вселенной пришла к выводу, что пространство, где мы с вами живем, обладает отрицательной кривизной. И именно геометрия Лобачевского описывает его лучше всего.
Без геометрии Лобачевского у нас не было бы теории относительности Эйнштейна, исследований Клейна и Пуанкаре. Его работы расширили наше представление о мире и дали возможность составить о нем более точное представление.
Великие ученые: Николай Лобачевский.Русский математик, создатель неевклидовой геометрии, деятель университетского образования и народного просвещения.
Иными словами, параллельные – это те, у которых нет ни одной общей точки. Обратите внимание на то, что данное определение справедливо только в том случае, если прямые находятся в одной плоскости, если же они не имеют общих точек, находясь в разных плоскостях, то они считаются скрещивающимися.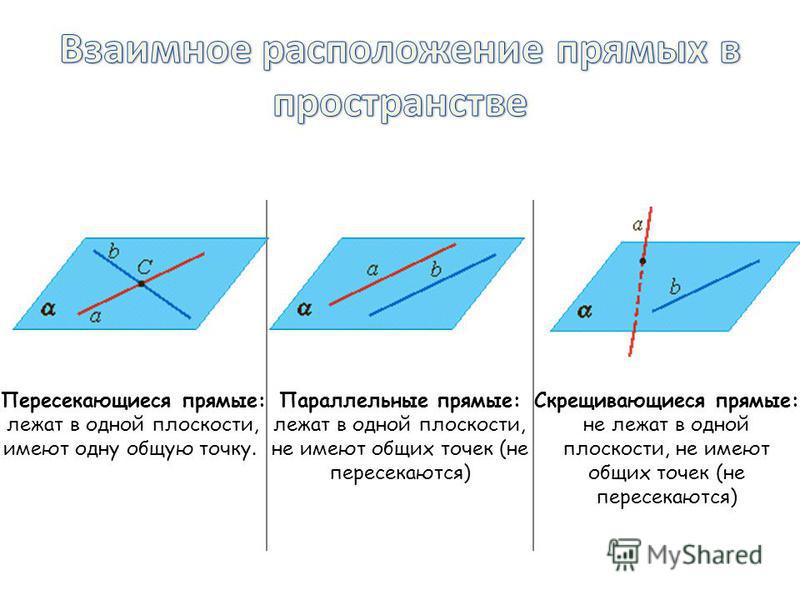
Как доказать что 2 параллельные прямые пересекаются в бесконечности?
Лобачевский сумел доказать ложность этого посыла.
Xn—-8sbanwvcjzh9e. xn--p1ai
05.04.2018 19:51:01
2018-04-05 19:51:01
Источники:
Https://xn—-8sbanwvcjzh9e. xn--p1ai/raznoe/dve-pryamye-parallelnye-peresekayutsya. html
Сколько параллельных прямых в геометрии Лобачевского — Наука — ТАСС » /> » /> .keyword { color: red; }
Кто из великих математиков доказал что параллельные прямые могут пересекаться
Все мы слышали про параллельные прямые. Сначала нас учат, что они никогда не пересекаются, а потом где-то на факультативах в районе старших классов тихо добавляют, что из этого правила бывают исключения. Например, в геометрии, придуманной нашим соотечественником Николаем Лобачевским. Так ли это на самом деле, как вообще это возможно и при чем здесь Эйнштейн — разобрались вместе с редакцией научно-популярного портала «Чердак».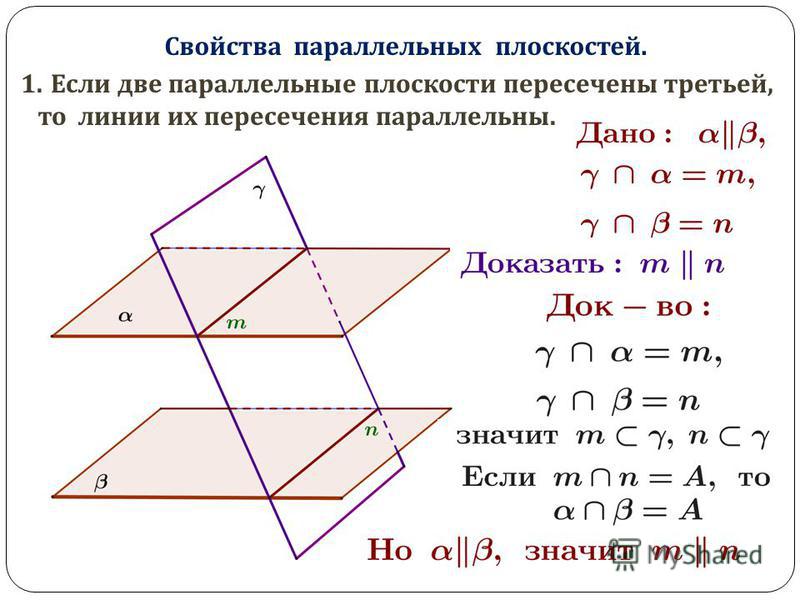
Что не так с пятым постулатом
Более 2300 лет назад древнегреческий математик Евклид собрал все имевшиеся до него знания о геометрии в одну большую книгу — «Начала». Именно в ней содержались знаменитые пять постулатов — недоказуемые утверждения, на фундаменте которых возводились все дальнейшие рассуждения и теоремы.
Первые четыре постулата были лаконичны и стройны. В их истинности, наверное, никто не сомневался за всю историю мира, но пятый постулат звучал гораздо более запутанно и мало напоминал неоспоримую истину.
Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых
Это утверждение в разных формулировках (самая распространенная из них гласит, что в плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной) пытались доказать десятки математиков, но все они втягивались в одну и ту же историю.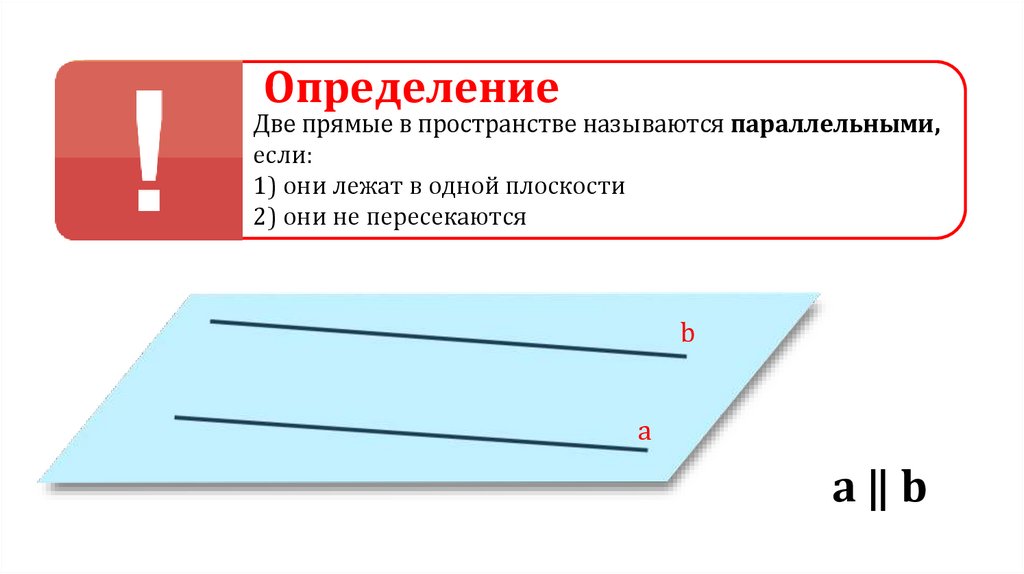 Их доказательства упирались в утверждения, доказать которые без самого пятого постулата было абсолютно невозможно.
Их доказательства упирались в утверждения, доказать которые без самого пятого постулата было абсолютно невозможно.
Лобачевского пятый постулат смущал не столько своей неаккуратностью, сколько философской нагрузкой: он поселял материю в какое-то застывшее абсолютное пространство. Твердый материалист, он не мог принимать исключительно на веру, что параллельные прямые не пересекаются где-нибудь в бесконечности космоса. Ученый обратился к доказательству от противного. Он попробовал заменить пятый постулат на его зеркальное отражение («Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие ее»). Лобачевский ждал, не появится ли во всей системе геометрических теорем внутренних противоречий, косвенно указывающих на то, что изначальная версия пятого постулата — была все-таки неизбежно верна в нашем пространстве? Но такого не случилось — противоречий не нашлось.
7 февраля 1826 года (по старому стилю) Лобачевский представил перед ученой комиссией Казанского университета свой труд — «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных».
Геометрия новая — проблемы старые
Доклад Лобачевского от 7 февраля провалился.
Незадолго до выступления новый император Николай I сместил Михаила Магницкого с должности попечителя Казанского университета, и все члены комиссии думали, как это повлияет на их жизнь, и почти не обращали внимания на странноватого математика, рассказывавшего на французском о какой-то инопланетной геометрии. Дальше рукопись была отдана на рецензию некоторым членам комиссии, но они, видимо, просто позабыли о ней, и сам доклад так и не был одобрен к публикации. Тогда вся геометрия Лобачевского могла навсегда остаться внутри его головы, если бы не одна неожиданность: новым ректором университета вскоре был избран именно он. Вряд ли у Лобачевского стало после этого меньше работы и больше сил, но постепенно он оформил свои идеи в законченный труд «О началах геометрии», который сначала напечатали в журнале «Казанский вестник», а потом представили на отзыв в Академию наук, где рецензия досталась одному из самых сильных русских математиков того времени — Михаилу Остроградскому.
Автор, по-видимому, задался целью написать таким образом, чтобы его нельзя было понять. Он достиг этой цели; большая часть книги осталась столь же неизвестной для меня, как если бы я никогда не видел ее…
Новая геометрия остается непонятной. Блуждание продолжается.
Позже Лобачевский публиковал свои труды в европейских журналах, где их заметил великий немец Гаусс, который сам не один год втайне ото всех занимался неевклидовой геометрией. Чтобы лучше понять казанского ученого, он оперативно выучил русский и потом, впечатленный смелостью и ясностью мыслей Лобачевского, выдвинул того в члены-корреспонденты Геттингенского королевского научного общества. Признание встречает своего гения, хотя на родине Остроградский и люди его окружения раз за разом отклоняют все работы по неевклидой геометрии вплоть до самой смерти Лобачевского в 1856 году.
Отложенное признание
Проходит 12—15 лет, и математики находят сразу несколько реальных моделей, в которых работает именно геометрия Лобачевского.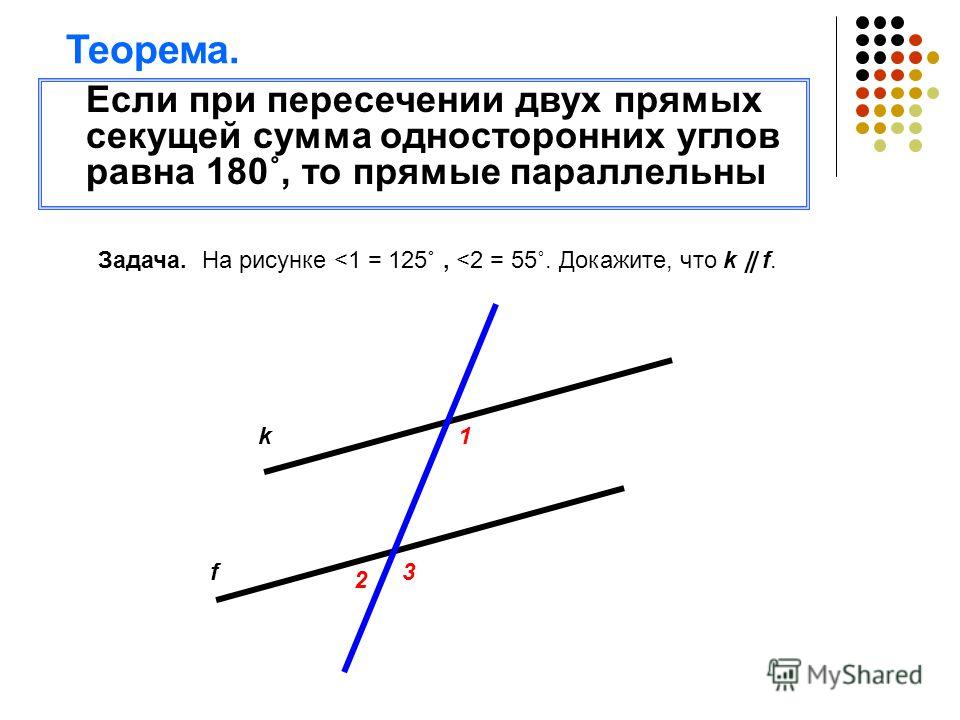 В самой простой из них, проективной, за плоскость принимают внутренность круга, а за прямую — его хорду. В результате тот факт, что через одну точку, лежащую внутри круга, можно провести сколько угодно хорд, не пересекающихся с одной фиксированной хордой, автоматически становится иллюстрацией пятого начала геометрии Лобачевского.
В самой простой из них, проективной, за плоскость принимают внутренность круга, а за прямую — его хорду. В результате тот факт, что через одну точку, лежащую внутри круга, можно провести сколько угодно хорд, не пересекающихся с одной фиксированной хордой, автоматически становится иллюстрацией пятого начала геометрии Лобачевского.
Он достиг этой цели; большая часть книги осталась столь же неизвестной для меня, как если бы я никогда не видел ее.
Nauka. tass. ru
03.02.2020 4:03:21
2020-02-03 04:03:21
Источники:
Https://nauka. tass. ru/nauka/4775456
Николай Лобачевский: параллельные прямые все-таки пересекаются! KP. Ru » /> » /> .keyword { color: red; }
Кто из великих математиков доказал что параллельные прямые могут пересекаться
Николай Лобачевский известен тем, что создал новую геометрию, в которой параллельные прямые запросто пересекаются. На самом деле все не совсем так. Он просто внимательно изучил имеющуюся на тот момент геометрию Евклида и внес в нее кое-какие коррективы.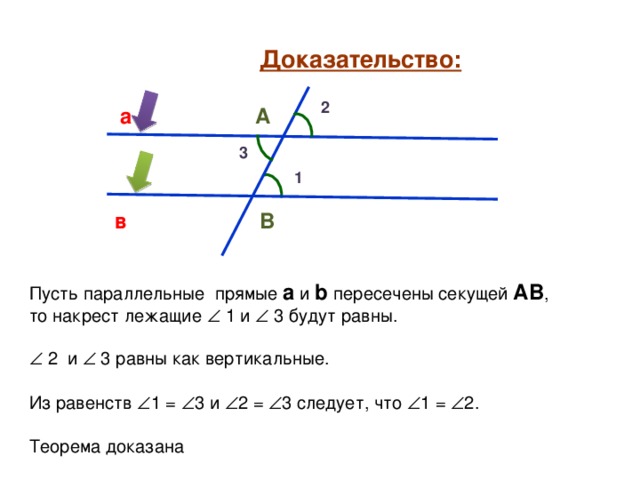 Учитывая, что этой науке к тому моменту уже исполнилось 2 с лишним тысячи лет, без обновлений было не обойтись…
Учитывая, что этой науке к тому моменту уже исполнилось 2 с лишним тысячи лет, без обновлений было не обойтись…
Николай Иванович Лобачевский родился 20 ноября 1792 года в Нижнем Новгороде. Семья была из простых. Дедушка будущего ученого был поляком, о бабушке известно лишь то, что она была крепостной крестьянкой у князя Михаила Долгорукого. Отец ученого служил чиновником в геодезическом департаменте и умер, когда Николаю было 8 лет.
С деньгами в семье было совсем плохо, и мать отправила Николая и двух его братьев в казанскую гимназию, где они смогли учиться за госсчет. В 16 лет Николай окончил учебу и попробовал поступить в только что открывшийся Казанский университет. С первого раза не выходит, зато со второй попытки Николая зачисляют на первый курс.
Из-за того, что университет только-только открылся, в первые годы там царила неразбериха. Доходило до того, что преподавать математику приходилось самим студентам! Впрочем, Лобачевский к паинькам не относился. Его современники туманно намекают на «студенческие шалости», в которых он участвовал на 1 — 2-м курсах. Но смогли доказать его участие только в одной проделке, когда Николай с приятелями под видом пиротехнических опытов запустили ракету прямо в аудитории! В наказание ему пришлось несколько дней просидеть в карцере.
Но смогли доказать его участие только в одной проделке, когда Николай с приятелями под видом пиротехнических опытов запустили ракету прямо в аудитории! В наказание ему пришлось несколько дней просидеть в карцере.
С тех пор будущий ученый взялся за ум. Засел за учебу, увлекся химией и математикой… Но совсем без приключений не обошлось. Например, в 1811 году Лобачевский чересчур увлекся празднованием Нового года — настолько, что администрация даже хотела его отчислить. А это, как и сейчас, означало для юноши только одно — армию!
«В генваре месяце Лобачевский оказался самого худого поведения, — гласил рапорт, поданный университетскому начальству. — Несмотря на приказание начальства не отлучаться из университета, он в новый год, а потом еще раз ходил в маскарад и многократно в гости, за что опять наказан написанием имени на черной доске и выставлением оной в студентских комнатах на неделю. Несмотря на сие, он после того снова еще был в маскараде».
Но благодаря заступничеству преподавателей, Лобачевского оставили в университете.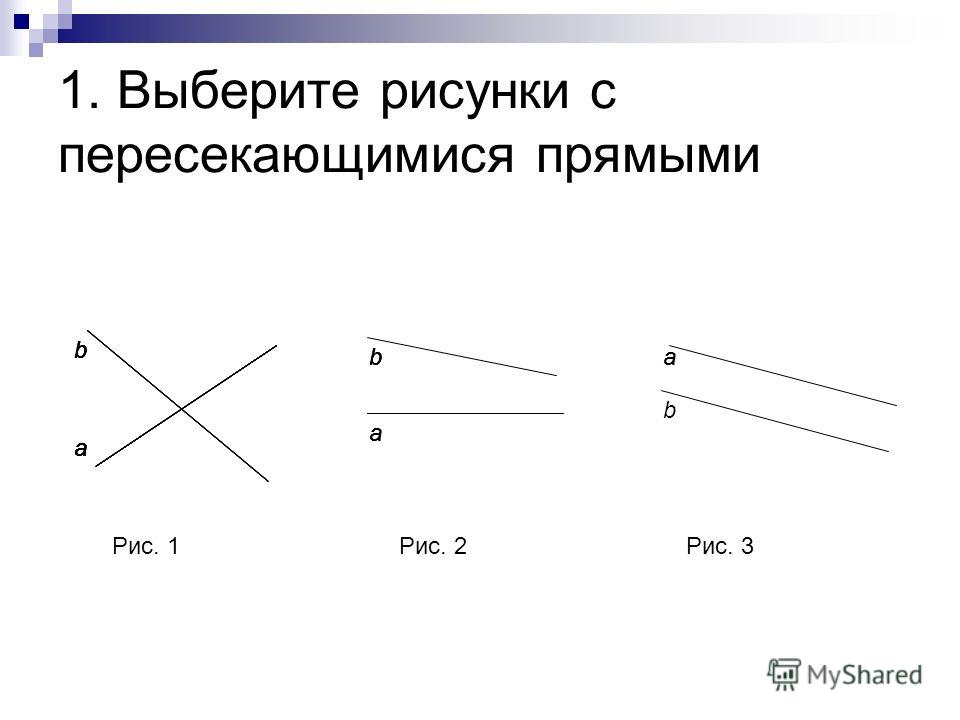 Правда, лишили пособия на учебники, так что теперь ему приходилось покупать их за свой счет. Доучиться оставалось всего полгода, так что Лобачевский без особых проблем получил степень магистра по математике и физике с отличием.
Правда, лишили пособия на учебники, так что теперь ему приходилось покупать их за свой счет. Доучиться оставалось всего полгода, так что Лобачевский без особых проблем получил степень магистра по математике и физике с отличием.
Отправлять талантливого студента восвояси никому не хотелось. Поэтому с Лобачевского взяли обещание, что он будет вести себя хорошо, и заставили покаяться во всех прошлых проделках. На этих условиях его взяли преподавать арифметику и геометрию, а также заниматься научной работой.
Сперва карьера пошла вверх: в 1820 году Лобачевский стал деканом физико-математического факультета. Но потом в Казанский университет прислали проверку. Ревизор отчитался об «отсутствии благочестия» в вузе и взялся устанавливать новые порядки. В университете открылась кафедра богословия, все достойные ученые и профессора либо разъехались, либо были уволены.
В такой атмосфере первый труд Лобачевского остался незамеченным. Еще в студенческие годы он пытался доказать пятый постулат Евклида, который звучит так:
«Если на плоскости при пересечении двух прямых третьей сумма внутренних односторонних углов меньше 180, то эти прямые при достаточном продолжении пересекаются».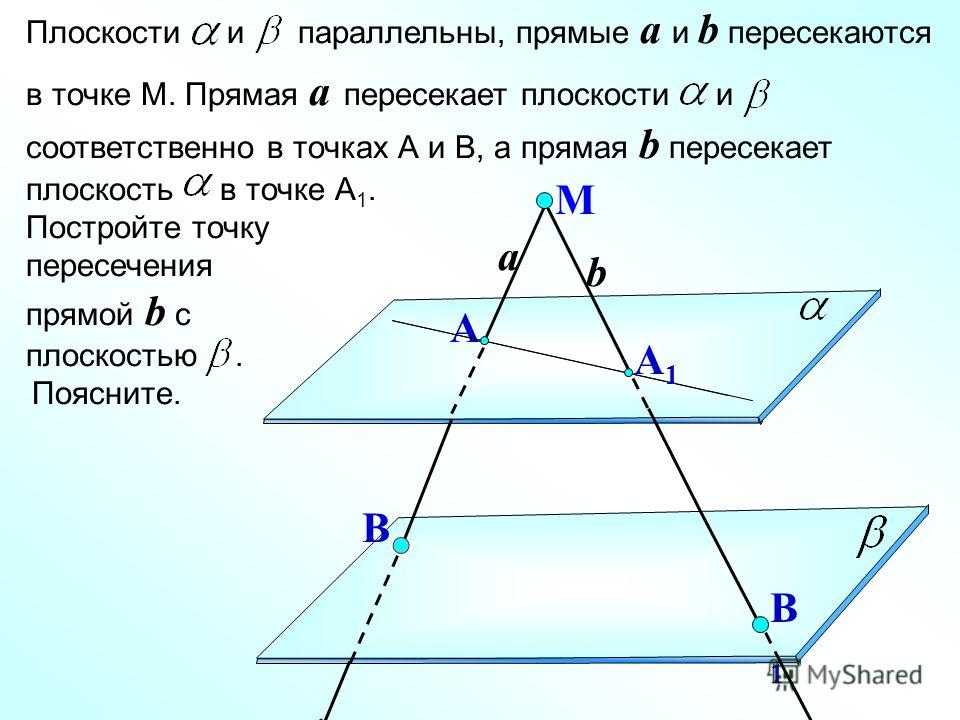
То есть о параллельных прямых тут речи нет вообще! Речь идет лишь о непересекающихся. Разница в том, что между параллелями должно быть одинаковое расстояние по всей их длине. А для непересекающихся прямых это необязательно!
Над этим постулатом математики бились не одну сотню лет. Дело в том, что доказать его математическими средствами невозможно! Поэтому ученые и пытались создать свою геометрию, которая была бы лишена этого недостатка.
В первом своем учебнике, написанном в 1823 году, Лобачевский попытался это сделать и опровергнуть это утверждение. Но рецензентов возмутили такие вольности. Да и то, что ученый использовал метрическую систему, не добавило ему баллов. После такого разгрома Лобачевский еще долго не брался за написание учебников… Следующее пособие, по алгебре, он опубликовал только через 10 лет.
В 1826 году попечители Казанского университета осознали, что что-то идет не так, и ревизора отстранили «за злоупотребления властью». И в 1827 году новым ректором университета выбрали Николая Лобачевского.
Ученый получает карт-бланш. Он активно погружается во все хозяйственные дела, не забывая при этом и про научные изыскания. Ведет занятия по алгебре, физике, началам анализа, теории вероятностей. И параллельно с этим читает открытые лекции по неевклидовой геометрии.
Одной из главных обязанностей Лобачевский считал наведение порядка в университете. По воспоминаниям современников, профессора сперва жаловались на строгие правила и формализм математика. Но вскоре поняли, что Лобачевский не злоупотребляет властью. «Когда он видел, что члены совета начинали спорить и спору их не предвиделось конца, Лобачевский обыкновенно прерывал заседание, оставлял спорный вопрос открытым до следующего раза; затем он приглашал к себе на дом спорщиков и у себя в кабинете в мирной беседе за чашкой чаю приводил их к соглашению. Этот прием всегда имел хорошие последствия, и на другом совете дело обходилось уже без всяких споров», — отзывался о нем попечитель университета Мусин-Пушкин.
В 1829 году Лобачевский публикует серьезный научный труд «О началах геометрии». Именно он дал старт новому разделу науки — неевклидовой геометрии.
Именно он дал старт новому разделу науки — неевклидовой геометрии.
Если говорить просто, то Лобачевский считает неправильным, что непересекающихся прямых может быть только две. И предлагает свою аксиому:
«На плоскости через точку, не лежащую на данной прямой, проходит более, чем одна прямая, не пересекающая данную».
Дело в том, что Евклид в прямом смысле слова плоско мыслил! Свой постулат он сформулировал только для плоскости. Если нарисовать прямую А и точку на листе бумаги, то через эту точку и правда можно провести всего одну прямую В, не пересекающую предыдущую.
А вот на кривой поверхности таких прямых будет гораздо больше. То есть Евклид описал лишь один частный случай, а не все существующие варианты. Пространство может быть и в форме седла, и в форме воронки. И геометрия Лобачевского описывает лучше всего именно такие формы — «с отрицательной кривизной».
Лобачевский предположил, что в трехмерном пространстве параллельные прямые вполне могут иметь общие точки
Но современники Лобачевского понять этой логики не смогли.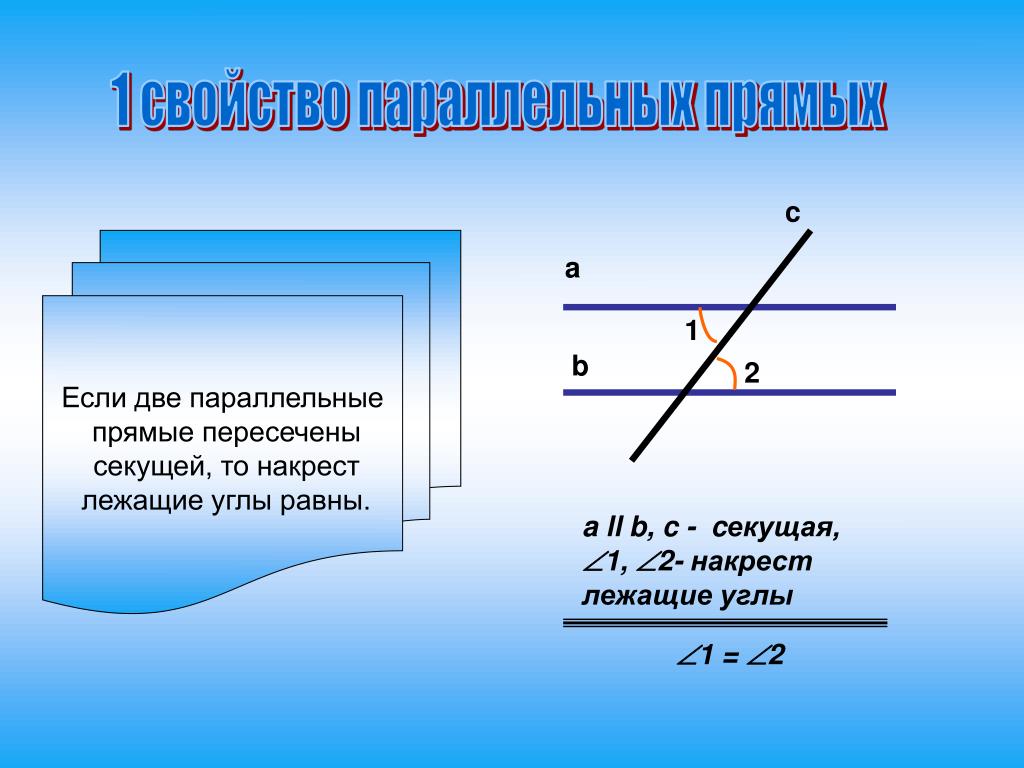 На него обрушился целый вал пасквилей и карикатур. Никто не мог поверить, что провинциальный педагог смог всерьез опровергнуть античную аксиому.
На него обрушился целый вал пасквилей и карикатур. Никто не мог поверить, что провинциальный педагог смог всерьез опровергнуть античную аксиому.
В 1832 году ученый женился на Варваре Моисеевой, которая была почти на 20 лет моложе его. В имении жены, недалеко от Казани, он развел большой сад. По преданию, Лобачевский сам посадил кедры и с грустью сказал, что не дождется их плодов. Предсказание сбылось — первые орехи были сняты в год смерти ученого. А кедровая роща на том месте сохранилась до сих пор.
В 1846 году Николая Ивановича отстраняют от должности ректора и лишают профессорской кафедры. Семья лишается значительной части дохода, имение жены приходится продать за долги. Здоровье ученого начинает слабеть, зрение падает. Последний свой труд, «Пангеометрию», Лобачевский создал в 1855 году. Текст записывали под диктовку его ученики — сам Николай Иванович к тому моменту уже ослеп.
Николай Иванович Лобачевский скончался 12 февраля 1856 года, и был похоронен в Казани, на Арском кладбище.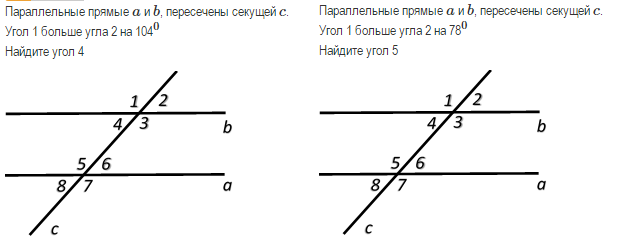 Сочинения ученого оценили по достоинству только после его смерти, во второй половине 1860-х годов.
Сочинения ученого оценили по достоинству только после его смерти, во второй половине 1860-х годов.
Современная физика Вселенной пришла к выводу, что пространство, где мы с вами живем, обладает отрицательной кривизной. И именно геометрия Лобачевского описывает его лучше всего.
Без геометрии Лобачевского у нас не было бы теории относительности Эйнштейна, исследований Клейна и Пуанкаре. Его работы расширили наше представление о мире и дали возможность составить о нем более точное представление.
Великие ученые: Николай Лобачевский
Русский математик, создатель неевклидовой геометрии, деятель университетского образования и народного просвещения.
Читайте также
Возрастная категория сайта 18 +
Сетевое издание (сайт) зарегистрировано Роскомнадзором, свидетельство Эл № ФС77-80505 от 15 марта 2021 г. Главный редактор — Сунгоркин Владимир Николаевич. Шеф-редактор сайта — Носова Олеся Вячеславовна.
Сообщения и комментарии читателей сайта размещаются без предварительного редактирования. Редакция оставляет за собой право удалить их с сайта или отредактировать, если указанные сообщения и комментарии являются злоупотреблением свободой массовой информации или нарушением иных требований закона.
Редакция оставляет за собой право удалить их с сайта или отредактировать, если указанные сообщения и комментарии являются злоупотреблением свободой массовой информации или нарушением иных требований закона.
АО «ИД «Комсомольская правда». ИНН: 7714037217 ОГРН: 1027739295781 127015, Москва, Новодмитровская д. 2Б, Тел. +7 (495) 777-02-82.
Великие ученые: Николай Лобачевский
Русский математик, создатель неевклидовой геометрии, деятель университетского образования и народного просвещения.
Возрастная категория сайта 18 +
Сетевое издание (сайт) зарегистрировано Роскомнадзором, свидетельство Эл № ФС77-80505 от 15 марта 2021 г. Главный редактор — Сунгоркин Владимир Николаевич. Шеф-редактор сайта — Носова Олеся Вячеславовна.
Сообщения и комментарии читателей сайта размещаются без предварительного редактирования. Редакция оставляет за собой право удалить их с сайта или отредактировать, если указанные сообщения и комментарии являются злоупотреблением свободой массовой информации или нарушением иных требований закона.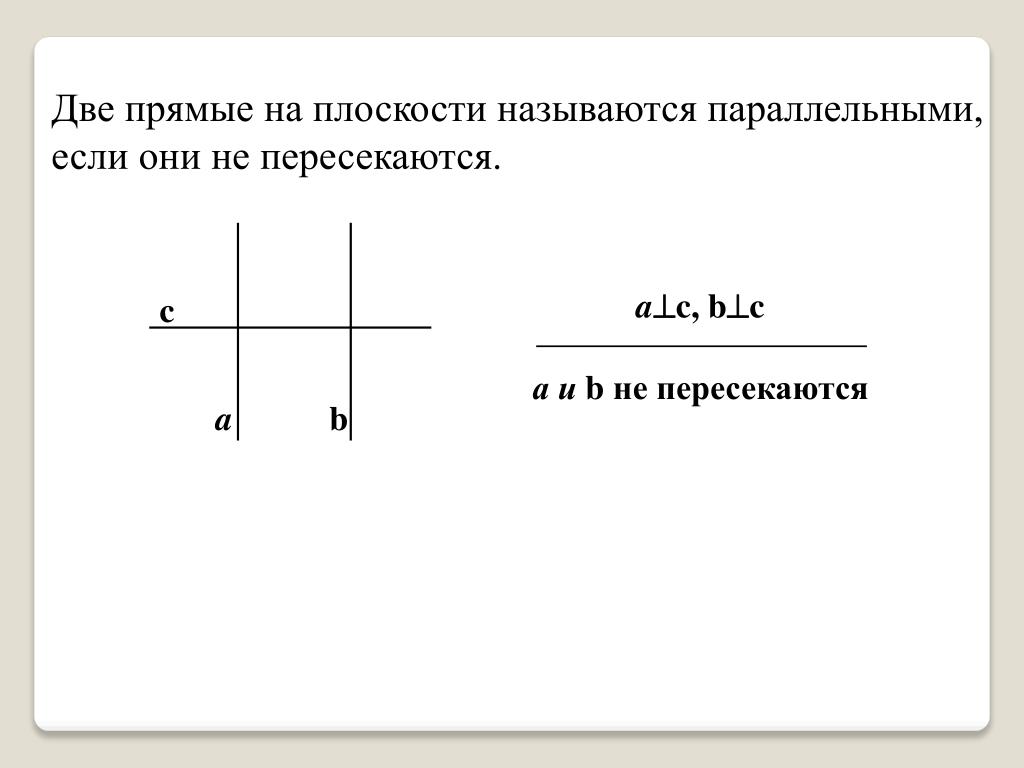
АО «ИД «Комсомольская правда». ИНН: 7714037217 ОГРН: 1027739295781 127015, Москва, Новодмитровская д. 2Б, Тел. +7 (495) 777-02-82.
В наказание ему пришлось несколько дней просидеть в карцере.
Www. kp. ru
07.07.2020 21:00:41
2020-07-07 21:00:41
Источники:
Https://www. kp. ru/daily/26341.4/3224135/
А «параллельные» прямые пересекаются в проективной геометрии: olegchagin — LiveJournal
Наверняка вы когда–нибудь слышали, что в геометрии Лобачевского параллельные прямые пересекаются. Конечно же, это не так. И даже наоборот.
Из школьного курса геометрии мы знаем, что [далее менторским тоном] «через точку, не лежащую на прямой, можно провести прямую, параллельную данной, и только одну».
Это утверждение – наиболее популярное перефразирование пятого постулата Евклида, который в своё время подложил здоровенную свинью своим последователям. Дело в том, что в его «Началах» первые четыре постулата сформулированы очень просто и очевидно. Вот они:
Вот они:
- От всякой точки до всякой точки можно провести прямую [и только одну]
- Ограниченную прямую можно непрерывно продолжать по прямой.
- Из всякого центра всяким раствором может быть описан круг.
- Все прямые углы равны между собой.
В пятом же постулате Евклид решил потроллить математиков, и вместо того, чтобы написать что–нибудь столь же простое, например, «Прямоугольники существуют» (и баста!), он начал запутывать: «Если прямая, пересекающая две прямые, образует внутренние односторонние углы… бла–бла–бла…»
И все подумали: что–то он здесь темнит, не может быть аксиома такой сложной. Не распознав подвох, математики в течение 2 тысяч лет пытались избавиться от этого постулата и доказать его через другие постулаты и аксиомы. Сначала древние греки, потом арабы, потом европейцы. И каждый думал, что он успешно доказал этот постулат, но потом выяснялось, что его доказательство базируется на каком–нибудь очевидном, но не доказанном утверждении, равнозначном самому постулату.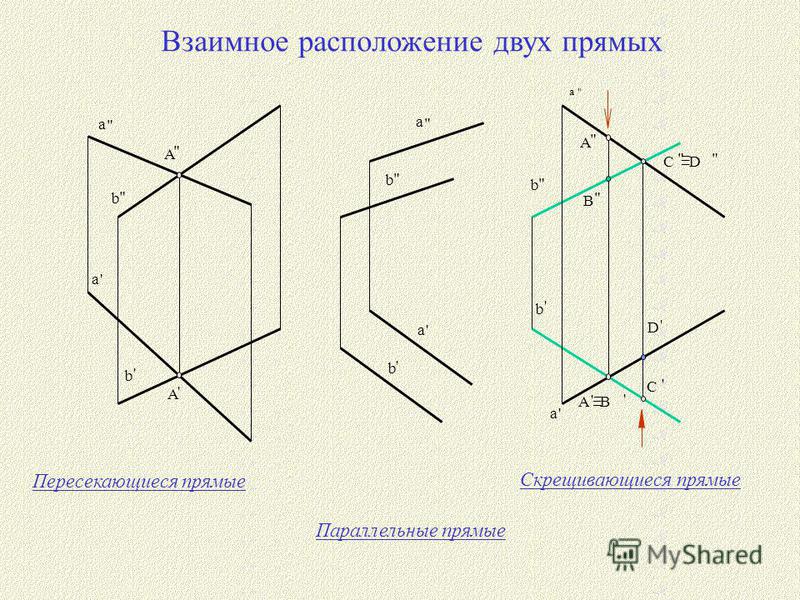 Таких утверждений набралось огромное множество. Вот ещё некоторые из них:
Таких утверждений набралось огромное множество. Вот ещё некоторые из них:
- Существуют треугольники сколь угодно большой площади
- Существуют подобные треугольники
- Сумма углов треугольник равна 180°
- Теорема Пифагора верна
- Отношение длины окружности к диаметру – константа и равно π
- Две прямые, параллельные третьей, параллельны друг другу
Последний пункт и играет ключевую роль в путанице с геометрией Лобачевского. Но об этом чуть позже.
Наконец, наиболее продвинутые из математиков стали пытаться применить доказательство от противного[Евклида] – то есть, предположить, что пятый постулат не верен, и вывести из этого какое–нибудь противоречие. Первым был итальянец Саккери (первая половина XVIII в.), который очень досадовал, что никак не может найти это противоречие. В конце концов, он сделал ошибку в вычислениях, получил противоречие и радостно вздохнул.
Мало–помалу математики стали что–то подозревать.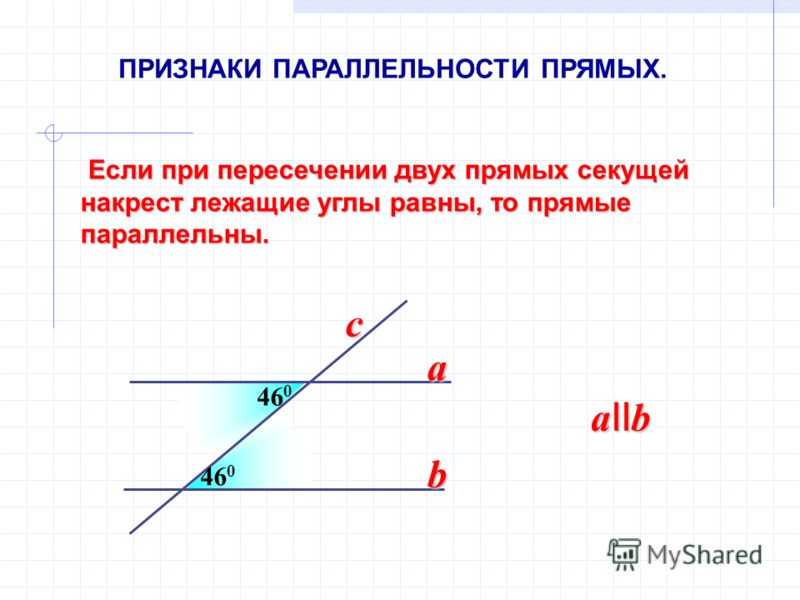 И уже начались попытки отказаться от пятого постулата не в целях найти противоречие, а просто посмотреть, что же получится. Первых успехов добился Ламберт, который во второй половине XVIII в. построил непротиворечивую геометрию на сфере, в которой сумма углов треугольника всегда больше 180° и все прямые пересекаются. Однако в сферической геометрии нарушается не только пятый постулат, но и как минимум первые три. Кстати, четвёртый всё–таки был доказан и исключен из постулатов.
И уже начались попытки отказаться от пятого постулата не в целях найти противоречие, а просто посмотреть, что же получится. Первых успехов добился Ламберт, который во второй половине XVIII в. построил непротиворечивую геометрию на сфере, в которой сумма углов треугольника всегда больше 180° и все прямые пересекаются. Однако в сферической геометрии нарушается не только пятый постулат, но и как минимум первые три. Кстати, четвёртый всё–таки был доказан и исключен из постулатов.
Ламберт также исследовал геометрию, в которой сумма углов треугольника всегда меньше 180°, не нашёл в ней противоречий, но не смог представить себе этакую мнимую сферу. Поэтому он не стал развивать тему, ограничившись заявлением, что доказать пятый постулат невозможно.
Дальше над этим работали Швейкарт и Гаусс. Гаусс отлично всё понимал, но понимал также и то, что втирать подобное почтенному научному сообществу – себе дороже. Заминусуют, потом вообще ничего не сможешь постить. Поэтому они оба тихо молчали себе в трубочку.
Первым, кто во всеуслышание заявил о неевклидовой геометрии, был Лобачевский. Сначала в докладе в 1826 году, затем в публикации 1829 года. Естественно на него посыпались все шишки, и он чуть было не лишился поста ректора Казанского университета. Он был не понят и осмеян, как в России, так и за рубежом. Но продолжал настаивать и отстаивать, и продвинулся в исследовании новой геометрии дальше всех. И с тех пор она носит его имя.
Почти как в песне поётся:
One deserves the credit, one deserves the blame
And Nikolai Ivanovich Lobachevsky is his name
Независимо от Лобачевского, но на три года позже него, публикует работу о неевклидовой геометрии венгерский математик Бойяи, которая также остаётся незамеченной.
Гаусс высоко оценивал работу Лобачевского, но только в частной переписке. Он даже пытался учить русский язык, чтобы почитать его русскоязычные публикации. В 1860–х годах (уже после смерти и Гаусса, и Лобачевского) переписка Гаусса становится достоянием общественности, и его восторженные отзывы о Лобачевском привлекают внимание к русскому учёному и его идеям. В общем, справедливость восторжествовала, но как всегда посмертно.
В общем, справедливость восторжествовала, но как всегда посмертно.
Итак, в геометрии Лобачевского через одну точку можно провести как минимум две прямые, параллельные данной, а вообще бесконечно много. Казалось бы, раз параллельные прямые проходят через одну точку, то они пересекаются. Да, они пересекаются, но фокус в том, что они не параллельны друг другу, хоть обе параллельны третьей прямой.
Ну и кроме этого, как вы, наверное, догадываетесь, сумма углов треугольника всегда меньше 180°, площадь треугольника ограничена константой, отношение длины окружности к диаметру растёт с увеличением окружности и т.д. Всё в таком духе. Да и теорема Пифагора не работает.
Как же представить такую поверхность, на которой работает геометрия Лобачевского? А вот она – на КДПВ, с очень сексуальным треугольничком на ней. Это так называемая гиперболическая плоскость. Если сфера – повсюду выпуклая поверхность, то гиперболическая плоскость – повсюду вогнутая, как какая–нибудь воронка или седло, только бесконечная. Как у сферы есть радиус (кривизны), так и у плоскости Лобачевского есть некий показатель кривизны. Только у сферы эта кривизна положительна, а у плоскости Лобачевского – отрицательна.
Как у сферы есть радиус (кривизны), так и у плоскости Лобачевского есть некий показатель кривизны. Только у сферы эта кривизна положительна, а у плоскости Лобачевского – отрицательна.
На очень маленьком масштабе, либо при увеличении показателя кривизны, геометрия Лобачевского приближается к евклидовой. Так что, вполне может оказаться, что мы живём в пространстве Лобачевского с достаточно большим показателем кривизны, поэтому не замечаем этого в наших масштабах. В частности, из теории относительности следует, что при равномерном распределении массы во вселенной, наше пространство вполне может иметь геометрию Лобачевского. Если это действительно окажется так, то Лобачевского можно назвать Эйнштейном математики.
А позавчера 228 лет со дня рождения Николая Ивановича Лобачевского. С чем вас и поздравляю!
P.S. А «параллельные» прямые пересекаются в проективной геометрии, но это уже совсем другая история.
Параллельные прямые пересекаются: миф или реальность?
Слайд 1
Автор: Панкратов Влад Научный руководитель: Попова Е. А . Параллельные прямые пересекаются: миф или реальность?
А . Параллельные прямые пересекаются: миф или реальность?
Слайд 2
Актуальность: параллельные прямые не пересекаются в школьном курсе геометрии, но почему рельсы на горизонте сходятся? И есть предположение , что параллельные прямые пересекаются. Так ли это? Я и решил выяснить.
Слайд 3
Происхождение понятия параллельных прямых . От Евклида Евкли́д ( 300 г. до н. э.) — древнегреческий математик, автор “Начал”. Начала Евклида- это сборник математических трудов, который состоит из 13 книг. В первой книге рассматриваются 5 важных постулатов .
Слайд 4
Рассмотрим примечательные 5 постулатов “Начал” Евклида: 1. От всякой точки до всякой точки можно провести прямую. 2. Ограниченную прямую можно непрерывно продолжать по прямой. 3. Из всякого центра всяким раствором может быть описан круг. 4. Все прямые углы равны между собой. 5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых
Слайд 5
Необычность 5 постулата Евклида В течение двух тысячелетий не прекращались попытки исключить 5 постулат из списка аксиом и вывести как теорему, как получилось с 4 постулатом. Все эти попытки окончились неудачей.
Все эти попытки окончились неудачей.
Слайд 6
Источник понятия “ параллельные прямые ” Следствием 5 постулата является понятие параллельных прямых , не пересекающихся на всем их протяжении; и, далее, аксиома параллельности: через точку, не лежащую на заданной прямой, нельзя провести более одной прямой, параллельной этой заданной прямой .
Слайд 7
В результате безуспешных попыток доказать 5 постулат возникли неевклидовые геометрии. Рассмотрим их: Геометрия Николая Ивановича Лобачевского. Сферическая геометрия древних греков. Геометрия Георгия Римана.
Слайд 8
Лобачевский Николай Иванович Годы жизни : 1792 – 1856 ( Нижний Новгород – Казань) Ректор Казанского университета “ Коперник геометрии ”
Слайд 9
Геометрия Лобачевского Ответ с улицы: «Лобачевский доказал, что параллельные прямые пересекаются.» «Лобачевский открыл, что параллельные прямые могут и пересечься». «А что такое параллельные прямые?» «Параллельные — это такие прямые, которые лежат в одной плоскости и не пересекаются». Несовместимые ответы!
Несовместимые ответы!
Слайд 10
Ф ольклор ( folklore — народная мудрость): Однажды Лобачевский думал, кутаясь в пальто: Как мир прямолинеен, видно, что-то здесь не то! И он вгляделся пристальней в безоблачную высь, И там все параллельные его пересеклись.
Слайд 11
Диалоги на “ Эхе Москвы ” В е н е д и к т о в . Вот вы скажите, параллельные прямые пересекаются? С л у ш а т е л ь . Нет. В е н е д и к т о в . А вот у Лобачевского пересекаются, там другая система отсчёта. Леонид Радзиховский : «Вот когда Лобачевский придумал свою неевклидову геометрию, что две параллельные прямые могут пересечься, — это был действительно переворот в области геометрии и физики».
Слайд 12
Аксиомы о параллельных Правильная формулировка : через точку, не лежащую на заданной прямой, нельзя провести более одной прямой, параллельной этой заданной прямой . В школьном курсе ( Атанасян Л.С.): через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. В версии Лобачевского: через точку, не лежащую на заданной прямой, можно провести более одной прямой, параллельной этой заданной прямой . Правда, как известно, у каждого своя, но истина одна. Истина состоит в том, что параллельные друг другу прямые не пересекаются даже у Лобачевского!
В версии Лобачевского: через точку, не лежащую на заданной прямой, можно провести более одной прямой, параллельной этой заданной прямой . Правда, как известно, у каждого своя, но истина одна. Истина состоит в том, что параллельные друг другу прямые не пересекаются даже у Лобачевского!
Слайд 13
Важно: А ксиому о параллельных доказать нельзя . В третьем десятилетии XIX в. два великих геометра — российский математик Николай Иванович Лобачевский и венгерский математик Янош Б о йаи —независимо друг от друга построили геометрическую теорию, основанную на отрицании аксиомы о параллельных. Эту теорию за рубежом, как правило, называют геометрией Лобачевского– Бойаи , а в России — геометрией Лобачевского . У нее есть и «обезличенное» название — гиперболическая геометрия . Геометрия Лобачевского применима в космологии, если учесть, что наше пространство искривлено гиперболически .
Слайд 14
“ Плоскость ” Лобачевского — “ седло ” , “ воронка ” Лобачевский Николай Иванович умер, не дожив до признания своей теории 10 лет, осмеянный, больной, в нищете, его уволили из университета. Янош Бойаи сошел с ума, не получив отклика и поддержки своих идей у математиков того времени (у Карла Гаусса – короля математиков)
Янош Бойаи сошел с ума, не получив отклика и поддержки своих идей у математиков того времени (у Карла Гаусса – короля математиков)
Слайд 15
Сферическая геометрия Древних Греков. Сферическая геометрия — раздел геометрии, изучающий геометрические фигуры на поверхности сферы. Сферическая геометрия возникла в древности в связи с потребностями географии и астрономии. Сферическая геометрия нужна не только астрономам, штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, а также при геодезических съемках больших территорий поверхности Земли, когда становится необходимым учитывать ее шарообразность.
Слайд 16
I век нашей эры Древняя Греция Геометрический труд “ Сферика ” – аналогично “ Началам ” Евклида Менелай Александрийский
Слайд 17
Особенности сферической геометрии Прямые – большие круги (меридианы, экватор, параллели – малые круги ) Есть двуугольник У сферического треугольника могут быть все три угла прямыми Сумма углов треугольника меньше 3П, но больше П Две прямые пересекаются дважды (например, на северном и южном полюсах) Нет понятия параллельности
Слайд 18
Геометрия Римана Геометрия Римана (эллиптическая геометрия) — одна из трёх «великих геометрий» (Евклида, Лобачевского и Римана).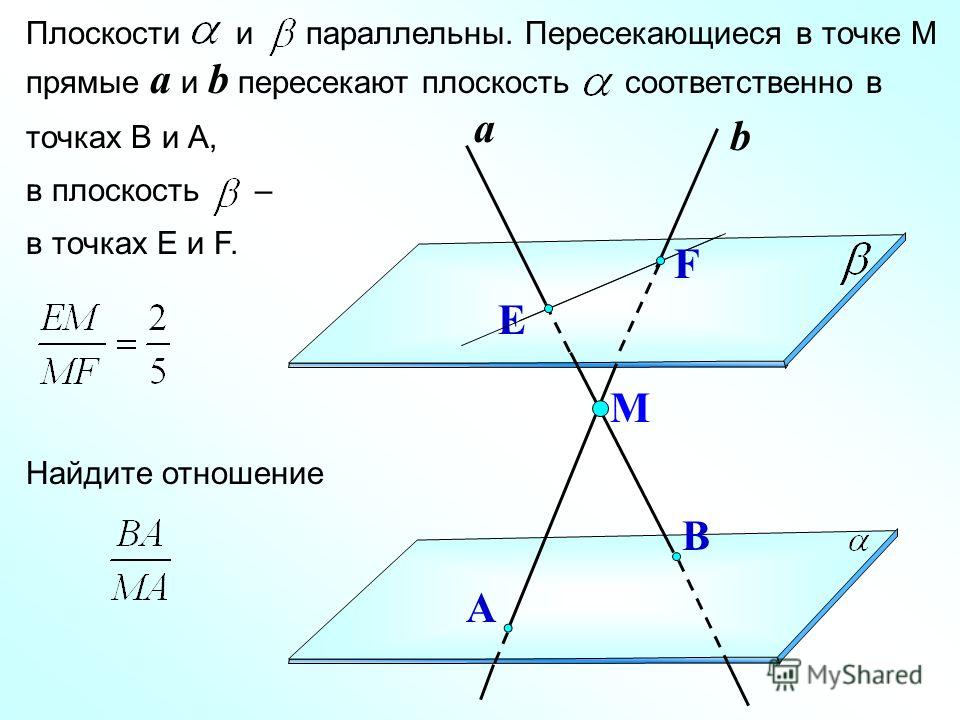 Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, то геометрия Римана реализуется на поверхностях с постоянной положительной гауссовой кривизной, т.е. на сферах. Исторически геометрия Римана появилась позже двух других геометрий (в 1854 г.).
Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, то геометрия Римана реализуется на поверхностях с постоянной положительной гауссовой кривизной, т.е. на сферах. Исторически геометрия Римана появилась позже двух других геометрий (в 1854 г.).
Слайд 19
Годы жизни: 1826 – 1866 (Германия – Италия) Место работы: Гёттингенский университет Научная сфера: математика, механика, физика Основатель римановой геометрии Георг Фридрих Бернхард Риман
Слайд 20
Геометрия Римана похожа на сферическую геометрию, но отличается тем, что любые две «прямые» имеют не две, как в сферической, а только одну точку пересечения. Поэтому иногда геометрией Римана называют геометрию на сфере, в которой противоположные точки отождествлены. В геометрии Римана любые прямые пересекаются , и таким образом, в ней нет параллельных прямых . Геометрия Римана не является абсолютной геометрией, ей нет практического применения.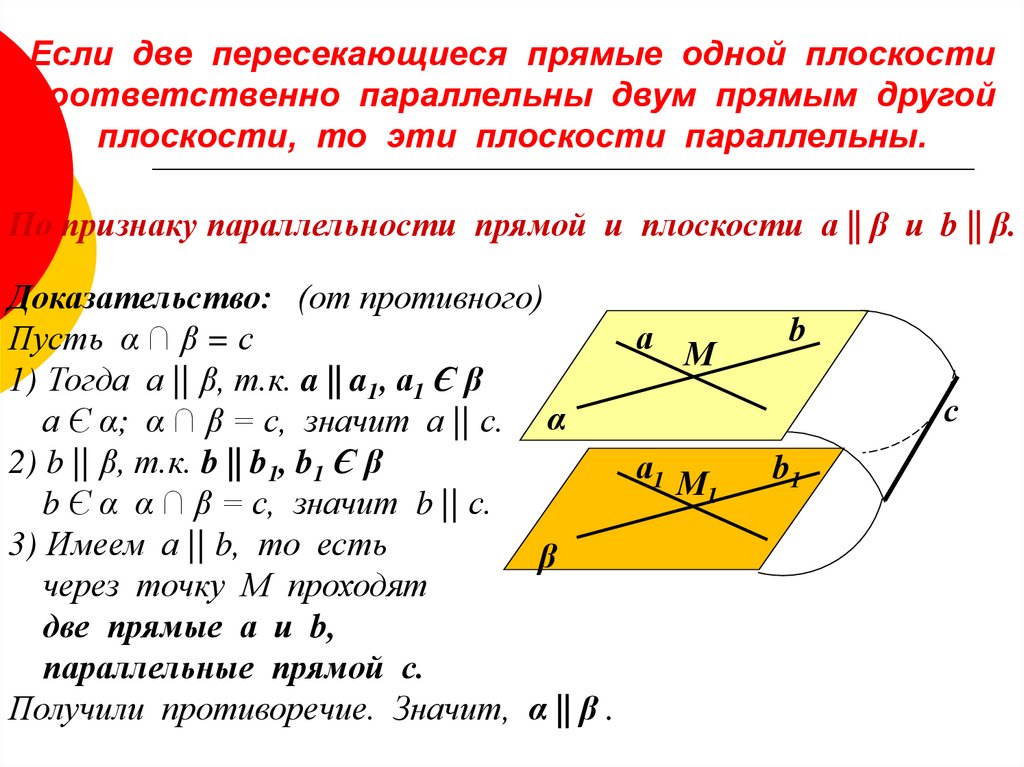
Слайд 21
Заключение : Итак, подводя итоги, ответим на вопрос: “Параллельные прямые пересекаются”? Нет , в идеале они не пересекаются ни у Евклида (2 параллельные прямые), ни у Лобачевского (прямая и пучок прямых в незримо больших масштабах) – это миф. Но нет дыма без огня: параллельных прямых не существует в сферической геометрии древних греков и в геометрии Римана. А в реальности: нет прямых, как нет и других объектов геометрии, поэтому одна прямая или их несколько, параллельных данной?..
Слайд 22
Спасибо за внимание!!!!!!
Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия
| Справочник по математике | Геометрия (Стереометрия) | Прямые и плоскости в пространстве |
| Взаимное расположение двух прямых в пространстве |
| Признак скрещивающихся прямых |
| Угол между скрещивающимися прямыми |
Взаимное расположение двух прямых в пространстве
Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.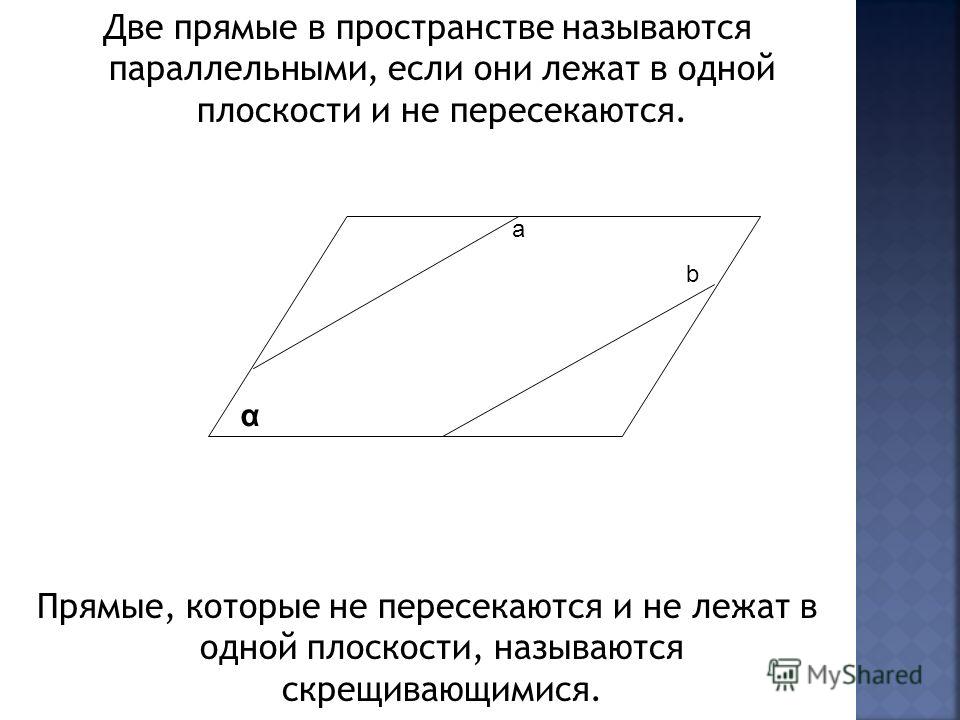
| Фигура | Рисунок | Определение |
| Две пересекающиеся прямые | Две прямые называют пересекающимися прямыми, если они имеют единственную общую точку. | |
| Две параллельные прямые | Две прямые называют параллельными прямыми, если они лежат в одной плоскости и не имеют общих точек | |
| Две скрещивающиеся прямые | Две прямые называют скрещивающимися прямыми, если не существует плоскости, содержащей обе прямые. |
| Две пересекающиеся прямые |
Две прямые называют пересекающимися прямыми, если они имеют единственную общую точку. |
| Две параллельные прямые |
Две прямые называют параллельными прямыми, если они лежат в одной плоскости и не имеют общих точек |
| Две скрещивающиеся прямые |
Две прямые называют скрещивающимися прямыми, если не существует плоскости, содержащей обе прямые. |
С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.
| Фигура | Рисунок | Тип утверждения и формулировка |
| Две различные точки | Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия. | |
| Прямая линия и точка, не лежащая на этой прямой | Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой. | |
| Две пересекающиеся прямые | Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые. | |
| Две параллельные прямые | Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые. 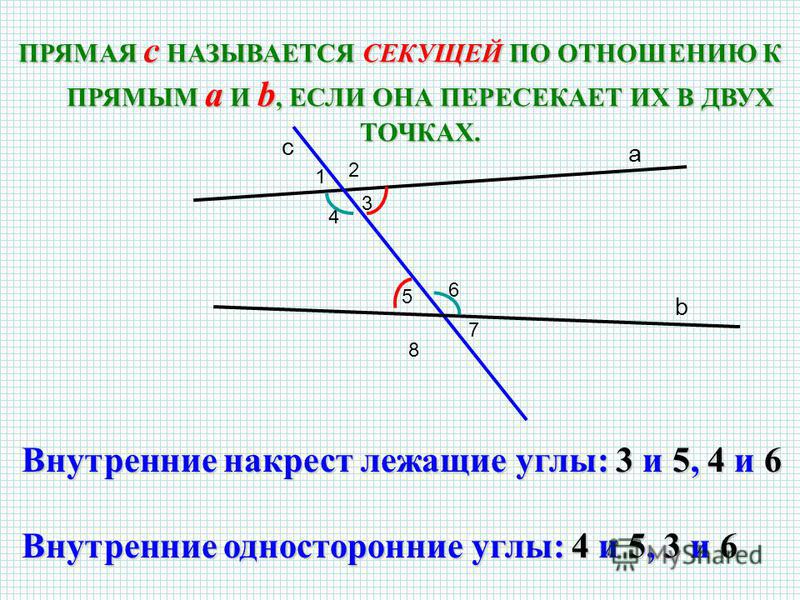 |
| Две различные точки |
Аксиома о прямой линии, заданной двумя точками |
| Прямая линия и точка, не лежащая на этой прямой |
Аксиома о параллельных прямых |
| Две пересекающиеся прямые |
Теорема о плоскости, определяемой двумя пересекающимися прямыми |
| Две параллельные прямые |
Теорема о плоскости, определяемой двумя параллельными прямыми |
Признак скрещивающихся прямых
Признак скрещивающихся прямых. Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).
Рис.1
Доказательство. Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».
Для этого предположим, что прямая a, пересекающая плоскость в точке K, и прямая b, лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α. Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K, не лежащую на этой прямой, то они совпадают.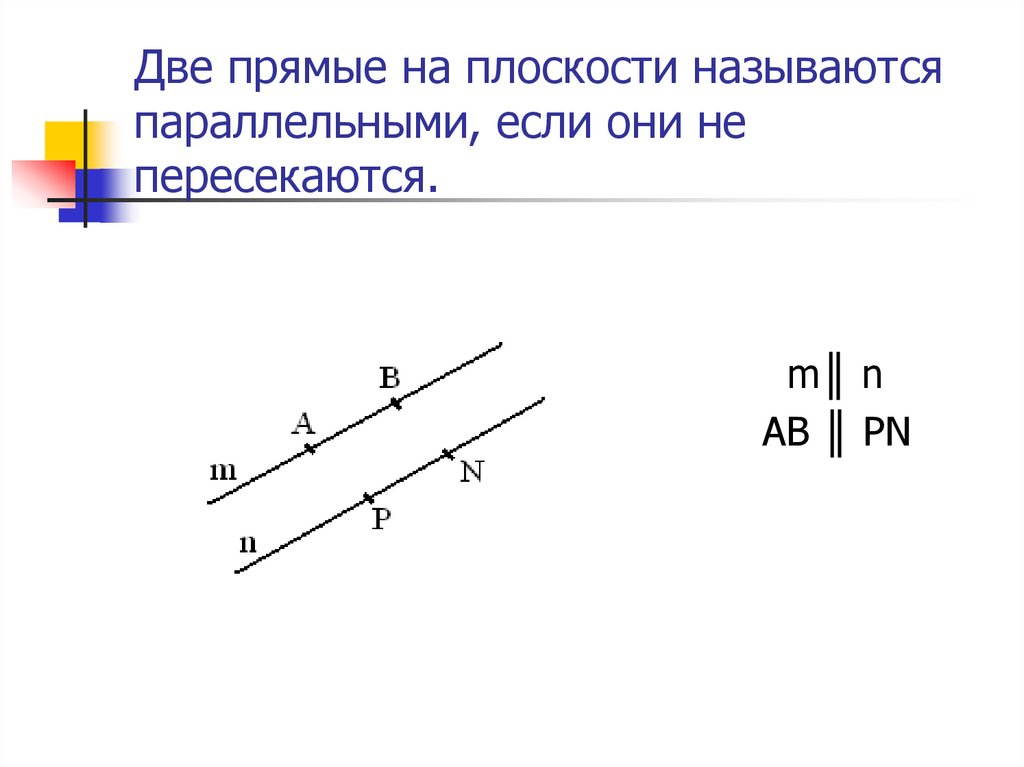 Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости. Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость, а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.
Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости. Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость, а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.
Угол между скрещивающимися прямыми
Углом между скрещивающимися прямыми называют угол между пересекающимися прямыми пересекающимися прямыми, соответственно параллельными параллельными данным скрещивающимся прямым скрещивающимся прямым (рис. 2).
Рис.2
На рисунке 2 изображены скрещивающиеся прямые a и b. Прямая a’ параллельна прямой a, прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b.
Задача. В кубе кубе ABCDA1B1C1D1 найти угол между прямыми AB1 и BC1.
Решение. Поскольку прямая AB1 пересекает плоскость BB1C1 в точке B1, которая не лежит на прямой BC1, то по признаку скрещивающихся прямых прямые AB1 и BC1 скрещиваются (рис. 3).
Рис.3
Для того, чтобы найти угол между прямыми AB1 и BC1, проведем в кубе диагональ боковой грани AD1 и диагональ верхнего основания D1B1 (рис. 4).
Рис.4
По определению угла между скрещивающимися прямыми угол D1AB1 и является углом между прямыми AB1 и BC1. Поскольку треугольник AD1B1 равносторонний, угол D1AB1 равен 60°.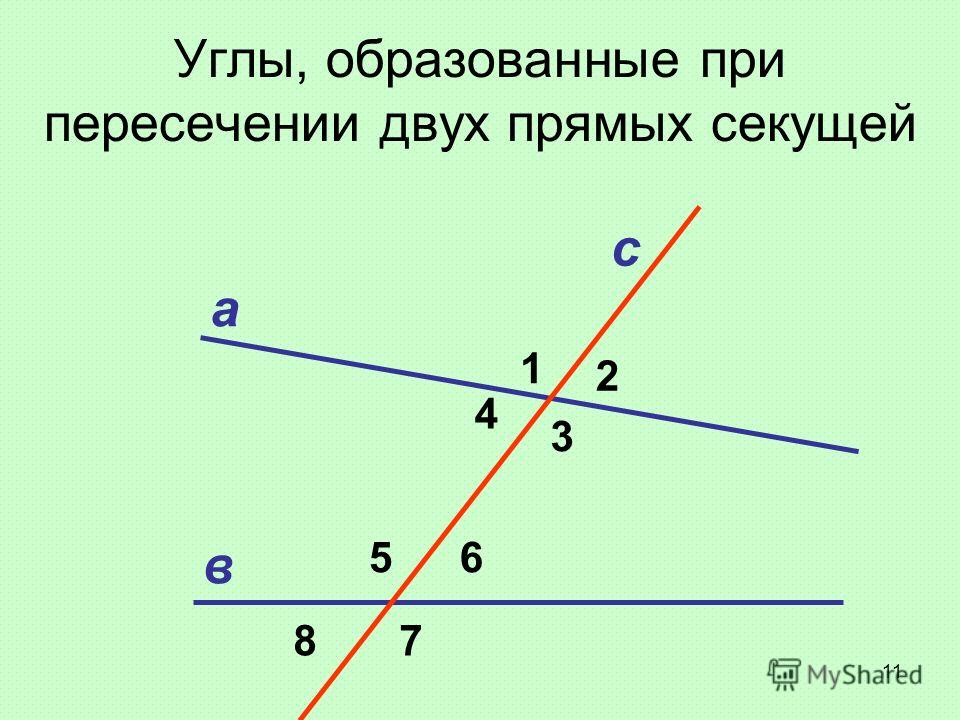
Ответ. 60°.
Замечание. Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ по математике.
геометрия — Пересечение двух параллельных прямых
Это неверно в обычной плоской геометрии и поэтому не может быть доказано.
Это является верным, в некотором роде, в другой форме геометрии, известной как проективная геометрия , однако.
В качестве быстрого интуитивного введения в проективную геометрию представьте, что вы стоите на обычной евклидовой плоскости. Ваша голова находится на высоте около 2 метров над плоскостью, поэтому, когда вы смотрите на вниз на , вы видите все, что нарисовано на плоскости, простирающееся до горизонта. Детали самолета прямо там, где вы стоите, кажутся вам большими; те же самые детали на большом расстоянии будут казаться вам маленькими и будут видны очень близко к горизонту.
Детали самолета прямо там, где вы стоите, кажутся вам большими; те же самые детали на большом расстоянии будут казаться вам маленькими и будут видны очень близко к горизонту.
Достаточно распространено ощущение, что если мы начертим параллельные бесконечные линии на плоскости, когда мы посмотрим на них из точки над плоскостью, будет казаться, что они встречаются на горизонте. Мы можем решить считать точки на линии горизонта «равно реальными» точками на плоскости. Затем горизонт становится «линией в бесконечности», и параллельные линии на плоскости действительно встречаются в точке на линии в бесконечности. Тогда всегда встречаются любые две строки. Каждая линия на плоскости встречается с бесконечно удаленной линией в точке, определяемой ее направлением; две прямые на плоскости с разными направлениями пересекаются в самой плоскости, а две прямые на плоскости с одно и то же направления пересекаются с бесконечно удаленной линией в одной и той же точке и, следовательно, встречаются там.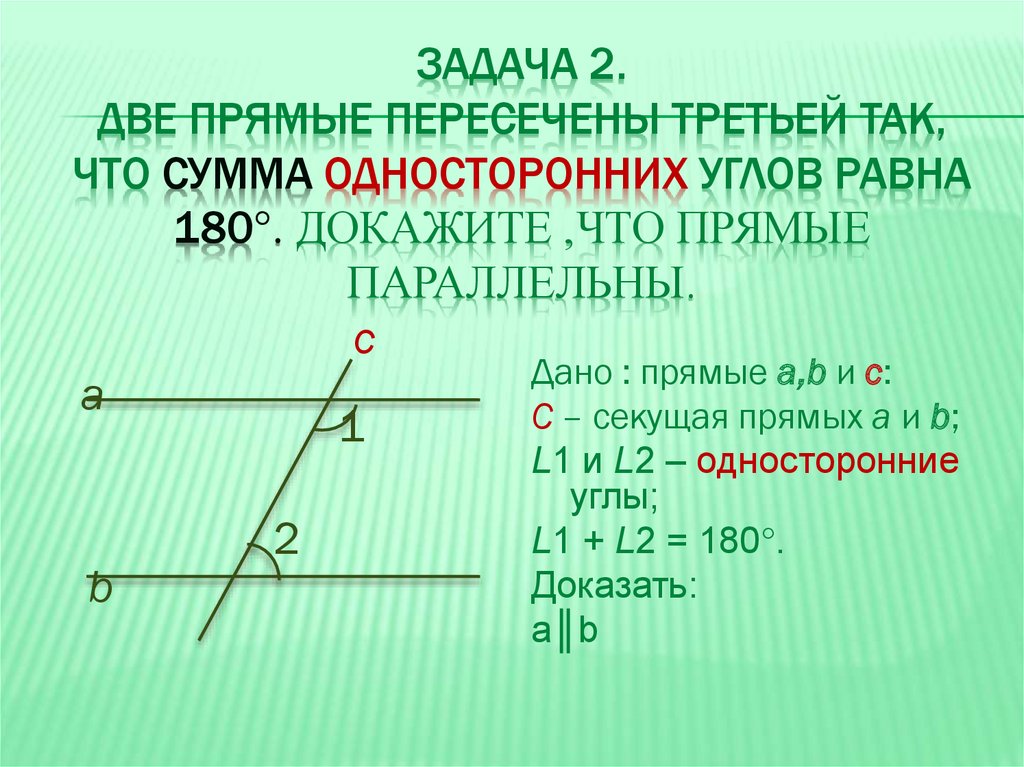
Пока с точками на горизонте происходит странная вещь: они находятся на «крае света», под ними плоскость, а над ними ничего. Это немного неаккуратно, и есть два способа это исправить. Один из них — просто решить нарисовать что-нибудь на небе. Это приводит к сферической геометрии , древней и почитаемой области исследования, которая является основой астрономии. Но не об этом сегодняшняя лекция.
В проективной геометрии мы стоим на евклидовой плоскости, но находимся в виртуальной реальности, созданной небрежным и/или ленивым программистом. Когда мы смотрим в любом направлении , наш шлем VR вычисляет бесконечную линию через нашу голову в том направлении, в котором мы смотрим, и выясняет, где эта бесконечная линия пересекает плоскость под нами. Что бы ни было в самолете, это то, что мы видим. Итак, когда мы смотрим на небо, мы видим самолет позади нашей головы! Только когда мы смотрим в совершенно горизонтальном направлении, эта процедура не работает, но мы утверждаем, что все же есть некоторые точки, на которые можно смотреть, которые, как и раньше, образуют «бесконечную линию».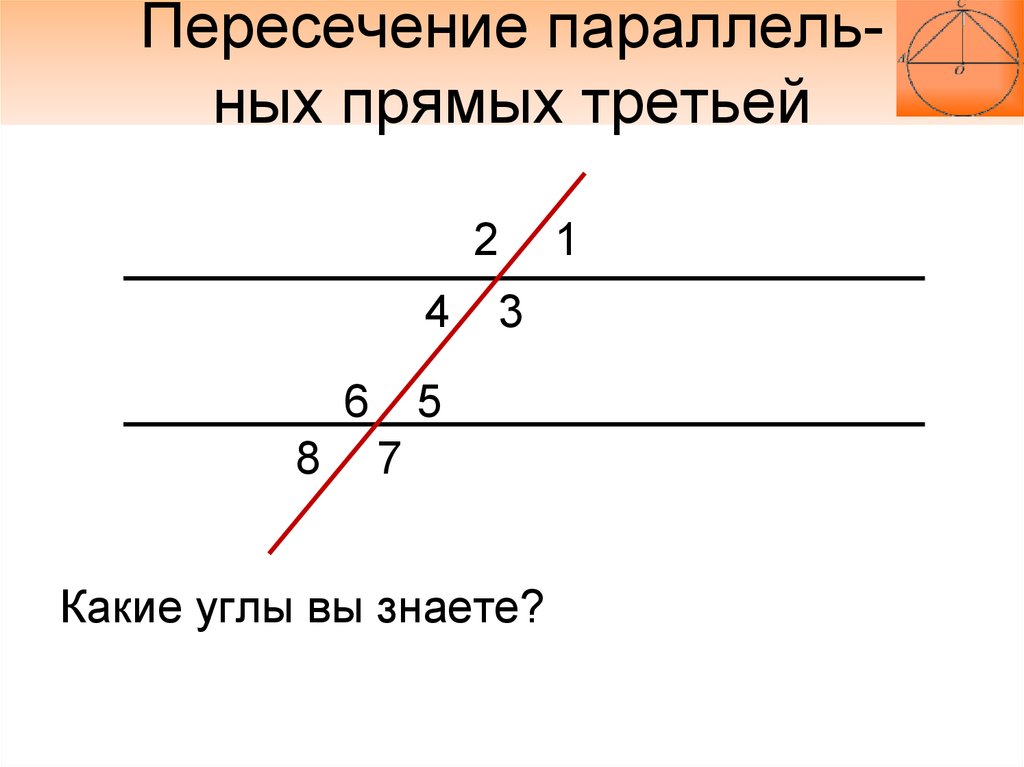 Поскольку мы не различаем точки перед собой и точки позади нас, всего горизонта всего 180°; если мы повернемся на 180°, мы будем смотреть на те же точки на бесконечности.
Поскольку мы не различаем точки перед собой и точки позади нас, всего горизонта всего 180°; если мы повернемся на 180°, мы будем смотреть на те же точки на бесконечности.
(Другой способ взглянуть на это — представить, что мы взяли копию обычного евклидова самолета и подняли его на 2 метра над нашей головой, а затем повернули его на 180° вокруг вертикальной оси Обратите внимание, что поскольку мы смотрим на небесную плоскость снизу , объекты в небе будут зеркальным отражением того же объекта, если вместо этого повернуться и посмотреть на них сверху вниз).
В проективной геометрии любые две разные линии имеют ровно одну общую точку. Если это непараллельные линии в исходной плоскости, они один раз пересекутся на земле, и мы также увидим это пересечение в небе — но это всего лишь два изображения одной и той же точки на проективной плоскости. Две параллельных прямых пересекутся ровно один раз на бесконечно удаленной линии — снова мы видим два изображения этого пересечения, когда поворачиваемся, но по определению это одна и та же точка. И любая линия на плоскости пересечет эту линию в бесконечности один раз.
И любая линия на плоскости пересечет эту линию в бесконечности один раз.
Главное, что делает это крутым, это то, что линия в бесконечности теперь не имеет особых свойств . Если мы наклоним голову и забудем, где верх, а где низ, мы никак не сможем вывести из геометрических свойств того, что мы видим, в каком направлении лежит «истинный» горизонт. Проективная геометрия касается свойств фигур, которые инвариантны к вращению нашего взгляда на мир. Это также касается свойств фигур, которые не меняются, когда мы ходим по плоскости или приближаем (или удаляем) голову от плоскости. Таким образом, у него также нет понятия масштаба или расстояния.
Эти движения сохраняют линии (линия остается линией в нашем поле зрения, когда мы наклоняем голову и/или ходим вокруг), поэтому «линия» — это проективное понятие. Они не сохраняют круги — если мы встанем над центром круга, он будет выглядеть круглым, но когда мы отойдем от него, он вместо этого начнет выглядеть как эллипс. Итак, «окружность» и «эллипс» не являются проективными понятиями. С другой стороны, как ни странно, «невырожденное коническое сечение» есть проективное понятие, и все невырожденные коники эквивалентны. Эллипс — это просто круг, видимый издалека. Парабола – это окружность, касающаяся прямой на бесконечности. Гипербола – это круг или эллипс, дважды пересекающий прямую на бесконечности.
Итак, «окружность» и «эллипс» не являются проективными понятиями. С другой стороны, как ни странно, «невырожденное коническое сечение» есть проективное понятие, и все невырожденные коники эквивалентны. Эллипс — это просто круг, видимый издалека. Парабола – это окружность, касающаяся прямой на бесконечности. Гипербола – это круг или эллипс, дважды пересекающий прямую на бесконечности.
Параллельные прямые — определение, свойства, символы, уравнения
Две или более прямых, которые лежат в одной плоскости и никогда не пересекаются друг с другом, называются параллельными прямыми . Они равноудалены друг от друга и имеют одинаковый наклон. Давайте узнаем больше о параллельных линиях в этой статье.
| 1. | Что такое параллельные линии? |
| 2. | Параллельные линии и поперечные |
| 3. | Свойства параллельных линий |
4. | Часто задаваемые вопросы о параллельных линиях |
Что такое параллельные линии?
Параллельные линии — это прямые линии, которые никогда не пересекаются, независимо от того, как долго мы их продлеваем. Обратите внимание на следующий рисунок, на котором показаны параллельные линии. Линия «а» параллельна линии «b», а линия «p» параллельна линии «q».
Параллельные линии и поперечные
При пересечении любых двух параллельных прямых другой прямой, называемой секущей, образуется много пар углов. В то время как некоторые углы конгруэнтны (равны), другие являются дополнительными. Обратите внимание на следующий рисунок, чтобы увидеть параллельные линии, обозначенные как L1 и L2, которые пересекаются секущей. Восемь отдельных углов были образованы двумя параллельными прямыми и секущей. Каждый угол был помечен с помощью алфавита.
Ниже приведены пары углов, образованных двумя параллельными прямыми L1 и L2.
- Соответствующие углы: Следует отметить, что пара соответствующих углов равна по размеру. На данном рисунке четыре пары соответствующих углов, то есть ∠a = ∠e, ∠b = ∠f, ∠c = ∠g и ∠d = ∠h
- Альтернативные внутренние углы: Альтернативные внутренние углы образованы внутри двух параллельных линий, которые пересекаются секущей. Они равны в меру. На этом рисунке ∠c = ∠e, ∠d = ∠f
- Альтернативные внешние углы: Альтернативные внешние углы образованы по обе стороны от поперечной, и они равны по размеру. На этом рисунке ∠a = ∠g, ∠b = ∠h
- Последовательные внутренние углы: Последовательные внутренние углы или совмещенные внутренние углы образуются на внутренней стороне поперечной и являются дополнительными. Здесь ∠c + ∠f = 180°, а ∠d + ∠e = 180°
- Вертикально-противоположные углы: Вертикально-противоположные углы образуются, когда две прямые пересекают друг друга, и они равны по размеру. Здесь ∠a = ∠c, ∠b = ∠d, ∠e = ∠g, ∠f = ∠h
Свойства параллельных линий
Параллельные линии можно легко идентифицировать по основным свойствам, приведенным ниже.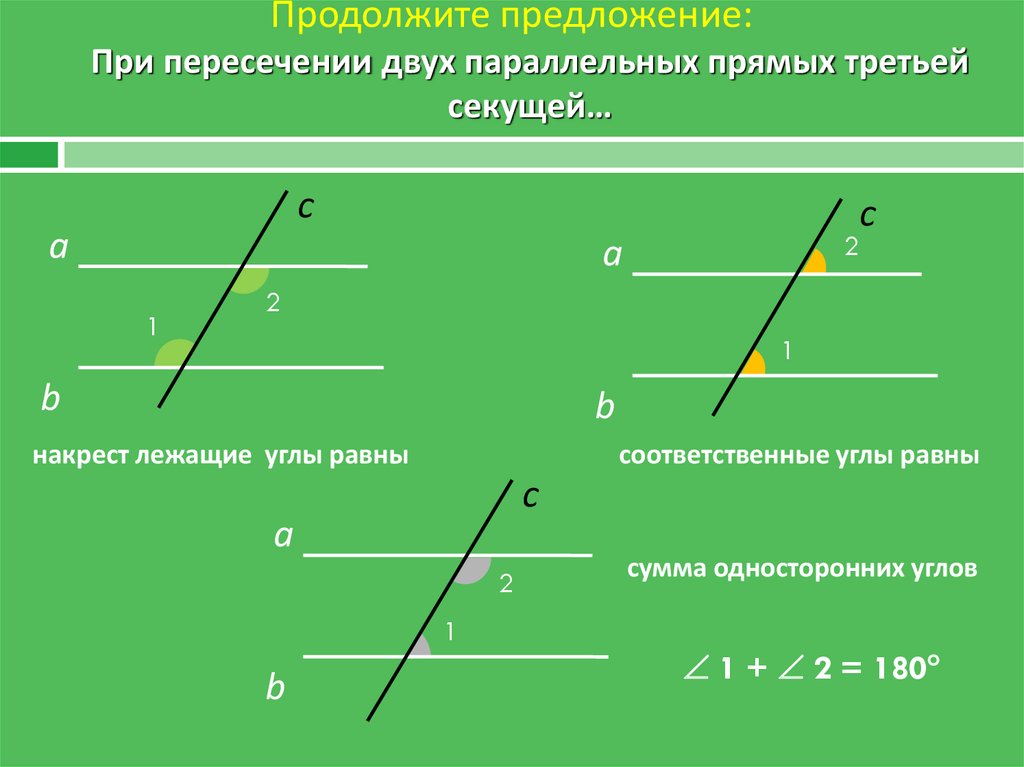
- Параллельные линии — это прямые линии, которые всегда находятся на одинаковом расстоянии друг от друга.
- Параллельные линии никогда не пересекаются, независимо от того, насколько они вытянуты в любом направлении.
Как узнать, параллельны ли линии?
Помимо характеристик, приведенных выше, когда любые две параллельные прямые пересекаются секущей, их можно идентифицировать по следующим свойствам.
- Любые две прямые называются параллельными, если соответствующие углы, образованные таким образом, равны.
- Любые две прямые называются параллельными, если образованные таким образом альтернативные внутренние углы равны.
- Любые две прямые называются параллельными, если образованные таким образом альтернативные внешние углы равны.
- Любые две прямые называются параллельными, если смежные внутренние углы по одну сторону от секущей являются дополнительными.
Параллельные линии Уравнение
Уравнение прямой линии обычно записывается в форме точки пересечения с наклоном, представленной уравнением y = mx + b, где «m» — наклон, а «b» — точка пересечения с осью y. Значение «m» определяет наклон или градиент и сообщает нам, насколько крута линия.
Значение «m» определяет наклон или градиент и сообщает нам, насколько крута линия.
Следует отметить, что наклон любых двух параллельных линий всегда одинаков. Например, если наклон линии с уравнением y = 4x + 3 равен 4. Следовательно, любая линия, параллельная y = 4x + 3, будет иметь одинаковый наклон, то есть 4. Параллельные прямые имеют разные y- пересекаются и не имеют общих точек.
Параллельные линии Символ
Параллельные линии — это линии, которые никогда не пересекаются друг с другом, независимо от того, как долго мы их продлеваем. Для обозначения параллельных прямых используется символ || . Например, AB II PQ указывает, что линия AB параллельна линии PQ. Символ, обозначающий непараллельные прямые, равен ∦ .
☛ Ссылки по теме
- Точки и линии
- Пересекающиеся линии
- Линейный сегмент
- Свойства параллельных линий
- Параллельные и перпендикулярные линии
- Уравнение прямой
Часто задаваемые вопросы о параллельных линиях
Что такое параллельные линии в геометрии?
Параллельные линии — это линии, которые всегда находятся на одном и том же расстоянии друг от друга и никогда не пересекаются. Для обозначения параллельных прямых используется символ || . Например, AB || CD означает, что линия AB параллельна линии CD.
Для обозначения параллельных прямых используется символ || . Например, AB || CD означает, что линия AB параллельна линии CD.
Что такое параллельные линии и перпендикулярные линии?
Параллельные линии — это линии, которые равноудалены друг от друга и никогда не пересекаются, независимо от того, насколько они могут быть продлены в любом направлении. Например, противоположные стороны прямоугольника представляют собой параллельные линии. С другой стороны, если любые две прямые пересекаются друг с другом под углом 90°, они называются перпендикулярными прямыми. Например, смежные стороны прямоугольника являются перпендикулярными прямыми, потому что они пересекают друг друга под углом 9.0°.
Какие бывают типы углов в параллельных линиях?
Когда любые две параллельные прямые пересекаются секущей, они образуют множество пар углов, таких как соответствующие углы, чередующиеся внутренние углы, чередующиеся внешние углы и последовательные внутренние углы.
Что происходит, когда параллельные прямые пересекаются секущей?
При пересечении любых двух параллельных прямых секущей образуются следующие углы.
- Соответственные углы, равные по размеру.
- Чередующиеся внутренние углы, равные по размеру.
- Альтернативные внешние углы, равные по размеру.
- Последовательные внутренние углы, которые являются дополнительными.
Как выглядят параллельные линии?
Параллельные линии выглядят как железнодорожные пути, которые никогда не пересекаются и всегда равноудалены. Противоположные стороны прямоугольника также представляют собой параллельные линии, находящиеся на равном расстоянии друг от друга.
Что такое наклон параллельных линий?
Если две прямые параллельны, они имеют одинаковый наклон. Например, если уравнение прямой линии y = 1/2x + 17, ее наклон равен 1/2. Теперь, если линия имеет одинаковый наклон 1/2 в той же плоскости, она будет параллельна данной линии.
Каковы реальные примеры параллельных линий?
Реальные примеры параллельных линий включают железнодорожные пути, края тротуаров, перила лестницы, бесконечные рельсовые пути, противоположные стороны линейки, противоположные края ручки, ластика и т. д.
Каково правило параллельных линий?
Правило для параллельных линий состоит в том, что линии не должны пересекаться друг с другом. Другими словами, если две прямые в одной плоскости находятся на одинаковом расстоянии друг от друга и никогда не пересекаются, то такие прямые называются параллельными.
Что такое символ параллельных линий?
Для обозначения параллельных линий используется символ ||. Любые две параллельные прямые AB и CD изображаются как AB||CD.
Параллельные прямые пересекаются в бесконечности?
Нет, само определение предполагает, что параллельные линии никогда не пересекаются. Следовательно, параллельные прямые не пересекались бы даже на бесконечности.
Параллельные прямые имеют одно и то же уравнение?
Нет, параллельные прямые не имеют одинакового уравнения, но имеют одинаковый наклон. Например, если уравнение линии представлено как y = 4x + 2, это означает, что наклон этой линии равен 4. Таким образом, другая прямая линия в той же плоскости с таким же наклоном 4 будет параллельна заданная линия.
Например, если уравнение линии представлено как y = 4x + 2, это означает, что наклон этой линии равен 4. Таким образом, другая прямая линия в той же плоскости с таким же наклоном 4 будет параллельна заданная линия.
Параллельные прямые равны по длине?
Нет, параллельные линии могут быть разной длины, но они должны находиться на одинаковом расстоянии друг от друга.
Есть ли в треугольнике параллельные линии?
Нет, в треугольнике нет параллельных прямых. Так как треугольник всегда имеет 3 пересекающиеся стороны; а мы знаем, что параллельные прямые никогда не пересекаются друг с другом, следовательно, в треугольнике не может быть параллельных прямых.
Сколько параллельных линий имеет шестиугольник?
Шестиугольник — это шестиугольник. В правильном шестиугольнике три пары параллельных прямых.
Что такое параллельные линии? Определение, свойства, примеры, факты
В геометрии параллельные прямые можно определить как две прямые в одной плоскости, находящиеся на одинаковом расстоянии друг от друга и никогда не пересекающиеся. Они могут быть как горизонтальными, так и вертикальными.
Они могут быть как горизонтальными, так и вертикальными.
Мы можем видеть примеры параллельных линий в нашей повседневной жизни, например, на пешеходном переходе, на линиях ноутбуков и на железнодорожных путях вокруг нас.
Как выглядят параллельные линии?
На рисунке ниже линия «AB» параллельна линии «CD».
Перпендикулярное расстояние между двумя параллельными линиями всегда одинаково.
Стороны различной формы параллельны друг другу. В приведенном ниже прямоугольнике линии с одинарными стрелками параллельны друг другу, и аналогичным образом линии с двойными стрелками также параллельны друг другу.
Параллельные линии представляются парой вертикальных линий между названиями линий с использованием знака: ︳︳
Поем!
Рисование параллельных линий на листе,
Используйте линейку, чтобы сделать их аккуратными!
Пусть их концы с концами никогда не сойдутся!
Что такое трансверсаль?
Секущая – это прямая, которая пересекает две параллельные прямые (или прямые на плоскости) в разных точках пересечения, образуя углы.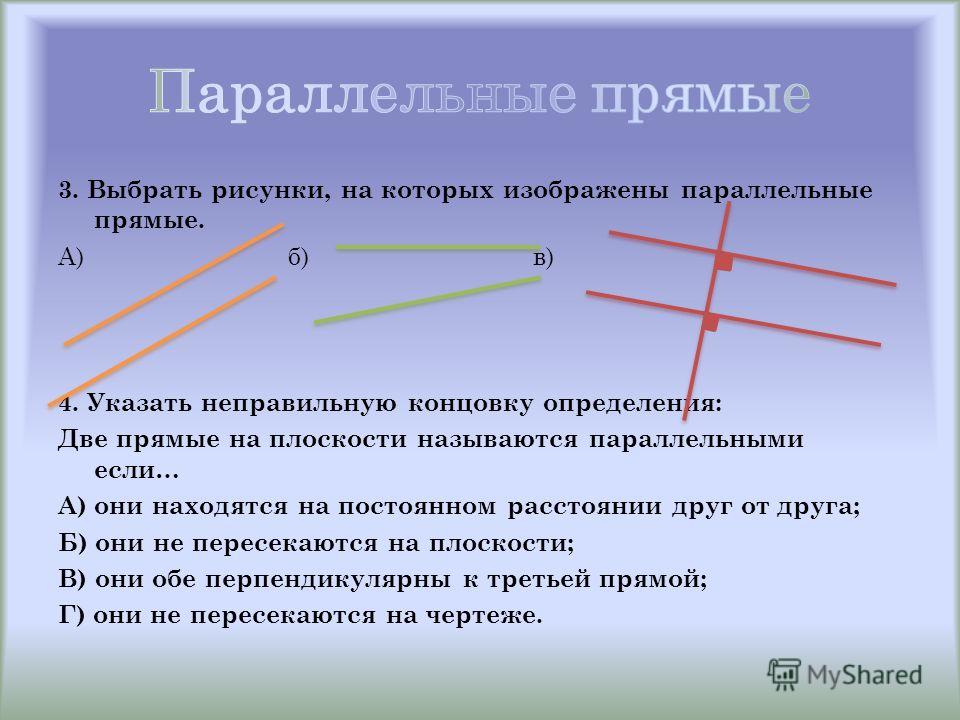
Свойства параллельных линий
Параллельные линии можно легко определить, используя следующие основные свойства и характеристики:
- Это всегда прямые линии с одинаковым расстоянием друг от друга.
- Это копланарные линии.
- Они никогда не пересекаются, независимо от того, как далеко вы пытаетесь расширить их в любом заданном направлении.
- Если есть поперечная линия, которая пересекает две параллельные прямые в двух разных точках, то она образует 4 угла в каждой точке.
- Соответствующие углы, образованные двумя параллельными прямыми и секущей, равны.
- Пары внутренних уголков на одной стороне пересечения являются дополнительными.
- Вертикально противоположные углы/углы при вершине равны.
- Чередующиеся внутренние/внутренние углы равны.
- Альтернативные внешние/внешние углы также равны.
Уравнения параллельных прямых
Линейные уравнения обычно описываются пересечением наклона, представленным уравнением $y = mx + b$.
Где «m» — наклон, «b» — точка пересечения с осью y, а y и x — переменные.
Значение «m» определяет наклон и указывает крутой наклон линии.
Обратите внимание, что наклоны двух параллельных линий всегда одинаковы.
Например, если наклон прямой в уравнении y $= 4x + 3$ равен 4, то все прямые, параллельные $y = 4x + 3$, имеют одинаковый наклон или 4.
Параллельные прямые имеют различные y-пересечения и не имеют общих точек или углов.
Решенные примеры
Пример 1: Выясните, какие прямые на данном рисунке параллельны друг другу.
Решение: Все три линии с проходящими через них стрелками параллельны друг другу, что означает:
a || б || c
Прямые с двойными стрелками, т. е. прямые d и e, являются секущими прямых a, b и c, но параллельны друг другу.
Итак, мы можем сказать, что d || e
Пример 2: Найти, параллельны ли заданные прямые, пересекаемые секущей на рисунке, или нет.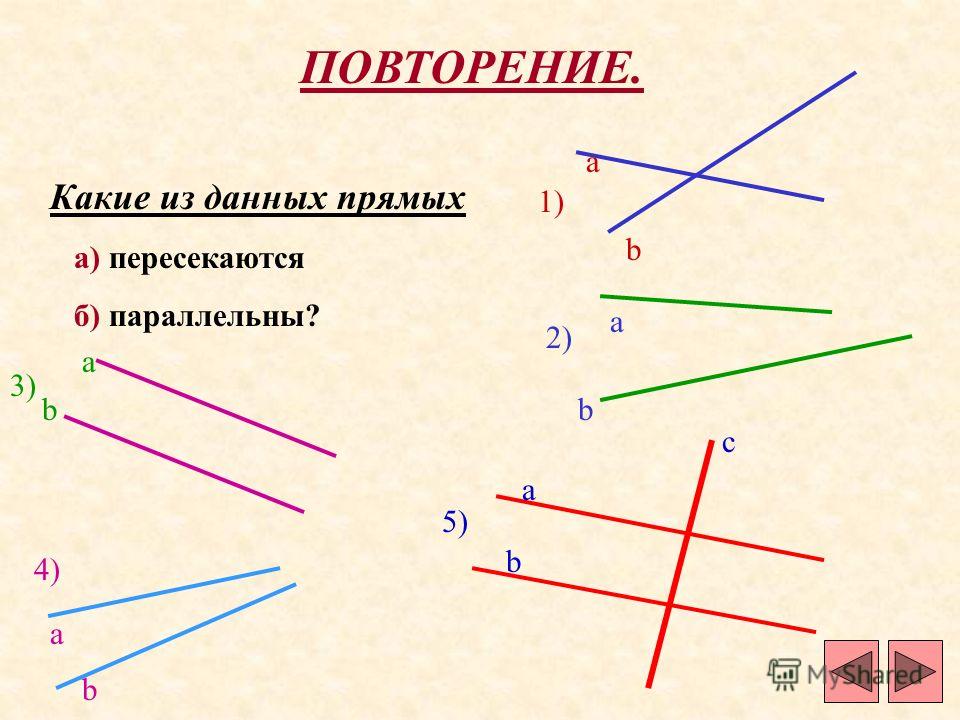
Решение: Две прямые параллельны, поскольку они удовлетворяют одному из свойств параллельных прямых: «когда чередующиеся внутренние углы равны, прямые параллельны».
$∠a$ равен $∠c$, и оба они являются альтернативными внутренними углами.
Это доказывает, что две прямые параллельны.
Пример 3: Параллельны ли прямые, пересекаемые секущей на этом рисунке?
Решение : Согласно заданным свойствам параллельных прямых, чередующиеся, соответствующие и последовательные углы должны быть одинаковыми, чтобы образовать параллельные прямые.
В этом случае $∠a$ не равно $∠d $
Таким образом, эти две прямые не параллельны.
Практические задачи
Некомпланарные
Компланарные
Равноотстоящие
Линии, идущие в одном направлении
Правильный ответ: Некомпланарные
Это указывает на то, что параллельные прямые не компланарны.
Стрелки часов
Дворники автомобиля
Лестницы и перила
Струны сетки теннисной ракетки
Правильный ответ: Стрелки часов
Стеклоочиститель автомобиля, лестница, перила и струны ракетки имеют одинаковую ориентацию и не пересекаются.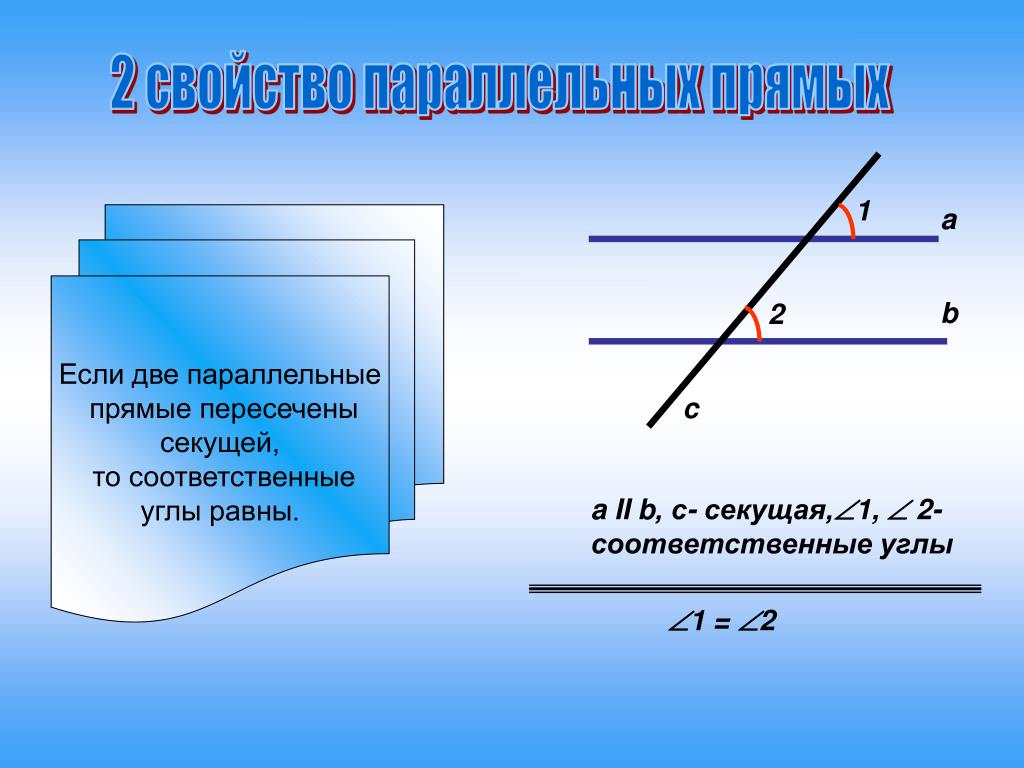 Все они находятся в одной плоскости (то есть струны в сети находятся в одной плоскости).
Все они находятся в одной плоскости (то есть струны в сети находятся в одной плоскости).
Однако стрелки часов пересекаются в центре часов и не представлены парой параллельных линий.
$120°$
$0°$
$112°$
$224°$
Правильный ответ: $112°$
Если обе прямые параллельны, то по одному из свойств параллельных прямых соответствующие углы и образующиеся чередующиеся внутренние и внешние углы равны.
В этом случае, поскольку альтернативные внешние углы будут равны,
$∠X = 112°$ как задано.
Часто задаваемые вопросы
Какие существуют типы параллельных линий?
Параллельные линии могут быть вертикальными, диагональными и горизонтальными.
Как параллельные линии используются в координатной геометрии?
Если графики двух линейных уравнений координатной геометрии параллельны, то эти два уравнения не имеют общего решения.
Наклоны двух параллельных линий одинаковы и всегда равны в координатной геометрии.
Как доказать, что две прямые параллельны?
Вы можете использовать некоторые геометрические отношения, чтобы доказать, что две линии параллельны.
Секущей называется линия, пересекающая две или более прямых. Когда прямая пересекает пару параллельных прямых, образуется пара разных углов.
Эти различные типы углов используются, чтобы доказать, параллельны ли две линии друг другу в соответствии с заданными свойствами параллельных линий.
Параллельные линии и пересечения — GeeksforGeeks
Вы, наверное, видели набор железнодорожных путей, лестницу или набор клавиш пианино. Есть ли что-то общее между ними? Две дорожки никогда не пересекаются, и две стороны лестницы никогда не встречаются. Клавиши пианино всегда параллельны друг другу. Рассмотрим подробнее параллельные и поперечные линии, а также углы, которым они соответствуют.
Параллельные линии: Комбинация двух или более линий, вытянутых в бесконечность и никогда не пересекающихся друг с другом, называется параллельной линией или копланарными линиями .
Параллельные прямые обозначаются специальным символом || .
Сечение: Сечение любой заданной прямой — это линия, которая пересекает две или более данных прямых в различных точках.
Соответствующие углы: Углы, образующиеся при пересечении секущей с любой парой параллельных прямых, называются соответствующих углов.
На рисунке ниже показаны как параллельные, так и поперечные прямые, а также соответствующие углы, образованные ими:
Параллельные прямые и поперечная
Рассмотрим прямую l, которая пересекает прямые m и n в точках P и Q соответственно. . Следовательно, прямая l является секущей для прямых m и n, где получается восемь различных углов. Восемь углов вместе образуют четыре пары соответствующих углов . Как видно на рисунке ниже, ∠2 и ∠6 составляют пару соответствующих углов. Все углы, находящиеся в одинаковом положении относительно прямых и секущей, называются пара соответствующих уголков .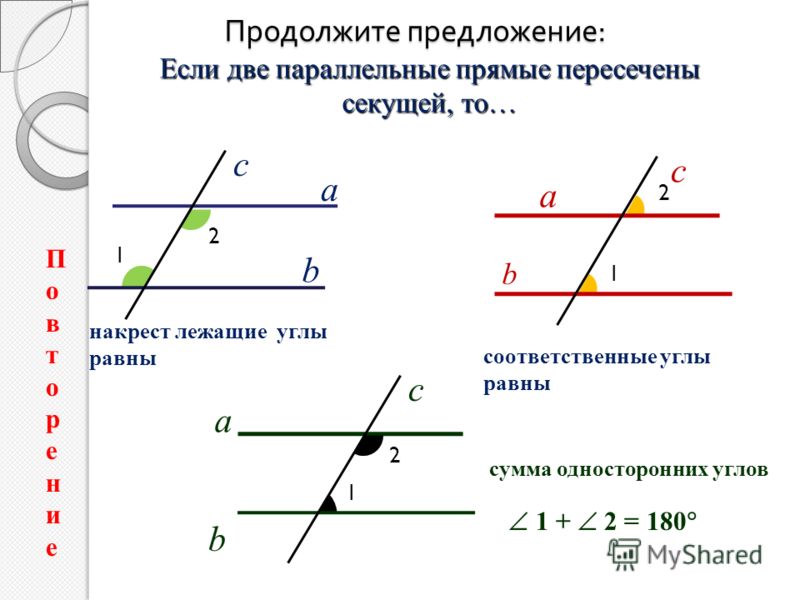
Кроме того, углы, находящиеся в области между линиями, напр. ∠4 и ∠5 называются внутренними углами , тогда как углы, которые находятся на внешней стороне двух линий, например. ∠1 и ∠8 называются внешними углами . Углы, которые находятся на противоположных сторонах поперечной, называются альтернативными углами например. ∠4 и ∠6. Углы, которые имеют одну и ту же вершину и имеют общий луч, например. углы ∠1 и ∠2 или ∠6 и ∠5 на рисунке называются смежные уголки . В этом случае, когда смежные углы образованы двумя прямыми, пересекающими две пары смежных углов, которые являются дополнительными. Два угла, противоположные друг другу как ∠1 и ∠3 на рисунке, называются вертикальными углами .
Углы, образованные Параллельными прямыми и секущей
Следовательно, пара соответствующих углов, чередующихся внутренних углов, чередующихся внешних углов, Внутренних углов по одну сторону от секущей такова:
- Соответствующие углы: ∠ 1 и ∠ 5, ∠ 2 и ∠ 6, ∠ 4 и ∠ 8 и ∠ 3 и ∠ 7.
- Альтернативные внутренние углы: и ∠ 3 и ∠ 3 ∠ 5.
- Альтернативные внешние углы: ∠ 1 и ∠ 7, и ∠ 2 и ∠ 8.
- Внутренние углы на одной стороне поперечной: ∠ 4 и ∠ 5 и ∠ 3
Аксиома соответственных углов
Выясним, как соотносятся углы в этих парах, когда прямая m параллельна прямой n.
Пара соответствующих углов.
Следовательно, аксиома соответственных углов формулируется так:
Если секущей пересекаются две параллельные прямые, так что пара соответствующих углов равна, то две прямые параллельны друг другу.
Доказать: Соответственные углы равны.
Доказательство: Прямые m и n параллельны друг другу, а прямая l является пересечением.
Так как прямые m и n параллельны.
Следовательно,
♂ 3 + ♂ 6 = 180 ° (соседний угол параллелограмма) …… (1)
тий 7 + ♂ 6 = 180 ° (дополнительные углы) …… (2)
потрясти 2 = 180 ° (дополнительный угол) …… (3)
Таким образом, из уравнения (1) и (2) делается вывод, что:
тий 3 = ♂ 7
Аналогично, из (1) и (3) делается вывод:
∠ 6 = ∠ 2
Таким образом, также можно доказать, что:
∠ 1 = ∠ 5
∠ 4 = ∠ 8
Отсюда следует, что все четыре пары соответствующих углов равны друг другу.
Обращение аксиомы соответствующих углов
Обращение аксиомы соответствующих углов формулируется как:
друг друга.
Пара соответствующих углов.
Доказать: Если соответствующие углы равны, то прямые параллельны.
Доказательство: Линия l является обходом линий m и n.
Следовательно,
♂ 3 = ♂ 7 (указано, соответствующие углы равны) …… (1)
♂ 7 + ♂ 6 = 180 ° (дополнительный угол) …… (2)
Итак, из уравнения ( 1) и (2) делается вывод о том, что:
∠ 3 + ∠ 6 = 180°
Так как сумма смежных углов является дополнительной.
Следовательно, прямые параллельны.
Аксиома альтернативных углов
Аксиома альтернативных углов формулируется следующим образом:
Если секущая пересекает две параллельные прямые, то каждая пара альтернативных внутренних углов равна.
Пара альтернативных углов.
Доказать: Смежные внутренние углы равны.
Доказательство: Прямые m и n параллельны друг другу, а прямая l является пересечением.
♂ 3 = ♂ 7 (соответствующая аксиома углов) …… (1)
♂ 7 = ♂ 5 (вертикально противоположные углы) …… (2)
Итак, из уравнения (1) и (2) что:
∠ 3 = ∠ 5
Точно так же это можно записать как:
∠ 4 = ∠ 6
Значит, внутренние углы равны.
Обращение аксиомы альтернативных углов
Обращение аксиомы альтернативных углов формулируется как:
.
Пара альтернативных углов.
Доказать: Если параллельные внутренние углы равны, то две прямые параллельны.
Доказательство: Прямые m и n параллельны друг другу, а прямая l является пересечением.
Следовательно,
♂ 3 = ♂ 5 (альтернативные внутренние углы) …….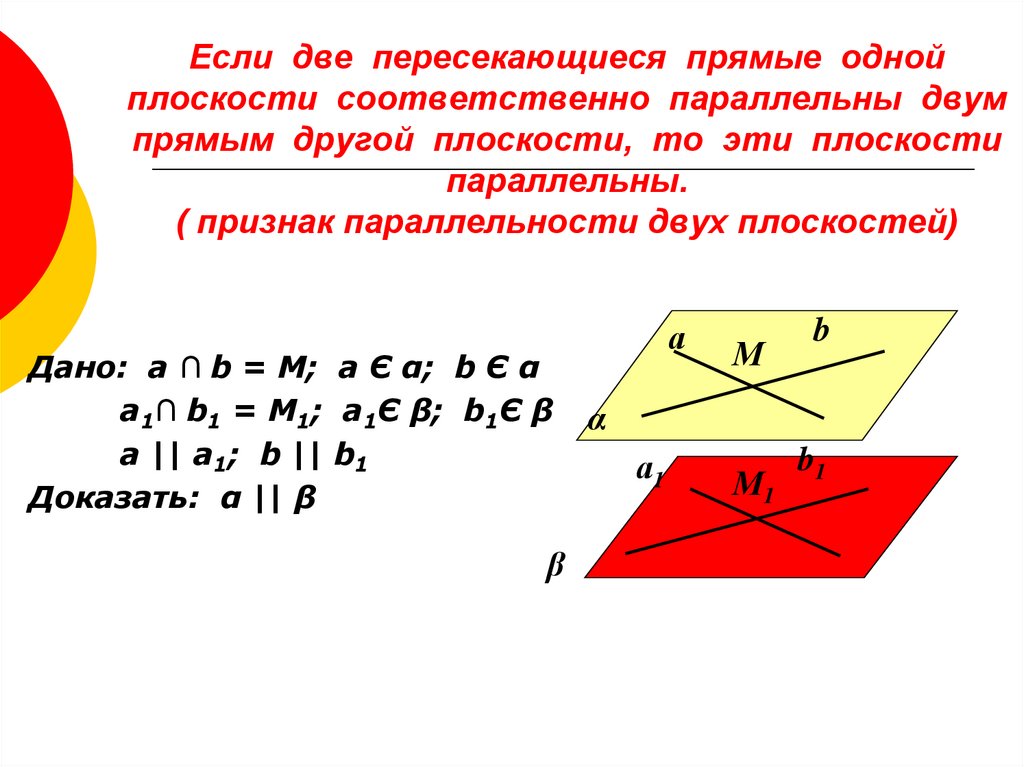 (1)
(1)
♂ 7 = ♂ 5 (вертикально противоположные углы) ……. (2)
Итак, из уравнения (1) и и (2) делается вывод, что:
∠ 3 = ∠ 7
Согласно обращенной аксиоме соответственных углов: если секущая пересекает две прямые так, что пара соответствующих углов равна, то две прямые параллельны каждой Другой.
Следовательно, две прямые параллельны.
Свойство внутренних углов по одну сторону от секущей
Свойство внутренних углов выражается следующим образом:
Если секущая пересекает две параллельные прямые, то каждая пара внутренних углов по одну сторону от секущей равна дополнительный.
Пара внутренних углов
Доказать: Если секущая пересекает две параллельные прямые, то каждая пара внутренних углов по одну сторону от секущей является дополнительной.
Доказательство: Прямые m и n параллельны друг другу, а прямая l является пересечением.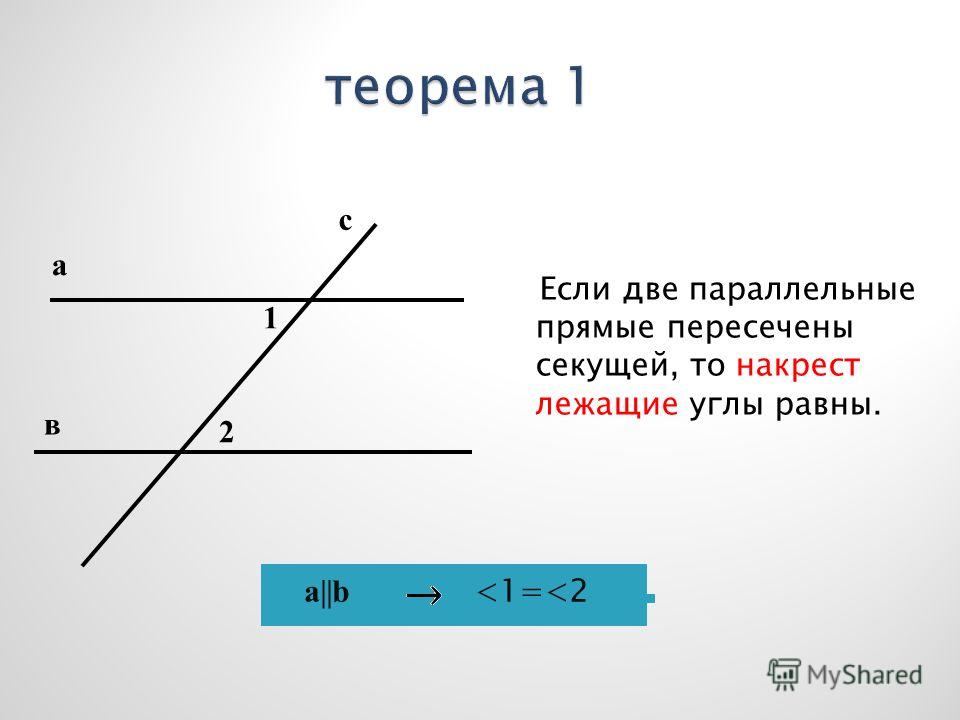
Следовательно,
♂ 3 = ♂ 7 (соответствующая аксиома углов) …… (1)
♂ 6 + ♂ 7 = 180 ° (дополнительный угол) …… (2)
Итак, из уравнения (1) и и (2) делается вывод, что:
∠ 6 + ∠ 3 = 180°
Значит, каждая пара внутренних углов по одну сторону от секущей является дополнительной.
Обратное свойство внутренних углов по ту же сторону от поперечной
Обратное свойство внутренних углов формулируется как:
углы по одну сторону от секущей добавочные, то обе прямые параллельны.
Пара внутренних уголков.
Доказать: Если секущая пересекает две прямые так, что пара внутренних углов по одну сторону от этой секущей является дополнительной, то эти две прямые параллельны.
Доказательство: Пара внутренних углов по одну сторону от секущей является дополнительной.
секрета.0005
Итак, из уравнения (1) и (2) следует, что:
∠ 7 = ∠ 3
Следовательно, две прямые параллельны.
Прямые, параллельные одной и той же прямой
Теорема о прямых, параллельных одной и той же прямой, формулируется следующим образом:
Прямые, параллельные одной и той же прямой, параллельны друг другу.
Линии, параллельные одной линии.
Доказать: Прямые, параллельные одной прямой, параллельны друг другу (p || q || r).
Доказательство: Прямые p и r параллельны, прямые p и q параллельны друг другу, а прямая l является пересечением.
Сейчас, п || д и р || р
С м || Q Следовательно,
♂ 1 = ♂ 2 (соответствующая аксиома углов) …… (1)
секрет 1 = ♂ 3 (соответствующие углы аксиомы) …… (2)
Итак, из уравнения (1) и (2) делается вывод, что:
∠ 2 = ∠ 3
Однако, согласно обратной аксиоме соответственных углов, если секущая пересекает две прямые так, что пара соответствующих углов равна, то две прямые параллельны друг другу.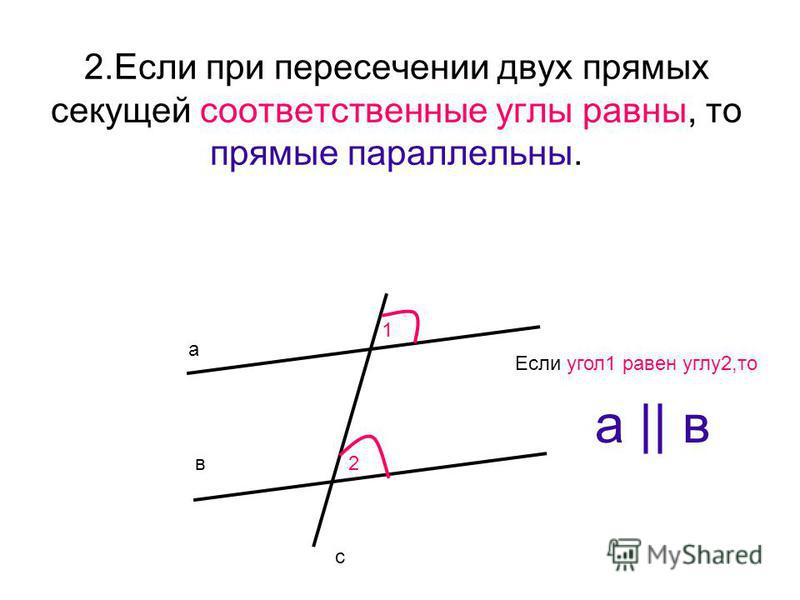
Следовательно, две прямые q и r параллельны и, значит, параллельны r.
Примеры задач
Задача 1: на рисунке, если PQ || RS, ∠ MXQ = 135° и ∠ MYR = 40°, найти ∠ XMY.
Решение:
Построим прямую AB, параллельную прямой PQ, через точку M.
Теперь AB || ПК и ПК || RS
⇒ AB || РС || PQ (теорема 5)
∠ QXM + ∠ XMB = 180° (AB || PQ, внутренние углы по одну сторону от поперечной XM)
As, ∠ QXM = 135°
135° + ∠ XMB = 180 °
∠ XMB = 45°
Теперь, ∠ BMY = ∠ MYR (AB || RS, Альтернативные углы)
∠ BMY = 40°
As, ∠ XMB + ∠ BMY = 45° + 405° 90
2 Следовательно,
∠ XMY = 85° .
Задача 2. Если секущая пересекает две прямые так, что биссектрисы пары соответствующих углов параллельны, то докажите, что эти две прямые параллельны.
Решение:
Пусть трансверсаль AD пересекает две прямые PQ и RS в точках B и C соответственно.
Луч BE — биссектриса ∠ ABQ, а луч CG — биссектриса ∠ BCS и BE || КГ.
Доказать: PQ || РС.
При этом луч BE является биссектрисой ∠ ABQ.
Следовательно, ∠ ABE = ½ ∠ ABQ .
Следовательно, ♂ BCG = ½ ♂ BCS …… (2)
с использованием соответствующих углов аксиомы,
♂ ABE = ♂ BCG (BE || CG, а AD — походные) …… (3)
Используя (1) и (2) в (3), получаем
½ ∠ ABQ = ½ ∠ BCS
То есть ∠ ABQ = ∠ BCS
Так как они являются соответствующими углами, образованными поперечными AD с PQ и РС.
Следовательно, PQ || РС. (Аксиома преобразования соответствующих углов)
Задача 3. На рисунке AB || CD и CD || ЭФ. Также ЕА ⊥ АВ. Если ∠ BEF = 55°, найдите значения x, y и z.
Решение:
Так как, AB || CD и CD || ЭФ
⇒ АВ || компакт-диск || EF ( Прямые, параллельные одной и той же прямой, параллельны друг другу )
И, EB и AE являются трансверсальными.
y + 55° = 180° (CD || EF, внутренние углы по одну сторону от поперечной EB)
y = 180° – 55° = 125°
As, x = y (AB || CD, соответствующие углы аксиома)
x = y = 125º
Теперь ∠ EAB + ∠ FEA = 180° (внутренние углы на одной стороне поперечного EA)
90° + z + 55° = 180°
Следовательно, z = 35°.
Задача 4. Найдите на рисунке значения x и y и покажите, что AB || CD.
Решение:
Здесь,
x+50 ° = 180 ° (линейная пара равна 180 °)
x = 130 °
и y = 130 ° (вертикально противоположное уголов равны)
Здесь мы можем наблюдать, что
x = y = 130°
В двух параллельных прямых внутренние углы равны.
Таким образом, это доказывает, что альтернативные внутренние углы равны и, таким образом, AB || CD.
Задача 5: На рисунке, если AB || CD, ∠ APQ = 50° и ∠ PRD = 127°, найти x и y.
Решение:
Здесь, APQ = PQR (альтернативные внутренние углы)
x = 50 °
и,
APR = PRD (alternate interior nagles)
APQ+QPR = 127°
127° = 50°+ y
y = 77°
Следовательно, значения равны x = 50° и y = 77°.
Параллельные линии (геометрия) | Brilliant Math & Science Wiki
Содержание
- Основные свойства параллельных линий
- Обходы параллельных линий
Параллельные прямые никогда не пересекаются. На языке линейных уравнений это означает, что они имеют одинаковый наклон. Другими словами, при некотором изменении независимой переменной каждая строка будет иметь идентичное друг другу изменение зависимой переменной.
В трехмерном пространстве параллельные линии — это (неподвижные) линии, лежащие в одной плоскости и не пересекающиеся. Важно отметить, что некоторые другие линии в трехмерном пространстве могут не пересекаться, но и не лежать в одной плоскости; они известны как наклонные линии.
Важно отметить, что некоторые другие линии в трехмерном пространстве могут не пересекаться, но и не лежать в одной плоскости; они известны как наклонные линии.
Imgur
На этом рисунке добавлена поперечная (линия PQ↔\overleftrightarrow{PQ}PQ). Пусть XXX и YYY будут точками пересечения секущей с AB↔\overleftrightarrow{AB}AB и CD↔,\overleftrightarrow{CD},CD соответственно. Теперь, учитывая, что AB↔∥CD↔,\overleftrightarrow{AB}\parallel\overleftrightarrow{CD},AB∥CD, всегда следует, что ∠PXB=∠PYD.\angle PXB=\angle PYD.∠PXB=∠PYD . Углы в этом виде отношений известны как соответствующие углы . Обратите внимание, что ∠PXB=∠AXY,\угол PXB=\угол AXY,∠PXB=∠AXY, так как они являются противоположными углами. Тогда мы имеем ∠AXY=∠XYD,\угол AXY=\угол XYD,∠AXY=∠XYD, которые называются альтернативными углами .
Обратные свойства вышеприведенных также верны. Если две прямые имеют соответствующие углы, то эти две прямые параллельны.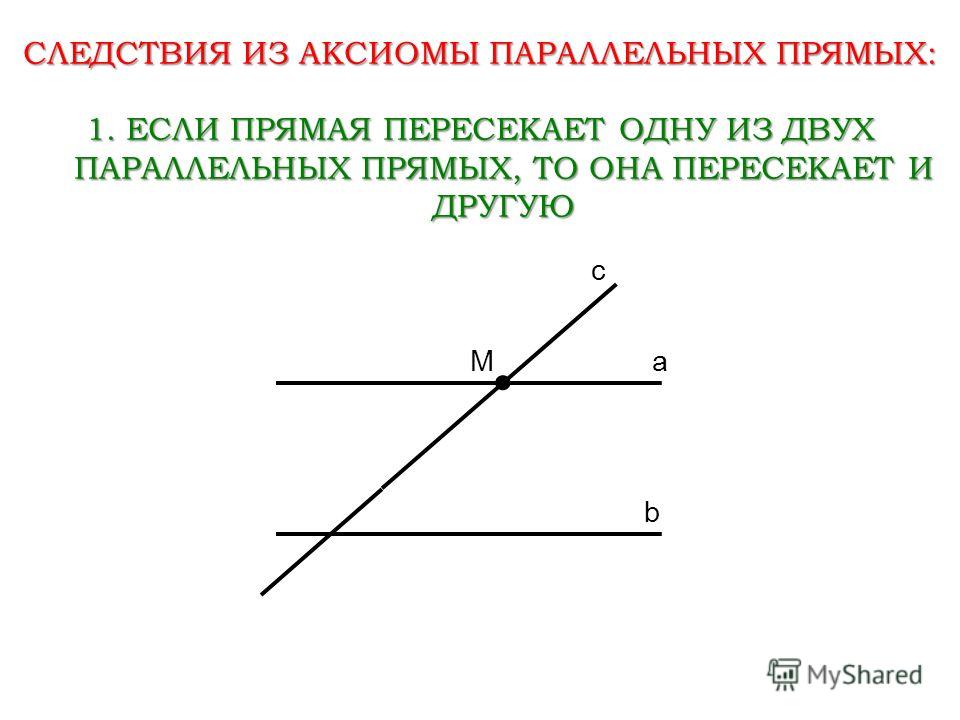 Кроме того, если две прямые имеют альтернативные углы, то мы можем сказать, что эти две прямые параллельны.
Кроме того, если две прямые имеют альтернативные углы, то мы можем сказать, что эти две прямые параллельны.
Изображение
Теперь представьте, что вы рисуете поперечную (линия PQ↔\overleftrightarrow{PQ}PQ), которая пересекается перпендикулярно двум параллельным линиям, как показано на рисунке выше. Тогда длина XY‾\overline{XY}XY будет кратчайшим расстоянием между двумя параллельными прямыми. Теперь мы проводим дополнительную секущую (прямая P′Q′↔\overleftrightarrow{P’Q’}P’Q′), которая также перпендикулярно пересекается с двумя параллельными прямыми. Обратите внимание, что PQ↔\overleftrightarrow{PQ}PQ и P′Q′↔\overleftrightarrow{P’Q’}P′Q′ параллельны (попробуйте доказать это, используя понятие соответствующих углов и альтернативных углов!). Теперь у нас также есть длина P′Q′‾\overline{P’Q’}P′Q′ как кратчайшее расстояние между двумя параллельными прямыми, и, следовательно, верно, что ∣PQ‾∣=∣P′Q ′‾∣.\lvert\overline{PQ}\rvert=\lvert\overline{P’Q’}\rvert. ∣PQ∣=∣P′Q′∣. Это означает, что две параллельные линии всегда находятся на постоянном расстоянии друг от друга, что является еще одной важной характеристикой параллельных линий.
∣PQ∣=∣P′Q′∣. Это означает, что две параллельные линии всегда находятся на постоянном расстоянии друг от друга, что является еще одной важной характеристикой параллельных линий.
Рассуждая более интуитивно, это должно быть правдой, поскольку, если бы линии отдалялись друг от друга, то на противоположной стороне линии сближались бы (и, в конце концов, встречались), что противоречит определению, согласно которому две параллельные линии никогда не встретиться. Обратите внимание, что расстояние между двумя отдельными линиями можно определить, только если линии параллельны. Если линии не параллельны, то расстояние будет продолжать изменяться.
Обсуждение чуть выше, к вашему сведению, на самом деле соответствует Пятый постулат Евклида , или параллельный постулат . Он гласит, что если отрезок пересекает две прямые линии, образующие два внутренних угла на одной стороне, сумма которых меньше 180 градусов, то две прямые, если их продолжить бесконечно, пересекутся на той стороне, на которой сумма углов меньше 180 градусов. . Другими словами, две прямые параллельны, если сумма внутренних углов на одной стороне равна ровно 180 градусам.
. Другими словами, две прямые параллельны, если сумма внутренних углов на одной стороне равна ровно 180 градусам.
Таким образом,
Углы, лежащие на одной и той же стороне секущей и между параллелями (называемые соответствующими углами), равны. Верно и обратное: если две прямые имеют равные соответствующие углы, то прямые параллельны.
Углы, лежащие на противоположных сторонах секущей и между параллелями (называемые параллельными углами), равны. Верно и обратное: если противоположные углы равны, прямые параллельны.
Две параллельные прямые находятся на постоянном расстоянии друг от друга, поэтому любая пара прямых, пересекающих их под одним и тем же углом, образует отрезки одинаковой длины.
Если на следующей диаграмме отрезки QUQUQU и RTRTRT параллельны, что мы можем сказать об углах PVQPVQPVQ и TWSTWSTWS?
У нас есть
∠PVQ=∠PWR (соответствующие углы) =∠TWS.
(противоположные углы) \begin{array} { l l l } \angle PVQ & = \angle PWR & \text{ (соответствующие углы) } \\ & = \angle TWS. & \text{ (противоположные углы) } \\ \end{массив} ∠PVQ=∠PWR=∠TWS. (соответствующие углы) (противоположные углы)
Следовательно, эти углы равны. □ _\квадрат □
Изображение 9\circ.x=45∘+65∘=110∘. □_\квадрат□
Имгур
На рисунке выше две линии XY↔\overleftrightarrow{XY}XY и AD↔\overleftrightarrow{AD}AD параллельны. Если площадь △ABY\треугольника ABY△ABY равна 5, то какова площадь △CDX?\треугольника CDX?△CDX?
Поскольку XY↔\overleftrightarrow{XY}XY и AD↔\overleftrightarrow{AD}AD параллельны, высоты двух треугольников будут равны. Поскольку основание △CDX\треугольника CDX△CDX в три раза больше основания △ABY,\треугольника ABY,△ABY, ответ равен 3×5=15,3\times5=15,3×5=15.
□_\квадрат□
Процитировать как: Параллельные линии (геометрия). Brilliant.org . Извлекаются из https://brilliant.org/wiki/parallel-lines/
Видео-урок: Параллельные прямые и сечения: применение углов
Стенограмма видео
использовать угловые отношения, образованные параллельными линиями и секущими, для решения задач
с использованием алгебраических выражений и уравнений. Прежде всего, давайте вспомним некоторые
свойства параллельных прямых и секущих. Прежде всего, когда любые две строки
пересекаются, мы знаем, что противоположные по вертикали углы будут равны
еще один. Противоположные углы это два угла
между секущими линиями, которые имеют общую вершину, как мы видим здесь. Мера угла 𝐴 будет
равной мере угла 𝐶, а мера угла 𝐵 будет равна
мера угла 𝐷.
Когда любые две секущие линии пересекаются, мы также можем сказать, что сумма смежных углов будет равна 180 градусам. В этом случае мера угла 𝐴 плюс мера угла 𝐷 должны быть равны 180 градусам. Можно также сказать, что мера угол 𝐷 плюс мера угла 𝐶 должны быть 180 градусов. В самом деле, любая пара смежных сумма углов на этом изображении равна 180 градусам.
Но теперь мы хотим расширить это на
посмотрите, что получится, если две параллельные прямые пересечь одной и той же секущей. Здесь вторая и третья строки
параллельны, и они оба пересекаются поперечной линией. Если мы просто смотрим на первую строку
и строка два, мы уже показали, что вертикально противоположные углы конгруэнтны
для другого. Но когда мы расширим это до параллели
прямые, пересекаемые секущей, мы говорим, если две или более параллельных прямых пересекаются одним и тем же
поперечной, соответствующие углы равны.
Глядя на пересечение линии один и два, мы могли бы обозначить углы, созданные как позиции один, два, три и четыре. И затем, поскольку мы знаем эту строку три параллельна линии два и также пересекается с линией один, когда мы маркируйте их в одном направлении — вверху слева, вверху справа, внизу справа, внизу слева — соответствующие углы будут конгруэнтны, что означает, что углы в положении один равны конгруэнтны друг другу, углы в положении два конгруэнтны друг другу, и скоро.
Есть еще кое-что, что мы
следует отметить. Когда две параллельные прямые пересекаются
поперечной, противоположные углы равны. это углы на противоположных сторонах
поперечного. Показанные здесь являются альтернативными
внутренние углы, так как они находятся по обе стороны от поперечной, но между
две параллельные линии. Когда две параллельные прямые
пересеченная секущей, имеет две пары чередующихся внутренних углов. Также есть две пары
параллельные внешние углы, равные друг другу. Они находятся по обе стороны от
поперечной и на внешней стороне двух параллельных прямых.
Когда две параллельные прямые
пересеченная секущей, имеет две пары чередующихся внутренних углов. Также есть две пары
параллельные внешние углы, равные друг другу. Они находятся по обе стороны от
поперечной и на внешней стороне двух параллельных прямых.
Давайте посмотрим на последнюю пару углов
отношение. Последовательные внутренние углы, или
иногда называемые ковнутренними углами, это углы, лежащие по одну сторону от поперечной
и между двумя параллельными линиями. Сумма этих углов равна 180
градусов. Также стоит отметить, что все
эти свойства распространяются на несколько параллельных линий, а не только на две. На этом изображении у нас есть три
параллельны, и для всех трех пересечений соответствующие углы
будет конгруэнтным. Но что, если у нас есть дополнительный
поперечный? Для этой другой поперечной
конечно верно, что соответствующие углы будут конгруэнтны. Однако только потому, что мы знаем
что-то об углах одной из трансверсалей не означает, что мы можем сказать
что-нибудь об отношениях углов в другой секущей. Поэтому мы должны помнить, чтобы применить
эти свойства по одной трансверсали за раз. Давайте посмотрим на некоторые примеры.
Однако только потому, что мы знаем
что-то об углах одной из трансверсалей не означает, что мы можем сказать
что-нибудь об отношениях углов в другой секущей. Поэтому мы должны помнить, чтобы применить
эти свойства по одной трансверсали за раз. Давайте посмотрим на некоторые примеры.
Определите значение 𝑥 в фигура.
Прежде всего, давайте подумаем о тип линий, которые мы видим на рисунке. У нас есть две параллельные линии, которые пересечение секущей, в результате чего угол 61 градус и угол 𝑥 чередуются внутренние углы. И когда две параллельные линии разрезаны у секущей параллельные внутренние углы равны. Это означает, что оба эти угла равны равны по мере, а 𝑥 должно быть равно 61.
Мы можем рассмотреть другой пример с другой набор пар углов.
Определите значение 𝑥 в фигура.
Прежде всего, давайте подумаем о
что мы можем сказать об этих строках. Имеем две параллельные прямые, пересеченные
поперечной, и вот два угла, которые мы рассматриваем. Они на одной стороне
поперечны, и они находятся в одном и том же положении на обоих пересечениях, что означает, что мы
называть их соответствующими углами. И когда две параллельные линии разрезаны
секущей соответствующие углы равны, поэтому 𝑥 должны быть равны
до 72,
Имеем две параллельные прямые, пересеченные
поперечной, и вот два угла, которые мы рассматриваем. Они на одной стороне
поперечны, и они находятся в одном и том же положении на обоих пересечениях, что означает, что мы
называть их соответствующими углами. И когда две параллельные линии разрезаны
секущей соответствующие углы равны, поэтому 𝑥 должны быть равны
до 72,
В нашем следующем примере мы не только есть две параллельные прямые, но у нас также будут две секущие.
Ответить на вопросы по данному фигура. Найдите значение 𝑥 и найдите значение 𝑦.
Прежде всего, давайте подумаем о
что мы знаем об этих линиях. У нас есть две параллельные линии. Назовем их первая линия и линия
два. И тогда у нас есть трансверсаль,
третья линия, которая пересекает первую и вторую линии. И у нас есть второй трансверсаль мы
может вызвать четвертую линию, которая также пересекает первую и вторую линии. Во-первых, давайте просто рассмотрим строку
один, два и три, левая сторона изображения. Поскольку третья линия является поперечной
которая пересекает первую и вторую линии, угол 𝑥 и угол 60 градусов равны
последовательные внутренние углы, иногда называемые ковнутренними углами. И мы знаем, что эти углы должны
в сумме 180 градусов, а это значит, что 𝑥 плюс 60 должно быть равно 180.
Во-первых, давайте просто рассмотрим строку
один, два и три, левая сторона изображения. Поскольку третья линия является поперечной
которая пересекает первую и вторую линии, угол 𝑥 и угол 60 градусов равны
последовательные внутренние углы, иногда называемые ковнутренними углами. И мы знаем, что эти углы должны
в сумме 180 градусов, а это значит, что 𝑥 плюс 60 должно быть равно 180.
Если вычесть 60 с обеих сторон
этого уравнения мы видим, что 𝑥 должно быть равно 120. Чтобы найти 𝑦, мы можем посмотреть на
строка первая, вторая и четвертая. Имеем две параллельные прямые, пересеченные
поперечные, и парные отношения углов 𝑦 и 110 будут соответствующими
углы. Они на одной стороне
поперечно и по одну сторону от их параллельных прямых соответственно. Они находятся в том же положении в
оба пересечения и соответствующие углы равны друг другу, что
означает, что 𝑦 должно быть равно 110.
Теперь, когда у нас есть все это информации, можно было бы найти этот четвертый угол внутри этого четырехугольник. Этот угол является последовательным внутренний угол со 110 градусами, что означает, что 110 плюс этот угол должны равняться 180. 70 плюс 110 равно 180. Если бы мы хотели выполнить один финальный проверить, правильно ли мы все посчитали, мы смогли просуммировать четыре внутренних углы, образованные этими линиями. Мы знаем, что четыре внутренних сумма углов внутри четырехугольника должна составлять 360 градусов. В этом случае они делают, и что подтверждает, что 𝑥 равно 120, а 𝑦 равно 110.
Мы готовы рассмотреть еще один пример.
На данном рисунке показана пара
параллельные прямые и две секущие, одна из которых пересекается под прямым углом. Напишите выражение для 𝑑 в терминах
из 𝑏. Используя это выражение для 𝑑, найдите
полностью упрощенное выражение для 𝑎 через 𝑏.
Посмотрим, что у нас есть. У нас есть две параллельные линии. Мы могли бы назвать их первой линией и
линия два, а затем у нас есть две трансверсали, которые мы могли бы назвать линией три и линией
четыре. Первое, что мы хотим сделать, это
напишите выражение для 𝑑 через 𝑏. 𝑑 и 𝑏 встречаются на пересечении
строки один и строки три. Это смежные углы на
той же стороне первой линии. Это делает их дополнительными
углы. В сумме они должны составлять 180
градусов. Если мы знаем, что 𝑏 градусов плюс 𝑑
градусы должны равняться 180 градусам, и мы хотим 𝑑 с точки зрения 𝑏, это означает, что мы хотим
попытайтесь получить 𝑑 само по себе и получить 𝑏 с другой стороны уравнения. Для этого мы можем вычесть 𝑏
градусов с обеих сторон уравнения, значит 𝑑 градусов будет равно 180
градусов минус 𝑏 градусов, поэтому 𝑑 будет равно 180 минус 𝑏. На этом первая часть, наша первая
выражение.
На этом первая часть, наша первая
выражение.
Теперь, используя это выражение для 𝑑, нам нужно найти полностью упрощенное выражение для 𝑎 через 𝑏, что означает, что мы сначала нужно посмотреть на соотношение между 𝑎 градусами и 𝑑 градусами. Когда дело доходит до 𝑎 и 𝑑, они находятся между двумя параллельными прямыми и по одну сторону от поперечной. Они последовательные внутренние углы, иногда называемые ковнутренними углами. И когда две параллельные прямые пересеченная секущей, последовательные внутренние углы являются дополнительными. В сумме получается 180. А это значит 𝑎 градусов плюс 𝑑 градусы должны равняться 180 градусам.
Для этого выражения мы хотим
выразить 𝑎 через 𝑏, а это значит, что нам нужно получить 𝑎 само по себе. Сначала мы вычитаем 𝑑 из обоих
сторон, что дает нам 𝑎 градусов равно 180 градусов минус 𝑑 градусов или 𝑎 равно
180 минус 𝑑. Но помните, мы хотим заменить
наше выражение мы уже нашли для 𝑑. Мы знаем, что 𝑑 равно 180 минус
𝑏. Помните, однако, мы вычитаем
все 𝑑, поэтому нам нужно сохранить это в круглых скобках, а затем распределить это
вычитание, что означает вычитание 180. Но вычитание отрицательного 𝑏 будет
добавить 𝑏, и это означает, что 𝑎 равно 180 минус 180 плюс 𝑏. 180 минус 180 равно нулю, а ноль
плюс 𝑏 равно 𝑏. Полностью упрощенное выражение для
𝑎 с точки зрения 𝑏 состоит в том, что 𝑎 равно 𝑏.
Но помните, мы хотим заменить
наше выражение мы уже нашли для 𝑑. Мы знаем, что 𝑑 равно 180 минус
𝑏. Помните, однако, мы вычитаем
все 𝑑, поэтому нам нужно сохранить это в круглых скобках, а затем распределить это
вычитание, что означает вычитание 180. Но вычитание отрицательного 𝑏 будет
добавить 𝑏, и это означает, что 𝑎 равно 180 минус 180 плюс 𝑏. 180 минус 180 равно нулю, а ноль
плюс 𝑏 равно 𝑏. Полностью упрощенное выражение для
𝑎 с точки зрения 𝑏 состоит в том, что 𝑎 равно 𝑏.
На самом деле, если присмотреться в 𝑎 и 𝑏 мы видим, что отношения между этими двумя углами чередуются внутренние углы, и мы знаем, что альтернативные внутренние углы будут конгруэнтными. Таким образом, 𝑑 с точки зрения 𝑏 будет 𝑑 равно 180 минус 𝑏, а 𝑎 с точки зрения 𝑏 будет 𝑎 равно 𝑏.
Теперь мы готовы взглянуть на наш
последний пример.
На следующем рисунке 𝑧 равно два 𝑥 минус 69а 𝑤 равно двум 𝑦 минус 59. Найдите 𝑥 и 𝑦.
Прежде всего, давайте посмотрим, что мы
имеют. У нас есть две параллельные линии. Если мы продлим их немного дальше,
мы можем назвать их первой и второй строками. И тогда у нас есть две трансверсали,
которые мы можем назвать третьей и четвертой строками. Сначала кажется, что у нас есть
много переменных и не так много информации. Но когда мы смотрим на
отношения 𝑤 градусов и 𝑧 градусов, мы можем сказать, что 𝑧 градусов плюс 𝑤
градусы должны равняться 180 градусам. Кроме того, третья строка
пересекает линию один и линию два. А значит этот четвертый интерьер
угол также будет равен 𝑧 градусам, так как эти два угла
соответствующий. А это значит, что наши две трансверсали
и наши две параллельные прямые дали нам четырехугольник. А внутренние углы
четырехугольник должен в сумме давать 360 градусов. Таким образом, мы можем сказать, что 𝑧 градусов плюс
𝑤 градусов плюс 83 градуса плюс 𝑥 должно равняться 360 градусам.
А внутренние углы
четырехугольник должен в сумме давать 360 градусов. Таким образом, мы можем сказать, что 𝑧 градусов плюс
𝑤 градусов плюс 83 градуса плюс 𝑥 должно равняться 360 градусам.
Но мы уже знаем, что 𝑧 плюс 𝑤 равно. Так как 𝑧 плюс 𝑤 равно 180 градусов, мы можем сказать, что 180 плюс 83 плюс 𝑥 должно равняться 360. Таким образом, 263 градуса плюс 𝑥 градусов равняется 360 градусам. Если вычесть 263 градуса из с обеих сторон, 𝑥 градусов равно 97 градусам, а 𝑥 должно равняться 97. И поскольку мы знаем, что 𝑧 равно два 𝑥 минус 69, мы можем подставить 97 вместо 𝑥, и мы обнаружим, что 𝑧 равно 125. Подставив 𝑧 равно 125 на нашем рисунке и 𝑥 равно 97, мы можем использовать эту информацию, чтобы найти 𝑤. Мы знаем, что 𝑧 плюс 𝑤 равно 180. Подставляем 125. И когда из обоих вычитаем 125 сторон, находим 𝑤 равно 55.
Но помните, наша цель найти
𝑥 и 𝑦, а это значит, что нам нужно подставить то, что мы знаем о 𝑤, чтобы найти 𝑦.

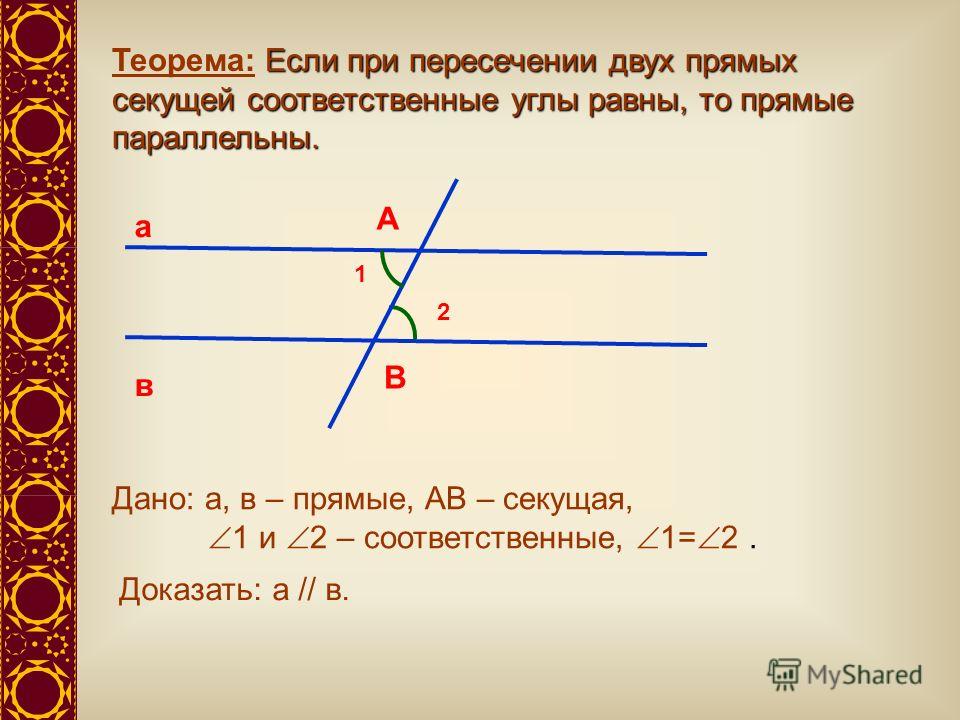
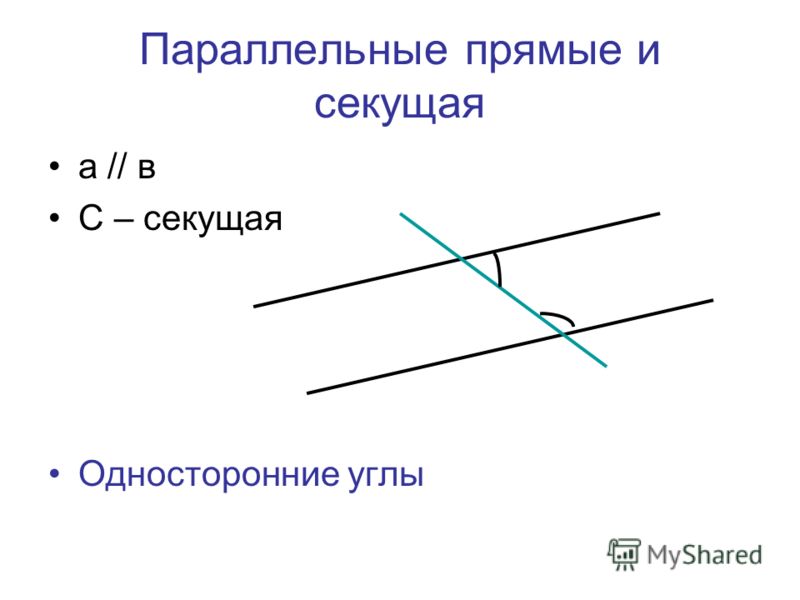
 Параллельные прямые обозначаются специальным символом || .
Параллельные прямые обозначаются специальным символом || .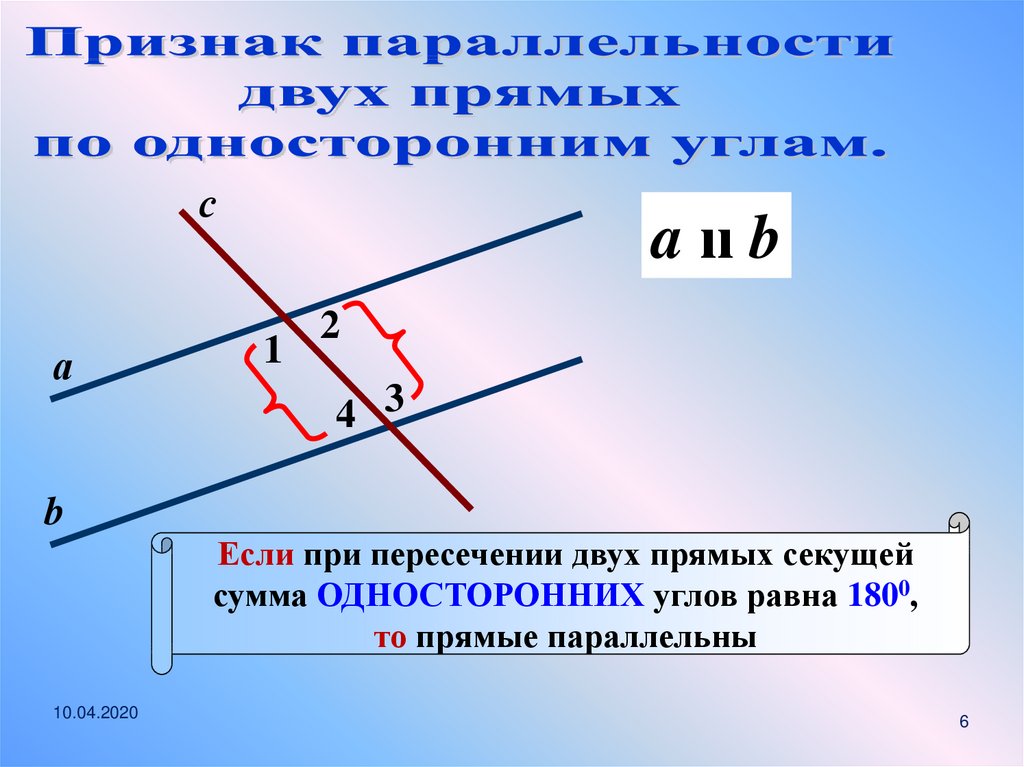

 Луч BE — биссектриса ∠ ABQ, а луч CG — биссектриса ∠ BCS и BE || КГ.
Луч BE — биссектриса ∠ ABQ, а луч CG — биссектриса ∠ BCS и BE || КГ.