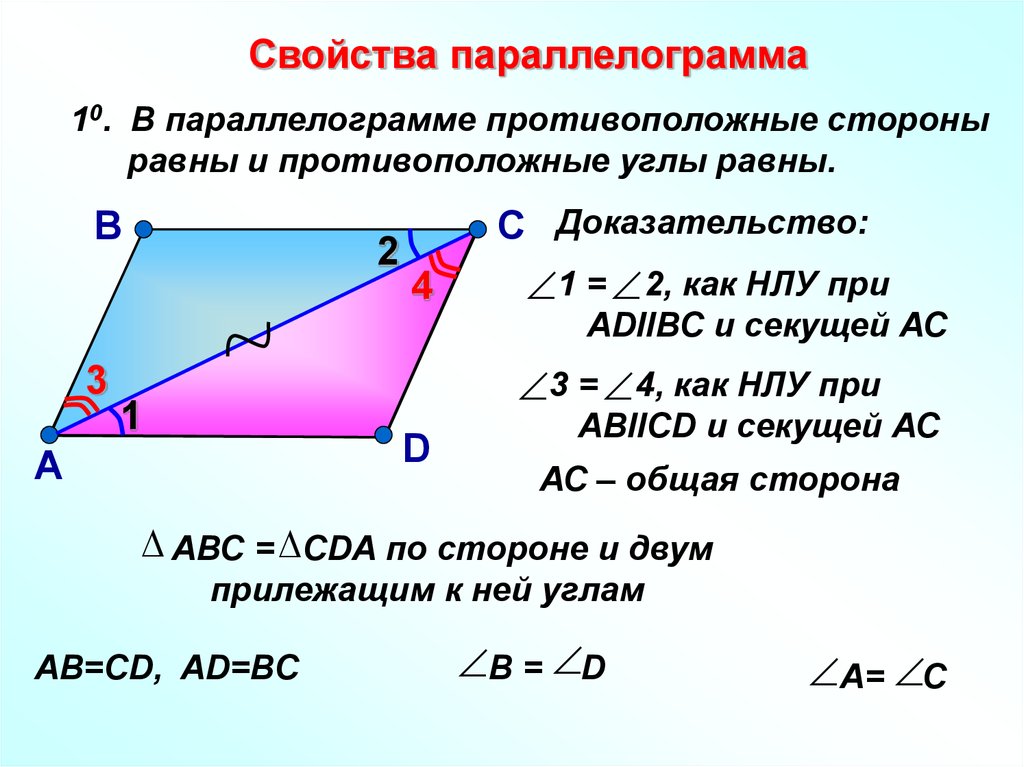
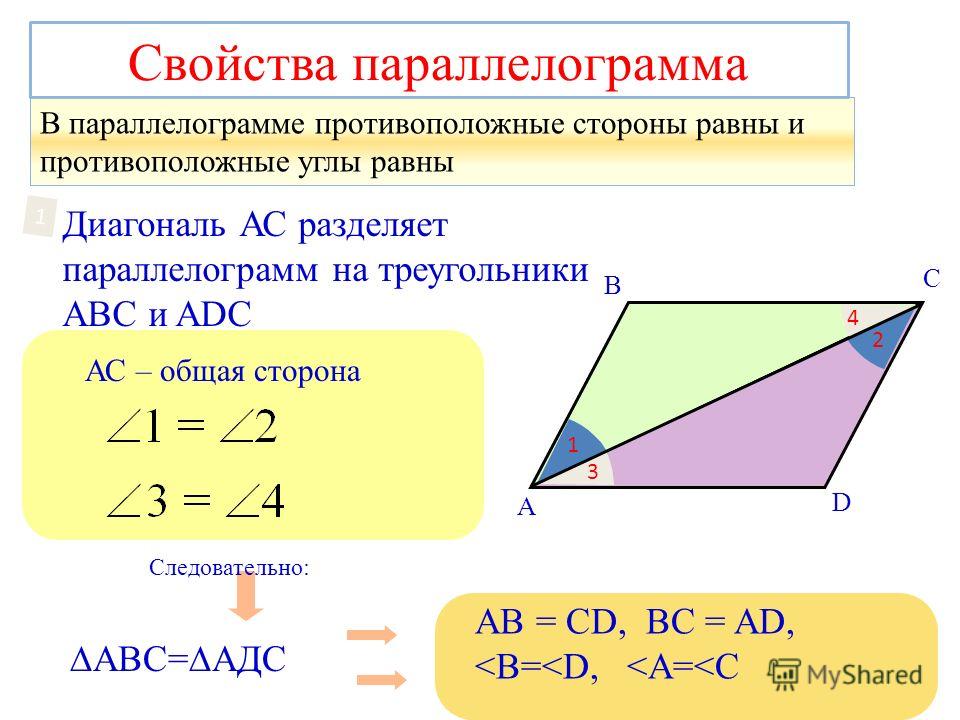
Какие свойства параллелограмма включены в его определение. Параллелограмм в задачах
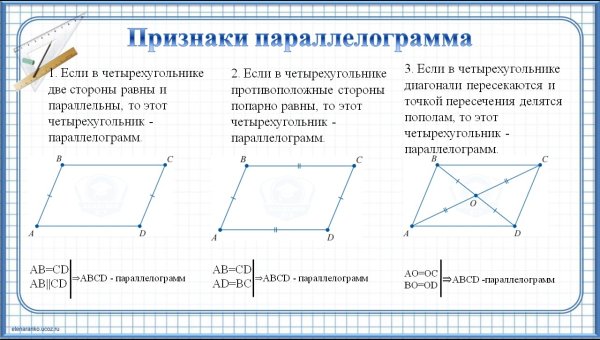
Для того, чтобы определить является ли данная фигура параллелограммом существует ряд признаков. Рассмотрим три основных признака параллелограмма.
1 признак параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти треугольники равны между собой по двум сторонам и углу между ними (BD — общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.
А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
2 признак параллелограмма
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти два треугольника буду равны между собой по трем сторонам (BD — общая сторона, AB = CD и BC = AD по условию). Из этого можно сделать вывод, что угол1 = угол2. Отсюда следует, что AB параллельна CD. А так как AB = CD и AB параллельна CD, то по первому признаку параллелограмма, четырехугольник ABCD будет являться параллелограммом.
3 признак параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Рассмотрим четырехугольник ABCD.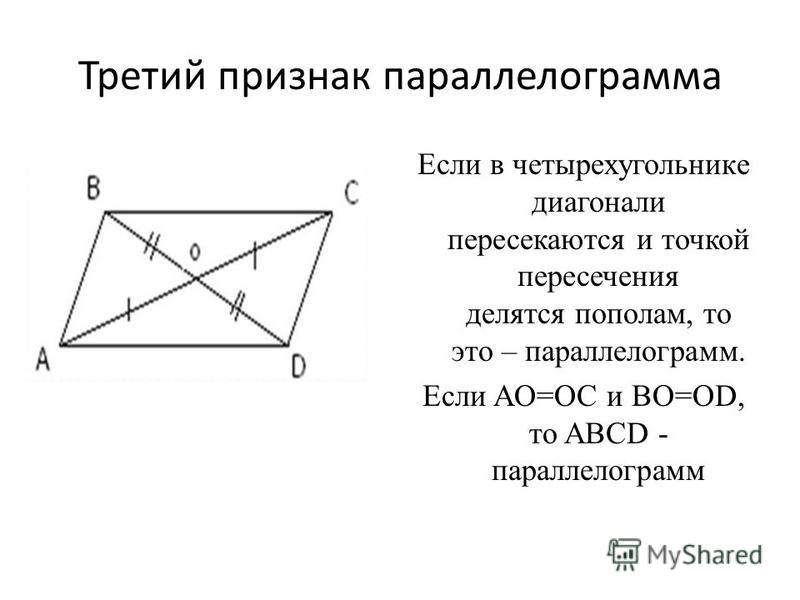
Треугольники AOB и COD будут равны между собой, по первому признаку равенства треугольников. (AO = OC, BO = OD по условию, угол AOB = угол COD как вертикальные углы.) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
Муниципальное бюджетное общеобразовательное учреждение
Савинская средняя общеобразовательная школа
Исследовательская работа
Параллелограмм и его новые свойства
Выполнила: ученица 8Б класса
МБОУ Савинская СОШ
Кузнецова Светлана,14 лет
Руководитель: учитель математики
Тульчевская Н.А.
п. Савино
Ивановская область, Россия
2016г.
I . Введение __________________________________________________стр 3
II . Из истории параллелограмма ___________________________________стр 4
III Дополнительные свойства параллелограмма ______________________стр 4
IV . Доказательство свойств _____________________________________ стр 5
V . Решение задач с использованием дополнительных свойств __________стр 8
VI . Применение свойств параллелограмма в жизни ___________________стр 11
VII . Заключение _________________________________________________стр 12
VIII . Литература _________________________________________________стр 13
Введение
«Среди равных умов
при одинаковости прочих условий
превосходит тот, кто знает геометрию»
(Блез Паскаль).
Во время изучения темы «Параллелограмм» на уроках геометрии мы рассмотрели два свойства параллелограмма и три признака, но когда мы начали решать задачи, то оказалось, что этого недостаточно.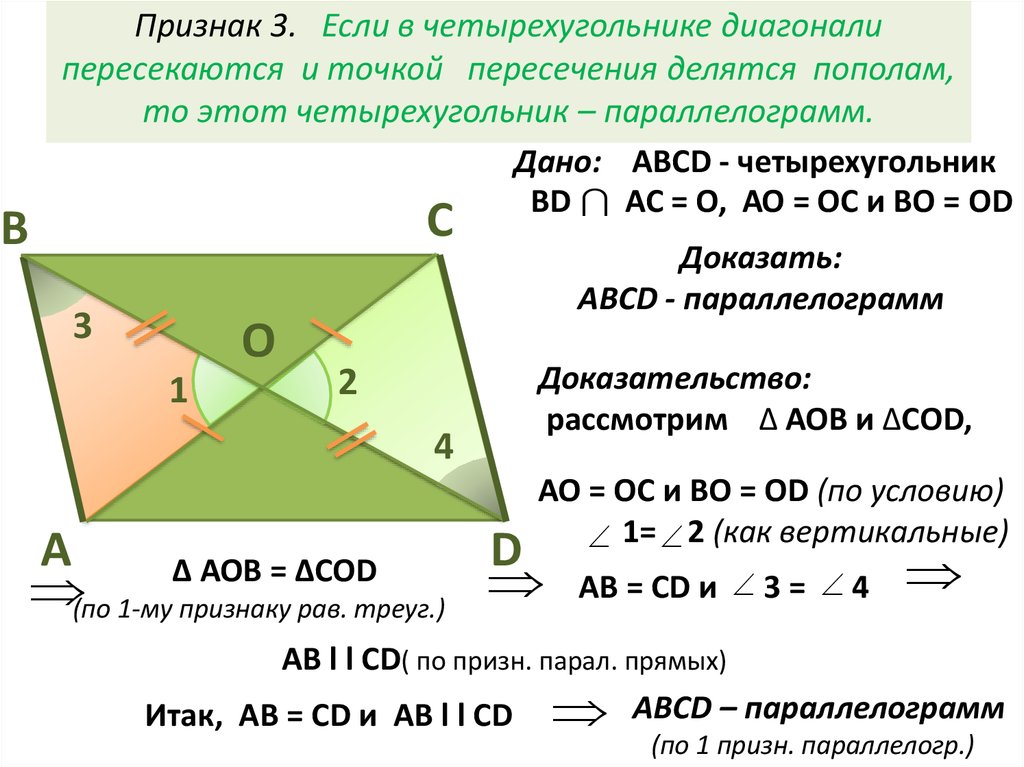
У меня возник вопрос, а есть ли у параллелограмма еще свойства, и как они помогут при решении задач.
И я решила изучить дополнительные свойства параллелограмма и показать, как их можно применить для решения задач.
Предмет исследования : параллелограмм
Объект исследования : свойства параллелограмма
Цель работы:
формулировка и доказательство дополнительных свойств параллелограмма, которые не изучаются в школе;
применение этих свойств для решения задач.
Задачи:
Найти дополнительную литературу по исследуемому вопросу;
Изучить дополнительные свойства параллелограмма и доказать их;
Показать применение этих свойств для решения задач;
Рассмотреть применение свойств параллелограмма в жизни.
Методы исследования:
Работа с учебной и научно – популярной литературой, ресурсами сети Интернет;
Изучение теоретического материала;
Выделение круга задач, которые можно решать с использованием дополнительных свойств параллелограмма;
Наблюдение, сравнение, анализ, аналогия.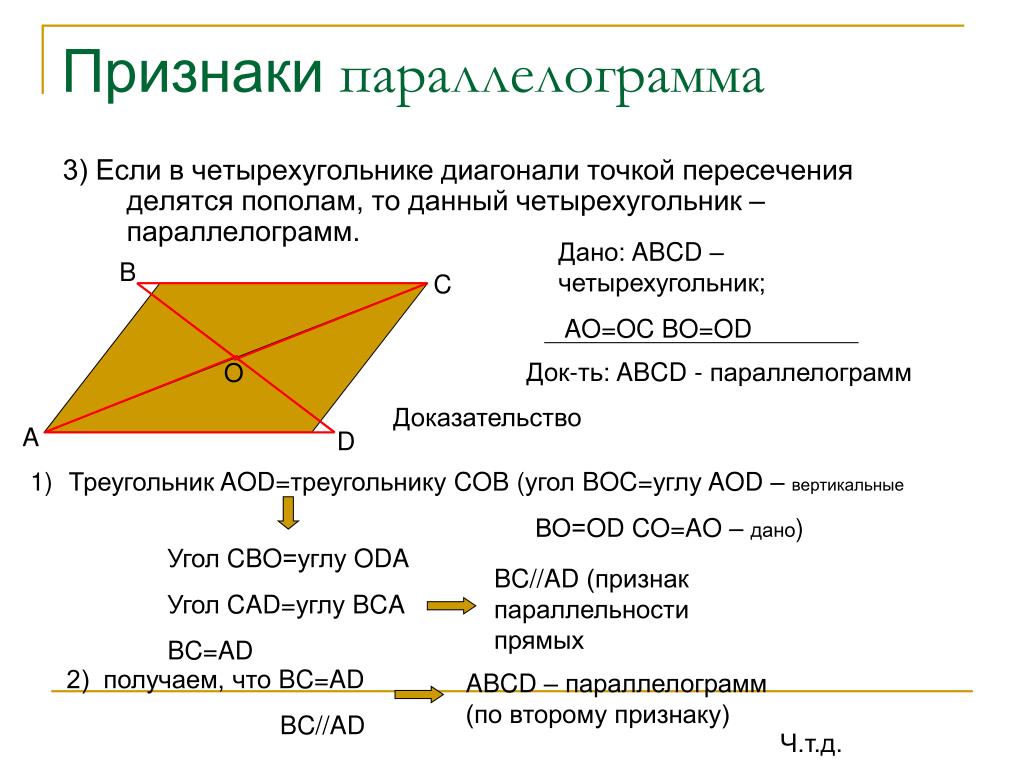
Продолжительность исследования : 3 месяца: январь-март 2016г
Из истории параллелограмма
В учебнике геометрии мы читаем следующее определение параллелограмма: параллелограмм – это такой четырехугольник, у которого противоположные стороны попарно параллельны
Слово «параллелограмм» переводится как «параллельные линии» (от греческих слов Parallelos — параллельный и gramme — линия), этот термин был введен Евклидом. В своей книге «Начала» Евклид доказал следующие свойства параллелограмма: противоположные стороны и углы параллелограмма равны, а диагональ делит его пополам. О точке пересечения параллелограмма Евклид не упоминает. Только к концу средних веков была разработана полная теория параллелограммов И лишь в XVII веке в учебниках появились теоремы о параллелограммах, которые доказываются с помощью теоремы Евклида о свойствах параллелограмма.
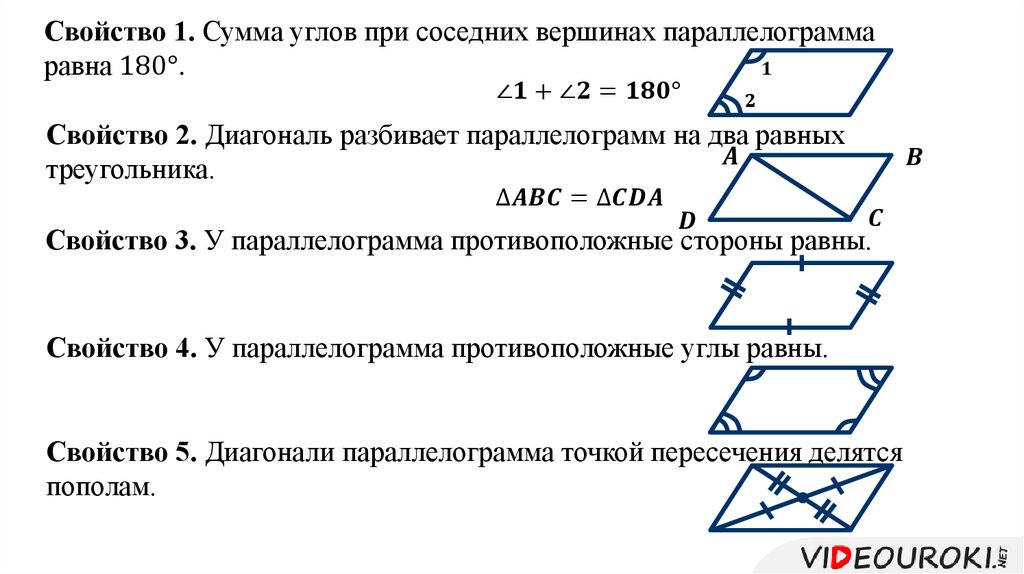
III Дополнительные свойства параллелограмма
В учебнике по геометрии даны только 2 свойства параллелограмма:
Противоположные углы и стороны равны
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
В различных источниках по геометрии можно встретить следующие дополнительные свойства:
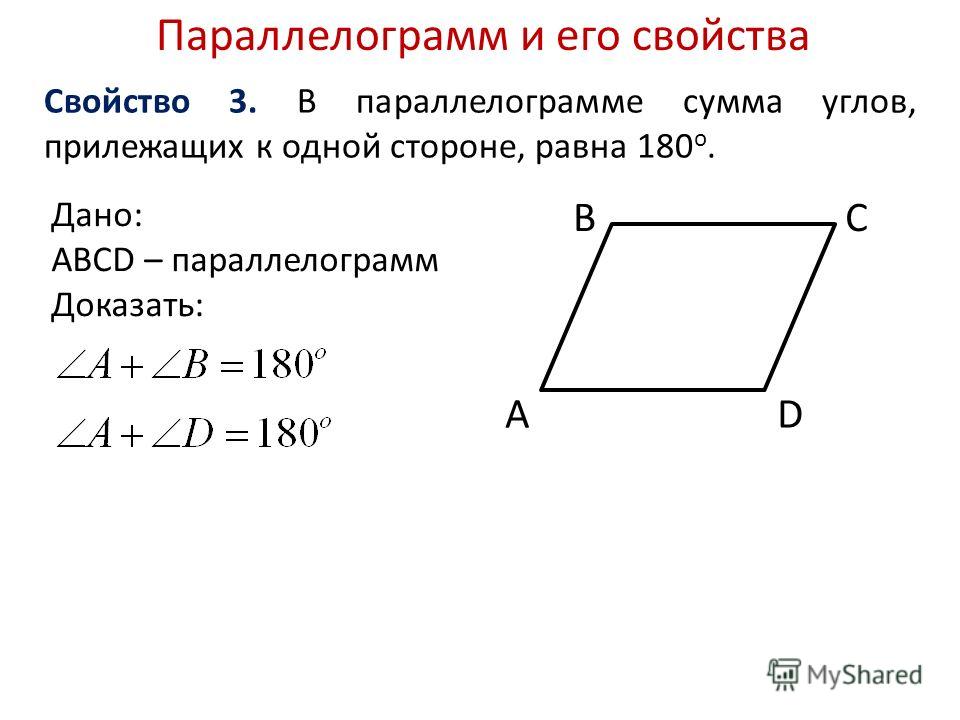
Сумма соседних углов параллелограмма равна 180 0
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник;
Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых;
Биссектрисы соседних углов параллелограмма пересекаются под прямым углом;
Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник;
Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.
Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.
Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.
IV Доказательство свойств параллелограмма
Сумма соседних углов параллелограмма равна 180 0
Дано :
ABCD – параллелограмм
Доказать:
A
+
B
=
Доказательство:
А и
B
–внутренние односторонние углы при параллельных прямых ВС АD
и секущей АВ, значит,
A
+
B
=
2
Дано: АBCD — параллелограмм,
АК -биссектриса
А.
Доказать: АВК – равнобедренный
Доказательство:
1)
1=
3 (накрест лежащие при ВСAD
и секущей AK
),
2)
2=
3 т.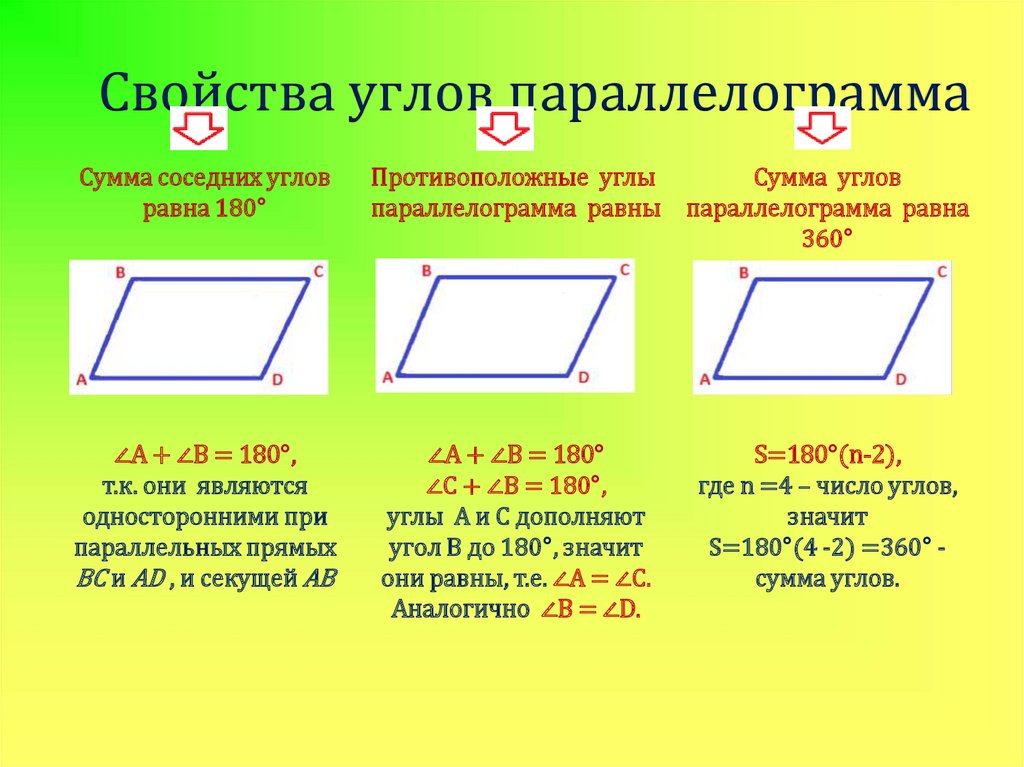 к. АК – биссектриса,
к. АК – биссектриса,
значит 1=
2.
3) АВК – равнобедренный т. к. 2 угла треугольника равны
. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольникДано: АВСD – параллелограмм,
АК – биссектриса A,
СР — биссектриса C.
Доказать: АК ║ СР
Доказательство:
1) 1=2 т. к. АК-биссектриса
2) 4=5 т.к. СР – биссектриса
3) 3=1 (накрест лежащие углы при
ВС ║ АD и АК-секущей),
4) A =C (по свойству параллелограмма), значит2=3=4=5.
4) Из п. 3 и 4 следует, что 1=4, а эти углы соответственные при прямых АК и СР и секущей ВС,
значит, АК ║ СР (по признаку параллельности прямых)
. Биссектрисы противоположных углов параллелограмма лежат на параллельных прямыхБиссектрисы соседних углов параллелограмма пересекаются под прямым углом
Дано: АВСD — параллелограмм,
АК-биссектриса A,
DР-биссектриса D
Доказать: DР АК.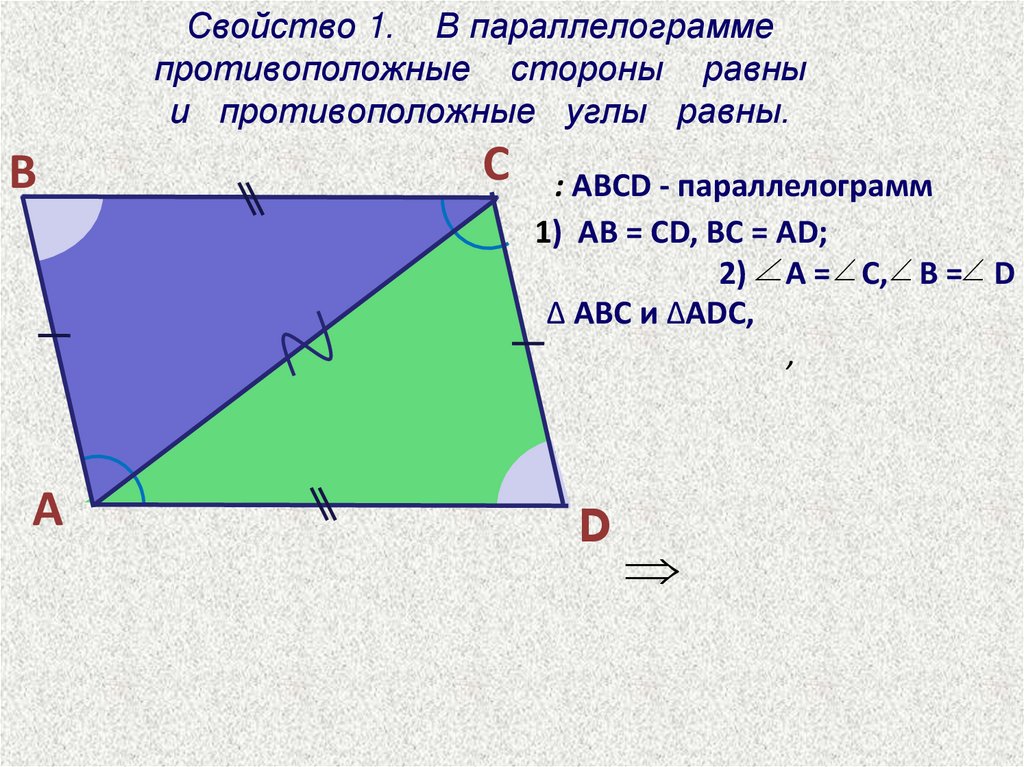
Доказательство:
1) 1=2, т.к. АК — биссектриса
Пусть, 1=2=x, тогда А=2x,
2) 3=4, т.к. D Р – биссектриса
Пусть, 3=4= у, тогда D =2y
3) A +D =180 0 , т.к. сумма соседних углов параллелограмма равна 180
2) Рассмотрим A ОD
1+3=90 0 , тогда
5. Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник
Дано: АВСD — параллелограмм, АК-биссектриса A,
DР-биссектриса D,
CM -биссектриса C ,
BF -биссектриса B .
Доказать : KRNS -прямоугольник
Доказательство:
Исходя из предыдущего свойства 8=7=6=5=90 0 ,
значит KRNS -прямоугольник.
Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.
Дано: ABCD-параллелограмм, АС-диагональ.
ВК АС, DPAC
Доказать: BК=DР
Доказательство: 1)DCР=КAB, как внутренние накрест лежащие при АВ ║ СD и секущей АС.
2) AКB=CDР (по стороне и двум прилежащим к ней углам АВ=СD CD Р=AB К).
А в равных треугольниках соответственные стороны равны, значит DР=BК.
Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.
Дано: ABCD-параллелограмм.
Доказать: ВКDР – параллелограмм.
Доказательство:
1) BР=КD (AD=BC, точки К и Р
делят эти стороны пополам)
2) ВР ║ КD (лежат на АD BC)
Если в четырехугольнике противоположные стороны равны и параллельны, значит, этот четырехугольник -параллелограмм.
Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.
Дано: ABCD – параллелограмм. BD и AC — диагонали.
Доказать: АС 2 +ВD 2 =2(AB 2 + AD 2 )
Доказательство: 1)АСК: AC ²=
+
2)B Р D : BD 2 = B Р 2 + Р D 2 (по теореме Пифагора)
3) AC ²+ BD ²=СК²+ A К²+ B Р²+Р D ²
4) СК = ВР = Н (высота)
5) АС 2 +В D 2 = H 2 + A К 2 + H 2 +Р D 2
6) Пусть D К= A Р=х , тогда C К D : H 2 = CD 2 – х 2 по теореме Пифагора)
7) АС²+В D ² = С D 2 — х²+ АК 1 ²+ CD 2 -х 2 +Р D 2 ,
АС²+В D ²=2С D 2 -2х 2 + A К 2 +Р D 2
8) A К =AD+ х , Р D=AD- х ,
АС²+В D ² =2 CD 2 -2х 2 +(AD +х) 2 +(AD -х) 2 ,
АС ²+ В D²=2 С D²-2 х ² +AD 2 +2AD х + х 2 +AD 2 -2AD х + х 2 ,
АС ²+ В D²=2CD 2 +2AD 2 =2(CD 2 +AD 2 ).
V . Решение задач с использованием этих свойств
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5 . Найдите его большую сторону.
Дано: ABCD – параллелограмм,
АК – биссектриса
А,
D
К – биссектриса
D
, АВ=5
Найти : ВС
ешениеРешение
Т.к. АК — биссектриса
А, то АВК – равнобедренный.
Т.к. D
К – биссектриса
D
, то DCK
— равнобедренный
DC =C К= 5
Тогда, ВС=ВК+СК=5+5 = 10
Ответ: 10
2. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
1 случай
Дано:
А,
ВК=14 см, КС=7 см
Найти: Р параллелограмма
Решение
ВС=ВК+КС=14+7=21 (см)
Т.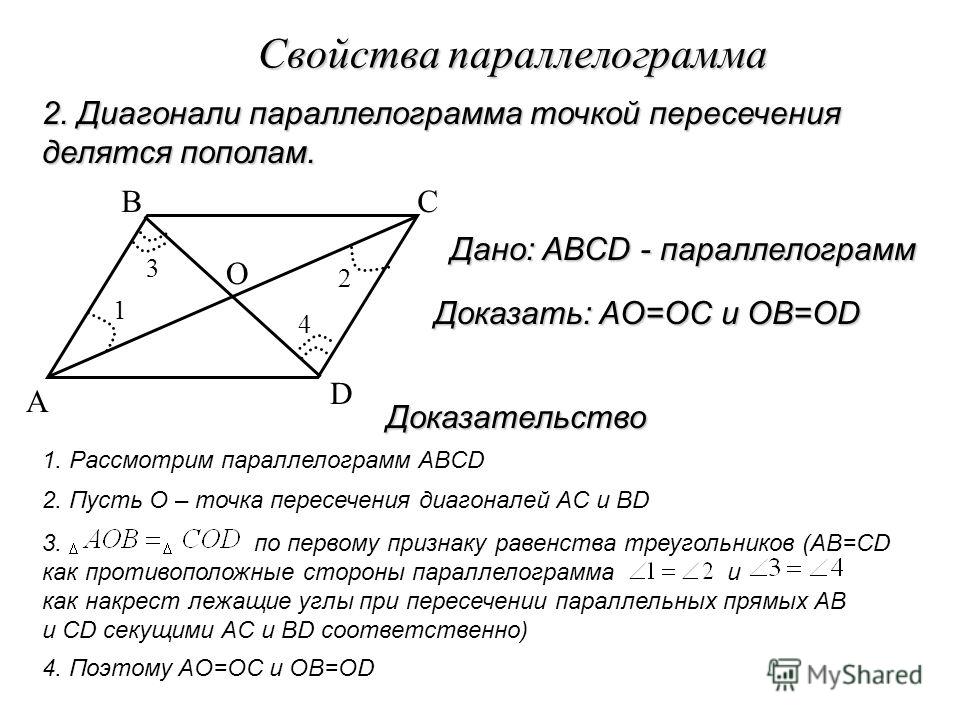 к. АК – биссектриса
к. АК – биссектриса
А, то АВК – равнобедренный.
АВ=ВК= 14 см
Тогда Р=2 (14+21) =70 (см)
случайДано: ABCD – параллелограмм,
D
К – биссектриса
D
,
ВК=14 см, КС=7 см
Найти : Р параллелограмма
Решение
ВС=ВК+КС=14+7=21 (см)
Т.к. D
К – биссектриса
D
, то DCK
— равнобедренный
DC =C К= 7
Тогда, Р= 2 (21+7) = 56 (см)
Ответ: 70см или 56 см
3.Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.
1 случай: биссектрисы пересекаются вне параллелограмма
Дано: ABCD
– параллелограмм, АК – биссектриса
А,
D
К – биссектриса
D
, АВ=3 см, ВС=10 см
Найти : ВМ, МN , NC
Решение
Т.к. АМ — биссектриса
А, то АВМ – равнобедренный.
Т.к. DN
– биссектриса
D
, то DCN
— равнобедренный
DC =CN = 3
Тогда, МN = 10 – (BM +NC ) = 10 – (3+3)=4 см
2 случай: биссектрисы пересекаются внутри параллелограмма
Т.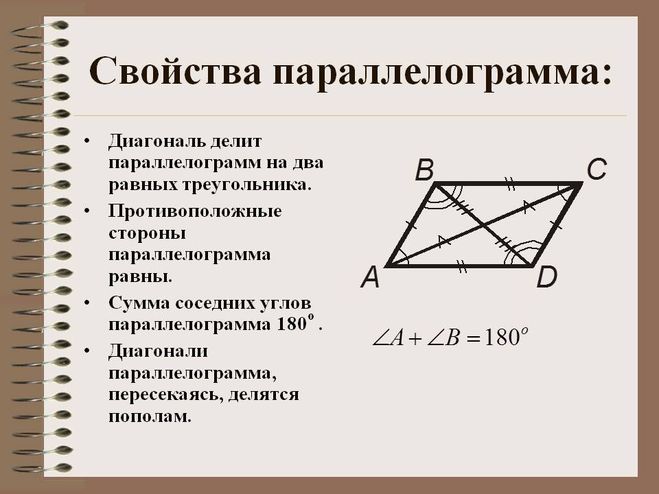 к. АN
— биссектриса
к. АN
— биссектриса
А, то АВN
– равнобедренный.
АВ=В N = 3 D
А раздвижную решетку – отодвигать на необходимое расстояние в дверном проеме
Параллелограммный механизм — четырёхзвенный механизм, звенья которого составляют параллелограмм. Применяется для реализации поступательного движения шарнирными механизмами.
Параллелограмм с неподвижным звеном — одно звено неподвижно, противоположное совершает качательное движение, оставаясь параллельным неподвижному. Два параллелограмма, соединённых друг за другом, дают конечному звену две степени свободы, оставляя его параллельным неподвижному.
Примеры: стеклоочистители автобусов, погрузчики, штативы, подвесы, автомобильные подвески.
Параллелограмм с неподвижным шарниром — используется свойство параллелограмма сохранять постоянное соотношение расстояний между тремя точками. Пример: чертёжный пантограф — прибор для масштабирования чертежей.
Ромб — все звенья одинаковой длины, приближение (стягивание) пары противоположных шарниров приводит к раздвиганию двух других шарниров. Все звенья работают на сжатие.
Все звенья работают на сжатие.
Примеры — автомобильный ромбовидный домкрат, трамвайный пантограф.
Ножничный или X-образный механизм , также известный как Нюрнбергские ножницы — вариант ромба — два звена, соединённые посередине шарниром. Достоинства механизма — компактность и простота, недостаток — наличие двух пар скольжения. Два (и более) таких механизма, соединённые последовательно, образуют в середине ромб(ы). Применяется в подъёмниках, детских игрушках.
VII Заключение
Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг,
свою волю, воспитывает в себе настойчивость
и упорство в достижении цели
А. Маркушевич
В ходе работы я доказала дополнительные свойства параллелограмма.
Я убедилась, что применяя эти свойства, можно решать задачи быстрее.
Я показала, как применяются эти свойства на примерах решения конкретных задач.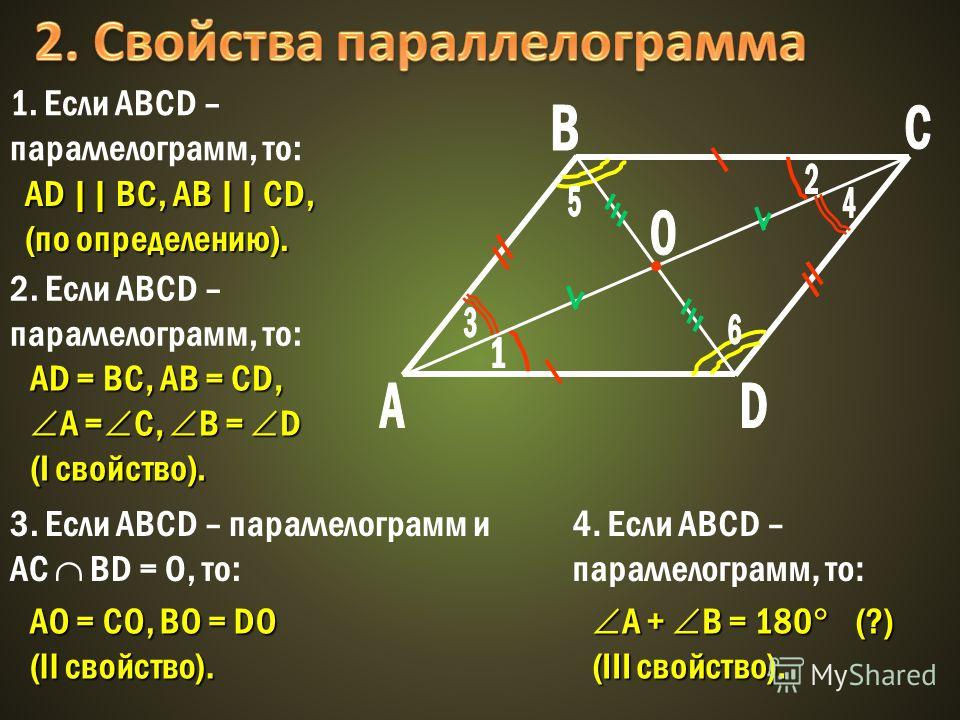
Я узнала много нового о параллелограмме, чего нет в нашем учебнике геометрии
Я убедилась в том, что знания геометрии очень важны в жизни на примерах применения свойств параллелограмма.
Цель моей исследовательской работы выполнена.
О том, насколько важны математические знания, говорит тот факт, что была учреждена премия тому, кто издаст книгу о человеке, который всю жизнь прожил без помощи математики. Эту премию до сих пор не получил ни один человек.
VIII Литература
ПогореловА.В. Геометрия 7-9: учебник для общеобразоват. учреждений-М.: Просвещение, 2014г
Л.С.Атанасян и др. Геометрия. Доп. Главы к учебнику 8 кл.: учеб. пособие для учащихся школ и классов с углубл. изуч.математики. – М.: Вита-пресс, 2003
Ресурсы сети Интернет
материалы Википедии
Конспект урока.
Алгебра 8 класс
Учитель Сысой А.К.
Школа 1828
Тема урока: «Параллелограмм и его свойства»
Тип урока: комбинированный
Цели урока:
1) Обеспечить усвоение нового понятия – параллелограмм и его свойств
2) Продолжить развитие навыков и умений решения геометрических задач;
3) Развитие культуры математической речи
План урока:
1. Организационный момент
Организационный момент
(Слайд 1)
На слайде демонстрируется высказывание Льюиса Кэрролла. Ученикам сообщается о цели урока. Проверяется готовность учеников к уроку.
2. Актуализация знаний
(Слайд 2)
На доске задачи для устной работы. Учитель предлагает ученикам подумать над этими задачами и поднять руку тем, кто понял, как задачу решать. После решения двух задач, на доказательство теоремы о сумме углов вызывается к доске ученик, который самостоятельно делает дополнительные построения на чертеже и доказывает устно теорему.
Учениками используется формула суммы углов многоугольника:
3. Основная часть
(Слайд 3)
На доске определение параллелограмма. Учитель говорит о новой фигуре и формулирует определение, делая с помощью чертежа необходимые пояснения. Затем на клетчатой части презентации, с помощью маркера и линейки, показывает, как можно рисовать параллелограмм (возможно несколько случаев)
(Слайд 4)
Учитель формулирует первое свойство параллелограмма.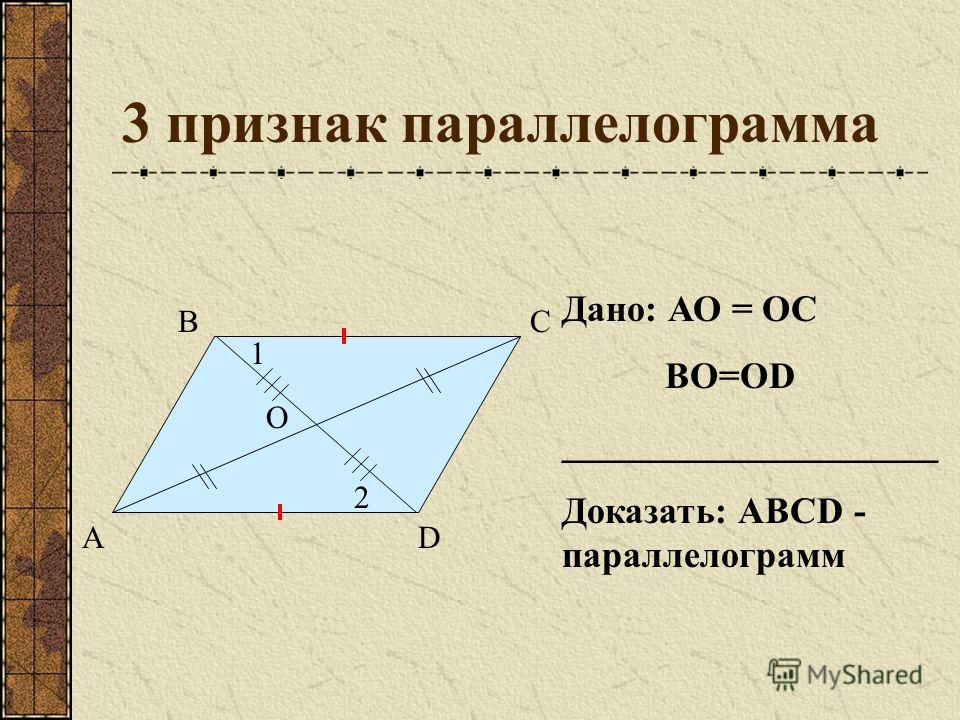 Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ). Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.
Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ). Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.
(Слайд 5)
Учитель формулирует второе свойство параллелограмма. На доске появляется рисунок параллелограмма. Учитель предлагает по рисунку сказать что дано, что необходимо доказать. После того как ученики правильно сообщают о том, что дано и что необходимо доказать, появляется условие теоремы. Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников
AOB
и
COD
. С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон
AB
и
CD
. Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.
Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников
AOB
и
COD
. С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон
AB
и
CD
. Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.
(Слайд 6)
Учитель формулирует третье свойство параллелограмма. В зависимости от времени, которое остаётся до конца урока, учитель может дать возможность ученикам самостоятельно доказать это свойство, или ограничится его формулировкой, а само доказательство оставить ученикам в качестве домашней работы. Доказательство может опираться на сумму углов вписанного многоугольника, которая повторялась в начале урока, или на сумму внутренних односторонних углов при двух параллельных прямых
AD
и
BC
, и секущей, например
AB
.
4. Закрепление материала
На этом этапе учащиеся, используя ранее изученные теоремы, решают задачи. Идеи к решению задачи подбирают ученики самостоятельно. Так как возможных вариантов оформления немало и все они зависят от того каким образом ученики будут искать решение задачи, визуализации решения задач нет, а ученики самостоятельно оформляют каждый этап решения на отдельной доске с записью решения в тетрадь.
(Слайд 7)
Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После того, как ученики, верно составят краткую запись условия на доске появляется «Дано». Ход решения задачи может выглядеть следующим образом:
Проведём высоту BH (визуализировано)
Треугольник AHB – прямоугольный. Угол A равен углу C и равен 30 0 (по свойству о противоположных углах в параллелограмме). 2BH =AB (по свойству катета, лежащего напротив угла в 30 0 в прямоугольном треугольнике). Значит AB = 13 см.
AB
= CD
, BC
= AD
(по свойству противоположных сторон в параллелограмме) Значит AB
=CD
=13см.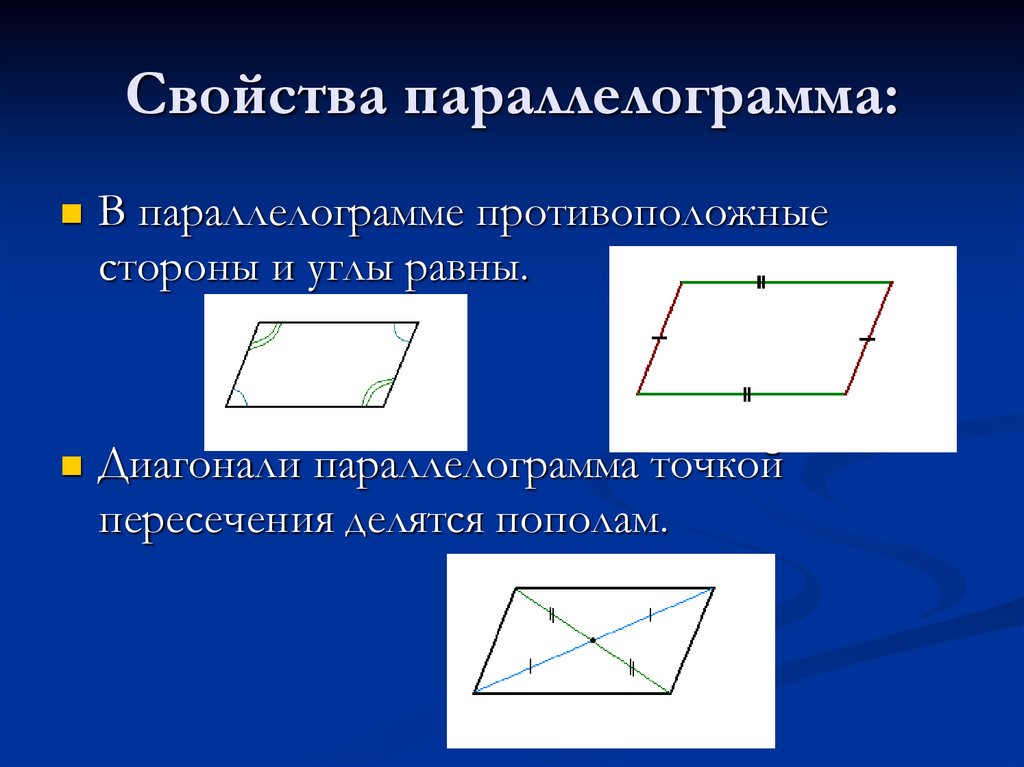 Так как периметр параллелограмма равен 50 см, то BC
=AD
=(50 – 26):2=12см.
Так как периметр параллелограмма равен 50 см, то BC
=AD
=(50 – 26):2=12см.
Ответ: AB = CD = 13 см, BC = AD = 12 см.
(Слайд 8)
Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После появляется «Дано» на экране. С помощью красных линий выделяется четырёхугольник, про который нужно доказать, что он параллелограмм. Ход решения задачи может выглядеть следующим образом:
Т.к. BK и MD перпендикуляры к одной прямой, то прямы BK и MD параллельны.
Через смежные углы можно показать, что сумма внутренних односторонних углов при прямых BM и KD и секущей MD равна 180 0 . Поэтому данные прямые параллельны.
Так как у четырехугольника BMDK противоположные стороны попарно параллельны, то данный четырехугольник параллелограмм.
5. Окончание урока. Поведение итогов.
(Слайд 8)
На слайде появляются вопросы по новой теме, на которые ученики отвечают.
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны.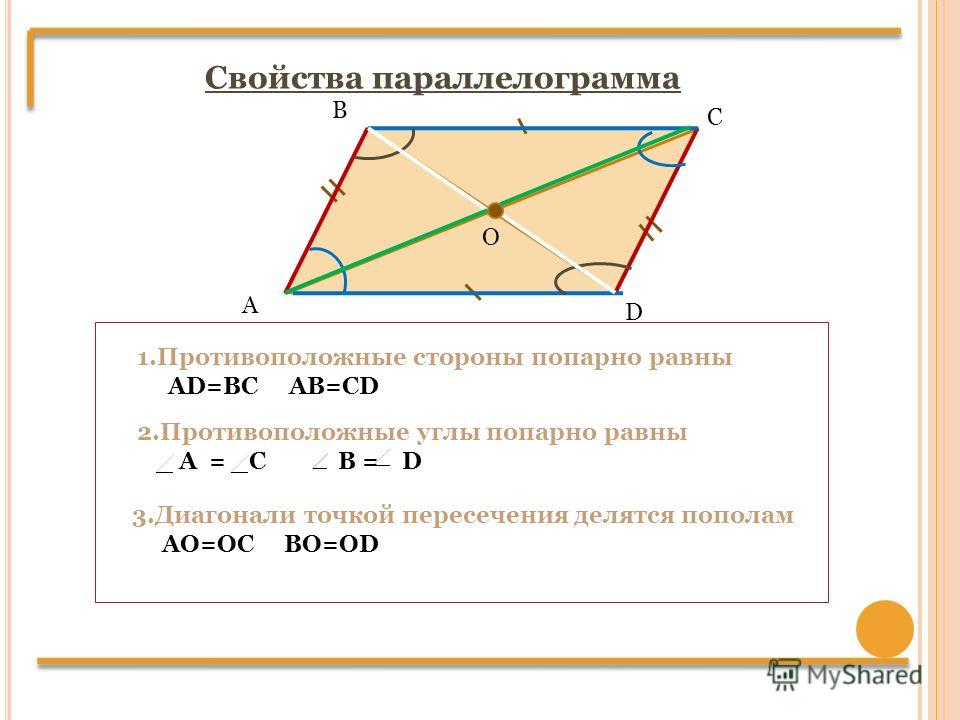 На следующем рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.
На следующем рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.
Как вы уже успели догадаться, параллелограмм является выпуклым четырехугольником. Рассмотрим основные свойства параллелограмма.
Свойства параллелограмма
1. В параллелограмме противоположные углы и противоположные стороны равны. Докажем это свойство — рассмотрим параллелограмм, представленный на следующем рисунке.
Диагональ BD разделяет его на два равных треугольника: ABD и CBD. Они равны по стороне BD и двум прилежащим к ней углам, так как углы накрест лежащие при секущей BD параллельных прямых BC и AD и AB и CD соответственно. Следовательно, AB = CD и
BC = AD. А из равенства углов 1, 2 ,3 и 4 следует, что угол A = угол1 +угол3 = угол2 + угол4 = угол С.
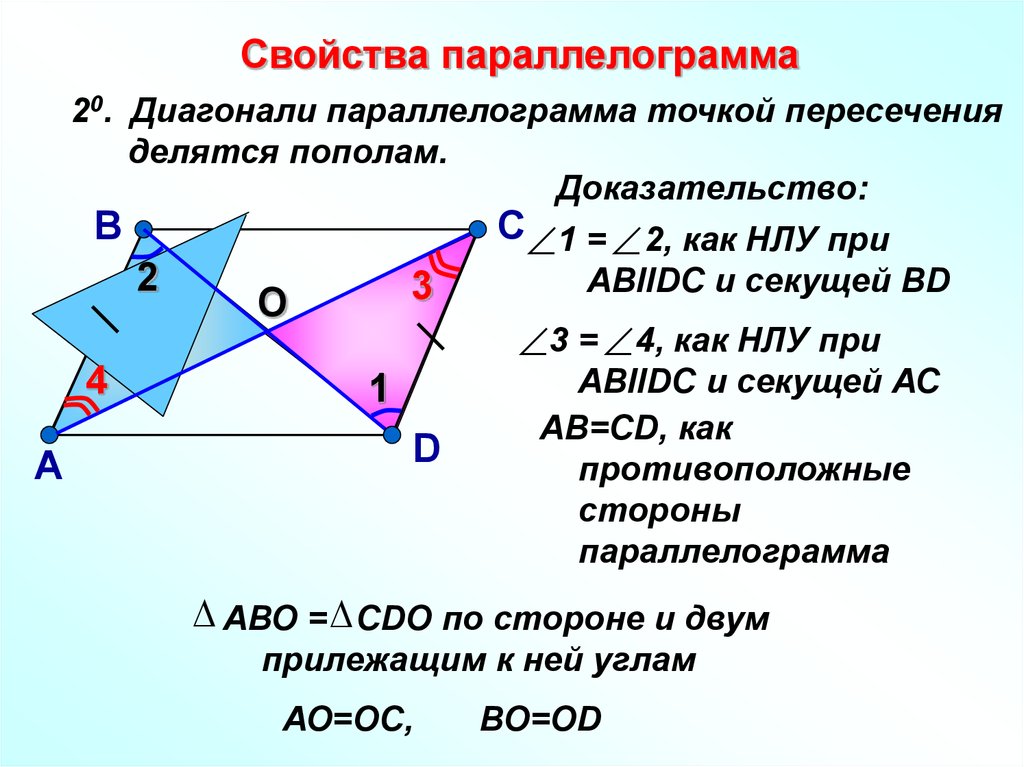
2. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть точка О есть точка пересечения диагоналей AC и BD параллелограмма ABCD.
Тогда треугольник AOB и треугольник COD равны между собой, по стороне и двум прилежащим к ней углам.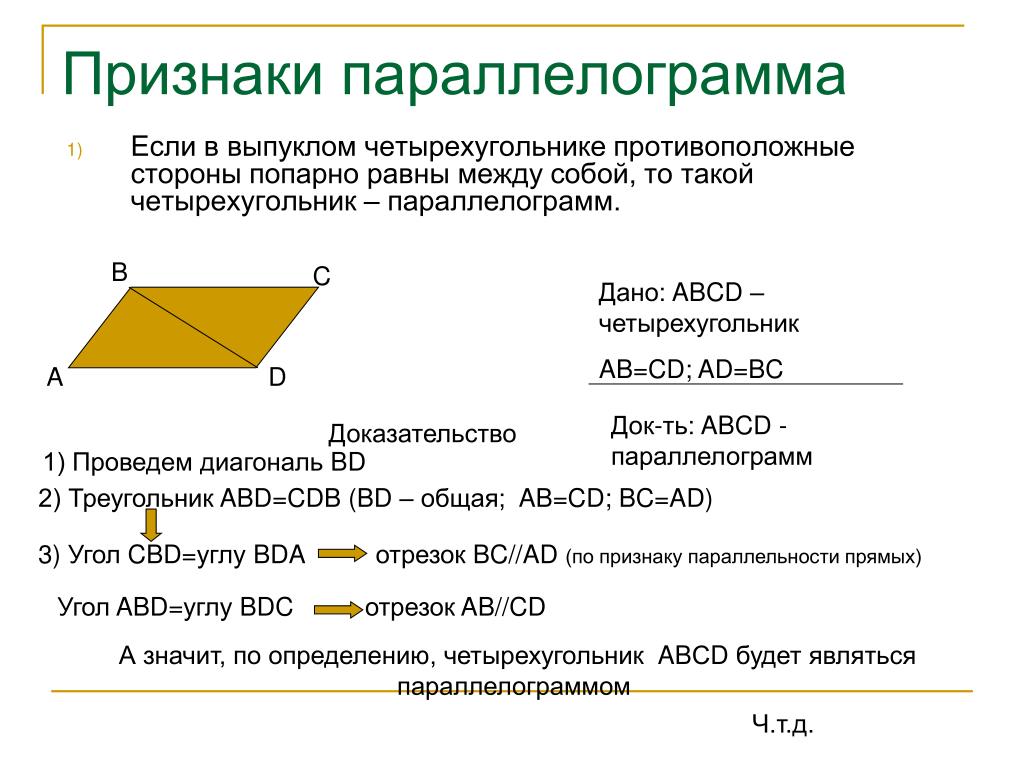 (AB=CD так как это противоположные стороны параллелограмма. А угол1 = угол2 и угол3 = угол4 как накрест лежащие углы при пересечении прямых AB и CD секущими AC и BD соответственно.) Из этого следует, что AO = OC и OB = OD, что и требовалось доказать.
(AB=CD так как это противоположные стороны параллелограмма. А угол1 = угол2 и угол3 = угол4 как накрест лежащие углы при пересечении прямых AB и CD секущими AC и BD соответственно.) Из этого следует, что AO = OC и OB = OD, что и требовалось доказать.
Все основные свойства проиллюстрированы на следующих трех рисунках.
Параллелограмм. Свойства параллелограмма с доказательством — Студопедия
Поделись с друзьями:
Определение. Параллелограмм – это четырёхугольник, противоположные стороны которого попарно параллельны.
Свойство 1. Любая диагональ параллелограмма делит его на два равных треугольника.
Доказательство. По II признаку (накрест лежащие углы и общая сторона).
Теорема доказана.
Свойство 2. В параллелограмме противолежащие стороны равны, противолежащие углы равны.
Доказательство.
Аналогично,
Теорема доказана.
Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.
Доказательство.
Теорема доказана.
Свойство 4. Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. – вершину – два равнобедренных?-ка).
Доказательство.
Теорема доказана.
Свойство 5. В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.
Доказательство.
Теорема доказана.
Свойство 6. Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.
Доказательство.
Теорема доказана.
Свойство 7. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Доказательство.
Теорема доказана.
Построение биссектрисы угла. Свойства биссектрисы угла треугольника.
1) Построить произвольный луч DE.
2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.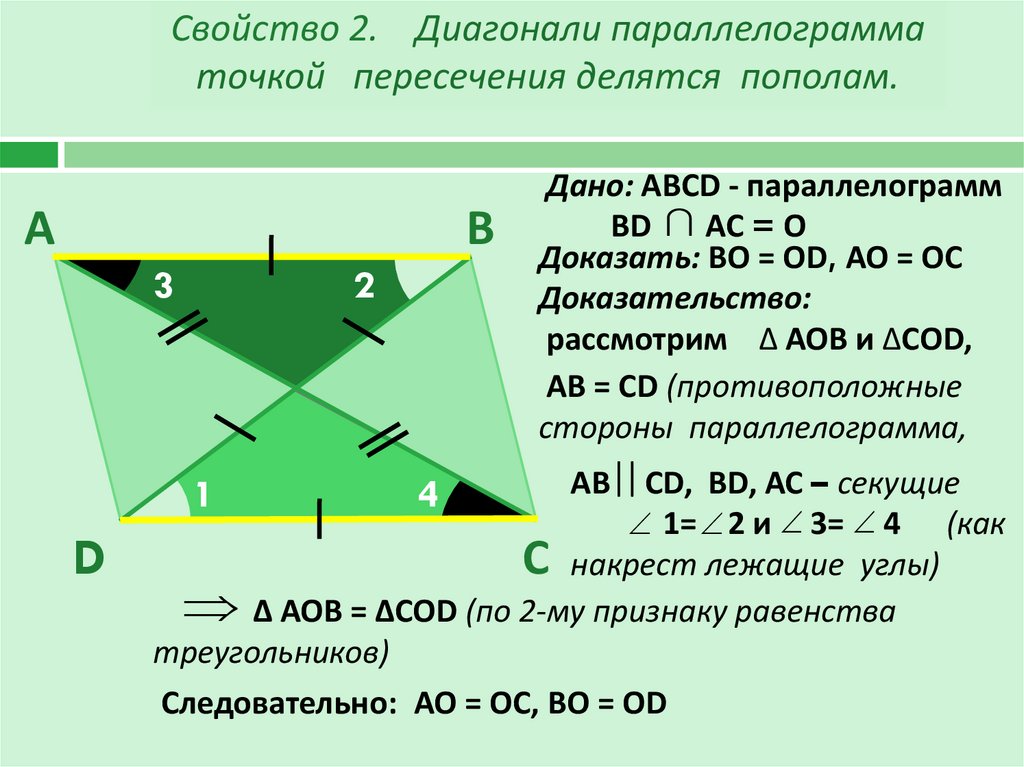
3) F и G – точки пересечения окружности со сторонами данного угла, H – точка пересечения окружности с построенным лучом
Построить окружность с центром в точке H и радиусом, равным FG.
5) I – точка пересечения окружностей построенного луча.
6) Провести прямую через вершину и I.
IDH – требуемый угол.
(
)
Свойство 1. Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.
Доказательство. Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.
Теорема доказана.
Свойство 2. Биссектриса – ГМТ равноудалённых от прилежащих сторон треугольника.
Свойство 3. Биссектрисы треугольника пересекаются в одной точке, и эта точка – центр вписанной окружности треугольника. (Из предыдущего свойства)
Свойство 4. Биссектрисы делятся точкой пересечения в отношении суммы прилежащих сторон к противолежащей стороне, считая от вершины.
Доказательство. Рассмотрим треугольник CBC1:
Теорема доказана.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Свойства параллелограмма — теоремы, доказательства, примеры
свойства параллелограмма помогают нам легко и быстро идентифицировать параллелограмм из заданного набора фигур. Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.
| 1. | Каковы свойства параллелограмма? |
| 2. | Свойства диагоналей параллелограмма |
| 3. | Теоремы о свойствах параллелограмма |
4. | Часто задаваемые вопросы о свойствах параллелограмма |
Каковы свойства параллелограмма?
Параллелограмм — это тип четырехугольника, в котором противоположные стороны параллельны и равны. В параллелограмме при вершинах четыре угла. Понимание свойств параллелограмма помогает легко связать его углы и стороны. Кроме того, свойства полезны для вычислений в задачах, касающихся сторон и углов параллелограмма.
Свойства углов параллелограмма
Важными свойствами параллелограммов, связанными с углами, являются следующие:
- Противоположные углы параллелограмма равны, т. е. ∠A = ∠C и ∠B = ∠D.
- Сумма всех углов параллелограмма составляет 360°, т. е. ∠A + ∠B + ∠C + ∠D = 360°.
- Последовательные углы параллелограмма являются дополнительными, т. е.
∠А + ∠В = 180°
∠В + ∠С = 180°
∠С + ∠D = 180°
∠D + ∠А = 180°
Свойства сторон параллелограмма
Противоположные стороны параллелограмма равны и параллельны друг другу.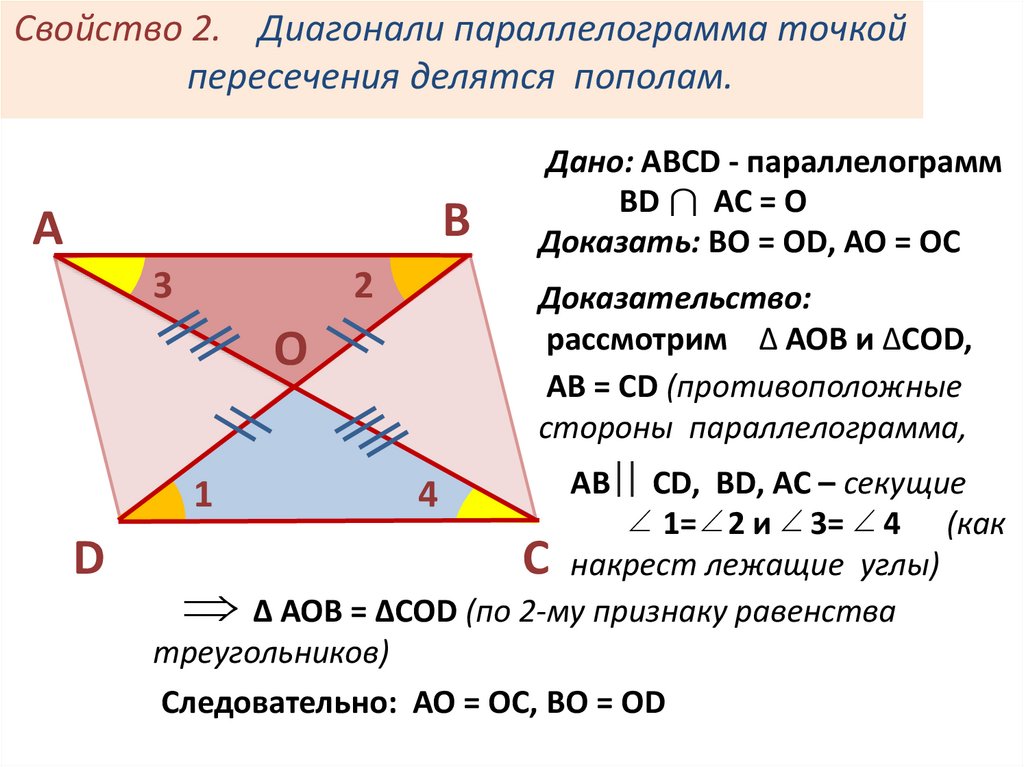
Обратите внимание на следующий рисунок, чтобы понять свойства параллелограмма.
Все вышеперечисленные свойства справедливы для всех типов параллелограммов, но теперь давайте также узнаем об индивидуальных свойствах некоторых специальных параллелограммов. Три разных параллелограмма — квадрат, прямоугольник и ромб, которые отличаются друг от друга из-за своих свойств, но все они подпадают под категорию параллелограммов.
Свойства квадрата
- Все четыре стороны квадрата равны.
- Все четыре угла равны и по 90 градусов каждый.
- Диагонали квадрата делят его углы пополам.
- Обе диагонали квадрата имеют одинаковую длину.
- Противоположные стороны квадрата равны и параллельны друг другу.
Свойства прямоугольника
- Противоположные стороны прямоугольника равны и параллельны.
- Все четыре угла прямоугольника равны и равны 90° каждый.
- Обе диагонали прямоугольника имеют одинаковую длину.

Свойства ромба
- Все стороны ромба равны по длине.
- Диагонали ромба пересекаются под углом 90°.
- Сумма любых двух смежных внутренних углов равна 180°.
- Противоположные стороны ромба равны и параллельны друг другу.
Теперь давайте расширим наши знания, изучив свойства диагоналей параллелограммов в следующем разделе.
Свойства диагоналей параллелограмма
Сначала вспомним значение диагонали. Диагонали — это отрезки, соединяющие несмежные вершины любого многоугольника. В параллелограмме ABCD (см. рисунок выше) диагонали AC и BD. Предположим, что O — точка пересечения диагоналей AC и BD. Свойства диагоналей параллелограмма следующие:
- Диагонали параллелограмма делят друг друга пополам, т. е. OB = OD и OA = OC.
- Каждая диагональ делит параллелограмм на два конгруэнтных треугольника, т. е. ΔCDA ≅ ΔABC и ΔBAD ≅ ΔDCB.
- Закон параллелограмма: Сумма квадратов сторон равна сумме квадратов диагоналей, т.
 е. AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + БД 2
е. AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + БД 2
Теоремы о свойствах параллелограмма
Теоремы о свойствах параллелограмма помогают определить правила решения задач на параллелограммы. Свойства, относящиеся к сторонам и углам параллелограмма, легко понять и применить для решения различных задач. Кроме того, эти теоремы также поддерживают понимание концепций других четырехугольников. Ниже приведены четыре важные теоремы, относящиеся к свойствам параллелограмма:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Диагонали параллелограмма делятся пополам.
- Если в четырехугольнике одна пара противоположных сторон равна и параллельна, то это параллелограмм.
Теорема 1: В параллелограмме противоположные стороны равны.
Доказательство:
Дано: ABCD — параллелограмм.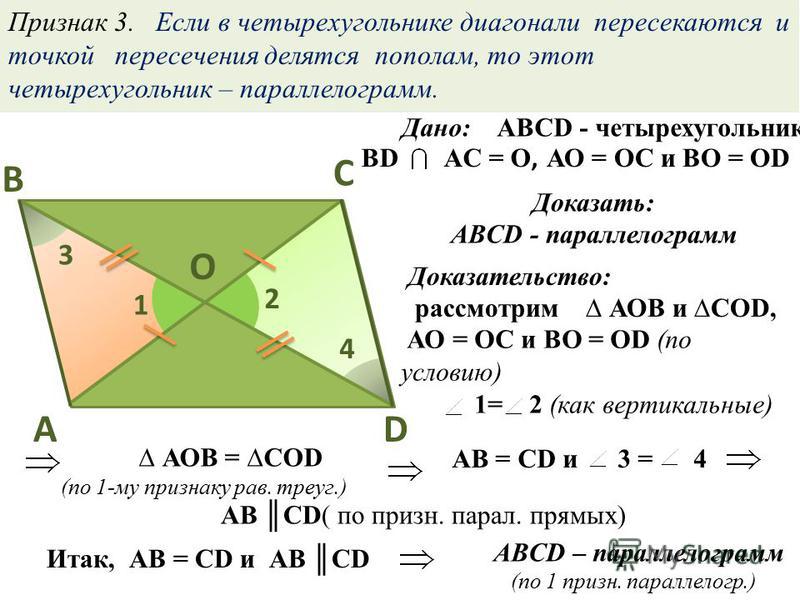
Доказать: Противоположные стороны равны, AB = CD и BC = AD.
В параллелограмме ABCD сравните треугольники ABC и CDA. В этих треугольниках:
- AC = CA (общая сторона)
- ∠BAC = ∠DCA (альтернативные внутренние углы)
- ∠BCA = ∠DAC (альтернативные внутренние углы)
Следовательно, по критерию ASA оба треугольника конгруэнтны и соответствующие стороны равны. Следовательно, мы имеем AB = CD и BC = AD.
Обратное к теореме 1: если в четырехугольнике противоположные стороны равны, то это параллелограмм.
Доказательство:
Дано: В четырехугольнике ABCD противоположные стороны равны, AB = CD и BC = AD.
Доказать: ABCD — параллелограмм.
В четырехугольнике ABCD дано, что AB = CD и AD = BC. Теперь сравните два треугольника ABC и CDA. Здесь мы имеем
- AC = AC (общие стороны)
- AB = CD (поскольку внутренние углы равны)
- г.
 н.э. = до н.э. (дано).
н.э. = до н.э. (дано).
Таким образом, по критерию SSS оба треугольника равны и соответствующие углы равны. Отсюда можно сделать вывод, что ∠BAC = ∠DCA, а ∠BCA = ∠DAC.
Поэтому AB || CD, Британская Колумбия || AD, ABCD — параллелограмм.
Теорема 2. В параллелограмме противоположные углы равны.
Доказательство:
Дано: ABCD — параллелограмм, а ∠A, ∠B, ∠C, ∠D — четыре угла.
Доказать: ∠A = ∠C и ∠B = ∠D
Предположим, что ABCD — параллелограмм. Теперь сравните треугольники ABC и CDA. Здесь у нас есть,
- AC = CA (общая сторона)
- ∠1 = ∠4 (чередующиеся внутренние углы)
- ∠2 = ∠3 (чередующиеся внутренние углы)
Таким образом, согласно ASA, два треугольника конгруэнтны, а это означает, что ∠B = ∠D. Точно так же мы можем показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны.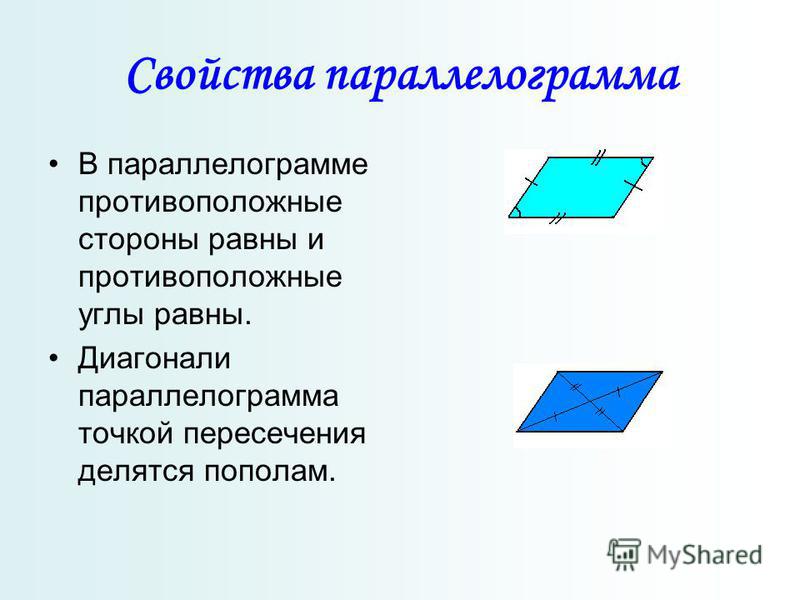
Обратное к теореме 2: Если в четырехугольнике противоположные углы равны, то это параллелограмм.
Доказательство:
Дано: ∠A = ∠C и ∠B = ∠D в четырехугольнике ABCD.
Доказать: ABCD — параллелограмм.
Предположим, что ∠A = ∠C и ∠B = ∠D в приведенном выше параллелограмме ABCD. Нам нужно доказать, что ABCD — параллелограмм. Имеем:
∠A + ∠B + ∠C + ∠D = 360º
2(∠A + ∠B) =360º
∠А + ∠В = 180º.
Это должно означать, что AD || ДО Н.Э. Аналогично можно показать, что AB || CD. Следовательно, АД || до н.э. и АВ || CD. Следовательно, ABCD — параллелограмм.
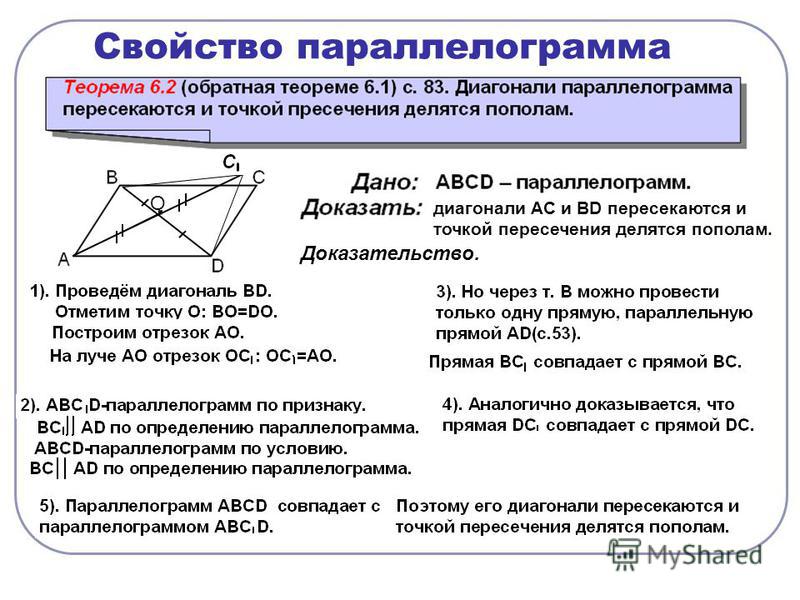
Теорема 3. Диагонали параллелограмма делят друг друга пополам.
Доказательство:
Дано: PQTR — параллелограмм. PT и QR — диагонали параллелограмма.
Доказать: Диагонали PT и RQ делят друг друга пополам, т.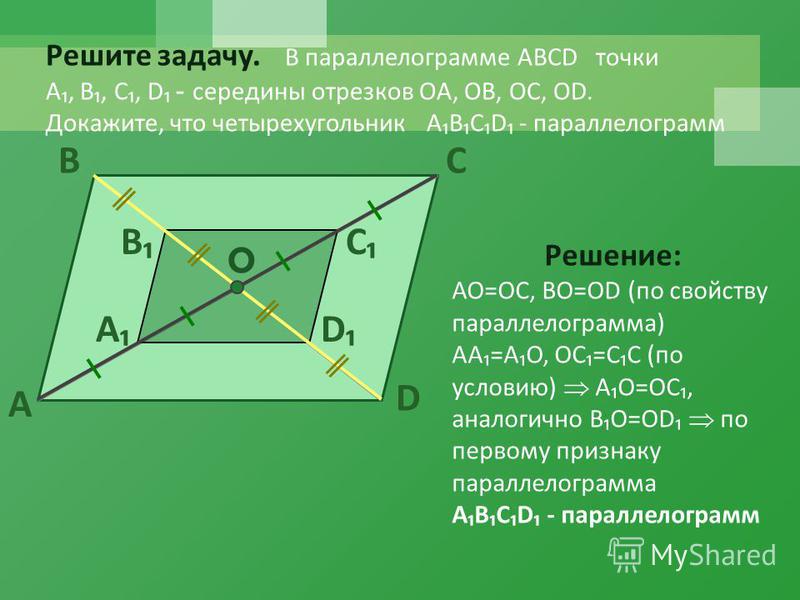 е. PE = ET и ER = EQ.
е. PE = ET и ER = EQ.
Во-первых, предположим, что PQTR — параллелограмм. Сравните треугольники TER и треугольник PEQ. Имеем,
- PQ = RT (противоположные стороны параллелограмма PQTR)
- ∠QRT = ∠PQR (альтернативные внутренние углы)
- ∠PTR = ∠QPT (альтернативные внутренние углы).
По критерию ASA два треугольника конгруэнтны, что означает по CPCTC, PE = ET и RE = EQ. Таким образом, две диагонали PT и RQ делят друг друга пополам, а PE = ET и ER = EQ.
Обратное к теореме 3: Если диагонали в четырехугольнике делят друг друга пополам, то это параллелограмм. В четырехугольнике PQTR, если PE=ET и ER=EQ, то это параллелограмм.
Дано: Диагонали PT и QR делят друг друга пополам.
Доказать: PQRT — параллелограмм.
Доказательство: Предположим, что диагонали PT и QR делят друг друга пополам. Еще раз сравните треугольник RET и треугольник PEQ.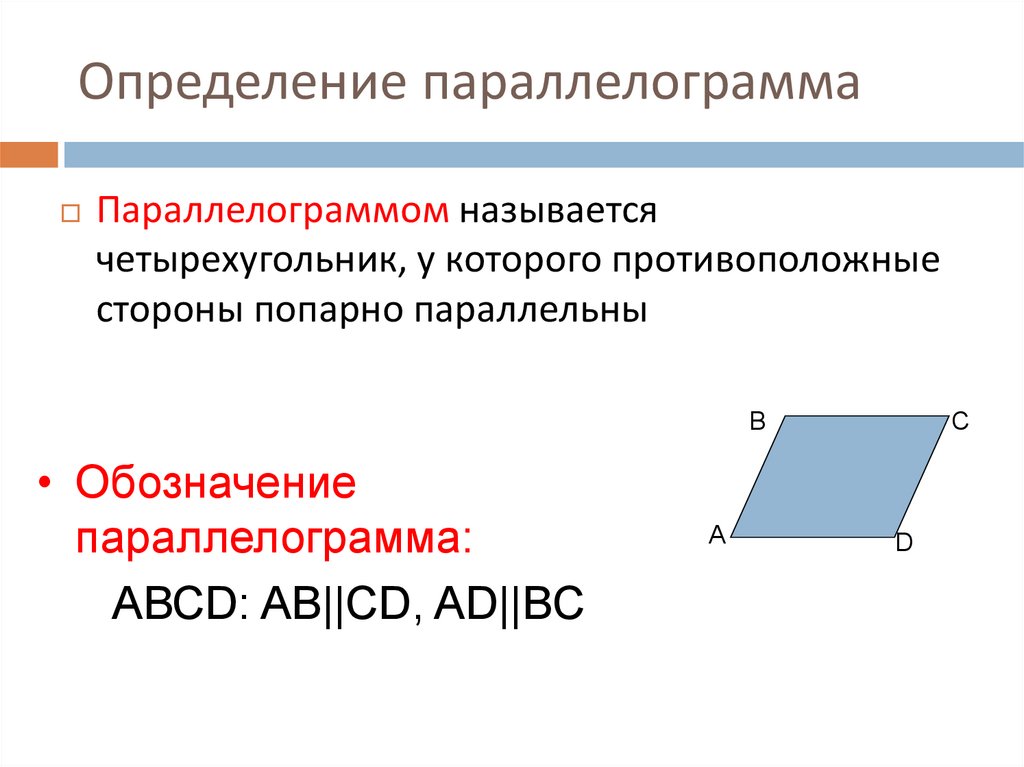 У нас есть:
У нас есть:
- RE = EQ
- ET = PE (диагонали делят друг друга пополам)
- ∠RET =∠PEQ (вертикально противоположные углы).
Следовательно, по критерию SAS два треугольника конгруэнтны. Это означает, что ∠QRT = ∠PQR и ∠PRT = ∠QPT. Следовательно, PQ || РТ и РТ || КТ. Таким образом, PQRT является параллелограммом.
Теорема 4: Если одна пара противоположных сторон равна и параллельна в четырехугольнике, то это параллелограмм.
Доказательство:
Дано: Дано, что AB = CD и AB || CD.
Доказать: ABCD — параллелограмм.
Сравним треугольник AEB и треугольник CED. Имеем,
- AB = CD (дано)
- ∠1 = ∠3 (чередующиеся внутренние углы)
- ∠2 = ∠4 (чередующиеся внутренние углы)
Таким образом, по критерию ASA два треугольника конгруэнтны. Отсюда можно сделать вывод, что по CPCTC AE = EC, а BE = ED. Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.
Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.
Важные примечания:
Четырехугольник является параллелограммом, если:
- Противоположные стороны четырехугольника равны и параллельны.
- Противоположные углы четырехугольника равны.
- Диагонали делятся пополам.
- Одна пара противоположных сторон равна и параллельна.
☛ Статьи по теме
- Формула параллелограмма
- Площадь параллелограмма
- Свойства прямоугольника
- Разница между прямоугольником и параллелограммом
Часто задаваемые вопросы о свойствах параллелограмма
Каковы 7 свойств параллелограмма?
Семь свойств параллелограмма таковы:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.

- Последовательные углы параллелограмма являются дополнительными.
- Если один угол параллелограмма прямой, то все углы прямые.
- Диагонали параллелограмма делятся пополам.
- Каждая диагональ параллелограмма делит его пополам на два равных треугольника.
- Если одна пара противоположных сторон четырехугольника равна и параллельна, то четырехугольник является параллелограммом.
Каковы свойства диагоналей параллелограмма?
Диагонали параллелограмма обладают двумя важными свойствами. Диагональ параллелограмма делит параллелограмм на два равных треугольника. А диагонали параллелограмма делят друг друга пополам.
Диагонали параллелограмма равны?
Диагонали параллелограмма НЕ равны. Противоположные стороны и противоположные углы параллелограмма равны. Диагонали квадрата и прямоугольника равны, что является особым типом параллелограмма.
Запись свойств параллелограмма.
Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны.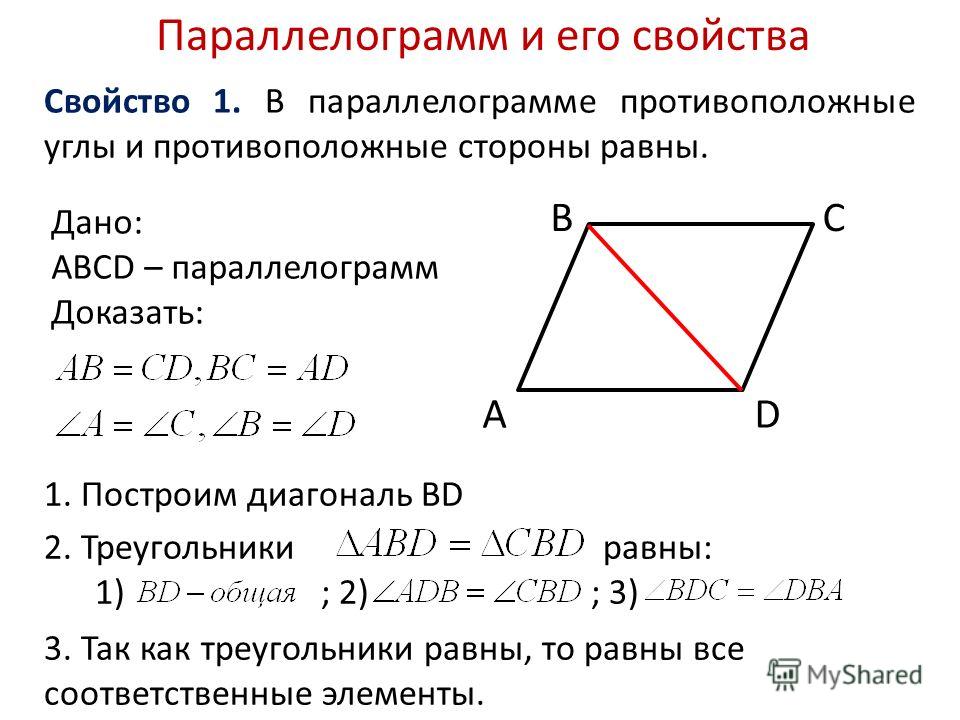 Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы:
Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Смежные углы параллелограмма дополнительные.
- Диагонали параллелограмма делятся пополам.
Можно ли прямоугольник назвать параллелограммом?
Противоположные стороны прямоугольника равны и параллельны. Таким образом, прямоугольник удовлетворяет всем свойствам параллелограмма, поэтому его можно назвать параллелограммом.
Каковы уникальные свойства параллелограммов?
Уникальные характеристики параллелограмма, отличающие его от других четырехугольников, приведены ниже:
- Противоположные стороны каждого параллелограмма равны и параллельны.
- Противоположные углы всегда равны.

- Сумма последовательных внутренних углов всегда равна 180°.
Каковы различные свойства каждого специального параллелограмма?
Существует три особых типа параллелограммов — квадрат, прямоугольник и ромб. Квадрат – это четырехугольник, у которого все стороны и углы равны. У прямоугольника противоположные стороны равны и параллельны. Все углы квадрата и прямоугольника равны и равны 90° каждый. Ромб — это параллелограмм с четырьмя равными сторонами, но его углы не обязательно должны быть прямыми.
Как отличить параллелограмм от четырехугольника по свойствам параллелограмма?
Каждый параллелограмм можно назвать четырехугольником, но не каждый четырехугольник можно назвать параллелограммом. Трапецию и воздушного змея можно назвать четырехугольниками, но они не полностью удовлетворяют свойствам параллелограмма и, следовательно, не могут быть названы параллелограммом.
Что составляют противоположные углы параллелограмма?
Противоположные углы параллелограмма всегда равны.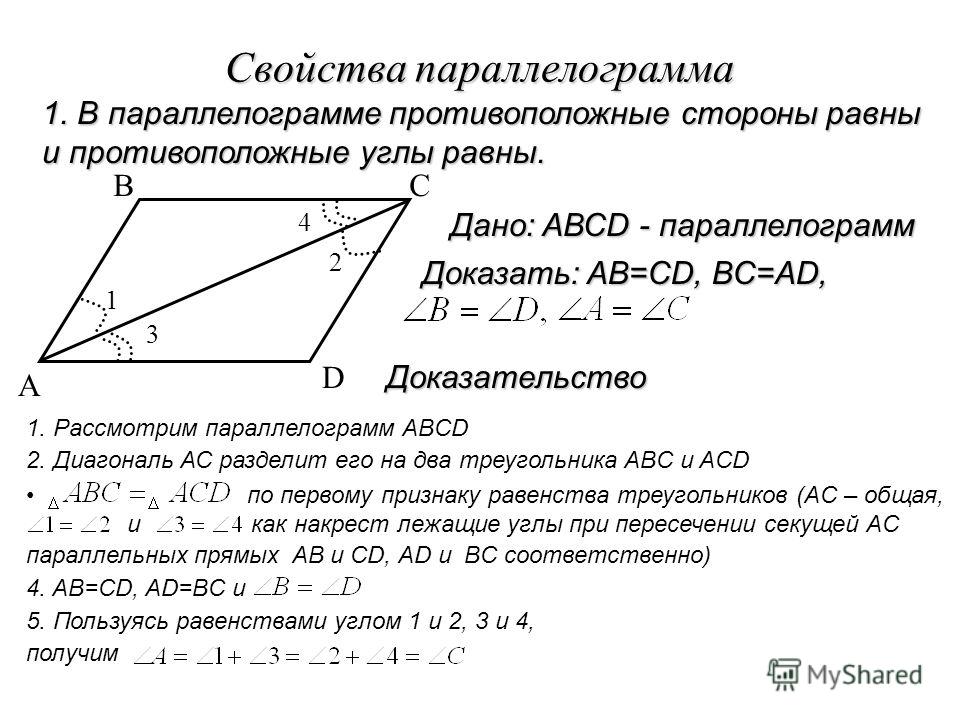 Однако следует отметить, что сумма последовательных внутренних углов параллелограмма всегда составляет 180°.
Однако следует отметить, что сумма последовательных внутренних углов параллелограмма всегда составляет 180°.
Каковы правила параллелограмма?
Правила параллелограмма — это характеристики параллелограмма, которые отличают его от других многоугольников. Другими словами, это все свойства параллелограмма, которые помогают нам его идентифицировать. Основные характеристики параллелограмма приведены ниже:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Последовательные углы параллелограмма являются дополнительными.
- Диагонали параллелограмма делятся пополам.
- Каждая диагональ параллелограмма делит его пополам на два равных треугольника.
Свойства параллелограммов — макеты
Автор: Марк Райан и
Обновлено: 26 марта 2016 г.
Основы геометрии для чайников
Исследуйте книгу Купить на Amazon
Свойства параллелограмма — это просто то, что о нем верно.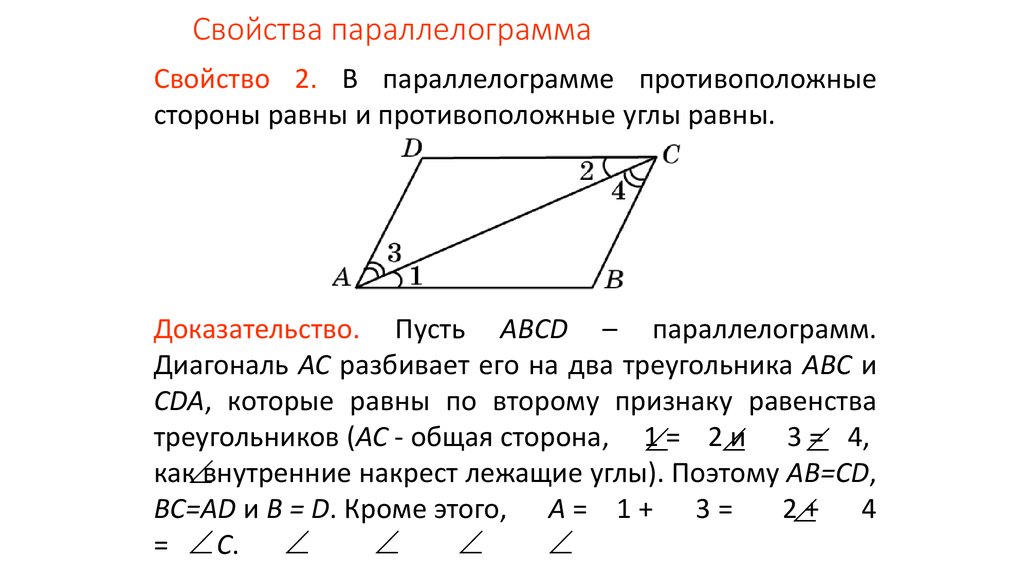 Эти свойства касаются его сторон, углов и диагоналей.
Эти свойства касаются его сторон, углов и диагоналей.
Параллелограмм обладает следующими свойствами:
Противоположные стороны параллельны по определению.
Противоположные стороны равны.
Противоположные углы равны.
Смежные углы являются дополнительными.
Диагонали делят друг друга пополам.
Если вы просто посмотрите на параллелограмм, то вещи, которые кажутся истинными (а именно, вещи в этом списке), истинны и, следовательно, являются свойствами, а вещи, которые не выглядят так, как будто они истинны, свойствами не являются.
Если вы рисуете рисунок, который поможет вам разобраться в свойствах четырехугольника, сделайте свой набросок как можно более общим. Например, когда вы рисуете свой параллелограмм, убедитесь, что он не является почти ромбом (с четырьмя почти конгруэнтными сторонами) или почти прямоугольником (с четырьмя углами, близкими к прямым).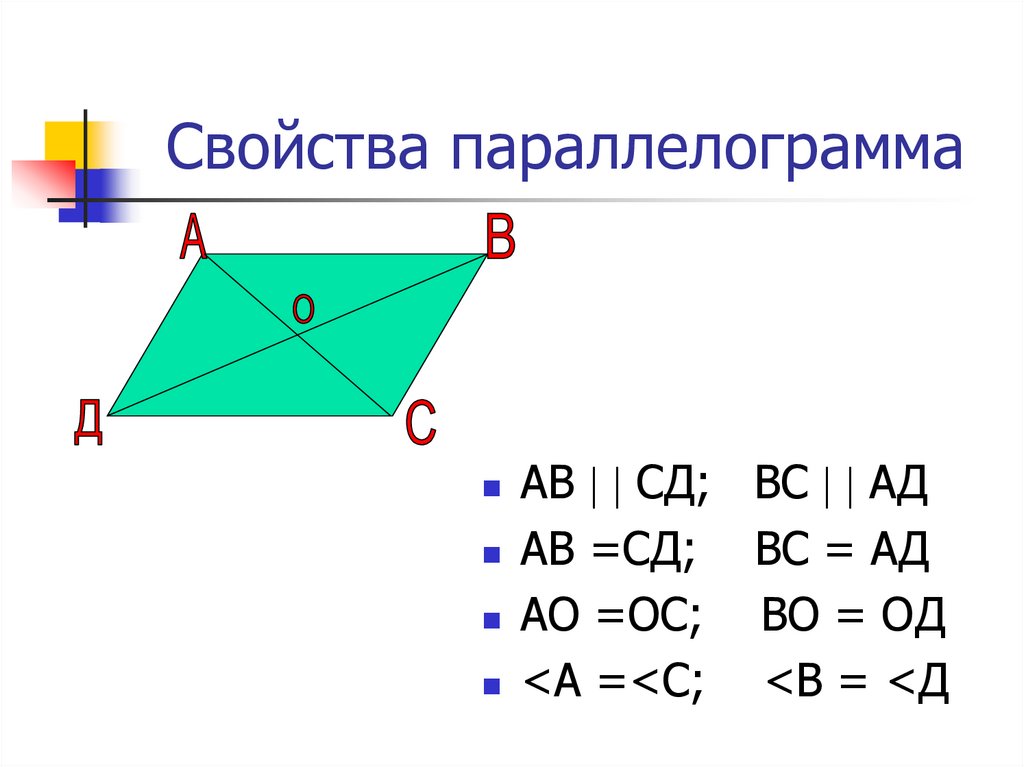 Если ваш набросок параллелограмма близок, скажем, к прямоугольнику, то что-то, что верно для прямоугольников, но не верно для всех параллелограммов (например, конгруэнтность диагоналей), может выглядеть правдой и, таким образом, привести к ошибочному выводу, что это свойство параллелограммов. Капиш?
Если ваш набросок параллелограмма близок, скажем, к прямоугольнику, то что-то, что верно для прямоугольников, но не верно для всех параллелограммов (например, конгруэнтность диагоналей), может выглядеть правдой и, таким образом, привести к ошибочному выводу, что это свойство параллелограммов. Капиш?
Представьте, что вы не можете вспомнить свойства параллелограмма. Вы можете просто набросать один (как на рисунке выше) и просмотреть все, что может быть свойствами. (Обратите внимание, что этот параллелограмм не похож на прямоугольник или ромб.)
Следующие вопросы касаются сторон параллелограмма (см. предыдущий рисунок).
Стороны кажутся конгруэнтными?
Да, противоположные стороны выглядят конгруэнтными, и это свойство. Но соседние стороны не выглядят конгруэнтными, и это , а не свойство.
Стороны кажутся параллельными?
Да, противоположные стороны выглядят параллельными (и, конечно, вы знаете это свойство, если знаете определение параллелограмма).

Следующие вопросы исследуют углы параллелограмма (снова обратитесь к рисунку).
Какие углы кажутся равными?
Да, противоположные углы выглядят конгруэнтными, и это свойство. (Углы A и C кажутся примерно 45°, а углы B и D примерно 135°).
Какие углы кажутся дополнительными?
Да, последовательные углы (например, углы A и B ) выглядят как дополнительные, и это свойство. (Используя параллельные линии
УголкиA и B являются односторонними внутренними углами и поэтому являются дополнительными.)
Какие углы кажутся прямыми?
Очевидно, что нет, и это не свойство.
Следующие вопросы касаются утверждений о диагоналях параллелограмма
.Диагонали кажутся конгруэнтными?
Даже не близко (на приведенном выше рисунке один примерно в два раза длиннее другого, что удивляет большинство людей) — не свойство.


 е. AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + БД 2
е. AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + БД 2 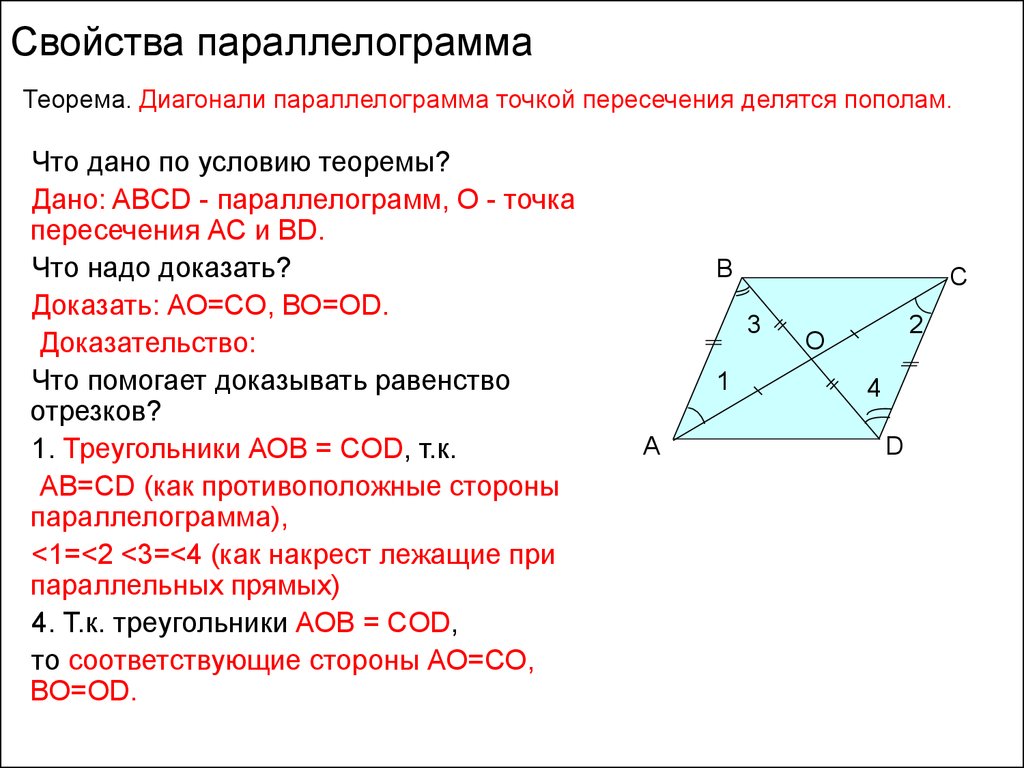 н.э. = до н.э. (дано).
н.э. = до н.э. (дано).