как выглядит, свойства диагоналей, как найти, признаки равенства
Содержание:
-
Что такое выпуклый четырехугольник
- Основные свойства
- Виды выпуклых прямоугольников
-
Свойства диагоналей, признаки выпуклости
- 1 свойство
- 2 свойство
- Еще один признак выпуклости
- Признаки равенства
- Сумма квадратов диагоналей
Содержание
-
Что такое выпуклый четырехугольник
- Основные свойства
- Виды выпуклых прямоугольников
-
Свойства диагоналей, признаки выпуклости
- 1 свойство
- 2 свойство
- Еще один признак выпуклости
- Признаки равенства
- Сумма квадратов диагоналей
Статья поможет разобраться в свойствах и видах выпуклых четырехугольников.
Научит отличать их от невыпуклых фигур. Вы узнаете, как определить, равны фигуры друг другу или нет, найдете ссылки на подробные доказательства всех пунктов равенства.
Что такое выпуклый четырехугольник
Определение
Это почти любой знакомый нам четырехугольник. Потому что в обычной общеобразовательной школе изучают только выпуклые фигуры.
Основные свойства
Для начала проверьте наличие четырех вершин, из которых три не лежат на одной прямой. Также должно быть четыре отрезка, которые эти вершины последовательно соединяют. Если все это есть, значит перед нами четырехугольник.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Дальше нужно отличить выпуклый от невыпуклого. Сделать это очень легко — достаточно просто посмотреть на данную вам фигуру: вся она должна быть расположена с одной стороны от любой из своих сторон.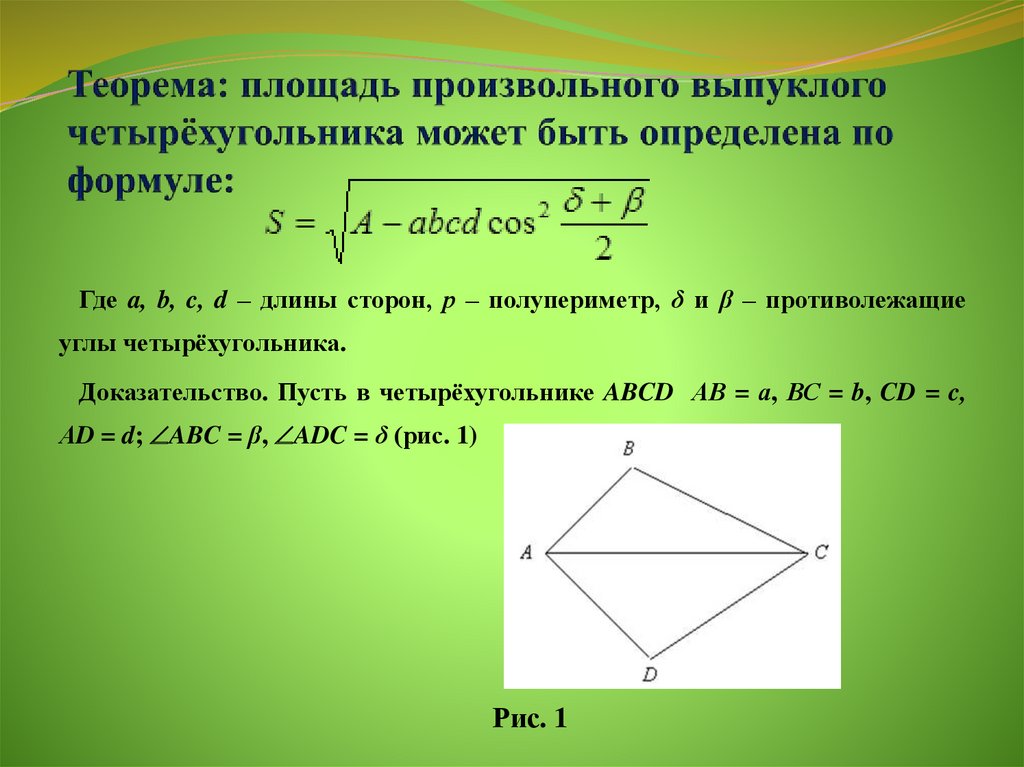
На рисунке ниже видно, что для невыпуклой фигуры это условие невыполнимо.
Виды выпуклых прямоугольников
Существуют две большие группы.
1 вид — параллелограммы:
- квадрат,
- прямоугольник,
- ромб,
- параллелограмм.
2 вид — трапеции:
- произвольная,
- прямоугольная,
- равнобедренная.
Свойства диагоналей, признаки выпуклости
Можно сказать, что это, за небольшим исключением, одно и то же, поэтому объединим их в один блок.
1 свойство
Пересечение всех диагоналей.
Примечание
Точка пересечения должна быть общая. Если хотя бы одна диагональ не пересекается с остальными в одной точке, то этот четыреугольник невыпуклый.
В основе этого свойства лежит соответствующая теорема, но здесь мы ее подробно не рассматриваем.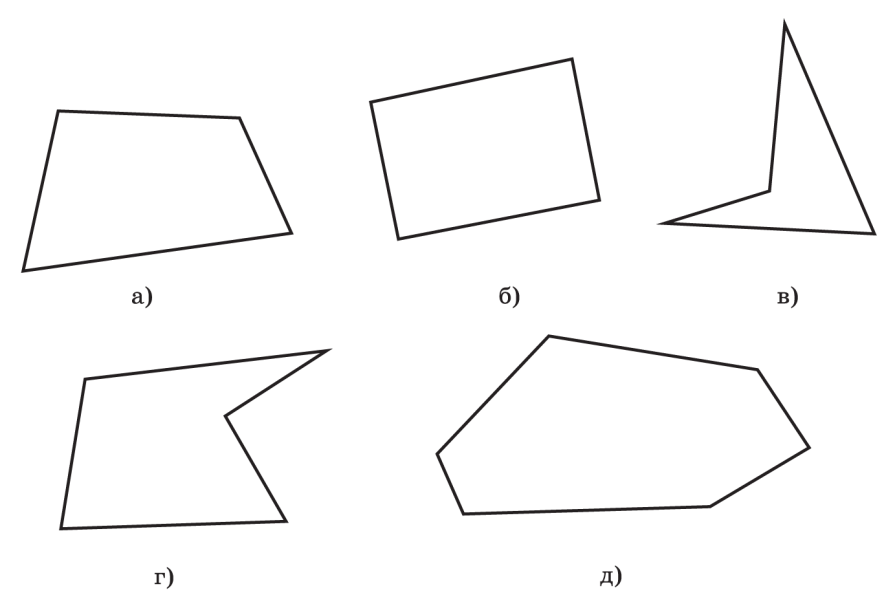
2 свойство
Любая из диагоналей разделит четырехугольник на 2 треугольника. Можно воспользоваться рисунками, данными в первом блоке статьи, и мысленно провести одну диагональ в каждой из фигур. Результат будет подтверждением написанного в этом пункте.
Еще один признак выпуклости
Если сложить градусные меры всех углов фигуры, получится величина, равная 360º.
Признаки равенства
Выпуклые четырехугольники равны, если у них соответственно равны:
- четыре стороны и один угол;
- три стороны и два угла между ними;
- три стороны и два угла, которые не лежат между этими сторонами;
- три стороны и два противолежащих угла;
- три угла и две стороны между ними;
- три угла и две смежные сороны, которые не лежат между этими углами;
- три угла и две смежные стороны, причем одна из них лежит между этими углами;
- фигуры равны, если площадь одной равна площади другой.
Подробные доказательства по каждому пункту с иллюстрациями можно найти здесь: https://yadi.sk/i/V0X_9c1DY1Wehg
https://yadi.sk/i/NFnvRwWep3TwKg https://yadi.sk/i/LyoMWkB872mcSQ
Сумма квадратов диагоналей
Если сумма квадратов диагоналей и сумма квадратов всех сторон фигуры равны, то это параллелограмм. Это свойство относится ко всем видам параллелограмма (ромб, квадрат, прямоугольник, собственно параллелограмм).
Насколько полезной была для вас статья?
Рейтинг: 3.08 (Голосов: 12)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Урок математики в 5-м классе по теме: «Выпуклые и невыпуклые четырехугольники»
- Пелевина Галина Николаевна
org/BreadcrumbList»> Разделы:Цели: Познакомить учащихся с понятием выпуклого и невыпуклого четырёхугольника.
Научить учащихся различать данные четырёхугольники, находить сумму углов четырёхугольника.
Ход урока
I. Организация класса.
II. Проверка знаний учащихся.
Устная работа
1) Подставьте вместо звёздочек нужные числа:
а) 1/4 : * = 1/12; б) 3/4 : * = 1/8; в) 2/* : 2 = 1/5; г) */6 : 20 = 1/24
*) Найдите дробное и натуральные числа, чтобы их произведение равнялось 16.
| X · n = 16 |
2) Найдите периметр и площадь дачного
прямоугольного участка, если его длина 10м и 8? м.
| Р = (а + в) · 2 | Р = (10 + 8?) · 2 = 18? · 2 = 37 (м) |
| S = а · в | S = 10 · 8? = 85 (м?) |
III. Изучение нового материала.
– Скажите, пожалуйста, чаще всего какую геометрическую фигуру вы увидите, если посмотрите на свою дачу сверху?
– Какие четырёхугольники вам уже известны из курса начальной школы? Что вы о них можете сказать?
– Помимо этих четырёхугольников существует ещё несколько видов четырёхугольников, с которыми мы познакомимся дальше в курсе математики.
Стр. 162
№322. Работаем вместе с детьми.
- 1, 7, 11 – два соседних угла тупые, две стороны параллельны
- 2, 12, 9, 8, 6, 3 – противоположные стороны попарно параллельны
- 3, 6 – прямоугольники
- 5 – все стороны разные
- 4, 10 – Что можно сказать об этих четырёхугольниках?
Рассматриваем вопросы 3), 4), 5).
– Как можно назвать остальные четырёхугольники?
[Надутенькие. – Можно?]
– А теперь изобразите в тетради несколько четырёхугольников (выпуклых и невыпуклых).
– А теперь давайте всё-таки попробуем сделать вывод, какой – же четырёхугольник является выпуклым, а какой – невыпуклым?
№325. (чертёж на доске).
– Сделайте вывод: Какие же четырёхугольники являются выпуклыми, а какие невыпуклыми?
– Что такое диагональ? Какой отрезок мы так называем?
– Какой вывод можно сделать?
– А теперь измерьте углы первого выпуклого четырёхугольника и найдите их сумму.
– А как измерить углы в невыпуклом четырёхугольнике? Можно это сделать сразу же?
– Чему равна сумма углов треугольника?
– На сколько треугольников разделит одна диагональ выпуклый четырёхугольник?
– Так, как по вашему, чему должна равняться сумма углов четырёхугольника?
– Получилось это значение у вас или нет?
IV.
Итог урока. Задание на дом.
– С какими геометрическими фигурами мы сегодня познакомились?
– Как определить, какой четырёхугольник является выпуклым, а какой — невыпуклым?
– Как расположены диагонали в этих четырёхугольниках?
Геометрия
— Четырехугольные конечные элементы должны быть выпуклыми и не самопересекающимися. Но почему?
Связанные вопросы и ответы @ Mathematics Stack Exchange, на самом деле исследования, предшествующие этому ответу:
- Четырехсторонняя интерполяция
- Определитель Якоби для билинейных четырехугольников
Пожалуйста, обратите внимание, потому что я не буду повторять все, что уже есть в этих ссылках.
Тогда взгляните на картинку ниже.
Фигура в локальных координатах $(\xi,\eta)$ слева представляет собой
$\left[-\frac{1}{2},+\frac{1}{2}\right] \times \left[-\frac{1}{2},+\frac{1}{2} \право]$
квадрат.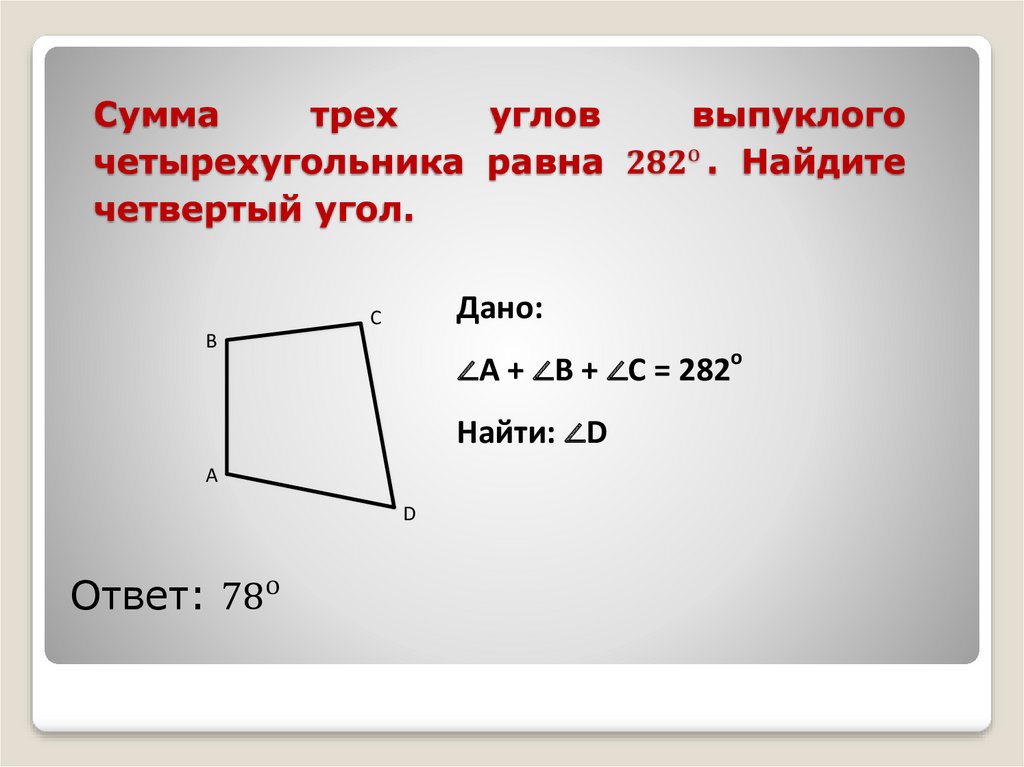
А вот элемент в глобальных координатах $(x,y)$ может иметь совсем другую форму,
как тот, что справа:
Сопутствующая алгебра — изопараметрическое отображение с билинейной интерполяцией — уже должна быть хорошо известна:
$$
\begin{случаи}
x(\xi,\eta) = N_1 x_1 + N_2 x_2 + N_3 x_3 + N_4 x_4 \\
y(\xi,\eta) = N_1 y_1 + N_2 y_2 + N_3 y_3 + N_4 y_4
\end{случаи}
$$
Где:
$$
\begin{случаи}
N_1 = (\frac{1}{2}-\xi)(\frac{1}{2}-\eta)\\
N_2 = (\frac{1}{2}+\xi)(\frac{1}{2}-\eta)\\
N_3 = (\frac{1}{2}-\xi)(\frac{1}{2}+\eta)\\
N_4 = (\frac{1}{2}+\xi)(\frac{1}{2}+\eta)\\
\end{случаи}
$$
Также было отображено отображение $\color{red}{\mbox{диагоналей и средней точки}}$.
Значение точки $\color{green}{\mbox{green}}$ в вершине $(4)$ и самой правой
$\color{blue}{\mbox{blue}}$ точка будет объяснена в ближайшее время.
Получается, что определение обратного преобразование $\,\xi(x,y),\eta(x,y)$ , вообще говоря, сложно , как это было
пример в ответе
по номинальному животному.
Лучше особый случай, чем вообще никакого.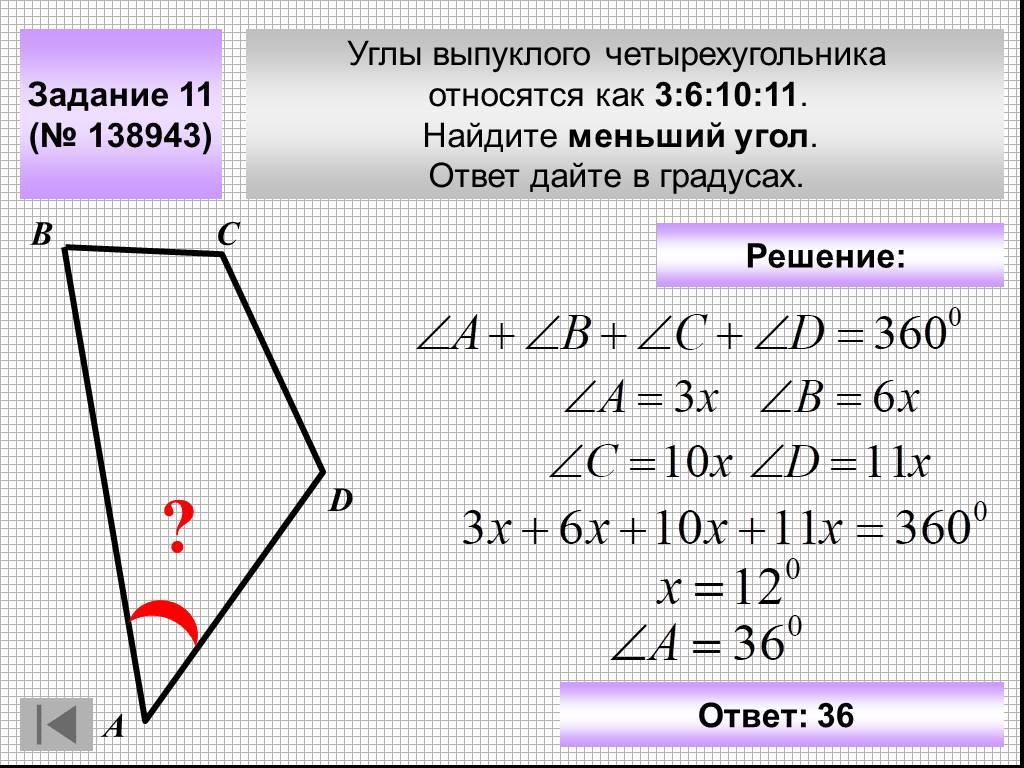
2+b\,\xi + c \quad \mbox{с} \; \begin{case} a = x_1-x_2-x_3+x_4 \\ b = x_4-x_1 \\ c = (x_1+x_2+x_3+x_4)/4 \end{case}
$$
$\color{red}{\mbox{красное пятно}}$ находится в точке $\,\xi=0$ . Следовательно: $x_{красный} = (x_1+x_2+x_3+x_4)/4$. Помимо $y = 0$, еще одна красная линия
есть отображение диагонали $\xi = -\eta$ . Можно доказать, что это отображение является параболой. 92 + (x_4-x_1)\,\xi + \frac{1}{4}(x_1+x_2+x_3+x_4) = x_4
$$
Поскольку $x_4$ является вершиной, мы знаем, что другой корень всегда находится в точке $\,\xi = 1/2$ . Воспользовавшись этим фактом, находим:
$$
\left[\xi-\frac{1}{2}\right]\left[(x_1-x_2-x_3+x_4)\xi — \frac{1}{2}(x_1+x_2+x_3-3x_4)\ справа] = 0
$$
Пришло время представить наши последние упрощения:
$$
(x_1,y_1) = (-\frac{1}{2},0) \quad ; \quad (x_2,y_2) = (+\frac{1}{2},-\frac{1}{2}) \quad ; \четверка
(x_3,y_3) = (+\frac{1}{2},+\frac{1}{2}) \\ (x_4,y_4) = (H>0,0) = \mbox{переменная}
$$
Тогда $\color{green}{\mbox{green}}$ корень уравнения для вершины (4) принимает вид:
$$
\left(-\frac{3}{2}+H\right)\xi — \frac{1}{2}\left(\frac{1}{2}-3H\right) = 0 \quad \Longrightarrow \quad \xi_{зеленый} = \frac{1-6H}{4H-6}
$$
Оказывается, нулевой знаменатель соответствует параллелограмму и линейной, а не квадратичной интерполяции.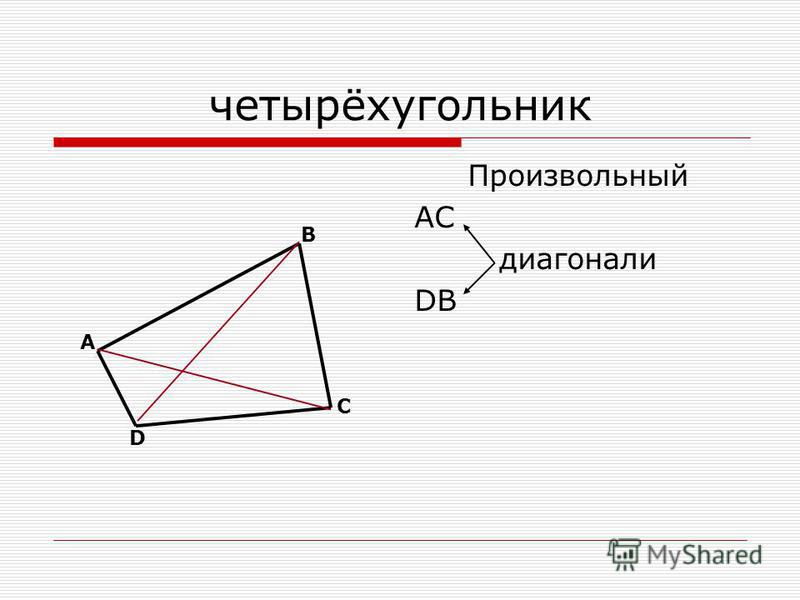
Наше текущее исследование не охватывает этот случай.
Ниже представлена анимация формы четырехугольника вместе с параболой, соответствующей отображению $\,\xi \rightarrow x$ ,
для значений $H$, начиная с $0$ с размером шага $1/8$.
Точка $\color{green}{\mbox{green}}$ слева соответствует линиям $\color{green}{\mbox{green}}$ справа: позиция $(0,H )$ вершины $(4)$.
Видно, что существует двух значений $\xi$ с одним значением $x$ для всех $0 < H < 1/2$ , что просто соответствует двум корням нашего квадратного уравнения.
Таким образом, отображение в этой вершине не уникально. Самая правая точка $\color{blue}{\mbox{blue}}$ слева соответствует максимуму параболы справа.
Тривиально, что эта точка $\color{blue}{\mbox{blue}}$ должна находиться на границе, ограничивающей область $\color{gray}{\mbox{gray}}$, которая является отображением
$(-1/2 < \xi < +1/2,-1/2 < \eta < + 1/2) \to (x,y)$ .
Исходный код бесплатного программного обеспечения, сопровождающего все это, находится на моем веб-сайте.
Разница между выпуклым и невыпуклым
Ключевое отличие: Выпуклый относится к кривизне, которая простирается наружу, тогда как невыпуклый относится к кривизне, которая простирается внутрь. Невыпуклые также называются вогнутыми.Выпуклость и невыпуклость определяют типы кривизны. Выпуклая определяет кривизну, которая выходит наружу или выпирает. С другой стороны, невыпуклость определяет кривизну, которая расширяется или изгибается внутрь. Таким образом, расширение кривой используется для различения двух форм. Выпуклые и невыпуклые часто используются в качестве прилагательных для определения объектов, связанных с формой или кривой, определяемой ими.
Например, с точки зрения многоугольника, две общие категории включают выпуклые и невыпуклые многоугольники. Выпуклый многоугольник не имеет внутреннего угла больше 180 градусов. Однако если существует многоугольник с одним или несколькими внутренними углами больше 180 градусов, то такой многоугольник называется невыпуклым или вогнутым многоугольником.
В евклидовом пространстве объект называется выпуклым, если для каждой пары точек, лежащих в объекте, каждая точка соединяющего их отрезка прямой также попадает внутрь объекта. Однако, если какой-либо отрезок выходит за пределы формы или набора, то он считается невыпуклым. Сплошной куб является примером выпуклости, тогда как серповидная форма не является выпуклой (вогнутой).
Концепция выпуклости и невыпуклости также была распространена на функции и переменные для решения связанных проблем. Пусть f будет функцией многих переменных, определенных на выпуклом множестве S . Тогда F —
(не выпуклый) вогнутый на комплекте S , если для всех x ∈ S , все x ‘∈ S и все λ (0,1).
f ((1−λ) x + λ x ‘) ≥ (1−λ) f ( x ) + λ f ( x ‘)
convex on the set S if for all x ∈ S , all x ‘ ∈ S , and для всех λ ∈ (0,1) имеем
f ((1 − λ) x + λ x ‘) ≤ (1 − λ) f 3 λ 4 f 9004 + ( х ‘).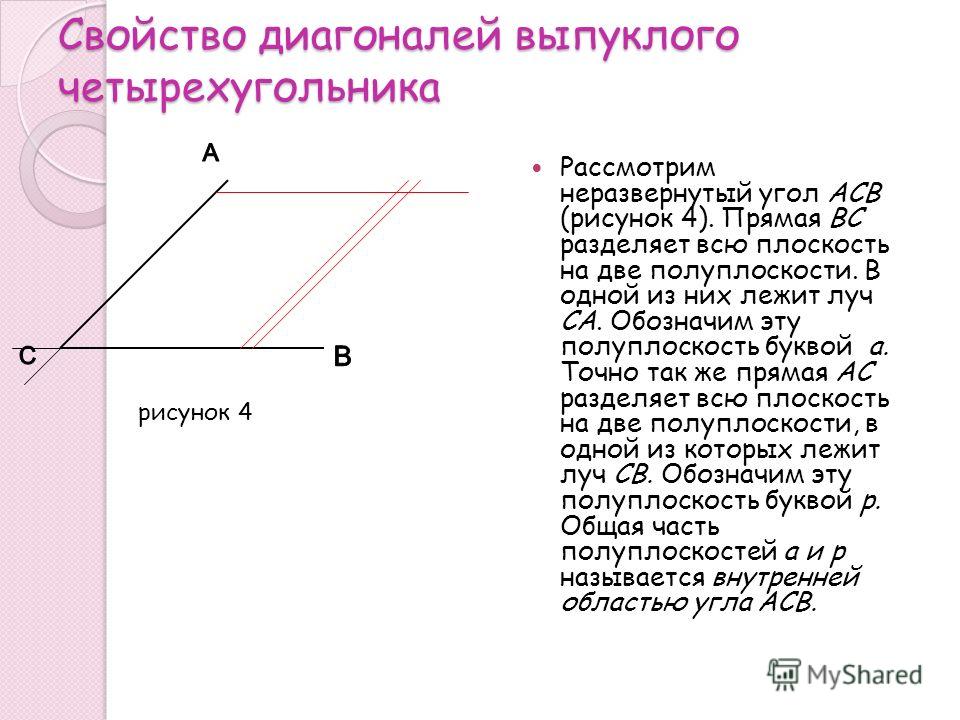
Выпуклые и невыпуклые также связаны с линзами и зеркалами. Выпуклая линза – это линза, толщина которой в середине больше, чем по краям. С другой стороны, невыпуклая линза по краям толще, чем в середине. Выпуклые зеркала — это изогнутые зеркала, в которых посеребренная поверхность выпирает наружу. Невыпуклые зеркала содержат внутреннюю серебряную поверхность.
Таким образом, эти термины используются в контексте многих типов объектов, но все они основаны на базовом определении выпуклости и невыпуклости.
Сравнение выпуклых и невыпуклых поверхностей:
| Выпуклая | Невыпуклый |
Определение | Выпуклая кривизна округляется, как внешняя сторона сферы. | Вогнутая (невыпуклая) кривизна закруглена внутрь |
Аналогия | Гора | Долина |
Полигон | Две точки, лежащие в многоугольнике, соединены отрезком, и если этот отрезок также полностью лежит в многоугольнике, то многоугольник считается выпуклым многоугольником. |
