Площадь бублика формула: Формулы, как найти площадь круга

Площадь кольца — формула, пример расчета

Кольцо – это плоская геометрическая фигура, которая представляет собой часть плоскости между двумя окружностями с общим центром, но имеющими разный радиус.

Площадь кольца, выраженная через внешний и внутренний радиусы

Пусть дана окружность радиуса R и окружности радиуса r. Причем R>r. Совместим центры этих окружностей. Фигура, заключенная между этими окружностями и будет кольцо, у которого R является внешним радиусом, r -внутренним радиусом.
Тогда площадь этой фигуры будет равна разницы между площадью круга с большим радиусом и площадью круга с меньшим радиусом.

Площадь круга с радиусом r выражается формулой:

Площадь круга с радиусом R выражается формулой:

Тогда площадь кольца будет равна:

Таким образом, площадь кольца равна произведению числа на разницу квадратов внешнего и внутреннего радиусов:

Пример расчета площади кольца, если известны его радиусы.
Найдите площадь кольца, если его внешний радиус равен 3, а внутренний – 2
Площадь кольца вычисляется по формуле:

Подставив значения из условия задачи, имеем:

Площадь кольца, выраженная через внешний и внутренний диаметры

Иногда при решении задач удобней использовать формулу площади кольца, выраженную через внутренний и внешний диаметры.

Пусть D – внешний диаметр кольца, d -внутренний диаметр кольца, тогда:

Выразим радиус через диаметр. Имеем:

Площадь кольца вычисляется по формуле:

Подставив выраженные через диаметр радиусы, получим:

Таким образом, площадь кольца равна четверти произведения числа на разницу квадратов внешнего и внутреннего диаметров:

Пример расчета площади кольца, если известны его диаметры.
Найдите площадь кольца, если его внешний диаметр равен 10, а внутренний – 6
Площадь кольца вычисляется по формуле:

Подставив значения из условия задачи, имеем:

Площади кольца, выраженная через средний радиус и ширину кольца

Пусть k– ширина кольца, являющийся разницей между большим и меньшим радиусом, то есть k=R-r-средний радиус кольца, равный

Площадь кольца вычисляется по формуле:

Применив формулу разности квадратов, имеем:

Но R-r=k, а
Подставим правые части равенства в формулу площади кольца.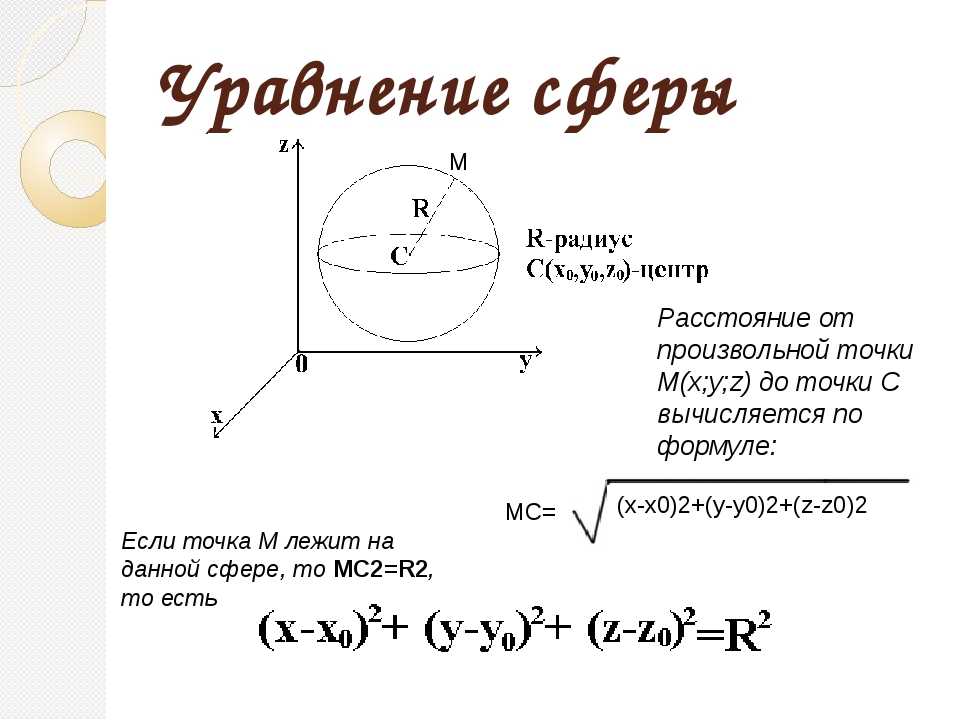
Получим:

Площадь кольца равна удвоенному произведению числа среднего радиуса на ширину кольца.

Пример расчета площади кольца, если известны его средний радиус и ширина.
Найдите площадь кольца, если его средний радиус равен 5, а ширина – 2

Площадь кольца вычисляется по формуле:

Подставив значения из условия задачи, имеем:

Площади кольца через длину самого большого отрезка, проведенного внутри кольца

Пусть AB –самый большой отрезок, лежащий внутри кольца. Точка С – половина этого отрезка. Этот отрезок будет являться касательной к кругу меньшего радиуса. Касательная перпендикулярна радиусу меньшей окружности, проведенного в точку каcания C. Тогда
Следовательно, треугольник ACO –прямоугольный, где

По теореме Пифагора имеем:



Площадь кольца равна:

Подставив, получим:

Следовательно, площадь кольца равна произведению числа на квадрат половины самого большого отрезка кольца.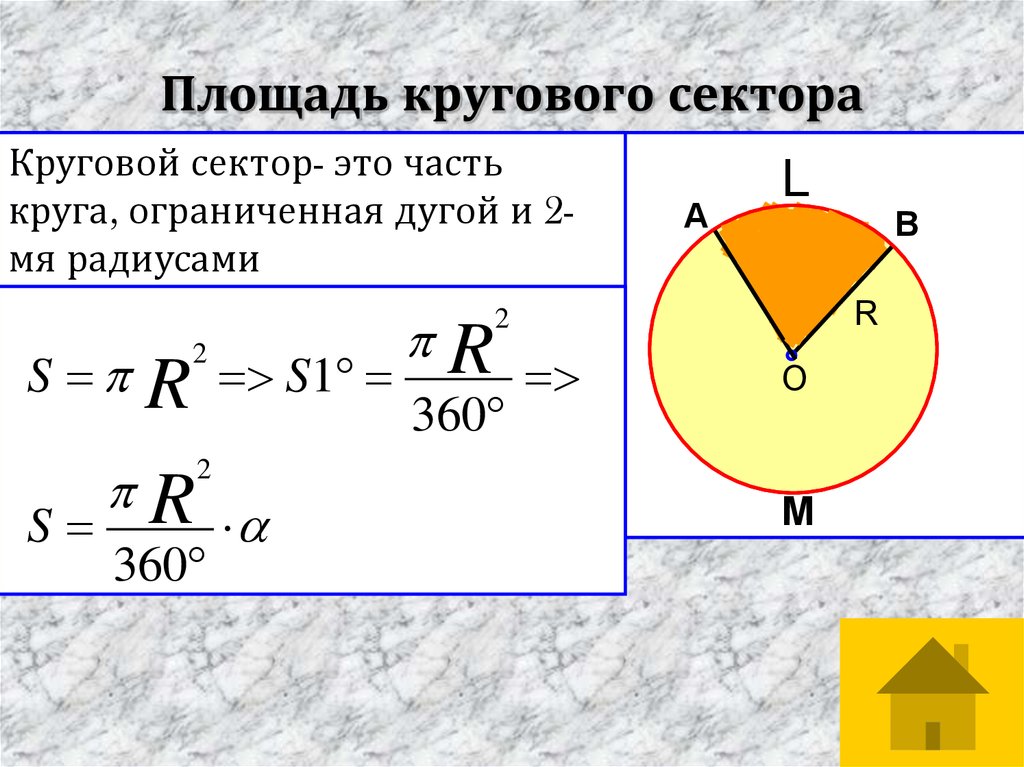

Площадь поверхности тела вращения формула интеграл. Нахождение площади поверхности тел вращения

Поэтому сразу перейду к основным понятиям и практическим примерам.

Посмотрим на лаконичную картинку

И вспомним: что можно вычислить с помощью

определённого интеграла ?

В первую очередь, конечно, площадь криволинейной трапеции . Знакомо со школьных времён.

Если же данная фигура вращается вокруг координатной оси, то речь уже идёт о нахождении объёма тела вращения . Тоже просто.

Что ещё? Не так давно была рассмотрена задача о длине дуги кривой .

И сегодня мы научимся рассчитывать ещё одну характеристику – ещё одну площадь. Представьте, что линия вращается вокруг оси . В результате этого действия получается геометрическая фигура, называемая поверхностью вращения . В данном случае она напоминает такой горшок без дна. И без крышки. Как бы сказал ослик Иа-Иа, душераздирающее зрелище =)

Чтобы исключить двусмысленную трактовку, сделаю занудное, но важное уточнение:

с геометрической точки зрения наш «горшок» имеет бесконечно тонкую стенку и две поверхности с одинаковыми площадями – внешнюю и внутреннюю.

Так вот, все дальнейшие выкладки подразумевают площадь только внешней поверхности .

В прямоугольной системе координат площадь поверхности вращения рассчитывается по формуле:

или, если компактнее: .

К функции и её производной предъявляются те же требования, что и при нахождении длины дуги кривой , но, кроме того, кривая должна располагаться выше оси . Это существенно! Нетрудно понять, что если линия располагается под осью , то подынтегральная функция будет отрицательной : , и поэтому к формуле придётся добавить знак «минус» дабы сохранить геометрический смысл задачи.

Рассмотрим незаслуженно обойденную вниманием фигуру:

Площадь поверхности тора

В двух словах, тор – это бублик . Хрестоматийный пример, рассматриваемый практически во всех учебниках по матану, посвящён нахождению объёма тора, и поэтому в целях разнообразия я разберу более редкую задачу о

площади его поверхности . Сначала с конкретными числовыми значениями:

Пример 1

Вычислить площадь поверхности тора, полученного вращением окружности вокруг оси .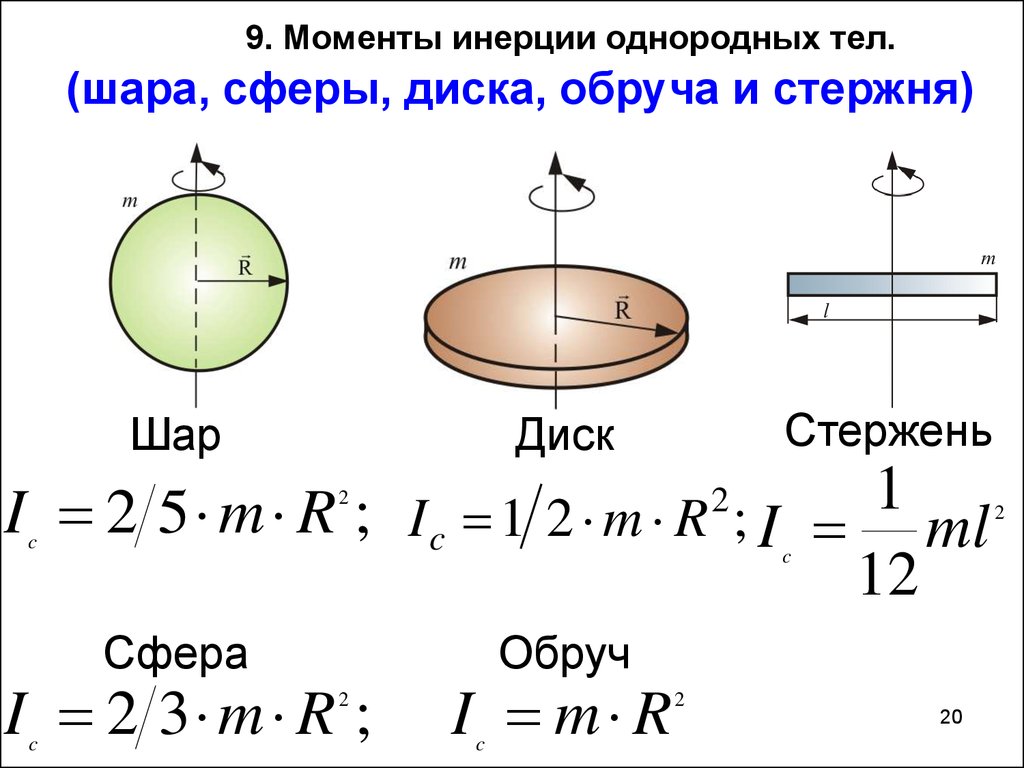

Решение : как вы знаете, уравнение задаёт окружность единичного радиуса с центром в точке . При этом легко получить две функции:

– задаёт верхнюю полуокружность;
– задаёт нижнюю полуокружность:

Суть кристально прозрачна: окружность вращается вокруг оси абсцисс и образует поверхность бублика. Единственное, здесь во избежание грубых оговорок следует проявить аккуратность в терминологии: если вращать круг , ограниченный окружностью , то получится геометрическое тело , то есть сам бублик. И сейчас разговор о площади его поверхности

, которую, очевидно, нужно рассчитать как сумму площадей:

1) Найдём площадь поверхности, которая получается вращением «синей» дуги вокруг оси абсцисс. Используем формулу . Как я уже неоднократно советовал, действия удобнее проводить поэтапно:

Берём функцию и находим её производную :

И, наконец, заряжаем результат в формулу:

Заметьте, что в данном случае оказалось рациональнее удвоить интеграл от чётной функции по ходу решения, нежели предварительно рассуждать о симметрии фигуры относительно оси ординат.

2) Найдём площадь поверхности, которая получается вращением «красной» дуги вокруг оси абсцисс. Все действия будут отличаться фактически только одним знаком. Оформлю решение в другом стиле, который, само собой, тоже имеет право на жизнь:

3) Таким образом, площадь поверхности тора:

Ответ

:

Задачу можно было решить в общем виде – вычислить площадь поверхности тора, полученного вращением окружности вокруг оси абсцисс, и получить ответ . Однако для наглядности и бОльшей простоты я провёл решение на конкретных числах.

Если вам необходимо рассчитать объём самого бублика, пожалуйста, обратитесь к учебнику, в качестве экспресс-справки:

Согласно теоретической ремарке, рассматриваем верхнюю полуокружность. Она «прорисовывается» при изменении значения параметра в пределах (легко видеть, что на данном промежутке), таким образом:

Ответ :

Если решить задачу в общем виде, то получится в точности школьная формула площади сферы , где – её радиус.

Что-то больно простая задачка, даже стыдно стало…. предлагаю вам исправить такую недоработку =)

Пример 4

Вычислить площадь поверхности, полученной вращением первой арки циклоиды вокруг оси .

Задание креативное. Постарайтесь вывести или интуитивно догадаться о формуле вычисления площади поверхности, полученной вращением кривой вокруг оси ординат. И, конечно, снова следует отметить преимущество параметрических уравнений – их не нужно как-то видоизменять; не нужно заморачиваться с нахождением других пределов интегрирования.

График циклоиды можно посмотреть на странице Площадь и объем, если линия задана параметрически . Поверхность вращения будет напоминать… даже не знаю с чем сравнить… что-то неземное – округлой формы с остроконечным углублением посередине. Вот для случая вращения циклоиды вокруг оси ассоциация в голову мгновенно пришла – продолговатый мяч для игры в регби.

Решение и ответ в конце урока.

Завершаем наш увлекательный обзор случаем полярных координат . Да, именно обзор, если вы заглянете в учебники по математическому анализу (Фихтенгольца, Бохана, Пискунова, др. авторов), то сможете раздобыть добрый десяток (а то и заметно больше) стандартных примеров, среди которых вполне возможно найдётся нужная вам задача.

Как вычислить площадь поверхности вращения,
если линия задана в полярной системе координат?

Если кривая задана в полярных координатах уравнением , и функция имеет непрерывную производную на данном промежутке, то площадь поверхности, полученной вращением данной кривой вокруг полярной оси, рассчитывается по формуле , где – угловые значения, соответствующие концам кривой.

В соответствии с геометрическим смыслом задачи подынтегральная функция , а это достигается только при условии ( и заведомо неотрицательны). Следовательно, необходимо рассматривать значения угла из диапазона , иными словами кривая должна располагаться выше полярной оси и её продолжения. Как видите, та же история, что и в двух предыдущих параграфах.

Пример 5

Вычислить площадь поверхности, образованной вращением кардиоиды вокруг полярной оси.

Решение : график данной кривой можно посмотреть в Примере 6 урока о полярной системе координат . Кардиоида симметрична относительно полярной оси, поэтому рассматриваем её верхнюю половинку на промежутке (что, собственно, обусловлено и вышесказанным замечанием).

Поверхность вращения будет напоминать яблочко.

Техника решения стандартна. Найдём производную по «фи»:

Составим и упростим корень:

Надеюсь, с заштатными

Приветствую вас, уважаемые студенты вуза Аргемоны!

Сегодня мы продолжим учиться материализации предметов. В прошлый раз мы вращали плоские фигуры и получали объёмные тела. Некоторые из них — очень даже заманчивые и полезные. Думаю, что многому, что изобретает маг, можно в дальнейшем найти применение.

Сегодня мы будет вращать кривые. Понятно, что таким образом мы можем получить какой-то предмет с очень тонкими гранями (колбочка или флакон для зелий, ваза для цветов, стакан для напитков и т.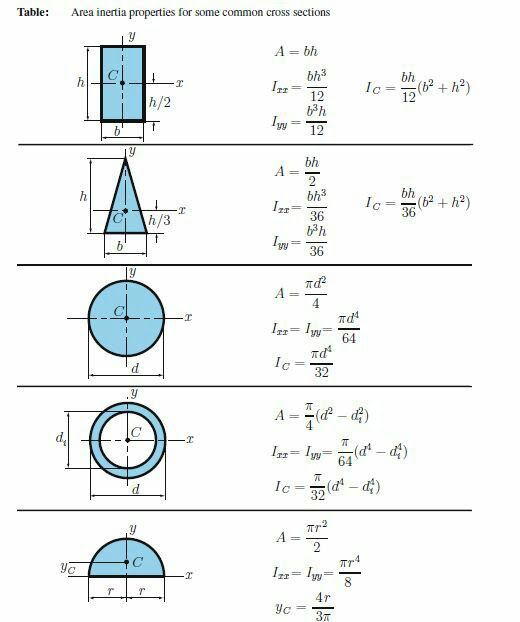 п.), потому как вращающаяся кривая именно такого рода предметы и может сотворить. Другими словами, вращением кривой мы можем получить какую-то поверхность — замкнутую со всех сторон или нет. Почему прямо сейчас вспомнилась дырявая чаша, из которой всё время пил сэр Шурф Лонли-Локли.

Вот мы и сотворим дырявую чашу и недырявую, и подсчитаем площадь сотворённой поверхности. Думаю, для чего-то она (вообще площадь поверхности) ведь будет нужна — ну хотя бы для нанесения специальной магической краски. А с другой стороны, площади магических артефактов могут потребоваться для расчёта приложенных к ним магических сил или ещё чего-то. Мы научимся это находить, а уж где применить — найдём.

Итак, форму чаши вполне нам может дать кусок параболы. Возьмём самую простейшую y=x 2 на промежутке . Видно, что при вращении её вокруг оси OY получается как раз чаша. Без дна.

Заклинание для расчёта площади поверхности вращения выглядит следующим образом:

Здесь |y| — это расстояние от оси вращения до любой точки кривой, которая вращается.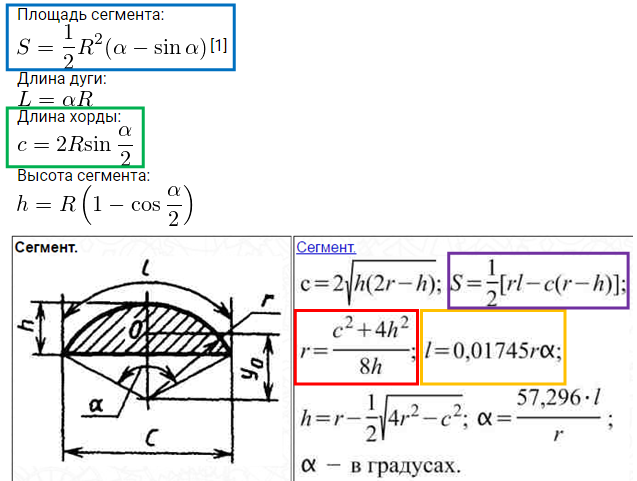 2. Для нашего случая площадь круга будет равна пи), но вычислим его по новой формуле — для проверки.
Расстояние от оси вращения до любой точки этого кусочка кривой также равно х.

Ну вот, расчёты наши верны, что радует.

А теперь домашнее задание .

1. Найти площадь поверхности, полученной вращением ломаной ABC, где A=(1; 5), B=(1; 2), C=(6; 2), вокруг оси ОХ.
Совет. Записать все отрезки в параметрическом виде.
AB: x=1, y=t, 2≤t≤5
BC: x=t, y=2, 1≤t≤6
Кстати, на что похож получившийся предмет?

2. Ну а теперь придумайте что-то сами. Трёх предметов, думаю, хватит.

I. Объемы тел вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п°п° 197, 198* Разберите подробно примеры, приведенные в п° 198.

508. Вычислить объем тела, образуемого вращением эллипсаВокруг оси Ох.

Таким образом,

530. Найти площадь поверхности, образованной вращением вокруг оси Ox дуги синусоиды у = sin х от точки X = 0 до точки X = It.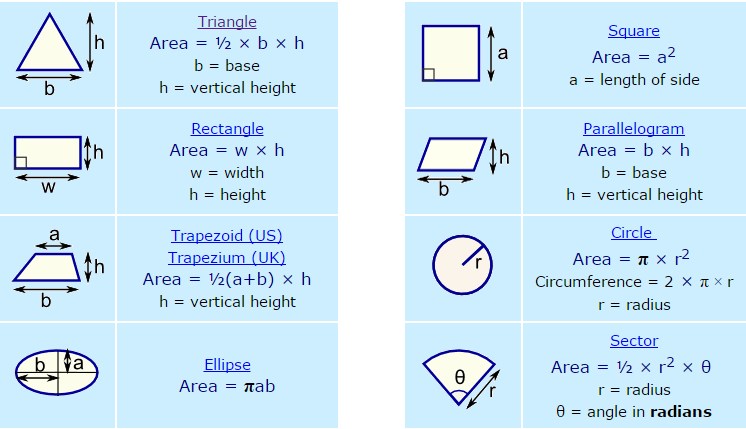

531. Вычислить площадь поверхности конуса с высотой h и радиусом г.

532. Вычислить площадь поверхности, образованной

вращением астроиды х3 -)- у* — а3 вокруг оси Ох.

533. Вычислить площадь поверхности, образованной цращением петли кривой 18 уг — х (6 — х)г вокруг оси Ох.

534. Найти поверхность тора, производимого вращением круга X2 — j — (у—З)2 = 4 вокруг оси Ох.

535. Вычислить площадь поверхности, образованной вращением окружности X = a cost, y = asint вокруг оси Ох.

536. Вычислить площадь поверхности, образованной вращением петли кривой х = 9t2, у = St — 9t3 вокруг оси Ох.

537. Найти площадь поверхности, образованной вращением дуги кривой х = е*sint, у = el cost вокруг оси Ox

от t = 0 до t = —.

538. Показать, что поверхность, производимая вращением дуги циклоиды х = a (q> —sin ф), у = а (I — cos ф) вокруг оси Oy, равна 16 и2 о2.

539. Найти поверхность, полученную вращением кардиоидыВокруг полярной оси.

540. Найти площадь поверхности, образованной вращением лемнискатыВокруг полярной оси.

Дополнительные задачи к главе IV

Площади плоских фигур

541. Найтивсю площадь области, ограниченной кривойИ осью Ох.

542. Найти площадь области, ограниченной кривой

И осью Ох.

543. Найти часть площади области, расположенной в первом квадранте и ограниченной кривой

л осями координат.

544. Найти площадь области, содержащейся внутри

петли:

545. Найти площадь области, ограниченной одной петлей кривой:

546. Найти площадь области, содержащейся внутри петли:

547. Найти площадь области, ограниченной кривой

И осью Ох.

548. Найти площадь области, ограниченной кривой

И осью Ох.

549. Найти площадь области, ограниченной осью Oxr

прямойИ кривой

Данная формула называется формулой объема тела по площади параллельных сечений.

Пример. Найти объем эллипсоида x 2 + y 2 + z 2 = 1 . a 2b 2c 2

Рассекая эллипсоид плоскостью, параллельной плоскости Oyz и на расстояниих от нее (-а ≤х ≤а ), получим эллипс (см. рис. 15):

Площадь этого эллипса равна

S(x) = π bc1

Поэтому, по формуле (16), имеем

Пусть кривая АВ является графиком функцииу = f (x ) ≥ 0, гдех [а ,b ], a функцияу = f (x ) и её производнаяу» = f» (x ) непрерывны на этом отрезке.

Тогда площадь S поверхности, образованной вращением кривойАВ вокруг осиОх вычисляется по формуле

		2 π			1 +(y ′) 2 dx .

Если кривая АВ задана параметрическими уравнениямих = x (t ),у = у (t ),t 1 ≤t ≤t 2 , то формула для площади поверхности вращения принимает вид

S x = 2 π ∫ y (t )(x ′ (t ))2 + (y ′ (t ))2 dt .

Пример Найти площадь поверхности шара радиуса R. Решение:

Можно считать, что поверхность шара образована вращением полуокружности y = R 2 − x 2 ,- R ≤х ≤R , вокруг осиОх. По формуле (19) находим

			− x
S = 2 π		R 2− x 21 +						dx =
					− x
	− R

2 π ∫ R2 − x2 + x2 dx= 2 π Rx− R R = 4 π R2 .

−R

Пример . Дана циклоида x = a (t − sin t ) , 0 ≤ t ≤ 2 π . y = a (1− cost ) ,

Найти площадь поверхности, образованной вращением её вокруг оси Ох.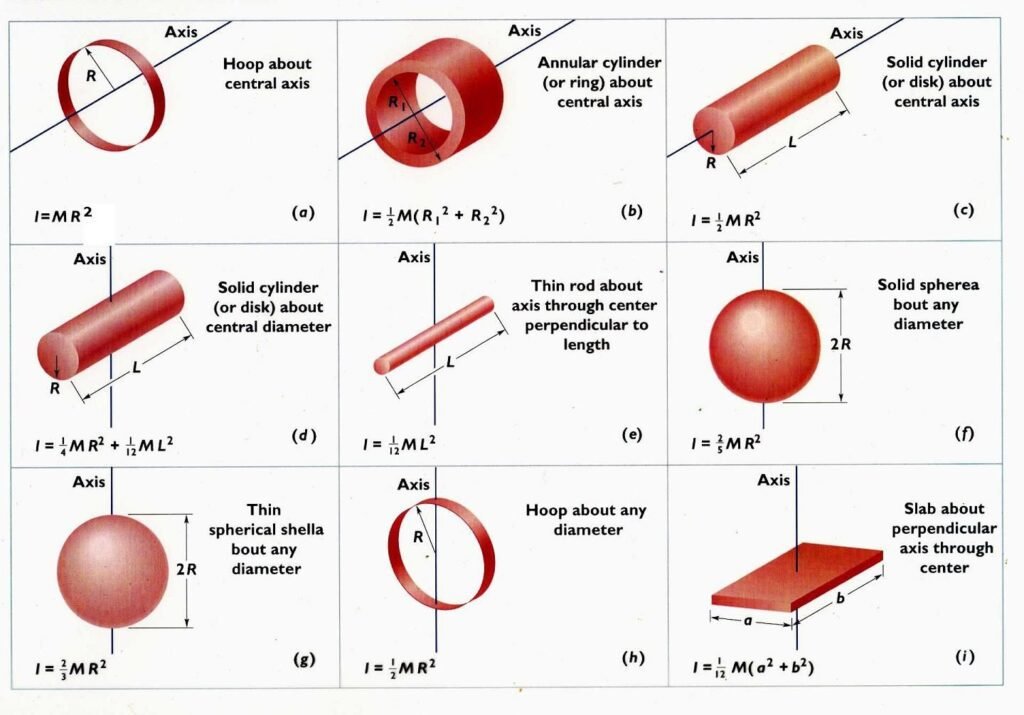 Решение:

При вращении половины дуги циклоиды вокруг оси Ох площадь поверхности вращения равна

1 S x

2π π ∫ a (1− cost )

(a(1 − cos t)) 2 + (asin t) 2 dt=

2π ∫ π a 2

2 sin2 t

2 cost + cos2

t + sin 2 tdt=

4 π a 2

π ∫ sin2

2 2sin2 t dt = 8π a 2

π ∫ sin2 t

sin t

dt =

= −8 π a 2 ∫

− cos

d cos

= − 16 π a

32π a

= −16 π a

0 −

1− 0+

= −16 π a

1 S x = 32 π a 2 . Следовательно,

64 π a 2 .

Вычисление длины дуги плоской кривой

Прямоугольные координаты

Пусть в дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего прямоугольных координатах дана плоская кривая АВ, уравнение которой у = f(x), где, а ≤ х≤ b.

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту звена ее стремится к нулю. Покажем, что если функция у = f(x) и ее производная y′ = f′ (x) непрерывны на отрезке [а ,b ], то криваяАВ имеет длину, равную

Если уравнение кривой АВ задано в параметрической форме

x = x(t) , α ≤ t ≤ β , y= y(t) ,

где x (t ) иy (t ) – непрерывные функции с непрерывными производными иx (α ) =а, x (β ) =b , то длинаl кривойАВ находится по формуле

(x ′ (t ))2 + (y ′ (t ))2 dt . = R arcsin

π .

− x

Значит, l = 2π R. Если уравнение окружности записать в параметрическом видех = R cost, у = R sint (0 ≤t ≤ 2π ), то

	(− Rsin t) 2 + (Rcos t) 2 dt= Rt0 2 π = 2 π R.
l = ∫

Полярные координаты

Пусть кривая АВ задана уравнением в полярных координатахr =r (ϕ ),α ≤ ϕ ≤ β . Предположим, чтоr (ϕ ) иr» (ϕ ) непрерывны на отрезке [α ,β ].

Если в равенствах х = r cosϕ ,у =r sinϕ , связывающих полярные и декартовы координаты,

параметром считать угол ϕ , то кривуюАВ можно задать параметрическиx = r (ϕ ) cos ϕ ,

y = r (ϕ ) sinϕ .

Применяя формулу (15), получаем l = ∫ r 2 + r ′ 2 d ϕ .

Пример Найти длину кардиоиды r =a (1 + cosϕ ). Решение:

Кардиоида r =a (1 + cosϕ ) имеет вид, изображенный на рисунке 14. Она симметрична относительно полярной оси. Найдем половину длины кардиоиды:

1 l =	π∫	(a (1 + cos ϕ ))2 + (a (− sin ϕ ))2 d ϕ =
A π ∫	2 + 2cosϕ d ϕ =a π ∫		2 2cos2 ϕ d ϕ =
2a π ∫ cosϕ d ϕ = 4a sinϕ

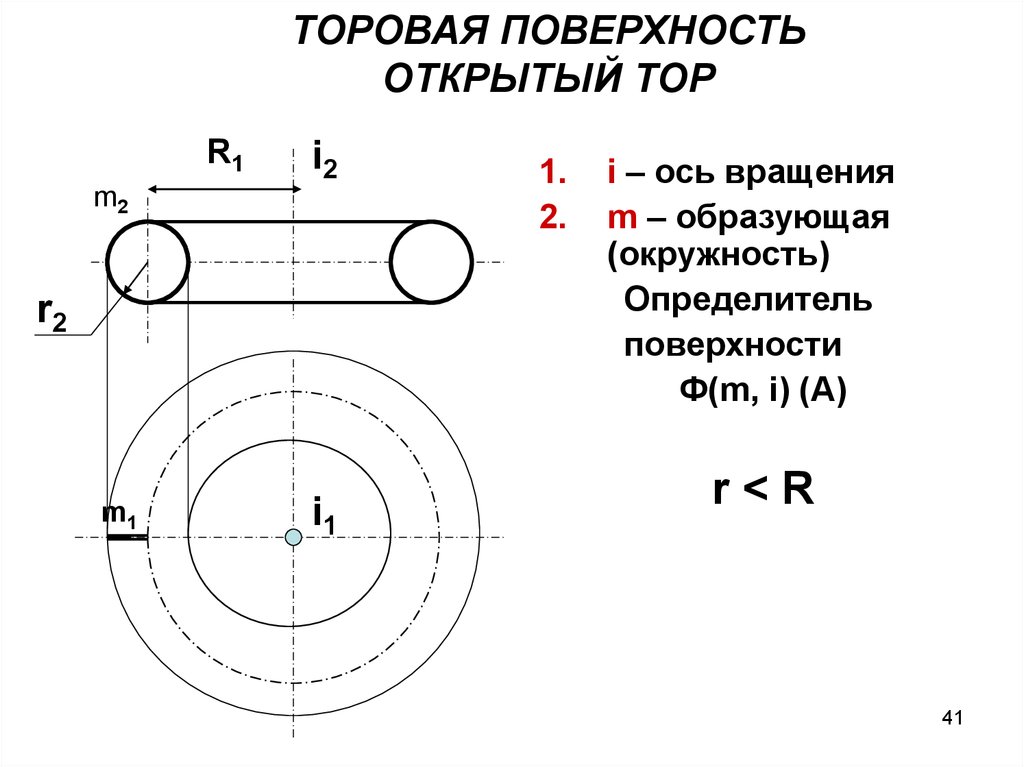
Таким образом, 1 2 l = 4 a . Значит,l = 8а.

Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостныйгиперболоид вращения. Одна и та же поверхность может быть получена вращением самых разнообразных кривых. Площадь поверхности вращения, образованной вращением плоской кривой конечной длины вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равна произведению длины кривой на длину окружности с радиусом, равным расстоянию от оси до центра масс кривой. Это утверждение называется второй теоремой Гюльдена, или теоремой Паппа о центроиде.

Площадь поверхности вращения, образованной вращением кривой вокруг оси можно вычислить по формуле

Для случая, когда кривая задана в полярной системе координат действительна формула

Механические приложения определённого интеграла (работа сил, статические моменты, центр тяжести).

Вычисление работы сил

Материальная точка движется по непрерывно дифференцируемой кривой, при этом на нее действует сила, направленная по касательной к траектории в направлении движения. Полная работа, совершаeмая силой F(s):

Если положение точки на траектории движения описывается другим параметром, то формула приобретает вид:

Вычисление статических моментов и центра тяжести
Пусть на координатной плоскости Оху некоторая масса М распределена с плотностью р = р(у) на некотором множестве точек S (это может быть дуга кривой или ограниченная плоская фигура). Обозначим s(у) — меру указанного множества (длина дуги или площадь).

Определение 2. Число называется k-м моментом массы М относительно оси Ох.
При k = 0 М 0 = М — масса,
k = 1 М 1 — статический момент,
k = 2 М 2 — момент инерции.

Аналогично вводятся моменты относительно оси Оу. В пространстве подобным же образом вводятся понятия моментов массы относительно координатных плоскостей.
Если р = 1, то соoтветствующие моменты называются геометрическими. Координаты центра тяжести однородной (р — const) плоской фигуры определяются по формулам:

где М 1 y , М 1 x — геометрические статические моменты фигуры относительно осей Оу и Ox; S — площадь фигуры.

Калькулятор площади поверхности тора — Найдите площадь поверхности вашего тора

Создано Rahul Dhari

Отзыв Стивена Вудинга

Последнее обновление: 23 ноября 2022 г.

Содержание:

• Что такое тор?
• Как пользоваться калькулятором площади поверхности тора?
• Пример: Как рассчитать площадь поверхности тора?
• Часто задаваемые вопросы

Этот калькулятор площади поверхности тора поможет вам оценить площадь поверхности тора для заданной пары радиусов. Вы наверняка встречали эту форму в повседневной жизни на своей тарелке в виде пончика или рогалика, или на дорогах под автомобилями 😉. Спасательная трубка или кольцо, также известное как спасательный буй , тоже тор. Тор также имеет значение в математике и физике. Читайте дальше, чтобы понять, что такое тор и как вычислить площадь поверхности тора.

Что такое тор?

Тор — это трехмерная фигура, полученная путем вращения окружности вокруг оси. Эта форма обычно встречается в пончиках, кольцах, шинах, трубах. Если вы возьмете кольцо и обведете его вокруг карандаша , вы получите тор. В современном программном обеспечении для проектирования их довольно легко нарисовать, используя команду вращения с кругом в качестве поперечного сечения. Тор имеет два радиуса – первый радиус равен радиусу поперечного сечения r , а второй радиус R — это радиус вращения, который представляет собой расстояние между центральной осью и центром поперечного сечения.

Любая точка на торе определяется с помощью модифицированной системы координат, имеющей два направления – тороидальное (красная стрелка) и полоидальное (зеленая стрелка) .

Направления тора

На основе комбинаций двух радиусов мы можем получить несколько типов торов . Такой, что:

• Кольцевого типа ( R > r )
• Рупорный тип ( R = r )
• Тип шпинделя ( R < r )

В дополнение к этим радиусам тор также может быть выражен в виде двух радиусов, таких как внутренний (a) и внешний (b) радиусы тора. Математически это:

a = R - r
b = R + r

Площадь поверхности A указанного тора:
A = 4 * π² 59 площадь также можно записать через внутренний и внешний радиусы:
A = π² * ( b - a ) * (b + a)
Приведенное выше уравнение используется в калькуляторе для определения площади поверхности, где:
r = (b - a) / 2
R = (a + b) / 2

Примечание. Этот калькулятор применим только к торам кольцевого или рогового типа. Кроме того, в случае тора рогового типа, т. е. R = r , малый радиус a становится равным нулю.

Как пользоваться калькулятором площади поверхности тора?

Выполните три простых шага, чтобы узнать площадь поверхности тора.

• Шаг 1: Введите внутренний радиус тора, a .
• Шаг 2: Введите внешний радиус тора, b .
• Шаг 3: Калькулятор теперь будет использовать приведенную выше формулу для вычисления площади поверхности тора.

Пример: Как рассчитать площадь поверхности тора?

Найти площадь поверхности рогового тора с радиусом поперечного сечения r = 1 м .
Примечание: тор рогового типа, т. е. р = р .

Давайте сначала преобразуем радиусы во внутренний и внешний радиус, a и b .

a = R - r = 0 м
b = R + r = 1 м

• Шаг 1: Введите внутренний радиус тора, a = 0 м .
• Шаг 2: Введите внешний радиус тора, b = 1 м .
• Шаг 3: Калькулятор площади поверхности тора теперь возвращает:

V = π² * ( b - a ) * (b + a)
V = π² * (1 - 0) * (1 + 0) = 9,87 м²
Площадь поверхности тора 9,87 м² . Вас также может заинтересовать определение объема тора.

Часто задаваемые вопросы

Что такое тор?

Тор представляет собой трехмерную круглую форму с кругом в качестве поперечного сечения. Форма обычно встречается в пончиках, шинах и обручах. Форма получается, когда вы вращаете круг по круговой траектории вдоль оси, нормальной к кругу.

Как образуется тор?

Полноторный тор образуется, когда вы проводите окружность по другой окружности на плоскости без самопересечения.

Что такое уравнение тора?

Уравнение тора: (R - √(x² + y²))² + z² = r꜀². Точка (x, y, z) на торе может быть представлена ​​с помощью уравнения.

Как вычислить площадь поверхности тора?

Площадь поверхности тора вычисляется путем умножения длины окружности поперечного сечения на длину окружности кольца. Объем = 2 × π × r꜀ × 2 × π × R.

Рахул Дхари

Внутренний радиус (a)

Внешний радиус (b)

Радиус трубы (r)

Радиус вращения (R)

Площадь поверхности

Ваш тор рогового типа.

Ознакомьтесь с 21 похожим калькулятором 3D-геометрии 📦

Площадь полушарияКубКуб Рассчитать: найти v, a, d… Еще 18

Что такое кольцевая диаграмма?

Кольцевая диаграмма в своей простейшей форме представляет собой круговую диаграмму с вырезанным центром, похожим на пончик. На первый взгляд может показаться, что это не служит гораздо большей цели, чем создание эстетического разнообразия. Однако кольцевая диаграмма помогает избежать путаницы с параметром площади, которая часто сбивает людей с толку на круговой диаграмме.

Глядя на круговую диаграмму, легко спутать область каждого слайда со всем кругом и делать выводы на основе этой визуальной подсказки. Вместо этого в кольцевой диаграмме центр удален, что побуждает читателя вместо этого сосредоточиться на длине дуги, а не сравнивать ее с общей площадью, которую представляет круг.

Другим визуальным преимуществом кольцевой диаграммы является то, что пространство внутри кольцевой диаграммы можно использовать для представления данных, меток и т. д., что упрощает чтение диаграммы.

Каждый фрагмент кольцевой диаграммы представляет разные фрагменты данных, часто для облегчения понимания они имеют цветовую кодировку.

Зачем использовать кольцевую диаграмму?

В большинстве случаев кольцевая диаграмма может заменить круговую диаграмму, так как варианты их использования не сильно отличаются. Кольцевая диаграмма обычно показывает пропорции категориальных данных, где размер каждой части пончика сообщает долю каждой категории.

Простейшим примером может быть расширение элементарной математической задачи. Предполагая, что у нас есть двадцать яблок, десять бананов, пятнадцать апельсинов и семь ананасов, доля каких фруктов в корзине наибольшая? Пончик с самой длинной дугой представляет собой фрукт, который присутствует, как это бывает, в изобилии.

Но сказать, что кольцевая диаграмма используется только в этом случае, было бы слишком упрощенно. В целом, кольцевая диаграмма занимает гораздо меньше места, чем круговая диаграмма, что делает ее идеальной для размещения на информационных панелях, которые уже содержат много информации для обработки, а также в бизнес-отчетах, где данные необходимо визуализировать одновременно, чтобы получить наилучшие результаты. идеи.

Например, кольцевую диаграмму продаж электроники для компании в 2020 году можно поместить внутрь кольцевой диаграммы продаж электроники в 2021 году. Это позволяет разместить таблицу данных рядом с диаграммой и передать больше информации, чем было бы можно, поместив две диаграммы рядом друг с другом и соответствующую им таблицу данных под ними.

Как превратить данные в кольцевую диаграмму

Кольцевая диаграмма работает в двух измерениях, поэтому для нее требуются два набора информации с общими отношениями. Первое измерение представляет атрибут, а второе — его значение. Например, в кольцевой диаграмме электронных продаж количество проданных телевизоров является измерением, а число (например, триста) — его значением.

Оба измерения важны, потому что они связаны между собой. Для тех, кто читает кольцевую диаграмму продаж электроники, полезно знать, сколько товаров было продано по разным категориям. Кроме того, сравнение с кольцевыми диаграммами других лет также помогает им увидеть, значительно ли изменились продажи товаров.

Один из наиболее частых вопросов, возникающих в связи с кольцевой диаграммой, заключается в том, должны ли значения в необработанных данных составлять в сумме 100 процентов. Простой ответ - да. Кольцевую диаграмму лучше всего использовать для представления частей целого, но ее не следует путать с суммированием до сотни. Любое значение, даже если оно достигает нескольких миллионов, может быть представлено в виде кольцевой диаграммы, если все значения в сумме представляют части целого или 100 процентов.

В большинстве программных продуктов кольцевую диаграмму можно создать, выделив всю таблицу данных и выбрав вариант кольцевой диаграммы. После этого значения обычно располагаются от самого высокого (самая длинная дуга) до самого низкого (самая короткая дуга) сверху по часовой стрелке. Однако этот параметр часто является гибким, и создатель диаграммы может изменить порядок этих сегментов.

Преимущества использования кольцевой диаграммы

Кольцевая диаграмма — это одно из самых простых представлений данных, которое также широко известно. При представлении информации большим и разнообразным группам людей круговая диаграмма часто является лучшим вариантом, если представляемые данные представляют собой целый набор с несколькими различными частями внутри.

В отчетах о продажах кольцевую диаграмму можно использовать для изучения количества открытых, упущенных или выигранных возможностей, а полученный доход можно представить в виде кольцевой диаграммы. Это позволяет лицам, принимающим решения, увидеть, вносят ли выигранные лиды достаточный вклад в итоговую прибыль, или потерянные лиды обходятся слишком дорого, чтобы их терять.

В дополнение к этой функциональности кольцевая диаграмма может быть динамической. Любое изменение значений данных может изменить внешний вид кольцевой диаграммы, что может быть полезно при прогнозировании.

Кольцевые диаграммы можно рисовать разных размеров и цветов, помещать друг в друга и маркировать в области диаграммы для экономии места, что делает их более интерактивными и предоставляет читателям доступ к более подробным данным.

Кольцевые диаграммы считаются одной из самых удобных форм представления данных. Сегменты кольцевой диаграммы можно выделить, сделав их толще, чтобы представить более важные сегменты. Некоторые программные продукты также автоматически рассчитывают процентные доли сегментов при использовании кольцевой диаграммы.

Проще говоря, те, кто плохо знаком с информационными панелями и отчетами, могут использовать кольцевую диаграмму с такой же легкостью и скоростью, как и их более опытные коллеги, и при этом получать правильные выводы.

Проблемы при использовании кольцевой диаграммы

Как и в большинстве других форм представления данных, кольцевая диаграмма может быть загромождена слишком большим количеством сегментов. Если имеется слишком много сегментов для представления, и каждый из них занимает лишь небольшую часть общих данных, сегменты могут быть трудночитаемыми.

Кольцевая диаграмма — не лучший формат для представления отрицательных значений. Например, задолженность может быть представлена ​​на кольцевой диаграмме финансового планирования только как часть целого, а не с точки зрения ее влияния на общий денежный поток.

Кроме того, хотя кольцевая диаграмма отлично подходит для сравнения данных, анализ с использованием только кольцевой диаграммы часто затруднен, поскольку визуальные подсказки являются единственным средством чтения диаграммы. Однако эту проблему можно решить, вставив метки процентов рядом с каждым сегментом диаграммы.

Если необходимо отслеживать изменения с течением времени, кольцевая диаграмма — не лучший вариант для использования, поскольку в отличие от средства отслеживания пузырьковой диаграммы она не может сохранять информацию, которую представляет, в течение определенного периода времени.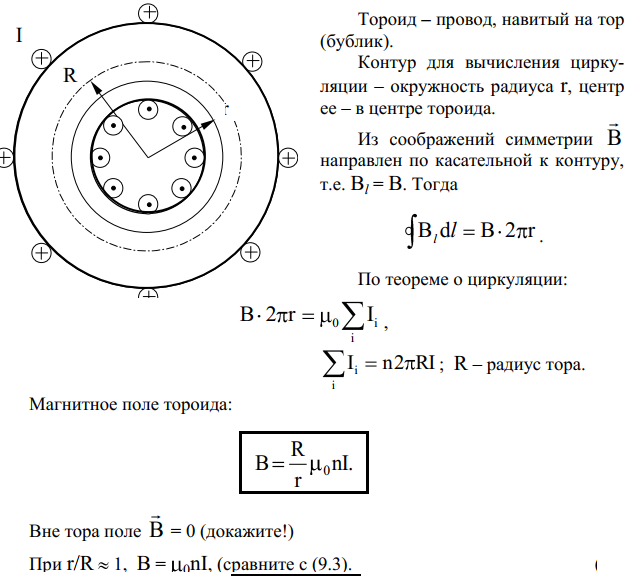 Например, кольцевая диаграмма годовых расходов продолжает изменяться по мере внесения корректировок в ее источник данных без сохранения какой-либо информации, существовавшей до внесения изменений. В результате читатель не может увидеть, как расходы выросли с течением времени.

Альтернативы кольцевым диаграммам

Круговая диаграмма может заменить кольцевую диаграмму почти во всех приложениях, где особое преимущество кольцевой диаграммы — сравнение областей как абсолютных величин — не является обязательным.

Помимо круговой диаграммы, данные на кольцевой диаграмме также могут быть представлены в виде других типов графиков:

Процентная гистограмма

Это служит почти той же цели, что и кольцевая диаграмма. Однако его также можно использовать при ограниченном пространстве или когда сумма всех сегментов не составляет 100 процентов. Например, гистограмму в процентах можно использовать для сравнения выбросов парниковых газов в 2010 г. с выбросами в 2020 г.