Площадь четырехугольника онлайн калькулятор по четырем сторонам: Площадь четырехугольника по четырем сторонам и двум противолежащим углам

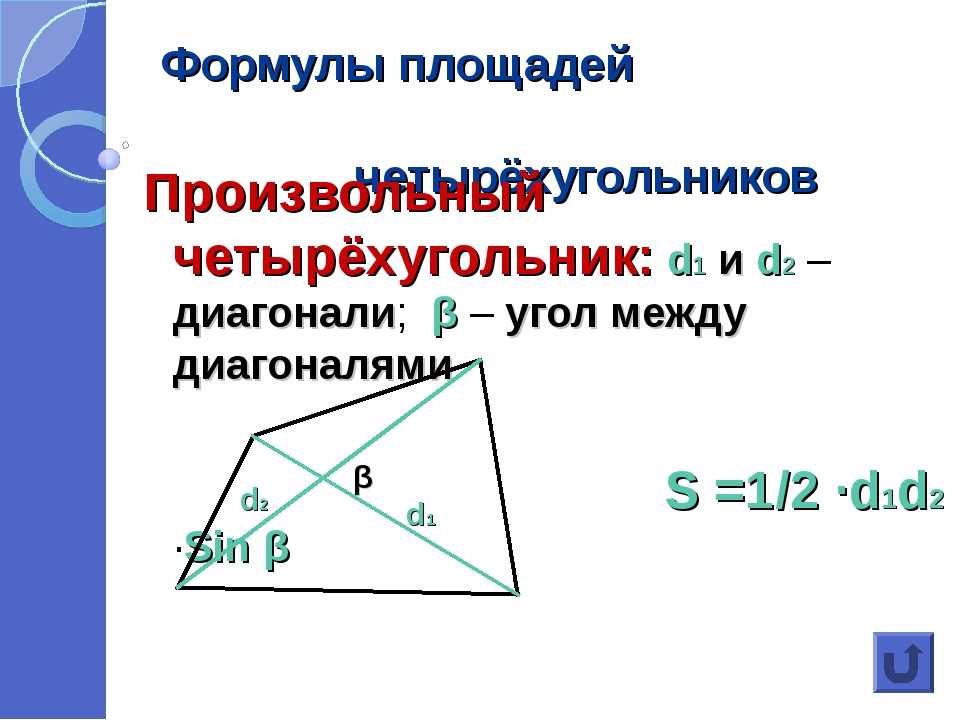
Площадь прямоугольника калькулятор онлайн

Категория: Калькуляторы

– Автор: Игорь (Администратор)

С помощью данного бесплатного онлайн калькулятора вы сможете рассчитать площадь прямоугольника разными методами. Преимуществом сервиса является то, что расчет осуществляется автоматически. Просто вводите значения в соответствующие поля.

 

1. Площадь прямоугольника, зная две стороны

Сторона (a)

Сторона (b)

 

Площадь прямоугольника 0.000

 

 

2. Площадь прямоугольника, зная периметр и одну из сторон

Периметр (P)

Сторона (a)

 

Площадь прямоугольника 0.000

 

 

3. Площадь прямоугольника, зная диагональ и одну из сторон

Диагональ (d)

Сторона (a)

 

Площадь прямоугольника 0. 000

 

 

4. Площадь прямоугольника, зная диагональ и угол между диагоналями

Диагональ (d)

Угол (A)

 

Площадь прямоугольника 0.000

 

 

5. Площадь прямоугольника, зная сторону и радиус описанной окружности

Сторона (a)

Радиус (R)

 

Площадь прямоугольника 0.000

 

 

6. Площадь прямоугольника, зная сторону и диаметр описанной окружности

Сторона (a)

Диаметр (D)

 

Площадь прямоугольника 0.000

 

 

Округлять до знаков после запятой (от 0 до 10)

 

Прямоугольник — это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.

Как самостоятельно узнать площадь прямоугольника?

Для вычисления площади прямоугольника можно воспользоваться следующими формулами:

1. Зная две стороны:

Площадь прямоугольника (S) = Сторона (a) * Сторона (b) = a * b

2. Зная периметр и одну из сторон:

Площадь прямоугольника (S) = 1/2 * ( Периметр (P) * Сторона (а) — 2 * Сторона (a)² ) = 1/2 * ( P * a — 2 * a² )

3. Зная диагональ и одну из сторон:

Площадь прямоугольника (S) = Сторона (a) * КОРЕНЬ ( Диагональ (d)² — Сторона (a)² ) = a * √ ( d² — a² )

4. Зная диагональ и угол между диагоналями:

Площадь прямоугольника (S) = 1/2 * Диагональ (d)² * sin ( Угол (A) ) = 1/2 * d² * sin(A)

5. Зная сторону и радиус описанной окружности:

Площадь прямоугольника (S) = Сторона (a) * КОРЕНЬ ( 4 * Радиус (R)² — Сторона (a)² ) = a * √ ( 4 * R² — a² )

6. Зная сторону и диаметр описанной окружности:

Площадь прямоугольника (S) = Сторона (a) * КОРЕНЬ ( Диаметр (D)² — Сторона (a)² ) = a * √ ( D² — a² )

Теперь, у вас всегда есть под рукой удобный и легкий калькулятор для расчетов.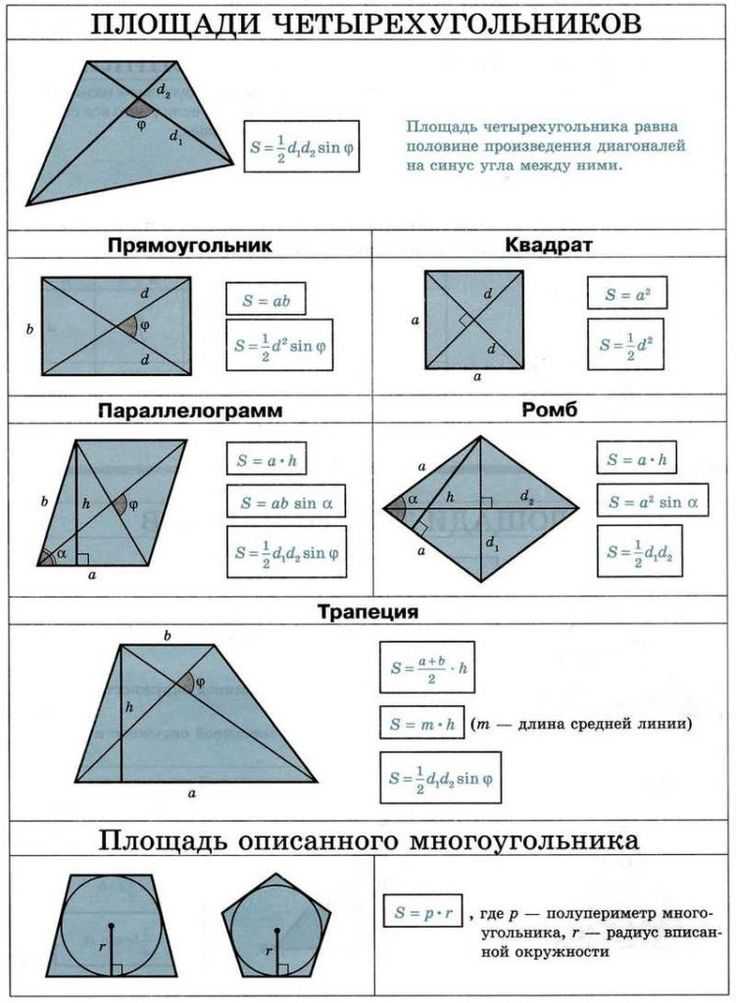

Понравилась заметка? Тогда время подписываться в социальных сетях и делать репосты!

☕ Понравился обзор? Поделитесь с друзьями!

• Площадь ромба калькулятор онлайн
• Площадь параллелограмма калькулятор онлайн

Добавить комментарий / отзыв

Калькулятор площади треугольника онлайн

Предлагаем простой и удобный калькулятор для расчета площади треугольника в режиме онлайн. Он может оказаться полезным не только для школьников, изучающих базовый курс геометрии, но и для строителей, дизайнеров, архитекторов и многих других специалистов, чья работа так или иначе связана с проектированием и изготовлением различных инженерных конструкций. Вы можете посчитать площадь произвольного треугольника, зная основные размеры, однозначно определяющие его конфигурацию.

Формула расчета площади треугольника по стороне и высоте, проведенной из противолежащей вершины

Зная длину одной из сторон треугольника (основания) и высоту, проведенную к этой стороне, его площадь можно посчитать, перемножив эти величины друг на друга и разделив результат на 2. То есть площадь треугольника — это полупроизведение основания на высоту. Это наиболее известная формула, она применима к любым треугольникам.

Площадь треугольника по трем сторонам, формула Герона

Одна из самых полезных на практике формул, незаслуженно обойденная вниманием во многих популярных источниках. Она позволяет рассчитать площадь треугольника, зная длины трех его сторон. В реальных условиях очень часто трудно провести измерения углов или каких-то линейных размеров конструкций, требующие дополнительных геометрических построений. Что же касается сторон, то они, как правило, или известны, или относительно легко поддаются измерению, поэтому площадь треугольника во многих случаях рассчитывают именно этим способом.

Для определения площади необходимо рассчитать полупериметр треугольника — сумму его сторон, деленную на 2. Далее из него поочередно вычитают длину каждой стороны, а результаты перемножают. Затем полученное значение умножают на полупериметр и из итогового числа извлекают квадратный корень. Это довольно сложный расчет, но с помощью нашего калькулятора вы проделаете его всего за несколько мгновений, введя длины сторон треугольника в предназначенные для этого поля.

Как рассчитать площадь треугольника, если известны две стороны и угол между ними

Эта формула также имеет широкое практическое применение. Например, с ее помощью можно посчитать площадь треугольного фронтона в доме с двускатной крышей. Угол наклона скатов и их длины обычно известны, их достаточно подставить в формулу и получить результат. Наш онлайн-калькулятор сделает это для вас моментально. Алгоритм расчета следующий: площадь треугольника вычисляется как половина произведения длин известных сторон на синус угла, который находится между ними.

Формула площади треугольника по его известной стороне и двум прилежащим углам

Наш калькулятор посчитает площадь треугольника и по этим параметрам. В расчете применяется довольно громоздкая формула, использовать которую при ручном подсчете довольно затруднительно. Поэтому, если вы знаете только эти характеристики треугольника, открывайте нужную вкладку и вводите значения в соответствующие поля калькулятора. Это поможет вам сэкономить время и избежать ошибок, исправлять которые будет сложно и дорого.

Как найти площадь треугольника по его периметру и радиусу вписанной окружности

Если вы знаете длины всех сторон треугольника, лучше использовать приведенную выше формулу Герона. Но если известен только полный периметр (сумма сторон, а не длины каждой из них по отдельности), площадь можно рассчитать как произведение радиуса вписанной окружности на половину периметра. Дизайнеры и проектировщики довольно часто помещают в треугольные фигуры круглые детали, при этом радиусы окружностей обычно бывают известны.

Формула площади произвольного треугольника по трем сторонам и радиусу описанной окружности

Радиус описанной окружности — избыточный параметр. Если длины всех трех сторон треугольника известны, его площадь определяется по формуле Герона. Тем не менее есть возможность несколько упростить расчет: нужно перемножить длины сторон друг на друга и разделить результат на учетверенный радиус описанной окружности. Наш онлайн-калькулятор при необходимости вычисляет площадь фигуры и по этой формуле.

Расчет площади прямоугольного треугольника

Прямоугольный треугольник — это частный случай произвольной треугольной фигуры, один из его углов равен 90°. Для вычисления его площади можно применять любую из приведенных выше формул, при этом многие из них заметно упрощаются. Например, синус прямого угла равен единице, поэтому площадь такого треугольника будет равна полупроизведению прилежащих сторон, которые называются катетами. Радиус описанной окружности для любого прямоугольного треугольника равен половине длины третьей стороны — гипотенузы, так что соответствующая формула также сводится к полупроизведению катетов. Если известен другой параметр — радиус вписанной окружности r, то площадь равна r · (r + c), где c — длина гипотенузы.

Площадь равнобедренного треугольника

В математике треугольник, две стороны которого равны, называется равнобедренным. Третья сторона при этом называется основанием, кроме того, известно, что углы при этом основании равны. Если боковые стороны обозначить буквой b, а находящийся между ними угол — α, то площадь будет равна ½ · b² · sin (α). Это частный случай формулы расчета площади произвольного треугольника по двум известным сторонам и углу между ними. Наш калькулятор использует именно ее.

Формулы для равностороннего треугольника

Если у треугольника все стороны равны, вычисление его площади еще больше упрощается. Достаточно знать длину стороны a или измерить радиус вписанной окружности r. Калькулятор использует одну из следующих формул:

• S = √3 / 4 · a²;
• S = 3√3 · r².

В основе расчета площади треугольника во всех случаях лежит довольно простая математика. Но при этом часто требуется вычислять тригонометрические функции, радикалы и произведения больших чисел. Поэтому самое простое решение — снять все необходимые размеры и воспользоваться нашим калькулятором. Это быстро, точно и бесплатно. Никаких ограничений на количество расчетов и требований по авторизации у нас нет. Если у вас появятся вопросы, вы можете задать их в комментариях.

Калькулятор четырехугольника — Найдите площадь четырехугольника

Калькулятор четырехугольника

Хотите узнать площадь вашей четырехугольной комнаты для меблировки?   Или даже если вам нужно решить задачи по геометрии к следующему уроку, воспользуйтесь этим четырехугольником.

Этот онлайн-инструмент поможет вам с легкостью вычислить площадь четырехугольника. Не имеет значения, если вы не знаете, с каким типом четырехугольника вы имеете дело. Просто заполните необходимые поля, и он рассчитает площадь вашего четырехугольника.

Вам интересно узнать о четырехугольниках? Потому что мы собираемся объяснить, как найти площадь четырехугольника с помощью нашего калькулятора, определение четырехугольника и его виды, формулу площади четырехугольника, и как вы можете вычислить площадь четырехугольника самостоятельно.

Как пользоваться калькулятором четырехугольника?

Используя приведенный выше калькулятор неправильного четырехугольника, вы можете легко узнать площадь четырехугольника без каких-либо усилий. Это экономит ваше время и помогает вам в вычислении площади четырехугольника.

Чтобы использовать этот калькулятор, выполните следующие действия:

• Выберите вариант, для которого вы хотите рассчитать четырехугольник.
• Выберите набор заданных параметров.
• Введите указанные значения в соответствующие поля ввода.
• Нажмите кнопку «Рассчитать   », чтобы получить результат расчета.

Он мгновенно вычисляет площадь, а также предоставляет формулу для каждого шага расчета. Таким образом, он не только вычисляет площадь, но и помогает подготовить тему к уроку или экзамену.

Что такое четырехугольник?

В евклидовой плоской геометрии четырехугольник — это многоугольник с четырьмя сторонами или ребрами и четырьмя углами или вершинами. Википедия.

Или четырехугольник можно определить просто как:

В геометрии четырехугольник можно определить как двумерную замкнутую форму с четырьмя прямыми сторонами.

Свойства четырехугольника

Ниже приведены свойства четырехугольника.

• Сумма всех внутренних углов четырехугольника равна 360°.
• Четырехугольник имеет 4 вершины, 4 угла и 4 стороны.
• Четырехугольник может быть правильным или неправильным.

Какие существуют типы четырехугольников?

В геометрии существует несколько типов четырехугольников. Некоторые из них перечислены ниже в таблице с картинками.

Название четырехугольника:	Изображение четырехугольника:	Свойства четырехугольника:
Параллелограмм	Противоположные стороны параллельны.  Противоположные стороны равны.  Противоположные углы равны.
Воздушный змей	Соседние стороны равны. Пара диагонально противоположных углов равны. Диагонали пересекаются под углом 90°.
Квадрат	Все стороны равны.  Все углы равны 90°.
Равнобедренная трапеция	Оба основания параллельны. Противоположные стороны равны. Углы равны.
Прямоугольник	Противоположные стороны параллельны.  Противоположные стороны равны.  Все углы равны и равны 90°.
Ромб	Все стороны равны.  Противоположные углы равны.
Трапеция	Противоположные стороны параллельны. Смежные углы в сумме дают 180°.

Все вышеперечисленные формы, которые мы видим в нашей повседневной жизни, являются четырехугольными. Вам может быть интересно узнать, как вычислить площадь любого из вышеперечисленных четырехугольников. Не волнуйся! Мы вас прикрыли.

У нас есть калькулятор площади прямоугольника, калькулятор площади ромба, калькулятор площади трапеции, калькулятор площади параллелограмма, калькулятор площади воздушного змея или калькулятор квадрата, если вы хотите вычислить площадь определенного четырехугольника.

Формула четырехугольника

Площадь формулы четырехугольника можно разделить на три категории на основе заданных значений. Ниже вы можете найти три разные формулы для вычисления площади четырехугольника.

1. Если даны диагонали и угол между ними

Если даны диагонали и угол между этими диагоналями, формула площади четырехугольника для этого случая может быть выражена как:

Площадь = \(p \times q \times \sin(angle)\)

Где:

p и q представляют диагонали.

2. Если известны бимедианы и угол между ними

Если известны бимедианы и угол между ними, площадь четырехугольника можно вычислить по следующей формуле:

Площадь = \(м \умножить на n \умножить на \sin(угол)\)

Где:

м и n представляют бимедианы.

Примечание. Бимедианы   — это линии, соединяющие центры противоположных сторон.

3. Если известны два противоположных угла и четыре стороны

Если известны два противоположных угла и четыре стороны, площадь четырехугольника можно вычислить по формуле Бретшнейдера.

Площадь = \(√[(s - a) \times (s - b) \times (s - c) \times (s - d) - a \times b \times c \times d \times cos2 ( 0,5 \раз (угол1 + угол2))]\)

Где:

a, b, c,  и d  представляют стороны четырехугольника,

s  представляет выражение ( + 0 2 c)0 ad (ad )   , который является полупериметром, угол 1 и угол 2 представляют собой два противоположных угла четырехугольника.

Как найти площадь четырехугольника?

Площадь четырехугольника можно рассчитать по любой из приведенных выше формул в зависимости от заданных значений. Возможно, вы захотите измерить площадь своего заднего двора или газона и столкнуться с трудностями, чтобы правильно составить уравнения. Ну, вы всегда можете использовать наш калькулятор выше для этой цели.

Здесь мы пройдем весь процесс вычисления площади четырехугольника. Выполните следующие шаги, чтобы найти площадь четырехугольника:

• Запишите данные значения.
• Запишите соответствующую формулу сверху.
• Подставьте значения в формулу и рассчитайте площадь вашего четырехугольника.

Пример:

Вычислите площадь четырехугольника, две стороны которого равны 6 см и 4 см соответственно при угле 30°?

Решение:

Шаг 1:  Запишите указанные значения.

p = 6 см, q = 4 см, угол = 30°

Шаг 2:  Запишите соответствующую формулу, приведенную выше.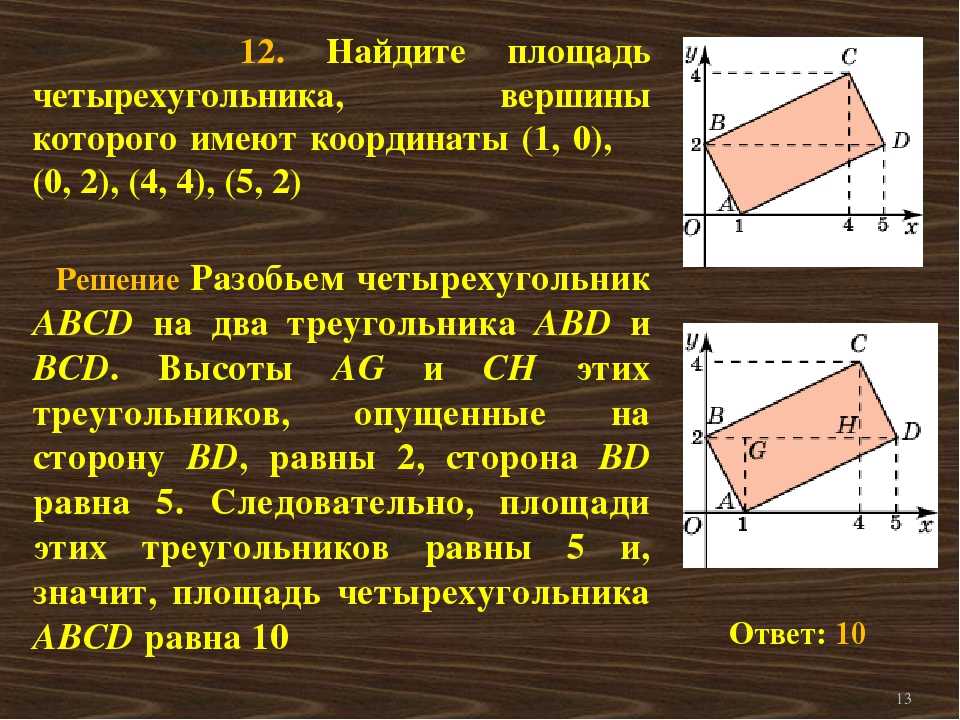

Площадь = \(p \times q \times \sin(angle)\)

Шаг 3:  Подставьте значения в формулу и рассчитайте площадь вашего четырехугольника.

Площадь = \(6 \умножить на 4 \умножить на \sin (30°)\)

Площадь =

\)

Итак, четырехугольник со сторонами 6 см и 4 см и углом 30°   будет иметь площадь 12 см ² .

Часто задаваемые вопросы

Какова формула площади четырехугольника ABCD?

Площадь четырехугольника ABCD можно представить как:

Площадь четырехугольника ABCD= ½ d (h ₁ +h ₂ )

Какова формула площади четырехугольника?

Ниже приведены формулы четырехугольника.

1. Если даны диагонали и углы

Площадь = \(p \times q \times \sin(angle)\)

p  и q  являются диагоналями.

2. Когда бимедианы и углы заданы

3. Когда даны противоположные углы и все стороны

Площадь = \(√[(s - a) \times (s - b) \times (s - c) \times (s - d) - a \ умножить на b \раз c \раз d \раз cos2 (0,5 \раз (угол1 + угол2))]\)

a, b, c,  и d  являются сторонами четырехугольника, угол 1 и угол 2 представляют собой два противоположных угла четырехугольника, а s  представляет выражение (0,5 × c + (a) )   , что является полупериметром.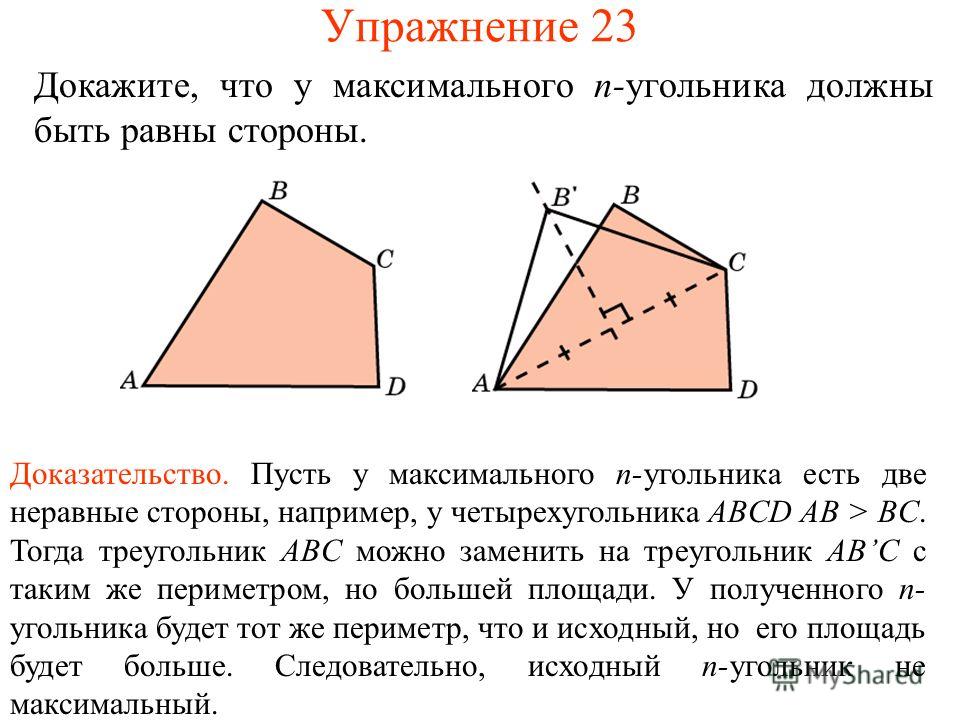

Как найти площадь неправильного четырехугольника?

Выполните следующие действия, чтобы вычислить площадь неправильного четырехугольника.

• Разделите неправильный четырехугольник на два треугольника, проведя диагональ.
• Вычислите площадь треугольника, угол которого известен.
• Найдите длину диагонали по закону косинусов.
• Найдите площадь второго треугольника по формуле Герона.
• Теперь добавьте площади обоих треугольников, что даст вам площадь неправильного четырехугольника.

Каковы периметр и площадь четырехугольника?

Здесь площадь и периметр различных четырехугольников.

92 \)	\ (l \ times h \)	\ (½ \ Times D1 \ Times D2 \)	\ (½ times (Сум. ) \times height\)
Perimeter	\(2 \times (l + b)\)	\(4a\)	\(2 \раз (l + b)\)	\(4a\)	Сумма всех сторон

Какой пример неправильного четырехугольника?

Неправильный четырехугольник состоит из неравных сторон. Некоторые примеры неправильных четырехугольников:

• Прямоугольник
• Параллелограмм
• Воздушный змей
• Ромб
• Трапеция

Этот документ был составлен с помощью бесплатного конвертера HTML. Нажмите здесь, чтобы попробовать.

Включите JavaScript для просмотра комментариев с помощью Disqus.

Калькулятор площади неправильного четырехугольника | Найдите площадь четырехугольника?

Площадь неправильного четырехугольника Калькулятор: Вам нужна помощь при решении задач по геометрии любого класса? Тогда вы находитесь в правильном месте. На этой странице представлена ​​полная информация о площади неправильного четырехугольника. Вы можете получить информацию о том, что подразумевается под неправильным четырехугольником, формулу для расчета площади и простую процедуру для решения вопросов о неправильном четырехугольнике.

Выбрать Площадь неправильного четырехугольника Площадь неправильного четырехугольника

Диагональ (е) сммкминмийдфтмм

Диагональ (f) сммкминмийдфтмм

Угол α градусы радиан

Вот некоторые примеры расчетов площади неправильного четырехугольника

Площадь неправильного четырехугольника диагональ-e 27 см диагональ-f 22 см с углом 2,4 радиана

Площадь неправильного четырехугольника, диагональ e 29 см, диагональ f 68 см, угол 96 градусов

Площадь неправильного четырехугольника диагональ-e 75 футов, диагональ-f 58 футов с углом 0,7 радиана

Площадь неправильного четырехугольника диагональ-e 28 футов, диагональ-f 75 футов с углом 104 градуса

Площадь неправильного четырехугольника диагональ-e 87 дюймов, диагональ-f 30 дюймов с углом 85 градусов

Площадь неправильного четырехугольника диагональ-e 74 дюйма, диагональ-f 50 дюймов с углом 2,1 радиана

Площадь неправильного четырехугольника диагональ-e 82 м, диагональ-f 99 м с углом 2,5 радиана

Площадь неправильного четырехугольника диагональ-e 84 м, диагональ-f 98 м с углом 1,9 радиана

Площадь неправильного четырехугольника диагональ-e 87 ярдов по диагонали-f 68 ярдов с углом 138 градусов

Площадь неправильного четырехугольника с диагональю e 92 ярда по диагонали-f 45 ярдов под углом 122 градуса

Площадь неправильного четырехугольника диагональ-e 9 ярдов по диагонали-f 7 футов с углом 2,4 радиана

Площадь неправильного четырехугольника, диагональ-e 2 фута, диагональ-f 5 м с углом 96 градусов

Площадь неправильного четырехугольника, диагональ-e, диагональ 4 м, f, 3 фута, угол 0,7 радиана

Площадь неправильного четырехугольника по диагонали-e 5 ярдов по диагонали-f 2 см с углом 104 градуса

Площадь неправильного четырехугольника диагональ-e 7 м диагональ-f 6 см с углом 85 градусов

Площадь неправильного четырехугольника, диагональ-e, диагональ 6 м, f, 8 ярдов, угол 2,1 радиан

Площадь неправильного четырехугольника диагональ-e 8 ярдов по диагонали-f 4 м с углом 2,5 радиана

Площадь неправильного четырехугольника по диагонали-e 3 фута по диагонали-f 9 м с углом 1,9 радиан

Площадь неправильного четырехугольника по диагонали-e 3 дюйма по диагонали-f 27 футов с углом 138 градусов

Площадь неправильного четырехугольника, диагональ-e, диагональ 2 м, f, 29 футов, угол 122 градуса

Площадь неправильного четырехугольника по диагонали-e 6 футов по диагонали-f 75 см с углом 1,4 радиана

Площадь неправильного четырехугольника, диагональ-e, диагональ 4 м, f, 28 ярдов, угол 158 градусов

Площадь неправильного четырехугольника с диагональю e 9yd диагональ-f 87 см с углом 2,2 радиана

Площадь неправильного четырехугольника, диагональ-e, диагональ 8 футов, f, 74 дюйма, угол 2,3 радиана

Площадь неправильного четырехугольника диагональ-e диагональ 5 см-f 82 ярда с углом 1,1 радиана

Площадь неправильного четырехугольника, диагональ-e 7 дюймов, диагональ-f 84 см с углом 159 градусов

Площадь неправильного четырехугольника по диагонали-e 4 см по диагонали-f 87 дюймов с углом 47 градусов

Площадь неправильного четырехугольника диагональ-e диагональ 5 см-f 92 ярда с углом 3,1 радиана

Площадь неправильного четырехугольника, диагональ-e 7 дюймов, диагональ-f 22 фута с углом 118 градусов

Площадь неправильного четырехугольника, диагональ-e, диагональ 6 см, f, 68 ярдов, угол 18 градусов

Площадь неправильного четырехугольника по диагонали e 57 см по диагонали f 59 дюймов с углом 31 градус

Площадь неправильного четырехугольника диагональ-e 69 см, диагональ-f 67 м с углом 130 градусов

Площадь неправильного четырехугольника диагональ-e 30 дюймов, диагональ-f 29 м с углом 126 градусов

Площадь неправильного четырехугольника, диагональ-e, диагональ 16 м, f, 91 ярд, угол 0,8 радиана

Площадь неправильного четырехугольника с диагональю е 65 дюймов и диагональю f 43 м с углом 1,6 радиана

Площадь неправильного четырехугольника по диагонали-e 40 футов по диагонали-f 54 дюйма с углом 0,3 радиана

Площадь неправильного четырехугольника диагональ-e 61 фут, диагональ-f 65 м с углом 0,9 радиана

Площадь неправильного четырехугольника по диагонали-e 41 ярд по диагонали-f 78 см с углом 147 градусов

Площадь неправильного четырехугольника с диагональю e 66 дюймов, диагональю f 68 футов и углом 2,6 радиана

Площадь неправильного четырехугольника диагональ-e 16 м диагональ-f 84 см с углом 100 градусов

Используйте этот онлайн-инструмент, чтобы получить мгновенный результат.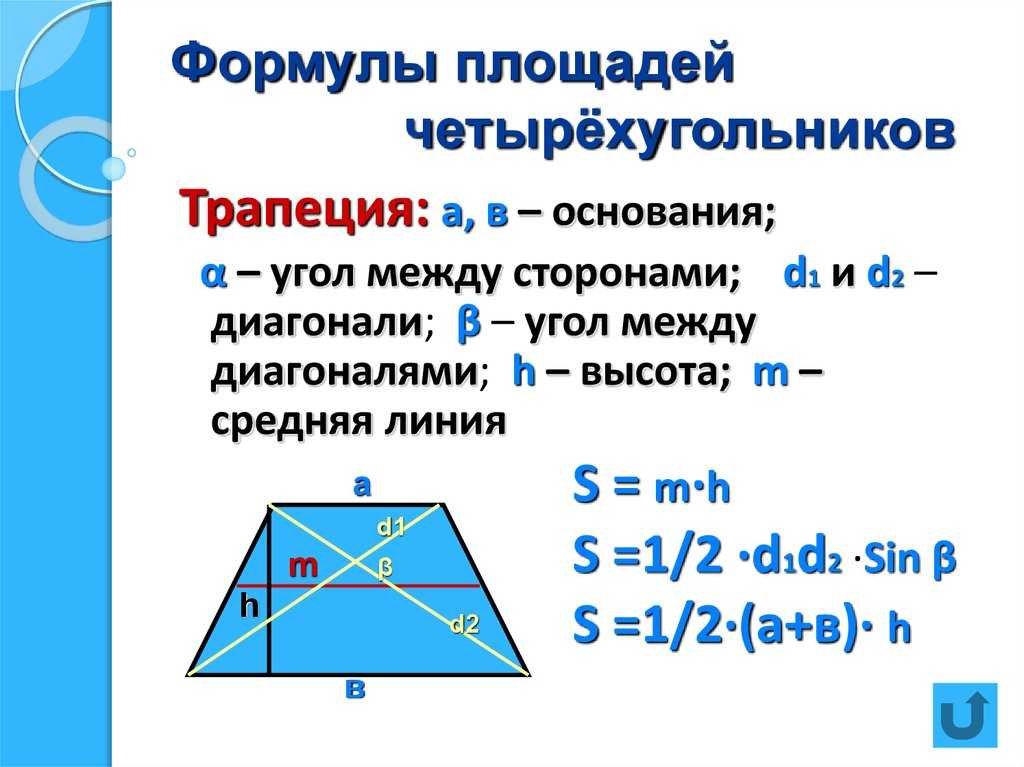

Введите длину двух диагоналей и угол между ними в полях ввода и нажмите кнопку расчета. Затем удобный калькулятор вычисляет площадь четырехугольника для заданных значений за доли секунды.

Мы приводим несколько важных формул, которые помогут вам найти площадь неправильного четырехугольника. Зная приведенные ниже формулы, вы без труда сможете решить любой вопрос.

1. Если даны диагонали четырехугольника и угол между ними,

Площадь = e * f * sin(α)

Где,

e, f — длины двух диагоналей неправильного четырехугольника.

α угол между углами.

2. Если даны четыре стороны и два противоположных угла, то 92(θ/2)]

Где,

a, b, c, d — стороны четырехугольника

s = (a + b + c + d) / 2, θ = θ ₁ + θ ₂

3. Если даны бимедианы и угол между ними,

Площадь = m * n * sin(θ)

Где,

m, n — бимедианы

r — угол между бимедианами

07 четырехугольник – это четырехугольник, у которого все стороны и углы не равны. Выполните следующие шаги и получите инструкции по вычислению площади неправильного четырехугольника. Воспользуйтесь любым из этих процессов и получите ответ.

Процесс 1:

• Сначала разделите четырехугольник на два треугольника, проведя диагональ, не нарушающую известный внутренний угол.
• Рассчитайте площадь каждого треугольника по формуле 1/2 * (основание) * (высота)
• Сложите площади этих двух треугольников, чтобы получить площадь четырехугольника.

Процесс 2:

• Из заданного вопроса обратите внимание на длины двух диагоналей и угол между ними.
• Найдите функцию синуса угла.
• Умножьте длины диагоналей и умножьте произведение на sin(угол).
• Полученное значение называется площадью неправильного четырехугольника.

Пример 1: Диагональ четырехугольника равна 42 см, а два перпендикуляра к нему из других вершин равны 8 см и 9 см соответственно. Найдите площадь четырехугольника?

Решение:

Учитывая, что

AC = 42 см

BN = 9 см

DM = 8 см

Площадь ABCD = площадь Δ 0 0 4 * 9 0 0 ACD 42 + ½ * 8 * 42

= 9 * 21 + 4 * 42

= 189 + 168 = 357

∴ Площадь четырехугольника 357 см²

Пример 2: Найдите площадь неправильного четырехугольника? Если длина диагоналей 10 см, то 15 см при угле 60 градусов.

Решение:

Учитывая, что

Длина диагонали e = 10 см, f = 15 см

Угол α = 60 градусов формула.

A = 10 * 15 * sin(60)

= 150 * (√3 / 2)

= 129,90

∴ Площадь четырехугольника составляет 129,90 см² для решения любых задач по геометрии. На нашем сайте вы получите бесплатные калькуляторы для любых тем по геометрии.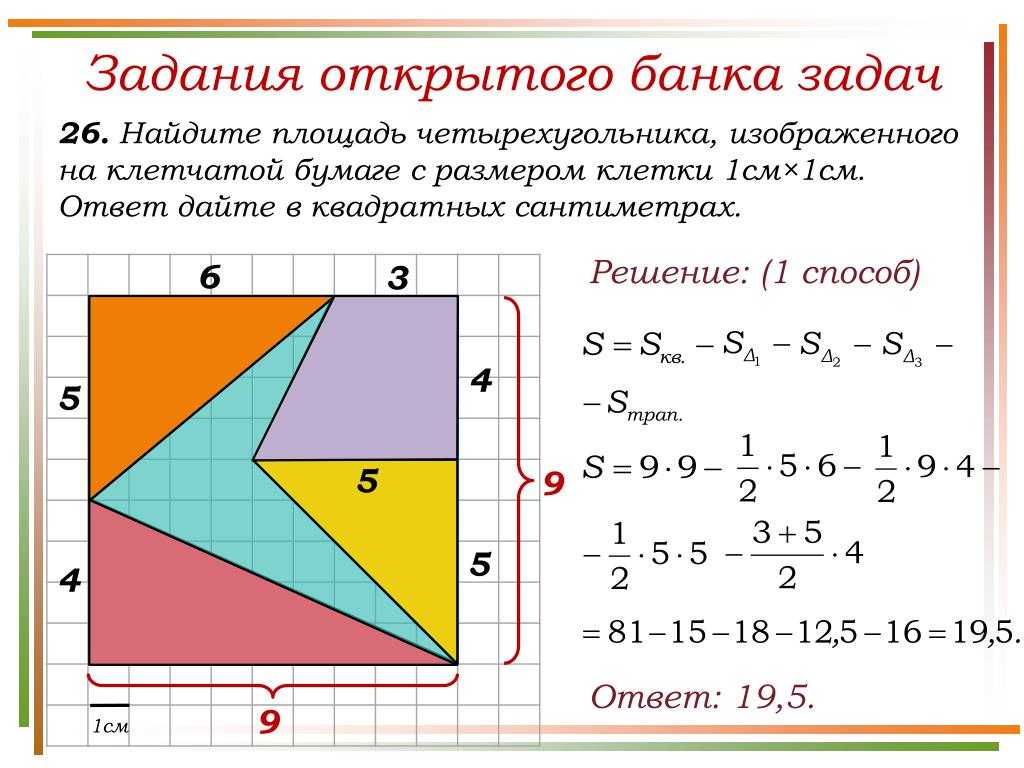

1. Чем отличается правильный четырехугольник от неправильного?

Четырехугольники бывают двух типов: правильные и неправильные. Правильный четырехугольник – это четырехугольник, у которого все стороны имеют одинаковую длину. Неправильный четырехугольник прямо противоположен правильному. Примерами правильного четырехугольника являются квадрат, пятиугольник и т. д. Примерами неправильного четырехугольника являются прямоугольник, воздушный змей, параллелограмм.

2. Как определить площадь неправильного четырехугольника?

Неправильный четырехугольник — это замкнутая фигура, имеющая четыре стороны и четыре угла. Длины всех сторон и углов неодинаковы. Чтобы найти площадь неправильного четырехугольника, необходимо знать либо длину всех сторон, либо диагонали и угол между диагоналями.

3. Какой пример неправильного четырехугольника?

Некоторыми неправильными четырехугольниками в реальном времени являются трапеция, прямоугольник, воздушный змей, ромб и параллелограмм.