Таблица синусов и косинусов полная: синусы и косинусы, тангенсы, котангенсы

Таблица косинусов

Главная » Математика

Автор admin На чтение 6 мин Просмотров 2.6к. Опубликовано

Таблица косинусов — значения косинусов углов записаны в таблицу от 0° до 360°. Используя таблицу косинусов вы сможете провести расчеты даже если под рукой не окажется инженерного калькулятора.

Таблица косинусов является одной из основных таблиц, которые используются в геометрии. В ней представлены косинусы углов от 0 до 360 градусов. Таблица позволяет решать математические задачи, в которых необходимо использовать тригонометрические данные без применения расчетов и калькулятора.

Содержание

Скачать таблицу для распечатки

Таблица косинусовСкачать

Таблица косинусов в радианах

α	0	π6	π4	π3	π2	π	3π2	2π
cos α	1	√32	√22	12	0	-1	0	1

Таблица косинусов углов от 0° до 180°

cos(0°) = 1 cos(1°) = 0. 999848 cos(2°) = 0.999391 cos(3°) = 0.99863 cos(4°) = 0.997564 cos(5°) = 0.996195 cos(6°) = 0.994522 cos(7°) = 0.992546 cos(8°) = 0.990268 cos(9°) = 0.987688 cos(10°) = 0.984808 cos(11°) = 0.981627 cos(12°) = 0.978148 cos(13°) = 0.97437 cos(14°) = 0.970296 cos(15°) = 0.965926 cos(16°) = 0.961262 cos(17°) = 0.956305 cos(18°) = 0.951057 cos(19°) = 0.945519 cos(20°) = 0.939693 cos(21°) = 0.93358 cos(22°) = 0.927184 cos(23°) = 0.920505 cos(24°) = 0.913545 cos(25°) = 0.906308 cos(26°) = 0.898794 cos(27°) = 0.891007 cos(28°) = 0.882948 cos(29°) = 0.87462 cos(30°) = 0.866025 cos(31°) = 0.857167 cos(32°) = 0.848048 cos(33°) = 0.838671 cos(34°) = 0.829038 cos(35°) = 0.819152 cos(36°) = 0.809017 cos(37°) = 0.798636 cos(38°) = 0.788011 cos(39°) = 0.777146 cos(40°) = 0.766044 cos(41°) = 0.75471 cos(42°) = 0.743145 cos(43°) = 0.731354 cos(44°) = 0. 71934 cos(45°) = 0.707107

cos(46°) = 0.694658 cos(47°) = 0.681998 cos(48°) = 0.669131 cos(49°) = 0.656059 cos(50°) = 0.642788 cos(51°) = 0.62932 cos(52°) = 0.615661 cos(53°) = 0.601815 cos(54°) = 0.587785 cos(55°) = 0.573576 cos(56°) = 0.559193 cos(57°) = 0.544639 cos(58°) = 0.529919 cos(59°) = 0.515038 cos(60°) = 0.5 cos(61°) = 0.48481 cos(62°) = 0.469472 cos(63°) = 0.45399 cos(64°) = 0.438371 cos(65°) = 0.422618 cos(66°) = 0.406737 cos(67°) = 0.390731 cos(68°) = 0.374607 cos(69°) = 0.358368 cos(70°) = 0.34202 cos(71°) = 0.325568 cos(72°) = 0.309017 cos(73°) = 0.292372 cos(74°) = 0.275637 cos(75°) = 0.258819 cos(76°) = 0.241922 cos(77°) = 0.224951 cos(78°) = 0.207912 cos(79°) = 0.190809 cos(80°) = 0.173648 cos(81°) = 0.156434 cos(82°) = 0.139173 cos(83°) = 0.121869 cos(84°) = 0.104528 cos(85°) = 0.087156 cos(86°) = 0. 069756 cos(87°) = 0.052336 cos(88°) = 0.034899 cos(89°) = 0.017452 cos(90°) = 0

cos(91°) = -0.017452 cos(92°) = -0.034899 cos(93°) = -0.052336 cos(94°) = -0.069756 cos(95°) = -0.087156 cos(96°) = -0.104528 cos(97°) = -0.121869 cos(98°) = -0.139173 cos(99°) = -0.156434 cos(100°) = -0.173648 cos(101°) = -0.190809 cos(102°) = -0.207912 cos(103°) = -0.224951 cos(104°) = -0.241922 cos(105°) = -0.258819 cos(106°) = -0.275637 cos(107°) = -0.292372 cos(108°) = -0.309017 cos(109°) = -0.325568 cos(110°) = -0.34202 cos(111°) = -0.358368 cos(112°) = -0.374607 cos(113°) = -0.390731 cos(114°) = -0.406737 cos(115°) = -0.422618 cos(116°) = -0.438371 cos(117°) = -0.45399 cos(118°) = -0.469472 cos(119°) = -0.48481 cos(120°) = -0.5 cos(121°) = -0.515038 cos(122°) = -0.529919 cos(123°) = -0.544639 cos(124°) = -0.559193 cos(125°) = -0.573576 cos(126°) = -0. 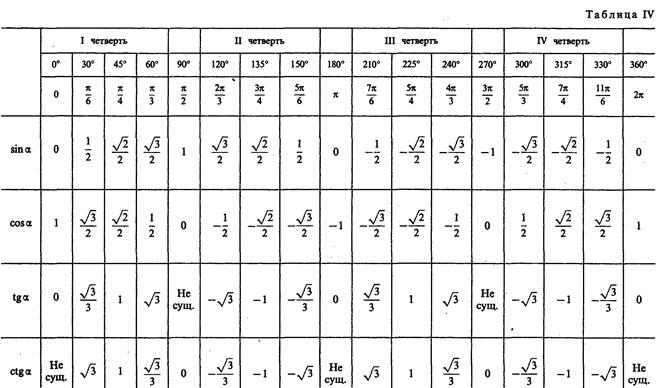587785 cos(127°) = -0.601815 cos(128°) = -0.615661 cos(129°) = -0.62932 cos(130°) = -0.642788 cos(131°) = -0.656059 cos(132°) = -0.669131 cos(133°) = -0.681998 cos(134°) = -0.694658 cos(135°) = -0.707107

cos(136°) = -0.71934 cos(137°) = -0.731354 cos(138°) = -0.743145 cos(139°) = -0.75471 cos(140°) = -0.766044 cos(141°) = -0.777146 cos(142°) = -0.788011 cos(143°) = -0.798636 cos(144°) = -0.809017 cos(145°) = -0.819152 cos(146°) = -0.829038 cos(147°) = -0.838671 cos(148°) = -0.848048 cos(149°) = -0.857167 cos(150°) = -0.866025 cos(151°) = -0.87462 cos(152°) = -0.882948 cos(153°) = -0.891007 cos(154°) = -0.898794 cos(155°) = -0.906308 cos(156°) = -0.913545 cos(157°) = -0.920505 cos(158°) = -0.927184 cos(159°) = -0.93358 cos(160°) = -0.939693 cos(161°) = -0.945519 cos(162°) = -0.951057 cos(163°) = -0.956305 cos(164°) = -0.961262 cos(165°) = -0. 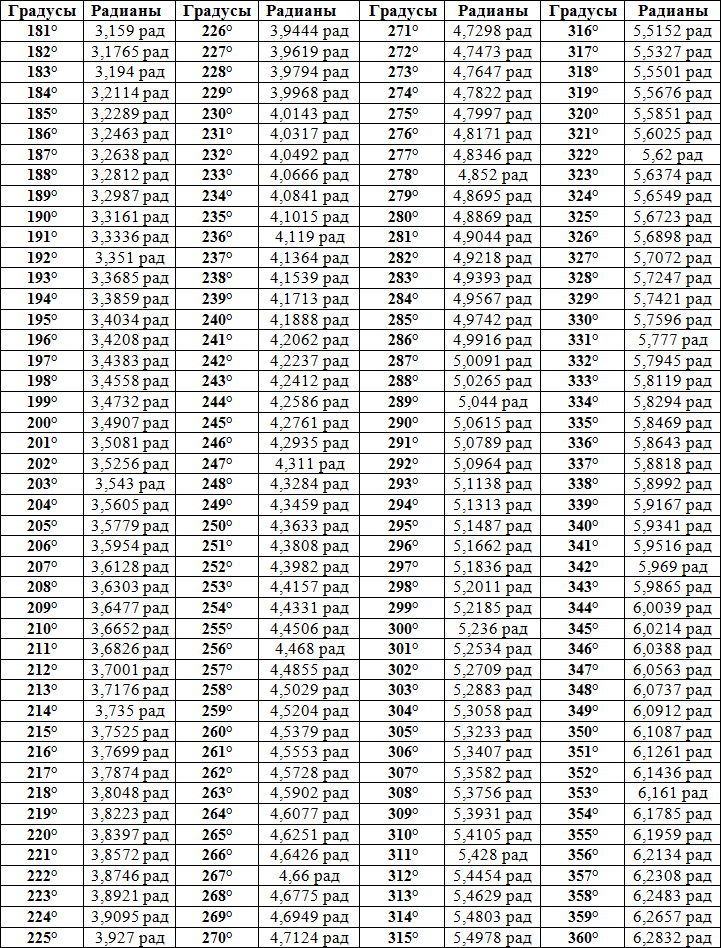965926 cos(166°) = -0.970296 cos(167°) = -0.97437 cos(168°) = -0.978148 cos(169°) = -0.981627 cos(170°) = -0.984808 cos(171°) = -0.987688 cos(172°) = -0.990268 cos(173°) = -0.992546 cos(174°) = -0.994522 cos(175°) = -0.996195 cos(176°) = -0.997564 cos(177°) = -0.99863 cos(178°) = -0.999391 cos(179°) = -0.999848 cos(180°) = -1

Таблица косинусов углов от 181° до 360°

cos(181°) = -0.999848 cos(182°) = -0.999391 cos(183°) = -0.99863 cos(184°) = -0.997564 cos(185°) = -0.996195 cos(186°) = -0.994522 cos(187°) = -0.992546 cos(188°) = -0.990268 cos(189°) = -0.987688 cos(190°) = -0.984808 cos(191°) = -0.981627 cos(192°) = -0.978148 cos(193°) = -0.97437 cos(194°) = -0.970296 cos(195°) = -0.965926 cos(196°) = -0.961262 cos(197°) = -0.956305 cos(198°) = -0.951057 cos(199°) = -0.945519 cos(200°) = -0.939693 cos(201°) = -0. 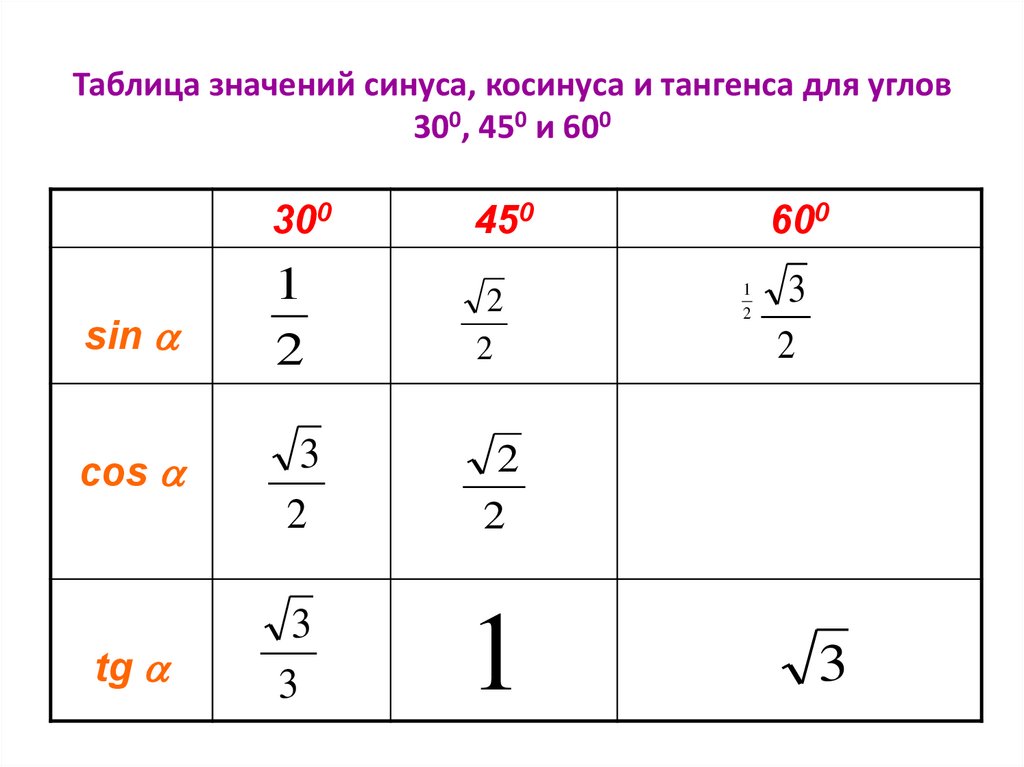93358 cos(202°) = -0.927184 cos(203°) = -0.920505 cos(204°) = -0.913545 cos(205°) = -0.906308 cos(206°) = -0.898794 cos(207°) = -0.891007 cos(208°) = -0.882948 cos(209°) = -0.87462 cos(210°) = -0.866025 cos(211°) = -0.857167 cos(212°) = -0.848048 cos(213°) = -0.838671 cos(214°) = -0.829038 cos(215°) = -0.819152 cos(216°) = -0.809017 cos(217°) = -0.798636 cos(218°) = -0.788011 cos(219°) = -0.777146 cos(220°) = -0.766044 cos(221°) = -0.75471 cos(222°) = -0.743145 cos(223°) = -0.731354 cos(224°) = -0.71934 cos(225°) = -0.707107

cos(226°) = -0.694658 cos(227°) = -0.681998 cos(228°) = -0.669131 cos(229°) = -0.656059 cos(230°) = -0.642788 cos(231°) = -0.62932 cos(232°) = -0.615661 cos(233°) = -0.601815 cos(234°) = -0.587785 cos(235°) = -0.573576 cos(236°) = -0.559193 cos(237°) = -0.544639 cos(238°) = -0.529919 cos(239°) = -0.515038 cos(240°) = -0. 5 cos(241°) = -0.48481 cos(242°) = -0.469472 cos(243°) = -0.45399 cos(244°) = -0.438371 cos(245°) = -0.422618 cos(246°) = -0.406737 cos(247°) = -0.390731 cos(248°) = -0.374607 cos(249°) = -0.358368 cos(250°) = -0.34202 cos(251°) = -0.325568 cos(252°) = -0.309017 cos(253°) = -0.292372 cos(254°) = -0.275637 cos(255°) = -0.258819 cos(256°) = -0.241922 cos(257°) = -0.224951 cos(258°) = -0.207912 cos(259°) = -0.190809 cos(260°) = -0.173648 cos(261°) = -0.156434 cos(262°) = -0.139173 cos(263°) = -0.121869 cos(264°) = -0.104528 cos(265°) = -0.087156 cos(266°) = -0.069756 cos(267°) = -0.052336 cos(268°) = -0.034899 cos(269°) = -0.017452 cos(270°) = -0

cos(271°) = 0.017452 cos(272°) = 0.034899 cos(273°) = 0.052336 cos(274°) = 0.069756 cos(275°) = 0.087156 cos(276°) = 0.104528 cos(277°) = 0.121869 cos(278°) = 0.139173 cos(279°) = 0.156434 cos(280°) = 0. 173648 cos(281°) = 0.190809 cos(282°) = 0.207912 cos(283°) = 0.224951 cos(284°) = 0.241922 cos(285°) = 0.258819 cos(286°) = 0.275637 cos(287°) = 0.292372 cos(288°) = 0.309017 cos(289°) = 0.325568 cos(290°) = 0.34202 cos(291°) = 0.358368 cos(292°) = 0.374607 cos(293°) = 0.390731 cos(294°) = 0.406737 cos(295°) = 0.422618 cos(296°) = 0.438371 cos(297°) = 0.45399 cos(298°) = 0.469472 cos(299°) = 0.48481 cos(300°) = 0.5 cos(301°) = 0.515038 cos(302°) = 0.529919 cos(303°) = 0.544639 cos(304°) = 0.559193 cos(305°) = 0.573576 cos(306°) = 0.587785 cos(307°) = 0.601815 cos(308°) = 0.615661 cos(309°) = 0.62932 cos(310°) = 0.642788 cos(311°) = 0.656059 cos(312°) = 0.669131 cos(313°) = 0.681998 cos(314°) = 0.694658 cos(315°) = 0.707107

cos(316°) = 0.71934 cos(317°) = 0.731354 cos(318°) = 0.743145 cos(319°) = 0.75471 cos(320°) = 0.766044 cos(321°) = 0. 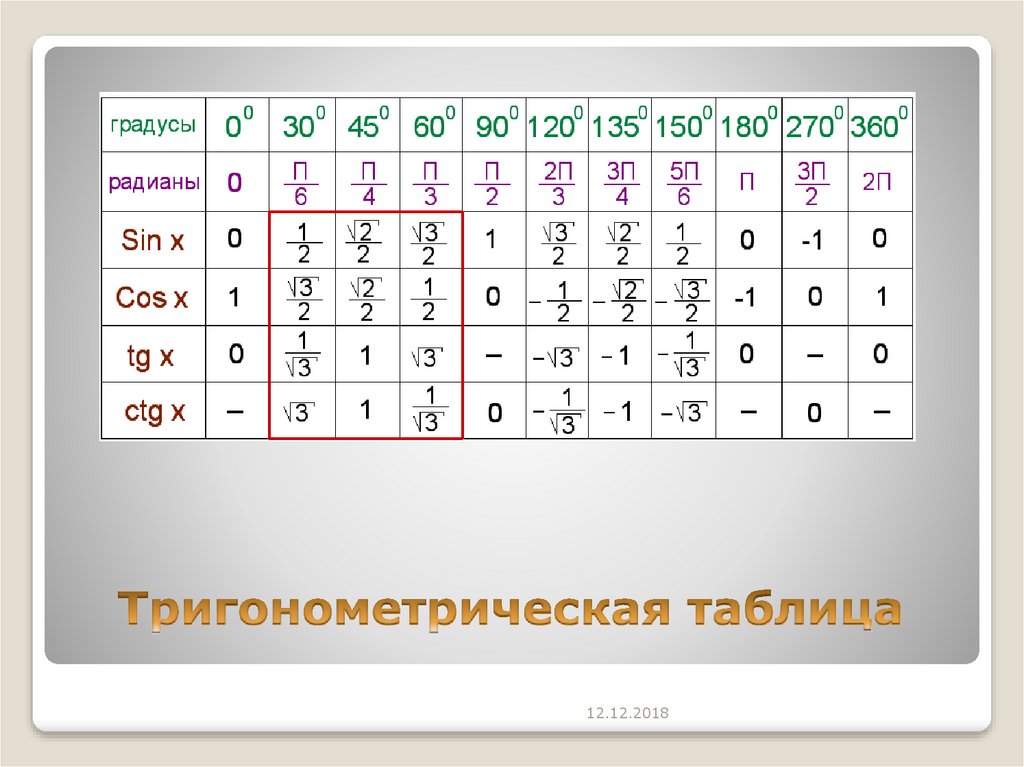777146 cos(322°) = 0.788011 cos(323°) = 0.798636 cos(324°) = 0.809017 cos(325°) = 0.819152 cos(326°) = 0.829038 cos(327°) = 0.838671 cos(328°) = 0.848048 cos(329°) = 0.857167 cos(330°) = 0.866025 cos(331°) = 0.87462 cos(332°) = 0.882948 cos(333°) = 0.891007 cos(334°) = 0.898794 cos(335°) = 0.906308 cos(336°) = 0.913545 cos(337°) = 0.920505 cos(338°) = 0.927184 cos(339°) = 0.93358 cos(340°) = 0.939693 cos(341°) = 0.945519 cos(342°) = 0.951057 cos(343°) = 0.956305 cos(344°) = 0.961262 cos(345°) = 0.965926 cos(346°) = 0.970296 cos(347°) = 0.97437 cos(348°) = 0.978148 cos(349°) = 0.981627 cos(350°) = 0.984808 cos(351°) = 0.987688 cos(352°) = 0.990268 cos(353°) = 0.992546 cos(354°) = 0.994522 cos(355°) = 0.996195 cos(356°) = 0.997564 cos(357°) = 0.99863 cos(358°) = 0.999391 cos(359°) = 0.999848 cos(360°) = 1

Скачать таблицу для распечатки

Таблица косинусовСкачать

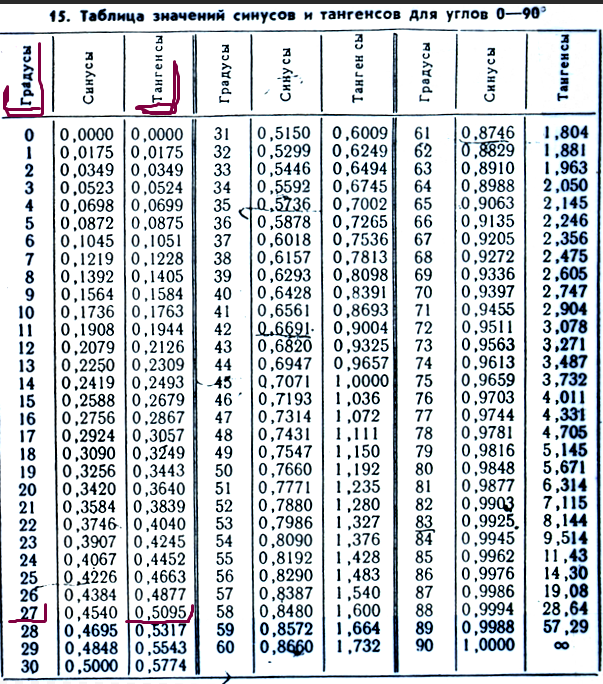
cos 45 градусов равен таблица брадиса

Вы искали cos 45 градусов равен таблица брадиса? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и sin 30 градусов равен таблица, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «cos 45 градусов равен таблица брадиса».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как cos 45 градусов равен таблица брадиса,sin 30 градусов равен таблица,sin 60 градусов равен таблица,tg 30 tg 45 tg 60,арккосинус таблица брадиса,брадиса,брадиса косинус,брадиса косинусы,значения синуса и косинуса таблица,калькулятор брадиса,калькулятор таблица брадиса,косинус 30 градусов равен таблица брадиса,косинус брадиса,косинус и синус 0,косинусы брадиса,косинусы и синусы таблица,онлайн таблица брадиса косинусы,полная таблица брадиса,син 30 градусов таблица,синус 30 градусов таблица,синус 30 таблица,синус 60 градусов равен таблица брадиса,синус косинус тангенс котангенс таблица значений,синус таблица брадиса,синусы и косинусы 30 45 и 60,таблица брадис,таблица брадиса,таблица брадиса арккосинус,таблица брадиса для косинусов,таблица брадиса для синусов,таблица брадиса калькулятор,таблица брадиса калькулятор онлайн,таблица брадиса косинус 30 градусов таблица,таблица брадиса косинусы и синусы онлайн,таблица брадиса косинусы онлайн,таблица брадиса косинусы онлайн калькулятор,таблица брадиса косинусы от 0 до 180,таблица брадиса котангенсы,таблица брадиса онлайн,таблица брадиса онлайн калькулятор,таблица брадиса онлайн калькулятор косинусы,таблица брадиса онлайн косинусы,таблица брадиса онлайн тангенсы,таблица брадиса полная,таблица брадиса распечатать,таблица брадиса синус,таблица брадиса синусов,таблица брадиса синусов и косинусов,таблица брадиса синусы,таблица брадиса синусы косинусы тангенсы,таблица брадиса тангенсы онлайн,таблица брадиса тангенсы онлайн калькулятор,таблица значение синуса косинуса тангенса и котангенса,таблица син 30 градусов,таблица синус 30,таблица синусов брадиса,таблица синусов и косинусов от 0 до 90,таблице брадиса,таблиці брадіса,таблицы брадиса,таблицы брадиса косинусы,таблицы брадиса онлайн,таблицы брадиса синусы,таблицы брадиса синусы косинусы,таблиця брадіса,таблиця косинусів і синусів,тангенс таблица брадиса,углы синуса косинуса тангенса таблица,четырехзначная таблица брадиса синусы косинусы и тангенсы котангенсы,четырехзначные таблицы брадиса.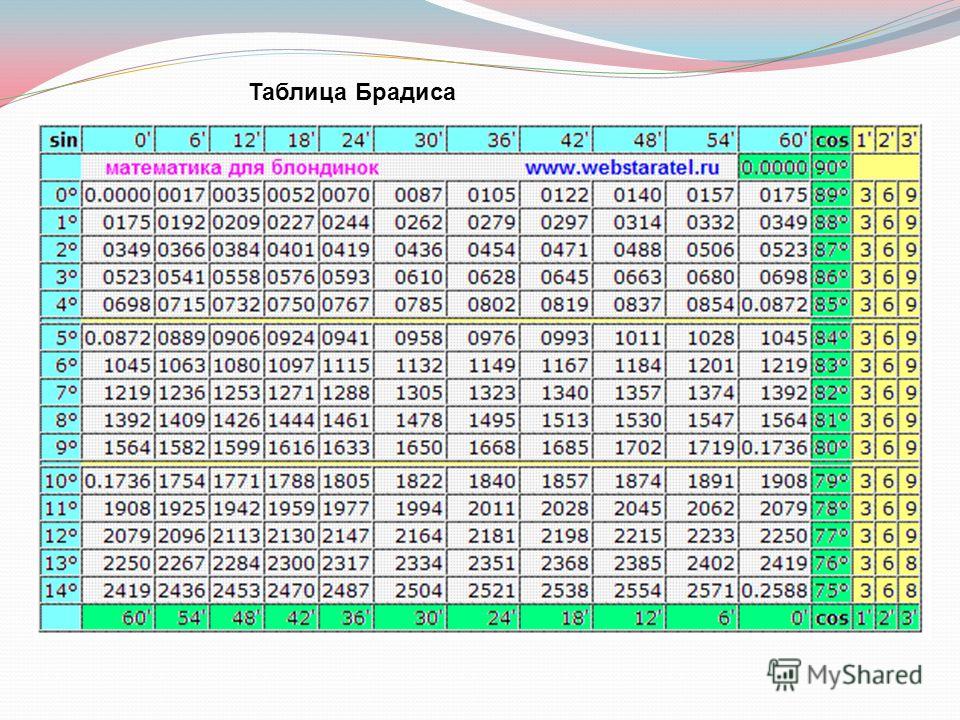

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и cos 45 градусов равен таблица брадиса. Просто введите задачу в окошко и нажмите «решить» здесь (например, sin 60 градусов равен таблица).

Решить задачу cos 45 градусов равен таблица брадиса вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Построение таблицы синусов голыми руками | Тригонометрия: очень краткое введение

Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаОчень короткое введениеКнигиЖурналы Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаОчень короткое введениеКнигиЖурналы Введите поисковый запрос

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения
• Делиться
  • Твиттер
  • Подробнее

Укажите

Ван Браммелен, Глен, «Построение таблицы синусов голыми руками», Trigonometry: A Very Short Introduction , Very Short Introductions (

Oxford

, 2020; онлайн-издание, Oxford Academic, 23 января 2020 г. ), https:/ /doi.org/10.1093/actrade/9780198814313.003.0003, по состоянию на 22 апреля 2023 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаОчень короткое введениеКнигиЖурналы Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Oxford AcademicТригонометрия: очень краткое введениеОчень краткое введениеЧистая математикаОчень короткое введениеКнигиЖурналы Введите поисковый запрос

Advanced Search

Abstract

Технологические достижения, которые так широко распространены почти во всех аспектах нашей современной жизни, почти мгновенно становятся для нас обыденными. Как вычислитель, по-видимому, без особых усилий выясняет, что sin 33° = 0,5446? Внутри калькулятора не нарисованы прямоугольные треугольники, так откуда взялось это число? «Построение таблицы синуса голыми руками» показывает, как различные значения синуса вычислялись на протяжении истории без каких-либо механических вспомогательных средств. Он вводит законы суммы синусов и разностей, формулы половинного и двойного угла, золотой треугольник и одно из самых замечательных чисел во всей математике, золотое сечение, которое встречается в ослепительном множестве областей математики, естественных наук. явлений, произведений искусства и архитектуры.

Ключевые слова: угол, Генри Бриггс, круг, формула половинного угла, отношение, Региомонтан, квадрат, Франсуа Виет

Предмет

Чистая математика

Ряд

Краткие введения

Коллекция: Очень короткие вступления

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Щелкните Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или купить в библиотеках и учреждениях.

Информация о покупке

Тригонометрический стол | Britannica

Ключевые люди:

Генри Бриггс Эдмунд Гюнтер

Похожие темы:

тригонометрия

См. весь соответствующий контент →

тригонометрическая таблица , табличные значения для некоторых или всех шести тригонометрических функций для различных угловых значений. Тригонометрические таблицы, которые когда-то были важным инструментом для ученых, инженеров, геодезистов и мореплавателей, устарели с появлением компьютеров. (Для справки, на рисунке показаны шесть тригонометрических функций относительно прямоугольного треугольника.)

Греческий астроном Гиппарх (ум. ок. 127 г. до н. э.) первым составил таблицу тригонометрических функций (на основе хорд в окружности), которые он вычислил с шагом 7° 30′. Птолемей (145 г. н. э.) улучшил таблицы Гиппарха, рассчитывая значения с шагом 30 футов. « Альмагест » Птолемея, величайшее астрономическое произведение древности, было бы невозможно представить без его таблицы аккордов.

Викторина «Британника»

Числа и математика

Самая ранняя таблица синусоидальной функции (хотя и не с ее современным определением) находится в Surya Siddhanta , индуистском астрономическом справочнике 4-го или 5-го века нашей эры.

Астрономы средневекового ислама были непревзойденными вычислителями, составившими таблицы всех шести тригонометрических функций в качестве основы для астрономии и астрономического хронометрирования. Венцом этого начинания стали таблицы Султана Улугбека, изданные в 1440 году в Самарканде (ныне Узбекистан). Функции синуса и тангенса (хотя до сих пор не даны их современные определения в терминах отношений), рассчитанные с шагом 1 ′, были точными до эквивалента 9десятичные знаки.

Из мусульманской Испании тригонометрические таблицы распространились в латинскую Европу. Региомонтан (1436–1476 гг.), немецкий астроном и математик, составил первые таблицы с десятичными значениями. Точно так же Георг Иоахим Ретикус (1514–1574 гг.), ученик Николая Коперника, подготовил великолепный набор таблиц всех шести тригонометрических функций с шагом 10 дюймов с точностью до 10 знаков после запятой. Ретикус также предпринял решительные шаги по определению тригонометрических функций в терминах углов, а не дуг, и в виде отношений, а не длин.

Французский математик Франсуа Виет опубликовал таблицы всех шести тригонометрических функций в Canon Mathematicus (1579). Однако ценность этой работы заключалась не в таблицах, в которых он вычислял функции с шагом в 1 ′ с точностью до пяти знаков после запятой. Наоборот, работа Виета была важна, потому что он открыл различные тригонометрические соотношения, с помощью которых продемонстрировал, как использовать тригонометрию для решения уравнений третьей степени и выше.