Расчет стенок цилиндра. Как найти площадь цилиндра
Формула радиуса цилиндра:
где V — объем цилиндра, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb — площадь боковой поверхности, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая).
Формула радиуса цилиндра:
где S — площадь полной поверхности, h — высота
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Площадь поверхности цилиндра — онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры.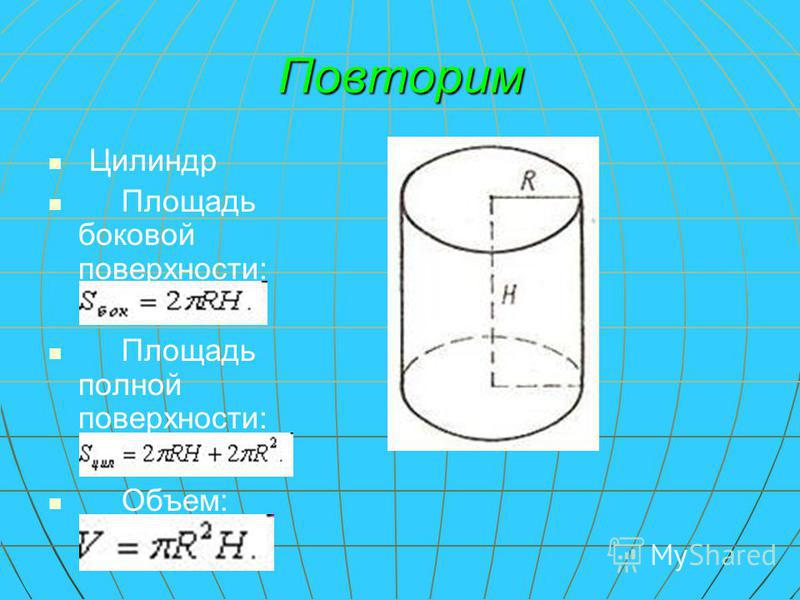 Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
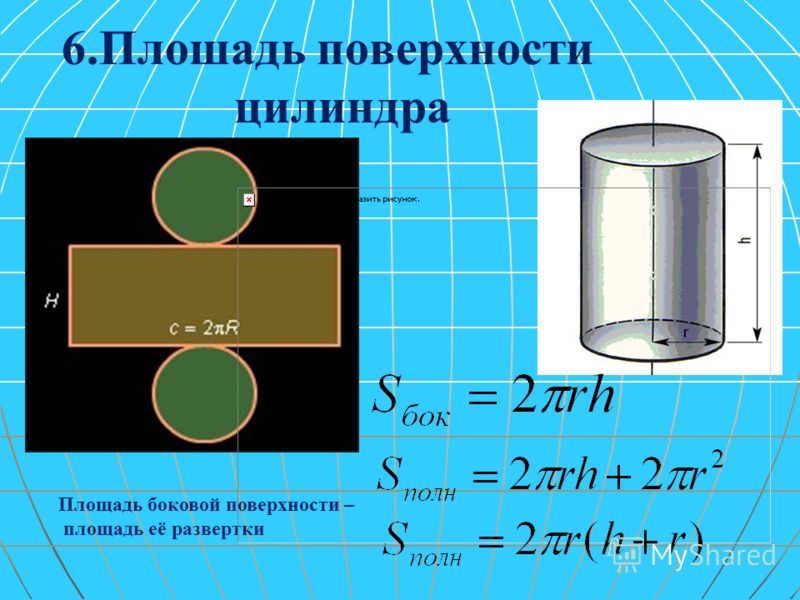
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r , где r — радиус окружности. Другая сторона прямоугольника равна высоте h . Найти искомое не составит труда.
S бок = 2π * r * h ,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной S бок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S о = 2π * r 2 .
Конечная формула выглядит следующим образом:
S пол = 2π * r 2 + 2π * r * h.
Площадь цилиндра — формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.
Например, имеется кусок полой трубы известного диаметра.
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
S пол = 2 π * r 2 + 2 π * r * h = 2 π * d 2 /4 + 2 π * h * d /2 = π * d 2 /2 + π * d * h ,
Вместо r в полную формулу нужно вставить значение r = d/2 .
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
S пол = 2 * 3.14 * 24 2 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм 2).
Переводим в привычные м 2 и получаем 0,01868928, приблизительно 0.02 м 2 .
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:
S пол = 3.14 * 0.2 2 /2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м 2 .
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
S бок = 2 * 3.14 * 1 * 1 = 6.28 м 2 .
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.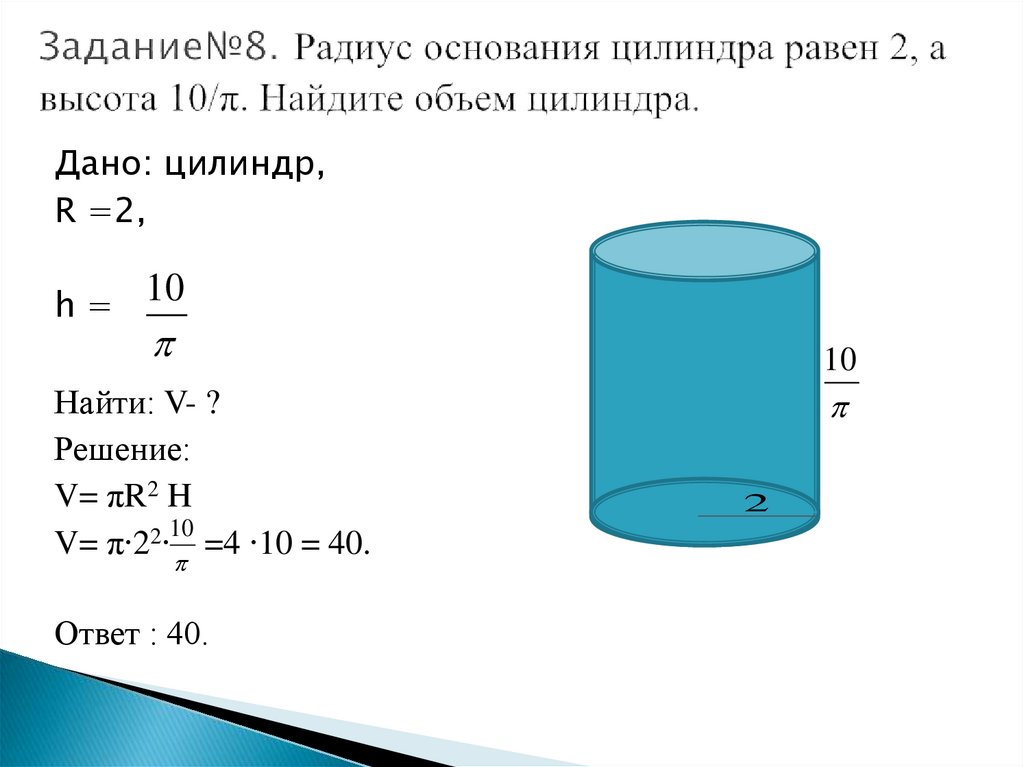
У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Вершина и основание цилиндра являются окружностями, их легко определить.
Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .
Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr 2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.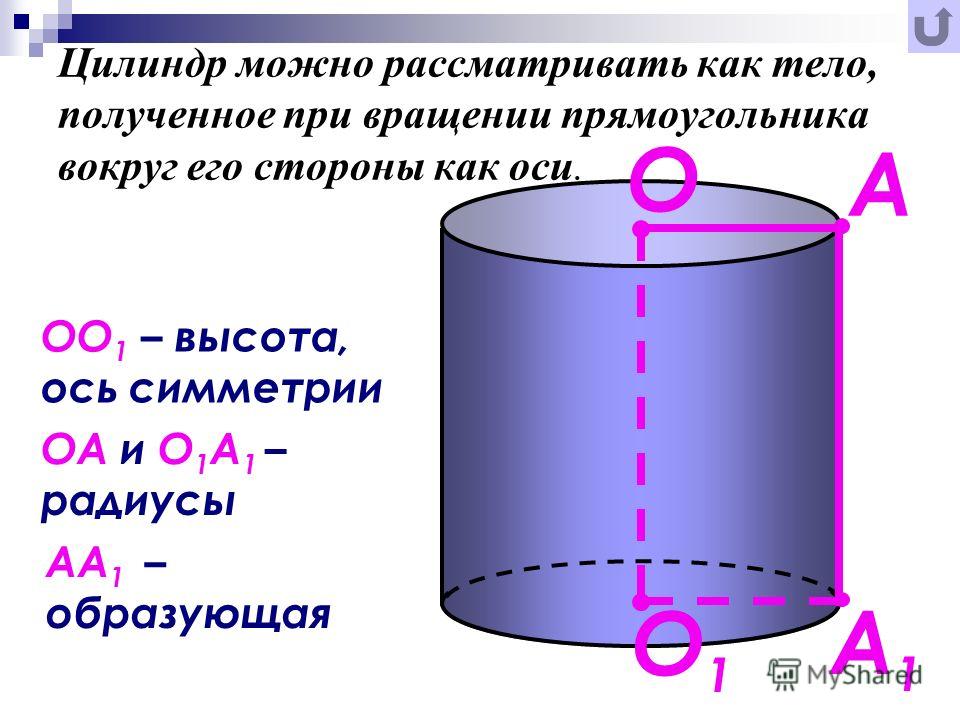
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь полной поверхности рассчитывается по формуле: S бок. = 2πrh
S бок. = 2 * 3,14 * 2 * 3
S бок. = 6,28 * 6
S бок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr 2 + 2πrh
S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
Площадь каждого основания цилиндра равна πr 2 , площадь обоих оснований составит 2πr 2 (рис.).
Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr , а высота равна высоте цилиндра h , т. е. 2πrh .
Полная поверхность цилиндра составит: 2πr 2 + 2πrh = 2πr (r + h ).
За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле
S б.ц. = 2πRH, (1)
Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра
S полн. =2πRH + 2πR 2 = 2πR (H + R).
Объем прямого цилиндра
Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту , т. е.
где Q — площадь основания, а Н — высота цилиндра.
Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n и Q’ n таких, что
\(\lim_{n \rightarrow \infty}\) Q n = \(\lim_{n \rightarrow \infty}\) Q’ n = Q.
Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H.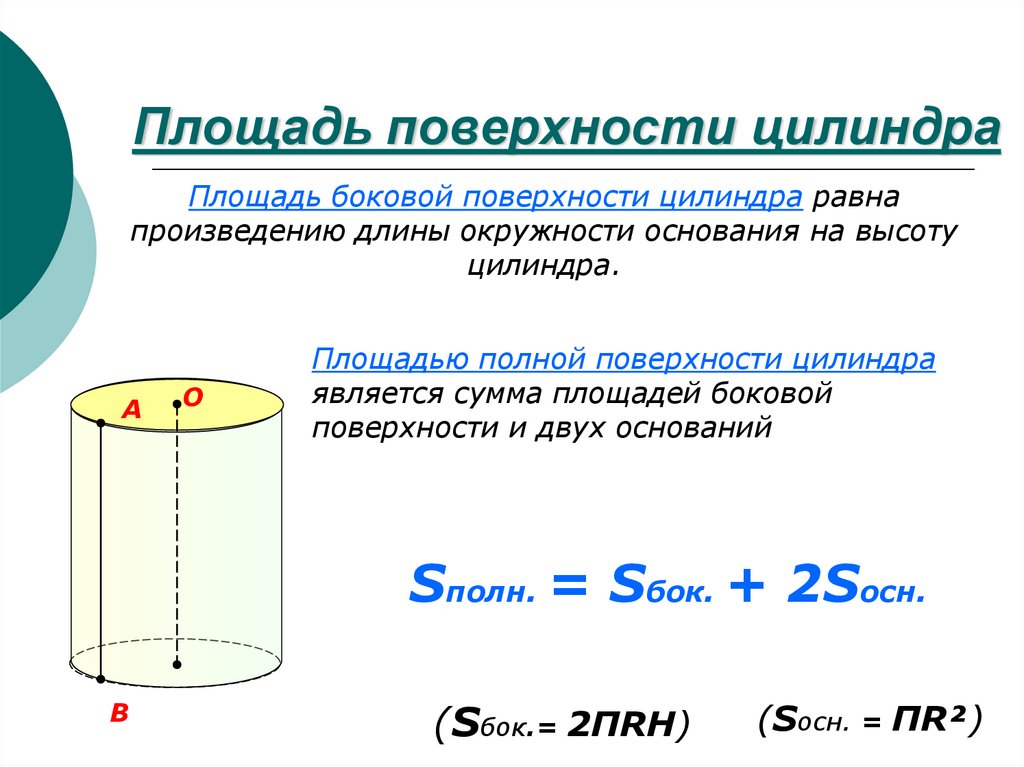
V n = Q n H и V’ n = Q’ n H.
Следовательно,
V= \(\lim_{n \rightarrow \infty}\) Q n H = \(\lim_{n \rightarrow \infty}\) Q’ n H = QH.
Следствие.
Объем прямого кругового цилиндра вычисляется по формуле
V = π R 2 H
где R — радиус основания, а H — высота цилиндра.
Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому
Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы.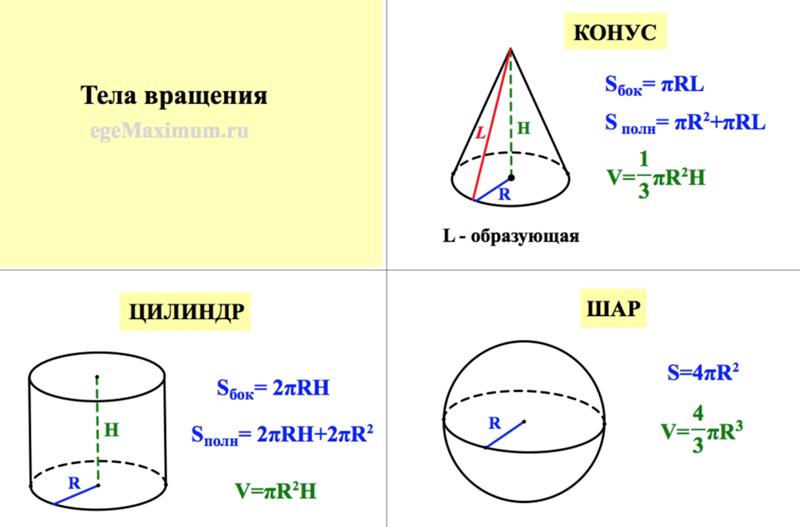 Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
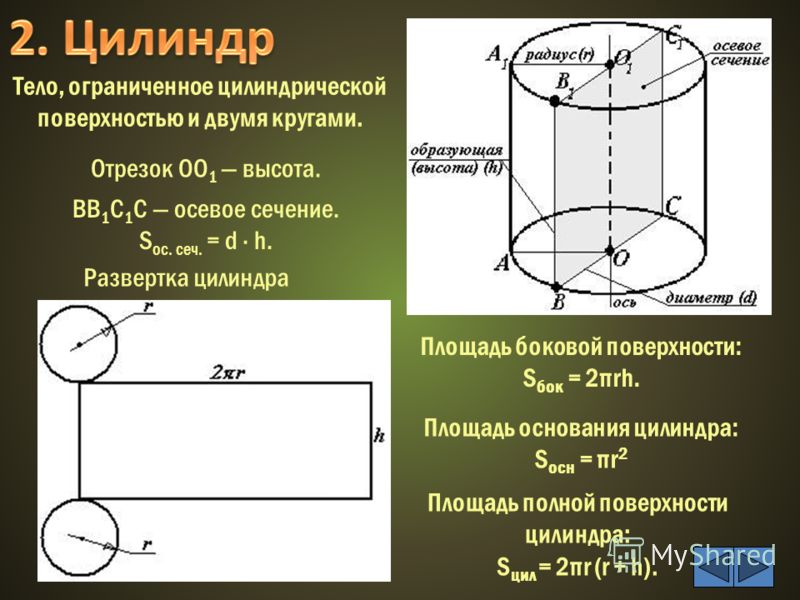
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета :
Периметр основания цилиндра. Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
Цилиндр – это фигура, состоящая из цилиндрической поверхности и двух окружностей, расположенных параллельно. Расчет площади цилиндра – это задача геометрического раздела математики, которая решается достаточно просто. Существует несколько методов ее решения, которые в результате всегда сводятся к одной формуле.
Как найти площадь цилиндра – правила вычисления
- Чтобы узнать площадь цилиндра, необходимо две площади основания сложить с площадью боковой поверхности: S= Sбок.+ 2Sосн. В более развернутом варианте данная формула выглядит так: S= 2 π rh+ 2 π r2= 2 π r(h+ r).
- Площадь боковой поверхности данного геометрического тела можно высчитать, если известны его высота и радиус окружности, лежащей в основании.
 В данном случае можно выразить радиус из длины окружности, если она дана. Высота может быть найдена, если в условии задано значение образующей. В этом случае образующая будет равна высоте. Формула боковой поверхности данного тела выглядит так: S= 2 π rh.
В данном случае можно выразить радиус из длины окружности, если она дана. Высота может быть найдена, если в условии задано значение образующей. В этом случае образующая будет равна высоте. Формула боковой поверхности данного тела выглядит так: S= 2 π rh. - Площадь основания считается по формуле нахождения площади круга: S osn= π r 2 . В некоторых задачах может не даваться радиус, но задаваться длина окружности. С данной формулы радиус выражается достаточно легко. С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра.
- При выполнении всех этих расчетов число π обычно не переводится в 3,14159… Его нужно просто дописывать рядом с числовым значением, которое было получено в результате проведения вычислений.
- Далее необходимо лишь умножить найденную площадь основания на 2 и прибавить к полученному числу вычисленную площадь боковой поверхности фигуры.
- Если в задаче указывается, что в цилиндре есть осевое сечение и это – прямоугольник, то решение будет немного другим.
 В таком случае ширина прямоугольника будет являться диаметром окружности, лежащей в основании тела. Длина фигуры будет равна образующей или высоте цилиндра. Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π.
В таком случае ширина прямоугольника будет являться диаметром окружности, лежащей в основании тела. Длина фигуры будет равна образующей или высоте цилиндра. Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π. - Можно высчитать площадь данного геометрического тела через его объем. Для этого нужно из формулы V=π r 2 h вывести недостающую величину.
- В вычислении площади цилиндра нет ничего сложного. Нужно только знать формулы и уметь выводить из них величины, необходимые для проведения расчетов.
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Площадь поверхности цилиндра — онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r , где r — радиус окружности. Другая сторона прямоугольника равна высоте h .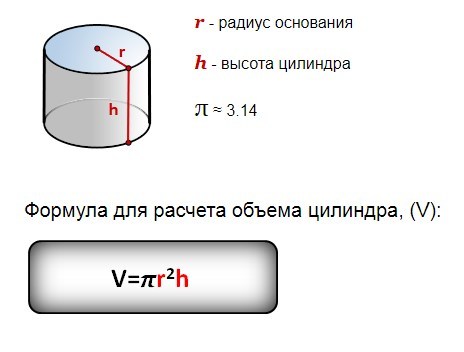 Найти искомое не составит труда.
Найти искомое не составит труда.
S бок = 2π * r * h ,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной S бок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S о = 2π * r 2 .
Конечная формула выглядит следующим образом:
S пол = 2π * r 2 + 2π * r * h.
Площадь цилиндра — формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
S пол = 2 π * r 2 + 2 π * r * h = 2 π * d 2 /4 + 2 π * h * d /2 = π * d 2 /2 + π * d * h ,
Вместо r в полную формулу нужно вставить значение r = d/2 .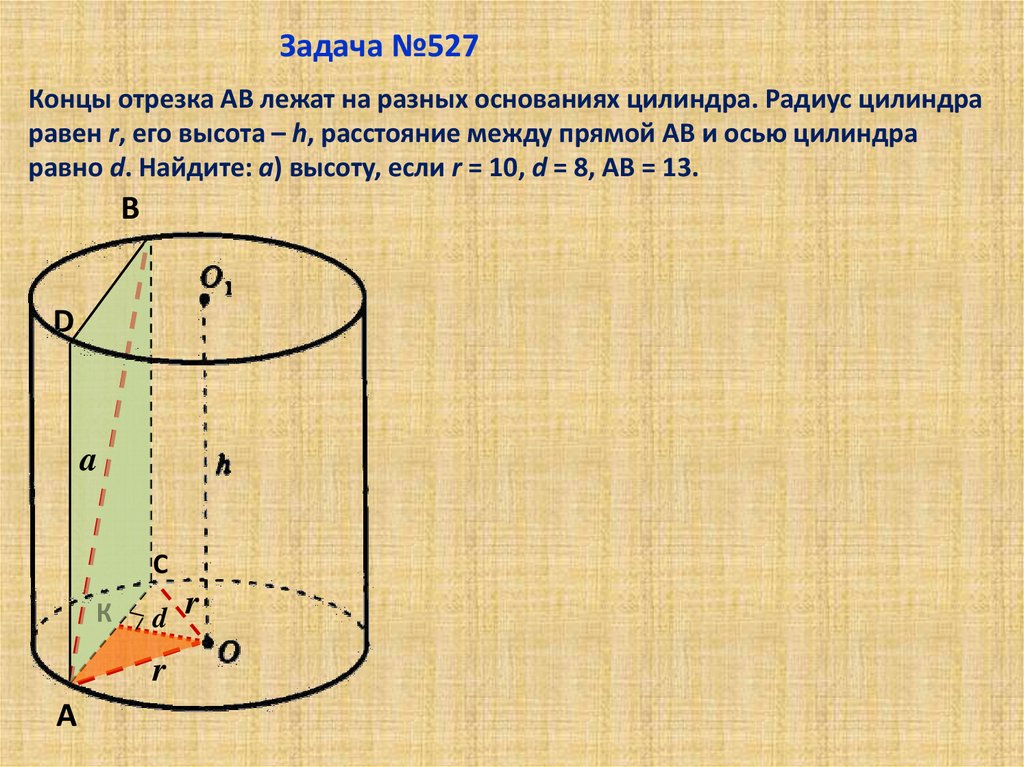
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
S пол = 2 * 3.14 * 24 2 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм 2).
Переводим в привычные м 2 и получаем 0,01868928, приблизительно 0.02 м 2 .
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:
S пол = 3.14 * 0.2 2 /2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м 2 .
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
S бок = 2 * 3.14 * 1 * 1 = 6.28 м 2 .
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.
Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Планиметрия — раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье — цилиндр.
Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже — коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец — знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения — самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a , расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a . Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.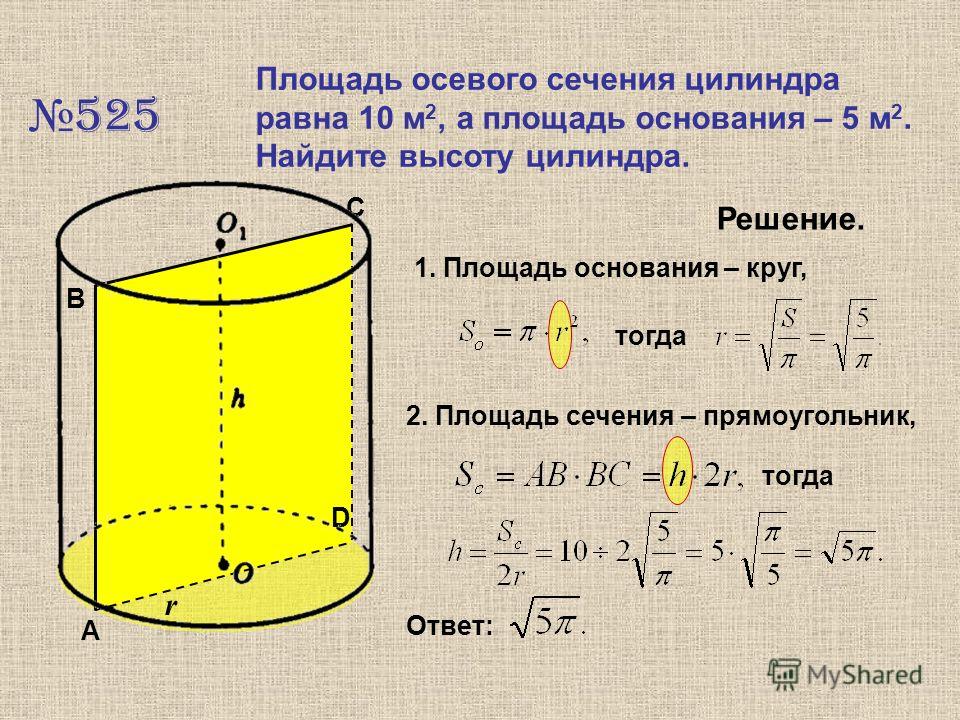
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг — шар и т.д.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.
Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N . Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями — перпендикулярный отрезок, построенный между ними.
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Как построить развёртку цилиндра
В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.
Следует учитывать, что рисунок приведен без учёта швов.
Отличия скошенного цилиндра
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.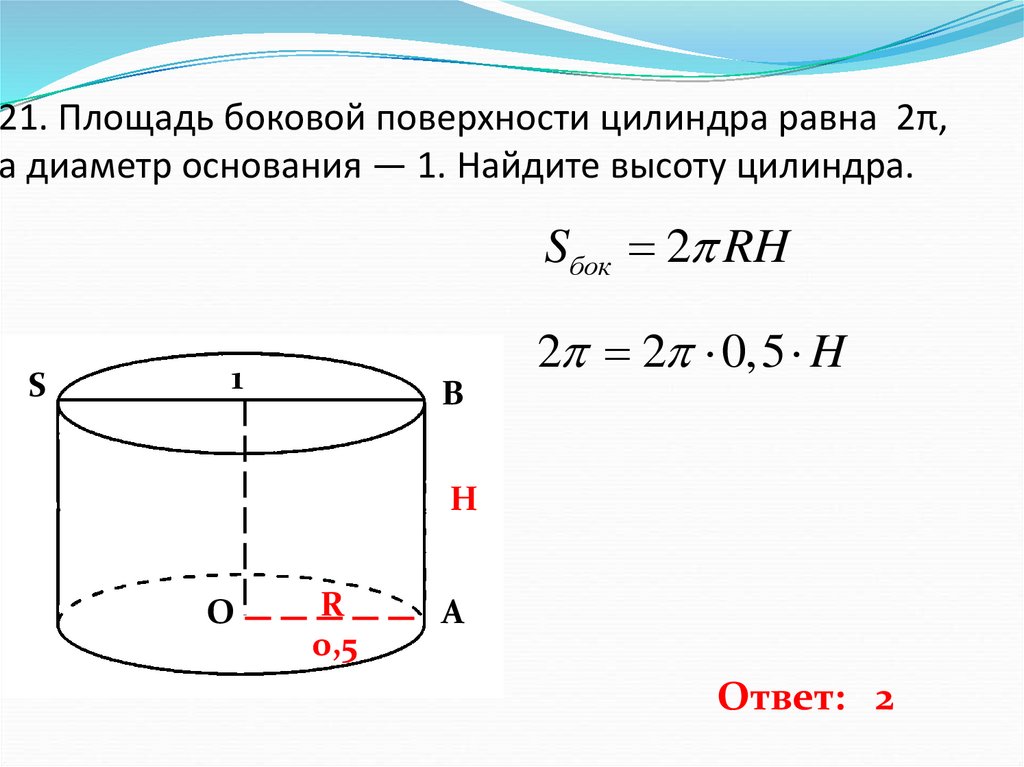
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.
Геометрические характеристики скошенного цилиндра
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.
Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета :
Площадь каждого основания цилиндра равна πr 2 , площадь обоих оснований составит 2πr 2 (рис.).
Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr , а высота равна высоте цилиндра h , т. е. 2πrh .
Полная поверхность цилиндра составит: 2πr 2 + 2πrh = 2πr (r + h ).
За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.
Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле
S б.ц. = 2πRH, (1)
Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра
S полн. =2πRH + 2πR 2 = 2πR (H + R).
Объем прямого цилиндра
Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту , т. е.
Объем прямого цилиндра равен произведению площади его основания на высоту , т. е.
где Q — площадь основания, а Н — высота цилиндра.
Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n и Q’ n таких, что
\(\lim_{n \rightarrow \infty}\) Q n = \(\lim_{n \rightarrow \infty}\) Q’ n = Q.
Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам
V n = Q n H и V’ n = Q’ n H.
Следовательно,
V= \(\lim_{n \rightarrow \infty}\) Q n H = \(\lim_{n \rightarrow \infty}\) Q’ n H = QH.
Следствие.
Объем прямого кругового цилиндра вычисляется по формуле
V = π R 2 H
где R — радиус основания, а H — высота цилиндра.
Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому
Радиус цилиндра. Калькулятор
Автор Dominik Czernia, PhD
Отзыв от Bogna Szyk и Adena Benn
Последнее обновление: 20 ноября 2022 г.
Содержание:- Что такое радиус формулы цилиндра?
- Как найти радиус цилиндра?
- Часто задаваемые вопросы
Этот калькулятор радиуса цилиндра быстро находит радиус правильного кругового цилиндра с восемью различными уравнениями . Вам нужно решить конкретную математическую задачу, но вы не знаете, как найти радиус цилиндра? Попробуйте ввести пару параметров и посмотрите, как просто работает этот калькулятор.
Существует множество различных способов оценки радиуса цилиндра. В следующем тексте мы представили восемь формул радиуса цилиндра, которые используются нашим калькулятором. В большинстве случаев вам понадобятся только два из следующих количеств:
- высота ;
- том ;
- самая длинная диагональ ;
- площадь основания ;
- площадь боковой поверхности ;
- общая площадь поверхности ; или
- отношение поверхности к объему .

Этот калькулятор радиуса цилиндра является удобным инструментом, который может вычислить параметры правильных круговых цилиндров . Под радиусом цилиндра мы подразумеваем радиус двух конгруэнтных окружностей, которые составляют оснований цилиндра. Вот почему этот тип цилиндра называется круговым .
Следует помнить, что слово цилиндр может соответствовать разным формам (обобщенный цилиндр). Однако обычно мы имеем в виду правильный круговой цилиндр. Цилиндр 9.0017 справа , когда одно из оснований лежит точно над другим. В противном случае цилиндр косой .
Этот калькулятор подготовлен для ответа на вопрос как найти радиус цилиндра . В другом нашем правом расчете цилиндров вы можете найти более общую информацию о цилиндрах. Обязательно проверьте это!
Какова формула радиуса цилиндра?
Для описания свойств цилиндра мы обычно используем радиус r и высоту ч .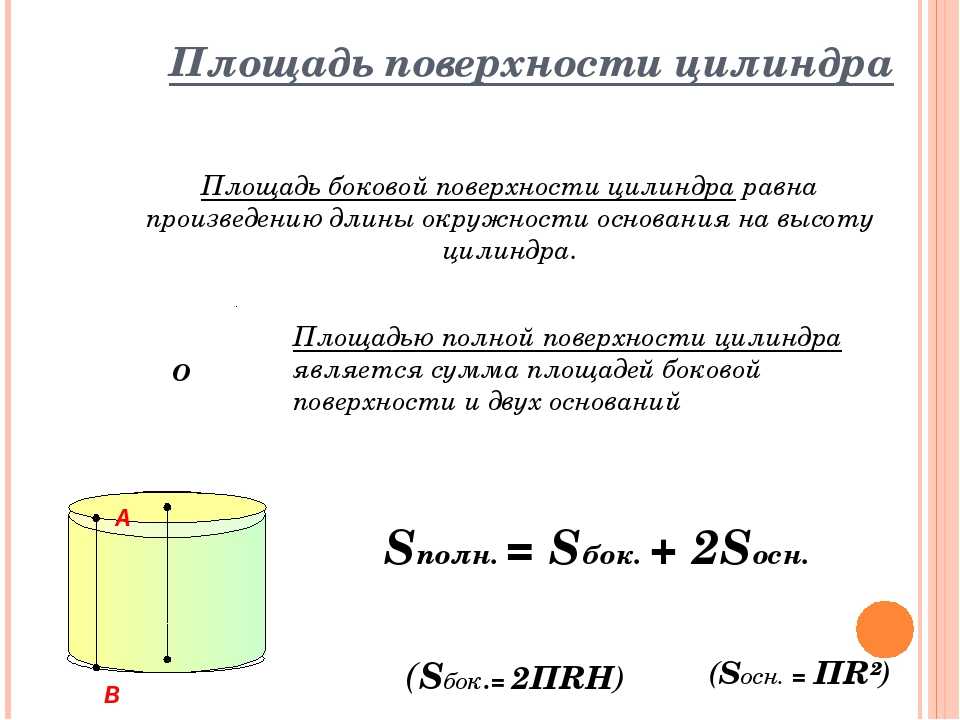 Ниже мы перечислили шесть основных уравнений, которые использовались для вывода явных формул радиуса цилиндра:
Ниже мы перечислили шесть основных уравнений, которые использовались для вывода явных формул радиуса цилиндра:
- Объем цилиндра:
V = π × r² × h, - Площадь основания цилиндра:
A_b = 2 × π × r², - Площадь боковой поверхности цилиндра:
A_l = 2 × π × r × h, - Общая площадь поверхности цилиндра:
A = A_b + A_l, - Наибольшая диагональ цилиндра:
d² = 4 × r² + h², - Отношение площади поверхности к объему цилиндра:
SA:V = A / V = 2 × (r + h) / (r × h)
Радиус цилиндра не всегда легко оценить. Однако с помощью нашего калькулятора радиуса цилиндра теперь вы можете быстро вычислить его с помощью следующих формул восьми радиусов цилиндра . Все они были получены непосредственно из приведенных выше уравнений.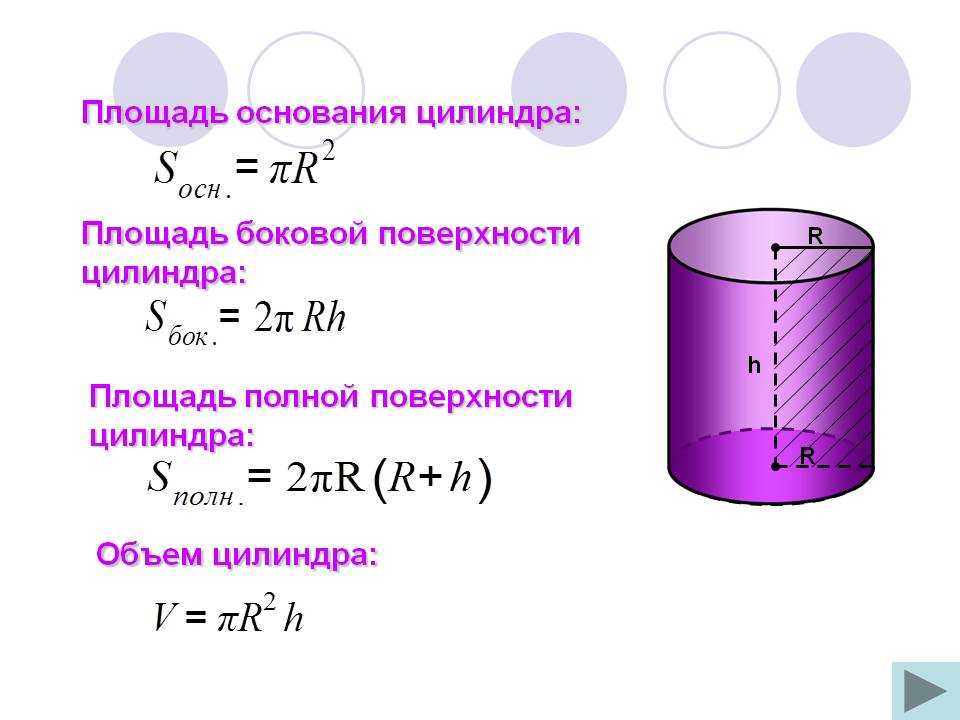
- Учитывая высоту и объем :
r = √(V / (π × h)); - Дано высоты и поперечной площади :
r = A_l / (2 × π × h); - Учитывая высоту и общую площадь :
r = (√(h² + 2 × A / π) - h) / 2; - Учитывая высоту и диагональ :
r = √(h² + d²) / 2; - Учитывая высоту и отношение площади поверхности к объему :
r = 2 × h / (h × SA:V - 2); - Учитывая объем и боковую площадь :
r = 2 × V / A_l; - Учитывая базовую площадь :
r = √(A_b / (2 × π)); и - Даны боковой площади и общей площади :
r = √((A - A_l) / (2 × π)).
Вам нужно рассчитать еще один параметр цилиндра? Вам обязательно нужно проверить наш калькулятор площади поверхности цилиндра и калькулятор высоты цилиндра!
Как найти радиус цилиндра?
Калькулятор радиуса цилиндра является полезным инструментом, предназначенным для решения широкого круга различных задач. Иногда вы будете знать высоту и объем цилиндра, но не будете знать его радиус. В другой раз вам придется столкнуться с более сложной проблемой. Например, вы узнаете, какова высота цилиндра и отношение площади поверхности к объему. Если вам когда-нибудь придется решать такую задачу, не забудьте использовать этот калькулятор радиуса цилиндра. Вам нужно выполнить всего три основных шага:
Иногда вы будете знать высоту и объем цилиндра, но не будете знать его радиус. В другой раз вам придется столкнуться с более сложной проблемой. Например, вы узнаете, какова высота цилиндра и отношение площади поверхности к объему. Если вам когда-нибудь придется решать такую задачу, не забудьте использовать этот калькулятор радиуса цилиндра. Вам нужно выполнить всего три основных шага:
- Определите какие параметры цилиндра вам известны.
- Введите значений выбранных величин.
- Считать результат вычислений.
Разве это не просто? Кроме того, с помощью нашего калькулятора вы можете выбрать единицы измерения любого параметра, который вам нужен. Это может быть очень полезно во многих вычислениях! Если вы хотите узнать больше о преобразовании единиц измерения, обязательно ознакомьтесь с преобразователем длины и инструментом преобразования объема!
Часто задаваемые вопросы
Как найти радиус цилиндра, зная его объем?
Чтобы определить радиус цилиндра по его объему, нужно также знать высоту (высоту) этого цилиндра:
- Умножить высоту на
π ≈ 3,14.
- Разделите объем на результат шага 1.
- Извлеките квадратный корень из результата шага 2.
- У вас есть радиус! Это было не так уж сложно, не так ли?
Как найти радиус, зная диаметр?
Чтобы определить радиус окружности (например, основания цилиндра), нужно диаметр разделить на 2 . Например, если диаметр равен 7 , то радиус равен 3,5 .
Каков радиус цилиндра?
Цилиндр — это твердое тело, имеющее два одинаковых круглых основания. Радиус цилиндра — это радиус основания этого цилиндра.
Доминик Черня, PhD
Высота (h)
Объем
Диагональный (D)
Свеча к объему к объему
Площади поверхности
Площадь базовой поверхности
Площадь боковой поверхности
Общая площадь поверхности
Радиус
Радиус (R)
Проверьте 21 Аналогичные геометрические калькуляторы 📦
Радиус (R).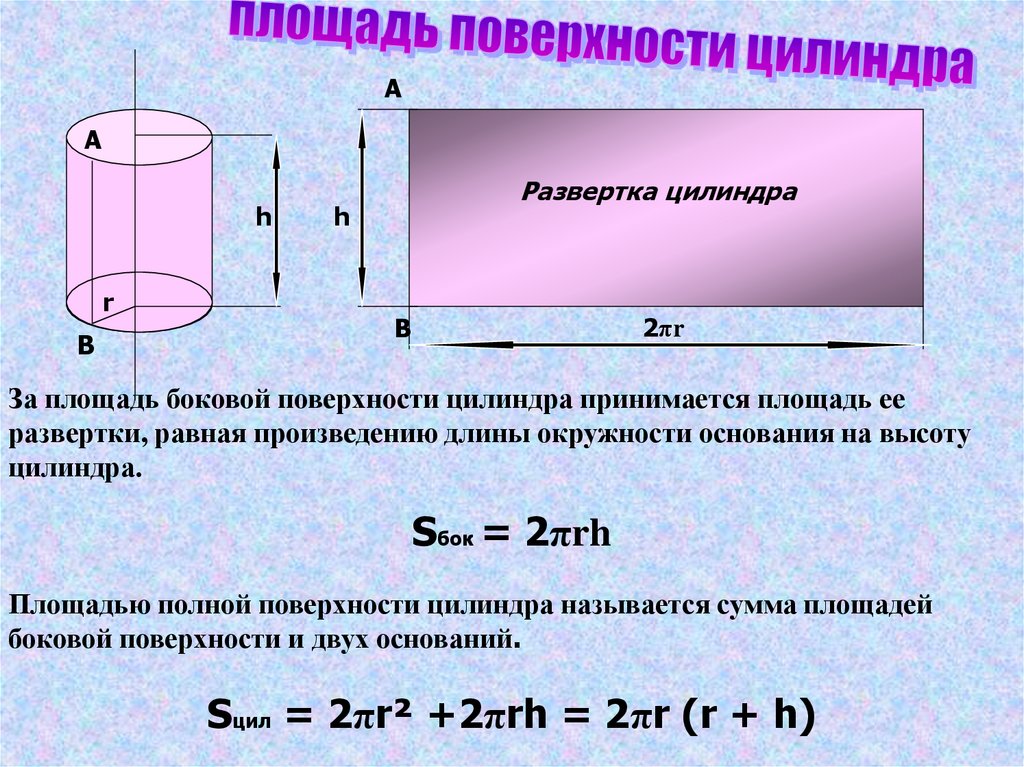
Площадь полушарияКубКуб Рассчитать: найти v, a, d… Еще 18
Как найти площадь круга и площадь поверхности цилиндра. Какую формулу вы используете?
Какова площадь круга?Площадь определяется как объем пространства, занимаемый двумерной формой или поверхностью. Площадь измеряется путем взятия общего количества квадратов 1 на 1 единицу, которые могут поместиться в двумерную форму или поверхность.
Площадь круга может быть рассчитана с использованием следующей формулы:
Площадь круга для площади круга
A = Area of Circle
π = 3.14 (rounded down) or 22/7
r = radius круга
Пример задачи 1: Найдите площадь круга, радиус которого равен 12 см.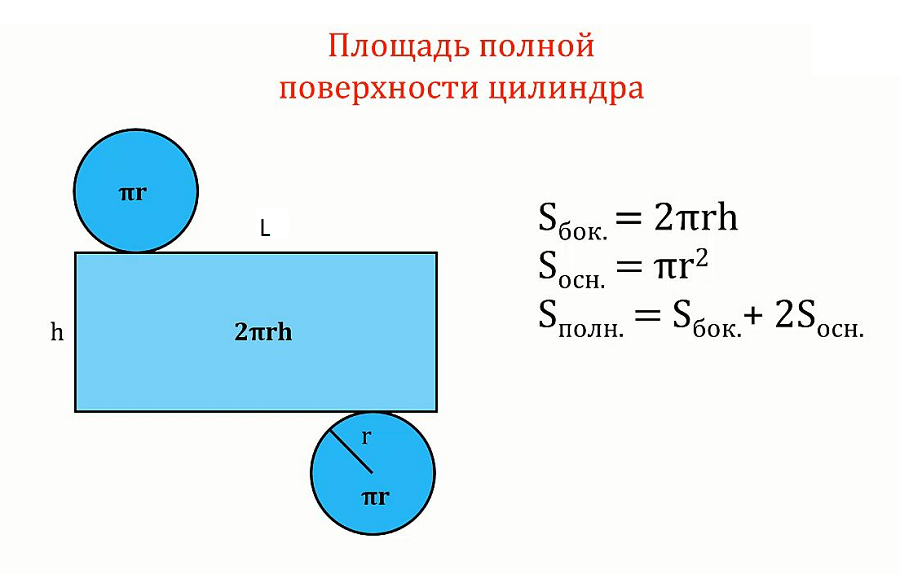 Используйте 3.14 как π.
Используйте 3.14 как π.
Шаг 1 : Подставим радиус и π в формуле. Радиус равен 12, а π равно 3,14.
Шаг 2 : Упростите и запишите ответ в единицах измерения в квадрате.
Значит, площадь круга с радиусом 12 см равна 452,16 см в квадрате!
Пример задачи 2:
Найдите площадь круга, диаметр которого равен 28 дюймам. Давайте на этот раз используем 22/7 для π .
Ответ:Шаг 1 : Найдите радиус. Если диаметр 28 дюймов, то радиус равен 14. Это половина длины диаметра.
Шаг 2 : Подставим радиус и π в формулу. Радиус равен 12, а π равно 22/7.
Шаг 3: Просто рассчитайте площадь!
Итак, площадь круга диаметром 28 дюймов равна 616 дюймов в квадрате!
Как площадь круга связана с нахождением площади поверхности цилиндра? Площадь поверхности представляет собой сумму площадей всех поверхностей трехмерной фигуры. Лучший способ представить площадь поверхности — это взять трехмерную фигуру и сгладить ее, чтобы увидеть все грани. Его еще называют сеткой. Посмотрите на следующий пример с использованием цилиндра:
Лучший способ представить площадь поверхности — это взять трехмерную фигуру и сгладить ее, чтобы увидеть все грани. Его еще называют сеткой. Посмотрите на следующий пример с использованием цилиндра:
В примере выше, в примере. фигура прямоугольной формы, которая на самом деле изогнута. Вам нужно будет найти площадь каждой части, а затем добавить сумму, чтобы получить площадь поверхности. В то время как для кругов используется нормальная формула площади круга, изогнутая прямоугольная фигура использует формулу длины окружности. Напомним, что площадь прямоугольника равна площади = длине х высоте, или A = l x h 9.0003
Как найти площадь поверхности цилиндра:
Площадь кругов + Площадь изогнутого прямоугольника = Площадь поверхности
Формула для расчета площади цилиндра цилиндра с радиусом 4 дюйма и высотой 6 дюймов . Используйте 3.14 как π
Используйте 3.14 как π
Ответ:Шаг 1 : Определите радиус и высоту.
r= 4 дюйма
h= 6 дюймов
Шаг 2: Подставьте значения в формулу.
Шаг 3: Упрощение.
SA = 2 ((3,14 * 16) + 2 (3,14) (4) (6)
SA = 2 (3,14 * 16) + 2 (75,36)
SA = 2 (50,24) + 2 (75,36)
SA = 100,48 + 150,72
SA = 251,2 дюйма в квадрате
Таким образом, площадь поверхности цилиндра с радиусом 4 дюйма и высотой 6 дюймов равна 251,2 дюйма в квадрате.
Пример задачи 4. Цилиндр:
Найдите площадь поверхности этого цилиндра. Используйте 3,14 как π.
Ответ:Шаг 1 : Определите радиус и высоту.
r= 5 см и h=9,5 см
Шаг 2: Подставьте значения в формулу.
Шаг 3 : Упрощение.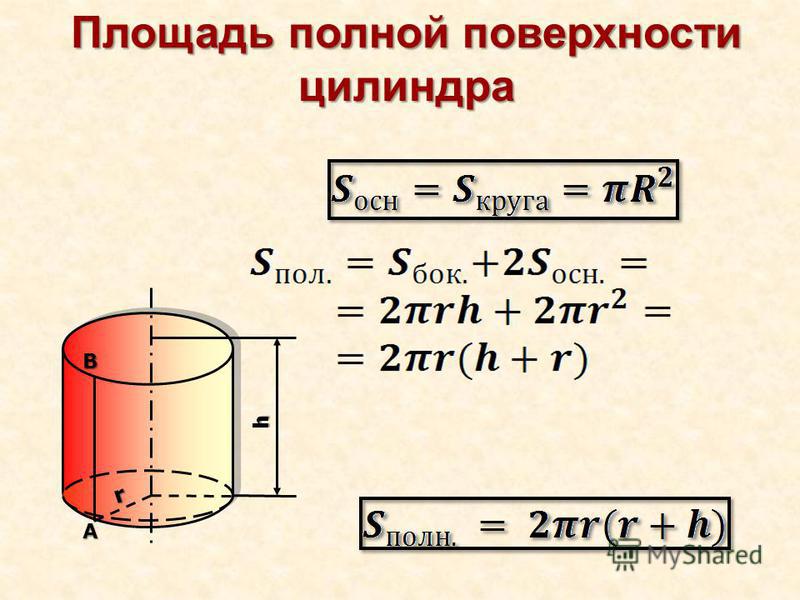

 В данном случае можно выразить радиус из длины окружности, если она дана. Высота может быть найдена, если в условии задано значение образующей. В этом случае образующая будет равна высоте. Формула боковой поверхности данного тела выглядит так: S= 2 π rh.
В данном случае можно выразить радиус из длины окружности, если она дана. Высота может быть найдена, если в условии задано значение образующей. В этом случае образующая будет равна высоте. Формула боковой поверхности данного тела выглядит так: S= 2 π rh. В таком случае ширина прямоугольника будет являться диаметром окружности, лежащей в основании тела. Длина фигуры будет равна образующей или высоте цилиндра. Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π.
В таком случае ширина прямоугольника будет являться диаметром окружности, лежащей в основании тела. Длина фигуры будет равна образующей или высоте цилиндра. Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π.