Анекдот : 1 курс. Первая пара по матанализу в техническом вузе… Преподаватель: — Поздравляю Всех с началом учебного года…!!!…Записываем первую тему: Действительная функция действительной переменной. Сюръективные, инъективные и биективные функции… Голос с задней парты: — Алло, военкомат..?!..Я передумал…Заберите меня в армию…:joy::thumbsup: — Обсуждай
Анекдот : 1 курс. Первая пара по матанализу в техническом вузе… Преподаватель: — Поздравляю Всех с началом учебного года…!!!…Записываем первую тему: Действительная функция действительной переменной. Сюръективные, инъективные и биективные функции… Голос с задней парты: — Алло, военкомат..?!..Я передумал…Заберите меня в армию…:joy::thumbsup: — ОбсуждайАС
Александр Соловейчик
Анекдот : 1 курс. Первая пара по матанализу в техническом вузе… Преподаватель: — Поздравляю Всех с началом учебного года…!!!…Записываем первую тему: Действительная функция
действительной переменной. Сюръективные,
Сюръективные,
инъективные и биективные функции…
Голос с задней парты:
— Алло, военкомат..?!..Я передумал…Заберите меня в армию…год
голос
анекдот
армия
начало
тема
курс
пара
функция
преподаватель
вуз
военкомат
парта
201
10
11
Ответы
ОС
Олег Сорокин
От таких иностранных ругательств и на марс сбежишь ))))))))))))))))))))))
0
АС
Александр Соловейчик
Спасибо…за проявленный интерес. .Лайки приветствуются..по закону..Справа от анекдота,загадки или вопроса жмите на сердечко-значок «понравилось», а то они без оценокскучают! Заходите на мою страничку… подписывайтесь при желании -там много интересных загадок, анекдотов убойных- штук 200..пока…будет больше и др…Не пожалеете.Настроение гарантирую
.Лайки приветствуются..по закону..Справа от анекдота,загадки или вопроса жмите на сердечко-значок «понравилось», а то они без оценокскучают! Заходите на мою страничку… подписывайтесь при желании -там много интересных загадок, анекдотов убойных- штук 200..пока…будет больше и др…Не пожалеете.Настроение гарантирую
1
Александр Гончар
щя умру нахер от смеха
0
АС
Александр Соловейчик
Спасибо…за проявленный интерес..Лайки приветствуются..по закону..Справа от анекдота,загадки или вопроса жмите на сердечко-значок «понравилось», а то они без оценокскучают! Заходите на мою страничку… подписывайтесь при желании -там много интересных загадок, анекдотов убойных- штук 200..пока…будет больше и др. ..Не пожалеете.Настроение гарантирую
..Не пожалеете.Настроение гарантирую
1
Александр Гончар
Спасибо!
1
АС
Александр Соловейчик
Рад если буду полезен
1
Soso Motsonelidze
Molodec nahel svoio prednognahenie
0
АС
Александр Соловейчик
Да
1
Soso Motsonelidze
O.k
1
Валентина Карих
Трясусь от смеха!!!
0
Валентина Карих
https://ok. ru/video/189753657869
ru/video/189753657869
0
Дмитрий Паул
Мда, из двух зол…
0
АС
Александр Соловейчик
Спасибо…за проявленный интерес..Лайки приветствуются..по закону..Справа от анекдота,загадки или вопроса жмите на сердечко-значок «понравилось», а то они без оценокскучают! Заходите на мою страничку… подписывайтесь при желании -там много интересных загадок, анекдотов убойных- штук 200..пока…будет больше и др…Не пожалеете.Настроение гарантирую
1
Зоя Михайлова
0
RV
Rusu Victor
0
АС
Александр Соловейчик
1
RV
Rusu Victor
1
Татьяна0
Колокольчик.
1
Сестрица Алёнушка
)))
0
АС
Александр Соловейчик
Спасибо…за проявленный интерес..Лайки приветствуются..по закону..Справа от анекдота,загадки или вопроса жмите на сердечко-значок «понравилось», а то они без оценокскучают! Заходите на мою страничку… подписывайтесь при желании -там много интересных загадок, анекдотов убойных- штук 200..пока…будет больше и др…Не пожалеете.Настроение гарантирую
1
Зоя Овосиенко
…только ОБЩЕНИЯ, которое ЭТОТ сайт предполагает, НЕ получается после Ваших анекдотов, потому они и запрещены правилами сайта. ..
..
Но, пока, Вас, вроде, на блокируют…
1
АС
Александр Соловейчик
Им тоже наверное нравятся
1
Зоя Овосиенко
Вполне возможно.
1
АС
Александр Соловейчик
У меня элитарные все
1
Отображения. Тождественное отображение — презентация онлайн
1. ОТОБРАЖЕНИЯ
Определение 1.Говорят, что задано отображение f: A B, если
заданы, во-первых, множество А (называемое
областью определения), во-вторых, множество В
(называемое областью значений), и, в третьих,
правило f, которое каждому элементу а из множества
A ставит в соответствие ровно один элемент f(a) из
множества B.
 Элемент f(a) называют образом
Элемент f(a) называют образомэлемента a при отображении f, сам элемент a при
этом называется аргументом. Множество f(C),
состоящее из образов всех точек множества C A,
называется образом множества С.
Упражнение 1.
Петя сопоставил каждому городу России, где
он бывал, число 1, каждому городу России,
где бывал его друг Вася, число 2, а каждому
городу России, где не бывали ни он ни Вася,
— число 0. Является ли такое сопоставление
отображением из множества всех городов
России в множество {0, 1, 2}?
Упражнение 2
«Вершины A и C параллелограмма ABCD
жестко закреплены, а вершина B пробегает
прямую l. Какую фигуру «вычерчивает»
вершина D?»
Какое отображение работает в этой задаче?
Z0 – центральная симметрия с центром O
(O – середина отрезка BD).
Она является отображением плоскости в себя, как и
все другие движения и подобия плоскости.
D = Z0(B)
A
m = Z0(l)
O
С
B
l
Упражнение 3
«a1 = 1, an+1 = an+1/n(n+1) при всех n 1.
 Чему
Чемуравно a2018?»
О каком отображении идет речь в этой
задаче?
• Отображение, область определения
которого — множество всех натуральных
чисел, называется последовательностью.
• У последовательностей аргумент по
традиции пишут как индекс: an вместо a(n).
• Последовательность в упражнении 3 задана
рекуррентно (индуктивно). Чтобы, работая с
ней, обойтись без длинных вычислений, её
надо задать формулой, выражающей образ
натурального числа n (то есть n-ый член
последовательности) через само это число.
Упражнение 4
Задайте формулами последовательности:
а) 2, 5, 8, 11, …;
б) 2, 5, 10, 17, …;
в) 1, 2, 6, 24, …;
г) 1, 2, 3, …
Упражнение 5
Имеются три автомата. Первый прибавляет к
любому введённому в него числу единицу,
второй — возводит введённое в него число в
квадрат, третий — вычитает 3. В первый
автомат ввели число x, результат y ввели во
второй автомат, а новый результат z — в
третий.
 Получилось число t.
Получилось число t.• а) Выразите t через x.
• б) Можно ли по известному t восстановить x?
• в) Каким будет ответ на вопрос б), если второй автомат возводит не в квадрат, а в куб?
f(x) = x+1, g(y) = y2, h(z) = z-3.
h(g(f(x))) = (x+1)2-3
• Отображение из числового множества в
числовое называется числовой функцией, а
образы аргументов – значениями функции.
• В упражнении 5 функции были заданы
описаниями. Решая его, мы заменили эти
описания формулами. Именно так числовые
функции обычно и задают.
Определение 2.
Пусть заданы отображения f: A B и g: B C.
Сопоставим каждому элементу x A элемент
y = f(x) B, а тому — элемент z = g(y) C. Получится
«сквозное» отображение h: A C, заданное
правилом h(x) = g(f(x)). Оно называется композицией
отображений g и f. Операция композиции
обозначается кружочком: пишут h = g f.
У функций, заданных формулами, легко искать
композицию: достаточно подставить одну
формулу в другую, что мы в упр.
 5 и сделали.
5 и сделали.• Отображения из числовых множеств в числовые
называют числовыми функциями.
• В упражнении 5 функции были заданы
описаниями. Решая его, мы заменили эти
описания формулами. Именно так числовые
функции обычно и задают: из школьного курса
Вам известны линейные функции f(x) = ax+b,
квадратичная функция f(x) = x2, обратная
пропорциональность f(x) = 1/x.
• У функций, заданных формулами, легко искать
композицию: достаточно подставить одну
формулу в другую.
Тождественное отображение
• Последовательность г) из упражнения 4 —
пример тождественного отображения, при
котором каждый элемент переходит в себя, а
область определения совпадает с областью
значений. Тождественное отображение
множества А обозначается idA.
• Упражнение 6. Пусть f: A B — произвольное
отображение. Найдите композиции idB f и f idA.
Упражнение 7
Докажите, что все точки графика
арифметической прогрессии an = a+nd
(n = 0, 1, …) лежат на одной прямой.

• Доказательство: Это график линейной
функции y = dx+a.
• Как видим, графики у арифметической
прогрессии и функции из R в R, заданной
тем же законом, различны, то есть
отображения, заданные одной и той же
формулой, но с разными областями
определения, имеют разные свойства
(ещё пример различия в свойствах:
линейную функцию из R в R рекуррентно не
задашь).
Упражнение 8
Проказница Мартышка, Осел, Козел и косолапый
Мишка, а также Коза с баяном расселись, чтобы
сыграть концерт. Играли они отвратительно, и
потому дважды менялись местами. Сначала
Мартышка села на место Осла, Осел — на место
Козла, Козел — на место Козы, а Коза — на место
Мишки, а Мишка — на оставшееся место. Затем
Коза поменялась местами с Ослом, а Козел — с
Мартышкой. Выясните, кто на чьем месте в итоге
оказался.
Отображения из упражнения 8 удобно
задавать орграфом или таблицей.
1
2
3
4
5
2
5
3
4
5
2
1
1
4
3
Определение 3
Если развернуть все стрелочки на их графах,
задающих отображения в упражнении 8, то
снова получатся отображения.
 Такие
Такиеотображения называются обратимыми, а
отображение f–1: B A, получающееся из
обратимого отображения f: A B «разворотом
всех стрелочек» — обратным к отображению f.
Аналитически определение обратного
отображения записывается так:
x = f–1(y) y = f(x).
Упражнение 9
Докажите следующие свойства обратных
отображений:
а) Если отображение f обратимо, то обратимо и
отображение f–1, и обратным к нему является
отображение f.
б) Отображения g: B A и f: A B являются
взаимно обратными тогда и только тогда, когда
g f = idA и f g = idB.
в) Если отображения f: A B и g B C обратимы, то
обратима и их композиция, причём (g f)–1 = f–1 g–1.
Очевидно, отображение f: A B обратимо тогда и только
тогда, когда одновременно обладает двумя свойствами:
1) в каждый элемент множества B «входит стрелочка», то
есть каждый элемент из B является образом какого-то
элемента из A;
2) ни в какой элемент множества B не входит двух стрелочек,
то есть разные элементы множества A переходят в разные
элементы множества B.

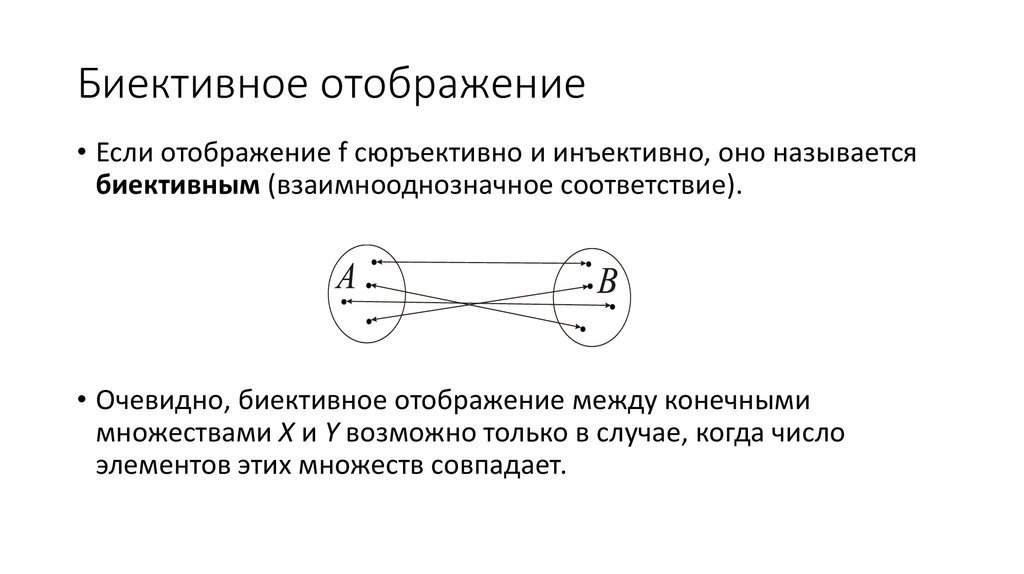
Первое свойство называется сюръективностью, второе —
инъективностью, а оба вместе — биективностью или
взаимной однозначностью.
Инъективные, сюръективные и биективные отображения
коротко называют инъекциями, сюръекциями и биекциями.
Биекции множества на себя называют ещё
преобразованиями этого множества. Например, движения и
подобия плоскости являются её преобразованиями.
Определение 4
Отображение f: A B называется
инъективным/сюръективным, если в при
этом отображении каждый элемент множества
B переходит не больше/не меньше одного
элемента множества A. Отображение, которое
одновременно и инъективно, и сюръективно,
называется биективным или взаимнооднозначным.
Отображение имеет обратное тогда и
только тогда, когда оно биективно.
Упражнение 10.
Обратима ли композиция отображений
h(g(f(x))) = (x+1)2-3
из упражнения 5?
Упражнение 11
Подберите в качестве областей определения и
значений такие числовые множества, чтобы
формула f(x) = x2 задавала отображение,
которое
• а) биективно;
• б) инъективно, но не сюръективно;
• в) сюръективно, но не инъективно;
• г) не сюръективно и не инъективно.

Упражнение 12
Многие комбинаторные задачи можно понимать как задачи
о подсчёте тех или иных отображений. Так преобразования
конечного множества известны вам под названием его
перестановок. Сформулируйте как задачи о подсчёте
количества отображений задачи о нахождении
• а) числа размещений с повторениями n предметов по m
местам;
• б) числа размещений (без повторений) n предметов по m
местам;
• в) числа перестановок с повторениями n1 предметов типа
1, n2 предметов типа 2, …, nk предметов типа k;
• г) числа всех подмножеств данного конечного множества;
• д) числа разбиений множества {1, 2, …, n} на k непустых
подмножеств, выстроенных в ряд.
Множества, связанные биективным отображением,
называются равномощными. Для конечных
множеств равномощность означает, что в них
поровну элементов. На этом основан известный
принцип кодировки, когда подсчет числа каких-либо
объектов заменяется подсчетом числа присвоенных
им кодов, находящихся с ними в биективном
соответствии.

Например, в упражнении 12г мы кодировали
подмножества данного множества отображениями
этого множества в множество {0, 1}.
Инъективные, сюръективные и биективные функции
\(\require{mathrsfs}\newcommand{\abs}[1]{\left| #1 \right|} \renewcommand{\emptyset}{\varnothing} \DeclareMathOperator{\dom}{dom} \DeclareMathOperator{\range}{rng} \DeclareMathOperator{\пермь}{пермь} \новая команда{\lt}{<} \новая команда{\gt}{>} \newcommand{\amp}{&} \)
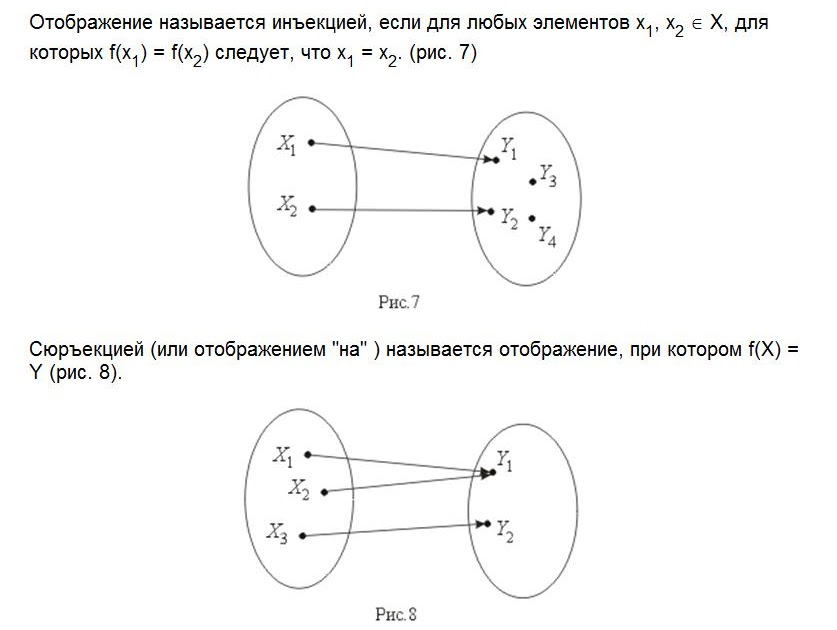
¶Определение 4.2.1
Говорят, что функция \(f : A \to B\) является инъективной (или однозначной , или 1-1 ), если для любого \(x,y \in A\text {,}\) \(f(x) = f(y)\) подразумевает \(x = y\text{.}\) В качестве альтернативы мы можем использовать противоположную формулировку: \(x \not= y\) подразумевает \(f(x) \not= f(y)\text{,}\), хотя на практике обычно более эффективно первое. 9{-1}|_{\range(f)}\) — это функция.
Определение 4.2.3
Функция \(f : A \to B\) называется
 }\) То есть для каждого \( b \in B\) существует некоторое \(a \in A\), для которого \(f(a) = b\text{.}\)
}\) То есть для каждого \( b \in B\) существует некоторое \(a \in A\), для которого \(f(a) = b\text{.}\)Определение 4.2.4
Функция \(f : A \to B\) называется биективной (или взаимно однозначной и на ), если она одновременно инъективна и сюръективна. Мы также говорим, что \(f\) есть индивидуальная переписка .
Теорема 4.2.5
Композиция инъективных функций инъективна, а композиция сюръективных функций сюръективна, поэтому композиция биективных функций биективна. То есть пусть \(f: A \to B\) и \(g: B \to C\text{.}\)
- Если \(f,g\) инъективны, то и \(g \circ f\text{.}\)
- Если \(f,g\) сюръективны, то \(g \circ f\text{.}\) сюръективны
- Если \(f,g\) биективны, то и \(g \circ f\text{.}\)
Предположим, что \(f,g\) инъективны и что \((g \circ f)(x) = (g \circ f)(y)\text{.}\) Это означает, что \(g(f(x )) = g(f(y))\text{.}\) Поскольку \(g\) инъективно, \(f(x) = f(y)\text{.}\) Поскольку \(f\) инъективно, \(x = y\text{. }\) Таким образом, \(g \circ f\) инъективно.
}\) Таким образом, \(g \circ f\) инъективно.
Предположим, что \(f,g\) сюръективны, и предположим, что \(z \in C\text{.}\) Поскольку \(g\) сюръективно, существует некоторое \(y \in B\) с \(g (y) = z\text{.}\) Так как \(f\) сюръективен, существует некоторый \(x \in A\) такой, что \(f(x) = y\text{.}\) Поэтому \ (z = g(f(x)) = (g \circ f)(x)\) и, следовательно, \(z \in \range(g \circ f)\text{.}\) Таким образом, \(g \circ f\) сюръективен. 9{-1}\) сюръективен.
Определение 4.2.8
Пусть \(A\) — непустое множество. перестановка \(A\) является биекцией из \(A\) в себя.
Обратите внимание, что теперь у нас есть два разных экземпляра слова перестановка, не кажется ли это запутанным? Что ж, давайте посмотрим, что они не так уж и отличаются в конце концов. Пусть \(A\) — непустое конечное множество с \(n\) элементами \(a_1,\ldots,a_n\text{.}\). Тогда пусть \(f : A \to A\) будет перестановкой (как определено выше). Тогда \(f(a_1),\ldots,f(a_n)\) есть некоторый порядок элементов \(A\text{,}\), т. е. перестановка в смысле комбинаторики. Обратите внимание, что в этом списке ничего не повторяется (поскольку \(f\) инъективен), и каждый элемент \(A\) указан (поскольку \(f\) сюръективен). Таким образом, каждая перестановка функций дает нам комбинаторную перестановку.
е. перестановка в смысле комбинаторики. Обратите внимание, что в этом списке ничего не повторяется (поскольку \(f\) инъективен), и каждый элемент \(A\) указан (поскольку \(f\) сюръективен). Таким образом, каждая перестановка функций дает нам комбинаторную перестановку.
Однако нам нужно пойти и другим путем. Пусть \(b_1,\ldots,b_n\) будет (комбинаторной) перестановкой элементов \(A\text{.}\) Определим функцию \(f: A \to A\) с помощью \(f(a_1 ) = b_1\text{.}\) Поскольку любой элемент \(A\) указан в списке \(b_1,\ldots,b_n\text{,}\) только один раз, то \(f\) инъективен. Поскольку каждый элемент \(A\) встречается где-то в списке \(b_1,\ldots,b_n\text{,}\), то \(f\) сюръективен.
Итак, в чем разница между комбинаторной перестановкой и функциональной перестановкой? Ну, две вещи: одна — это то, как мы об этом думаем, но здесь каждая точка зрения дает некоторый взгляд на другую. Однако другое отличие, пожалуй, гораздо интереснее: комбинаторные перестановки можно применить только к конечных множеств, в то время как перестановки функций могут применяться даже к бесконечным множествам! Это означает, что перестановку \(f : \mathbb{N} \to \mathbb{N}\) можно рассматривать как «переупорядочение» элементов \(\mathbb{N}\text{. }\)
}\)
Теорема 4.2.9
Пусть \(A\) — непустое множество.
- Карта тождества \(I_A\) является перестановкой.
- Композиция перестановок есть перестановка.
- Обратная перестановка является перестановкой. 9{-1}\текст{.}\)
Все эти утверждения напрямую следуют из уже доказанных результатов.
Приведенная выше теорема, вероятно, является одной из самых важных, с которыми мы сталкивались. По сути, он говорит, что перестановки множества \(A\) образуют математическую структуру, называемую группой . Группа — это просто набор вещей (в данном случае перестановок) вместе с бинарной операцией (в данном случае композицией функций), которые удовлетворяют нескольким свойствам:
- бинарная операция ассоциирована (мы уже доказали это о композиции функций),
- применение бинарной операции к двум элементам в наборе сохраняет вас в наборе (пункт 2 выше),
- существует идентификатор для бинарной операции, т.
 е. такой элемент, что применение операции с чем-то еще оставляет эту вещь неизменной (пункт 1 и пункт 4 выше),
е. такой элемент, что применение операции с чем-то еще оставляет эту вещь неизменной (пункт 1 и пункт 4 выше), - у каждого элемента есть обратная операция для бинарной операции, т. е. такой элемент, что применение операции к элементу и ее обратной дает идентичность (пункт 3 и пункт 5 выше),
Скорее всего, вы никогда не слышали о группе, но они являются фундаментальным инструментом современной математики и основой современной алгебры. Группы будут единственным объектом изучения на протяжении всего курса MATH-320!
Группы были изобретены (или открыты, в зависимости от вашей метаматематической философии) Эваристом Галуа, французским математиком, который погиб на дуэли (из-за девочки) в возрасте 20 лет 31 мая 1832 года, в разгар Французской революции. Галуа изобрел группы, чтобы решать, вернее, 92 + cx + d = 0\) через коэффициенты \(a,b,c,d\) и используя только операции сложения, вычитания, умножения, деления и извлечения корней. Есть и другая аналогичная формула для уравнений четвертой степени, но кубическая и формала четвертой степени были открыты только в середине второго тысячелетия нашей эры!
Затем еще несколько сотен лет математики ищут формулу уравнения пятой степени, удовлетворяющую тем же свойствам. Галуа изобрел группы, чтобы решить эту проблему. Хотя вместо того, чтобы найти формулу, он доказал, что такой формулы не существует для квинтики, да и для любого полинома более высокой степени. Когда мы говорим, что такой формулы не существует, мы имеем в виду, что не существует формулы, включающей только упомянутые коэффициенты и упомянутые операции; есть и другие способы нахождения корней многочленов более высоких степеней. Следует отметить, что Нильс Хенрик Абель также доказал неразрешимость квинтики, причем его решение появилось раньше, чем решение Галуа, хотя Абель не обобщил свой результат на все многочлены высших степеней. Ясно, однако, что Галуа не знал решения Абеля, а идея группы была революционной.
Галуа изобрел группы, чтобы решить эту проблему. Хотя вместо того, чтобы найти формулу, он доказал, что такой формулы не существует для квинтики, да и для любого полинома более высокой степени. Когда мы говорим, что такой формулы не существует, мы имеем в виду, что не существует формулы, включающей только упомянутые коэффициенты и упомянутые операции; есть и другие способы нахождения корней многочленов более высоких степеней. Следует отметить, что Нильс Хенрик Абель также доказал неразрешимость квинтики, причем его решение появилось раньше, чем решение Галуа, хотя Абель не обобщил свой результат на все многочлены высших степеней. Ясно, однако, что Галуа не знал решения Абеля, а идея группы была революционной.
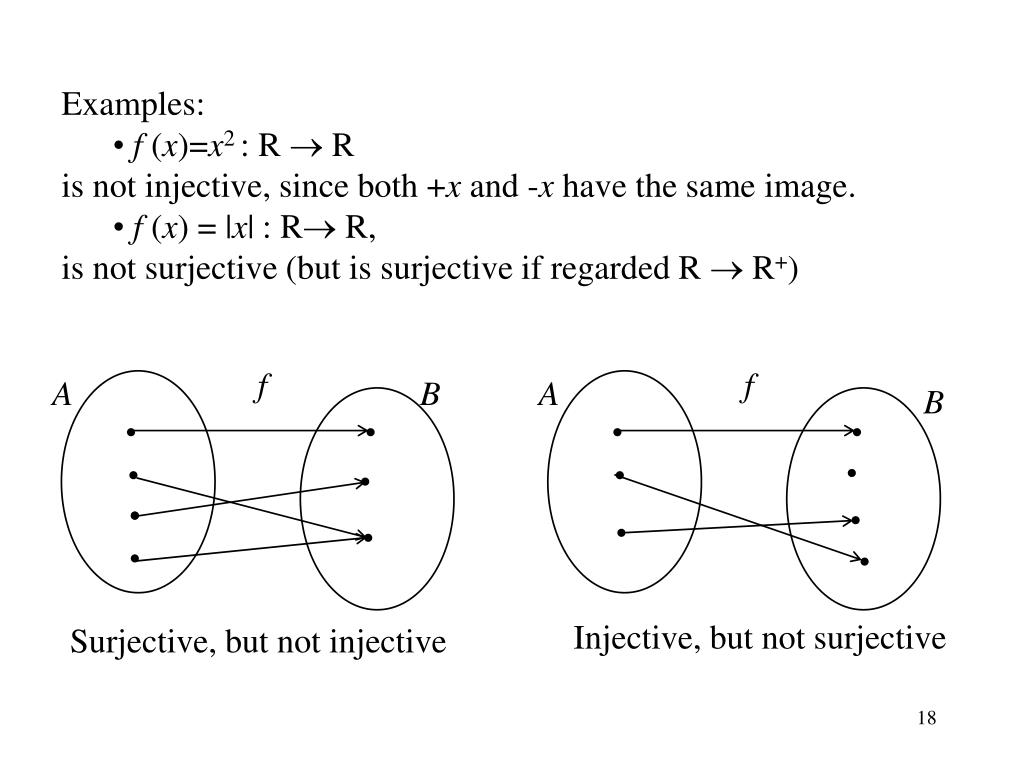
Типы функций: инъективные, сюръективные и биективные
письменные в maths
Вы, вероятно, знакомы с тем, что такое функция: это формула или правило, описывающее отношение между одним числом и другим. Например, функция \(f(x) = |x| + 1\) описывает отношение между числом и его абсолютным значением плюс 1. Если вы вспомните нашу предыдущую запись в блоге, вы увидите, что мы фактически описывающим является отношение, где \(x\mathrel{R}f(x)\) задается как \(f(x) = |x| + 1\).
Например, функция \(f(x) = |x| + 1\) описывает отношение между числом и его абсолютным значением плюс 1. Если вы вспомните нашу предыдущую запись в блоге, вы увидите, что мы фактически описывающим является отношение, где \(x\mathrel{R}f(x)\) задается как \(f(x) = |x| + 1\).
Если мы возьмем три элемента из \(x\), \(\{-1, 0, 1\}\) и пропустим их через \(f(x)\), мы получим набор упорядоченных пар \ (f = \{(-1, 2), (0, 1), (1, 2)\}\). Однако мы также можем представить эту связь в форме ниже, где мы берем набор, созданный нашими входными элементами, и сопоставляем их с набором, заданным нашими выходными элементами.
Приведенный выше пример иллюстрирует несколько важных особенностей функций, отличающих их от отношений. Во-первых, как вы, наверное, уже поняли, функция предназначена для отображения элементов из одного множества \(A\) в другое \(B\), которое обозначается как \(f: A \rightarrow B\). В нашем примере выше мы просто отображали набор из трех чисел \(\{-1, 0, 1\}\) в другой набор из трех чисел \(\{2, 1, 2\}\ ).
Однако функции могут использоваться (и обычно используются) для описания отношений между бесконечными множествами, такими как натуральные или действительные числа. На самом деле, мы можем продолжить наш пример функции, чтобы подумать о таком отображении. Поскольку наш входной набор включает как -1, так и 0, давайте представим, что наш входной набор — это целые числа \(\mathbb{Z}\). Каким тогда будет набор, на который мы сопоставляем? Поскольку любой \(f(x)\) никогда не может быть меньше 1, то выходным набором будут все натуральные числа \(\mathbb{N}\). Таким образом, наша функция \(f(x) = |x| + 1\) будет определена как \(f: \mathbb{Z} \rightarrow \mathbb{N}\).
Это приводит к еще двум наблюдениям о функциях. Хотя входной и выходной наборы могут быть одинаковыми, они не обязательно должны быть одинаковыми, как в случае с нашим примером. Этот пример также показывает, что входной набор влияет на то, что будет содержать выходной набор. В нашем примере входной набор содержал только целые числа, поэтому выходной набор может содержать только положительные целые числа. Однако, если бы наш входной набор был действительными числами, то наш выходной набор был бы набором положительных действительных чисел больше 1.
Однако, если бы наш входной набор был действительными числами, то наш выходной набор был бы набором положительных действительных чисел больше 1.
Последнее, что нужно отметить о функциях, касается того, как входные элементы соотносятся с выходными элементами. В отличие от отношений, каждое входное значение \(x\) может сопоставляться только с одним значением выходного значения \(f(x)\). Это означает, что, например, отношение, включающее \((1, 2)\) и \((1, 3)\), будет допустимым отношением, но не функцией.
Домен, кодовый домен и диапазон
Давайте начнем давать имена этим частям функций. Наш входной набор называется доменом 9.0160 функции, а выходной набор называется кодовым доменом . Наконец, все элементы в кодовом домене, заданные \(f(x)\) для каждого \(x\) в домене, называются диапазоном функции. В зависимости от функции кодовый домен и диапазон могут быть равны или диапазон может быть подмножеством кодового домена. Это можно увидеть в приведенном ниже примере для \(g(x) = 2x\), если мы представим, что и домен, и кодовый домен являются набором целых чисел.
Это можно увидеть в приведенном ниже примере для \(g(x) = 2x\), если мы представим, что и домен, и кодовый домен являются набором целых чисел.
Вы видите, что домен сопоставляется только с некоторыми элементами в домене кодов, для которых \(g(x)\) в два раза больше элементов в домене. В этом случае диапазон (показан розовым) будет состоять из всех четных целых чисел, подмножества \(\mathbb{Z}\).
Типы функций
Вы, наверное, уже заметили, глядя на две функции, о которых мы говорили до сих пор, что существуют разные шаблоны в том, как элементы в домене связаны с элементами в кодовом домене. В случае \(f(x) = |x|+ 1\) все элементы в домене сопоставляются со значением в домене, но между ними нет уникальной однозначной связи. Например, \(f(-1) = f(1) = 2\). Напротив, в случае \(g(x) = 2x\) в домене нет значения для каждого значения в домене кодов. Например, нет \(a\) в области, для которой \(g(a) = 1\).
Эти способы, которыми элементы в домене и кодовом домене связаны друг с другом, имеют определенные имена. Когда каждое значение \(a, a’\) в домене \(A\) отображается в другое \(f(a), f(a’)\) в домене кодов \(B\), мы говорим, что эта функция инъективная . Из наших двух примеров \(g(x) = 2x\) является инъективным, так как каждое значение в домене отображается в другое значение в кодовом домене, но \(f(x) = |x| + 1\) не является инъективным, так как разные элементы в домене могут сопоставляться с одним и тем же значением в домене кода.
Когда каждое значение \(a, a’\) в домене \(A\) отображается в другое \(f(a), f(a’)\) в домене кодов \(B\), мы говорим, что эта функция инъективная . Из наших двух примеров \(g(x) = 2x\) является инъективным, так как каждое значение в домене отображается в другое значение в кодовом домене, но \(f(x) = |x| + 1\) не является инъективным, так как разные элементы в домене могут сопоставляться с одним и тем же значением в домене кода.
И наоборот, когда каждое значение \(b\) в домене кодов \(B\) отображается в значение \(a\) в домене \(A\), тогда мы говорим, что эта функция сюръективна . Снова взглянув на наши примеры, мы видим, что \(g(x) = 2x\) не является сюръективным, так как все нечетные целые числа в домене кодов не отображаются ни в какое значение в домене. Однако \(f(x) = |x| + 1\) является сюръективным для \(f: \mathbb{Z} \rightarrow \mathbb{N}\), поскольку каждое натуральное число в кодовой области отображается в целое число в домен. Это поднимает важный вопрос: является ли функция сюръективной, зависит от того, как определен кодовый домен.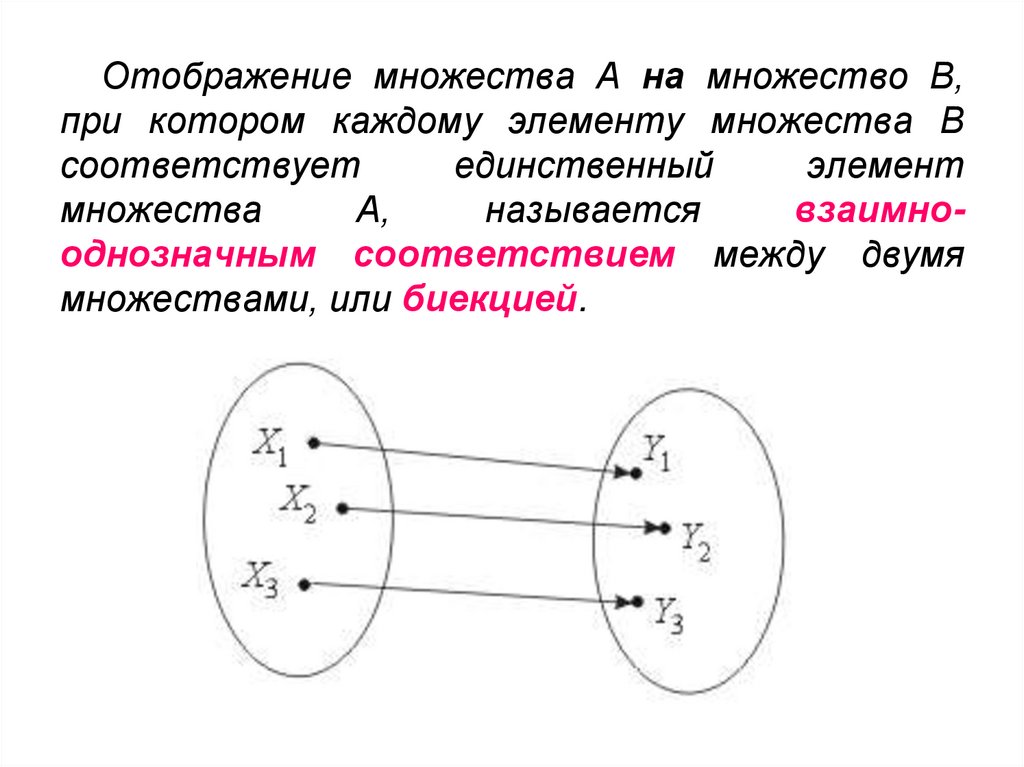 Если бы мы определили домен и домен \(f(x) = |x| + 1\) как \(f: \mathbb{Z} \rightarrow \mathbb{Z}\), то это не было бы сюръективным, как любой значение кодового домена \(\leq 0\) не будет сопоставляться ни с чем в домене.
Если бы мы определили домен и домен \(f(x) = |x| + 1\) как \(f: \mathbb{Z} \rightarrow \mathbb{Z}\), то это не было бы сюръективным, как любой значение кодового домена \(\leq 0\) не будет сопоставляться ни с чем в домене.
Функции также могут быть ни инъективными, ни сюръективными, или одновременно инъективными и сюръективными. Это можно увидеть на диаграмме ниже. В последнем случае эта функция называется bijective , что означает, что эта функция обратима (то есть мы можем создать функцию, которая обращает отображение из домена в домен кода).
Давайте теперь посмотрим, как мы доказываем, является ли функция инъективной или сюръективной.
Доказательство инъекции, сюръекции и биекции
Чтобы посмотреть, как доказать инъекцию и сюръекцию, давайте рассмотрим пример задачи.
Докажите, что функция \(f: \mathbb{R} — {2} \rightarrow \mathbb{R} — {5}\), определяемая равенством \(f(x) = \frac{5x + 1}{ x — 2}\) биективно.
Мы знаем, что если функция биективна, то она должна быть и инъективной, и сюръективной. Что нам нужно сделать, так это доказать их по отдельности, и, сделав это, мы можем сделать вывод, что функция должна быть биективной.
Начнем с доказательства инъективности функции. Для этого нам нужно доказать, что для любых двух элементов \(a, a’\) в области \(A\), если \(a \neq a’\), то \( f(a) \neq f(a’)\). Другими словами, нам нужно доказать, что любые два различных элемента в домене не сопоставляются с одним и тем же значением в домене кода.
Легче всего это сделать с контрапозитивным доказательством. Мы начнем с предположения, что \(a, a’ \in A\) и \(f(a) = f(a’)\), и мы хотим показать, что отсюда следует, что \(a = a’\) , указывая на то, что единственный способ, которым два элемента в домене кода могут быть равны, — это если они сопоставляются с одним и тем же элементом в домене. Давайте применим это к нашей проблеме.
Поскольку мы знаем, что \(f(x) = \frac{5x + 1}{x — 2}\), то \(f(a) = \frac{5a + 1}{a — 2}\) и \(f(a’) = \frac{5a’ + 1}{a’ — 2}\). Мы исходим из предположения, что \(f(a) = f(a’)\), поэтому подставляя в наши определения, мы получаем:
Мы исходим из предположения, что \(f(a) = f(a’)\), поэтому подставляя в наши определения, мы получаем:
$$ \begin{выровнено} \frac{5a + 1}{a — 2} = \frac{5a’ + 1}{a’ — 2} \end{выровнено} $$
Теперь нам нужно упростить это выражение, чтобы получить \(a = a’\).
$$ \begin{выровнено} \frac{5a + 1}{a — 2} &= \frac{5a’ + 1}{a’ — 2} \\ (5а + 1)(а’ — 2) &= (5а’ + 1)(а — 2) \\ 5аа’ — 10а + а’ — 2 &= 5аа’ — 10а’ + а — 2 \\ -10а + а’ &= -10а’ + а \\ -9а &= -9а’ \\ а &= а’ \end{выровнено} $$
Таким образом, мы показали, что если мы выберем любые два произвольных \(a, a’\) в домене, единственный способ, которым они связаны \(f(a), f(a’)\) в кодовом домене может быть равным, если \(a, a’\) равны. Следовательно, наша функция инъективна.
С помощью сюръекции мы пытаемся показать, что для любого произвольного \(b\) в нашем кодовом домене \(B\) должен быть элемент \(a\) в нашем домене \(A\), для которого \ (f(a) = b\). Самый простой способ показать это — решить \(f(a) = b\) для \(a\) и проверить, является ли полученная функция допустимым элементом \(A\).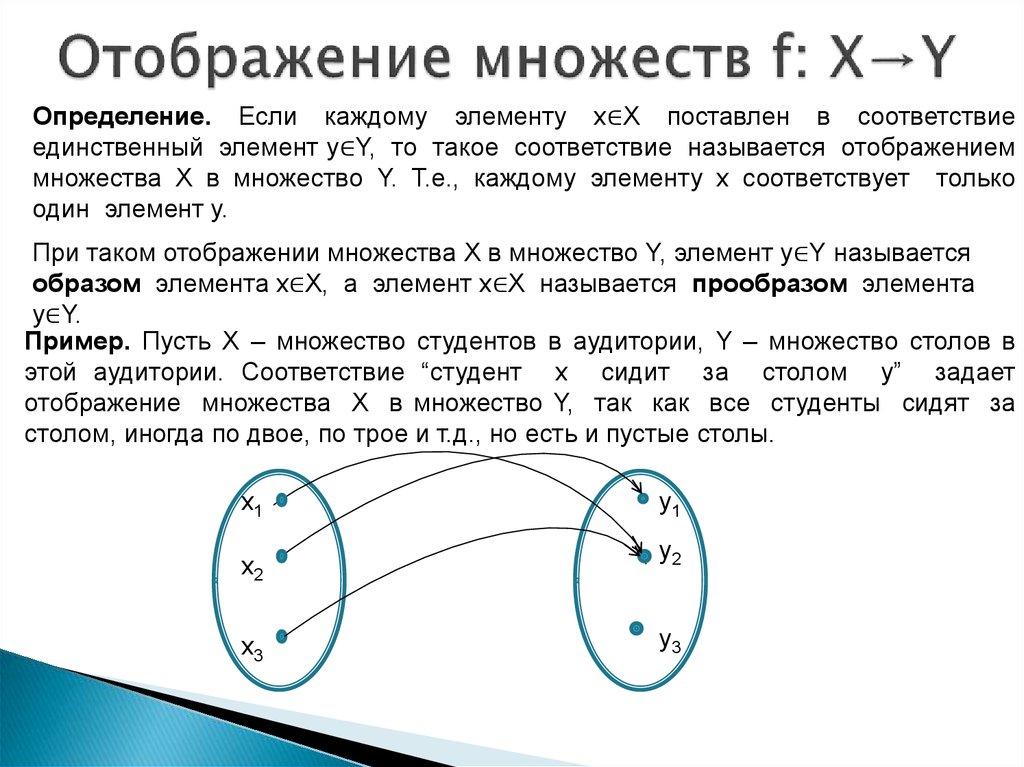

 е. такой элемент, что применение операции с чем-то еще оставляет эту вещь неизменной (пункт 1 и пункт 4 выше),
е. такой элемент, что применение операции с чем-то еще оставляет эту вещь неизменной (пункт 1 и пункт 4 выше),