Геометрия 7-9 класс. Средняя линия треугольника — math200.ru
Skip to contentГеометрия 7-9 класс. Средняя линия треугольникаadmin2022-12-23T20:51:30+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Средняя линия треугольника
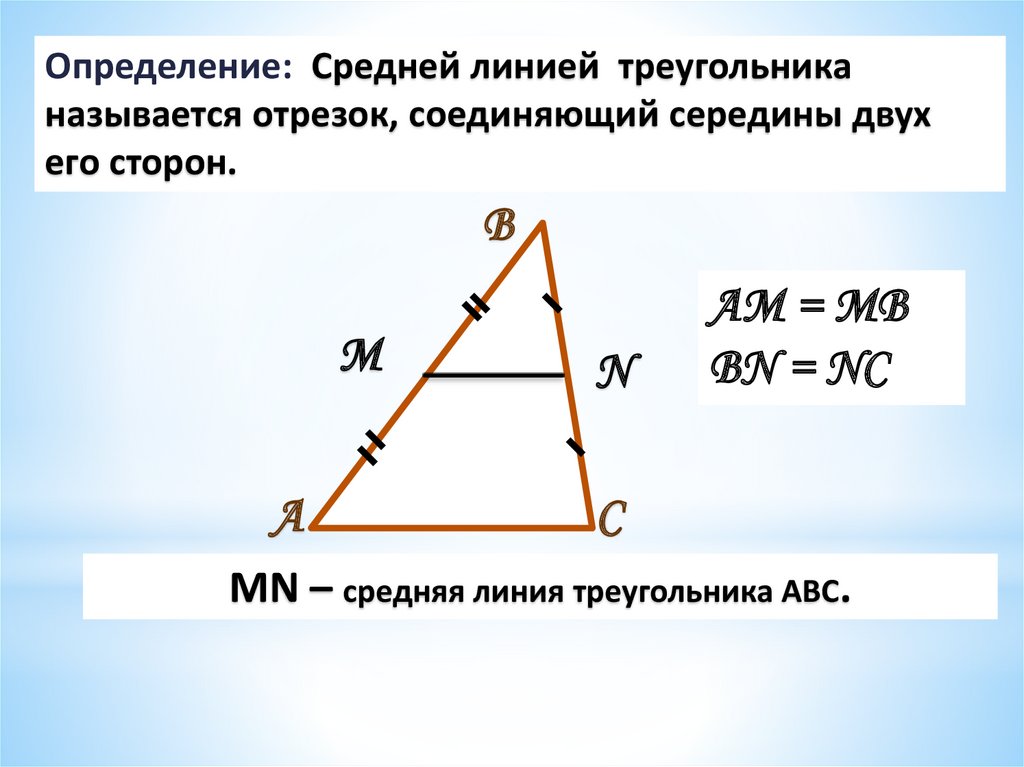
Средняя линия треугольника: отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
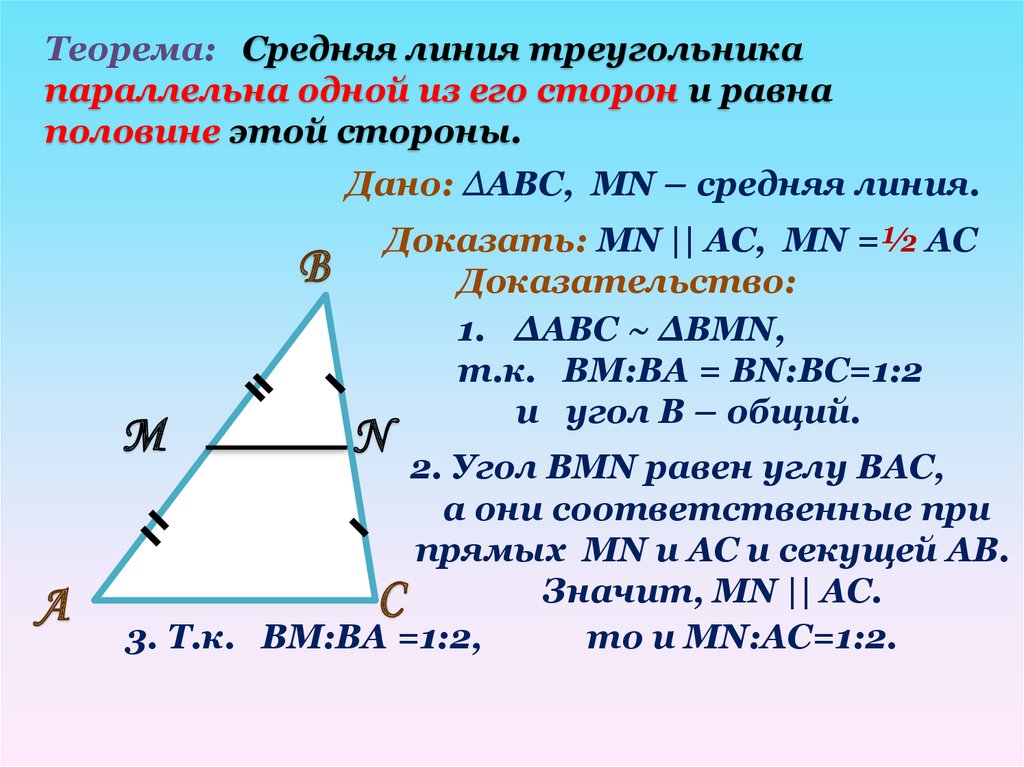
Теорема о средней линии треугольника: средняя линия треугольника параллельна стороне треугольника и равна её половине.
| Задача 1. В треугольнике АВС точки М и К середины сторон АВ и ВС соответственно. Найдите длину отрезка МК, если АС = 12. Ответ ОТВЕТ: 6. |
Задача 2. В треугольнике АВС точки М и К середины сторон АВ и ВС соответственно. Найдите длину стороны АС, если Найдите длину стороны АС, если Ответ ОТВЕТ: 5,6. |
| Задача 3. В треугольнике АВС точки М, К и N середины сторон АВ, ВС и АС соответственно. Найдите периметр треугольника MNK, если АВ = 7, АС = 12, ВС = 10. Ответ ОТВЕТ: 14,5. |
| Задача 4. В треугольнике АВС точки М, К и N середины сторон АВ, ВС и АС соответственно. Найдите периметр треугольника АВС, если периметр треугольника MNK равен 15. Ответ ОТВЕТ: 30. |
| Задача 5. В прямоугольнике ABCD диагонали пересекаются в точке О. Отрезок ОН = 12 является высотой треугольника AOD. Найдите длину стороны АВ. Ответ ОТВЕТ: 24. |
Задача 6. В прямоугольнике ABCD точки М, К, О и Р середины сторон АВ, ВС, CD и AD соответсnвенно. Найдите периметр четырёхугольника МКОР, если АС = 12. В прямоугольнике ABCD точки М, К, О и Р середины сторон АВ, ВС, CD и AD соответсnвенно. Найдите периметр четырёхугольника МКОР, если АС = 12.Ответ ОТВЕТ: 24. |
| Задача 7. В треугольнике АВС точки М и N середины сторон АВ и ВС. Периметр треугольника MNB равен 10. Найдите периметр треугольника ABC. Ответ ОТВЕТ: 20. |
| Задача 8. В равнобедренном треугольнике АВС с основанием АС точки М и N середины сторон АВ и ВС. Периметр треугольника АВС равен 16, а MN = 3. Найдите АВ. Ответ ОТВЕТ: 5. |
Задача 9. В параллелограмме ABCD диагонали пересекаются в точке 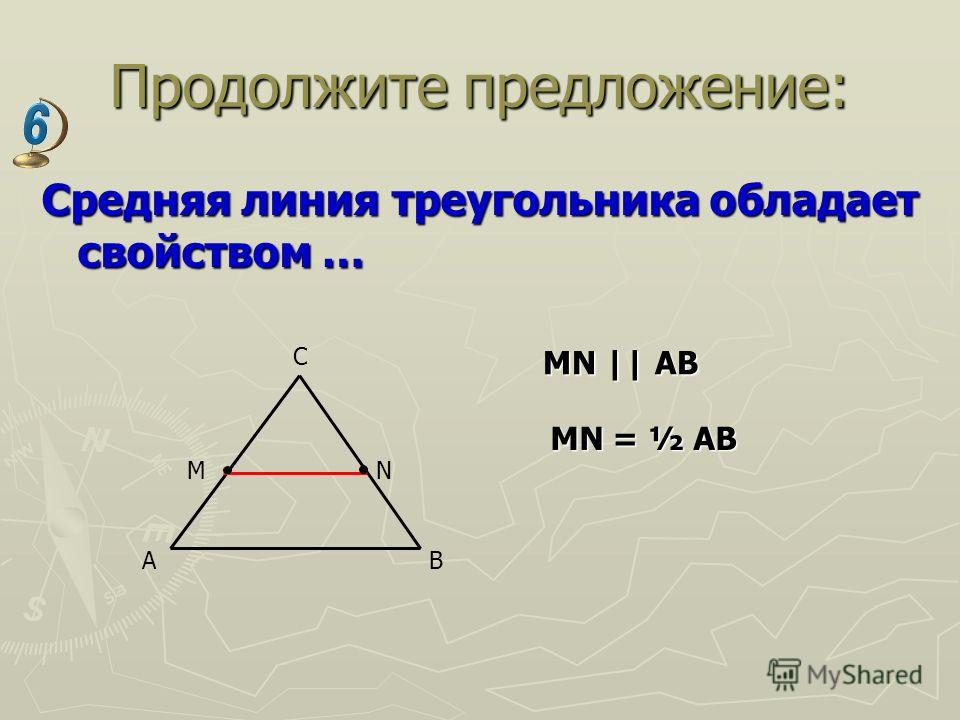 Найдите периметр параллелограмма, если ОМ = 4 и АМ = 5. Найдите периметр параллелограмма, если ОМ = 4 и АМ = 5.Ответ ОТВЕТ: 36. |
| Задача 10. В трапеции ABCD с основаниями ВС = 12 и AD = 16 точка М принадлежит основанию AD. Через середины отрезков ВМ и СМ проведена прямая пересекающая АВ и CD в точках Е и F соответственно. Найдите длину отрезка EF. Ответ ОТВЕТ: 14. |
| Задача 11. В треугольнике АВС точки М и К середины сторон АВ и ВС соответственно. Известно, что АС – МК = 12. Найдите АС. Ответ ОТВЕТ: 24. |
Задача 12. В квадрате ABCD точки M, N, P и K середины сторон АВ, ВС, CD и AD соответственно. Во сколько раз площадь квадрата ABCD больше площади четырехугольника MNPK.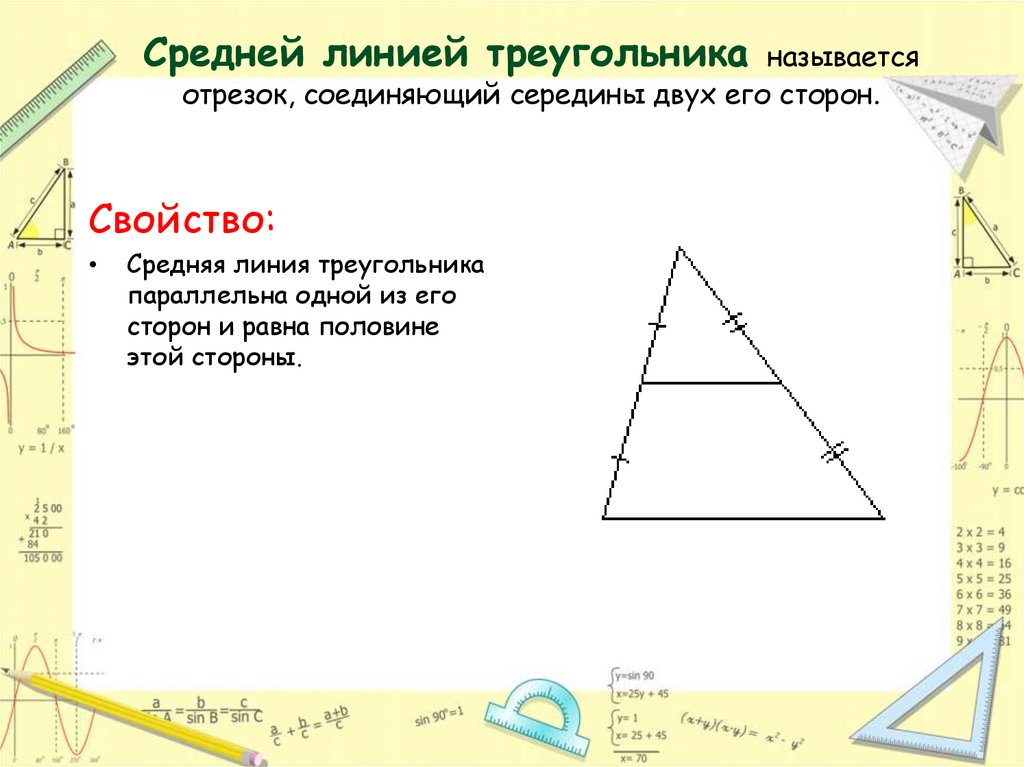 Ответ ОТВЕТ: 2. |
| Задача 13. В треугольнике АВС через точку пересечения медиан треугольника проведена прямая параллельная стороне АС и пересекающая стороны АВ и ВС в точках М и К. Найдите длину отрезка МК, если АС = 15. Ответ ОТВЕТ: 10. |
| Задача 14. В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке М, АМ = 13, ВМ = 10. Найдите площадь треугольника АВС. Ответ ОТВЕТ: 180. |
| Задача 15. В четырёхугольнике ABCD М, N, K и Р середины сторон АВ, ВС, CD и AD соответственно. Найдите площадь четырёхугольника ABCD, если площадь четырёхугольника MNKP равна 23. Ответ ОТВЕТ: 46. |
Задача 16.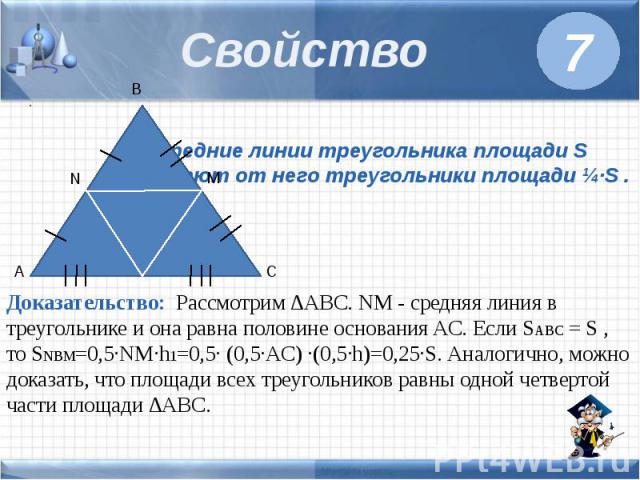 \circ },\) АВ = 12. Найдите периметр треугольника с вершинами в серединах сторон треугольника АВС. \circ },\) АВ = 12. Найдите периметр треугольника с вершинами в серединах сторон треугольника АВС.Ответ ОТВЕТ: \(9 + 3\sqrt 3 .\) |
| Задача 18. В равнобедренном прямоугольном треугольнике гипотенуза равна 10. Найдите периметр треугольника с вершинами в серединах сторон исходного треугольника. Ответ ОТВЕТ: \(5 + 5\sqrt 2 .\) |
Реклама
Поддержать нас
ОглавлениеВВЕДЕНИЕЧасть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня.  § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. 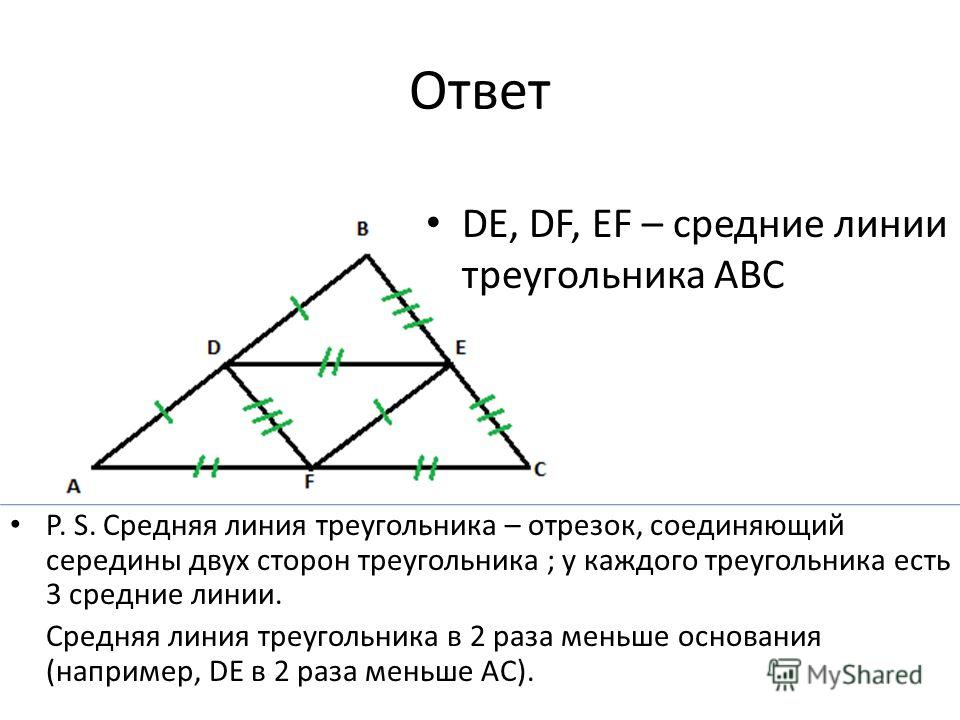 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 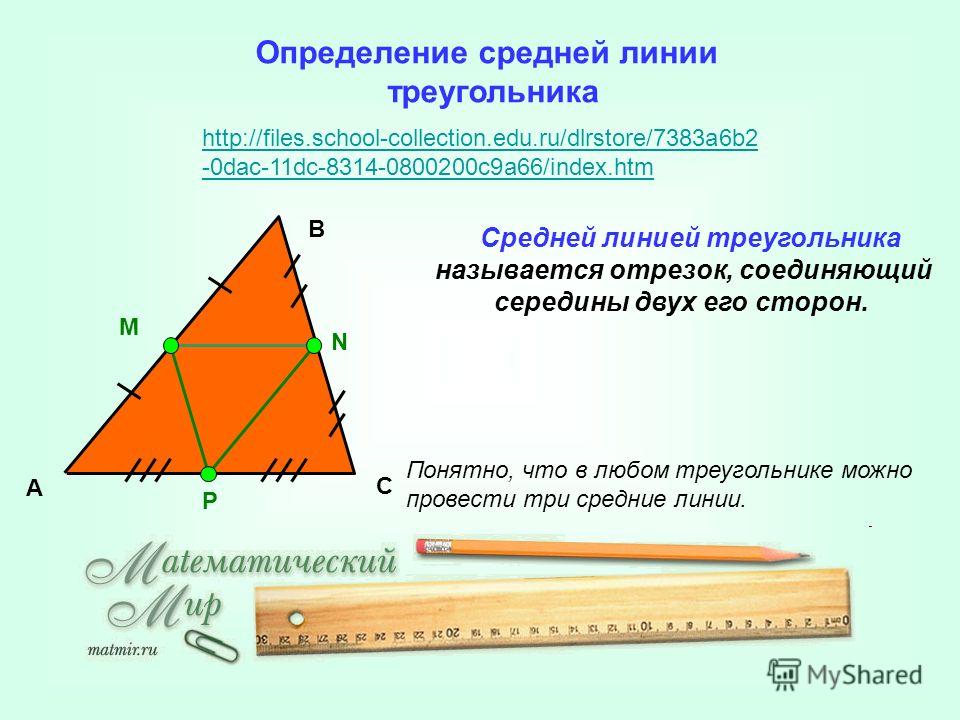 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства. Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора.  94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. 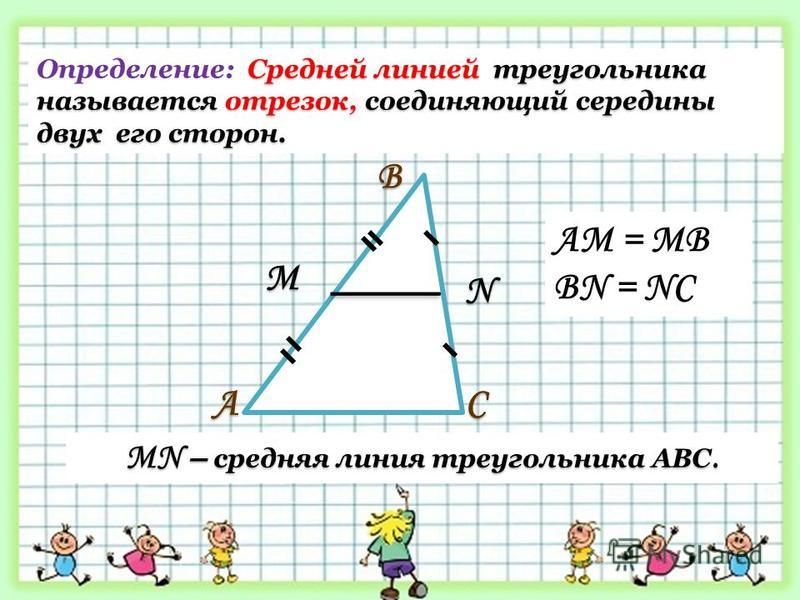 Тригонометрические функции числового аргумента Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.  121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137.  Функция у = arcsin (sin x). Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства.  155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла.  176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. 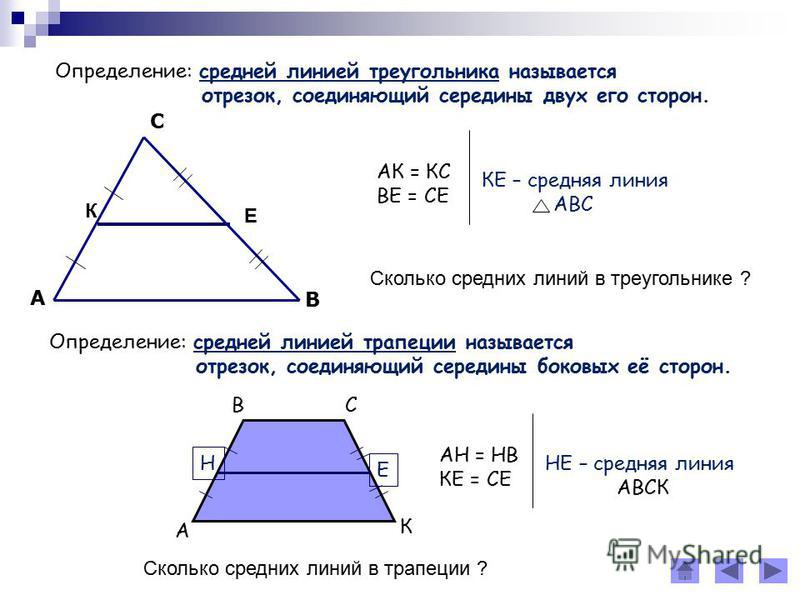 § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора. Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса.  253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
Раздел 4.4: Средняя линия треугольника
Section_4_4Мы начнем здесь с мощной теоремы о специальная линия в треугольнике.
- Определение: Средняя линия треугольника – это отрезок, концы которого являются серединами двух сторон треугольника.
Теорема о средней линии для треугольников полезна для установления некоторых неожиданные результаты о четырехугольниках, а также предоставление полезного теорема о трапециях.
- Теорема 4.13:
Теорема о средней линии
Отрезок, соединяющий середины двух сторон треугольник параллелен третьей стороне и равен половине третьей стороны сторона.
| Дано: $\треугольник
ABC$ с серединами $D$ и $E$ $\overline{AB}$ и $\overline{AC}$,
соответственно. Доказать: $\overline{DE}\parallel\overline{BC}$ и $DE=\dfrac{1}{2}BC$ | |
Доказательство:
Дан $\треугольник ABD$ с серединами $D$ и $E$. Продлевать
$\overline{DE}$ в точку $F$ такую, что $DE=EF$. Так как $E$
середине $\overline{AC}$, мы знаем, что диагонали
четырехугольники $ADCF$ делят друг друга пополам. Тогда теорема 4.8 говорит нам
этот четырехугольник должен быть параллелограммом. Свойства
параллелограмма говорят нам, что $\overline{ADB}\parallel\overline{CF}$
и $\overline{AD}\cong \overline{CF}$. Но
$\overline{AD}\cong\overline{DB}$, так как $D$ является средней точкой
$\overline{AB}$. Поэтому $\overline{DB}\cong\overline{CF}$ и
$\overline{DB}\parallel\overline{CF}$. Это делает $BCFD$
параллелограмм. Теперь по определению,
$\overline{DEF}\parallel\overline{BC}$. Кроме того, $DF=BC$.
Поскольку $E$ — это середина $\overline{DF}$, мы знаем, что
$DE=\frac{1}{2}DF$ и заменой $DE=\frac{1}{2}BC$.
Кроме того, $DF=BC$.
Поскольку $E$ — это середина $\overline{DF}$, мы знаем, что
$DE=\frac{1}{2}DF$ и заменой $DE=\frac{1}{2}BC$.
В предыдущей главе при обсуждении параллельных прямые, отсекающие конгруэнтные отрезки на одной секущей, мы столкнулся со следующим следствием. Так как это частично обратная теорема о средней линии, мы повторяем ее здесь.
- Следствие:
Если прямая проходит через середину одной из сторон треугольника и
параллельна второй стороне, то прямая проходит через середину
третья сторона треугольника.
| Дано: $\треугольник
ABC$ с $P$ серединой $\overline{AB}$ и
$\overline{PQ}\parallel\overline{BC}$. Докажите: $Q$ середина $\overline{AC}$. | |
Доказательство: Мы
даны $\треугольник ABC$ с серединой стороны $P$
$\overline{AB}$ и $\overline{PQ}\parallel\overline{BC}$.
Ввести прямую $\ell$ через $A$ так, чтобы
$\ell\parallel\overline{BC}$. Теперь $\ell$, $\overline{PQ}$ и
$\overline{BC}$ — это три параллельные прямые, пересекающие конгруэнтные
сегменты на $\overline{AB}$. Затем должны отрезать конгруэнтные
отрезки на любой трансверсали, в частности на $\overline{AC}$.
Это делает $Q$ средней точкой $\overline{AC}$.
Теперь $\ell$, $\overline{PQ}$ и
$\overline{BC}$ — это три параллельные прямые, пересекающие конгруэнтные
сегменты на $\overline{AB}$. Затем должны отрезать конгруэнтные
отрезки на любой трансверсали, в частности на $\overline{AC}$.
Это делает $Q$ средней точкой $\overline{AC}$.
Теорема о средней линии позволяет нам установить множество иногда неожиданных результатов. Одним из них является следующий факт о прямоугольные треугольники — середина гипотенузы всегда равноудалена из всех трех вершин треугольника.
- Теорема 4.14:
Если $M$ — середина гипотенузы $\overline{AB}$ прямоугольного треугольника
$\overline{ABC}$, затем $MA=MB=MC$.
| Дано: Правильно
$\треугольник ABC$ с $M$ серединой гипотенузы $\overline{AB}$ Доказать: $MA=MB=MC$ | |
Доказательство: Мы
задано, что $M$ — середина гипотенузы $\overline{AB}$.
Пусть $P$ — середина $\overline{BC}$. По теореме 4.13
$\overline{MP}\parallel\overline{AC}$. Так как $\треугольник ABC$ является
прямоугольный треугольник с прямым углом $C$, мы знаем, что
$\overline{BC}\perp\overline{AC}$. Затем
$\overline{BC}\perp\overline{MP}$, потому что если линия
перпендикулярно одной из двух параллельных прямых, то оно перпендикулярно
другой. Тогда по определению $\overline{MP}$ — это перпендикуляр
биссектриса $\overline{BC}$. Теорема о перпендикулярной биссектрисе
затем сообщает нам, что $MB=MC$. Поскольку $M$ является серединой
$\overline{AB}$, тогда мы имеем $MA=MB=MC$.
По теореме 4.13
$\overline{MP}\parallel\overline{AC}$. Так как $\треугольник ABC$ является
прямоугольный треугольник с прямым углом $C$, мы знаем, что
$\overline{BC}\perp\overline{AC}$. Затем
$\overline{BC}\perp\overline{MP}$, потому что если линия
перпендикулярно одной из двух параллельных прямых, то оно перпендикулярно
другой. Тогда по определению $\overline{MP}$ — это перпендикуляр
биссектриса $\overline{BC}$. Теорема о перпендикулярной биссектрисе
затем сообщает нам, что $MB=MC$. Поскольку $M$ является серединой
$\overline{AB}$, тогда мы имеем $MA=MB=MC$.
Эта теорема появилась в последнем наборе задач, где предложенный подход полностью отличался от принятого здесь.
Анатомия, голова и шея, подбородочный треугольник — StatPearls
Муртаджа З. Аль-Миссри; Ясир Аль Халили.
Информация об авторе и организациях
Последнее обновление: 4 июня 2022 г.
Введение
Подподбородочный треугольник — единственный непарный треугольник переднего треугольника шеи. Она ограничена телом подъязычной кости и передними брюшками двубрюшной мышцы. Дно подбородочного пространства образуют челюстно-подъязычные мышцы. Однако подбородочный треугольник может отсутствовать или быть искаженным, поскольку переднее брюшко двубрюшной мышцы различается по анатомии и может отсутствовать [1]. Эта область имеет клиническое значение, поскольку содержит важные анатомические структуры, такие как подбородочные лимфатические узлы, которые могут служить хорошими индикаторами для определения метастазов [1].
Она ограничена телом подъязычной кости и передними брюшками двубрюшной мышцы. Дно подбородочного пространства образуют челюстно-подъязычные мышцы. Однако подбородочный треугольник может отсутствовать или быть искаженным, поскольку переднее брюшко двубрюшной мышцы различается по анатомии и может отсутствовать [1]. Эта область имеет клиническое значение, поскольку содержит важные анатомические структуры, такие как подбородочные лимфатические узлы, которые могут служить хорошими индикаторами для определения метастазов [1].
Строение и функции
Шея анатомически ограничена нижним краем нижней челюсти, верхним краем ключицы, средней линией и передним краем трапециевидной мышцы. Между этими границами описаны два основных шейных треугольника, передний и задний. Задний треугольник делится на затылочный и надключичный треугольники; передний треугольник содержит три парных треугольника (мышечный, сонный и поднижнечелюстной) и одно непарное пространство: подбородочный треугольник . На шее также находятся позвоночная артерия и лестничные треугольники в глубоких слоях, а также треугольники Лессера, Пирогова, Фарабефа и Беклара [1].
На шее также находятся позвоночная артерия и лестничные треугольники в глубоких слоях, а также треугольники Лессера, Пирогова, Фарабефа и Беклара [1].
Границы переднего шейного треугольника включают передний край грудино-ключично-сосцевидной мышцы, среднюю линию шеи и нижний край нижней челюсти [1]. Подподбородочный треугольник расположен в этой области и отличается от других треугольников тем, что он непарный. Вершиной треугольника является подбородок, основанием является тело подъязычной кости, а стороны образованы передними брюшками двубрюшной мышцы. Кроме того, левая и правая челюстно-подъязычные мышцы составляют пол. Они прикрепляются к челюстно-подъязычной линии нижней челюсти и проходят медиально и вниз, чтобы прикрепиться к телу подъязычной кости. Подментальный треугольник содержит подбородочные лимфатические узлы , которые дренируют подбородочную область, кончик языка, нижнюю губу и резцы. Кроме того, челюстно-подъязычный нерв и вены , которые впадают в переднюю яремную жила пересекает этот регион [2]. Передние брюшки двубрюшной мышцы, прикрепляющиеся к двубрюшной ямке, отделяют подбородочный треугольник от поднижнечелюстного.
Передние брюшки двубрюшной мышцы, прикрепляющиеся к двубрюшной ямке, отделяют подбородочный треугольник от поднижнечелюстного.
Эмбриология
Переднее брюшко двубрюшной мышцы начинает эмбриональное развитие на четвертой неделе беременности от первой глоточной дуги [2]. Точно так же челюстно-подъязычная мышца развивается на четвертой неделе беременности из первой глоточной дуги.
Кровоснабжение и лимфатическая система
Подбородочные лимфатические узлы собирают лимфу из центральной области нижней губы, кожи подбородочной области, кончика языка и резцов. Далее они впадают в подчелюстные лимфатические узлы и глубокую шейную группу, которая в конечном итоге впадает в яремный лимфатический ствол.
Подподбородочная артерия является самой крупной из шейных ветвей лицевой артерии. Она появляется сразу после выхода лицевой артерии из поднижнечелюстной железы. Подподбородочная артерия обеспечивает кровоснабжение кожи подподбородочной области и мышц, граничащих с подподбородочным треугольником, и анастомозирует с нижней альвеолярной артерией и подъязычной артерией. Он проходит между челюстно-подъязычной мышцей и нижней челюстью; он проходит либо глубоко, либо поверхностно по отношению к переднему брюшку двубрюшной мышцы [3].
Он проходит между челюстно-подъязычной мышцей и нижней челюстью; он проходит либо глубоко, либо поверхностно по отношению к переднему брюшку двубрюшной мышцы [3].
Нервы
Челюстно-подъязычный нерв и язычный нерв могут сообщаться в подбородочном треугольнике. Челюстно-подъязычный нерв проникает в челюстно-подъязычную мышцу; затем он проходит параллельно подподбородочной артерии и подподбородочной вене. Подподбородочный нерв проходит под подподбородочной артерией и подподбородочной веной [4].
Мышцы
челюстно-подъязычная мышца состоит из двух единиц, левой и правой. Он начинается от челюстно-подъязычной линии, расположенной на внутренней поверхности нижнечелюстной кости, и оба сегмента встречаются в челюстно-подъязычном шве по средней линии. Точка прикрепления этой мышцы расположена на теле подъязычной кости. Подъязычная мышца также отделяет поднижнечелюстную область от подъязычной. Кроме того, он поддерживает и поднимает дно рта и поднимает подъязычную кость [5].
Двубрюшные мышцы представляют собой парные мышцы, образованные передней и задней брюшными мышцами, соединяющими височную, нижнюю и подъязычную кости. Переднее брюшко берет начало от двубрюшной ямки нижней челюсти и прикрепляется к подъязычной кости, где встречается с задним брюшком у промежуточного сухожилия. Заднее брюшко начинается от сосцевидной вырезки на медиальной стороне сосцевидного отростка височной кости. Затем он направляется к подъязычной кости, чтобы встретиться с передней частью живота. Передние брюшки выстилают боковые стороны поднижнечелюстного треугольника, открывают рот (путем опускания нижней челюсти) и поднимают подъязычную кость [6].
Челюстно-подъязычный нерв , ветвь нижнего альвеолярного нерва , иннервирует мышцы, ограничивающие подподбородочный треугольник: переднее брюшко двубрюшной мышцы и челюстно-подъязычную мышцу [2][6]. Однако переднее брюшко двубрюшной мышцы также может получать иннервацию от лицевого нерва [7].
За кровоснабжение переднего брюшка двубрюшной мышцы отвечают подбородочная и лицевая артерии [6]. Напротив, челюстно-подъязычные мышцы орошаются челюстно-подъязычная артерия , ветвь нижней альвеолярной артерии [5].
Физиологические варианты
Исследователи обнаружили у некоторых трупов дополнительные мышечные пучки, пересекающие среднюю линию подподбородочного треугольника. Эти дополнительные мышечные пучки иннервирует челюстно-подъязычный нерв. Исследователи полагали, что эти сверхштатные мышечные пучки представляли собой комбинацию переднего брюшка двубрюшной мышцы и первичных остатков челюстно-подъязычной мышцы [8].
Хирургические соображения
Недостаток дифференцировки первой глоточной дуги является причиной некоторых вариаций переднего брюшка двубрюшной мышцы. Эти изменения необходимо учитывать при проведении операции в области подбородочного треугольника [2].
При проведении операции по удалению переднего брюшка двубрюшной мышцы от челюстно-подъязычной мышцы необходимо учитывать наличие язычного нерва и подъязычного нерва, поскольку они часто имеют сложное расположение как в подбородочном, так и в поднижнечелюстном треугольнике [4].
Клиническое значение
Подподбородочный треугольник имеет клиническое значение, поскольку в его пределах развиваются опухоли и кисты, а абсцессы из других областей распространяются на эту область. Кроме того, увеличенные подбородочные лимфатические узлы вызывают подозрение на злокачественные образования в их притоках. Однако поражения подподбородочного треугольника обычно развиваются из локальной и доброкачественной патологии головы и шеи [9].
Исследование 24 новообразований, обнаруженных в подбородочном треугольнике, выявило различные состояния, включая липому, саркоидоз, неходжкинскую лимфому, гемангиому, абсцесс, дермоидную кисту и реактивную лимфоидную гиперплазию [9].]. Они также обнаружили, что образования подподбородочного треугольника могут осложняться стоматологическими проявлениями и хейлитом [9]. Объемные образования, ограниченные подподбородочным треугольником, диагностируются с помощью тонкоигольной аспирации, а основным методом лечения является хирургическое иссечение, за исключением абсцессов, которые лечат дренированием и системными антибиотиками.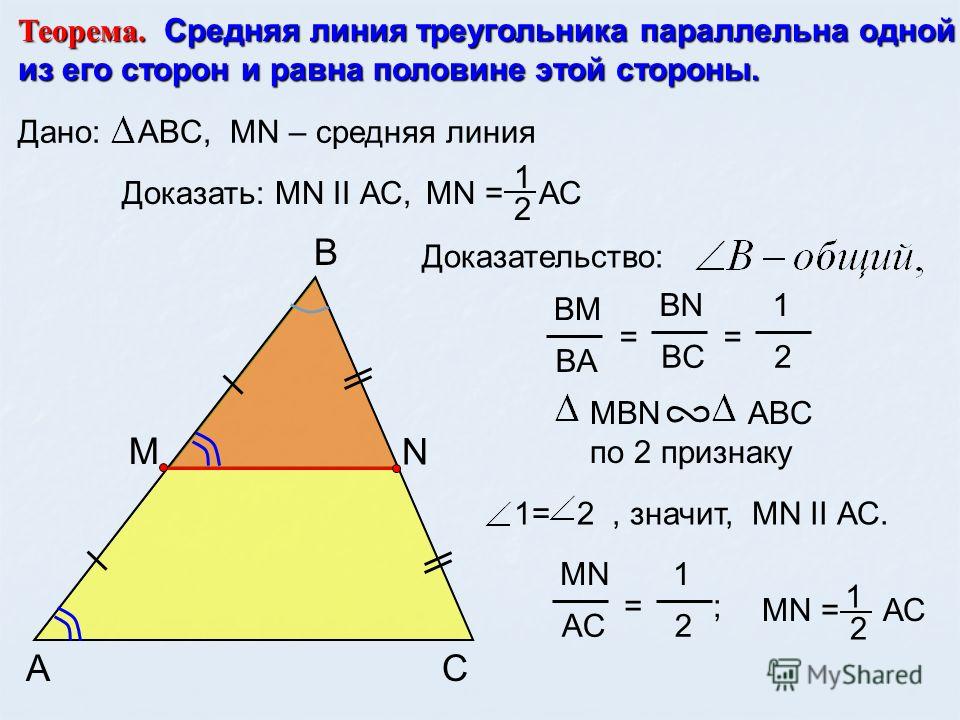 Так обстоит дело с одонтогенными инфекциями, которые иногда могут распространяться на подбородочное пространство и образовывать абсцесс. При необходимости клиницист дренирует его через чрескожные разрезы, а поскольку в треугольнике отсутствуют артерии и содержится лишь несколько структур, риск повреждения во время разрезов невелик [1].
Так обстоит дело с одонтогенными инфекциями, которые иногда могут распространяться на подбородочное пространство и образовывать абсцесс. При необходимости клиницист дренирует его через чрескожные разрезы, а поскольку в треугольнике отсутствуют артерии и содержится лишь несколько структур, риск повреждения во время разрезов невелик [1].
Врожденная лимфатическая мальформация может проявляться как объемное образование подподбородочного пространства, о чем свидетельствует прозрачная жидкость при тонкоигольной аспирации и низкопотоковое поражение при ультразвуковом исследовании с допплерографией [10].
Подподбородочные лимфатические узлы обычно вовлекаются в метастазирование рака полости рта [11]. Но они являются необычным местом туберкулезного шейного лимфаденита [12].
Оценка подбородочных лимфатических узлов
Пороговое значение размера подбородочных лимфатических узлов при измерении отношения короткой оси к длинной оси составляет 0,5 [13]. Существует удовлетворительный уровень воспроизводимости измерений подбородочных лимфатических узлов с использованием 3-D УЗИ [14].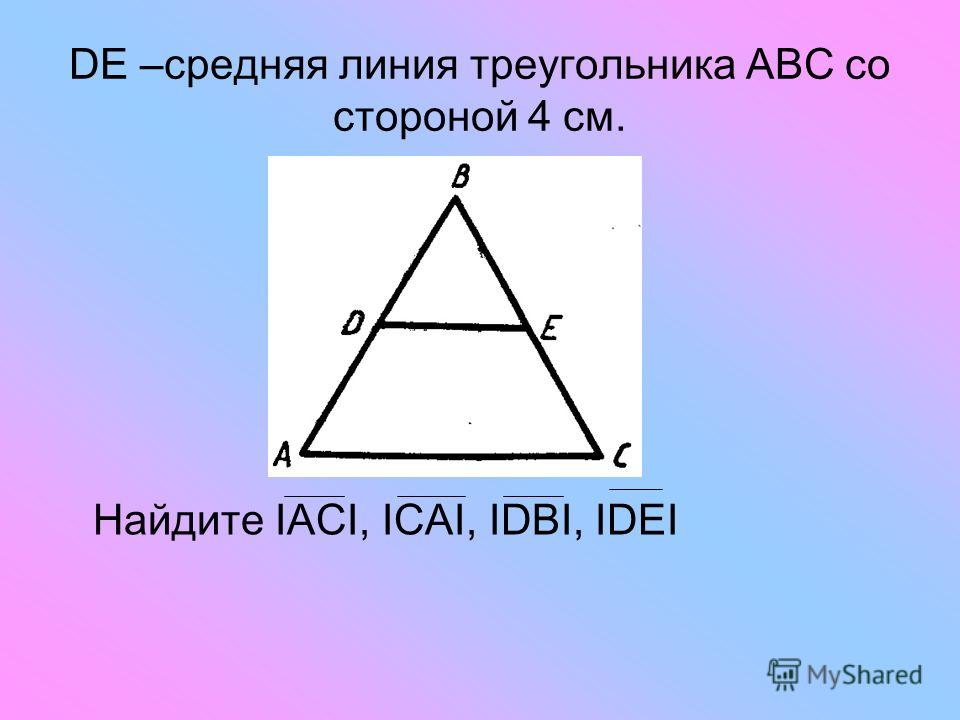 УЗИ чувствительно и специфично для оценки подбородочных лимфатических узлов. Напротив, компьютерная томография не особенно чувствительна для определения состояния подбородочных лимфатических узлов, но обладает специфичностью [15].
УЗИ чувствительно и специфично для оценки подбородочных лимфатических узлов. Напротив, компьютерная томография не особенно чувствительна для определения состояния подбородочных лимфатических узлов, но обладает специфичностью [15].
Контрольные вопросы
Доступ к бесплатным вопросам с несколькими вариантами ответов по этой теме.
Комментарий к этой статье.
Рис. M. Scalenus (подробнее…)
Рисунок
Подподбородочный треугольник. Изображение предоставлено доктором Чайгасаме
Ссылки
- 1.
Кикута С., Иванага Дж., Кусукава Дж., Таббс Р.С. Треугольники шеи: обзор с клиническим/хирургическим применением. Анат Селл Биол. 2019 июнь;52(2):120-127. [PMC free article: PMC6624334] [PubMed: 31338227]
- 2.
Кальниев М., Крастев Д., Крастев Н., Видинов К., Вельчев Л., Апостолов А., Милева М. Редкий вариант двубрюшной мышцы. Клужул Мед. 2013;86(4):327-9. [Бесплатная статья PMC: PMC4462457] [PubMed: 26527971]
- 3.

Фалтаус А.А., Йетман Р.Дж. Лоскут подподбородочной артерии: анатомическое исследование. Plast Reconstr Surg. 1996 г., январь; 97 (1): 56–60; обсуждение 61-2. [PubMed: 8532806]
- 4.
Сато И., Сунохара М., Уэно Р., Йошида С. Ветви челюстно-подъязычного и язычного нервов на поднижнечелюстном и подбородочном треугольниках. Окадзимас Фолиа Анат Jpn. 2004 г., август; 81 (2–3): 45–8. [PubMed: 15455728]
- 5.
Тот Дж., Лаппин С.Л. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 11 июня 2022 г. Анатомия, голова и шея, челюстно-подъязычная мышца. [В паблике: 31424877]
- 6.
Ким С.Д., Лукас М. Анатомия и варианты двубрюшной мышцы. Анат Селл Биол. 2019 март; 52(1):1-11. [PMC бесплатная статья: PMC6449592] [PubMed: 30984445]
- 7.
Асами Ю., Каваи К., Канох Т., Коидзуми М., Хонма С., Токиёси А., Кодама К. Двойная иннервация передней брюшной стенки двубрюшной мышца.
 Анат Научный Международный 2006 г., июнь; 81 (2): 130-3. [PubMed: 16800298]
Анат Научный Международный 2006 г., июнь; 81 (2): 130-3. [PubMed: 16800298]- 8.
Сакамото Ю., Акита К. Нештатные мышечные пучки в подподбородочном треугольнике: их позиционные отношения в зависимости от иннервации. Сур Радиол Анат. 2004 г., июнь; 26 (3): 245–53. [В паблике: 14872289]
- 9.
Урал А., Имамоглу М., Умит Ишик А., Бахадыр О., Бекташ Д., Чобаноглу Б., Чобаноглу У. Массы шеи ограничены субментальным пространством: наш опыт с 24 случаями. Ухо, нос, горло, Дж. 2011, ноябрь; 90 (11): 538-40. [PubMed: 22109923]
- 10.
Shah GH, Deshpande MD. Лимфатическая мальформация у взрослого пациента: редкий случай. J Maxillofac Oral Surg. 2010 Сентябрь;9(3):284-8. [Бесплатная статья PMC: PMC3177438] [PubMed: 22190807]
- 11.
Тривич А., Крейович-Тривич С., Милованович Дж., Джукич В., Арсович Н., Димитриевич М., Петрович З., Микич А. [Распределение шейных метастазов рака шейно-лицевой области].




 Анат Научный Международный 2006 г., июнь; 81 (2): 130-3. [PubMed: 16800298]
Анат Научный Международный 2006 г., июнь; 81 (2): 130-3. [PubMed: 16800298]