Площадь треугольника через медиану: Нахождение площади через медианы

По каким формулам можно вычислить площадь треугольника

Геометрия 8 класса — это, в основном, площади фигур. Во многих задачах фигурирует треугольник, некоторые элементы которого известны, и требуется найти площадь.

Здесь мы систематизируем формулы площади треугольника, грамотно применяя которые вы сможете решить любую задачу 8 класса по геометрии, а то и олимпиадную геометрическую задачу в 8, 9 или 10 классе.

1. Формула площади треугольника по основанию и высоте

Если в треугольнике известны основание a и проведённая к нему высота h_a, то площадь его будет равна полупроизведению основания на высоту.

$S=\frac{1}{2}a h_a$

2. Формула площади треугольника по двум сторонам и углу между ними

Если в треугольнике известны две стороны a и b и угол между ними $\alpha$, то его площадь равна полупроизведению сторон на синус угла между ними.

$S=\frac{1}{2}ab\sin\alpha$

3. Формула площади треугольника по трём сторонам (формула Герона)

Если в треугольнике известны три стороны, a, b, c то для определения площади у него нужно найти полупериметр $p=\frac{a+b+c}{2}$ и вычислить площадь по формуле Герона:

$S=\sqrt{p(p-a)(p-b)(p-c)}$

Иногда формулу Герона ещё записывают так:
$S=\frac{1}{4}\sqrt((a+b+c)(a+b-c)(a+c-b)(b+c-a))$

Кстати, сущесвтует и формула Герона для четырёхугольника. 2\sqrt{3}}{4}$

7. Формула площади треугольника по сторонам и радиусу описанной окружности

Если дополнительно к сторонам a, b, c треугольника известен и его радиус описанной окружности R, то площадь можно найти без формулы Герона, просто разделив произведение сторон на четыре радиуса описанной окружности.

$S=\frac{abc}{4R}$

8. Формула площади треугольника по сторонам и радиусу вписанной окружности

Если у треугольника известны все стороны и ещё радиус вписанной окружности, то снова формула Герона будет не нужна. Площадь будет равна полупоризведению радиуса списанной окружности на пеример (ну или полупериметра на радиус описанной окружности).

$S=\frac{(a+b+c)r}{2}=pr$

9. Формула площади треугольника по стороне и прилежащим к ней углам

Бывает, что в треугольнике известна только одна строна a, зато два прилежащих к ней угла: $\beta$ и $\gamma$. В этом случае площадь находится как половина квадрата стороны на произведение синусов прилежащих углов, делённое на синус суммы этих углов. 2}$

11. Формула площади треугольника, который задан координатами своих вершин на плоскости

Если треугольник задан на плоскости координатами своих вершин: $(x_0; y_0)$, $(x_1; y_1)$, $(x_2; y_2)$, то его площадь можно вычислить как определитель матрицы:

$S=\frac{1}{2}\begin{vmatrix}x_0&y_0&1\\x_1&y_1&1\\x_2&y_2&1\end{vmatrix}$

При этом если точки взяты по часовой стрелке, результат будет положительным, а если против часовой — отрицательным.

12. Формула площади треугольника, стороны которого заданы векторами

Если две стороны треугольника заданы векторами с общим началом и координатами $(x_1; y_1)$ и $(x_2; y_2)$, то его площадь можно вычислить по формуле:

$\frac{1}{2}|x_1 y_2 — x_2 y_1|$

13. Формула площади треугольника по трём медианам

Если у треугольника известны все медианы $m_a$, $m_b$, $m_c$, то его площадь можно найти по формуле, аналогичной формуле Герона:

$S = \frac{4}{3} \sqrt{\sigma (\sigma — m_a)(\sigma — m_b)(\sigma — m_c)}$,
где $\sigma$ — полусумма медиан. {2} \sin \alpha \sin \beta\sin \gamma$

16. Формула площади треугольника, нарисованного на клетчатой бумаге

Если треугольник нарисован на клетчатой бумаге и все его вершины находятся в углах сетки, то площадь его можно вычисляить по формуле Пика:
S = В+Г/2-1,
где В — количество узлов сетки, находящихся внутри треугольника,
Г — количество узлов сетки, находящихся на границе треугольника.

Геометрия 8-го класса в планиметрических задача ЕГЭ

Цели занятий:

• Образовательные: систематизировать знания учащихся при подготовке экзаменам, применять теоретический при решении задач.
• Развивающие: развитие познавательного интереса, внимания, логического мышления.
• Воспитательные: воспитание настойчивости для преодоления возникающих трудностей, повышение самооценки учащихся.

Тип занятий: обобщающее повторение на факультативах и уроках геометрии при подготовке к ЕГЭ по учебнику Атанасяна Л. С., Бутузова В.Ф.и других, Москва, “Просвещение”, 2006г.

I блок. Свойство медианы треугольника.

Теория:

1. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины (п. 62).

2. Задача № 571:

значит, .

3. Медианы разбивают заданный треугольник на шесть равновеликих.

Доказательство:

т.к. OC₁— медиана _то

т.к. 1=2 (п.52), значит

Аналогично рассуждая, получим: .

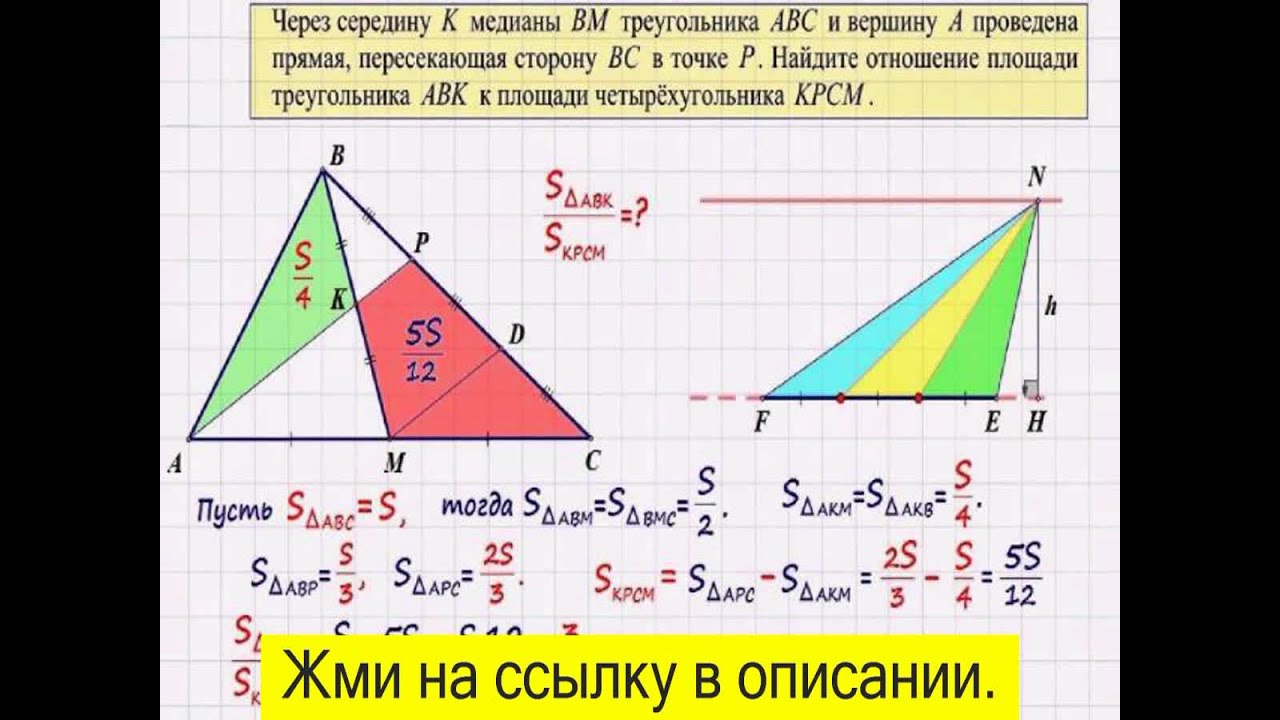
Задача 1. Площадь треугольника ABC равна 60. Точка C является серединой отрезка AC₁. Медиана AA₁ треугольника ABC₁ пересекает сторону BC в точке M. Найдите площадь четырёхугольника CMA₁C₁.

По условию задачи AA₁ и BC – медианы .

Провели медиану C₁K. разбился на 6 равновеликих треугольников.

Тогда .

Ответ: 40

Задача 2. В треугольнике медианы, длины которых 3 и 4, пересекаются под прямым углом. Найти площадь треугольника.

BB₁ и CC₁ — медианы,

BB_{1 CC1 ; BB1 = 4; CC1= 3.}

По свойству медиан C₁O = , тогда C₁O = 1; ; .

Ответ: 8.

II блок. Вписанная окружность.

Теория:

1. Свойство касательных: отрезки касательных к окружности, проведённые из одной из одной точки, равны и составляют равные углы с прямой, проходящей через центр и эту точку (п. 69).
2. Радиус, проведённый в точку касания, перпендикулярен касательной.
3. Суммы длин противоположных сторон описанных четырёхугольников равны (п.74).
4. Центром вписанной окружности является точка пересечения биссектрис описанного многоугольника.
5. Формула площади описанного многоугольника: , где r – радиус вписанной окружности, P – периметр многоугольника.

Задача 3. Дан прямоугольный треугольник ABC с прямым углом С. Через центр О вписанной окружности проведён луч ВО, пересекающий катет АС в точке М. Известно, что . Найдите гипотенузу.

Т.к. О – точка пересечения биссектрис, то ABM=CBM, значит MAB=MBA, следовательно, — равнобедренный, тогда .

C=90⁰ ,A=MBC, т.е.

Из по теореме Пифагора

Составим уравнение

Из по т. Пифагора: =

Ответ: 24

Задача 4. В равнобедренном треугольнике АВС с основанием ВС вписана окружность. Она касается стороны АВ в точке М. найдите радиус окружности, если АМ=6, ВМ=24

Т.к - равнобедернный, то AB=AC=30

По свойству касательных: АМ=АЕ=6,СЕ=СК=24,ВМ=КВ=24,значит ВС=48

По формуле Герона

Ответ: 8

Задача 5.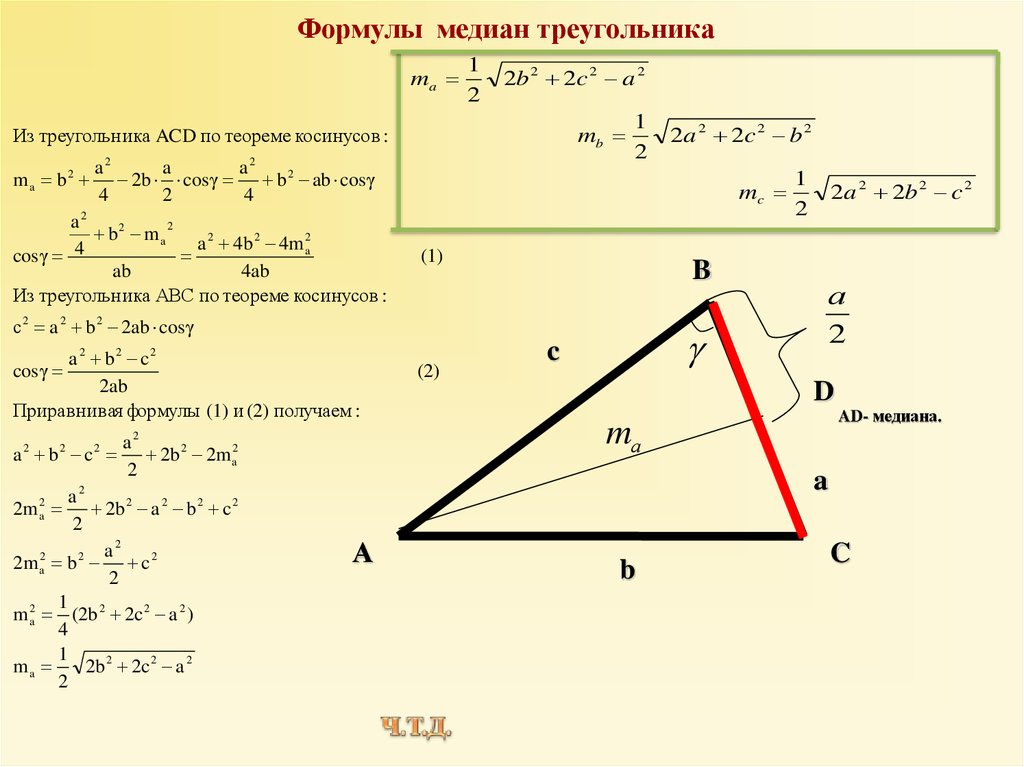 прямоугольная трапеция описана около окружности радиусом 2. Найдите площадь трапеции, если одно из её оснований больше другого основания на 3.

; М, Е, К, N – точки касания, О — точка пересечения биссектрис, С+D=180⁰ , тогда , значит,

M – точка касания, OM – радиус, проведённый в точку касания, следовательно , OMCD.Воспользуемся пропорциональностью отрезков в прямоугольном треугольнике (п. 63). OM – среднее геометрическое для отрезков CM и MD:

 Примем , тогда . По свойству касательных 

Так как трапеция прямоугольная , то OK=BN=BK, OE=AN=AE. Т. к. AD>BC на 3, то AD=BC+3

Задача 6. В прямоугольную трапецию вписана окружность. Точка касания делит боковую сторону на отрезки длинной 1 и 9 . Найти площадь трапеции.

Аналогично решению задачи №5

По свойству сторон описанного четырехугольника , тогда P=32

Ответ: 48.

III блок. Описанная окружность

Теория:

1. Центральный угол измеряется величиной дуги, на которую он опирается (п.70)
2. Вписанный угол измеряется половиной дуги, на которую он опирается.
3. Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды (п.71)

Задача 7. Высоты АН и ВК остроугольного треугольника АВС пересекаются в точке М, АВМ=105⁰ . Найдите градусную меру угла АВО, где О- центр окружности, описанной около треугольника АВС

Задача 8. в треугольнике ABC угол В равен 30⁰ . около треугольника описана окружность радиуса 12. хорда ВК проходит через середину М стороны АС, причем МК=2. Найдите ВМ

IV Блок. Подобные треугольники. (пп 59, 60, 61)

Задача 9. В прямоугольном треугольнике ABC (C=90⁰ ), из вершины прямого угла проведена высота CH. Периметры треугольников ACH и BCH равны соответственно 3 см и 4 см. Найдите периметр треугольника ABC.

Примем CH=x, x>0, тогда

В треугольнике ABC BC – среднее геометрическое для AB и BH . По условию P периметр равен 4 см, тогда , X=1

Значит, CH=1см; P_ABC= 7 – 5 = 5. Ответ: 5

Задача 10. Найти периметр равнобедренного треугольника, если радиус вписанной окружности равен 3, а высота, проведённая к основанию, равна 8.

P_ABC = 2AB + AC

M – точка касания. Проведём ОМ. ОМОС (как радиус, проведённый в точку касания).

( OBM – общий, BMO = BHC = 90⁰ )

Из по теореме Пифагора

Из по теореме Пифагора .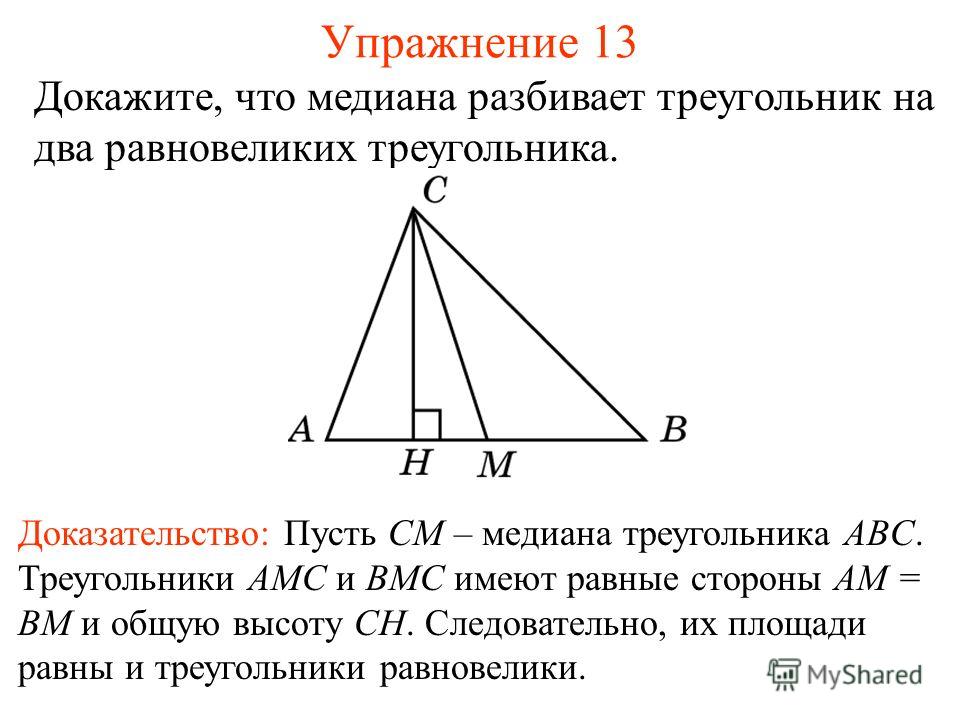

Ответ: 32

V Блок. Свойства биссектрисы треугольника.

Теория:

1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон (п. 72)
2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника (№ 535)

Задача11. В равнобедренном треугольнике АВС с основанием АС высоты ВМ и АН пересекаются в точке К, причём АК=5, КН=3. Найдите площадь треугольника АВК. Проведём высоту СЕ. Она проходит через точку К (п. 73).

S_АВК=. Так как треугольник АВС – равнобедренный, то высота ВМ является биссектрисой.

КЕ=КН=3. Из треугольника АЕК по т. Пифагора . В треугольнике АВН  ВН — биссектриса и делит сторону АН на отрезки, пропорциональные сторонам АВ и ВН:.

Примем ВН = х, где х>0, тогда . АВ = 6+4=10.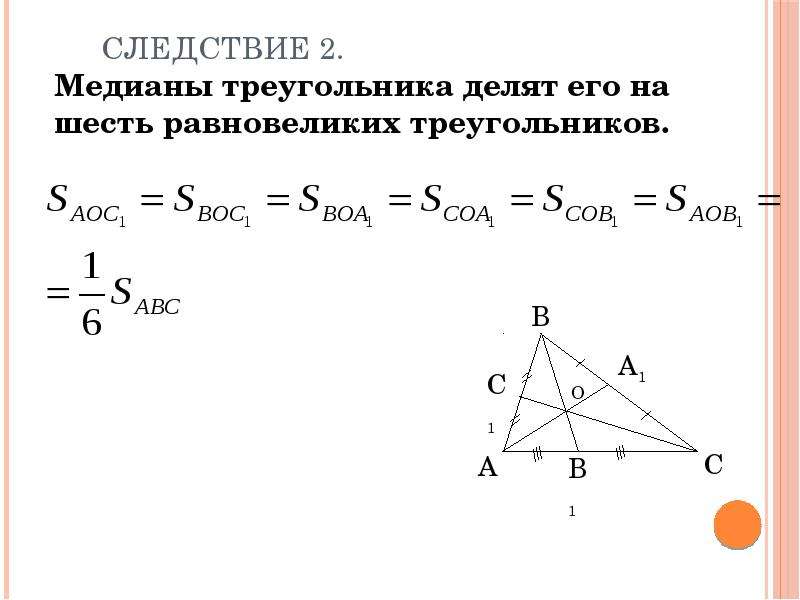

. Ответ 15.

Задача 12. В ромбе АВСD из вершины тупого угла В проведена высота ВН к стороне АD. Она пересекает диагональ АС в точке М. Сторона ромба равна 15, а его площадь равна 135.

Найдите площадь треугольника АМН

.

. S_ABCD= AD^. BH. ВН = 135:15 = 9. Из треугольника АВН по теореме Пифагора,. Так как диагональ ромба является биссектрисой (п.46), то по свойству биссектрисы треугольника АВН  получим Примем МН=х, х>0, тогда

Ответ:24.

Задача 13. Площадь равнобедренного треугольника АВС равна 20. К основанию АС и стороне ВС проведены высоты BD и АН, пересекающиеся в точке К. Найдите площадь треугольника ВКН, если

.

тогда  АВ=ВС (так как треугольник АВС-равнобедренный). Из треугольника АВН :

1) по т. Пифагора

2) ВК – биссектриса, поэтому .

Примем КН = х, х>0, тогда ,, КН = . . Ответ: 4,5.

Литература:

1. Учебник для общеобразовательных учреждений “Геометрия 7-9”, Л.С. Атанасян,В.Ф. Бутузов и другие. Москва, “Просвещение”, 2006г.
2. КИМ “ЕГЭ -2006” под редакцией Л.О.Денищевой. Москва, “Просвещение”, 2006г
3. “Типовые тестовые задания ЕГЭ” — 2007г, Т.А. Корешкова, Ю.А.Глазков, В.В. Мирошин, Н.В. Шевелёва. Москва, “Экзамен”, 2007
4. КИМ “ ЕГЭ – 2007”, Ю.А. Глазков, Т.А. Корешкова, В.В. Мирошин, Н.В.Шевелёва. Москва, “Экзамен” -2007г
5. “Тренировочные задания ЕГЭ” -2008, Т.А. Корешкова, Н.В.Шевелёва, В.В. Мирошин. Москва, “Эксмо” -2008.

Центроид треугольника | Brilliant Math & Science Wiki

Бой (보이), Даниэль Лю, Александр Кац, и

способствовал

Содержимое

• Нахождение центроида
• Доказательство существования
• Характеристики
• Отношения с другими центрами треугольника
• Другие полигоны
• Смотрите также

Центр тяжести легко найти с помощью координат: треугольник с вершинами в точках \((x_1, y_1), (x_2, y_2), (x_3, y_3)\) имеет центроид в точке \(\left(\frac{x_1+x_2) +x_3}{3}, \frac{y_1+y_2+y_3}{3}\right). \)

Треугольник \(ABC\) имеет вершины \(A = (3,4)\), \(B=(5,12)\) и \(C=(8,15)\). Каковы координаты центра тяжести треугольника \(ABC\)?

---

Центр тяжести находится на

\[\left(\frac{3+5+8}{3}, \frac{4+12+15}{3}\right)=\left(\frac{16}{3}, \frac{ 31}{3}\справа).\ _\квадрат\]

Простейшее доказательство является следствием теоремы Чевы, которая утверждает, что \(AD, BE, CF\) совпадают тогда и только тогда, когда

\[\frac{AE}{EC} \cdot \frac{CD}{ DB} \cdot \frac{BF}{FA} = 1.\]

В этом случае \(D,E,F\) являются серединами соответствующих сторон. Следовательно, \(AE=EC, CD=DB,\) и \(BF=FA,\), поэтому вышеприведенное равенство сразу верно, что демонстрирует существование центроида.

Медиана треугольника — это отрезок прямой между вершиной треугольника и серединой противоположной стороны. Каждая медиана делит треугольник на два равновеликих треугольника. Центроид — это пересечение трех медиан.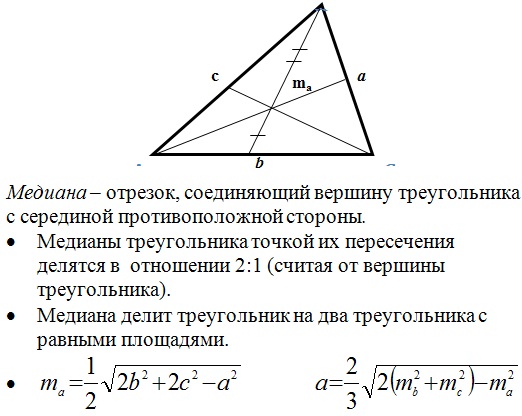

Три медианы также делят треугольник на шесть треугольников, каждый из которых имеет одинаковую площадь. 92 = 70\). Геометрическое место \(P\) представляет собой окружность радиуса \(r\), где \(r\) может быть выражено в форме \(\frac{m}{n}\) для некоторых относительно простых натуральных чисел \ (м\) и \(п\). Найдите \(100m+n\).

Аналогичное свойство следующее: если любая линия, проходящая через центроид, попадает в \(AB\) в точке \(D\) и \(AC\) в точке \(E\), то

\[\frac{BD}{DA}+\frac{CE}{EA}=1.\]

Можно также вычислить длину медианы из длин сторон:

92\большой)\).

На приведенной выше диаграмме прямая \(l\) проходит через центр тяжести \(\треугольника ABC.\)

Если расстояние по перпендикуляру между \(A\) и линией \(l\) равно 2, а расстояние по перпендикуляру между \(B\) и линией \(l\) равно 6, тогда каково расстояние по перпендикуляру между \(C\) и линией \(l?\)

Пусть \(a, b, c\) — длины сторон треугольника \(ABC\) выше, а \(d, e, f\) — расстояния от его центра тяжести \(O\) до вершин . (Красные линии — медианы.) 92}?\)

В треугольнике \(ABC\) случайная прямая проходит через его центр тяжести (пересечение трех медиан), разделяя его на две области. Найдите минимально возможное отношение площади меньшей области к площади большей области.

Другие центры треугольника включают

• ортоцентр
• в центре
• центр окружности.

Ортоцентр — это точка, где сходятся три высоты треугольника. Высота — это отрезок, проведенный из одной вершины в противоположную сторону и перпендикулярный противоположной стороне. 92\большой).\ _\квадрат \конец{выравнивание}\]

Центроид также лежит на линии Эйлера треугольника, поэтому

\[GH = \frac{2}{3}OH,\quad GO=\frac{1}{3}OH,\]

где \(H\) — ортоцентр треугольника.

Если \(A’, B’, C’\) являются центрами описанных окружностей треугольников \(BCG, ACG, ABG,\) соответственно, то

\(O\) — центр тяжести треугольника \(A’B’C’\). Кроме того, \(G\) является симедианой точки \(\треугольника A’B’C’\).

Наконец, медианы \(\треугольника A’B’C’\) проходят через середины \(AB, BC,\) и \(CA\), поэтому медианы \(\треугольника A’B ‘C’\) и \(\треугольник ABC\) пересекаются в середине исходного треугольника.

Рассмотрим равнобедренный \(\треугольник ABC\) с \(AB=AC=5, BC=6,\), где \(I,O,H\) обозначают его центр вписанной окружности, центр описанной окружности, ортоцентр соответственно.

Найдите площадь \(\треугольника IOH\).

Другие многоугольники имеют аналогичную интерпретацию центроида; он остается центром масс вершин многоугольника.

Однако центр тяжести больше не является (обязательно) пересечением медиан; на самом деле медианы не обязательно пересекаются в больших многоугольниках.

• Циркумцентр
• Инцентр
• Ортоцентр

Процитировать как: Центроид треугольника. Brilliant. org . Извлекаются из https://brilliant.org/wiki/triangles-centroid/

Калькулятор треугольников

Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д.

Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.

Засечки на ребрах треугольника — общепринятое обозначение, отражающее длину стороны, где одинаковое количество засечек означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны одинаковой длины. Обратите внимание, что треугольник, представленный в калькуляторе, показан не в масштабе; хотя он выглядит равносторонним (и имеет маркировку углов, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто изображение треугольника. При вводе фактических значений выходные данные калькулятора будут отражать форму входного треугольника.

Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямоугольные и косоугольные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.

Факты, теоремы и законы треугольника

• Зная длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что значения a, b и c известны.

Площадь треугольника

Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна.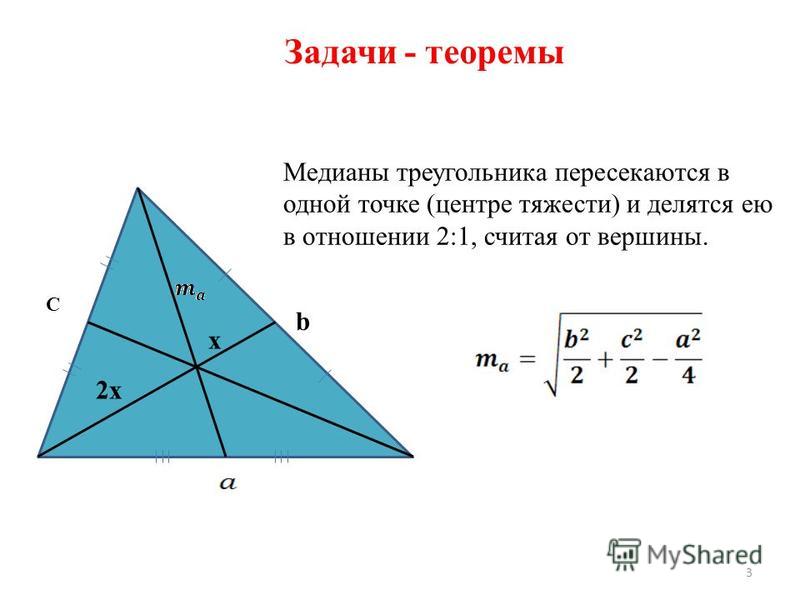 Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена ​​длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.

Зная длину двух сторон и угол между ними, можно использовать следующую формулу для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше. Учитывая а = 9, b = 7 и C = 30°:

Другой метод вычисления площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат. Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, в отношении треугольника, представленного в калькуляторе, если a = 3, b = 4 и c = 5:

Медиана, внутренний радиус и радиус описанной окружности

Медиана

Медиана треугольника определяется как длина отрезка, проходящего от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.

Медианы треугольника представлены отрезками m _a , m _б и м _с . Длину каждой медианы можно рассчитать следующим образом:

Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.

Например, учитывая, что a=2, b=3 и c=4, медиану m _a можно рассчитать следующим образом: круг, который поместится внутри заданного многоугольника, в данном случае треугольника. Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вписанной стороны и одной из сторон треугольника.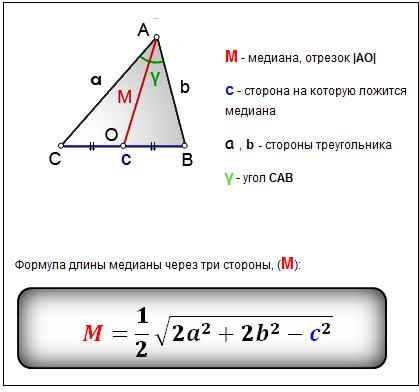 Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.

Для целей этого калькулятора внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (s) треугольника по следующим формулам:

внутренний радиус =

с =	а + б + в 2

где a, b и c — стороны треугольника

Радиус окружности

Радиус окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника. Центр этой окружности, где встречаются все серединные перпендикуляры каждой стороны треугольника, является центром описанной окружности треугольника и является точкой, от которой измеряется радиус описанной окружности.