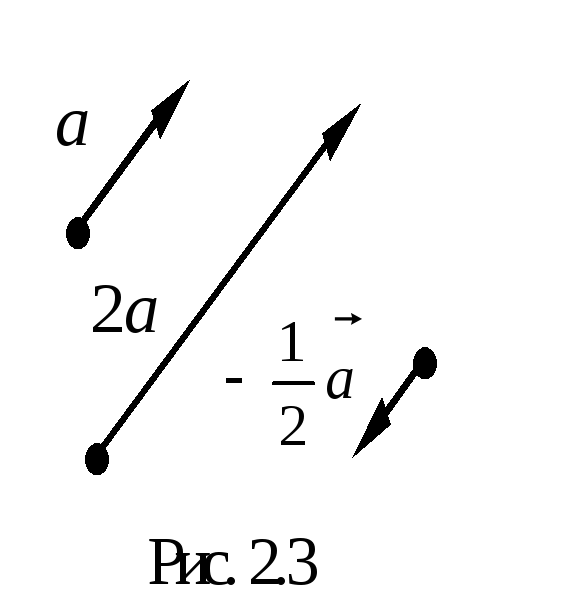Самостоятельные работы по теме Векторы | Учебно-методическое пособие по геометрии (9 класс):
Опубликовано 30.10.2020 — 12:00 — Маршева Ирина Владимировна
Самостоятельные работы предназначены для закрепления основных понятий по теме «Векторы». Представлены в двух вариантах. Рассчитаны на 12-15 минут урока.
Скачать:
Предварительный просмотр:
Вариант-1 Тема: «Понятие вектора. Равные векторы»
| Вариант-2 Тема: «Понятие вектора.
|
Вариант-1 Тема: «Понятие вектора. Равные векторы»
| Вариант-2 Тема: «Понятие вектора. Равные векторы»
|
Предварительный просмотр:
Самостоятельная работа по теме: «Координаты вектора»
I вариант
- Запишите координаты данных векторов, если их разложение по координатным векторам имеет вид: .
- Запишите разложение данного вектора по координатным векторам.
- Найдите координаты векторов , если ,
- Найдите координаты вектора , если
- Начертите прямоугольную систему координат ХОУ, выберите координатные векторы и .
 Постройте векторы , , , .
Постройте векторы , , , .
Самостоятельная работа по теме: «Координаты вектора»
II вариант
- Запишите координаты данных векторов, если их разложение по координатным векторам имеет вид: .
- Запишите разложение данного вектора по координатным векторам.
- Найдите координаты векторов , если ,
- Найдите координаты вектора , если
- Начертите прямоугольную систему координат ХОУ, выберите координатные векторы и . Постройте векторы , , , .
Самостоятельная работа по теме: «Координаты вектора»
III вариант
- Запишите координаты данных векторов, если их разложение по координатным векторам имеет вид: .
- Запишите разложение данного вектора по координатным векторам.
- Найдите координаты векторов , если ,
- Найдите координаты вектора , если
- Начертите прямоугольную систему координат ХОУ, выберите координатные векторы и .
 Постройте векторы , , , .
Постройте векторы , , , .
Самостоятельная работа по теме: «Координаты вектора»
IV вариант
- Запишите координаты данных векторов, если их разложение по координатным векторам имеет вид: .
- Запишите разложение данного вектора по координатным векторам.
- Найдите координаты векторов , если ,
- Найдите координаты вектора , если
- Начертите прямоугольную систему координат ХОУ, выберите координатные векторы и . Постройте векторы , , , .
Предварительный просмотр:
Вариант 1 Задание 1 Постройте вектор .
Задание 2 Постройте векторы а) ; б) .
Задание 3 Постройте вектор .
Вариант 2 Задание 1 Постройте вектор
Задание 2 Постройте векторы а) ; б) .
Задание 3 Постройте вектор .
По теме: методические разработки, презентации и конспекты
Самостоятельная работа по теме «Координаты вектора» 11 класс.
Самостоятельная работа по теме «Координаты вектора».в 11 классе расчитана на 20 мин. Два варианта. Учебник «Геометрия» 10-11, автор Атанасян….
Самостоятельная работа по теме «Координаты вектора» 11 класс.
Самостоятельная работа по теме «Координаты вектора».в 11 классе расчитана на 20 мин. Два варианта. Учебник «Геометрия» 10-11, автор Атанасян….
Самостоятельная работа по теме «Координаты вектора»
Самостоятельная работа по теме «Координаты вектора» для 11 класса…
Самостоятельная работа по теме «Векторы».
Презентация для проведения самостоятельной работы по теме «Векторы»…
9 класс.Геометрия.Самостоятельная работа по теме: Векторы.
Самостоятельная работа в двух вариантах на сложение и вычитание векторов….
Задания для подготовки к самостоятельной работе по теме: «Векторы» 9 класс
9 класс. ..
..
Самостоятельная работа по теме: «Вектор. Сложение, вычитание, умножение вектора на число. Линейная зависимость векторов. Координаты вектора» (с учетом индивидуальной структуры мышления обучающихся)
Учет индивидуальной подструктуры мышления у обучающихся ведет к усвоению математического материала и привитию устойчивого интереса к математике. Разработала учитель математики высшей к.к. МБОУ СОШ №19…
Поделиться:
Координаты вектора 9 класс онлайн-подготовка на Ростелеком Лицей
Определение вектора
Вектором (от лат. vector – «переносчик») называется направленный отрезок, имеющий длину и определенное направление. Графически векторы изображаются в виде направленных отрезков прямой определенной длины (см. Рис. 1).
Рис. 1. Вектор
Вектор, начало которого есть точка , а конец – точка , обозначается (см. Рис. 1). Также векторы обозначают одной маленькой буквой, например .
Рис. 1). Также векторы обозначают одной маленькой буквой, например .
Коллинеарные векторы. Сонаправленные и противоположно направленные векторы
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых: (см. Рис. 2).
Рис. 2. Коллинеарные векторы
Два коллинеарных вектора и называются сонаправленными векторами, если их направления совпадают: (см. Рис. 2).
Два коллинеарных вектора и называются противоположно направленнымивекторами, если их направления противоположны: (см. Рис. 2).
Равные векторы
Векторы и называются равными, если они сонаправлены и их абсолютные величины равны (см. Рис. 3).
, если: 1.
2.
Рис. 3. Равные векторы
3. Равные векторы
Умножение вектора на число
Произведение ненулевого вектора начисло – это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа (см. Рис. 4).
Рис. 4. Произведение вектора на число
Сложение векторов
(см. Рис. 5)
Рис. 5. Сложение векторов
Координаты коллинеарных векторов
Даны два коллинеарных вектора и (см. Рис. 6), причем .
Рис. 6. Коллинеарные векторы
– это коэффициент пропорциональности (число), для нахождения этого числа необходимо:
1. Если и – это сонаправленные векторы:
2. Если и – это противоположно направленные векторы:
Если и – это противоположно направленные векторы:
Задание произвольного вектора на плоскости
На плоскости для задания произвольного вектора необходимы две координаты и пара неколлинеарных векторов.
Теорема
Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом, то есть для любых неколлинеарных , и для любого найдется единственная пара действительных чисел таких, что .
Доказательство теоремы
Дано: , (см. Рис. 7)
Доказать:
1. ,
2. равенство верно для единственной пары чисел .
Рис. 7. Иллюстрация к доказательству
Доказательство
1. Из точки проведем прямую (параллельно ), на пересечении с осью получим точку (см. Рис. 8). Вектор будет равен:
Рис. 8). Вектор будет равен:
Рис. 8. Иллюстрация к доказательству
Вектор коллинеарен вектору , следовательно, найдется такое число , которое при умножении на вектор даст нам вектор .
Вектор коллинеарен вектору , следовательно, найдется такое число , которое при умножении на вектор даст нам вектор .
Следовательно:
То есть существует такая пара чисел , что: .
2. Методом от противного докажем, что пара чисел единственна.
Имеем: для
Предположим, что существует другая пара чисел такая, что . Вычтем из первого равенства второе:
Пусть , то есть . Тогда:
Получили, что векторы и коллинеарные: , а это противоречит условию ().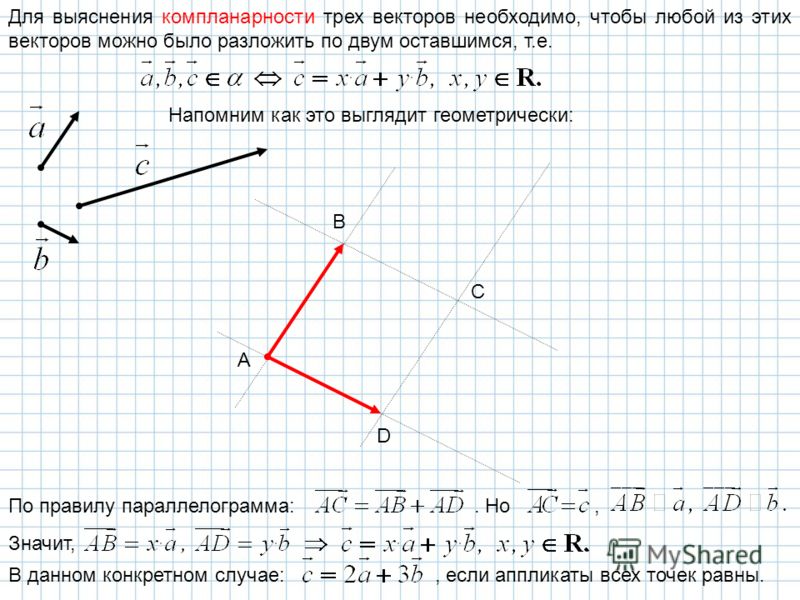 Следовательно, .
Следовательно, .
Аналогично доказывается, что . Таким образом:
Что и требовалось доказать.
Теорему можно сформулировать также следующим образом:
Неколлинеарные векторы и образуют систему координат . Любой третий вектор однозначно представляется в виде линейной комбинации векторов и : .
Пара действительных чисел – это координаты вектора. То есть вектор имеет координаты .
Задача 1
В системе координат с координатными и построить заданный с координатами .
Решение
Вектора и задают ось и . Необходимо построить вектор :
Эта запись означает:
Рис. 9. Иллюстрация к задаче
Отложим на оси вектор (см. Рис. 9). На оси отложим вектор . Проведем из точки прямую, параллельную оси , а из точки – прямую, параллельную оси . На пересечении этих прямых будет находиться точка . Вектор – это искомый вектор.
Проведем из точки прямую, параллельную оси , а из точки – прямую, параллельную оси . На пересечении этих прямых будет находиться точка . Вектор – это искомый вектор.
Если задана система координат, то под координатами точки на плоскости подразумеваются координаты вектора, проведенного из начала координат в эту точку. Например, в задаче 1 точка имеет координаты .
Задача 2
Построить с координатами .
Решение
Векторы и задают ось и . Необходимо построить вектор :
Эта запись означает:
Рис. 10. Иллюстрация к задаче
Отложим на оси вектор (см. Рис. 10). На оси отложим вектор . Проведем из конца вектора прямую, параллельную оси , а из конца вектора – прямую, параллельную оси . На пересечении этих прямых будет находиться точка . Вектор – это искомый вектор.
Задача 3
Выписать координаты вектора.
Дано:
Решение
Координатами вектора являются числа .
Ответ: .
Задача 4
Найти недостающие координаты и , если известно, что .
Решение
Данное равенство означает, что это один и тот же разложенный по векторам вектор, но записанный иначе. Следовательно, этому вектору соответствует единственная пара . Поэтому:
Ответ: ; .
Задача 5
Найти и , если .
Решение
Нулевой вектор равен:
Следовательно, можно записать
Поэтому:
Ответ: ; .
Список литературы
1. Атанасян Л.С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А.В. Тесты по геометрии: 9 класс. К учебнику Л.С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А.В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт ru.onlinemschool.com (Источник)
2. Интернет-сайт mathprofi.ru (Источник)
3. Интернет-сайт YouTube (Источник)
Домашнее задание
1. Задачи 911, 913 – Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия, 7-9 (Источник)
2. Какие векторы называют равными?
3. Построить с координатами .
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления. Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒ Вектор – это направленный отрезок. Векторы могут обозначаться как 2-мя прописными буквами, так и одной строчной с чертой или стрелкой. Длина вектора называется его модулем и обозначается Если Если Векторы, лежащие на одной прямой или на параллельных прямых, называют коллинеарными. Если начало и конец вектора совпадают , то такой вектор называется нулевым и обозначается Длина нулевого вектора равна нулю: , а направление – неопределенно. Сложение векторов
Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора , отложенного из конца вектора (правило треугольника). Суммой векторов и называется такой третий вектор , что при совмещенных началах этих трех векторов, векторы и служат сторонами параллелограмма, а вектор – его диагональю (называется сложением по правилу параллелограмма). Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего. При сложении векторов выполняется переместительныйзакон, т.е. + = +
и сочетательныйзакон, т.е. ( + )+ = +( + ) Вычитание векторов Под разностью векторов и понимается вектор такой, что (см. рис. 5).
Умножение вектора на число Произведением вектора на число k называется такой вектор , длина которого равна |k|⋅| |, причем векторы сонаправлены, если k>0, и противоположно направлены, если k<0. Произведение нулевого вектора на любое число есть нулевой вектор. Обозначение Вектора и коллинеарны для любого k. Если два вектора и коллинеарны – то существует такое число k, что =k . Для любых векторов и и чисел k и l справедливы следующие законы: Сочетательный: (kl)a→=k(l ) Первый распределительный: k( + )=k +k Второй распределительный: (k+l) =k +l
Разложение вектора по базисным ортам. Единичные векторы выходящие из начала координат в положительных направлениях осей OX, OYи OZназываются ортами этих осей. Любой вектор можно разложить по ортам осей координат: , или (на плоскости). Пример: Задание. Вектор задан своими координатами: . Записать разложение данного вектора по ортам осей координат. Решение. Числа называются направляющими косинусами вектора .
Направляющие косинусы вектора определяются соотношениями: , ясно что Пример: а = (3; -6; 2). Длина вектора называется его модулем и обозначается Если Если Пример: а = (3; -6; 2).
17. Два вектора называются ортогональными, если в пересечении они образуют прямой угол, т.е. угол в 90о. Два вектора называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых. Три вектора называются компланарными , если они лежат в одной плоскости либо в параллельных плоскостях. Условие ортогональности векторов. Два вектора и ортогональны (перпендикулярны), если их скалярное произведение равно нулю. · = 0 Условия коллинеарности Ø Два вектора a и b коллинеарны, если существует число n такое, что Ø Два вектора коллинеарны, если отношения их координат равны. Ø Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
Условия компланарности векторов Ø Три вектора компланарны если их смешанное произведение равно нулю. Ø Три вектора компланарны если они линейно зависимы. Ø Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.
(НУЖНЫ ПРИМЕРЫ)
⇐ Предыдущая1234Следующая ⇒ Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. |
отрицательных векторов – объяснение и примеры
Если есть отрицательные скаляры, возможно ли также иметь отрицательный вектор ? Это! На самом деле отрицательный вектор:
«Вектор, величина которого такая же, как у опорного вектора, но его направление противоположно направлению опорного вектора».
В этой статье мы обсудим следующие подтемы, связанные с отрицательными векторами:
- Что такое отрицательный вектор?
- Как найти отрицательный вектор
Что такое отрицательный вектор?
Векторы, имеющие ту же длину, что и конкретный вектор, но в противоположном направлении, называются отрицательными векторами. Отрицательный знак изменит направление вектора и сделает его отрицательным вектором. Векторы отрицательны только по отношению к другому вектору.
Например, , если вектор PQ указывает слева направо, то вектор QP будет указывать справа налево.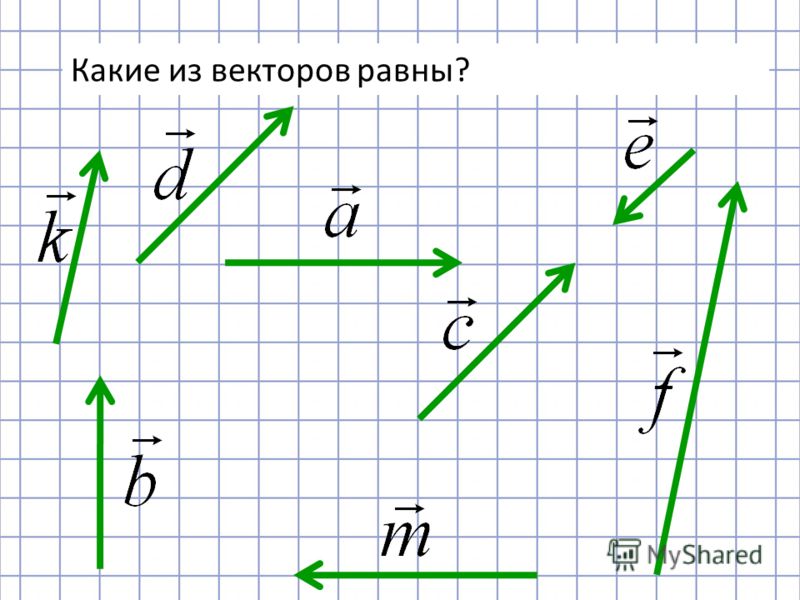 Поскольку эти направления противоположны, мы говорим, что PQ = – QP. То есть QP является отрицательным вектором для PQ, , как показано на рисунке ниже. Важно отметить, что вектор PQ и вектор QP имеют одинаковую величину, но противоположные направления, что делает их отрицательными векторами друг друга.
Поскольку эти направления противоположны, мы говорим, что PQ = – QP. То есть QP является отрицательным вектором для PQ, , как показано на рисунке ниже. Важно отметить, что вектор PQ и вектор QP имеют одинаковую величину, но противоположные направления, что делает их отрицательными векторами друг друга.
Величина или длина вектора не может быть отрицательной; он может быть нулевым или положительным. Знак минус используется здесь, чтобы указать, что вектор имеет направление, противоположное опорному вектору.
Математически можно сказать, что два вектора A и B являются отрицательными друг другу, если они удовлетворяют следующим двум условиям:
A = – B («Вектор вектор A” )
If
|A| = |В| (одинаковая величина) и
A ↑ и B ↓ или A↓ и B ↑ (противоположные направления).
Еще один простой способ узнать, являются ли два вектора отрицательными значениями друг друга, — это сравнить их координаты. Если координаты векторов равны по значению, но имеют противоположные знаки, то векторы будут отрицательными друг другу. Например, рассмотрим векторы A = (ax1, ay1) и B = (bx1, by1). Мы говорим, что вектор B является отрицательным вектором A , или:
A = – B
If
ax1 = -bx1 и ay1 = -by1.y1 = -by1.ay1
Этого критерия достаточно, чтобы показать, что B является отрицательным вектором A и наоборот.
Как найти отрицательный вектор?
Основная идея нахождения отрицательного вектора данного вектора состоит в том, чтобы найти две компоненты данного вектора (т. е. величину вектора и направление), а затем найти вектор той же длины, который указывает в противоположном направлении.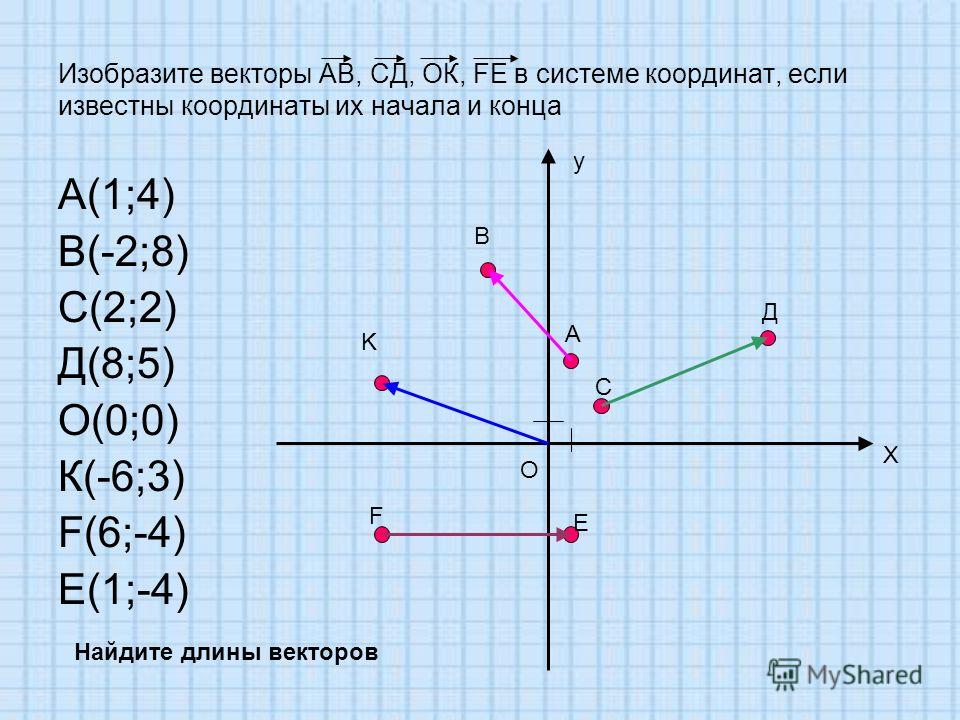 Два таких вектора будут отрицательными векторами друг друга.
Два таких вектора будут отрицательными векторами друг друга.
Нахождение отрицательного вектора заданного вектора можно выполнить, поставив перед ним знак минус. Например, пусть X будет вектором. Чтобы получить отрицательный вектор X , , мы умножаем X на -1, что дает X. Помните, что величина вектора X такая же, как у вектора X .
Примеры
В этом разделе сначала будут рассмотрены различные примеры, в которых мы находим отрицательные векторы путем сравнения компонентов опорного вектора. Затем мы обсудим еще несколько примеров и их пошаговые решения, чтобы развить еще более глубокое понимание негативных векторов.
Пример 1
Учитывая вектор P = (2, 4), определить отрицательное значение P. как направление, противоположное опорному вектору. В этом случае опорный вектор равен P, и его направление на 2 точки вправо по оси x и на 4 точки вверх по оси y. Таким образом, чтобы найти отрицательный вектор P , мы сохраняем ту же величину и умножаем опорный вектор P на -1. Это дает нам:
Таким образом, чтобы найти отрицательный вектор P , мы сохраняем ту же величину и умножаем опорный вектор P на -1. Это дает нам:
– P = (-2,-4)
Или
– P = – (2, 4)
Теперь направление отрицательного вектора можно интерпретировать как 2 точки на влево по оси x и на 4 точки вниз по оси y. Это явно противоположно направлению опорного вектора P.
Пример 2
Учитывая параллелограмм ABCD на изображении ниже, определите, какие векторы равны друг другу и являются отрицательными.
Решение
По определению два вектора могут быть равны, только если они имеют одинаковую величину и направлены в одном направлении. В параллелограмме ABCD вектор AB параллелен вектору CD, , тогда как вектор BC параллелен вектору DA. Кроме того, вектор AB и вектор CD указывают в одном направлении.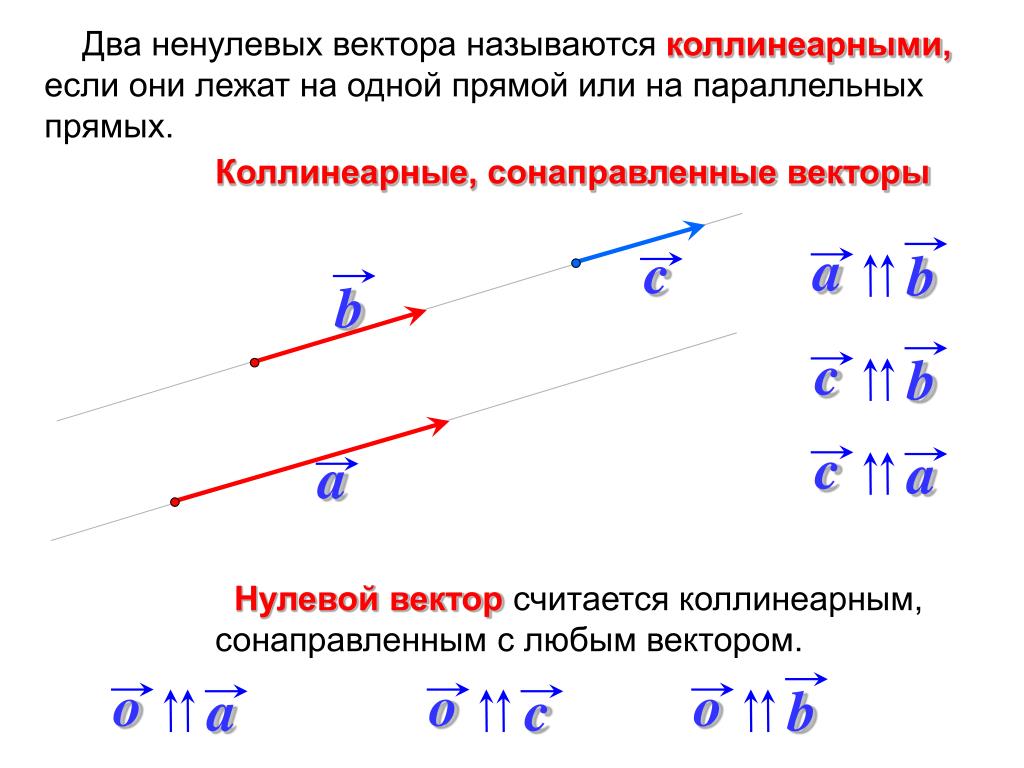 Следовательно, можно сказать, что это равные векторы, т.е.:
Следовательно, можно сказать, что это равные векторы, т.е.:
AB = CD (равные векторы)
Аналогично, вектор BC и вектор DA имеют одинаковую длину, но противоположные направления. Следовательно, они отрицательны друг относительно друга, то есть:
BC = – DA (отрицательные векторы)
Пример 3
Рассмотрим изображение, приведенное ниже. Сравните два вектора P и Q и определите, являются ли они отрицательными друг для друга или нет.
Решение
Этот пример прост. На изображении выше видно, что вектор P и вектор Q имеют одинаковую величину. Оба вектора также указывают в одном направлении. Таким образом, быстрое сравнение двух векторов показывает, что они равны, но не являются минусами друг друга.
P = Q
Пример 4
Определить отрицательное значение вектора OW, , начальная точка которого O = (2, 5), а конечная точка W = (5, 2).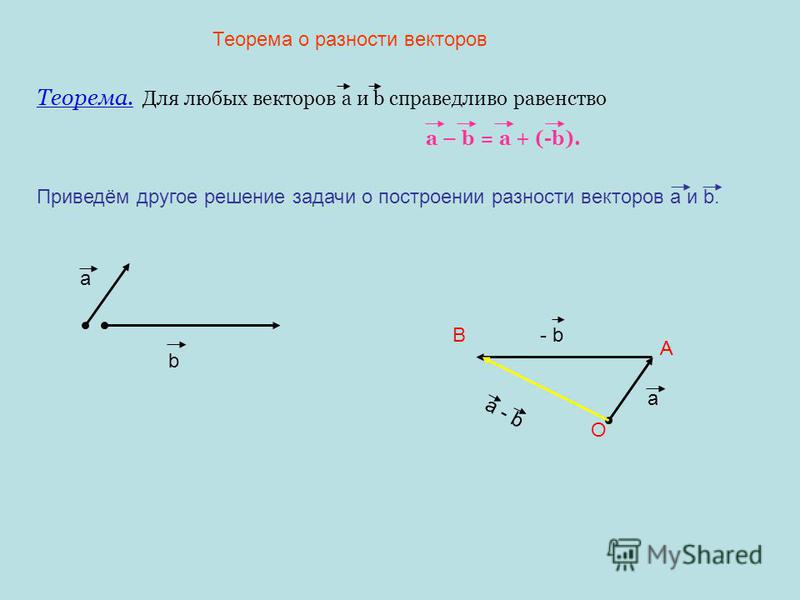
Решение
Для определения отрицательного вектора заданного вектора OW, умножим его координаты на -1 и получим – OW. Таким образом, начальная и конечная точки отрицательного вектора равны:
-O = (-2, -5) и -W = (-5, -2)
Далее определяем модуль обоих векторов для проверьте, что они все те же. 92
|- OW | = √ 18
Таким образом, модуль вектора – OW также оказывается примерно равным 4,242 единицы. Следовательно, два вектора имеют одинаковую длину, но противоположные направления, а это означает, что вектор – OW является отрицательным вектором OW.
OW = – OW
Пример 5
Определите, какие из следующих векторов равны, а какие отрицательные:2
| с | = √10
Очевидно, что | и | = | б |, | и | = | с |, и | б | = | с |. Таким образом, величины векторов a, , векторов b, и вектора c одинаковы.
Таким образом, величины векторов a, , векторов b, и вектора c одинаковы.
Чтобы сравнить направление, мы можем нанести три вектора на координатную плоскость, как показано на рисунке ниже. Можно заметить, что векторы a и c имеют одинаковую величину и указывают в одном направлении. С другой стороны, вектор b указывает в противоположном направлении. Следовательно, можно сделать следующий вывод:
Векторы а и с являются равными векторами,
а = с
и пара векторов а и b и c — отрицательные векторы.
и = – B
C = — B
Пример 6
Определите значение x, для которых два вектора A = (4, 10) и B = ( 2x, 5x) являются негативами друг друга.
Решение
Мы знаем, что два вектора являются отрицательными по отношению друг к другу, если их величины одинаковы, а их направления противоположны друг другу. Мы используем это, чтобы определить значение неизвестного x следующим образом:
A = – B => (2, 10) = – (2x, 5x)
Приравняв соответствующие компоненты, получим:
2 = -2x
А
2
10 = -5x
Упрощая приведенное выше уравнение, мы получаем:
x = -2
Таким образом, когда x = -2, два вектора A и B являются отрицательными значениями друг друга.
Пример 7
Определите значение n, для которого два вектора A = (-5, -1, 3n) и B = (-5, -1, -9) являются минусами друг друга.
Решение
Мы знаем, что два вектора равны, если их величины одинаковы, а их направления противоположны друг другу. Мы используем это, чтобы определить значение неизвестного n следующим образом:
Мы используем это, чтобы определить значение неизвестного n следующим образом:
A = – B => (-5, -1, -3n) = – (-5, -1, -9)
Установив соответствующие компоненты равными друг другу, получим:
-5 = 5, -1 = 1 и 3n = 9
-3n = -9
Упрощая приведенное выше уравнение, мы получаем:
n = 3
Таким образом, когда n = 3, два вектора A и B являются негативами друг друга.
Практические вопросыНайдите отрицательные значения следующих векторов: В = (2, 5) и Д = (3, -2). Кроме того, проверьте, являются ли два вектора отрицательными друг для друга или нет.
Ответы
- Отрицательное значение вектора A будет – A = (1, 2/3, 0).
- Минус вектора T будет равен – T = (0, -2, 1).
- Минус вектора В будет – В = (-2, -5), минус вектора D будет – D = (-3, 2). Ясно, что два вектора не являются негативами друг друга.
- Негатив вектора F будет – F = (-4, -10). Минус вектора G будет – G = (-5,-5), а минус вектора H будет – H = (4,10). Ясно, что два вектора F и G не являются отрицательными друг другу, но векторы F и H равны F = – H.

- Сравнивая компоненты двух векторов, мы находим, что при n = 4 два вектора A и B, будут негативами друг друга.
- Величина вектора OA равна | ОА |= 7 единиц, а минус вектора ОА будет – ОА. Его величина должна быть такой же, как у вектора OA . Таким образом, вектор – ОА будет начинаться в точке -О = (1, 0, -3) и заканчиваться в точке -А = (-5, -2, 0).
- Величина вектора UV | UV |= 5 единиц, а отрицательный вектор УФ будет – УФ. Его величина должна быть такой же, как у вектора UV. Таким образом, вектор – UV будет начинаться в точке -U = (-1, 2, 0) и заканчиваться в точке -V = (2, -2, 0).
Векторы и базисы
Вектор — это стрелка длины и
направление. Точно так же, как позиции, векторы существуют до того, как мы
измерить или описать их. В отличие от позиций, векторы могут
означают много разных вещей, таких как векторы положения,
скорости и т. д. Векторы не привязаны к конкретным
позиции в пространстве, так что мы можем двигать вектор вокруг и
найти его в любом месте.
Точно так же, как позиции, векторы существуют до того, как мы
измерить или описать их. В отличие от позиций, векторы могут
означают много разных вещей, таких как векторы положения,
скорости и т. д. Векторы не привязаны к конкретным
позиции в пространстве, так что мы можем двигать вектор вокруг и
найти его в любом месте.
Изменять:
Два вектора, которые могут совпадать или не совпадать вектор. Перемещение вектора не меняет его: это еще тот же вектор.
Добавление и масштабирование векторов
Векторы можно умножать на скалярное число, которое умножает их длину. Также можно добавить векторы вместе, используя закон параллелограмма дополнение или правило «голова к хвосту «.
Добавление и масштабирование векторов для получения новых векторов.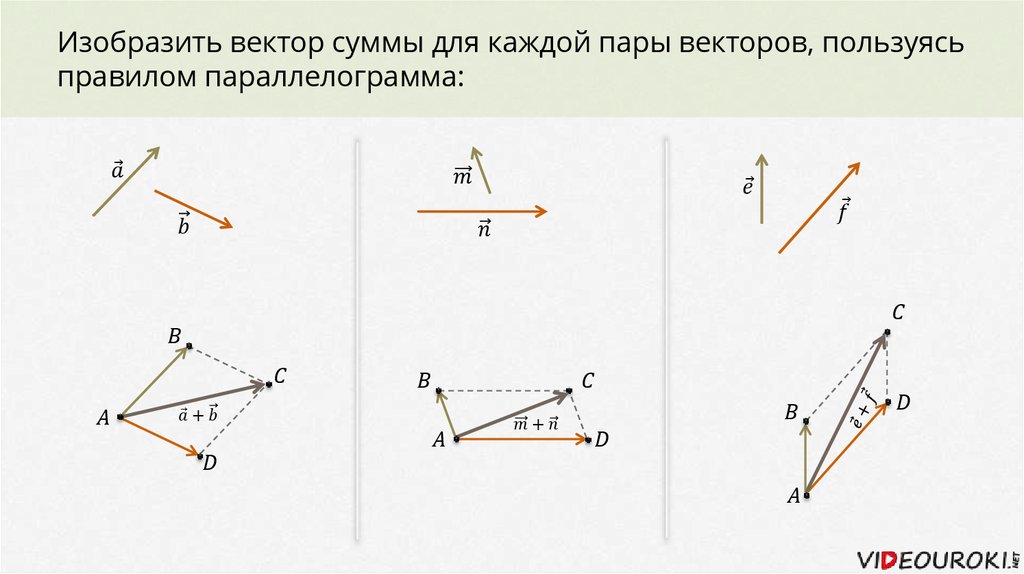
Векторные базы
Для математического описания векторов мы записываем их как
комбинация базисных векторов . ортонормированный
базис представляет собой набор из двух (в 2D) или трех (в 3D) базисов
векторов, которые
Любой другой вектор можно записать в виде линейного числа . комбинация базисных векторов:
\[\vec{a} = a_1 \,\hat{\imath} + a_2 \,\шляпа{\jmath} + a_3 \,\шляпа{k}\]
Числа $a_1, a_2, a_3$ называются компонент $\vec{a}$ в $\,\hat{\imath},
\hat{\jmath}, \hat{k}$ базис. Если мы находимся в 2D, то мы будем
имеют только две компоненты для вектора.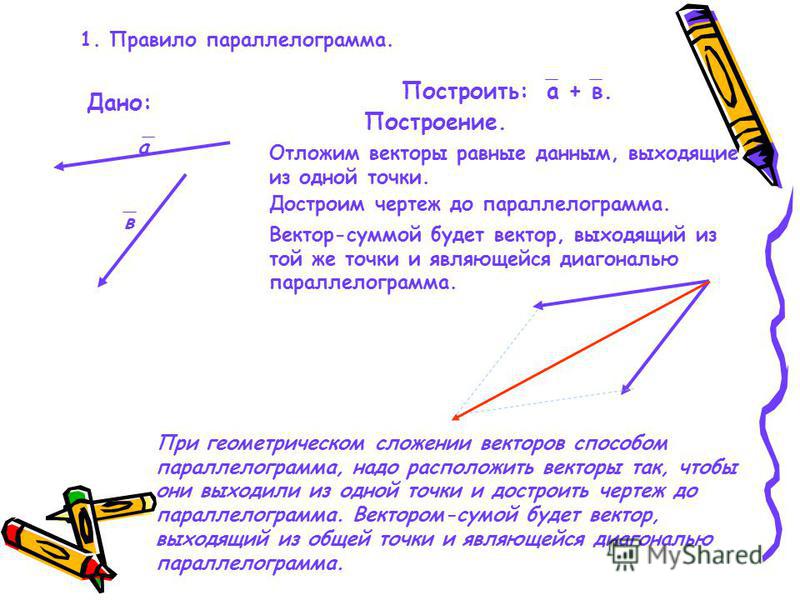
Запись вектора в виде суммы масштабированных базисных векторов. масштабные коэффициенты являются компонентами вектора. Здесь $\vec{a} = 3\hat\imath + 2\hat\jmath$, поэтому компоненты $\vec{a}$ равны $a_1 = 3$ и $a_2 = 2$.
Мы рисуем символ $\odot$ (кончик стрелки), чтобы указать вектор выход со страницы и $\otimes$ (стрелка оперения) чтобы указать стрелку, идущую на страницу.
Два стандартных расположения базисных векторов при работает в 2D. Либо $\hat\jmath$ является вертикальным и $\hat{k}$ находится за пределами страницы или $\hat{k}$ является вертикальным и $\hat\jmath$ находится на странице. В обоих случаях $\hat\imath$ расположен горизонтально.
Длина векторов
Длина вектора $\vec{a}$ записывается
либо $\|\vec{a}\|$, либо просто $a$. длина может быть вычислена с помощью 92.
\конец{выровнено}\]
длина может быть вычислена с помощью 92.
\конец{выровнено}\]
Нажмите и перетащите, чтобы повернуть.
Формула длины Пифагора может быть использована только в том случае, если все компоненты записываются в одном ортонормированном основа.
Вычисление длины вектора с помощью Пифагора теорема.
Некоторые общие целочисленные длины векторов $\vec{a} = 4\hat\imath + 3\hat\jmath$ (длина $a = 5$) и $\vec{b} = 12\hat\imath + 5\hat\jmath$ (длина $b = 13$).
Если $\vec{c} = \vec{a} + \vec{b}$, то $\|\vec{c}\| \ne \|\vec{а}\| + \|\vec{b}\|$, если только $\vec{a}$ и $\vec{b}$ параллельны и имеют одинаковое направление.
Однако всегда будет верно, что $\|\vec{c}\| \ле
\|\vec{а}\| + \|\vec{b}\|$. Этот факт известен как неравенство треугольника , по причинам, которые должны быть
очевидный.
Этот факт известен как неравенство треугольника , по причинам, которые должны быть
очевидный.
Единичные векторы
Единичный вектор — это любой вектор длиной один. Мы используем специальное обозначение $\hat{a}$ для указать, когда вектор является единичным вектором. Любой ненулевой вектор $\vec{a}$ задает единичный вектор $\hat{a}$, определяющий направление $\vec{a}$.
\[\begin{выровнено} \шляпа{а} = \frac{\vec{a}}{a}\end{выровнено}\]
Если мы вычислим длину $\hat{a}$, то найдем:
\[
\| \шляпа{а} \| = \слева\| \frac{\vec{a}}{a} \right\|
= \frac{\|\vec{a}\|}{a} = \frac{a}{a} = 1,
\]
так что $\hat{a}$ действительно является единичным вектором, и он находится в
того же направления, что и $\vec{a}$, поскольку они отличаются только на
скалярный фактор.
Любой вектор можно представить в виде произведения его длины на направление:
\[\begin{выровнено} \vec{a} = a \шляпа{а}\конец{выровнено}\]
Это следует из перестановки #rvv-eu.
Три вектора и их разложения на длины и направленные единичные векторы.
Векторы и единицы
При использовании векторов для описания физических величин нам необходимо
чтобы иметь правильные единицы, связанные с ними, так же, как для положения
координаты. Базисные векторы, такие как
$\hat\imath,\hat\jmath,\hat{k}$ не имеют единиц (они также
безразмерные), поэтому компоненты должны иметь единицы измерения. За
например, вектор скорости $\vec{v} = (4\hat\imath +
3\hat\jmath){\rm\ m/s}$ имеет компоненты $v_1 = 4{\rm\ m/s}$
и $v_2 = 3{\rm\ m/s}$, которые затем умножают
безразмерные (и безразмерные) базисные векторы $\hat\imath$ и
$\шляпа\jmath$. Для удобства, когда все компоненты
вектор имеет одинаковые единицы измерения, мы будем часто писать единицы измерения
только один раз в конце, так что все следующие
выражения эквивалентны:
\[\ начало {выровнено}
\vec{v} &= (4{\rm\ м/с})\,\шляпа\imath + (3{\rm\ м/с})\,\шляпа\jmath \\
&= (4\шапка\imath + 3\шляпа\jmath){\rm\m/s} \\
&= 4\шляпа\imath + 3\шляпа\jmath {\rm\ м/с}.
\конец{выровнено}\]
92}} = 5{\rm\ м/с}.
\]
Тогда единичный вектор равен
\[
\ шляпа {v} = \ гидроразрыва {\ vec {v}} {v}
= \ frac {(4 {\ rm \ м / с}) \, \ шляпа \ imath + (3 {\ rm \ м / с}) \, \ шляпа \ jmath} {5 {\ rm \ м / с} }
= 0.8\,\hat\imath + 0.6\,\hat\jmath.
\]
Для удобства, когда все компоненты
вектор имеет одинаковые единицы измерения, мы будем часто писать единицы измерения
только один раз в конце, так что все следующие
выражения эквивалентны:
\[\ начало {выровнено}
\vec{v} &= (4{\rm\ м/с})\,\шляпа\imath + (3{\rm\ м/с})\,\шляпа\jmath \\
&= (4\шапка\imath + 3\шляпа\jmath){\rm\m/s} \\
&= 4\шляпа\imath + 3\шляпа\jmath {\rm\ м/с}.
\конец{выровнено}\]
92}} = 5{\rm\ м/с}.
\]
Тогда единичный вектор равен
\[
\ шляпа {v} = \ гидроразрыва {\ vec {v}} {v}
= \ frac {(4 {\ rm \ м / с}) \, \ шляпа \ imath + (3 {\ rm \ м / с}) \, \ шляпа \ jmath} {5 {\ rm \ м / с} }
= 0.8\,\hat\imath + 0.6\,\hat\jmath.
\]
Скалярное произведение
Скалярное произведение (также называемое внутренним числом ). произведение или скалярное произведение ) определяется как
\[\vec{a} \cdot \vec{b} = а_1 б_1 + а_2 б_2 + а_3 б_3\]
Альтернативное выражение для скалярного произведения может быть заданы через длины векторов и угол между ними:
\[\vec{a} \cdot \vec{b} = а б \cos\тета\]
Здесь мы представим простое 2D-доказательство. Более полное доказательство в 3D использует закон косинусов.
Более полное доказательство в 3D использует закон косинусов.
Начните с двух векторов $\vec{a}$ и $\vec{b}$ с угол $\theta$ между ними, как показано ниже.
Заметим, что угол $\theta$ между векторами $\vec{a}$ и $\vec{b}$ — это разница между $\theta_a$ и $\theta_b$ от горизонтали.
Если мы используем формулу суммы углов для косинуса, мы имеем
\[\begin{align} a b \cos\theta &= a b \cos(\theta_b — \theta_a) \\ &= a b (\cos\theta_b \cos\theta_a + \sin\theta_b \sin\theta_a) \конец{выровнено}\]
Теперь мы хотим выразить синус и косинус $\theta_a$ и $\theta_b$ с точки зрения $\vec{a}$ и $\vec{b}$.
Переформулируем выражение так, чтобы можно было использовать факт
что $a_1 = a \cos\theta_a$ и $a_2 = a \sin\theta_a$,
и аналогично для $\vec{b}$. 2$, что
дает первое уравнение для длины через
скалярное произведение.
9\circ$ вращение $\vec{a}$.
2$, что
дает первое уравнение для длины через
скалярное произведение.
9\circ$ вращение $\vec{a}$.
Перекрестный продукт
Перекрестный продукт может быть определен с точки зрения компонентов следующим образом:
\[ \vec{a} \times \vec{b} = (a_2 b_3 — a_3 b_2) \,\шляпа{\imath} + (a_3 b_1 — a_1 b_3) \,\шляпа{\jmath} + (a_1 b_2 — a_2 b_1) \,\шляпа{k} \]
Иногда удобнее работать с перекрестными произведениями отдельных базисных векторов, которые связаны следующим образом.
\[\ начало {выровнено} \hat\imath \times \hat\jmath &= \hat{k} & \hat\jmath \times \hat{k} &= \hat\imath & \hat{k} \times \hat\imath &= \hat\jmath \\ \hat\jmath \times \hat\imath &= -\hat{k} & \hat{k} \times \hat\jmath &= -\hat\imath & \hat\imath \times \hat{k} &= -\hat\jmath \\ \конец{выровнено}\]
Запись базисных векторов через самих себя дает
составные части:
\[\ начало {выровнено}
i_1 &= 1 & i_2 &= 0 & i_3 &= 0 \\
j_1 &= 0 & j_2 &= 1 & j_3 &= 0 \\
k_1 &= 0 & k_2 &= 0 & k_3 &= 1. \конец{выровнено}\]
Теперь эти значения можно подставить в определение #rvv-ex. Например,
\[\ начало {выровнено}
\ шляпа \ имат \ раз \ шляпа \ jmath
&= (i_2 j_3 — i_3 j_2) \,\шляпа{\imath}
+ (i_3 j_1 — i_1 j_3) \,\шляпа{\jmath}
+ (i_1 j_2 — i_2 j_1) \,\шляпа{k} \\
&= (0 \times 0 — 0 \times 1) \,\hat{\imath}
+ (0 \times 0 — 1 \times 0) \,\hat{\jmath}
+ (1 \times 1 — 0 \times 0) \,\hat{k} \\
&= \шляпа{к}
\конец{выровнено}\]
Аналогично рассчитываются и другие комбинации.
\конец{выровнено}\]
Теперь эти значения можно подставить в определение #rvv-ex. Например,
\[\ начало {выровнено}
\ шляпа \ имат \ раз \ шляпа \ jmath
&= (i_2 j_3 — i_3 j_2) \,\шляпа{\imath}
+ (i_3 j_1 — i_1 j_3) \,\шляпа{\jmath}
+ (i_1 j_2 — i_2 j_1) \,\шляпа{k} \\
&= (0 \times 0 — 0 \times 1) \,\hat{\imath}
+ (0 \times 0 — 1 \times 0) \,\hat{\jmath}
+ (1 \times 1 — 0 \times 0) \,\hat{k} \\
&= \шляпа{к}
\конец{выровнено}\]
Аналогично рассчитываются и другие комбинации.
Перекрестное произведение не ассоциативно,
значит в общем
\[\vec{a} \times (\vec{b} \times \vec{c})
\ne (\vec{a} \times \vec{b}) \times \vec{c}.\]
Например,
\[\ начало {выровнено}
\ шляпа {\ imath} \ раз (\ шляпа {\ imath} \ раз \ шляпа {\ jmath})
&= \ шляпа {\ imath} \ раз \ шляпа {k} = — \ шляпа {\ jmath} \\
(\ шляпа {\ imath} \ раз \ шляпа {\ imath}) \ раз \ шляпа {\ jmath}
&= \vec{0} \times \hat{\jmath} = \vec{0}.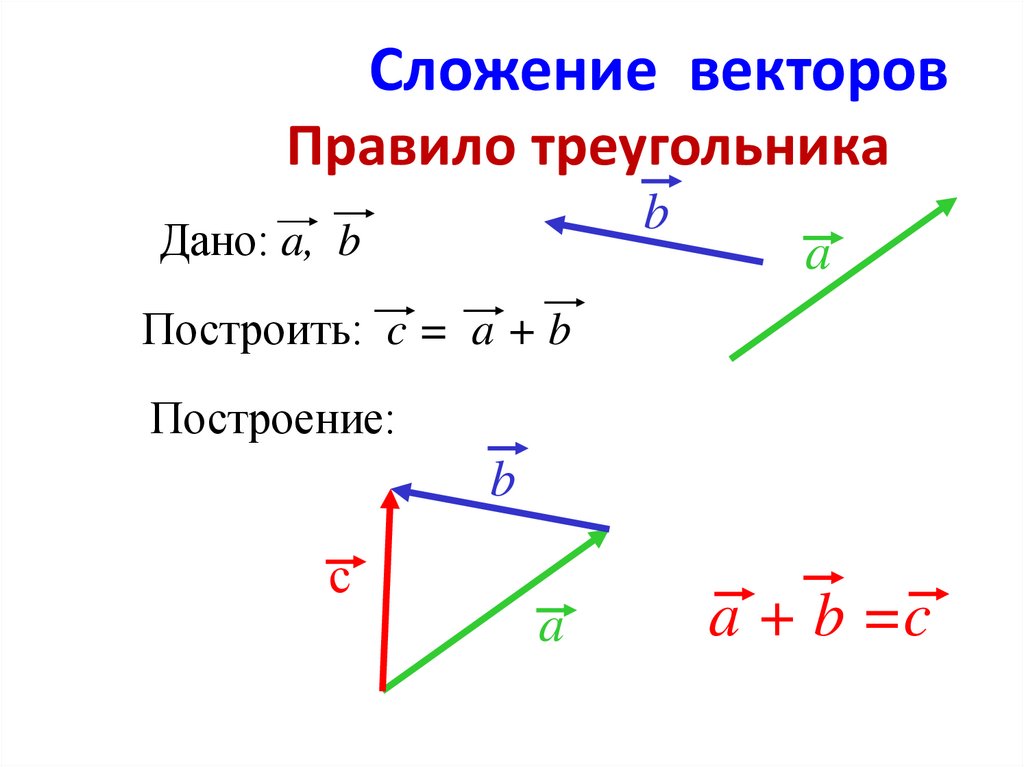 \конец{выровнено}\]
Это означает, что мы никогда не должны писать выражение типа
\[\vec{a} \times \vec{b} \times \vec{c}\]
потому что непонятно, в каком порядке мы должны выполнять
перекрестные произведения. Вместо этого, если у нас есть более одного
перекрестное произведение, мы всегда должны использовать круглые скобки для
указать порядок.
\конец{выровнено}\]
Это означает, что мы никогда не должны писать выражение типа
\[\vec{a} \times \vec{b} \times \vec{c}\]
потому что непонятно, в каком порядке мы должны выполнять
перекрестные произведения. Вместо этого, если у нас есть более одного
перекрестное произведение, мы всегда должны использовать круглые скобки для
указать порядок.
Вместо того, чтобы использовать компоненты, перекрестный продукт может быть определяется указанием длины и направления результирующий вектор. Направление $\vec{a} \times \vec{b}$ ортогонален как $\vec{a}$, так и $\vec{b}$, причем направление, заданное правилом правой руки. Величина перекрестное произведение определяется как:
\[\| \vec{a} \times \vec{b} \| = a b \sin\theta\]
Используя тождество Лагранжа, мы можем вычислить:
\[\ начало {выровнено}
\| \vec{a} \times \vec{b} \|^2
&= \|\vec{a}\|^2 \|\vec{b}\|^2
— (\vec{a} \cdot \vec{b})^2 \\
&= a^2 b^2 — (a b \cos\theta)^2 \\
&= a^2 b^2 (1 — \cos^2\тета) \\
&= а^2 б^2 \sin^2\тета. \конец{выровнено}\]
Извлечение квадратного корня из этого выражения дает
желаемая формула длины перекрестного произведения.
\конец{выровнено}\]
Извлечение квадратного корня из этого выражения дает
желаемая формула длины перекрестного произведения.
Эта вторая форма определения перекрестного произведения также может быть относится к площади параллелограмма.
Площадь параллелограмма равна длине основания умножается на высоту перпендикуляра, которая также является величина векторного произведения боковых векторов.
Полезный частный случай векторного произведения возникает, когда вектор $\vec{a}$ лежит в двумерной плоскости $\hat\imath,\hat\jmath$ а другой вектор находится в ортогональном $\hat{k}$ направление. В этом случае векторное произведение вращает $\vec{a}$ на 9 долларов\ перп. \конец{выровнено}\]
Проекция и дополнительная проекция
Проекция и дополнительная проекция:
\[\operatorname{Proj}(\vec{a},\vec{b}) = (\vec{a} \cdot \шляпа{b}) \шляпа{b} = (а \cos\тета) \, \шляпа{b} \]
\[\ начало {выровнено} \operatorname{Comp}(\vec{a}, \vec{b}) &= \vec{a} — \operatorname{Proj}(\vec{a}, \vec{b}) = \vec{a} — (\vec{a} \cdot \шляпа{b}) \шляпа{b} \\ \влево\| \operatorname{Comp}(\vec{a}, \vec{b}) \right\| &= а \sin\тета \конец{выровнено}\]
Добавление проекции и дополнительной проекции
вектор просто дайте тот же вектор снова, как мы можем видеть на
рисунок ниже.
Проекция $\vec{a}$ на $\vec{b}$ и дополнительная проекция.
Как мы видим на диаграмме выше, дополнительная проекция ортогонален опорному вектору:
\[\operatorname{Comp}(\vec{a}, \vec{b}) \cdot \vec{b} = 0\]
Используя определения дополнительной проекции rvv-em и проекции rvv-ep, мы вычисляем: \[\ начало {выровнено} \operatorname{Comp}(\vec{a}, \vec{b}) \cdot \vec{b} &= \Big(\vec{a} — (\vec{a} \cdot \hat{b}) \шляпа{b}\Большой) \cdot \vec{b} \\ &= \vec{a} \cdot \vec{b} — (\vec{a} \cdot \hat{b}) (\шляпа{b} \cdot \vec{b}) \\ &= a b \cos\theta — (a\cos\theta) b \\ &= 0. \конец{выровнено}\]
Смена баз
Чтобы изменить базис, в котором записывается вектор, нам нужно
узнать, как связаны базисные векторы.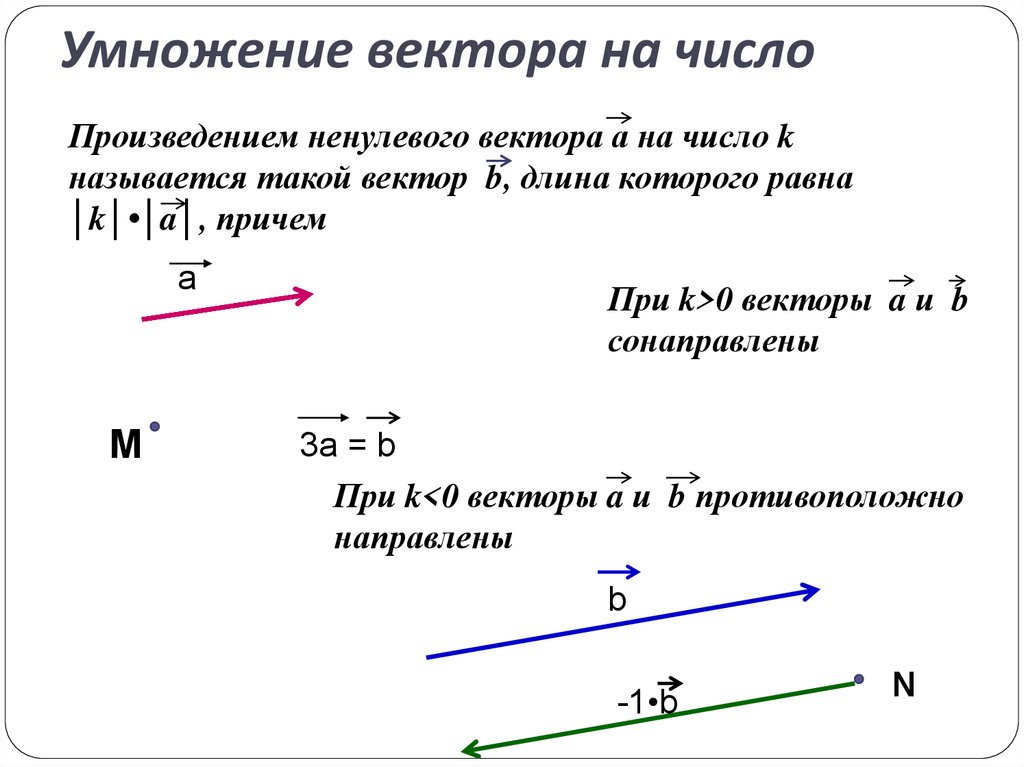 Мы делаем это по
запись одного набора базисных векторов через другой
базисные векторы. Если мы хотим перейти от
$\hat\imath,\hat\jmath$ в $\hat{u},\hat{v}$, то мы
нужно написать $\hat\imath,\hat\jmath$ в терминах
$\hat{u},\hat{v}$, а затем подставьте выражения.
Мы делаем это по
запись одного набора базисных векторов через другой
базисные векторы. Если мы хотим перейти от
$\hat\imath,\hat\jmath$ в $\hat{u},\hat{v}$, то мы
нужно написать $\hat\imath,\hat\jmath$ в терминах
$\hat{u},\hat{v}$, а затем подставьте выражения.
Например, если у нас есть $\vec{a} = 3\,\hat{\imath} + 2\,\hat{\jmath}$ и мы хотим напишите это в $\,\hat{u}, \,\hat{v}$ базисе, то нам нужно знать $\,\hat{\imath}, \,\hat{\jmath}$ через $\,\hat{u}, \,\шляпа{v}$.
Сверху мы видим, что:
\[\begin{выровнено} \шляпа{\imath} &=
\cos\theta \, \hat{u} — \sin\theta \, \hat{v}
= \frac{1}{\sqrt{2}} \,\hat{u} — \frac{1}{\sqrt{2}}
\,\шляпа{v} \\
\шляпа{\jmath} &=
\sin\theta \, \hat{u} + \cos\theta \, \hat{v}
= \ гидроразрыва {1} {\ sqrt {2}}
\,\шляпа{и} + \фракция{1}{\sqrt{2}}
\,\шляпа{v}.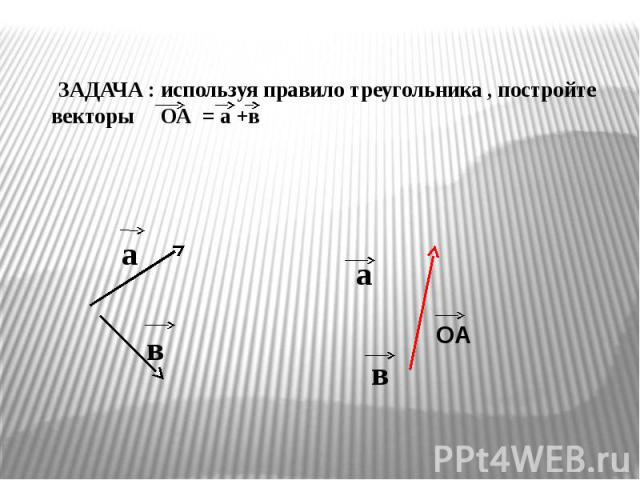 \end{выровнено}\]
\end{выровнено}\]
Затем мы можем заменить и переставить:
\[\begin{выровнено} \vec{a} &= 3\,\шляпа{\imath} + 2\,\шляпа{\jmath} \\ &= 3\left(\frac{1}{\sqrt{2}} \,\шляпа{u} — \frac{1}{\sqrt{2}} \,\шляпа{v}\right) + 2\left(\frac{1}{\sqrt{2}} \,\шляпа{u} + \frac{1}{\sqrt{2}} \,\hat{v}\right) \\ &= \left(\frac{3}{\sqrt{2}} + \frac{2}{\sqrt{2}} \right) \,\шляпа{u} + \left(-\frac{3}{\sqrt{2}} + \frac{2}{\sqrt{2}} \right) \,\hat{v} \\ &= \frac{5}{\sqrt{2}} \,\hat{u} — \frac{1}{\sqrt{2}} \,\шляпа{v}.\end{выровнено}\]
Если мы хотим преобразовать обратно, то мы бы
нужно знать $\,\hat{u}, \,\hat{v}$ с точки зрения
$\,\шляпа{\imath}, \,\шляпа{\jmath}$. Мы можем найти это по
решение для $\,\hat{u}, \,\hat{v}$ выше, что дает:
\[\begin{выровнено} \шляпа{u} &=
\cos\theta \, \hat\imath + \sin\theta \, \hat\jmath
= \frac{1}{\sqrt{2}} \,\hat\imath + \frac{1}{\sqrt{2}}
\,\шляпа\jmath\\
\шляпа{v} &=
-\sin\theta \, \hat\imath + \cos\theta \, \hat\jmath
= -\frac{1}{\sqrt{2}}
\,\hat\imath + \frac{1}{\sqrt{2}}
\,\шляпа\jmath. \end{выровнено}\]
\end{выровнено}\]
Мы также можем написать общие выражения для изменения базиса, как показано ниже.
\[\ начало {выровнено} \vec{а} &= a_i \, \hat\imath + a_j \, \hat\jmath + a_k \, \hat{k} & \vec{а} &= a_u \, \шляпа{u} + a_v \, \шляпа{v} + a_w \, \шляпа{w} \\[1em] a_i &= a_u u_i + a_v v_i + a_w w_i & a_u &= a_i i_u + a_j j_u + a_k k_u \\ a_j &= a_u u_j + a_v v_j + a_w w_j & a_v &= a_i i_v + a_j j_v + a_k k_v \\ a_k &= a_u u_k + a_v v_k + a_w w_k & a_w &= a_i i_w + a_j j_w + a_k k_w \конец{выровнено}\]
Выведем первую систему уравнений (вторую
набор выводится аналогично). Вектор $\vec{a}$ может быть
написано как на $\hat\imath,\hat\jmath,\hat{k}$, так и на
Основания $\шляпа{u},\шляпа{v},\шляпа{w}$:
\[\ начало {выровнено}
\vec{a} &= a_i \hat\imath + a_j \hat\jmath + a_k \hat{k}
& \vec{a} &= a_u \hat{u} + a_v \hat{v} + a_w \hat{w}. \конец{выровнено}\]
\конец{выровнено}\]
Мы можем записать каждый базисный вектор $\hat{u},\hat{v},\hat{w}$
с точки зрения базиса $\hat\imath,\hat\jmath,\hat{k}$:
\[\ начало {выровнено}
\hat{u} &= u_i \hat\imath + u_j \hat\jmath + u_k \hat{k} \\
\шляпа{v} &= v_i \шляпа\imath + v_j \шляпа\jmath + v_k \шляпа{k} \\
\hat{w} &= w_i \hat\imath + w_j \hat\jmath + w_k \hat{k}.
\конец{выровнено}\]
Подстановка этих выражений в $\vec{a}$ дает:
\[\ начало {выровнено}
\vec{a} &= a_u \hat{u} + a_v \hat{v} + a_w \hat{w} \\
&= a_u (u_i \шляпа\imath + u_j \шляпа\jmath + u_k \шляпа{k})
+ a_v (v_i \шляпа\imath + v_j \шляпа\jmath + v_k \шляпа{k})
+ a_w (w_i \шляпа\imath + w_j \шляпа\jmath + w_k \шляпа{k}) \\
&= (a_u u_i + a_v v_i + a_w w_i) \шляпа\imath
+ (a_u u_j + a_v v_j + a_w w_j) \шляпа\jmath
+ (a_u u_k + a_v v_k + a_w w_k) \шляпа{k} \\
&= a_i \hat\imath + a_j \hat\jmath + a_k \hat{k}. \конец{выровнено}\]
Сравнение последних двух строк дает формулы компонентов.
\конец{выровнено}\]
Сравнение последних двух строк дает формулы компонентов.
В 2D изменение между двумя ортонормированными основаниями представляет собой поворот на угол $\theta$, что приводит к изменению базиса выражение ниже.
\[\ начало {выровнено} \vec{а} &= a_i \, \hat\imath + a_j \, \hat\jmath & \vec{а} &= a_u \, \шляпа{u} + a_v \, \шляпа{v} \\[1em] a_i &= \cos\theta \, a_u — \sin\theta \, a_v & a_u &= \cos\theta \, a_i + \sin\theta \, a_j \\ a_j &= \sin\theta \, a_u + \cos\theta \, a_v & a_v &= -\sin\theta \, a_i + \cos\theta \, a_j \конец{выровнено}\]
Элементарная геометрия дает отношения между
базисные векторы:
\[\ начало {выровнено}
\hat\imath &= \cos\theta \, \hat{u} — \sin\theta \, \hat{v}
& \hat{u} &= \cos\theta \, \hat\imath + \sin\theta \, \hat\jmath \\
\hat\jmath &= \sin\theta \, \hat{u} + \cos\theta \, \hat{v}
& \hat{v} &= -\sin\theta \, \hat\imath + \cos\theta \, \hat\jmath. \конец{выровнено}\]
Итак, у нас есть компоненты:
\[\ начало {выровнено}
i_u &= \cos\theta & i_v &= -\sin\theta
& u_i &= \cos\theta & u_j &= \sin\theta \\
j_u &= \sin\theta & j_v &= \cos\theta
& v_i &= -\sin\theta & v_j &= \cos\theta.
\конец{выровнено}\]
Подставив их в #rvv-eg
а игнорирование третьих компонентов дает желаемое
выражения.
\конец{выровнено}\]
Итак, у нас есть компоненты:
\[\ начало {выровнено}
i_u &= \cos\theta & i_v &= -\sin\theta
& u_i &= \cos\theta & u_j &= \sin\theta \\
j_u &= \sin\theta & j_v &= \cos\theta
& v_i &= -\sin\theta & v_j &= \cos\theta.
\конец{выровнено}\]
Подставив их в #rvv-eg
а игнорирование третьих компонентов дает желаемое
выражения.
Векторные выражения истинны независимо от того, какой базис мы пишем векторы в, даже если они записаны в разных основаниях.
Добавление $\vec{a}$ и $\vec{b}$ для получения результата
$\vec{c}$ — хорошо определенная операция еще до того, как
используется базис, поэтому он не может зависеть от базиса
выбран. Как мы видим ниже, мы можем сделать расчет в
либо $\hat\imath,\hat\jmath$, либо $\hat{u},\hat{v}$
основа.
Показать компоненты: никто $\шляпа\imath,\шляпа\jmath$ $\шляпа{и},\шляпа{в}$ смешанный
\[\ начало {выровнено} \vec{c} &= \vec{a} + \vec{b} \\ &= (3\шляпа\имат + 2\шляпа\jmath) + (3\шляпа\имат — \шляпа\jмат) \\ &= 6\шляпа\имат + \шляпа\jmath \\ \vec{c} &= \vec{a} + \vec{b} \\ &= (3,5\шляпа{u} — 0,7\шляпа{v}) + (1,4\шляпа{u} — 2,8\шляпа{v}) \\ &= 4,9\шляпа{и} — 3.5\шляпа{в} \\ \vec{c} &= \vec{a} + \vec{b} \\ &= (3\шапка\imath + 2\шляпа\jmath) + (1.4\шляпа{u} — 2.8\шляпа{v}) \\ &= 3\шляпа\имат — 2,8\шляпа{v} + 2\шляпа\jmath + 1,4\шляпа{и}. \конец{выровнено}\] Порядок компонентов в смешанном выражении произвольный.
Рассмотрим два вектора, показанные ниже, и их компоненты в двух основаниях вместе с их длинами: 92} = 3,2 \конец{выровнено}\]
Показать компоненты: никто $\шляпа\imath,\шляпа\jmath$ $\шляпа{и},\шляпа{в}$
Вычислите векторное произведение $\vec{a} \times \vec{b}$
используя: (1) формулу угла #rvv-el; (2) формула компонента
#rvv-ex с $\vec{a},\vec{b}$
как в базисе $\hat\imath,\hat\jmath$, так и в
$\hat{u},\hat{v}$, а с $\vec{a}$ в
Базис $\hat\imath,\hat\jmath$ и $\vec{b}$ в
Базис $\hat{u},\hat{v}$. 9\circ$. Теперь используем #rvv-el
дает:
\[\ начало {выровнено}
\vec{a} \times \vec{b} &= a b \sin\theta ( -\hat{k}) \\
&= -9 \шляпа{к}.
\конец{выровнено}\]
(2) Использование формулы компонента #rvv-ex дает:
\[\ начало {выровнено}
(3\шляпа\имат + 2\шляпа\jmath) \times (3\шляпа\имат — \шляпа\jmath)
&= -3 \hat\imath \times \hat\jmath + 6 \hat\jmath \times \hat\imath \\
&= -3 \шляпа{к} — 6 \шляпа{к} \\
&= -9\ шляпа {к} \\
(3,5 \ шляпа {u} — 0,7 \ шляпа {v}) \ раз (1,4 \ шляпа {u} — 2,8 \ шляпа {v})
&= — (3,5 \times 2,8) \hat{u} \times \hat{v}
— (0,7 х 1,4) \шляп{в} \раз \шляп{у} \\
&= -10 \шляпа{к} + \шляпа{к} \\
&= -9 \шляпа{к} \\
(3\шапка\imath + 2\шляпа\jmath) \times (1.
9\circ$. Теперь используем #rvv-el
дает:
\[\ начало {выровнено}
\vec{a} \times \vec{b} &= a b \sin\theta ( -\hat{k}) \\
&= -9 \шляпа{к}.
\конец{выровнено}\]
(2) Использование формулы компонента #rvv-ex дает:
\[\ начало {выровнено}
(3\шляпа\имат + 2\шляпа\jmath) \times (3\шляпа\имат — \шляпа\jmath)
&= -3 \hat\imath \times \hat\jmath + 6 \hat\jmath \times \hat\imath \\
&= -3 \шляпа{к} — 6 \шляпа{к} \\
&= -9\ шляпа {к} \\
(3,5 \ шляпа {u} — 0,7 \ шляпа {v}) \ раз (1,4 \ шляпа {u} — 2,8 \ шляпа {v})
&= — (3,5 \times 2,8) \hat{u} \times \hat{v}
— (0,7 х 1,4) \шляп{в} \раз \шляп{у} \\
&= -10 \шляпа{к} + \шляпа{к} \\
&= -9 \шляпа{к} \\
(3\шапка\imath + 2\шляпа\jmath) \times (1. \circ \, \шляпа{k} \\
&= — 9\шляпа{к}.
\конец{выровнено}\]
\circ \, \шляпа{k} \\
&= — 9\шляпа{к}.
\конец{выровнено}\]
Уравнение #rvv-ed делает ясно, что скалярное произведение не зависит от какой базис мы используем для записи $\vec{a}$ и $\vec{b}$, если мы используем один и тот же ортонормированный базис для них обоих. Это потому что скалярное произведение зависит только от длины и угла между векторами, которые являются реальными физическими величины, которые не меняются только потому, что мы используем разная основа.
Однако мы также можем проверить непосредственно, что компонента уравнение #rvv-es для точки продукт не зависит от того, какую основу мы используем. Хранить короткая алгебра, мы будем делать это только в 2D.
Мы вычисляем скалярное произведение, используя #rvv-es в $\hat\imath,\hat\jmath$ и заменить в выражения изменения основы #rvv-eg, дающие:
\[\begin{выровнено} \vec{a} \cdot \vec{b}
&= a_i b_i + a_j b_j \\
&= (u_i a_u + v_i a_v ) (u_i b_u + v_i b_v) + (u_j a_u + v_j a_v) (u_j b_u + v_j b_v) \\
&= (u_i^2 + u_j^2) a_u b_u + (v_i^2 + v_j^2) a_v b_v + (u_i v_i + u_j b_j) (a_u b_v + a_v b_u) \\
&= \| \шляпа{и} \|^2 a_u b_u + \| \шляпа{v} \|^2 a_v b_v + (\шляпа{u} \cdot \шляпа{v}) (a_u b_v + a_v b_u) \\
&= a_u b_u + a_v b_v. \конец{выровнено}\]
\конец{выровнено}\]
Чтобы получить последнюю строку, мы использовали тот факт, что $\hat{u}$ и $\hat{v}$ образуют орторнормальный базис, так что каждая из них имеет длину 1 (т.е. $\|\шляпа{и}\| = \|\шляпа{v}\| = 1$) и они ортогональные (то есть $\hat{u} \cdot \hat{v} = 0$).
Затем это показывает, что
\[\ начало {выровнено} a_i b_i + a_j b_j &= a_u b_u + a_v b_v \конец{выровнено}\]
и поэтому не имеет значения, какую основу мы используем для вычислить $\vec{a} \cdot \vec{b}$, поэтому пока мы используем ортонормированный базис.
Векторы и базисы, зависящие от времени
У нас могут быть динамические векторы, которые меняются со временем, поэтому их
компоненты тоже меняются. В качестве альтернативы, мы можем иметь фиксированный
вектор, но динамическая основа. Поскольку мы используем ортонормированный
базиса, единственный тип изменения базиса, который может произойти, это
жесткое вращательное движение основания.
В качестве альтернативы, мы можем иметь фиксированный
вектор, но динамическая основа. Поскольку мы используем ортонормированный
базиса, единственный тип изменения базиса, который может произойти, это
жесткое вращательное движение основания.
Движение: вектор основа
Изменяющийся во времени вектор или базис. Будь то вектор или базис меняется со временем, в любом случае компоненты также меняется со временем.
Векторы 101 | ASGCT — Американское общество генной и клеточной терапии |
Генная терапия — это способ лечения или предотвращения определенного заболевания с использованием генетического материала. Один из распространенных способов, который исследователи нашли для достижения этой цели, — использование вектора. Векторы — это, по сути, носители, предназначенные для доставки терапевтического генетического материала, такого как рабочий ген, непосредственно в клетку. Существует четыре основных типа вирусных векторов (аденоассоциированные вирусы, аденовирусы, лентивирусы и ретровирусы), каждый из которых имеет свои уникальные характеристики, области применения и ограничения.
Один из распространенных способов, который исследователи нашли для достижения этой цели, — использование вектора. Векторы — это, по сути, носители, предназначенные для доставки терапевтического генетического материала, такого как рабочий ген, непосредственно в клетку. Существует четыре основных типа вирусных векторов (аденоассоциированные вирусы, аденовирусы, лентивирусы и ретровирусы), каждый из которых имеет свои уникальные характеристики, области применения и ограничения.
Использование вирусов
Векторы обычно получают из вирусов, поскольку вирусы доказали свою эффективность при попадании в клетки. Чтобы сделать векторы безопасными для использования, все вирусные гены удаляются, а вектор модифицируется для доставки только терапевтических генов. Выбор вирусов для использования в качестве векторов основывается на трех критериях:
- Насколько хорошо исследователи понимают вирус
- Насколько хорошо вирус может воздействовать на определенные типы клеток
- Как безопасно использовать вирус
Векторы используют оболочку вируса, также известную как капсид, чтобы помочь транспортировать рабочие гены в клетку-мишень.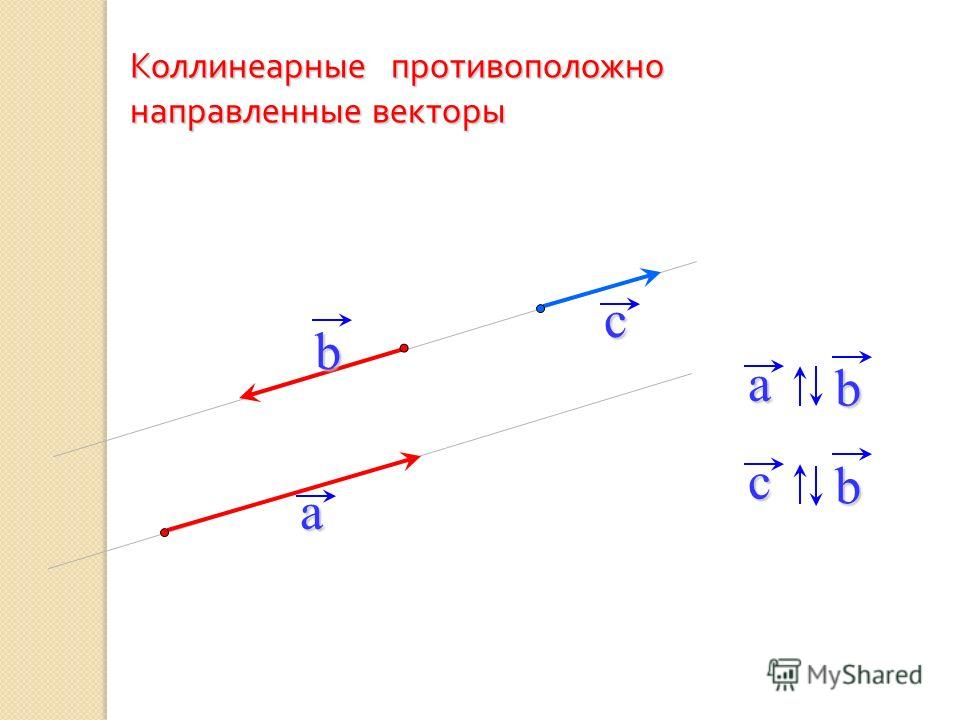 Думайте о векторах как о конвертах, используемых для доставки определенного сообщения. Конверт позволяет доставить сообщение, а сообщение внутри предоставляет клетке новые инструкции о том, как правильно функционировать. Использование вируса для лечения болезни может показаться устаревшим, но использование векторов подтверждено многолетними исследованиями и доказало свою безопасность, что всегда является главным приоритетом.
Думайте о векторах как о конвертах, используемых для доставки определенного сообщения. Конверт позволяет доставить сообщение, а сообщение внутри предоставляет клетке новые инструкции о том, как правильно функционировать. Использование вируса для лечения болезни может показаться устаревшим, но использование векторов подтверждено многолетними исследованиями и доказало свою безопасность, что всегда является главным приоритетом.
Генная терапия с использованием вирусных векторов дает больше, чем просто лечение симптомов. Векторы с генетической информацией, которую они несут, могут напрямую воздействовать на причину болезни и изменять способ функционирования клетки. Кроме того, их обычно нужно вводить только один раз, и они обычно используются для лечения редких наследственных заболеваний, для которых практически нет других вариантов лечения.
Аденоассоциированные вирусные (AAV) векторы Аденоассоциированные вирусные векторы, также известные как AAV, обычно используются для доставки небольших пакетов ДНК или генов. Размер этого вектора может быть фактором, определяющим, на какие редкие заболевания он может воздействовать. Известно, что они безопасны и эффективны при использовании в течение подходов генной терапии in vivo . Терапия In vivo включает введение генной терапии в определенные части тела, чтобы новые генетические инструкции могли быть доставлены непосредственно в клетки тела.
Размер этого вектора может быть фактором, определяющим, на какие редкие заболевания он может воздействовать. Известно, что они безопасны и эффективны при использовании в течение подходов генной терапии in vivo . Терапия In vivo включает введение генной терапии в определенные части тела, чтобы новые генетические инструкции могли быть доставлены непосредственно в клетки тела.
AAV обычно не интегрируются . Это означает, что ДНК, которую они несут, обычно не встраивается в геном клетки. Таким образом, если вектор поглощается делящейся клеткой, терапевтический ген не будет копироваться при каждом клеточном делении и со временем может быть потерян, что ослабит лечебный эффект. Из-за этого AAV обычно используются для нацеливания на неделящиеся клетки, такие как клетки печени, нервной системы, глаз и скелетных мышц. ААВ могут сохраняться у пациентов в течение длительного периода времени, возможно, даже всю жизнь.
Врожденный иммунитет является одним из ограничений AAV, поскольку многие люди могли ранее подвергаться воздействию AAV через естественные инфекции. Это означает, что ранее существовавшие антитела могут отстранить от 30 до 70 процентов пациентов от участия в клинических испытаниях в зависимости от типа используемого AAV. Для этих пациентов их иммунная система может атаковать или уничтожить вектор до того, как он сможет доставить свой терапевтический пакет, что сделает его бесполезным. Кроме того, пациенты часто ограничиваются однократным введением терапии, поскольку у них могут вырабатываться антитела после первого введения. Тестирование на врожденный иммунитет становится все более распространенным и используется в качестве критерия исключения для участия в клинических испытаниях. На данный момент ученые работают над различными стратегиями, помогающими справиться с этой проблемой, такими как создание синтетических капсидов, которые не будут атакованы иммунной системой, или использование фермента, который может расщеплять антитела в краткосрочной перспективе. Эти решения основаны на знании того, что существует короткий промежуток времени (часы), в течение которого вектор вводится, а затем перемещается в клетку-мишень, и как только вектор попадает внутрь клетки, он защищен от антител.
Это означает, что ранее существовавшие антитела могут отстранить от 30 до 70 процентов пациентов от участия в клинических испытаниях в зависимости от типа используемого AAV. Для этих пациентов их иммунная система может атаковать или уничтожить вектор до того, как он сможет доставить свой терапевтический пакет, что сделает его бесполезным. Кроме того, пациенты часто ограничиваются однократным введением терапии, поскольку у них могут вырабатываться антитела после первого введения. Тестирование на врожденный иммунитет становится все более распространенным и используется в качестве критерия исключения для участия в клинических испытаниях. На данный момент ученые работают над различными стратегиями, помогающими справиться с этой проблемой, такими как создание синтетических капсидов, которые не будут атакованы иммунной системой, или использование фермента, который может расщеплять антитела в краткосрочной перспективе. Эти решения основаны на знании того, что существует короткий промежуток времени (часы), в течение которого вектор вводится, а затем перемещается в клетку-мишень, и как только вектор попадает внутрь клетки, он защищен от антител.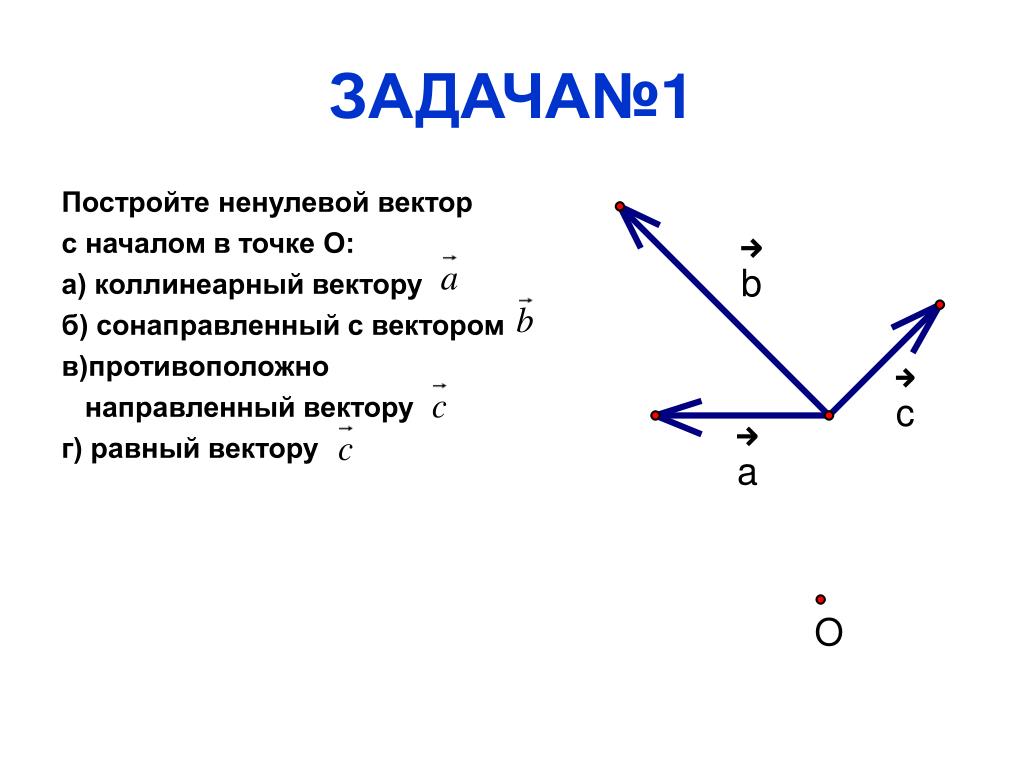
В некотором смысле аденовирусные векторы сходны с векторами AAV. Например, они чаще всего используются для доставки пакетов ДНК в неделящиеся клетки. Однако аденовирусные векторы крупнее и способны доставлять генетические пакеты почти в восемь раз больше, чем AAV. Аденовирусные векторы могут вызывать сильных иммунных ответа , что приводит к потенциально опасному воспалению во всем организме и снижению эффективности терапии. В последние годы ученые работали над созданием аденовирусных векторов, вызывающих более мягкий иммунный ответ, чтобы доставлять более крупные пакеты с меньшим риском.
Лентивирусные и ретровирусные векторыЛентивирусные и ретровирусные векторы могут нести более крупные генетические пакеты РНК, которые преобразуются в ДНК. Во время этого процесса векторы интегрируют в геном клетки-мишени, в отличие от AAV и аденовирусных векторов.
Способность интегрироваться в геном клетки делает лентивирусные и ретровирусные векторы наиболее подходящими для деления клеток, которые являются мишенями ex vivo лечения .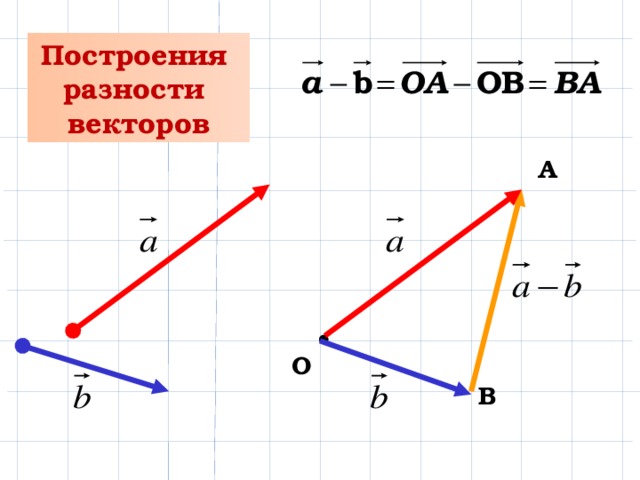 Например, эти векторы используются для нацеливания на Т-клетки, которые являются типом иммунных клеток, и стволовые клетки, которые являются особыми клетками, которые могут развиваться во многие типы клеток. В отличие от in vivo обработок, ex vivo обработка клеток происходит вне организма. Клетки удаляются из организма и культивируются на чашках, что позволяет им реплицироваться и расширяться. Затем эти клетки обрабатывают векторами и модифицируют новыми генетическими инструкциями, такими как рабочий ген. Затем модифицированные клетки возвращаются в организм. После этого обработанные клетки начинают делиться и генерировать новые клетки. Благодаря интеграции новый генетический материал копируется во все новые клетки и продолжает функционировать за пределами исходной клетки.
Например, эти векторы используются для нацеливания на Т-клетки, которые являются типом иммунных клеток, и стволовые клетки, которые являются особыми клетками, которые могут развиваться во многие типы клеток. В отличие от in vivo обработок, ex vivo обработка клеток происходит вне организма. Клетки удаляются из организма и культивируются на чашках, что позволяет им реплицироваться и расширяться. Затем эти клетки обрабатывают векторами и модифицируют новыми генетическими инструкциями, такими как рабочий ген. Затем модифицированные клетки возвращаются в организм. После этого обработанные клетки начинают делиться и генерировать новые клетки. Благодаря интеграции новый генетический материал копируется во все новые клетки и продолжает функционировать за пределами исходной клетки.
Генная терапия с использованием вирусных векторов обладает большим потенциалом, но не лишена определенного риска. Эти примеры являются дополнением к ограничениям, которые обсуждались выше, включая врожденный иммунитет и сильный иммунный ответ.
Нецелевые эффекты — когда после введения могут быть затронуты ткани, отличные от основной ткани-мишени. Векторы, которые вставляют свой генетический пакет в геном хозяина, потенциально могут интегрироваться в неправильном месте генома и вызывать непредвиденные последствия. Чтобы сохранить как можно больший контроль над процессом, исследователи разработали методы таргетинга. Кроме того, у них есть возможность отслеживать долгосрочные эффекты вектора у пациентов в месте введения.
Производство — еще одна задача, которую решают профессионалы в этой области. Создание очень большого количества безопасных вирусных векторов требует времени, усилий и ресурсов. Сложность процесса увеличивает производственные затраты и затрудняет эффективную оптимизацию производства. Исследователи будут продолжать работать над более эффективными методами производства по мере того, как будут исследованы и одобрены для использования все больше генных терапий.
Невирусные векторы Исследователи также разрабатывают больше невирусных векторов для устранения (или устранения) этих ограничений. Невирусные векторы дешевле в производстве, чем их вирусные аналоги. Они потенциально могут доставлять более крупные генетические пакеты, позволяют многократно дозировать и упрощают контроль качества. Преимуществом невирусных векторов также является пониженная вероятность запуска неблагоприятных иммунных реакций.
Невирусные векторы дешевле в производстве, чем их вирусные аналоги. Они потенциально могут доставлять более крупные генетические пакеты, позволяют многократно дозировать и упрощают контроль качества. Преимуществом невирусных векторов также является пониженная вероятность запуска неблагоприятных иммунных реакций.
Несмотря на то, что невирусные переносчики имеют большие перспективы, у ученых просто меньше опыта работы с ними. Многие из невирусных механизмов быстро развиваются, но все еще остаются проблемы, такие как пропускная способность и способность воздействовать на определенные органы или ткани. На данный момент их нельзя использовать для in vivo подходы, общие для AAV и аденовирусных векторов.
Генная терапия и онкология Подход к генной терапии очень отличается, когда речь идет об онкологии и лечении рака. Существующие векторы не могут воздействовать на 100 % клеток, поэтому стратегии добавления генов или специфического нацеливания на гены, которые используются для лечения редких заболеваний, таких как добавление рабочего гена, просто не так эффективны для лечения рака.

 Равные векторы»
Равные векторы»
 Постройте векторы , , , .
Постройте векторы , , , . Постройте векторы , , , .
Постройте векторы , , , . ..
..

 Направляющие косинусы. Длины векторов. Примеры.
Направляющие косинусы. Длины векторов. Примеры. Ортогональные, коллинеарные и компланарные векторы: определения и примеры. Условия ортогональности, коллинеарности и компланарности.
Ортогональные, коллинеарные и компланарные векторы: определения и примеры. Условия ортогональности, коллинеарности и компланарности.