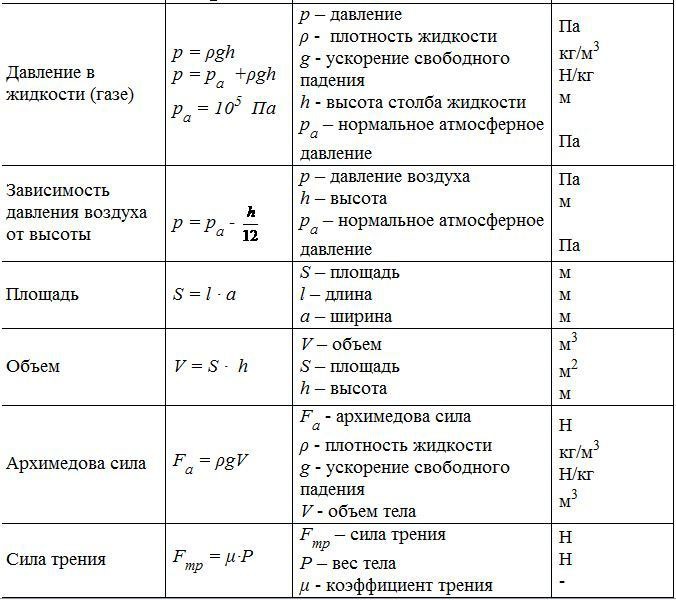
Как найти работу в физике все формулы. Механическая работа
Прежде чем раскрывать тему «В чём измеряется работа», необходимо сделать небольшое отступление. Всё в этом мире подчиняется законам физики. Каждый процесс или явление можно объяснить на основе тех или иных законов физики. Для каждой измеряемой величины существует единица, в которой её принято измерять. Единицы измерения являются неизменными и имеют единое значение во всём мире.
Причиной этого является следующее. В тысяча девятьсот шестидесятом году на одиннадцатой генеральной конференции по мерам и весам была принята система измерений, которая признана во всём мире. Эта система получила наименование Le Système International d’Unités, SI (СИ система интернационал). Эта система стала базовой для определений принятых во всём мире единиц измерения и их соотношения.
Физические термины и терминология
В физике единица измерения работы силы называется Дж (Джоуль), в честь английского учёного физика Джеймса Джоуля, сделавшего большой вклад в развитие раздела термодинамики в физике. Один Джоуль равен работе, совершаемой силой в один Н (Ньютон), при перемещении её приложения на один М (метр) в направлении действия силы. Один Н (Ньютон) равен силе, массой в один кг (килограмм), при ускорении в один м/с2 (метр в секунду) в направлении силы.
Один Джоуль равен работе, совершаемой силой в один Н (Ньютон), при перемещении её приложения на один М (метр) в направлении действия силы. Один Н (Ньютон) равен силе, массой в один кг (килограмм), при ускорении в один м/с2 (метр в секунду) в направлении силы.
К сведению. В физике всё взаимосвязано, выполнение любой работы связано с выполнением дополнительных действий. В качестве примера можно взять бытовой вентилятор. При включении вентилятора в сеть лопасти вентилятора начинают вращаться. Вращающиеся лопасти воздействуют на поток воздуха, придавая ему направленное движение. Это является результатом работы. Но для выполнения работы необходимо воздействие других сторонних сил, без которых выполнение действия невозможно. К ним относятся сила электрического тока, мощность, напряжение и многие другие взаимосвязанные значения.
Электрический ток, по своей сути, – это упорядоченное движение электронов в проводнике в единицу времени. В основе электрического тока лежит положительно или отрицательно заряжённые частицы. Они носят название электрических зарядов. Обозначается буквами C, q, Кл (Кулон), названо в честь французского учёного и изобретателя Шарля Кулона. В системе СИ является единицей измерения количества заряженных электронов. 1 Кл равен объёму заряженных частиц, протекающих через поперечное сечение проводника в единицу времени. Под единицей времени подразумевается одна секунда. Формула электрического заряда представлена ниже на рисунке.
Они носят название электрических зарядов. Обозначается буквами C, q, Кл (Кулон), названо в честь французского учёного и изобретателя Шарля Кулона. В системе СИ является единицей измерения количества заряженных электронов. 1 Кл равен объёму заряженных частиц, протекающих через поперечное сечение проводника в единицу времени. Под единицей времени подразумевается одна секунда. Формула электрического заряда представлена ниже на рисунке.
Сила электрического тока обозначается буквой А (ампер). Ампер – это единица в физике, характеризующая измерение работы силы, которая затрачивается для перемещения зарядов по проводнику. По своей сути, электрический ток – это упорядоченное движение электронов в проводнике под воздействием электромагнитного поля. Под проводником подразумевается материал или расплав солей (электролит), имеющий небольшую сопротивляемость прохождению электронов. На силу электрического тока влияют две физические величины: напряжение и сопротивление. Они будут рассмотрены ниже.
Как было сказано выше, электрический ток – это упорядоченное движение электронов в проводнике. Но есть один нюанс: для их движения нужно определённое воздействие. Это воздействие создаётся путём создания разности потенциалов. Электрический заряд может быть положительным или отрицательным. Положительные заряды всегда стремятся к отрицательным зарядам. Это необходимо для равновесия системы. Разница между количеством положительно и отрицательно заряжённых частиц называется электрическим напряжением.
Мощность – это количество энергии, затрачиваемое на выполнение работы в один Дж (Джоуль) за промежуток времени в одну секунду. Единицей измерения в физике обозначается как Вт (Ватт), в системе СИ W (Watt). Так как рассматривается мощность электрическая, то здесь она является значением затраченной электрической энергии на выполнение определённого действия в промежуток времени.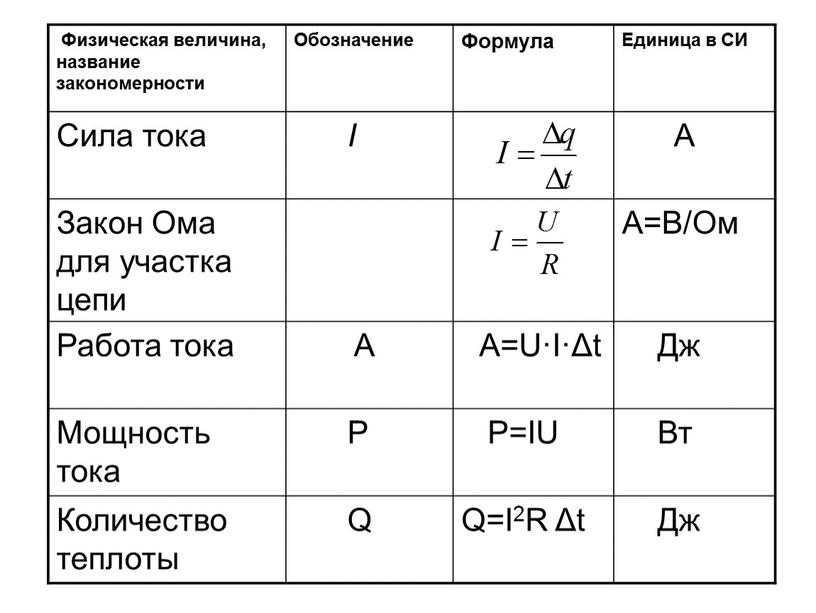
Лошадь тянет телегу с некоторой силой, обозначим её F тяги. Дедушка, сидящий на телеге, давит на неё с некоторой силой. Обозначим её F давл. Телега движется вдоль направления силы тяги лошади (вправо), а в направлении силы давления дедушки (вниз) телега не перемещается. Поэтому в физике говорят, что F тяги совершает работу над телегой, а F давл не совершает работу над телегой.
Итак, работа силы над телом или механическая работа – физическая величина, модуль которой равен произведению силы на путь, пройденный телом вдоль направления действия этой сил ы:
В честь английского учёного Д.Джоуля единица механической работы получила название 1 джоуль (согласно формуле, 1 Дж = 1 Н·м).
Если на рассматриваемое тело действует некоторая сила, значит, на него действует некоторое тело. Поэтому работа силы над телом и работа тела над телом – полные синонимы. Однако, работа первого тела над вторым и работа второго тела над первым – частичные синонимы, поскольку модули этих работ всегда равны, а их знаки всегда противоположны. Именно поэтому в формуле присутствует знак «±». Обсудим знаки работы более подробно.
Именно поэтому в формуле присутствует знак «±». Обсудим знаки работы более подробно.
Числовые значения силы и пути – всегда неотрицательные величины. В отличие от них механическая работа может иметь как положительный, так и отрицательный знаки. Если направление силы совпадает с направлением движения тела, то
Рассмотрите три иллюстрации по трём аспектам механической работы.
Совершение силой работы может выглядеть по-разному с точек зрения различных наблюдателей. Рассмотрим пример: девочка едет в лифте вверх. Совершает ли она механическую работу? Девочка может совершать работу только над теми телами, на которые действует силой. Такое тело лишь одно – кабина лифта, так как девочка давит на её пол своим весом.
Пусть сначала мальчик-наблюдатель сидит на земле. По отношению к нему кабина лифта движется вверх и проходит некоторый путь. Вес девочки направлен в противоположную сторону – вниз, следовательно, девочка совершает над кабиной отрицательную механическую работу: A дев A дев = 0.
Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.
Формула механической работы
Определяется механическая работа формулой:
где A – работа, F – сила, s – пройденный путь.
ПОТЕНЦИА́Л (потенциальная функция), понятие, характеризующее широкий класс физических силовыхполей (электрических, гравитационных и т.
35.
Проводники в электрическом поле.
Электроемкость. Проводники
в электрическом поле. Проводники
— это вещества, характеризующиеся
наличием в них большого количества
свободных носителей зарядов, способных
перемещаться под действием электрического
поля. К проводникам относятся металлы,
электролиты, уголь. В металлах носителями
свободных зарядов являются электроны
внешних оболочек атомов, которые при
взаимодействии атомов полностью
утрачивают связи со «своими» атомами
и становятся собственностью всего
проводника в целом. Свободные электроны
участвуют в тепловом движении подобно
молекулам газа и могут перемещаться по
металлу в любом направлении. Электри́ческая
ёмкость —
характеристика проводника,
мера его способности накапливать электрический
заряд. В теории электрических цепей ёмкостью
называют взаимную ёмкость между двумя
проводниками; параметр ёмкостного
элемента электрической схемы,
представленного в виде двухполюсника.
Такая ёмкость определяется как отношение
величины электрического заряда к разности
потенциалов между
этими проводниками
В теории электрических цепей ёмкостью
называют взаимную ёмкость между двумя
проводниками; параметр ёмкостного
элемента электрической схемы,
представленного в виде двухполюсника.
Такая ёмкость определяется как отношение
величины электрического заряда к разности
потенциалов между
этими проводниками
36. Емкость плоского конденсатора.
Емкость плоского конденсатора.
Т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.
37. Магнитное
взаимодействие токов в вакууме. Закон
Ампера. Закон
Ампера. В 1820 году Ампер (французский ученый
(1775-1836)) установил экспериментально
закон, по которому можно рассчитать
где
–
вектор магнитной индукции,– вектор элемента длины проводника,
проведенного в направлении тока.
Модуль силы , где– угол между направлением тока в проводнике и направлением индукции магнитного поля.Для прямолинейного проводника длиной с токомв однородном поле
Направление действующей силы может быть определено с помощью правила левой руки :
Если ладонь левой руки расположить так, чтобы нормальная (к току) составляющая магнитного поля входила в ладонь, а четыре вытянутых пальца направлены вдоль тока, то большой палец укажет направление, в котором действует сила Ампера.
38.Напряженность магнитного поля. Закон Био-Савара-Лапласа Напряжённость магни́тного по́ля (стандартное обозначение Н ) — векторная физическая величина , равная разности вектора магнитной индукции B и вектора намагниченности J .
В Международной системе единиц (СИ) : где-магнитная постоянная .
Закон
БСЛ. Закон,
определяющий магнитное поле отдельного
элемента тока
39. Приложения
закона Био-Савара-Лапласа. Для
поля прямого тока
Приложения
закона Био-Савара-Лапласа. Для
поля прямого тока
Для кругового витка.
И для соленоида
40. Индукция магнитного поля Магнитное поле характеризуется векторной величиной, которая носит название индукции магнитного поля (векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства). МИ. (В) это не сила, действующая на проводники, это величина, которая находится через данную силу по следующей формуле: B=F / (I*l) (Словестно:
 2/R
играет роль центростремительной силы.
Период обращения равен T=2пиR/V=2пиm/qB
и он не зависит от скорости частицы (Это
справедливо только при V
2/R
играет роль центростремительной силы.
Период обращения равен T=2пиR/V=2пиm/qB
и он не зависит от скорости частицы (Это
справедливо только при VСила
Л. определяется соотношением:
Fл = q·V·B·sina (q — величина движущегося
заряда; V — модуль его скорости; B —
модуль вектора индукции магнитного
поля; aльфа — угол между вектором V
и вектором В)
Сила
Лоренца перпендикулярна скорости и
поэтому она не совершает работы, не
изменяет модуль скорости заряда и его
кинетической энергии. Но направление
скорости изменяется непрерывно.
Сила
Лоренца перпендикулярна векторам В и v ,
и её направление определяется с помощью
того же правила левой руки, что и
направление силы Ампера: если левую
руку расположить так, чтобы составляющая
магнитной индукции В, перпендикулярная
скорости заряда, входила в ладонь, а
четыре пальца были направлены по движению
положительного заряда (против движения
отрицательного), то отогнутый на 90
градусов большой палец покажет направление
действующей на заряд силы Лоренца F л.
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Определение 1
Работа А, совершаемая постоянной силой F → , — это физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α , располагаемого между векторами силы F → и перемещением s → .
Данное определение рассматривается на рисунке 1 . 18 . 1 .
Формула работы записывается как,
A = F s cos α .
Работа – это скалярная величина. Это дает возможность быть положительной при (0 ° ≤ α
Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.
Рисунок 1 . 18 . 1 . Работа силы F → : A = F s cos α = F s s
При проекции F s → силы F → на направление перемещения s → сила не остается постоянной, а вычисление работы для малых перемещений Δ s i суммируется и производится по формуле:
A = ∑ ∆ A i = ∑ F s i ∆ s i .
Данная сумма работы вычисляется из предела (Δ s i → 0) , после чего переходит в интеграл.
Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком F s (x) рисунка 1 . 18 . 2 .
Рисунок 1 . 18 . 2 . Графическое определение работы Δ A i = F s i Δ s i .
Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F → , модуль которой пропорционален удлинению пружины. Это видно на рисунке 1 . 18 . 3 .
Рисунок 1 . 18 . 3 . Растянутая пружина. Направление внешней силы F → совпадает с направлением перемещения s → . F s = k x , где k обозначает жесткость пружины.
F → у п р = — F →
Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.
Рисунок 1 . 18 . 4 . Зависимость модуля внешней силы от координаты при растяжении пружины.
Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид
Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F → у п р равняется работе внешней силы F → , но с противоположным знаком.
Определение 2
Если на тело действует несколько сил, то формула общей работы будет выглядеть, как сумма всех работ, совершаемых над ним. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.
Рисунок 1 . 18 . 5 . Модель механической работы.
Определение мощности
Определение 3
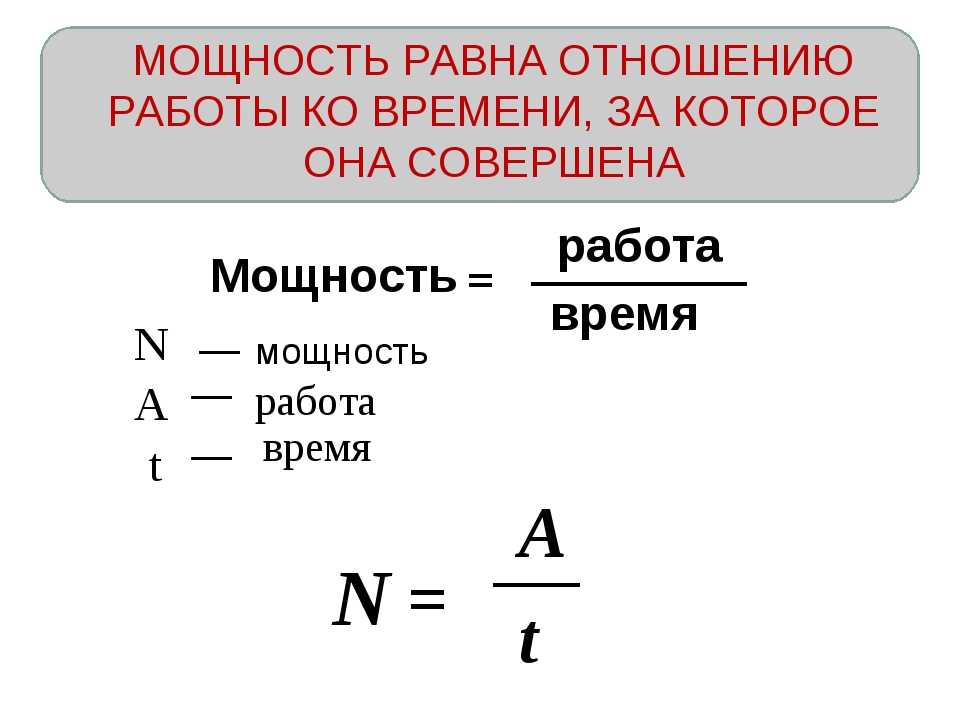
Мощностью называют работу силы, совершаемую в единицу времени.
Запись физической величины мощности, обозначаемой N , принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:
Определение 4
Система С И использует в качестве единицы мощности ватт (В т) , равняющийся мощности силы, которая совершает работу в 1 Д ж за время 1 с.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Основные формулы по физике — МЕХАНИКА
Формулы механики. Механика делится на три раздела: кинематику, динамику и статику. В разделе кинематика рассматриваются такие кинематические характеристики движения, как перемещение, скорость, ускорение. Здесь необходимо использовать аппарат дифференциального и интегрального исчисления.
В основе классической динамики лежат три закона Ньютона. Здесь необходимо обратить внимание на векторный характер действующих на тела сил, входящих в эти законы.
Динамика охватывает такие вопросы, как закон сохранения импульса, закон сохранения полной механической энергии, работа силы.
При изучении кинематики и динамики вращательного движения следует обратить внимание на связь между угловыми и линейными характеристиками. Здесь вводятся понятия момента силы, момента инерции, момента импульса и рассматривается закон сохранения момента импульса.
Смотрите также основные формулы по термодинамике
Таблица основных формул по механике
|
Физические законы, формулы, переменные |
Формулы механики |
||||||||
|
Скорость мгновенная: где r — радиус-вектор материальной точки, t — время;
|
|||||||||
|
Модуль вектора скорости: где s — расстояние вдоль траектории движения (путь) |
|||||||||
|
Скорость средняя (модуль): |
|||||||||
|
Ускорение мгновенное: |
|||||||||
|
Модуль вектора ускорения при прямолинейном движении: |
|||||||||
|
Ускорение при криволинейном движении: 1) нормальное где R — радиус кривизны траектории, 2) тангенциальное 3) полное (вектор) 4) (модуль) |
|
||||||||
|
Скорость и путь при движении: 1) равномерном 2) равнопеременном V0— начальная скорость; а > 0 при равноускоренном движении; а < 0 при равнозамедленном движении. |
|
||||||||
|
Угловая скорость: где φ — угловое перемещение. |
|||||||||
|
Угловое ускорение: |
|||||||||
|
Связь между линейными и угловыми величинами: |
|||||||||
|
Импульс материальной точки: где m — масса материальной точки. |
|||||||||
|
Основное уравнение динамики поступательного движения (II закон Ньютона): где F — результирующая сила, <> |
|||||||||
|
Формулы сил: тяжестиP где g — ускорение свободного падения трения Fтр где μ — коэффициент трения, N — сила нормального давления, упругости Fупр где k — коэффициент упругости (жесткости), Δх — деформация (изменение длины тела). |
|
||||||||
|
Закон сохранения импульса для замкнутой системы, состоящей из двух тел: где — скорости тел до взаимодействия; — скорости тел после взаимодействия. |
|||||||||
|
Потенциальная энергия тела: 1) поднятого над Землей на высоту h 2) упругодеформированного |
|
||||||||
|
Кинетическая энергия поступательного движения: |
|||||||||
|
Работа постоянной силы: где α — угол между направлением силы и направлением перемещения. |
|||||||||
|
Полная механическая энергия: |
|||||||||
|
Закон сохранения энергии: силы консервативны силы неконсервативны где W1 — энергия системы тел в начальном состоянии; W2 — энергия системы тел в конечном состоянии. |
|
||||||||
|
Момент инерции тел массой m относительно оси, проходящей через центр инерции (центр масс): 1) тонкостенного цилиндра (обруча) где R — радиус, 2) сплошного цилиндра (диска) 3) шара 4) стержня длиной l, если ось вращения перпендикулярна стержню и проходит через его середину |
|
||||||||
|
Момент инерции тела относительно произвольной оси (теорема Штейнера): где — момент инерции тела относительно оси, проходящей через центр масс, d — расстояние между осями. |
|||||||||
|
Момент силы(модуль): где l — плечо силы. |
|||||||||
|
Основное уравнение динамики вращательного движения: где — угловое ускорение, — результирующий момент сил. |
|||||||||
|
Момент импульса: 1) материальной точки относительно неподвижной точки где r — плечо импульса, 2) твердого тела относительно неподвижной оси вращения |
|
||||||||
|
Закон сохранения момента импульса: где L1 — момент импульса системы в начальном состоянии, L2 — момент импульса системы в конечном состоянии. |
|||||||||
|
Кинетическая энергия вращательного движения: |
|||||||||
|
Работа при вращательном движении где Δφ — изменение угла поворота. |
Все Основные Формулы по Физике
Вы можете сразу скачать готовые шпаргалки по физике в разных форматах
- Шпора (все формулы по физике) в формате PDF
- Шпора (все формулы по физике) в формате DOC (Текстовый документ)
- Шпора (все формулы по физике) в формате JPG (картинка)
Или воспользоваться готовой подробной таблицей расположенной внизу
Существует огромное количество формул по физике, которые часто используют для решения различных физических задач.
Что бы было легче ориентироваться в них на этой странице собраны все основные формулы по физике.
Эта шпаргалка с формулами будет полезна учащимся средней школы, студентам, а так же школьникам, которые планируют учиться в вузах или сузах.
Эту информацию можно использовать при подготовке к егэ, экзаменам или олимпиадам по физике.
Все формулы рассортированы по классам и физическим темам.
Для быстрого перехода на эту страницу добавьте сайт в закладки.
Раздел постоянно обновляется!
Формулы физики для 7-8 классов
Основные формулы для 7 классов на новой странице.
Основные формулы для 8 классов.
Электрические и электромагнитные явления
 Постоянный ток
Постоянный токФормулы физики для 8-9 классов
Основные формулы для 9 классов на новой странице.
Формулы физики для 10-11 классов
Основные формулы для 10-11 классов.
Данная шпаргалка по физике включает в себя формулы физики по следующим темам:
Фундаментальные константы.

Название константы. | Обозн. | Значение. | Измерение |
|---|---|---|---|
Гравитационная постоянная. | G | 6,672*10-11 | Н*м2/кг2 |
Ускорение свободного падения | G | 9,8065 | м/с2 |
Атмосферное давление | p0 | 101325 | Па |
Постоянная Авогадро | Na | 6,022045*1023 | Моль-1 |
Объем 1моль идеального газа | V0 | 22,41383 | м3/моль |
Газовая постоянная | R | 8,31441 | |
Постоянная Больцмана | K | 1,380662*10-23 | Дж/К |
Скорость света в вакууме | C | 2,99792458*108 | м/с |
Магнитная постоянная | μ0 | 4π*10-7= 1,25663706*10-6 | Гн/м |
Электрическая постоянная | ε0 | 8,8541878*10-12 | Ф/м |
Масса покоя электрона | me | 9,109534*10-31 | кг |
Масса покоя протона | mp | 1,6726485*10-27 | кг |
Масса покоя нейтрона | mn | 1,6749543*10-27 | кг |
Элементарный заряд | E | 1,6021892*10-19 | Кл |
Отношение заряда к массе | e/me | 1,7588047*1011 | Кл/кг |
Постоянная Фарадея | F | 9,648456*104 | Кл/моль |
Постоянная Планка | H | 6,626176*10-34 1,054887*10-34 | Дж*с Дж*с |
Радиус 1 боровской орбиты | a0 | 0,52917706*10-10 | м |
Энергия покоя электрона | mec2 | 0. | МэВ |
Энергия покоя протона | mpc2 | 938.2796 | МэВ |
.Энергия покоя нейтрона | mnc2 | 939.5731 | МэВ |
Система единиц.
Приставки Си.
пристав. | поряд. | пристав. | поряд. | пристав. | порядок | Пристав. | порядок | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
экса | Э | 18 | мега | М | 6 | деци | д | -1 | Нано | н | -9 |
пета | П | 15 | кило | к | 3 | санти | с | -2 | пико | п | -12 |
тера | Т | 12 | гекто | г | 2 | милли | м | -3 | фемто | ф | -15 |
гига | Г | 9 | дека | да | 1 | микро | мк | -6 | атто | а | -18 |
Вернуться к оглавлению
Механика.
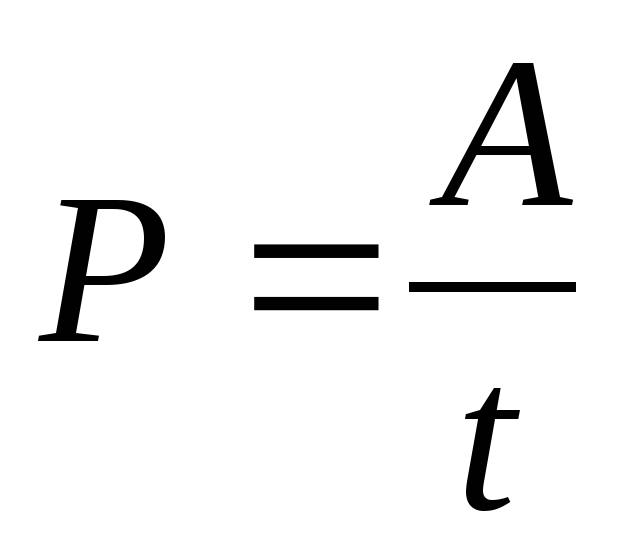
Кинематика.
Обозн. | Изм. | Смысл |
|---|---|---|
S | м | пройденный путь |
v | м/с | скорость |
t | с | время |
x | м | координата |
a | м/с2 | ускорение |
ω | с-1 | угловая скорость |
T | с | период |
Гц | частота | |
ε | с-2 | угловое ускорение |
R | м | радиус |
Скорость и ускорение.
, ,
Равномерное движение:
, ;
Равнопеременное движение:
a=const, , ;
, ; v=v0+at , ;
;
Криволинейное движение.

,
Вращательное движение.
, , ; ;
, ; , ;
, , , ;
Вернуться к оглавлению
Динамика и статика.
Обозн. | Изм. | Смысл |
|---|---|---|
F | Н | сила |
P | кг*м/с | импульс |
a | м/с2 | ускорение |
m | кг | масса |
v | м/с | скорость |
p | Н | вес тела |
g | м/с2 | ускорение свободного падения |
E | Дж | энергия |
A | Дж | работа |
N | Вт | мощность |
t | с | время |
I | кг*м2 | момент инерции |
L | кг*м2/с | момент импульса |
M | Н*м | момент силы |
ω | с-1 | угловая скорость |
Первый закон Ньютона:
Второй закон Ньютона.

, , при m=const ➔
Третий закон Ньютона.
Основной закон динамики для неинерциальных систем отчета.
ma=ma0+Fинерц ,где а- ускорение в неинерциальной а0- в инерциальной системе отчета.
Силы разной природы.
Скорость центра масс ;
Закон всемирного тяготения.
,
— ускорение свободного падения на планете.
— первая космическая скорость.
Вес тела.
p=mg — вес тела в покое.
p=m(g+a) — опора движется с ускорением вверх.
p=m(g-a) — опора движется с ускорением вниз.
p=m(g-v2/r) — движение по выпуклой траектории.
p=m(g+v2/r) — движение по вогнутой траектории.
Сила трения.
,
Закон Гука.
Fупр=–kx, — сила упругости деформированной пружины.
— механическое напряжение
— относительное продольное удлинение (сжатие)
— относительное поперечное удлинение (сжатие)
, где μ- коэффициент Пуассона.
Закон Гука:, где Е- модуль Юнга.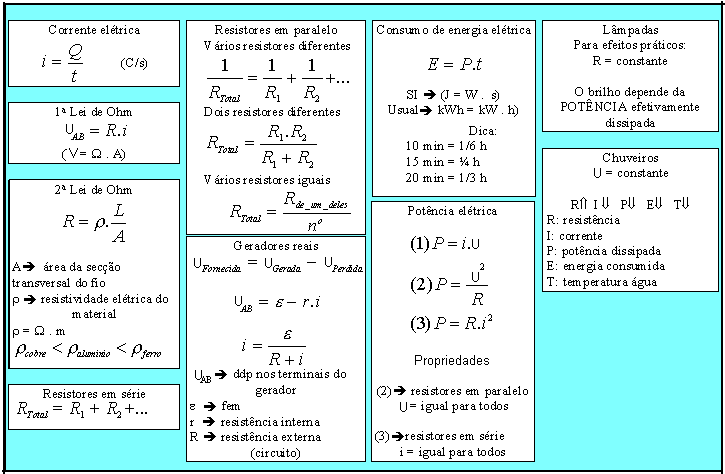
, кинетическая энергия упругорастянутого (сжатого) стержня. (V- объем тела)
Динамика и статика вращательного движения.
— момент импульса
; — момент силы
L=const — закон сохранения момента импульса.
M=Fl, где l- плечо
I=I0+mb2 — теорема Штейнера
система | ось | I |
|---|---|---|
точка по окружности | ось симметрии | mR2 |
стержень | через середину | 1/12 mR2 |
стержень | через конец | 1/3 mR2 |
шар | через центр шара | 2/5 mR2 |
сфера | через центр сферы | 2/3 mR2 |
кольцо или тонкостенный цилиндр | ось симметрии | mR2 |
диск сплошной цилиндр | ось симметрии | 1/2 mR2 |
Условие равновесия тел
Законы сохранения.

Закон сохранения импульса.
P=mv; — импульс тела.
Ft=ΔP
Потенциальная и кинетическая энергия. Мощность.
— работа силы F
A=ΔE
— мощность
— кинетическая энергия
— кинетическая энергия вращательного движения.
Ep=mgh — потенциальная энергия поднятого над землей тела.
— потенциальная энергия пружины
Закон сохранения энергии.
Eк1+Eр1=Eк2+Eр2
Вернуться к оглавлению
Молекулярная физика. Свойства газов и жидкостей.
Обозн. | Изм. | Смысл |
|---|---|---|
p | Па | давление |
V | м3 | объем |
T | К | температура |
N | – | число молекул |
m | кг | масса |
кг/Моль | молярная масса | |
Моль | кол-во вещества | |
U | Дж | вн. |
Q | Дж | кол-во теплоты |
η | – | КПД |
Вернуться к оглавлению
Уравнение состояния.
pV=NkT — уравнение состояния (уравнение Менделеева- Клайперона)
, , ;
, — полная внутренняя энергия системы.
Число атомов | i | |
|---|---|---|
1 | 3 | 5/3 |
2 | 7 | 9/7 |
3 | 13 (12) | 15/13 (7/6) |
— основное уравнение молекулярно- кинетической теории.
— закон Дальтона для давления смеси газов.
, p=nkT ;
при N=const ➔
T=const | изотерма | PV=const | закон Бойля-Мариотта |
p=const | изобара | V/T=const | закон Гей-Люсака |
V=const | изохора | p/T=const | закон Шарля |
Броуновское движение.

среднеквадратичная скорость молекул.
— наиболее вероятная скорость молекул.
— средняя арифметическая скорость молекул.
— Закон Максвелла для распределения молекул идеального газа по скоростям.
Среднее число соударений молекулы за 1с:
Средняя длинна свободного пробега молекул
— средний путь молекулы за время t.
Вернуться к оглавлению
Распределение в потенциальном поле.
— барометрическая формула.
— распределение Больцмана.
Термодинамика.
— первое начало термодинамики.
— работа газа.
— уравнение адиабаты.
Теплоемкость , удельная теплоемкость с=С/m.
Название | Опред. | Уравнение | A | Q | C |
|---|---|---|---|---|---|
Изохора | V=const | Q=ΔU | 0 | NkΔT/(γ-1) | Nk/(γ-1) |
Изобара | p=const | ΔU=Q+pΔV | pΔV | γpΔV/(γ-1) | γNk/(γ-1) |
Изотерма | T=const | Q=A | A | ∞ | |
Адиабата | Q=const | ΔU=-A | 0 | 0 |
Вернуться к оглавлению
Тепловой баланс.

Qотд=Qполуч
Q=cmΔT — теплота на нагрев (охлаждение)
Q=rm — Теплота парообразования (конденсации)
Q=λm — плавление (кристаллизация)
Q=qm — сгорание.
Тепловое расширение.
l=l0(1+αΔT) V=V0(1+βΔT)
Тепловые машины.
— коэффициент полезного действия
,
Гидростатика, гидродинамика.
Обозн. | Изм. | Смысл |
|---|---|---|
p | Па | давление |
V | м3 | объем |
m | кг | масса |
σ | Н/м | коэффициент поверхностного натяжения |
v | м/с | скорость жидкости |
S | м2 | площадь |
ρ | кг/м3 | плотность |
h | м | высота столба жидкости. |
, (давление на глубине h).
— плотность.
( сила Архимеда ).
— (гидравлический пресс).
— закон сообщающихся сосудов.
— уравнение неразрывности.
— уравнение Бернулли ( — динамическое, р — статическое, — гидростатическое давление.)
— сила и энергия поверхностного натяжения.
— высота подъема жидкости в капилляре.
Вернуться к оглавлению
Электрические и электромагнитные явления.
Электростатика.
— закон Кулона.
, — напряженность электрического поля
— принцип суперпозиции полей.
— поток через площадку S.
— теорема Гаусса.
— теорема о циркуляции.
, — потенциал.
плоскость | ||
сфера | ||
шар | ||
цилиндр (пустой) |
,
, ,
— электроемкость уединенного проводника.
, , плоский конденсатор.
— электроемкость заряженного шара.
— электроемкость сферического конденсатора.
— батарея конденсаторов. p=qd — дипольный момент.
поляризованность диэлектрика.
P=жε0E где ж- диэлектрическая восприимчивость.
ε=1+ж ε- диэлектрическая проницаемость.
— теорема Гаусса для диэлектриков.
Электродинамика. Постоянный ток.
, ,
, , Закон Ома.
; — температурное изменение температуры.
, ,
— закон Джоуля–Ленца.
— правило Кирхгофа для узлов.
— правило Кирхгофа для контуров.
Параллельное соединение проводников: I=const, ,
Последовательное соединение: , U=const,
Вернуться к оглавлению
Законы электролиза.
m=kq=kΔT — первый закон Фарадея.
— второй закон Фарадея.
Вернуться к оглавлению
Электромагнетизм.

, — сила Лоренца.
— сила Ампера, действующая на проводник длиной l.
,
магнитная индукция поля в точке.
— магнитная индукция в центре витка.
— индукция внутри соленоида.
индукция поля проводника на расстоянии R от оси.
связь между магнитной индукцией и напряженностью магнитного поля.
— принцип суперпозиции магнитных полей.
— сила взаимодействия двух проводников.
магнитный поток.
— энергия магнитного поля.
ЭДС индукции в замкнутом контуре.
ЭДС самоиндукции.
Вернуться к оглавлению
Колебания и волны. Оптика. Акустика.
Механические и электромагнитные колебания.
— уравнение гармонических колебаний.
,n.3
— полная энергия колеблющейся точки.
Вернуться к оглавлению
Система. | Период | Цикл. частота | Уравнение |
|---|---|---|---|
Математический маятник. | |||
Пружинный маятник. | |||
Физический маятник. | |||
Колебательный контур. |
Сложение колебаний.
, при ω1=ω2
— период пульсации.
Затухающие колебания.
,
Переменный ток.
Z=ZR+ZL+ZC — полный импеданс цепи.
ZR=R, ZL=iΩL,
— модуль полного импеданса цепи.
, — действующие значения.
Упругие волны.
Скорость волны в газе: , в твердом теле:
,
уравнение плоской волны:
Отражение | ||
Преломление | Δφ=0 lim αпад=arcsin(c2/c1) |
Интерференция: ,
фазовая v и групповая u скорости: ,,
— эффект Доплера.
Электромагнитные волны.
— фазовая скорость
Отражение | ||
Преломление | Δφ=0 lim αпад=arcsin(c2/c1) |
Вернуться к оглавлению
Оптика
— разность хода.
— скорость света в среде
— закон преломления.
— формула линзы.
— увеличение линзы.
Вернуться к оглавлению
Квантовая физика и теория относительности.
— энергия фотона. h- постоянная Планка
— фотоэффект
— полная энергия.
Атомная физика.
— закон распада
Вернуться к оглавлению
Формула ускорения с примерами и решенными задачами
Когда стоящая машина внезапно трогается с места, нас толкает назад, а при торможении нас толкает вперед, к нашему сиденью, или когда наша машина резко поворачивает направо, нас толкает влево. Мы сталкиваемся с такими ситуациями, потому что наша машина ускоряется.
Мы сталкиваемся с такими ситуациями, потому что наша машина ускоряется.
Просто когда есть изменение скорости, будет и ускорение. Давайте разберемся с концепцией ускорения на наглядных примерах.
Предположим, у меня есть автомобиль, движущийся по прямой с постоянной скоростью 90 км/ч. Я вижу вертолет, летящий со скоростью примерно 20 000 км/ч. Если бы я спросил вас об этом в этих двух случаях, где вы нашли Ускорение? Ваш ответ, безусловно, будет отрицательным, потому что оба они движутся с постоянной скоростью, поэтому ускорение в обоих случаях отсутствует.
Теперь, если я спрошу вас, что Ускорение равно высокой скорости. Каким будет ваш ответ? Вы можете сказать да, но это не точно. Хотите знать, почему? Это потому, что Ускорение — это скорость изменения Скорости. Теперь давайте разберемся с формулой ускорения.
Общая формула ускорения
Мы уже знаем, что скорость — это скорость с направлением; следовательно, это векторная величина. Ускорение «a» задается как:
Ускорение «a» задается как:
\[ a = \frac{\text{Изменение скорости}}{\text{Затраченное время}}\]
Эта формула утверждает, что скорость изменения скорости равна Ускорение, или если скорость объекта изменяется от его начального значения ‘u’ до конечного значения ‘v’, то выражение можно просто записать как:
\[a = \frac{(v — u)}{t}\]
В физике ускорение описывается как скорость изменения скорости объекта независимо от того, ускоряется он или замедляется . Если он ускоряется, ускорение считается положительным, а если замедляется, то ускорение отрицательным. Это вызвано суммарной неуравновешенной силой, действующей на объект в соответствии со вторым законом Ньютона. Ускорение является векторной величиной, поскольку оно описывает скорость изменения во времени скорости, которая является векторной величиной. Ускорение обозначается а. Его единица СИ — \[\frac{m}{s^{2}}\], а размеры — \[[M^{0}L^{1}T^{–2}]\].
Если \[v_{0}, v_{t}\] и t представляют начальную скорость, конечную скорость и время, необходимое для изменения скорости, то ускорение определяется как:
\[\overrightarrow{ a} = \frac{\overrightarrow{v_t} — \overrightarrow{v_0}}{t}\]
В одномерном движении мы можем использовать;
\[a = \frac{v_t — v_0}{t}\]
Формула ускорения
Если \[\overrightarrow{r} \]представляет вектор смещения и \[\overrightarrow{v} = \frac {\overrightarrow{\text{d}r}}{\text{d}t}\] представляет скорость, тогда; 9{2}} \]
2. Девушка начинает движение по прямой со скоростью 30 \[\frac{м}{с}\], ее скорость изменяется с постоянной скоростью. Если она остановится через 60 с, каково ее ускорение?
Ответ: Здесь начальная скорость девушки была 30 \[\frac{m}{s}\] и она останавливается, поэтому ее конечная скорость станет равной 0 м/с. Теперь происходит замедление или запаздывание, что прямо противоположно Ускорению и может быть определено как: {с^{2}} \]
Вопрос 3. Автомобиль движется по круговой траектории с постоянной скоростью; будет ли он испытывать ускорение?
Автомобиль движется по круговой траектории с постоянной скоростью; будет ли он испытывать ускорение?
Ответ: Здесь скорость постоянна; однако направление постоянно меняется, что означает, что скорость также меняется. В нем говорится, что автомобиль будет испытывать ускорение.
Как подготовиться к тесту по ускорению с использованием Веданту
Вы можете войти в Веданту и просмотреть имеющиеся учебные материалы
Вы можете нажать на формулу ускорения с примерами и решенной задачей
После прочтения этого учебного материала концепции станут намного яснее
Внимательно изучите решенные примеры
Дело позаботится о том, чтобы вы хорошо подготовились к экзаменам
Почему стоит выбрать Vedantu?
Vedantu — это ведущая платформа электронного обучения, которая размещает на своем веб-сайте только лучшие учебные материалы. Он чрезвычайно надежен, так как все учащиеся делают ставку на него, прежде чем приступить к проверке или тестированию. Учебный материал на нем бесплатен и может быть загружен, а затем пройден в офлайн-режиме. Вы должны выбрать Vedantu, если вам нужно хорошо подготовиться перед тестами и изучить все сложные концепции.
Он чрезвычайно надежен, так как все учащиеся делают ставку на него, прежде чем приступить к проверке или тестированию. Учебный материал на нем бесплатен и может быть загружен, а затем пройден в офлайн-режиме. Вы должны выбрать Vedantu, если вам нужно хорошо подготовиться перед тестами и изучить все сложные концепции.
Формула постоянной пружины с использованием закона Гука
Springs — это то, с чем мы все знакомы. Обычно мы видим их в ручках, игрушках и других бытовых предметах. Одной из отличительных особенностей пружины является ее способность сохранять свою длину даже после растяжения. Он просто возвращается в свою первоначальную форму и завораживает. В этом разделе учащийся получит возможность глубже изучить эту концепцию.
Всякий раз, когда пружина растягивается, прикладывается усилие для удлинения пружины в направлении от центра пружины. Это происходит всякий раз, когда кто-то или что-то тянет за пружину, и это создает напряжение в пружине, которое заставляет ее возвращаться к центру пружины, когда сила прекращается, то есть когда человек или предмет, удерживающий ее, отпускает. Это сила, которую ученик вычислит по закону Гука.
Это сила, которую ученик вычислит по закону Гука.
Прежде чем вывести формулу для жесткости пружины, давайте просто объясним, почему пружина ведет себя таким образом. Константа пружины — это числовое представление внутреннего свойства пружины, которое позволяет ей сохранять свою форму и длину даже после растяжения.
Формула жесткости пружины является неотъемлемой частью простого гармонического движения. Чтобы понять формулу для постоянной пружины, сначала мы рассмотрим, что такое SHM или то, что мы называем простым гармоническим движением. После того, как мы подробно изучим концепцию SHM, мы рассмотрим, как пружины связаны с простым гармоническим движением, а затем, наконец, выведем формулу жесткости пружины. Подробное объяснение, представленное здесь, также является попыткой разработать формулу жесткости пружины с использованием закона Гука.
Простое гармоническое движение
Простое гармоническое движение — это повторяющееся движение вперед и назад через центральное положение, при котором максимальное смещение с одной стороны этого положения равно максимальному смещению с другой стороны. Интервал времени каждой полной вибрации одинаков. Сила, ответственная за движение, всегда направлена в сторону равновесия и прямо пропорциональна расстоянию от него.
Интервал времени каждой полной вибрации одинаков. Сила, ответственная за движение, всегда направлена в сторону равновесия и прямо пропорциональна расстоянию от него.
Некоторыми распространенными примерами SHM являются маятники. Если принять положение покоя маятника за центр, то при движении маятника наблюдается, что расстояние, которое он проходит по обе стороны от центра, одинаково, и маятник всегда движется к центру после прохождения максимального расстояния. . Будем называть центр равновесием.
Пружины обычно имеют SHM. Пружины имеют свои собственные естественные «пружинные константы», которые определяют их жесткость. Закон Гука — известный закон, который объясняет SHM и дает формулу для силы, приложенной с использованием жесткости пружины.
Применительно к пружине мы можем наблюдать, что когда пружина растягивается в обоих направлениях, оба конца пружины возвращаются к равновесию. Это очень похоже на то, как ведет себя маятник, хотя он и не движется по кругу.
Закон Гука
Закон Гука определяет соотношение между приложенной силой и расстоянием, на которое растянулась пружина. Сила, необходимая для сжатия или растяжения пружины, прямо пропорциональна расстоянию, на которое она растягивается.
Это основано на третьем законе движения Ньютона, который гласит, что на каждое действие есть равное и противоположное противодействие. Думайте о растяжении пружины как о действии, а о естественном сжатии пружины как о противодействии.
Согласно третьему закону движения Ньютона, при растяжении пружины она оттягивается с возвращающей силой. Эта восстанавливающая сила подчиняется закону Гука, который связывает силу пружины с постоянной пружины. Это соотношение, представленное математически, называется формулой жесткости пружины.
(Изображение будет загружено в ближайшее время)
Сила пружины = -(Постоянная пружины) x (Перемещение)
F=−K*X
F=−KX
Знак минус указывает на противоположное направление сила реакции.
Где,
F: восстанавливающая сила пружины, направленная к равновесию.
K: Постоянная пружины в Н.м-1.
X: Смещение пружины от положения равновесия.
Жесткость пружины (K)
Теперь константа пружины определяется как сила, необходимая для восстановления исходной формы пружины на единицу растяжения пружины. Это также означает, что, зная постоянную пружины, мы можем легко определить, какая сила необходима для деформации пружины. Потому что, если мы приложим больше силы, чем та, с которой может справиться пружина, она больше не сможет проявлять СГМ.
K=−F * x
K=−Fx
Единицей измерения является Н/м (Ньютон на метр).
Как жесткость пружины зависит от длины?
Предположим, у нас есть пружина 6 см с жесткостью k. Что произойдет, если мы разделим пружину на два бита одинакового размера? Для одной из этих более коротких пружин будет новая константа пружины, которая будет равна 2k. В более общем случае жесткость пружины обратно пропорциональна длине пружины, если мы говорим о пружине из определенного материала и ее толщине.
В более общем случае жесткость пружины обратно пропорциональна длине пружины, если мы говорим о пружине из определенного материала и ее толщине.
Это означает, что чем больше длина пружины, тем меньшая сила потребуется ей для достижения состояния равновесия, и наоборот.
Итак, предположим, что в приведенном выше примере мы разрезали пружину ровно пополам, получив две более короткие пружины по 3 см каждая. Для пружин меньшего размера будет применяться жесткость пружины, вдвое превышающая исходную. Это потому, что она обратно пропорциональна жесткости пружины и длине пружины. Это означает, что на более короткой пружине первоначальная масса в 30 г даст растяжение только на 1 мм. Чем больше постоянная пружины, тем меньше растяжение, создаваемое данной силой. Вот почему пружины меньшего размера труднее растянуть!
График закона Гука
График закона Гука представлен ниже. Здесь материал проявляет упругое поведение до предела текучести, после чего материал теряет эластичность и проявляет пластичность.
Это означает, что как только мы успешно приложим силу, превышающую пороговое значение, пружина потеряет свою эластичность, и поэтому дальнейшее приложение силы заставит пружину изменить свою форму и сохранить ее. Когда материал меняет свою форму и сохраняет эту форму при приложении к нему какой-либо силы, то это свойство называется пластичностью.
Подумайте о пластиковых предметах, которые вы видели. Как только вы прикладываете силу, он либо сгибается, либо ломается. Он не пытается растянуться или вернуться в свою первоначальную форму, как хорошо функционирующая пружина.
(Изображение будет загружено в ближайшее время)
Прямая линия означает, что материал следует закону Гука от начала до пропорционального предела, приближающегося к пределу текучести. Материал теряет свою эластичность за пределом упругости между пределом пропорциональности и пределом текучести и начинает проявлять пластичность. Площадь от начала координат до предела пропорциональности под кривой находится ниже диапазона эластичности. В диапазоне пластичности площадь под кривой находится от пропорционального предела до точки разрыва/разрушения.
Площадь от начала координат до предела пропорциональности под кривой находится ниже диапазона эластичности. В диапазоне пластичности площадь под кривой находится от пропорционального предела до точки разрыва/разрушения.
Чтобы помочь учащимся с некоторыми быстрыми и простыми советами по изучению физики, мы перечислили несколько пунктов, которые считаются успешными при подготовке.
Сосредоточьтесь больше на основах темы, поскольку вы укрепляете основные понятия, последующее путешествие становится легче.
Обратите внимание на мелкие детали, упущение любой из концепций может стоить вам очень дорого.
Всегда старайтесь использовать некоторые визуальные методы обучения, такие как блок-схемы, рисунки, диаграммы и т. д., чтобы сделать процесс обучения легким и увлекательным.

Постарайтесь упростить ситуацию и сосредоточьтесь на понимании сути вопросов. Без этого вы не сможете точно на них ответить.
Используйте различные учебные ресурсы, такие как онлайн-учебные материалы, викторины, ваши учебные заметки, видео в классе и т. д.
В физике много практических занятий, и она включает в себя использование уравнений. Студенты должны убедиться, что выучили и поняли уравнения и связанные с ними формулы.
Другим важным навыком, который нужно улучшить в этом предмете, является укрепление ваших математических навыков. Поскольку в нем много вопросов, основанных на числах, вы должны быть быстрыми и точными в расчетах.
Формула массы — что такое формула массы
Масса — это величина, которая дает представление о том, сколько материи присутствует в объекте. Это количественная мера инерции. А ускорение обратно пропорционально инерции.
Это количественная мера инерции. А ускорение обратно пропорционально инерции.
Связь между силой и массой определяется выражением:
F = ma или m = F/a
Связь между плотностью, массой и объемом определяется формулой:
𝛒 = m/V или m = 𝛒V
K = ½ mv2 или m = 2K/v2
Связь между потенциальной энергией, массой, ускорением свободного падения и высотой определяется по формуле:
P = mgh или m = P/gh 9000 хорошо известное соотношение массы и энергии Эйнштейна, которое обеспечивает формулу массы и энергии,
m = E / c2
Где, E = энергия, m = масса, c = скорость света
Связь между массой (m), скоростью (v) и импульсом (p) определяется формулой: = mv или m = p/v
Разница между массой и весом
Вес – это сила тяжести, действующая на массу. Таким образом, масса остается постоянной, а вес изменяется в соответствии с изменением гравитационного поля.
Таким образом, масса остается постоянной, а вес изменяется в соответствии с изменением гравитационного поля.
W = мг или m = Вт/г
Примеры решения
1. Рассчитайте массу тела, если плотность и объем тела равны 2 кг/м 3 и 5 м 3 .
ANS:
Здесь масса = плотность x объем
= 2 x 5
= 10 кг
2. Если объект движется со скоростью 5 м/с и имеет кинетическую энергию 100J, найдите масса.
Решение: Мы знаем, что KE = ½ mv2
100 = ½ x m x 5 x 5
100 = 25 м/2
m = 100×2/25 = 200/25 = 8 кг
Почему масса остается неизменной, а вес меняется на разных планетах?
Масса объекта — это мера его содержимого, а вес — это сила гравитации. И сила гравитации меняется на разных планетах.
Мы знаем, что на Земле g = 9,8 м/с 2
А на Луне g = 1,6 м/с 2
Поясним это на примере:
Пример:
1.
Вычислите вес объекта на Луне, который весит 50 кг на Земле.
ANS:
Здесь вес = масса x гравитационное ускорение
= M x G
= 50 кг x 1,6 м/с 2
= 80 кг м/с 2
. из этого примера, если ваш друг весит 50 кг на этой планете, он будет весить 80 кг на Луне!
Теперь рассчитайте свой вес на Луне.
Знаете ли вы?
Подобно тому, как большинство объектов на Земле или в земном гравитационном поле испытывают гравитационное притяжение и поэтому приобретают атрибут «веса»; есть какие-то особые обстоятельства, которые могут дать ощущение «невесомости».
Невесомость — это явление, при котором ощущение веса полностью или почти полностью отсутствует. Это также называется невесомостью, хотя более подходящим термином будет «нулевая перегрузка». Возникает при отсутствии контактных сил, действующих на объект, в том числе и на тело человека.
Возникает при отсутствии контактных сил, действующих на объект, в том числе и на тело человека.
Вес, как мы понимаем, является мерой силы, действующей на покоящийся объект под действием гравитационного поля (например, для объектов на поверхности Земли). Это «ощущение веса» может возникнуть из-за контакта с опорными полами, сиденьями, кроватями, весами и т. д.
Ощущение веса также можно испытать, когда гравитационное поле равно нулю; в таких случаях объект находится под действием контактных сил, действующих на него. Эти силы помогают преодолеть инерцию тела (состояние покоя) за счет некоторого механического и негравитационного воздействия, такого как центробежная сила в центрифуге, на орбитальной космической станции или в ускоряющемся транспортном средстве.
Именно в этих обстоятельствах (когда сила гравитации равна нулю) говорят, что тело находится в «свободном падении».
Подобно тому, как большинство объектов на Земле или в земном гравитационном поле испытывают гравитационное притяжение и поэтому приобретают атрибут «веса»; есть какие-то особые обстоятельства, которые могут дать ощущение «невесомости».
Невесомость — это явление, при котором ощущение веса полностью или почти полностью отсутствует. Это также называется невесомостью, хотя более подходящим термином будет «нулевая перегрузка». Возникает при отсутствии контактных сил, действующих на объект, в том числе и на тело человека.
Возникает при отсутствии контактных сил, действующих на объект, в том числе и на тело человека.
Вес, как мы понимаем, является мерой силы, действующей на покоящийся объект под действием гравитационного поля (например, для объектов на поверхности Земли). Это «ощущение веса» может возникнуть из-за контакта с опорными полами, сиденьями, кроватями, весами и т. д.
Ощущение веса также можно испытать, когда гравитационное поле равно нулю; в таких случаях объект находится под действием контактных сил, действующих на него. Эти силы помогают преодолеть инерцию тела (состояние покоя) за счет некоторого механического и негравитационного воздействия, такого как центробежная сила в центрифуге, на орбитальной космической станции или в ускоряющемся транспортном средстве.
Именно в этих обстоятельствах (когда сила гравитации равна нулю) говорят, что тело находится в «свободном падении».





 511034
511034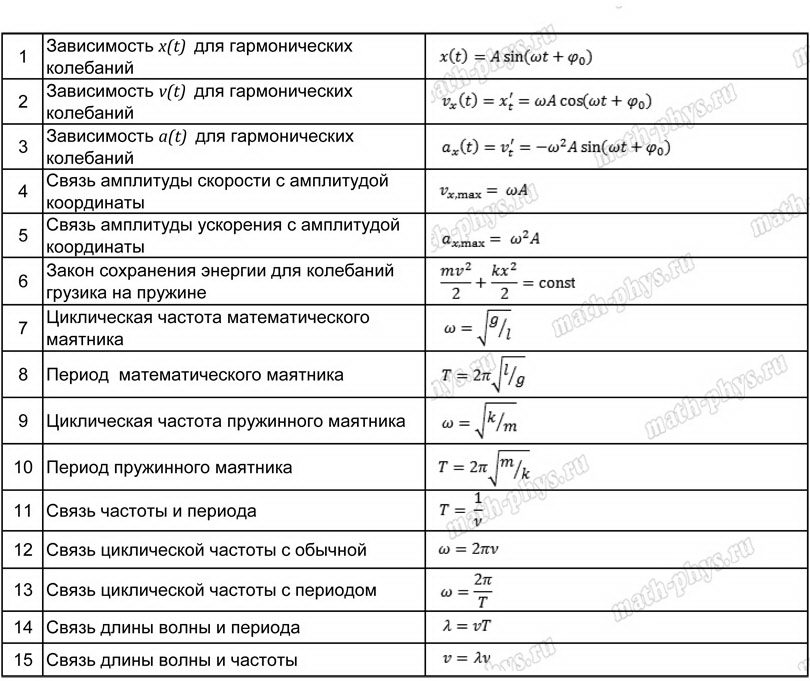 энергия газа
энергия газа