Подобие фигур 6 класс: Презентация по математике на тему «Подобие фигур» ( 6 класс)

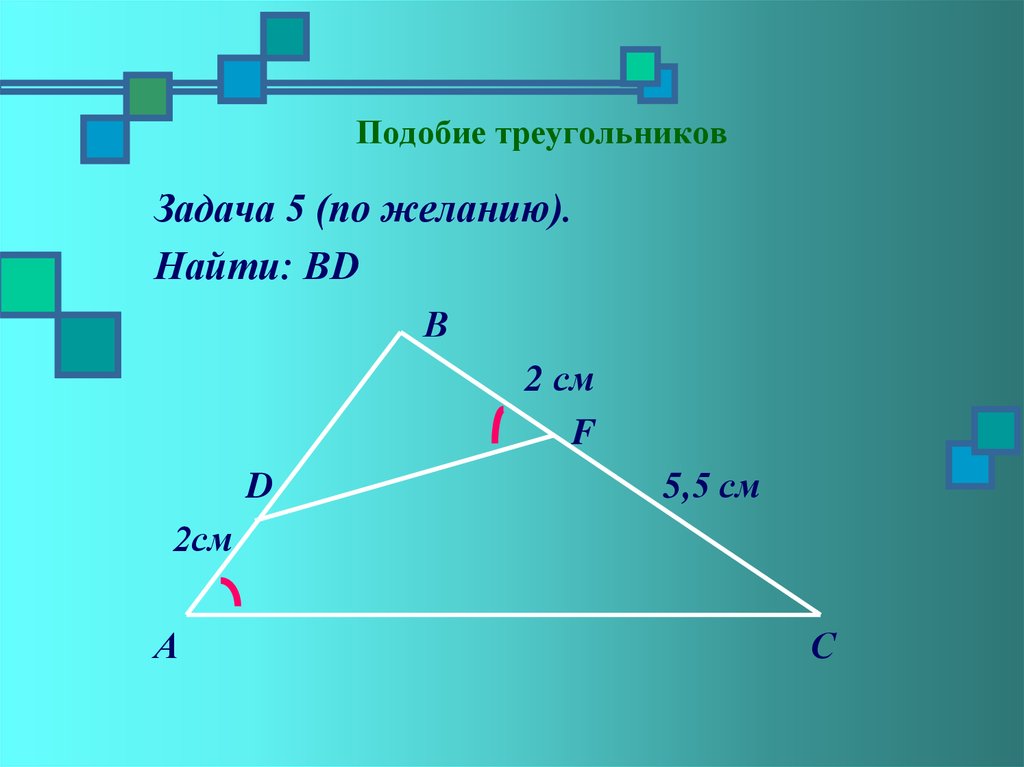
Презентация «Подобие фигур»

Преобразование подобия.

Скажи мне — и я забуду, покажи мне — и я запомню, дай мне сделать — и я пойму.

Конфуций

Конфуций

древний мыслитель,

философ Китая

Д

В

И

Ж

Е

Н

И

Е

• ОСЕВАЯ СИММЕТРИЯ

• ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

• ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС

• ПОВОРОТ

а

А

4

а

5

А

6

Свойства движения:

• При движении прямая переходит в прямую, луч – в луч, отрезок – в отрезок.
• Сохраняются расстояния между точками.
• Сохраняются углы между лучами.

7

Что такое подобие и где оно встречается?

• Посмотрите на эту картинку.

Все матрешки имеют одинаковое лицо,

костюмы и пропорции. Значит они являются

ПОДОБНЫМИ ФИГУРАМИ. Что такое подобные фигуры? Простым языком

Это те фигуры, которые

имеют разные массы, размеры, но

одинаковые формы!

.

Где встречается подобие? Посмотрите вокруг.

Мы живем в мире подобия. В самом Человеке заложен Принцип Подобия, каждый его орган или часть тела подобна всему телу. Даже все люди похожи. У каждого из нас одинаковый набор органов. У каждого два уха, два глаза и тп.

Мы живем на планете Земля, наша планета подобна другим планетам. Она такая же круглая как и все планеты во вселенной.

Вот некоторые подобия которые встречаем мы в жизни:

• Посмотрите на рисунке 4 вида мячей. Они все имеют разные размеры и массы, но одинаковую форму — круга.

В геометрии фигуры одинаковой формы принято называть подобными.

А для чего нам нужно подобие?

• Для решения задач. А вы знали, что при помощи зеркала можно найти высоту рядом находящегося предмета. Как измерить высоты дерева с которым мы стоим рядом?

• Отойдя на некоторое расстояние от дерева, зеркало следует положить на землю так, чтобы оно приняло горизонтальное положение. Затем нужно постепенно отходить назад до тех пор, пока в зеркале удастся увидеть отражение вершины дерева.

• Высота дерева будет во столько раз больше роста человека (до высоты глаз), во сколько расстояние от зеркала до дерева больше расстояние от зеркала до места стояния человека .

Подобие фигур

Преобразование фигуры F в фигуру F’ называется преобразованием подобия , если при этом преобразовании расстояния между точками изменяются в одно и то же число раз.

число k называется коэффициентом подобия.

Х  Х’

Х’Y’ = k  ХY

Y  Y’

Х’

Y’

Y

Две фигуры F и F’ называются подобными, если одна из них переводится в другую подобием.

В режиме слайдов ответы появляются после кликанья мышкой

Х

F’

F

Свойства подобия

Подобие сохраняет порядок точек на прямой, то есть если точка лежит между точками — соответствующие их образы при некотором подобии, то также лежит между точками.

Точки, не лежащие на прямой, при любом подобии переходят в точки, не лежащие на одной прямой.

Подобие преобразует прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность.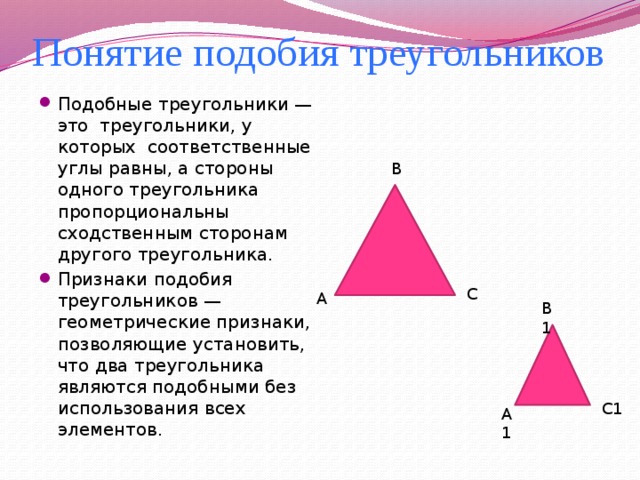

При подобии угол сохраняет величину.

Подобие с коэффициентом , преобразующее каждую прямую в параллельную ей прямую, является гомотетией с коэффициентом.

Каждое подобие можно рассматривать как композицию движения и некоторой гомотетии с положительным коэффициентом.

Подобие называется собственным (несобственным), если движение является собственным (несобственным). Собственное подобие сохраняет ориентацию фигур, а несобственное — изменяет ориентацию на противоположную.

Два треугольника являются подобными, если их соответственные углы равны, или стороны пропорциональны.

Площади подобных фигур пропорциональны квадратам их сходственных линий (например, сторон). Так, площади кругов пропорциональны отношению квадратов их диаметров (или радиусов).

Преобразование подобия сохраняет углы между полупрямыми.

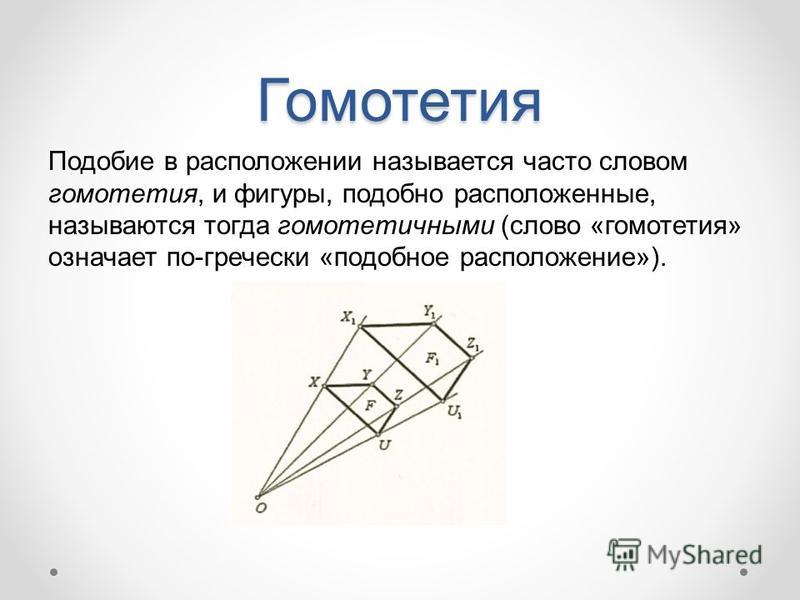
Гомотетия

O

Х

Фигуры F и F´ называются гомотетичными.

Х’

В режиме слайдов ответы появляются после кликанья мышкой

Преобразование фигуры F, при котором каждая ее точка Х переходит в точку Х’ , построенную указанным способом, называется

гомотетией относительно центра O.

Зафиксируем точку O и положительное число k . Каждой точке Х плоскости, отличной от O сопоставим точку Х’ на луче OХ так, что OХ’ = k  OХ . Точке O сопоставим ее саму.

Число k называется коэффициентом гомотетии.

В′

О – центр гомотетии

ОВ′ = k∙ОВ

k – коэффициент гомотетии.

В

С′

С

О

А

А ′

0 а) k 1 б) k 2 случай: k «

Рассмотрим случаи:

• 1 случай:
  k 0

а) k 1

б) k

• 2 случай: k

Построение фигуры

гомотетичной данной

О

О – центр гомотетии,

Дано: ∆АВС,

k = 3.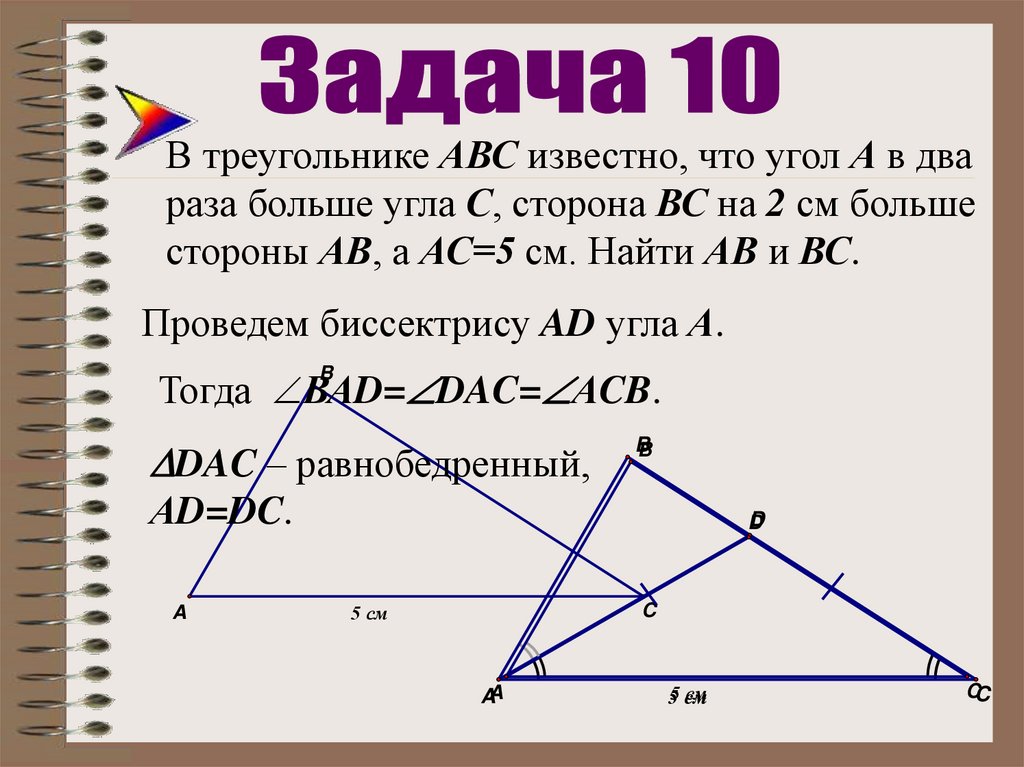

В

Построить: ∆ А ´В´С´, гомотетичный ∆ АВС.

А

Построение.

Проведем луч ОА.

С

Отложим на нем отрезок ОА ´ = 3 ∙ОА.

В ´

Проведем луч ОВ.

Отложим на нем отрезок ОВ´ = 3 ∙ОВ.

А ´

Проведем луч ОС.

Отложим на нем отрезок ОС´ = 3 ∙ОС.

С ´

Достроим ∆

А´В´С´ — искомый.

1 случай: б) k = 1 / 3

А

А ′

О

В ′

С ′

В

С

ОА′ = 1 / 3 ∙ОА = 1 / 3 ___ = ___

ОВ′ = 1 / 3 ∙ОВ = 1 / 3 ∙___ = ___

ОС′ = 1 / 3 ∙ОС = 1 / 3 ∙___ = ___

2 случай: k = -2

С′

В′

А

О

В

С

А′

ОА′ = |-2|∙ОА = 2∙___ = ___

ОВ′ = |-2|∙ОВ = 2∙___ = ___

ОС′ = |-2|∙ОС = 2∙___ = ___

Подобными являются любые два круга, два квадрата.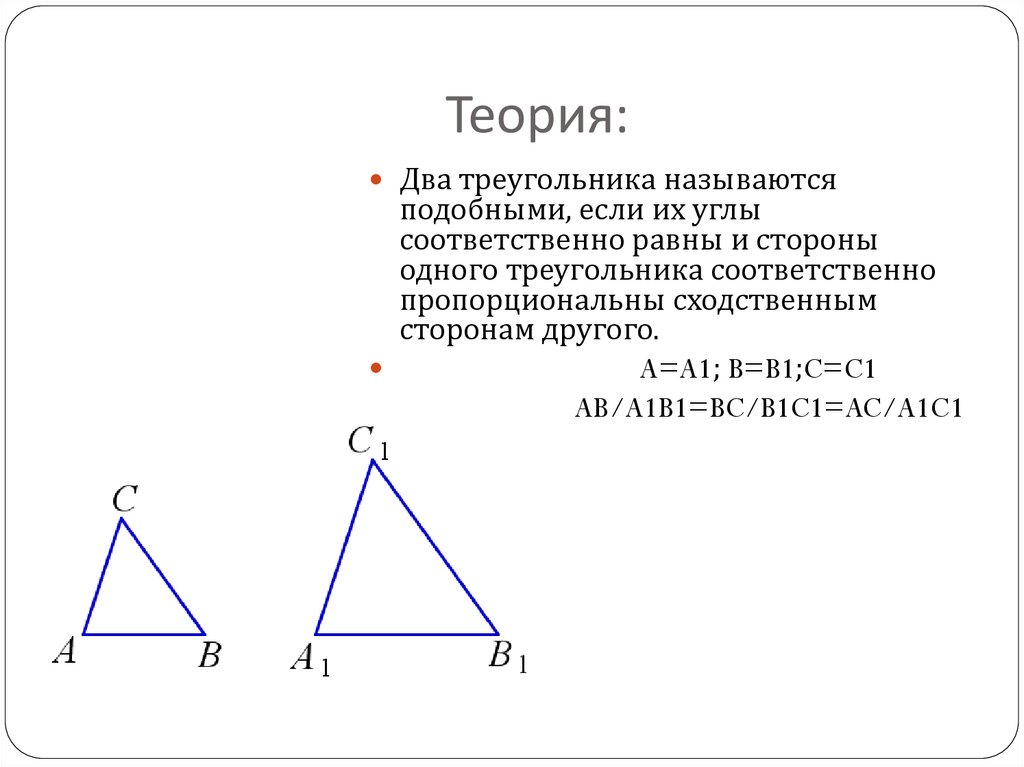

Подобие фигур.

ЕСЛИ ФИГУРА F1 ПОДОБНА ФИГУРЕ F2, А ФИГУРА F2 ПОДОБНА ФИГУРЕ F3, ТО ФИГУРЫ F1 И F3 ПОДОБНЫ.

• Преобразование подобия имеет широкое практическое применение, в частности, при выполнении деталей машин, составлении карт и планов местности. При этом коэффициент подобия называется  масштабом.

Подобие в жизни

( карты местности )

Преобразование подобия

Преобразование одной фигуры в другую называется преобразованием подобия , если при этом преобразовании расстояние между точками изменится в одно и то же число раз

Свойства преобразования подобия

Проверь себя

Иллюстрация определения

Задание 1

Задание 2

8см

32 см

Пример преобразования подобия

5 см

• Расстояние между соответствующими точками изменилось в 4 раза, значит, фигуры были подвергнуты преобразованию подобия

О

С

В

А

Н

К

20 см

М

Р

Задание 1

Квадрат F1 был подвергнут некоторому преобразованию. В результате была получена фигура F2. Будет ли данное преобразование являться преобразованием подобия? Свой ответ обоснуйте.

F 2

F 1

Подобные треугольники:

В

В

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника

В 1

В 1

С

С

А

А

С 1

А 1

С 1

Стороны АВ и А 1 В 1

ВС и В 1 С 1

СА и С 1 А 1 называются сходными

Подобные треугольники:

∆ КМР  ∆ СОВ

• Найдите равные углы
• Назовите пропорциональные стороны

I вариант

II вариант

∆ DEO  ∆NRM

∆ СВР  ∆КМО

Подобие фигур. 8 класс — презентация онлайн

1. ПОДОБИЕ В ГЕОМЕТРИИ

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
8 класс

2. ТЕМА «ПОДОБИЕ»

Теоретический материал.
Задачи.

3.

ПЛАНПропорциональные отрезки.
Свойство биссектрисы
треугольника.
Определение подобных
треугольников.
Отношение периметров подобных
фигур.
Отношение площадей подобных
фигур.
Признаки подобия треугольников.

4. ЗАДАЧИ

Разминка.
Решение задач.
Задачи на признаки подобия.
Тест

5. Пропорциональные отрезки

Отношением
отрезков называется
отношение их длин.
Отрезки AB и CD
пропорциональны
отрезкам A1B1 и
C1D1,, если
AB A1B1
CD C1D1
B
A
D
C
AB
CD
A
A1
B
С
D
B1 С1
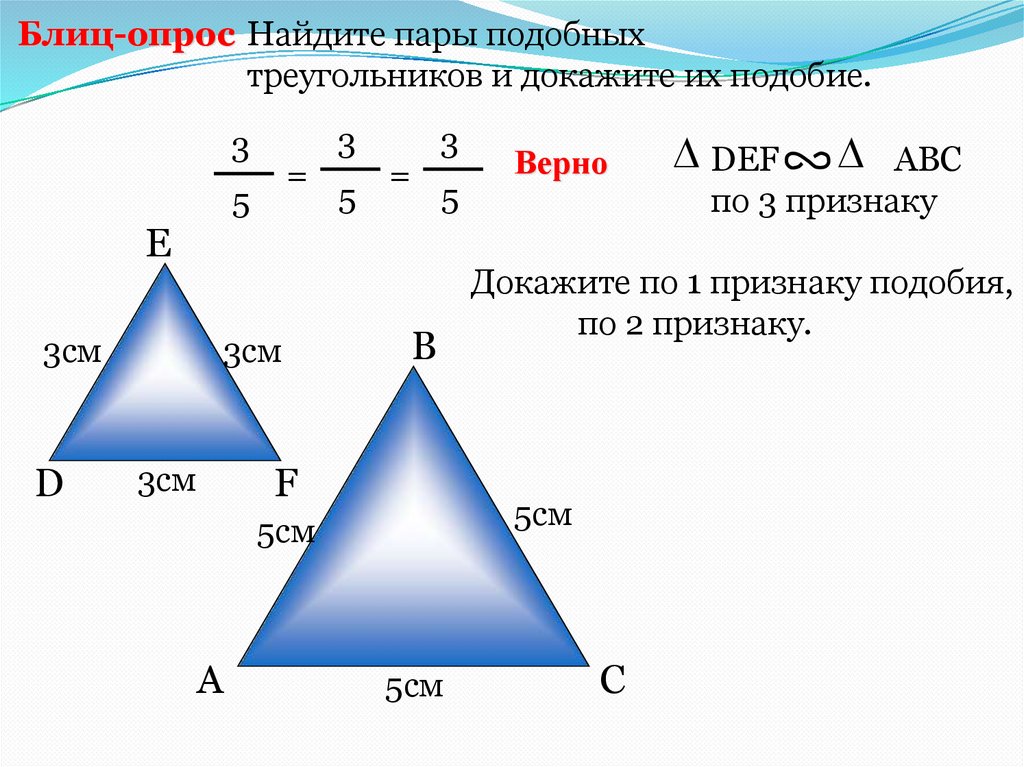
ПРИМЕР
D1

6. ПРИМЕР

Даны два прямоугольных треугольника
Стороны ΒC и CA пропорциональны MN и MK,
так как
B
5
BC
3
MN 15
3
C
A
4
N
т.е.
?
15
M
K
20
и
AC
4
MK 20
BC AC 1
MN MK 5
НАЙДИТЕ ГИПОТЕНУЗУ БОЛЬШЕГО
ТРЕУГОЛЬНИКА.

7. Пропорциональность отрезков

Понятие пропорциональности вводится
для любого числа отрезков.
B
например
5
3
C
A
BC AC AB
MN MK NK
4
N
25
15
M
K
20

8. Подобные фигуры

Предметы
одинаковой формы,
но разных размеров
Фотографии, отпечатанные
с одного негатива, но с
разными увеличениями;
Здание и его макет
Планы,
географические
карты одного и того
же района,
выполненные в
разных масштабах.

9. Подобные фигуры

В геометрии фигуры одинаковой формы называют подобными
фигурами
Подобными
являются любые
два квадрата
Подобными
являются любые
два круга
два куба
два шара

10. Подобные треугольники

Даны два треугольника AΒC и A1Β1C1,
у которых A = A1, Β = Β1, C = C1.
Стороны AΒ и A1Β1 , AC и A1C1 , ΒC и Β1C1,
лежащие против равных углов, называют
сходственными
Β1
Β
A
C
A1
C1

11. Определение

Два треугольника называются подобными,
если их углы соответственно равны и
стороны одного треугольника
пропорциональны сходственным
сторонам другого.
Β
ΔAΒC ~ ΔA1Β1C1
A
C
A1
Β1
A = A1, Β = Β1, C = C1.
AB
BC
AC
A1 B1 B1C1 A1C1
C1

12. Коэффициент подобия

Β
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
Β1
C
A1
k – коэффициент подобия.
Число k , равное отношению сходственных
сторон, называется коэффициентом
подобия.
C1

13. Дополнительные свойства

Отношение высот подобных треугольников,
проведенных к сходственным сторонам,
равно коэффициенту подобия.
Отношение медиан подобных треугольников,
проведенных к сходственным сторонам,
равно коэффициенту подобия.
Отношение биссектрис подобных
треугольников, проведенных к сходственным
сторонам, равно коэффициенту подобия.

14. Отношение периметров

Β
Β1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
C
A1
PABC
k
PA1B1C1
ДОКАЗАТЕЛЬСТВО
Отношение периметров
подобных треугольников равно
коэффициенту подобия.
C1

15. Отношение периметров

ΔAΒC ~ ΔA1Β1C1
Β
Β1
A
AB
BC
AC
k
A1B1 B1C1 A1C1
AB kA1B1
C
A1
C1
BC kB1C1
AC kA1C1
PABC
AB BC AC
kA1B1 kB1C1 kA1C1
PA1B1C1 A1B1 B1C1 A1C1
A1B1 B1C1 A1C1
Выносим общий множитель за скобку и
сокращаем дробь.
PABC
k
PA1B1C1

16. Отношение площадей

Β
Β1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
Отношение площадей
подобных треугольников
равно квадрату
коэффициента подобия.
C
A1
SABC
2
k
SA1B1C1
ДОКАЗАТЕЛЬСТВО
C1

17. Отношение площадей

Пусть ΔAΒC ~ ΔA1Β1C1,
коэффициент подобия k
AB
BC
AC
k
A1B1 B1C1 A1C1
Β
Β1
A
A = A1, по теореме об отношении
площадей треугольников, имеющих по
равному углу, имеем
C
A1
SABC
AB AC
AB AC
k k k2
SA1B1C1 A1B1 A1C1 A1B1 A1C1
C1

18. Свойство биссектрисы треугольника

Биссектриса треугольника
делит противоположную
сторону на отрезки,
пропорциональные
прилежащим сторонам
треугольника.
BD DC
AB AC
или
A
ПРИМЕР
B
BD AB
DC AC
ДОКАЗАТЕЛЬСТВО
D
C

19. Свойство биссектрисы треугольника

A
2
1
H
B
ИМЕЕМ
D
BD AB
DC AC
C
ΔABD и ΔACD имеют
общую высоту AH
S ABD DB
S ACD DC
ΔABD и ΔACD имеют
равные углы 1 = 2
SABD AB AD AB
SACD AD AC AC

20. Свойство биссектрисы треугольника

Дано: ΔABC
AD – биссектриса
A
AB = 14 см
BC = 20 см
1
2
AC = 21 см
Найти: BD,CD.
Решение:
B
D
20см
C

21. Свойство биссектрисы треугольника

A
1
B
D
20см
2
Решение:
Пусть BD = x см,
тогда CD = (20 – x) см.
По свойству биссектрисы
треугольника BD DC
AB AC
имеем
x
20 x
C
14
21
Решая уравнение, получим х = 8
BD = 8 см, CD = 12 см.

22. Признаки подобия треугольников

Первый признак подобия треугольников.
(по двум углам)
Второй признак подобия треугольников.
(по углу и двум пропорциональным
сторонам)
Третий признак подобия треугольников.
(по трем пропорциональным сторонам)

23. Первый признак подобия треугольников.

Если два угла одного треугольника
соответственно равны двум углам другого
треугольника, то такие треугольники подобны.
C1
C
A
B
A1
B1

24. Первый признак подобия треугольников.

Дано:
C
ΔABC и ΔA1B1C1, A = A1, B = B.
Доказать:
ΔABC ~ ΔA1B1C1
A
A1
B
C1
Доказательство:
B1

25. Первый признак подобия треугольников.

Доказательство:
C
A = A1, B = B1.
C = 180º – A – B,
C1 = 180º – A1 – B1.
A
A1
C = C1
C1B
Таким образом углы треугольников
соответственно равны.
B1

26. Первый признак подобия треугольников.

Доказательство:
A = A1,
B = B1.
SABC
AB AC
SA1B1C1 A1B1 A1C1
SABC
AB BC
SA1B1C1 A1B1 B1C1
C
A
B
Имеем BC
AC
B1C1 A1C1
Аналогично, рассматривая равенство углов
BC
AB
C= C1, A= A1, получим
B1C1 A1B1
Итак, сходственные стороны пропорциональны.

27. Второй признак подобия треугольников.

Если две стороны одного треугольника
пропорциональны двум сторонам другого
треугольника и углы, заключенные между этими
сторонами, равны, то такие треугольники
подобны.
Β
A
A = A1
AB
AC
A1B1 A1C1
Β1
C
A1
C1

28. Второй признак подобия треугольников.

Дано:
ΔABC и ΔA1B1C1,
Β
A = A1,
Доказать:
ΔABC ~ ΔA1B1C1
Β1
A
Доказательство:
C
A1
AB
AC
A1B1 A1C1
C1

29. Второй признак подобия треугольников.

С
Доказательство:
Достаточно доказать, что B = B1.
A
1
2 B
C1
С2
A1
ΔABC2, 1= A1, 2= B1,
ΔABC2 ~ ΔA1B1C1 по двум углам.
AB
AC2
(из подобия).
A1B1 A1C1 AB
AC
По условию
A1B1 A1C1
AC=AC2.
B1
ΔABC=ΔABC2, т.е. B = B1.

30. Третий признак подобия треугольников.

Если три стороны одного треугольника
пропорциональны трем сторонам другого
треугольника, то такие треугольники подобны.
Β1
Β
A1
A
C
AB
BC
AC
A1B1 B1C1 A1C1
C1

31. Третий признак подобия треугольников.

Дано:
Β1
ΔABC и ΔA1B1C1,
AB
BC
AC
A1B1 B1C1 A1C1
A1
C1
Β
A
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
C

32. Третий признак подобия треугольников.

С
Доказательство:
Достаточно доказать, что A= A1
ΔABC2, 1= A1, 2= B1,
A
1
2 B ΔABC2 ~ ΔA1B1C1 по двум углам.
Отсюда
С2
A1
AB BC2 AC2
Β1
A1B1 B1C1 A1C1
По условию
AB
BC
AC
A1B1 B1C1 A1C1
ΔABC=ΔABC2 по трем
C1
сторонам,
т.е. A = A1

33. Разминка

1
Отрезки AB и CD пропорциональны отрезкам MN и PK.
Найдите MN,
если AB = 3, CD = 4, PK = 2.
AB MN
CD PK
3 MN
4
2
MN = 1,5

34. Разминка

2
• Даны два подобных прямоугольных
треугольника.
• Коэффициент подобия 1,5
• Стороны одного из них 3, 4 и 5.
• Найдите гипотенузу другого.
5 · 1,5 = 7,5
7,5

35. Разминка

3
• По данным на
рисунке найдите х.
х
12
5
х
12
5
4
4
х = 15

36. Разминка

4
• Длины двух окружностей 2π и 8π.
• Найдите отношение их радиусов.
2π : 8π = 1 : 4
0,25

37. Разминка

5
• Отношение площадей двух квадратов
равно 9 : 1.
• Найдите сторону большего их них, если
сторона меньшего равна 2.
k2 = 9, k = 3
Коэффициент подобия
3·2=6
сторона большего квадрата
6

38. Решение задач

Пропорциональные
отрезки
1
2
3
Свойство
биссектрисы
4
5
6
7
8
9
10
11
12
13
14
15
Определение
подобных
треугольников
Отношение
периметров
подобных фигур
Отношение
площадей подобных
фигур

39. 1 задача

Отрезки AB и CD пропорциональны
отрезкам EF и MN.
Найдите EF,
если AB = 5 см, CD = 80 мм, MN = 1 дм.

40.

4 задачаB
В треугольнике АВС
АС = 6 см,
1
2
ВС = 7 см,
AB = 8 см,
A
D
C
BD – биссектриса.
Найдите, AD, CD.

41. 7 задача

Треугольник со сторонами 2 см, 3 см, 4 см
подобен треугольнику
со сторонами 5 мм, 7,5 мм и 1 см.
Найдите коэффициент подобия.

42. 10 задача

Сходственные стороны подобных
треугольников относятся как 1 : 3.
Найдите периметр большего
треугольника, если периметр
меньшего 15 см.

43. 13 задача

ΔABC ~ ΔA1B1C1 ,
AB : A1B1 = k = 4
SΔABC= 48 м2.
Найдите площадь треугольника A1B1C1 .

44. 2 задача

B
C
O
A
10
D
В параллелограмме
ABCD диагонали
пересекаются в точке О,
CD = 10 см.
Найдите периметр
параллелограмма, если
BC
AC
CD OC

45. 5 задача

B
M
12
A
18
C
Основание
равнобедренного
треугольника равно 18 мм,
а биссектриса делит
боковую сторону на
отрезки, из которых
прилежащий к основанию
равен 12 мм. Найдите
периметр треугольника

46. 8 задача

Треугольники KPF и ЕМТ подобны, причем
T
M
40°
E
P
20°
F
K
KP
PF
KF
ME MT ET
F = 20°, E = 40°.
Найдите остальные
углы этих
треугольников.

47. 11 задача

Периметры подобных треугольников
12 мм и 108 мм соответственно.
Стороны одного из них 3 мм, 4 мм и 5 мм.
Найдите стороны другого и
определите его вид.

48. 14 задача

Площади двух подобных треугольников
равны 16 см2 и 25 см2.
Одна из сторон первого треугольника
равна 2 см.
Найдите сходственную ей сторону
второго треугольника.

49. 3 задача

В треугольнике ABC
B
точка K лежит на стороне
10
АС. Площади
треугольников АВK и
KВС относятся
.
A
K
C
как 1 : 3,
ВС = 10 см. Найдите AC ,
BC
AK
если
AC KC

50. 6 задача

B
AD = 4
1
BC = 5
2
AB + DC = 12
Найти AB, DC, AC
4
A
D
C

51.

9 задачаНа рисунке
B
ΔВЕС ~ ΔАВС,
АЕ = 16 см,
A
C
16
E
9
СЕ = 9 см. Углы
ABC и ВЕС тупые.
Найдите ВС.

52. 12 задача

Масштаб плана 1 : 1000.
Какова длина ограды участка,
если на плане размеры
прямоугольника,
изображающего участок 2 см х 5 см.

53. 15 задача

Периметры подобных треугольников
относятся как 2 : 3,
сумма их площадей равна 260 см2.
Найдите площадь каждого
треугольника.

54. ЗАДАЧИ

1.
Диагонали трапеции ABCD пересекаются в точке O. Площади
треугольников BOC и AOD относятся как 1 : 9. Сумма оснований
BC и AD равна 4,8 см. Найдите основания трапеции.
Решение:

55. Решение

B
C
2
4
3
O
1
A
Рассмотрим ΔAOD и
ΔBOC:
1= 2 (накрест
лежащие при AD ||
BC, и секущей AC;
3= 4 (вертикальные)
ΔAOD ~ ΔBOC (по двум
углам)
D
AO OD AD = k
OC OB BC

56. Решение

B
C
2
4
3
S AOD
9
2
k
S BOC
1
.
k=3
O
AD + BC =
= 3BC + BC = 4BC
AD + BC = 4,8см
(по условию)
1
D
A
BC = 1,2 см
AD = 3,6 см
Ответ:
BC = 1,2 см AD = 3,6 см

57. ЗАДАЧИ

B
2,5
4
20
A
2.
5
C
D
E
16
10
F
Докажите, что треугольники, изображенные на рисунке, подобны, и
выясните взаимное положение прямых CB и DF.
Решение:

58. Решение

B
2,5
4
20
A
5
C
D
E
16
10
Отсюда
BС AC AB
DF DE EF
F
ΔABC~ΔDEF
по трем
пропорциональным
сторонам
Найдем
отношение
сходственных
сторон данных
треугольников
AB 2,5
0,25
EF 10
AC 5
0,25
ED 20
BС 4
0,25
DF 16

59. Решение

B
.
E
1
A
C
D
2
ΔABC~ΔDEF
Соответственно
A = E
B = F
ACB = EDF
F
Рассмотрим
прямые BC и DF,
секущую AE
1 = 2
(внешние накрест
лежащие)
BC || DF.

60. ЗАДАЧИ

3.
Отрезки AB и CD пересекаются
AO DO
в точке O, причем OB OC .
Докажите, что CBO = DAO.
Решение:

61. Решение

Рассмотрим ΔAOD и
ΔCOB
DOA = COB
(вертикальные).
D
A
O
B
C
AO DO
OB OC
.
ΔAOD ~ ΔCOB по углу и
двум пропорциональным
сторонам.
CBO = DAO (из
подобия).

62. ЗАДАЧИ

4.
В треугольнике ABC
AB = 4, BC = 6, AC = 7.
Точка E лежит на стороне AB.
Внутри треугольника взята точка M так,
что MB = 5,25, ME = 4,5, AE = 1.
Прямая BM пересекает AC в точке P.
Докажите, что ΔAPB равнобедренный.
Решение:

63. Решение

.
A
4 E
Рассмотрим ΔBEM и ΔABC
1
BE = AB − AE = 4 – 1 = 3
BE : AB = 3 : 4 = 0,75
B
4,5
5,25
M
EM : BC = 4,5 : 6 = 0,75
7
BM : AC = 5,25 : 7 = 0,75,
т.е. стороны треугольников
P
пропорциональны
6
C
Решение
ΔBEM ~ ΔABC по трем
пропорциональным сторонам.
Следовательно, BME = AСB
EBM = BAC
BEM = ABC.
Рассмотрим треугольник ABP:
EBM = BAC, т.е. ABP = BAP.
ΔABP – равнобедренный, что и
требовалось доказать.

65. ЗАДАЧИ

5.
Диагональ AC параллелограмма ABCD равна 90.
Середина M стороны AB соединена с вершиной D.
Отрезок MD пересекает AC в точке O.
Найдите отрезки AО и CО.
Решение:

66. Решение

C
B
M
A
O
D
Рассмотрим
ΔAOM и ΔCОD
AOM = CОD
(вертикальные),
MAO = ОCD
(накрест лежащие
при AB || DC и
секущей AC).
Отсюда ΔAOM ~
ΔCОD
по двум углам.

67. Решение

C
B
M
A
O
D
AO OM AM
1
OC OD CD
2
.
AM = ½ AB (по условию)
AB = CD (ABCD параллелограмм),
AM : CD = 1 : 2
ΔAOM ~ ΔCОD
т.е. AO = 0,5CО
AO = ⅓AC = ⅓·90 = 30
CO = ⅔AC = ⅔·90 = 60
Решите задачи, отметьте нужные ячейки
А
1
2
3
4
5
Б
В
Г
1. По данным рисунка х равен
А) 7
7
Б) 14
В) 3,5
х
Г) 14/3
2) По данным рисунка периметр
ΔABC равен
В
А) 9
Б) 27
3
В) 36
2
А
4
Г) 18
С
3) По данным рисунка отрезок BC
равен
В
А) 3,75
3
Б) 7,5
3
В) 5
2,5
Г) 4,5
А
4
0,5
С
B
E
12
9
3
A
18
C
D
4
6
4) По данным рисунка площади данных
треугольников относятся
А) 3 : 1
Б) 9 : 1
В) 6 : 1
Г) 9 : 4
F
B
E
12
9
3
A
18
C
D
4
6
F
5) По данным рисунка прямые AB и DE
А) нельзя ответить
Б) пересекаются
В) параллельны
ОТВЕТЫ:
А
1
2
3
4
5
Б
В
Г

75.

Помощь в управлении презентацией• управление презентацией
осуществляется с помощью левой
клавиши мыши
• переход от одного слайда к другому и на
гиперссылки по одиночному щелчку
• завершение презентации при нажатии
кнопки выход
Возврат в содержание
Переход по слайдам
Возврат к гиперссылке
Справка

Как найти похожие фигуры?

Похожие цифры означают, что две фигуры имеют одинаковую форму, но разные размеры. В этом руководстве вы узнаете больше о поиске похожих фигур.

Две формы называются похожими, если обе имеют одинаковые свойства, но могут не совпадать. Например, солнце и луна могут казаться одного размера, но на самом деле они разных размеров.

Похожие темы

• Как найти похожие и конгруэнтные фигуры?

Пошаговое руководство по Поиск похожих фигур

В геометрии, когда две формы, такие как треугольник, многоугольник, четырехугольник и т. д., имеют общие размеры или пропорции, но отличаются по размеру или длине, они считаются похожими фигурами. . Например, два круга (любого радиуса) имеют одинаковую форму, но разные размеры, потому что они подобны. Посмотрите на картинку ниже.

Символ для обозначения одинаковых фигур — это тот же символ конгруэнтности, т. е. «\(∼\)», но точно так же он не означает одинакового размера. Когда отношения соответствующих сторон равны, фигуры считаются подобными, то есть при делении каждого набора длин соответствующих сторон полученное число является масштабным коэффициентом. Это число помогает увеличить или уменьшить размер фигур, но не по форме, оставляя их похожими на фигуры.

Подобие треугольников

Два треугольника будут подобны, если углы равны (соответствующие углы) и стороны в равной пропорции (соответствующие стороны). Подобные треугольники могут иметь разную длину сторон треугольников, но их углы должны быть равны и их соответствующее отношение длин сторон, или масштабный коэффициент должен быть одинаковым.

Если два треугольника подобны, это означает, что

• Все соответствующие пары углов треугольников равны.
• Все соответствующие стороны треугольников пропорциональны.

\(AA\) критерий сходства

Критерий сходства треугольников АА утверждает, что если три угла одного треугольника соответственно равны трем углам другого треугольника, то два треугольника будут подобны.

Рассмотрим следующий рисунок, на котором \(ΔABC\) и \(ΔDEF\) равноугольны, т.е. \(∠С = ∠F\)

Мы можем сказать, что эти треугольники подобны, используя критерий \(AA\).

\(SSS\) критерий подобия

\(SSS\) критерий подобия утверждает, что если три стороны треугольника пропорциональны трем другим сторонам треугольника соответственно, то два треугольника подобны. Это означает, что любая такая пара треугольников также будет равноугольной (все соответствующие пары углов равны).

Рассмотрим следующий рисунок, на котором стороны двух треугольников \(ΔABC\) и \(ΔDEF\) пропорциональны соответственно:

То есть дано, что:

\(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\)

\(SAS\) критерий подобия

Критерий подобия \(SAS\) утверждает, что если две стороны треугольника пропорциональны двум сторонам, соответствующим другому треугольнику, соответственно, и если углы между ними равны, то два треугольника подобны. Если равный угол не включен, то два треугольника могут быть не подобны. Рассмотрим следующий рисунок:

Дано, что:

\(\frac{AB}{DE}=\frac{AC}{DF}\)

\(∠A = ∠D\)

Критерий \(SAS\) говорит нам, что \(ΔABC ~ ΔDEF\).

Подобие многоугольников

Подобные многоугольники имеют одинаковую форму, но различаются по размеру. В подобных полигонах будут определенные одинаковые соотношения. Другими словами, соответствующие углы равны, но соответствующие стороны пропорциональны.

У подобных многоугольников есть два важных свойства:

• Соответствующие углы равны. (Внутренний и внешний углы одинаковы)
• Соотношение соответствующих сторон одинаково для всех сторон. Следовательно, периметры разные.

Четырехугольники — это многоугольники, имеющие четыре стороны. Сумма внутренних углов четырехугольника равна \(360\) градусов. Два четырехугольника подобны, если три соответствующих угла равны и две смежные стороны имеют равные отношения.

Поиск похожих фигур – Пример 1:

Рассмотрим следующий рисунок и найдем значение \(∠E\).

Сопоставьте самую длинную сторону с самой длинной стороной и самую короткую сторону с самой короткой стороной и проверьте все три соотношения:

• \(\frac{DE}{AB}=\frac{4.2}{6}=0.7\)
• \(\frac {DF}{AC}=\frac{2.8}{4}=0.7\)
• \(\frac{EF}{BC}=\frac{3.5}{5}=0.7\)

Таким образом, по \(SAS\) критерию подобия, \(ΔABC ~ ΔDEF\).

Это означает, что они также равноугольные. Обратите внимание, что равные углы будут следующими:

\(∠A = ∠D = 55,77°\)

\(∠C = ∠F = 82,82°\)

\(∠B = ∠E\)

Наконец,

\(∠E = ∠B = 180° – (55,77° + 82,82°)\)

\(∠E = 41,41°\)

Упражнения на нахождение подобных фигур

Каждая пара фигур подобна. Найдите недостающую сторону.

1. \(\color{blue}{100}\)
2. \(\color{blue}{9}\)
3. \(\color{blue}{12}\)

Похожие цифры — Подобие треугольников, определение, примеры

Похожие фигуры означают, что две фигуры одинаковой формы, но разных размеров. Другими словами, две фигуры называются подобными, когда они обе имеют много одинаковых свойств, но все же могут не быть идентичными. Например, солнце и луна могут казаться одинакового размера, но на самом деле они разные. Тем не менее, мы похожи, поскольку обе фигуры имеют круглую форму. Это явление рассматривается как свойство сходства с учетом формы и расстояния. Давайте узнаем больше об этом интересном понятии, определив подобные фигуры, их роль в геометрии и решив несколько примеров.

1.	Определение похожих фигур
2.	Применение подобных фигурок
3.	Подобие треугольников
4.	Подобие многоугольников
5.	Разница между сходством и соответствием
6.	Часто задаваемые вопросы по подобным фигуркам

Определение похожих фигур

Когда два или более объектов или фигур кажутся одинаковыми или равными из-за их формы, это свойство называется сходством или подобными фигурами. Когда мы увеличиваем или уменьшаем эти фигуры, они всегда накладываются друг на друга. В геометрии, когда две фигуры, такие как треугольники, многоугольники, четырехугольники и т. д., имеют одинаковую размерность или общее соотношение, но разные размеры или длину, они считаются похожими фигурами. Например, два круга (любого радиуса) имеют одинаковую форму, но разные размеры, потому что они подобны. Посмотрите на изображение ниже.

Символ для обозначения похожих фигур — это тот же символ конгруэнтности, т. е. «∼», но похожие не означают одинаковые по размеру. Формы также считаются подобными, когда отношения соответствующих сторон эквивалентны, т. Е. При делении каждого набора соответствующих длин сторон полученное число является масштабным коэффициентом. Это число помогает увеличивать или уменьшать фигуры по размеру, но не по форме, делая их похожими на фигуры. Например, прямоугольник имеет длину 5 единиц и ширину 2 единицы. Теперь, если мы увеличим размер этого прямоугольника с коэффициентом масштабирования 2, стороны станут равными 10 единицам и 4 единицам соответственно. Следовательно, мы можем использовать масштабный коэффициент, чтобы получить размеры измененных фигур.

Применение подобных фигурок

Ниже перечислены некоторые приложения с похожими или похожими цифрами.

• Подобие широко используется в архитектуре.
• Решение задач связано с высотой и расстоянием.
• Решение математических задач на треугольники.

Подобие треугольников

Два треугольника будут подобны, если углы равны (соответствующие углы) и стороны находятся в одинаковом соотношении или пропорции (соответствующие стороны). Подобные треугольники могут иметь разные индивидуальные длины сторон треугольников, но их углы должны быть равны, и их соответствующее отношение длин сторон или масштабный коэффициент должны быть одинаковыми. Если два треугольника подобны, значит,

• Все соответствующие пары углов треугольников равны.
• Все соответствующие стороны треугольников пропорциональны.

Поймем сходство треугольников с тремя теоремами по их углам и сторонам.

Критерий подобия AA

Критерий подобия треугольников AA утверждает, что если три угла одного треугольника соответственно равны трем углам другого, то два треугольника будут подобны. Короче говоря, равноугольные треугольники подобны. В идеале имя этого критерия должно быть критерием AAA (угол-угол-угол), но мы называем его критерием AA, потому что нам нужно, чтобы только две пары углов были равными — тогда третья пара автоматически будет равна критерию Свойство суммы углов треугольников.

Рассмотрим следующий рисунок, на котором ΔABC и ΔDEF равноугольны, т. е.

• ∠A = ∠D
• ∠В = ∠Е
• ∠С = ∠Ф

Используя критерий АА, мы можем сказать, что эти треугольники подобны.

Критерий подобия SSS

Критерий подобия SSS утверждает, что если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то эти два треугольника подобны. По сути, это означает, что любая такая пара треугольников также будет равноугольной (все соответствующие пары углов равны). Рассмотрим следующий рисунок, на котором стороны двух треугольников ΔABC и ΔDEF соответственно пропорциональны:

То есть дано, что:

\[\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}} = \frac{{AC}}{ {DF}}\]

Критерий подобия SAS

Критерий подобия SAS утверждает, что если две стороны одного треугольника соответственно пропорциональны двум соответствующим сторонам другого и если углы между ними равны, то два треугольника подобны. Обратите внимание на ударение на слове «включено». Если равный угол является невключенным углом, то два треугольника могут быть не подобны. Рассмотрим следующий рисунок:

Дано, что

\[\begin{align}& \frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} \end{align}\]

∠A = ∠D

Критерий SAS говорит нам, что ΔABC ~ ΔDEF

Сходство полигонов

Подобные многоугольники имеют одинаковую форму, но разные размеры. В подобных полигонах должны быть определенные одинаковые соотношения. Другими словами, соответствующие углы равны, но соответствующие стороны пропорциональны. Многоугольники — это двумерные фигуры, состоящие из прямых линий. Говорят, что они имеют замкнутую форму, так как все линии соединены. Есть два важных свойства подобных многоугольников:

• Соответствующие углы равны. (Внутренний и внешний углы одинаковые)
• Соотношение соответствующих сторон одинаково для всех сторон. Следовательно, периметры разные.

Четырехугольники — это многоугольники с четырьмя сторонами. Сумма внутренних углов четырехугольника равна 360 градусов. Два четырехугольника являются подобными четырехугольниками, когда три соответствующих угла одинаковы (четвертые углы автоматически становятся равными, поскольку сумма внутренних углов равна 360 градусам), а две смежные стороны имеют равные отношения.

Разница между сходством и соответствием

Слова сходство и конгруэнтность связаны с формой и размером в геометрии. Конгруэнтность означает одинаковую структуру, размер и форму, тогда как подобные фигуры означают одинаковую форму, но разный размер. Давайте посмотрим на разницу между обоими терминами.

Конгруэнтность	Подобие
Конгруэнтностью называют фигуры одинаковой формы и размера.	Под подобными или подобными фигурами понимаются фигуры одинаковой формы, но разных размеров.
Конгруэнтные фигуры равны по размеру и накладываются друг на друга. 2}\) Связанные темы Ниже перечислены несколько тем, связанных с похожими цифрами, взгляните. Геометрия расширения Теорема о сходстве треугольников ЦПКТС Внутренние углы с одной стороны Часто задаваемые вопросы по похожим фигуркам Как сходство используется в реальной жизни? Подобие используется при проектировании, решении задач на высоту и расстояние и т. д. Что такое правила сходства? Три правила сходства: сходство SSS, сходство SAS и сходство AA или AAA. Является ли SSA теоремой подобия? Нет, SSA не является теоремой подобия. Что такое заявление о сходстве? Когда два или более объектов или фигур кажутся одинаковыми или равными из-за их формы, это свойство называется сходством. Что такое теорема подобия SSS? Критерий подобия SSS утверждает, что если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то эти два треугольника подобны. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт