Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Поиск по сайту:
| Справочник по математике | Алгебра | Координатная плоскость |
| Гипербола на координатной плоскости |
| Примеры графиков дробно-линейных функций |
Гипербола на координатной плоскости
Определение 1. Гиперболой (равносторонней гиперболой) называют график функции
| (1) |
где k – любое, отличное от нуля, число.
Функция (1) обладает следующими свойствами:
- областью определения функции (1) является вся числовая ось за исключением точки x = 0, в которой знаменатель обращается в нуль;
- функция (1) является нечетной функцией, поскольку для всех значений аргумента выполнено равенство
- при k > 0 функция (1) убывает на интервале и на интервале ;
при k < 0 функция возрастает на интервале и на интервале ; - прямая x = 0 является вертикальной асимптотой графика функции (1), так как в формуле (1) при x = 0 знаменатель обращается в нуль;
- прямая y = 0 является горизонтальной асимптотой графика функции (1), так как в формуле (1) дробь (1) стремится к нулю, когда знаменатель стремится в бесконечность дробь (1) стремится к нулю, когда знаменатель стремится в бесконечность.

y (x) = – y (– x) ;
Рассмотрим теперь функцию, заданную формулой
| (2) |
где a, b, c, d – произвольные числа, а число c не равно нулю.
Определение 2. Дробно-линейной функцией называют функцию, заданную формулой (2), если дробь, стоящая в правой части формулы (2), несократима.
Графиком дробно–линейной функции является гипербола.
Примеры графиков дробно–линейных функций
| Функция | График |
Асимптоты: x = 0, y = 0. | |
Асимптоты: x = 0, y = 0. | |
Асимптоты: x = 2, y = 0. | |
Асимптоты: x = 2, y = 0. | |
Асимптоты: x = – 2, y = 0. | |
Асимптоты: x = – 1, y = 3. | |
Асимптоты: x = – 1, y = – 3. | |
Асимптоты: . |
Функция: Асимптоты: x = 0, y = 0. График: |
Функция: Асимптоты: x = 0, y = 0. График: |
Функция: Асимптоты: x = 2, y = 0. График: |
Функция: Асимптоты: x = 2, y = 0. График: |
Функция: Асимптоты: x = – 2, y = 0. График: |
Функция: Асимптоты: x = – 1, y = 3. График: |
Функция: Асимптоты: x = – 1, y = – 3. График: |
Функция: Асимптоты: . График: |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Гипербола и ее свойства, урок по алгебре в 8 классе, презентация
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Урок и презентация на тему: Гипербола и её свойства (PPTX)
Гипербола, определение
Ребята, сегодня мы с вами изучим новую функцию и построим ее график.
Рассмотрим функцию: $y=\frac{k}{x}$, $k≠0$.
Коэффициент $k$ – может принимать любые действительные значения, кроме нуля. Для простоты начнем разбор функции со случая, когда $k=1$.
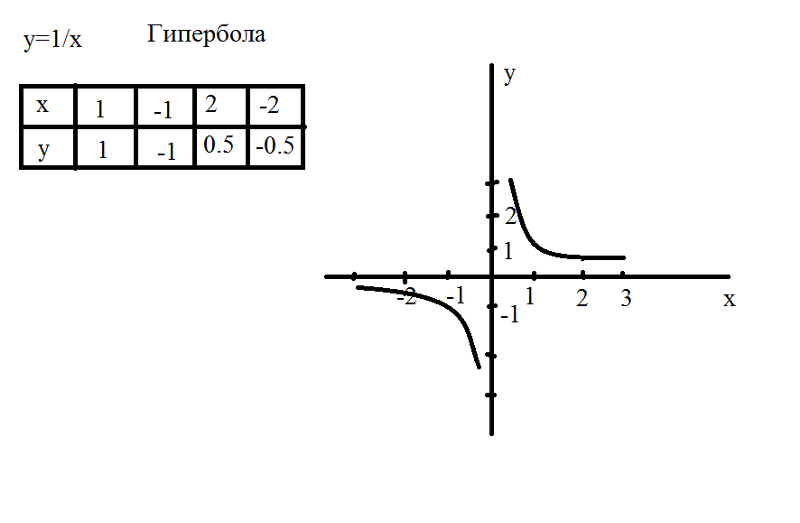
Построим график функции: $y=\frac{1}{x}$.
Как всегда начнем с построения таблицы. Правда в этот раз придется разделить нашу таблицу на две части.
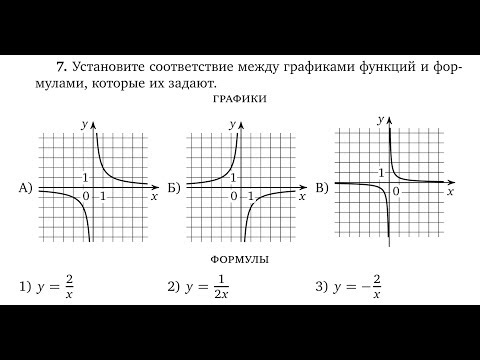 Рассмотрим случай, когда $x>0$.
Рассмотрим случай, когда $x>0$.Нам нужно отметить шесть точек с координатами $(x;y)$, которые приведены в таблице и соединить их линией.
График функции $y=\frac{1}{x}$.
График такой функции называется «Гиперболой».
Свойства гиперболы
Согласитесь, график выглядит довольно-таки красиво, и он симметричен относительно начала координат. Если провести любую прямую, проходящую через начало координат, из первой в третью четверть, то она пересечет наш график в двух точках, которые будут одинаково отдалены от начала координат.
Гипербола состоит из двух, симметричных относительно начала координат, частей. Эти части называются, ветвями гиперболы.
Ветви гиперболы в одном направлении (влево и вправо) все больше и больше стремятся к оси абсцисс, но никогда не пересекут ее. В другом направлении (вверх и вниз) стремятся к оси ординат, но также никогда не пересекут ее (так как на ноль делить нельзя).
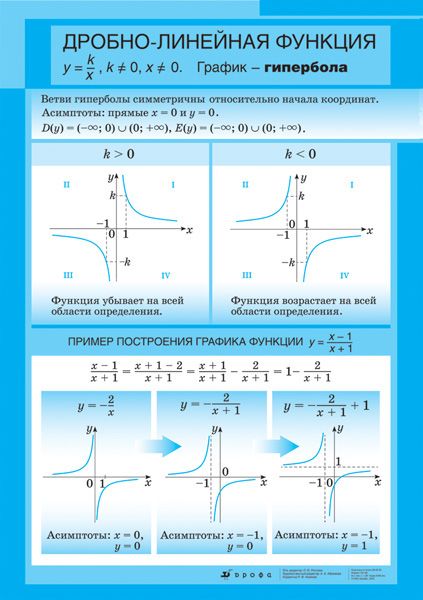 В таких случаях, соответствующие линии называются асимптотами. График гиперболы имеет две асимптоты: ось х и ось у.
В таких случаях, соответствующие линии называются асимптотами. График гиперболы имеет две асимптоты: ось х и ось у.У гиперболы есть не только центр симметрии, но и ось симметрии. Ребята, проведите прямую $y=x$ и посмотрите, как разделился наш график. Можно заметить, что если часть, которая расположена выше прямой $y=x$, наложить на часть, которая располагается ниже, то они совпадут, это и означает симметричность относительно прямой.
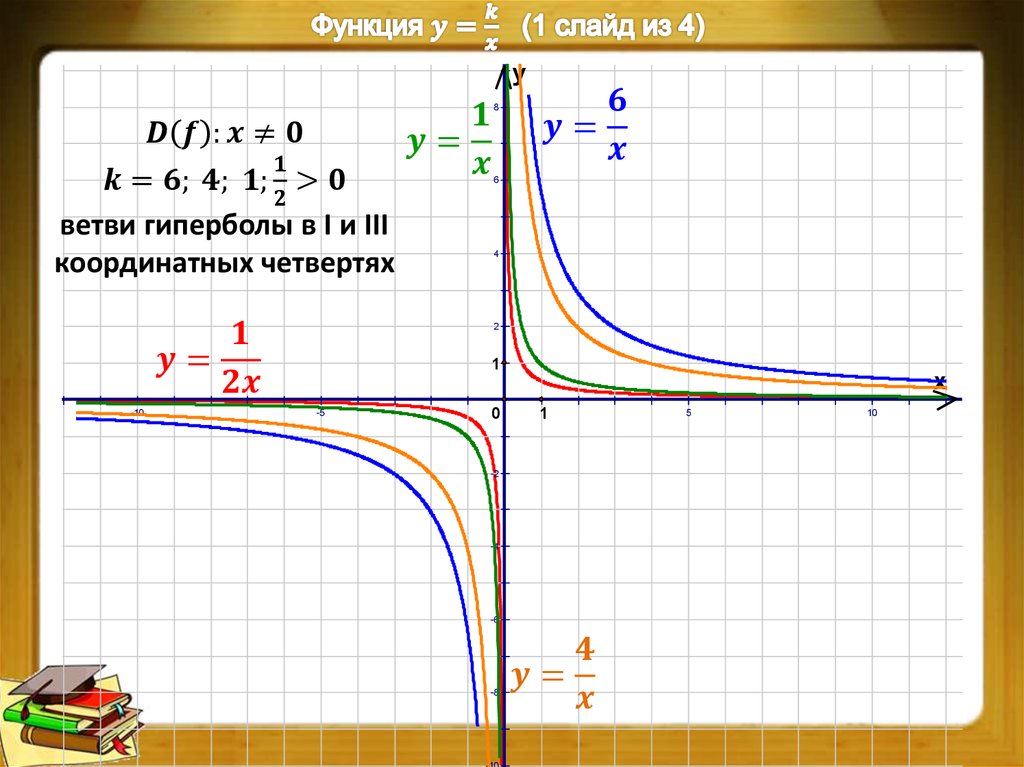
Мы построили график функции $y=\frac{1}{x}$, но что будет в общем случае $y=\frac{k}{x}$, $k>0$.
Графики практически не будут отличаться. Будет получаться гипербола с теми же ветвями, только чем больше $k$, тем дальше будут удалены ветви от начала координат, а чем меньше $k$, тем ближе подходить к началу координат.
Например, график функции $y=\frac{10}{x}$ выглядит следующим образом. График стал «шире», отдалился от начала координат.

Давайте воспользуемся этим свойством и построим график функции $y=-\frac{1}{x}$.
Обобщим полученные знания.
Графиком функции $y=\frac{k}{x}$, $k≠0$ является гипербола, расположенная в первой и третье (второй и четвертой) координатных четвертях, при $k>0$ ($k
Свойства функции $y=\frac{k}{x}$, $k>0$
1. Область определения: все числа, кроме $х=0$.
2. $y>0$ при $x>0$, и $y 3. Функция убывает на промежутках $(-∞;0)$ и $(0;+∞)$.
4. Функция не ограничена ни сверху, ни снизу.
5. Наибольшего и наименьшего значений нет.
6. Функция непрерывна на промежутках $(-∞;0)U(0;+∞)$ и имеет разрыв в точке $х=0$.
7. Область значений: $(-∞;0)U(0;+∞)$.
Свойства функции $y=\frac{k}{x}$, $k
1. Область определения: все числа кроме $х=0$.
2. $y>0$ при $x0$.
3. Функция возрастает на промежутках $(-∞;0)$ и $(0;+∞)$.
4. Функция не ограничена ни сверху, ни снизу.
5. Наибольшего и наименьшего значений нет.
6. Функция непрерывна на промежутках $(-∞;0)U(0;+∞)$ и имеет разрыв в точке $х=0$.
7. Область значений: $(-∞;0)U(0;+∞)$.
Алгебра — Гипербола
Онлайн-заметки Пола
Главная
/
Алгебра
/
Общие графики
/ Гиперболы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4.4: Гиперболы
Следующим графиком, на который нам нужно взглянуть, является гипербола. Существуют две основные формы гиперболы. Вот примеры каждого.
Гиперболы состоят из двух частей в форме параболы, которые открываются либо вверх и вниз, либо вправо и влево. Кроме того, как и в случае с параболой, каждая часть имеет вершину. Обратите внимание, что на самом деле это не параболы, они просто напоминают параболы.
На каждом графике также две линии. Эти линии называются асимптотами, и, как показывают графики, по мере того, как мы делаем \(x\) большими (как в положительном, так и в отрицательном смысле), график гиперболы становится все ближе и ближе к асимптотам. Асимптоты официально не являются частью графика гиперболы. Тем не менее, они обычно включаются, чтобы мы могли убедиться и получить правильный эскиз. Точка пересечения двух асимптот называется центром гиперболы. 92}}} = 1\)
Обратите внимание, что разница между двумя формами заключается в том, какой член имеет знак минус. Если член \(y\) стоит со знаком минус, то гипербола будет открываться влево и вправо. Если член \(x\) стоит со знаком минус, то гипербола будет открываться вверх и вниз. 92}}}{{49}} = 1\) Показать решение
Если член \(y\) стоит со знаком минус, то гипербола будет открываться влево и вправо. Если член \(x\) стоит со знаком минус, то гипербола будет открываться вверх и вниз. 92}}}{{49}} = 1\) Показать решение
Теперь обратите внимание, что член \(y\) имеет знак минус, и поэтому мы знаем, что находимся в первом столбце таблицы выше и что гипербола будет раскрываться влево и вправо.
Первое, что мы должны получить, это центр, так как почти все остальное строится вокруг него. Центр в данном случае это \(\left( {3, — 1} \right)\) и как всегда следите за знаками! Когда у нас есть центр, мы можем получить вершины. Это \(\left( {8, — 1} \right)\) и \(\left( { — 2, — 1} \right)\).
Далее мы должны получить наклоны асимптот. Это всегда квадратный корень числа под термином \(y\), деленный на квадратный корень числа под термином \(x\), и всегда будет положительный и отрицательный наклон. Тогда наклоны равны \( \pm \frac{7}{5}\).
Теперь, когда у нас есть центр и наклоны асимптот, мы можем получить уравнения для асимптот.
\[y = — 1 + \frac{7}{5}\left( {x — 3} \right)\hspace{0,25 дюйма}{\mbox{and}}\hspace{0,25 дюйма}y = — 1 — \frac{7}{5}\left( {x — 3} \right)\] 92} = 1\) Показать решение
В этом случае гипербола будет открываться вверх и вниз, так как член \(x\) имеет знак минус. Теперь центр этой гиперболы равен \(\left( { — 2,0} \right)\). Помните, что поскольку существует сам по себе терм y 2 , мы должны были иметь \(k = 0\). На данный момент мы также знаем, что вершинами являются \(\left( { — 2,3} \right)\) и \(\left( { — 2, — 3} \right)\).
Чтобы увидеть наклоны асимптот, немного перепишем уравнение. 92}}}{1} = 1\]
Итак, наклоны асимптот равны \( \pm \frac{3}{1} = \pm 3\). Тогда уравнения асимптот будут такими:
\[y = 0 + 3\left( {x + 2} \right) = 3x + 6\hspace{0,25 дюйма}{\mbox{and}}\hspace{0,25 дюйма}\,\,y = 0 — 3 \влево( {х + 2} \вправо) = — 3х — 6\]
Вот эскиз этой гиперболы.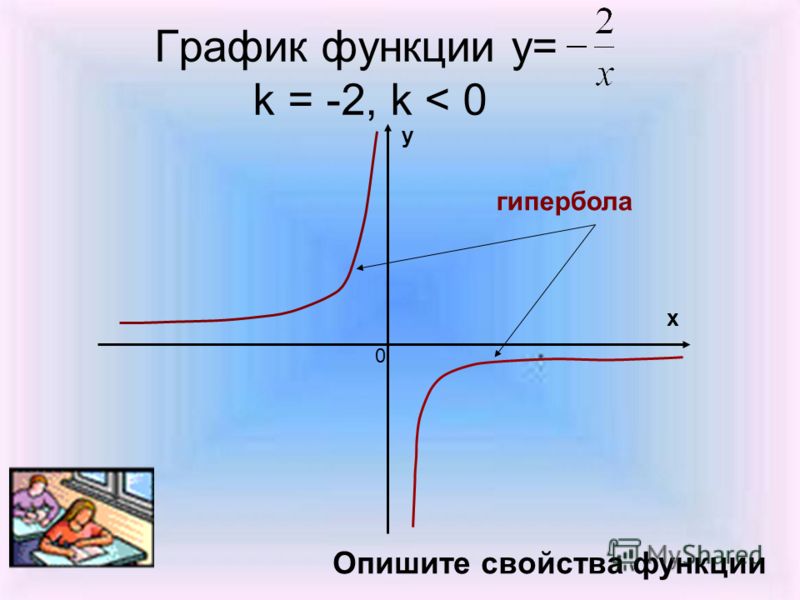
Определение и значение гиперболы — Merriam-Webster
hy·per·bo·la hī-ˈpər-bə-lə
: плоская кривая, образованная точкой, движущейся так, что разница расстояний от двух фиксированных точек является постоянной : кривая, образованная пересечением двойного прямого кругового конуса с плоскостью, пересекающей обе половины конуса
Иллюстрация гиперболы
- AB
- оси CD; Ф
- F’ очаги; ху
- zw асимптоты; ч
- ч’
- ч″
- h»’ гипербола
Примеры предложений
Недавние примеры в Интернете
Клэра Чонг может изобразить гиперболой , но не может выписать чек. Карина Блэнд, Республика Аризона , 22 апр. 2021 г.
Та же взаимосвязь между денежными агрегатами и стоимостью валюты (гипербола для тех, кто помнит геометрию) применима к другим странам с развитой экономикой и к другим денежным показателям, таким как денежная масса М2.
Дуглас Карр, National Review , 14 сентября 2020 г.
Графиками таких кривых являются конические сечения — окружности, параболы, эллипсы и гипербол . Журнал Quanta , 9 июля 2013 г.
По словам Гуруле, курс не охватывает некоторые уроки по кругам, гиперболам и эллипсам, но эти темы больше относятся к предварительному исчислению.
Шайна Кавазос, The Atlantic , 9 февраля 2018 г.
Облака никогда не бывают сферами, горные конусы и пондерозовые сосны;
кора не гладкая; и где земля и море
так разнообразно врут друг о друге
и слегка поцелуй, нет гипербола .
Карина Блэнд, Республика Аризона , 22 апр. 2021 г.
Та же взаимосвязь между денежными агрегатами и стоимостью валюты (гипербола для тех, кто помнит геометрию) применима к другим странам с развитой экономикой и к другим денежным показателям, таким как денежная масса М2.
Дуглас Карр, National Review , 14 сентября 2020 г.
Графиками таких кривых являются конические сечения — окружности, параболы, эллипсы и гипербол . Журнал Quanta , 9 июля 2013 г.
По словам Гуруле, курс не охватывает некоторые уроки по кругам, гиперболам и эллипсам, но эти темы больше относятся к предварительному исчислению.
Шайна Кавазос, The Atlantic , 9 февраля 2018 г.
Облака никогда не бывают сферами, горные конусы и пондерозовые сосны;
кора не гладкая; и где земля и море
так разнообразно врут друг о друге
и слегка поцелуй, нет гипербола .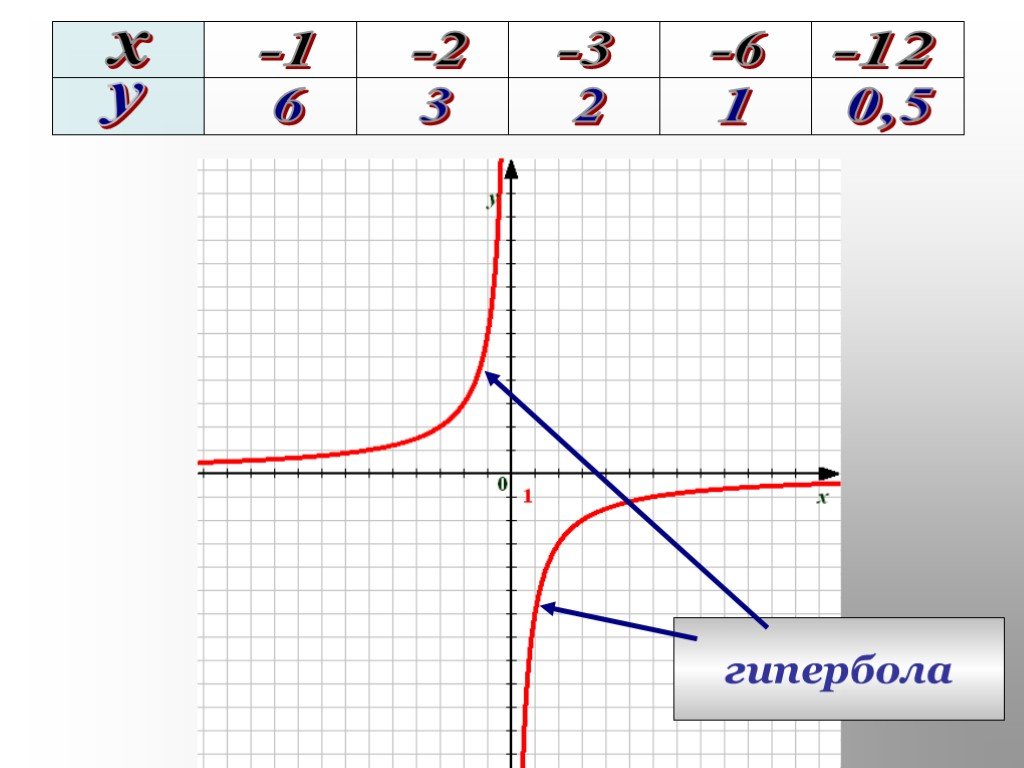 Эвелин Лэмб, Smithsonian , 24 апреля 2018 г.
Эвелин Лэмб, Smithsonian , 24 апреля 2018 г.
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «гипербола». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Этимология
Новая латынь, от греческого гипербола
Первое известное использование
1668, в значении, определенном выше
Путешественник во времени
Первое известное использование гиперболы было
в 1668 г.
Посмотреть другие слова того же года
Словарные статьи Около
гиперболагипербатон
гипербола
гипербола
Посмотреть другие записи поблизости
Процитировать эту запись «Гипербола».
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/hyperbola. По состоянию на 11 декабря 2022 г.Copy Citation
Еще от Merriam-Webster о гиперболе
Britannica.com: Энциклопедическая статья о гиперболе
Подпишитесь на крупнейший словарь Америки и получите тысячи других определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
наполнять
См.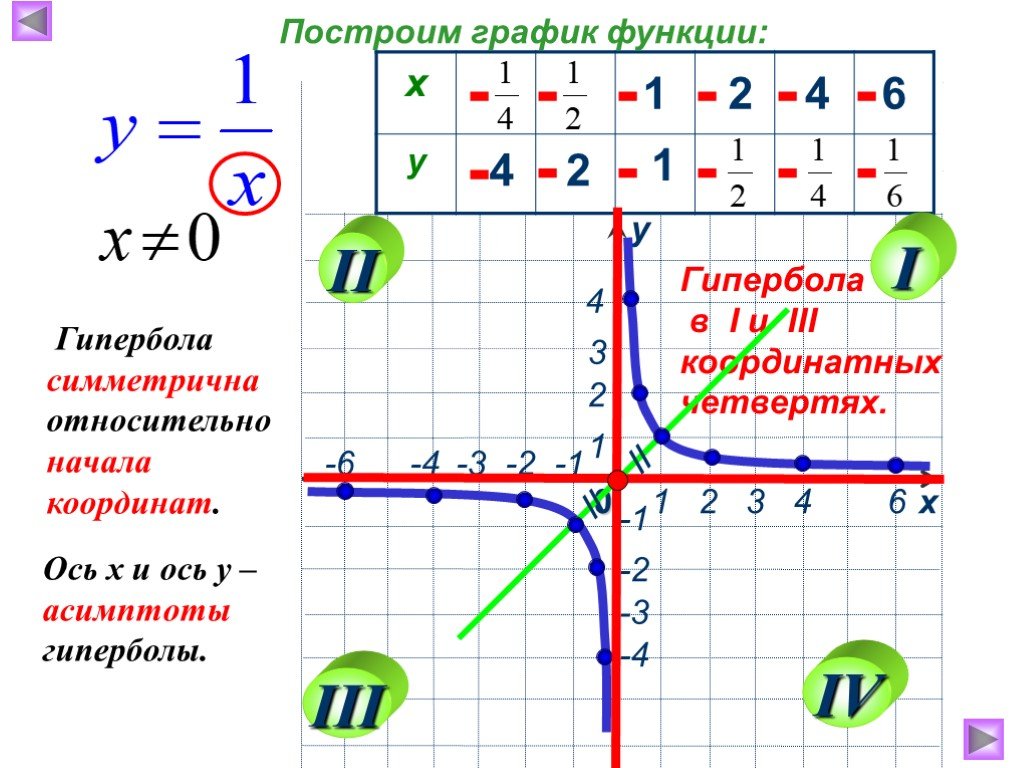


 Самаров
Самаров