Математический Калькулятор С Решением APK (Android App)
Вы не знаете как решать уравнения? Вы боитесь решать уравнения с дробями? Вы боитесь решить уравнение? Не позволяйте математике быть вашей одержимостью, используйте наше дифференциальные уравнения калькулятор приложение, чтобы решить свой страх. Наше калькулятор дробей с решением приложение поможет решить сложные математические задачи всего за 3 секунды с подробным описанием. Вы вряд ли найдете такое замечательное приложение чтобы решать уравнения.
⏩ Наше калькулятор математический приложение может решить множество проблем:
⋆ Уравнение
⋆ Система уравнения
⋆ Калькулятор дробей и десятичных
⋆ Интегралы калькулятор с решением
⋆ Производные
⋆ Алгебра калькулятор
⋆ Ограничения
⋆ Тригонометрия калькулятор
⋆ Логарифмы калькулятор
Кроме того, калькулятор решение уравнения приложение предоставляет некоторые примеры расчетов с тремя уровнями сложности, вы можете изучить и найти для себя самое быстрое решение.
⏩Как использовать уравнения калькулятор приложение:
После того, как вы загрузили уравнения решать приложение из магазина приложений, вы можете начать решать математику. Вам нужно ввести расчет, а затем выбрать решите неравенство в правом нижнем углу или выбрать рисунок в левом нижнем углу. Приложение математический калькулятор с решением даст вам ответ в течение 3 секунд, вы можете выбрать, если хотите, подробное решение.
⏩Выделение калькулятор графический приложения:
• Быстрое и точное решение
• Подробное пошаговое решение уравнений
• Простое понимание, интуитивное математическое решение
• Дайте разные решения
• Интегрированная функция графика
• Удерживайте несколько клавиш, чтобы добавить параметры.
• Поделитесь решением с друзьями
• Удобный интерфейс калькулятор тригонометрия приложения, простой в решить неравенство
• Малая емкость калькулятор логарифмы приложения, быстрая загрузка
Вы тратите много денег на покупку калькулятора, который поможет вам разобраться в результатах, но не решает сложные вычисления.
Тогда почему бы не использовать наше бесплатное дифференциальные уравнения решатель приложение для решения сложных расчетов. Приложение математика тригонометрия поможет вам решить самые сложные и сложные вычисления за очень короткое время.
Не позволяйте математике стать страхом в вашей школе, превратите ее в любимую с нашим математика производные приложением. Используя это математический решатель приложение, вы можете стать математиком, который решает сложные математические задачи в мгновение ока.
Если у вас есть какие-либо вопросы по поводу пошаговый решатель приложения, оставьте комментарий ниже. И не забудьте представить это системные уравнения приложение своим друзьям, чтобы они могли легко решить проблему.
Оцените 5⭐ уравнения с решением, чтобы поддержать усилия разработчика!
Подробнее…
Решение показательных уравнений. Видеоуроки
В этой статье вы познакомитесь со всеми типами показательных уравнений и алгоритмами их решения, научитесь распознавать, к какому типу принадлежит показательное уравнение, которое вам надо решить, и применять для его решения соответствующий метод.
Подробное решение примеров показательных уравнений каждого типа вы сможете посмотреть в соответствующих ВИДЕОУРОКАХ.
Показательным уравнением называется уравнение, в котором неизвестное содержится в показателе степени.
Прежде чем начать решать показательное уравнение, полезно сделать несколько предварительных действий, которые могут значительно облегчить ход его решения. Вот эти действия:
1. Разложите все основания степеней на простые множители.
2. Корни представьте в виде степени.
3. Десятичные дроби представьте в виде обыкновенных.
4. Смешанные числа запишите в виде неправильных дробей.
Пользу этих действий вы осознаете в процессе решения уравнений.
Рассмотрим основные типы показательных уравнений и алгоритмы их решения.
1. Уравнение вида
Это уравнение равносильно уравнению
Посмотрите в этом ВИДЕОУРОКЕ решение уравнения этого типа.
2. Уравнение вида
В уравнениях этого типа:
а) все степени имеют одинаковые основания
б) коэффициенты при неизвестном в показателе степени равны.
Пример решения уравнения этого типа:
посмотрите в ВИДЕОУРОКЕ.
3. Уравнение вида
Уравнения этого типа отличаются тем, что
а) все степени имеют одинаковые основания
б) коэффициенты при неизвестном в показателе степени разные.
Уравнения такого типа решаются с помощью замены переменных. Прежде чем вводить замену, желательно освободиться от свободных членов в показателе степени. (, , и т.д)
Посмотрите в ВИДЕОУРОКЕ решение уравнения этого типа:
youtube.com/embed/gxrmusJuW-w?rel=0″ frameborder=»0″ allowfullscreen=»»>
4. Однородные уравнения
видаОтличительные признаки однородных уравнений:
а) все одночлены имеют одинаковую степень,
б) свободный член равен нулю,
в) в уравнении присутствуют степени с двумя различными основаниями.
Однородные уравнения решаются по сходному алгоритму.
Чтобы решить уравнение такого типа, разделим обе части уравнения на (можно разделить на или на )
Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
В нашем случае, поскольку выражение не равно нулю ни при каких значениях неизвестного, мы можем делить на него без опаски. Разделим левую часть уравнения на это выражение почленно. Получим:
Сократим числитель и знаменатель второй и третьей дроби:
Введем замену:
, причем при всех допустимых значениях неизвестного.
Получим квадратное уравнение:
Решим квадратное уравнение, найдем значения , которые удовлетворяют условию , а затем вернемся к исходному неизвестному.
Смотрите в ВИДЕОУРОКЕ подробное решение однородного уравнения:
5. Уравнение вида
При решении этого уравнения будем исходить из того, что
Исходное равенство выполняется в двух случаях:
1. Если , поскольку 1 в любой степени равна 1,
или
2. При выполнении двух условий:
Посмотрите в ВИДЕОУРОКЕ подробное решение уравнения
И.В. Фельдман, репетитор по математике.
Решение уравнения: определение, понятия и примеры решения
- Автор Рачана
- Последнее изменение 14-11-2022
Решение уравнения: Математическое уравнение — это утверждение, что два выражения равны.
4 + 4=8 – это математическое выражение. Алгебраическое уравнение — это математическая формула, которая имеет одну или несколько переменных. В результате (2x + 5 = 35) представляет собой линейное уравнение с одной переменной. Он имеет переменную первой степени (x), а его график представляет собой прямую линию.
Решение уравнения — это процесс определения числа, которое представляет переменная. Полученное значение называется решением уравнения. Математический язык, который утверждает, что два алгебраических выражения должны быть равны по своей природе, известен как уравнение.
Решение уравнения – это массив всех значений, замена которых на неизвестные делает уравнение верным. Для уравнений, требующих одного неизвестного, возведенного в степень один, для определения их решений используются два основных правила алгебры, включающие свойство аддитивности и свойство мультипликативности.
Решение уравнения примечания поясняются ниже:
Методы решения линейного уравнения с одной переменной 1.
Метод транспонирования для решения линейных уравнений с одной переменной
2. Крест. -метод умножения для решения линейного уравнения с одной переменной
Иногда две части уравнения содержат переменную (неизвестную величину) и константу (числа). В таких случаях мы сначала упрощаем две стороны в их простейших формах, а затем транспонируем (сдвигаем) члены, содержащие переменные на \(RHS\) в \(LHS\) и постоянные члены на \(LHS\) в \(RHS\). под переносом термина из одной стороны в другую мы имеем в виду смену его знака и перенос его на другую сторону.
Метод перестановки включает следующие шаги:
Шаг I: Получите линейное уравнение.
Шаг II: Распознайте переменные и константы.
Шаг III: Сократите \(левая\) и \(правая\) до их наиболее простой формы, удалив скобки.
самая основная форма, так что каждая сторона содержит только один член. Шаг VI: Решите уравнение, полученное на шаге \(V\), разделив две части на коэффициент при переменной \(LHS.\)
Например, \(3x + 3 = 2x + 4\)
\( \Стрелка вправо 3x – 2x = 4 – 3 \Стрелка вправо x = 1\)
Метод перекрестного умножения для решения линейного уравнения с одной переменной
Процедура умножения числителя в \(левой части\) на знаменатель в \(правой части\) и приравнивания его к произведению общего знаменателя в \(левой части\) на числитель в \(правой части\) называется кросс- умножение.
\(\frac{{ax + b}}{{cx + d}} = \frac{m}{n}\)
в линейное уравнение \(n\left({ax + b} \right) = m\left({cx + d} \right.
)\) Например, \(\ frac{{x + 1}}{{2x + 3 }} = \frac{2}{3}\)
Ответ: \(3\left({x + 1} \right) = 2\left({2x + 3} \right)\)
\( \Rightarrow 3x + 3 = 4x + 6\)
\( \Стрелка вправо x = – 3\) Правила решения линейных уравнений с одной переменной
Решить уравнение означает найти его корни, т. е. определить значение переменной, которое ему удовлетворяет.
Правила решения линейных уравнений с одной переменной: Правило 1: К обеим частям уравнения можно добавить одну и ту же величину без изменения равенства.
Правило 2: Одна и та же величина может быть вычтена из любой части уравнения без изменения равенства.
Правило 3: Обе части уравнения можно умножить на одинаковое ненулевое число без изменения равенства.
Правило 4: Обе части уравнения можно разделить на одинаковое ненулевое число без изменения равенства.
Следует отметить, что некоторые сложные уравнения можно решить, используя два или более этих правил вместе.
Например, \(\frac{{2x}}{3} + 2 = \frac{3}{2}\)
Ответ: \(\frac{{2x}}{3} + 2 – 2 = \ frac{3}{2} – 2\) (вычитая обе стороны на \(2\))
\( \Стрелка вправо \frac{{2x}}{3} = \frac{{3 – 4}}{2}\)
\( \Стрелка вправо \frac{{2x}}{3} \times 3 = \ frac{{ – 1}}{2} \times 3\) (Умножая обе части на \(3\))
\( \Стрелка вправо 2x = \frac{{ – 3}}{2}\)
\( \Rightarrow \frac{{2x}}{2} = \frac{{ – 3}}{4}\) (делим обе стороны на \(2\))
\( \Rightarrow x = \frac{{ – 3}}{4}\)
В этом разделе мы рассмотрим постановку и решение некоторых практических задач. Эти задачи связаны с отношениями между неизвестными величинами, а числа часто задаются словами.
Чтобы найти решение задачи со словами, необходимо выполнить следующие шаги:
Шаг I: Внимательно прочтите задачу и отметьте, что дано и что требуется.
Шаг II: Обозначьте неизвестную величину определенными буквами, скажем \(x,y,z,\) и т. д.
Шаг III: Переведите формулировку задачи в математические слова.
Шаг IV: При использовании условия (условий), представленных в задаче, сформируйте уравнение.
Шаг V: Решите уравнение для неизвестного.
Шаг VI: Проверьте, удовлетворяет ли решение уравнению.
Например,
Рави теперь на \(7\) лет старше Махеша. Если сумма их возрастов равна \(33\) лет, найдите возраст каждого из них.
Ответ: Пусть возраст Махеша \( = x\) лет
Тогда возраст Рави \( = \) возраст Махеша \( + 7 = \left({x + 7} \right)\) лет
Согласно задаче, Возраст Рави \( + \) Возраст Махеша \(= 33.\) т.е. \(x + \left({x + 7} \right) = 33\)
\(\Стрелка вправо 2x + 7 = 33 \Стрелка вправо 2x = 26 \Стрелка вправо x = 13\)
Следовательно, возраст Махеша \(= 13\) лет, возраст Рави \(= 20\) лет.
Непротиворечивая система: Система одновременных линейных уравнений непротиворечива, если она имеет хотя бы одно решение.
1. При \(\frac{{{a_1}}}{{{a_2}}} \ne \frac{{{b_1}}}{{{b_2}}},\) мы получаем единственное решение . В этом случае две линии, представляющие уравнения, пересекаются друг с другом.
2. Когда \(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} = \frac{{{c_1}}}}{ {{c_2}}},\) решений бесконечно много. В этом случае две линии, представляющие уравнения, перекрывают друг друга.
Несовместная система: Система одновременных линейных уравнений считается несовместной, если она не имеет решения.
1. Когда \(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}} }{{{c_2}}},\) решения нет. В этом случае две линии, представляющие уравнения, параллельны друг другу.
Говорят, что пара линейных уравнений с двумя переменными образует одновременные линейные уравнения.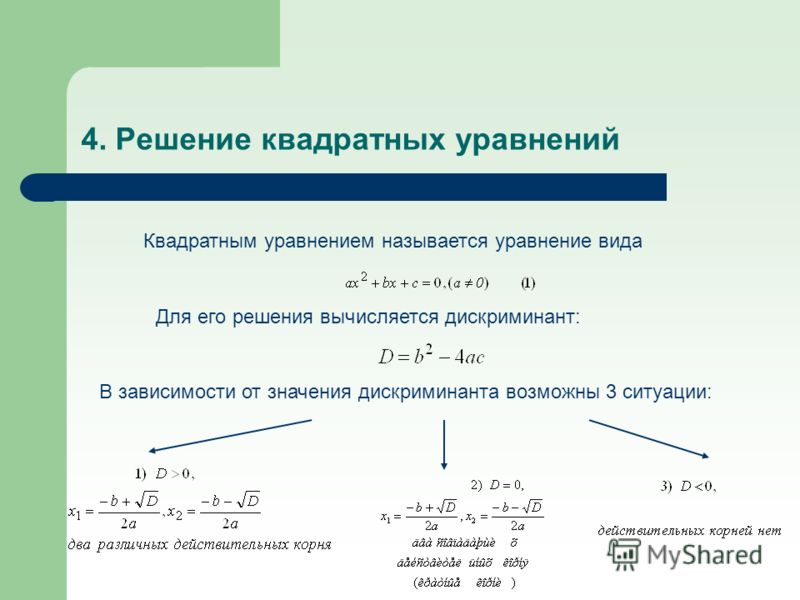
Пара значений переменных \(х\) и \(у\), удовлетворяющая каждому из уравнений каждой системы двух одновременных линейных уравнений относительно \(х\) и \(у\), называется решением уравнения система.
Наиболее часто используемые алгебраические методы решения одновременных линейных уравнений с двумя переменными:
1. Метод устранения путем замены.
2. Метод исключения приравниванием коэффициентов.
3. Метод перекрестного умножения.
Метод исключения путем замены: В этом методе мы выражаем одну из переменных через другую переменную из каждого из двух уравнений. Это выражение подставляется в другое уравнение, чтобы получить уравнение с одной переменной, как поясняется в следующем алгоритме.
Шаг I: Получите два уравнения.
Пусть уравнения будут \({a_1}x + {b_1}y + {c_1} = 0 — — — (1)\) и \({a_2}x + {b_2}y + {c_2} = 0 — — – (2)\)
Шаг II: Выберите любое из двух уравнений, скажем, \(\left( 1 \right)\) и найдите значение одной переменной, скажем, \(y,\) через другое, т.
е. \(x.\)
Шаг III: Подставить значение \(y,\), полученное на шаге \(II,\), в другое уравнение, т.е. \(\left( 2 \right), \), чтобы получить уравнение в \(x.\)
Шаг IV: Решите уравнение, полученное в шаге \(III\), чтобы получить значение \(x.\)
Шаг V: Подставьте значение \(x\), полученное на этапе \(IV\), в выражение для \(y\) через \(x\), полученное на этапе \(II\), чтобы получить значение \(у.\)
Шаг VI: Значения \(х\) и \(у\), полученные на этапах \(IV\) и \(V,\) соответственно, составляют решение задачи заданная система двух линейных уравнений.
В этом методе мы удаляем одну из двух переменных, чтобы получить уравнение с одной переменной, которое можно легко решить. Затем, подставляя значение этой переменной в любое из указанных уравнений, можно получить значение другой переменной.
Следующий алгоритм объясняет процедуру.
Шаг I: Получите два уравнения.
Шаг II: Умножьте уравнения, чтобы коэффициенты переменной исключались одинаково.
Шаг III: Сложите или вычтите уравнения, полученные на шаге \(II\), в соответствии с условиями, имеющими одинаковые коэффициенты, противоположного или одного знака.
Шаг IV: Решить уравнение с одной переменной, полученное на шаге \(III.\)
Шаг V: Подставить найденное на шаге \(IV\) значение в любое из данных уравнений и найти значение другой переменной.
Значения переменных в шагах \(IV\) и \(V\) образуют решение системы уравнений.
Например,
Найдите \(x\) и \(y,\) в \(2x + 3y = 5\) и \(3x – y = 0\)
Ответ: пусть \(2x + 3y = 5 – – – (1)\) и \(3x – y = 0 – – – (2)\)
Теперь, умножая уравнение \(\left( 2 \right)\) на \(3,\) получаем получить \(9x – 3y = 0 – – – – – \left( 3 \right)\)
Добавив уравнение \(\left( 1 \right)\) и \(\left( 3 \right)\), мы имеем \(2x + 3y + \left({9x – 3y} \right) = 5\)
\( \Rightarrow 11x = 5 \Rightarrow x = \frac{5}{{11}}\) Тогда \( 3 \times \frac{5}{{11}} – y = 0 \Rightarrow y = \frac{{15}}{{11}}\)
Следовательно, \(x = \frac{5}{{11}}\) и \(y = \frac{{15}}{{11}}.
\)
Пусть \({a_1}x + {b_1}y + {c_1} = 0\) и \({a_2}x + {b_2}y + {c_2} = 0\) — система одновременных линейных уравнений с двумя переменными \(x\) и \(y.\)
Чтобы найти решения, используя метод перекрестного умножения, мы имеем,
\(x = \frac {{\left({{b_1}{c_2} – {b_2}{c_1 }} \right)}}{{\left({{a_1}{b_2} – {a_2}{b_1}} \right)}}\) и \(y = \frac{{\left({{c_1}) {a_2} – {c_2}{a_1}} \right)}}{{\left({{a_1}{b_2} – {a_2}{b_1}} \right)}}\) 92} + bx + c = 0,\), где \(a,b,c \in R\) и \(a \ne 0.\)
Корни квадратного уравнения: Пусть \(p\left ( x \right) = 0\) — квадратное уравнение, то корни функции \(p\left( x \right)\) называются корнями уравнения \(p\left( x \right) = 0.\)
Таким образом, \(x = k\) является корнем \(p\left( x \right) = 0\) тогда и только тогда, когда \(p\left( k \right) = 0.\ )
Нахождение корней квадратного уравнения известно как решение квадратного уравнения.
92} + ax} \right) + (bx + q)\) и вынесите в каждой скобке общие множители.
Как найти \(a\) и \(b:\)
\(p\) будет разбит на \(a\) и \(b\) таким образом, что \(p = a + b\) и \(q = a \times b\)
Если знак \(q\) положителен, то оба множителя \(a\) и \(b\) из \(q\) будут иметь знак такой же, как у \(p,\), т. е. если \(p\) положительно, то и \(a\), и \(b\) будут положительными, но если \(p\) отрицательно, тогда и \(a\), и \(b\) будут отрицательными.
Если \(q\) отрицательно, то найти \(\left| q \right|\) (числовое значение \(q \)), тогда численно больший множитель \(q\) будет иметь тот же знак, что и знак \(p,\) и меньшего множителя будет иметь знак, противоположный знаку \(p.\) 92} – 4 \times 1 \times \left({ – 1} \right)} }}{{2 \times 1}}\)
\(\Rightarrow x = \frac{{ – 1 \pm \sqrt 5 }}{2}\)
\( \Rightarrow x = \frac{{ – 1 + \sqrt 5 }}{2}\) или \(x = \frac{{ – 1 – \sqrt 5 }}{2 }\)
Следовательно, корни данного квадратного уравнения равны \(x = \frac{{ – 1 + \sqrt 5 }}{2}\) и \(x = \frac{{ – 1 – \sqrt 5 }}{2.}\) Решение квадратного уравнения методом заполнения квадратов
Мы можем использовать следующий алгоритм для получения корней квадратного уравнения методом заполнения квадратов.
92}}}} \)
Шаг VII: Получите значения \(x\) сдвигом постоянного члена \(\frac{b}{{2a}}\) на \(RHS.\)
Q.1. Решите \(2\влево({5x — 2} \вправо) = 4x + 8.\)
Ответ: Данное уравнение имеет вид \(2\влево({5x — 2} \вправо) = 4x + 8\)
\( \Стрелка вправо 10x — 4 = 4x + 8\)
\( \Стрелка вправо 10x — 4x = 8 + 4\)
\( \Стрелка вправо 6x = 12\)
\( \Стрелка вправо x = 2\)
Следовательно, значение \(x\) равно \(2.\)
Q.2. Решите \(\frac{{7y + 2}}{5} = \frac{{6y – 5}}{{11}}\)
Ответ: Данное уравнение имеет вид \(\frac{ {7y + 2}}{5} = \frac{{6y – 5}}{{11}}\)
\( \Стрелка вправо 11\left({7y + 2} \right) = 5\left({6y – 5} \right)\)
\( \Стрелка вправо 77y + 22 = 30y – 25\)
\( \Стрелка вправо 77y – 30y = – 25 – 22\)
\( \Стрелка вправо 47y = – 47\) 92} = \frac{{19}}{{25}}\)
\(\Стрелка вправо x – \frac{3}{5} = \pm \frac{{\sqrt {19} }}{5}\ )
\( \Rightarrow x = \frac{3}{5} \pm \frac{{\sqrt {19}}}}{5} = \frac{{3 \pm \sqrt {19}}}}{5} \)
\( \Rightarrow x = \frac{{3 + \sqrt {19} }}{5}\) или \(x = \frac{{3 – \sqrt {19} }}{5}\)
Следовательно, корни данного уравнения равны \(x = \frac{{3 + \sqrt {19} }}{5}\) и \(x = \frac{{3 – \sqrt {19} }} {5.
}\)
Q.4. Решите следующую систему линейных уравнений \(x – y = 1\) и \(2x + y = 8.\)
Ответ: Пусть \(x – y = 1 – – – (1)\) и \(2x + y = 8 – – – (2 )\)
Из уравнения \(\left( 1 \right),\) путем решения значения \(x\) через \(y,\) имеем
\(x = 1 + y – – – (3 )\)
Подставив уравнение \(\left( 3 \right)\) в уравнение \(\left( 2, \right)\) получим
\(2\left({1 + y} \right) + y = 8\)
\( \Стрелка вправо 2 + 2y + y = 8\)
\( \Стрелка вправо 3y = 6\)
\( \Стрелка вправо y = 2\)
Подставив \(y = 2\) в уравнение \(\left( 3, \right)\) получаем 92} = 0\)
\(\Стрелка вправо \влево({x + 3} \вправо)\влево({x – 3} \вправо) = 0\)
\(\Стрелка вправо \влево({x + 3} \right) = 0\) или \(\left({x – 3} \right) = 0\)
\( \Rightarrow x = – 3\) или \(x = 3\)
Таким образом, \(x = 3\) и \(x = -3\) являются корнями данного уравнения.
Вы можете использовать математические уравнения для решения уравнения или системы уравнений.
Уравнение — это утверждение, в котором утверждается, что два выражения равны. В подавляющем большинстве случаев можно найти точные решения представленных математических уравнений. Однако в большинстве случаев получить точный ответ невозможно, но можно найти приближенные решения, которые по точности равны точному решению. Он имеет дело с квадратичными математическими задачами и конкретными инструкциями. Математический язык, который утверждает, что два алгебраических выражения должны быть равны по своей природе, известен как уравнение.
В нем мы узнали об определении решения уравнения, заметках о решении уравнения, правилах решения линейных уравнений с одной переменной, приложениях линейных уравнений к практическим задачам, решении одновременных линейных уравнений с двумя переменными , решение квадратного уравнения, решаемые примеры на решение уравнения.
Результат обучения этой статьи помогает перевести слово проблема в виде уравнения, известного как формулировка проблемы.
Таким образом, процедура решения текстовой задачи состоит из двух частей, таких как постановка и решение.
Q.1. Что такое решение алгебраического уравнения?
Ответ: Решение уравнения – это массив всех значений, замена которых на неизвестные делает уравнение верным. Для уравнений, требующих одного неизвестного, возведенного в степень один, для определения их решений используются два основных правила алгебры, включающие свойство аддитивности и свойство мультипликативности.
Q.2. Как решать уравнения с переменной?
Ответ : Одним из методов решения уравнений с переменной является метод транспонирования. Метод перестановки включает \(6\) шагов.
Шаг I: Получите линейное уравнение.
Шаг II: Распознайте переменные и константы.
Шаг III: Сократите \(левая\) и \(правая\) до их наиболее простой формы, удалив скобки.
Шаг IV: Транспонируйте все члены, которые включают переменную в \(LHS\) и постоянные члены в \(RHS.\)
Шаг V: Упростите \(LHS\) и \(RHS\) в самой простой форме, чтобы каждый сторона содержит только одно слагаемое.
Шаг VI: Решить уравнение, полученное на шаге \(V\), путем деления двух частей на коэффициент при переменной \(LHS.\)
Q.3. Каковы \(4\) правила решения уравнения?
Ответ: Правило 1: К обеим частям уравнения можно добавить одно и то же количество без изменения равенства.
Правило 2: Одинаковую величину можно вычесть из любой части уравнения без изменения равенства.
Правило 3: Обе части уравнения можно умножить на одинаковое ненулевое число без изменения равенства.
Правило 4: Обе части уравнения можно разделить на одинаковое ненулевое число без изменения равенства.
Следует отметить, что некоторые сложные уравнения можно решить, используя два или более этих правил вместе.
Q.4. Какова формула отсутствия решения?
Ответ: Система одновременных линейных уравнений считается несовместной, если она не имеет решения.
Когда \(\frac{{{a_1}}}{{{a_2}}} = \frac{{{b_1}}}{{{b_2}}} \ne \frac{{{c_1}}}{{ {c_2}}},\) две прямые параллельны и, следовательно, решения нет.
Q.5. Как решить пару одновременных уравнений с двумя переменными?
Ответ: Одним из методов решения уравнения с двумя переменными является метод исключения.
Шаг I: Получите два уравнения.
Шаг II: Умножьте уравнения, чтобы коэффициенты переменной исключались одинаково.
Шаг III: Сложите или вычтите уравнения, полученные на шаге \(II\), в соответствии с условиями, имеющими одинаковые коэффициенты, противоположного или одного знака.
Шаг IV: Решить уравнение с одной переменной, полученное на шаге \(III.\)
Шаг V: Подставьте значение, найденное в шаге \(IV\), в любое из данных уравнений и найдите значение другой переменной.
Значения переменных в шагах \(IV\) и \(V\) образуют решение системы уравнений.
Мы надеемся, что эта подробная статья о решении уравнения поможет вам в подготовке. Если вы застряли, сообщите нам об этом в разделе комментариев ниже, и мы свяжемся с вами в ближайшее время.
1.17: Уравнения и их решения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 45473
- Самар ЭльХитти, Марианна Бонаноме, Холли Карли, Томас Тредлер и Лин Чжоу Технологический колледж Нью-Йорка
- Нью-Йоркский технологический колледж Нью-Йорка технологий в CUNY Academic Works 9{2}+x+1=0\)
g) \(2 x-5>3\) не является уравнением.
.
Это неравенство, и оно будет обсуждаться в главе 21Решением уравнения является любое значение переменной, которое удовлетворяет равенству, то есть оно делает левую (левую) и правую (правую) части уравнения одинаковыми значениями.
Чтобы решить уравнение , нужно найти решение(я) для этого уравнения. Метод решения уравнения зависит от вида уравнения. Мы будем учиться:
- решить линейные уравнения в главах 16 и 17
- решить квадратные уравнения в главе 20
Пример 15.2
Решения уравнений:
-4=6\), что равно \(\mathrm{RHS}\).
b) Решением для \(5 x-6=4 x+2\) будет \(x=8\), потому что LHS, вычисленное при \(x=8\), равно \(5(8)-6= 40-6=34\), а правая сторона, оцененная как \(x=8\), равна \(4 x+2=4(8)+2=32+2=34,\), и они равны!
Таким образом, при заданном значении \(x\) мы можем проверить, является ли оно решением, путем одновременного вычисления левой и правой сторон уравнения.
Это неравенство, и оно будет обсуждаться в главе 21