Полином жегалкина как построить: Что нам стоит полином Жегалкина построить… / Хабр

2.2.6. Полиномы Жегалкина

Полином вида , где — элементарные конъюнкции различных переменных без отрицаний (среди может быть константа 1), называется Полиномом Жегалкина.

Например, .

Теорема (Жегалкин). Любая булева функция представляется в виде полинома Жегалкина, причем единственным образом с точностью до порядка следования элементарной конъюнкции (слагаемых) и до порядка следования переменных в элементарных конъюнкциях.

Доказательство. Если функция , то полиномом Жегалкина для данной функции является константа 0. В остальных случаях представим функцию в виде СДНФ: .

Преобразуем СДНФ в полином Жегалкина. Прежде всего, все знаки дизъюнкции можно заменить на знак суммы по модулю 2 :

.

Это можно сделать по следующей причине: дизъюнкция (проверить).

Если и заменить элементарными конъюнкциями из СДНФ, то получим , так как . Действительно и имеют одинаковые наборы переменных, которые отличаются только расстановкой отрицания, поэтому в произведении найдется переменная , которая встречается с отрицанием и без отрицания.

А конъюнкция таких переменных: равна нулю: .

Далее в полученной формуле преобразуем отрицания по формуле: (проверить). После этого останется раскрыть скобки, что можно сделать ввиду следующего дистрибутивного закона: (проверить). После раскрытия всех скобок мы получим сумму элементарных конъюнкций без отрицаний. Если среди полученных конъюнкций есть одинаковые, то все их (за исключением, может быть, одной из группы одинаковых) можно убрать по следующему правилу: . В итоге получим полином Жегалкина.

Чтобы убедиться в единственности полинома Жегалкина для данной функции, подсчитаем количество различных полиномов от переменных. Заметим, что можно составить элементарных конъюнкций из переменных без отрицания. (Действительно для каждой из Переменной имеется две возможности: данная переменная входит в данную конъюнкцию или нет). Далее для каждой конъюнкции существует также 2 возможности: она входит в данный полином Жегалкина или нет. Поэтому количество различных полиномов Жегалкина равно , т.

е. ровно столько, сколько существует различных булевых функций от переменных. Из данного совпадения вытекает единственность полинома Жегалкина. Действительно, если бы какую-то функцию можно было представить двумя или несколькими полиномами Жегалкина, то некоторые функции нельзя было бы представить полиномом Жегалкина. А уже доказано, что любую функцию можно представить полиномом Жегалкина.

Пример. Пусть функция задана следующей таблицей истинности.

					Строим полином Жегалкина сразу Преобразовывая соответствующую СДНФ:
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

< Предыдущая		Следующая >

Программа — Полином Жегалкина

org/BreadcrumbList» itemprop=»breadcrumb»>
1. Файлы
2. Академическая и специальная литература
3. Математика
4. Дискретная математика

Дискретная математика

• Комбинаторика

• Теория графов

• Теория конечных автоматов

Математика

• Вариационное исчисление

• Векторный и тензорный анализ

• Высшая геометрия

• Высшая математика (основы)

• Вычислительная математика

• Дискретная математика

• Дифференциальные уравнения

• Задачники и решебники

• Интегральные уравнения

• Исследование операций

• История математики

• Комплексное исчисление

• Конформные отображения

• Линейная алгебра и аналитическая геометрия

• Математическая логика

• Математическая физика

• Математические олимпиады

• Математический анализ

• Материалы конференций

• Методы оптимизации

• Нелинейная динамика

• Общая алгебра

• Операционное исчисление

• Оптимальное управление

• Периодика по математике

• Популярная математика

• Программное обеспечение

• Прочие разделы математики

• Решения по Кузнецову

• Решения по Рябушко

• Решения по Чудесенко

• Решения прочие

• Справочники, каталоги, таблицы

• Теория вероятностей и математическая статистика

• Теория игр

• Теория принятия решений (ТПР)

• Теория чисел

• Топология

• Философия математики

• Функциональный анализ

• Элементарная математика

software

• формат jar, txt
• размер 34. 5 КБ
• добавлен 20 сентября 2011 г.

Программа позволяет построить полином Жегалкина для логической функции 2 — 5 переменных. Логическая функция задается в виде таблицы истинности.
Работа выполнена в Воткинском филиале Ижевского ГТУ.

Похожие разделы

1. Академическая и специальная литература
2. Математика
3. Математическая логика

1. Академическая и специальная литература
2. Математика
3. Математическая логика
4. Теория множеств

Смотрите также

Лабораторная

• формат rtf
• размер 163. 19 КБ
• добавлен 13 января 2008 г.

Составить таблицы истинности для формул,Записать формулы в ДНФ и СДНФ, Построить полином Жегалкина для функций,..

Статья

• формат doc
• размер 913 КБ
• добавлен 11 января 2012 г.

Содержание. Булевы переменные и функции +примеры решений. Элементарные булевы функции. Равносильности +примеры решений. Дизъюнктивные нормальные формы +примеры решений. Минимизация Днф +примеры решений. Конъюнктивные нормальные формы +примеры решений. Минимизация Кнф +примеры решений. Полиномиальное разложение булевых функций +примеры решений. Разложение булевых функций в канонический полином Жегалкина +примеры решений. Арифметическое разложение…

Лабораторная

• формат doc
• размер 107.77 КБ
• добавлен 01 февраля 2010 г.

Построение таблицы истинности, СКНФ и СДНФ, полином Жегалкина, карты Карно, Построение ориентированного графа, алгоритм Прима и Дейкстры

Статья

• формат doc
• размер 734.14 КБ
• добавлен 13 марта 2009 г.

МГТУ «Станкин», кафедра прикладной математики Двузначная логика: — Функции алгебры логики. — Суперпозиция и формулы. — Булева алгебра. — Алгебра Жегалкина. — Нормальные формы логических функций.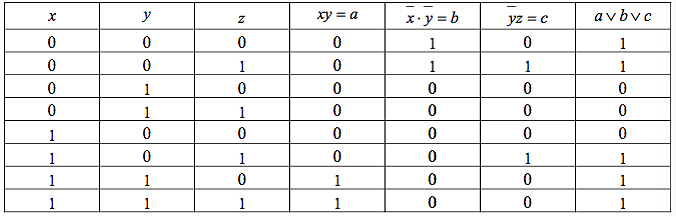 — Минимизация функций. — Полнота и замкнутость. К-значная логика: — Элементарные функции. — Основные свойства элементарных функций. — Основные формы функций. — Представление функций полиномами. — Полнота и замкнутость. Элементы теории графов:…

software

• формат exe
• размер 367.04 КБ
• добавлен 15 апреля 2011 г.

Бета-версия. Отображает заданные пользователем логические функции в виде диаграммы Эйлера- Венна. Функции могут быть заданы выражением, таблицей истинности или картой Карно. Программа позволяет рассчитать СДНФ, СКНФ и полином Жегалкинаrn

• формат docx
• размер 229.11 КБ
• добавлен 04 февраля 2010 г.

Пособие разработано БФ НГТУ. Содержит конспект лекций с примерами, а также решение типовых задач по темам: Логические (булевы) функции. Свойства конъюнкции, дизъюнкции и отрицания. ДНФ, СДНФ, КНФ, СКНФ. Представление логических функций в виде СДНФ (СКНФ). Полиномы Жегалкина. Нахождение сокращенной ДНФ по таблице истинности (карты Карно). Суперпозиция функций. Графы. Деревья.

• формат pdf
• размер 557.33 КБ
• добавлен 30 октября 2008 г.

Полиномы Жегалкина и поляризованные полиномы. Реализация булевых функций обобщенными полиномами. Распознавание свойств функций, заданных полиномами. Предствление булевых функций полиномами над Z.

pottee

• формат doc
• размер 970 КБ
• добавлен 29 сентября 2009 г.

«Дискретный анализ» Понятие множества, элементов множества, подмножество, универсальное множество, пустое множество. Операции над множествами и их семействами: объединение, пересечение, дополнение, разность. Понятие графа. Полный граф. Вершина, степень вершины. Теорема о сумме степеней вершин графа. Теорема о числе нечетных вершин графа. Цикл. Путь. Длина пути. Связность графа. Мост. Деревья, лес. Плоский граф. Формула Эйлера о числе ребер и числ…

pottee

• формат doc
• размер 115.04 КБ
• добавлен 23 марта 2005 г.

Комбинаторные задачи. Перестановки. Размещения. Размещения с повторениями. Перестановки с повторениями. Сочетания с повторениями. Замыкание и замкнутые классы. Принцип двойственности. Полнота, примеры полных систем. Элементарные функции алгебры логики. Разложение булевой функции по переменным. Полином Жегалкина. rn

pottee

• формат doc
• размер 249.5 КБ
• добавлен 03 октября 2008 г.

Множества, основные понятия, способы задания. Операции над множествами. Булева алгебра множеств. Отношения. Отображение и функции. Двойственность. Принцип двойственности. Разложение функции по переменным. Реализация функций многочленом Жегалкина. Замкнутость и полнота. Графы.

Из чего нам строить полином Жегалкина… / Хабр

Главная особенность этих полиномов состоит в том, что любая булева функция может быть представлена ​​полиномом Жегалкина, причем единственным образом.

Чаще всего для построения полиномов Жегалкина учащимся предлагается два метода построения таких полиномов: метод неопределенных коэффициентов и метод эквивалентных преобразований.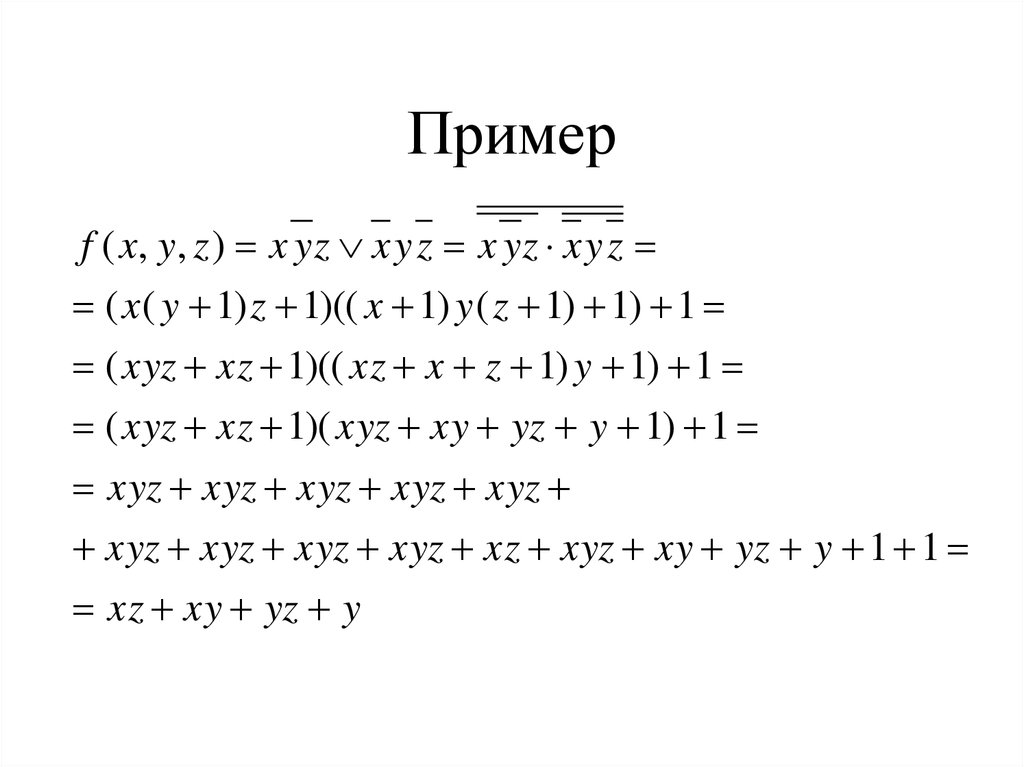

Расчеты с использованием этих методов часто громоздки. По невнимательности ошибиться не сложно.

Под катом один удобный алгоритм построения полиномов Жегалкина, который ученики воспринимают на ура, т.к. требует только выполнения «механических действий» без применения каких-либо умственных усилий. Краткое описание метода можно найти в Википедии, но по моему не совсем понятно по нему как быстро производить расчеты. Этот метод известен мне как «Метод Треугольника Паскаля».

Порядок вычислений проще показать на примере. Далее я по шагам покажу, как должен выглядеть расчет на бумаге (или как удобно его проводить).

Метод треугольника Паскаля

Требуется построить многочлен Жегалкина для функции f. В качестве примера возьмем функцию голосования как функцию f .

Шаг 1. Строим таблицу значений функции (строки в таблице расположены в порядке возрастания двоичных кодов). Таблицу лучше расположить с левой стороны листа.

Шаг 2. Построение треугольника.

Для этого возьмем вектор значения функции и запишем его напротив первой строки таблицы:

Далее заполним треугольник, сложив попарно соседние значения по модулю 2, запишем результат дополнение ниже.

Продолжаем вычисления до тех пор, пока в строке не останется только одна цифра.

Шаг 3. Построение полинома Жегалкина.

Нас интересует левая сторона треугольника (значения выделены жирным):

Числа в левой части треугольника (выделены жирным шрифтом) — это коэффициенты многочлена для монотонных конъюнкций, соответствующих множествам значений переменных.

Теперь выпишем эти союзы для ясности. Выписываем союзы с помощью бинарных множеств в левой части таблицы по следующему принципу: если противоположность переменной xi равна 1, то переменная входит в союз; в противном случае переменная не находится в конъюнкции. Набор (0,0,0) соответствует константе 1.

Если принцип получения конъюнкций понятен, то столбец с ними можно (даже лучше) не выписывать, а сразу переходить к построению полинома.

Для построения многочлена нужны только соединения строк с единицами в левой части треугольника.

Это соединения, из которых состоит многочлен Жегалкина. Осталось только выписать сам полином:

Если переменных в функции не 3, а 4 и более, то метод работает без изменений, только увеличится размер таблиц. Тем не менее, в отличие от метода неопределенных коэффициентов, расчеты можно производить без особых усилий на листе бумаги. 9n \to \mathbb{B}\$, который проверяет, находится ли число его истинных аргументов в \$S\$, т.е. е. функция \$f_S\$ такая, что

$$f_S(\alpha_1, \alpha_2, \ldots, \alpha_n) = \left(\sum_{1 \le i \le n}\alpha_{i}\right) \in S$$

или эквивалентно

$$f_S(\alpha_1, \alpha_2, \ldots, \alpha_n) = |\{ i : \alpha_i \}| \in S. $$

Эти функции называются симметричными булевыми функциями, поскольку все они являются булевыми функциями, не зависящими от порядка аргументов.

Набор логических чисел образует поле , условно обозначаемое \$GF(2)\$, где умножение является логическим и (\$\wedge\$), а сложение — исключающим или (\$\oplus\$).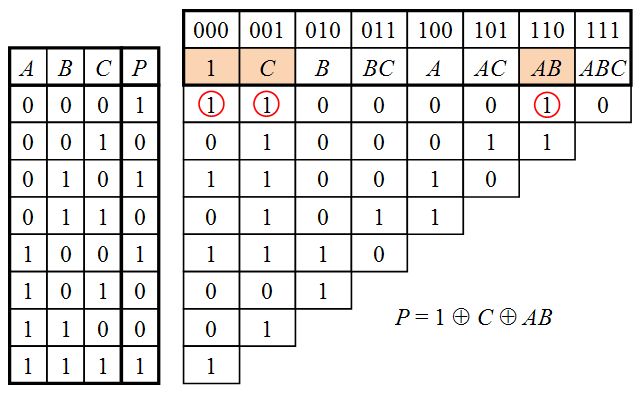 Это поле имеет такие свойства, как \$-\alpha = \alpha\$, \$\alpha / \beta = \alpha \wedge \beta\$ (для всех \$\beta \neq 0\$), \$\ alpha \oplus \alpha = 0\$ и \$\alpha \wedge \alpha = \alpha\$ для всех \$\alpha\$ в дополнение к свойствам поля. Для удобства я буду писать \$\oplus\$ как \$+\$ и опускать \$\wedge\$ в следующих абзацах. Например, я буду писать \$\alpha\oplus\beta\oplus\alpha\wedge\beta\$ как \$\alpha + \beta + \alpha\beta\$.

Любая логическая функция может быть выражена в виде многочлена над полем логических чисел. Такой полином называется полиномом Жегалкина, представление каноническое, т.е. е. существует ровно один многочлен, представляющий данную логическую функцию. Вот несколько примеров булевых функций и соответствующих им полиномов Жегалкина:

• \$\alpha \vee \beta = \alpha + \beta + \alpha\beta\$
• \$\альфа\клин\отриц\бета = \альфа + \альфа\бета\$
• \$(\alpha\to\beta) \oplus\gamma = 1 + \alpha + \gamma + \alpha\beta\$
• \$\neg(\alpha\wedge\beta) \vee\gamma = 1 + \alpha\beta + \alpha\beta\gamma\$
• \$f_{\{1, 4\}}(\alpha, \beta, \gamma, \delta) = \alpha + \beta + \gamma + \delta + \alpha\beta\gamma + \alpha\beta \delta + \alpha\gamma\delta + \beta\gamma\delta + \alpha\beta\gamma\delta\$
  , где тройные члены \$(\alpha\beta\gamma + \alpha\beta\delta + \ alpha\gamma\delta + \beta\gamma\delta)\$ необходимы, поскольку в противном случае мы имели бы \$f(1,1,1,0) = 1\$ и \$3 \not\in \{1, 4\}\$.

  No related posts.