Как найти площадь поверхности прямого кругового конуса: боковую, основания, полную
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение площади поверхности конуса: формула и задачи
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого кругового конуса (боковую, полную и основания), а также разберем примеры решения задач для закрепления материала.
- Формула вычисления площади конуса
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
Формула вычисления площади конуса
1. Боковая поверхность
Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.
Sбок. = πRl
Образующая (l) соединяет вершину конуса и границу основания, другими словами, точку на окружности.
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
Основанием конуса является круг, площадь которого вычисляется так:
Sосн. = πR2
Учитывая то, что диаметр круга равняется двум его радиусам (d = 2R), данную формулу можно представить в виде:
Sосн. = π(d/2)2
3. Полная площадь
Для вычисления суммарной площади конуса следует сложить площади боковой поверхности и основания:
Sполн. = πRl + πR2 = πR(l + R)
Примеры задач
Задание 1
Вычислите площадь боковой поверхности конуса, если известно, что его радиус равен 16 см, а длина образующей – 5 см.
Решение:
Используем соответствующую формулу с известными нам величинами:
S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см2.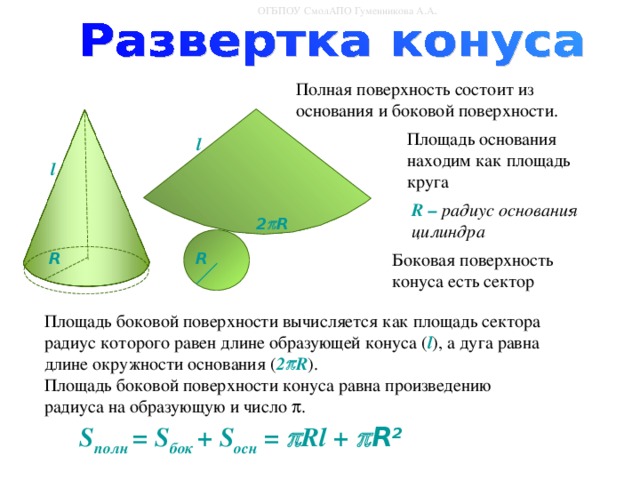
Задание 2
Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если рассмотреть конус в сечении, то можно заметить, что его высота, радиус и образующая представляют собой прямоугольный треугольник. Следовательно, воспользовавшись теоремой Пифагора, можно найти длину образующей (является гипотенузой):
l2 = (4 см)2 + (3 см)2 = 25 см2.
l = 5 см.
Осталось только использовать найденное и известные по условиям задачи значения, чтобы рассчитать площадь:
S = 3,14 ⋅ 3 см ⋅ (5 см + 3 см) = 75,36 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиакаНахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Площадь поверхности конуса — формулы, пример расчета
Пусть α– плоскость, точка S– точка, не лежащая в этой плоскости.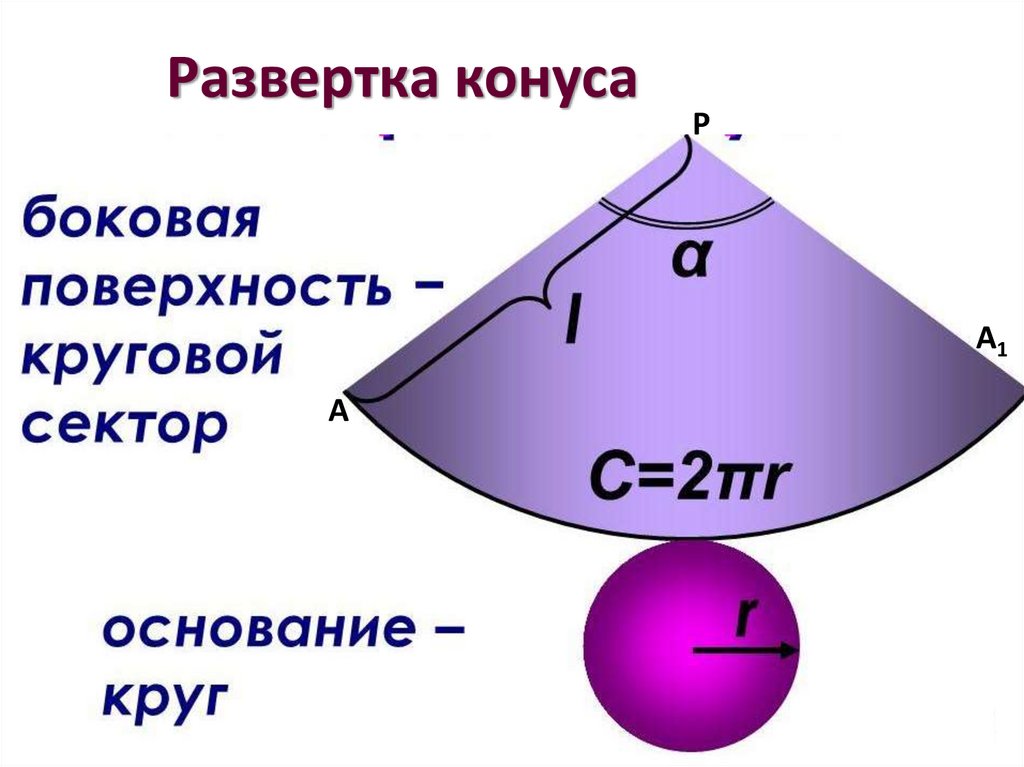
Границей конуса является круг радиуса R и боковая поверхность конуса.
Боковую поверхность описывает отрезок AS , когда точка A описывает круг.
Точка S является вершиной конуса. Множество отрезков AS, соединяющих вершину с окружностью основания являются направляющими конуса.Если перпендикуляр, опущенный из точки S, совпадает с центром основания, то конус называется прямым.Очень часто говорят, что прямой конус образуется в результате вращения прямоугольного треугольника вокруг оси, содержащий его катет.
На данном рисунке прямой конус получился в результате вращения прямоугольного треугольника AOS вокруг катета SO. Тогда говорят, что
- Катет SO –это высота конуса;
- Гипотенуза AS –образующая конуса;
- Катет AO – радиус конуса.

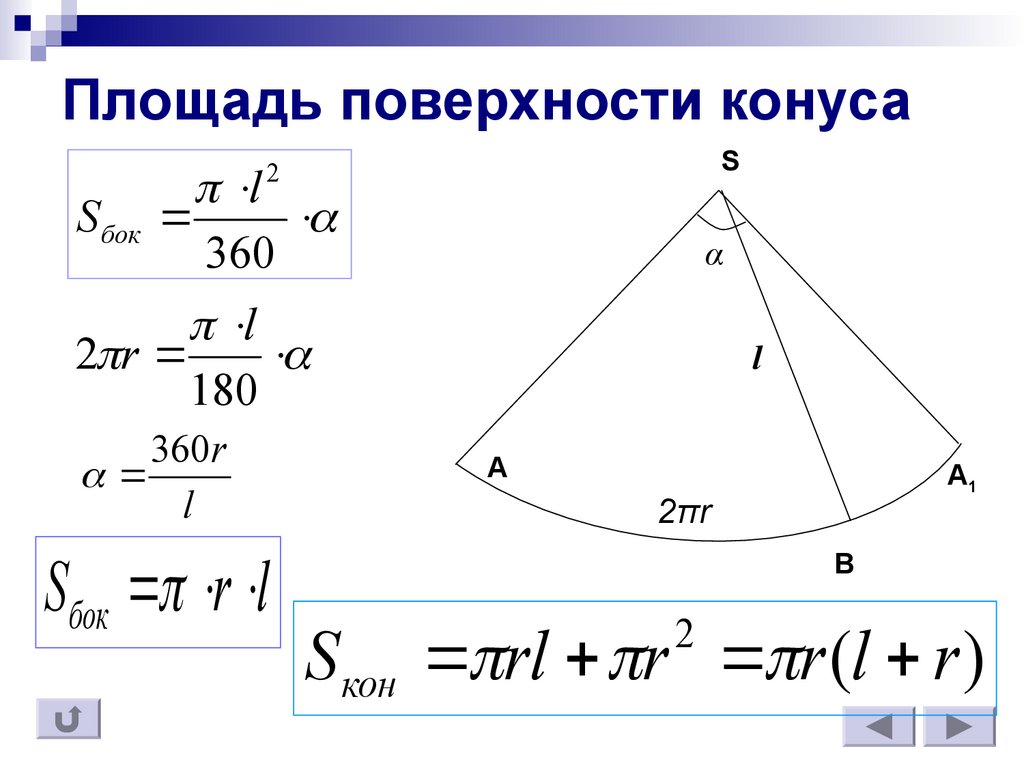
Площадь боковой поверхности конуса через его радиус и направляющую
Пусть дан конус с радиусом R и образующей L
AS=L, AO=R
Разрежем конус по образующей L и развернем его боковую поверхность.
В результате получим криволинейный треугольник ASA` , где AS=L, A`S=L.
Дуга AA` -это вытянутая окружность основания конуса с радиусом R. Следовательно, длина дуги AA` будет равна 2πR
Площадь боковой поверхности будет равна площади сектора круга с радиусом R.
Если угол α – радиальная мера угла, то:
где α=∠{ASA`}
Чтобы найти угол ∠{ASA`} воспользуемся формулой длины дуги, которая стягивает данный угол:
Но с другой стороны:
Приравняем правые части равенств. Имеем:
Выразим α:
Подставим полученное выражение в формулу площади сектора:
Следовательно, боковая поверхность конуса равна произведению числа π на радиус конуса и его образующую.
Формула боковой поверхности конуса будет иметь следующий вид:
Пример расчета площади боковой поверхности конуса, если известны его радиус и направляющая
Найти площадь боковой поверхности конуса с радиусом равным 3 см, образованным направляющей равной 7 см
По условию задачи L = 5см, R=3см
Формула боковой поверхности конуса:
Подставив в формулу значения из условия задачи, имеем:
Площадь боковой поверхности конуса через его радиус и высоту
Очень часто в задачах на вычисление площади боковой поверхности конуса известна высота конуса вместо его направляющей.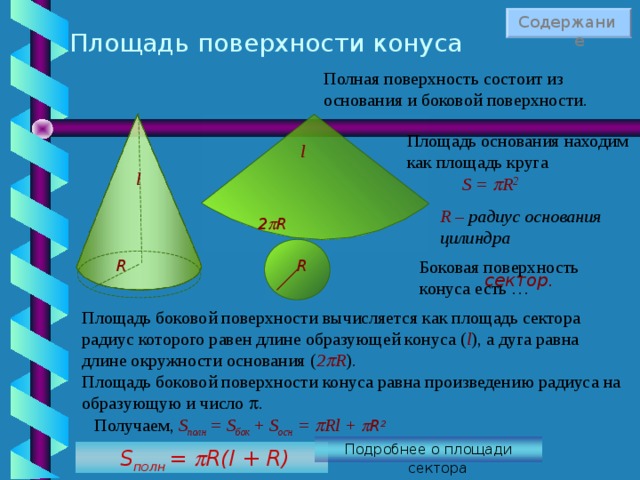
Так как конус прямой, то треугольник AOS – прямоугольный, где AO и OS – катеты, а AS –гипотенуза. Воспользовавшись теоремой Пифагора, получаем:
Отсюда:
Но
Тогда:
Подставим данное выражение в формулу площади боковой поверхности конуса:
Боковая поверхность конуса равна произведению числа на радиус конуса и корень квадратный из суммы квадратов радиуса и высоты конуса
Пример расчета площади боковой поверхности конуса, если известны его радиус и высота.
Найти площадь боковой поверхности конуса с радиусом равным 1 см и высотой, равной 5 см
По условию задачи Н = 5см, R=1см
Формула боковой поверхности конуса:
Подставив в формулу значения из условия задачи, имеем:
Полная поверхность конуса
Полная поверхность конуса – это сумма площади его боковой поверхности и площади основания конуса:
Основанием конуса является круг с радиусом R. Его площадь равна произведению числа π на квадрат его радиуса:
Площадь боковой поверхности вычисляется по формуле: или
Тогда площадь полной поверхности конуса равна:
или
Таким образом, площадь полной поверхности конуса равна произведению числа {pi} на радиус конуса и сумму направляющей и радиуса.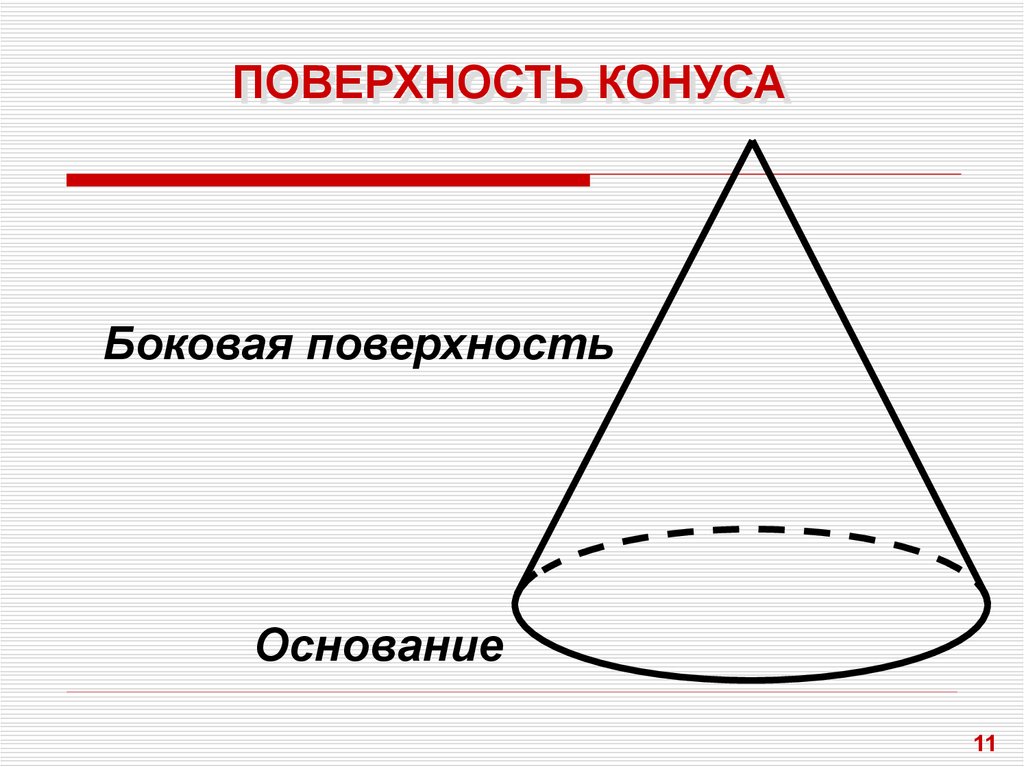
Формула имеет следующий вид:
Площадь полной поверхности конуса равна произведению числа π на радиус конуса и сумму корня квадратного из суммы квадратов радиуса и высоты конуса и радиуса конуса.
Формула имеет следующий вид:
Площадь поверхности конуса
Площадь поверхности конуса – это общая площадь, занимаемая поверхностями конуса. Конус представляет собой геометрическую фигуру объемной формы, которая имеет плоскую грань и криволинейную поверхность с заостренным концом. Форма конуса получается путем складывания нескольких треугольников и последующего вращения их вокруг оси. Заостренный конец конуса называется вершиной или вершиной. Расстояние по перпендикуляру между центром основания и вершиной конуса называется высотой, а наклонная высота — это расстояние от вершины конуса до любой точки на окружности основания. Нормальный конус также называют прямым круговым конусом. В этой статье обсуждается площадь прямого кругового конуса. Конусы для мороженого, дорожные конусы, воронки, шляпы на день рождения и т. д. — вот некоторые примеры конусов, которые мы видим в нашей повседневной жизни.
д. — вот некоторые примеры конусов, которые мы видим в нашей повседневной жизни.
Какова площадь поверхности конуса?
Площадь поверхности конуса визуализируется как площадь, занимаемая конусом, когда он разрезается. Он образован круглым основанием и изогнутой поверхностью. Площадь поверхности конуса зависит от радиуса его основания и высоты конуса. Кроме того, объем конуса зависит от его радиуса и высоты.
Площадь поверхности конуса Формула
Площадь поверхности конуса определяется как площадь, занимаемая границей или поверхностью конуса. Конус имеет два типа площадей поверхности, а именно: криволинейную площадь поверхности и общую площадь поверхности.
Площадь криволинейной поверхности конусаКриволинейная поверхность конуса определяется как площадь криволинейной части конуса, т. е. площадь конуса без его основания.
Общая площадь поверхности конусаПлощадь криволинейной поверхности (S) = πrl квадратных единиц
, где
« r » — радиус основания конуса, а
« l » — наклонная высота конуса.
Общая площадь поверхности конуса определяется как общая площадь, занимаемая конусом в трехмерном пространстве, т. е. площадь криволинейной поверхности и площадь круглая основа.
Общая площадь поверхности = πr (r + l) квадратных единиц
где
« r » — радиус основания конуса, а
« l » — наклонная высота конуса. .
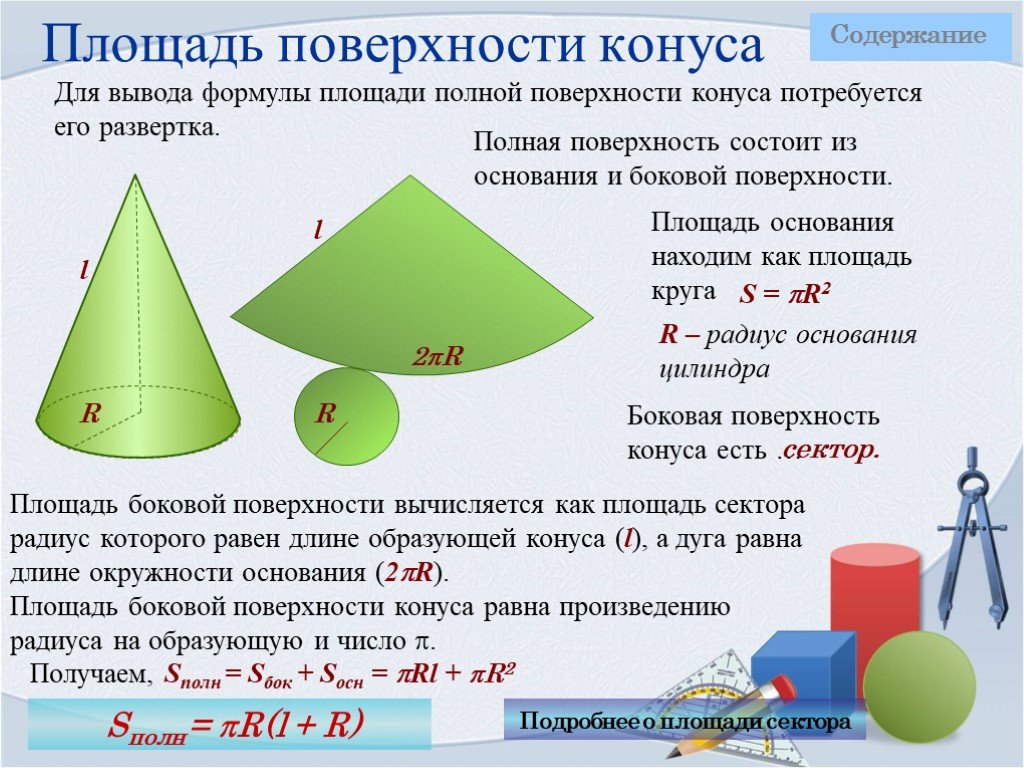
Расчет площади поверхности конуса
Чтобы увидеть фигуру, образованную поверхностью конуса, возьмите бумажный конус и разрежьте его по наклонной высоте. Теперь отметьте A и B как две конечные точки и O как точку пересечения двух линий. Теперь, если мы его откроем, он будет выглядеть как сектор круга.
Итак, чтобы найти площадь криволинейной поверхности конуса, нужно найти площадь сектора.
Площадь сектора по длине дуги = (длина дуги × радиус)/ 2 = ((2πr) × l)/2 = πrl.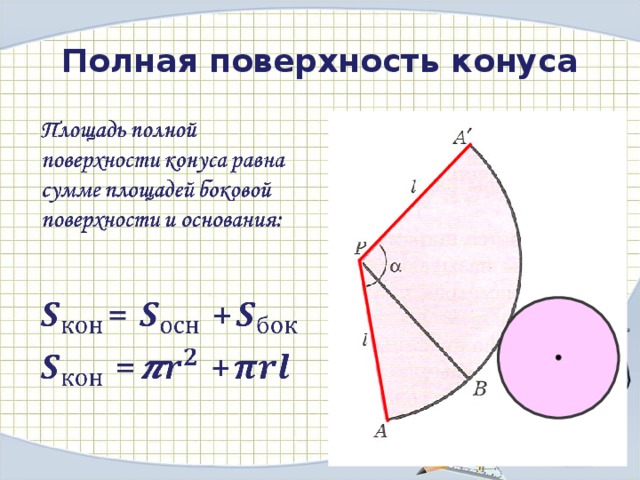
Таким образом,
Площадь криволинейной поверхности конуса (S) = πrl квадратных единиц
Общая площадь поверхности конуса (T) = площадь основания + площадь криволинейной поверхности круг, площадь основания = πr 2
⇒ T = πr 2 + πrl = πr(r + l)
Следовательно,
Общая площадь поверхности конуса = πr (r + l) квадратных единиц
6 Узнайте об усеченном конусе здесь.Связь между площадью поверхности конуса и его высотой
Мы знаем, что наклонная высота конуса (l) = √(r 2 + h 2 )
Итак, заменив значение наклона в формулах площадей конуса, получаем
Как найти площадь поверхности конуса?Площадь криволинейной поверхности (S) = πr√(r 2 + h 2 ) квадратных единиц h 2 ) квадратных единиц
Давайте рассмотрим пример, чтобы увидеть, как найти площадь поверхности конуса, используя его формулу.
Пример: Найдите общую площадь поверхности конуса, если его радиус равен 5 дюймам, а высота наклона равна 12 дюймам. (Используйте π = 3,14)
Шаг 1: Запишите размеры данного конуса. Здесь наклонная высота конуса равна 12 дюймам, а его радиус равен 5 дюймам.
Шаг 2: Мы знаем, что общая площадь поверхности конуса = πr (r + l). Итак, подставьте значение заданных размеров в уравнение = (3,14) × 5 × (5 + 12) = 266,9 кв. дюйма
Шаг 3: Следовательно, общая площадь поверхности конуса равна 266,9 квадратных дюймов.
Решенные примеры на площади поверхности конуса
Пример 1. Найдите общую площадь поверхности конуса, если его радиус равен 15 см, а высота наклона равна 10 см. (Используйте π = 3,14)
Решение:
Приведенные данные,
Радиус конуса (r) = 15 см
Наклонная высота (l) = 10 см Мы знаем, что 90 20 3 9000 Общая площадь поверхности конуса = πr (r + l) квадратных единиц
= (3,14) × 15 × (15 + 10)
= 1177,5 кв.
см
Следовательно, общая площадь поверхности конуса равна 1 177,5 кв. см.
Пример 2. Какова высота конуса, если его радиус равен 14 единицам, а площадь криволинейной поверхности равна 1100 квадратных единиц? (Используйте π = 22/7)
Решение:
Данные,
Радиус конуса (r) = 14 единиц
Площадь криволинейной поверхности конуса = 1100 квадратных единиц
3 Пусть наклонная высота конуса равна «l», а высота конуса — «h».
Мы знаем, что
Площадь криволинейной поверхности конуса = πrl квадратных единиц
⇒ 1100 = (22/7) × 14 × l
⇒ 44 × l = 1100
⇒ l = 1100/44 = 25 единиц
Мы знаем, что
наклонная высота (l) = 2 + R 2 )
⇒ H = √ (L2 — R2)
= √ (25 2 — 14 2 ) = √429 = 20,71 единицы
Таким составляет 20,71 ед.
Пример 3: Определите наклонную высоту конуса, если общая площадь поверхности конуса составляет 525 кв.
см, а радиус равен 7 см. (Используйте π = 22/7)
Решение:
Данные,
Радиус конуса (r) = 7 см
Общая площадь поверхности конуса = 525 кв. л».
Мы знаем, что
Общая площадь поверхности конуса = πr (r + l) квадратных единиц
⇒ (22/7) × 7 × (7 + l) = 525
⇒ 22 × (7 + l) = 525
⇒ 7 + l = 25
⇒ l = 18 см
Следовательно, наклонная высота конуса равна 18 см.
Пример 4. Рассчитайте площадь боковой поверхности конуса, радиус которого равен 24 дюймам, а высота — 7 дюймам. (Используйте π = 3,14)
Решение:
Приведенные данные,
Радиус конуса (r) = 24 дюйма
Высота конуса (h) = 7 дюймов.
Мы знаем, что
наклонная высота (l) = √(h 2 + r 2 )
l = √(7 2 + 24 2)2 = 5 (6 дюймов) 2
Мы знаем, что
Площадь криволинейной поверхности конуса = πrl квадратных единиц
= 3,14 × 24 × 25
= 1884 кв.
в
Следовательно, площадь криволинейной поверхности конуса равна 1884 кв.
Часто задаваемые вопросы о площади поверхности конуса
Вопрос 1: Что произойдет с площадью криволинейной поверхности конуса, если его высоту удвоить?
Ответ:
Площадь криволинейной поверхности конуса напрямую зависит от радиуса его основания.
Площадь криволинейной поверхности = πrl
Если радиус конуса удвоить, площадь его криволинейной поверхности также удвоится.
CSA = π(2r)(l)
= 2πrl
= 2 × площадь исходной кривизны
Вопрос 2. Как найти площадь поверхности конуса?
Ответ:
Площадь поверхности con можно рассчитать двумя способами:
CSA = πrl
TSA = πrl(r+l)
где,
r радиус конуса
l высота наклона конуса
Вопрос по вычислению высоты наклона конус.

Ответ:
Высота наклона конуса определяется формулой
L = √ (R 2 + H 2 ),
, где ‘R’ ) —
, где ‘R’ ) —
, где ‘R’ ). радиус и «h» высота конуса.
Вопрос 4: Напишите формулу базовой поверхности конуса.
Ответ:
Поверхность основания конуса круглая и формула основания поверхности конуса πr 2 квадратных единиц.
Вопрос 5: Что мы подразумеваем под площадью поверхности конуса?
Ответ:
Площадь поверхности конуса — это область, занимаемая поверхностью конуса в трехмерном пространстве. Его можно рассчитать, найдя сумму боковой площади и площади основания конуса.
Связанные ресурсы
- Площадь поверхности цилиндра
- Площадь поверхности сферы
- Площадь поверхности куба
Площадь поверхности конуса
11 Бывший блестящий член, Пи Хан Го, Ян Браун, а такжеспособствовал
Содержимое
- Вывод формулы
- Примеры
На конусе внизу hhh — высота, LLL — наклонная высота, ccc — окружность основания, rrr — радиус основания.
Как это выглядит, когда мы разворачиваем его?
Если развернуть, форма будет следующей: Это сектор окружности с радиусом LLL и длиной дуги ccc. Таким образом, площадь криволинейной поверхности конуса равна площади верхнего сектора. Площадь сектора с заданной длиной дуги ccc и радиусом LLL определяется как A=12cLA=\dfrac{1}{2}cLA=21cL. Теперь применив это к конусу, мы имеем A=12cL,A=\frac{1}{2}cL,A=21cL, где LLL – высота наклона, а ccc – длина окружности основания. После некоторых манипуляций A=πLr,A=\pi Lr,A=πLr, как указано в определении. 92\big)=540 \pi.\ _\squareA=360θ(площадь круга)=360150(π)(362)=540π. □
Куча песка имеет форму правильного круглого конуса. Он имеет высоту 333 фута и диаметр основания 888 футов. Найдите площадь его поверхности в квадратных метрах.
После некоторых манипуляций мы видим, что образовался прямоугольный треугольник 3-4-5.



 см
см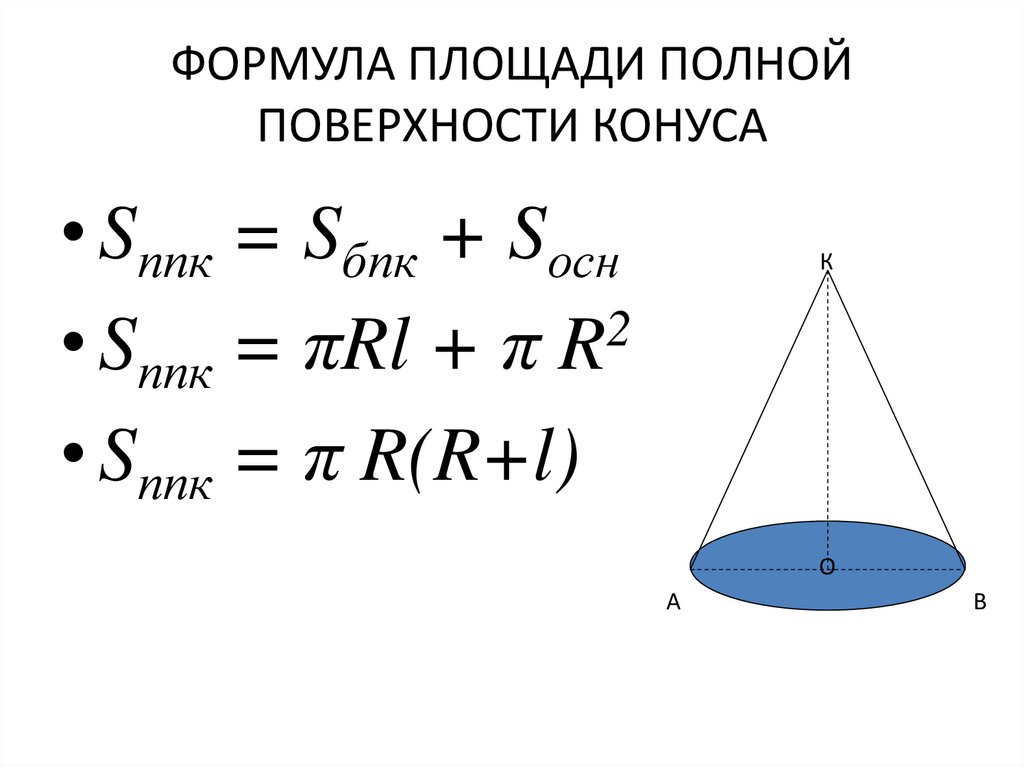 см, а радиус равен 7 см. (Используйте π = 22/7)
см, а радиус равен 7 см. (Используйте π = 22/7)  в
в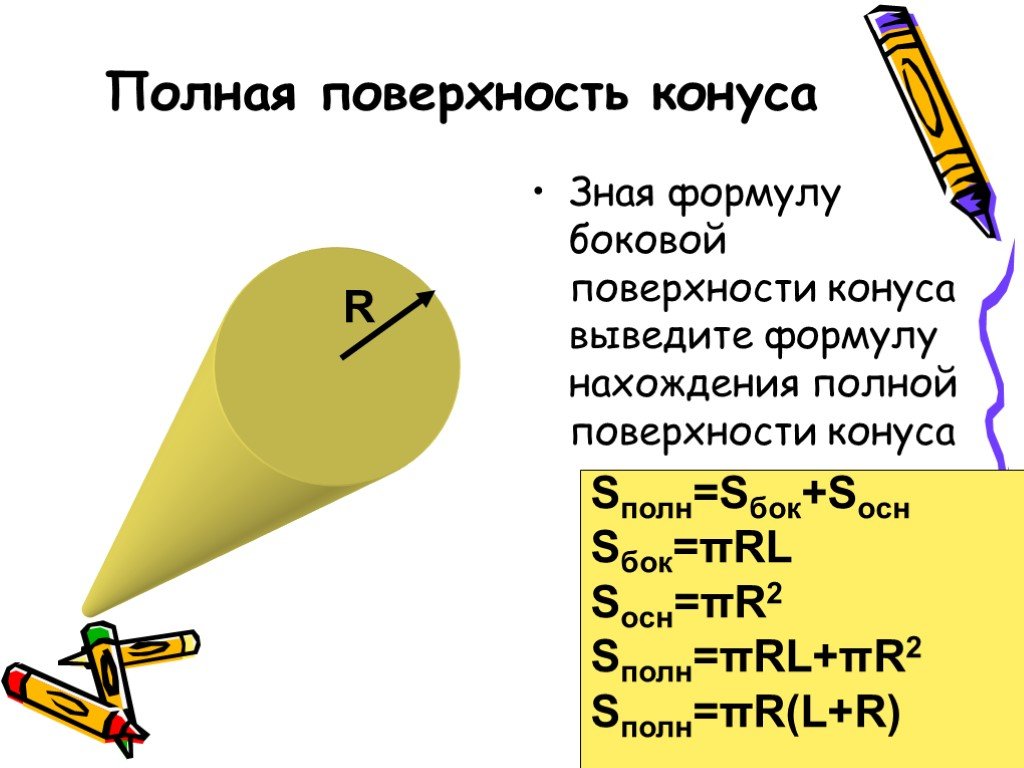
 Как это выглядит, когда мы разворачиваем его?
Как это выглядит, когда мы разворачиваем его?