Целые числа: положительные и отрицательные. Сравнение целых чисел
- Положительные и отрицательные числа
- Сравнение целых чисел
Целые числа — это положительные и отрицательные числа, не имеющие дробной части и число нуль.
Число 0 целое, но не является ни положительным, ни отрицательным числом.
Ставить перед числом нуль какой-либо знак (+ или -) не имеет смысла, так как записи
+0, -0 и 0
представляют собой одно и тоже число:
+0 = -0 = 0.
Положительные и отрицательные числа
Существуют величины, отсчёт которых производиться в двух противоположных направлениях.
Пример. Температура отсчитывается в двух противоположных направлениях от температуры тающего льда, принимаемой за нулевую:
1) Уровень ртути при нулевой температуре (температуре тающего льда).
2) Уровень ртути при температуре, более низкой, чем нулевая.
3) Уровень ртути при температуре, более высокой, чем нулевая.
Если мы имеем какую-либо величину, отсчёт которой производится в двух противоположных направлениях, то одно из направлений, безразлично какое, принято называть положительным, а другое отрицательным.
Положительное число — это число, полученное в результате измерения величины, отсчитанной в положительном направлении. Положительное число изображается в виде числа со знаком +
(плюс) впереди. Например, +16 — положительное число.
Пример.
16 °C тепла
или +16 °C
.
Примечание: все градусы пишутся с буквой C
(Цельсия), знак градуса отделяется от числа пробелом. Например, +7 °C.
Наименьшее целое положительное число – это 1 (единица).
Отрицательное число — это число, полученное в результате измерения величины, отсчитанной в отрицательном направлении. Отрицательное число изображается в виде числа со знаком —
(минус) впереди.
Пример.
16 °C мороза
или -16 °C
.
Наибольшее целое отрицательное число – это -1 (минус один).
Все числа, кроме нуля, записанные со знаком +
(плюс) впереди, являются положительными, а записанные со знаком —
(минус) — отрицательными.
Пример.
+1, +15, +57 и т. д. — положительные числа;
-1, -15, -57 и т. д. — отрицательные числа.
Положительные числа можно обозначать предшествующим знаком +
(плюс) или опускать его. Числа, перед которыми не стоит знака (+ или -), считаются положительными числами. Например, вместо
+8, +14, +100 и т. д.
можно написать просто
8, 14, 100 и т. д.
Сравнение целых чисел
Сравнить два целых числа — значит, узнать, какое из них больше, какое меньше, или определить, что числа равны.
Сравнивать целые числа можно с помощью ряда целых чисел, так как числа в нём расположены от меньшего к большему, если двигаться по ряду слева направо. Поэтому в ряду целых чисел можно заменить запятые на знак меньше:
Поэтому в ряду целых чисел можно заменить запятые на знак меньше:
… -5 < -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5 < …
Следовательно, из двух целых чисел больше то число, которое в ряду стоит правее, и меньше то, которое стоит левее, значит:
1) Любое положительное число больше нуля и больше любого отрицательного числа:
1 > 0; 15 > -16.
2) Любое отрицательное число меньше нуля:
-7 < 0; -357 < 0.
3) Из двух отрицательных чисел больше то, которое в ряду целых чисел стоит правее:
-31 < -28.
какие так называют, что такое в математике, чем отличаются
Содержание:
- Какие числа называются положительными и отрицательными
- Сравнение положительных и отрицательных чисел
- Правила действий с отрицательными и положительными числами
- Примеры задач с решением
Содержание
- Какие числа называются положительными и отрицательными
- Сравнение положительных и отрицательных чисел
- Правила действий с отрицательными и положительными числами
- Примеры задач с решением
Какие числа называются положительными и отрицательными
Отрицательными числами в алгебре являются числа со знаком минус (-). Например, к таким числам относят -1, -2, -3. Прочитать запись можно, как минус один, минус два, минус три.
Например, к таким числам относят -1, -2, -3. Прочитать запись можно, как минус один, минус два, минус три.
Отрицательное число — это какое-либо число меньше нуля, перед которым ставится знак минус.
Положительные числа — числа, состоящее в множестве положительных чисел, являются числами без знака минус в обозначении и не являются нулем.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В системе отрицательных чисел так же, как и среди положительных есть дроби: обыкновенные и десятичные, целые числа, корни и так далее. Почти все подвиды чисел, которые встречаются среди положительных чисел, есть и среди отрицательных. Стоит отметить, что, согласно понятию, число 0 не является ни положительным, ни отрицательным числом.
Положительные числа — это числа, соответствующие точкам в той части координатной прямой, которая лежит с правой стороны относительно начала отсчета.
Отрицательные числа — являются числами, соотносящимися с точками в части координатной прямой, которая расположена с левой стороны относительно начала отсчета (нуля).
Наглядным примером использования отрицательных чисел является термометр. Прибор демонстрирует температуру тела, воздуха, почвы, воды. Зимой при холодной погоде температура воздуха снижается до отрицательных значений. К примеру, -10 градусов мороза:
Обычные числа, в том числе, 1, 2, 3 называют положительными. Данные числа имеют знак (+). Обычно, его не записывают.
Координатная прямая — является прямой линией, на которой размещены все числа, включая отрицательные и положительные.
Координатная прямая имеет следующий вид:
В данном случае отмечены только числа от −5 до 5. В действительности координатная прямая бесконечна. На изображении можно увидеть только фрагмент этой прямой. Для того чтобы отметить на координатной прямой числа, использую точки. Началом отсчета является нуль. С левой стороны от нуля отмечают отрицательные числа, а с правой — положительные.
С левой стороны от нуля отмечают отрицательные числа, а с правой — положительные.
Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом \(\infty\). Отрицательное направление будет обозначаться символом −\(\infty\), а положительное — символом +\(\infty\). Таким образом, координатная прямая содержит все числа от минус бесконечности до плюс бесконечности:
\((−\infty; +\infty)\)
Каждая точка на координатной прямой обладает определенным именем и координатой. Именем является какая-либо латинская буква. Координата представляет собой число, указывающее на положение точки на прямой. Таким образом, координатой является то число, которое требуется отметить на координатной прямой. К примеру, точка А(2) читается, как «точка А с координатой 2» и обозначается на координатной прямой таким образом:
При рассмотрении изображения координатной прямой можно заметить, что отрицательные числа лежат левее относительно начала отсчета, а положительные числа — правее. С каждым шагом в левую сторону число будет уменьшаться в меньшую сторону. При каждом шаге в правом направлении число будет увеличиваться.
С каждым шагом в левую сторону число будет уменьшаться в меньшую сторону. При каждом шаге в правом направлении число будет увеличиваться.
Сравнение положительных и отрицательных чисел
Положительные числа, то есть те, которые больше 0, можно рассматривать в качестве прибыли, прибавки, увеличения количества чего-либо. Отрицательные числа можно представить, как недостаток, убыток, расход, долг. Предположим, что имеется 55 неких предметов, например, яблок. Цифра 55 является положительной. В том случае, когда требуется отдать кому-то 5 яблок, данной действие можно обозначить, как -5. На градуснике рост температуры на 4,5 значений можно описать как +4,5, а снижение, в свою очередь, как −4,5. В приборах, которые используют для измерений, часто применяют положительные и отрицательные числа. Это объясняется удобством отображения изменения величин.
Любое отрицательное число меньше, чем любое положительное число. К примеру, если сравнить -5 и 3, то минус пять меньше трех.
На прямой -5 расположено левее относительно числа 3. Согласно правилу, любое отрицательное число меньше любого положительного числа. Отсюда следует, что:
−5 < 3
Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. К примеру, при сравнении чисел -4 и -1 можно сделать вывод, что минус четыре меньше, чем минус единица. Причина заключается в том, что на координатной прямой -4 располагается левее, чем -1.
Видно, что -4 лежит левее, а -1 правее. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Таким образом:
-4 < -1
Ноль больше, чем любое отрицательное число. К примеру, при сравнении 0 и -3 можно сделать вывод, что ноль больше, чем минус три. Это объясняется тем, что на координатной прямой 0 располагается правее, чем -3.
При рассмотрении координатной прямой можно заметить, что 0 лежит правее, а -3 левее. Согласно правилу, нуль больше любого отрицательного числа. Таким образом:
0 > -3
Нуль меньше любого положительного числа. К примеру, можно сравнить 0 и 4. Ноль меньше, чем 4.
На координатной прямой 0 располагается левее, а 4 правее. Исходя из правила, ноль меньше, чем какое-либо положительное число. Таким образом:
0 < 4
Правила действий с отрицательными и положительными числами
Существуют следующие правила знаков при умножении и делении отрицательных чисел:
- Умножение или деление отрицательного числа на отрицательное приводит в результате к получению положительного числа.
- Если требуется умножить или разделить отрицательное число на положительное, то получится отрицательное число.

В процессе сложения отрицательных чисел следует руководствоваться аналогичными правилами знаков в несколько ином виде. По общей формулировке правило знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». В таком случае, при сложении отрицательного числа с другим, получится:
-а+(-в)=-а-в — то есть из отрицательного числа вычитается положительное.
Аналогичное правило применимо для примеров с вычитанием отрицательных чисел:
-а-(-в)=-а+в — к отрицательному числу в итоге прибавляется положительное.
В том случае, когда требуется сложить два отрицательных числа, следует сложить два числа и поставить знак минус. К примеру:
(−2)+(−3)=−5(−2)+(−3)=−5
Если первое число положительное, а второе отрицательное, требуется определить, какое число по модулю больше. Далее нужно отнять от большего меньшее число и поставим знак большего числа. Например:
(−8)+4=4−8=−4
9+(−4)=9−4=5
Каждое число, за исключением 0, соответствует противоположному элементу. В сумме с ним число дает 0. Например:
В сумме с ним число дает 0. Например:
−9+9=0
7,1+(−7,1)=0
При вычитании двух отрицательных чисел следует руководствоваться правилом: минус на минус дает плюс. Таким образом, когда стоят рядом два минуса, в сумме получается плюс. К примеру:
(−7)−(−6)=(−7)+6=(−1)
В том случае, когда первое число положительное, а второе число является отрицательным, вычитание выполняют по тому же принципу, что и сложение. Нужно определить, какое число по модулю больше. Далее следует отнять от большего меньшее число и поставить знак большего числа.
7−9=−2
так как 9>7
Одним из ключевых свойств является то, что минус на минус дает плюс:
7−(−9)=7+9=16
Примеры задач с решением
Задача 1
Задача
Нужно решить: (+3) + (+4)
Решение:
(+3) + (+4) = +7
Ответ: 7
Задача 2
Задача
Требуется решить: (-4) + (-3)
Решение:
(-4) + (-3) = -7
Ответ: -7
Задача 3
Задача
Необходимо выполнить сложение: (+15) + (-7)
Решение:
(+15) + (-7) = 15 — 7 = 8
Ответ: 8
Задача 4
Задача
Нужно выполнить вычитание: (+7) — (+4)
Решение:
(+7) — (+4) = +3
Ответ: 3
Задача 5
Задача
Требуется найти разность чисел: -17 — (-14)
Решение:
-17 — (-14) = -17 + 14 = -3
Ответ: -3
Задача 6
Задача
Необходимо решить пример: (+5) ⋅ (-8)
Решение:
(+5) ⋅ (-8) = -40
Ответ: -40
Задача 7
Задача
Нужно найти произведение двух чисел: -9 ⋅ (-9)
Решение:
-9 ⋅ (-9) = 81
Ответ: 81
Задача 8
Задача
Требуется решить пример: -6 ⋅ 5
Решение:
-6 ⋅ 5 = -30
Ответ: -30
Задача 9
Задача
Нужно выполнить деление двух чисел: 40 : (-8)
Решение:
40 : (-8) = -5
Ответ: -5
Задача 10
Задача
Требуется найти разность: (-6) — (+6) — (-8)
Решение:
(-6) — (+6) — (-8) = -12 — (-8) = -12 + 8 = -4
Ответ: -4
Задача 11
Задача
Необходимо решить пример: (-5) ⋅ (-4) + (+3) ⋅ (-2)
Решение:
(-5) ⋅ (-4) + (+3) ⋅ (-2) = 20 + (-6) = 14
Ответ: 14
Задача 12
Задача
Нужно найти ответ: (-15) ⋅ [-3 + (-15)] : (+5)
Решение:
(-15) ⋅ [-3 + (-15)] : (+5) = -15 ⋅ (-18) : 5 = (-15 : 5) ⋅ (-18) = -3 ⋅ (-18) = 54
Ответ: 54
Задача 13
Задача
Требуется выполнить деление: -18 : [-20 — (30 — 56)]
Решение:
-18 : [-20 — (30 — 56)] = -18 : [-20 — (-26)] = -18 : (-20 + 26) = -18 : 6 = -3
Ответ: -3
Задача 14
Задача
Нужно найти значение выражения:
(−1)−(−512)⋅(+411)=(−1)−(−521)⋅(+114)
Решение:
(−1)−(−512)⋅411=−1−(−112)⋅411=(−1)−(−521)⋅114=−1−(−211)⋅114=−1−(−2)=−1+2=1−1−(−2)=−1+2=1
Ответ: 1
Задача 15
Задача
Необходимо вычислить:
Вычислить |a| — |b| + |c|
при a = -8, b = -5, c = 1
Решение:
|-8| — |-5| + |1| = 8 — 5 + 1 = 4
Ответ: 4
Задача 16
Задача
Требуется решить пример:
[2,4−(0,3−0,21)⋅2+0,44:(−2)]:45=[2,4−(0,3−0,21)⋅2+0,44:(−2)]:54
Решение:
[2,4−(0,3−0,21)⋅2+0,44:(−2)]:45=[2,4−(0,3−0,21)⋅2+0,44:(−2)]:54=
[2,4−0,09⋅2+(−0,22)]:45=[2,4−0,09⋅2+(−0,22)]:54= (2,4−0,18−0,22):25=
2:45=52=2,5(2,4−0,18−0,22):52=2:54=25=2,5
Ответ: 2,5
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Арифметика, математика и статистика — Набор академических навыков
Положительные и отрицательные числа (Психология)
ContentsToggle Главное меню 1 Введение 2 Примеры работы 3 Проверка себя 4 Внешние ресурсы
Введение
Положительные числа — это те, которые больше нуля. Отрицательные числа — это те, которые меньше нуля. Ниже приведена таблица, которая поможет вам запомнить, что делать со знаком при использовании умножения или деления, сложения или вычитания.
\begin{array}{ccccc} \text{Положительный} & \times / \div & \text{Положительный} & = & \text{Положительный} \\ \text{Отрицательный} & \times / \div & \ text{Отрицательный} & = & \text{Положительный} \\ \text{Положительный} & \times / \div & \text{Отрицательный} & = & \text{Отрицательный} \\ \text{Отрицательный} & \times / \div & \text{Положительный} & = & \text{Отрицательный} \\ \end{массив}
\begin{массив}{ccccc} + (-\text{Число}) &= -\text{Число} \\ — (+\text{Число}) &= -\text{Число} \\ + (+\text{Число}) &= +\text{Число} \\ — (-\text{Число}) & = +\text{Число} \\ \end{массив}
Для получения дополнительной информации см. положительные и отрицательные числа в нашем разделе «Счет».
положительные и отрицательные числа в нашем разделе «Счет».
Рабочие примеры
Сначала у нас есть рабочий пример сложения и вычитания отрицательных чисел.
Пример работы
В начале года вы открыли собственную клинику. Вам осталось потратить $\large\unicode{xA3}\normalsize 20,\!000$. Как и большинство вновь созданных предприятий, в первые месяцы вы несете убытки. В январе вы потеряли $\large\unicode{xA3}\normalsize4,\!500$, в феврале вы потеряли в три раза больше, чем в январе, а в марте вы потеряли вдвое меньше, чем в феврале. За это время вы получили три гранта размером $\large\unicode{xA3}\normalsize1,\!000$ каждый.
У вас уже есть овердрафт к концу марта? Если да, то насколько? Если нет, то сколько вам осталось потратить?
Решение
Сначала подсчитайте, сколько вы потеряли в феврале и марте:
В феврале: вы потеряли в три раза больше, чем в январе: $\large\unicode{xA3}\normalsize 4, \!500 \times 3 =\large\unicode{xA3}\normalsize 13,\!500$
‘ В марте: ‘ вы потеряли вдвое меньше, чем в феврале: $\large\unicode{xA3}\normalsize13 ,\!500 \div 2=\large\unicode{xA3}\normalsize6,\!750$
Ваши потери за этот период: $\large\unicode{xA3}\normalsize4,\!500+ \large\unicode{xA3}\normalsize13,\!500+ \large\unicode{xA3}\normalsize6,\! 750 = \large\unicode{xA3}\normalsize 24,\!750$.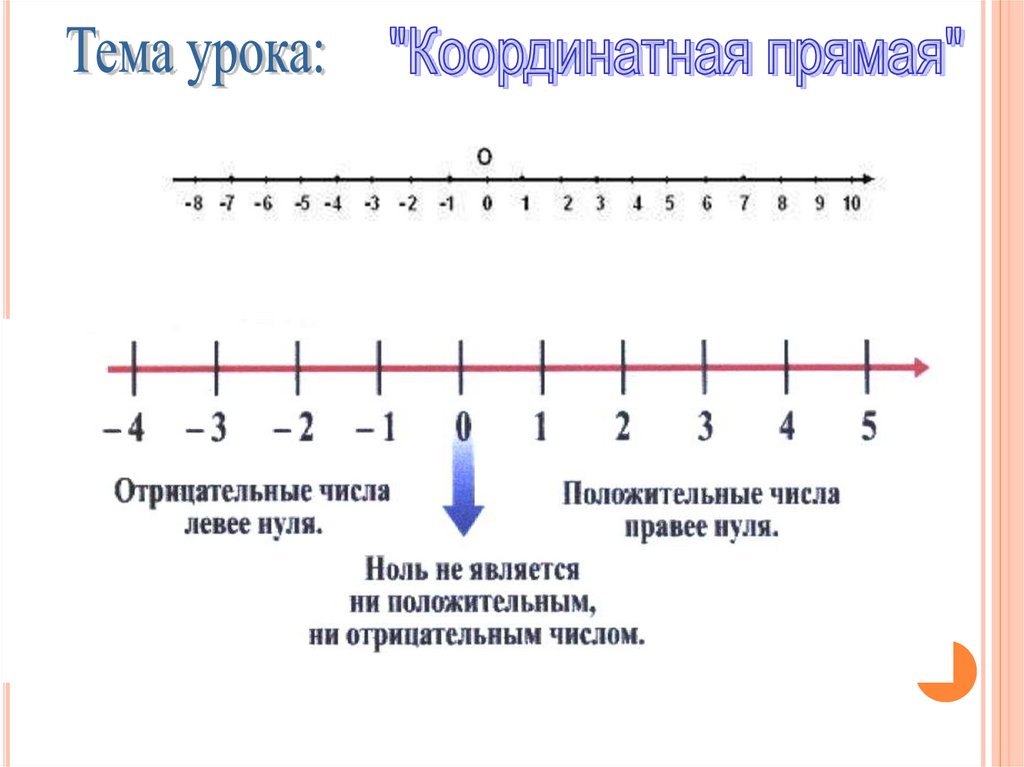 Но вы получаете всего три гранта: $\large\unicode{xA3}\normalsize1,\!000 \times 3 = \large\unicode{xA3}\normalsize3,\!000$. Следовательно, у вас есть: $\large\unicode{xA3}\normalsize20,\!000 + \large\unicode{xA3}\normalsize3,\!000 + (- \large\unicode{xA3}\normalsize24,\!750) = — \large\unicode{xA3}\normalsize1,\!750$ осталось на конец марта. Таким образом, к концу марта ваш овердрафт составит $\large\unicode{xA3}\normalsize1,\!750$.
Но вы получаете всего три гранта: $\large\unicode{xA3}\normalsize1,\!000 \times 3 = \large\unicode{xA3}\normalsize3,\!000$. Следовательно, у вас есть: $\large\unicode{xA3}\normalsize20,\!000 + \large\unicode{xA3}\normalsize3,\!000 + (- \large\unicode{xA3}\normalsize24,\!750) = — \large\unicode{xA3}\normalsize1,\!750$ осталось на конец марта. Таким образом, к концу марта ваш овердрафт составит $\large\unicode{xA3}\normalsize1,\!750$.
Теперь у нас есть второй пример умножения/деления на отрицательные числа.
Рабочий пример
У администратора на столе есть диспенсер с водой, чтобы ожидающие могли выпить, пока ждут.
В настоящее время в баке 2500$млн. Администратор знает, что каждый день выпивается 500 миллионов долларов.
а) Насколько полным был бак $4$ дней назад?
б) Вы находитесь в жару и выпиваете в два раза больше воды. Хватит ли воды в дозаторе еще на 3$ дней?
Раствор
a)
Мы знаем, что количество воды в дозаторе меняется на -500$мл каждый день. Чтобы рассчитать количество в баке, мы вычитаем это количество $4$ раз (чтобы вернуться назад на $4$ дней).
Чтобы рассчитать количество в баке, мы вычитаем это количество $4$ раз (чтобы вернуться назад на $4$ дней).
Таким образом, общее изменение равно: $-4\times -500=2000$ml.
Следовательно, $4$ дня назад в баке было: $2500+2000=4500$мл.
b)
Ежедневное потребление воды удвоилось. Таким образом, общее изменение каждый день составляет $-1000 $млн.
Через $3$ дня мы можем подсчитать, что в баке будет: $2500 — 3\x 1000 = -500$мл в баке.
Следовательно, в дозаторе недостаточно воды, чтобы продержаться еще $3$ дней, так как число отрицательное.
Проверьте себя
Попробуйте наши тесты Numbas по фоновой математике.
Внешние ресурсы
- Сложение и вычитание отрицательных значений в математике — это весело.
- Умножение на минусы из Математики — это весело.
Положительные и отрицательные числа | SkillsYouNeed
Стандартные числа, большие нуля, описываются как «положительные» числа. Мы не ставим перед ними знак плюс (+), потому что нам это не нужно, так как общее понимание таково, что числа без знака положительны.
Мы не ставим перед ними знак плюс (+), потому что нам это не нужно, так как общее понимание таково, что числа без знака положительны.
Числа меньше нуля называются «отрицательными». Перед ними стоит знак минус (-), указывающий, что они меньше нуля (например, -10 или ‘ минус 10 ‘).
Визуализация отрицательных и положительных чисел
Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую прямую, инструмент, с которым вы, возможно, хорошо знакомы, особенно если ваши дети учатся в начальной школе.
Это выглядит примерно так:
Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними выполнять.
Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания).
Эта числовая линия является упрощенной версией, но вы можете нарисовать их, включив в них все числа, если хотите. Большим преимуществом числовой линии является то, что ее очень легко нарисовать самому себе на обратной стороне конверта или на клочке бумаги, а также очень сложно ошибиться в расчетах. Пока вы внимательно подсчитываете количество мест, которые вы перемещаете, вы получите правильный ответ.
Вычитание отрицательных чисел
Если вы вычитаете отрицательное число, два отрицательных числа объединяются, чтобы получить положительное.
−10−(−10) не равно −20. Вместо этого вы можете думать об этом как о повороте одного из отрицательных знаков вертикально, чтобы пересечь другой и сделать плюс. Тогда сумма будет равна −10+10 = 0.
Краткое примечание о скобках
Для ясности: вы никогда не будете писать два отрицательных знака рядом без скобок.
Таким образом, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли видеть, что использование двух отрицательных знаков было преднамеренным.
-10—10 неправильно (и сбивает с толку)
-10-(-10) правильно (и более ясно)
Умножение и деление с положительными и отрицательными числами
При умножении или делении с комбинациями положительные и отрицательные числа, вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или разделяя числа, как если бы они оба были положительными. Получив числовой ответ, вы можете применить очень простое правило для определения знака ответа:
- Когда знаки двух чисел совпадают с , ответ будет положительным .
- Когда знаки двух чисел отличаются , ответ будет отрицательным .
Итак:
(положительное число) × (положительное число) = положительное число
(отрицательное число) × (отрицательное число) = положительное число
Но:
(положительное число) число) = отрицательное число
В качестве побочного вопроса, это каким-то образом объясняет, почему вы не можете получить квадратный корень из отрицательного числа (подробнее об этом читайте на нашей странице Специальные числа и понятия ). Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Правило работает так же, когда у вас есть более двух чисел для умножения или деления. Четное количество отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.
Почему умножение двух отрицательных чисел дает положительный ответ?
Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто сбивает с толку и кажется нелогичным.
Чтобы объяснить, почему это так, вернитесь к числовым линиям, использованным ранее в этой статье, поскольку они помогают объяснить это визуально.
- Во-первых, представьте, что вы стоите на числовой прямой в нулевой точке и смотрите в положительном направлении, то есть в сторону 1, 2 и так далее.
 Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
Следовательно, положительный × положительный = положительный - Теперь вернитесь к нулю и повернитесь лицом в отрицательном направлении, то есть к −1, −2 и т. д. Сделайте два шага вперед, затем еще два. Теперь вы стоите на −4. Вы переместились на 2 × -2 шага = -4 шага.
Отсюда отрицательный × положительный = отрицательный
В обоих этих примерах вы двигались вперед (т. е. в том направлении, в котором смотрели), положительное движение.
- Снова вернитесь к нулю, но на этот раз вы пойдете назад (негативное движение). Снова повернитесь лицом в положительном направлении и сделайте два шага назад. Теперь вы стоите на −2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Следовательно, положительный × отрицательный = отрицательный - Наконец, снова вернитесь к нулю, повернитесь лицом в отрицательном направлении.
 Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два негатива ), вы достигли положительного результата.
Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два негатива ), вы достигли положительного результата.
Отсюда отрицательный × отрицательный = положительный
- Два отрицания компенсируют друг друга. Вы можете увидеть это в речи:
- «Просто сделай это!» позитивное побуждение к действию.
- «Не делай этого!» просит кого-то не делать что-то. Это минус.
- «Не делай этого» означает «пожалуйста, сделай это». Два отрицания компенсируются и дают положительный результат как в математике, так и в речи.
- Знаки складываются физически. Когда у вас есть два отрицательных знака, один переворачивается, и они складываются вместе, чтобы получить положительный. Если у вас есть положительный и отрицательный, остается одна черточка, и ответ отрицательный.



 Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага. 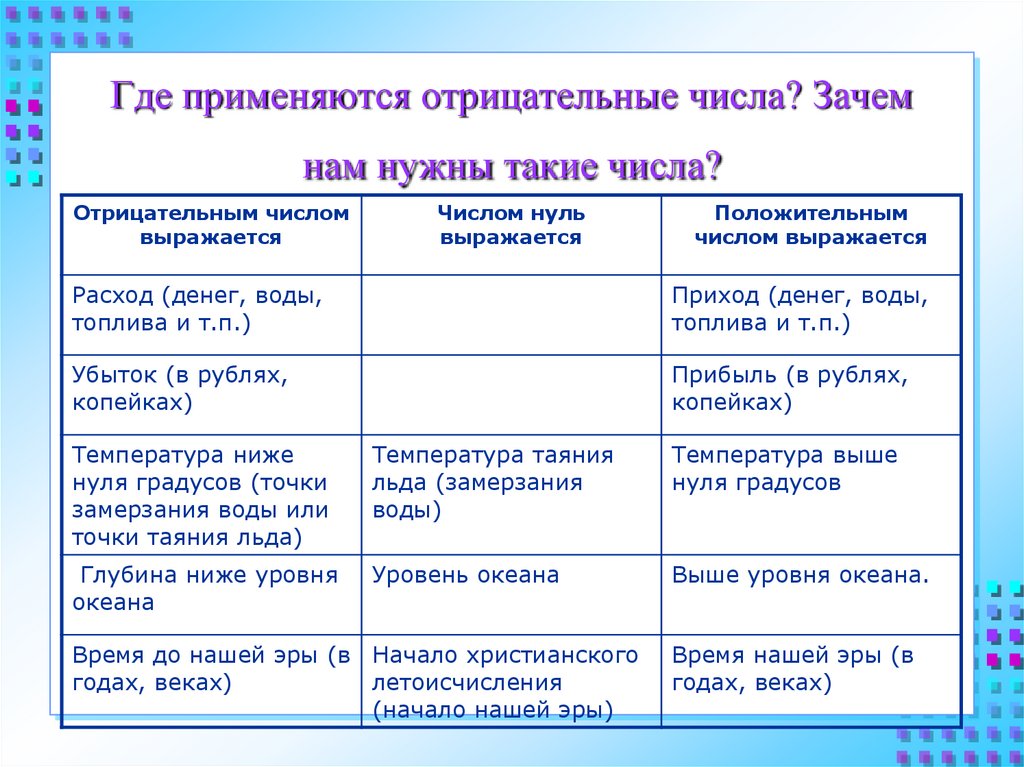 Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два негатива ), вы достигли положительного результата.
Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два негатива ), вы достигли положительного результата. 