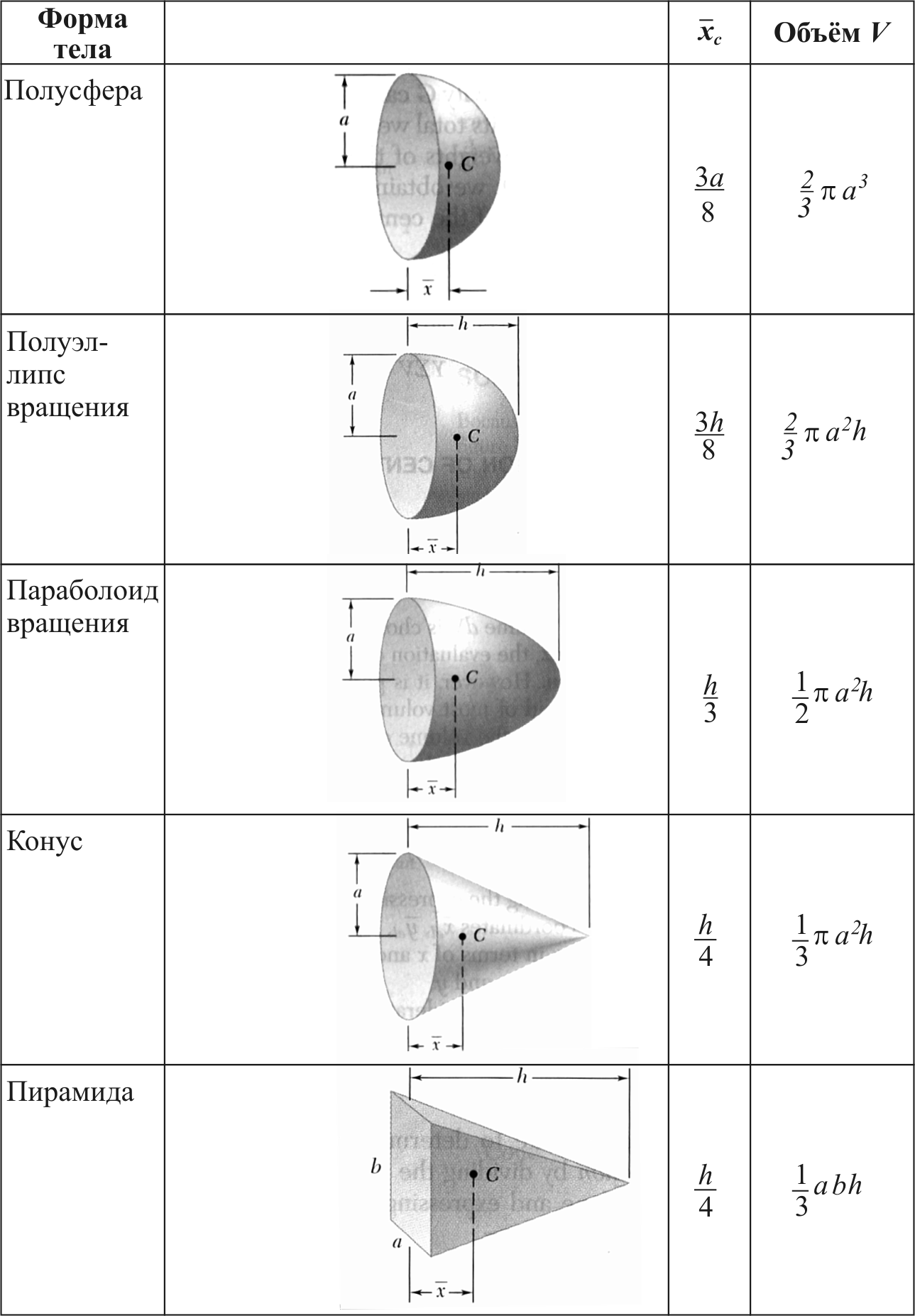
Полусфера, как форма обладающая приятным видом не имеющим углов и граней, часто используется в качестве малых архитектурных форм для оформления детских площадок, загородных участков, газонов и рекреационных зон. Цветные бетонные полусферы эстетично подходят под любой стиль оформления пространства, одновременно выполняя роль ограничителя проезда для транспорта. Полусфера яркого цвета, раскрашенная в виде арбуза, божий коровки, цветка, глобуса или любого другого предмета схожей формы, станет заметным и долговечным примером малых архитектурных форм.
Среди множества вариантов ограждений для тротуаров и парковочных зон, золотой серединой в соотношении цены, качества и долговечности являются бетонные полусферы. Бетонные полушары обладают всеми качествами которыми должны обладать дорожные ограждения. Это прочный долговечный материал устойчивый к ультрафиолету, воздействию химических реагентов и солей, не поддающийся коррозии и обладающий хорошим весом. Гладкая не травмоопасная форма полушара идеально подходит для применения в качестве ограждения для пешеходных зон, тротуаров, детских площадок, площадей перед станциями метрополитена и других мест скопления людей.
Особенностью бетонной полусферы как преграды для проезда автомобиля является ее прочность и долгое сохранение первоначального вида. Это несомненно делает выгодным установку бетонных полусфер перед другими вариантами ограждений из пластика или металла. Для фиксации полусферы из бетона на устанавливаемой поверхности используется арматурный штырь который вставляется в засверленное отверстие в тротуаре, асфальте, бетоне или плитке. То есть без разрушения поверхности дороги или тротуара и проведения сложных черновых работ. Таким образом полусфера аккуратно и прочно фиксируется, но в любой момент может быть демонтирована с помощью специальных средств. После снятия полусферы на месте установки остается малозаметное отверстие.
Во все эпохи и времена примером самой прочной архитектурной формы являлась пирамида, конус и полусфера/полушар. По сей день жители севера выстраивают свои жилища (иглу) в форме половины шара с заниженным входом у основания. Сферическая форма позволяет распределять возможные нагрузки по всей конструкции по принципу яичной скорлупы, и дает возможность разведения костра, без опасения задымления помещения.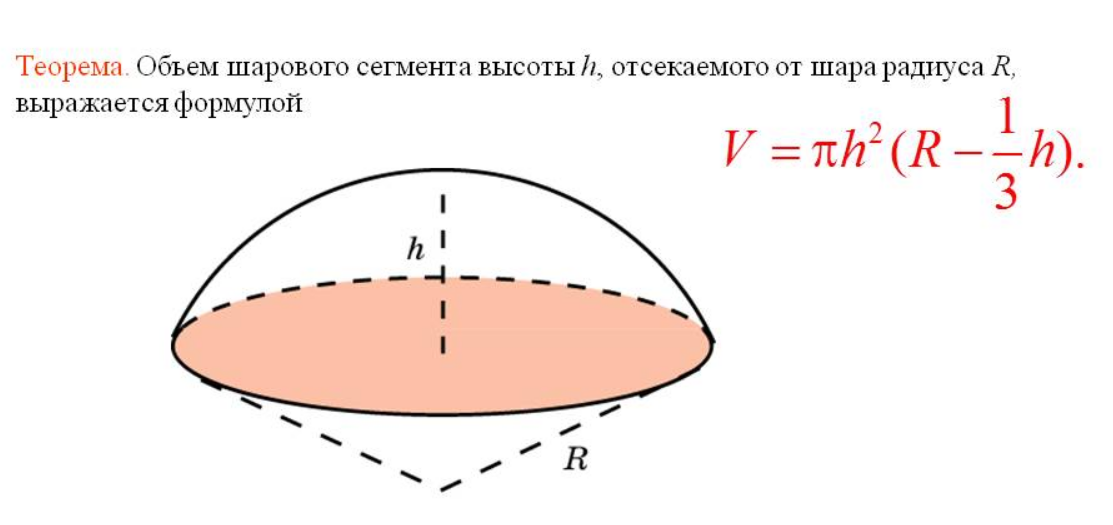
В современной архитектуре полусфере отведена особенная роль. Полукруглые дома и шатры, или как еще их называют купольные дома, выстраиваются во всех уголках планеты.Футуристичный вид зданий в виде полусферы используется в частном загородном строительстве, при строительстве городских зданий и сооружений, при возведении шатров и куполов с внутренней эко системой. Примером здания в виде полушара (сферической формы) в Москве является дом на Ленинградском проспекте.
В Санкт-Петербурге строение полушар вмещает в себя целый аквапарк. Конструкция выполнена по современной технологии повышенной прочности с симпатичной иллюминацией снаружи.
Совсем новый, но быстро обретающий популярность вид уличных и домашних светильников — светящаяся полусфера. Полушары правильной формы имеют внушительные размеры от 40 см в диаметре и излучают на выбор 14 цветов при четырех режимах свечения. Выбор цвета и режима свечения осуществляется при помощи пульта дистанционного управления.
В основе светящийся полусферы установлен прочный пластиковый патрон с RGB светодиодной лампой и специальным фильтром. Сверху на патрон с фильтром устанавливается пластиковый купол высокой прочности. Питание светящегося уличного полушара осуществляется от сети 220 В.
Особенностью таких ламп является их обычный вид при дневном свете и совсем необычное свечение в темное время суток. Днем эти полусферы выглядят как бетонные или каменные, а ночью сияют мягким светом.
Рабочий диапазон полусферических ламп от -40 до +80 градусов C. Корпус полусферы влагонепроницаем, устойчив к физическим воздействиям и легко моется. По вопросу установки светящихся полусфер для улицы и помещения или как купить, обращайтесь по эл адресу: radair[собака]yandex.ru или по телефону в контактах сайта.
Самыми удобными креслами в мире считаются именно кресла в виде полусфер. Придуманное неизвестным изобретателем кресло полусфера Papasan обрело популярность еще в 50 годах двадцатого века.
Основа кресла плелась из ротанга (испанского тростника), а вельветовый чехол в качестве подушки набивался хлопковым пухом.
К началу двадцать первого века появилось множество кресел и диванов в виде полушаров/полусфер не только из разных видов древесины, но из пластика, стеклопластика и даже металла. Кресло полусфера не редкий элемент дизайнерской мебели в современном доме. Ведь именно такая форма, по мнению владельцев, придает чувство особенной расслабленности и комфорта.
Во многих смыслах универсальный тренажер для развития координации, равновесия и не только. Все та же форма полусферы, но на это раз из резины, в народе более известный как полу-мяч. Изобретатель резиновой полусферы для фитнеса утверждает, что все упражнения совершаемые на неустойчивой поверхности, на такой как резиновая полусфера, заставляют работать большое количество мелких мышц, улучшает координацию и положительно влияет на работу вестибулярного аппарата.
То есть воздействие мяча повышает тонус опорно-двигательного аппарата и улучшает осанку. Регулировать жесткость полушара можно при помощи воздуха, накачивая или спуская через специальный клапан, это в свою очередь регулирует сложность выполнения упражнений используя резиновую полусферу для фитнеса.
Если не все, то многие выросшие в СССР помнят этот атрибут каждой детской площадки во дворе. Пользующаяся огромной популярностью, на ровне с качелями, горка в виде металлической паутинки полусферической формы — прекрасное спортивное и развлекательное сооружение в одном флаконе. Детвора кружилась по ней как стая обезьян, играя в салки, перебиралась на руках с одного края на другой. Достаточно подобных детских паутинок сохранилось и по сей день, что в очередной раз является примером прочности конструкции с применением формы полушара, полусферы.
Еще одно воплощение в виде полусферической формы направленное на развитие и образование деток дошкольного и школьного возраста.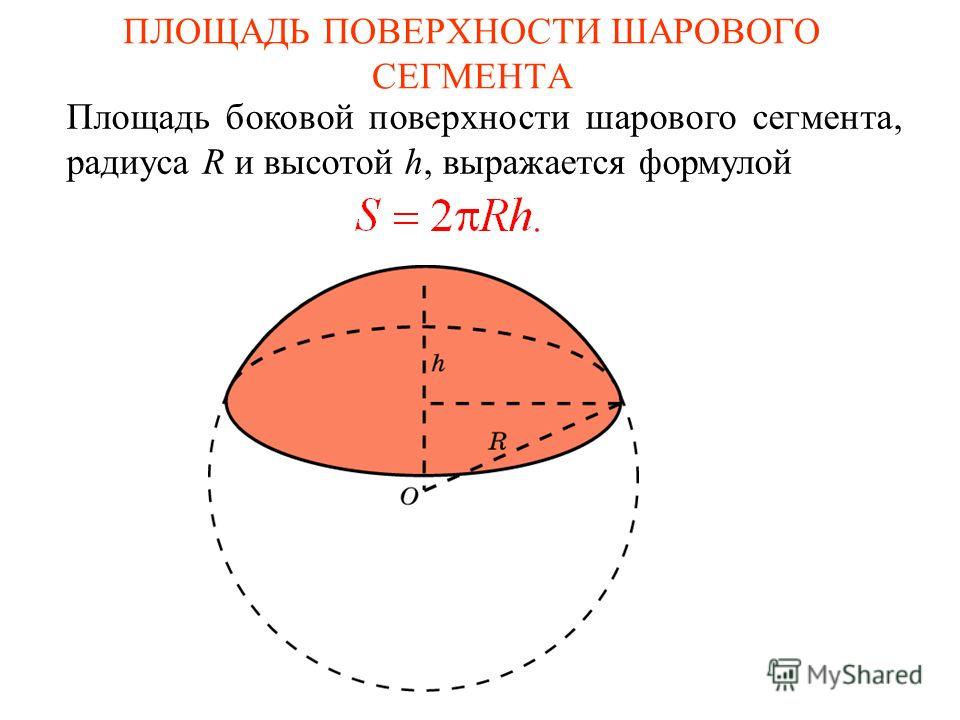
Под куполом мобильных планетариев читаются интереснейшие лекции с сопровождением анимации при помощи проектора. Форма полусферы как нельзя лучше подходит для имитации небесного пространства.
Сфера, шар, сегмент и сектор. Формулы и свойства
Навигация по странице: Определение сферы Определение шара Объём шара Площадь поверхности сферы Уравнение сферы Основные свойства сферы и шара Секущая, хорда, секущая плоскость и их свойства Касательная, касательная плоскость и их свойства Сегмент шара Срез шара Сектор шара Касательные сферы Концентрические сферы
Определение.
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула.
Объём шара:
| V = | 4 | πR3 = | 1 | πD3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4πR2 = πD2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:
x2 + y2 + z2 = R2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0, y0, z0) в декартовой системе координат:
(x — x0)2 + (y — y0)2 + (z — z0)2 = R2
3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0):
x = x0 + R · sin θ · cos φy = y0 + R · sin θ · sin φz = z0 + R · cos θгде θ ϵ [0,π], φ ϵ [0,2π].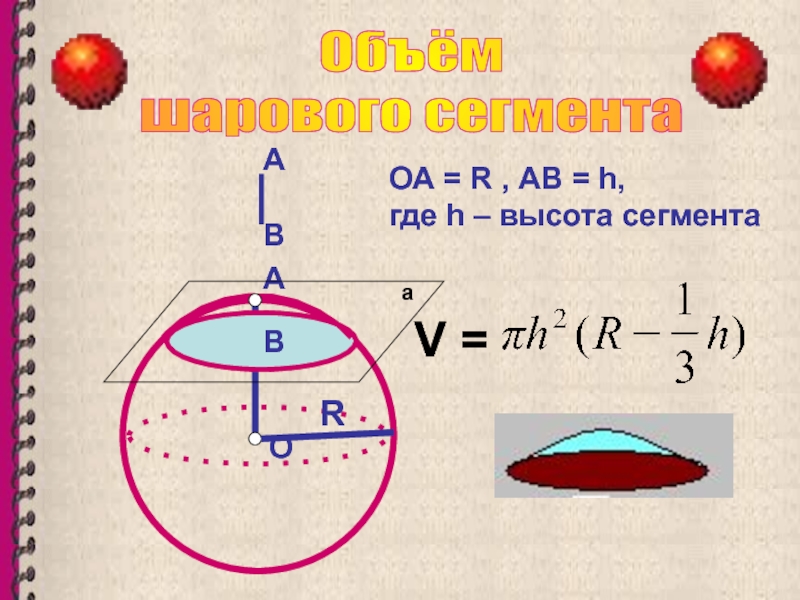
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m < R
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг.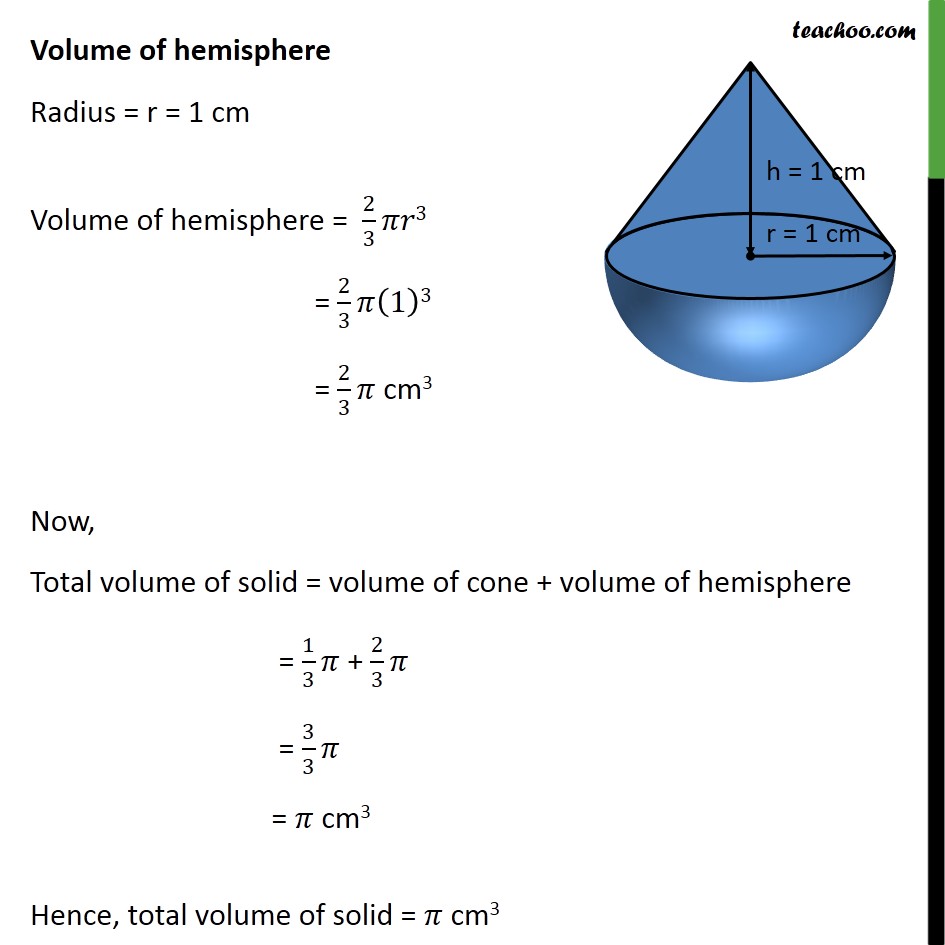
Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R2 — m2,
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение.
Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2πRh
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
| V = | h2π | (3R — h) |
| 3 |
Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.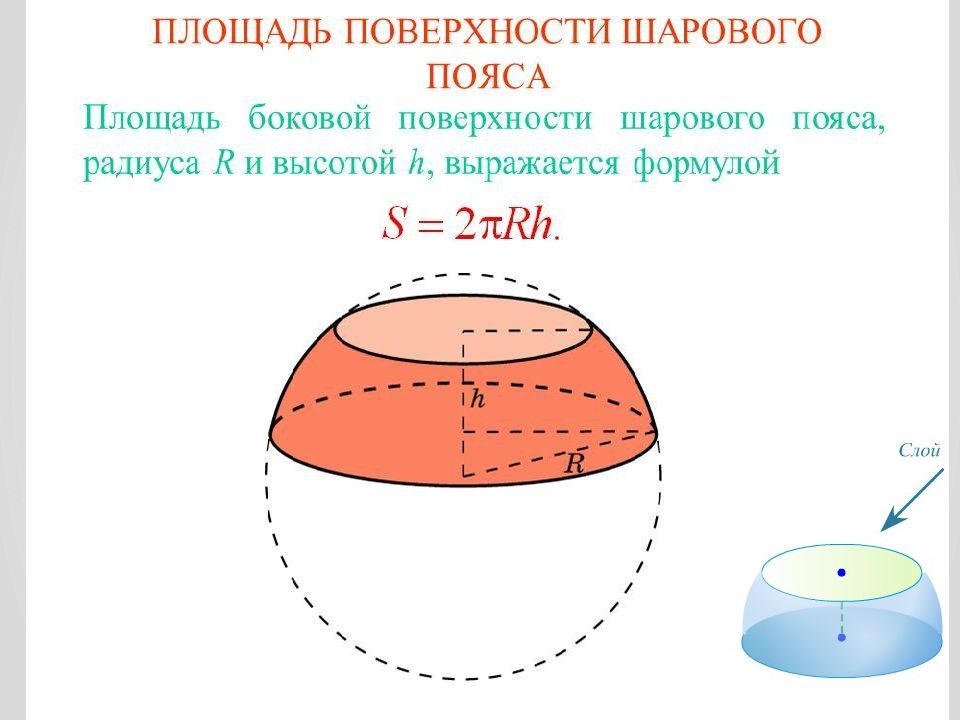
Формула. Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R):
S = πR(2h + √2hR — h2)
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
| V = | 2πR2h |
| 3 |
Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.
Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.
Все таблицы и формулы
Калькулятор полушария
Форма полушария
r = радиус
C = окружность основания
В = объем
A = площадь изогнутой поверхности
B = площадь базовой поверхности
К = общая площадь поверхности
π = пи = 3,1415926535898
√ = квадратный корень
Калькулятор Использование
Этот онлайн-калькулятор рассчитает различные свойства полушария по любой 1 известной переменной.
Он также вычисляет переменные с точки зрения PI π. Полушарие составляет 1/2 часть
шар разрезать пополам, проведя плоскость через центр шара. Объем V и площадь А рассчитаны по существу для половины сферы. Видеть
Полушария в Mathworld.
Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на расчеты. Единицы используются для указания порядка результатов, таких как футы, футы 2 или фут 3 . Например, если вы начинаете с мм и знаете, что r в мм, ваши расчеты дадут A в мм 2 , V в мм 3 и C в мм.
Полушарие Формулы для радиуса r:
- Объем полушария:
- В = (2/3)πr 3
- Окружность основания полушария:
- С = 2πr
- Площадь криволинейной поверхности полусферы (1 сторона, только внешняя):
- А = 2πr 2
- Рассчитайте площадь основания полусферы (окружности):
- В = πr 2
- Суммарная площадь поверхности полушария:
- К = (2πr 2 ) + (πr 2 ) = 3πr 2
Расчет полушария:
Используйте следующие дополнительные формулы вместе с формулами выше.
- Зная радиус полушария, рассчитайте объем, площадь кривизны поверхности, длину окружности и общую площадь поверхности.
Дано r найти V, A, C, K- используйте формулы выше
- Зная объем полушария, рассчитайте радиус, площадь криволинейной поверхности, длину окружности и общую площадь поверхности.
По данному V найти r, A, C , K- r = кубический корень (3V / 2π)
- Зная площадь криволинейной поверхности полушария, рассчитайте радиус, объем, длину окружности и общую площадь поверхности.
Дано A найти r, V, C, K- г = √(А / 2π)
- Зная общую площадь поверхности полушария, рассчитайте радиус, объем, площадь криволинейной поверхности и длину окружности.
По данным K найти r, V, A, C- г = √(К / 3π)
- Зная длину окружности полушария, рассчитайте радиус, объем, площадь криволинейной поверхности и общую площадь поверхности.
По данному C найти r, V, A , K- г = С / 2π
Калькулятор площади поверхности полушария
Автор Dominik Czernia, PhD
Отзыв от Bogna Szyk и Adena Benn сфера?
Наш калькулятор площади поверхности полушария представляет собой удобный инструмент, который находит различные типы площади поверхности полушария. Вы ищете ответ на вопрос, как найти площадь поверхности полушария? Или, может быть, вам просто нужно быстро оценить его? Что бы вы ни планировали сделать, попробуйте этот калькулятор полушарий, который включает в себя несколько различных площадей полушария формулы .
Полусферы создаются путем разделения сферы на две равные половины, как вы можете видеть на рисунке ниже. В отличие от полной сферы, полусфера имеет два типа площадей поверхности: площадь основания (которая представляет собой круг) и площадь крышки . Обозначения, которые мы использовали в этом калькуляторе площади поверхности полушария, следующие:
- r — радиус полушария;
- d — диаметр полусферы;
- V — объем полусферы;
- А — общая площадь поверхности полушария;
- Ab — площадь базовой поверхности полушария;
- Ac — площадь поверхности крышки полусферы; и
- А/В — отношение поверхности к объему полусферы.
🙋 Интересно, что суммарный объем двух полушарий равен объему одной полной сферы. Однако это не относится к площади поверхности.
Суммарная площадь двух полушарий больше , чем площадь сферы. Причина проста: полушария имеют дополнительных площадей основания .
Если вам нужно проанализировать полные сферы, наш калькулятор сфер — это то, что вам нужно!
Как найти площадь поверхности полушария?
Когда мы разделим сферу пополам и возьмем одну из получившихся частей , мы получим полусферу. В каждом полушарии мы можем назвать две области поверхности: основания и крышки (см. рисунок выше). Из калькулятора площади сферы мы знаем, что площадь поверхности сферы следующая:
A(сфера) = 4 × π × r² .
Вы можете думать об этом как о , в два раза превышающем площадь поверхности крышки полушария . Следовательно, площадь шапки полушария равна:
Ac = A(сфера) / 2 ,
Ac = 2 × π × r² .
Площадь базовой поверхности представляет собой круг с тем же радиусом, что и полусфера .
Таким образом, согласно кругу вычислить: найти A, можно выразить так:
Ab = π × r² .
Наконец, общая площадь поверхности равна сумма этих двух вкладов :
A = Ac + Ab ,
A = 2 × π × r² + π × r² ,
A = 3 × π × r² .
Этот калькулятор площади полушария позволяет найти все три типа площадей поверхности определенного полушария. Кроме того, вы можете делать каждый расчет в различных единицах (SI и имперские единицы). Если вы хотите узнать больше о преобразовании единиц площади, ознакомьтесь с нашим конвертером площади!
Какова площадь полушария?
Теперь, когда мы знаем, что такое площадь поверхности полушария и как ее найти, давайте попробуем вывести различные формулы площади полушария. Они могут быть полезны в ситуациях, когда у нас нет радиуса . Прежде всего, есть некоторые основные уравнения полушария, которые вы должны знать:
- Диаметр полушария:
d = 2 × r, - Объем полушария:
В = 2/3 × π × r³, - Площадь основания полушария:
Ab = π × r², - Площадь поверхности крышки полусферы:
Ac = 2 × π × r², - Полная площадь поверхности полушария:
A = 3 × π × r², - Отношение поверхности к объему полушария:
A / V = 9 / (2 × r).
Формула площади полушария (для общей площади) может быть получена из приведенных выше уравнений. Мы можем получить даже шесть из них! Уравнения, используемые калькулятором площади полушария, следующие:
- Дан радиус :
A = 3 × π × r²; - Учитывая диаметр :
A = 3/4 × π × d²; - Дан объем :
A = ³√[243/4 × π × V²]; - Дана площадь основания :
A = 3 × Ab; - Учитывая площадь крышки :
A = 3/2 × Ac; и - Учитывая отношение поверхности к объему :
A = 243 × π / (4 × (A/V)²).
Как известно, Земля приблизительно представляет собой сферу с радиусом почти 6400 км , в которой можно указать северное и южное полушария (конкретно говоря, Земля — это геоид). Этот раздел играет важную роль в географии и физике.