Как найти длину отрезка по координатам точек: Размещение рекламы на Studygide.ru

Формула длины отрезка в координатах. Нахождение координат середины отрезка, примеры, решения

Приведу подробный пример, как можно определить длину отрезка по заданным координатам, воспользовавшись сервисом онлайн на сайте Контрольная работа Ру.

Допустим, вам надо найти длину отрезка на плоскости

(в пространстве вы можете по-аналогии расчитывать, только надо изменить точку на размерность трёх)

Отрезок AB имеет концы с координатами A (1, 2) и B (3, 4).

Для того, чтобы вычислить длину отрезка AB воспользуйтесь следующими шагами:

1. Перейдите на страницу сервиса по нахождению расстояния между двумя точками онлайн:

Мы можем этим пользоваться, т.к. длина отрезка по коорд. как раз и равна расстоянию между точками A и B.

Чтобы задать правильную размерность точки A, то потяните за нижний правый край влево, как показано на рис.

После того, как ввели координаты первой точки A(1, 2), то нажмите на кнопку

3. На втором шаге вы увидите форму для ввода второй точки B, введите её координаты, как рис.

ниже:

Точки a и b введены! Решение:

Даны точки a =

и b =

Найдем расстояние между точками (s)

Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.

Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.

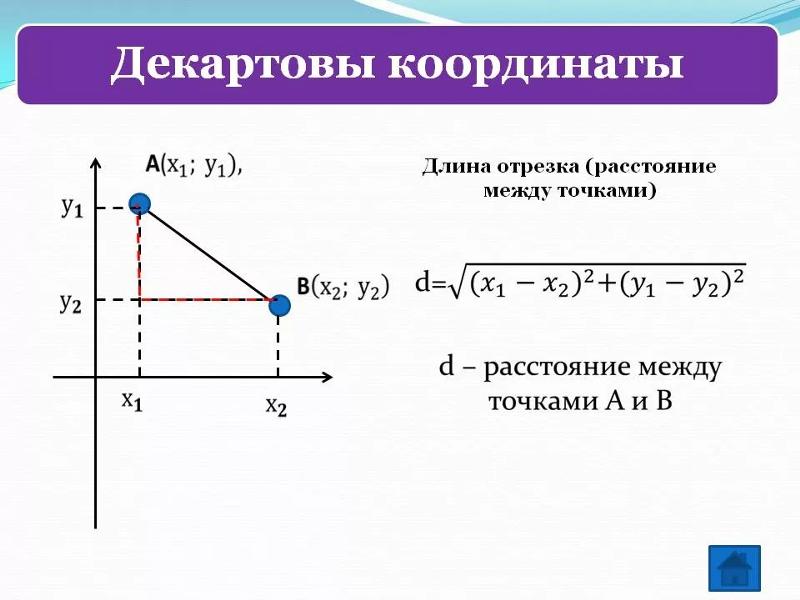
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.

Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.

Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .

Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.

Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .

Рассчитаем длину отрезка А

, для этого найдем квадратный корень:

A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .

Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .

Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат каждая точка имеет три координаты. 2))

Пусть отрезок задан двумя точками в плоскости координат, тогда можно найти его длину с помощью теоремы Пифагора.

Инструкция

Пусть заданы координаты концов отрезка (x1- y1) и (x2- y2). Начертите отрезок в системе координат.

Опустите перпендикуляры из концов отрезка на оси X и Y. Отрезки, отмеченные на рисунке красным, являются проекциями исходного отрезка на оси координат.

Если выполнить параллельный перенос, отрезков-проекций к концам отрезков, то получится прямоугольный треугольник. Катетами этого треугольника будут являться перенесенные проекции, а гипотенузой — сам отрезок AB.

Длины проекций легко вычисляются. Длина проекции на ось Y будет равна y2-y1, а длина проекции на ось X — x2-x1. Тогда по теореме Пифагора |AB|²- = (y2 — y1)²- + (x2 — x1)²-, где |AB| — длина отрезка.

Представив эту схему нахождения длины отрезка в общем случае, легко вычислять длину отрезка, не строя отрезок. Посчитаем длину отрезка, координаты концов которого (1-3) и (2-5). 1/2.

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле

Если даны две точки пространства и , то длину отрезка можно вычислить по формуле

Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант

Пример 3

Решение: по соответствующей формуле:

Ответ:

Для наглядности выполню чертёж

Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:

Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».

Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:

Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.

Вот другие распространенные случаи:

Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся.

Пробуем поделить на девять: . В результате:
Готово.

Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.

В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.

Давайте заодно повторим возведение корней в квадрат и другие степени:

Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.

Задание для самостоятельного решения с отрезком в пространстве:

Пример 4

Даны точки и . Найти длину отрезка .

Решение и ответ в конце урока.

Измерить отрезок — значит найти его длину. Длина отрезка — это расстояние между его концами.

Измерение отрезков производится путём сравнения данного отрезка с другим отрезком, принятым за единицу измерения.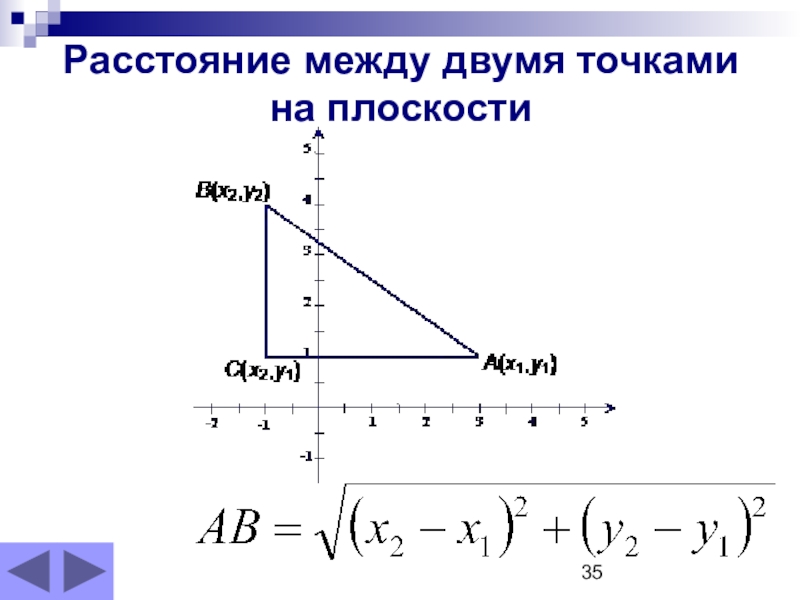 Отрезок, принятый за единицу измерения, называется единичным отрезком .

Если за единичный отрезок принят сантиметр, то для определения длины данного отрезка надо узнать, сколько раз в данном отрезке помещается сантиметр. В этом случае измерение удобно производить с помощью сантиметровой линейки.

Начертим отрезок AB и измерим его длину. Приложим шкалу сантиметровой линейки к отрезку AB так, чтобы её нулевая точка (0) совпала с точкой A :

Если при этом окажется, что точка B совпадает с некоторым делением шкалы — например, 5, то говорят: длина отрезка AB равна 5 см, и пишут:

AB = 5 см.

Свойства измерения отрезков

Когда точка делит отрезок на две части (на два отрезка), длина всего отрезка равна сумме длин этих двух отрезков.

Рассмотрим отрезок AB :

Точка C делит его на два отрезка: AC и CB . Мы видим, что AC = 3 см, CB = 4 см и AB = 7 см. Таким образом, AC + CB = AB .

Любой отрезок имеет определённую длину, большую нуля.

Как найти длину по координатам точек. Нахождение координат середины отрезка: примеры, решения

Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.

Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.

Итак, в системе координат начертим отрезок с заданными координатами его концов

(x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.

Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.

Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .

Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.

Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .

Рассчитаем длину отрезка А , для этого найдем квадратный корень:

A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .

Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .

Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.

Длина отрезка с помощью линейки

Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.

Метод координат на плоскости

Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.

Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.

Метод координат в пространстве

Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?

1. Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
2. После этого нужно возвести каждую координату вектора в квадрат.
3. Затем складываем квадраты координат.
4. Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).

Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.

Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .

Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.

Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.

Вам понадобится

• Декартовы, полярные и сферические координаты концов отрезка

Инструкция

1. Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами этой точки.Пускай у вас сейчас есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и 2-й точки. Видимо, что расстояние между этими двумя точками будет равно модулю вектора r = r1-r2, где (r1-r2) – векторная разность.Координаты вектора r, видимо, будут следующими: x1-x2, y1-y2, z1-z2. Тогда модуль вектора r либо расстояние между двумя точками будет равно: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)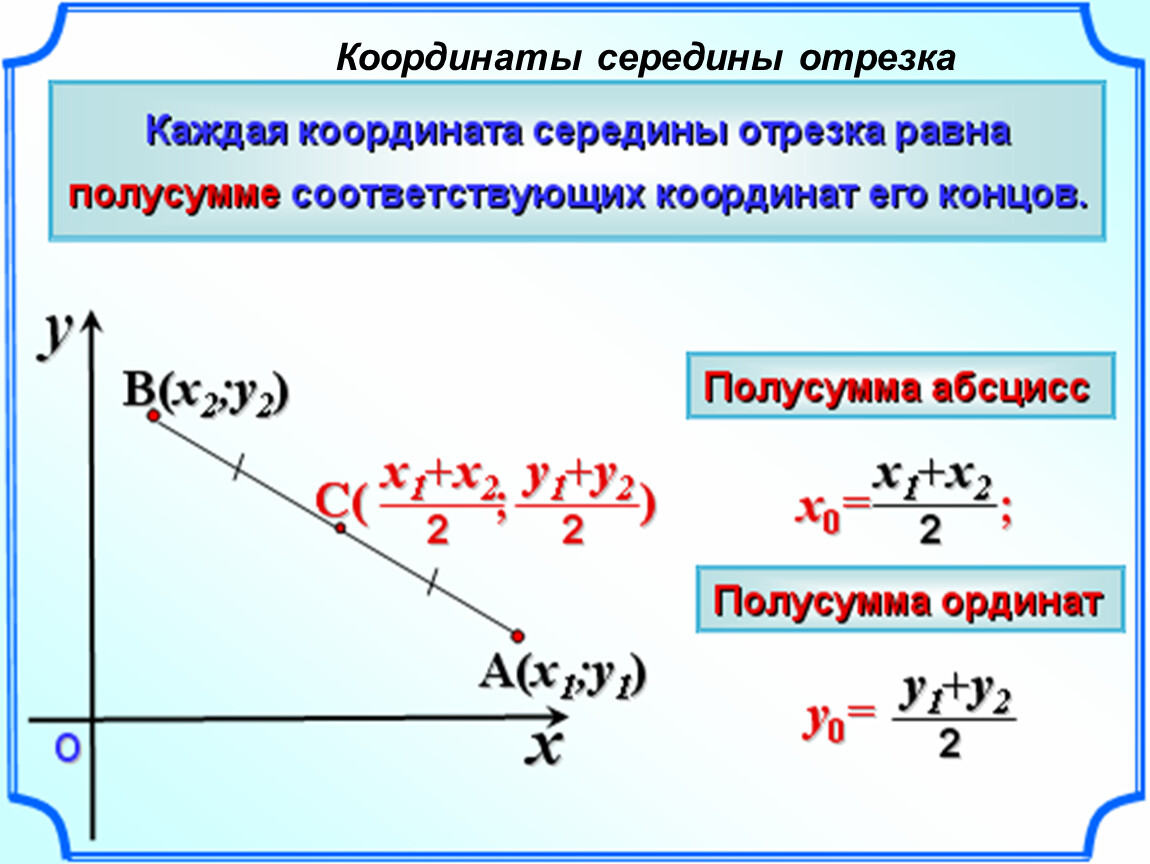^2)). 2))

Видео по теме

Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).

Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой. Большинству эти задания будут не интересны. Но изложить их считаю необходимым.

Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н емного теории.

Построим на координатной плоскости точку А с координатами х= 6, y=3.

Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.

Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.

То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.

Длина отрезка на координатной плоскости

Формула для определения длины отрезка, если известны координаты его концов:

Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными

Х В – Х А и У В – У А

* * *

Середина отрезка. Её Координаты.

Формула для нахождения координат середины отрезка:

Уравнение прямой проходящей через две данные точки

Формула уравнения прямой походящей через две данные точки имеет вид:

где (х 1 ;у 1 ) и (х 2 ;у 2 ) координаты заданных точек.

Подставив значения координат в формулу, она приводится к виду:

y = kx + b , где k — это угловой коэффициент прямой

Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!

Что ещё можно добавить?

Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.

Рассмотрим задачи.

Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.

Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.

Ответ: 8

Найдите расстояние от точки A с координатами (6;8) до оси ординат.

Расстояние от точки А до оси ординат равно абсциссе точки А.

Ответ: 6.

A (6;8) относительно оси Ox .

Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).

Ордината равна минус восьми.

Ответ: – 8

Найдите ординату точки, симметричной точке A (6;8) относительно начала координат.

Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).

Её ордината равна – 8.

Ответ: –8

Найдите абсциссу середины отрезка, соединяющего точки O (0;0) и A (6;8).

Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).

Вычисляем по формуле:

Получили (3;4). Абсцисса равна трём.

Ответ: 3

*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.

Найдите абсциссу середины отрезка, соединяющего точки A (6;8) и B (–2;2).

Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).

Вычисляем по формуле:

Получили (2;5). Абсцисса равна двум.

Ответ: 2

*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.

Найдите длину отрезка, соединяющего точки (0;0) и (6;8).

Длина отрезка при данных координатах его концов вычисляется по формуле:

в нашем случае имеем О(0;0) и А(6;8). Значит,

*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:

Ответ:10

Найдите косинус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.

Угол наклона отрезка – это угол между этим отрезком и осью оХ.

Из точки А опустим перпендикуляр на ось оХ:

То есть, угол наклона отрезка это угол ВОА в прямоугольном треугольнике АВО.

Косинусом острого угла в прямоугольном треугольнике является

отношение прилежащего катета к гипотенузе

Необходимо найти гипотенузу ОА.

По теореме Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Таким образом, косинус угла наклона равен 0,6

Ответ: 0,6

Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.

Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ .

Найдите расстояние от точки A с координатами (6;8) до оси абсцисс.

Найдите расстояние от точки A с координатами (6;8) до начала координат.

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле

Если даны две точки пространства и , то длину отрезка можно вычислить по формуле

Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант

Пример 3

Решение: по соответствующей формуле:

Ответ:

Для наглядности выполню чертёж

Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:

Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».

Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:

Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.

Вот другие распространенные случаи:

Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.

Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.

В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.

Давайте заодно повторим возведение корней в квадрат и другие степени:

Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.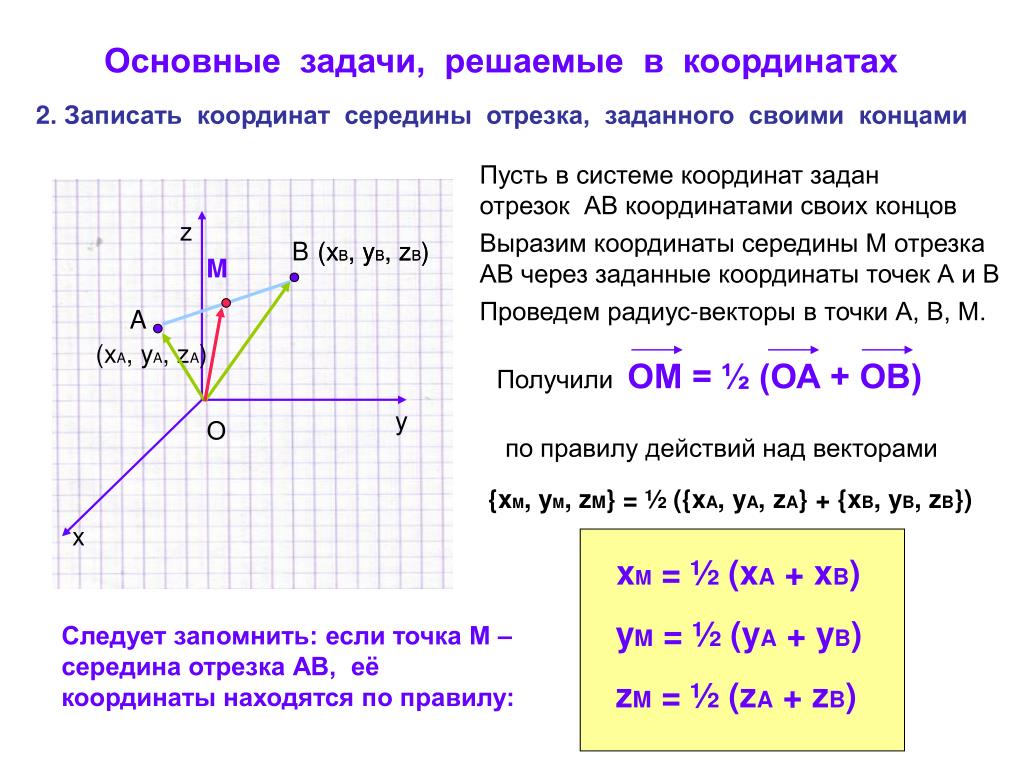

Задание для самостоятельного решения с отрезком в пространстве:

Пример 4

Даны точки и . Найти длину отрезка .

Решение и ответ в конце урока.

Отрезок линии

— определение, примеры

Отрезок линии — это часть линии, имеющая две конечные точки и фиксированную длину. Она отличается от линии, которая может быть продолжена в обоих направлениях и не имеет ни начала, ни конца. В этом уроке давайте узнаем больше об определении сегмента линии, символе сегмента линии и о том, как найти длину сегмента линии.

1.	Что такое линейный сегмент?
2.	Как измерить отрезки линии?
3.	Формула сегмента линии
4.	Разница между линией, сегментом линии и лучом
5.	Часто задаваемые вопросы по линейному сегменту

Что такое линейный сегмент?

Отрезок линии — это путь между двумя точками, который можно измерить. Поскольку отрезки имеют определенную длину, они могут образовывать стороны любого многоугольника. На приведенном ниже рисунке показан отрезок AB, где длина отрезка AB относится к расстоянию между его конечными точками A и B.

Определение сегмента линии

Сегмент линии может быть определен как часть линии фиксированной длины, которую можно измерить.

Символ сегмента линии

Сегмент линии представлен полосой сверху, которая является символом сегмента линии. Записывается как \(\overline{AB}\).

Как измерить отрезки линии?

Отрезки можно измерять с помощью линейки (шкалы). Давайте посмотрим, как измерить данный отрезок линии и назвать его PQ.

• Шаг 1: Аккуратно расположите кончик линейки так, чтобы ноль оказался в начальной точке P данного отрезка.
• Шаг 2: Теперь начните читать значения, указанные на линейке, и найдите число, которое находится на другой конечной точке Q.
• Шаг 3: Таким образом, длина отрезка равна 4 дюймам, что можно записать как \(\overline{PQ}\) = 4 дюйма.

Линейный сегмент Формула

В приведенном выше примере мы измерили длину отрезка линии PQ как 4 дюйма. Это записывается как \(\overline{PQ}\) = 4 дюйма. Теперь давайте посмотрим, как найти длину отрезка, когда заданы координаты двух конечных точек. В этом случае мы используем формулу расстояния, то есть D = √[(\(x_{2}-x_{1}\)) ² + (\(y_{2}-y_{1}\) ) ² ]. Здесь (\(x_{1}\), \(y_{1}\)) и (\(x_{2}\), \(y_{2}\)) — координаты заданных точек.

Например, отрезок имеет следующие координаты: (-2, 1) и (4, –3). Применим формулу расстояния, чтобы найти длину отрезка. Здесь \(x_{1}\) = -2; \(х_{2}\) = 4; \(у_{1}\) = 1; \(у_{2}\) = -3. После подстановки этих значений в формулу расстояния получаем: D =√[(4-(-2)) ² + (-3-1) ² ) = √((4+2) ² + (-3-1) ² ] = √(6 ² + (-4) ² ) = √(36 + 16) = √52 = 7,21 ед. Следовательно, используя формулу расстояния, мы нашли, что длина отрезка с координатами (-2, 1) и (4, –3) равна 7,21 ед.

Разница между линией, сегментом линии и лучом

Обратите внимание на приведенные ниже рисунки, чтобы понять разницу между линией, сегментом линии и лучом.

Строка	Линейный сегмент	Рэй
Линия — это набор точек, бесконечно простирающихся в двух противоположных направлениях.	Отрезок линии является частью линии и имеет начальную и конечную точки.	Луч — это часть линии, которая имеет начальную точку, но не имеет определенной конечной точки.
Обозначается стрелками на обоих концах, чтобы показать, что это продолжается вечно.	Имеет определенную длину и обозначается двумя концами.	Он показывает одну начальную точку и стрелку на другом конце, что означает, что он будет продолжаться вечно в одном направлении.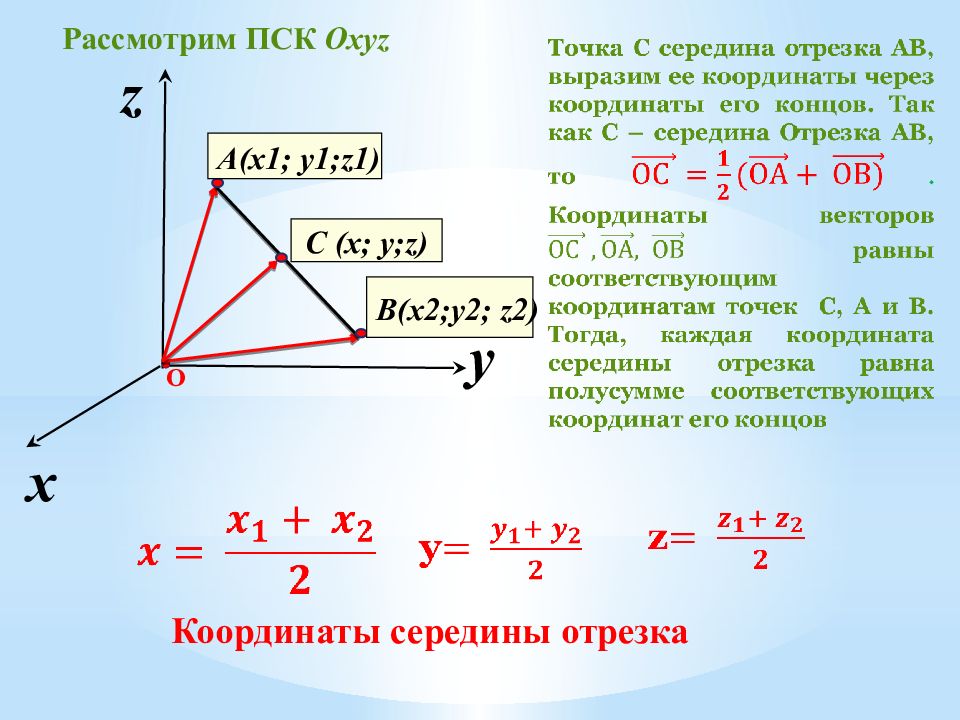
Он не имеет конечных точек и записывается как \(\overleftrightarrow{AB}\).	Обозначается полосой сверху, которая является символом сегмента линии. Записывается как \(\overline{CD}\).	Записывается как \(\overrightarrow{\mathrm{EF}}\).

Важные примечания

• Линия имеет бесконечные концы и не может быть измерена.
• Отрезок имеет начальную и конечную точки, поэтому его можно измерить.
• Отрезки имеют определенную длину, следовательно, они образуют стороны любого многоугольника.
• Луч имеет только одну начальную точку и не имеет конечной точки, поэтому его нельзя измерить.
• Понятие лучей можно понять на примере солнечных лучей, у которых есть начальная точка, но нет конечной.

☛Связанные темы

Ознакомьтесь со следующими страницами, посвященными линейному сегменту.

• Разница между линией и линейным сегментом
• Рабочие листы «Линии, лучи и сегменты линий»
• Как узнать, перпендикулярны ли два отрезка прямой?

 

Примеры линейных сегментов

1. Пример 1: Определите, является ли данная фигура отрезком, линией или лучом.

   Решение:

   Рисунок имеет одну начальную точку, но стрелку на другом конце. Это показывает, что это не отрезок или линия, это луч. Следовательно, LM — луч.

2. Пример 2: Назовите отрезки в данном треугольнике.

   Решение:

   Треугольник образуют отрезки \(\overline{PQ}\), \(\overline{QR}\) и \(\overline{PR}\).
   Следовательно, отрезки в данном треугольнике равны \(\overline{PQ}\), \(\overline{QR}\) и \(\overline{PR}\).

3. Пример 3: Найдите длину отрезка PQ, если координаты P и Q равны (3, 4) и (2, 0) соответственно.

   Решение:

   Координаты P и Q: (3, 4) и (2, 0). Применим формулу расстояния: D = √[(\(x_{2}-x_{1}\)) ² + (\(y_{2}-y_{1}\)) ² ]. Здесь \(x_{1}\) = 3; \(х_{2}\) = 2; \(у_{1}\) = 4; \(y_{2}\) = 0. Следовательно, длина отрезка D =√[(2-3) ² +(0-4) ² ] = √((-1) ² +(-4) ² ) = √(1 + 16) = √17 = 4,123 единицы.
   Следовательно, \(\overline{PQ}\) = 4,123 единицы.

перейти к слайдуперейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатное пробное занятие

Практические вопросы в онлайн-сегменте

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по линейному сегменту

Что такое отрезок в математике?

Отрезок линии — это часть линии, соединяющая две точки, которые считаются ее конечными точками. Это расстояние между двумя точками, которое можно измерить. Поскольку отрезки имеют определенную длину, они могут образовывать стороны любого многоугольника.

В чем разница между линией и сегментом линии?

Линия не имеет конечных точек и может быть продолжена в оба конца, тогда как отрезок линии имеет две фиксированные конечные точки. Линия бесконечна, тогда как отрезок линии имеет определенную длину, поэтому его можно измерить.

Как нарисовать отрезок?

Существует два основных метода построения отрезка любой длины. Первый метод построения отрезка прост, в котором мы берем линейку (шкалу) и отмечаем начальную точку как P, затем нам нужно отметить конечную точку как Q с необходимой длиной отрезка. Например, если требуемая длина составляет 4 дюйма, мы отмечаем Q равным 4 дюймам с помощью линейки. После этого шага две точки соединяются вместе, что показывает отрезок линии желаемой длины. Посетите страницу «Методы рисования сегмента линии» для подробного объяснения.

Что такое середина отрезка?

Под серединой отрезка понимается точка, которая делит его на две равные части и находится в середине отрезка.

Как найти середину отрезка?

Середину отрезка можно вычислить, если известны координаты конечных точек. Например, если (x ₁ , y ₁ ) и (y _1, y ₂ ) являются двумя конечными точками, то середину отрезка можно вычислить по формуле Midpoint = [( х ₁ + x ₂ )/2, (y ₁ + y ₂ )/2]

Каковы примеры линейных сегментов в реальной жизни?

Мы знаем, что отрезки имеют фиксированную длину или меру. Таким образом, примерами отрезков в реальной жизни являются стороны многоугольника, края линейки, края бумаги и т. д.

Что такое символ отрезка?

Отрезок линии обозначается чертой сверху (—), например \(\overline{AB}\). Эта полоса считается символом сегмента линии.

Как найти длину отрезка линии?

Чтобы найти длину отрезка, мы используем шкалу (линейку) для измерения его размеров. В некоторых случаях, если координаты концов отрезка заданы, то мы применяем формулу расстояния, D = √[(\(x_{2}-x_{1}\)) ² + (\( y_{2}-y_{1}\)) ² ], где ‘D’ — расстояние между конечными точками отрезка и (\(x_{1}\), \(y_{1}\) ) и (\(x_{2}\), \(y_{2}\)) — координаты двух точек.

Когда отрезки конгруэнтны?

Две фигуры называются конгруэнтными, если они имеют одинаковый размер и форму. Таким образом, любые два отрезка можно считать конгруэнтными, если они имеют одинаковую длину.

Можно ли расширить сегмент линии?

Нет, отрезок нельзя удлинить, потому что он имеет фиксированную и определенную длину. Хотя линию можно бесконечно продолжать в двух противоположных направлениях, а луч можно продолжать и с одного конца.

Как выглядит сегмент линии?

Отрезок выглядит как прямая линия с фиксированными концами. Например, если мы посмотрим на стороны любого многоугольника, такого как треугольник, квадрат или даже пятиугольник, мы увидим, что стороны этих многоугольников являются отрезками.

Счет, математика и статистика — Комплект академических навыков

Свойства сегментов прямой линии

ContentsToggle Главное меню 1 Расстояние между двумя точками1.1 Определение1.2 Рабочий пример 2 Точка на линии2.1 Определение2.2 Рабочий пример 3 Середина3. 1 Определение 3.2 Рабочий пример 4 Пример видео 5 Рабочая тетрадь 6 Внешние ресурсы 92}\\\\ &=\sqrt{9+4}\\\\ &=\sqrt{13} \end{align}

Точка на линии

Определение

Две точки $A(x_1,y_1 )$ и $B(x_2,y_2)$ соединены линией, и мы хотим найти на этой линии третью точку $C(x_3,y_3)$, которая находится на расстоянии $\lambda$ единиц от $A$.

|400px|center

Сначала найдите длину отрезка $AB$ (см. выше), затем найдите отношение отрезка: $\lambda$ как часть длины $AB$: \[r = \ frac{\lambda}{AB}\].

Точка $C$ находится в точке $A+r(B-A) = (1-r)A + rB$, поэтому ее координаты \begin{align} x_3 &= r \times x_1 + (1 — r) \ раз x_2 \\ y_3 &= r \times y_1 + (1 — r) \times y_2 \end{align} 92}\\ &=\sqrt{9+16}\\ &=\sqrt{25}\\ &=5 \end{align}

Затем найдите $\lambda$ как часть длины $AB$. \begin{align} r &= \frac{\lambda}{AB}\\ &=\frac{2}{5} \end{align}

Теперь мы можем найти координаты $C$. \begin{align} x_3 &= r \times x_1 + (1 — r) \times x_2\\ &=\frac{2}{5}\times(-2) + \left(1-\frac{2} {5}\right) \times 1\\ &=-\frac{4}{5}+\frac{3}{5}\\ &=-\frac{1}{5} \end{align}

\begin{align} y_3 &= r \times y_1 + (1 — r) \times y_2\\ &=\frac{2}{5}\times 3 + \left(1-\frac{2}{5) }\right) \times 7\\ &=\frac{6}{5} + \frac{21}{5}\\ &=\frac{27}{5} \end{align}

Таким образом, координаты точки $C$ равны $\left(-\dfrac{1}{5}, \dfrac{27}{5}\right)$.

Середина

Определение

Середина $P$ линии, соединяющей две точки $A(x_1,y_1)$ и $B(x_2,y_2)$, находится на полпути между двумя точками. Формула получена из приведенной выше формулы «точка на прямой», когда $r=\frac{1}{2}$/

\[P=\left(\frac{1}{2}(x_1+ x_2),\frac{1}{2}(y_1+y_2)\right)\]

Рабочий пример

Пример 1

Найдите середину $P$ прямой $AB$, где $A(2, -2)$ и $B(-4,3)$.

Решение

\begin{align} P&=\left(\frac{1}{2}(x_1+x_2),\frac{1}{2}(y_1+y_2)\right)\\ &=\ влево(\frac{1}{2}\Bigl(2+(-4)\Bigr),\frac{1}{2}\Bigl((-2)+3\Bigr)\right)\\ &= \left(\frac{1}{2}(-2),\frac{1}{2}(1)\right)\\ &=\left(-1,\frac{1}{2}\right ) \end{align}

Пример видео

Хейли Бишоп находит длину и середину отрезка между $A(-2,1)$ и $B(3,0)$.

Рабочая тетрадь

Эта рабочая тетрадь, созданная HELM, является хорошим пособием по повторению, содержащим ключевые моменты для исправления и множество рабочих примеров.