Посчитать онлайн среднее квадратичное отклонение: Среднее квадратичное отклонение | Онлайн калькулятор

Как рассчитать среднее и стандартное отклонение в Google Sheets

Редакция Кодкампа

17 авг. 2022 г. читать 2 мин

---

Среднее значение представляет собой среднее значение в наборе данных. Это дает нам хорошее представление о том, где находится центр набора данных.

Стандартное отклонение показывает, насколько разбросаны значения в наборе данных. Это дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.

Используя только эти два значения, мы можем многое понять о распределении значений в наборе данных.

Чтобы вычислить среднее значение набора данных в Google Таблицах, мы можем использовать функцию =СРЗНАЧ(диапазон) , где диапазон — это диапазон значений.

Чтобы вычислить стандартное отклонение набора данных, мы можем использовать функцию =STDEV. S(Range)

, где Range — это диапазон значений.

В этом руководстве объясняется, как использовать эти функции на практике.

Техническое примечание

Обе функции СТАНДОТКЛОН() и СТАНДОТКЛОН.С() вычисляют стандартное отклонение выборки .

Вы можете использовать функцию STDEV.P() для вычисления стандартного отклонения совокупности , если ваш набор данных представляет всю совокупность значений.

Однако в большинстве случаев мы работаем с выборочными данными, а не со всей совокупностью, поэтому мы используем функцию СТАНДОТКЛОН.С().

Пример 1: Среднее и стандартное отклонение одного набора данных

На следующем снимке экрана показано, как рассчитать среднее значение и стандартное отклонение одного набора данных в Google Таблицах:

Среднее значение набора данных составляет 16,4 , а стандартное отклонение — 9,127 .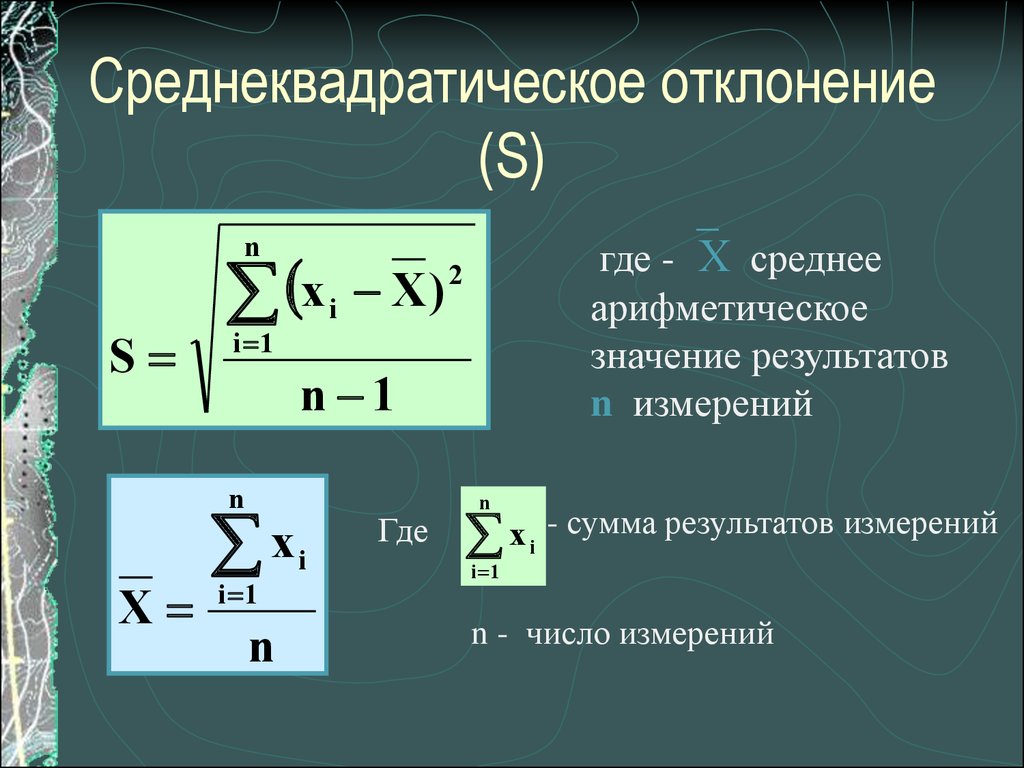

Столбец E показывает формулы, которые мы использовали для расчета как среднего, так и стандартного отклонения набора данных.

Пример 2: Среднее и стандартное отклонение нескольких наборов данных

Предположим, у нас есть несколько наборов данных в Google Sheets :

Чтобы вычислить среднее значение и стандартное отклонение первого набора данных, мы можем использовать следующие две формулы:

• Среднее значение: =СРЗНАЧ(B2:B21)
• Стандартное отклонение: =STDEV.S(B2:B21)

Затем мы можем выделить ячейки B22: B23 и перетащить формулы в следующие два столбца:

Результаты показывают среднее значение и стандартное отклонение для каждого из трех наборов данных.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в Google Таблицах:

Как рассчитать межквартильный диапазон в Google Sheets
Как рассчитать сводку из пяти чисел в Google Sheets
Как найти 10% лучших значений в Google Sheets

что за характеристика, как можно рассчитать, формула, пример

Что такое среднеквадратичное отклонение

Рассматривая какие-либо величины или их изменения, используют такие критерии как среднеарифметическая величина и ее отклонение. Различные понятия позволяют оценить разброс измеряемой величины и ее отклонение. К ним относится абсолютная погрешность, которая показывает насколько каждая конкретная величина отличается от среднего значения. Но так как сумма всех абсолютных погрешностей равна нулю, то этот критерий не позволяет показать разброс измеряемых величин. И для решения этой задачи был введен новый показатель — среднее квадратичное отклонение.

Для того чтобы объяснить его смысл необходимо вспомнить некоторые основные математические понятия.

Определение

Средней величиной или средним арифметическим называется число, полученное в результате деления суммы всех величин на их количество.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Пример

Среднеарифметическое для 3 чисел b₁, b₂

и b₃ определяется как:

\(M=\frac{b_1+b_2+b_3}3\)

Со средней величиной непосредственно связана и другая характеристика — математическое ожидание.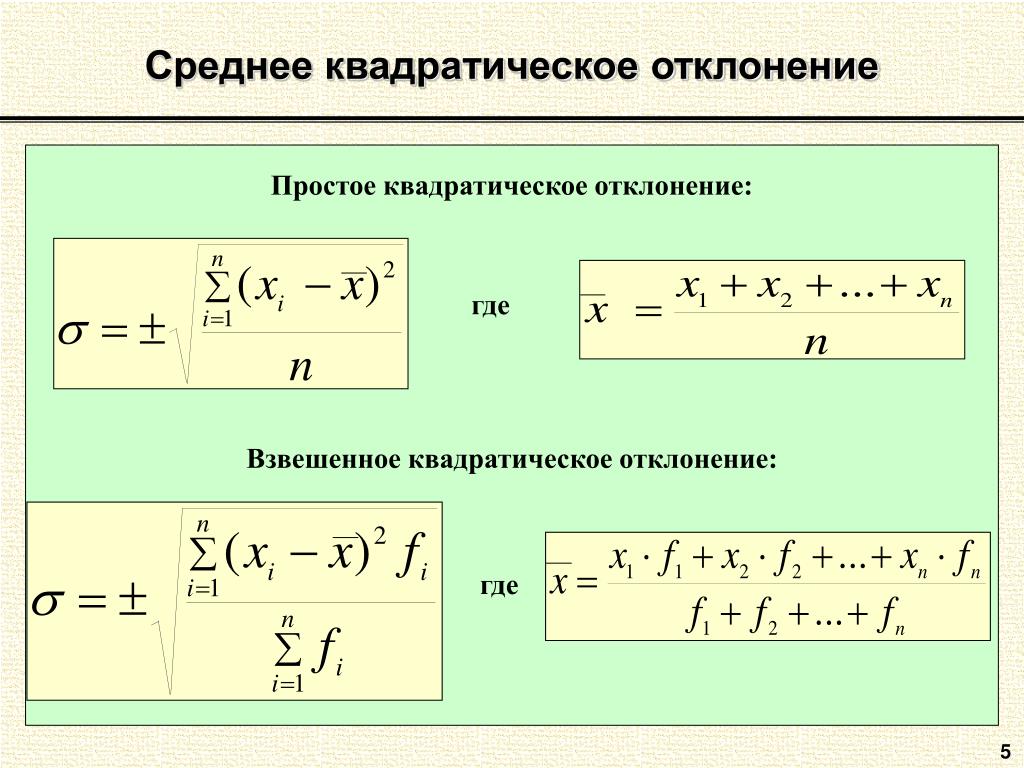

Определение

Значение среднего арифметического некоторого множества при стремлении его членов к бесконечности называется математическим ожиданием (М).

А оценкой математического ожидания является среднее арифметическое определенного числа измерений изучаемой величины.

Определение

Вариантой или абсолютной погрешностью называется разность измеряемой величины со средним значением.

Она обозначается греческой буквой D. Для того чтобы найти варианту единичного измерения ai следует отнять от ее значение среднее арифметическое:

\(Da_i=a_i-M\)

Также для оценки единичного измерения используется и относительная погрешность

, значение которой выражается в процентах. Ее вычисление проводят по формуле:

\(\sigma=\frac{\left|\triangle a_i\right|}M\times100\%\)

Относительная погрешность каждой величины позволяет отбросить из вариации измерений значения с очень большой погрешностью и проводить дальнейший анализ только величин с незначительной относительной погрешностью.

Характеристикой распределения значений некоторой измеряемой величины является дисперсия (D).

Определение

Дисперсией называется среднее арифметическое квадратов всех абсолютных погрешностей.

Теперь можно дать определение и «среднеквадратичному отклонению».

Определение

Значение корня квадратного из дисперсии случайной величины называется среднеквадратичным отклонением и обозначается «ϭ».

Оно вычисляется по формуле:

\(\sigma=\sqrt{D_{\left|x\right|}}\)

Единицей измерения среднеквадратического отклонения является единица измерения исследуемой величины. Данный критерий используется при измерении линейной функции, статической проверки гипотезы, расчете стандартной ошибки среднего арифметического, а также при построении доверительных интервалов.

Как найти среднеквадратическое отклонение

Вычисление среднеквадратичного отклонения на первый взгляд может показаться достаточно сложным и запутанным. Но этот процесс можно облегчить, если воспользоваться следующим алгоритмом действий:

1. Найти среднее арифметическое всех членов множества.
2. Для каждого элемента вычислить варианту.
3. Сложить все полученные на предыдущем этапе значения.
4. Разделить число, полученное при выполнении третьего шага, на количество элементов множества.
5. Из полученного в предыдущем шаге числа извлечь корень квадратный.

Формула, примеры решения задач

Для четырех измеренных значений величины b формула среднеквадратичного отклонения будет выглядеть следующим образом:

\(\sigma=\sqrt{\frac{\triangle b_1+\triangle b_2+\triangle b_3+\triangle b_4}4}\)

где Db₁ — Db₄ являются абсолютными погрешностями каждой исследуемой величины.

Рассмотрим пример решения конкретной задачи.

Задача

При проведении лабораторной работы по физике школьники несколько раз измерили напряжение электрического тока и получили следующие значения:

\(U_1=4. 22B\\U_2=4.30B\\U_3=4.27B\\U_4=4.23B\\U_5=4.20B\)

Необходимо рассчитать погрешности (абсолютные и относительные) каждого измерения, дисперсию и среднеквадратическое отклонение.

Решение

Определим среднее арифметическое значение напряжения в данной работе:

\(U_c=\sqrt{\frac{U_1+U_2+U_3+U_4+U_5}5}=\frac{4.22+4.30+4.27+4.23+4.20}5=4.244B\)

Теперь рассчитаем для каждого полученного измерения абсолютную и относительную погрешности. Так как абсолютная погрешность определяется как разница между средним арифметическим и полученным значением, то

\(\triangle U_1=0.024\\\triangle U_2=-0.056\\\triangle U_3=-0.026\\\triangle U_4=0.014\\\triangle U_5=0.044\)

Находим относительную погрешность:

\(\sigma_1=\frac{\left|U_1\right|}{U_c}\times100\%=0.50\%\\\sigma_2=\frac{\left|U_2\right|}{U_c}\times100\%=1.06\%\\\sigma_3=\frac{\left|U_3\right|}{U_c}\times100\%=0.50\%\\\sigma_4=\frac{\left|U_4\right|}{U_c}\times100\%=0.25\%\\\sigma_5=\frac{\left|U_5\right|}{U_c}\times100\%=0.

2}5=0.001304\\\)

Теперь можно вычислить среднеквадратичное отклонение:

\(\sigma=\sqrt D=0.0361\\\)

Калькулятор стандартного отклонения и дисперсии

Введите набор данных, разделяя каждое отдельное значение запятыми, чтобы определить стандартное отклонение и дисперсию.

Что такое стандартное отклонение и дисперсия?
Стандартное отклонение и дисперсия являются статистическими функциями, используемыми для измерения дисперсии или отклонения значений в наборе данных от его среднего значения. Проще говоря, стандартное отклонение и вариация показывают, насколько близко или далеко значения, составляющие набор данных, друг от друга и, таким образом, указывают на их отклонение от среднего или среднего значения. Чем больше стандартное отклонение и дисперсия, тем больше несоответствие в наборе данных и наоборот.

При расчете стандартное отклонение равно квадратному корню из дисперсии.

Формула стандартного отклонения:

При расчете для совокупности

Здесь
σ = стандартное отклонение совокупности
N = общее количество значений в наборе данных
x _i = индивидуальное значение в данных set
µ = Среднее значение

При расчете для выборки

Здесь
s = Стандартное отклонение выборки
N = Общее количество значений в наборе данных
x _i = Индивидуальное значение в наборе данных
x¯ = Среднее значение выборки

Формула дисперсии:

Здесь
σ ² = дисперсия генеральной совокупности
N = общее количество значений в наборе данных
x _i = индивидуальное значение в наборе данных
µ = среднее значение

При расчете выборки

с ² = ∑(xi — x̄) ² / (N — 1)

Здесь,
s ² = Выборочная дисперсия
N = Общее количество значений в наборе данных
x _i = Индивидуальное значение в наборе данных
x¯ = Среднее значение выборки

Что такое стандарт калькулятор отклонения и дисперсии?
Приведенный выше калькулятор представляет собой цифровой инструмент, который вычисляет стандартное отклонение, дисперсию и некоторые другие статистические функции, такие как среднее значение заданного набора данных. Пользователям необходимо ввести набор данных, где каждое отдельное значение отделяется запятой, чтобы определить значение вышеупомянутых статистических функций.

Как работает этот калькулятор?
Этот калькулятор представляет собой онлайн-инструмент, к которому можно получить доступ со смартфона или компьютера с активным подключением к Интернету. Вот пошаговое руководство по использованию этого калькулятора стандартного отклонения и дисперсии:

• Поле ввода предназначено для ввода набора данных. Здесь все отдельные значения набора данных должны быть разделены запятой. Введенные значения могут быть как положительными, так и отрицательными числами.
• Выберите вкладку «Население», если набор данных учитывает все население рассматриваемой группы
• Выберите вкладку «Выборка», если набор данных представляет только часть соответствующего населения или группы
• После ввода всех необходимых данных нажмите кнопку «Рассчитать», чтобы просмотреть результат
• Нажмите «Очистить» кнопка для нового ввода

Что показывает страница результатов?
В разделе результатов вверху отображается «стандартное отклонение», за которым следует «количество» отдельных значений, «сумма» значений, «среднее» набора данных и, наконец, « дисперсия предоставленных данных.

В разделе ниже показаны этапы расчета, за которыми следует предел погрешности или доверительный интервал расчета. Под ним находится таблица частот, которая показывает частоту появления каждого из отдельных значений.

Калькулятор стандартного отклонения — StdDev Измерение списка

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Стандартное отклонение

Инструмент для расчета стандартного отклонения списка значений. Стандартное отклонение — статистическая величина, характеризующая дисперсию выборки или распределения.

Результаты

Стандартное отклонение — dCode

Тег(и) : Статистика

Поделиться

dCode и многое другое день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор стандартного отклонения

Загрузка…
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

См. {2}\right] } $$ 92 \right) } = \sqrt{ 14/2 = 7 } \примерно 2,646 $

Какая связь между стандартным отклонением и дисперсией?

Значение стандартного отклонения представляет собой квадратный корень из дисперсии. Зная значение дисперсии $ V $, $ \sigma $ можно рассчитать по соотношению: $$ \sigma(X) = \sqrt{ V(X) } $$

Исходный код

Исходный код «Стандартное отклонение». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Стандартное отклонение», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Стандартное отклонение» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или доступ к API для «Стандартного отклонения» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!

Напоминание: dCode можно использовать бесплатно.