Параллельные прямые. Признаки параллельности прямых
Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).
Определение 1. Две прямые на плоскости называются параллельными, если они не пересекаются.
Если прямые a и b параллельны, то это обозначают так:
На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).
Понятие параллельности можно распространять и на отрезки.
Определение 2. Два отрезка называются параллельными, если они лежат на параллельных прямых (Рис.2).
Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.
На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок
На рисунке Рис.4 отрезок
Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.
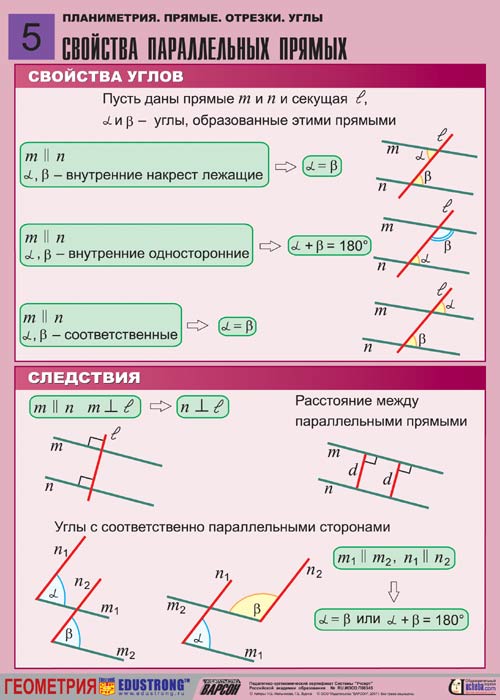
При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):
- накрест лежащие углы: 3 и 5, 4 и 6;
- односторонние углы: 4 и 5, 3 и 6;
- соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Определим признаки параллельности двух прямых, связанные с этими парамы углов.
Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: (Рис.8).
Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: (Рис.8).
Докажем, что .
Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).
Предположим, что углы 1 и 2 не прямые (Рис.10).
Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, . Тогда и .
означает, что точка N лежит на продолжении луча MO, т.е. точки M, O, N
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например (Рис.11).
Так как углы 2 и 3 вертикальные, то . Тогда из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1, прямые a и b параллельны.
Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например (Рис.11). Из рисунка видно, что углы 4 и 3 смежные, т.е. . Из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1 прямые a и b параллельны.
Раздел недели: Обезжиривающие водные растворы и органические растворители. Составы для очистки и обезжиривания поверхности. | |||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  Перпендикуляр и наклонные. Виды углов, свойства углов, признаки параллельности прямых, Теорема Фалеса. Перпендикуляр и наклонные. Виды углов, свойства углов, признаки параллельности прямых, Теорема Фалеса.Поделиться:
 Введите свой запрос: Введите свой запрос: | ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||
Узнайте о параллельных прямых и углах, образованных
В этом видео мы узнаем о взаимосвязях между углами, образованными при пересечении пары параллельных прямых секущей. Образовавшиеся углы называются вертикальными, дополнительными, чередующимися внутренними, чередующимися внешними, односторонними внутренними, односторонними внешними и соответствующими углами.
Образовавшиеся углы называются вертикальными, дополнительными, чередующимися внутренними, чередующимися внешними, односторонними внутренними, односторонними внешними и соответствующими углами.
Вот список часто используемых терминов для описания углов, образованных двумя параллельными прямыми, пересекаемыми секущей.
- Вертикальные углы: — углы, образованные пересекающимися линиями; противоположны друг другу и также конгруэнтны
- Дополнительные углы: — два угла, сумма которых всегда равна .
- Альтернативные внутренние углы: — углы, расположенные между двумя параллельными линиями, но находящиеся на противоположных сторонах поперечной. Они всегда конгруэнтны.
- Альтернативные внешние углы: Углы, находящиеся снаружи по разные стороны от двух параллельных линий и по разные стороны от поперечной. Они всегда конгруэнтны.
- Односторонние внутренние углы: Углы между параллельными линиями и на одной стороне поперечной.
 Они всегда являются дополнительными.
Они всегда являются дополнительными. - Односторонние внешние углы: Углы, находящиеся снаружи по разные стороны от двух параллельных прямых, но по одну сторону от поперечной. Они всегда являются дополнительными.
- Соответствующие углы: Углы, соответствующие углам пересечения противоположных параллельных линий. Графически они обращены в одну сторону и всегда конгруэнтны.
В этом уроке мы рассмотрим отношения углов, возникающие в результате пересечения двух параллельных прямых секущей.
У нас есть прямые и которые параллельны друг другу.
У нас также есть линия, которая является поперечной.
Когда секущая пересекает две параллельные прямые, возникает множество взаимосвязей углов.
Во-первых, если игнорировать нижнюю линию и сосредоточиться на верхней линии и поперечной , углов уже много.
Теперь, если мы сосредоточимся на нижней линии и поперечной , образующиеся здесь углы соответствуют углам, образованным верхней линией.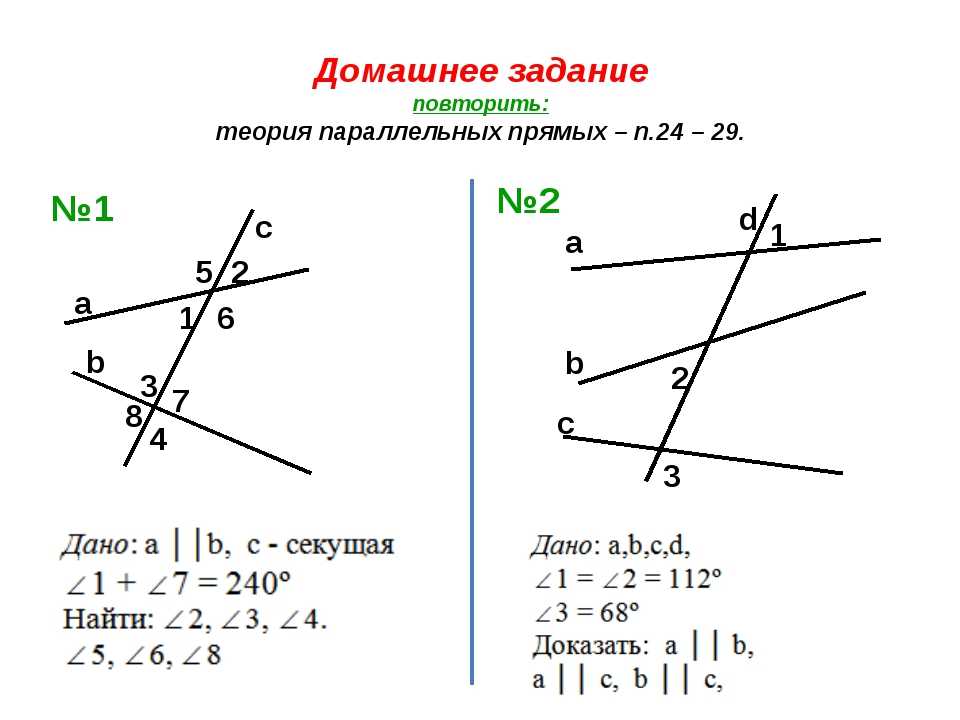
Углы, соответствующие группе, называются соответствующими углами. Соответствующие углы равны. Это означает, что они имеют одинаковые точные измерения.
Посмотрите на рисунок.
Углы и являются соответственными углами, поэтому они равны. Это означает, что они имеют одинаковые точные измерения.
Следовательно, мы можем сказать, что
Аналогично, угол находится вверху справа, как и угол .
Эти два
Теперь давайте посмотрим на угол , который находится внизу слева так же, как и угол . Таким образом, мы можем сказать, что эти два понятия совпадают.
Наконец, угол находится внизу справа точно так же, как угол . Что делает их совместимыми друг с другом.
Соответствующие углы — это углы, которые совпадают на диаграмме. Верхний левый в верхний левый. Верхний правый в верхний правый. И так далее.
Давайте рассмотрим еще несколько терминов.
Углы между двумя параллельными прямыми называются внутренними углами.
Те, которые находятся за пределами этого, известны как внешние углы.
Если мы идем от одной стороны трансверсали к другой, это называется альтернативой.
Углы по одну сторону от секущей называются односторонними.
Давайте рассмотрим альтернативные внутренние углы.
Альтернативный означает другую сторону поперечного сечения. В то время как интерьер означает между параллельными линиями.
Итак, альтернативные внутренние углы равны и . Эти углы также равны.
Угол, а также альтернативные внутренние углы. Это означает, что они также совпадают.
Теперь давайте посмотрим на альтернативные внешние углы.
Внешний означает внешний и альтернативный означает противоположные стороны поперечного сечения.
Альтернативные внешние углы также равны.
Теперь давайте посмотрим на односторонние углы.
Односторонние внутренние углы являются дополнительными.
Аналогично, односторонние внешние углы также являются дополнительными.
Теперь посмотрим на схему в целом.
Если подумать, мы просто прыгаем туда-сюда, словно зигзагами по диаграмме.
Углы, в которые вы прыгнули, равны.
Это лучший способ определения равных углов.
Если два угла не равны, то они должны быть смежными.
Уголки с параллельными линиями — A Plus Topper
A поперечная — это линия, пересекающая две или более линий (в одной плоскости). При пересечении линий в нескольких местах образуются углы. Некоторым углам даны «имена», которые описывают, «где» углы расположены по отношению к линиям. Эти имена описывают углы независимо от того, параллельны ли задействованные линии или нет.
Помните, что:
слово ИНТЕРЬЕР означает МЕЖДУ линиями.
слово ЭКСТЕРЬЕР означает ВНЕШНИХ строк.
слово ЧЕРЕДОВАНИЕ означает « чередующиеся стороны » поперечной.
Названия «чередующиеся внутренние углы», «чередующиеся внешние углы», «соответствующие углы» и «внутренние углы на одной стороне поперечной» используются для описания конкретных углов, образованных при пересечении прямых.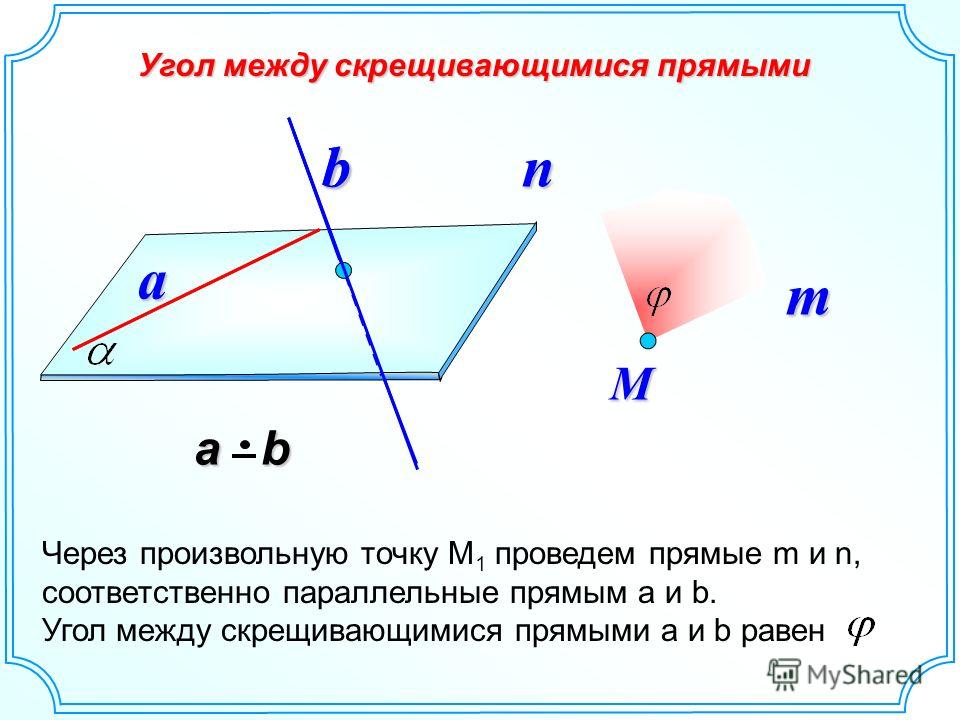 Эти имена используются как для параллельных, так и для непараллельных линий.
Эти имена используются как для параллельных, так и для непараллельных линий.
Давайте рассмотрим эти и другие углы, когда прямые параллельны.
Когда прямые параллельны:
Альтернативные внутренние углы (размеры равны)
Название четко описывает, «где» эти углы расположены.
Посмотрите внимательно на диаграмму ниже:
Подсказка: если вы нарисуете Z на диаграмме, чередующиеся внутренние углы находятся в углах Z. Z также может быть обратной Z.
Теорема:
Если две параллельные прямые пересечены секущей, то внутренние углы равны.
Теорема:
Если две прямые пересечены секущей и внутренние углы равны, то прямые параллельны.
Когда прямые параллельны:
Альтернативные внешние углы (меры равны)
Название четко описывает, «где» эти углы расположены.
Посмотрите внимательно на диаграмму ниже:
Теорема:
Если две параллельные прямые пересечены секущей, противоположные внешние углы равны.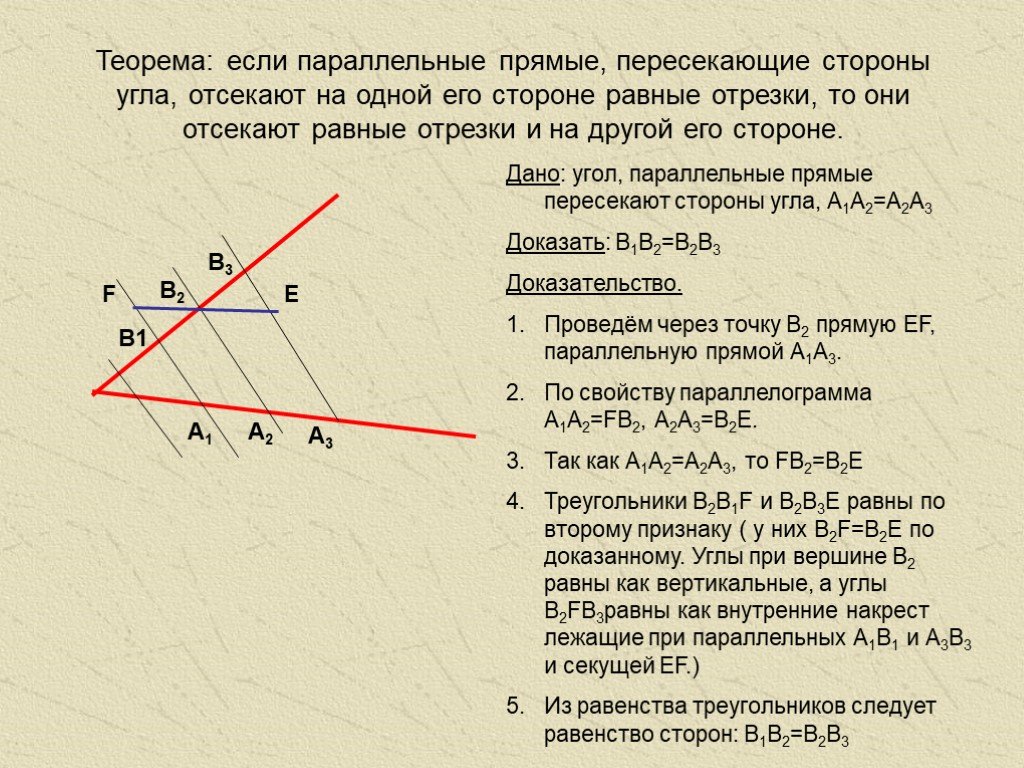
Теорема:
Если две прямые пересечены секущей и прилежащие внешние углы равны, то прямые параллельны.
Когда прямые параллельны:
Соответствующие углы (меры равны)
К сожалению, название этих углов не ясно указывает, «где» они расположены. Они расположены:
- на ОДНОЙ СТОРОНЕ поперечной
- одна ВНУТРЕННЯЯ и одна НАРУЖНАЯ
- и НЕ являются смежными (не соприкасаются).
(Они лежат на одной стороне поперечной в соответствующих положениях.)
Подсказка: Если вы сфотографировали один соответствующий угол и сдвинули угол вверх (или вниз) по той же стороне поперечной, вы пришли бы к другому соответствующему углу.
Также: Если вы нарисуете на диаграмме букву F, соответствующие углы можно найти в «углах» буквы F. Буква F может быть перевернутой и/или перевернутой.
Теорема:
Если две параллельные прямые пересечены секущей, то соответствующие углы равны.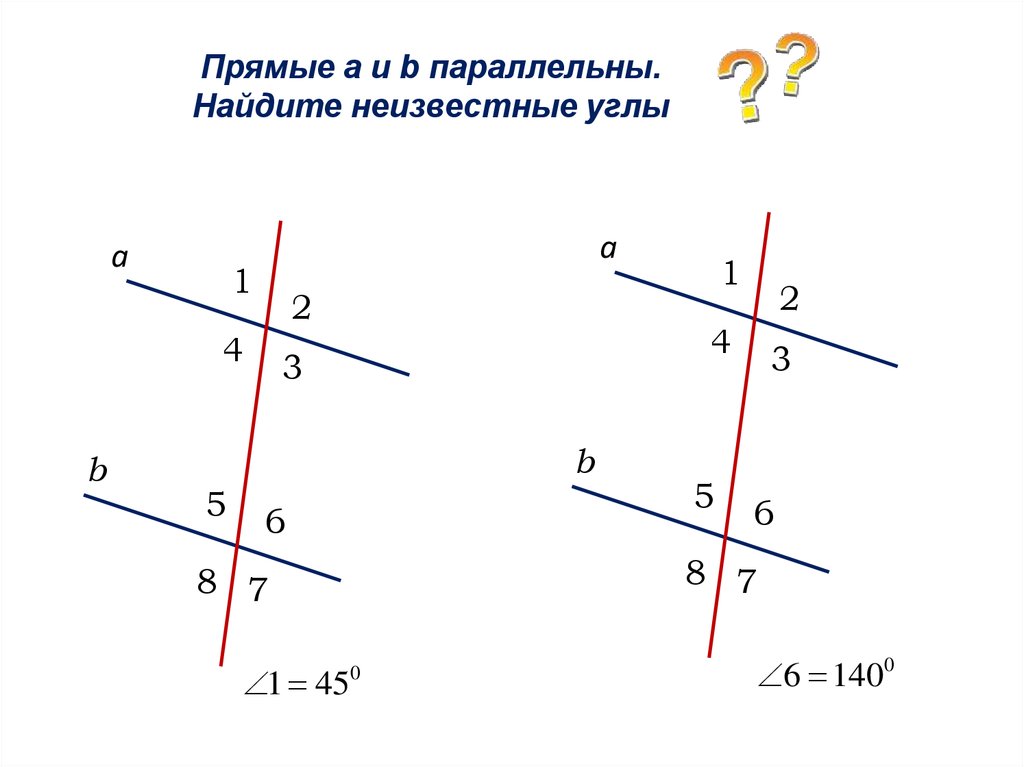
Теорема:
Если две прямые пересечены секущей и соответствующие углы равны, то прямые параллельны.
Когда прямые параллельны:
Внутренние углы на одной стороне от поперечной (размеры дополнительные)
Их «название» — это просто описание того, где расположены углы.
Теорема:
Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей являются дополнительными.
Теорема:
Если две прямые пересечены секущей и внутренние углы по одну сторону от этой секущей смежны, то прямые параллельны.
Конечно, при работе с параллельными линиями возникают и другие соотношения углов.
Вертикальные углы (меры равны)
Вертикальные углы ВСЕГДА равны, независимо от того, параллельны ли у вас линии или нет.
Освежите свою память, используя схему ниже:
Теорема:
Вертикальные углы равны.

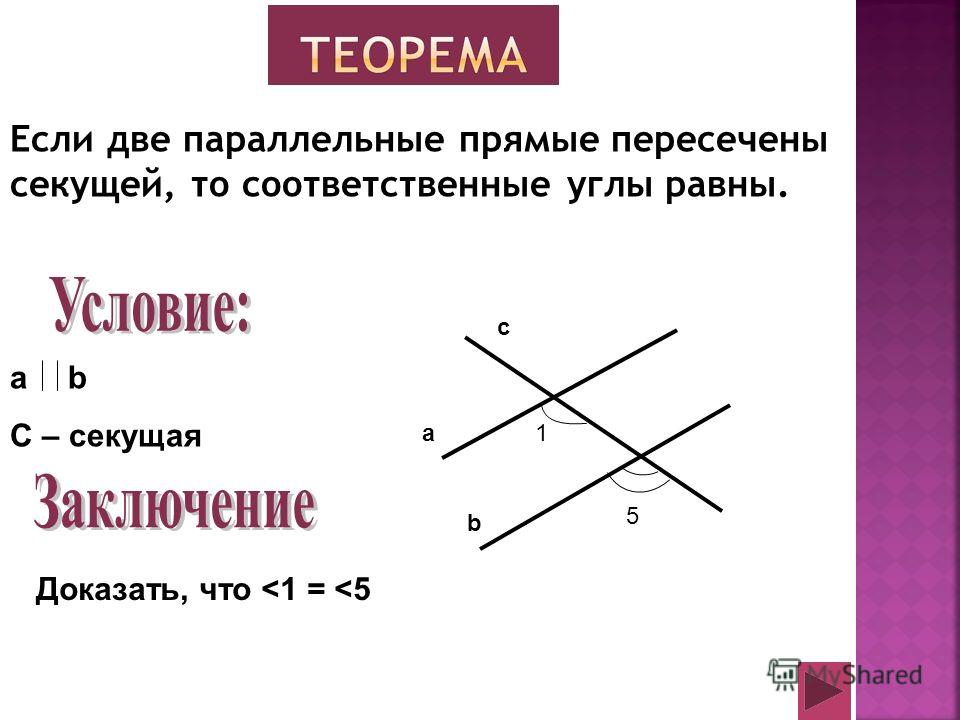 Виды углов, свойства углов, признаки параллельности прямых, Теорема Фалеса.
Виды углов, свойства углов, признаки параллельности прямых, Теорема Фалеса. Они всегда являются дополнительными.
Они всегда являются дополнительными.