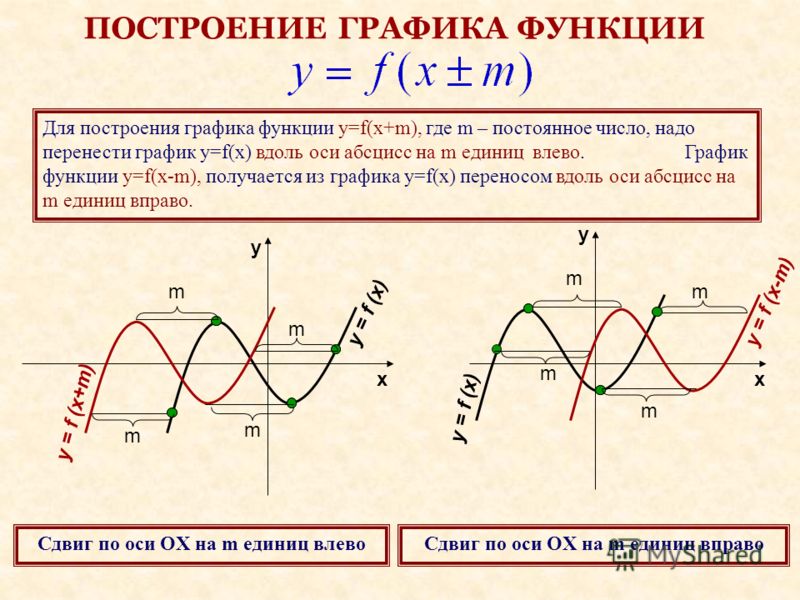
АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ГРАФИКАМИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ГРАФИКАМИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
2.1 «Сложение» («вычитание») графиков функций.
Общий метод построения графиков суммы и разности двух функций заключается в том, что предварительно строят два графика для обеих функций, а затем складывают или вычитают ординаты этих кривых при одних и тех же значениях (удобно – в характерных точках). По полученным точкам строят искомый график и выполняют проверку в нескольких контрольных точках.
В отдельных случаях построение графиков сумы и разности функций можно выполнять так.
Если надо построить график суммы двух функций, то сначала стоят график одной, более простой, функции, затем пристраивают график второй функции, ординаты которого откладываются от соответствующих точек первого графика.
Ели надо построить график разности
двух функций, то строят сначала график функции-уменьшаемого, а затем от него
откладывают ординаты функции вычитаемого, взятые с противоположным знаком.
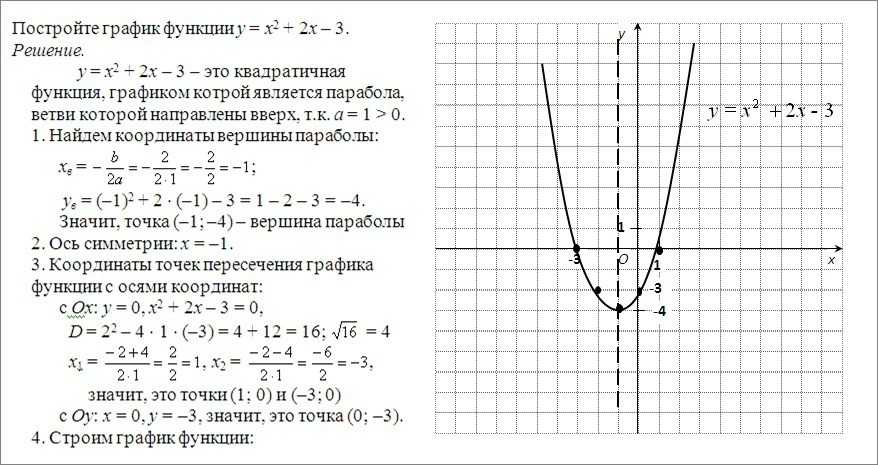
Пример 2.1. Построить график функции .
Решение. Так как исследуемая функция нечетная (она является суммой двух нечетных вспомогательных функций ,), график симметричен относительно начала координат и его достаточно построить только для .
При алгебраическом сложении ординат графиков вспомогательных функций, соответствующих одному и тому же значению аргументы, необходимо иметь в виду следующее:
1) так как , то исследуемый график будет располагаться между прямыми и ;
2) точки исследуемого графика с абсциссами ,лежат на прямой ;
3) точки исследуемого графика с абсциссами (там, где ), лежат на прямой ;
4) точки исследуемого графика с абсциссами (там, где ), лежат на прямой .
График построения функции приведен на рисунке 17.
Рисунок 17.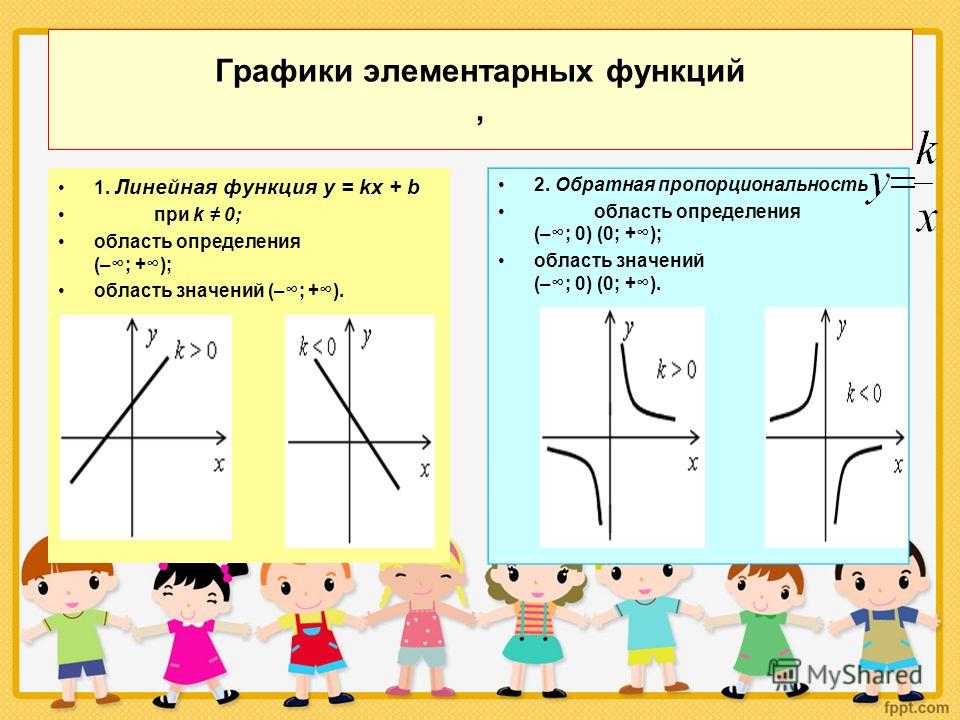
График построения функции
Пример 2.2. Построить график функции .
Решение. Функция нечетная, поэтому ограничимся случаем . Вспомогательными функциями являются и. ординаты исходного графика получаются алгебраическим сложением ординат графика вспомогательных функций. Так как ординаты графика отрицательны, то они откладываются вниз от графика . Прямая является асимптотой для искомого графика, причем правая ветвь графика приближается к этой асимптоте снизу. Кроме того,
1) если справа, то ;
2) если слева, то ;
3) если , то .
График построения функции приведен на рисунке 18.
Рисунок 18. График построения функции
Пример 2.3 Построить график функции .
Решение. Вспомогательная функция существует лишь при . Учитывая, что первая вспомогательная
функция определена на ,
область определения исследуемой функции является бесконечный интервал .
Так как модули не могут принимать
отрицательные значений, то график исследуемой функции будет расположен в первом
квадранте.
При сложении графиков вспомогательных функций необходимо иметь в виду следующее:
1) точка исследуемого графика с абсциссой лежит на синусоиде, так как ;
2) точки исследуемого графика с абсциссами ,лежат на графике вспомогательной функции , так кА в этих точках синус обращается в ноль;
3) в точках с абсциссами точки графика искомой функции совпадают с графиком функции .
График построения функции приведен на рисунке 19.
Рисунок 19. График построения функции
Пример 2.4. Построить график функции.
Решение. Имеем две функции: и .
Строим график функции , затем от него (а не от оси
абсцисс) откладываем ординаты второй функции. Поскольку ,
то целесообразно провести две вспомогательные прямые: и
. В точках, где (т.е.
при ), , а это значит, что соответствующие точки
графика заданной функции лежат на прямой .
В тех
точках, где (т.е. при ,), , а это
значит, что соответствующие точки графика заданной функции лежат на прямой . В точках, где (т.е.
при ,), , а это означает, что соответствующие
точки лежат на прямой . Следовательно, на прямых и лежат
вершины синусоиды.
График построения функции изображен на рисунке 20.
Рисунок 20. График построения функции
Пример 2.5. Построить график функции.
Решение. Строим графики функций-слагаемых и. затем складываем ординаты кривых при одинаковых значениях . Возьмем значения 0,5, 1, 1,5, 2, 2,5,… Складывая ординаты обоих графиков для каждого из этих значениях , получаем точки графика заданной функции. Соединив их плавной линией, получим одну ветвь графика функции (при ). Обе построенные ветви графика дадут график заданной функции.
График построения функции изображен на рисунке 21.
Рисунок
21.
График построения функции
Пример 2.6. построить график функции.
Решение. Строим графики двух функций и . Затем от графика первой функции откладываем ординаты второй функции, по характерным точкам функции . Соединив плавной линией, получим график заданной функции.
График построения функции изображен на рисунке 22.
Рисунок 22. График построения функции
2.2 «Умножение» («деление») графиков функций.
Областью определение исследуемой
функции является пересечение областей определения
вспомогательных функций и . Для построения графика функции надо построить на одном чертеже графики
вспомогательных функций и перемножить значения ординат, соответствующих одному
и тому же значению аргумента. При этом необходимо учитывать, что там, где
каждая из вспомогательных функций обращается в нуль, графики их произведения
пресекает ось абсцисс.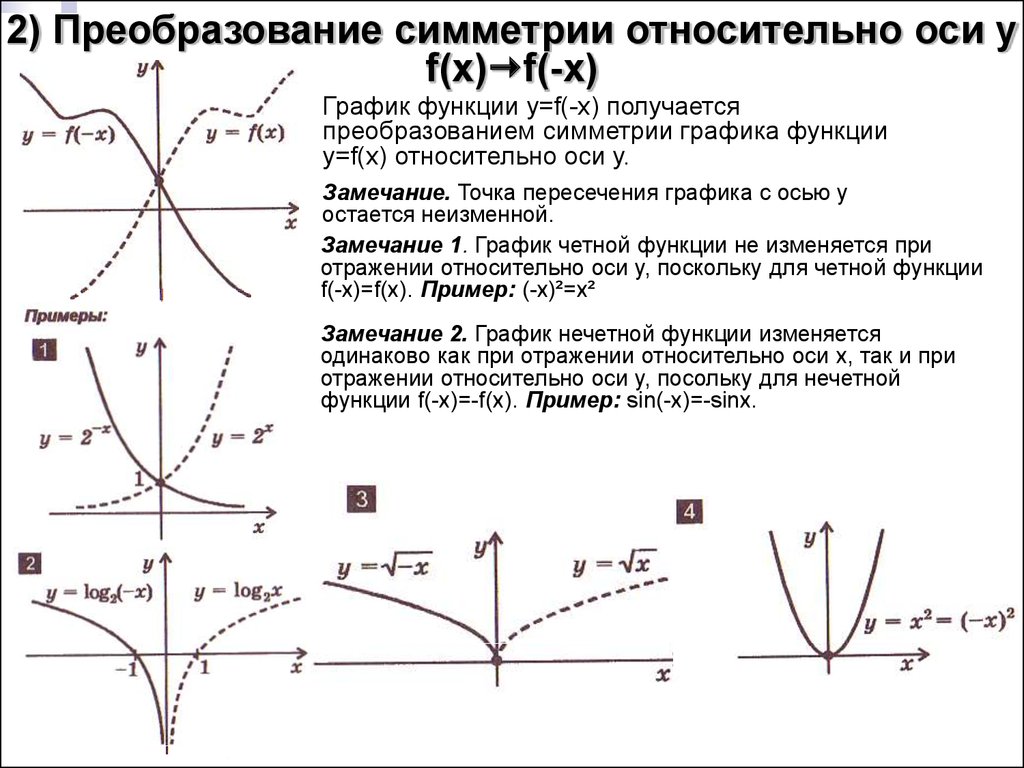
Построение графика функции сводится к построению графиков вспомогательных функции и и последующему их перемножению.
Для построения графика следует построить на одном чертеже и, деля на единицу на численные значения ординат , с учетом знака по точкам построить график данной функции. Необходимо использовать следующие правила.
1) Областью определения исследуемой функции является область определения функции за исключением тех значений аргумента, где последняя обращается в нуль.
2) Через точки, где функции обращается в нуль, проходят вертикальные асимптоты – прямые, к которым неограниченно приближаются ветви исследуемого графика. Поэтому в окрестности таких точек стремиться к в зависимости от знака .
3) Там, где функция возрастает (убывает), функция убывает (возрастает).
4) Там, где функция стремится к , исследуемая функция стремится к нулю.
Пример 2.7. Построить график функции .
Решение. Исследуемая функция
является нечетной, так как представляет собой произведение нечетной и четной
вспомогательных функций соответственно и Выполняем построение для .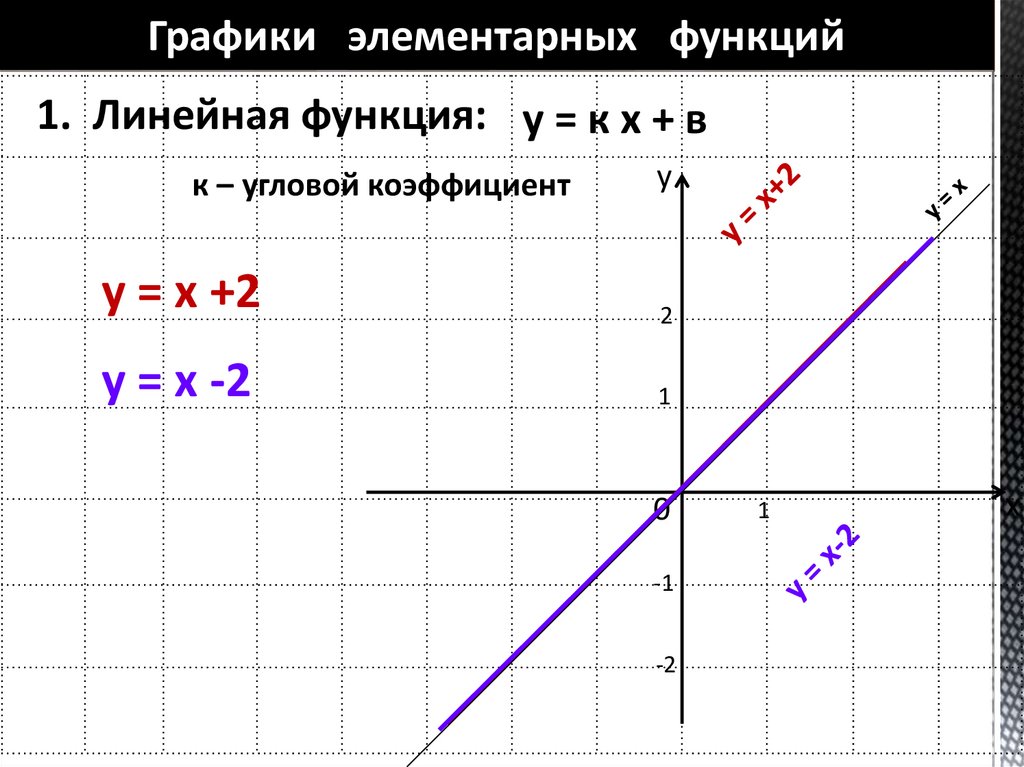
Рисунок 23. График функции
Пример 2.8. Построить график функции .
Решение. Вначале строим график вспомогательной функции . Этот квадратный трехчлен не имеет действительных корней и принимает положительные значения. Деля единицу на значение ординат этого графика, получаем график исследуемой функции. Замечаем, что там, где вспомогательная функция имеет минимум и возрастает, исследуемая функция имеет максимум и убывает. Там, где вспомогательная функция стремиться к бесконечности, исследуемая функция стремится к нулю. График построения функции приведен на рисунке 24.
Рисунок 24. График функции
Пример 2.
9. Построить график
функции .
Решение. Строим график функции и . Умножение этих графиков упрощается благодаря тому, что функции периодически принимает значения 0, 1, -1. При () функции , тогда , т.е. соответствующая точка графика функции находится на оси абсцисс. При () функция , тогда , т.е. соответствующая точка графика функции лежит на прямой . При () функция , тогда , т.е. соответствующая точка графика функции лежит на прямой .
Поскольку заданная функция четная, то указанное построение производим только для правой части графика, левую часть графика (для ) строим симметрично правой относительно оси ординат. Найденные точки соединим плавной линией, получим график заданной функции. График построения функции приведен на рисунке 25.
Рисунок 25. График функции
Пример 2.10. Построить график функции .
Решение. Представим функцию в виде . Строим графики и
и, перемножая значения их ординат,
получаем график исходной функции.
При функция
убывает быстрее, чем возрастает функция , поэтому при , т.е. ось является
горизонтальной асимптотой графика. При , при . При функция
имеет максимум. График построения функции приведен
на рисунке 26.
Рисунок 26. График функции
Пример 2.11. Построить график функции .
Решение. Строим графики и и, перемножая значения их ординат, получаем график исходной функции. Функция определена при всех значениях , кроме . Функция четная, поэтому достаточно построить график функции при . В точках ; при , т.е ось ординат является вертикальной асимптотой. Для график достраивается отражением относительно оси ординат. График построения функции приведен на рисунке 27.
Рисунок 27. График функции
Пример 2.12. Построить график функции .
Решение. Строим графики функции и .
Поскольку при ,
график функции проходит через точки . Кроме того, следует иметь в виду, что
при и
график функции касается графика функции сверху.
При и график функции касается
графика функции снизу. Следовательно, график
функции располагается между графиками функций и и
периодически касается их. График построения функции приведен
на рисунке 28.
Рисунок 28. График функции
Преобразование графиков элементарных функций
Руководитель:
Синякова Елена Александровна
МБОУ СОШ №67
г.Владивосток
Оглавление
- Основные определения
- Основные характеристики функции
- Основные элементарные функции
- Преобразования графиков функций
- Порядок выполнения преобразования графиков функций
- Переменная у является функцией от переменной х, если задана такая зависимость между этими переменными, которая позволяет для каждого значения х однозначно определить значение у.
- Графиком функции f называется множество точек плоскости с координатами (х ;f(x)), где х пробегает область определения функции f.
Основные характеристики функции
1.Область определения, т.е. множество значений аргумента, при которых задана функция.
2.Корни, т.е. точки, в которых функция обращается в нуль, или иначе решение уравнения f(x)=0.
1.Проекция графика на ось х .
2.Точки пересечения графика с осью х.
3.Участки оси х, соответствующие точкам графика, лежащим выше (ниже) оси х.
4.Симметричность относительно оси у или начала координат.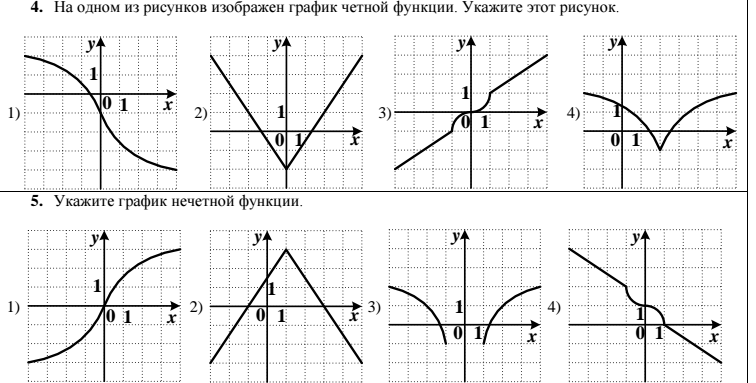
5. ” Вершины ” на графике функции.
6.Участки оси х, где график идет вверх или вниз.
7.Ординаты самой высокой и самой низкой точек графика.
8.Проекция графика на ось у.
3 .Промежутки постоянного знака, т.е. промежутки, на которых функция положительна(отрицательна), или иначе решение неравенства f(x)0 (f(x)
4. Четность( f(x)=f(-x)) и нечетность( f(x)=-f(x)) .
5 .Точки экстремума, т.е. точки, лежащие внутри области определения, в которых функция принимает самое большое(максимум) или самое маленькое(минимум) значение по сравнению со значениями в близких точках.
6 .Промежутки монотонности, т.е. промежутки, на которых функция или возрастает, или убывает.
7.Наибольшее и наименьшее значение функции(по сравнению со всеми возможными точками).
8.Область значений функции, т.е. множество чисел, состоящее из всех значений функции.
Основные элементарные функции
- Y=kx+b — линейная функция
- Y=k/x — обратная пропорциональность
- Y=ax 2 +bx+c — квадратичная функция
- Y=sin x — тригонометрическая функция
- Y=cos x — тригонометрическая функция
- Y=tg x — тригонометрическая функция
- Y=a x — показательная функция
- Y=log a x — логарифмическая функция
1.Область определения — множество всех действительных чисел . 2. Область значений – множество R. 3.Функция возрастает на R , если k0 , убывает, если k4. Графиком функции является прямая линия. 5.Если k=0 , графиком функции является прямая , параллельная оси Ох. «
Свойства функции у =kx+b и ее график
Пример :k=3, 30, b=5.
1.Область определения — множество всех действительных чисел .
2. Область значений – множество R.
3.Функция возрастает на R , если k0 , убывает, если k
4. Графиком функции является прямая линия.
5.Если k=0 , графиком функции является прямая , параллельная оси Ох.
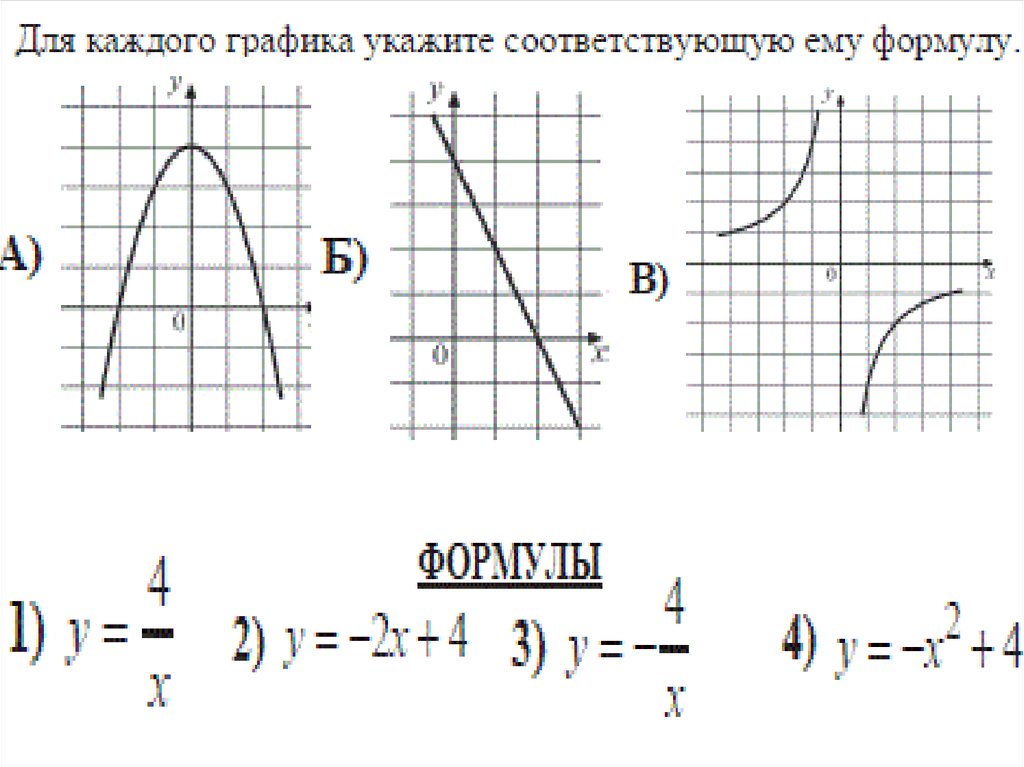
Свойства функции у = k/ х и ее график
Пример :k=3, k0.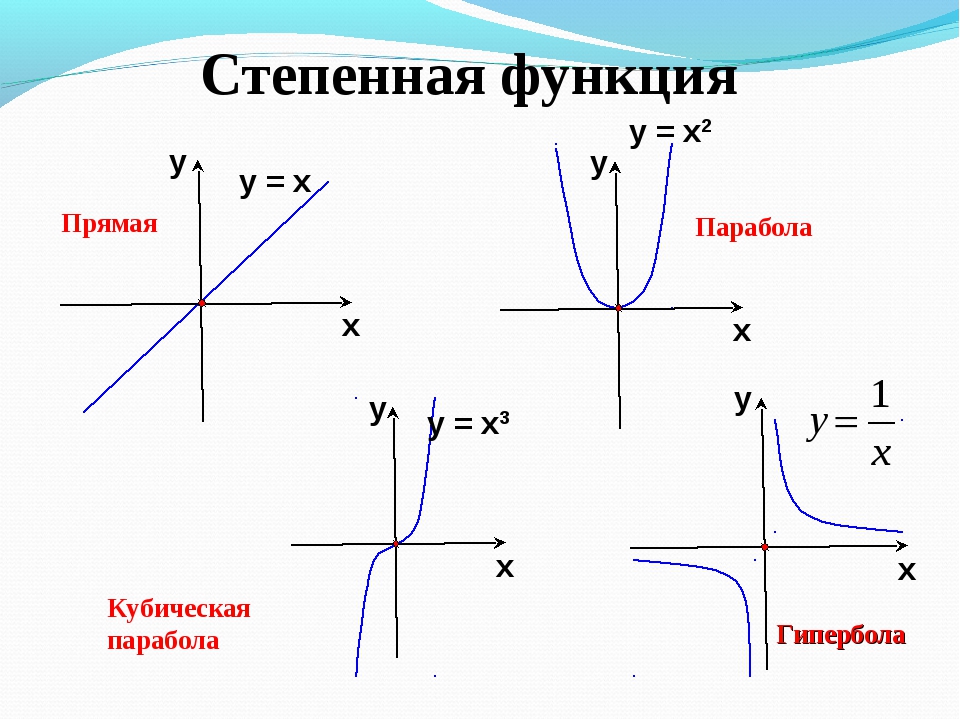
1. Область определения : все действительные числа, кроме 0.
2. Область значений : все действительные числа, кроме 0.
3. Функция возрастает при k0.
4. Функция нечетная, т.к. f(-x)=-f(x).
5. Графиком функции является гипербола.
Свойства функции y= ах 2 + bx+c и ее график
1. Область определения – множество всех действительных чисел.
2. Графиком функции является парабола, ветви которой направлены вверх при а 0, вниз при a
Пример :a=2, b=3, c=-5.
Свойства функции y=cos x и ее график
1.Область определения – множество R всех действительных чисел .
2 .Множество значений – отрезок [-1;1].
3. Функция y=cos x периодическая с периодом 2П .
4. Функция y=cos x четная.
5.Функция y=cos x принимает :
- значение, равное 0, при х = П/2+П n , n- целое.
- наибольшее значение, равное 1, при х = 2П n , n- целое.
- наименьшее значение, равное -1, при х = П+2П n , n- целое.
- положительные значения на интервале(-П/2,П/2) и на интервалах, получаемых сдвигами этого интервала на 2П n , n -целое.
- отрицательные значения на интервале(П/2 ;3 П/2) и на интервалах, получаемых сдвигами этого интервала на 2П n , n -целое.
6.Функция y=cos x:
- возрастает на отрезке [ П ; 2П ] и на отрезках, получаемых сдвигами этого отрезка на 2П n , n- целое.
- убывает на отрезке [ 0 ; П ] и на отрезках, получаемых сдвигами этого отрезка на 2П n , n- целое.
Свойства функции y=sin x и ее график
1.Область определения – множество R всех действительных чисел .
2 .Множество значений – отрезок [-1;1].
3. Функция y=sin x периодическая с периодом 2П .
4. Функция y=sin x нечетная.
5.Функция y=sin x принимает :
- значение, равное 0, при х = П n , n- целое.
- наибольшее значение, равное 1, при х =П/2+2П n , n- целое.
- наименьшее значение, равное -1, при х = -П/2+2П n , n- целое.
- положительные значения на интервале(0 ; П) и на интервалах, получаемых сдвигами этого интервала на 2П n , n -целое.
- отрицательные значения на интервале(П ; 2П) и на интервалах, получаемых сдвигами этого интервала на 2П n , n -целое.
6.Функция y=sin x:
- возрастает на отрезке [ -П/2 ; П/2 ] и на отрезках, получаемых сдвигами этого отрезка на 2П n , n- целое.
- убывает на отрезке [ П/2 ; 3П/2 ] и на отрезках, получаемых сдвигами этого отрезка на 2П n , n- целое.
Свойства функции y=tg x и ее график
1.Область определения – множество всех действительных чисел, кроме х = П/2+П n , n -целое.
2 .Множество значений – множество R всех действительных чисел .
3. Функция y=tg x периодическая с периодом П .
4. Функция y=tg x нечетная.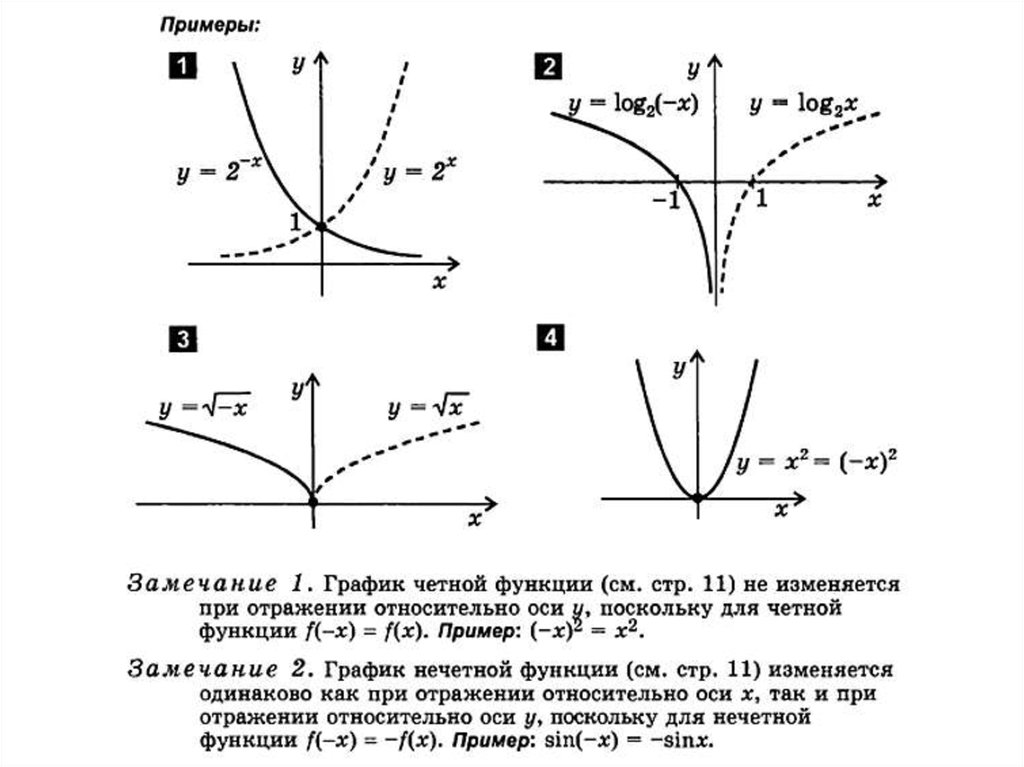
5.Функция y=tg x принимает :
- значение, равное 0, при х = П n , n- целое.
- положительные значения на интервалах ( П n; П/2+П n ), n- целое.
- отрицательные значения на интервалах ( -П/2+П n; П n ), n- целое.
6.Функция y=tg x возрастает на интервалах(-П/2+П n; П/2+П n) , n- целое .
Свойства функции у =a x и ее график
1.Область определения – множество R всех действительных чисел .
2 .Множество значений – множество всех положительных чисел .
3.Показательная функция y=a x является возрастающей на множестве всех действительных чисел, если a1, и убывающей, если 0
Пример :a=3.
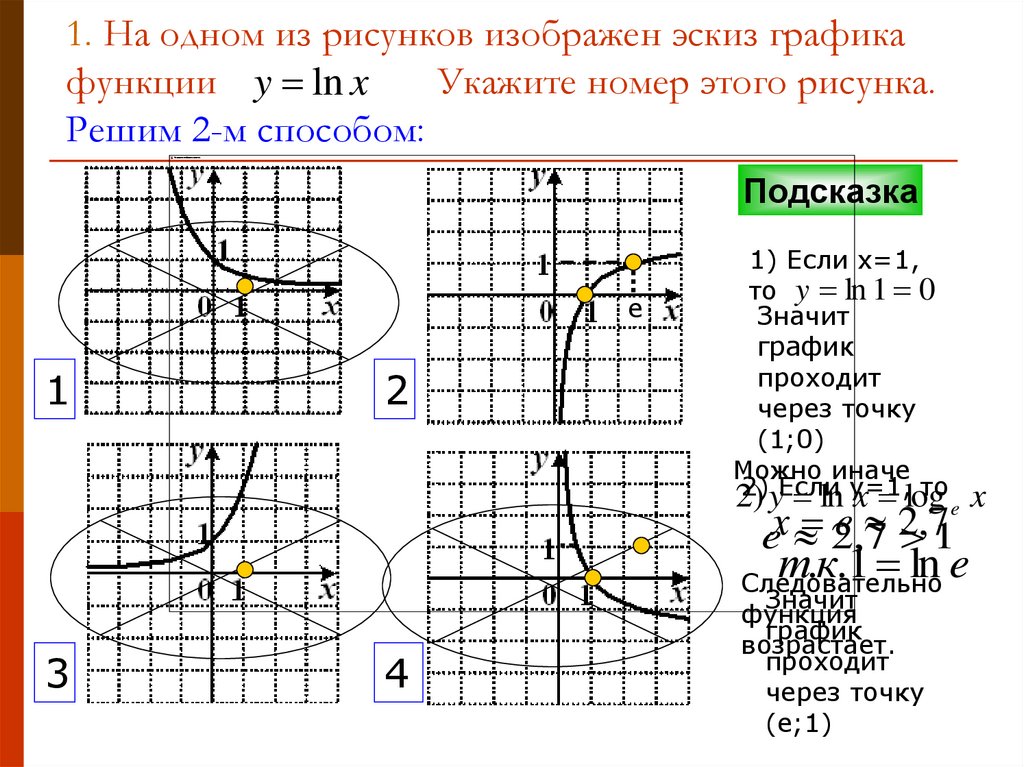
Свойства функции у =log a x и ее график
Пример :a=2.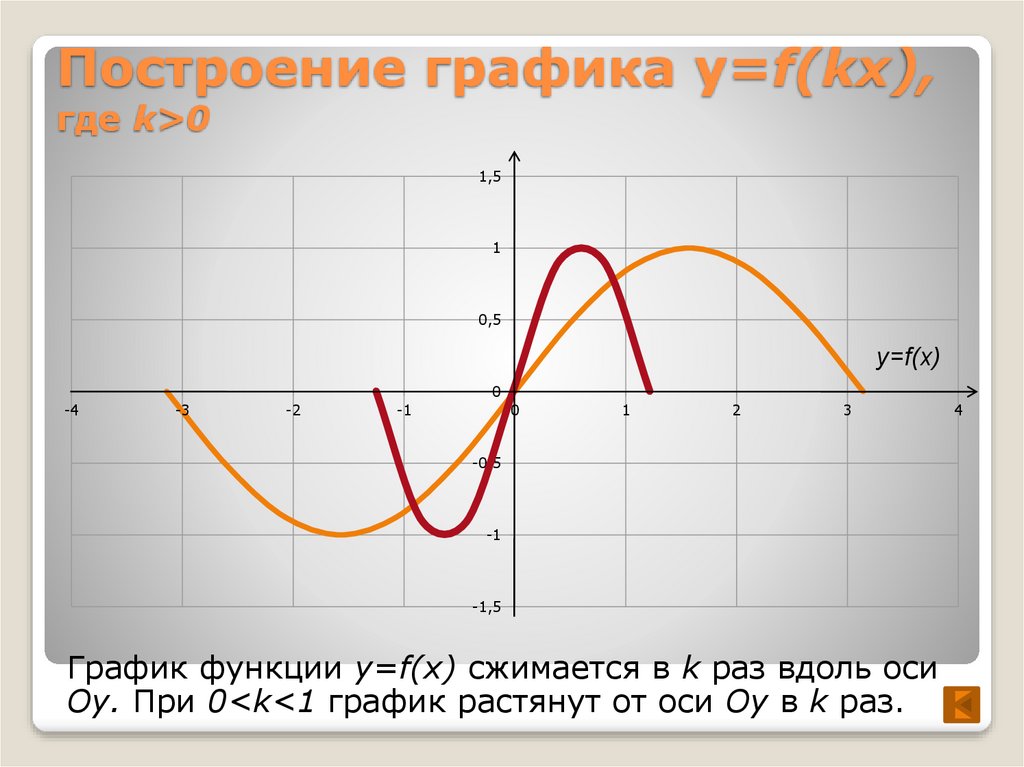
8
1.Область определения – множество всех положительных чисел .
2 .Множество значений – множество R всех действительных чисел .
3.Логарифмическая функция y=log a x является возрастающей на промежутке x0 , если a1, и убывающей, если 0
4. Если a1, то функция у =log a x принимает положительные значения при x1, отрицательные при 01.
Преобразования графиков функций
- Установим связь между графиками функций y =f(x) и …
- у = f(x-a)
- у = f(x) + b
- y = f(x-a) + b
- Y=f(|x|)
- Y=|f(x)|
График функции y=f(x-a)
- Для построения графика функции y=f(x-a) надо изобразить график исходной функции f(x) и сдвинуть его вдоль оси Ох на а единиц вправо (если а 0) или влево (если а 0).
Примеры:
- у = 1/x, y=1/(x-3), y=1/(x+2)
- y=sin(x), y=sin(x-1), y=sin(x+0.5)
- y=2 x, y=2 (x+2) ,y=2 (x-3)
y=2 x
Y=2 x-3
y=2 x+2
График функций у = f(x) + b
- Для построения графика функции у = f(x) +b надо изобразить график функции y= f (х) и сдвинуть его на b единиц вверх (если b 0) вдоль оси О y или вниз (если b ).
Примеры:
1) у = 1/x, y=(1/x)-3, y=(1/x)+2
2) y=sin(x), y=sin(x)-3, y=sin(x)+2
3) Y=2 x ,y=2 x +1,y=2 x -3
y=2 x +1
y=2 x
y=2 x -3
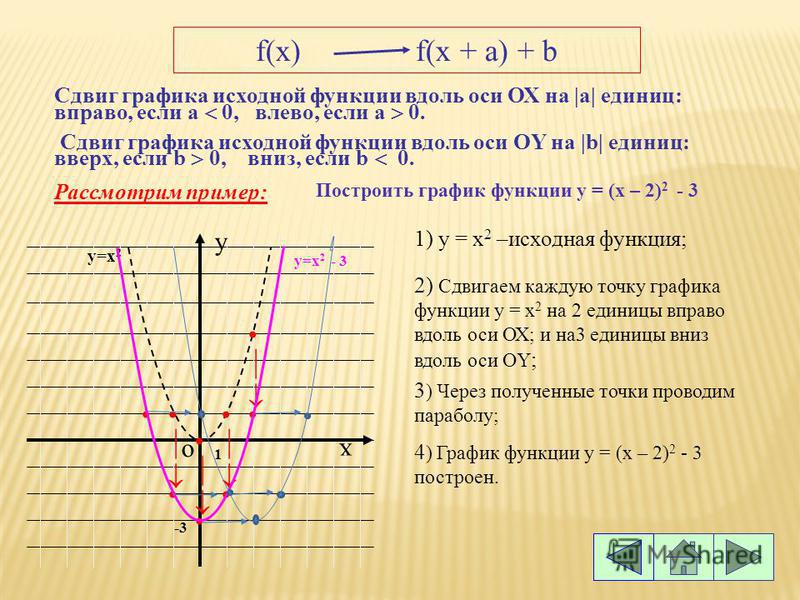
График функции y=f(x-a)+b
Для построения графика функции Y= f (x-a)+b
надо изобразить график исходной функции y= f (x) и сдвинуть его вдоль оси О x на a единиц в право(если a0 ) или в лево (если a 0), и вдоль оси О y на b единиц вверх (если b0 ) или вниз (если b .
НАПРИМЕР:
1) y=1/x; y=(1/(x-3))+2; y=(1/(x+1))-3 )
2) y=sinx,y=sin(x-2)+3, y=sin(x-3)+2
3 ) y=2x,y=2 (x-3) +2,y=2 (x+2) -2
y=2 x
Y=2 x-3 +2
y=2 x+2 -2
График функции y= f ( k x)
▪ Для построения графика функции y= f ( k x) необходимо построить график исходной функции y= f (x) и растянуть или сжать его вдоль оси Ox .
Если k 1 производится сжатие в k раз, при 0 k производится растяжение в k раз. При k 0 производится отображение графика относительно оси О y.
НАПРИМЕР:
1) y=1/x; y=1/3x; y= — (1/x)
2) y=sin x ; y=sin( 2 x) ; y=sin( 0,4 x)
3) y=2x,y=2 0,4x ,y=2 3x
y=2 x
y=2 0.4x
y=2 3x
Если k при этом отрицательное, то необходимо отобразить график относительно оси О x НАПРИМЕР: 1) y=1/x; y=2/x; y=- 3 /x 2)y=sin x; y=2sin x; y=0.6sin x 3)y=2x,y=2*2 x ,y=-3*2 x «
График функции y= kf (x)
▪ Для построения графика функции y= kf (x) исходный график y= f (x) нужно растянуть (если k 0 ) или сжать(если 0 k 1 ) вдоль оси О y в k раз. Если k при этом отрицательное, то необходимо отобразить график относительно оси О x
НАПРИМЕР:
1) y=1/x; y=2/x; y=- 3 /x
2)y=sin x; y=2sin x; y=0.
6sin x
3)y=2x,y=2*2 x ,y=-3*2 x
y=2 x
y=2*2 x
y=-3*2 x
График функции y=|f(x)|
Чтобы построить график функции y=|f(x)| , надо :
- Построить график базовой функции y=f(x) для всех х из ее области определения.
- Оставить без изменения ту часть графика, которая лежит выше оси Ох(т.к. если f(x)=0 , то |f(x)|=f(x)).
- Часть графика, лежащую ниже оси Ох, отразить симметрично относительно оси абсцисс(т.к. при f(x)
Примеры :
1)y=sinx,y=|sinx|
2)y=1/x,y=|1/x|
3)y=2 x ,y=|2 x |
y=2 x
y=|2x|
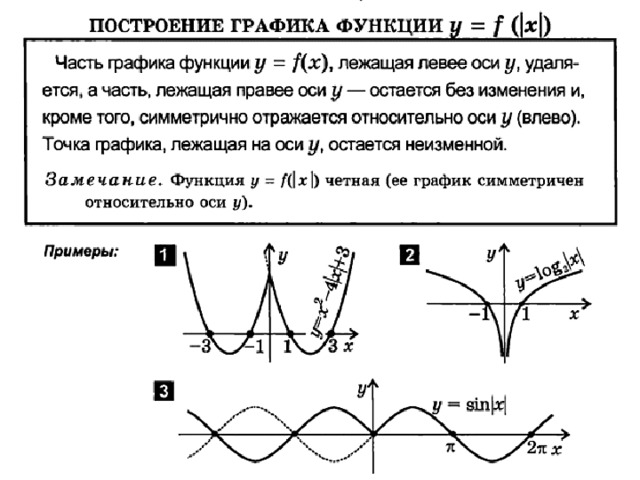
График функции y=f(|x|)
Чтобы построить график функции y=f(|x|) , надо :
- Построить график базовой функции y=f(x) .
- Оставить без изменения ту часть графика, которая лежит правее оси Oy.
- Часть графика функции y=f(x) , лежащую левее оси Oy, удалить, вместо нее построить часть графика, симметричную относительно оси Oy, оставленной неизменной части графика функции f.
- Примеры :
- 1)y=sinx,y=sin|x|
- 2)y=1/x,y=1/|x|
- 3)y=2 x ,y=2 |x|
y=2 |x|
y=2 x
Порядок выполнения преобразования графиков функций.
При выполнении преобразований графиков функций следует придерживаться следующих правил :
1. При выполнении преобразований вида y=f(ax+b) необходимо вынести множитель a в выражении ax+b за скобку, т.е. представить функцию в виде y=f(a(x+b/a)). Таким образом, параллельный перенос вдоль оси абсцисс будет проводиться не на |b| единиц, а на |b/a| единиц в нужном направлении.
2.Преобразования сжатия(растяжения ) выполняются всегда до преобразований сдвига(параллельного переноса) , т.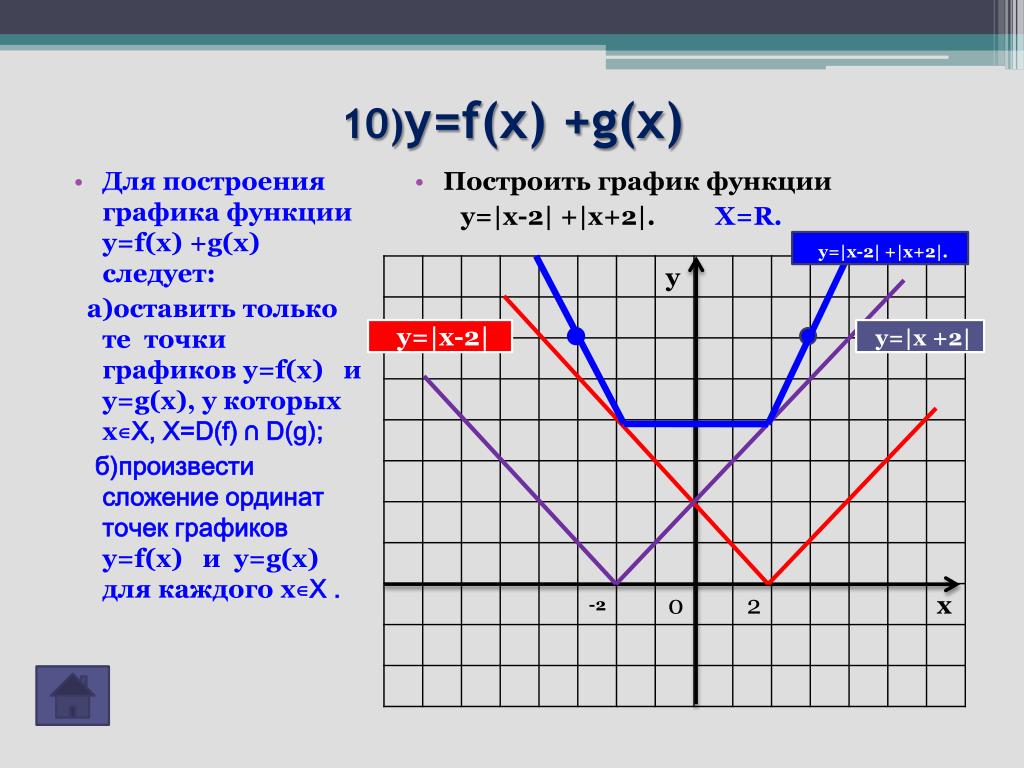
е. обладают приоритетом.
3.При выполнении преобразований вида y=f(k|x|+b) удобно придерживаться следующего порядка действий :
- f(x) f(kx) ( преобразование сжатия)
- f(kx) f(k(x+b/k)) ( преобразование сдвига)
- Y=f(k(x+b/k)) y=f(k(|x|+b/k)) ( преобразование «модуль аргумента»).
4.При выполнении преобразований вида y=f|kx+b| стоит придерживаться следующего порядка действий :
- y=f(x) y=f(|x|) ( преобразование «модуль аргумента»)
- Y=f(|x|) y=f(|kx|) ( преобразование сжатия)
- Y=f(|kx|) y=f(|k(x+b/k)|) ( преобразование сдвига).
Building Bar Graphs-NCES Kids’ Zone
Построение гистограмм Гистограммы можно использовать, чтобы показать, как что-то меняется с течением времени, или для сравнения разных периодов времени. Гистограммы хороши для отображения данных, которые охватывают многие годы (или дни, недели. Название Заголовок предлагает краткое объяснение того, что находится на вашем графике. Это помогает читателю определить, на что он собирается смотреть. Он может быть творческим или простым, если он говорит о том, что находится на графике. Название этого графика сообщает читателю, что он содержит информацию об уровне безработицы в 2004 г. среди лиц в возрасте 25 лет и старше в разбивке по высшему уровню образования. Источник Источник объясняет, где вы нашли информацию, которая находится на вашем графике. Важно отдать должное тем, кто собирал ваши данные! На этом графике источник говорит нам, что мы нашли нашу информацию из общего ядра данных NCES. Ось X Гистограммы имеют ось X и ось Y. В большинстве гистограмм, таких как приведенная выше, ось X проходит горизонтально (плоско). Иногда гистограммы делаются так, что столбцы располагаются сбоку, как на графике ниже. Затем на оси X есть числа, представляющие разные периоды времени или названия сравниваемых вещей. На этих графиках ось x имеет названия состояний. Ось Y В большинстве гистограмм, таких как приведенная выше, ось Y проходит вертикально (нас и вниз). Иногда гистограммы делаются так, что столбцы располагаются боком, как на графике слева. Тогда ось Y горизонтальна (плоская). Как правило, ось Y имеет числа для количества измеряемого материала. Ось Y обычно начинает отсчет с 0 и может быть разделена на любое количество равных частей. На этих гистограммах ось Y измеряет количество школ. Данные Наиболее важной частью вашего графика является содержащаяся в нем информация или данные. Легенда Легенда говорит нам, что представляет собой каждая полоса. Как и на карте, легенда помогает читателю понять, на что он смотрит. Примеры условных обозначений можно найти на втором и третьем графиках выше. Закрыть окно |
..), имеют действительно большие изменения из года в год (или изо дня в день…), или их можно использовать для сравнения различных элементов в таблице. связанная категория (например: сравнение чего-либо между разными состояниями). На следующих страницах описываются различные части гистограммы.
Гистограммы могут представлять данные разными способами и могут одновременно отображать более одной группы данных. Первый график представляет собой обычную гистограмму с одной группой данных. Второй график имеет две группы данных, которые сложены. Последний график — это еще один график с двумя группами данных, но они представлены рядом, а не стопкой.Способность построения и интерпретации графиков Фрэнка А. Черрето, Юнга Ли и Вонди Геремью – Визуальная грамотность сегодня
Frank A. Cerreto, Jung Lee, and Wondi Geremew
Abstract
Цель этого исследования состояла в том, чтобы выяснить, существует ли какая-либо связь между способностью построения графа и способностью интерпретации.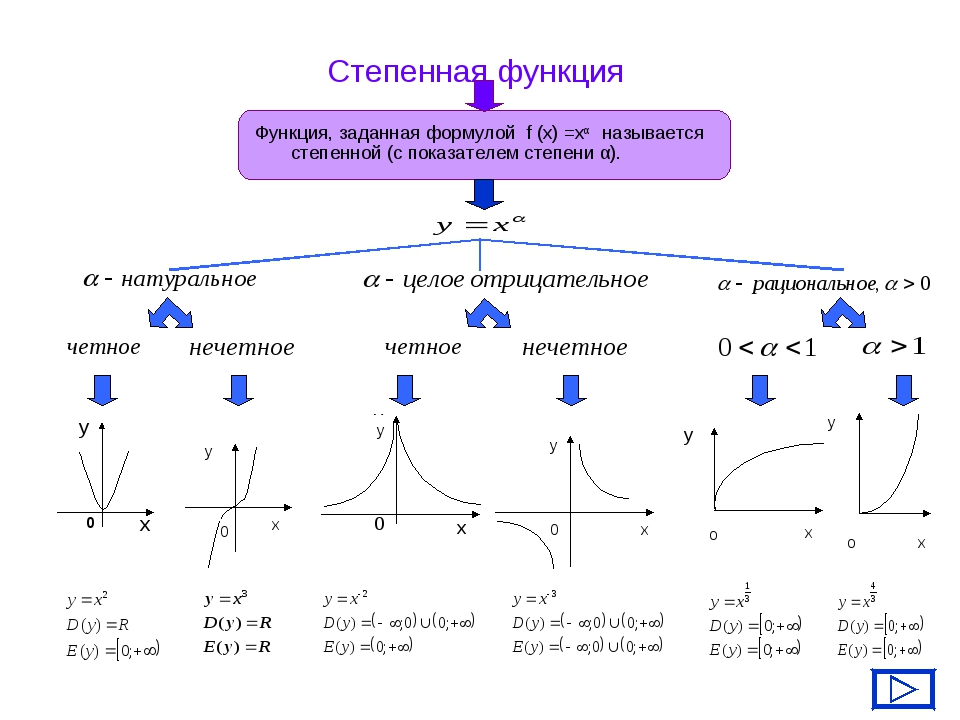
Шестьдесят семь студентов колледжа выполнили два задания по построению графиков, одно из которых включало построение, а другое интерпретацию графиков, причем оба задания основаны на реальных данных. Статистический анализ баллов не показал значимой корреляции между общими баллами по двум заданиям и существенных взаимосвязей между конкретными компонентами способности построения графика и способности интерпретации графика. Эти результаты предполагают, что эти две способности отличаются друг от друга. Результаты исследования дополняют наше понимание способности построения графов и имеют практическое значение для преподавания и обучения.
Ключевые слова
построение графов, интерпретация графов, графические данные, графическая грамотность , Mayer, & Hegarty, 1999), поскольку они могут помочь зрителям понять числовую информацию (Winn, 1987). Графики обеспечивают визуальную среду для выявления закономерностей и взаимосвязей в числовых данных и широко используются, когда люди принимают решения (Raschke & Steinbart, 2008).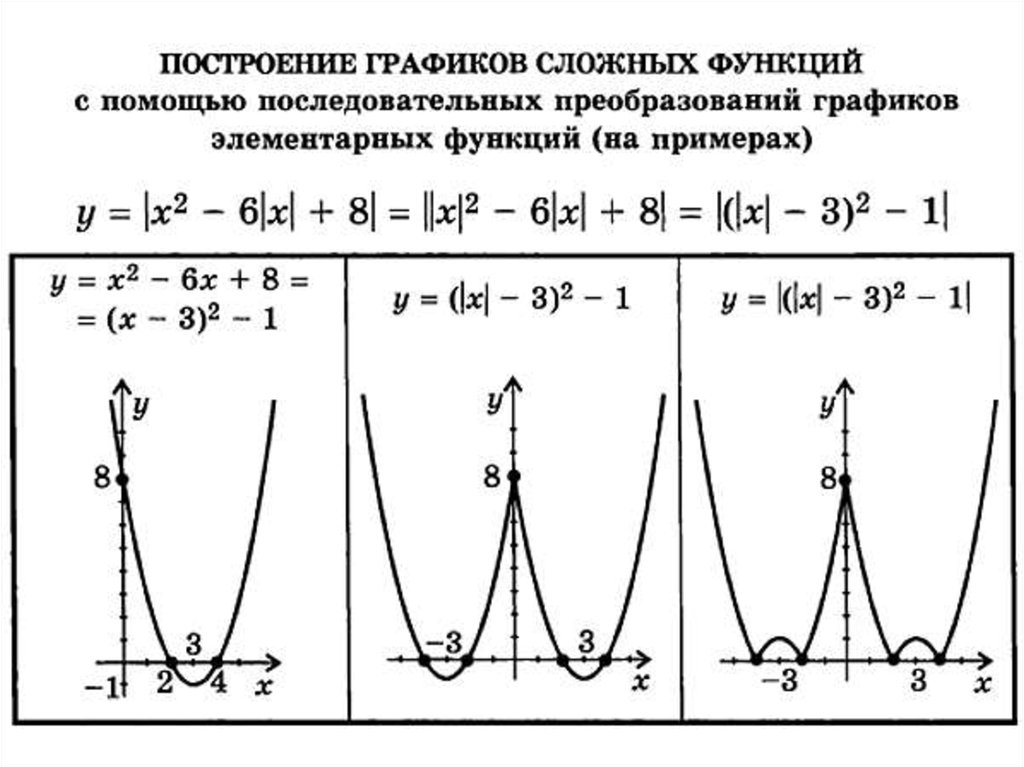
В то же время, если графики неправильно составлены или интерпретированы, они могут повлиять на наше восприятие реальной ситуации и наши результирующие суждения. Tufte (1983) представил множество примеров графиков, которые приводят к неправильной интерпретации данных. Трактинский и Мейер (1999) утверждали, что вводящие в заблуждение графики иногда могут быть созданы преднамеренно, а Битти и Джонс (2002a, 2002b) также добавили, что такие графики могут снизить качество решений. Особенно в наши дни, когда создание графиков так же просто, как пара кликов, люди часто создают неполные, предвзятые или неправильные графики.
В школе учащиеся часто занимаются интерпретацией и построением графиков. Например, преподаватели часто представляют результаты научных лабораторий в графическом виде, чтобы облегчить сложность и позволить понять закономерности и взаимосвязи между научными переменными (Hardy, Schneider, Jonen, Stern, & Möller, 2005), а также ожидается, что учащиеся будут строить графики.
(Шах и Хоффнер, 2002). Таким образом, графики считаются сильным средством коммуникации между учителями и учащимися, а графическая интерпретация и представление информации являются важными навыками количественной грамотности.
Существует множество исследований трудностей, с которыми зрители сталкиваются при восприятии графиков (Carpenter & Shah, 1998; Cleveland & McGill, 1985; Gattis & Holyoak, 1996; Guthrie, Weber, & Kimmerly, 1993; Leinhardt, Zaslavsky, & Stein, 1990; Maichle, 1994; Shah & Carpenter, 1995; Shah, Mayer, & Hegarty, 1999; Wang, Wei, Ding, Chen, Wang, & Hu, 2012), а также их значение для обучения в классе (Friel & Curcio, 2001; Глейзер, 2011; Шарма, 2006). Однако, как отмечают Амодео и Визнер (2012) и Лейнхардт и ее коллеги (1990), мало исследований, посвященных построению графов.
Тем не менее, исследования выявили некоторые различия между интерпретацией графиков и возможностями их построения. Лейнхардт и ее коллеги (1990) заявили: «Конструирование сильно отличается от интерпретации.
В то время как интерпретация зависит от данной части данных и требует реакции на нее, построение требует создания новых частей, которые не даны (стр. 12)». Берг и Смит (1994) обнаружили повсеместное отсутствие у школьников естественных наук навыков интерпретации и построения графиков. Тайраб и Аль-Накби (2004) обнаружили, что интерпретация графиков старшеклассниками была намного лучше, чем их способность строить графики. Тем не менее, недостаточно исследований, посвященных взаимосвязи между конкретными навыками и пониманием, лежащими в основе этих двух способностей.
Черрето и Ли (2012) сосредоточились на способности студентов колледжа строить графики и показали, что способность строить графики — это четко определенная конструкция, которая отделена от общей математики и вербальных способностей. В этом исследовании между всеми парами пяти компонентов графической задачи были обнаружены корреляции от умеренной до сильной, что подтверждает достоверность конструкции построения графа.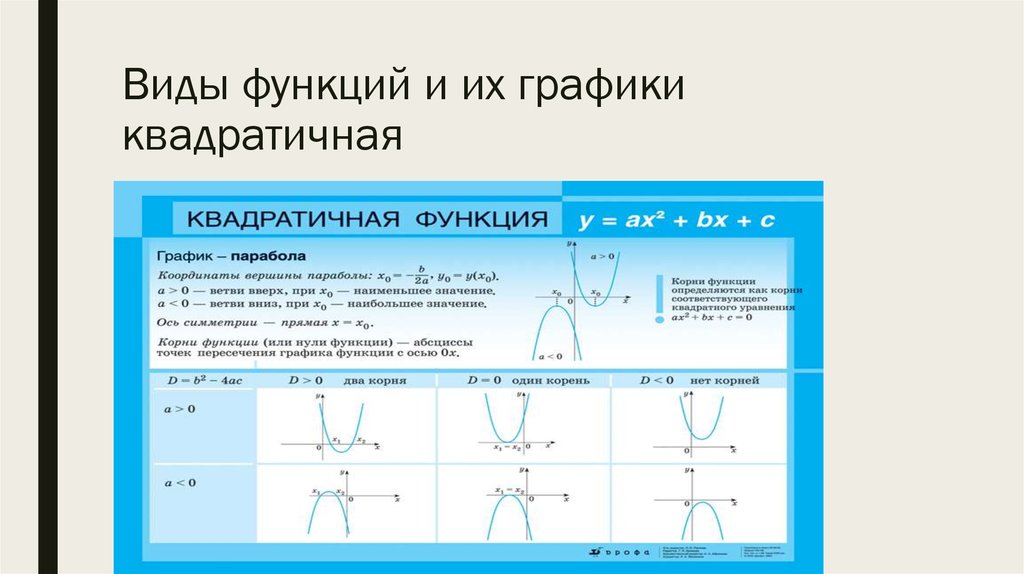
Цель и вопросы исследования
Целью данного исследования является изучение возможных взаимосвязей между способностью интерпретации графа и способностью построения графа.
Мы попытались ответить на следующие два исследовательских вопроса:
- В какой степени общая способность построения графов связана со способностью интерпретации графов?
- В какой степени определенные компоненты способности построения графа связаны с соответствующими компонентами способности интерпретации графа?
Участники и метод
Участниками этого исследования являются 67 студентов, которые были зачислены в четырехлетний государственный общеобразовательный университет в Нью-Джерси. Студенты были зачислены в один из трех классов: курс предварительного исчисления, средний курс алгебры и семинар для первокурсников, не связанный с математикой.
Студентам было дано два задания: построение графика (см. Приложение А) и интерпретация графика (Приложение Б).
Студенты сначала прошли тест на построение графиков, чтобы избежать возможности увидеть какие-либо графики в тесте на интерпретацию.
В тесте на строительство им были предоставлены числовые данные о населении и земельных площадях трех стран. Предоставив им линейки, транспортиры, калькуляторы и карандаши, их попросили построить графики, которые можно было бы использовать для ответа на три вопроса об этих странах.
В первом вопросе им предлагалось провести сравнение, во втором — выразить части целого, а в третьем — описать тенденцию. После построения каждого из трех графиков студентов попросили описать свои выводы. Задача построения графика была несвоевременной; большинство студентов закончили в течение 45 минут.
После сдачи первого теста студенту был дан второй, интерпретационный, тест. Тест на интерпретацию графиков состоял из 12 вопросов с несколькими вариантами ответов, основанных на заданных гистограммах, линейных графиках и круговых диаграммах. Это также было несвоевременным; большинство студентов закончили за 15 минут.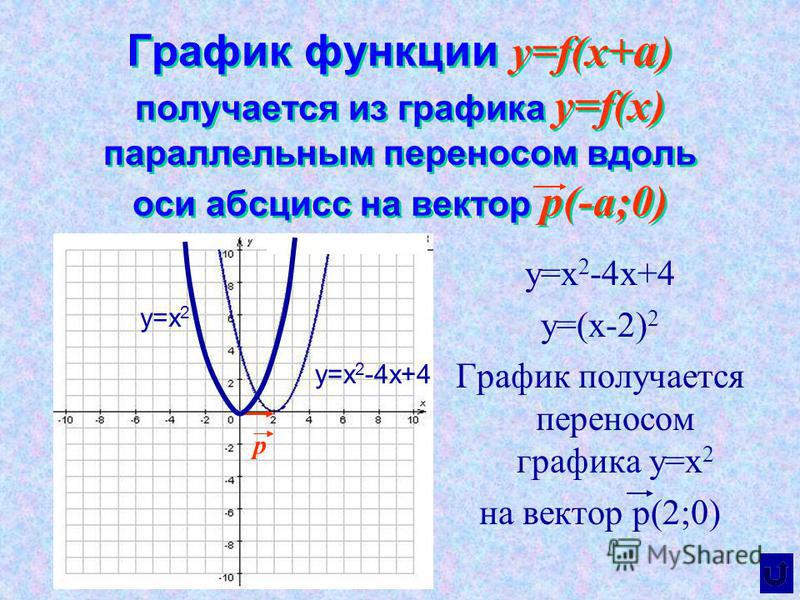
Для оценки построения графа использовались рубрики для каждой из пяти составляющих: соответствие построенного графа вопросу (Тип), качество и полнота разметки графа (Ярлыки), правильность шкалы осей (Scales), точность чертежа (Accuracy), а также правильность и полноту письменного ответа на вопрос (Explanation).
По каждому из трех вопросов два оценщика независимо присваивали баллы. Четыре, три, два или один балл означают отличную, хорошую, удовлетворительную или плохую работу соответственно. Ответы не по теме или пустые ответы получали нулевой балл. Сумма баллов от нуля до восьми использовалась для всего последующего анализа.
Чтобы ответить на два вопроса исследования, мы провели корреляционный анализ и анализ хи-квадрат.
Результаты
Сравнение общих баллов
В таблице 1 показан корреляционный анализ между общими баллами по задачам построения графика и интерпретации графика. Обратите внимание, что коэффициент корреляции не является статистически значимым (r = 0,051; p = 0,683), что указывает на отсутствие связи между двумя оценками.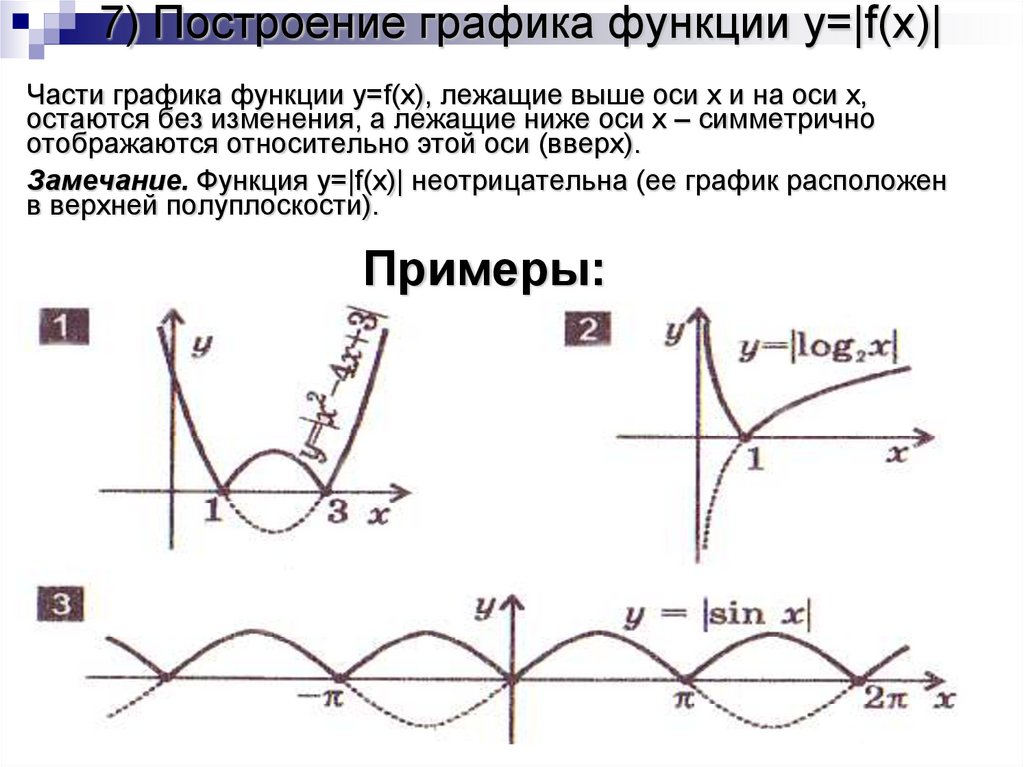
| Таблица 1: Корреляции общих баллов: построение и интерпретация графика | |||
| Общая конструкция | Общая интерпретация | ||
| Общая конструкция | Корреляция Пирсона | 1 | .051 |
| Знак. (двухвостый) | .683 | ||
| Н | 67 | 67 | |
| Общая интерпретация | Корреляция Пирсона | .051 | 1 |
| Знак. (двухвостый) | .683 | ||
| Н | 67 | 67 | |
Сравнение конкретных компонентов
Чтобы более тщательно изучить возможные взаимосвязи между этими двумя способностями, мы определили определенные элементы в задаче интерпретации графа, которые должны соответствовать конкретным компонентам способности построения графа, измеренной в задаче построения графа.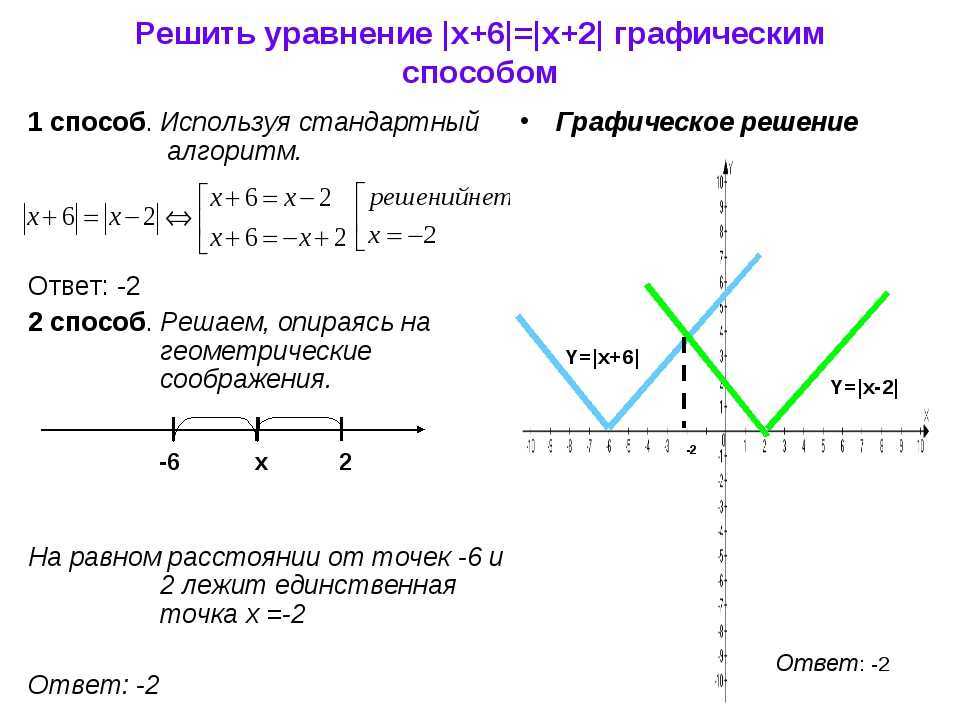
Например, пункты D1, D2 и D3 в задании на интерпретацию графика измеряли степень, в которой учащиеся были в состоянии определить наиболее подходящий тип графика для использования. В таблице 2 показаны результаты анализа хи-квадрат между баллами по компоненту «Тип» построения графика и баллами по пунктам D1, D2 и D3 в задаче интерпретации графика. Результат не показывает существенной связи в компоненте «Тип» между построением графика и его интерпретацией.
| Таблица 2: Тесты хи-квадрат: ТИП построения графика и элементы интерпретации графика D1, D2 и D3 | |||
| Значение | дф | Асимп. Сиг. (двухсторонний) | |
| Хи-квадрат Пирсон | 1,026 | 2 | .599 |
| Отношение правдоподобия | 1,029 | 2 | .598 |
| Количество действительных ящиков | 67 | ||
Точно так же пункты A1, A3, B1 и B2 в задании на интерпретацию графиков измеряли точность и способность учащихся маркировать.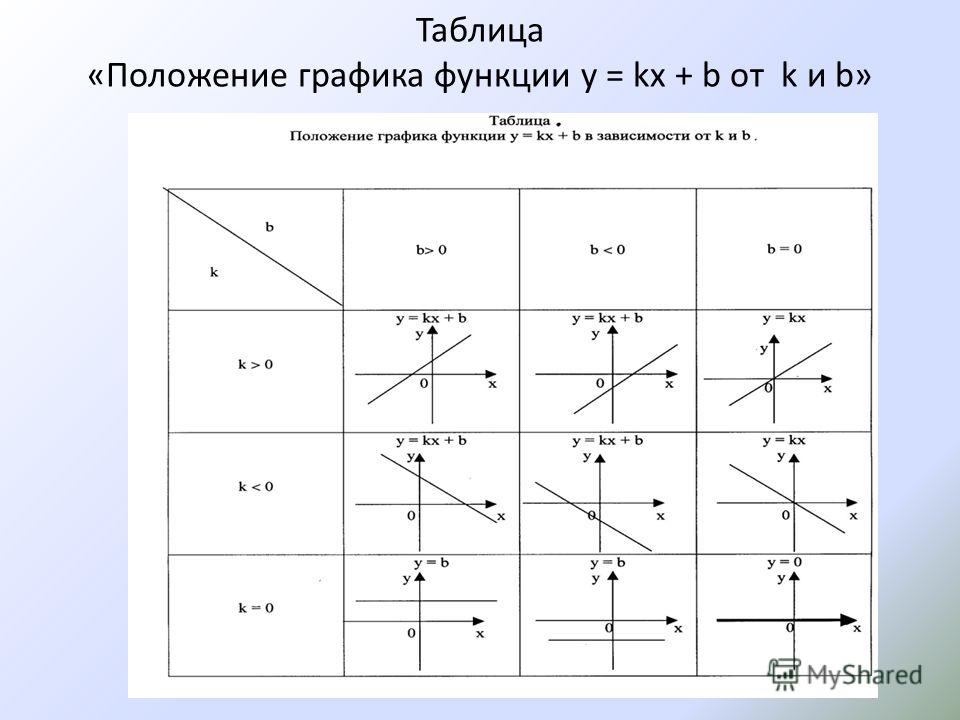
Как показано в Таблице 3, анализ хи-квадрат указывает на отсутствие связи в компонентах Точность и Метки между построением графика и интерпретацией графика.
| Таблица 3. Тесты хи-квадрат : точность построения графика/метки и элементы интерпретации графика A1, A3, B1 и B2 | |||
| Значение | дф | Асимп. Сиг. (двухсторонний) | |
| Хи-квадрат Пирсон | .383 | 2 | .826 |
| Отношение правдоподобия | .388 | 2 | .824 |
| Количество действительных ящиков | 67 | ||
Наконец, пункты A2 и A6 связаны со способностью учащихся объяснять значения графиков. Как показано в Таблице 4, анализ хи-квадрат предполагает отсутствие связи в компоненте «Объяснение» между построением графика и интерпретацией графика.
| Таблица 4: Тесты хи-квадрат: построение графика Объяснение и интерпретация графика Элементы A2 и A6 | |||
| Значение | дф | Асимп. Сиг. (двухсторонний) | |
| Хи-квадрат Пирсон | 1,192 | 2 | .551 |
| Отношение правдоподобия | 1,163 | 2 | .559 |
| Количество действительных ящиков | 67 | ||
Выводы
Цель этого исследования состояла в том, чтобы изучить возможную взаимосвязь между построением графика и способностью интерпретации графика. Хотя общепринятое мнение предполагает, что построение и интерпретация графов — две стороны одной медали, данное исследование опровергает это утверждение. Полученные данные свидетельствуют о том, что построение и интерпретация графов представляют собой разные способности, независимо от того, сравниваются ли они в глобальном масштабе или с точки зрения отдельных графических компонентов.
Хотя поначалу эти выводы могут показаться неожиданными, при дальнейшем рассмотрении мы можем их оправдать.
В этом исследовании студентов просили построить графики из заданных числовых данных и сделать числовые выводы из данных графиков. В некотором смысле это обратные операции. В изучении математики есть много других примеров, когда навыки и понимание, необходимые для движения в одном направлении, отличаются от тех, которые необходимы для движения в противоположном направлении. Например, процедуры и базовые концепции, используемые для разложения полиномов на множители, отличаются от тех, которые используются для их умножения. Точно так же знание того, как читать шкалу на данном графике, отличается от способности выбрать полезную и справедливую шкалу для использования в создаваемом графике.
Это исследование имеет важные последствия для класса и вызывает вопросы об оптимальном порядке обучения интерпретации и построению, подробном обучении графических компонентов и способах помочь учащимся установить связи между построением графа и интерпретацией. Ли и Гус (2011) утверждали, что построение графа является частью интерпретации графа.
Глейзер (2011) предположил, что если студентов нужно научить интерпретировать графики до их создания, то нам необходимо понять, что мы подразумеваем под интерпретацией графиков. Мы утверждаем, что независимо от предпочтительного порядка обучения одинаково важно понимать, что влечет за собой построение графа.
Кроме того, хотя в этом исследовании студентов просили использовать «низкотехнологичные» графические инструменты, мы должны учитывать, что преобладающее использование компьютера может изменить методы обучения построению графиков и изменить их интерпретацию. Например, когда они создают графики на компьютере, учащиеся больше внимания уделяют внешнему виду графика, а не его содержанию и значению (Li & Goos, 2011). В то же время, как утверждал Glazer (2011), создание графиков с помощью компьютеров не отменяет потребности учащихся в понимании графики.
Ссылки
Amodeo, V. & Wizner, F. (2012), Scientific Graphing A Review of the Literature, получено с http://www.
albany.edu/etap/files/Graphs_in_Science_Education.pdf
Beattie, V. ., & Jones, MJ (2002a). Влияние наклона графика на оценку скорости изменения в корпоративных отчетах . Абак (июнь), 177–199.
Битти В. и Джонс М. Дж. (2002b). Измерение искажения графиков в корпоративных отчетах: экспериментальное исследование. Журнал бухгалтерского учета, аудита и отчетности (специальный выпуск) , 546–564.
Карпентер, П.А., и Шах, П. (1998). Модель перцептивных и концептуальных процессов понимания графа. Journal of Experimental Psychology Applied, 4 (2), 75–100.
Черрето, Ф. А., и Ли, Дж. (2012). Графики, построенные учащимися, и академические способности. В MD Avgerinou (Ed.) Новые горизонты визуальной грамотности: Избранные материалы для чтения 43-й Международной конференции ассоциации визуальной грамотности , 62-72. ИВЛА.
Кливленд, Вашингтон и Макгилл, Р. (1985). Графические восприятия и графические методы анализа научных данных.
Наука, 229 , 828-833.
Фрил, С. Н., Курсио, Ф. Р., и Брайт, Г. В. (2001). Осмысление графиков: критические факторы, влияющие на понимание и последствия для обучения», Journal for Research in Mathematics Education, 32 (2), 124–158.
Гаттис, М., и Холиок, К. (1996). Отображение концептуальных пространственных отношений в визуальном мышлении. Журнал экспериментальной психологии: обучение, память и познание, 22 (1), 231-239.
Глейзер, Н. (2011). Проблемы с интерпретацией графиков: обзор литературы. Исследования в области естественнонаучного образования , 47, 183-210
Гатри, Дж. Т., Вебер, С., и Киммерли, Н. (1993). Поиск документов: когнитивный процесс и дефицит понимания графиков, таблиц и иллюстраций. Современная педагогическая психология, 18 (2), 186-221.
Лейнхардт, Г., Заславский, О., и Штейн, М.К. (1990). Функции, графики и графики: задачи, обучение и преподавание. Review of Educational Research, 60 (1).
1–64.
Левандовски С. и Беренс Дж. Т. (1999). Статистические графики и карты. В Ф. Дюрсо, С. Дюме, Р. Никерсон, Р. Шваневельдт, М. Чи и С. Линдси (ред.), The Handbook of Applied Cognitive Psychology , стр. 513–549. Чичестер, Англия: Wiley.
Ли, К., и Гус, М. (2011). Укрепление корреляционного понимания учащихся. Международный журнал обучения , 17, 261-274.
Майхле, У. (1994). Когнитивные процессы в понимании линейных графиков. В W. Schnotz, & RW Kulhavy (Eds.), Понимание графики , 207-226. Амстердам: Эльзевир.
Рашке, Р.Л. и Стейнбарт, П.Дж. (2008). Смягчение влияния вводящих в заблуждение графиков на решения путем обучения пользователей принципам построения графиков. Журнал информационных систем, 22 (2), 23-52.
Шах, П., и Карпентер, П.А. (1995). Концептуальные ограничения в понимании линейных графиков. Журнал экспериментальной психологии: Общие, 124 (1), 43-61.
Шах, П., и Хоффнер, Дж.
(2002). Обзор исследований понимания графов: значение для обучения. Обзор психологии образования, 14 (1). 47-69.
Шах П., Майер Р. Э. и Хегарти М. (1999). Графики как средства построения знаний: методы сигнализации для управления процессом понимания графов. Журнал педагогической психологии, 91 (4), 690–702.
Шарма С.В. (2006). Учащиеся старших классов, интерпретирующие таблицы и графики: значение для исследований. Международный журнал науки и математического образования, 4 , 241-268.
Тайраб, Х., и Халаф Аль-Накби, А. (2004). Как учащиеся средней школы интерпретируют и строят научные графики? Журнал биологического образования, 38 (3), 127-132.
Трактинский Н. и Мейер Дж. (1999). «Junkchart или Goldgraph? Влияние целей презентации и желательности содержания на представление информации», MIS Quarterly, 23, 397-420.
Тафте, Э. Р. (1983 ). Визуальное отображение количественной информации , Графика, Чешир, Коннектикут.
Ван, З. Х., Вэй, С., Дин, В., Чен, X., Ван, X., и Ху, К. (2012). Когнитивное рассуждение студентов о графиках: характеристики и развитие. Международный журнал научного образования , 34 (13), 2015-2041.
Винн, В. (1987). Диаграммы, графики и диаграммы в учебных материалах. В D. Willows, & HA Houghton (Eds.), The Psychology of Illustration , 152-198. Нью-Йорк: Спрингер.
ПРИЛОЖЕНИЕ A: Задача построения графика
Имя:________________________________________________ Дата: _________________
Следующие таблицы содержат данные по трем основным странам Северной Америки (Sourceus.gov).
Таблица 1: Районы стран Северной Америки
| Страна | Площадь (кв. км) |
| Канада | 9 984 670 |
| Мексика | 1 964 375 |
| США | 9 629 091 |
Таблица 2: Среднегодовое население Канады
| Год | Население | человек
| 1950 | 14 011 000 |
| 1960 | 18 267 000 |
| 1970 | 21 750 000 |
| 1980 | 24 593 000 |
| 1990 | 27 791 000 |
| 2000 | 30 689 000 |
| 2010 | 33 760 000 |
Таблица 3: Среднегодовое население Мексики
| Год | Население | человек
| 1950 | 24 485 000 |
| 1960 | 38 579 000 |
| 1970 | 52 775 000 |
| 1980 | 68 347 000 |
| 1990 | 84 914 000 |
| 2000 | 99 927 000 |
| 2010 | 112 469 000 |
Таблица 4: Среднегодовое население США
| Год | Население | человек
| 1950 | 151 868 000 |
| 1960 | 179 979 000 |
| 1970 | 203 984 000 |
| 1980 | 227 225 000 |
| 1990 | 249 623 000 |
| 2000 | 282 172 000 |
| 2010 | 308 282 000 |
На следующих страницах вам будет предложено нарисовать графики, которые можно использовать для ответов на вопросы об этих трех странах, и использовать эти графики для ответов на вопросы.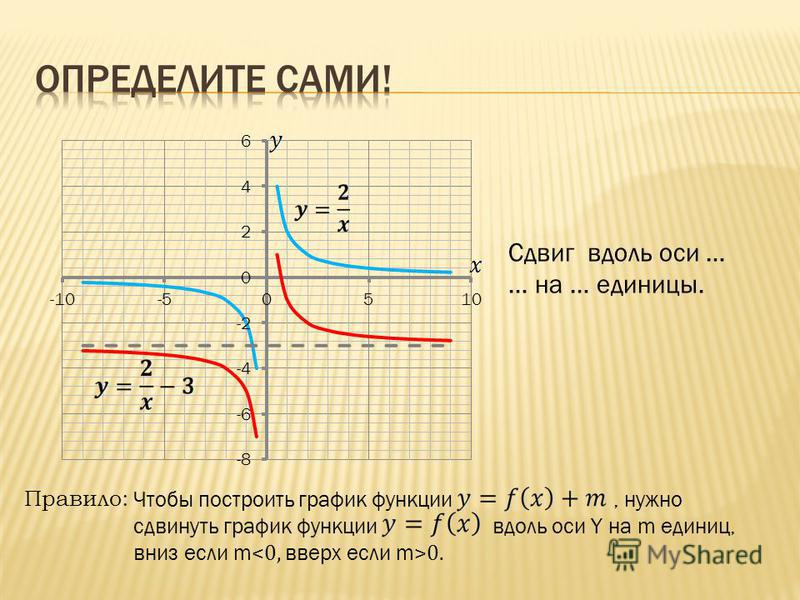
Вам дадут транспортир и линейку. Пожалуйста, нарисуйте графики как можно точнее и четче.
1. Предположим, вы хотите сравнить население трех стран в 2000 году.
- На основе графика напишите несколько предложений, сравнивающих население трех стран.
- Нарисуйте полезный график.
2. Предположим, вы хотите выяснить, какую часть общей площади Северной Америки занимает каждая из трех стран.
- Нарисуйте полезный график в этом пространстве.
- На основе графика напишите несколько предложений о долях общей площади, занимаемой каждой страной.
3. Предположим, вы хотите определить, какая из трех стран имела самые высокие темпы прироста населения с 1950 по 2010 год.
- Нарисуйте полезный график в этом пространстве.
- На основе графика напишите несколько предложений, сравнивая темпы прироста населения этих трех стран за этот период.
Имя________________________________________ Дата____________________
Часть A.
Этот график содержит информацию о недавнем населении трех вымышленных городов: Аллентаун, Браунсвилл и Кроуэлл.
1. Какова была приблизительная численность населения Браунсвилля в 2008 году?
- 60
- 65
- 60 000
- 65 000
- Невозможно определить по этому графику.
2. В каком городе наблюдалось наиболее устойчивое изменение численности населения с 2000 по 2012 г.?
- Аллентаун
- Браунсвилл
- Кроуэлл
- Невозможно определить по этому графику.
3. На сколько примерно человек увеличилось население Аллентауна с 2004 по 2012 год?
- 10
- 15
- 10 000
- 15 000
- Невозможно определить по этому графику.
4. В каком городе было больше всего населения более чем за один год?
- Аллентаун
- Браунсвилл
- Кроуэлл
- Невозможно определить по этому графику.
5. Какой город имеет наибольшую площадь?
- Аллентаун
- Браунсвилл
- Кроуэлл
- Невозможно определить по этому графику.
6. Население какого города за 2000 -2004 гг. сократилось быстрее всего?
- Аллентаун
- Браунсвилл
- Кроуэлл
- Невозможно определить по этому графику.
Часть B. Этот график содержит информацию о земельных площадях трех вымышленных городов: Аллентаун, Браунсвилл и Кроуэлл.
- Какова приблизительная площадь Кроуэлла в квадратных милях?
- 8,5
- 9
- 850
- 900
- Невозможно определить по этому графику.
- Насколько примерно Аллентаун больше, чем Браунсвилл, в квадратных милях?
- 4
- 5
- 400
- 500
- Невозможно определить по этому графику.
Часть C. Объединение
1.
Используя оба графика в частях A и B, определите, в каком городе была самая высокая плотность населения (количество человек на квадратную милю) в 2000 году?
- Аллентаун
- Браунсвилл
- Кроуэлл
- Невозможно определить по двум графикам.
Часть D. На этих графиках представлена информация о возрастных группах населения Аллентауна в 2012 г.
1. Какой график труднее всего использовать, если вы хотите точно определить значения?
- Круговая диаграмма
- Гистограмма
- Линейный график
- Трехмерная гистограмма
- Невозможно определить.
2. Какой график будет наименее подходящим , если вы хотите сравнить количество людей в двух разных возрастных группах?
- Круговая диаграмма
- Гистограмма
- Линейный график
- Трехмерная гистограмма
- Невозможно определить.
