Уравнение прямой найти: Уравнение прямой онлайн

описание, примеры, решение задач, общий вид уравнения прямой

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой (общее уравнение прямой на плоскости и его исследование). Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и его исследование, как осуществлять переходы от общего уравнения к другим типам уравнений прямой (неполного уравнения, полного уравнения). Всю теорию закрепим иллюстрациями и решением практических задач на уравнения.

Общее уравнение прямой: основные сведения

Как найти уравнение прямой? Пусть на плоскости задана прямоугольная система координат Oxy.

Теорема 1

Любое уравнение первой степени, имеющее вид Ax+By+C=0, где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид Ax+By+C=0 при некотором наборе значений А, В, С.

Доказательство 

указанная теорема состоит из двух пунктов, докажем каждый из них.

1. Докажем, что уравнение Ax+By+C=0 определяет на плоскости прямую.

Пусть существует некоторая точка М0(x0, y0), координаты которой отвечают уравнению Ax+By+C=0. Таким образом: Ax0+By0+C=0. Вычтем из левой и правой частей уравнений Ax+By+C=0 левую и правую части уравнения Ax0+By0+C=0, получим новое уравнение, имеющее вид A(x-x0)+B(y-y0)=0. Оно эквивалентно Ax+By+C=0.

Полученное уравнение A(x-x0)+B(y-y0)=0 является необходимым и достаточным условием перпендикулярности векторов n→=(A, B) и M0M→=(x-x0, y-y0). Таким образом, множество точек M(x, y)  задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n→=(A, B). Можем предположить, что это не так, но тогда бы векторы n→=(A, B) и M0M→=(x-x0, y-y0) не являлись бы перпендикулярными, и равенство A(x-x0)+B(y-y0)=0 не было бы верным.

Следовательно, уравнение A(x-x0)+B(y-y0)=0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение Ax+By+C=0 определяет ту же прямую. Так мы доказали первую часть теоремы.

2. Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени Ax+By+C=0.

Зададим в прямоугольной системе координат на плоскости прямую a; точку M0(x0, y0), через которую проходит эта прямая, а также нормальный вектор этой прямой n→=(A, B).

Пусть также существует некоторая точка M(x, y) – плавающая точка прямой. В таком случае, векторы n→=(A, B) и M0M→=(x-x0, y-y0) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:

n→, M0M→=A(x-x0)+B(y-y0)=0

Перепишем уравнение Ax+By-Ax0-By0=0, определим C: C=-Ax0-By0 и в конечном результате получим уравнение  Ax+By+C=0.

Так, без какой-либо помощи онлайн мы смогли доказать и вторую часть теоремы, и доказали всю теорему в целом.

Определение 1

Уравнение, имеющее вид Ax+By+C=0 – это общее уравнение прямой на плоскости в прямоугольной системе координат Oxy (уравнение прямой параллельной оси ox).

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой Ax+By+C=0.

Рассмотрим конкретный пример общего уравнения прямой.

Пусть задано уравнение 2x+3y-2=0, которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n→= (2, 3). Изобразим заданную прямую линию из уравнения с вектором на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2x+3y-2=0, поскольку координаты всех точек заданной прямой отвечают этому уравнению.

Мы можем получить уравнение λ·Ax+λ·By+λ·C=0, умножив обе части общего уравнения прямой на число λ, не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.

Неполное уравнение общей прямой

Определение 2

Полное общее уравнение прямой – такое общее уравнение прямой Ax+By+C=0, в котором числа А, В, С отличны от нуля. В ином случае уравнение является неполным.

Разберем все вариации неполного общего уравнения прямой.

1. Когда А=0, В≠0, С≠0, общее уравнение принимает вид By+C=0. Такое неполное общее уравнение задает в прямоугольной системе координат Oxy прямую, которая параллельна оси Ox, поскольку при любом действительном значении x переменная y примет значение -CB . Иначе говоря, общее уравнение прямой Ax+By+C=0, когда А=0, В≠0, задает геометрическое место точек (x, y), координаты которых равны одному и тому же числу -CB.
2. Если А=0, В≠0, С=0, общее уравнение принимает вид y=0. Такое неполное уравнение определяет ось абсцисс Ox.
3. Когда А≠0, В=0, С≠0, получаем неполное общее уравнение Ax+С=0, задающее прямую, параллельную оси ординат.
4. Пусть А≠0, В=0, С=0, тогда неполное общее уравнение примет вид x=0, и это есть уравнение координатной прямой Oy.
5. Наконец, при А≠0, В≠0, С=0, неполное общее уравнение принимает вид Ax+By=0. И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел (0, 0) отвечает равенству Ax+By=0, поскольку А·0+В·0=0.

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Пример 1

Известно, что заданная прямая параллельна оси ординат и проходит через точку 27, -11. Необходимо написать общее уравнение заданной прямой. Попробуем его составить.

Решение

Решение лежит на поверхности. Прямая, параллельная оси ординат, задается уравнением вида Ax+C=0, в котором А≠0. Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения Ax+C=0, т. е. верно равенство:

A·27+C=0

Из него возможно определить C, если придать A какое-то ненулевое значение, к примеру, A=7. В таком случае получим: 7·27+C=0⇔C=-2. Нам известны оба коэффициента A и C, подставим их в уравнение Ax+C=0 и получим требуемое уравнение прямой: 7x-2=0

Ответ: 7x-2=0

Пример 2

 На чертеже изображена прямая, необходимо записать ее уравнение. Как будем это находить?

Решение

Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси Ox и проходит через точку (0, 3).

Прямую, которая будет являться параллельной оси абсцисс, определяет неполное общее уравнение By+С=0. Найдем значения B и C. Координаты точки (0, 3), поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой By+С=0, тогда справедливым является равенство: В·3+С=0. Зададим для В какое-то значение, отличное от нуля. Допустим, В=1, в таком случае из равенства В·3+С=0 можем найти С: С=-3. Используем известные значения В и С, получаем требуемое уравнение прямой: y-3=0.

Ответ: y-3=0.

Общее уравнение прямой, проходящей через заданную точку плоскости

Пусть заданная прямая проходит через точку М0(x0, y0), тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: Ax0+By0+C=0. Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A(x-x0)+B(y-y0)+C=0, это уравнение эквивалентно исходному общему, проходит через точку М0(x0, y0) и имеет нормальный вектор n→=(A, B).

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Пример 3

Даны точка М0(-3, 4), через которую проходит прямая, и нормальный вектор этой прямой  n→=(1, -2). Необходимо записать уравнение заданной прямой.

Решение

Исходные условия позволяют нам получить необходимые данные для составления уравнения: А=1, В=-2, x0=-3, y0=4. Тогда:

A(x-x0)+B(y-y0)=0⇔1·(x-(-3))-2·y(y-4)=0⇔⇔x-2y+22=0

Задачу можно решать иначе. Как она будет решаться? Общее уравнение прямой имеет вид Ax+By+C=0. Заданный нормальный вектор (векторная прямая) позволяет получить значения коэффициентов A и B в уравнении прямой, тогда:

Ax+By+C=0⇔1·x-2·y+C=0⇔x-2·y+C=0

Теперь найдем значение С, используя заданную условием задачи точку М0(-3, 4), через которую проходит прямая. Координаты этой точки отвечают уравнению x-2·y+C=0, т.е. -3 — 2·4+С=0. Отсюда С=11. Требуемое уравнение прямой принимает вид: x — 2·y + 11=0.

Ответ: x — 2·y + 11=0.

Пример 4

Задана прямая 23x-y-12=0 и точка М0, лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна -3. Необходимо определить ординату заданной точки.

Решение

Зададим обозначение координат точки М0 как x0 и y0. В исходных данных указано, что x0=-3. Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой.

Тогда верным будет равенство:

23×0-y0-12=0

Определяем y0: 23·(-3)-y0-12=0⇔-52-y0=0⇔y0=-52

Ответ: -52

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Для начала рассмотрим переход от общего уравнения вида Ax+By+C=0 к каноническому уравнению  x-x1ax=y-y1ay.

Если А≠0, тогда переносим слагаемое By в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: Ax+CA=-By.

Это равенство возможно записать как пропорцию: x+CA-B=yA .

В случае, если В≠0, оставляем в левой части общегь уравнения только слагаемое Ax, прочие переносим в правую часть, получаем: Ax=-By-C. Выносим –В за скобки, тогда: Ax=-By+CB.

Перепишем равенство в виде пропорции: x-B=y+CBA                             .

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Пример 5

Задано общее уравнение прямой 3y-4=0. Необходимо преобразовать его в каноническое уравнение.

Решение 

Запишем исходное уравнение как 3y-4=0. Далее действуем по алгоритму: в левой части остаётся слагаемое 0x; а в правой части выносим -3 за скобки; получаем: 0x=-3y-43.

Запишем полученное равенство как пропорцию: x-3=y-430. Так, мы получили уравнение канонического вида.

Ответ: x-3=y-430.

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Пример 6

Перед нами задание. Прямая задана уравнением 2x-5y-1=0. Запишите параметрические уравнения этой прямой.

Решение

Осуществим переход от общего уравнения к каноническому:

2x-5y-1=0⇔2x=5y+1⇔2x=5y+15⇔x5=y+152

Теперь примем обе части полученного канонического уравнения равными λ, тогда:

x5=λy+152=λ⇔x=5·λy=-15+2·λ, λ∈R

Ответ: x=5·λy=-15+2·λ, λ∈R

Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y=k·x+b, но только тогда, когда В≠0. Для перехода в левой части оставляем слагаемое By, остальные переносятся в правую. Получим: By=-Ax-C. Разделим обе части полученного равенство на B, отличное от нуля: y=-ABx-CB.

Пример 7

Задано общее уравнение прямой: 2x+7y=0. Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.

Решение

Произведем нужные действия по алгоритму:

2x+7y=0⇔7y-2x⇔y=-27x

Ответ: y=-27x .

Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида xa+yb=1. Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на –С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y:

Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1

Пример 8

Необходимо преобразовать общее уравнение прямой x-7y+12=0 в уравнение прямой в отрезках.

Решение

Перенесем 12  в правую часть: x-7y+12=0⇔x-7y=-12.

Разделим на -1/2 обе части равенства: x-7y=-12⇔1-12x-7-12y=1.

Преобразуем далее в необходимый вид: 1-12x-7-12y=1⇔x-12+y114=1.

Ответ: x-12+y114=1.

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.

Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:

xa+yb⇔1ax+1by-1=0⇔Ax+By+C=0y=kx+b⇔y-kx-b=0⇔Ax+By+C=0

Каноническое уравнение преобразуется к общему по следующей схеме:

x-x1ax=y-y1ay⇔ay·(x-x1)=ax(y-y1)⇔⇔ayx-axy-ayx1+axy1=0⇔Ax+By+C=0

Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:

x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔Ax+By+C=0

Пример 9

Заданы параметрические уравнения прямой x=-1+2·λy=4. Необходимо записать общее уравнение этой прямой.

Решение 

Осуществим переход от параметрических уравнений к каноническому:

x=-1+2·λy=4⇔x=-1+2·λy=4+0·λ⇔λ=x+12λ=y-40⇔x+12=y-40

Перейдем от канонического к общему:

x+12=y-40⇔0·(x+1)=2(y-4)⇔y-4=0

Ответ: y-4=0

Пример 10

Задано уравнение прямой в отрезках  x3+y12=1 . Необходимо осуществить переход к общему виду уравнения.

Решение:

Просто перепишем уравнение в необходимом виде:

x3+y12=1⇔13x+2y-1=0

Ответ: 13x+2y-1=0.

Составление общего уравнения прямой

Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A(x-x0)+B(y-y0)=0. Там же мы разобрали соответствующий пример.

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Пример 11

Задана прямая, параллельная прямой 2x-3y+33=0. Также известна точка M0(4, 1), через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.

Решение

Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n→=(2, -3): 2x-3y+33=0. Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:

A(x-x0)+B(y-y0)=0⇔2(x-4)-3(y-1)=0⇔2x-3y-5=0

Ответ: 2x-3y-5=0.

Пример 12

Заданная прямая проходит через начало координат перпендикулярно прямой x-23=y+45. Необходимо составить общее уравнение заданной прямой.

Решение

Нормальный вектором заданной прямой будет направляющий вектор прямой x-23=y+45.

Тогда n→=(3, 5). Прямая проходит через начало координат, т.е. через точку О(0, 0). Составим общее уравнение заданной прямой:

A(x-x0)+B(y-y0)=0⇔3(x-0)+5(y-0)=0⇔3x+5y=0

Ответ: 3x+5y=0. 2

y=mx+c — Уравнение прямой — GCSE Maths

Введение

Что такое y=mx+c?

Градиент м

Y-пересечение ‘c’

Как использовать y=mx+c

рабочий лист y=mx+c

Распространенные заблуждения

Практика y=mx+c вопросов

y=mx+c вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое y=mx+c?

Градиент м

Y-пересечение ‘c’

Как использовать y=mx+c

рабочий лист y=mx+c

Распространенные заблуждения

Практика y=mx+c вопросов

y=mx+c вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о y = mx + c , в том числе о том, как распознать градиент и точку пересечения y из уравнения y = mx + c и преобразовать уравнение в стандартную форму y = mx + c.

Существуют также рабочие листы y = mx + c, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое y=mx+c?

Уравнение y = mx + c — это общее уравнение любой прямой линии, где m — это градиент линии (насколько крута линия), а c — это точка пересечения по оси y ( точка, в которой линия пересекает ось Y).

y = mx + c является линейным уравнением, а переменные x и y относятся к координатам на линии.
Когда мы вводим значение x в уравнение y = mx + c, мы получаем результат для y.
Это означает, что x является независимой переменной , а y является зависимой переменной , поскольку она определяется значением x.

Давайте посмотрим на линию y = 2x + 1. 

Этот график имеет градиент 2 и точку пересечения 1 с координатой (0,1).

• Термин линейный используется для описания прямой линии, в которой переменные возводятся в степень не выше 1
• Если переменные возводятся в степень не выше 2 , мы называем его квадратичным
• Если переменные возводятся в степень не выше 3 , мы называем это кубическим и так далее.

Что такое y=mx+c?

Градиент «m»

Градиент линии говорит нам насколько крута линия .

Мы используем букву м для обозначения градиента.

Представьте, что вы поднимаетесь по лестнице. Если лестница очень близко к стене, уклон лестницы действительно крутой (вы будете карабкаться почти вертикально). Отведение основания лестницы от стены означает, что уклон наклона уменьшается, достигая более низкой точки на стене.

Чем больше градиент, тем круче линия.

Градиент 2 создаст линию, которая будет намного круче, чем градиент {\frac{1}{3}} .

См. схему ниже.

Градиент линии может представлять собой множество различных типов чисел, т. е. дроби, десятичные знаки, отрицательные значения и т. д. линия y = mx + c и ось y. Y-отрезок — это значение y, когда x = 0.

Например.
Давайте посмотрим на уравнение y = 5x + 7. 

Чтобы найти точку пересечения y, подставим x = 0 в уравнение.

\begin{выровнено} &у=(5\умножить на 0)+7\\\\ &у=7 \end{aligned}

Итак, когда x = 0, y = 7, мы получаем координату (0,7).

Это точка пересечения оси Y.

Вот краткий обзор некоторых уравнений в форме y = mx + c с выделенными градиентом и точкой пересечения y.

y = Mx+C

Y = 2x+4

Y = 6x-3

Y = -4x

Y = 6-x

Градиент M

2

6
9000
-4

-1

Y -интерцепт C

4

-3

0 (Происхождение)

6

Как использовать Y = MX+C

. -пересечение линии:

1. Переставьте уравнение, чтобы сделать y предметом
2. Подставьте x = 0 в уравнение, чтобы найти точку пересечения с осью y
3. Укажите коэффициент x (градиент)

Как использовать y=mx+c

Рабочий лист y=mx+c

Получите бесплатный рабочий лист y=mx+c, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Рабочий лист y=mx+c

Получите бесплатный рабочий лист y=mx+c, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

y = mx + c примеры

Пример 1: y=mx+c форма

Укажите градиент и точку пересечения с линией y = −3x + 8.

1. Измените уравнение, чтобы сделать y предметом

Уравнение y = −3x + 8 уже имеет общую форму y=mx+c, поэтому мы можем сразу перейти к шагу 2.

2 Подставьте x = 0 в уравнение, чтобы найти точку пересечения с осью y

Когда x = 0,

\begin{align} &y=(-3\times{0})+8\\\\ &y=0+8\\\\ &у=8 \end{aligned}

Y-пересечение линии y = −3x + 8 равно 8 или c = 8,

3 Укажите коэффициент при x (градиент)

Коэффициент при x равен −3.

Градиент линии y = −3x + 8 равен −3, или m = −3.

Решение: m = −3, c = 8

Пример 2: y=mx+c из

Укажите градиент и точку пересечения y линии y = 7 − x.

Переформулируйте уравнение так, чтобы y стало предметом

Здесь у нас есть два члена +7 и −x, поэтому нам нужно изменить порядок их появления справа от знака равенства, чтобы мы получили уравнение в виде y=mx+c.

\begin{выровнено} &у=7-х\\\\ &у=-х+7 \end{align}

Подставьте x = 0 в уравнение, чтобы найти точку пересечения с осью y

Когда x = 0,

\begin{align} &y=-0+7\\\\ &y=0+7\\\\ &у=7 \end{aligned}

Пересечение линии y = 7 − x равно 7 или c = 7.

Укажите коэффициент x (градиент)

Коэффициент x равен −1, поскольку −x совпадает с −1x.

Градиент линии y = 7 − x равен −1 или m = −1.

Решение: m = −1, c = 7.

Пример 3: переформулировать уравнение, когда x является предметом уравнение, чтобы сделать

y предмет

Здесь нам нужно сделать y предметом уравнения. Поэтому нам нужно убедиться, что мы изолируем y по одну сторону от знака равенства, чтобы выразить уравнение в форме y=mx+c.

Подставьте x = 0 в уравнение, чтобы найти точку пересечения с осью y

Когда x = 0,

\begin{align} &y=0-10\\\\ &у=-10 \end{aligned}

Y-пересечение линии x = y + 10 равно −10, или c = −10.

Укажите коэффициент x (градиент)

Коэффициент x равен 1, так как x равен 1x.

Градиент линии x = y + 10 равен 1 или m = 1.

Пример 4: изменение субъекта, включая дробь

Укажите градиент и точку пересечения с осью y линии 2x = 6y − 15.

Переформулируйте уравнение так, чтобы y стало предметом

Здесь нам нужно чтобы сделать y предметом уравнения. Поэтому нам нужно убедиться, что мы изолируем y по одну сторону от знака равенства, чтобы выразить уравнение в форме y=mx+c.

Подставьте x = 0 в уравнение, чтобы найти точку пересечения с осью y

Когда x = 0,

\begin{align} &y=(\frac{1}{3}\times{0})+\frac{5}{2}\\\\ &y=0+\frac{5}{2}\\\\ &y=\frac{5}{2} \end{align}

Y-пересечение линии 2x = 6y −15 равно

\[\frac{5}{2}, \quad \text{or} \quad c=\frac{5} {2}.\]

Укажите коэффициент x (градиент)

Коэффициент x равен

\[\frac{1}{3}.\]

Градиент строка 2x = 6y — 15 равна

\[\frac{1}{3}, \quad \text{or} \quad m=\frac{1}{3}. \]

Пример 5: изменение темы, включая скобки

Укажите градиент и y-пересечение прямой 3x = 4(y − 5).

Переформулируйте уравнение так, чтобы y стало субъектом

Здесь нам нужно сделать y субъектом уравнения. Поэтому нам нужно убедиться, что мы изолируем y по одну сторону от знака равенства, чтобы выразить уравнение в форме y=mx+c.

Подставьте x = 0 в уравнение, чтобы найти точку пересечения с осью y

Когда x = 0,

\begin{align} &y=(\frac{3}{4}\times{0})+5\\\\ &y=0+5\\\\ &у=5 \end{align}

Точка пересечения линии 3x = (y −5) равна 5 или c = 5.

Укажите коэффициент x (градиент) x равно

\[\frac{3}{4}.\]

Градиент линии 3x = (y − 5) равен

\[\frac{3}{4}, \quad \text{or} \quad m=\frac{3}{4}.\]

Пример 6: изменение темы, включая десятичные дроби

Укажите градиент

\[x=\frac{y+0. 85}{0.2}.\]

Преобразуйте уравнение так, чтобы y стало предметом

Здесь нам нужно сделать y предметом уравнения. Поэтому нам нужно убедиться, что мы изолируем y по одну сторону от знака равенства, чтобы выразить уравнение в форме y=mx+c.

Подставьте x = 0 в уравнение, чтобы найти точку пересечения с осью y

Когда x = 0,

\begin{align} &у=(0,2\раз{0})-0,85\\\\ &у=0-0,85\\\\ &у=-0,85 \end{align}

Y-пересечение линии

\[x=\frac{y+0.85}{0.2}\]

равно −0,85, или c = −0,85.

Укажите коэффициент при x (градиент)

Коэффициент при x равен 0,2.

Градиент линии

\[x=\frac{y+0,85}{0,2}\]

равен 0,2 или m = 0,2.

Распространенные заблуждения

• Неправильная обратная операция

При преобразовании уравнений вместо применения обратной операции к перемещаемому значению значение просто перемещается с другой стороны знака равенства.

y + 5 = 2x переставляется, чтобы получить y = 2x + 5 ✘

• Указание значения m и c

Распространенной ошибкой является неверное указание значений m и c из-за того, что уравнение не перестроено таким образом, чтобы оно имело форму y=mx+c.
Возьмем пример 3 выше, когда x = y + 10. Градиент будет указан как 1, так как это коэффициент x, однако значение точки пересечения y будет неправильно указано как 10.

Правильный ответ для Перехват y равен −10, так как мы можем изменить уравнение, чтобы сделать y субъектом. См. ниже.

• Смешение градиента и точки пересечения оси Y

Возьмем, например, уравнение y = 10 + 3x. Здесь коэффициент x равен 3, а значение y при x = 0 равно 10. Это означает, что градиент равен 3, а точка пересечения y равна 10, а не наоборот.

Практика y=mx+c вопросы

m=-5, \; с=9

m=9, \; с=5

m=9, \; с=-5

m=-5, \; c=4

Коэффициент x равен -5, поэтому m=-5

 

Когда x=0, y=9, значит, c=9.

м=6, \; с=-1

м=-1, \; с=6

m=5, \; с=6

m=0, \; с=5

у=6-х

 

у=-х+6

 

Коэффициент при x равен -1, поэтому m=-1

 

Когда x=0, y=6, поэтому c=6.

м=\frac{1}{2}, \; c=-\frac{5}{2}

м=2, \; с=5

м=-2, \; с=-5

м=1, \; с=7

y=\frac{1}{2}x-\frac{5}{2}

 

Коэффициент при x равен \frac{1}{2} , поэтому m=\frac{1}{2}

 

Когда x=0, y=-\frac{5}{2}, поэтому c=-\frac{5}{2}.

м=\frac{3}{5}, \; c=\frac{6}{5}

м=3, \; с=-6

м=2, \; с=-1

m=2y, \; с=5

y=\frac{3}{5}x+\frac{6}{5}

 

Коэффициент при x равен \frac{3}{5} , поэтому m=\frac{3}{5}

 

Когда x=0, y=\frac{6}{5}, поэтому c=\frac{6}{5}.

м=\frac{2}{3}, \; с=-3

м=2, \; с=0

м=6, \; c=9

м=\frac{2}{3}, \; с=3

у=\фракция{2}{3}х-3

 

Коэффициент при x равен \frac{2}{3} , поэтому m=\frac{2}{3}

 

Когда x=0, y=-3, поэтому c=-3.

м=-\frac{2}{3}, \; c=\frac{1}{3}

м=0,5, \; с=0,5

m=0,75,\; с=0,5

м=1,5, \; с=0,5

y=-\frac{2}{3}x+\frac{1}{3}

 

Коэффициент при x равен -\frac{2}{3} , поэтому m=-\frac{2}{3}

 

Когда x=0, y=\frac{1}{3} , поэтому c=\frac{1}{3}.

y=mx+c Вопросы GCSE

1. Учитывая, что координата (3,4) лежит на прямой y=3x+c, вычислить точку пересечения прямой по оси y.

(2 балла)

Показать ответ

Подставьте x=3 и y=4 в y=3x+c , чтобы получить

4=(3\times3)+c (1 балл)

(1)

 

4 = 9+0c

c=-5 (1 балл)

(1)

2. (a) Координата A=(0,2) лежит на прямой. Градиент линии равен 5 . Используя эту информацию, составьте уравнение прямой линии.

 

(b)  Запишите уравнение прямой, параллельной а), в форме y=mx+c .

 

(4 балла)

Показать ответ

(a)

A является точкой пересечения с осью y, поэтому c=2 или при x=0, y=2 , поэтому c=2

7 (9)

y = 5x+c (1mark)

(1)

Y = 5x+2 (1mark)

(1)

(B) 9003

(B) 9003

(B)

(B) . 5х+с где
с ≠ 2 (1 балл)

(1)

3. Покажите m=2 для прямой линии 8x-4y=12.

(3 балла)

Показать ответ

(3)

Контрольный список обучения

Вы уже узнали, как:

• форма y=mx+c

Все еще застрял?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения математики GCSE, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе повторения GCSE по математике.

Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой использования файлов cookie для получения информации о том, как мы используем файлы cookie и как управлять вашими настройками файлов cookie или изменять их. Принять

4.2 Уравнение линии | Аналитическая геометрия

4.2 Уравнение прямой (EMBG8)

Мы можем вывести различные формы уравнения прямой линии. Используются различные формы в зависимости от информация в задаче:

• Двухточечная форма уравнения прямой: \(\dfrac{y-y_1}{x-x_1} = \dfrac{y_2-y_1}{x_2-x_1}\)
• Градиентно-точечная форма уравнения прямой линии: \(y-y_1 = m(x-x_1)\)
• Градиентно-отрезочная форма уравнения прямой линии: \(y = mx + c\)

Двухточечная форма уравнения прямой линии (EMBG9)

Даны любые две точки \(\left({x}_{1};{y}_{1}\right)\) и \(\ left({x}_{2};{y}_{2}\right)\), мы можем определить уравнение линии, проходящей через две точки, используя уравнение:

\[\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\]

Рабочий пример 3: двухточечная форма уравнения прямой

Найдите уравнение прямой, проходящей через точки \(P\left(-1;-5\right)\) и \(Q\left(5;4\right)\).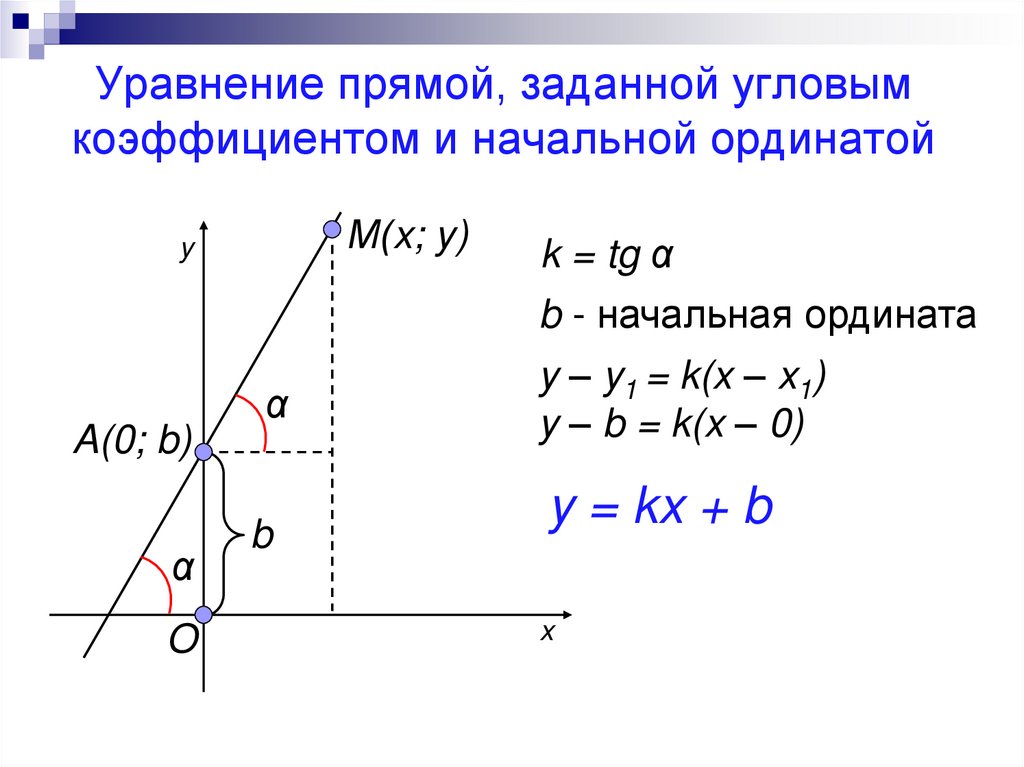

Нарисовать эскиз

Присвоить переменные координатам заданных точек

Пусть координаты \(P\) равны \((x_1;y_1)\) и \(Q(x_2;y_2)\)

\[x_1 = -1 ; \qquad y_1 = -5; \qquad x_2 = 5; \qquad y_2 = 4\]

Запишите двухточечную форму уравнения прямой

\[\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\]

Подставьте значения и сделайте \(y\) предметом уравнения

\begin{align*} \frac{y-(-5)}{x-(-1)} &= \frac{4-(-5)}{5-(-1)} \\ \frac{y+5}{x+1} &= \frac{9}{6} \\ y+5 &= \frac{3}{2}(x+1) \\ y+5 &= \frac{3}{2}x + \frac{3}{2} \\ y &= \frac{3}{2}x — \frac{7}{2} \end{выравнивание*}

Запишите окончательный ответ

\[y = \frac{3}{2}x — 3\frac{1}{2}\]

Двухточечная форма уравнения прямой

Учебник Упражнение 4.2

\((3;7)\) и \((-6;1)\)

\begin{align*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-7}{x-3} &= \frac{1-7}{-6-3} \\ \frac{y-7}{x-3} &= \frac{-6}{-9} \\ \frac{y-7}{x-3} &= \frac{2}{3} \\ y — 7 &= \frac{2}{3} \left( x — 3 \right) \\ y &= \frac{2}{3}x — 2 + 7 \\ \следовательно y &= \frac{2}{3}x + 5 \end{выравнивание*}

\((1;-\frac{11}{4})\) и \((\frac{2}{3}; -\frac{7}{4})\)

\begin{align *} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y + \frac{11}{4}}{x-1} &= \frac{-\frac{7}{4} + \frac{11}{4}}{\frac{2}{ 3} — 1} \\ \frac{y + \frac{11}{4}}{x-1} &= \frac{1}{-\frac{1}{3}} \\ \frac{y + \frac{11}{4}}{x-1} &= -3 \\ y + \frac{11}{4} &= -3 (x — 1) \\ y &= -3x + 3 — \frac{11}{4} \\ \поэтому y &= -3x + \frac{1}{4} \end{выравнивание*}

\((-2;1)\) и \((3;6)\)

\begin{align*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-1}{x+2} &= \frac{6-1}{3+2} \\ \frac{y-1}{x+2} &= \frac{5}{5} \\ у — 1 &= х + 2 \\ \поэтому у &= х + 3 \end{align*}

\((2;3)\) и \((3;5)\)

\begin{align*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-3}{x-2} &= \frac{5-3}{3-2} \\ \frac{y-3}{x-2} &= 2 \\ у — 3 &= 2(х — 2) \\ у &= 2х — 4 + 3\\ \поэтому y &= 2x — 1 \end{выравнивание*}

\((1;-5)\) и \((-7;-5)\)

\begin{align*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y+5}{x-1} &= \frac{-5+5}{-7-1} \\ \frac{y+5}{x-1} &= 0 \\ у + 5 &= 0\\ \поэтому у &= -5 \end{align*}

\((-4;0)\) и \((1;\frac{15}{4})\)

\begin{align*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-0}{x+4} &= \frac{\frac{15}{4}-0}{1+4} \\ \ frac {y} {x + 4} & = \ frac {\ frac {15} {4} {5} \\ \frac{y}{x+4} &= \frac{15}{20} \\ y &= \frac{3}{4} \left( x+4 \right) \\ \поэтому y &= \frac{3}{4}x + 3 \end{выравнивание*}

\((s;t)\) и \((t;s)\)

\begin{align*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-t}{x-s} &= \frac{s — t}{t — s}\\ \frac{y-t}{x-s} &= \frac{-(t — s)}{t — s}\\ \frac{y-t}{x-s} &= -1\\ y — t &= -(x — s)\\ у &= -х + с + т \end{align*}

\((-2;-8)\) и \((1;7)\)

\begin{align*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y+8}{x+2} &= \frac{7+8}{1+2} \\ \frac{y+8}{x+2} &= \frac{15}{3} \\ \frac{y+8}{x+2} &= 5 \\ у + 8 &= 5(х + 2)\\ у + 8 &= 5х + 10\\ у &= 5x + 2 \end{выравнивание*}

\((2p;q)\) и \((0;-q)\)

\begin{align*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-q}{x-2p} &= \frac{-q-q}{0 — 2p} \\ \frac{y-q}{x-2p} &= \frac{-2q}{-2p} \\ \frac{y-q}{x-2p} &= \frac{q}{p} \\ y — q &= \frac{q}{p} \left( x — 2p \right) \\ y — q &= \frac{q}{p}x — 2q \\ \поэтому y &= \frac{q}{p}x — q \конец{выравнивание*}

Градиентно-точечная форма уравнения прямой линии (EMBGB)

Мы выводим уравнение прямой линии в форме точки градиента, используя определение градиента и двухточечная форма уравнения прямой \[\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\]

Подставьте \(m = \dfrac{y_2-y_1}{x_2-x_1}\) в правой части уравнения \[\frac{y-y_1}{x-x_1} = m\]

Умножьте обе части уравнения на \((x-x_1)\) \[у-у_1 = м(х-х_1)\]

Чтобы использовать это уравнение, нам нужно знать градиент линии и координаты одной точки на линии.

Видео: 22K9

Рабочий пример 4: Градиентно-точечная форма уравнения прямой линии

Определите уравнение прямой с градиентом \(m = -\frac{1}{3}\) и проходящей через точка \((-1;1)\).

Нарисуйте эскиз

Заметим, что \(m < 0\), поэтому график уменьшается по мере увеличения \(x\).

Запишите уравнение прямой линии в форме точки градиента

\[y — y_1= m(x — x_1)\]

Подставьте значение градиента

\[y — y_1= -\frac{1 }{3}(x — x_1)\]

Подставить координаты заданной точки

\begin{align*} y — 1 &= -\frac{1}{3}(x — (-1)) \\ y — 1 &= -\frac{1}{3}(x + 1) \\ y &= -\frac{1}{3}x — \frac{1}{3} + 1\\ &= -\frac{1}{3}x + \frac{2}{3} \end{выравнивание*}

Напишите окончательный ответ

Уравнение прямой имеет вид \(y = -\frac{1}{3}x +\frac{2}{3}\).

Если нам даны две точки на прямой линии, мы также можем использовать форму точки градиента, чтобы определить уравнение прямой. Сначала мы вычисляем градиент, используя две заданные точки, а затем подставляем любую из двух точек в форму уравнения с точкой градиента.

Рабочий пример 5: Градиентно-точечная форма уравнения прямой линии

Определите уравнение прямой, проходящей через точки \(\left(-3;2\right)\) и \(\left(5;8\right)\).

Нарисовать эскиз

Присвоить переменные координатам заданных точек

\[x_1 = -3; \qquad y_1 = 2; \qquad x_2 = 5; \qquad y_2 = 8\]

Вычислить градиент, используя две заданные точки

\begin{align*} m &= \frac{y_2 — y_1}{x_2 — x_1} \\ &= \frac{8 — 2}{5 — (- 3)} \\ &= \фракция{6}{8} \\ &= \фракция{3}{4} \end{выравнивание*}

Запишите уравнение прямой линии в форме точки градиента

\[y — y_1= m(x — x_1)\]

Подставьте значение градиента

\[y — y_1= \frac{3} {4}(x — x_1)\]

Подставить координаты заданной точки

\begin{align*} y — y_1 &= \frac{3}{4}(x — x_1) \\ y — 2 &= \frac{3}{4}(x — (-3)) \\ у — 2 &= \ гидроразрыва {3} {4} (х + 3) \\ y &= \frac{3}{4}x + \frac{9}{4} + 2\\ &= \frac{3}{4}x + \frac{17}{4} \end{выравнивание*}

Напишите окончательный ответ

Уравнение прямой линии имеет вид \(y = \frac{3}{4}x +4\frac{1}{4}\).

Видео: 22 КБ

Градиентно-точечная форма уравнения прямой линии

Учебник Упражнение 4.3

, проходящий через точку \((-1;\frac{10}{3})\) и с \(m=\frac{2}{3}\).

\begin{выравнивание*} у — у_1 &= м (х — х_1)\\ y — \frac{10}{3} &= \frac{2}{3}(x + 1)\\ y — \frac{10}{3} &= \frac{2}{3}x + \frac{2}{3} \\ y &= \frac{2}{3}x + \frac{2}{3} + \frac{10}{3} \\ \следовательно y &= \frac{2}{3}x + 4 \end{выравнивание*}

с \(m= -1\) и проходящей через точку \((-2;0)\).

\begin{выравнивание*} у — у_1 &= м (х — х_1) \\ у — 0 &= -(х + 2) \\ \поэтому y &= -x — 2 \end{align*}

, проходящий через точку \((3;-1)\) и с \(m=-\frac{1}{3}\).

\begin{выравнивание*} у — у_1 &= м (х — х_1) \\ y + 1 &= -\frac{1}{3}(x — 3) \\ y + 1 &= -\frac{1}{3}x + 1 \\ \поэтому y &= -\frac{1}{3}x \end{выравнивание*}

параллельно оси \(x\) и проходящей через точку \((0;11)\).

\begin{выравнивание*} у — у_1 &= м (х — х_1) \\ у — 11 &= 0(х — 0) \\ \поэтому у &= 11 \end{align*}

, проходящий через точку \((1;5)\) и с \(m=-2\).

\begin{выравнивание*} у — у_1 &= м (х — х_1) \\ у — 5 &= -2(х — 1) \\ у — 5&=-2х+2\ \поэтому y &= -2x + 7 \end{выравнивание*}

перпендикулярно оси \(x\) и проходящей через точку \((-\frac{3}{2};0)\).

\(x = -\frac{3}{2}\)

с \(m = -\text{0,8}\) и проходящей через точку \((10;-7)\).

\begin{выравнивание*} у — у_1 &= м (х — х_1) \\ y + 7 &= -\frac{4}{5}(x — 10) \\ у + 7 &= -\frac{4}{5}х + 8 \\ \поэтому y &= -\frac{4}{5}x + 1 \end{align*}

с неопределенным градиентом и проходящей через точку \((4;0)\).

\(x = 4\)

с \(m= 3a\) и проходящей через точку \((-2;-6a+b)\).

\begin{выравнивание*} у — у_1 &= м (х — х_1) \\ у — (-6а + Ь) &= 3а(х + 2) \\ у + 6а — Ь &= 3ах + 6а \\ \поэтому y &= 3ax + b \конец{выравнивание*}

Градиентно-отрезковая форма уравнения прямой линии (EMBGC)

Используя форму точки градиента, мы также можем получить форму точки пересечения градиента прямой линии уравнение.

Начиная с уравнения

\[у — у_1 = м(х — х_1)\]

Раскройте скобки и сделайте \(y\) подлежащим формулы

\начать{выравнивать*} у — у_1 &= тх — тх_1 \\ у &= тх — тх_1 + у_1 \\ у &= тх + (у_1 — тх_1) \конец{выравнивание*}

Определим константу \(c\) таким образом, что \(c={y}_{1}-m{x}_{1}\) и получим уравнение

\[у = тх + с\]

Это также называется стандартная форма уравнения прямой линии.

Обратите внимание, что когда \(x=0\), у нас есть

\начать{выравнивать*} у &= т(0) + с \\ &= с \конец{выравнивание*}

Следовательно, \(с\) есть \(у\)-пересечение прямой.

Рабочий пример 6: Градиентно-отрезковая форма уравнения прямой линии

Определите уравнение прямой с уклоном \(m=-2\) и проходящей через точку \((-1;7)\).

Наклон линии

Заметим, что \(m < 0\), поэтому график уменьшается по мере увеличения \(x\).

Запишите уравнение прямой линии в форме пересечения градиента

\[y =mx + c\]

Подставьте значение градиента

\[y = -2x + c\]

Подставьте координаты заданную точку и найти \(c\)

\начать{выравнивать*} у &= -2х + с \\ 7 &= -2(-1) + с \\ 7 — 2 &=с\\ \поэтому с &= 5 \конец{выравнивание*}

Это дает \(y\)-перехват \((0;5)\).

Напишите окончательный ответ

Уравнение прямой линии \(y = -2x + 5\).

Если нам даны две точки на прямой линии, мы также можем использовать форму пересечения градиента, чтобы определить уравнение прямой линии. Мы решаем для двух неизвестных \(m\) и \(c\), используя одновременные уравнения — с использованием методов замены или исключения.

Рабочий пример 7: Градиентно-отрезковая форма уравнения прямой линии

Определите уравнение прямой, проходящей через точки \((-2;-7)\) и \((3;8)\).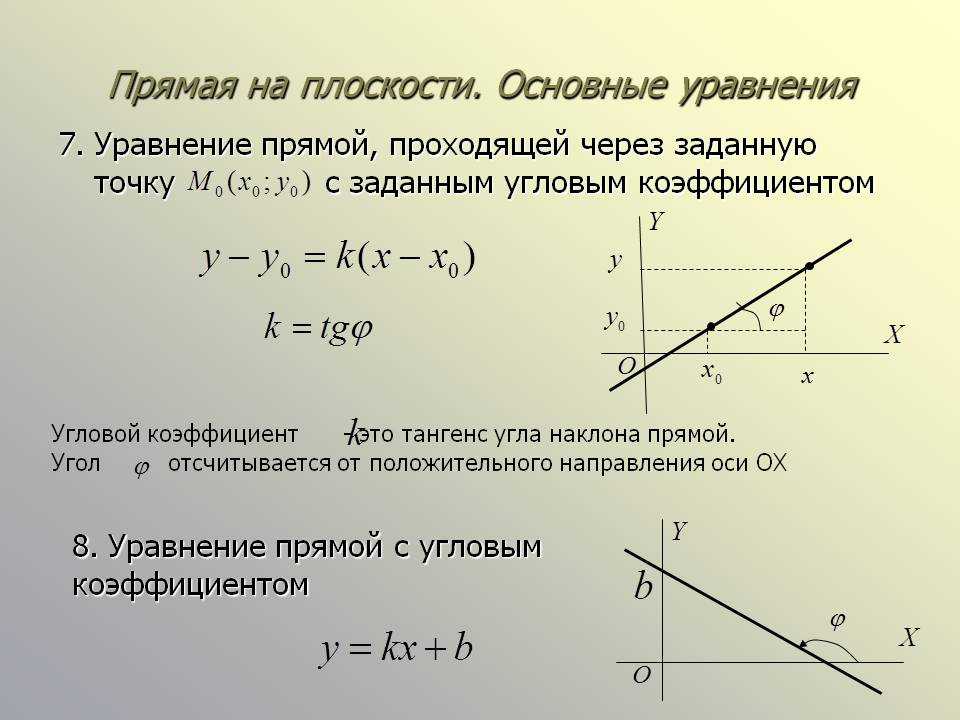

Нарисовать эскиз

Запишите уравнение прямой линии в форме пересечения градиента

\[y =mx + c\]

Подставить координаты заданных точек

\[\begin{массив}{rll} -7 & = m(-2) + c & \\ -7&=-2м+с&\ldots(1)\\ \\ 8 & = т(3) + с & \\ 8 & = 3m + c & \ldots (2) \конец{массив}\]

У нас есть два уравнения с двумя неизвестными; поэтому мы можем решить, используя одновременные уравнения.

Сделать коэффициент одной из переменных одинаковым в обоих уравнениях

Заметим, что коэффициент при \(c\) в обоих уравнениях равен \(\text{1}\), поэтому мы можем вычесть один уравнение от другого, чтобы исключить \(c\):

\начать{выравнивать*} -7&=-2м+с\ -( 8 &= 3м + с ) \\ -15 &= -5м\\ \поэтому 3 &= m \конец{выравнивание*}

Подставьте \(m=3\) в любое из двух уравнений и определите \(c\): \начать{выравнивать*} -7&=-2м+с\ -7 &= -2(3) + с \\ \поэтому с &= -1 \конец{выравнивание*} или \начать{выравнивать*} 8 &= 3м + с\ 8 &= 3(3) + с \\ \поэтому с &= -1 \конец{выравнивание*}

Напишите окончательный ответ

Уравнение прямой имеет вид \(y = 3x — 1\).

Градиентно-отрезковая форма уравнения прямой линии

Учебник Упражнение 4.4

, проходящий через точку \((\frac{1}{2};4)\) и с \(m=2\).

\begin{выравнивание*} у &= тх + с \\ у &= 2х + с \\ 4 &= 2\влево( \frac{1}{2} \вправо) + c \\ 4 &= 1 + с \\ \поэтому с &= 3 \\ \поэтому y &= 2x + 3 \end{выравнивание*}

, проходящей через точки \((\frac{1}{2};-2)\) и \((2;4)\).

\begin{выравнивание*} у &= тх + с \\ -2 &= m\left( \frac{1}{2} \right) + c \\ \text{Умножить на } 2: \quad -4 &= m + 2c \ldots (1)\\ 4 &= 2м + с\ \text{Умножить на } 2: \quad 8 &= 4m + 2c \ldots (2)\\ (2) — (1): \quad 8 + 4 &= 4m — m \\ 12 &= 3м\\ \поэтому 4 &= м \\ \поэтому с &= 4 — 2(4) \\ &= -4 \\ \поэтому y &= 4x — 4 \end{выравнивание*}

, проходящий через точки \((2;-3)\) и \((-1;0)\).

\begin{выравнивание*} у &= тх + с \\ -3 &= 2m + c \ldots (1) \\ 0 &= -m + c \ldots (2) \\ (1) — (2): \quad -3 &= 2m + m \\ -3 &= 3м\\ \поэтому -1 &= м \\ \поэтому с &= -1 \\ \поэтому y &= -x — 1 \end{align*}

, проходящий через точку \((2;-\frac{6}{7})\) и с \(m=-\frac{3}{7}\).

\begin{выравнивание*} у &= тх + с \\ y &= -\frac{3}{7}x + c \\ -\frac{6}{7} &= -\frac{3}{7}(2) + c \\ -\frac{6}{7} + \frac{6}{7} &= + c \\ \поэтому с &= 0 \\ \поэтому y &= -\frac{3}{7}x \end{align*}

, который пересекает ось \(y\) в точке \(y=-\frac{1}{5}\) и с \(m=\frac{1}{2}\) .

\begin{выравнивание*} у &= тх + с \\ y &= mx — \frac{1}{5} \\ \поэтому y &= \frac{1}{2}x -\frac{1}{5} \end{выравнивание*}

\begin{выравнивание*} у &= тх + с \\ 2 &= 2m + c \ldots (1) \\ -4 &= -m + c \ldots (2) \\ (1)-(2) \quad 2 + 4 &= 2m + m \\ 6 &= 3м\\ \поэтому m &= 2 \\ \поэтому c &= -4 +2 \\ &= -2\\ \поэтому y &= 2x -2 \end{align*}

\(y = -\frac{3}{2}\)

\begin{align*} с &= 4 \\ у &= тх + с \\ у &= тх + 4 \\ \text{См.

No related posts.