Построение графиков математических функций в OneNote с использованием помощника по преобразованию в математические выражения
OneNote
Создание заметок
Создание заметок
Построение графиков математических функций в OneNote с использованием помощника по преобразованию в математические выражения
OneNote для Интернета OneNote для Windows 10 Помощник по преобразованию в математические выражения Еще…Меньше
Постройте график рукописных или введенных уравнений, используя помощник по преобразованию в математические выражения в OneNote. Вы даже можете манипулировать переменными, чтобы увидеть визуальный эффект изменений, превратив помощник по преобразованию в математические выражения в эффективное средство обучения математике.
Примечание: Эта функция доступна только при наличии подписки на Microsoft 365. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.
-
Откройте настольное приложение OneNote или войдите в Office.com и выберите OneNote.
Совет: Если вы не видите OneNote прямо сейчас, откройте средство запуска , чтобы найти его.
-
Откройте существующую записную книжку или создайте новую.
-
Выберите вкладку «Рисование» и напишите или введите уравнение.
org/ListItem»>
-
Выберите «Математика«, чтобы открыть область помощника по математическим вычислениям.
-
В раскрывающемся меню «Выбор действия» в области «Математические вычисления» выберите «Граф в двухстроковом режиме» или «Граф с обеими сторонами в 2D».
Используйте средство Lasso Select для рисования круга вокруг уравнения.
Чтобы настроить граф, созданный помощником по математическим вычислениям, выполните одно из следующих действий, если доступно:
- org/ListItem»>
-
Измените значения параметров в уравнении, нажав или нажав кнопки «+» и «Лупа», чтобы увеличить и уменьшить масштаб.
Выберите (или нажмите и удерживайте) и перетащите граф в любом направлении, чтобы переместить его положение.
Примечание: Если вы используете OneNote на устройстве с сенсорным экраном, вы можете настроить граф пальцами. Для перемещения графа используйте один палец. Масштабирование сжатия двумя пальцами для изменения уровня увеличения. В OneNote для Интернета положение графа можно изменить с помощью стрелок, расположенных по сторонам графа.
-
Выберите или коснитесь значка сброса двойной стрелки, чтобы восстановить исходное состояние графа.

-
Когда график будет выглядеть так, как нужно, нажмите кнопку «Вставить на страницу», чтобы поместить его в качестве снимка экрана на текущую страницу.
Примечание: Чтобы изменить способ выражения графа (градус, радиан, градиенты), выберите или коснитесь параметров, пока открыта область «Математические вычисления».
Расширенные функции графизации
В зависимости от типа графа могут быть доступны следующие функции:
-
Чтение значений x-y: Чтобы увидеть значения x и y в OneNote для Windows 10, наведите указатель мыши на точку на линии графа. В OneNote для Интернета строка для просмотра значений.

-
Управление параметрами Если у вас есть уравнение с параметрами, например ax+b, используйте знаки + и — под графиком, чтобы изменить значения a и b.
-
Основные функции графа: Помощник по преобразованию в математические выражения рассчитывает интересные сведения о графе (нули, перехваты, минимум, максимум и т. д.). Установите флажки для тех возможностей, которые вы хотите отобразить на графе.
Дополнительные сведения
Создание математических формул с помощью рукописного ввода или текста с использованием помощника по преобразованию в математические выражения в OneNote
Решение математических уравнений с использованием помощника по преобразованию в математические выражения в OneNote
Типы задач, поддерживаемые помощником по преобразованию в математические выражения
Создание математического теста для практики
Типы проблем, которые можно создать на диаграмме в 2D
При использовании помощника по математике в OneNote вы заметите, что раскрывающийся список «Выбрать действие» под уравнением изменяется в зависимости от выбранного уравнения. Следующие типы проблем можно на диаграмме с помощью помощника по математическим вычислениям.
Следующие типы проблем можно на диаграмме с помощью помощника по математическим вычислениям.
Примечание: Эта функция доступна только в том случае, если у вас есть подписка на Microsoft 365. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.
|
Выражения (с переменной) |
|
|
Полиномиальный массив |
|
|
Формулы |
При работе с уравнениями можно использовать граф двух- или двухсторонние диаграммы. Выберите Graph в 2D, чтобы увидеть решение уравнения.
Выберите Graph с обеих сторон в двуме , чтобы просмотреть график двух функций на противоположных сторонах знака равенства.
|
|
Системы уравнений |
|
|
Полярные координаты |
Для графирования функции в полярных координатах r должен быть выражен как функция theta. |
| Неравенства |
При работе с неравенством можно использовать граф в двух- или двухстроковом режиме. Выберите Graph в 2D, чтобы увидеть решение неравенства.
Выберите Graph с обеих сторон в двуме, чтобы просмотреть график двух функций на противоположных сторонах знака сравнения.
|
|
Система неравенства |
|
Дополнительные сведения
Создание математического теста в Microsoft Forms
Создание математического теста для практики в OneNote с использованием помощника по преобразованию в математические выражения
Решение математических уравнений с помощью помощника по преобразованию в математические выражения в OneNote
Графики функций и их построение — ЗФТШ, МФТИ
Одним из разделов школьной математики является изучение функциональных зависимостей или функций.
Напомним, что функцией математики называют зависимость величины от одной или нескольких других величин. При этом независимые переменные величины принято называть аргументами, а зависимые – функциями. При этом важно не забывать, что каждому значению аргумента (или аргументов) ставится в соответствие единственное значение зависимой переменной (функции). Наглядно функции изображают с помощью графика – специального набора точек на плоскости. Пусть имеется функция $$ y=f\left(x\right)$$ одной переменной $$ x$$. На плоскости введём декартову систему координат $$ xOy$$ и рассмотрим множество точек $$ G$$ с координатами $$ (x,f(x\left)\right)$$, где $$ x$$ принадлежит некоторому множеству $$ M$$, которое называется областью определения функции. А множество $$ G$$ называется графиком функции $$ y=f\left(x\right)$$ (рис. 1).
В школьном курсе математики вы изучали такие типы функций:
- Линейные функции $$ f\left(x\right)=kx+b$$.
 {n}$$ при натуральных $$ n$$.
{n}$$ при натуральных $$ n$$. - Степенные функции вида $$ f\left(x\right)=\sqrt[n]{x}$$ при натуральных $$ n$$.
- Обратная пропорциональность $$ f\left(x\right)={\displaystyle \frac{k}{x}}$$, $$ k\ne 0$$.
График линейной функции можно построить по двум точкам, поскольку это прямая линия. Однако стоит заметить, что не всякая прямая будет графиком линейной функции. Если взять вертикальную прямую $$ x=a$$, то такая линия не может быть графиком никакой функции (рис. 2).
Действительно, здесь одному значению переменной $$ x$$ ставится в соответствие несколько значений переменной $$ y$$. Итак,
Напомним геометрический смысл коэффициентов $$ k$$ и $$ b$$ в уравнении прямой $$ y=kx+b:$$ $$ k=\mathrm{tg} \alpha $$ – тангенс угла наклона прямой к оси $$ Ox$$, $$ b$$ – ордината точки пересечения прямой с осью $$ Oy$$. Поэтому две невертикальные прямые $$ y={k}_{1}x+{b}_{1}$$ и $$ y={k}_{2}x+{b}_{2}$$:
- параллельны ⟺ $$ {k}_{1}={k}_{2}$$ и $$ {b}_{1}\ne {b}_{2}$$;
- совпадают ⟺ $$ {k}_{1}={k}_{2}$$ и $$ {b}_{1}={b}_{2}$$;
- перпендикулярны ⟺ $$ {k}_{1}{k}_{2}=-1$$.
 {n}$$, но при этом $$ x$$ и $$ y$$ меняются местами. Для чётных $$ n$$ при этом еще нужно учесть ОДЗ $$ x\ge 0$$. Поэтому график функции $$ f\left(x\right)=\sqrt[n]{x}$$ имеет следующий вид в зависимости от чётности натурального числа $$ n$$ (рис. 7, 8):
{n}$$, но при этом $$ x$$ и $$ y$$ меняются местами. Для чётных $$ n$$ при этом еще нужно учесть ОДЗ $$ x\ge 0$$. Поэтому график функции $$ f\left(x\right)=\sqrt[n]{x}$$ имеет следующий вид в зависимости от чётности натурального числа $$ n$$ (рис. 7, 8):Рассмотрим теперь функции вида $$ f\left(x\right)=\frac{k}{x}$$.
Поскольку функция $$ f$$ нечётна, то график должен быть симметричным относительно начала координат. Схематический вид графика этой функции показан на рисунке 9.
Если $$ k
Покажем, как меняется график функции $$ f\left(x\right)={\displaystyle \frac{k}{x}}$$ при изменении параметра $$ k$$. Если $$ \left|{k}_{2}\right|>\left|{k}_{1}\right|$$, то линия $$ f\left(x\right)={\displaystyle \frac{{k}_{2}}{x}}$$ более удалена от осей координат, чем $$ f\left(x\right)={\displaystyle \frac{{k}_{1}}{x}}$$. Схематично это изображено на рис. 11, 12.
Построение графика по точкам онлайн. График функции
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т.
 е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью.
 Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис.
 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика.
 И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
И, наконец, через построенные точки проводят кривую, используя свойства данной функции.Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ).
 При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая.
 Потому компьютер в данном случае – незаменимый помощник.
Потому компьютер в данном случае – незаменимый помощник.Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн.
 Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.

- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны.
 Но кому же хочется получать плохие оценки?
Но кому же хочется получать плохие оценки?Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т.
 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Построение графиков функций
Функции и их графики — одна из самых увлекательных тем в школьной математике.
 Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.
Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».
Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».

Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».
Темы для повторения:
Понятие функции
Типы элементарных функций
Преобразования графиков функций
Производная функции
1. Построим график функции
Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.
Упростим формулу функции:
при
График функции — прямая с выколотой точкой
2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.

3. Построим график функции
Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали
4. Построим график функции
Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:
Действуем по порядку:
1) График функции y=sinx сдвинем на влево;
2) сожмем в 2 раза по горизонтали,
3) растянем в 3 раза по вертикали,
4) сдвинем на 1 вверх
Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».
5. Построим график функции
Область определения функции:
Нули функции: и
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Прямая x = 0 (ось Y) — вертикальная асимптота функции. Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности.
 Асимптоты»)
Асимптоты»)Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.
Раскроем скобки в формуле функции:
Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.
6. Построим график функции
Это дробно-рациональная функция.
Область определения функции
Нули функции: точки — 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты:
Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.
Вот эскиз графика:
Еще один интересный прием — сложение графиков.
7. Построим график функции
Если x стремится к бесконечности, то стремится к нулю и график функции будет бесконечно близко подходить к наклонной асимптоте
Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:
Вот мы и построили график суммы функций.
 Теперь график произведения!
Теперь график произведения!8. Построим график функции
Область определения этой функции — положительные числа, поскольку только для положительных x определен
Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при
При значение cos x равно единице. Значение функции в этих точках будет равно при
9. Построим график функции
Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.
Нули функции — в точках, где то есть при при
Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное ?
Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».
А как же производная? Да, наконец-то мы до нее добрались.
 Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.
Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.10. Построим график функции
Область определения функции — все действительные числа, поскольку
Функция нечетна. Ее график симметричен относительно начала координат.
При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.
Если x стремится к бесконечности, то стремится к нулю.
Найдем производную функции
По формуле производной частного,если или
В точке производная меняет знак с «минуса» на «плюс», — точка минимума функции.
В точке производная меняет знак с «плюса» на «минус», — точка максимума функции.
Найдем значения функции при x=2 и при x=-2.
Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?
Общая схема построения графика функции:
1.
 Область определения функции
Область определения функции2. Область значений функции
3. Четность — нечетность (если есть)
4. Периодичность (если есть)
5. Нули функции (точки, в которых график пересекает оси координат)
6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).
7. Асимптоты (если есть).
8. Поведение функции в бесконечности
9. Производная функции
10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.
Построение графиков термодинамических процессов
I. Введение
Как известно, простейшие термодинамические системы описываются тремя параметрами: давлением P, объемом V и температурой T. Так как они связаны уравнением Менделеева-Клапейрона, то число независимых параметров уменьшается до двух и равновесные процессы, происходящие с системой, можно изображать графически в плоскостях PV, PT или VT.

Часто по ходу решения задачи необходимо перейти от графиков в одних осях к графикам в других. Подобные переходы являются прекрасными упражнениями, позволяющими глубже понять происходящие в системе процессы.
Если график задан в масштабированных осях с конкретными цифрами, то переход к другим осям не представляет никаких трудностей, так как из уравнения Менделеева-Клапейрона можно найти недостающие координаты для характерных точек графика, после чего легко построить график в любых осях.
Если же численных данных нет, то можно стоить графики из качественных соображений, основываясь на физике процессов. При этом получающиеся графики не вполне согласованы друг с другом: по имеющимся двум графикам со значениями Pi, Vi, Ti для характерных точек невозможно построить правильный третий график, так как получающиеся при этом линии не будут линиями изопроцессов.

Мною разработан геометрический алгоритм построения согласованных графиков, основанный на связи между параметрами системы, вытекающей из уравнения Менделеева-Клапейрона, и графическим изображением изопроцессов. Почти всегда изопроцессы изображаются прямыми линиями, кроме изотермы в осях PV. Поэтому необходимо правильно изображать гиперболу, а вернее, находить точки, принадлежащие одной гиперболе. Я обнаружил, что это легко сделать с помощью линейки.
II. Построение гиперболы с помощью линейки.
Все точки гиперболы первого порядка обладают следующим свойством: площадь любого прямоугольника, одна вершина которого принадлежит гиперболе, вторая – началу координат, а остальные – координатным осям, постоянна. Отсюда следует, что если строить такие равновеликие прямоугольники, то соответствующие вершины будут принадлежать одной гиперболе.

Пусть имеется точка A(x1, y1) (рис.1). Нужно найти координату x2 точки B(x2, y2), для которой известна координата y2 и которая принадлежит той же гиперболе, что и точка A. По условию равновеликости площадей,
x1 · y1 = x1 · y2=> x1/y2 = x2 /y1.
Последнее равенство похоже на соотношение сторон в подобных треугольниках: треугольник OA’A» подобен треугольнику OB’B». Отсюда видно, как найти точку B. Надо провести две прямые, параллельные оси абсцисс, через точки с ординатами y1 и y2, затем опустить перпендикуляр из точки A на ось абсцисс, а затем провести прямую через точку O и точку A’ — пересечение перпендикуляра и прямой с ординатой y2.
 Перпендикуляр из точки B’
(пересечение прямой OA’ и прямой с ординатой y1)
на ось абсцисс и дает координату x2.
Находя подобным образом ряд точек, можем по ним
построить гиперболу.
Перпендикуляр из точки B’
(пересечение прямой OA’ и прямой с ординатой y1)
на ось абсцисс и дает координату x2.
Находя подобным образом ряд точек, можем по ним
построить гиперболу.Можно поступить еще проще. Если провести через точку A две прямые (рис.2), параллельные координатным осям, то любая прямая, проходящая через начало координат, отсекает на них координаты точек гиперболы (на 1-й — абсциссы, а на 2-й – ординаты). Если эти прямые проходят в первой четверти, то получается одна ветвь гиперболы, а если во второй – то вторая ветвь гиперболы. В более общем случае прямые 1 и 2 проводятся параллельно абсциссам, а секущие прямые – через центр двух гипербол.
III. Алгоритм построения графиков.
Так как мы рассматриваем в основном графики, соответствующие последовательным изопроцессам, то нам достаточно находить недостающие координаты точек перехода от одного изопроцесса к другому.
 Если же мы имеем дело не с
изопроцессами, то тем более надо уметь находить
координаты любой точки.
Если же мы имеем дело не с
изопроцессами, то тем более надо уметь находить
координаты любой точки.Введем на осях P, V, T масштаб, то есть выберем произвольные отрезки OP0, OV0, OT0, которые будем считать единичными отрезками. Желательно выбирать их одинаковыми, так как в противном случае при возвращении к исходному графику через два построенных в других осях мы получим искажение. Преобразуем уравнение Менделеева-Клапейрона
PV = vRT (1)
в уравнение
PV = T ‘ (2).
Таким образом, мы просто изменили масштаб на оси T.
Рассмотрим процесс нахождения недостающих координат в случаях, когда заданы графики в осях PV, PT или VT. Для каждого случая мы рассмотрим две точки. У первой ордината больше выбранной единицы (точка A), у второй – меньше (т.
 A’
)
A’
)Оси PV (рис. 3а), PT (рис. 3б) и VT (рис. 3в).
Пусть имеются точки A и A’ в плоскости PV. Необходимо найти для них координаты T’. Из уравнения (2) следует, что значение T’ геометрически равно значению объема при P = P0 = 1. Поэтому надо провести изотермы через A и A’ до пересечения с прямой P = P0. Тогда абсциссы этих точек дадут геометрические значения T’A и T’A’ . Для точки A построение описано выше.
Для точки A’ построение ведется в обратном порядке по сравнению с A, так как PA’ < P0, а PA > P0. Проводим прямые, параллельные осям, через точку A’. Проводим линию через начало координат и пересечение вертикали из точки A’ с линией P = P0. Через точку пересечения этой линии с горизонталью из точки A’ проводим вертикаль, пересечение которой с осью 0V даёт значение VB’ , геометрически равное TA’ в выбранном нами масштабе.

Из уравнения (2) следует, что V = T’/P. При P = P0 = 1 получаем, что геометрически V = T’. Проведем через A и A’ изохоры. Тогда абсциссы точек пересечения их с прямой P = P0 дадут нам геометрическое значение объема.
Из уравнения (2) следует, что P = T’/V. Поэтому, построение в осях VT проводится аналогично, только теперь надо проводить изобары через точки A и A’ и пересечение искать с прямой V = V0.
Как видно, для нахождения недостающей координаты надо через интересующую нас точку провести линию того изопроцесса, чей неизменный параметр отсутствует на осях графика, до пересечения с прямой P = P0 или V = V0. Тогда вторая координата точки пересечения даст нам геометрическое значение искомой координаты.
Выбор P0, V0 и T0 влияет на величину получающихся графиков.
 Из рис. 3а
видно, что если PA > P0, то
геометрическое значение TA больше
геометрического значения VA, то есть
графики в осях PT и VT получатся более растянутыми.
Если PA < P0, то всё наоборот. Из рис. 3б
и 3в видно, что если PA > P0 (VA
> V0), то геометрическое значение VA (PA)
получится меньше геометрического значения TA,
то есть график в осях PV получается сжатым по оси V
(P). Если же PA < P0, то всё наоборот.
Исходя из этого, можно выбирать P0 (V0)
таким образом, чтобы получающиеся графики
укладывались в заранее определенные рамки. Это
легко сделать, так как всегда известно, в какой
точке исходного графика недостающий параметр
имеет наибольшее значение. Следует провести
через нее соответствующую изолинию и выбрать P0
или V0 так, чтобы точка пересечения прямой P =
P0 или V = V0 имела абсциссу нужной нам
величины.
Из рис. 3а
видно, что если PA > P0, то
геометрическое значение TA больше
геометрического значения VA, то есть
графики в осях PT и VT получатся более растянутыми.
Если PA < P0, то всё наоборот. Из рис. 3б
и 3в видно, что если PA > P0 (VA
> V0), то геометрическое значение VA (PA)
получится меньше геометрического значения TA,
то есть график в осях PV получается сжатым по оси V
(P). Если же PA < P0, то всё наоборот.
Исходя из этого, можно выбирать P0 (V0)
таким образом, чтобы получающиеся графики
укладывались в заранее определенные рамки. Это
легко сделать, так как всегда известно, в какой
точке исходного графика недостающий параметр
имеет наибольшее значение. Следует провести
через нее соответствующую изолинию и выбрать P0
или V0 так, чтобы точка пересечения прямой P =
P0 или V = V0 имела абсциссу нужной нам
величины.
Чтобы предложенный алгоритм работал, необходимо правильно строить исходный график в осях PV: конечные точки изотермы должны принадлежать одной гиперболе, что легко сделать, опираясь на алгоритм построения гиперболы.
Существует еще один класс графических задач – сравнение параметров, отсутствующих на осях графика для разных его точек. Для этого через эти точки проводятся соответствующие изолинии, что и позволяет сделать вывод, где соответствующий параметр больше.
До сих пор проблемы возникали для изотерм, так как не всегда было ясно, изотерма какой точки пойдет выше (рис. 4а). Теперь подобных затруднений нет (рис. 4б) и видно, что температура состояния в точке В выше, чем температура состояния в точке А.
График в декартовой системе координат
Построение графиков онлайн с помощью нашего сервиса является простой задачей.
 2/16=1)
2/16=1) - Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
- Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете
- Управление масштабом, цветом линий
- Возможность построения графиков по точкам, использование констант
- Построение одновременно нескольких графиков функций
- Построение графиков в полярной системе координат (используйте r и θ( heta) )
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Цели работы:
1. Научиться строить графики явно заданных функций в декартовой системе координат.

2. Научиться строить графики параметрически заданных функций в декартовой системе координат.
4.1. Построение графиков явно заданных функций
Если зависимость между переменными х и у выражена уравнением, разрешенным относительно у, то у называется явно заданной функцией и записывается в виде у=f(х) .
Для того чтобы построить график функции у=f(х), необходимо:
1. Определить х как дискретную переменную (в пределах области определения).
2. Задать функцию f(х) .
3. Щелкнуть мышью в свободном месте. Выбрать из меню «Графика» XYPlot (Декартов график).
4. В появившемся шаблоне напечатать х в среднем поле по оси абсцисс, напечатать f(х) в среднем поле по оси ординат. Остающиеся поля предназначены для ввода границ на осях. Если их оставить незаполненными, MathCAD заполнит их автоматически при создании графика.
5. Щелкнуть мышью вне графика.
Пример 1.
 Построим график функции .
Построим график функции .Решение.
График можно форматировать. Для этого необходимо:
1. Щелкнуть мышью по чертежу, чтобы выделить его (появляется синяя выделяющая рамка). Дважды щелкнуть мышью по выделенному чертежу. Появится окно форматирования.
2. В верхней части окна форматирования расположены закладки: «ХУ-оси», «Графики», «Надписи».
«ХУ-оси» позволяет форматировать оси. В частности, можно задать стиль оформления осей: рамка, пересечение, ничего. Рамка окружает график наружной рамкой. Пересечение покажет оси, пересекающиеся в начале координат. Ничего – оси не будут отражены вообще.
«Графики» позволяет форматировать отдельные кривые: указать цвет, тип, толщину и т.п. для каждой кривой.
«Надписи» позволяет оформить график: указать заголовок, подписать название осей.
На одном рисунке можно отображать графики нескольких функций. Если все функции зависят от одного и того же аргумента, то на одном рисунке можно построить до 16 графиков различных функций.
 Если же каждая функция зависит от своего аргумента, то на одном рисунке можно построить только 10 графиков.
Если же каждая функция зависит от своего аргумента, то на одном рисунке можно построить только 10 графиков.Чтобы построить несколько графиков функций одной и той же переменной, необходимо:
1. Определить независимую переменную и все функции, графики которых будем строить.
2. Создать шаблон декартового графика.
3. В появившемся шаблоне в среднем поле по оси абсцисс напечатать имя независимой переменной, в среднем поле по оси ординат напечатать через запятую имена всех функций.
4. Щелкнуть мышью вне графика.
Пример 2. Построим на одном чертеже графики функций у=1-х и у=0,3х 2 +0,66.
Решение.
Чтобы построить несколько графиков функций, зависящих от разных переменных, необходимо:
1. Определить все независимые переменные и все функции, графики которых будем строить.
2. Создать шаблон декартового графика.
3. В появившемся шаблоне в среднем поле по оси абсцисс напечатать через запятую имена независимых переменных, в среднем поле по оси ординат напечатать через запятую имена всех функций.
 Порядок следования переменных и функций должен быть согласован.
Порядок следования переменных и функций должен быть согласован.4. Щелкнуть мышью вне графика.
Пример 3.Построим на одном рисунке графики функций s(x1)=3 x1-1, g(x2)=3 x2 2 — 30, h(x3)=50 sin(x3).
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10072 — | 7513 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужноЧитайте также:
- II. Игра в системе трансляции деятельности и обучения
- IV. ОБРАБОТКА РЕЗУЛЬТАТОВ ГРУППОВОГО И ИНДИВИДУАЛЬНОГО ОБСЛЕДОВАНИЯ, ЗАПОЛНЕНИЕ ХАРАКТЕРИСТИКИ, ПОСТРОЕНИЕ ИНДИВИДУАЛЬНОГО ПРОФИЛЯ ГОТОВНОСТИ
- Автоматизированной системе управления
- Административная реформа в системе и структуре федеральных органов государственного экологического контроля 1 страница
- Административная реформа в системе и структуре федеральных органов государственного экологического контроля 2 страница
- Административное право в правовой системе
- Административное судопроизводство в системе судебной власти
- Азия в ХХI веке – перспективы эволюции и положения в системе международных отношений
- Алгоритм формирования систем координат звеньев
- Аналитические параметры сетевых графиков
- Апостериорная оценка точности рассчитанных координат
- Априорная оценка точности рассчитанных координат
Все основные типы графиков и инструменты работы с ними расположены на рабочей панели Graph (График) семейства Math (Математические).
 На этой панели вы можете найти ссылки на семь типов графиков. В данном разделе остановимся на декартовой системе координат.
На этой панели вы можете найти ссылки на семь типов графиков. В данном разделе остановимся на декартовой системе координат.В MathCAD существует несколько способов построения графиков, однако, первый шаг для всех способов будет один и тот же. Этим первым шагом является введение специальной заготовки для будущего графика – так называемой графической области. Ввести графическую область, как для декартового, так и для любого другого графика можно либо с панели Graph (Графические), либо командой одноименного подменю меню Insert (Вставка).
Графическая область представляет собой две вложенные рамки, как это показано на рис. 5.10, а. Во внутренней области отображаются непосредственно кривые зависимостей. Пространство между рамками служит для визуализации разного рода служебной информации. Графическую область можно увеличивать и уменьшать с помощью специальных маркеров, расположенных на ее внешней рамке. Перемещать по документу и удалять графические области можно точно так же, как простые формулы.

Рис. 5.10. Графическая область в декартовой системе координат
После того как графическая область будет введена, в общем случае требуется задать два соразмерных вектора, определяющих значения координат точек. Сделать это можно различными способами. Наиболее простым и часто используемым методом задания координатной сетки является так называемый быстрый метод. При его применении пользователь задает только имя переменной и вид функции, а шкалы осей и величину шага между узловыми точками автоматически определяет система.
Для построения графика функции по быстрому методу, необходимо выполнить следующую последовательность действий:
1. Введите графическую область.
2. В специальном маркере, расположенном в центре под внутренней рамкой графической области, задайте имя независимой переменной.
3. В центральный маркер, расположенный слева от внутренней рамки, введите функцию или имя функции (если функцию определить раньше переменной, то работа даже упрощается, так как независимая переменная будет задана автоматически).

На рис. 5.10, b показан график функции y=sin(t), построенный по быстрому методу.
К недостаткам рассматриваемого метода относится, прежде всего, то, что область изменения переменной для всех функций определяется одна и та же: от –10 до +10. В большинстве же случаев такие пределы будут неприемлемы по целому ряду причин. Например, если амплитуда экстремумов мала по сравнению с изменением величины функции на промежутке, что они становятся просто незаметными.
Чтобы справиться с возникшими трудностями, нужно просто уменьшить интервал изменения либо переменной, либо функции. Для этого выделите графическую область щелчком левой кнопкой мыши. При этом визуализируются все элементы, которые до этого были скрыты (рис. 5.11, а).
Рис. 5.11. Графическая область в декартовой системе координат
Непосредственно под крайними значениями (для оси X) или слева от них (для оси Y) появятся цифры, отражающие максимальные и минимальные величины координат узловых точек графика.
 Чтобы изменить их значения, просто удалите (точно так же, как при редактировании формул) старые величины и введите новые. Изменения пределов по оси X вызывает автоматический пересчет крайних значений по Y. Однако если вы переопределите область по оси Y, то область изменения переменной останется старой.
Чтобы изменить их значения, просто удалите (точно так же, как при редактировании формул) старые величины и введите новые. Изменения пределов по оси X вызывает автоматический пересчет крайних значений по Y. Однако если вы переопределите область по оси Y, то область изменения переменной останется старой.Графическую область можно отформатировать – изменить внешний вид и цветовую гамму. Для этого можно воспользоваться командой Properties (Свойства) из контекстного меню графика (вызывается щелчком правой кнопкой мыши на графической области), как это показано на рис. 5.11, b.
В окне Properties(Свойства) для подавляющего большинства пользователей объективно могут быть полезны два параметра, расположенных на вкладке Display (см. рис. 5.11, b):
· Highlight Region (Цветная область). Установив этот флажок, вы сможете на палитре Choose Color (Выбор цвета) определить наиболее подходящий цвет заливки для вашей графической области.

· Show Border (Показать границу). Параметр отвечает за отображение внешней границы графической области. По умолчанию она не визуализируется.
При исследовании функции большое применение находит команда Trace (След) из контекстного меню графика. Эта команда позволяет считать с графика текущее значение аргумента и соответствующего ему значение функции. В результате выполнения этой команды открывается окно «X-Y Trace», как это показано на рис. 5.12. Чтобы активизировать трассировку, нужно мышью щелкнуть по графику. В результате на графике появляются две линии – вертикальная и горизонтальная, которые легко с помощью мыши перемещаются по графической области, а координаты точки пересечения линий отражается в окне трассировки.
Рис. 5.12. Считывание координат точки на графике
Глава 6
ИСПОЛЬЗОВАНИЕ ПАКЕТА MATHCAD В ЗАДАЧЕ ИССЛЕДОВАНИЯ МАТЕМАТИЧЕСКИХ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙИсследование функции является одним из важнейших приложений теории пределов, непрерывности функции и производных.
 Полная схема исследования функции и построения ее графика объединяет в себе три этапа:
Полная схема исследования функции и построения ее графика объединяет в себе три этапа:1. Элементарное исследование.
2. Исследование графика функции с помощью первой производной.
3. Исследование графика функции с помощью второй производной.
При этом на каждом из этапов решаются частные задачи, которые позволяют в целом получить свойства функции и оценить ее поведение в различных областях ее определения:
1. Элементарное исследование.
1.1. Найти область определения функции.
1.2. Исследовать функцию на симметричность, периодичность, четность и нечетность.
1.3. Вычислить предельные значения функции в ее граничных точках.
1.4. Выяснить существование асимптот и получить их уравнения в том случае, если они есть.
1.5. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями.
1.6. Сделать эскиз графика функции, используя полученные результаты.
2. Исследование графика функции с помощью первой производной:
2.
 1. Найти точки, подозрительные на экстремум из решения уравнений и .
1. Найти точки, подозрительные на экстремум из решения уравнений и .2.2. Точки, «подозрительные» на экстремум, исследовать с помощью достаточного условия существования экстремума, определить вид экстремума.
2.3. Вычислить значения функции в точках экстремума.
2.4. Найти интервалы монотонности функции.
2.5. Нанести на эскиз графика экстремальные точки.
2.6. Уточнить вид графика функции согласно полученным результатам.
3. Исследование графика функции с помощью второй производной.
3.1. Найти точки, «подозрительные» на точки перегиба из решения уравнений: y”(х)=0 и y”(х)=¥.
3.2. Точки, «подозрительные» на перегиб, исследовать с помощью достаточного условия.
3.3. Вычислить значения функции в точках перегиба.
3.4. Найти интервалы выпуклости и вогнутости графика функции.
3.5. Нанести на эскиз графика точки перегиба.
3.6. Окончательно построить график функции.
Если исследование проведено без ошибок, то результаты всех этапов должны согласовываться друг с другом.
 Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.
Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.Очевидно, что проведение полного анализа – очень трудоемкая задача. А решение некоторых вопросов, например, проверка функции на периодичность, требует знаний из областей математики, не входящих в учебную программу. Тем не менее, пакет MathCAD может оказать большую помощь при исследовании функций, особенно в тех случаях, где требуется решение уравнений и неравенств. А технология построения графиков функций, используемая системой MathCAD, позволяет проверять найденные решения практически на любом из этапов исследования.
Дата добавления: 2014-11-29 ; Просмотров: 1641 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Параллельный график координат – из данных в визуализацию
Параллельный графикили график параллельных координат позволяет сравнивать признаки нескольких отдельных наблюдений (серии) по набору числовых переменных. Каждая вертикальная полоса представляет собой переменную и часто имеет собственный масштаб. (Единицы могут быть даже разными). Затем значения отображаются в виде серии линий, соединенных по каждой оси.
Каждая вертикальная полоса представляет собой переменную и часто имеет собственный масштаб. (Единицы могут быть даже разными). Затем значения отображаются в виде серии линий, соединенных по каждой оси.Набор данных
ìrisпредоставляет четыре функции (каждая представлена вертикальной линией) для 150 образцов цветов (каждая представлена цветной линией). Образцы сгруппированы по трем видам. На приведенной ниже диаграмме эффективно показано, что у сетозы лепестки меньше, но чашелистик, как правило, шире.# Библиотеки библиотека (tidyverse) библиотека (hrbrthemes) библиотека (пэчворк) библиотека (GGally) библиотека (виридис) # Набор данных изначально предоставлен R данные <- радужная оболочка # Сюжет данные %>% ggparcoord( столбцы = 1:4, groupColumn = 5, порядок = "любой класс", шоуПойнтс = ИСТИНА, title = "Параллельный график координат для данных радужной оболочки", альфа-линии = 0,3 ) + scale_color_viridis (дискретный = ИСТИНА) + тема_ipsum()+ тема( plot. title = element_text (размер = 10)
)
title = element_text (размер = 10)
) Примечание : Параллельный график эквивалентен паутинной диаграмме, но с декартовыми координатами. Таким образом, его часто предпочитают.
Параллельный график позволяет изучать особенности выборок по
нескольким количественнымпеременным. Его сила в том, что переменные могут быть даже совершенно разными: разныедиапазоныи даже разныеединицы.На приведенном выше рисунке признаки цветка сгруппированы по видам, все переменные нормализованы и имеют одну и ту же единицу измерения (см). Вот еще один пример, где бриллианты сравниваются по 4 переменным, использующим разные единицы измерения, например, цена в долларах или глубина в %. Обратите внимание на использование масштабирования, чтобы иметь возможность сравнивать их.
бриллианты %>% образец_n(10) %>% ggparcoord( столбцы = c(1,5:7), группаКолонка = 2, # заказ = "любой класс", шоуПойнтс = ИСТИНА, title = "Характеристики бриллиантов", альфа-линии = 0,3 ) + scale_color_viridis (дискретный = ИСТИНА) + тема_ipsum()+ тема( plot. title = element_text (размер = 10)
)
title = element_text (размер = 10)
) Вот обзор функций параллельных координат, с которыми вы можете поиграть:
- Масштабирование — масштабирование преобразует необработанные данные в новый масштаб, общий с другими переменными. Крайне важным шагом является сравнение переменных, которые не имеют одинаковых единиц измерения, но также могут помочь в других отношениях, как показано в примере ниже:
# Участок p1 <- данные %>% ggparcoord( столбцы = 1:4, groupColumn = 5, порядок = "любой класс", шкала = "глобальный минмакс", шоуПойнтс = ИСТИНА, title = "Без масштабирования", альфа-линии = 0,3 ) + scale_color_viridis (дискретный = ИСТИНА) + тема_ipsum()+ тема( легенда.позиция = "нет", plot.title = element_text (размер = 10) ) + xlab("") p2 <- данные %>% ggparcoord( столбцы = 1:4, groupColumn = 5, порядок = "любой класс", шкала = «униминмакс», шоуПойнтс = ИСТИНА, title = "Стандартизировать до минимального = 0 и максимального = 1", альфа-линии = 0,3 ) + scale_color_viridis (дискретный = ИСТИНА) + тема_ipsum()+ тема( легенда. позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p3 <- данные %>%
ggparcoord(
столбцы = 1:4, groupColumn = 5, порядок = "любой класс",
масштаб = "стандарт",
шоуПойнтс = ИСТИНА,
title = "Одномерно нормализовать (вычесть среднее и разделить на sd)",
альфа-линии = 0,3
) +
scale_color_viridis (дискретный = ИСТИНА) +
тема_ipsum()+
тема(
легенда.позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p4 <- данные %>%
ggparcoord(
столбцы = 1:4, groupColumn = 5, порядок = "любой класс",
масштаб = "центр",
шоуПойнтс = ИСТИНА,
title = "Стандартизация и центрирование переменных",
альфа-линии = 0,3
) +
scale_color_viridis (дискретный = ИСТИНА) +
тема_ipsum()+
тема(
легенда.позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p1 + p2 + p3 + p4 + plot_layout (ncol = 2)
позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p3 <- данные %>%
ggparcoord(
столбцы = 1:4, groupColumn = 5, порядок = "любой класс",
масштаб = "стандарт",
шоуПойнтс = ИСТИНА,
title = "Одномерно нормализовать (вычесть среднее и разделить на sd)",
альфа-линии = 0,3
) +
scale_color_viridis (дискретный = ИСТИНА) +
тема_ipsum()+
тема(
легенда.позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p4 <- данные %>%
ggparcoord(
столбцы = 1:4, groupColumn = 5, порядок = "любой класс",
масштаб = "центр",
шоуПойнтс = ИСТИНА,
title = "Стандартизация и центрирование переменных",
альфа-линии = 0,3
) +
scale_color_viridis (дискретный = ИСТИНА) +
тема_ipsum()+
тема(
легенда.позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p1 + p2 + p3 + p4 + plot_layout (ncol = 2) - Порядок осей — оптимизация порядка
вертикальной оси может уменьшить беспорядоквашего параллельного графика. По сути, цель состоит в том, чтобы свести к минимуму количество пересечений между сериями. На следующем рисунке левый график гораздо труднее понять, чем правый. Отличается только порядок переменных.
По сути, цель состоит в том, чтобы свести к минимуму количество пересечений между сериями. На следующем рисунке левый график гораздо труднее понять, чем правый. Отличается только порядок переменных.
# Участок p1 <- данные %>% ggparcoord( столбцы = 1:4, groupColumn = 5, порядок = c(1:4), шоуПойнтс = ИСТИНА, название = "Оригинал", альфа-линии = 0,3 ) + scale_color_viridis (дискретный = ИСТИНА) + тема_ipsum()+ тема( легенда.позиция="По умолчанию", plot.title = element_text (размер = 10) ) + xlab("") p2 <- данные %>% ggparcoord( столбцы = 1:4, groupColumn = 5, порядок = "любой класс", шоуПойнтс = ИСТИНА, title = "Повторно заказано", альфа-линии = 0,3 ) + scale_color_viridis (дискретный = ИСТИНА) + тема_ipsum()+ тема( легенда.позиция = "нет", plot.title = element_text (размер = 10) ) + xlab("") п1 + п2- Выделение — параллельный график представляет собой линейный график, главное предостережение — диаграмма спагетти, где слишком много линий перекрываются, что делает диаграмму нечитаемой.
 Существует несколько обходных путей, описанных на этой странице. Решение состоит в том, чтобы выделить конкретный образец или конкретную интересующую группу:
Существует несколько обходных путей, описанных на этой странице. Решение состоит в том, чтобы выделить конкретный образец или конкретную интересующую группу:
# Участок данные %>% ggparcoord( столбцы = 1:4, groupColumn = 5, порядок = "любой класс", шоуПойнтс = ИСТИНА, название = "Оригинал", альфа-линии = 0,3 ) + scale_color_manual (значения = с («# 69b3a2", "серый", "серый") ) + тема_ipsum()+ тема( легенда.позиция="По умолчанию", plot.title = element_text (размер = 10) ) + xlab("")- Как и для линейного графика, отображение слишком большого количества выборок приводит к загроможденной и нечитаемой спагетти-диаграмме.
- Отсортируйте переменные по оси X, имеет смысл избегать пересечений в линиях выборки.
- Попробуйте разные масштабы, чтобы найти тот, который лучше всего соответствует вашим данным.
Галереи графиков R и Python — это два веб-сайта, на которых представлены сотни примеров диаграмм, всегда предоставляющих воспроизводимый код.
 Нажмите кнопку ниже, чтобы узнать, как построить нужную диаграмму с помощью вашего любимого языка программирования.
Нажмите кнопку ниже, чтобы узнать, как построить нужную диаграмму с помощью вашего любимого языка программирования.Галерея графов R Галерея Python
Есть мысли по этому поводу? Нашли ошибку? Не согласен? Напишите мне пару слов в твиттере или в разделе комментариев ниже:
Включите JavaScript, чтобы просматривать комментарии, созданные с помощью Disqus.
Создание картографической диаграммы в Excel
Картографическую диаграмму можно использовать для сравнения значений и отображения категорий по географическим регионам. Используйте его, если в ваших данных есть географические регионы, такие как страны/регионы, штаты, округа или почтовые индексы.
Примечание. Эта функция доступна в Windows или Mac, если у вас есть Office 2019 или подписка на Microsoft 365. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.

Загрузите наши примеры
Вы можете загрузить рабочую книгу с несколькими примерами картографических диаграмм, подобных приведенным в этой статье.
Картографические диаграммы могут отображать как значения, так и категории, и каждый из них имеет разные способы отображения цвета. Значения представлены небольшими вариациями двух-трех цветов. Категории представлены разными цветами.
Например, в приведенной ниже таблице «Страны по налоговым доходам в %» используются значения. Значения представляют собой налоговые поступления в каждой стране, каждая из которых изображена с использованием градиентного спектра двух цветов. Цвет для каждой области определяется тем, где в спектре падает его значение. По умолчанию, чем выше значение, тем темнее будет соответствующий цвет.
В следующем примере «Страны по категориям» категории отображаются с использованием стандартной легенды для отображения групп или принадлежности.
 Каждая страна представлена своим цветом.
Каждая страна представлена своим цветом.Создание диаграммы карты с типами данных
Картографические диаграммы стали еще проще с географическими типами данных. Просто введите список географических значений, таких как страна, штат, округ, город, почтовый индекс и т. д., затем выберите свой список и перейдите на вкладку Данные > Типы данных > География . Excel автоматически преобразует ваши данные в географический тип данных и будет включать свойства, относящиеся к этим данным, которые вы можете отобразить на диаграмме карты. В следующем примере мы преобразовали список стран в географические типы данных, а затем выбрали поле Налоговые поступления (%) из Добавить элемент управления Column для использования на нашей карте.
org/ListItem»>
Теперь пришло время создать картографическую диаграмму, поэтому выберите любую ячейку в диапазоне данных, затем перейдите на вкладку Вставка > Диаграммы > Карты > Заполненная карта .
Если предварительный просмотр выглядит хорошо, нажмите OK . В зависимости от ваших данных Excel вставит карту значений или категорий.
Совет: Если ваши данные настроены как таблица Excel, а затем вы добавляете страну в список, Excel автоматически обновит ее как тип географических данных и обновит связанную диаграмму карты. Точно так же, если вы удалите страну, Excel также удалит ее из диаграммы.
Существует несколько опций серии для картографических диаграмм, однако они не поддерживаются в устройствах Android или Excel Mobile. Если вам нужны некоторые параметры серии карт, вы можете построить свою диаграмму в Excel для Windows или Mac и просмотреть ее на устройстве Android или в Excel Mobile.
Узнайте больше о форматировании картографических диаграмм.
Область карты — измените уровень масштабирования карты, начиная с вида штата/провинции и заканчивая видом мира.
Ярлыки карт — отображение географических названий ваших стран/регионов. Выберите отображение имен по размеру или отображение всех меток.
Для создания новых карт или добавления данных к существующим картам требуется подключение к сети (для подключения к службе карт Bing).
Существующие карты можно просматривать без подключения к сети.
Существует известная проблема, из-за которой картографические диаграммы, использующие типы географических данных, иногда могут отображаться неправильно.
 Пожалуйста, попробуйте включить поля администратора, такие как провинция или страна, при попытке отобразить их, пока проблема не будет устранена.
Пожалуйста, попробуйте включить поля администратора, такие как провинция или страна, при попытке отобразить их, пока проблема не будет устранена.Изменение масштаба горизонтальной оси Поскольку горизонтальная ось точечной диаграммы является осью значений, доступны дополнительные параметры масштабирования.
org/ListItem»>Отображение данных рабочей таблицы, которые включают пары или сгруппированные наборы значений. В точечной диаграмме можно настроить независимые шкалы осей, чтобы получить больше информации о сгруппированных значениях.
Показать закономерности в больших наборах данных Точечные диаграммы полезны для иллюстрации закономерностей в данных, например, для отображения линейных или нелинейных трендов, кластеров и выбросов.
org/ListItem»>Использовать текстовые метки вдоль горизонтальной оси Эти текстовые метки могут представлять равномерно распределенные значения, такие как месяцы, кварталы или финансовые годы.
Используйте небольшое количество числовых меток вдоль горизонтальной оси Если вы используете несколько равномерно расположенных числовых меток, представляющих временной интервал, например годы, вы можете использовать линейную диаграмму.

Используйте шкалу времени вдоль горизонтальной оси Если вы хотите отображать даты в хронологическом порядке с определенными интервалами или базовыми единицами, такими как количество дней, месяцев или лет, даже если даты на листе не в порядке или в тех же базовых единицах используйте линейную диаграмму.
Скопируйте данные рабочего листа примера на пустой рабочий лист или откройте рабочий лист, содержащий данные, которые вы хотите отобразить на точечной диаграмме.
1
2
3
4
5
6
7
8
9
10
11
А
Б
Ежедневное количество осадков
Твердые частицы
4.
 1
1122
4,3
117
5,7
112
5,4
114
5,9
110
5,0
114
3,6
128
1,9
137
7,3
104
org/ListItem»>Щелкните вкладку Вставить , а затем щелкните Вставить точечную (X, Y) или пузырьковую диаграмму .
Нажмите Скаттер .
Совет: Вы можете навести указатель мыши на любой тип диаграммы, чтобы увидеть его название.
Щелкните область диаграммы для отображения вкладок Design и Format .

Щелкните вкладку Design , а затем щелкните стиль диаграммы, который вы хотите использовать.
Щелкните заголовок диаграммы и введите нужный текст.
Чтобы изменить размер шрифта заголовка диаграммы, щелкните заголовок правой кнопкой мыши, выберите Font , а затем введите нужный размер в поле Size . Нажмите ОК .
org/ListItem»>На вкладке Design щелкните Добавить элемент диаграммы > Названия осей , а затем выполните следующие действия:
Чтобы добавить заголовок горизонтальной оси, нажмите Основной горизонтальный .
Чтобы добавить заголовок вертикальной оси, нажмите Основная вертикаль .

Щелкните каждый заголовок, введите нужный текст и нажмите клавишу ВВОД.
Для получения дополнительных параметров форматирования заголовка на вкладке Формат в поле Элементы диаграммы выберите заголовок из списка и нажмите Выбор формата . Появится панель Формат заголовка. Щелкните Размер и свойства , а затем выберите Выравнивание по вертикали , Направление текста или Пользовательский угол .
Щелкните область графика диаграммы или на вкладке Формат в поле Элементы диаграммы выберите Область графика из списка элементов диаграммы.

На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительно , а затем щелкните эффект, который вы хотите использовать.
Щелкните область диаграммы или на вкладке Формат в поле Элементы диаграммы выберите Область диаграммы из списка элементов диаграммы.
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительно , а затем щелкните эффект, который вы хотите использовать.

Если вы хотите использовать цвета темы, отличные от темы по умолчанию, применяемой к вашей книге, сделайте следующее:
На вкладке Макет страницы в группе Темы щелкните Темы .
В разделе Office выберите тему, которую хотите использовать.
Скопируйте данные рабочего листа примера на пустой рабочий лист или откройте рабочий лист, содержащий данные, которые вы хотите отобразить в линейной диаграмме.
1
2
3
4
5
6
7
8
9
10
11
А
Б
С
Дата
Ежедневное количество осадков
Твердые частицы
01.
 01.07
01.074.1
122
02.01.07
4,3
117
03.01.07
5,7
112
04.
 01.07
01.075,4
114
05.01.07
5,9
110
06.01.07
5,0
114
07.
 01.07
01.073,6
128
08.01.07
1,9
137
09.01.07
7,3
104
org/ListItem»>Щелкните вкладку Вставить , а затем щелкните Вставить линейную или диаграмму с областями .
Нажмите Линия с маркерами .
Щелкните область диаграммы, чтобы отобразить Design и Формат вкладок.
org/ListItem»>Щелкните заголовок диаграммы и введите нужный текст.
Чтобы изменить размер шрифта заголовка диаграммы, щелкните заголовок правой кнопкой мыши, выберите Font и введите нужный размер в поле Size . Нажмите ОК .
Щелкните область диаграммы на диаграмме.
org/ListItem»>Чтобы построить один из рядов данных вдоль вторичной вертикальной оси, щелкните ряд данных или выберите его из списка элементов диаграммы (на вкладке Формат в Текущий выбор , нажмите Элементы диаграммы ).
На вкладке Формат в группе Текущий выбор щелкните Формат выбора .
 Появится панель задач «Формат ряда данных».
Появится панель задач «Формат ряда данных».до 9 лет0099 Опции серии , выберите Второстепенная ось , а затем нажмите Закрыть .
На вкладке Дизайн в группе Макеты диаграмм щелкните Добавить элемент диаграммы , а затем выполните следующие действия:
Чтобы добавить заголовок основной вертикальной оси, нажмите Заголовок оси > Основная вертикаль . а затем на панели Формат заголовка оси щелкните Размер и свойства , чтобы настроить нужный тип заголовка вертикальной оси.

Чтобы добавить заголовок вторичной вертикальной оси, щелкните Заголовок оси > Второстепенная вертикаль , а затем на панели Формат заголовка оси щелкните Размер и свойства , чтобы настроить нужный тип заголовка вертикальной оси.
Щелкните каждый заголовок, введите нужный текст и нажмите клавишу ВВОД.
Щелкните область построения диаграммы или выберите ее из списка элементов диаграммы (вкладка Формат , группа Текущий выбор , поле Элементы диаграммы ).

На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительно , а затем щелкните эффект, который вы хотите использовать.
Щелкните область диаграммы на диаграмме.
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительно , а затем щелкните эффект, который вы хотите использовать.
org/ListItem»>На вкладке Макет страницы в группе Темы щелкните Темы .
В разделе Office выберите тему, которую хотите использовать.
Скопируйте данные рабочего листа примера на пустой рабочий лист или откройте рабочий лист, содержащий данные, которые вы хотите отобразить в точечной диаграмме.
1
2
3
4
5
6
7
8
9
10
11
А
Б
Ежедневное количество осадков
Твердые частицы
4.
 1
1122
4,3
117
5,7
112
5,4
114
5,9
110
5,0
114
3,6
128
1,9
137
7,3
104
org/ListItem»>На вкладке Вставка в группе Диаграммы нажмите Разброс .
Нажмите Скаттер только с маркерами .
Совет: Вы можете навести указатель мыши на любой тип диаграммы, чтобы увидеть его название.
Щелкните область диаграммы на диаграмме.

Отображает Инструменты диаграммы , добавляя вкладки Дизайн , Макет и Формат .
На вкладке Дизайн в группе Стили диаграмм щелкните стиль диаграммы, который вы хотите использовать.
Для нашей точечной диаграммы мы использовали Style 26 .
На вкладке Layout щелкните Chart Title , а затем выберите местоположение для заголовка из раскрывающегося списка.
Мы выбрали над таблицей .

Щелкните заголовок диаграммы и введите нужный текст.
Для нашей точечной диаграммы мы набрали Уровни твердых частиц в осадках .
Чтобы уменьшить размер заголовка диаграммы, щелкните его правой кнопкой мыши и введите нужный размер в поле Размер шрифта в контекстном меню.
Для нашей точечной диаграммы мы использовали 14 .
Щелкните область диаграммы на диаграмме.

На вкладке Макет в группе Метки щелкните Названия осей и выполните следующие действия:
Чтобы добавить заголовок горизонтальной оси, щелкните Заголовок основной горизонтальной оси , а затем щелкните Заголовок под осью 9.0100 .
Чтобы добавить заголовок вертикальной оси, щелкните Заголовок основной вертикальной оси , а затем щелкните нужный тип заголовка вертикальной оси.

Для нашей точечной диаграммы мы использовали Rotated Title .
Щелкните каждый заголовок, введите нужный текст и нажмите клавишу ВВОД.
Для нашей точечной диаграммы мы ввели Ежедневное количество осадков в заголовке по горизонтальной оси и Уровень твердых частиц в заголовке по вертикальной оси.
Щелкните область графика диаграммы или выберите Область графика из списка элементов диаграммы (вкладка Макет , группа Текущий выбор , поле Элементы диаграммы ).

На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительно , а затем щелкните эффект, который вы хотите использовать.
Для нашей точечной диаграммы мы использовали Тонкий эффект — Акцент 3 .
Щелкните область диаграммы на диаграмме.
На вкладке Формат в Стили формы , нажмите кнопку Еще , а затем щелкните эффект, который вы хотите использовать.

Для нашей точечной диаграммы мы использовали Тонкий эффект — Акцент 1 .
Если вы хотите использовать цвета темы, отличные от темы по умолчанию, применяемой к вашей книге, выполните следующие действия:
На вкладке Макет страницы в группе Темы щелкните Темы .
В разделе Встроенная выберите тему, которую хотите использовать.

Для нашей линейной диаграммы мы использовали тему Office .
Скопируйте данные рабочего листа примера на пустой рабочий лист или откройте рабочий лист, содержащий данные, которые вы хотите отобразить в линейной диаграмме.
1
2
3
4
5
6
7
8
9
10
11
А
Б
С
Дата
Ежедневное количество осадков
Твердые частицы
01.
 01.07
01.074.1
122
02.01.07
4,3
117
03.
 01.07
01.075,7
112
04.01.07
5,4
114
05.
 01.07
01.075,9
110
06.01.07
5,0
114
07.
 01.07
01.073,6
128
08.01.07
1,9
137
09.
 01.07
01.077,3
104
Выберите данные, которые вы хотите отобразить на линейной диаграмме.
На вкладке Вставка в группе Диаграммы щелкните Строка .

Нажмите Линия с маркерами .
Щелкните область диаграммы на диаграмме.
Отображает Инструменты диаграммы , добавляя вкладки Дизайн , Макет и Формат .
На вкладке Дизайн в группе Стили диаграмм щелкните стиль диаграммы, который вы хотите использовать.
Для нашей линейной диаграммы мы использовали Стиль 2 .

На вкладке Макет в группе Метки щелкните Заголовок диаграммы , а затем щелкните Над диаграммой .
Щелкните заголовок диаграммы и введите нужный текст.
Для нашей линейной диаграммы мы набрали 9009.9 Уровни твердых частиц в осадках .
Чтобы уменьшить размер заголовка диаграммы, щелкните заголовок правой кнопкой мыши и введите нужный размер в поле Размер в контекстном меню.

Для нашей линейной диаграммы мы использовали 14 .
На диаграмме щелкните легенду или выберите ее из списка элементов диаграммы (вкладка Макет , группа Текущий выбор , поле Элементы диаграммы ).
На вкладке Layout в группе Labels щелкните Legend , а затем выберите нужное положение.
Для нашей линейной диаграммы мы использовали Показать легенду наверху .
Чтобы построить один из рядов данных вдоль вторичной вертикальной оси, щелкните ряд данных для осадков или выберите его из списка элементов диаграммы (вкладка Макет , группа Текущий выбор , поле Элементы диаграммы ).

На вкладке Layout в группе Current Selection нажмите Format Selection .
В разделе «Параметры серии » выберите Второстепенная ось и нажмите «Закрыть» .
На вкладке Макет в группе Метки щелкните Названия осей и выполните следующие действия:
Чтобы добавить заголовок основной вертикальной оси, щелкните Заголовок основной вертикальной оси , а затем выберите нужный тип заголовка вертикальной оси.
Для нашей линейной диаграммы мы использовали Повернутое название .
Чтобы добавить заголовок вторичной вертикальной оси, щелкните Заголовок вторичной вертикальной оси , а затем щелкните нужный тип заголовка вертикальной оси.
Для нашей линейной диаграммы мы использовали Rotated Title .
org/ListItem»>Щелкните область построения диаграммы или выберите ее из списка элементов диаграммы (вкладка Макет , группа Текущий выбор , поле Элементы диаграммы ).
На вкладке Формат в группе Стили фигур нажмите кнопку Дополнительно , а затем щелкните эффект, который вы хотите использовать.

Для нашей линейной диаграммы мы использовали Тонкий эффект — темный 1 .
Щелкните область диаграммы на диаграмме.
На вкладке Формат в Стили формы , нажмите кнопку Еще , а затем щелкните эффект, который вы хотите использовать.
Для нашей линейной диаграммы мы использовали Тонкий эффект — Акцент 3 .
Если вы хотите использовать цвета темы, отличные от темы по умолчанию, применяемой к вашей книге, выполните следующие действия:
На вкладке Макет страницы в группе Темы щелкните Темы .
В разделе Встроенная выберите тему, которую хотите использовать.
Для нашей линейной диаграммы мы использовали тему Office .
Щелкните вкладку Вставить , затем щелкните X Y Scatter и в разделе Scatter выберите диаграмму.
Выбрав диаграмму, щелкните вкладку Chart Design , чтобы выполнить одно из следующих действий:
Щелкните Добавить элемент диаграммы , чтобы изменить такие детали, как заголовок, метки и легенда.
org/ListItem»>
Нажмите Quick Layout , чтобы выбрать один из предопределенных наборов элементов диаграммы.
Щелкните один из элементов предварительного просмотра в галерее стилей, чтобы изменить макет или стиль.
Нажмите Переключить строку/столбец или Выберите Данные , чтобы изменить представление данных.
Форматирование карты карты
После того, как ваша картографическая диаграмма была создана, вы можете легко настроить ее дизайн. Просто нажмите на карту, затем выберите на ленте вкладки Chart Design или Format . Вы также можете дважды щелкнуть диаграмму, чтобы запустить панель задач формата объекта , которая появится в правой части окна Excel. При этом также будут доступны опции серии , характерные для картографических диаграмм (см. ниже).
Просто нажмите на карту, затем выберите на ленте вкладки Chart Design или Format . Вы также можете дважды щелкнуть диаграмму, чтобы запустить панель задач формата объекта , которая появится в правой части окна Excel. При этом также будут доступны опции серии , характерные для картографических диаграмм (см. ниже).
Примечания:
- org/ListItem»>
Картографические проекции — изменение стиля проекции карты. По умолчанию Excel отображает наиболее эффективный стиль.
Часто задаваемые вопросы
Вопрос: Когда я использую определенные текстовые местоположения, я получаю пустую карту и ошибку, или некоторые из моих точек отображаются в других странах.
Ответ: Если вы используете данные, в которых может быть более одного похожего местоположения в мире, картографические диаграммы не обязательно смогут определить разницу без дополнительных указаний. Если возможно, добавьте к своим данным столбец с подробными сведениями более высокого уровня. Например, следующие местоположения не обязательно будут отображены так, как вы ожидаете, поскольку в мире есть много мест, где это действительные названия округов:
Если возможно, добавьте к своим данным столбец с подробными сведениями более высокого уровня. Например, следующие местоположения не обязательно будут отображены так, как вы ожидаете, поскольку в мире есть много мест, где это действительные названия округов:
Но данные должны сопоставляться правильно, если вы добавите еще один столбец для детализации более высокого уровня, в данном случае «Провинция». Это называется Значение:
При наличии нескольких уровней географической детализации каждый уровень необходимо разделить на отдельную ячейку/столбец. Например, «Вашингтон, Соединенные Штаты» (Штат, Страна) не создаст карту. В этом случае данные будут успешно сопоставлены при размещении «Вашингтон» и «США» в отдельных столбцах.
Данные, которые не сопоставляются (штат и страна объединены)
Данные для создания карты штата Вашингтон
Ограничения
- org/ListItem»>
Картографические диаграммы могут отображать только географические детали высокого уровня, поэтому отображение широты/долготы и адресов улиц не поддерживается. Диаграммы карты также поддерживают только одномерное отображение, но если вам нужны многомерные детали, вы можете использовать функцию трехмерной карты Excel.
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
Представление данных в виде точечной диаграммы или линейной диаграммы
Точечная диаграмма и линейная диаграмма выглядят очень похоже, особенно когда точечная диаграмма отображается с соединительными линиями. Однако способ, которым каждый из этих типов диаграмм отображает данные вдоль горизонтальной оси (также известной как ось X) и вертикальной оси (также известной как ось Y), сильно различается.
Примечание. Сведения о различных типах точечных и линейных диаграмм см. в разделе Доступные типы диаграмм в Office.
в разделе Доступные типы диаграмм в Office.
Прежде чем выбрать любой из этих типов диаграмм, вы можете узнать больше о различиях и выяснить, когда лучше использовать точечную диаграмму вместо линейной или наоборот.
Основное различие между точечными и линейными диаграммами заключается в том, как они отображают данные на горизонтальной оси. Например, когда вы используете следующие данные рабочего листа для создания точечной диаграммы и линейной диаграммы, вы можете видеть, что данные распределяются по-разному.
На точечной диаграмме ежедневные значения количества осадков из столбца A отображаются в виде значений x на горизонтальной оси (x), а значения твердых частиц из столбца B отображаются в виде значений на вертикальной оси (y). Точечная диаграмма, которую часто называют диаграммой xy, никогда не отображает категории на горизонтальной оси.
Точечная диаграмма всегда имеет две оси значений для отображения одного набора числовых данных по горизонтальной оси (значений) и другого набора числовых значений по вертикальной оси (значений). На диаграмме отображаются точки на пересечении числовых значений x и y, объединяя эти значения в отдельные точки данных. Эти точки данных могут быть распределены равномерно или неравномерно по горизонтальной оси, в зависимости от данных.
На диаграмме отображаются точки на пересечении числовых значений x и y, объединяя эти значения в отдельные точки данных. Эти точки данных могут быть распределены равномерно или неравномерно по горизонтальной оси, в зависимости от данных.
Первая точка данных, которая появляется на точечной диаграмме, представляет собой значение y, равное 137 (твердые частицы), и значение x, равное 1,9.(суточное количество осадков). Эти числа представляют значения в ячейках A9 и B9 на листе.
Однако на линейной диаграмме одни и те же ежедневные значения количества осадков и твердых частиц отображаются в виде двух отдельных точек данных, которые равномерно распределены по горизонтальной оси. Это связано с тем, что линейная диаграмма имеет только одну ось значений (вертикальную ось). Горизонтальная ось линейной диаграммы показывает только равномерно расположенные группы (категории) данных. Поскольку в данных не были указаны категории, они были созданы автоматически, например, 1, 2, 3 и т. д.
Это хороший пример того, когда не следует использовать линейную диаграмму.
Линейная диаграмма равномерно распределяет данные категорий по горизонтальной оси (категории) и распределяет все числовые данные по вертикальной оси (значений).
Значение y твердых частиц, равное 137 (ячейка B9), и значение x дневного количества осадков, равное 1,9 (ячейка A9), отображаются в виде отдельных точек данных на линейной диаграмме. Ни одна из этих точек данных не является первой точкой данных, отображаемой на диаграмме — вместо этого первая точка данных для каждого ряда данных относится к значениям в первой строке данных на листе (ячейки A2 и B2).
Тип оси и различия масштабирования
Поскольку горизонтальная ось точечной диаграммы всегда является осью значений, на ней могут отображаться числовые значения или значения дат (например, дни или часы), которые представлены в виде числовых значений. Чтобы отображать числовые значения вдоль горизонтальной оси с большей гибкостью, вы можете изменить параметры масштабирования на этой оси так же, как вы можете изменить параметры масштабирования вертикальной оси.
Поскольку горизонтальная ось линейного графика является осью категорий, она может быть только текстовой осью или осью дат. На текстовой оси отображается только текст (нечисловые данные или числовые категории, не являющиеся значениями) через равные промежутки времени. Ось дат отображает даты в хронологическом порядке с определенными интервалами или базовыми единицами, такими как количество дней, месяцев или лет, даже если даты на листе расположены не по порядку или в одних и тех же базовых единицах.
Возможности масштабирования оси категорий ограничены по сравнению с параметрами масштабирования оси значений. Доступные параметры масштабирования также зависят от типа используемой оси.
Точечные диаграммы обычно используются для отображения и сравнения числовых значений, таких как научные, статистические и инженерные данные. Эти диаграммы полезны для отображения отношений между числовыми значениями в нескольких рядах данных, и они могут отображать две группы чисел как один ряд координат xy.
Линейные диаграммы могут отображать непрерывные данные во времени в соответствии с общей шкалой и поэтому идеально подходят для отображения трендов данных через равные интервалы или во времени. На линейной диаграмме данные категорий распределяются равномерно по горизонтальной оси, а все данные о значениях равномерно распределяются по вертикальной оси. Как правило, используйте линейную диаграмму, если ваши данные имеют нечисловые значения x — для числовых значений x обычно лучше использовать точечную диаграмму.
Рассмотрите возможность использования точечной диаграммы вместо линейной диаграммы, если вы хотите:
Использовать логарифмическую шкалу на горизонтальной оси Горизонтальную ось можно преобразовать в логарифмическую шкалу.
Сравнивайте большое количество точек данных без учета времени Чем больше данных вы включаете в точечную диаграмму, тем точнее можно проводить сравнения.
Попробуйте использовать линейную диаграмму вместо точечной, если хотите:
Примечание. Следующая процедура применима к Office 2013 и более поздним версиям. Шаги Office 2010?
Создание точечной диаграммы
Итак, как мы создали эту точечную диаграмму? Следующая процедура поможет вам создать точечную диаграмму с аналогичными результатами. Для этой диаграммы мы использовали пример данных рабочего листа. Вы можете скопировать эти данные на свой рабочий лист или использовать свои собственные данные.
Выберите данные, которые вы хотите нанести на точечную диаграмму.
Щелкните область диаграммы на диаграмме.
Создание линейной диаграммы
Итак, как мы создали эту линейную диаграмму? Следующая процедура поможет вам создать линейную диаграмму с аналогичными результатами. Для этой диаграммы мы использовали пример данных рабочего листа. Вы можете скопировать эти данные на свой рабочий лист или использовать свои собственные данные.
Для этой диаграммы мы использовали пример данных рабочего листа. Вы можете скопировать эти данные на свой рабочий лист или использовать свои собственные данные.
Выберите данные, которые вы хотите отобразить на линейной диаграмме.
Щелкните вкладку Design , а затем щелкните стиль диаграммы, который вы хотите использовать.
На диаграмме щелкните легенду или добавьте ее из списка элементов диаграммы (на Design щелкните Add Chart Element > Legend , а затем выберите место для легенды).
Если вы хотите использовать цвета темы, отличные от темы по умолчанию, применяемой к вашей книге, выполните следующие действия:
Создание точечной или линейной диаграммы в Office 2010
Итак, как мы создали эту точечную диаграмму? Следующая процедура поможет вам создать точечную диаграмму с аналогичными результатами. Для этой диаграммы мы использовали пример данных рабочего листа. Вы можете скопировать эти данные на свой рабочий лист или использовать свои собственные данные.
Для этой диаграммы мы использовали пример данных рабочего листа. Вы можете скопировать эти данные на свой рабочий лист или использовать свои собственные данные.
Выберите данные, которые вы хотите нанести на точечную диаграмму.
Итак, как мы создали эту линейную диаграмму? Следующая процедура поможет вам создать линейную диаграмму с аналогичными результатами. Для этой диаграммы мы использовали пример данных рабочего листа. Вы можете скопировать эти данные на свой рабочий лист или использовать свои собственные данные.
Щелкните каждый заголовок, введите нужный текст и нажмите клавишу ВВОД.
Для нашей линейной диаграммы мы ввели Уровень твердых частиц в заголовке основной вертикальной оси и Ежедневное количество осадков в заголовке вторичной вертикальной оси.
Создать точечную диаграмму
- org/ListItem»>
Выберите данные, которые вы хотите отобразить на диаграмме.
Выбрав диаграмму, щелкните вкладку Design , чтобы при необходимости изменить заливку формы, контур или эффекты элементов диаграммы.
Создание линейной диаграммы
Выберите данные, которые вы хотите отобразить на диаграмме.
Щелкните вкладку Вставить , затем щелкните Линия и выберите вариант из доступных стилей линейной диаграммы.
Выбрав диаграмму, щелкните вкладку Chart Design , чтобы выполнить одно из следующих действий:
- org/ListItem»>
Щелкните Добавить элемент диаграммы , чтобы изменить такие детали, как заголовок, метки и легенда.
Нажмите Quick Layout , чтобы выбрать один из предопределенных наборов элементов диаграммы.
Щелкните один из вариантов предварительного просмотра в галерее стилей, чтобы изменить макет или стиль.
Нажмите Переключить строку/столбец или Выберите Данные , чтобы изменить представление данных.

Выбрав диаграмму, щелкните вкладку Design , чтобы при необходимости изменить заливку формы, контур или эффекты элементов диаграммы.
См. также
Сохранение пользовательской диаграммы в качестве шаблона
Создание карт Tableau из пространственных файлов
В Tableau Desktop вы можете подключаться к следующим типам пространственных файлов: шейп-файлы, таблицы MapInfo, файлы KML (Keyhole Markup Language), файлы GeoJSON, файлы TopoJSON и файловые базы геоданных Esri. Затем вы можете создавать точечные, линейные или полигональные карты, используя данные из этих файлов.
С лицензией Creator в Tableau Online или Tableau Server вы можете загружать пространственные форматы файлов, для которых требуется только один файл (KML, GeoJSON, TopoJSON, шейп-файлы Esri, упакованные в . , и базы геоданных Esri File с расширением  zip
zip . gdb.zip ) на вкладке «Файлы» при создании новой книги и подключении к данным.
Примечание: В текущих версиях Tableau вы можете подключаться только к точечной геометрии, линейной геометрии или полигонам. Вы не можете подключаться к смешанным типам геометрии.
Где найти пространственные файлы
Если у вас еще нет пространственных файлов, вы можете найти их на многих порталах открытых данных. Вы также можете найти их на сайтах своего города или конкретной организации, если они их предоставляют.
Вот несколько примеров:
- LONDON DATASTORE(Ссылка открывается в новом окне)
- EGIS Южная Африка (ссылка открывается в новом окне)
- Управление энергетической информации США (ссылка открывается в новом окне)
- Геологическая служба США по водным ресурсам (ссылка открывается в новом окне)
- Управление геопространственной информации Японии (ссылка открывается в новом окне)
- Data.
 gov(ссылка открывается в новом окне)
gov(ссылка открывается в новом окне) - Census.gov(ссылка открывается в новом окне)
Подключение к пространственным файлам
- В Tableau Desktop: щелкните значок «Новый источник данных» и выберите «Пространственный файл».
В Tableau Online или Tableau Server (роль Creator): выберите «Создать» > «Книга». Выберите вкладку «Файлы». Перейдите к папке, содержащей ваши пространственные данные, выберите пространственный файл, к которому вы хотите подключиться, а затем нажмите «Открыть».
Примечание : для подключения к пространственным файлам необходимо включить все следующие файлы в один и тот же каталог:
Для шейп-файлов Esri : папка должна содержать файлы
., shp
shp .shx,.dbfи.prj, а такжефайлы .zip. При подключении к шейп-файлам Esri в Tableau Online или Tableau Server файл должен быть упакован в.zip.Для файловых баз геоданных Esri : папка должна содержать файл
.gdbили файловой базы геоданных.0004 .zipфайловой базы геоданных.gdb.. При подключении к шейп-файлам Esri в Tableau Online или Tableau Server база геоданных Esri File должна быть упакована с расширением.gdb.zip.Для таблиц MapInfo (только Tableau Desktop): папка должна содержать
.TAB,.DAT,.MAPи.IDили.MIDи.MIFфайлы.Для файлов KML : папка должна содержать файл
.. (Другие файлы не требуются.) kml
kml Для файлов GeoJSON : Папка должна содержать файл
.geojson. (Другие файлы не требуются.)Для файлов TopoJSON : папка должна содержать файл
.jsonили.topojson. (Другие файлы не требуются.)
Как Tableau интерпретирует ваши пространственные данные
Как только вы подключаетесь к своим пространственным данным, Tableau считывает информацию о пространственной привязке набора данных и преобразует данные в координаты широты и долготы. Все данные, независимо от системы пространственной привязки, преобразуются в формат WGS84 (EPSG:4326) .
Примечание . Если в ваших данных неправильно отображаются диакритические знаки (знаки ударения на символах), убедитесь, что файл имеет кодировку UTF-8 .
Поле геометрии
Когда вы подключаетесь к пространственным данным, Tableau создает поле «Геометрия» для ваших точечных геометрий или полигонов. Вы используете поле Геометрия для создания карты с вашими пространственными данными.
Значения в этом поле отображают геометрический примитив — например, Point для точечной геометрии, Linestring или Multilinestring для линейных геометрий и Polygon или Multipolygon для полигонов. Но это просто псевдоним для базовых пространственных данных.
Для получения дополнительной информации о том, как построить карту с помощью поля «Геометрия», см. раздел «Построение представления карты из пространственных данных».
Объединение пространственных данных
Иногда ваши пространственные данные включают только информацию о геометрии и не включают демографическую или другую информацию. В этом случае вы можете соединить источник пространственных данных с другим типом источника данных или даже с другим файлом пространственных данных, который содержит дополнительные данные, необходимые для вашего анализа, если файлы имеют общий столбец (или поле).
В этом случае вы можете соединить источник пространственных данных с другим типом источника данных или даже с другим файлом пространственных данных, который содержит дополнительные данные, необходимые для вашего анализа, если файлы имеют общий столбец (или поле).
Например, вы можете соединить файл KML, содержащий пользовательские географические данные школьных округов в штате Орегон, США, с электронной таблицей Excel, содержащей демографическую информацию об этих школьных округах.
Дополнительные сведения о различных способах объединения пространственных данных см. в разделе Объединение пространственных файлов в Tableau.
Создание представления карты из пространственных данных
Открыть новый рабочий лист.
На панели «Данные» в разделе «Показатели» дважды щелкните поле «Геометрия».

Поле «Геометрия» добавлено в «Подробности» на карточке «Метки», а поля «Широта» (создано) и «Долгота» (сгенерировано) добавлены на полки «Столбцы» и «Ряды». Создается вид карты.
Фильтровать геометрию для улучшения производительности просмотра
При работе с большими наборами пространственных данных визуализация представления может занять много времени. В этом случае вы можете отфильтровать количество геометрий, добавляемых в представление, с помощью другого измерения в вашем источнике данных. Дополнительные сведения о фильтрации данных см. в разделе Фильтрация данных из ваших представлений (ссылка открывается в новом окне).
Например, на изображении ниже вид был отфильтрован до небольшого подмножества полигонов с использованием измерения (Family Nam). Источник данных из Списка исчезающих видов МСОП (ссылка открывается в новом окне) содержит данные о находящихся под угрозой исчезновения млекопитающих по всему миру. Таким образом, измерение Family Name содержит список названий семейств млекопитающих. Этот взгляд был сужен до одного семейства: носороги. На виде показаны полигоны только для носорогов.
Таким образом, измерение Family Name содержит список названий семейств млекопитающих. Этот взгляд был сужен до одного семейства: носороги. На виде показаны полигоны только для носорогов.
Без фильтра полигоны для каждого млекопитающего в источнике данных отображаются по всему миру, и представление занимает много времени для визуализации каждый раз, когда вы выполняете действие, например, выбираете метку в представлении.
Добавление уровней детализации в представление
Поле «Геометрия» является мерой и по умолчанию объединяется в одну метку с использованием агрегации COLLECT при добавлении в представление. Все ваши полигоны или метки будут в поле зрения, но они будут работать как одна метка. Поэтому вам необходимо:
Чтобы добавить дополнительные уровни детализации в вид :
Для разбивки данных:
Настройка внешнего вида геометрии
Вы можете настроить внешний вид точек, многоугольников и линий, добавив цвет, скрыв многоугольные линии, указав, какие многоугольники или точки данных должны отображаться сверху, и отрегулировав размер точек данных.
Добавить цвет
Чтобы добавить цвет точкам данных или полигонам, перетащите измерение или меру в поле Цвет на карточке Метки.
Например, на изображениях выше измерение (Присутствие) помещено в Цвет, чтобы показать присутствие животного в определенной области.
Скрыть полигональные линии
По умолчанию полигональные линии отображаются при создании полигональной карты из пространственных данных. Если вы хотите более чистый вид, вы можете удалить их.
Возьмите, например, следующие изображения. На первом изображении показаны полигональные линии. На втором изображении не показаны полигональные линии.
Полигональные линии показаны по умолчанию.
Линии многоугольника удалены.
Чтобы скрыть многоугольные линии:
На карточке Метки щелкните Цвет.

В разделе «Эффекты» выберите раскрывающийся список «Граница» и нажмите «Нет».
Укажите, какие полигоны или точки данных будут отображаться сверху
Ваши полигоны или точки данных могут перекрывать друг друга. Вы можете указать, какие полигоны или точки данных будут отображаться сверху, если у вас есть легенда цвета или размера в представлении.
Например, обратите внимание, что на изображении ниже есть меньший многоугольник, скрытый за большим бирюзовым многоугольником в южной части Африки.
Вы можете изменить порядок элементов легенды, чтобы контролировать, какие точки данных или многоугольники будут отображаться сверху. Для этого в легенде выберите элемент, который вы хотите разместить наверху, а затем перетащите его наверх списка.
Настройка размера точек данных
Если вы используете точечную геометрию, вы можете настроить размер точек на карте. Это полезно, если вы хотите сопоставить точки данных с количественными значениями, такими как средний объем продаж или прибыль.
Чтобы настроить размер точек данных:
На панели данных перетащите показатель в поле Размер на карточке Метки.
На карточке Метки щелкните раскрывающийся список Тип метки и выберите Круг.
Необязательно: из области Данные перетащите одно или несколько измерений в Детали на карточке Метки, чтобы добавить в представление дополнительные точки данных.

Примечание: Уровень детализации определяет размер точек данных. Добавьте дополнительные измерения в Детали на карточке Метки, чтобы добавить уровни детализации (больше точек данных), иначе вы можете получить одну большую точку данных.
Дополнительные сведения о добавлении уровней детализации в представление см. в разделе Добавление уровней детализации в представление.
Создание двухосевой карты из пространственных данных
Если вы соедините пространственный файл с другим пространственным файлом или файлом другого типа, вы можете создать двухосную карту, используя географические данные из этих файлов. Это позволяет вам создавать более одного слоя ваших данных на карте.
Например, ниже показано двухосное представление карты, созданное с использованием двух пространственных файлов. Он содержит две карты; на одной карте районы Нью-Йорка показаны в виде полигонов, а на другой показаны точки данных для входов в метро по всему городу. Данные входа в метро накладываются поверх полигонов городских районов.
Он содержит две карты; на одной карте районы Нью-Йорка показаны в виде полигонов, а на другой показаны точки данных для входов в метро по всему городу. Данные входа в метро накладываются поверх полигонов городских районов.
В Tableau Desktop откройте новый рабочий лист.
Подключитесь к своим источникам данных.
Создайте первый вид карты.
См. раздел Создание представления карты из пространственных данных выше, чтобы узнать, как создать представление карты из пространственных файлов.
На полке «Столбцы» перетащите поле «Долгота», удерживая нажатой клавишу «Control» (на Mac — «Command-перетаскивание»), чтобы скопировать его, и поместите его справа от первого поля «Долгота».

Важно : в этом примере используются поля Широта (сгенерированные) и Долготы (сгенерированные), которые Tableau создает при подключении к пространственным данным. Если ваш источник данных содержит собственные поля широты и долготы, вы можете использовать их вместо полей, сгенерированных Tableau, или в сочетании с полями, сгенерированными Tableau. Дополнительные сведения см. в разделе Создание двухосевых (многослойных) карт в Tableau.
Теперь у вас есть два одинаковых вида карты. Теперь на карточке Метки есть три вкладки: по одной для каждого представления карты и по одной для обоих представлений (Все). Вы можете использовать их для управления визуальными деталями представлений карты. Верхняя вкладка «Долгота» соответствует карте слева от вида, а нижняя вкладка «Долгота» соответствует карте справа от вида.
На карточке Метки щелкните одну из вкладок Долгота, а затем удалите все поля на этой вкладке.

Теперь одно из представлений карты пусто.
Создайте второй вид карты, перетащив соответствующие поля с панели данных на пустую вкладку Долгота на карточке Метки.
Когда ваши два представления карты будут готовы, на полке Столбцы щелкните правой кнопкой мыши поле Долгота справа и выберите Двойная ось.
Данные вашей карты теперь размещены слоями в одном представлении карты.
Чтобы изменить данные, отображаемые вверху, на полке «Столбцы» перетащите поле «Долгота» справа и поместите его перед полем «Долгота» слева.
См.
 также
такжеПространственный файл(ссылка открывается в новом окне)
С легкостью выполняйте геопространственный анализ в Tableau 10.2 (ссылка открывается в новом окне) (запись в блоге Tableau)
Объединить пространственные файлы в Tableau
Концепции картирования в Tableau(ссылка открывается в новом окне)
Создавайте двухосевые (многослойные) карты в Tableau
Виджет инфографики—ArcGIS Web AppBuilder | Документация
Виджет «Инфографика» предоставляет 16 графических шаблонов, которые можно использовать для визуализации и мониторинга атрибутов и статистических данных на карте и из дополнительных источников данных.
График визуализации, созданный виджетом «Инфографика», является динамическим, обновляется при изменении экстента карты или источника данных и может быть интерактивным с картой. Графики также напрямую реагируют на виджеты «Фильтр» и «Выбор», а также на результаты виджетов «Геообработка» и «Запрос». Цели и соответствующие индикаторы для данных поддерживаются в определенных шаблонах.
Графики также напрямую реагируют на виджеты «Фильтр» и «Выбор», а также на результаты виджетов «Геообработка» и «Запрос». Цели и соответствующие индикаторы для данных поддерживаются в определенных шаблонах.
Внимание!
Будьте осторожны при включении параметра Фильтровать по экстенту. Если ваше приложение общедоступно и может стать вирусным, включение этого параметра резко снизит производительность приложения из-за масштабирования сервера. Настоятельно рекомендуется вместо этого использовать другие виджеты, такие как фильтр и групповой фильтр, для увеличения объектов.
Однако, если эта опция включена автоматически и не может быть отключена, что означает, что статистика рассчитывается на стороне клиента, ваше приложение будет в порядке.
Шаблоны и их значения
перечислены в следующей таблице:
За исключением первых четырех шаблонов, перечисленных в таблице, в этом разделе шаблоны называются шаблонами диаграмм.
Процентная диаграмма с накоплением (столбец, столбец и область) является расширением составной диаграммы и сравнивает процентное соотношение каждого значения.
| Имя шаблона | Отображаемое значение | Support custom indicators |
|---|---|---|
Number |
| Yes |
Gauge |
| Да |
Вертикальный датчик |
| Yes |
Horizontal Gauge |
| Yes |
Pie | No | |
Donut | Нет | |
Бар |
| No |
Stacked Bar |
*Although the режим поддерживается, эффект сложения может быть не виден из-за одного ряда данных. | Нет |
Процентная линейка |
*Хотя режим поддерживается, эффект суммирования может быть не виден из-за одного ряда данных. | NO |
Столбец |
| No |
Stacked Column |
*Although the mode is supported, the stacked effect may not можно увидеть из-за одного ряда данных. | № |
процентный состав Сложный столбец |
*  серии. серии. | № |
Строка |
| NO |
Область | . Эффект суммирования может быть незаметен из-за одного ряда данных.Нет | |
Площадь штабеля |
*Хотя режим поддерживается, эффект суммирования может быть не виден из-за одного ряда данных. | NO |
Сделанная область | . не видно из-за одного ряда данных. | Нет |
Добавить источник данных
Виджет инфографики может визуализировать данные с карты или дополнительных источников данных. Перед настройкой виджета «Инфографика» решите, какой источник данных использовать для виджета. Интуитивно понятно использовать слои карты в качестве прямого источника данных. Рассмотрите вариант дополнительного источника данных, если вы хотите полностью контролировать параметр «Фильтровать по экстенту» для слоев или хотите визуализировать данные за пределами карты.
Внимание!
Будьте осторожны при включении параметра «Фильтровать по экстенту». Если ваше приложение общедоступно и может стать вирусным, включение этого параметра резко снизит производительность приложения из-за масштабирования сервера.
Если ваше приложение общедоступно и может стать вирусным, включение этого параметра резко снизит производительность приложения из-за масштабирования сервера. Когда используется источник данных карты, объекты на карте могут быть загружены в режиме моментального снимка или по запросу. Когда объекты загружаются в режиме по требованию, они фильтруются по текущему экстенту карты. Когда объекты загружаются в режиме моментальных снимков, вы можете выбрать, будут ли они фильтроваться по текущему экстенту карты. Все сервисы по умолчанию используют режим по запросу, за исключением размещенного сервиса объектов. Для точечного объекта, когда количество объектов меньше или равно 4000, включается режим моментального снимка; когда больше 4000, включается режим по требованию. Для объектов, размещенных в виде полилиний и полигонов, пороговое значение составляет 2 000 объектов с 250 000 вершин. Пока данные добавляются из дополнительного источника данных, функции загружаются так же, как и в режиме моментального снимка.
Первым шагом в настройке виджета «Инфографика» является выбор источника данных следующим образом:
Совет:
Что касается параметра «Фильтровать по экстенту», у вас есть возможность включить или отключить его с данными из дополнительных данных. источник и данные из источника данных карты, когда объекты загружаются в режиме моментального снимка. Параметр «Фильтровать по экстенту» всегда включен, когда вы выбираете данные из источника данных карты, а объекты загружаются в режиме по требованию.
При использовании виджета «Инфографика» связанную таблицу можно использовать как внешний источник данных. При этом связанная таблица рассматривается как отдельная таблица. Взаимодействие между таблицей, связанными функциями и диаграммами отсутствует.
Настройка шаблона номера
Этот виджет можно настроить на автоматическое открытие при
запускается приложение. Наведите курсор на виджет и щелкните Не открывать этот виджет, когда
кнопку запуска приложения, чтобы изменить настройку на Открывать этот виджет автоматически при запуске приложения. (Для виджетов, которые необходимо сначала добавить в приложение, этот параметр можно включить после настройки виджета.)
(Для виджетов, которые необходимо сначала добавить в приложение, этот параметр можно включить после настройки виджета.)
Следующие шаги описывают, как настроить график с помощью числового шаблона. Настройки трех шаблонов, связанных с датчиками, аналогичны шаблону «Число».
- Наведите указатель мыши на виджет и нажмите кнопку «Настроить этот виджет», чтобы открыть окно конфигурации.
- Щелкните миниатюру шаблона номера и нажмите кнопку ОК.
- Выберите источник данных.
Это может быть векторный слой на карте, выходной слой виджета или дополнительный источник данных, добавленный на вкладке Атрибут.
- Нажмите OK, и появится панель настроек шаблона.
- Нажмите кнопку Изменить виджет, чтобы заменить значок по умолчанию для этого виджета своим собственным изображением.
Появится окно проводника, позволяющее перейти к локальному файлу изображения для использования в качестве значка виджета.

- Установить условия взаимодействия, если источником данных является векторный слой текущей карты:
- Изменить компоновку элемента.
Левая панель — это не только предварительный просмотр графика, но и гибкий редактор макетов.
- Заголовок, описание, изображение и номер — это элементы, которые можно добавить в шаблон. Щелкните миниатюру элемента, чтобы скрыть или отобразить соответствующий элемент.
- Выберите элемент в предварительном просмотре, чтобы выделить его, и перетащите верхнюю и нижнюю границы, чтобы изменить его размер. Перетащите ручку в правом верхнем углу, чтобы переставить ее.
- Нажмите кнопку «Сброс», чтобы сбросить макеты.
- Щелкните Изменить шаблон, чтобы выбрать другой шаблон, например Gauge.
- Щелкните каждый элемент, чтобы установить его параметры.

Все изменения в предварительном просмотре вступают в силу синхронно.
- Нажмите OK, чтобы завершить настройку.
Настройка шаблона столбца
По сравнению с виджетом «Диаграмма» шаблоны диаграмм дополнены следующими функциями:
- Щелкните миниатюру шаблона столбца и нажмите «ОК».
- Повторите шаги с 3 по 7 в разделе Настройка шаблона номера.
- Щелкните каждый элемент, чтобы установить его параметры.
- Нажмите OK, чтобы завершить настройку.
Использование виджета «Инфографика»
Откройте виджет «Инфографика» в приложении, щелкнув значок виджета.
При использовании виджета имейте в виду следующее:
- Если во время настройки была отмечена опция Использовать выбор, число изменяется при выборе объектов из исходного слоя.
- Если во время настройки был установлен флажок Фильтровать по экстенту, число изменяется при панорамировании или масштабировании карты.

- Если при настройке были установлены индикаторы, цвет и значок меняются вместе с номером.
- График обновляется при обновлении данных.
Вы также можете сделать следующее с шаблонами диаграмм:
- Наведите указатель мыши на отдельные элементы диаграммы. Отобразятся значения категории и поля, а соответствующий объект будет выделен на карте.
- Переместите ползунок или перетащите его концы, чтобы настроить диапазон отображения, чтобы на диаграмме отображались все или часть записей.
- Нажмите кнопку «Настройки», чтобы включить или выключить легенду, метки данных и ось.
Отзыв по этой теме?
Как построить двухкоординатную диаграмму в Google Sheets
Создание двухкоординатной диаграммы в Google Sheets
- Выберите данные, которые вы хотите отобразить в виде диаграммы
- Создайте диаграмму
- Измените тип диаграммы
- Улучшите визуальные данные
- Настройте свой x-y graph
- Поделитесь диаграммой
Цифры важны для понимания рынков, клиентов и производительности, но давайте смотреть правде в глаза — смотреть в таблицу данных не всегда интересно. Визуализация данных имеет решающее значение для четкой и эффективной передачи информации. Также важно представить ваши данные в визуально приятном виде.
Визуализация данных имеет решающее значение для четкой и эффективной передачи информации. Также важно представить ваши данные в визуально приятном виде.
Вот где на помощь приходят Google Таблицы. Они позволяют пользователям создавать различные диаграммы и графики непосредственно из данных, которые они тщательно задокументировали.
Одним из самых полезных является график x-y. Прежде чем вы начнете создавать свой собственный, вот все, что вам нужно знать о том, как сделать график xy в Google Sheets.
Основные сведения о диаграмме x-y
Также известная как точечная диаграмма, диаграмма x-y отображает ряд точек данных, чтобы проиллюстрировать взаимосвязь между двумя наборами чисел.
Например, на диаграмме x-y о заработной плате и количестве отработанных лет по оси x будет указано количество лет, проработанных сотрудником в компании. На оси Y может быть указан диапазон зарплат от 25 000 до 100 000 долларов. Каждая точка данных будет представлять текущую зарплату и опыт работы человека.
Этот тип диаграммы имеет решающее значение для отображения детализированных данных способами, которые не могут быть представлены другими диаграммами, особенно среди больших наборов чисел.
Наконечник Pro
Соберите данные с помощью Jotform и автоматически синхронизируйте их с Google Таблицами с помощью нашей бесплатной интеграции.
Создание графика x-y в Google Sheets
Google Sheets предлагает различные инструменты для построения диаграмм, позволяющие быстро и легко создавать привлекательные визуализации данных.
Вот пошаговое руководство о том, как построить диаграмму x-y в Google Sheets.
1. Выберите данные, которые вы хотите построить на графике
Выберите два столбца чисел, которые вы хотите сравнить, щелкнув и выбрав имена столбцов. Для ПК удерживайте Shift для выбора нескольких столбцов. На Mac удерживайте клавишу Command во время щелчка.
2.
 Создайте диаграмму
Создайте диаграммуНажмите кнопку Вставить в верхней части экрана, чтобы открыть раскрывающееся меню. Выберите Диаграмму . Появится окно, которое будет автоматически заполнено диаграммой или графиком, отражающим выбранные данные.
3. Измените тип диаграммы
Диалоговое окно Редактор диаграмм появится в правой части экрана. Откройте выпадающее меню для Тип диаграммы, и прокрутите вниз, чтобы найти параметр Точечная диаграмма . Выберите его, и ваши данные будут преобразованы в график x-y.
4. Улучшение визуализации данных
В диалоговом окне Редактор диаграмм щелкните Настроить , чтобы открыть новое меню. Разверните подраздел серии и прокрутите вниз, чтобы найти флажки для линий тренда , меток данных , полос ошибок и . Вот как вы можете использовать каждый из них:
- Добавьте на диаграмму линию тренда, чтобы проиллюстрировать общее направление ваших чисел и помочь выявить закономерности даже среди самых, казалось бы, случайных точек данных.

- Настройте полосы погрешностей, чтобы показать потенциальный диапазон чисел, которые может занимать каждая точка данных. Это полезно для отображения пределов погрешности, например, для данных политических опросов.
- Применение меток данных к графикам x-y для идентификации каждой точки данных на диаграмме.
5. Настройте график x-y
Используйте меню Настройка в диалоговом окне Редактор диаграмм для изменения шрифтов, размера текста, имен осей, цветовых палитр и других элементов графика.
6. Поделитесь диаграммой
Нажмите на три точки в верхней правой части диаграммы, чтобы открыть раскрывающееся меню. Вы можете скачать график в формате PDF, в формате PNG или масштабируемой векторной графике. Вы также можете опубликовать диаграмму, чтобы поделиться ею со своего Google Диска в виде ссылки или встроить в другой документ.
Построение курса
Вооружившись знаниями о том, как построить диаграмму x-y в Google Таблицах, вы увидите, что находить тренды в собранных вами данных стало проще, чем когда-либо. Однако, если вы обнаружите, что параметры настройки в Google Таблицах отсутствуют, рассмотрите возможность создания графика xy с помощью построителя отчетов Jotform.
Однако, если вы обнаружите, что параметры настройки в Google Таблицах отсутствуют, рассмотрите возможность создания графика xy с помощью построителя отчетов Jotform.
Инструмент Jotform предлагает даже больше возможностей, чем Google Таблицы, позволяя пользователям точно управлять каждым отдельным элементом диаграммы с помощью функции перетаскивания. Кроме того, графики будут автоматически обновляться по мере того, как вы будете получать больше материалов через свои формы.
Независимо от платформы, графики x-y помогут вам и вашей команде лучше понять закономерности в данных, которые вы собираете, а также поделиться ими с заинтересованными сторонами и клиентами.
В конечном счете, надежная визуализация данных — это создание повествования, и четкая линия тренда на графике x-y — один из самых эффективных способов добиться этого.
Эта статья была первоначально опубликована 28 апреля 2021 г. и обновлена 19 сентября 2022 г.




 {n}$$ при натуральных $$ n$$.
{n}$$ при натуральных $$ n$$. {n}$$, но при этом $$ x$$ и $$ y$$ меняются местами. Для чётных $$ n$$ при этом еще нужно учесть ОДЗ $$ x\ge 0$$. Поэтому график функции $$ f\left(x\right)=\sqrt[n]{x}$$ имеет следующий вид в зависимости от чётности натурального числа $$ n$$ (рис. 7, 8):
{n}$$, но при этом $$ x$$ и $$ y$$ меняются местами. Для чётных $$ n$$ при этом еще нужно учесть ОДЗ $$ x\ge 0$$. Поэтому график функции $$ f\left(x\right)=\sqrt[n]{x}$$ имеет следующий вид в зависимости от чётности натурального числа $$ n$$ (рис. 7, 8):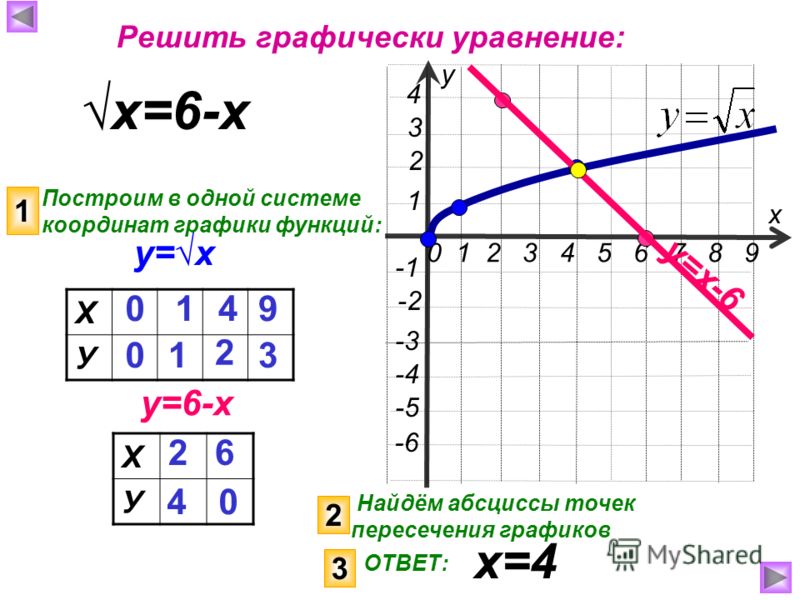
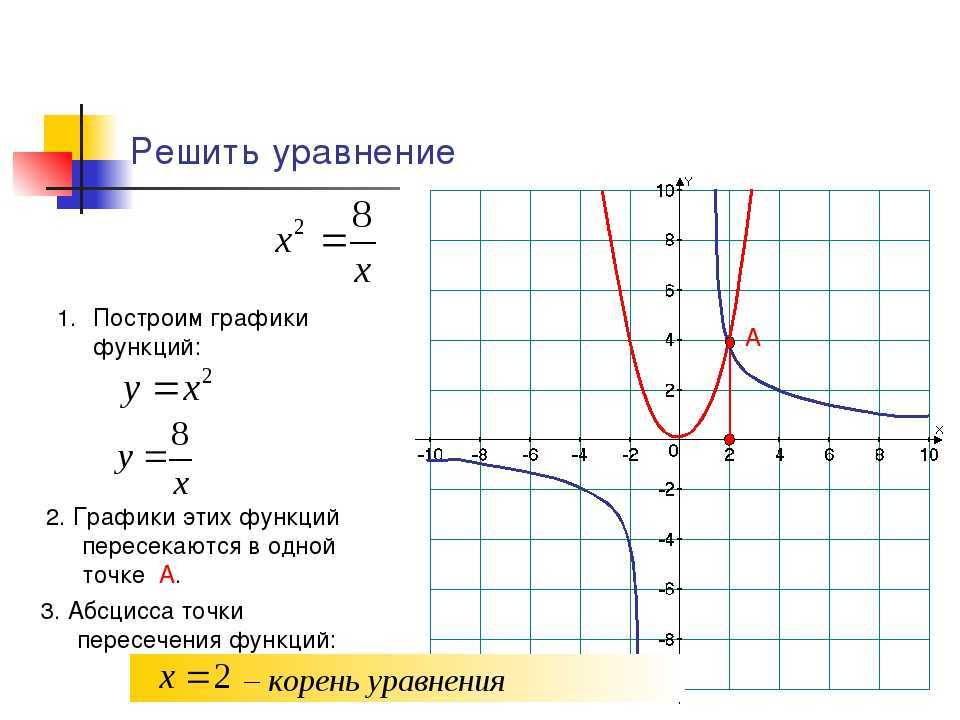 е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).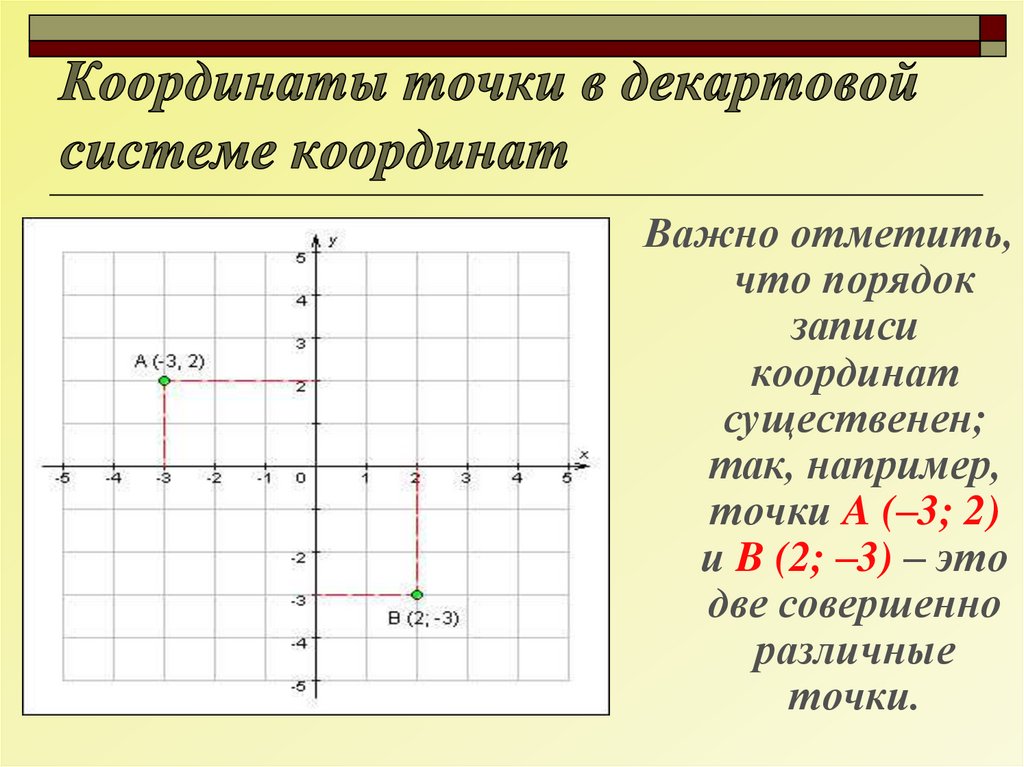 Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.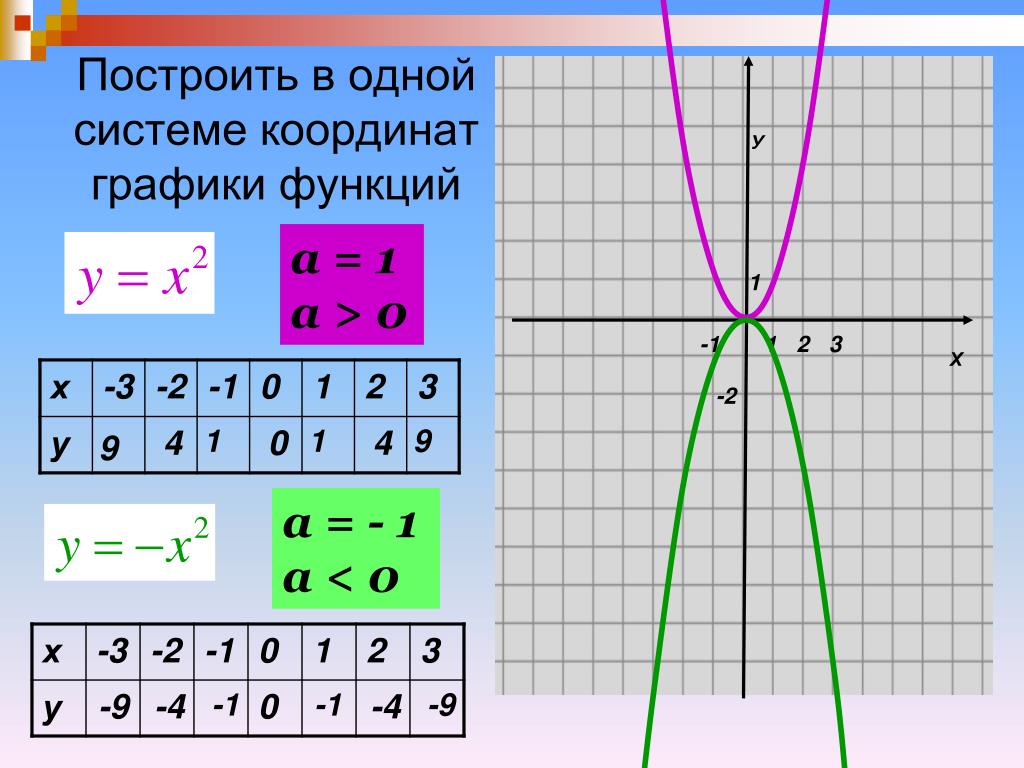 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
 При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) . Потому компьютер в данном случае – незаменимый помощник.
Потому компьютер в данном случае – незаменимый помощник.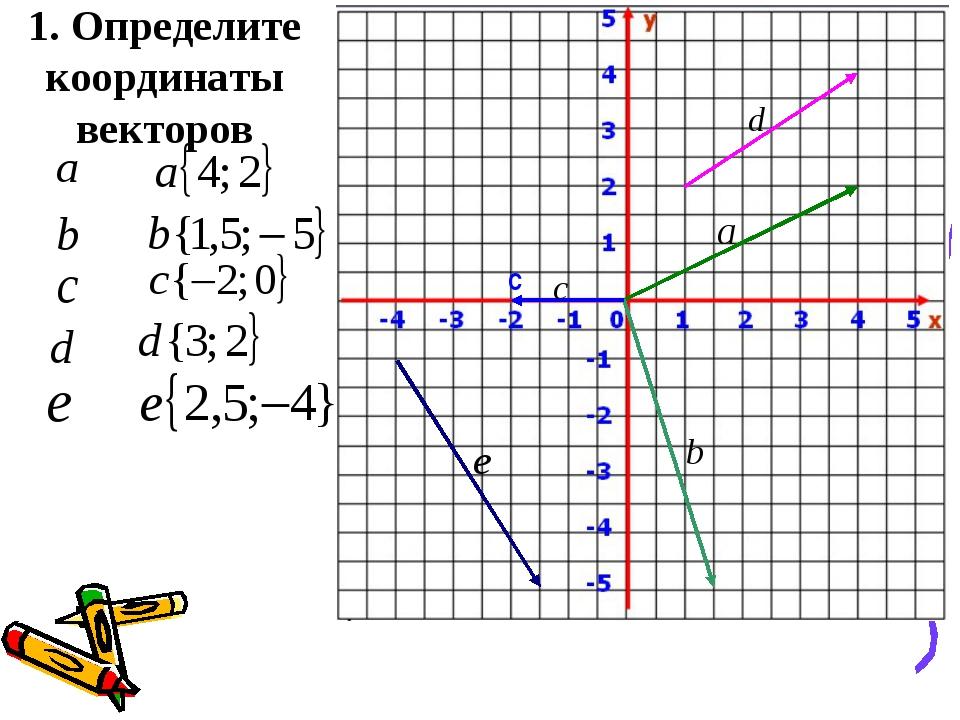 Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
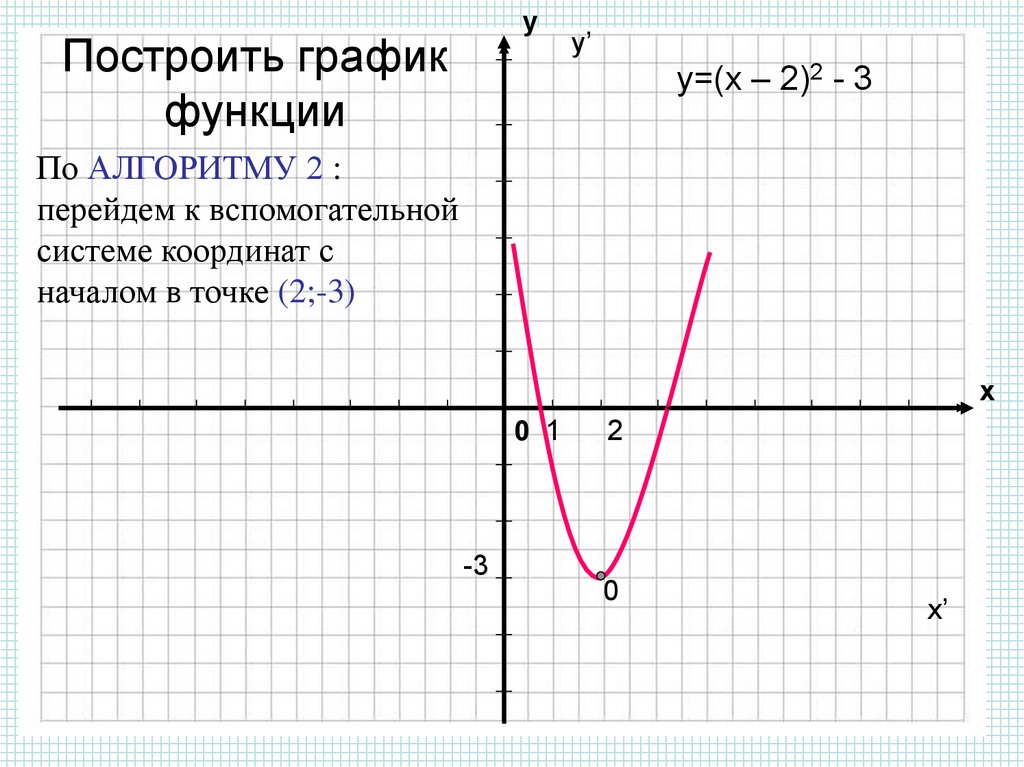
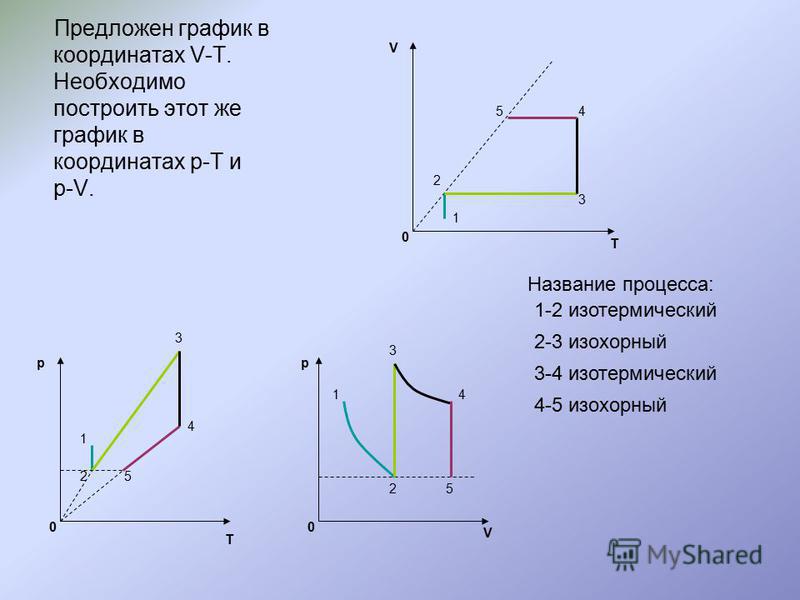 Но кому же хочется получать плохие оценки?
Но кому же хочется получать плохие оценки?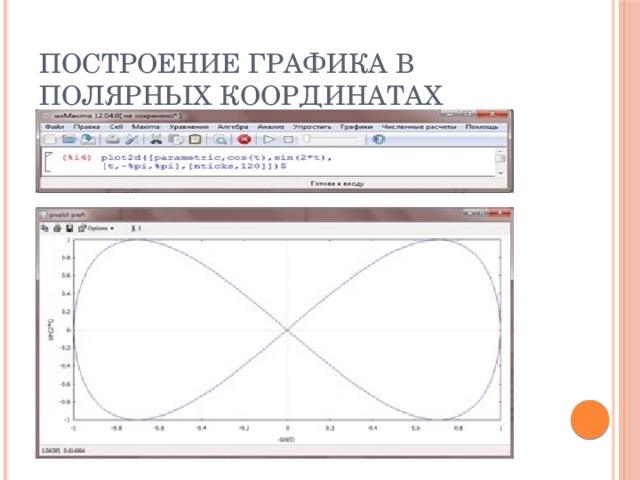 3$.
3$.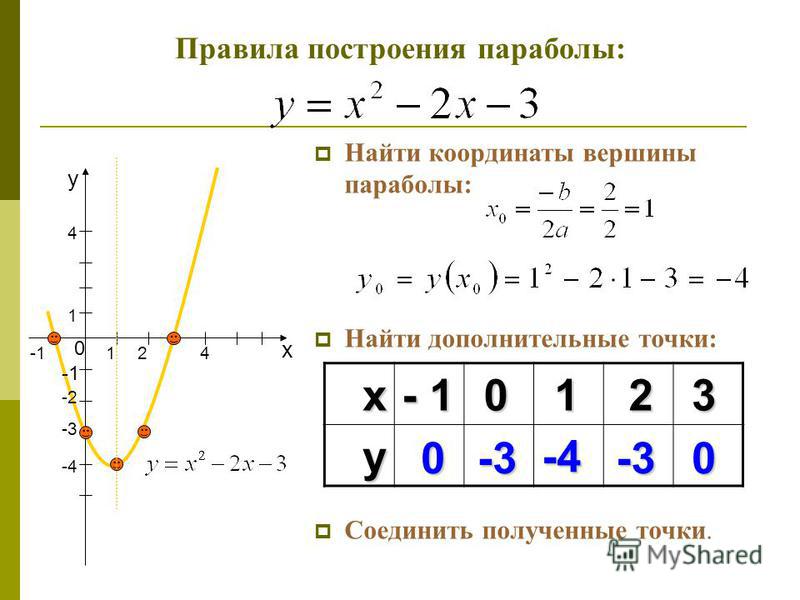 д.
д.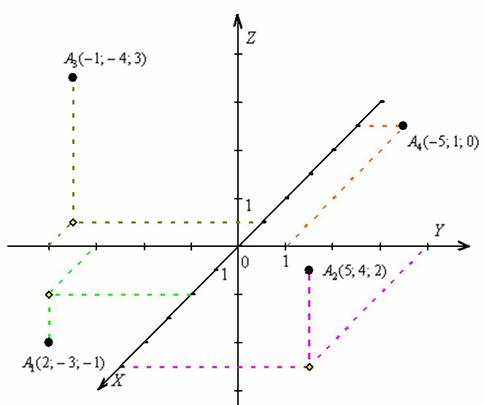 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.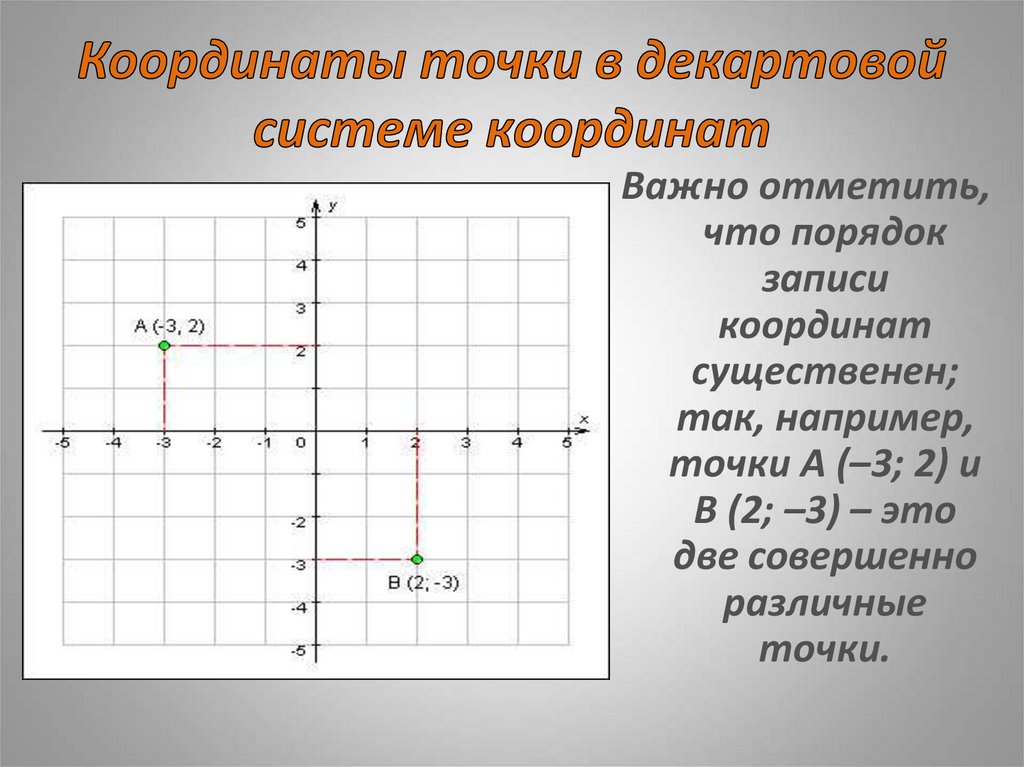 Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.
Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.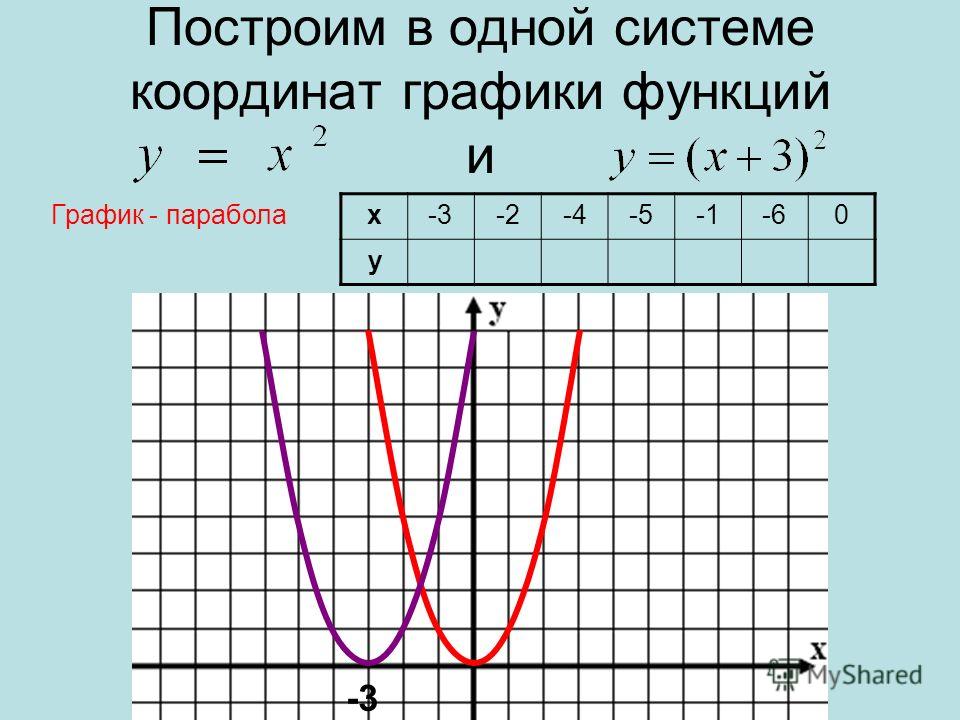
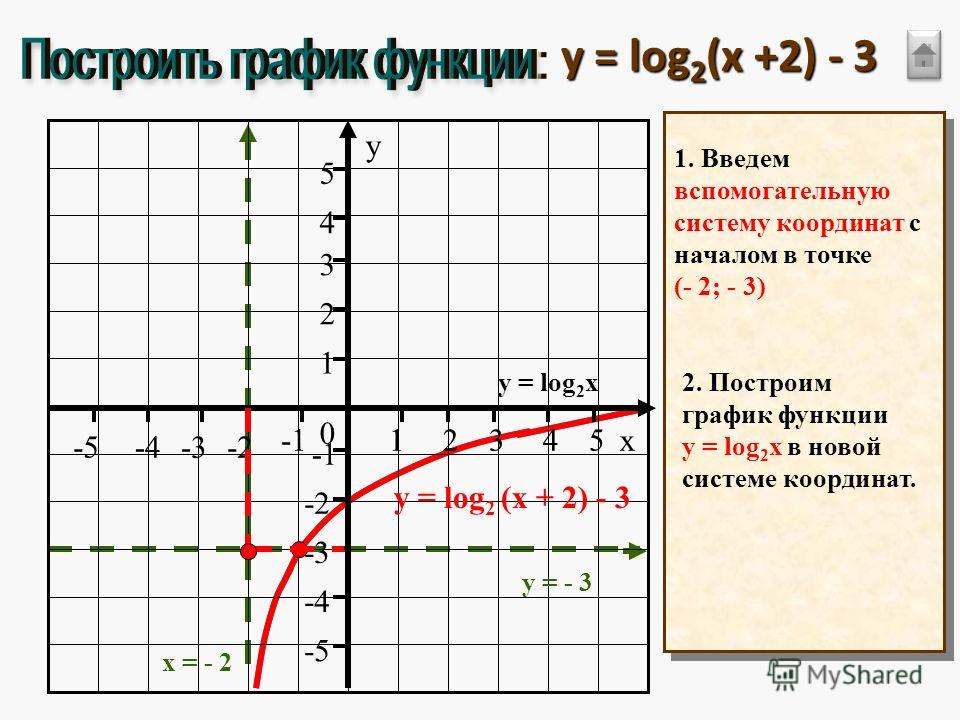
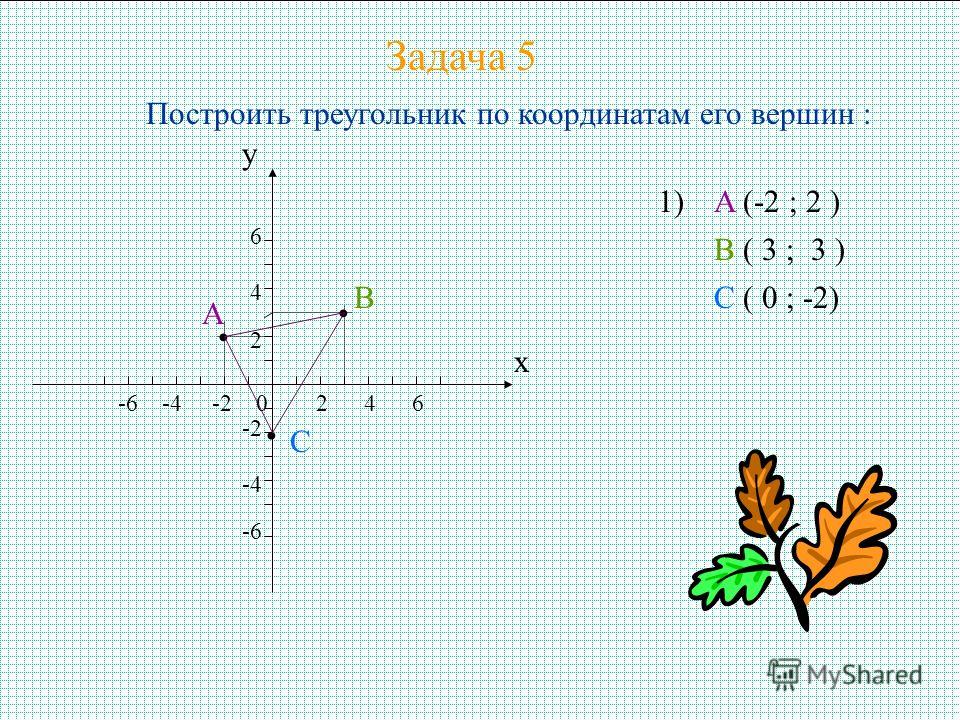 Асимптоты»)
Асимптоты») Теперь график произведения!
Теперь график произведения! Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.
Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках. Область определения функции
Область определения функции
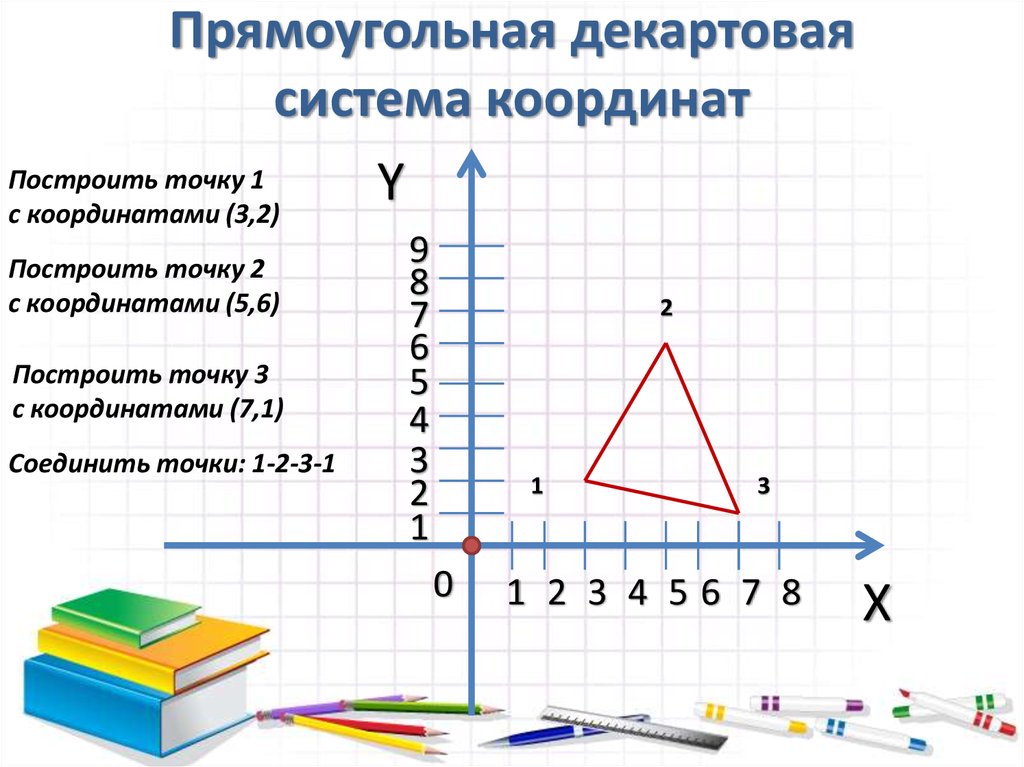
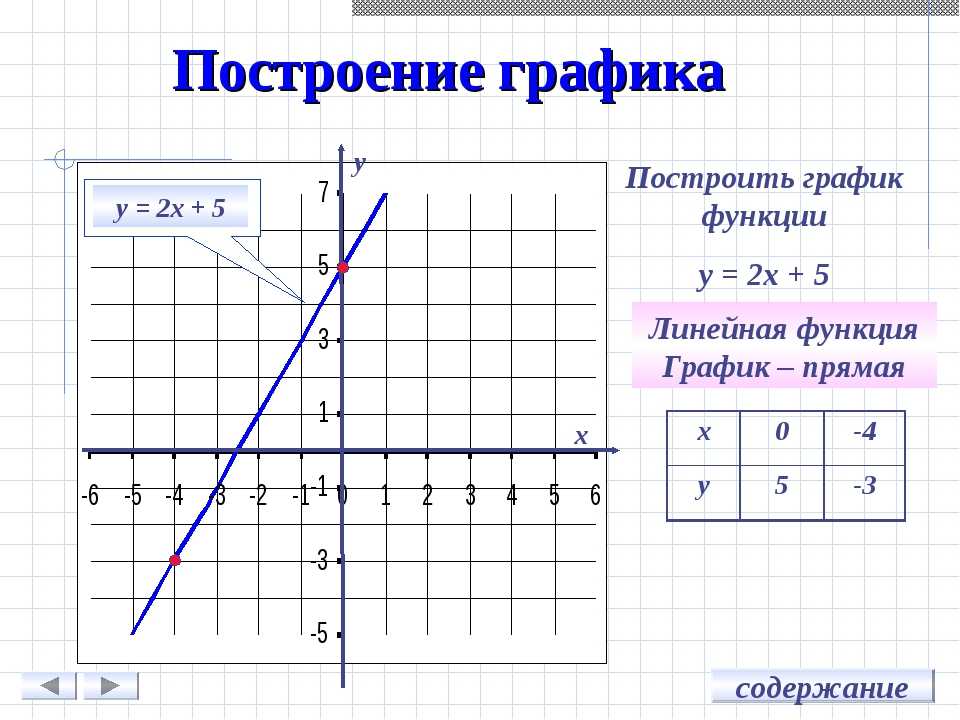
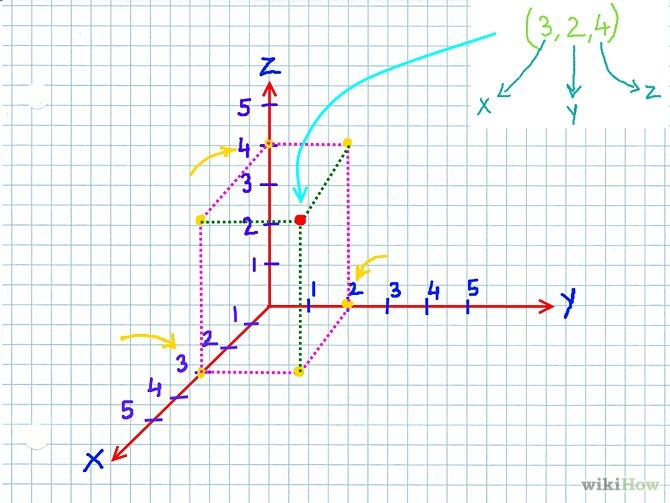 Перпендикуляр из точки B’
(пересечение прямой OA’ и прямой с ординатой y1)
на ось абсцисс и дает координату x2.
Находя подобным образом ряд точек, можем по ним
построить гиперболу.
Перпендикуляр из точки B’
(пересечение прямой OA’ и прямой с ординатой y1)
на ось абсцисс и дает координату x2.
Находя подобным образом ряд точек, можем по ним
построить гиперболу.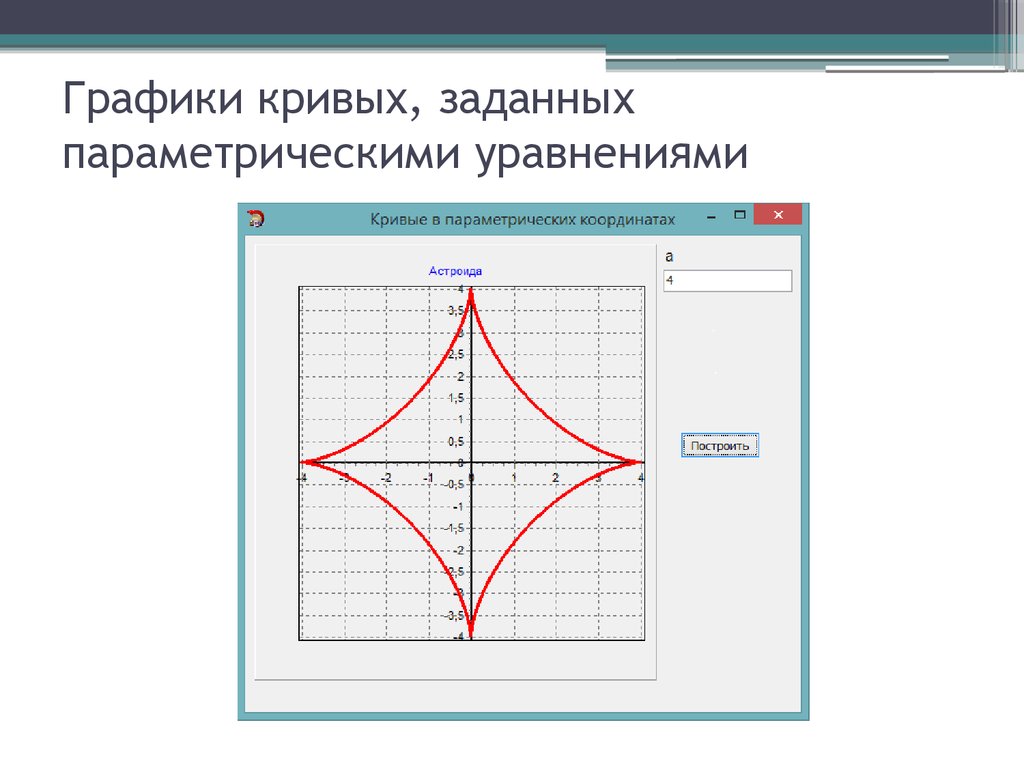 Если же мы имеем дело не с
изопроцессами, то тем более надо уметь находить
координаты любой точки.
Если же мы имеем дело не с
изопроцессами, то тем более надо уметь находить
координаты любой точки.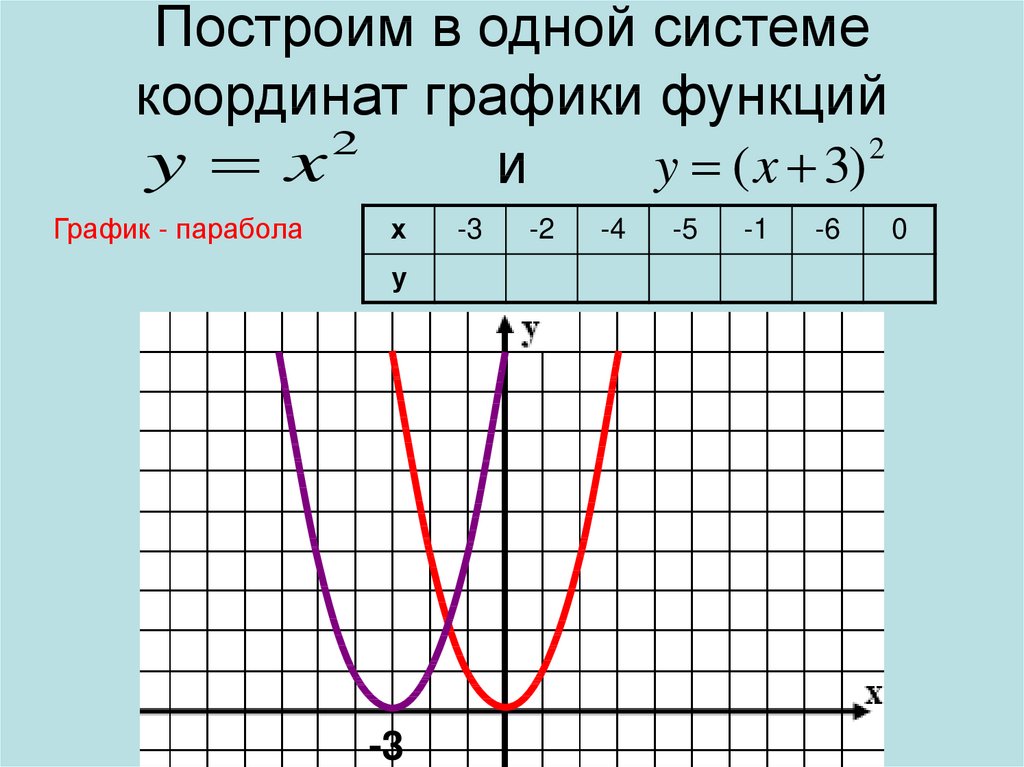 A’
)
A’
)
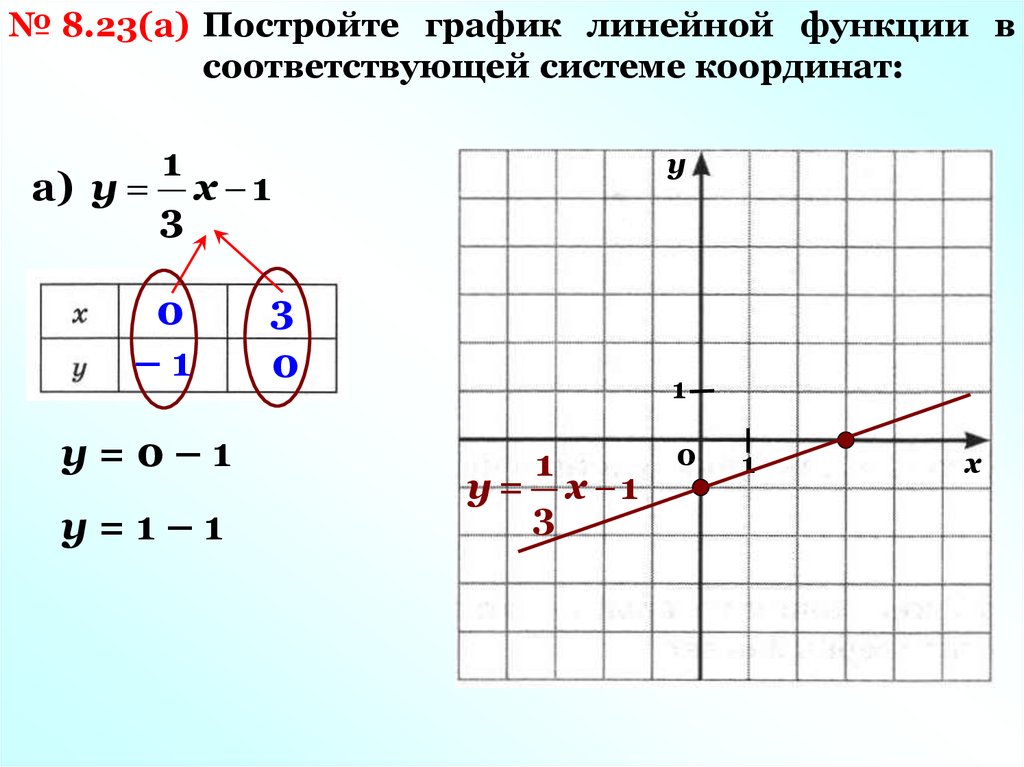 Из рис. 3а
видно, что если PA > P0, то
геометрическое значение TA больше
геометрического значения VA, то есть
графики в осях PT и VT получатся более растянутыми.
Если PA < P0, то всё наоборот. Из рис. 3б
и 3в видно, что если PA > P0 (VA
> V0), то геометрическое значение VA (PA)
получится меньше геометрического значения TA,
то есть график в осях PV получается сжатым по оси V
(P). Если же PA < P0, то всё наоборот.
Исходя из этого, можно выбирать P0 (V0)
таким образом, чтобы получающиеся графики
укладывались в заранее определенные рамки. Это
легко сделать, так как всегда известно, в какой
точке исходного графика недостающий параметр
имеет наибольшее значение. Следует провести
через нее соответствующую изолинию и выбрать P0
или V0 так, чтобы точка пересечения прямой P =
P0 или V = V0 имела абсциссу нужной нам
величины.
Из рис. 3а
видно, что если PA > P0, то
геометрическое значение TA больше
геометрического значения VA, то есть
графики в осях PT и VT получатся более растянутыми.
Если PA < P0, то всё наоборот. Из рис. 3б
и 3в видно, что если PA > P0 (VA
> V0), то геометрическое значение VA (PA)
получится меньше геометрического значения TA,
то есть график в осях PV получается сжатым по оси V
(P). Если же PA < P0, то всё наоборот.
Исходя из этого, можно выбирать P0 (V0)
таким образом, чтобы получающиеся графики
укладывались в заранее определенные рамки. Это
легко сделать, так как всегда известно, в какой
точке исходного графика недостающий параметр
имеет наибольшее значение. Следует провести
через нее соответствующую изолинию и выбрать P0
или V0 так, чтобы точка пересечения прямой P =
P0 или V = V0 имела абсциссу нужной нам
величины.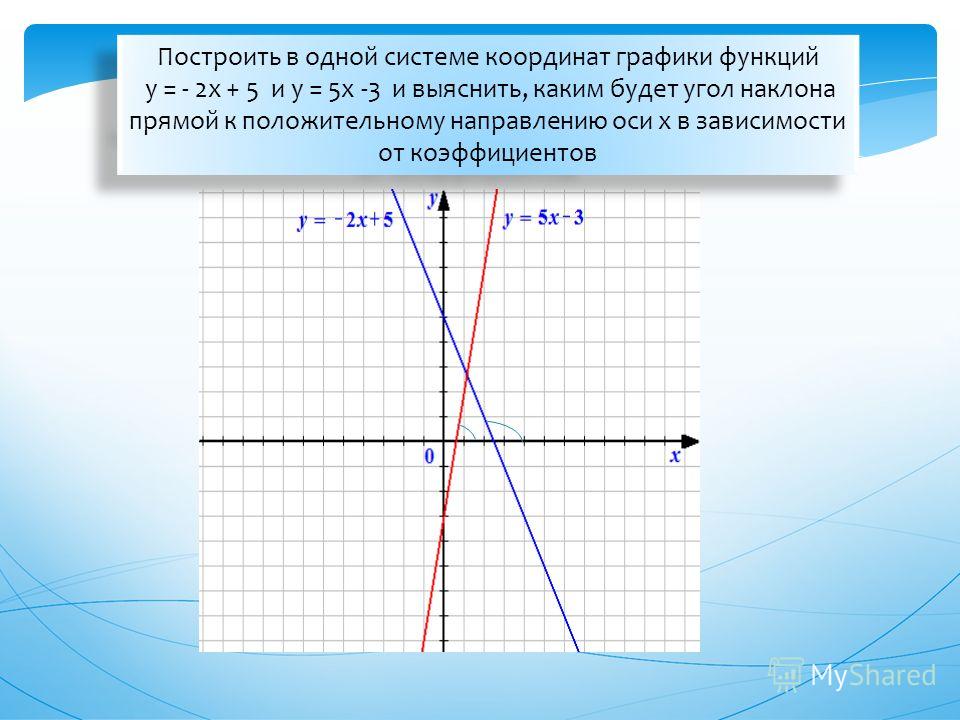
 2/16=1)
2/16=1)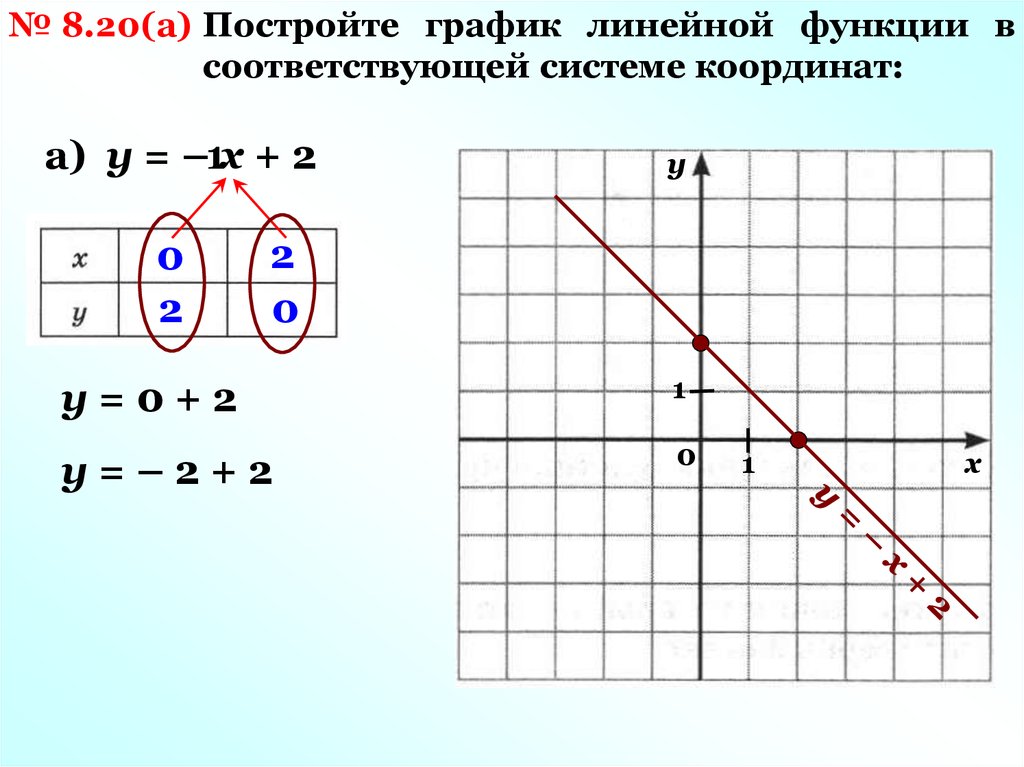
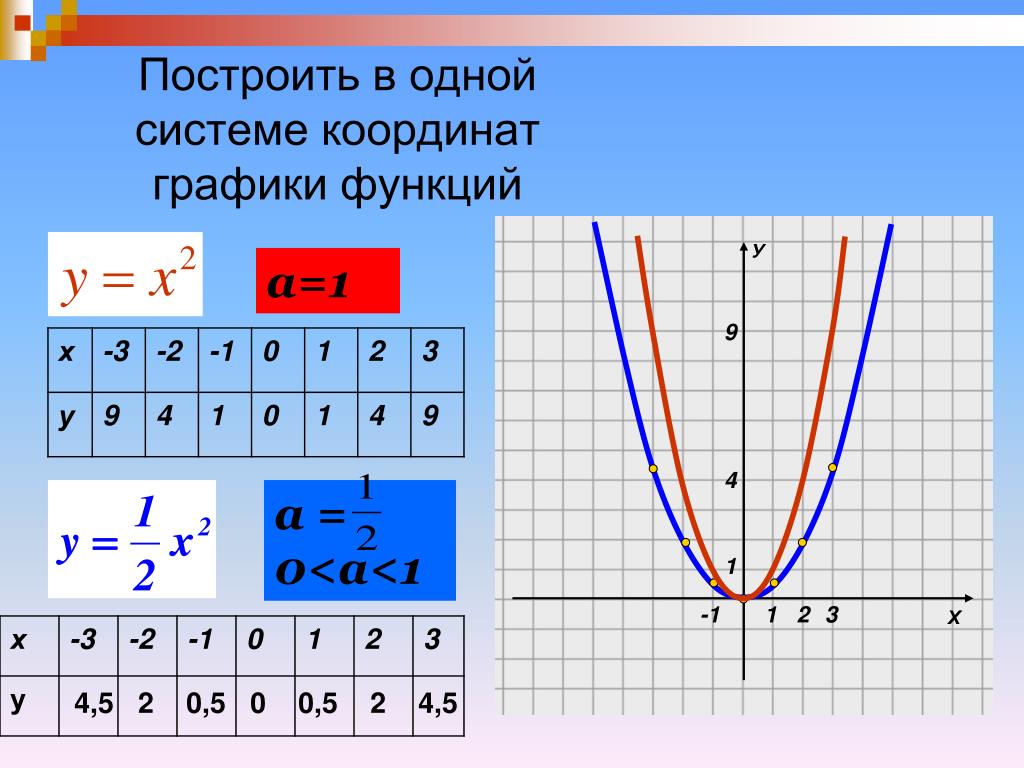 Построим график функции .
Построим график функции . Если же каждая функция зависит от своего аргумента, то на одном рисунке можно построить только 10 графиков.
Если же каждая функция зависит от своего аргумента, то на одном рисунке можно построить только 10 графиков. Порядок следования переменных и функций должен быть согласован.
Порядок следования переменных и функций должен быть согласован. На этой панели вы можете найти ссылки на семь типов графиков. В данном разделе остановимся на декартовой системе координат.
На этой панели вы можете найти ссылки на семь типов графиков. В данном разделе остановимся на декартовой системе координат.
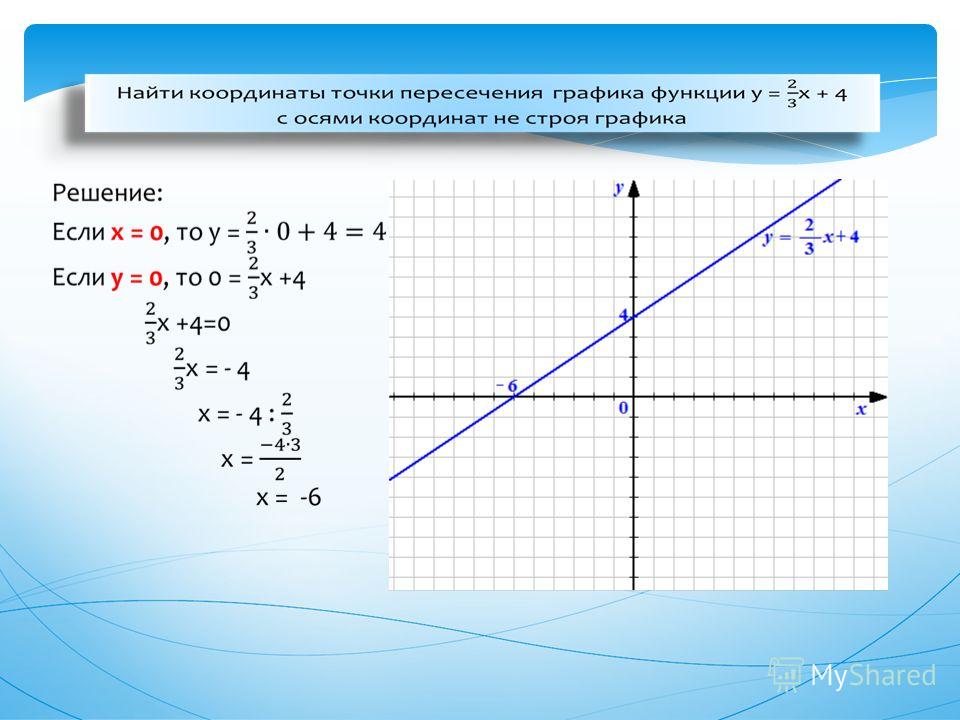
 Чтобы изменить их значения, просто удалите (точно так же, как при редактировании формул) старые величины и введите новые. Изменения пределов по оси X вызывает автоматический пересчет крайних значений по Y. Однако если вы переопределите область по оси Y, то область изменения переменной останется старой.
Чтобы изменить их значения, просто удалите (точно так же, как при редактировании формул) старые величины и введите новые. Изменения пределов по оси X вызывает автоматический пересчет крайних значений по Y. Однако если вы переопределите область по оси Y, то область изменения переменной останется старой.
 Полная схема исследования функции и построения ее графика объединяет в себе три этапа:
Полная схема исследования функции и построения ее графика объединяет в себе три этапа: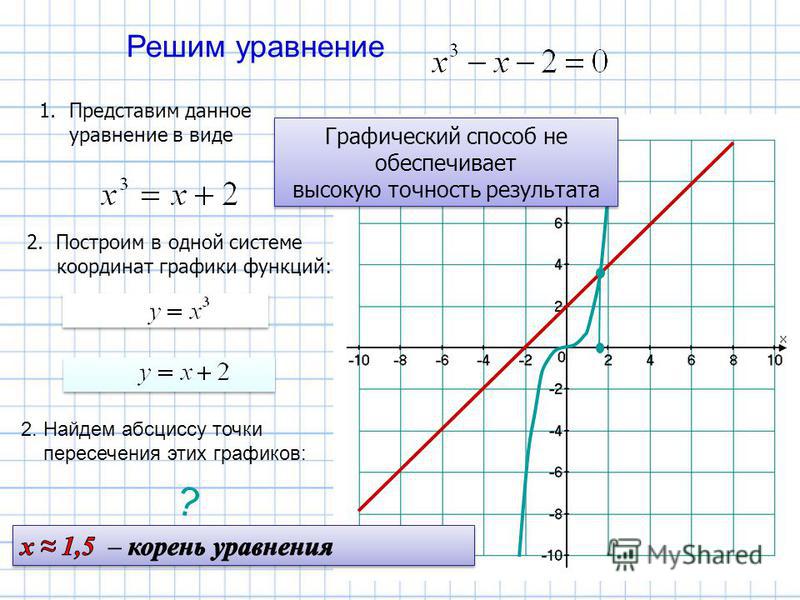 1. Найти точки, подозрительные на экстремум из решения уравнений и .
1. Найти точки, подозрительные на экстремум из решения уравнений и . Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.
Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.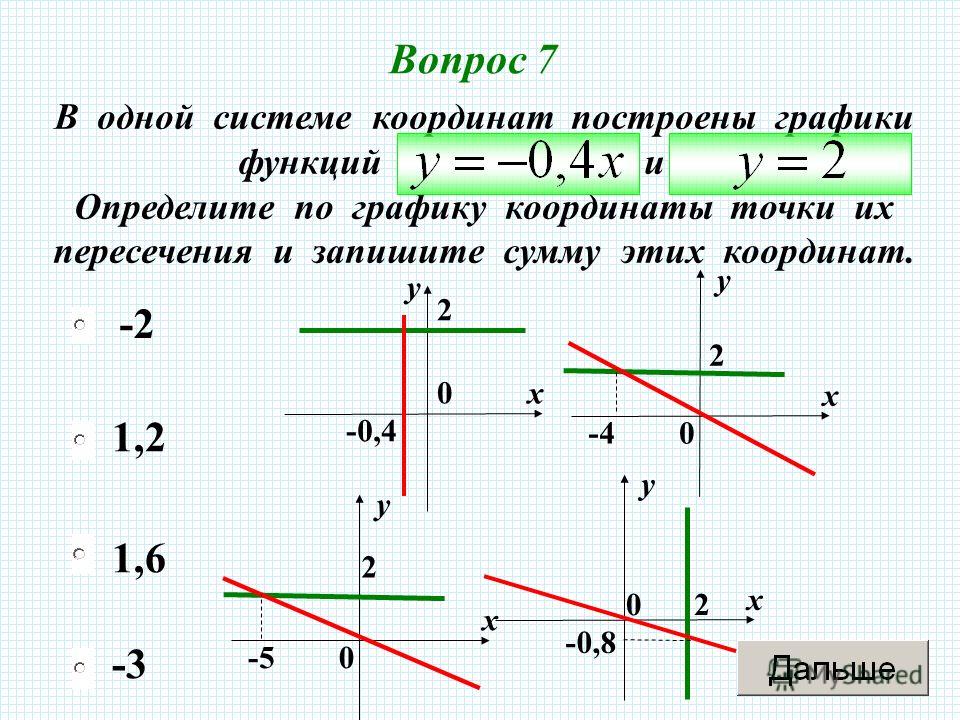 Каждая вертикальная полоса представляет собой переменную и часто имеет собственный масштаб. (Единицы могут быть даже разными). Затем значения отображаются в виде серии линий, соединенных по каждой оси.
Каждая вертикальная полоса представляет собой переменную и часто имеет собственный масштаб. (Единицы могут быть даже разными). Затем значения отображаются в виде серии линий, соединенных по каждой оси.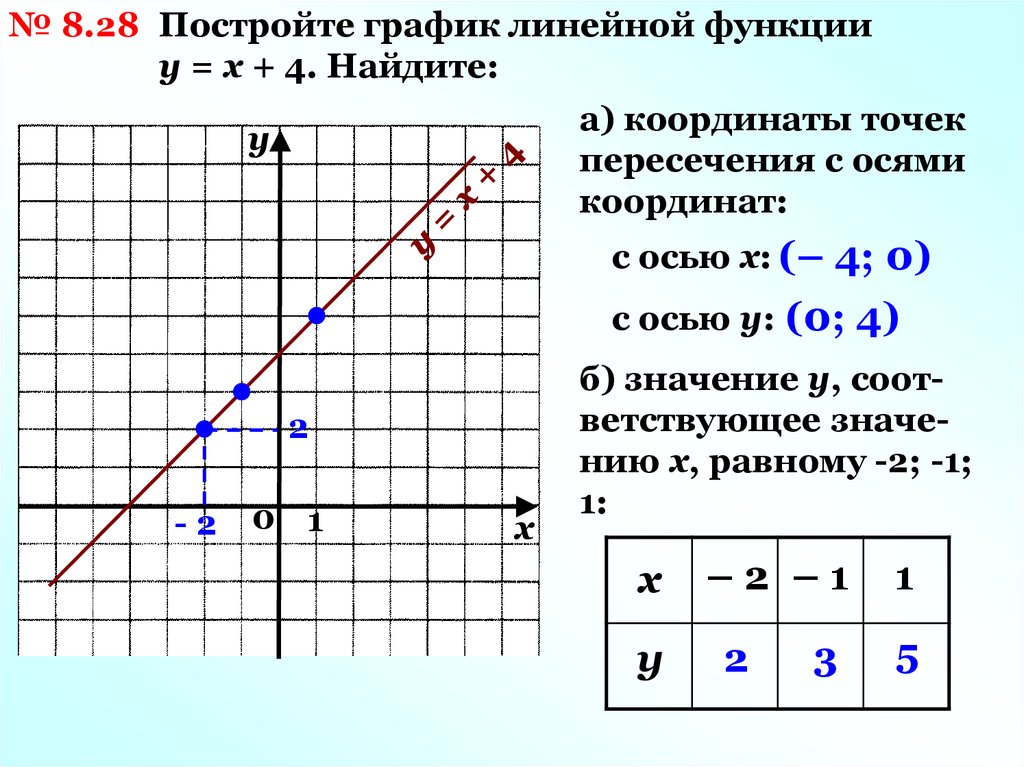 title = element_text (размер = 10)
)
title = element_text (размер = 10)
)  title = element_text (размер = 10)
)
title = element_text (размер = 10)
) 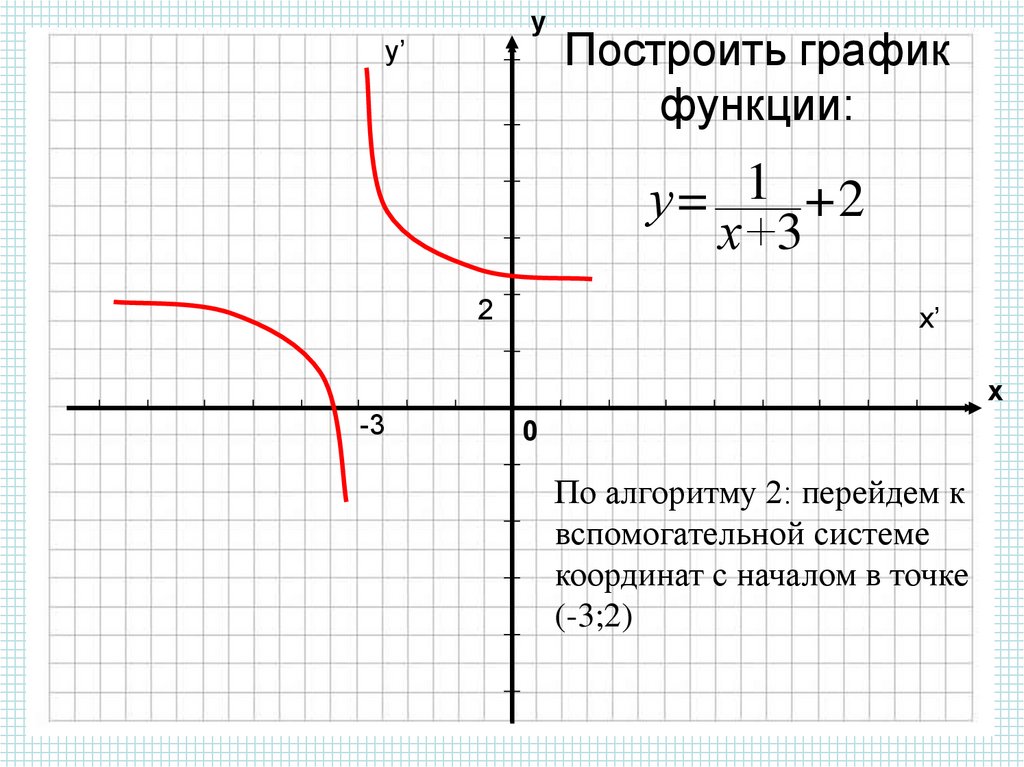 позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p3 <- данные %>%
ggparcoord(
столбцы = 1:4, groupColumn = 5, порядок = "любой класс",
масштаб = "стандарт",
шоуПойнтс = ИСТИНА,
title = "Одномерно нормализовать (вычесть среднее и разделить на sd)",
альфа-линии = 0,3
) +
scale_color_viridis (дискретный = ИСТИНА) +
тема_ipsum()+
тема(
легенда.позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p4 <- данные %>%
ggparcoord(
столбцы = 1:4, groupColumn = 5, порядок = "любой класс",
масштаб = "центр",
шоуПойнтс = ИСТИНА,
title = "Стандартизация и центрирование переменных",
альфа-линии = 0,3
) +
scale_color_viridis (дискретный = ИСТИНА) +
тема_ipsum()+
тема(
легенда.позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p1 + p2 + p3 + p4 + plot_layout (ncol = 2)
позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p3 <- данные %>%
ggparcoord(
столбцы = 1:4, groupColumn = 5, порядок = "любой класс",
масштаб = "стандарт",
шоуПойнтс = ИСТИНА,
title = "Одномерно нормализовать (вычесть среднее и разделить на sd)",
альфа-линии = 0,3
) +
scale_color_viridis (дискретный = ИСТИНА) +
тема_ipsum()+
тема(
легенда.позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p4 <- данные %>%
ggparcoord(
столбцы = 1:4, groupColumn = 5, порядок = "любой класс",
масштаб = "центр",
шоуПойнтс = ИСТИНА,
title = "Стандартизация и центрирование переменных",
альфа-линии = 0,3
) +
scale_color_viridis (дискретный = ИСТИНА) +
тема_ipsum()+
тема(
легенда.позиция = "нет",
plot.title = element_text (размер = 10)
) +
xlab("")
p1 + p2 + p3 + p4 + plot_layout (ncol = 2)