Найти площадь треугольника по трем сторонам — Онлайн калькулятор
Рассчитать площадь треугольника формулой по трем сторонам онлайн-калькулятором пригодится школьникам, студентам, преподавателям, специалистам различных специальностей. Вычисления производятся бесплатно. Пользователь сервиса получает не только готовый ответ, но и подробное решение. Используя данный способ, можно осуществлять самостоятельную подготовку к занятиям без привлечения репетиторов.
Чтобы найти площадь треугольника по трем сторонам онлайн:
- введите данные длины сторон треугольника в соответствующие поля;
- выберите единицы измерения для каждой стороны и для предполагаемой площади треугольника;
- для получения ответа нажмите кнопку «Рассчитать».
В автоматических вычислениях заложена формула Герона, в которой фигурируют величины трех сторон треугольника и его полупериметра.
Как найти площадь треугольника по трем сторонам с помощью онлайн-калькулятора
Онлайн-калькулятор позволяет вычислить площадь треугольника, зная длину его сторон. При этом не важно, является ли треугольник прямоугольным, равнобедренным, равносторонним, или вообще задан произвольно.
При этом не важно, является ли треугольник прямоугольным, равнобедренным, равносторонним, или вообще задан произвольно.
Рассмотрим простой пример, демонстрирующий работу калькулятора. Пусть нужно вычислить площадь треугольника, со сторонами a=5 см, b=4 см и с=3 см.
- Чтобы узнать площадь, введем значения в поля для значений сторон:
Обратите внимание, стороны можно задавать в метрах, сантиметрах и миллиметрах.
- После того, как мы ввели значения сторон треугольника, выберем единицы измерения, в которых хотим получить ответ. Это могут быть соответственно квадратные метры, сантиметры и миллиметры.
- Теперь нажмем кнопку «Найти»:
В результате калькулятор предоставит ответ с подробным решением:
Отметим, что в калькуляторе существуют ограничения. Например, в поле для значений сторон нельзя вводить отрицательные числа. Если вы введете некорректное значение, калькулятор предупредит вас об этом.
Материалы, которые помогут вам лучше разобраться в теме:
- Площадь фигуры: понятие площади, свойства площади, квадрируемые фигуры
- Вычисление площади фигуры в полярных координатах
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Площадь треугольника (по 2 сторонам и углу)
- Площадь треугольника (по стороне и высоте)
- Площадь прямоугольного треугольника
- Площадь равнобедренного треугольника
- Площадь равностороннего треугольника
- Площадь квадрата (по стороне квадрата)
- Площадь квадрата (по диагонали)
- Площадь прямоугольника
- Площадь треугольника (по 3 сторонам и радиусу описанной окружности)
- Площадь треугольника (по 3 сторонам и радиусу вписанной окружности)
- Площадь треугольника (по полупериметру и радиусу вписанной окружности)
- Площадь треугольника (по двум сторонам и одному углу)
- Площадь треугольника (по одной стороне и двум углам)
- Площадь треугольника (по радиусу описанной окружности и двум углам)
- Площадь круга (по радиусу)
- Площадь круга (по диаметру)
- Площадь круга (по длине окружности)
- Площадь ромба (по сторонам и углу между ними)
- Площадь ромба (по стороне и высоте)
- Площадь ромба (по диагоналям)
- Площадь параллелограмма (по сторонам и углу между ними)
- Площадь параллелограмма (по стороне и высоте)
- Площадь параллелограмма (по диагоналям и углу между ними)
- Площадь трапеции (по основаниям и высоте)
- Площадь трапеции (по средней линии и высоте)
- Площадь трапеции (по диагоналям и углу между ними)
- Площадь эллипса
- Площадь поверхности параллелепипеда
- Площадь поверхности сферы
- Площадь поверхности цилиндра
- Площадь поверхности конуса
Вычисление площади треугольника по трем сторонам онлайн-калькулятором
Для решения задачи используется формула Герона:
S=p*(p-a)*(p-b)*(p-c)
где
- a, b, c – длины сторон треугольника,
- p – полупериметр треугольника, который вычисляется по формуле p=(a+b+c)/2
Обратите внимание на то, что вводимая длина сторон может иметь отличные друг от друга единицы измерения. Нет необходимости их переводить самостоятельно. То же касается и полученного ответа. Все переводы осуществляются автоматически и приведены в решении.
Нет необходимости их переводить самостоятельно. То же касается и полученного ответа. Все переводы осуществляются автоматически и приведены в решении.
Если понадобилась помощь в написании работы по математике или другим дисциплинам, обратитесь к консультанту на сайте. Вам помогут быстро оформить заявку со скидкой.
Понравился калькулятор? Поделись с друзьями!
Площадь треугольника. Онлайн калькулятор.
- Площадь прямоугольного треугольника
- по двум катетам
- по катету и гипотенузе
- по катету и прилежащему углу
- по катету и противолежащему углу
- по гипотенузе и углу
- Площадь равнобедренного треугольника
- по основанию и боковой стороне
- по основанию и высоте
- по боковой стороне и углу прилежащему основанию
- по основанию и прилежащему углу
- по боковой стороне и углу противолежащему основанию
- по основанию и противолежащему углу
- по высоте и радиусу описанной окружности
- Площадь равностороннего треугольника
- по стороне
- по высоте
- по средней линии
- по радиусу описанной окружности
- по радиусу вписанной окружности
- по периметру
Площадь прямоугольного треугольника по катетам
Введите катет
Введите катет
Формула площади прямоугольного треугольника по катетам
Где a, b — катеты прямоугольного треугольника
Площадь прямоугольного треугольника по катету и гипотенузе
Введите катет
Введите гипотенузу
Формула площади прямоугольного треугольника по катету и гипотенузе
Где a — катет прямоугольного треугольника
c — гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника по катету и прилежащему углу
Введите катет
Введите угол
Формула площади прямоугольного треугольника по катету и прилежащему углу
Где b — катет прямоугольного треугольника
α — прилежащий угол
Площадь прямоугольного треугольника по катету и противолежащему углу
Введите катет
Введите угол
Формула площади прямоугольного треугольника по катету и противолежащему углу
Где a — катет прямоугольного треугольника
γ — противолежащий угол
Площадь прямоугольного треугольника по гипотенузе и острому углу
Введите гипотенузу
Введите угол
Формула площади прямоугольного треугольника по гипотенузе и острому углу
Где c — гипотенуза прямоугольного треугольника
α — острый угол прямоугольного треугольника
Площадь равнобедренного треугольника по основанию и боковой стороне
Введите основание
Введите сторону
Формула площади равнобедренного треугольника по основанию и боковой стороне
Где a — основание равнобедренного треугольника
b — боковые стороны
Площадь равнобедренного треугольника по основанию и высоте
Введите основание
Введите высоту
Формула площади равнобедренного треугольника по основанию и высоте
S=1/2*a*h
Где a — основание равнобедренного треугольника
h — высота равнобедренного треугольника
Площадь равнобедренного треугольника по боковой стороне и углу прилежащему основанию
Введите сторону
Введите угол
Формула площади равнобедренного треугольника по боковой стороне и углу прилежащему основанию
Где b — основание равнобедренного треугольника
γ — угол равнобедренного треугольника прилежащий основанию
Площадь равнобедренного треугольника по основанию и прилежащему углу
Введите сторону
Введите угол
Формула площади равнобедренного треугольника по основанию и прилежащему углу
Где a — основание равнобедренного треугольника
γ — прилежащий к основанию угол
Площадь равнобедренного треугольника по боковой стороне и углу противолежащему основанию
Введите сторону
Введите угол
Формула площади равнобедренного треугольника по боковой стороне и углу противолежащему основанию
Где a — боковая сторона равнобедренного треугольника
γ — угол равнобедренного треугольника противолежащий основанию
Площадь равнобедренного треугольника по основанию и противолежащему углу
Введите основание
Введите угол
Формула площади равнобедренного треугольника по основанию и противолежащему углу
Где a — основание равнобедренного треугольника
γ — угол равнобедренного треугольника противолежащий основанию
Площадь равнобедренного треугольника по высоте и радиусу описанной окружности
Введите высоту
Введите радиус
Формула площади равнобедренного треугольника по высоте и радиусу описанной окружности
Где h — высота равнобедренного треугольника
R — радиус описанной окружности
Площадь равностороннего треугольника по стороне
Введите сторону
Формула площади равностороннего треугольника по стороне
Где a — сторона треугольника
Площадь равностороннего треугольника по высоте
Введите высоту
Формула площади равностороннего треугольника по высоте
Где h — высота треугольника
Площадь равностороннего треугольника по средней линии
Введите длину средней линии
Формула площади равностороннего треугольника по средней линии
Где MN — средняя линия
Площадь равностороннего треугольника по радиусу описанной окружности
Введите радиус
Формула площади равностороннего треугольника по радиусу описанной окружности
Где R — радиус описанной окружности
Площадь равностороннего треугольника по радиусу вписанной окружности
Введите радиус
Формула площади равностороннего треугольника по радиусу вписанной окружности
Где r — радиус вписанной окружности
Площадь равностороннего треугольника по периметру
Введите периметр
Формула площади равностороннего треугольника по периметру
Где P — периметр
Площадь прямоугольного треугольника: онлайн калькулятор, формулы, примеры решений
Фигура
{$ main.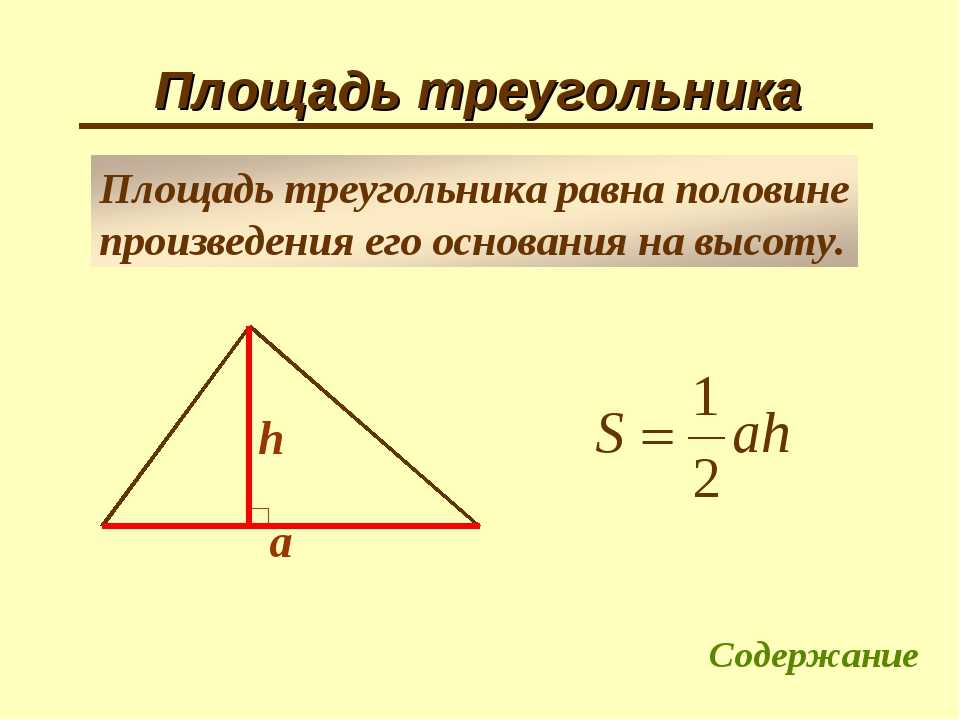 figures[data.figure] $}
figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Радиусили диаметр
Стороныили диагонали
Введите 2 величины
Сторона A
Сторона B
Диагонали
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Угол γ{$ main.angles[data.angle] $}
Введите 2 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 2 величины
Сторона
Высота
Диагональ 1
Диагональ 2
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.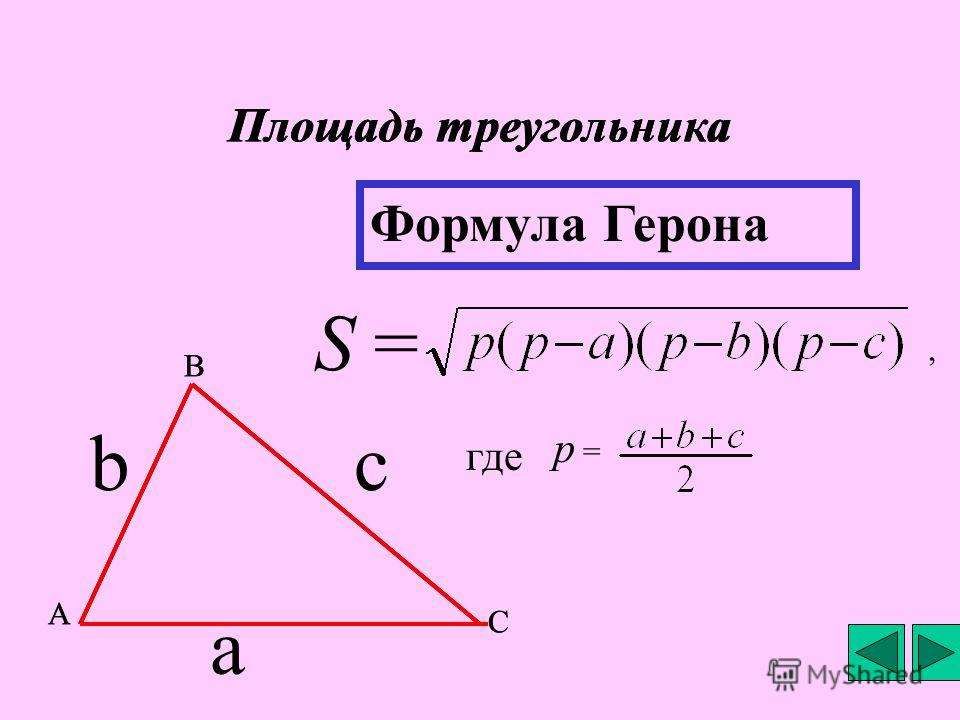 angles[data.angle] $}
angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Высота ha
Высота hb
Диагональ 1
Диагональ 2
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Основание A
Основание C
Высота H
Дополните боковые стороны для поиска периметра
Сторона B
Сторона D
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Количество сторон многоугольника
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Введите 1 величину
Сторона A = радиусу описанной окружности (R)
Радиус вписанной окружности (r)
Результат расчёта
- Периметр: {$ result.p|number:4 $} type == ‘area'»>Площать: {$ result.s|number:4 $}
Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.
Геометрия треугольника
В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии. В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:
- Гипотенуза — самая длинная сторона треугольника, лежащая напротив прямого угла.
- Катеты — отрезки, образующие прямой угол. В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла).
 Для непрямоугольных треугольников катетов не существуют.
Для непрямоугольных треугольников катетов не существуют.
Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.
Прямоугольный треугольник в реальности
Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности. Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.
Площадь треугольника
Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника. Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:
Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:
S = 0,5 a × h,
где a – сторона треугольника, h – его высота.
Формула для вычисления площади прямоугольного треугольника еще проще:
S = 0,5 a × b,
где a и b – катеты.
Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:
- два катета;
- катет и прилежащий угол;
- катет и противолежащий угол.
В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.
Примеры из реальной жизни
Керамическая плитка
Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника.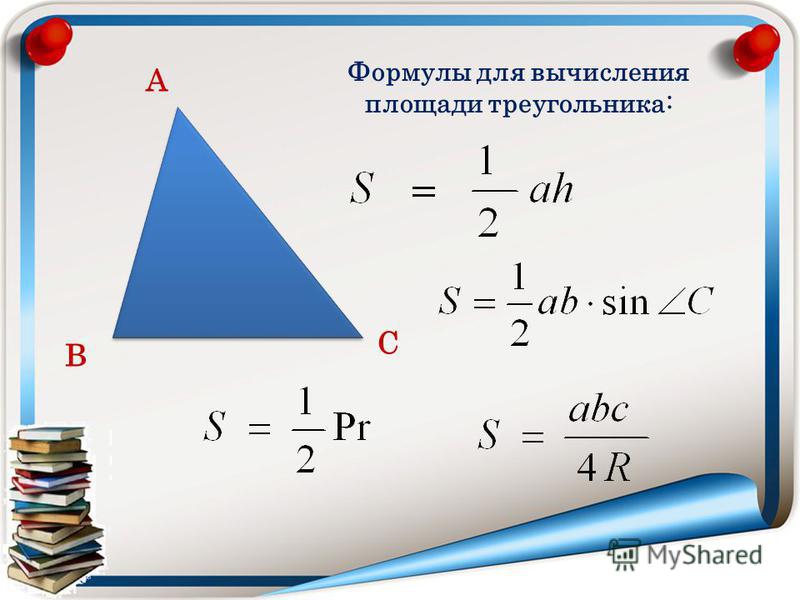 Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
S = 180,5
Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.
Школьная задача
Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:
S= 21,65
Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.
Заключение
Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.
Калькулятор площади треугольника по всем формулам расчета
Площадь треугольника — это численная характеристика, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц. В зависимости от типа треугольника и известных исходных данных, площадь треугольника можно рассчитать по различным формулам. Приведенные калькуляторы площади треугольника используют все известные методики и упрощают процесс вычислений.
Треугольник — это геометрическая фигура, образованная соединением отрезков трех точек, не лежащих на одной прямой. Точки называются вершинами треугольника, а отрезки — его сторонами.
Площадь треугольника — калькуляторы для всех видов
Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.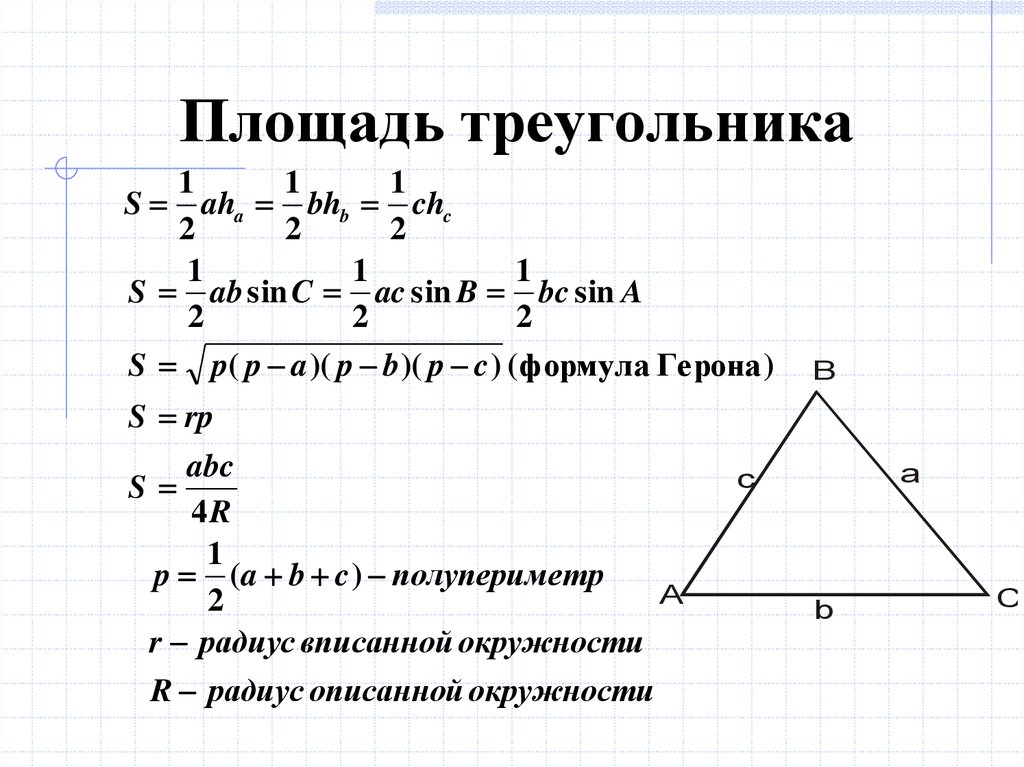 Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.
Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.
Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.
Площадь треугольника по основанию и высоте — калькулятор онлайн:
| Формула | Результат |
| S = ½ × a × h | |
Сторона a | |
Высота h |
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними. Угол α между сторонами может быть любым: тупым, острым, прямым.
Площадь треугольника по двум сторонам и углу между ними — расчет:
| Формула | Результат |
| S = ½ × a × b × α | |
Сторона a | |
Сторона b | |
Угол α° между сторонами a и b |
Если известно три стороны треугольника и радиус вписанной окружности, то площадь данного треугольника вычисляется, как половина суммы этих сторон (полупериметр p = ½ × (a + b + c)) умноженная на радиус вписанной окружности.
Площадь треугольника по радиусу вписанной окружности и трем сторонам — онлайн калькулятор:
| Формула | Результат |
| S = r × ½ × (a + b + c) | |
Сторона a | |
Сторона b | |
Сторона c | |
Радиус r вписанной окружности |
Если известно три стороны треугольника и радиус описанной окружности, то площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.
Площадь треугольника по радиусу описанной окружности и трем сторонам — расчет:
| Формула | Результат |
| S = (a × b × c) ⁄ (4 × R) | |
Сторона a | |
Сторона b | |
Сторона c | |
Радиус R описанной окружности |
Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c) на полупериметр.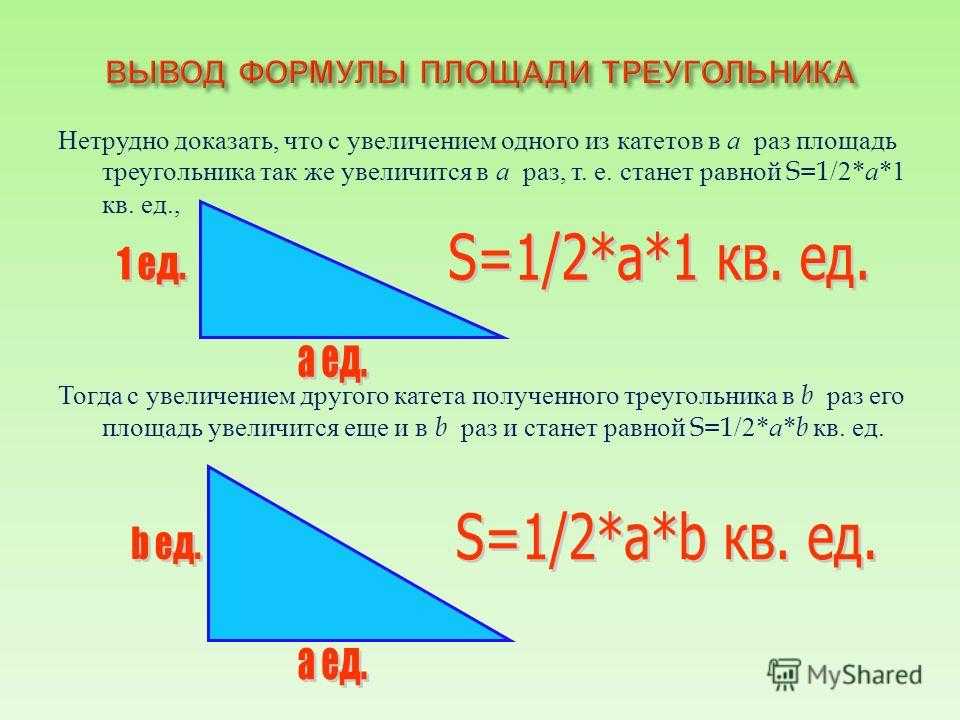 Полупериметр p = (a + b + c) × ½.
Полупериметр p = (a + b + c) × ½.
Площадь треугольника по формуле Герона — калькулятор онлайн:
| Формула | Результат |
| S = √ p × (p — a) × (p — b) × (p — c) | |
Сторона a | |
Сторона b | |
Сторона c |
Площадь произвольного треугольника по стороне и двум прилежащим углам — расчет:
| Формула | Результат |
| S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β)) | |
Сторона a | |
Угол β° | |
Угол α° |
Калькулятор площади для равнобедренных треугольников
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.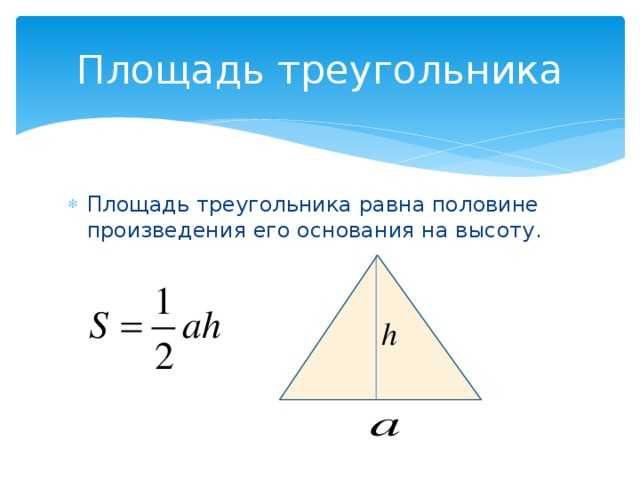 Боковыми называются равные стороны, а последняя неравная им сторона — основанием. Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
Боковыми называются равные стороны, а последняя неравная им сторона — основанием. Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
Площадь равнобедренного треугольника по боковым сторонам и основанию — калькулятор:
| Формула | Результат |
| S = ¼ × c × √ (4 × a² — c²) | |
Сторона a (a = b) | |
Сторона c |
Если известны боковые стороны и угол между ними, то площадь равнобедренного треугольника определяется, как половина произведения квадрата боковой стороны на синус угла между боковыми сторонами.
Площадь равнобедренного треугольника по боковым сторонам и углу между ними:
| Формула | Результат |
| S = ½ × a² × sin (α) | |
Боковая сторона a (a = b) | |
Угол α° между боковыми сторонами |
Если известна боковая сторона, основание и углу между ними, то площадь равнобедренного треугольника равна половине произведения боковой стороны и основания на синус угла между ними.
Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними — расчет:
| Формула | Результат |
| S = ½ ×a × c × sin (β) | |
Боковая сторона a (a = b) | |
Основание треугольника c | |
Угол β° между основанием и стороной |
Если известно основание и угол между боковыми сторонами, то площадь равнобедренного треугольника рассчитывается, как четверть отношения квадрата основания на тангенс половинного угла между боковыми сторонами.
Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами — онлайн:
| Формула | Результат |
| S = c² ⁄ (4 × tg (½ × α)) | |
Основание треугольника c | |
Угол α° между боковыми сторонами |
Площадь равнобедренного треугольника по высоте и основанию — калькулятор:
| Формула | Результат |
| S = ½ × c × h | |
Основание треугольника c | |
Высота h |
Площадь равносторонних треугольников — онлайн калькулятор, формулы
Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник, все стороны которого равны между собой, все углы также равны и составляют 60°.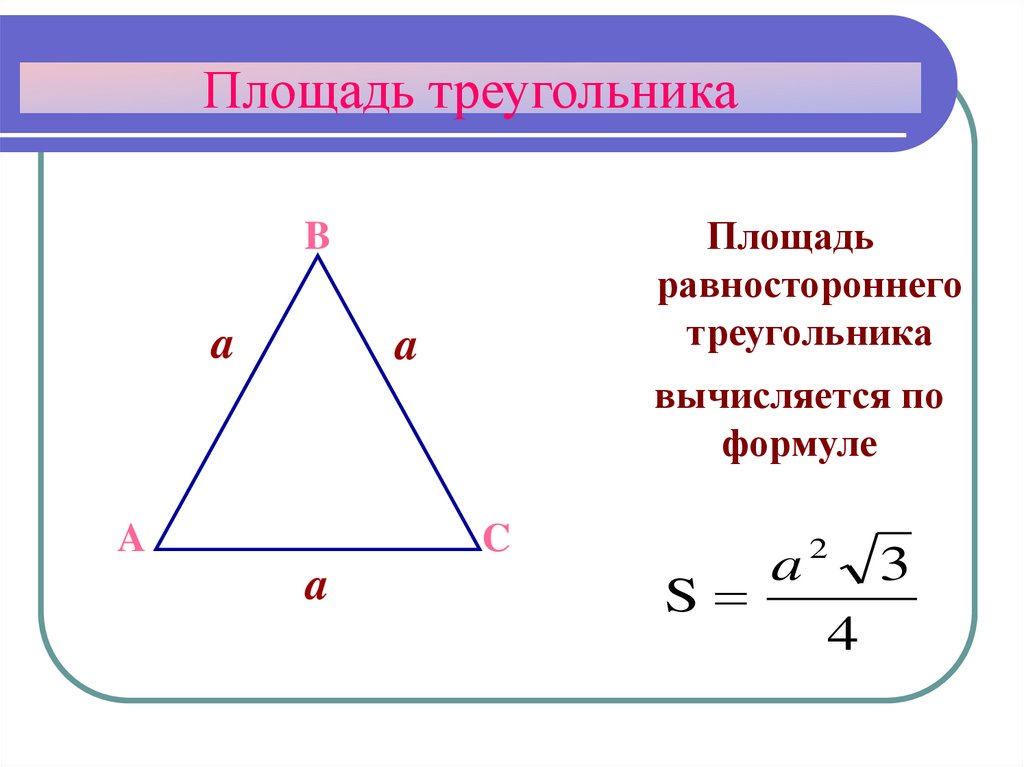 В равностороннем треугольнике высота является и биссектрисой, и медианой.
В равностороннем треугольнике высота является и биссектрисой, и медианой.
Площадь равностороннего треугольника по известной стороне равна произведению одной четвертой корня из трех на квадрат стороны.
Площадь равностороннего треугольника по стороне — онлайн расчет:
| Формула | Результат |
| S = ¼ × √(3) × a² | |
Сторона a (a = b = c) |
Если известна высота равностороннего треугольника, то его площадь равна отношению квадрата высоты к корню из трех.
Площадь равностороннего треугольника по высоте:
| Формула | Результат |
| S = h² ⁄ √(3) | |
Высота h |
Если известен радиус вписанной окружности, то площадь равностороннего треугольника равна произведению трех корней из трех на квадрат радиуса вписанной окружности.
Площадь равностороннего треугольника по радиусу вписанной окружности — калькулятор:
| Формула | Результат |
| S = 3 × √(3) × r² | |
Радиус r вписанной окружности |
По известному радиусу описанной окружности площадь равностороннего треугольника определяется, как произведение трех четвертей корня из трех на квадрат радиуса.
Площадь равностороннего треугольника по радиусу описанной окружности:
| Формула | Результат |
| S = ¾ × √(3) × R² | |
Радиус R описанной окружности |
Площадь прямоугольного треугольника — формулы и калькуляторы
Прямоугольный треугольник — это треугольник, в котором один угол прямой (90°).
По основанию и высоте площадь прямоугольно треугольника равна половине произведения катетов треугольника.
Площадь прямоугольного треугольника по двум катетам — расчет:
| Формула | Результат |
| S = ½ × a × b | |
Катет a | |
Катет b |
Площадь прямоугольного треугольника через гипотенузу и угол:
| Формула | Результат |
| S = ¼ × c² × sin (2α) | |
Сторона c | |
Угол α |
Площадь прямоугольного треугольника через катет и угол — онлайн калькулятор:
| Формула | Результат |
| S = ½ × b² × tg (α) | |
Сторона b | |
Угол α |
Если в треугольник вписана окружность и известны отрезки, на которые она делит гипотенузу, то площадь прямоугольно треугольника равна произведению этих отрезков.
Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность:
| Формула | Результат |
| S = d × e | |
Отрезок d | |
Отрезок e |
Площадь прямоугольного треугольника через гипотенузу и вписанную окружность — расчет:
| Формула | Результат |
| S = r × (r + c) | |
Сторона с | |
Радиус r |
Площадь прямоугольно треугольника по трем сторонам (формула Герона) равна произведению разностей полупериметра треугольника и каждого из катетов. Полупериметр p = ½ × (a + b + c)
Площадь прямоугольного треугольника по формуле Герона:
| Формула | Результат |
| S = ( ½ × (a + b + c) — a) × ( ½ × (a + b + c) — b) | |
Сторона a | |
Сторона b | |
Сторона c |
Таблица синусов (sin) для расчета площади треугольника
Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя ее вы сможете провести расчеты площади треугольника самостоятельно при помощи формул.
Используя ее вы сможете провести расчеты площади треугольника самостоятельно при помощи формул.
Таблица подходит для вычисления:
- Площади прямоугольного треугольника через гипотенузу и угол S = ¼ × c² × sin (2α).
- Площади равнобедренного треугольника по боковой стороне, основанию и углу между ними S = ½ ×a × c × sin (β).
- Площади равнобедренного треугольника по боковым сторонам и углу между ними S = ½ × a² × sin (α).
- Площади произвольного треугольника по стороне и двум прилежащим углам S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β)).
Таблица синусов (sin) углов от 0° до 180°:
| sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.  173648 173648sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 | sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.  788011 788011sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 | sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.  997564 997564sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.  707107 707107 | sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.  069756 069756sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов (sin) углов от 181° до 360°:
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.  515038 515038sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 | sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.  939693 939693sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 | sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.  945519 945519sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 | sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.  529919 529919sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
Таблица тангенсов (tg) для расчета площади треугольника
Таблица тангенсов — это записанные в таблицу посчитанные значения тангенсов углов от 0° до 360°. С ее помощью вы сможете провести расчеты площади треугольника самостоятельно по следующим формулам:
С ее помощью вы сможете провести расчеты площади треугольника самостоятельно по следующим формулам:
- S = ½ × b² × tg (α) — площадь прямоугольного треугольника через катет и угол.
- S = c² ⁄ (4 × tg (½ × α)) — площадь равнобедренного треугольника по основанию и углу между боковыми сторонами.
Таблица тангенсов (tg) углов от 0° до 180°:
| tg(0°) = 0 tg(1°) = 0.01746 tg(2°) = 0.03492 tg(3°) = 0.05241 tg(4°) = 0.06993 tg(5°) = 0.08749 tg(6°) = 0.1051 tg(7°) = 0.12278 tg(8°) = 0.14054 tg(9°) = 0.15838 tg(10°) = 0.17633 tg(11°) = 0.19438 tg(12°) = 0.21256 tg(13°) = 0.23087 tg(14°) = 0.24933 tg(15°) = 0.26795 tg(16°) = 0.28675 tg(17°) = 0.30573 tg(18°) = 0.32492 tg(19°) = 0.34433 tg(20°) = 0.36397 tg(21°) = 0.38386 tg(22°) = 0.40403 tg(23°) = 0.42447 tg(24°) = 0.44523 tg(25°) = 0.  46631 46631tg(26°) = 0.48773 tg(27°) = 0.50953 tg(28°) = 0.53171 tg(29°) = 0.55431 tg(30°) = 0.57735 tg(31°) = 0.60086 tg(32°) = 0.62487 tg(33°) = 0.64941 tg(34°) = 0.67451 tg(35°) = 0.70021 tg(36°) = 0.72654 tg(37°) = 0.75355 tg(38°) = 0.78129 tg(39°) = 0.80978 tg(40°) = 0.8391 tg(41°) = 0.86929 tg(42°) = 0.9004 tg(43°) = 0.93252 tg(44°) = 0.96569 tg(45°) = 1 tg(46°) = 1.03553 tg(47°) = 1.07237 tg(48°) = 1.11061 tg(49°) = 1.15037 tg(50°) = 1.19175 tg(51°) = 1.2349 tg(52°) = 1.27994 tg(53°) = 1.32704 tg(54°) = 1.37638 tg(55°) = 1.42815 tg(56°) = 1.48256 tg(57°) = 1.53986 tg(58°) = 1.60033 tg(59°) = 1.66428 tg(60°) = 1.73205 | tg(61°) = 1.80405 tg(62°) = 1.88073 tg(63°) = 1.96261 tg(64°) = 2.0503 tg(65°) = 2.14451 tg(66°) = 2.24604 tg(67°) = 2.35585 tg(68°) = 2.47509 tg(69°) = 2.60509 tg(70°) = 2.74748 tg(71°) = 2.  90421 90421tg(72°) = 3.07768 tg(73°) = 3.27085 tg(74°) = 3.48741 tg(75°) = 3.73205 tg(76°) = 4.01078 tg(77°) = 4.33148 tg(78°) = 4.70463 tg(79°) = 5.14455 tg(80°) = 5.67128 tg(81°) = 6.31375 tg(82°) = 7.11537 tg(83°) = 8.14435 tg(84°) = 9.51436 tg(85°) = 11.43005 tg(86°) = 14.30067 tg(87°) = 19.08114 tg(88°) = 28.63625 tg(89°) = 57.28996 tg(90°) = ∞ tg(91°) = -57.28996 tg(92°) = -28.63625 tg(93°) = -19.08114 tg(94°) = -14.30067 tg(95°) = -11.43005 tg(96°) = -9.51436 tg(97°) = -8.14435 tg(98°) = -7.11537 tg(99°) = -6.31375 tg(100°) = -5.67128 tg(101°) = -5.14455 tg(102°) = -4.70463 tg(103°) = -4.33148 tg(104°) = -4.01078 tg(105°) = -3.73205 tg(106°) = -3.48741 tg(107°) = -3.27085 tg(108°) = -3.07768 tg(109°) = -2.90421 tg(110°) = -2.74748 tg(111°) = -2.60509 tg(112°) = -2.47509 tg(113°) = -2.35585 tg(114°) = -2.24604 tg(115°) = -2.  14451 14451tg(116°) = -2.0503 tg(117°) = -1.96261 tg(118°) = -1.88073 tg(119°) = -1.80405 tg(120°) = -1.73205 | tg(121°) = -1.66428 tg(122°) = -1.60033 tg(123°) = -1.53986 tg(124°) = -1.48256 tg(125°) = -1.42815 tg(126°) = -1.37638 tg(127°) = -1.32704 tg(128°) = -1.27994 tg(129°) = -1.2349 tg(130°) = -1.19175 tg(131°) = -1.15037 tg(132°) = -1.11061 tg(133°) = -1.07237 tg(134°) = -1.03553 tg(135°) = -1 tg(136°) = -0.96569 tg(137°) = -0.93252 tg(138°) = -0.9004 tg(139°) = -0.86929 tg(140°) = -0.8391 tg(141°) = -0.80978 tg(142°) = -0.78129 tg(143°) = -0.75355 tg(144°) = -0.72654 tg(145°) = -0.70021 tg(146°) = -0.67451 tg(147°) = -0.64941 tg(148°) = -0.62487 tg(149°) = -0.60086 tg(150°) = -0.57735 tg(151°) = -0.55431 tg(152°) = -0.53171 tg(153°) = -0.50953 tg(154°) = -0.48773 tg(155°) = -0.46631 tg(156°) = -0.44523 tg(157°) = -0.  42447 42447tg(158°) = -0.40403 tg(159°) = -0.38386 tg(160°) = -0.36397 tg(161°) = -0.34433 tg(162°) = -0.32492 tg(163°) = -0.30573 tg(164°) = -0.28675 tg(165°) = -0.26795 tg(166°) = -0.24933 tg(167°) = -0.23087 tg(168°) = -0.21256 tg(169°) = -0.19438 tg(170°) = -0.17633 tg(171°) = -0.15838 tg(172°) = -0.14054 tg(173°) = -0.12278 tg(174°) = -0.1051 tg(175°) = -0.08749 tg(176°) = -0.06993 tg(177°) = -0.05241 tg(178°) = -0.03492 tg(179°) = -0.01746 tg(180°) = 0 |
Таблица тангенсов (tg) углов от 181° до 360°:
| tg(181°) = 0.01746 tg(182°) = 0.03492 tg(183°) = 0.05241 tg(184°) = 0.06993 tg(185°) = 0.08749 tg(186°) = 0.1051 tg(187°) = 0.12278 tg(188°) = 0.14054 tg(189°) = 0.15838 tg(190°) = 0.17633 tg(191°) = 0.19438 tg(192°) = 0.21256 tg(193°) = 0.23087 tg(194°) = 0.24933 tg(195°) = 0.  26795 26795tg(196°) = 0.28675 tg(197°) = 0.30573 tg(198°) = 0.32492 tg(199°) = 0.34433 tg(200°) = 0.36397 tg(201°) = 0.38386 tg(202°) = 0.40403 tg(203°) = 0.42447 tg(204°) = 0.44523 tg(205°) = 0.46631 tg(206°) = 0.48773 tg(207°) = 0.50953 tg(208°) = 0.53171 tg(209°) = 0.55431 tg(210°) = 0.57735 tg(211°) = 0.60086 tg(212°) = 0.62487 tg(213°) = 0.64941 tg(214°) = 0.67451 tg(215°) = 0.70021 tg(216°) = 0.72654 tg(217°) = 0.75355 tg(218°) = 0.78129 tg(219°) = 0.80978 tg(220°) = 0.8391 tg(221°) = 0.86929 tg(222°) = 0.9004 tg(223°) = 0.93252 tg(224°) = 0.96569 tg(225°) = 1 tg(226°) = 1.03553 tg(227°) = 1.07237 tg(228°) = 1.11061 tg(229°) = 1.15037 tg(230°) = 1.19175 tg(231°) = 1.2349 tg(232°) = 1.27994 tg(233°) = 1.32704 tg(234°) = 1.37638 tg(235°) = 1.42815 tg(236°) = 1.48256 tg(237°) = 1.53986 tg(238°) = 1.60033 tg(239°) = 1.  66428 66428tg(240°) = 1.73205 | tg(241°) = 1.80405 tg(242°) = 1.88073 tg(243°) = 1.96261 tg(244°) = 2.0503 tg(245°) = 2.14451 tg(246°) = 2.24604 tg(247°) = 2.35585 tg(248°) = 2.47509 tg(249°) = 2.60509 tg(250°) = 2.74748 tg(251°) = 2.90421 tg(252°) = 3.07768 tg(253°) = 3.27085 tg(254°) = 3.48741 tg(255°) = 3.73205 tg(256°) = 4.01078 tg(257°) = 4.33148 tg(258°) = 4.70463 tg(259°) = 5.14455 tg(260°) = 5.67128 tg(261°) = 6.31375 tg(262°) = 7.11537 tg(263°) = 8.14435 tg(264°) = 9.51436 tg(265°) = 11.43005 tg(266°) = 14.30067 tg(267°) = 19.08114 tg(268°) = 28.63625 tg(269°) = 57.28996 tg(270°) = ∞ tg(271°) = -57.28996 tg(272°) = -28.63625 tg(273°) = -19.08114 tg(274°) = -14.30067 tg(275°) = -11.43005 tg(276°) = -9.51436 tg(277°) = -8.14435 tg(278°) = -7.11537 tg(279°) = -6.31375 tg(280°) = -5.67128 tg(281°) = -5.14455 tg(282°) = -4.  70463 70463tg(283°) = -4.33148 tg(284°) = -4.01078 tg(285°) = -3.73205 tg(286°) = -3.48741 tg(287°) = -3.27085 tg(288°) = -3.07768 tg(289°) = -2.90421 tg(290°) = -2.74748 tg(291°) = -2.60509 tg(292°) = -2.47509 tg(293°) = -2.35585 tg(294°) = -2.24604 tg(295°) = -2.14451 tg(296°) = -2.0503 tg(297°) = -1.96261 tg(298°) = -1.88073 tg(299°) = -1.80405 tg(300°) = -1.73205 | tg(301°) = -1.66428 tg(302°) = -1.60033 tg(303°) = -1.53986 tg(304°) = -1.48256 tg(305°) = -1.42815 tg(306°) = -1.37638 tg(307°) = -1.32704 tg(308°) = -1.27994 tg(309°) = -1.2349 tg(310°) = -1.19175 tg(311°) = -1.15037 tg(312°) = -1.11061 tg(313°) = -1.07237 tg(314°) = -1.03553 tg(315°) = -1 tg(316°) = -0.96569 tg(317°) = -0.93252 tg(318°) = -0.9004 tg(319°) = -0.86929 tg(320°) = -0.8391 tg(321°) = -0.80978 tg(322°) = -0.78129 tg(323°) = -0.75355 tg(324°) = -0.  72654 72654tg(325°) = -0.70021 tg(326°) = -0.67451 tg(327°) = -0.64941 tg(328°) = -0.62487 tg(329°) = -0.60086 tg(330°) = -0.57735 tg(331°) = -0.55431 tg(332°) = -0.53171 tg(333°) = -0.50953 tg(334°) = -0.48773 tg(335°) = -0.46631 tg(336°) = -0.44523 tg(337°) = -0.42447 tg(338°) = -0.40403 tg(339°) = -0.38386 tg(340°) = -0.36397 tg(341°) = -0.34433 tg(342°) = -0.32492 tg(343°) = -0.30573 tg(344°) = -0.28675 tg(345°) = -0.26795 tg(346°) = -0.24933 tg(347°) = -0.23087 tg(348°) = -0.21256 tg(349°) = -0.19438 tg(350°) = -0.17633 tg(351°) = -0.15838 tg(352°) = -0.14054 tg(353°) = -0.12278 tg(354°) = -0.1051 tg(355°) = -0.08749 tg(356°) = -0.06993 tg(357°) = -0.05241 tg(358°) = -0.03492 tg(359°) = -0.01746 tg(360°) = 0 |
Площадь треугольника можно посчитать самостоятельно по формулам, или воспользоваться для этого онлайн калькулятором. В рассмотренном материале приведены как формулы и таблицы синусов, тангенсов, так и калькуляторы с возможностью расчета площади 21 способом.
В рассмотренном материале приведены как формулы и таблицы синусов, тангенсов, так и калькуляторы с возможностью расчета площади 21 способом.
Площадь треугольника | Онлайн калькулятор
Площадь треугольника — формулы и калькулятор онлайн
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали 21 калькулятор для нахождения площади любого треугольника — равнобедренного, равностороннего, прямоугольного или обыкновенного.
Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулами площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
— Формула для нахождения площади треугольника через основание и высоту:
где a — основание треугольника, h — высота треугольника.
— Формула для нахождения площади треугольника по формуле Герона (если известны 3 стороны):
где a, b, c — стороны треугольника, p — полупериметр треугольника.
— Формула для нахождения площади треугольника через 2 стороны и угол:
где a, b — стороны треугольника, α — угол между ними.
— Формула для нахождения площади треугольника через вписанную окружность и стороны:
где p — полупериметр треугольника, r — радиус вписанной окружности, a, b, c — стороны треугольника.
— Формула для нахождения площади треугольника через описанную окружность и стороны:
где a, b, c — стороны треугольника, R — радиус описанной окружности.
— Формула для нахождения площади треугольника через сторону и 2 прилежащих угла:
где a — сторона треугольника, α и β — прилежащие углы, γ — противолежащий угол.
Площадь прямоугольного треугольника
— Формула для нахождения площади прямоугольного треугольника по двум сторонам:
где a, b — стороны треугольника.
— Формула Герона для прямоугольного треугольника выглядит так:
где a, b — катеты треугольника, p — полупериметр прямоугольного треугольника/
— Формула для нахождения площади прямоугольного треугольника по вписанной окружности:
где e и d — отрезки на гипотенузе.
— Формула для нахождения площади прямоугольного треугольника по радиусу вписанной окружности и гипотенузе:
где c — гипотенуза треугольника, r — радиус вписанной окружности.
— Формула для нахождения площади прямоугольного треугольника по гипотенузе и острому углу:
где c — гипотенуза треугольника, α — любой из прилегающих острых углов.
— Формула для нахождения площади прямоугольного треугольника по катету и прилежащему углу:
где a — катет треугольника, α — прилежащий угол.
Площадь равнобедренного треугольника
— Формула площади равнобедренного треугольника через основание и сторону:
где a — боковая сторона треугольника, b — основание треугольника.
— Формула площади равнобедренного треугольника через основание и угол между боковыми сторонами:
где b — основание треугольника, α — угол между боковыми сторонами.
— Формула площади равнобедренного треугольника через боковые стороны и угол между ними:
где a — боковая сторона треугольника, α — угол между боковыми сторонами.
— Формула площади равнобедренного треугольника через основание и высоту:
где b — основание треугольника, h — высота, проведенная к основанию.
— Формула площади равнобедренного треугольника через основание и угол:
где a — боковая сторона треугольника, b — основание треугольника, α — угол между основанием и стороной.
Площадь равностороннего треугольника
— Формула площади равностороннего треугольника через сторону:
где a — сторона треугольника.
— Формула площади равностороннего треугольника через высоту:
где h — высота треугольника.
— Формула площади равностороннего треугольника через радиус вписанной окружности:
где r — радиус вписанной окружности.
— Формула площади равностороннего треугольника через радиус описанной окружности:
где R — радиус описанной окружности.
Полезен ли материал?
#Калькуляторы#Математика
Площадь треугольника
На данной странице вы сможете не только ознакомиться со всеми формулами нахождения площади треугольника, но и воспользоваться достаточно удобными калькуляторами и рассмотреть примеры решения задач. Это очень рационально и полезно для того, чтобы вспомнить уже давно забывшиеся формулы и сверить свой ответ с ответом необходимого калькулятора.
Площадь треугольника по основанию и высоте
Формула площади треугольника по основанию и высоте выглядит, как
$S = \frac{1}{2}\cdot a \cdot h$ , где
$S$ — площадь,
$a$ — основание,
$h$ — высота.
Рассмотрим наглядно на примере, в котором используется данная формула, как просто и быстро самостоятельно или с помощью калькулятора вычислить площадь в одно действие по данным элементам.
Пример 1
Дано: основание — $6$, высота — $10$.
Найти: площадь треугольника.
Решение:
$S = \frac12 \cdot 6 \cdot 10$
$S = 30$.
Ответ:
$S = 30$.
Площадь треугольника по двум сторонам и углу между ними
Формула площади треугольника по двум сторонам и углу между ними выглядит следующим образом:
$S = \frac12 \cdot a \cdot b \cdot \sin (α)$, где
$S$ — площадь треугольника,
$a$ — сторона номер 1,
$b$ — сторона номер 2,
$α$ — угол между сторонами 1 и 2.
По радиусу описанной окружности и трем сторонам
Площадь треугольника по радиусу описанной окружности и трем сторонам вычисляется по следующей формуле:
$S = \frac{a \cdot b \cdot c}{4 \cdot R}$, где
$S$ — площадь треугольника,
$a, b, c$ — стороны треугольника,
$R$ — радиус описанной около данного треугольника окружности. 2$.
2$.
Площадь треугольника по формуле Герона
Площадь треугольника по формуле Герона вычисляется следующим образом:
$S = \sqrt{p \cdot (p — a) \cdot (p — b) \cdot (p — c)} $, где
$S$ — площадь треугольника,
$a, b, c$ — стороны треугольника,
$p$ — полупериметр треугольника, вычисляемый по формуле:
$p = \frac{a + b + c}{2}$.
Площадь прямоугольного треугольника по формуле Герона
Рассчитать площадь прямоугольного треугольника по формуле Герона можно следующим образом:
$S = (p — a) \cdot (p — b)$, где
$S$ — площадь треугольника,
$a$ — первый катет,
$b$ — второй катет,
$p$ — полупериметр данного треугольника, вычисляемый по формуле:
$p = \frac{a + b + c}{2}$.
Калькулятор треугольника – площадь в квадратных футах
Что такое треугольник?
Треугольник – это особая замкнутая форма или многоугольник, который имеет три вершины, три стороны и три угла. Вершина — это точка, в которой встречаются две линии или стороны. Поскольку у треугольника три стороны, у него также есть три вершины a, b и c. Сумма внутренних углов всегда равна 180°. Треугольники можно классифицировать по длине стороны и внутреннему углу.
Поскольку у треугольника три стороны, у него также есть три вершины a, b и c. Сумма внутренних углов всегда равна 180°. Треугольники можно классифицировать по длине стороны и внутреннему углу.
Например, треугольник с равными длинами сторон может быть идентифицирован как равносторонний треугольник или треугольник, ни одна из линий / сторон, имеющих одинаковую длину, не является разносторонним треугольником.
Треугольники, определяемые по длинам сторон:
Треугольники, определяемые по углам:
Типы треугольников:
Треугольники можно разделить на 6 различных типов в зависимости от длины их сторон и углов.
Остроугольный треугольник:
Треугольник, у которого все три угла меньше 90°.
∠ABC, ∠ACB и ∠BAC — острые углы.Прямоугольный треугольник:
Треугольник, у которого один угол равен 90°.
∠ABC = один прямой угол.Тупоугольный треугольник:
В тупоугольном треугольнике любой из треугольников больше 90°.

∠АВСРавносторонний треугольник:
Когда длины всех сторон треугольника равны. Он называется равносторонним.
Здесь АВ = ВС = СА.Равнобедренный треугольник:
Треугольник, у которого хотя бы две стороны равны, является равнобедренным.
Здесь АВ = АС.Разносторонний треугольник:
Треугольник, у которого все стороны разной длины.
Факты о треугольнике:
Треугольник не может иметь более одной стороны, больше или равной 90°. Как упоминалось выше в определении треугольника, треугольник — это замкнутый путь.
Сумма всех внутренних треугольников всегда равна 180°.
Сумма длин любых двух сторон всегда больше длины третьей стороны.
Теорема Пифагора:
Теорема Пифагора — это теорема о прямоугольном треугольнике. Согласно теореме Пифагора, квадрат длины по стороне гипотенузы (наибольшая сторона) равен сумме двух других сторон. Любой треугольник, удовлетворяющий этому условию, является прямоугольным.
Любой треугольник, удовлетворяющий этому условию, является прямоугольным.
Уравнение Пифагора:
a 2 + b 2 = c 2
ПРИМЕР: Учитывая a = 5, c = 7, найдите b:
5 2 + b 2 = 7 2
25 + b 2 = 49
b 2 = 24 => b = 4,8989
Закон синусов:
синус противолежащего ему угла постоянный. Закон синусов помогает найти любую недостающую длину или угол треугольника. Например: если известна длина стороны а и углы А и В. Мы можем легко найти длину стороны b, подставив данную информацию в формулы ниже:
В случае, когда известны все длины сторон, углы треугольников можно вычислить следующим образом:
Как вычислить площадь треугольника?
Существует множество способов вычисления площади треугольника. Выбор метода зависит от имеющейся информации. Самый распространенный метод определения площади треугольника:
В случае, когда известны длины всех сторон, углы треугольников можно вычислить следующим образом:
В сценарии, где две стороны и угол дано. Небольшое изменение в формуле можно сделать, чтобы получить площадь треугольника. Формула будет:
Небольшое изменение в формуле можно сделать, чтобы получить площадь треугольника. Формула будет:
Существует еще один метод расчета площади треугольника по формуле Герона, требующий знания всех трех сторон: вершины треугольника к середине противоположной стороны. Треугольник имеет три медианы, которые пересекаются в центре треугольника.
Центроид представляет собой среднее арифметическое положение всех точек треугольника.
Ma = медиана стороны a
Mb = медиана стороны b
Mc = медиана стороны c
Медиана каждой стороны может быть рассчитана следующим образом: внутри треугольника, который касается всех трех сторон треугольника, то есть вписанной окружности. Центром этой окружности является точка, в которой пересекаются две биссектрисы угла. Он перпендикулярен любой из трех сторон треугольника.
Формула для расчета радиуса:
Inradius = Площадь / s
Где s = a + b + c / 2
Где a, b и c — длины сторон треугольника.
Радиус окружности:
В случае треугольника радиус описанной окружности — это радиус окружности, проходящей через все вершины треугольника. Центр этой окружности называется центром описанной окружности. Центр окружности — это точка, в которой пересекаются все серединные перпендикуляры каждой стороны треугольника.
Формула для радиуса описанной окружности:
Радиус окружности = a / 2 * sin(A)
Где а — длина стороны, а А — угол, противоположный стороне а.
Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и соответствующие им противоположные углы.
Чтобы понять, как рассчитать квадратные метры, мы должны сначала начать с определения площади. Площадь – это размер двумерной поверхности. Площадь треугольника – это пространство, содержащееся внутри его трех сторон. Чтобы узнать площадь треугольника, нам нужно знать длины трех его сторон. Стороны должны быть измерены в футах (футах) для расчета квадратных метров и, при необходимости, преобразованы в дюймы (дюймы), ярды (ярды), сантиметры (см), миллиметры (мм) и метры (м).
Формула:
Площадь треугольника = (1/4) x √ [ (a+b+c) x (b+c-a) x (c+a-b) x (a+b-c)]
Длина треугольника сторона a (раскрывающаяся футы, дюймы, ярды, см, мм, м)
Длина стороны b (раскрывающаяся футы, дюймы, ярды, см, мм, м)
Длина стороны c (раскрывающаяся футы, дюймы, ярды , см, мм, м)
Ответ = ((1/4) x √ [ (a+b+c) x (b+c-a) x (c+a-b) x (a+b-c) ])
Сокращения единиц площади: футов 2 , дюймов 2 , ярдов 2 , см 2 , мм 2 , м 2
Где он нужен в повседневной жизни?
Наш Калькулятор Треугольника поможет вам рассчитать площадь, необходимую для треугольника. Хотя мы охватываем наиболее распространенный вариант использования, например. Вы можете знать две стороны и угол между ними, но хотели бы знать недостающую длину стороны. мы также недавно добавили калькулятор прямоугольного треугольника, который также часто используется в сценарии, где вы знаете две длины сторон треугольника, одна из которых составляет 90 ° градусов.
Какие размеры вам нужны?
Вам необходимо знать длину трех сторон треугольника в футах (футах), дюймах (дюймах), ярдах (ярдах), сантиметрах (см), миллиметрах (мм) или метрах (м).
Что можно рассчитать с помощью этого инструмента?
Вы можете рассчитать площадь треугольника в квадратных футах, квадратных дюймах, квадратных ярдах, квадратных сантиметрах, квадратных миллиметрах и квадратных метрах. Да, наш инструмент такой классный.
Наш калькулятор дает возможность рассчитать точную стоимость материалов. Все, что вам нужно сделать, это ввести цену за единицу площади и вуаля, у вас есть общая стоимость материалов в один клик!
Коэффициенты пересчета:
Для преобразования квадратных футов, квадратных дюймов, квадратных ярдов, квадратных сантиметров, квадратных миллиметров и квадратных метров вы можете использовать следующую таблицу преобразования.
| Квадратные футы в квадратные ярды | умножьте футы 2 на 0,11111, чтобы получить ярды 2 |
| Квадратные футы в Квадратные метры | умножьте футы 2 на 0,092903, чтобы получить м 2 |
| Квадратные ярды в квадратные футы | умножьте ярды 2 на 9, чтобы получить футы 2 |
| Квадратные ярды в Квадратные метры | умножить ярды 2 на 0,836127, чтобы получить м 2 |
| Квадратные метры в Квадратные футы | умножьте м 2 на 10,7639, чтобы получить футы 2 |
| Квадратные метры в Квадратные ярды | умножить m 2 на 1,19599 чтобы получить ярдов 2 |
| Квадратные метры в квадратные миллиметры | умножьте значение m 2 на 1000000, чтобы получить мм 2 |
| Квадратные метры в Квадратные сантиметры | умножьте значение m 2 на 10 000, чтобы получить см 2 |
| Квадратные сантиметры в Квадратные метры | умножьте значение см 2 на 0,0001, чтобы получить мм 2 |
| Квадратные сантиметры в Квадратные миллиметры | умножьте значение см 2 на 100, чтобы получить мм 2 |
| Квадратные миллиметры в квадратные сантиметры | умножьте значение мм 2 на 0,000001, чтобы получить см 2 |
| Квадратные миллиметры в Квадратные метры | умножьте значение мм 2 на 1000000, чтобы получить m 2 |
Калькулятор теорем треугольника
Фигура треугольника
Угол-Сторона-Угол (ASA)
А = угол А
B = угол B
С = угол С
а = сторона а
б = сторона б
с = сторона с
P = периметр
с = полупериметр
К = площадь
r = радиус вписанной окружности
R = радиус описанной окружности
Использование калькулятора
Каждый вариант расчета, показанный ниже, имеет подпункты, перечисляющие последовательность методов, используемых в этом калькуляторе для расчета неизвестных значений угла и стороны, включая
Сумма углов треугольника, закон синусов и
Закон косинусов. Это НЕ ЕДИНСТВЕННЫЕ последовательности, которые вы можете использовать для решения подобных проблем.
Это НЕ ЕДИНСТВЕННЫЕ последовательности, которые вы можете использовать для решения подобных проблем.
- См. также тригонометрические калькуляторы:
- Калькулятор закона косинусов
- Калькулятор закона синусов
Решение теорем о треугольниках
AAA is Angle, Angle, Angle
Указание трех углов треугольника не однозначно определяет один треугольник. Таким образом, задание двух углов треугольника позволяет вычислить только третий угол.
Зная размеры двух углов треугольника, вы можете вычислить размер третьего угла. Сумма будет равна 180° или π радиан.
C = 180° — A — B (в градусах)
C = π — A — B (в радианах)
AAS — Угол, Угол, Сторона
Дан размер 2 углов и 1 стороны, противоположной одному из по заданным углам можно вычислить размеры оставшегося 1 угла и 2 сторон.
используйте Правило суммы углов, чтобы найти другой угол, затем
Используйте закон синусов, чтобы решить для каждой из двух других сторон.
ASA is Angle, Side, Angle
Зная размер 2 углов и размер стороны, которая находится между этими 2 углами, вы можете рассчитать размеры оставшегося 1 угла и 2 сторон.
используйте правило суммы углов, чтобы найти другой угол, затем
используйте закон синусов, чтобы решить для каждой из двух других сторон.
ASS (или SSA) — это угол, сторона, сторона
Учитывая размер двух сторон (a и c, где a < c) и размер угла A, который не находится между этими двумя сторонами, вы можете рассчитать размеры оставшихся 1 стороны и 2 углов в зависимости от следующих условий.
Для A ≥ 90° (A ≥ π/2) :
Если a ≤ c нет возможных треугольников
Пример:
Если a > c существует 1 возможное решение
- используйте закон синусов для решения угла C
- используйте правило суммы углов, чтобы найти другой угол, B
- использовать закон синусов для решения последней стороны, b
- Пример:
Для A < 90° (A < π/2) :
Если a ≥ c существует 1 возможное решение
- используйте закон синусов, чтобы найти угол C
- используйте правило суммы углов, чтобы найти другой угол, B
- использовать закон синусов для решения последней стороны, b
- Пример:
Если a < c , у нас есть 3 возможных ситуации. «Если sin(A) < a/c , есть два возможных треугольника, удовлетворяющих заданным условиям. Если sin(A) = a/c , есть один возможный треугольник. Если sin(A) > a/c , возможных треугольников нет.» [1]
«Если sin(A) < a/c , есть два возможных треугольника, удовлетворяющих заданным условиям. Если sin(A) = a/c , есть один возможный треугольник. Если sin(A) > a/c , возможных треугольников нет.» [1]
sin(A) < a/c , возможны два треугольника
найти 2 возможных значения третьей стороны b = c*cos(A) ± √[ a 2 — c 2 sin 2 (A) ] [1]
для каждого набор решений, используйте закон косинусов, чтобы решить для каждого из двух других углов
представить 2 полных решения
Пример:
sin(A) = a/c , есть один возможный треугольник
используйте Закон синусов для нахождения угла C
используйте правило суммы углов, чтобы найти другой угол, B
используйте закон синусов, чтобы найти последнюю сторону, b
Пример:
sin(A) > a/c , возможных треугольников нет
Уведомление об ошибке: sin(A) > a/c, поэтому нет ни решений, ни треугольника!
Пример:
SAS — сторона, угол, сторона
Зная размер двух сторон (c и a) и размер угла B между этими двумя сторонами, вы можете рассчитать размеры оставшихся 1 стороны и 2 углов. .
.
используйте закон косинусов, чтобы найти оставшуюся сторону, b
определите, какая сторона, a или c, наименьшая, и используйте закон синусов, чтобы найти размер противоположного угла, A или C соответственно. [2]
используйте правило суммы углов, чтобы найти последний угол .
Используйте закон косинусов, чтобы найти углы. Вы также можете использовать правило суммы углов, чтобы найти окончательный угол, когда вы знаете 2 из них.
Сумма углов треугольника
В градусах A + B + C = 180°
В радианах A + B + C = π треугольника, противоположного углам А, В и С соответственно; тогда закон синусов гласит:
a/sin A = b/sin B = c/sin C
Решение, например, для угла, A = sin -1 [ a*sin(B) / b ]
Закон косинусов
Если a, b и c — длины катетов треугольника, противоположных углам A, B и C соответственно; тогда закон косинусов гласит:
a 2 = c 2 + b 2 — 2bc cos A, решение для cos A, cos A = ( b 2 + c 2 — c 1 2
b 2 = a 2 + c 2 — 2ca cos B, решение для cos B, cos B = ( c 2 + a 2 — b 2 )
c 2 = b 2 + a 2 — 2ab cos C, решение для cos C, cos C = ( a 2 + б 2 — в 2 ) / 2аб
Решение, например, для угла, A = cos -1 [ ( b 2 + c 2 — a 2 ) / 2bc ]
Другие характеристики треугольника
Периметр треугольника, P = a + b + c
Полупериметр треугольника, s = 0,5 * (a + b + c)
Площадь треугольника, K = √[ s*(s-a)* (s-b)*(s-c)]
Радиус вписанной окружности в треугольник, r = √[ (s-a)*(s-b)*(s-c) / s ]
Радиус описанной окружности вокруг треугольника, R = (abc) / (4K)
Ссылки/дополнительная литература
[1]
Вайсштейн, Эрик В. «Теорема ASS». Из MathWorld — Веб-ресурс Wolfram.
Теорема АСС.
«Теорема ASS». Из MathWorld — Веб-ресурс Wolfram.
Теорема АСС.
[2] Математика — это весело — Решение треугольников SAS
Цвиллингер, Даниэль (главный редактор). Стандартные математические таблицы и формулы CRC, 31-е издание Нью-Йорк, штат Нью-Йорк: CRC Press, с. 512, 2003.
Вайсштейн, Эрик В. «Свойства треугольника». Из MathWorld — Веб-ресурс Wolfram. Свойства треугольника.
Математика — это весело в Решение треугольников.
Расчет площади треугольника Герона
Расчет площади треугольника ГеронаДжеймс П. Дильдине, 19 лет99 Треугольники — увлекательные математические темы. Давайте рассмотрим некоторые аспекты треугольников в интерактивная мода. Этот сайт проведет вас через некоторые исторические исследования, некоторые интерактивные мероприятия, как а также некоторые интригующие связи в математике. Треугольник в типичной плоской геометрии описывается как трехсторонняя фигура или многоугольник, сумма внутренних углов которого равна равен 180 градусам. периметр треугольника есть сумма всех три стороны 1. Поэкспериментируйте с этим файл. Площадь треугольника весьма интересна. Часто это будет представлен Площадь=(1/2) x Основание x Высота . Где высота
высота, проведенная от основания до противоположного угла. Эта формула приписывается Герону Александрийскому, но может восходит к Архимеду. Эта формула представлена Площадь=SQRT(s(s-a)(s-b)(s-c)), , где s=(a+b+c)/2 или периметр/2. | ||||
Эту формулу можно использовать, когда высота неизвестна и его также можно использовать для изучения взаимосвязей между периметр и площадь треугольника. 2. Поэкспериментируйте с этим
файл. Приглашаю вас поэкспериментировать со сторонами треугольники, чтобы исследовать эти отношения. Используйте следующее ссылки для загрузки MS Excel файл, который вычисляет площадь треугольника после сторон вводятся, а также попробуйте файл Java, который показывает связь, которую формула Герона имеет с компьютером расчетная площадь (т.е. такая, о которой мы понятия не имеем, как она рассчитано-хороший тест, чтобы убедиться в точности техники), и типичная формула (1/2) * Основание * Высота. | ||||
Также может быть хорошим упражнением задать вопросы о
допустимость некоторых сторон треугольника. Excel-файл
может не дать правильных расчетов до определенного момента. Немного
расчеты тоже могут не иметь смысла. Это может привести к
исследование теоремы о неравенстве треугольника. Вы можете
установить диапазон, в котором третья сторона треугольника должна
упасть, если вам даны две другие стороны и вы можете проверить
это через файл excel и файл Java. СУММА ДВУХ СТОРОН ДОЛЖНА БЫТЬ БОЛЬШЕ, ЧЕМ ДЛИНА ОСТАВШЕЙСЯ ТРЕТЬЕЙ СТОРОНЫ. ИЛИ (со сторонами A,B,C):
Итак, может ли быть треугольник со сторонами 5, 12, 16? Как насчет 5, 12, 13? Как это выглядит? Интересно, что формула цапли тоже приводит нас к результату где мы можем вычислить высоту треугольника. С основание c и высота h высота равна,
Больше тем для размышлений. 1. Представьте себе треугольник с основанием и вершиной, не на основании, а на линии, параллельной этому основанию. Что бы произойдет с периметром и площадью этого треугольника, если база осталась прежней, но вершина была перетащена все время линия параллельна основанию? Вот действие для пытаться… 2. Можешь начать доказательство формулы Герона? это довольно приятно пройти и очень провокационно. Я призываю вас изучить его по крайней мере в этом текст, который я отсканировал. | ||||
Java-файл | ||||
Файл Excel | ||||
Файл блокнота | ||||
Файл калькулятора TI-83 | ||||
Доказательство формулы Герона | ||||
Пожалуйста, попробуйте ввести различные длины сторон
треугольник. Электронная почта Джеймс П. Дилдин, [email protected] с любым вопросы |
Калькулятор площади треугольника
Введите информацию
Решить для Выберите optionAreaBase «b»HeightSide «a»Side «c»Gamma «Y»Perimeter
Дано
Результат
Как пользоваться калькулятором площади треугольника?
С помощью этого калькулятора можно найти различные значения, относящиеся к треугольнику. Выполните следующие шаги:
- Выберите значение, которое вы хотите рассчитать, из раскрывающегося списка » Решить для «.
- Выберите набор значений, которые вы уже использовали для расчета, из списка » Учитывая «.
- Введите значения.
- Нажмите « Вычислить «.

Получить Индивидуальный калькулятор Для вашего веб-сайта
Получить сейчас
ИЛИ
Получить Калькулятор площади треугольника Для вашего веб-сайта
Получить сейчас
Содержание:
| 1 | Что такое треугольник? |
| 2 | Формула площади треугольника |
| 3 | Как вычислить площадь треугольника? |
| 4 | Пример 1: |
Калькулятор площади треугольника, также известный как калькулятор sss, поможет вам рассчитать площадь треугольника. Калькулятор не только площади, но и площади треугольника также дает вам возможность решить уравнение треугольника для любого значения, например:
• Основание b
• Площадь A
• Стороны
• Гамма γ
• Параметр
В посте ниже вы узнаете, как найти площадь треугольника, как вычислить длину треугольника и формулу площади треугольника.
Используя этот калькулятор прямоугольного треугольника, вычислите площадь, основание или высоту треугольника. Вы можете рассчитать центроид треугольника, используя наш калькулятор центроида треугольника.
Что такое треугольник?
Согласно Википедии
«Треугольник — это многоугольник с тремя ребрами и тремя вершинами. Это одна из основных фигур в геометрии. Треугольник с вершинами A, B и C обозначается через ∆ ABC».
Далее в нем говорится, что:
«В евклидовой геометрии любые три точки, если они не лежат на одной прямой, определяют уникальный треугольник и одновременно уникальную плоскость».
На приведенной ниже диаграмме A, B и C – это ребра, а a, b и c – вершины треугольника ABC.
Существует несколько типов треугольников, вот некоторые из них:
• Равносторонний
• Равнобедренный
• Прямоугольный треугольник
• Разносторонний
• Тупоугольный
Формула площади треугольника
Вот список различных методов вычисления площади треугольника с использованием различных уравнений.
• Когда известны основание и высота
Если известны основание b и высота h треугольника, его площадь можно рассчитать по следующей формуле:
Площадь треугольника = ½ × b × h
• Когда три стороны известны (ССС)
Формулу Герона можно использовать, если известны все три стороны треугольника.
Площадь = 0,25 × √ ((a + b + c) × (-a + b + c) × (a — b + c) × (a + b — c))
• Когда две стороны и угол известный (SAS)
Когда известны две стороны треугольника и угол между ними, Используйте следующее уравнение, чтобы найти площадь,
Площадь = 0,5 × a × b × sin (γ)
• Когда два угла и a сторона известна (ASA)
Если известны два угла и линия между ними, то площадь треугольника можно вычислить, используя вышеуказанное 45 45 90 калькулятор треугольника или приведенное ниже уравнение.
Площадь = a² × sin (β) × sin (γ) / (2 × sin (β + γ))
Примечание. Приведенные выше уравнения содержат несколько тригонометрических значений. Вы можете использовать наш научный калькулятор для оценки тригонометрических значений.
Вы можете использовать наш научный калькулятор для оценки тригонометрических значений.
Как вычислить площадь треугольника?
Чтобы найти площадь треугольника, выполните следующие действия:
• Определите и запишите данные значения.
• Запишите формулу площади треугольника.
• Подставьте данные значения и рассчитайте площадь.
Пример 1:
Вычислите площадь треугольника с основанием 5 см и высотой 9 см.
Решение:
Шаг 1: Определите и запишите указанные значения.
b = 5 см, h = 9 см
Шаг 2: Запишите формулу площади треугольника.
Площадь треугольника = ½ × b × h
Шаг 3: Подставьте данные значения и рассчитайте площадь.
Площадь треугольника = ½ × 5 × 9
Площадь треугольника = 22,5 см2
Значит, площадь этого треугольника равна 22,5 см2.
Рейтинги пользователей
- Всего отзывов 1
- Общий рейтинг 5/5
- Звезды
Спасибо! Для вашего рассмотрения
Ваш отзыв скоро появится.
Отправить свой отзыв Закрыть
Отзывы
Пожалуйста, заполните 1 строку
Обратная связь
Отправьте нам свой отзыв!
Нужна помощь? Вы можете связаться с нами в любое время.
Площадь треугольника – объяснение и примеры
В этой статье вы узнаете площадь треугольника и определите площадь различных типов треугольников . Площадь треугольника – это количество пространства внутри треугольника. Измеряется в квадратных единицах.
Прежде чем перейти к теме площади треугольника , давайте ознакомимся с такими терминами, как основание и высота треугольника.
Основание — сторона треугольника, которая считается основанием, а t высота треугольника — перпендикулярная линия, опущенная на его основание из вершины, противоположной основанию .
На приведенном выше рисунке пунктирными линиями показаны возможные высоты △ ABC. Обратите внимание, что каждый треугольник имеет, возможно, три высоты или высоты.
- Высота треугольника △ ABC равно h 1 , когда основание является стороной.
- Высота треугольника △ ABC равна h3 при основании AB.
- Высота треугольника △ ABC равна h 3 , когда основание равно
- Высота треугольника △ ABC может быть вне треугольника ( 1 h 49102), 1 h 49102 то же, что высота h 1 .
Из приведенных выше рисунков можно сделать следующие выводы:
- Высота треугольника зависит от его основания.
- Перпендикуляр к основанию треугольника равен высоте треугольника.
- Высота треугольника может быть вне треугольника.
Обсудив концепцию высоты и основания треугольника, давайте теперь приступим к вычислению площади треугольника.
Площадь прямоугольника нам хорошо известна, т. е. длина * ширина . Что произойдет, если мы разделим прямоугольник пополам по диагонали (разрежем пополам)? Какова будет его новостная область? Например, в прямоугольнике с основанием и высотой 6 единиц и 12 единиц соответственно площадь прямоугольника составляет 72 квадратных единицы.
Теперь, если вы разделите его на две равные половины (после деления прямоугольника пополам по диагонали), площадь двух новых фигур должна быть 36 квадратных единиц каждая. Две формы новостей представляют собой треугольники. Это означает, что если прямоугольник разрезать по диагонали на две равные половины, две новые образовавшиеся фигуры будут треугольниками, где каждый треугольник имеет площадь, равную ½ площади прямоугольника.
Площадь треугольника – это общее пространство или область, ограниченная определенным треугольником.
Площадь треугольника равна произведению основания и высоты, деленному на 2.
Стандартной единицей измерения площади являются квадратные метры (м 2 ).
Другие единицы включают:
- Квадратные миллиметры (мм 2 )
- Квадратные дюймы (в 2 )
- Квадратные километры (км 2 1 90 90)0021 Квадратные ярды.
Формула площади треугольника
Общая формула для вычисления площади треугольника:
Площадь (A) = ½ (b × h) квадратных единиц, где; A — площадь, b — основание, h — высота треугольника. Треугольники могут быть разными по своей природе, но важно отметить, что эта формула применима ко всем треугольникам. Различные типы треугольников имеют разные формулы площади.
Примечание. База и высота должны быть выражены в одних и тех же единицах измерения, т. е. в метрах, километрах, сантиметрах и т. д.
Площадь прямоугольного треугольника
Площадь треугольника = (½ × основание × высота) квадратных единиц.
Пример 1
Найдите площадь прямоугольного треугольника, основание которого равно 9 м, а высота 12 м.
Решение
a = ¹/₂ × основание × высота
= ¹/₂ × 12 ×
= 54 см²
Пример 2
. 70 см и 8 м соответственно. Чему равна площадь треугольника?
Раствор
A = ½ × основание × высота
Здесь 70 см и 8 м. Вы можете выбрать работу с см или м. Давайте поработаем в метрах, заменив 70 см на метры.
Разделите 70 см на 100.
70/100 = 0,7 м.
⇒ a = (½ × 0,7 × 8) M 2
⇒ a = (½ x 5,6) M 2
⇒ a = 2,8 м 2
Область Isosceles Triangle
ANHAR81
. равнобедренный треугольник — это треугольник, у которого две стороны равны, а также два угла равны. Формула площади равнобедренного треугольника:
⇒A = ½ (основание × высота).
Если высота равнобедренного треугольника не указана, то для ее нахождения используется следующая формула:
Высота = √ (a 2 − b 2 /4)
Где;
b = основание треугольника
a = длина двух равных сторон.
Следовательно, площадь равнобедренного треугольника может быть;
⇒ A = ½ [√ (a 2 − b 2 /4) × b]
Кроме того, площадь равнобедренного прямоугольного треугольника определяется как: 9Пример 3
Решение
⇒A = ½ × основание × Высота
⇒ 1/2 × 12 × 17
⇒ 1/2 × 204
= 102 мм 2
7 Пример 40080 2
16. Пример 40080 2
. Найдите площадь равнобедренного треугольника с длинами сторон 5м и 9см.м Решение Пусть основание b = 9 м, a = 5 м. ⇒ a = ½ [√ (A 2 — B 2 /4) × B] ⇒ ½ [√ (5 2 — 2 /4) × 9] = 9.81 m 2 Равносторонний треугольник – это треугольник, у которого три стороны равны и три внутренних угла равны. Площадь равностороннего треугольника: A = (a 2 √3)/4 Где а = длина сторон. Пример 5 Вычислите площадь равностороннего треугольника со стороной 4 см. Решение ⇒ a = (A 2 /4) √3 ⇒ (4 2 /4) √3 ⇒ (16/4) √3 = 4√3 СМ. 2 Пример 6 Найдите площадь равностороннего треугольника, периметр которого равен 84 мм. Решение Периметр равностороннего треугольника = 3а. ⇒ 3a = 84 мм ⇒ a = 84/3 ⇒ a = 28 мм Область = (A 2 /4) √3 ⇒ (28 2 /4) √3 ⇒ (28 2 /4) √3 ⇒ (28 2 /4) √3 = 196√3 мм 2 Разносторонний треугольник — это треугольник с 3 различными длинами сторон и 3 различными углами. Площадь разностороннего треугольника можно вычислить по формуле Герона. , где «p» — полупериметр, а a, b, c — длины сторон. ⇒ p = (a + b + c) / 2 Пример 7 Решение ⇒ p = (a + b + c) / 2 Косой треугольник определяется как любой треугольник без прямого угла (угол 90 градусов).
Косоугольные треугольники используют набор формул, уникальный для прямоугольных треугольников. С помощью калькулятора косоугольного треугольника можно рассчитать все значения, если либо
1 сторона и любые два других значения известны. Получите значения треугольника и формулы для: Закон синусов и закон косинусов необходимы для процесса вычислений. Эти формулы показаны ниже. Просто введите длину одной стороны и любые два других значения, и наш калькулятор вернет отсутствующие значения в точном и десятичном виде в дополнение к пошаговому процессу расчета для каждого из этих отсутствующих значений. Если вам нужно найти недостающие стороны и углы треугольника с углом А, равным 34 градусам, углом В, равным 58 градусам, и стороной а, равной длине 16, вы
начнет решать проблему, определив значение, которое нужно найти в первую очередь. Поскольку две угловые меры уже известны, третий угол будет самым простым и быстрым.
рассчитать. Чтобы найти третий угол (угол C), вы можете применить закон, согласно которому все треугольники в сумме дают 180 градусов. этот процесс показан ниже: 9{\circ } \text{(в простейшей форме)} Чтобы найти значения двух других сторон, сторон b и c, необходимо использовать закон синусов. Расчетный процесс нахождения этих значений
показано ниже: \frac{\text{sideA}}{\sin (\text{angleA})}=\frac{\text{sideB}}{\sin (\text{angleB})}=\frac {\ text {sideC}} {\ sin (\ text {angleC})} \ text {sideB} = \ frac {(16) \ sin ((58))} {\ sin ((34))} \text{sideB}=\frac{16\sin (58)}{\sin (34)} \text{(в точной форме)} 24. \text{(в десятичной аппроксимации)} \text{sideC}=\frac{\text{sideA}\cdot \sin (\text {angleC})}{\sin (\text{angleA})} \text{sideC}=\frac{(16)\sin ((88))}{\sin ((34))} \ text{sideC}=\frac{16\sin (88)}{\sin (34)} \text{(в форме точного значения)} 28,5952363362601811 \text{(в форме десятичной аппроксимации)} Теперь, когда все стороны и углы треугольника вычислены, можно вычислить площадь и периметр треугольника.
Процесс расчета площади и периметра показан ниже: \text{area}=\frac{1}{2}\cdot \text{sideA}\cdot \text{sideB}\cdot \sin (\text{angleC}) \text{area}=\ frac{1}{2}(16)(\frac{16\sin (58)}{\sin (34)})\sin ((88)) \text{area}=\frac{128\sin (58)\sin (88)}{\sin (34)} \text{(в простейшей форме)} 194.0010858728679993 \text{(в десятичной аппроксимации)} Если даны один угол треугольника и две стороны, возможно существование двух треугольников при одинаковых размерах. \text{(в десятичном приближении)} Так как это правда, что синус дополнительных углов имеет одинаковые значения, и функция sin использовалась для нахождения угла B, вы должны проверить, может ли существовать другой треугольник с
угол А, равный 19 градусам, и угол В, равный 18 градусам. Дополнительные углы — это углы, сумма которых равна 180 градусам. Если сумма дополнения угла B
и угол А меньше 180 градусов, возможно существование двух треугольников. Чтобы проверить это, вы можете выполнить следующий процесс: 9{-1}(18,5621602382506538))+(19)<180 180,43783976174936>180 Так как сумма дополнения угла B
и угол А больше 180 градусов, существование другого треугольника невозможно. Площадь равностороннего треугольника

Площадь разностороннего треугольника
Формула Герона дается формулой;
⇒ Площадь = √ {p (p — a) (p — b) (p — c)}
Вычислите площадь треугольника, стороны которого равны 18 мм, 20 мм и 12 мм.
Подставьте значения a, b и c.
⇒ p = (12 + 18 + 20) / 2
⇒ p = 50/2
⇒ p = 25
⇒ Площадь = √ {p (p – a) (p – b) (p – c)}
= √ {25 x (25 – 12) x (25 – 18) x (25 – 20)}
= √ (25 x 13 x 7 x 5)
= 5√455 мм 2 9
Калькулятор треугольника
(любой треугольник): Получите помощь по Trig здесь


Решение треугольников с двумя углами и одной стороной
 26491726609088
26491726609088 Решение треугольников с одним углом и две стороны (закон синусов)
 Например, если сказали найти пропавшего
стороны и углы треугольника, если угол А равен 19\circ
Например, если сказали найти пропавшего
стороны и углы треугольника, если угол А равен 19\circ

 Для непрямоугольных треугольников катетов не существуют.
Для непрямоугольных треугольников катетов не существуют.