» Исследование некоторых кривых в полярной системе координат.»
Слайд 1
XXII городская конференция учащихся «Виват, молодая наука!» «Исследование некоторых кривых в полярной системе координат.» Выполнил: Ученик 11 класса «Б» МБОУ «СОШ №14» Норман Роман Михайлович Научный руководитель – Козлова Наталья Борисовна
Слайд 2
Цель работы: Изучение принципов построения графиков в полярной системе координат. Задачи: — организовать поиск и отбор материала по теме; — научиться строить графики в полярной системе координат, — сравнить полярную и декартовую прямоугольную системы координат; — научиться переводить график кривой из одной системы в другую; провести собственное исследование
Слайд 3
Объект исследования: полярная система координат. Предмет исследования: элементарные преобразования кривых, заданных в ПСК на примере кардиоиды. Методы исследования: — обзор литературы по теме; — анализ различных систем координат; — анкетирование одноклассников; — эксперимент.
Гипотеза: Некоторые элементарные преобразования кривых в ПСК будут соответствовать элементарным преобразованиям в ДСК.
Слайд 4
При изучении уравнений с двумя переменными, графического способа решения систем уравнений возникла необходимость построения графиков уравнений с двумя переменными типа 2х+3 y =5, x 2 + y 2 =9, x y =4 и т.п. Особый интерес вызвали графики уравнений ( x 2 + y 2 ) 2 =2( x 2 — y 2 ). В декартовой системе координат это построение будет весьма сложным. В полярной же системе координат эта процедура намного упрощается. Кроме непосредственного интереса эта тема привлекает внимание ещё и тем, что найдёт свое приложение в «Интегральном исчислении». Актуальность:
Слайд 5
Существуют разные версии о том, как и когда формально ввели полярную систему координат. Ещё в древности намёки на полярные координаты появлялись у греческого астронома Гиппарха, у Архимеда. Динострат использовал их в неявном виде при исследовании квадратрисы в IV веке до н.э . Введение термина «полярные координаты» приписывают Грегорио Фонтана.
Чёткое представление об определении точки на плоскости при помощи полярных координат имеется у Л. Эйлера и С.Е. Гурьева.
Слайд 6
Система координат Системой координат называется совокупность одной, двух, трёх или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, — начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат.
Слайд 7
Любая отличная от начала координат точка М однозначно определяется своим расстоянием ОМ = r от полюса и ориентированным углом между полярной осью и отрезком ОМ. Кроме того, задаётся единица масштаба для измерения длин отрезков. Полярная система координат – двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.
Слайд 8
Перевод полярных координат в декартовы и обратно. Установим связь между полярными координатами точки и её прямоугольными координатами.
При этом будем предполагать, что начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Рассмотрим АОМ
Слайд 9
Перевод полярных координат в декартовы и обратно. Пример 1. Требуется построить точку М ( 2 ; ) в полярной системе координат. Проведем луч ОР под углом к полярной оси ОЕ и отложим от полюса отрезок ОМ, равный двум единицам масштаба. Конец М этого отрезка и будут искомой точкой . Пример 2. Найти прямоугольные координаты точки, полярные координаты которой М ( ; ). Решение: По формулам получаем Ответ: М( 3; )
Слайд 10
Перевод полярных координат в декартовы и обратно. Пример 3. Прямоугольные координаты точки А (1; ). Требуется найти ее полярные координаты. Решение: По формуле получаем . Зная получим откуда Ответ: А( 2 ; )
Слайд 11
Некоторые кривые в полярных координатах. Окружность. Уравнение вида r = K = const определяет окружность с центром в полюсе радиуса K .
Слайд 12
2) Спираль Архимеда
Слайд 13
3) Кардиоида
Слайд 14
Преобразования кардиоиды.
Слайд 15
Преобразования кардиоиды.
Слайд 19
Прямоугольная СК Полярная СК Наиболее простая, часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению. Уравнения некоторых кривых (окружности) в ПСК записываются проще. Распределяются на пространство путем добавления еще одного угла. Сравнение полярной и прямоугольной системы координат.
Слайд 20
Прямоугольная СК Полярная СК Прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Началом координат служит точка пересечения координатных осей. В ПСК фиксируется точка, являющаяся началом координат, и координатная ось, — прямая, проходящая через это начало.
Слайд 21
Прямоугольная СК Полярная СК Прямоугольная система координат может быть двухмерной или трехмерной.
Полярная система координат может быть только двухмерной. В прямоугольной системе координат отношения между точками можно установить только путем применения тригонометрических преобразований. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов.
Слайд 22
Полярная система координат в жизни Полярную систему координат часто применяют в навигации , поскольку пункт назначения можно задать как расстояние и направление движения от отправной точки. В авиации , для навигации применяют несколько изменённую версию полярных координат. Графики в полярной системе координат помогут нам лучше понять смысл квадратурной модуляции . Полярные координаты нередко возникают при решении различных задач в электротехнике , акустике , гидростатике и механике .
Слайд 23
Материал, представленный в работе, расширяет кругозор, пополняет теоретические знания и практические навыки. Мы рассмотрели некоторые примеры, показывающие необходимость и актуальность изученной темы, и пришли к выводу: В ряде случаев при указании места расположения какого-нибудь объекта удобнее определять не его декартовы координаты, а направление и расстояние до объекта, то есть полярные координаты.
Я убедился, что все они играют важнейшую роль в различных средах деятельности человека. Построение некоторых линий в полярной системе координат намного проще, а элементарные преобразования уравнений кривых схожи, чем в декартовой СК. Заключение:
Слайд 24
СПАСИБО ЗА ВНИМАНИЕ
Замечательные кривые | matematicus.ru
Artman Аналитическая геометрия в пространстве
Семейство роз Гранди
Уравнение имеет вид:
ρ=asinkφ
a — радиус лепестка;
k — положительный параметр, отвечает за количество лепестков.
Свойство:
|sin(kφ)| ≤1
Рисунок 1 — роза с тремя лепестками ρ=sin3φ
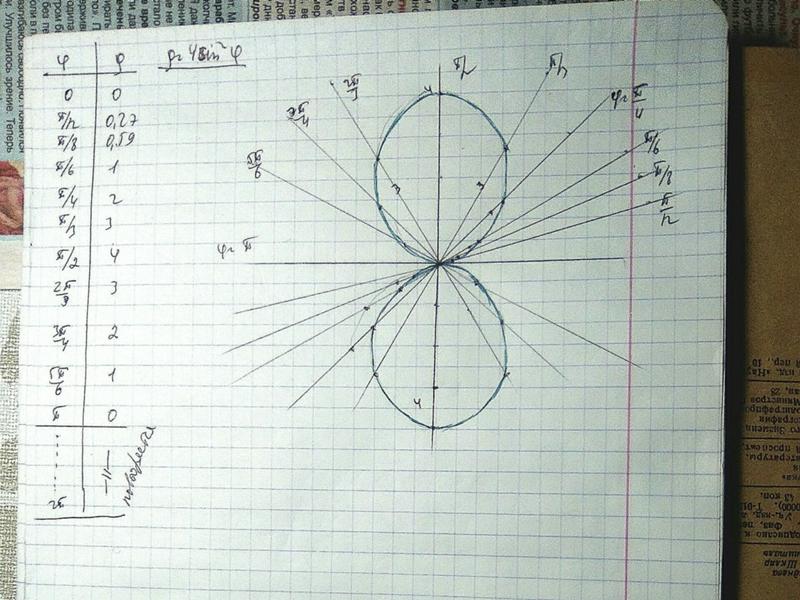
Рисунок 2 — роза с 16 лепестками ρ=sin8φ
Рисунок 3 — семейство роз Гранди — напоминает ромашку ρ=sin20φ
Рисунок 4 — семейство роз Гранди — линия похожа на зрачок глаза ρ=sin100φ
Уравнение логарифмическая спираль (трансцендентная кривая) в полярных координатах:
ρ = 2aφ
Кардиоида частный случай улитки Паскаля.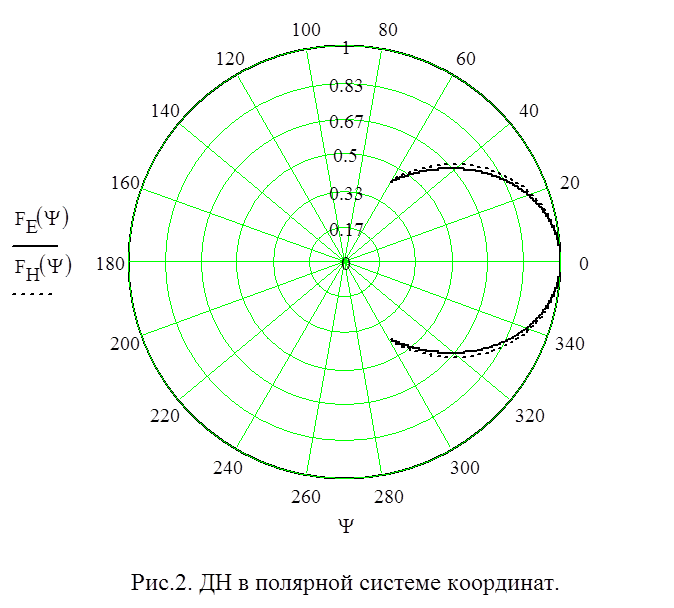
2}\varphi }}{{\cos \varphi }}$$
Параметрическое уравнение циклоиды:
x = R (t — sint)
y = R (1 — cost)
Уравнение кохлеоиды (трансцендентная кривая) в полярных координатах:
$\rho = \frac{{\pi a}}{2}\frac{{\sin \varphi }}{\varphi }$
Лемниската Бернулли
Уравнение лемниската Бернулли в прямоугольных координатах:
(x2 + y2)2 = a2 (x2 — y2)
Уравнение лемниската Бернулли в полярных координатах:
р2 = a2соs2φ
Архимедова спираль рассмотрена здесь подробно.
Применяя математические уравнения замечательных кривых, можно получить вот такие геометрические линии.
Математическое уравнение сердца имеет вид:
Лист клена, уравнение:
7800
Длина дуги в полярных координатах: проект Calculus 3, Мередит Лапидас расположение часовой стрелки относительно минутной, что бы вы сказали? Вместо того чтобы измерять расстояние
между обоими числами с помощью точных измерений, было бы намного проще сказать, что 3 и 6 отстоят друг от друга на 90 градусов.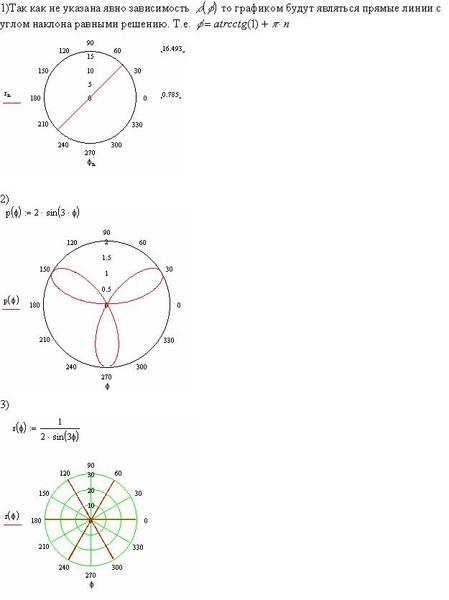
Как и в этом примере с часами, полярные координаты можно использовать для упрощения поиска точек на графике.
A Полярная координата — это набор значений, определяющих местоположение точки на основе как расстояния между точкой и фиксированным исходным положением, так и угла между точкой и направлением.
Полярные кривые — это точки, находящиеся на заданном расстоянии от начала координат/полюса в зависимости от угла, измеренного против часовой стрелки от полярной оси
Примерами полярных кривых являются эллипсы, кардиоиды и лемнискаты:
Любое уравнение, записанное в декартовых координатах, может быть преобразовано в уравнение в полярных координатах с помощью тригонометрических соотношений:
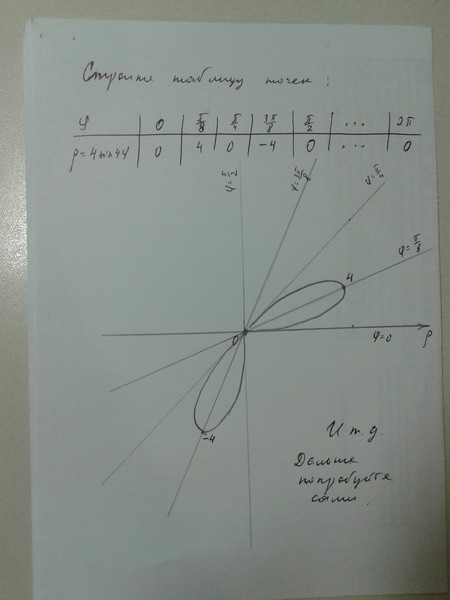{d}{t}\right.}\)- Чтобы найти длину дуги в полярных координатах , сначала запишите кривую в терминах параметрических уравнений:
\(r=f(\theta) \\ x=rcos(\theta)=f(\theta)\cos(\theta) \\ x=rsin (\theta)=f(\theta)\sin(\theta )\)
- Параметрическую формулу для определения длины дуги можно вывести, заменив параметр t на θ:
{2}{\left(\frac{\theta}{{2}}\right)}}~d \theta =~8 }\)
Приложения
Полярные координаты подходят в ситуациях, когда объект рассматриваемое связано с направлением и длиной от центральной точки плоскости.
В небесной механике полярные координаты могут использоваться для построения планетарных орбит. Поскольку есть тела, движущиеся вокруг центральной точки, для таких планет проще всего использовать полярные координаты.
2}\)Где h — смещение кривой по горизонтали, k — смещение кривой по вертикали, a — радиус кривой в направлении x, а b — радиус кривой в направлении y.
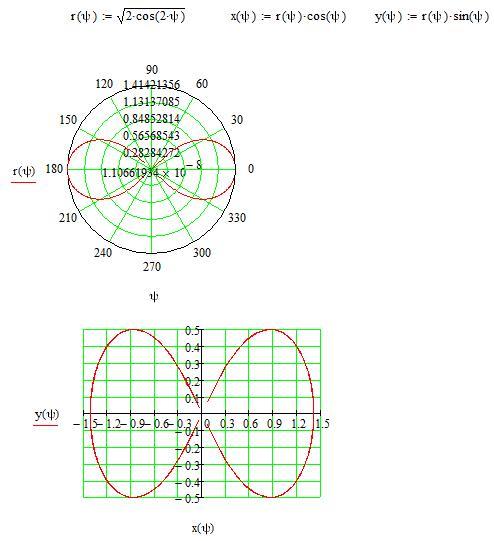
В орбитальной кривой планеты нет смещения в направлении y. Следовательно, значение k равно 0.
Можно преобразовать уравнение Декарта в параметрическую форму эллиптической кривой за несколько простых шагов:
Наконец, можно использовать значения из планетарных данных (значения a,b , и c) чтобы получить Полярная форма кривой для любой планеты:
Теперь мы можем подключить каждую значения для каждой планеты …
. Системная динамика: орбиты и законы Кеплера
Ссылки
//study.com/academy/lesson/polar-coordinates-definition-equation-examples.html
Полярные кривые: определение, формула и типы
Вы когда-нибудь внимательно рассматривали подсолнух? Кривые, которые вы видите перекрещивающимися друг с другом в подсолнухе, на самом деле расположены в виде логарифмических спиралей, типа полярной кривой.
1
Рисунок 1. Семена подсолнуха, расположенные в виде логарифмических спиралей — Pixabay
Другие природные явления, форма которых может быть описана с помощью логарифмических спиралей, включают раковины наутилуса и даже некоторые галактики.
Рисунок 2. Галактика, имеющая форму логарифмической спирали — Pixabay
В этой статье будут представлены полярные кривые, включая важные примеры полярных кривых, некоторые их симметрии и способы их построения.
Полярная кривая Формула
Вы можете использовать для записи функций в форме
\[ y=f(x),\]
, где отношение между \( x \) и \( y \) приводит к кривой на плоскости. Когда функция записывается в терминах \(x\) и \(y\), мы говорим, что она записана в декартовых координатах, , также известных как прямоугольных координат.
С другой стороны, полярные кривые представляют собой кривые, записанные в терминах полярных координат \( r \) и \( \theta.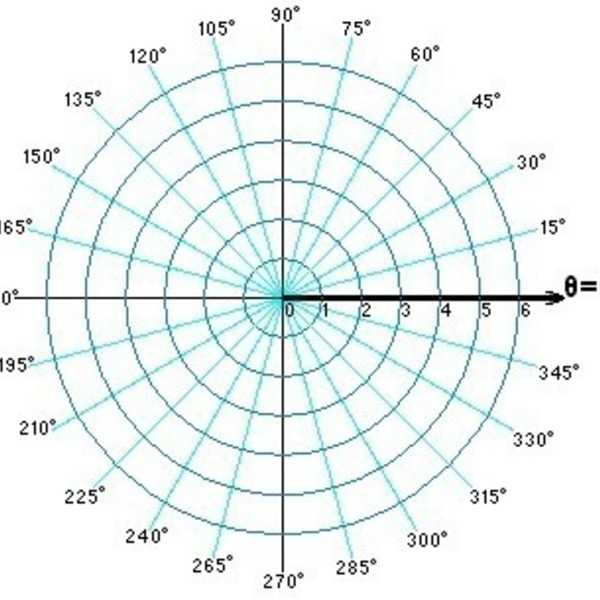
\) Чтобы лучше описать полярные координаты, рассмотрим точку на плоскости. 92},\]
— расстояние от начала координат до точки на плоскости (длина отрезка, показанного на диаграмме), а
\[ \theta = \arctan{\frac{y}{x} },\]
— это угол между положительной осью \(x-\) и линией, соединяющей начало координат с точкой.
Изображение 3. Графическое представление полярных координат.
Другой способ описания полярных координат — с помощью уравнений
\[ x = r\,\cos{\theta}\]
и
\[ y = r\,\sin{\theta}.\]
A полярная кривая представляет собой функцию, описанную в терминах полярных координат, которая может быть выражена в общем виде как
\[ f(r,\theta ).\]
Обратите внимание, что функции, описываемые полярными координатами, обычно не проходят
проверку вертикальной линии. Проверка вертикальной линии применяется только к функциям, которые записываются как \(y=f(x)\)!Уравнение
\[ r = 3\sin{\left(\frac{2}{3}\theta\right)}\]
определяет полярную кривую.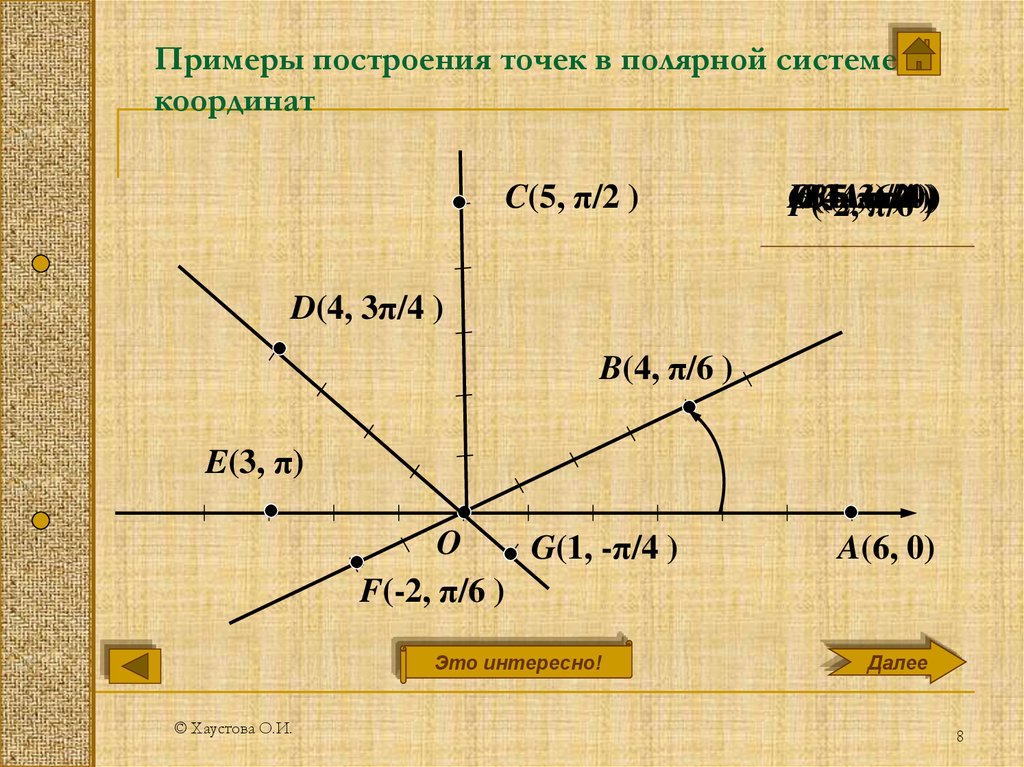
Его график выглядит следующим образом:
Рисунок 3. Кривая-роза
Вы можете видеть приведенную выше кривую как набор всех пар \( (r,\theta)\), которые удовлетворяют уравнению
\[ r = 3\ sin{\left(\frac{2}{3}\theta\right)}.\]
Для получения дополнительной информации о полярных координатах, что они собой представляют и как преобразовать полярные координаты в прямоугольные, см. наши статьи о полярных координатах. Координаты и производные функции, записанные в полярных координатах.
Типы полярных кривых
Некоторые типы кривых могут быть более естественно выражены в полярных координатах, чем в прямоугольных. Six important classes of such curves are,
- Limaçons
- Cardioids
- Rose curves
- Archimedean spirals
- Logarithmic spirals
- Lemniscates
Limaçons
A limaçon is a polar curve defined by the equation
\[ г = а \pm b \sin{\theta}\]
или
\[ r = a \pm b \cos{\theta},\]
, где \( a \) и \( b \) — константы.
Лимасоны бывают трех типов:
- Петлевые (лимасоны, где \( a
- Кардиоидные (лимасоны, где \( a = b \)),
- Ямочки (лимасоны, где \( a > b \) )).
Лимасон с петлей
Например, лимасон, определенный как
\[ r = 2 + 3 \sin{\theta},\]
, является лимасоном с петлей, потому что \( 2 < 3. \) Вот его график.
Рис. 4. Лимасон с петлями
Лимасон с ямочками
Другой пример: кривая
\[ r = 4 — \cos{\theta}\]
является лимасоном с ямочками, потому что \( 4 > 1. \ ) Это выглядит так:
Рисунок 5. Лимасон с ямочками
Обратите внимание, что лимасоны, определенные с помощью косинуса, симметричны относительно горизонтальной оси, а лимасоны, определенные с помощью синуса, симметричны относительно вертикальной оси.
Лимасон — странное имя, не так ли? Есть причина, почему это имя используется!
Название limaçon в переводе с французского буквально означает «улитка».
Это название происходит от некоторых видов лимасонов, которые выглядят как раковины улиток.
Кардиоиды
Кардиоиды — это особые экземпляры лимасонов, названные в честь их сердцевидной формы. Уравнение для кардиоиды:
\[ r = a(1-\cos{\theta}),\]
, где \( a \) — некоторая константа. Например, кардиоида
\[ 1- \cos{\theta}\] выглядит так,
Рис. 6. Кардиоида
Кривые розы
Кривые розы — это полярные кривые, названные Гвидо Гранди, итальянским математиком, изучавшим их в начале 1700-х годов. Они определяются уравнениями вида
\[ r = a\sin{\left(n\theta\right)},\]
или
\[ r = a\cos{\left(n\theta \right)},\]
где \( a \) — константа, определяющая размер цветка, а \( n \) — константа, определяющая количество и расположение лепестков. Например, кривая розы
\[ r = \cos{\left( 9\theta \right)},\]
выглядит так, 3
\[ r = 3 \sin{\left( 9 \theta \right) } ,\]
выглядит так,
.
Это связано с тем, что \( n \) установлено равным 9 в обоих уравнениях. Однако одна роза масштабируется с коэффициентом 3, что соответствует тому факту, что она имеет \( a=3.\). Вы также можете заметить, что одна роза повернута относительно другой, что соответствует тому факту, что одна определяется в терминах функции синуса, а другой записывается с использованием функции косинуса.
Значение \(n\) не обязательно должно быть целым числом. Например, кривая розы
\[ r = 3 \cos{\left(\frac{4}{7}\theta \right)},\]
выглядит так,
Рис. 9. Кривая розы с нецелым значением \( n\)
Кривые Розы с иррациональными значениями для \(n\) (например, \(\pi\)) могут быть особенно интересными, потому что они никогда не заканчиваются. Для данной иррациональной розы \(f\) и произвольной точки \(P\) в круге, содержащем \(f\), независимо от того, насколько близко вы подходите к \(P\), найдется точка \(f \) ближе к \(P\), чем вы. \(f\) является примером плотный набор ; другой пример — набор рациональных чисел на прямой.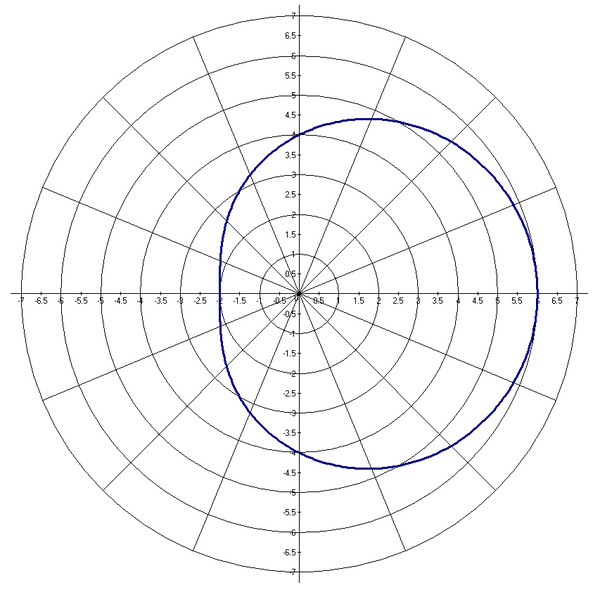
Спирали Архимеда
Спираль Архимеда представляет собой полярную кривую, определяемую уравнением
\[r = b\theta.\]
Существует обобщенная версия спирали Архимеда, называемая неоидом, определяемая уравнением
\[ r = a + b\theta, \]
где \( a \) и \( b \) — константы. Константа \(a\) определяет значение кривой при \(\theta = 0\) (положительная \(x-\)ось), а \(b\) соответствует размеру спирали.
Спирали Архимеда имеют еще одну особенность, так как существует постоянное расстояние между последовательными сегментами спирали, равное \(2\pi b\). Например, неоид
\[ r = 1 + 3\theta,\]
выглядит так, 4
Рисунок 10. Неоид, описываемый \( r = 1 + 3\theta \)
Архимедовы спирали — это полярные кривые, названные в честь древнегреческого математика Архимеда. Архимед написал целую книгу « На спирали 9».2 = 4\cos{\left( 2 \theta \right)},\]
выглядит так,
Рис. 13. Лемниската, использующая функцию косинуса
с точки зрения косинуса, просто повернутой на 45 градусов.
Рис. 14. Лемниската, использующая функцию синуса
Полярные кривые появляются в некоторых интересных и, возможно, неожиданных местах. Например, вы, возможно, слышали о множестве Мандельброта. Множество Мандельброта — это пример фрактала, формы, которая содержит копии самого себя в разных масштабах.
Множество Мандельброта содержит несколько кривых, о которых мы говорили. Например, основная лампочка набора имеет форму кардиоиды. 5
Рис. 15. Граница участка множества Мандельброта
При приближении к краю множества можно увидеть логарифмические спирали. 5
Рис. 16. Логарифмические спирали можно найти в множестве Мандельброта
Граница множества Мандельброта, хотя она невероятно сложна, на самом деле может быть построена с помощью последовательности лемнискат.
Симметрии полярных кривых
Полярные кривые часто имеют симметрию, которую можно использовать при построении графика и изучении их свойств.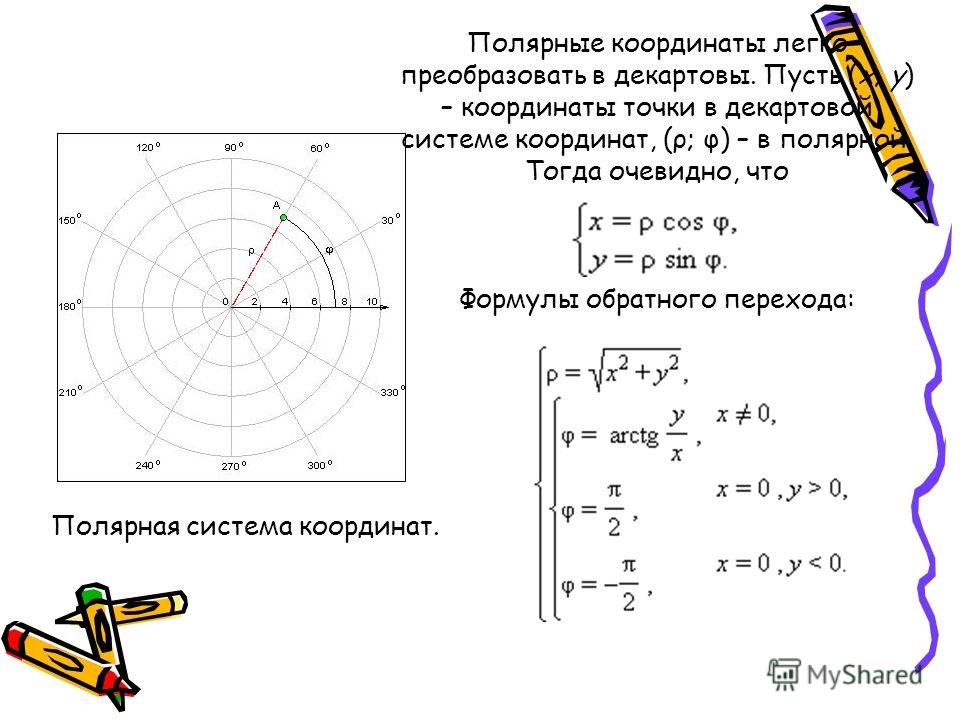
Обычно при работе с полярными кривыми используются три симметрии:
- Симметрия относительно полярной оси,
- Симметрия относительно полюса,
- S ymметрия относительно вертикальной оси.
В таблице ниже приведены различные симметрии и способы их поиска. 6
Имя | Ось симметрии | Тест |
| Симметрия about about able | $ $Замените \(r\) на \(-r\) или (эквивалентно) замените \(\theta\) на \(\pi + \theta\). | |
| Симметрия относительно полярной оси | $$\theta = \pi$$ | Замените \(r\) на \(-r\) и \(\theta\) на \(\pi — \theta \) или (эквивалентно) заменить \(\theta\) на \(-\theta\). |
| Симметрия относительно вертикальной оси | $$\theta = \frac{\pi}{2}$$ | Заменить \(r\) на \(-r\) и \(\theta\) на \(-\theta\) или (эквивалентно) заменить \(\theta\) на \(\pi — \theta\). |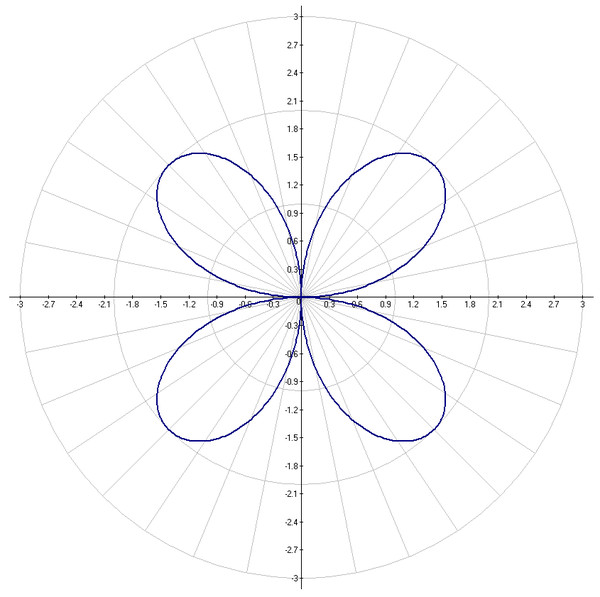
Симметрия относительно полярной оси
Симметрия относительно полярной оси аналогична симметрии относительно линии \( \theta = \pi,\) горизонтальной оси. Полярная кривая симметрична относительно полярной оси, если вы можете перевернуть график относительно горизонтальной оси и получить тот же график, с которого вы начали. Эквивалентно, это означает, что если точка \( (r,\theta)\) находится на полярной кривой, то точка \( (r,-\theta) \), полученная переворачиванием \( (r,\theta) \ ) вокруг горизонтальной оси также находится на кривой.
Есть несколько тестов, которые можно использовать для проверки симметричности кривой относительно полярной оси. Если вам дано уравнение для полярной кривой и вы можете заменить каждое вхождение \(\theta\) на \(-\theta, \) и получить то же самое уравнение, то кривая симметрична относительно полярной оси. Это то же самое, что проверять, находится ли точка \((r,\theta)\) на кривой и точка \((r,-\theta)\) также на полярной кривой.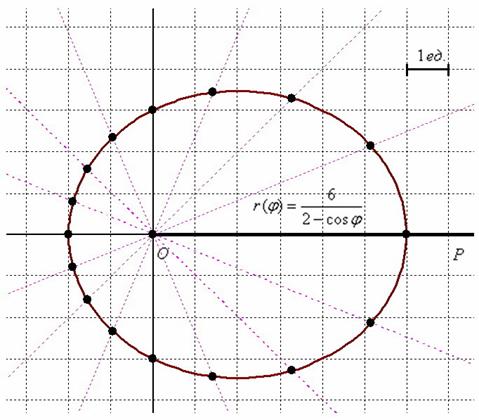
Другой тест, который вы можете попробовать, это заменить \( r \) на \( -r \) и \( \theta \) на \( \pi — \theta.\) Этот тест работает, потому что точка \( (-r ,\pi-\theta) \) совпадает с точкой \( (r,-\theta),\), только представленной несколько иначе.
Проверить кривую розы
\[ r = 3 \cos{\left(2\theta\right)},\]
на симметрию относительно полярной оси.
Решение
Начните с \( \theta \) с помощью \( -\theta.\) Это даст вам
\[ \begin{align} r &= 3\cos{\left(2(— \theta)\right)} \\ &= 3\cos{(-2\theta)}. \end{align}\]
Функция косинуса имеет свойство
\[\cos{(-\theta)}=\cos{\theta}\]
для любого значения \( \theta,\) так
\[ \begin{align} r &= 3 \cos{(-2\theta)} \\ &= 3\cos{(2\theta)}. \end{align}\]
Поскольку это то же самое уравнение, с которого вы начали, этот тест проходит успешно. Итак, эта кривая розы симметрична относительно полярной оси.
Рис. 17. Кривая-роза с симметрией относительно полярной оси
Если полярная кривая проходит тест на симметрию, то она определенно имеет такую симметрию.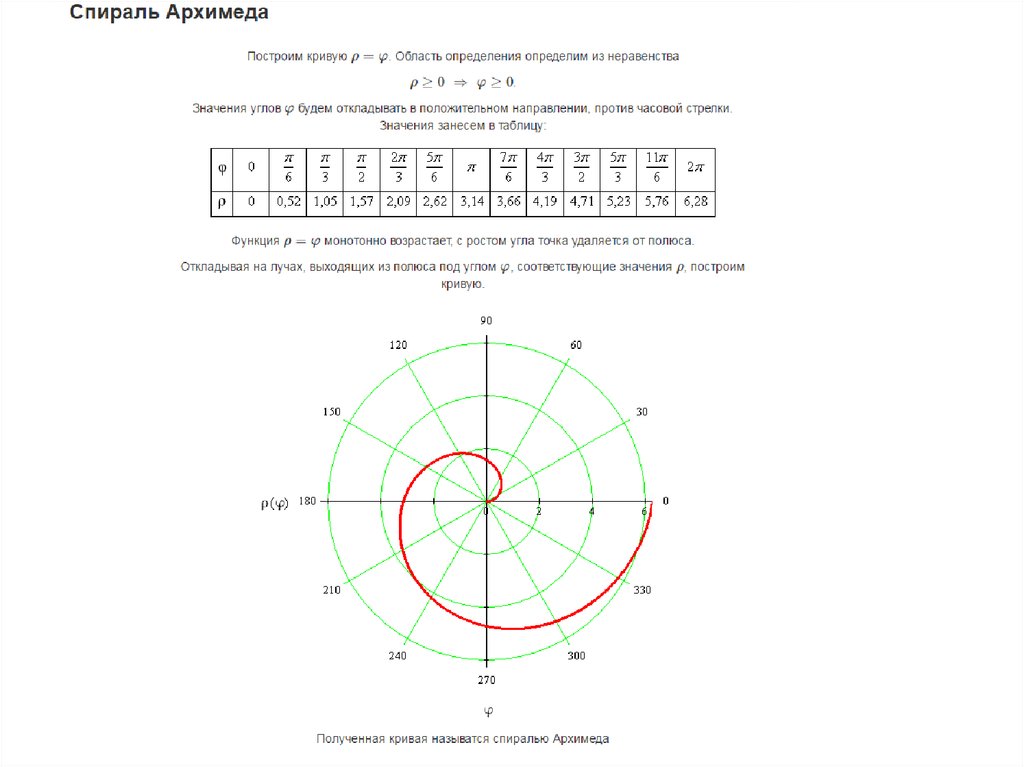
Однако, даже если полярная кривая не проходит все тесты на симметрию, которые вы пытаетесь выполнить, она все равно может иметь эту симметрию. Это происходит из-за того, что полярные кривые имеют много эквивалентных алгебраических представлений, и вы не всегда сможете сказать, просто взглянув на два уравнения, описывают ли они одну и ту же кривую.
Симметрия относительно полюса
Если полярная кривая симметрична относительно полюса, то ее переворачивание относительно прямой
\[ \theta = \frac{3\pi}{4}\]
не меняет ее график . Эквивалентно, полярная кривая симметрична относительно полюса, если для любой точки \((r,\theta)\) на кривой точка \((-r,\theta)\) также находится на кривой. Чтобы проверить симметрию относительно полюса, вы можете заменить \( r \) на \( -r \) и посмотреть, получится ли то же самое уравнение. Вы также можете попробовать заменить \(\theta\) на \(\theta + \pi.\) 92 = 4 \sin{(2\theta)}.\]
Уравнение снова такое же, как и исходное, поэтому кривая имеет симметрию относительно полюса.
Рис. 18. Лемниската с симметрией относительно полюса
Симметрия относительно вертикальной оси
Наконец, симметрия относительно вертикальной оси совпадает с симметрией относительно прямой
\[ \theta = \frac{\pi}{ 2}.\]
Чтобы проверить симметрию относительно вертикальной оси, попробуйте заменить \( r \) на \( -r \) и \( \theta \) на \( -\theta.\) Вы также можете попробовать замена \(\theta\) на \(\pi-\theta.\)
Проверить лимасон
\[ r = 2+3\sin{\theta},\]
на симметрию относительно вертикальной оси.
Решение
Начните с замены \( r \) на \( -r \) и \( \theta \) на \( -\theta,\), то есть
\[ -r = 2 + 3 \sin{(-\theta)},\]
, где вы можете использовать тот факт, что функция синуса является нечетной функцией, что означает, что
\[ \sin{(-\theta)}=-\sin{ \theta}\]
для любого значения \( \theta,\) поэтому
\[ \begin{align} -r &= 2 -3\sin{\theta} \\r &= -2+3\sin{\theta}.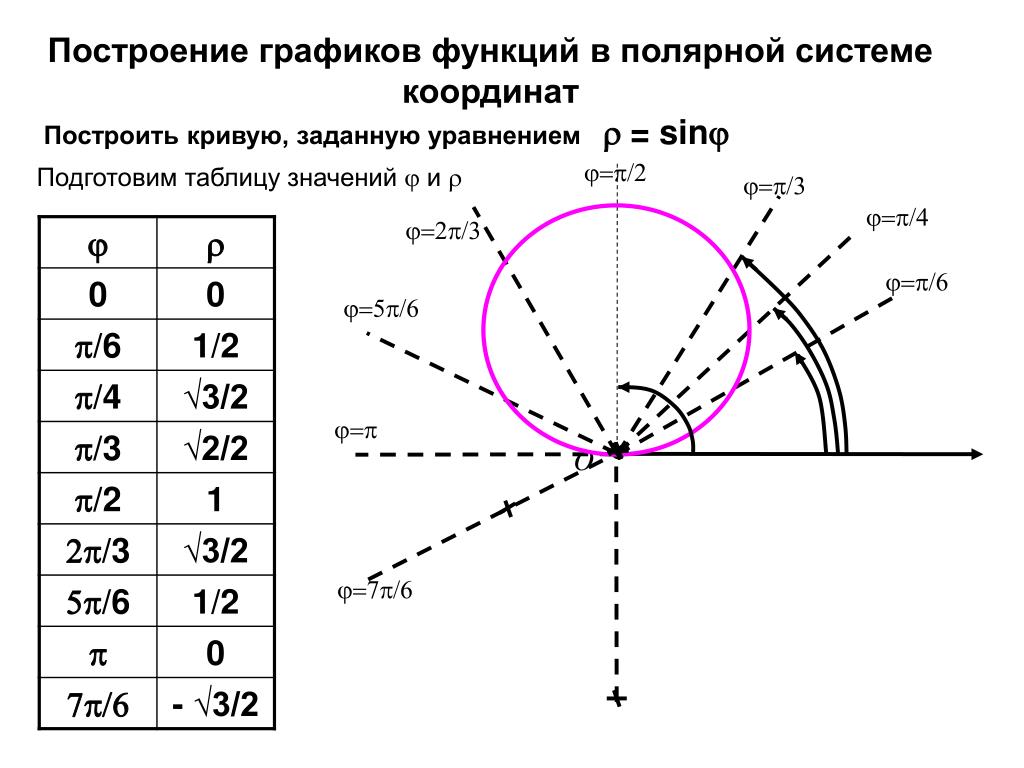
\end{align}\]
Поскольку приведенное выше уравнение отличается от исходного, этот тест не говорит вам, симметрична ли кривая относительно вертикальной оси. Однако, если вы попытаетесь заменить \(\theta\) на \(\pi-\theta,\), вы получите
\[ r = 2 +3 \sin{(\pi-\theta)},\]
, и теперь вы можете использовать тождество
\[ \sin{(\pi-\theta)} = \sin{\theta},\]
, так что
\[ r = 2 + 3 \sin{\theta }.\]
Приведенное выше уравнение эквивалентно исходному уравнению, доказывая, что этот лимасон симметричен относительно вертикальной оси.
Рисунок 19. Лимасон с симметрией относительно вертикальной оси
Построение полярных кривых
Вы видели большое разнообразие полярных кривых и их графиков. Теперь предположим, что вам дана формула и вы хотите построить график полярной кривой.
Одна из стратегий состоит в том, чтобы выучить формулы для важных примеров полярных кривых и понять соответствующие им графики. Многие из кривых, с которыми вас могут попросить поработать, являются вариантами полярных кривых, рассмотренных выше, поэтому знание этих кривых, их уравнений и их свойств может оказаться весьма полезным.
Однако есть вероятность, что не каждая полярная кривая, с которой вы столкнетесь, будет иметь формулу, которую вы узнаете. Не говоря уже о задаче запоминания всех форм и формул!
Здесь вы можете ознакомиться с некоторыми альтернативными вариантами построения полярных кривых.
Построение полярных кривых вручную
Существует несколько стратегий, которые можно использовать при построении полярных кривых вручную. В этих случаях первое, что вы можете сделать, это проверить периодичность. Если функция, которую вы рисуете, является периодической, то вам нужно построить график функции только за один период. Затем найдите точки на кривой для различных значений \(\theta.\). После того, как вы начертите эти значения, соедините точки, чтобы аппроксимировать кривую.
Вы также можете проверить симметрию. Это может значительно сократить объем работы, которую вам необходимо выполнить. Например, если вы знаете, что полярная кривая симметрична относительно вертикальной оси, вы должны нарисовать кривую только в одной полуплоскости, а затем отразить ее поперек оси, чтобы получить другую половину.
Нарисуйте полярную кривую, описанную выражением
\[ r = 1 + 2\cos{\theta}.\]
Решение
Начните с проверки симметрии. Во-первых, проверьте симметрию относительно полярной оси, заменив \(\theta\) на \(-\theta,\), так что
\[ r = 1 + 2\cos{(-\theta)},\]
поскольку функция косинуса является четной функцией, это означает, что
\[ \cos{(-\theta)} = \ cos{\theta},\]
so
\[ r = 1 + 2\cos{\theta}.\]
Поскольку это уравнение такое же, как исходное, кривая симметрична относительно полярной оси. Прежде чем проверять дополнительные симметрии, попробуйте подставить в уравнение несколько хороших значений \(\theta\).
| \[ \theta \] | \[ 1 + 2\cos{\theta} \] | \[ r \] |
| \[ 0 \] | \[ 1 + 2 \cos{0} \] | \[ 3 \] |
| \[ \frac{\pi}{ 4}\] | \[ 1 + 2 \cos{\frac{\pi}{4}}\] | \[ 1 + \sqrt{2}\] |
| \[ \frac{\pi {2}\] | \[ 1 + 2 \cos{\frac{\pi}{2}}\] | \[ 1 \] |
| \[ \frac{3\pi}{2 }\] | \[ 1 + 2\cos{\frac{3\pi}{2}}\] | \[ 1 — \sqrt{2}\] |
| \[ \pi \] | \[ 1 + 2 \cos{\pi}\] | \[-1\] |
Для построения графика отрицательных значений \(r,\) просто перейдите к противоположной стороне \( \ тета\) угол, который вы используете.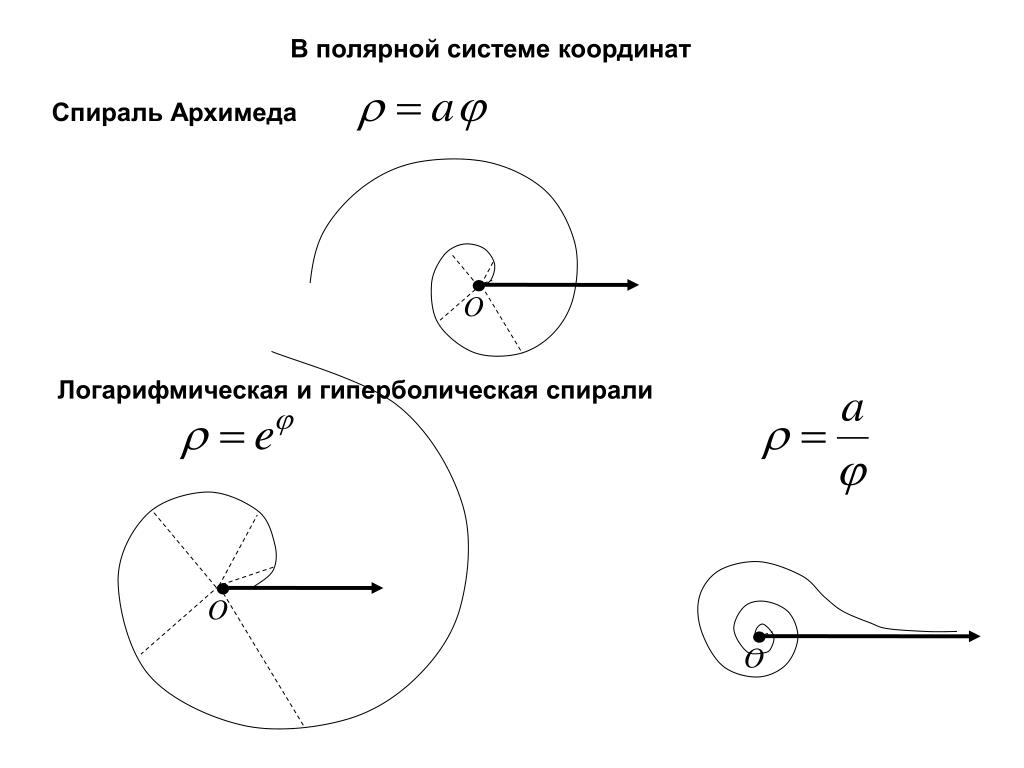
Построение этих точек даст вам.
Рисунок 20. Построение полярных кривых путем соединения точек
Затем соедините точки. Вы должны помнить, что вы рисуете полярную кривую, поэтому попробуйте соединить точки в извилистом делении!
Рис. 21. Построение полярных кривых путем соединения точек
Ранее вы обнаружили, что график имеет полярную симметрию, поэтому отразите график вдоль оси \(x-\).
Рис. 22. Симметрия при построении полярных кривых
Онлайн-графики полярных кривых
Существует множество бесплатных онлайн-инструментов, таких как Geogebra и Desmos, для построения полярных кривых. Чтобы построить полярные кривые в любом из этих инструментов, просто введите уравнение для кривой в поле ввода.
Например, чтобы нарисовать розу с тремя листьями в Geogebra или Desmos с использованием полярных координат, введите
\[ r = \cos{(3\theta)}\]
и нажмите Enter.
Чтобы ввести символ \( \theta \) в Geogebra, используйте математическую клавиатуру, которую можно открыть, щелкнув символ клавиатуры в нижней левой части поля ввода.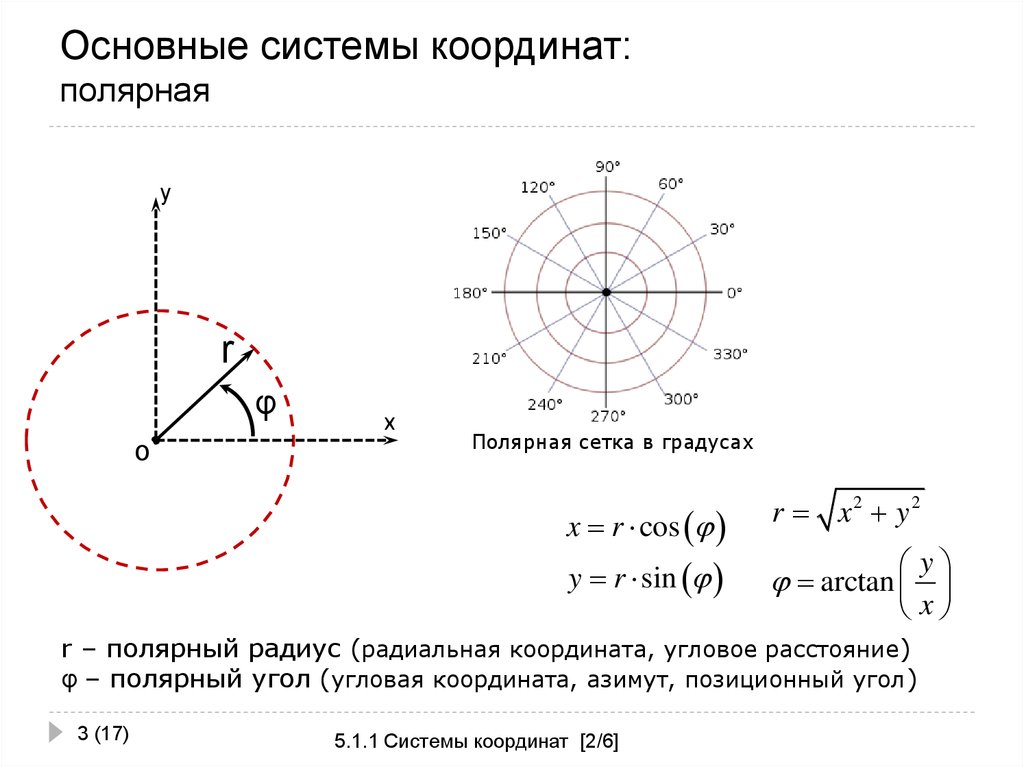
Чтобы ввести символ \(\theta\) в Desmos, введите слово ‘theta’.
Конечно, существует множество других способов построения полярных кривых. Если у вас есть графический калькулятор, он, вероятно, имеет функцию, позволяющую отображать функции в полярных координатах. Вы также можете использовать языки программирования и программное обеспечение, такое как Python, Matlab и Octave.
Если у вас возникли проблемы с построением полярной кривой, проверьте диапазон тета-значений, которые вы начертили. Иногда вам нужно расширить диапазон значений тета, которые вы используете, чтобы убедиться, что кривая построена правильно.
Площадь полярных кривых
Предположим, у вас есть полярная кривая, заданная выражением
\[ r = f(\theta). \]
Чтобы найти площадь, ограниченную линией \( \theta = \theta_1,\) кривой \( f(\theta),\) и линией \( \theta=\theta_2, \), вам нужно используйте формулу 92}\,\mathrm{d}\theta.\]
Нужна дополнительная информация о том, как работать с этой формулой? См.
нашу статью о длине дуги в полярных координатах!
Полярные кривые — ключевые выводы
- Полярные кривые определяются соотношениями в терминах полярных координат.
- Важные типы полярных кривых включают лимасоны, кардиоиды, кривые-розы, спирали Архимеда, логарифмические спирали, овалы Кассини и лемнискаты.
- Полярная кривая может иметь три типа симметрии: симметрия относительно полярной оси, симметрия относительно полюса и симметрия относительно вертикальной оси.
- Чтобы изобразить полярные кривые, узнайте распространенные типы полярных кривых и их свойства, проверьте периодичность, проверьте симметрию, затем найдите несколько точек на кривой и соедините их.
1. Эли Маор, «e»: История одного числа , 1994.
2. Джон В. Раттер, Геометрия кривых , 2000.
Флорес 3. Гвидо Гранди, геометрический ex Rhodonearum, et Cloeliarum curvarum descriptione resultsantes, … , 1728 .