Построить кривую онлайн по уравнению: Построение графика функции онлайн

Содержание

Прямая на плоскости. Кривые второго порядка

Раздел «Аналитическая геометрия на
плоскости» курса «Высшая математика»
включает две основные темы:
1.
2.
Прямая на плоскости
Кривые 2-го порядка

2. Прямая на плоскости

Основные уравнения прямой на плоскости
1. Уравнение прямой, проходящей через заданную
точку M 0 ( x0 ; y0 ) перпендикулярно
N A; B
заданному вектору N A; B
A( x x0 ) B( y y0 ) 0
M 0 ( x0 ; y0 )
2. Общее уравнение прямой
N A; B
Ax By C 0
— вектор нормали
3. Уравнение прямой « в отрезках»
x y
1
a b
Y
b
X
a

3. Прямая на плоскости. Основные уравнения

4. Уравнение прямой, проходящей через заданную
точку M 0 ( x0 ; y0 ) параллельно заданному вектору s m; n
x x0 y y 0
m
n
— каноническое уравнение
s m; n — направляющий вектор
s m; n
5. Параметрические уравнения
x mt x0
y nt y 0
M 0 ( x0 ; y0 )
6. Уравнение прямой, проходящей через две
заданные точки M 1 ( x1 ; y1 ) и M 2 ( x2 ; y2 )
x x1
y y1
x2 x1 y2 y1
s M 1M 2
M 2 ( x2 ; y 2 )
M 1 ( x1 ; y1 )

4.

Прямая на плоскости. Основные уравнения7. Уравнение прямой, проходящей через заданную
точку M 0 ( x0 ; y0 ) с заданным угловым коэффициентом
y y0 k ( x x0 )
k tg
Y
y
y0
X
O
x0
x
Угловой коэффициент k — это тангенс угла наклона прямой.
Угол отсчитывается от положительного направления оси OX
8. Уравнение прямой с угловым
коэффициентом
y kx b
Y
b
O
X

5. Задачи на составление уравнений прямой , определение параметров уравнений

1. Составить уравнение прямой, проходящей через точку M 0 (2;4)
параллельно прямой
5x 3 y 15 0 . Построить прямую.
Решение. Нам задано уравнение прямой общего вида
Ax By C 0
N A; B
-вектор нормали
Сравнивая с заданным уравнением, получаем координаты
вектора нормали N 5; 3 Так как все параллельные прямые
можно охарактеризовать одним вектором нормали, то можно составить
уравнение параллельной прямой, проходящей через данную
в условии точку.

За основу берем уравнение A( x x0 ) B( y y0 ) 0
5( x 2) 3( y 4) 0
5x 10 3 y 12 0
5x 3 y 2 0
Y
Найдем угловой коэффициент
5x 2 3 y
5
2
y x
3
3
N 5; 3
s 3;5 -направляющий вектор
k
5
3
2
3
2
5
O
X
2. Составить уравнение прямой, проходящей через данную точку
M 0 ( 3;4) параллельно прямой x 1 y 3
2
5
Из канонического уравнения заданной прямой можно определить
ее направляющий вектор s 2; 5
Поскольку для всех параллельных прямых можно взять один и тот
же направляющий вектор, то берем за основу каноническое
уравнение x x0 y y 0 и подставляем в него координаты точки
m
n
и направляющего вектора
x 3 y 4
2
5
Это уравнение можно преобразовать к уравнению
общего вида и к уравнению с угловым коэффициентом
x
0
y
7
2
7
5
0
Y
5x 15 2 y 8
5( x 3) 2( y 4)
7
5x 2 y 7 0
7
5
5
( y 4) ( x 3)
2
2
5
k
N 5;2 — вектор нормали
угловой коэффициент
2
X
3.

Составить уравнение прямой, проходящей через точку A( 5;2)
параллельно прямой y 3x 5 .
В данном случае прямая задана уравнением с известным
угловым коэффициентом y=kx+b.
K=3
Все параллельные прямые имеют один угловой коэффициент.
Y
Т.о. нам известна точка на прямой и угловой коэффициент.
Y
Берем уравнение y y0 k ( x x0 )
Y
y 2 3( x 5)
17
y 2 3x 15
y 3x 17
Записав уравнение в виде
X
17 / 3
3x y 17 0 , определим вектор нормали
N 3; 1 и направляющий вектор
s 1;3
Для построения прямой используем таблицу
x
y
0
-17/3
17
0
4. Составить уравнение прямой, проходящей через точку M 0 (2;4)
перпендикулярно прямой 5x 3 y 15 0
N 5; 3
M 0 (2;4)
5x 3 y 15 0
Из рисунка видно, что вектор
нормали известной прямой
является направляющим для
искомой прямой, поэтому
используем каноническое уравнение
x x0 y y 0
m
n
3( x 2) 5( y 4)
x 2 y 4
5
3
3x 6 5 y 20
3x 5 y 26 0
Таким образом, получили общее уравнение прямой, из которого
определяем вектор нормали N 3;5
Из канонического уравнения можно перейти к уравнению
с угловым коэффициентом
x 2 y 4
5
3
3
x y 4
5
3
y x 4
5
k 3 / 5
5.

Составить уравнение прямой, проходящей через точку M 0 (4; 1)
перпендикулярно прямой
x 3t 1
y 2t 5
M 0 (4; 1)
s 3; 2
A( x x0 ) B( y y0 ) 0
3( x 4) 2( y 1) 0
Прямая задана параметрическими
уравнениями, из которых найдем
направляющий вектор s 3; 2
Из рисунка видно, что
направляющий вектор известной
прямой является вектором нормали
для искомой прямой, поэтому
используем уравнение прямой с
известной точкой и вектором
нормали
3x 12 2 y 2 0
3x 2 y 14 0
Получили общее уравнение прямой, из которого N 3; 2 ,
Записав уравнение в виде
3
( y 1) ( x 4) ,
2
3
найдем угловой коэффициент k
2
s 2;3
6. Составить уравнение прямой, проходящей через точку
перпендикулярно прямой y 1 x 3
5
M 0 (3;2)
Из уравнения заданной прямой можно взять угловой коэффициент
k
1
5
Из условия перпендикулярности прямых
можно найти угловой коэффициент
перпендикулярной прямой
k2
k1 k 2 1
1
1
5
k1
( 1 / 5)
Теперь берем уравнение прямой с угловым коэффициентом и
подставляем координаты точки и значение углового коэффициента
y y0 k ( x x0 )
y 5x 13
y 2 5( x 3) y 2 5x 15
Или 5x y 13 0 — общее уравнение N 5; 1 ,
s 1;5

11.

Взаимное расположение прямых на плоскостиЗадачи на взаимное расположение прямых включают слежующие
вопросы:
1.
Нахождение точки пересечения.
2.
Нахождение угла между прямыми
3.
Проверка условий параллельности и перпендикулярности
прямых
Для нахождения точки пересечения нужно решить систему,
составленную из уравнений этих прямых, например
2 x 5 y 4 0
3x 2 y 1 0
2 5
3
y
2
4 ( 15) 19
2 4
3
1
Систему можно решить методом Крамера
2 ( 12) 14
x
4 5
x
1
2
8 ( 5) 3
x 3
19
Точка пересечения
y
y
3 14
M ;
19 19
14
19

12. Нахождение угла между прямыми

.
1 Если прямые заданы общими уравнениями, то угол между
прямыми – это угол между векторами нормалей и используется
формула косинуса угла между векторами
cos
( N1 N 2 )
N1 N 2
A1 A2 B1 B2
A1 B12 A2 B22
2
2
2. Если прямые заданы каноническими уравнениями, то угол между
прямыми – это угол между направляющими векторами
( s1 s2 )
m1m2 n1n2
cos
2
2
s1 s2
m1 n12 m2 n22
3.

Если прямые заданы угловыми коэффициентами, то находят
тангенс угла
k k
tg 2 1
1 k1 k 2

13. Проверка условий параллельности и перпендикулярности прямых

1. Условия параллельности прямых
A1 B1
A2 B2
m1 n1
m2 n2
k1 k 2
2. Условия перпендикулярности прямых
1 k1 k 2 0
A1 A2 B1 B2 0
m1m2 n1n2 0
1
k2
k1
Расстояние от точки M 1 ( x1 ; y1 ) до прямой Ax By C 0
d
Ax1 By1 C
A2 B 2
Для нахождения расстояния от точки до прямой нужно координаты точки
Подставить в левую часть уравнения прямой, разделить на длину
вектора нормали и полученное значение взять по абсолютной величине.
Уравнение прямой должно быть приведены к общему виду
x 4 y 9
1. Найти угол между прямыми 2 x y 3 0 и
5
4
Из уравнения первой прямой определяем вектор нормали N1 2; 1
Из уравнения второй прямой находим направляющий вектор s 5;4
Тогда вектор нормали этой прямой N 2 4; 5
Используем формулу cos ( N1 N 2 )
N1 N 2
cos
A1 A2 B1 B2
A1 B12 A2 B22
2
2
2 4 ( 1) ( 5)
13
4 1 16 25
5 41
2.

Найти расстояние от точки M 0 ( 1; 4) до прямой
Приведем сначала уравнение прямой к общему виду
x y
1
5 7
7 x 5 y 35
или 7 x 5 y 35 0 . Теперь можно использовать формулу
Ax By C 7( 1) 5( 4) 35 62
62
d 1 2 1 2
74
74
A B
7 2 52

15. Кривые 2-го порядка

Общее уравнение прямой на плоскости – есть уравнение
линейное относительно переменных x и y
Ax By C 0
Уравнение кривой 2-го порядка
Ax 2 2 Bxy Cy 2 Dx Ey F 0
Ax 2 2 Bxy Cy 2 квадратичная часть
линейная часть
Dx Ey F 0
В дальнейшем
будем рассматривать уравнения кривых,
.
в которых отсутствует произведениеxy
Ax2 Cy 2 Dx Ey F 0
К кривым 2-го порядка относятся :
окружность, эллипс, гипербола и парабола.
Основная задача состоит в умении по уравнению определить
тип кривой, привести само уравнение к каноническому
виду и построить кривую в системе координат.

16. 1. Окружность

Определение. Окружностью называется множество точек
плоскости, равноудаленных от одной точки, называемой центром
Уравнение окружности с центром в начале координат
x2 y2 R2
Уравнение окружности со смещенным центромO ‘ ( x0 ; y0 )
( x x0 ) 2 ( y y 0 ) 2 R 2
!
В уравнение окружности входят квадраты переменных,
причем коэффициенты при квадратах и знаки
при них одинаковые.

Y
Y
y0
O
O’
X
O
x0
X

17. Построение окружностей

1. Построить окружность
2. Построить окружность
x2 y2 9
3
( x 1) 2 ( y 2) 2 9
Y
O
Y
R 3
3 X
2
O’
1
3. Построить окружность
y 1 x2
Y
y 2 ( 1 x 2 ) 2
y2 1 x2
y2 x2 1
O
y 0
1
1 X
O
X
2
2
Построить окружность x 6 x y 4 y 12
( x x0 ) 2 ( y y 0 ) 2 R 2
Каноническое уравнение
Формула квадрата суммы и разности двух чисел
( a b) 2 a 2 2 a b b 2
1. ( x 6 x) ( y 4 y ) 12
2
2
2
2
2
2
2. ( x 2 x 3 3 3 ) ( y 2 y 2 2 2 ) 12
2
2
Y
3. [( x 3) 9] [( y 2) 4] 12
2
4.
2
( x 3) 2 ( y 2) 2 9 4 12
2
2
(
x
3
)
(
y
2
)
25
5.
2
2
2
(
x
3
)
(
y
2
)
5
6.
O ( 3;2) центр окружности,
‘
R 5 радиус окружности
O’
3
2
O
X

19.

2. ЭллипсОпределение. Эллипсом называется множество точек
плоскости, сумма расстояний которых до двух данных точек,
называемых фокусами , есть величина постоянная, равная
длине большой оси 2a .
Каноническое уравнение эллипса
Y
b B1 M ( x; y)
x2 y2
2 1, причем
2
A2 F2
a
b
F1 A1
c
O
a c
a
X
B2
a 2 b2 c 2
b
A1 (a;0) A2 ( a;0)
F1 (c;0)
F2 ( c;0)
вершины эллипса
B1 (0; b) B2 (0; b)
фокусы эллипса
A1 A2 2a
большая ось эллипса
F1 F2 2c фокусное расстояние
B1 B2 2b
малая ось эллипса
В уравнение эллипса входят квадраты переменных,
причем знаки при квадратах одинаковые, а коэффициенты
при квадратах разные.
!

20. Разновидности эллипса

Уравнение эллипса со смещенным центром
Y
( x x0 ) 2 ( y y0 ) 2
1
2
2
a
b
O ‘ ( x0 ; y 0 ) — центр эллипса
b
a
x0
X
y0
a
O’
b
Если в уравнении эллипса b a , то большой осью будет ось
B1 B2 2b , фокусы эллипса будут
B1 b
.

лежать на этой оси и связь
между параметрами эллипса
будет такой:
b2 a 2 c 2
F1 c
a
O
.
F2 c
B2 b
a

21. Построение эллипса

1. Построить эллипс
x2 y2
1
4
2
Для построения эллипса нужно знать координаты центра и
размеры полуосей a и b
Y
Центр эллипса O(0;0)
2
Полуоси a 4 a 2,
b2 2 b 2
2
.
Расстояние между фокусами
2 2
c 2 a 2 b 2 4 2 2,
c 2 , т.е. 2c 2 2
O
.
2
X
2
2
Можно найти площадь фигуры, ограниченной эллипсом по формуле
S a b
Для данного примера получим
S 2 2 2 2
2. Построить эллипс
9 x 2 5 y 2 45
Для получения канонического уравнения делаем некоторые
преобразования:
1) Делим все члены уравнения на 45, так чтобы получит единицу
в правой части уравнения
9×2 5 y 2
1
45
45
2) Убираем в знаменатель коэффициенты из числителей
x2
y2
1
45 / 9 45 / 5
x2 y2
1
5
9
Получили уравнение эллипса, из которого определяем положение
Y
центра и размеры полуосей
3
O(0;0) — центр эллипса
a 2 5 a 5,
— полуоси
b2 9 b 3
b a
3) Строим эллипс
5
O
5
3
X
3.

Построить кривую
x 1 9 4 y 2
Y
2
2
1. ( x 1) 4 y 9
2. x 1
9 4 y2
3. ( x 1) 9 4 y
2
b
a
2
O’
1
O
X
2
2
(
x
1
)
4
y
9
4.
( x 1) 2 4 y 2
1
5.
9
9
( x 1) 2
y2
1
9
9/4
Таким образом, центр эллипса имеет координаты
Полуоси эллипса
O ‘ ( 1;0)
a 2 9 a 3,
b 2 9 / 4 b 3 / 2 , т.е. a b
При построении необходимо учесть, что уравнение определяет
Только правую половинку эллипса, так как по условию имеем x
1
3x 2 6 x 2 y 2 2 y 0
4. Построить кривую
Данное уравнение определяет эллипс, так как есть квадраты
переменных, знаки при которых одинаковые, а коэффициенты
различные. Кроме того, наличие линейной части уравнения
означает, что центр эллипса смещен от начала координат.
Приводим уравнение к каноническому виду
( x x0 ) 2 ( y y0 ) 2
1
2
2
a
b
Используем прием выделения полного квадрата согласно формуле
( a b) 2 a 2 2 a b b 2
2
2
1.

3( x 2 x) 2( y y ) 0
2. 3( x 2 x 1 1 1 ) 2( y 2 y 1/ 2 (1/ 2) (1/ 2) ) 0
3. 3[( x 1) 2 1] 2[( y 1 / 2) 2 1 / 4] 0
2
2
2
2
2
4. 3( x 1) 2( y 1 / 2) 3 1 / 2 0
5. 3( x 1) 2 2( y 1 / 2) 2 7 / 2
2
2
( x 1) 2 ( y 1 / 2) 2
6. 3( x 1) 2( y 1 / 2) 1
1
7/2
7/2
7/6
7/4
7
O ‘ ( 1;1/ 2) центр , a 7 / 6 , b
полуоси
2
2
2
Y
2
O’
1/ 2
1
O
X

25. 3. Гипербола

Определение. Гиперболой называется множество точек
плоскости, разность расстояний которых до двух данных точек,
называемых фокусами ,по абсолютной есть величина
постоянная, равная длине действительной оси 2a .
Каноническое уравнение гиперболы с центром в начале координат
x2 y2
2 1
2
a b
В этом случае
a действительная полуось
b мнимая полуось
Фокусы гиперболы всегда лежат на действительной оси.
Связь между параметрами гиперболы определяется соотношением
c 2 a 2 b2
!
В уравнение гиперболы входят квадраты
переменных, причем знаки при квадратах разные.

Асимптоты гиперболы – это прямые к которым гипербола
неограниченно приближается на бесконечности.

26. Построение гиперболы

x2 y2
2 1
2
a b
Построение гиперболы
Для построения гиперболы удобно пользоваться
вспомогательными построениями.
1. В системе координат строим прямоугольник с размерами 2a 2b
на осях OX и OY соответственно.
2. Проводим диагонали этого прямоугольника.
Уравнения диагоналей – это уравнения асимптот гиперболы
b
y x
a
3. На действительной оси отмечаем вершины гиперболы и от них
ведем ветви гиперболы к асимптотам.
Y
Y
Y
b
a
a
b
b
b
X
a
a
b
X
c a
a c
b
X

27. Виды гипербол

Y
Рассмотрим другие виды гипербол
Сопряженная гипербола
2
c
2
x
y
1
2
2
a b
b
a X
b действительная полуось
a мнимая полуось
c
Равнобочная гипербола
2
2
x
y
x 2 y 2 a 2 или 2 2 1
a
a
Y
b
Гипербола со смещенным центром O ( x0 ; y0 )
‘
( x x0 ) ( y y0 )
1
2
2
a
b
Гипербола, приведенная к своим асимптотам
2
xy a
2
или
a
y
x
X
a
O’
Y
X
Рассмотрим примеры построения гипербол
1.

Построить гиперболу 4 x 2 3 y 2 12
2
Y
2
4x 3y
1
12
12
2
x2
y2
1
12 / 4 12 / 3
X
3
x2 y2
1
3
4
2
O(0;0) центр гиперболы
a2 3
3
a 3 действительная полуось
b2 4 b 2
мнимая полуось
c 2 a 2 b 2 3 4 7,
c 7
2c 2 7
расстояние между фокусами
.
2 Построить кривую
y x2 4
Возведем в квадрат обе части уравнения
y2 x2 4
Собираем квадраты переменных в левую часть уравнения
x2 y2 4
Данное уравнение определяет гиперболу, так как знаки при квадратах
переменных разные. Кроме того, данная гипербола
является сопряженной и равнобочной
x2 y2
Можно записать уравнение в виде
1
Y
4
4
a 2 4 a 2 мнимая полуось
2
b 2 4 b 2 действительная
X
полуось
2
2
Оставляем только нижнюю ветвь
2
гиперболы, так как по условию
y 0
3. Построить кривую
4 x 2 3 y 2 12 8 x 12 y
Данное уравнение определяет гиперболу (знаки при квадратах
переменных различные) со смещенным центром (есть линейная часть)
Приведем уравнение к каноническому виду
( x x0 ) 2 ( y y 0 ) 2
1
a2
b2
4( x 2 2 x) 3( y 2 4 y) 12
4 x 2 8 x 3 y 2 12 y 12
Y
4( x 2 2 x 1 12 12 ) 3( y 2 2 y 2 2 2 2 2 ) 12
4[( x 1) 2 1] 3[( y 2) 2 4] 12
4( x 1) 2 4 3( y 2) 2 12 12
1
4( x 1) 2 3( y 2) 2 4
4( x 1) 2 3( y 2) 2
1
4
4
X
2
O’
( x 1) 2 ( y 2) 2
1
1
4/3
O ‘ ( 1; 2) центр гиперболы
4
2
b
мнимая полуось
a 1 действительная полуось
3
3

31.

4. ПараболаОпределение. Параболой называется множество точек
плоскости, равноудаленных от одной точки, называемой
фокусом, и от данной прямой, называемой директрисой.
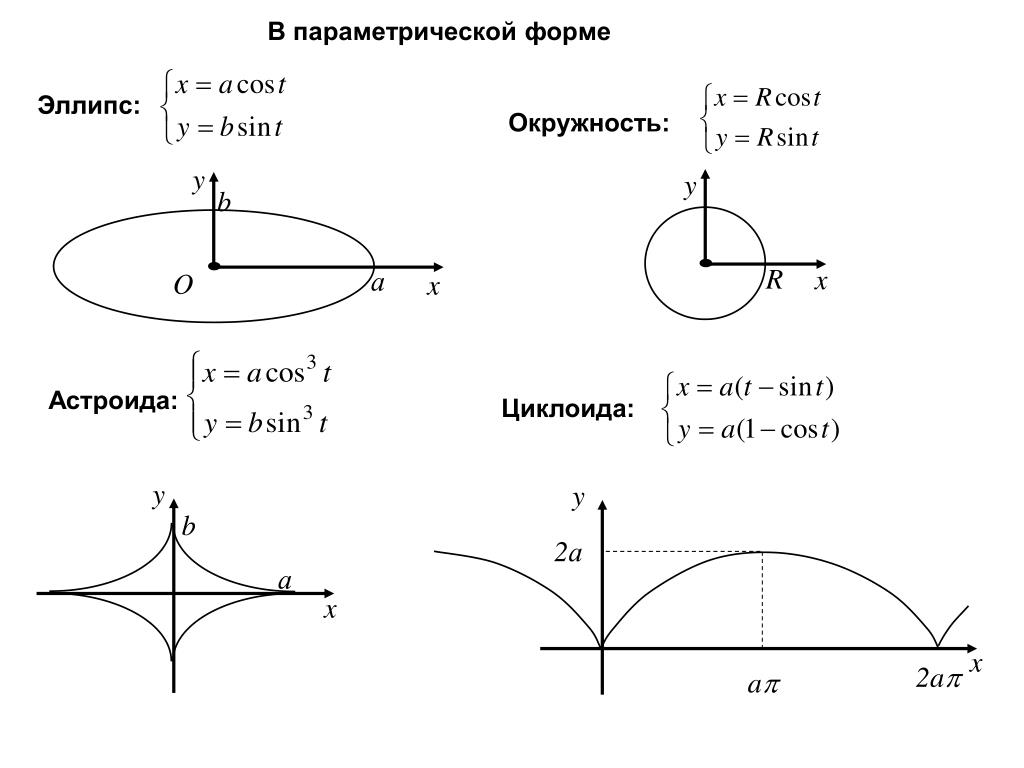
Виды парабол
Парабола с осью симметрии OX
x 2 2 py
y 2 px
2
Y
Y
y 2 px
2
Парабола c осью симметрии OY
y 2 2 px
X
x 2 2 py
X
x 2 2 py
Парабола со смещенной вершиной O’ ( x0 ; y0 )
Парабола с осью симметрии OX
Парабола c осью симметрии OY
( x x0 ) 2 2 p( y y0 )
( y y0 ) 2 2 p( x x0 )
Y
y0
Y
O’
x0
x0
!
X
y0
Отличительные признаки уравнения параболы:
отсутствует квадрат одной переменной.
O’
X

33. Построение парабол

Для построения параболы нужно знать:
O’ ( x0 ; y0 ) .
Координаты вершины
Ось симметрии параболы (определяется по той переменно,
квадрат которой отсутствует в уравнении)
Направление ветвей (определяется по знаку : если в правой
части канонического уравнения знак плюс, то ветви параболы
идут в положительном направлении оси симметрии, если знак
минус, то в отрицательном )
Параметр параболы p определяется по коэффициенту при
переменной, стоящей в каноническом уравнении в первой
степени, и определяет «ширину» параболы.

Знание параметра
помогает более качественно получить начальный участок
параболы.
2
(
y
2
)
4( x 1)
1. Построить параболу
Данное уравнение является каноническим уравнением параболы,
так как отсутствует квадрат переменной x . Поэтому осью
симметрии параболы будет ось OX.
Вершина параболы в точке O’ (1;2)
Ветви параболы направлены в положительном направлении оси OX,
так как в правой части уравнения знак “плюс”.
2 p 4 ширина параболы
p 2 параметр параболы
p
1
2
Y
p
2
O’ p p
2
1
X
2. Построить кривую
y 3 2 1 x
Y
y 3 2 1 x
( y 3) 2 4(1 x)
( y 3) 2 4( x 1)
y 3
3
O’
X
O
1
O’ (1;3) вершина параболы
Ось симметрии параболы OX, так как отсутствует квадрат
переменной x
Ветви параболы направлены влево, так как в правой части уравнения
получился знак “минус”
p 2 параметр параболы
Так как по условию y 3 , то уравнение определяет только
верхнюю ветвь параболы
3.

Построить кривую
y 2 x2
Преобразуем уравнение
x2 2 y
x 2 ( y 2)
Уравнение определяет параболу. Сравнивая с уравнением
( x x0 ) 2 2 p ( y y0 ) , определяем координаты вершины
O’ (0;2) . Ось симметрии OY. Ветви направлены вниз.
1 параметр параболы
p
2
Y
O’ 2
p
1
2
1 1
O
X
4. Построить параболу
4×2 6x 3 y 2 0
В уравнении отсутствует квадрат переменной y, поэтому оно
определяет параболу с осью симметрии OY.
Проведем преобразования уравнения, чтобы привести его к
каноническому виду ( x x0 ) 2 2 p ( y y0 )
6
4 x 2 x 3 y 2 0
4
3
2
4 x 2 x (3 / 4) 2 (3 / 4) 2 3 y 2 0
4
2
3 9
3
9
4 x 3 y 2 0
4 x 3 y 2 0
4 4
4 16
Y
2
3
1
O ‘ y0
4 x 3 y
4
4
X
x0 O
2
3
1
4 x 3 y или
4
12
2
3
3
1
x y
4
4
12
3
3 1
O ‘ ; вершина параболы p параметр параболы
8
4 12
Ветви параболы направлены вниз
2

Решение высшей математики онлайн

‹— Назад

Из школьного курса математики известно, что кривая, задаваемая уравнением , где — число, называется гиперболой.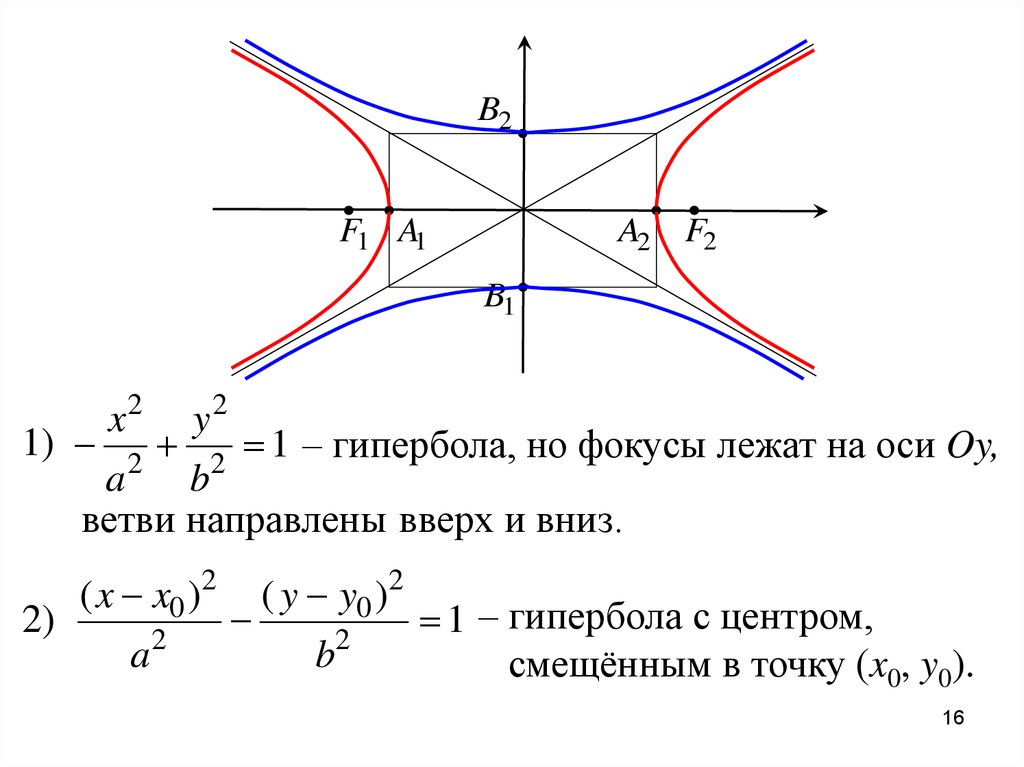 Однако это — частный случай гиперболы (равносторонняя гипербола).

Определение 12.5 Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.

Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось направим вдоль этого отрезка, а ось ординат — перпендикулярно к нему.

Теорема 12.3 Пусть расстояние между фокусами и гиперболы равно , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна . Тогда гипербола в выбранной выше системе координат имеет уравнение

(12.

где

(12.9)

Доказательство. Пусть — текущая точка гиперболы (рис. 12.9).

Рис.12.9.

Так как разность двух сторон треугольника меньше третьей стороны, то , то есть , . В силу последнего неравенства вещественное число , определяемое формулой (12.9), существует.

По условию, фокусы — , . По формуле (10.4) для случая плоскости получаем

По определению гиперболы

Это уравнение запишем в виде

Обе части возведем в квадрат:

После приведения подобных членов и деления на 4, приходим к равенству

Опять обе части возведем в квадрат:

Раскрывая скобку и приводя подобные члены, получим

С учетом формулы (12.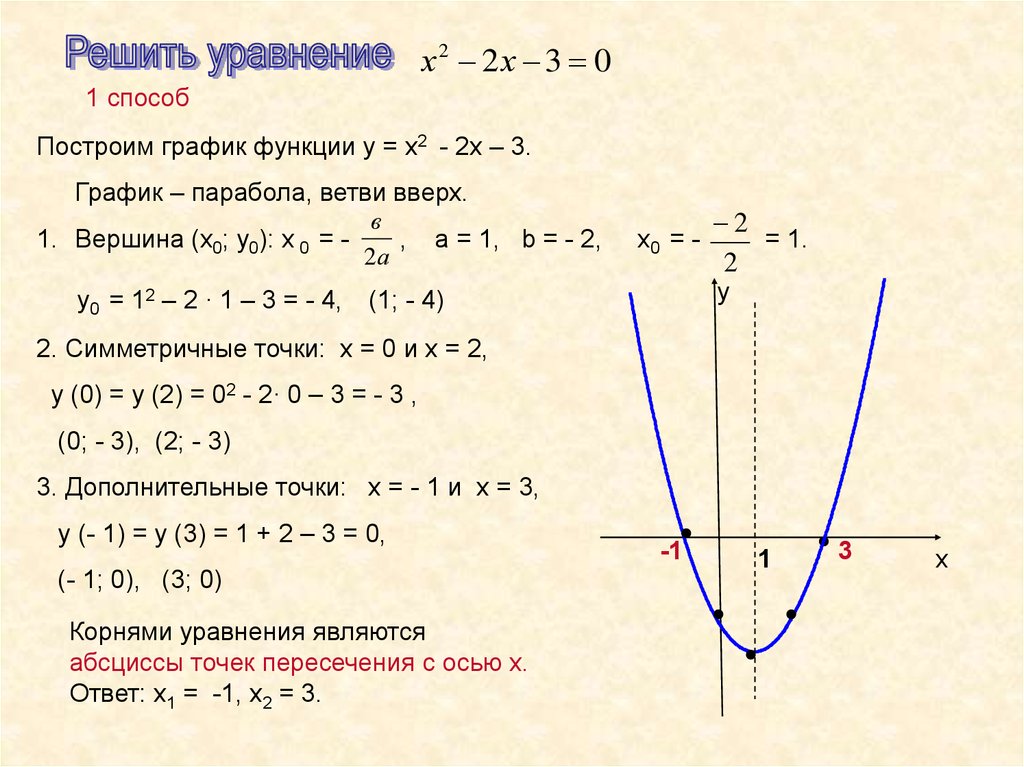 9) уравнение принимает вид

Разделим обе части уравнения на и получим уравнение (12.8)

Уравнение (12.8) называется каноническим уравнением гиперболы.

Предложение 12.3 Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси и , а начало координат — центр симметрии гиперболы.

Доказательство. Проводится аналогично доказательству предложения 12.1.

Проведем построение гиперболы, заданной уравнением (12.8). Заметим, что из-за симметрии достаточно построить кривую только в первом координатном угле. Выразим из канонического уравнения как функцию , при условии, что ,

и построим график этой функции.

Область определения — интервал , , функция монотонно растет. Производная

существует во всей области определения, кроме точки . Следовательно, график — гладкая кривая (без углов). Вторая производная

во всех точках интервала отрицательна, следовательно, график — выпуклый вверх.

Проверим график на наличие асимптоты при . Пусть асимптота имеет уравнение . Тогда по правилам математического анализа

Выражение под знаком предела домножим и разделим на . Получим

Итак, график функции имеет асимптоту . Из симметрии гиперболы следует, что — тоже асимптота. Остается неясным характер кривой в окрестности точки , а именно, образует ли график и симметричная ему относительно оси часть гиперболы в этой точке угол или гипербола в этой точке — гладкая кривая (есть касательная). Для решения этого вопроса выразим из уравнения (12.8) через :

Очевидно, что данная функция имеет производную в точке , , и в точке у гиперболы есть вертикальная касательная. По полученным данным рисуем график функции (рис. 12.10).

Рис.12.10.График функции

Окончательно, используя симметрию гиперболы, получаем кривую рисунка 12.11.

Рис.12.11.Гипербола

Определение 12.6 Точки пересечения гиперболы, заданной каноническим уравнением (12.8), с осью называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками и называется мнимой осью. Числа и называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина называется эксцентриситетом гиперболы.

Замечание 12.3 Из равенства (12.9) следует, что , то есть у гиперболы . Эксцентриситет характеризует угол между асимптотами, чем ближе к 1, тем меньше этот угол.

Замечание 12.4 В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами и может быть произвольным. В частности, при мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид , если взять , а оси и направить по биссектрисам четвертого и первого координатных углов (рис. 12.12).

Рис.12.12.Равносторонняя гипербола

Для отражения на рисунке качественных характеристик гиперболы достаточно определить ее вершины, нарисовать асимптоты и нарисовать гладкую кривую, проходящую через вершины, приближающуюся к асимптотам и похожую на кривую рисунка 12.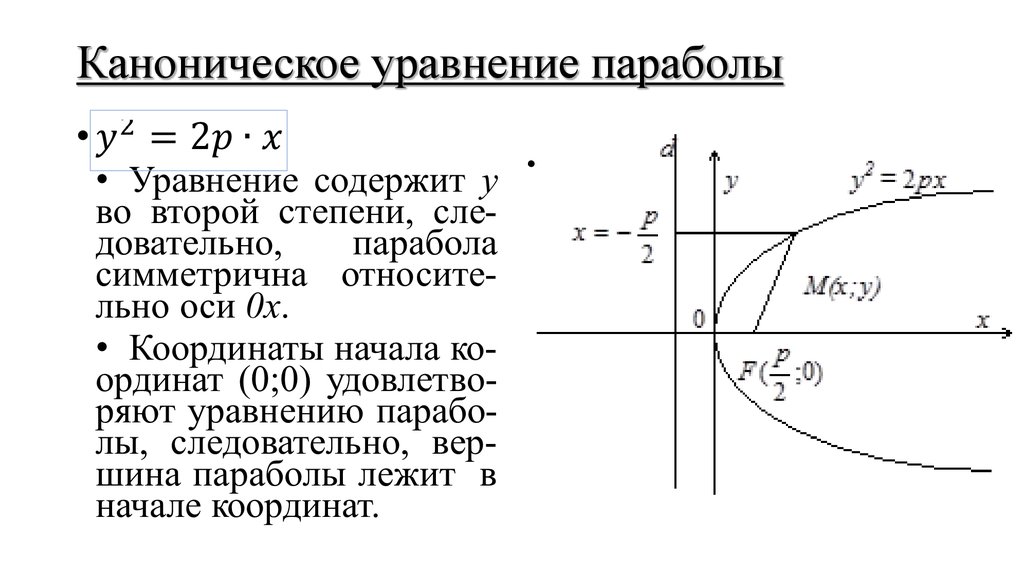 10.

Пример 12.4 Постройте гиперболу , найдите ее фокусы и эксцентриситет.

Решение. Разделим обе части уравнения на 4. Получим каноническое уравнение

, . Проводим асимптоты и строим гиперболу (рис. 12.13).

Рис.12.13.Гипербола

Из формулы (12.9) получим . Тогда фокусы — , , .

Пример 12.5 Постройте гиперболу . Найдите ее фокусы и эксцентриситет.

Решение. Преобразуем уравнение к виду

Данное уравнение не является каноническим уравнением гиперболы, так как знаки перед и противоположны знакам в каноническом уравнении. Однако, если переобозначить переменные , , то в новых переменных получим каноническое уравнение

Действительная ось этой гиперболы лежит на оси , то есть на оси исходной системы координат, асимптоты имеют уравнение , то есть уравнение в исходных координатах.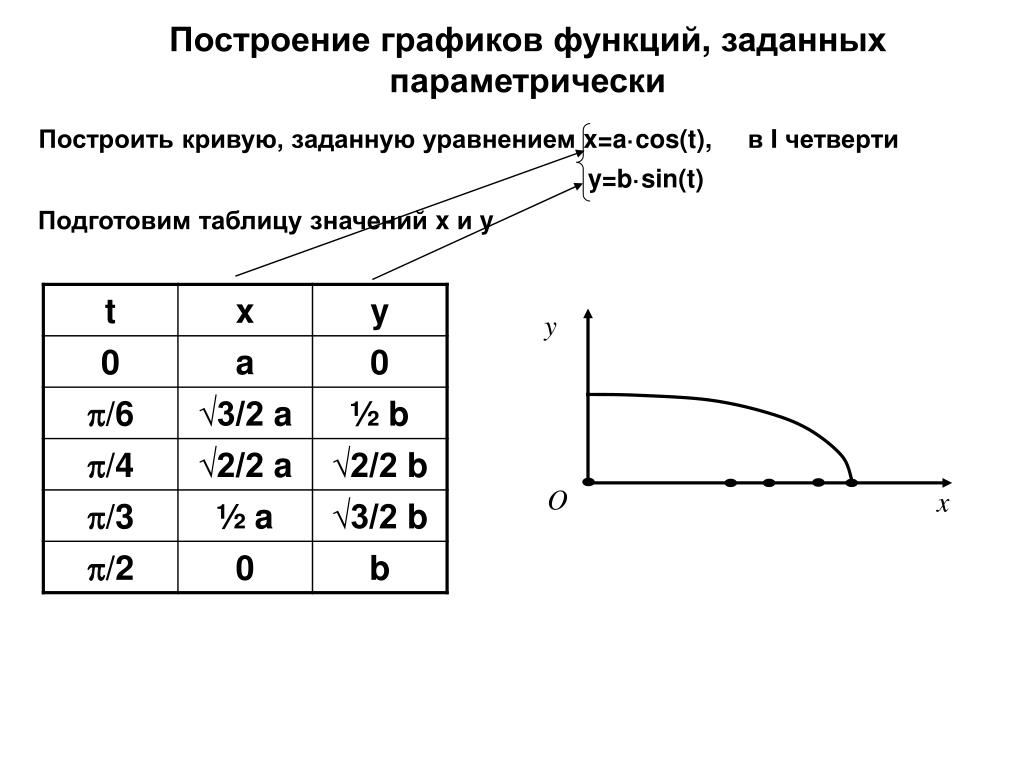 Действительная полуось равна 5, мнимая — 2. В соответствии с этими данными проводим построение (рис. 12.14).

Рис.12.14.Гипербола с уравнением

Из формулы (12.9) получим , , фокусы лежат на действительной оси — , , где координаты указаны в исходной системе координат.

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Подгонка кривой с использованием линейной и нелинейной регрессии

В регрессионном анализе подгонка кривой — это процесс определения модели, которая обеспечивает наилучшее соответствие конкретным кривым в вашем наборе данных. Криволинейные отношения между переменными не так просто подобрать и интерпретировать, как линейные отношения.

Для линейных отношений, когда вы увеличиваете независимую переменную на одну единицу, среднее значение зависимой переменной всегда изменяется на определенную величину. Это соотношение сохраняется независимо от того, где вы находитесь в пространстве наблюдения.

К сожалению, реальный мир не всегда так хорош и опрятен. Иногда ваши данные имеют кривые отношения между переменными. В криволинейной зависимости изменение зависимой переменной, связанное со сдвигом независимой переменной на одну единицу, варьируется в зависимости от местоположения в пространстве наблюдения. Другими словами, эффект независимой переменной не является постоянной величиной.

Прочтите мой пост, в котором я обсуждаю, как интерпретировать коэффициенты регрессии как для линейных, так и для криволинейных отношений, чтобы увидеть это в действии.

В этом посте я расскажу о различных методах подгонки кривой, используя как линейную регрессию, так и нелинейную регрессию.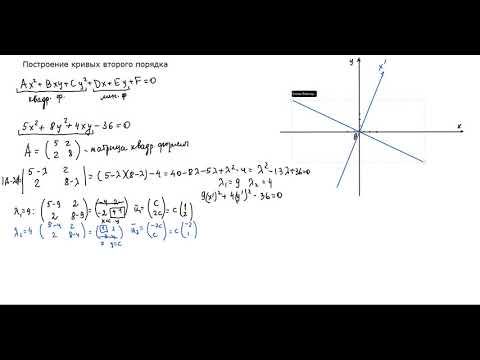 Я также покажу вам, как определить, какая модель подходит лучше всего.

Связанный пост : Что такое независимые и зависимые переменные?

Зачем нужно подгонять кривые в регрессионной модели

Приведенный ниже график с подгонкой иллюстрирует проблему использования линейной связи для подбора криволинейной зависимости. R-квадрат высокий, но модель явно неадекватна. Вам нужно сделать кривую подгонку!

Когда у вас есть одна независимая переменная, легко увидеть кривизну, используя построенный график. Однако при множественной регрессии искривленные отношения не всегда так очевидны. В этих случаях остаточные графики являются ключевым индикатором того, адекватно ли ваша модель отражает криволинейные отношения.

Если вы видите шаблон на остаточных графиках, ваша модель не обеспечивает адекватного соответствия данным. Распространенной причиной является то, что ваша модель неправильно моделирует кривизну. Построение остатков по каждой из ваших независимых переменных может помочь вам найти кривую зависимость.

Связанный пост : Проверьте остаточные графики, чтобы убедиться в достоверности результатов!

В других случаях вам может потребоваться знание предметной области для подбора кривой. Предыдущий опыт или исследования могут подсказать вам, что влияние одной переменной на другую зависит от значения независимой переменной. Возможно, существует предел, порог или точка убывающей отдачи, когда отношения меняются?

Чтобы сравнить методы подгонки кривой, я буду подгонять модели под кривую на приведенном выше графике подгонки, потому что это не так просто. Предположим, что эти данные получены из физического процесса с очень точными измерениями. Нам нужно производить точные прогнозы вывода для любого указанного ввода. Вы можете загрузить набор данных CSV для этих примеров: CurveFittingExample.

Аппроксимация кривых с использованием полиномиальных членов в линейной регрессии

Несмотря на свое название, вы можете аппроксимировать кривые с помощью линейной регрессии. Наиболее распространенным методом является включение полиномиальных членов в линейную модель. Полиномиальные члены — это независимые переменные, которые вы возводите в степень, например, члены в квадрате или в кубе. Узнайте больше о линейной регрессии.

Чтобы определить, какой член полинома следует включить, просто посчитайте количество изгибов линии. Возьмите количество изгибов на вашей кривой и добавьте один для нужного вам порядка модели. Например, квадратичные члены моделируют один изгиб, а кубические члены моделируют два. На практике кубические члены встречаются очень редко, и я никогда не видел членов четвертой степени или выше. Когда вы используете полиномиальные термины, подумайте о стандартизации ваших непрерывных независимых переменных.

Линейная

Квадратичная

Кубическая

Наши данные имеют один изгиб. Давайте подгоним линейную модель к квадратичному члену.

R-квадрат увеличился, но линия регрессии не совсем совпадает. Подогнанная линия предсказывает завышенные и заниженные данные в разных точках кривой. Высокий R-квадрат подтверждает то, что я делаю в своем посте о том, как интерпретировать R-квадрат. Высокие значения R-квадрата не всегда представляют собой хорошие модели, и вам необходимо проверить остаточные графики!

Попробуем другие модели.

Аппроксимация кривой с использованием обратных членов в линейной регрессии

Когда ваша зависимая переменная опускается до минимума или поднимается до потолка (т. е. приближается к асимптоте), вы можете попробовать аппроксимацию кривой, используя обратную величину независимой переменной (1/X). . Используйте обратный член, когда влияние независимой переменной уменьшается по мере увеличения ее значения.

Значение этого члена уменьшается по мере увеличения независимой переменной (X), поскольку оно находится в знаменателе. Другими словами, по мере увеличения X влияние этого члена уменьшается, и наклон становится более плоским. X не может равняться нулю для этого типа модели, потому что вы не можете делить на ноль.

Для наших данных увеличение выходных данных выравнивается по мере увеличения входных данных. Похоже, что асимптота находится около 20. Давайте попробуем подобрать кривую с обратным членом. В наборе данных я создал столбец для 1/Input (InvInput). Я подбираю модель с линейным обратным членом (вверху), а другую — с квадратичным обратным членом (внизу).

В нашем примере набора данных квадратичная обратная модель намного лучше соответствует кривизне. Графики меняют масштаб оси x на 1/Input, что затрудняет просмотр естественной кривой в данных.

Чтобы показать естественный масштаб данных, я построил диаграмму рассеяния ниже, используя уравнения регрессии. Ясно, что зеленые точки данных ближе к квадратичной линии.

На аппроксимированных графиках квадратичная обратная модель имеет более высокое значение R-квадрата (хорошо) и более низкое значение S (хорошо), чем квадратичная модель. Он также не отображает смещенные подогнанные значения. Эта модель обеспечивает наилучшее соответствие данным на данный момент!

Аппроксимация кривой с логарифмическими функциями в линейной регрессии

Логарифмическое преобразование позволяет линейным моделям соответствовать кривым, которые в противном случае возможны только с нелинейной регрессией.

Например, вы можете выразить нелинейную функцию:

Y = E ^B0 x ₁ ^B1 x ₂ ^B2

В линейной форме:

ln y = B ₀

в линейной форме:

ln y = b ₀

. + B ₁ lnX ₁ + B ₂ lnX ₂

Ваша модель может принимать логарифмы с обеих сторон уравнения, которое представляет собой двойную логарифмическую форму, показанную выше. Или вы можете использовать полулогарифмическую форму, в которой вы берете журнал только с одной стороны. Если вы берете журналы на стороне независимой переменной модели, это может быть для всех или подмножества переменных.

Использование логарифмических преобразований — мощный метод подбора кривых. Слишком много возможностей, чтобы охватить их все. Выбор между двойной логарифмической и полулогарифмической моделью зависит от ваших данных и предметной области. Если вы используете этот подход, вам нужно будет провести некоторое расследование.

Давайте применим это к нашей примерной кривой. Полулогарифмическая модель может соответствовать кривым, которые сглаживаются по мере увеличения независимой переменной. Давайте посмотрим, как полулогарифмическая модель соответствует нашим данным!

На приведенном ниже графике с подгонкой я преобразовал независимую переменную.

Подобно первой квадратичной модели, которую мы подогнали, полулогарифмическая модель обеспечивает смещенную подгонку к точкам данных. Кроме того, значения S и R-квадрата очень похожи на эту модель. Модель с квадратичным обратным членом по-прежнему обеспечивает наилучшее соответствие.

До сих пор мы выполняли подгонку кривой, используя только линейные модели. Давайте переключим передачу и попробуем модель нелинейной регрессии.

Связанный пост : Использование логарифмических графиков для определения того, имеет ли значение размер

Аппроксимация кривой с помощью нелинейной регрессии

Нелинейная регрессия — очень мощная альтернатива линейной регрессии. Это обеспечивает большую гибкость в подборе кривых, поскольку вы можете выбирать из широкого диапазона нелинейных функций. На самом деле существует так много возможных функций, что вся хитрость заключается в том, чтобы найти функцию, которая лучше всего соответствует конкретной кривой в ваших данных.

Большинство пакетов статистического программного обеспечения, выполняющих нелинейную регрессию, имеют каталог нелинейных функций. Вы можете использовать это, чтобы помочь выбрать функцию. Кроме того, поскольку нелинейная регрессия использует итеративный алгоритм для поиска наилучшего решения, вам может потребоваться указать начальные значения для всех параметров функции.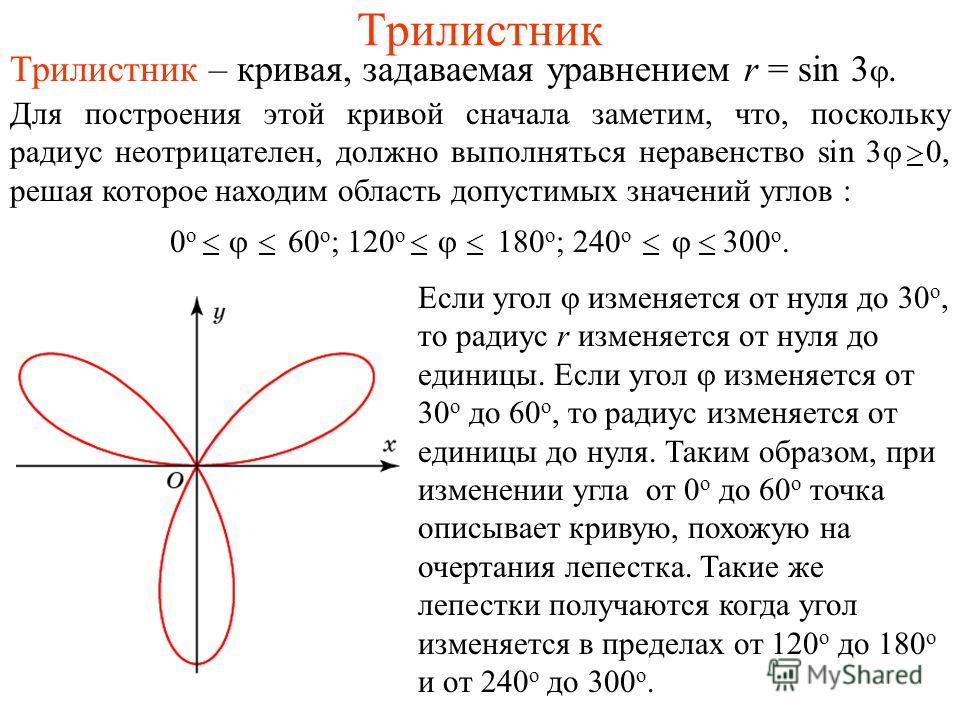

Наши данные приближаются к асимптоте, которая помогает нам выбрать нелинейную функцию из приведенного ниже каталога.

Диаграмма в каталоге помогает нам определить начальные значения. Theta1 – это асимптота. Для наших данных это около 20. Исходя из формы нашей кривой, Theta2 и Theta3 должны быть больше 0.

Следовательно, я буду использовать следующие начальные значения для параметров:

Тета1: 20
Тета2: 1
Тета3: 1

На приведенном ниже линейном графике показана модель нелинейной регрессии.

Нелинейная модель обеспечивает превосходное объективное соответствие данным. Давайте сравним модели и определим, какая из них лучше всего соответствует нашей кривой.

Сравнение эффективности подбора кривой различных моделей

R-квадрат недействителен для нелинейной регрессии. Таким образом, вы не можете использовать эту статистику для оценки соответствия этой модели. Однако стандартная ошибка регрессии (S) действительна как для линейных, так и для нелинейных моделей и служит отличным способом сравнения соответствия между этими типами моделей. Небольшая стандартная ошибка регрессии указывает на то, что точки данных ближе к подобранным значениям.

Модель	R-квадрат	С	Беспристрастный
Обратная – квадратичная	99,9	0,134828	Да
Нелинейный	н/д	0,179746	Да
Квадратичный	99,0	0,518387	№
Полубревно	98,6	0,565293	№
Обратная – Линейная	90,4	1.49655	№
Линейный	84,0	1.93253	№

У нас есть две модели наверху, которые одинаково хороши для получения точных и непредвзятых прогнозов.

Эти две модели представляют собой линейную модель, в которой используется квадратичный обратный член, и нелинейную модель.

Стандартная ошибка регрессии для нелинейной модели (0,179746) почти такая же низкая, как S для обратной модели (0,134828). Разница между ними настолько мала, что вы можете использовать любой из них. Однако с помощью линейной модели вы также получаете значения p для независимых переменных (не показаны) и R-квадрата.

Эти дополнительные статистические данные могут быть полезны для целей отчетности. Однако, если бы нелинейная модель давала гораздо лучшее соответствие, мы бы предпочли использовать ее даже без этой статистики. Узнайте, почему вы не можете получить значения P для переменных в нелинейной модели.

Похожие сообщения

: Разница между моделями линейной и нелинейной регрессии и как выбрать между линейной и нелинейной регрессией.

Заключительные мысли

Подгонка кривой не так уж сложна. Вы можете использовать различные методы, обеспечивающие большую гибкость для соответствия большинству типов кривых. Кроме того, определение лучшей модели включает оценку только нескольких статистических данных и остаточных графиков.

Подготовка исследования и сбор данных — это трудоемкий процесс. Определенно стоит усилий, чтобы найти модель, которая обеспечивает наилучшую посадку.

Каждый раз, когда вы определяете модель, вы должны руководствоваться знаниями предметной области и теорией. Кроме того, некоторые области исследования могут иметь стандартные методы и функции для моделирования данных.

И последнее предупреждение. Вам нужна хорошая подгонка, но вы не хотите переобучать свою регрессионную модель. Модель переобучения слишком сложна, она начинает моделировать случайную ошибку и ложно завышает R-квадрат. Скорректированный R-квадрат и прогнозируемый R-квадрат — это инструменты, которые помогут вам избежать этой проблемы.

Узнайте, как выбрать правильную модель регрессии!

Если вы изучаете регрессию, ознакомьтесь с моим руководством по регрессии!

Примечание. Я написал другую версию этого поста, которая появилась в другом месте. Я полностью переписал и обновил его для своего блога.

Вычисление площади под кривой в Excel (2 простых способа)

Площадь под кривой (AUC) — это широко используемая концепция в науках о данных во многих областях.

Несмотря на то, что концепция площади под кривой довольно проста – она заключается в вычислении общей площади, покрываемой между кривой/прямой и осью – в Excel нет прямого способа вычислить это.

Но это тоже не так уж и сложно!

В этом коротком уроке я покажу вам два способа расчета площади под кривой в Excel .

Итак, приступим!

В этом руководстве рассматриваются:

Формула для расчета площади под кривой в Excel

Как я уже упоминал, прямой формулы для расчета AUC нет, но мы можем вычислить ее, используя вспомогательный столбец и простую формулу.

Ниже у меня есть набор данных, и я создал линейную диаграмму, используя эти данные.

Хотя я не могу вычислить площадь под кривой для всего этого графика, я могу разбить его на маленькие трапеции (как показано ниже), а затем вычислить площадь каждой трапеции.

На приведенном выше изображении графика я разбил каждый интервал на отдельный участок (обозначенный другим цветом), и каждый из этих участков напоминает трапецию.

Хотя я не могу вычислить площадь под кривой линии напрямую, я могу вычислить площадь этих отдельных трапеций.

Как только у меня будет площадь всех этих трапеций, я могу просто добавить их все. Это даст мне очень близкое значение общей площади под графиком.

Ниже приведена формула для расчета площади трапеции

 A = (a+b)/2 * h

где:

a — длина основания одной стороны
b — длина основания другая сторона
h — это высота

Ниже приведена формула, которую я могу использовать (в соседнем столбце) для расчета площади трапеции на диаграмме для моего набора данных:

 =((B2+B3)/2)*(A3-A2)

Примените приведенную выше формулу ко всем ячейкам в столбце (кроме последней).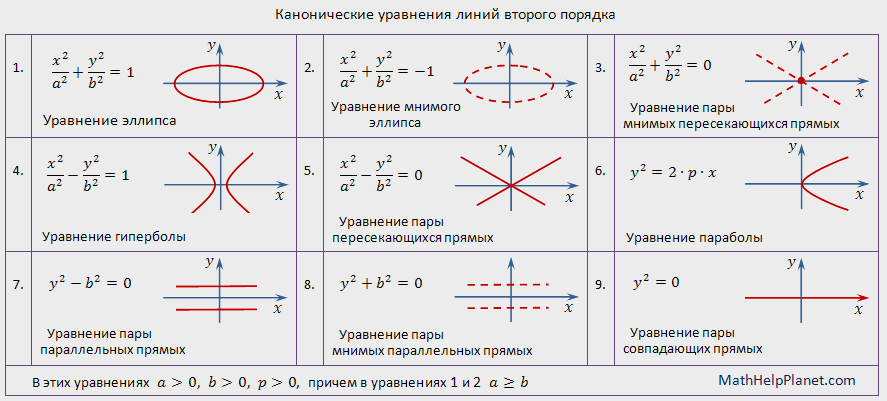

Теперь, когда у меня есть значение трапеции (которое также является площадью под значением кривой) для интервалов по оси X на диаграмме, я могу добавить все это, чтобы получить общую площадь под диаграммой.

Для этого я могу использовать простую формулу СУММ.

Вот как я могу рассчитать общую площадь под кривой для простой линейной диаграммы.

Обратите внимание, что результат этого метода будет очень близок к фактическому значению площади под кривой, он может немного отличаться. Это связано с тем, что область между линией и осью не является идеальной трапецией, но близка к ней.

Использование уравнения линии тренда для площади под кривой

Позвольте мне показать вам еще один метод расчета площади под кривой (AUC) для диаграммы в Excel.

Этот метод использует добавление линии тренда в диаграмму Excel, а затем использование уравнения, которое диаграмма Excel автоматически создает для линии тренда.

Ниже представлен набор данных, для которого я создал линейный график, и теперь я хочу рассчитать площадь под кривой для этого графика.

Ниже приведены шаги для получения уравнения линии тренда для нашего набора данных:

Выберите диаграмму
На вкладке «Дизайн диаграммы» выберите параметр «Добавить элемент диаграммы». Откроется панель «Формат линии тренда». Это покажет полиномиальное уравнение линии тренда на графике 9.0151

Теперь, когда у нас есть полиномиальное уравнение, мы можем использовать его для вычисления площади этой линейной диаграммы.

Но перед этим вам нужно сделать еще один шаг. Вам нужно получить определенный интеграл для полиномиального уравнения.

В моем случае уравнение будет таким:

 y = 1,0038x ² + 2,1826x - 1,85

Таким образом, определенный интеграл этого уравнения будет

 y = (1,0038/3)*x 909090 3 2.1826/2)*х ² - 1.85x + c

Хотя я не являюсь экспертом в области математических вычислений, исходя из моего ограниченного понимания, вы можете преобразовать уравнение в определенный интеграл, увеличив степень x на 1 и погрузив его в ту же степень значения.