Высшая математика Т2
Высшая математика Т2
ОглавлениеПРЕДИСЛОВИЕГлава 1. ВВЕДЕНИЕ § 1.1. Предмет математики. Переменные и постоянные величины, множества § 1.2. Операции над множествами § 1.3. Символика математической логики § 1.4. Действительные числа § 1.5. Определение равенства и неравенства § 1.6. Определение арифметических действий 1.6.1. Общие соображения 1.6.2. Стабилизирующиеся последовательности 1.6.3. Определение арифметических действий § 1.7. Основные свойства действительных чисел § 1.8. Аксиоматический подход к понятию действительного числа § 1.9. Неравенства для абсолютных величин § 1.10. Отрезок, интервал, ограниченное множество § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел Глава 2. Предел последовательности § 2.1. Понятие предела последовательности § 2.  2. Арифметические действия с переменными, имеющими предел§ 2.3. Бесконечно малая и бесконечно большая величины § 2.4. Неопределенные выражения § 2.5. Монотонные последовательности § 2.6. Число e § 2.7. Принцип вложенных отрезков § 2.8. Точные верхняя и нижняя грани множества § 2.9. Теорема Больцано-Вейерштрасса § 2.10. Верхний и нижний пределы § 2.11. Условие Коши сходимости последовательности § 2.12. Полнота и непрерывность множества действительных чисел Глава 3. Функция. Предел функции § 3.1. Функция 3.1.1. Функция от одной переменной. 3.1.2. Функции многих переменных. 3.1.3. Полярная система координат § 3.2. Предел функции § 3.3. Непрерывность функции § 3.4. Разрывы первого и второго рода § 3.6. Обратная непрерывная функция § 3.7. Равномерная непрерывность функции § 3.8. Элементарные функции § 3.9. Замечательные пределы § 3.10. Порядок переменной. Эквивалентность Глава 4.  Дифференциальное исчисление функций одной переменной§ 4.1. Производная § 4.2. Геометрический смысл производной § 4.3. Производные элементарных функций § 4.4. Производная сложной функции § 4.5. Производная обратной функции § 4.6. Производные элементарных функций (продолжение) § 4.7. Дифференциал функции 4.7.1. Дифференцируемые функции 4.7.2. Дифференциал функции 4.7.3. Приближенное выражение приращения функции § 4.8. Другое определение касательной § 4.9. Производная высшего порядка § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка § 4.11 Дифференцирование параметрически заданных функций § 4.12. Теоремы о среднем значении § 4.13. Раскрытие неопределенностей § 4.14. Формула Тейлора § 4.15. Ряд Тейлора § 4.16. Формулы и ряды Тейлора элементарных функций § 4.17. Локальный экстремум функции § 4.18. Экстремальные значения функции на отрезке § 4.19. Выпуклость кривой.  Точка перегиба§ 4.20. Асимптота графика функции § 4.21. Непрерывная и гладкая кривая § 4.22. Схема построения графика функции § 4.23. Вектор-функция. Векторы касательной и нормали Глава 5. неопределенные интегралы § 5.1. Неопределенный интеграл. Таблица интегралов § 5.2. Методы интегрирования § 5.3. Комплексные числа § 5.4. Теория многочлена n-й степени § 5.5. Действительный многочлен n-й степени § 5.6. Интегрирование рациональных выражений § 5.7. Интегрирование иррациональных функций § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение § 6.2. Свойства определенных интегралов § 6.3. Интеграл как функция верхнего предела § 6.4. Формула Ньютона – Лейбница § 6.5. Остаток формулы Тейлора в интегральной форме § 6.6. Суммы Дарбу. Условия существования интеграла § 6.7. Интегрируемость непрерывных и монотонных функций § 6.8. Несобственные интегралы § 6.  9. Несобственные интегралы от неотрицательных функций§ 6.10. Интегрирование по частям несобственных интегралов § 6.11. Несобственный интеграл с особенностями в нескольких точках Глава 7. Приложения интегралов. Приближенные методы § 7.1. Площадь в полярных координатах § 7.2. Объем тела вращения § 7.3. Гладкая кривая в пространстве. Длина дуги § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента § 7.5. Площадь поверхности вращения § 7.6. Интерполяционная формула Лагранжа § 7.7. Квадратурные формулы прямоугольников и трапеций § 7.8. Формула Симпсона Глава 8. Дифференциальное исчисление функций многих переменных § 8.1. Предварительные сведения § 8.2. Предел функции § 8.3. Непрерывная функция § 8.4. Частные производные и производная по направлению § 8.5. Дифференцируемые функции § 8.6. Применение дифференциала в приближенных вычислениях § 8.7. Касательная плоскость. Геометрический смысл дифференциала § 8.  8. Производная сложной функции. Производная по направлению. Градиент8.8.1. Производная сложной функции 8.8.2. Производная по направлению 8.8.3. Градиент функции 8.8.4. Однородные функции § 8.9. Дифференциал функции. Дифференциал высшего порядка § 8.10. Формула Тейлора § 8.12. Непрерывная функция на замкнутом ограниченном множестве § 8.13. Экстремумы § 8.14. Нахождение наибольших и наименьших значений функции § 8.15. Теорема существования неявной функции § 8.16. Касательная плоскость и нормаль § 8.17. Системы функций, заданных неявно § 8.18. Отображения § 8.19. Условный (относительный) экстремум Глава 9. Ряды § 9.1. Понятие ряда § 9.2. Несобственный интеграл и ряд § 9.3. Действия с рядами § 9.4. Ряды с неотрицательными членами § 9.5. Ряд Лейбница § 9.6. Абсолютно сходящиеся ряды § 9.7. Условно сходящиеся ряды с действительными членами § 9.8. Последовательности и ряды функций.  Равномерная сходимость§ 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов § 9.10. Перемножение абсолютно сходящихся рядов § 9.11. Степенные ряды § 9.12. Дифференцирование и интегрирование степенных рядов § 9.13. Функции exp(z), sinz, cosz от комплексного переменного § 9.14. Ряды в приближенных вычислениях § 9.15. Понятие кратного ряда § 9.16. Суммирование рядов и последовательностей |
Построение графика функции, заданной в параметрической форме. — Студопедия
Государственное образовательное учреждение высшего профессионального образования
Московский авиационный институт
(национальный исследовательский университет)
РАДИОВУЗ МАИ
О.М.Данченко
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
МОСКВА
О.
М. ДАНЧЕНКО
Методические указания по выполнению индивидуальных заданий по математическому анализу – М.; РАДИОВТУЗ, 2012г., — 36 с.
Данное пособие содержит типовые задачи для индивидуальных заданий студентов-заочников по курсу «Математический анализ» часть 1. Ко всем задачам приводятся подробные решения и указания. Приведенные задания в равной степени могут использоваться студентами очного отделения при подготовке к экзамену. В приложении приведена подробная программа курса по «Математическому анализу» часть 1.
РАДИОВТУЗ 2012
Содержание
Введение…………………………………………………………………………….
Построение графиков функций, заданных в полярной системе координат или в параметрической форме……………………………………………………………
Вычисление пределов последовательностей и функций…………………………
Исследование функций на непрерывность………………………………………..
Вычисление производных………………………………………………………….
Исследование функций с помощью производных, построение графиков функций…………………………………………………………………………….
.
Задания на вычисление интегралов……………………………………………….
Приложения…………………………………………………………………………
Введение
В процессе изучения курса «Математический анализ» предусмотрено выполнение студентами индивидуальных домашних заданий в каждом семестре. Индивидуальное домашнее задание 1-ого семестра содержит следующие задачи:
1. Построение графиков функций, заданных в полярной системе координат или заданных в параметрической форме.
2. Вычисление пределов последовательностей и функций.
3. Исследование функций на непрерывность.
4. Вычисление производных от сложных функций, функций, заданных неявно или в параметрической форме.
5. Исследование функций с помощью производных, построение графика функции.
6. Вычисление неопределенного и определенного интегралов.
Рассмотрим далее типовые примеры на каждое из заданий и укажем методы их решения.
Построение графиков функций, заданных в простой полярной системе координат.
Простая полярная система координат характеризуется следующим:
ρ=ρ(φ); 0≤ρ<+∞; 0≤φ≤2π(1)
Положительные углы φотсчитываются от полярной оси (совпадающей с положительным направлением оси ОХ) против часовой стрелки, отрицательные – по часовой стрелке. При построении графика функции в соответствии с уравнениями (1) следует придерживаться следующего порядка действий:
а) указать область допустимых значений (О.Д.З.), т.е. определить при каких углах φфункция ρ(φ) – неотрицательна, т.е. ρ(φ)≥ 0;
б) найти область изменения функции;
в) указать является ли функция четной или нечетной, т.е. если ρ(-φ) = ρ(φ),то график функции симметричен относительно полярной оси и, следовательно, достаточно сделать исследования для φ≥0.После данных исследований следует построить кривую по точкам.
Пример: построить график функции в простой полярной системе координатρ=2cos2φ
Так как в простой полярной системе координат ρ≥0, то О.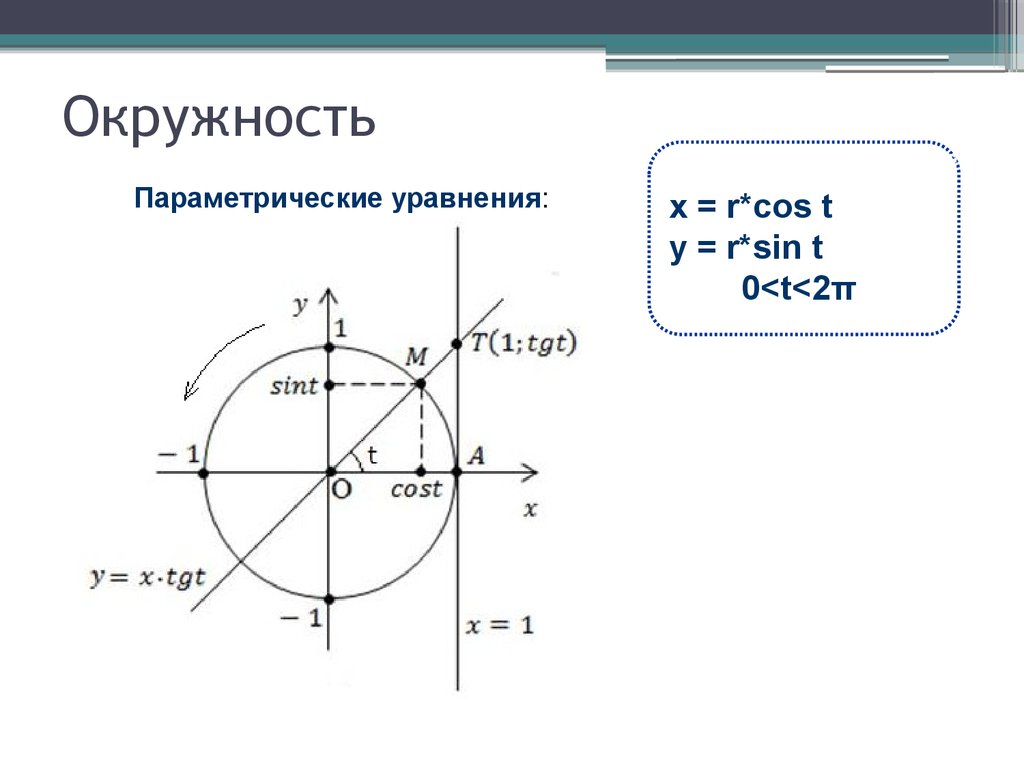
Д.З. будут являться только те углы φ,для которых cos2φ≥0,т.е. 0≤φ≤π/4; 3π/4≤φ≤5π/4; 7π/4≤φ≤2π. Функция будет ограничена, т.к. |cos2φ|≤1,т.е. |2cos2φ|≤2. Так как функция четная и периодическая то достаточно построить кривую только для 0≤φ≤π/4, а затем отразить кривую симметрично относительно полярной оси и в силу периодичности построить аналогичную петлю для 3π/4 ≤φ≤5π/4.Для 0≤φ≤π/4функция монотонно убывает от двух до нуля, для 3π/4≤φ≤πфункция монотонно возрастает от нуля до двух (рис. 1).
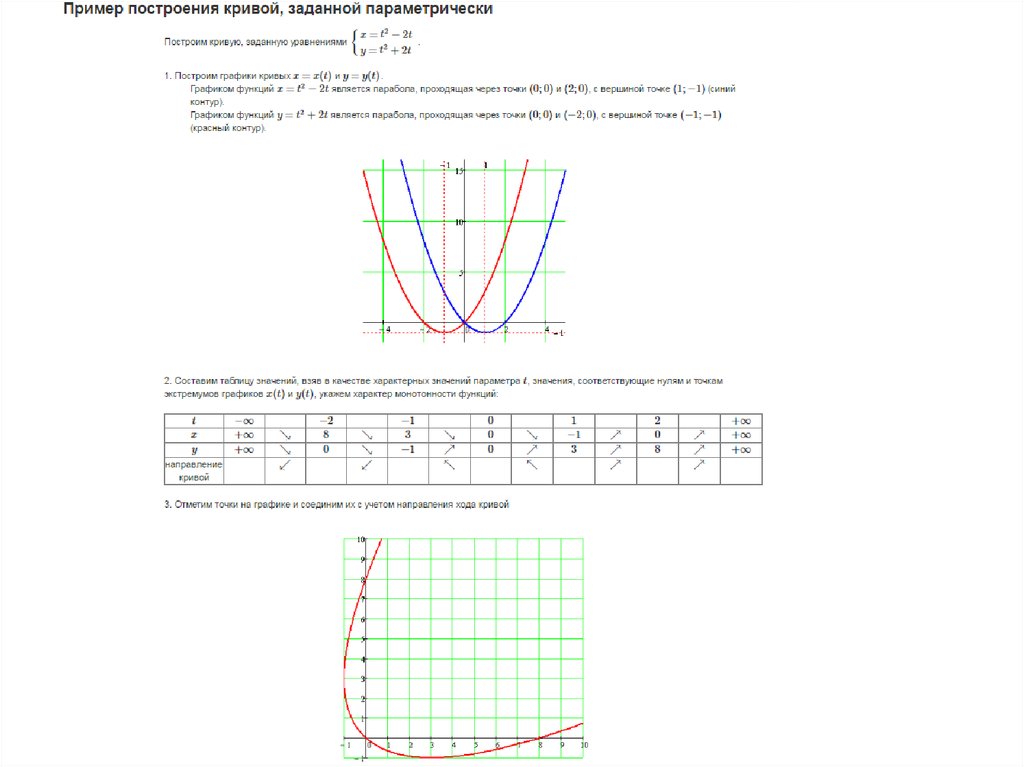
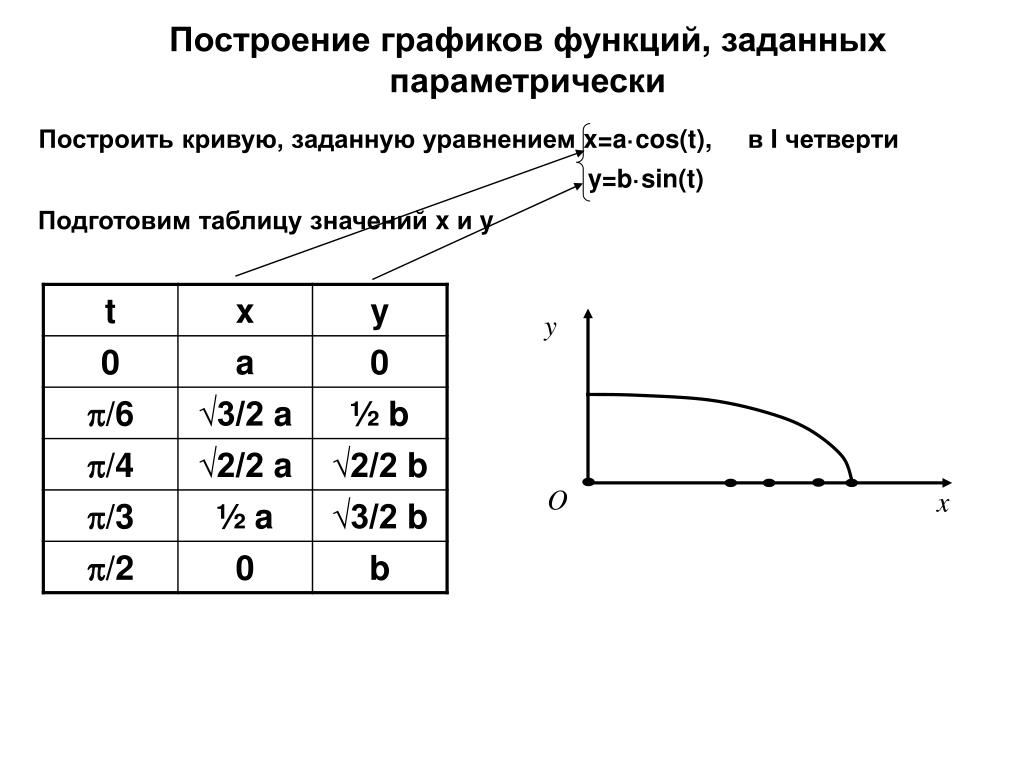
Построение графика функции, заданной в параметрической форме.
Пусть x=X(t)и y=Y(t), где параметр tизменяется в определенных заданных пределах. График функции, заданной в параметрической форме, строится по характерным точкам.
Пример: x=t², y= t∙(t²-3)/3
а) Заметим, что для любых значений аргумента t функция x(t)=t²≥0, следовательно, график функции расположен в правой полуплоскости.
б) В силу нечетности функции y(t), так как y(-t)=-y(t), график функции симметричен относительно оси ОХ.
в) Определим точки, в которых y(t) = 0: при t=0, y(0)=0 и x(0)=0
при t= + и t= — y=0, а x(+ ) = 3 – т.е. это точки пересечения графика функции с осью ОХ. Для более точного построения графика функции достаточно добавить еще 2-3 точки, например при t=1 y(1)=-2/3, x(1)=1; при t=2 y(2)=2/3, x(2)=4; при t =3 y(3)=6, x(3)=9 (рис.2.).
рис. 1 рис. 2
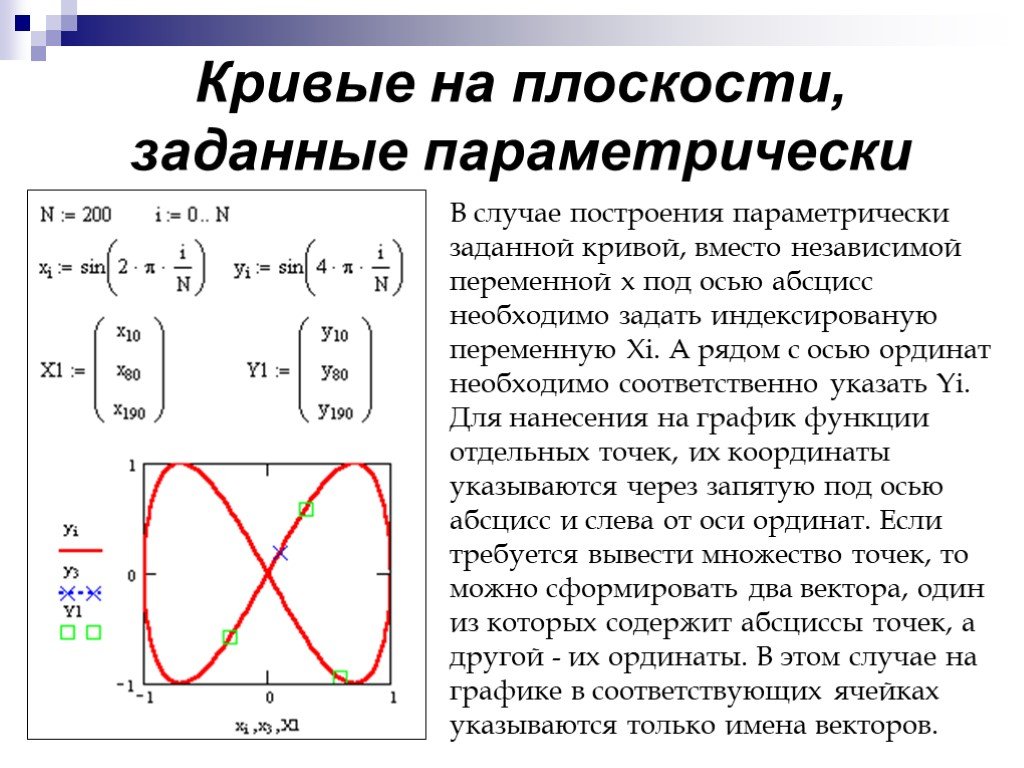
Параметрические уравнения и полярные координаты: Параметрические уравнения
До сих пор нарисованные нами графики определялись одним уравнением: функция с две переменные, x и y . Однако в некоторых случаях полезно ввести третью переменную, называемую параметром, и выразить x и y через параметр. Это приводит к двум уравнениям, называемым параметрическими уравнениями.
Пусть f и g — непрерывные функции
(функции, графики которых представляют собой сплошные кривые) переменной т .
Пусть f ( t ) =
Параметр может иметь положительные и отрицательные значения. Обычно плоская кривая рисуется по мере увеличения значения параметра. Направление плоской кривой по мере увеличения параметра называется ориентацией кривой. Ориентация плоской кривой может быть представлена стрелками, проведенными вдоль кривой. Изучите график ниже. Он определяется параметрическими уравнениями x = cos( t ), y = sin( t ), 0≤ t < 2 Π . Рисунок %: плоская кривая, определяемая параметрическими уравнениями Кривая такая же, как определено прямоугольным уравнением x 2 + y
2 = 1.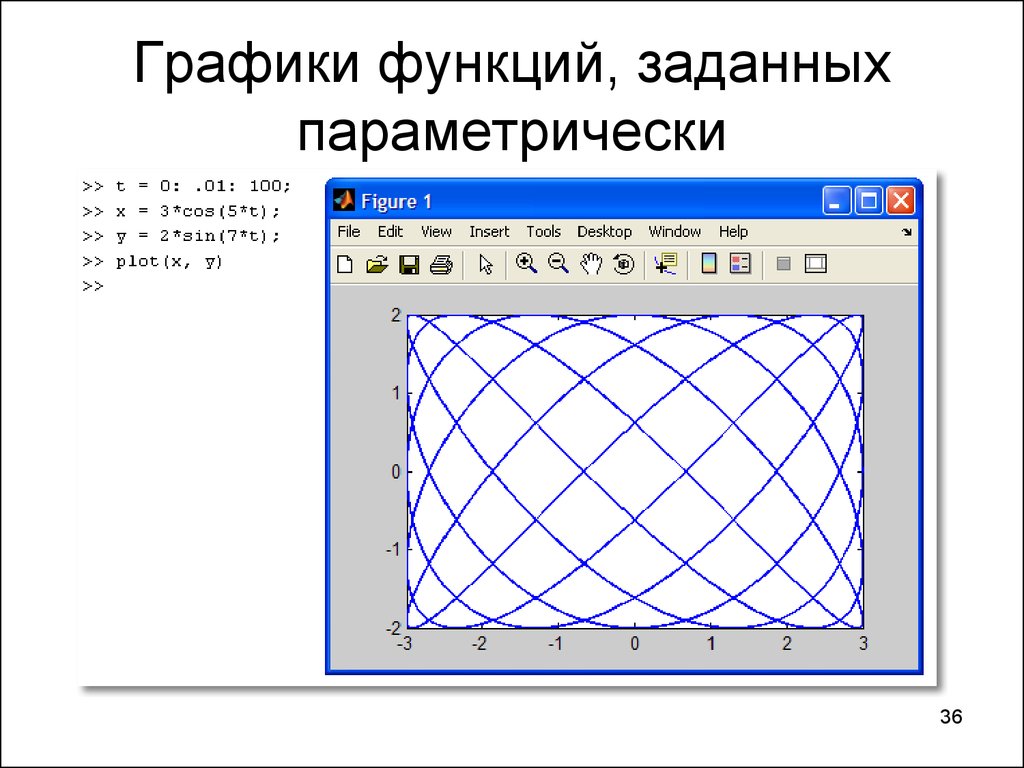
Это единичный круг. Проверьте значения x и y в ключевых точках, таких как t = , Π , и . Обратите внимание на ориентацию
кривая: против часовой стрелки.Единичная окружность является примером кривой, которую можно легко нарисовать с помощью параметрические уравнения. Одним из преимуществ параметрических уравнений является то, что их можно использовать для построения кривых, которые не являются функциями, например единичный круг.
Еще одним преимуществом параметрических уравнений является то, что параметр можно использовать для представляют собой что-то полезное и, следовательно, предоставляют нам дополнительную информацию о графике. Часто плоская кривая используется для отслеживания движения объекта. через определенный промежуток времени. Предположим, что положение частицы дается приведенными выше уравнениями,
Начальное положение частицы (когда t = 0) равно (cos(0), sin(0)) = (1, 0). Подставив количество секунд
для t положение частицы можно найти в любое время между 0 и
2 Π секунды. Подобную информацию нельзя было бы найти, если бы все это было известно
было прямоугольным уравнением для пути частицы, х 2 + у 2 = 1.Полезно уметь преобразовывать прямоугольные уравнения в параметрические. уравнения. Преобразование из прямоугольного в параметрическое может быть сложным, и требует некоторого творчества. Здесь мы обсудим, как преобразовать параметрический в прямоугольные уравнения.
Процесс преобразования параметрических уравнений в прямоугольное уравнение таков:
обычно называется удалением параметра. Во-первых, вы должны решить для
параметр в одном уравнении. Затем подставьте прямоугольное выражение вместо
параметр в другом уравнении и упростить. Изучите пример ниже, в
что параметрические уравнения x = 2 t — 4, y = t + 1, — аау < t < аау
преобразуются в прямоугольное уравнение.
параметрический
| х = 2 т — 4, у = т + 1 |
| т = |
| у = + 1 |
| у = х + 3 |
Решая параметр в одном параметрическом уравнении и подставляя в
другого параметрического уравнения было найдено эквивалентное ему прямоугольное уравнение.
Одна вещь, которую следует отметить в отношении параметрических уравнений, заключается в том, что существует более одной пары уравнений. параметрические уравнения могут представлять одну и ту же плоскую кривую. Иногда ориентация разная, а иногда и отправная точка, но график может остаться прежним. Когда параметром является время, различные параметрические уравнения можно использовать, например, для отслеживания одной и той же кривой на разных скоростях.
Непараметрические графовые методы
Непараметрические графовые методы Понятие сходства между объектами данных играет фундаментальную роль во многих методах машинного обучения. Методы на основе графов вызывают сходство между объектами данных.
из (1) локальных подобий, которые сначала соблюдаются в графе подобия и (2)
спектральное разложение этого графа, целью которого является объединение эффектов локального сходства
в глобальную (управляемую данными) метрику подобия (или ядро) между объектами. А
прямым следствием этого является то, что алгоритмы машинного обучения, предназначенные для
работа с абсолютными расстояниями теперь может быть применена к задачам с расстояниями, управляемыми данными.
Наше исследование основанной на графах методологии охватывает:
- Разработка метрики подобия текста для поддержки выводов в тексте на основе низкоразмерных вложений слов и понятий на основе спектрального графа-лапласиана
- Разработка методов аппроксимации крупномасштабных и многомерных данных
- Применение методов к клиническим данным.
Текстовые метрики на основе графов Методы, основанные на графах, могут использоваться для определения сходства произвольного набора объектов из их локальное сходство. Мы использовали этот подход, определяя сходство между терминами или понятиями в корпусе документов. Вкратце, мы использовали количество совпадений двух терминов в предложении или абзаце в корпусе, чтобы определить их локальное сходство. Затем глобальное подобие было индуцировано с использованием методов спектрального разложения и полученных на их основе гладких ядер.
Это позволит
мы строим сходство между парами понятий. После этого мы разработали новый способ определения сходства между наборами терминов.
которые позволяют сравнивать предложения, абзацы или даже целые документы. Чтобы эффективно вычислить этот показатель,
мы разработали метод аппроксимации, основанный на предварительно скомпилированных сходствах терминов. Мы продемонстрировали
преимущества всей структуры в двух задачах текстового вывода: (1) предсказание терминов
в биомедицинской статье из ее реферата и (2) расширения запроса при поиске информации; и на задаче расстановки приоритетов генов, где
наша цель состояла в том, чтобы вывести из текста гены, которые, скорее всего, связаны с болезнью Альцгеймера. Этот подход (разработанный в 2010 г.) является альтернативным подходом к популярным моделям skip-gram и CBOW.
для определения подобия терминов, слов или понятий, который использует собственные векторы спектрального разложения лапласиана графа для определения вложений более низкой размерности.
Связанные публикации:
- С. Ван, М. Хаускрехт.
Аннотация ключевых слов биомедицинских документов с помощью графических методов подобия.
Международная конференция IEEE по биоинформатике и биомедицине (BIBM) , Филадельфия, октябрь 2012 г. - С. Амизаде, С. Ван и М. Хаускрехт.
Эффективная структура для создания обобщенного локально индуцированного текста Метрики, Международная объединенная конференция по ИИ (IJCAI) , Барселона, Испания, июль 2011 г. - С. Ван и М. Хаускрехт.
Расширение эффективного запроса с помощью показателя сходства терминов на основе устойчивости,
Материалы 33-й международной конференции ACM SIGIR по исследованиям и разработкам в области информационного поиска , Женева, Швейцария, июль 2010 г., стр. 715-716. - С. Ван, М. Хаускрехт, С. Висвесваран.
Приоритизация генов-кандидатов с использованием вероятностных моделей на основе сети.
Саммит AMIA по трансляционной биоинформатике , март 2010 г.
Связанные публикации:
- А. Амизаде, Б. Тиссон, М. Хаускрехт.
Вариационная структура двойного дерева Брегмана.
29-я Международная конференция по неопределенности в области искусственного интеллекта (UAI) , Сиэтл, Вашингтон, июль 2013 г. - С. Амизаде, Б. Тиссон и М. Хаускрехт.
Вариационная структура двойного дерева для крупномасштабной аппроксимации матрицы перехода.
28-я Международная конференция по неопределенности в области искусственного интеллекта (UAI) , остров Каталина, Калифорния, август 2012 г. - С. Амизаде, Х. Вализадеган и М. Хаускрехт.
Аппроксимация факторизованной диффузионной карты.
15-я Международная конференция по искусственному интеллекту и Статистические данные (AISTATS) , Ла-Пальма, Канарские острова, апрель 2012 г. ( приложение)
