| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |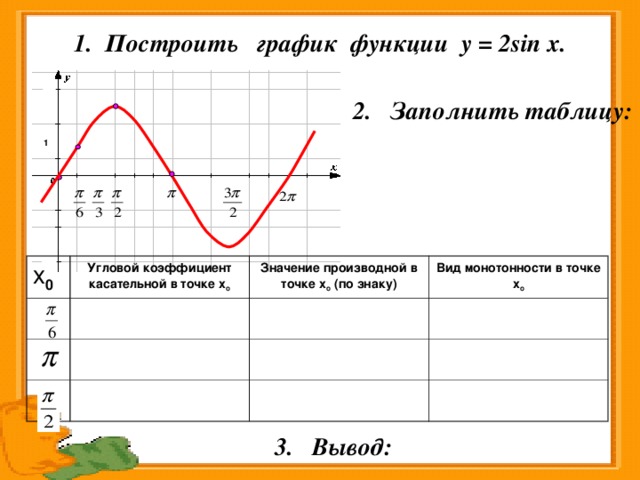
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |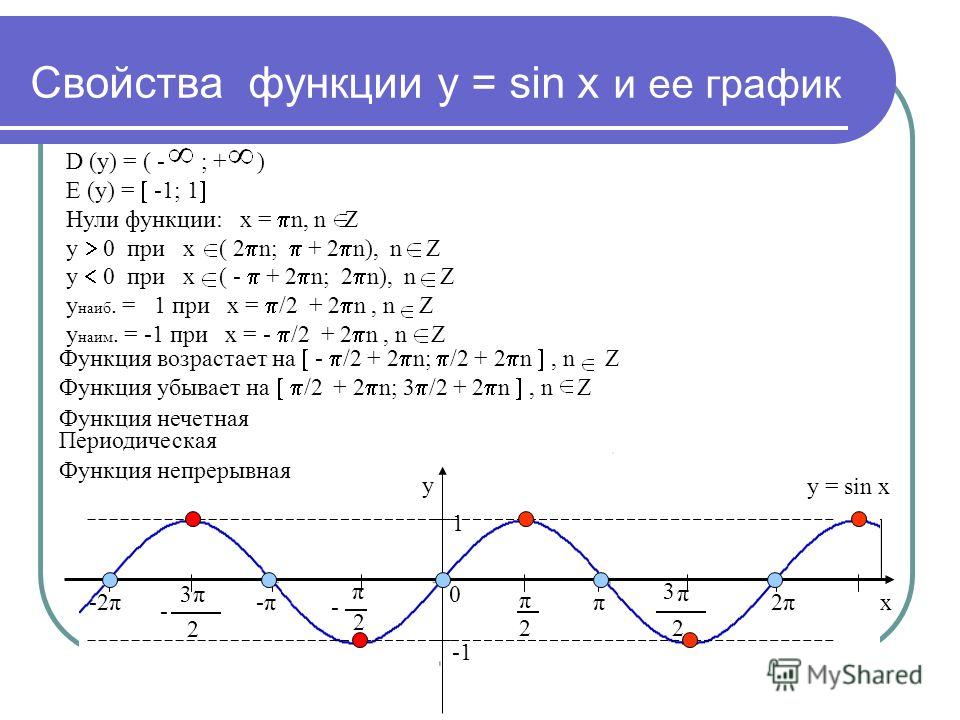
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |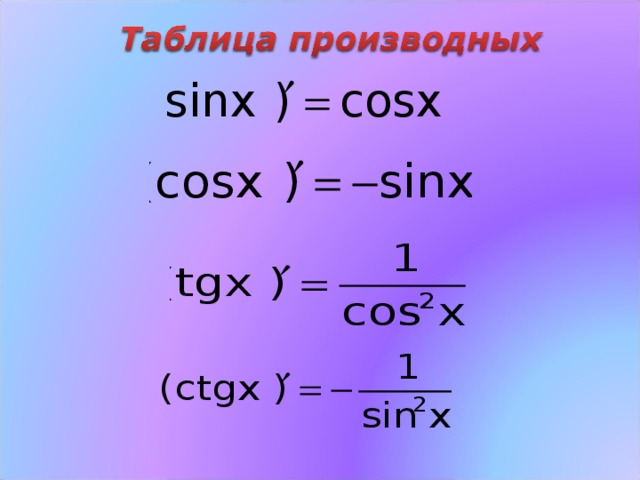
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |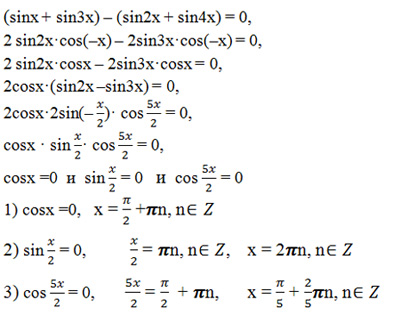
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
06.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
В классе 27 детей, из них 12 ходят на вокал, 19 на танцы, 5 человек участвуют в обоих кружках.
2x-4log2x+3=0 решите уравнение
Решено
Кто сможет решить?
Решено
Изобразите график функции у=1+cos(pi/3 + x)
Решено
сумма цифр трёхзначного натурального числа А делится на 12.Сумма цифр числа А+6 также делится на 12.Найти наименьшее возможное число А
Пользуйтесь нашим приложением
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Уравнения с бесконечными решениями (6 примеров и пояснений) – JDM Educational
Решая уравнение, мы можем обнаружить, что решения нет, одно решение, несколько решений или бесконечное количество решений (можно также сказать «бесконечное множество решений»).
Полезно знать, как выглядят некоторые из них, чтобы вы могли узнать их в случае, если вы столкнетесь с ними.
Итак, какие есть уравнения с бесконечными решениями? Некоторые уравнения с тригонометрическими функциями (например, sin(x) = 0) имеют бесконечно много решений. Есть некоторые уравнения с одной переменной (например, (x+1) 2 = x 2 + 2x + 1), которые имеют бесконечно много решений. Существуют также уравнения с двумя или более переменными (например, x = y), которые имеют бесконечно много решений.
Конечно, существует множество уравнений с бесконечными решениями — приведенные выше лишь несколько примеров.
В этой статье мы поговорим о том, что означает, что уравнение имеет бесконечные решения. Мы также рассмотрим несколько примеров и объясним, почему в этих случаях существует бесконечное число решений.
Начнем.
Уравнения с бесконечными решениями
Существуют некоторые общие признаки того, что уравнение может иметь бесконечные решения.
Например:
- Если обе части уравнения равны (или эквивалентны после перестановки членов), то всегда есть бесконечные решения. Это может произойти для уравнений с одной или несколькими переменными. Например, 2(x + 3) = 2x + 6 одинаково с обеих сторон после того, как мы используем Распределительное свойство слева. Значит, она имеет бесконечные решения.
- Если в уравнении две или более переменных, то может быть бесконечное количество решений. Например, y = x 2 имеет бесконечные решения: для любого действительного числа x мы можем легко найти решение y, возведя x в квадрат.
- Если имеется осциллирующая или периодическая функция (например, синус или косинус), то решений может быть бесконечно много. Например, sin(x) = 0 имеет бесконечно много решений, поскольку каждое целое число, кратное π радианам, является решением (таким образом, π, 2π, 3π, 4π,… все являются решениями).
*Примечание: когда мы говорим, что уравнение имеет бесконечные решения (или бесконечно много решений), мы не имеем в виду, что ∞ является решением уравнения. Мы имеем в виду, что существует неограниченное число решений уравнения (каждое решение — конечное число).
Теперь давайте рассмотрим несколько примеров уравнений с бесконечными решениями, а также объяснение каждого из них.
Когда квадратное уравнение не имеет решения…
Пожалуйста, включите JavaScript
Когда у квадратного уравнения нет решения?
Пример 1. Уравнение с одной переменной и бесконечным числом решений
Рассмотрим следующее уравнение с одной переменной:
Нам нужно будет выполнить некоторую работу (используя FOIL и комбинируя подобные термины), чтобы увидеть, существуют ли бесконечные решения:
- (x 2 + 2x + 1) + 4x = (x + 3) 2 – 8 [(x + 1) 2 = (x 2 + 2x + 1), по ФОЛЬГЕ]
- (x 2 + 2x + 1) + 4x 91 = (0x 901 + 6x + 9) – 8 [(x + 3) 2 = (x 2 + 6x + 9), по ФОЛЬГЕ]
- x 2 + 6x + 1 = x + 2 6x + 1 [объединить одинаковые члены с обеих сторон]
- 0 = 0
Последнее утверждение всегда верно, независимо от того, какое значение x мы выбираем.
Итак, исходное уравнение имеет бесконечное число решений — подойдет любое реальное значение x!
Пример 2. Уравнение с двумя переменными и бесконечным числом решений
Рассмотрим следующее уравнение с двумя переменными:
- y = 2x 2 – 5x + 1
У этого уравнения бесконечно много решений. . В этом случае мы можем выбрать любое реальное значение x и найти y, подставив выбранное значение x в уравнение.
Например:
- Для x = 0 получаем y = 2(0) 2 – 5(0) + 1 = 2*0 – 0 + 1 = 0 – 0 + 1 = 1
- Для x = 1 получаем y = 2(1) 2 – 5(1) + 1 = 2*1 – 5 + 1 = 2 – 5 + 1 = -2
- Для x = 2, получаем y = 2(2) 2 – 5(2) + 1 = 2*4 – 10 + 1 = 8 – 10 + 1 = -1
- и т. д.
График ниже показано множество решений (парабола, которая является графиком квадратного).
График квадратного уравнения y = 2x 2 – 5x + 1, имеющего бесконечно много решений.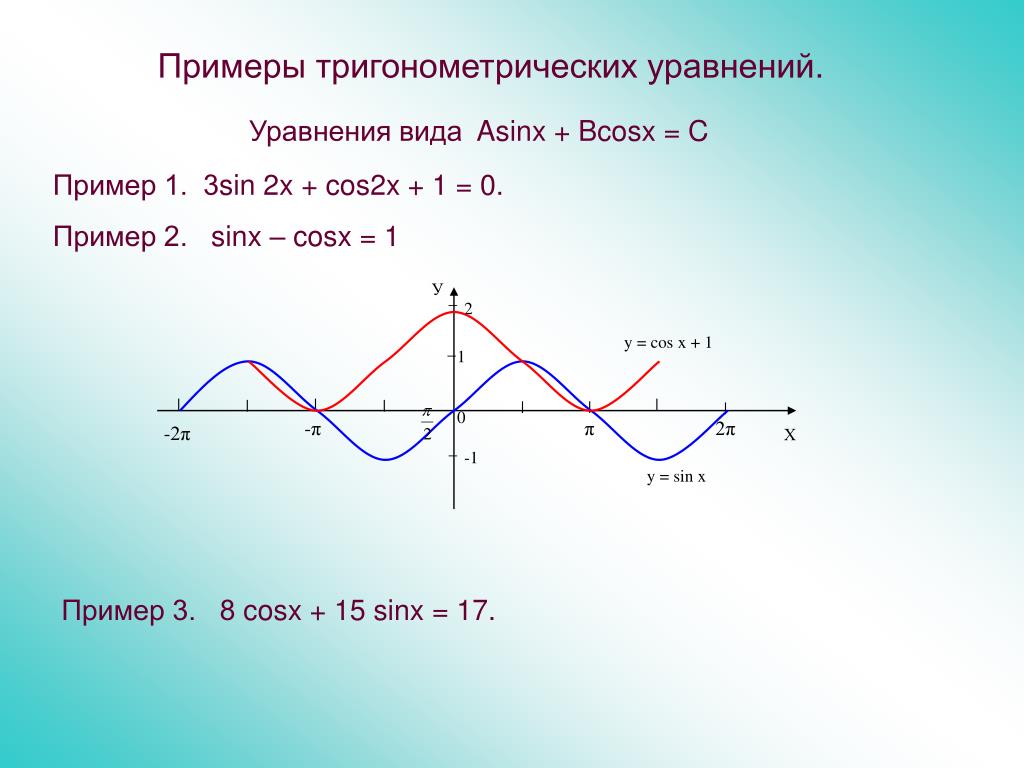
Пример 3. Уравнение с тремя переменными и бесконечным числом решений
Рассмотрим следующее уравнение с двумя переменными:
- z = x + y
У этого уравнения бесконечно много решений. В этом случае мы можем выбрать любое действительное значение для x и любое действительное значение для y и найти z, подставив выбранные нами значения x и y в уравнение.
Например:
- Для x = 0 и y = 0 получаем z = 0 + 0 = 0
- Для x = 0 и y = 1 получаем z = 0 + 1 = 1
- Для x = 1 и y = 1 мы получаем z = 1 + 1 = 2
- и т. д.
График уравнения z = x + y будет представлять собой целую плоскость при отображении в 3D космос.
Плоскость (например, z = x + y) отображается в трехмерном пространстве. У уравнения z = x + y есть бесконечные решения.Пример 4. Уравнение с триггерными функциями с бесконечным числом решений
Рассмотрим следующее уравнение с тригонометрической функцией:
- 2sin(x) = 1
- sin(x) = ½
- x = (12k + 1)π/6, (12k + 5)π/6 для любого целого числа k
Поскольку k может быть любым целым числом, существует бесконечно много решений уравнения.
Ниже вы можете увидеть график, показывающий некоторые точки пересечения y = 2sin(x) и y = 1.
Обратите внимание, что тот же самый тип шаблона будет иметь место для любой периодической функции (синуса, косинуса и т. д.)
Пример 5. Уравнение с триггерными функциями с бесконечным числом решений
Рассмотрим следующее уравнение с тригонометрической функцией:
- cos(x) = 1
- x = kπ для любого целого числа k
Поскольку k может быть любым целым числом, у уравнения существует бесконечно много решений. Ниже вы можете увидеть график, показывающий некоторые точки пересечения y = cos(x) и y = 1.
Здесь показаны некоторые решения уравнения cos(x) = 1. Синяя кривая — часть графика y = cos(x), а красная линия — горизонтальная линия y = 1.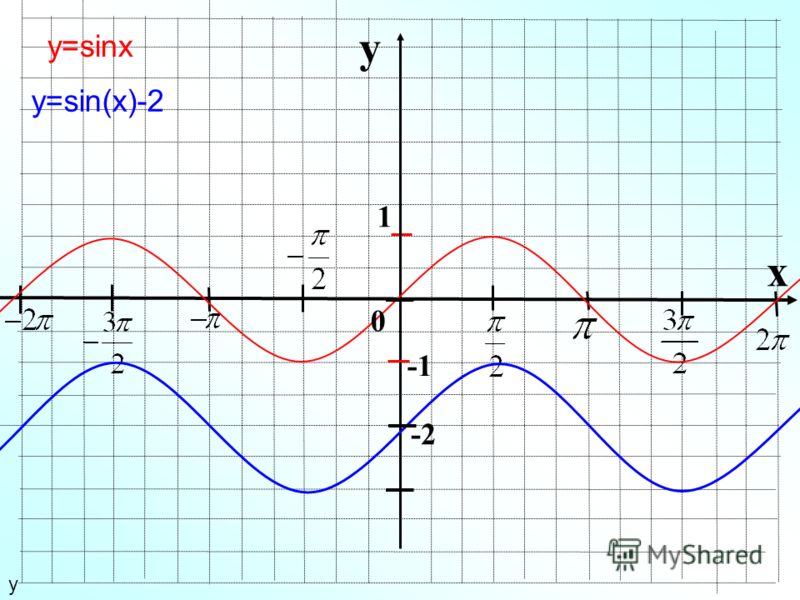
Существует бесконечное количество решений уравнения уравнение cos(x) = 1.Пример 6. Уравнение с тригонометрическими функциями с бесконечным числом решений
Рассмотрим следующее уравнение с тригонометрической функцией:
- sin(x) = cos(x)
- sin(x)/cos(x) = cos(x)/cos(x)
- tan(x) = 1
Это происходит, когда x = (8k+1)π/4 и x = (8k+5)π/4 для каждого целого числа k.
*Примечание: поскольку мы делили на cos(x), мы должны проверить случай, когда cos(x) = 0, что имеет место, когда x = kπ/2 для каждого k. В этом случае sin(x) равен 1, что не равно 0.
Поскольку k может быть любым целым числом, у уравнения существует бесконечно много решений. Ниже вы можете увидеть график, показывающий некоторые точки пересечения y = cos(x) и y = 1.
Здесь показаны некоторые решения уравнения sin(x) = cos(x). Синяя кривая является частью графика y = sin(x), а красная линия является частью графика y = cos(x).