Ускорение свободного падения — Без Сменки
15 июня, 2022
1 мин
Физ 🔬
🚶Свободное падение — падение тел в вакууме из состояния покоя под действием притяжения Земли.
Падение тел в воздухе можно приближенно считать свободным лишь при условии, что сопротивление воздуха мало и им можно пренебречь.
Ускорение свободного падения — это ускорение, которое приобретают все тела при свободном падении вблизи поверхности Земли независимо от их массы. Обозначается буквой g.
🌍 Ускорение свободного падения на Земле приблизительно равно g = 9,81 м/с2.
Свободное падение — это равноускоренное движение. Его ускорение всегда направлено к центру Земли.
Вектор ускорения при свободном падении всегда направлен вертикально вниз 👀
Ускорение при свободном падении тел является постоянной величиной. Кстати, его можно вычислить с помощью формулы (смотри на картинке)👇
Это означает какое бы тело не летело вверх или вниз, его скорость будет изменяться одинаково.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
44 подписчиков
+ Подписаться
Редакция Без Сменки
19 мая, 2022
1 мин
Общ 👨👩👧
Норма права
У правовой нормы есть определенная структура, в состав которой входят гипотеза, диспозиция и. ..
..
Редакция Без Сменки
01 июля, 2022
1 мин
Лит 📚
А.П. Чехов
Разбираем прекрасные произведения А.П. Чехова ниже
Редакция Без Сменки
29 июня, 2022
1 мин
определения
Если коротко и по делу, то химия — это наука о веществах, их свойствах и превращениях. Разберем это…
Редакция Без Сменки
15 июня, 2022
1 мин
Инф 💻
Траектории
🔈Задача:
Исполнитель Фибо преобразуется число на экране. У исполнителя есть две команды, которым…
У исполнителя есть две команды, которым…
Редакция Без Сменки
30 июня, 2022
1 мин
Мтмт 📈ПАРАЛЛЕЛЕПИПЕД
✨Параллелепипедом называется призма, основанием которой служит параллелограмм. С его определением…
Редакция Без Сменки
06 июня, 2022
1 мин
Общ 👨👩👧
Особенности гражданского процесса
📄 Принципы гражданского процесса: — осуществление правосудия только судами — равенство всех…
СТАНДОТКЛОН.Г (функция СТАНДОТКЛОН.
 Г) — Служба поддержки Майкрософт
Г) — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Синтаксис
СТАНДОТКЛОН.Г(число1;[число2];…)
Аргументы функции СТАНДОТКЛОН.Г описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий генеральной совокупности.
org/ListItem»>
Число2… Необязательный. Числовые аргументы 2—254, соответствующие генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОН.Г предполагает, что аргументы — это вся генеральная совокупность. Если данные являются только выборкой из генеральной совокупности, для вычисления стандартного отклонения следует использовать функцию СТАНДОТКЛОН.
-
Для больших выборок функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г возвращают примерно равные значения.
org/ListItem»>
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
org/ListItem»>
-
Чтобы включить логические значения и текстовые представления чисел в ссылку для вычисления, используйте функцию СТАНДОТКЛОНПА.
-
Функция СТАНДОТКЛОН.Г вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 | ||
|
1299 |
||
|
Формула |
Описание |
Результат |
|
=СТАНДОТКЛОН. |
Стандартное отклонение предела прочности при условии, что произведено только 10 инструментов. |
26,05455814 |
Причинно-следственный вывод с помощью параметрической g-формулы • предельные эффекты
Источник: виньетки/gformula.Rmd
gformula.Rmd
В этой виньетке 3 гола:
- Дайте краткое введение в идею «параметрической g-формулы»
- Подчеркните эквивалентность между одной формой g-оценки и «Средними контрастами», рассчитанными с помощью
предельных эффектов - Покажите, как получить оценки, стандартные ошибки и доверительные интервалы с помощью параметрической g-формулы, используя одну строку из
маргинальные эффектыкод. Это удобно, потому что, как правило, аналитикам приходится вручную создавать наборы неверных данных и загружать свои оценки.
Это удобно, потому что, как правило, аналитикам приходится вручную создавать наборы неверных данных и загружать свои оценки.
«Параметрическая g-формула» часто используется для причинно-следственной связи в данных наблюдений.
Объяснения и иллюстрации, которые следуют, во многом опираются на главу 13 этой превосходной книги (бесплатная копия доступна в Интернете):
Эрнан М.А., Робинс Дж.М. (2020). Причинный вывод: что, если. Бока-Ратон: Чепмен и Холл/CRC.
Что такое параметрическая g-формула?
Параметрическая g-формула — это метод стандартизации, который можно использовать для решения сложных проблем при выводе о причинно-следственных связях с данными наблюдений. Он основан на тех же предположениях идентификации, что и взвешивание обратной вероятности (IPW), но использует другие предположения моделирования. В то время как IPW моделирует уравнение лечения, стандартизация моделирует уравнение среднего результата. Как отмечают Эрнан и Робинс:
Как отмечают Эрнан и Робинс:
.«И взвешивание IP, и стандартизация являются оценками g-формулы, общего метода причинно-следственного вывода, впервые описанного в 1986. … Мы говорим, что стандартизация — это «подключаемый модуль оценки g-формулы», потому что она просто заменяет условное среднее значение в g-формуле ее оценками. Когда, как в главе 13, эти оценки исходят из параметрических моделей, мы называют этот метод параметрической g-формулой».
Как это работает?
Представьте себе такую причинно-следственную модель:
Мы хотим оценить влияние бинарной обработки \(X\) на результат \(Y\), но есть смешанная переменная \(W\). Мы можем использовать стандартизацию с параметрической g-формулой, чтобы справиться с этим. Грубо говоря, процедура такова:
- Используйте наблюдаемые данные, чтобы подобрать регрессионную модель с \(Y\) в качестве результата, \(X\) в качестве лечения и \(W\) в качестве контрольной переменной (возможно, с некоторыми полиномами и/или взаимодействиями, если есть несколько управляющих переменных).

- Создайте новый набор данных, полностью идентичный исходным данным, но с \(X=1\) в каждой строке.
- Создайте новый набор данных, полностью идентичный исходным данным, но с \(X=0\) в каждой строке.
- Используйте модель, полученную на этапе 1, для вычисления скорректированных прогнозов в двух контрфактических наборах данных, полученных на этапах 2 и 3.
- Интересующая величина представляет собой разницу между средними значениями скорректированных прогнозов в двух контрфактических наборах данных.
Это эквивалентно вычислению «Среднего контраста», в котором значение \(X\) изменяется от 0 до 1. Благодаря этой эквивалентности мы можем применить параметрический метод g-формулы, используя одну строку кода в marginaleffects и автоматически получать стандартные ошибки дельта-метода.
Пример с реальными данными
Давайте проиллюстрируем этот метод, повторив пример из главы 13 книги Эрнана и Робинса. Данные получены из Национального эпидемиологического исследования данных I обследования здоровья и питания (NHEFS). Результат
Результат wt82_71 , показатель прибавки в весе. Лечение составляет qsmk , бинарный показатель отказа от курения. Есть много путаницы.
Шаг 1 заключается в подгонке регрессионной модели результатов для лечебных и контрольных переменных:
библиотека (загрузочная)
библиотека (маргинальные эффекты)
f <- wt82_71 ~ qsmk + пол + раса + возраст + I(возраст * возраст) + фактор(образование) +
интенсивность дыма + I(интенсивность дыма * интенсивность дыма) + дымность +
I(smokeyrs * smokeyrs) + фактор(упражнение) + фактор(активный) + wt71 +
I(wt71 * wt71) + I(qsmk * интенсивность дыма)
URL <- "https://raw.githubusercontent.com/vincentarlbundock/modelarchive/main/data-raw/nhefs.csv"
nhefs <- read.csv(url)
nhefs <- na.опустить(nhefs[ all.vars(f)])
fit <- glm(f, data = nhefs) Шаги 2 и 3 требуют, чтобы мы воспроизвели полный набор данных, установив обработку qsmk на неверные значения. Мы можем сделать это автоматически, вызвав сравнения() .
TLDR
Эти простые команды делают все, что нужно для применения параметрической g-формулы:
avg_comparisons(fit, variable = list(qsmk = 0:1))
## ## Термин Оценка контрастности Std. Ошибка z Pr(>|z|) 2,5 % 97,5 % ## qsmk 1 - 0 3,517 0,4403 7,989 1.3613e-15 2.654 4.38 ## ## Тип прогноза: ответ ## Столбцы: тип, термин, контраст, оценка, std.error, статистика, p.value, conf.low, conf.high
В остальной части виньетки процесс рассматривается более подробно и сравнивается с кодом репликации. от Эрнана и Робинса.
Скорректированные прогнозы
Мы можем вычислить средние прогнозы в исходных данных и средние прогнозы в двух контрфактических наборах данных следующим образом:
# средний прогнозируемый результат в исходных данных p <- прогнозы (подходят) среднее (p $ оценка)
## [1] 2,6383
# средний прогнозируемый результат в двух контрфактических наборах данных p <- прогнозы (подходят, новые данные = datagrid (qsmk = 0: 1, grid_type = «контрфактический»)) агрегат(оценка ~ qsmk, данные = p, FUN = среднее значение)
## оценка qsmk ## 1 0 1.756213 ## 2 1 5.273587
В коде R , который прилагается к их книге, Эрнан и Робинс вычисляют одни и те же величины вручную следующим образом:
# создают набор данных с 3 копиями каждого субъекта nhefs$interv <- -1 # 1-я копия: равна исходной interv0 <- nhefs # 2-я копия: обработка установлена на 0, результат отсутствует интервал0$интерв <- 0 Interv0$qsmk <- 0 interv0$wt82_71 <- нет данных interv1 <- nhefs # 3-я копия: обработка установлена на 1, результат отсутствует интервал1$интерв <- 1 интервал1$qsmk <- 1 interv1$wt82_71 <- нет данных onesample <- rbind(nhefs, interv0, interv1) # объединение наборов данных # линейная модель для оценки среднего результата в зависимости от лечения и искажающих факторов # параметры оцениваются только с использованием исходных наблюдений (nhefs) # оценки параметров используются для прогнозирования среднего результата для наблюдений с # обработка установлена на 0 (interv=0) и на 1 (interv=1) std <- glm(f, data = onesample) onesample$predicted_meanY <- прогнозировать(стандартное, одновыборочное) # оценить средний результат в каждой из групп interv=0 и interv=1 # этот средний результат представляет собой средневзвешенное значение средних результатов в каждой комбинации # значений лечения и вмешивающихся факторов, то есть стандартизированный результат среднее (один образец [который (один образец $ интервал == -1), ] $ прогнозируемое_среднее значение Y)
## [1] 2.6383
mean(onesample[what(onesample$interv == 0), ]$predicted_meanY)
## [1] 1.756213
mean(onesample[what(onesample$interv == 1) ), ]$predicted_meanY)
## [1] 5.273587
Может быть полезно отметить, что функция datagrid() , предоставляемая marginaleffects , может автоматически создавать гипотетические наборы данных. Это эквивалентно набору данных onesample :
nd <- datagrid(
модель = подходит,
qсмк = с(0, 1),
grid_type = "неправдоподобный") Контраст
Теперь мы хотим вычислить эффект лечения с помощью параметрической g-формулы, который представляет собой разницу в средних предсказанных результатах в двух наборах данных, основанных на гипотетических данных. Это эквивалентно получению средней контрастности с помощью функции сравнения() . В следующей команде следует отметить три важных момента:
- Аргумент
переменныхиспользуется для указания того, что мы хотим оценить «контраст» между скорректированными прогнозами, когдаqsmkравно 1 или 0.
-
сравнения()автоматически производит оценки неопределенности.
avg_comparisons(стандарт, переменные = список(qsmk = 0:1))
## ## Термин Оценка контрастности Std. Ошибка z Pr(>|z|) 2,5 % 97,5 % ## qsmk 1 - 0 3,517 0,4403 7,989 1,3613e-15 2,654 4,38 ## ## Тип прогноза: ответ ## Столбцы: тип, терм, контраст, оценка, std.error, статистика, p.value, conf.low, conf.high
Под капотом, сравнения() сделали именно то, что мы описали выше в шагах g-формулы: $interv == 1), ]$predicted_meanY) -
mean(onesample[what(onesample$interv == 0), ]$predicted_meanY)
## [1] 3,517374
Хотя ручное вычисление простое, оно не дает оценок неопределенности. Напротив, сравнения() уже вычислил стандартную ошибку и доверительный интервал с помощью дельта-метода.
Вместо дельта-метода большинство аналитиков будут полагаться на самозагрузку. Например, код репликации от Hernán and Robins делает следующее:
# функция для вычисления разницы в средних значениях
стандартизация <- функция (данные, индексы) {
# создать набор данных с 3 копиями каждого субъекта
d <- data[indices, ] # 1-я копия: равна исходной`
d$интерв <- -1
d0 <- d # 2-я копия: обработка установлена на 0, результат отсутствует
d0$интерв <- 0
d0$qsmk <- 0
d0$wt82_71 <- нет данных
d1 <- d # 3-я копия: обработка установлена на 1, результат отсутствует
d1$интерв <- 1
d1$qsmk <- 1
d1$wt82_71 <- нет данных
d. onesample <- rbind(d, d0, d1) # объединение наборов данных
# линейная модель для оценки среднего результата в зависимости от лечения и искажающих факторов
# параметры оцениваются только с использованием исходных наблюдений (interv= -1)
# оценки параметров используются для прогнозирования среднего результата для наблюдений с набором
# лечение (interv=0 и interv=1)
fit <- glm(f, data = d.onesample)
d.onesample$predicted_meanY <- прогнозировать(подходить, d.onesample)
# оценить средний результат в каждой из групп interv=-1, interv=0 и interv=1
return(mean(d.onesample$predicted_meanY[d.onesample$interv == 1]) -
среднее (d.onesample$predicted_meanY[d.onesample$interv == 0]))
}
# начальная загрузка
результаты <- загрузка (данные = nhefs, статистика = стандартизация, R = 1000)
# создание доверительных интервалов
se <- sd (результаты $ t [ 1])
означает0 <- результаты$t0
ll <- означает 0 - qнорма(0,975) *сэ
ul <- означает0 + qnorm(0,975) * se
начальная загрузка <- data.
onesample <- rbind(d, d0, d1) # объединение наборов данных
# линейная модель для оценки среднего результата в зависимости от лечения и искажающих факторов
# параметры оцениваются только с использованием исходных наблюдений (interv= -1)
# оценки параметров используются для прогнозирования среднего результата для наблюдений с набором
# лечение (interv=0 и interv=1)
fit <- glm(f, data = d.onesample)
d.onesample$predicted_meanY <- прогнозировать(подходить, d.onesample)
# оценить средний результат в каждой из групп interv=-1, interv=0 и interv=1
return(mean(d.onesample$predicted_meanY[d.onesample$interv == 1]) -
среднее (d.onesample$predicted_meanY[d.onesample$interv == 0]))
}
# начальная загрузка
результаты <- загрузка (данные = nhefs, статистика = стандартизация, R = 1000)
# создание доверительных интервалов
se <- sd (результаты $ t [ 1])
означает0 <- результаты$t0
ll <- означает 0 - qнорма(0,975) *сэ
ul <- означает0 + qnorm(0,975) * se
начальная загрузка <- data. frame(
" " = "Лечение - Без лечения",
оценка = означает 0,
стандартная ошибка = SE,
conf.low = ll,
конф.высокая = ул,
check.names = ЛОЖЬ)
bootstrap
frame(
" " = "Лечение - Без лечения",
оценка = означает 0,
стандартная ошибка = SE,
conf.low = ll,
конф.высокая = ул,
check.names = ЛОЖЬ)
bootstrap ## оценка std.error conf.low conf.high ## 1 Обработка - Без обработки 3.517374 0.4960004 2.545231 4.489517
Результаты близки к результатам, полученным с помощью сравнений() , но доверительный интервал немного отличается из-за разницы между бутстрэппингом и дельта-методом.
avg_comparisons(подгонка, переменные = список(qsmk = 0:1))
## ## Термин Оценка контрастности Std. Ошибка z Pr(>|z|) 2,5 % 97,5 % ## qsmk 1 - 0 3,517 0,4403 7,989 1,3613e-15 2,654 4,38 ## ## Тип прогноза: ответ ## Столбцы: тип, термин, контраст, оценка, стандартная ошибка, статистика, p.value, conf.low, conf.high
G-вычислений в причинно-следственном выводе | by Yao Yang
Алгоритм G-вычисления был впервые представлен Робинсом в 1986 году [1] для оценки причинно-следственного эффекта изменяющегося во времени воздействия в присутствии изменяющихся во времени искажающих факторов, на которые воздействует воздействие, сценарий, в котором традиционная регрессия- основанные методы потерпят неудачу.
G-вычисление или G-формула относится к семейству G-методов [2], которое также включает маргинальные структурные модели, взвешенные по обратной вероятности, и g-оценку структурной вложенной модели. Они обеспечивают согласованные оценки контрастов (например, различий, соотношений) средних потенциальных результатов при менее строгом наборе условий идентификации, чем стандартные методы регрессии.
В этом посте я более подробно объясню, как G-вычисления работают в причинно-следственном анализе.
Подумайте о примере: при лечении ВИЧ способ измерения эффекта лечения заключается в проверке количества CD4, чем больше количество CD4 в вашей крови, тем лучше эффект лечения. Мы называем результат (количество CD4) Y . У нас есть две группы пациентов: A = 1 означает, что они получают определенное лечение, A = 0 означает другое. Мы тестируем пациентов перед любым лечением в качестве базового уровня, а также проводим последующий тест A_1 . У нас также есть ковариата Z — повышенная вирусная нагрузка ВИЧ, которая по замыслу постоянна на исходном уровне и измерена один раз во время последующего наблюдения непосредственно перед вторым лечением (Z_1). Помимо этого, у нас также есть неизмеряемая общая причина ( U ) вирусной нагрузки ВИЧ (Z) и CD4 (Y).
У нас также есть ковариата Z — повышенная вирусная нагрузка ВИЧ, которая по замыслу постоянна на исходном уровне и измерена один раз во время последующего наблюдения непосредственно перед вторым лечением (Z_1). Помимо этого, у нас также есть неизмеряемая общая причина ( U ) вирусной нагрузки ВИЧ (Z) и CD4 (Y).
Чтобы измерить разницу, мы обычно используем средний причинный эффект E(Y1-Y0), это предельный эффект, поскольку он усредняет все эффекты на индивидуальном уровне в популяции.
Как определить изменения количества CD4 ( Y ) вызвано обработкой ( A=1 ), а не чем-то другим?
Причинно-следственная диаграмма, представляющая связь между лечением во время 0 (A0), вирусной нагрузкой ВИЧ непосредственно перед вторым раундом лечения (Z1), статусом лечения во время 1 (A1), числом CD4, измеренным в конце наблюдения -up (Y) и неизмеряемая общая причина (U) вирусной нагрузки ВИЧ и CD4.
Мы используем средний эффект для измерения разницы, однако мы не можем получить всю информацию, потому что некоторые люди подвергаются лечению, а некоторые нет. Мы не проводим сопоставление показателей склонности, поэтому мы не можем гарантировать, что все остальные условия, которые есть у людей, одинаковы. Нам нужно обосновать, что средний эффект, который мы принимаем для измерения, будет наблюдаться во всей популяции. Это достигается путем принятия следующих допущений:
Допущение 1: Контрфактическая непротиворечивость
Правило непротиворечивости утверждает, что потенциальный результат человека при гипотетических условиях, которые материализовались, является в точности результатом, переживаемым этим человеком. Это позволяет нам написать: P(Yx = y|Z = z,X = x) = P(Y = y|Z = z,X = x) и определить наш средний причинный эффект
Допущение 2: взаимозаменяемость
Обмениваемость подразумевает, что потенциальные результаты под рисками не зависят от фактических рисков A_0 или A_1. Это предположение гласит: «Данные получены из рандомизированного контролируемого исследования». Если это предположение верно, вы увидите случайное подмножество распределения Ya=0 в группе, где A=0, и случайное подмножество распределения Ya=1 в группе, где A=1.
Это предположение гласит: «Данные получены из рандомизированного контролируемого исследования». Если это предположение верно, вы увидите случайное подмножество распределения Ya=0 в группе, где A=0, и случайное подмножество распределения Ya=1 в группе, где A=1.
Допущение3: положительность
Положительность — это предположение о том, что любой человек имеет положительную вероятность получения всех значений лечебной переменной. Это предположение полезно для того, чтобы эффекты существовали. Предположение будет выполнено, когда во всех искажающих факторах есть экспонированные и неэкспонированные индивидуумы.
Исходя из этих предположений, g-методы могут быть использованы для оценки гипотетических величин с помощью данных наблюдений
Чтобы оценить влияние различных компонентов лечения на количество CD4, мы выполнили следующие шаги:
3 шага для G-вычисления Идея состоит в том, чтобы использовать контрфактуальные значения (каким был бы результат, если бы пациенты, получавшие лечение, не получали лечения, а пациенты, которые не получали лечения, получали) для создания оценки среднего эффекта, чтобы соответствовать в нашу модель измерения разницы.

 Г(A3:A12)
Г(A3:A12) Это удобно, потому что, как правило, аналитикам приходится вручную создавать наборы неверных данных и загружать свои оценки.
Это удобно, потому что, как правило, аналитикам приходится вручную создавать наборы неверных данных и загружать свои оценки.
 756213
## 2 1 5.273587
756213
## 2 1 5.273587  6383
6383 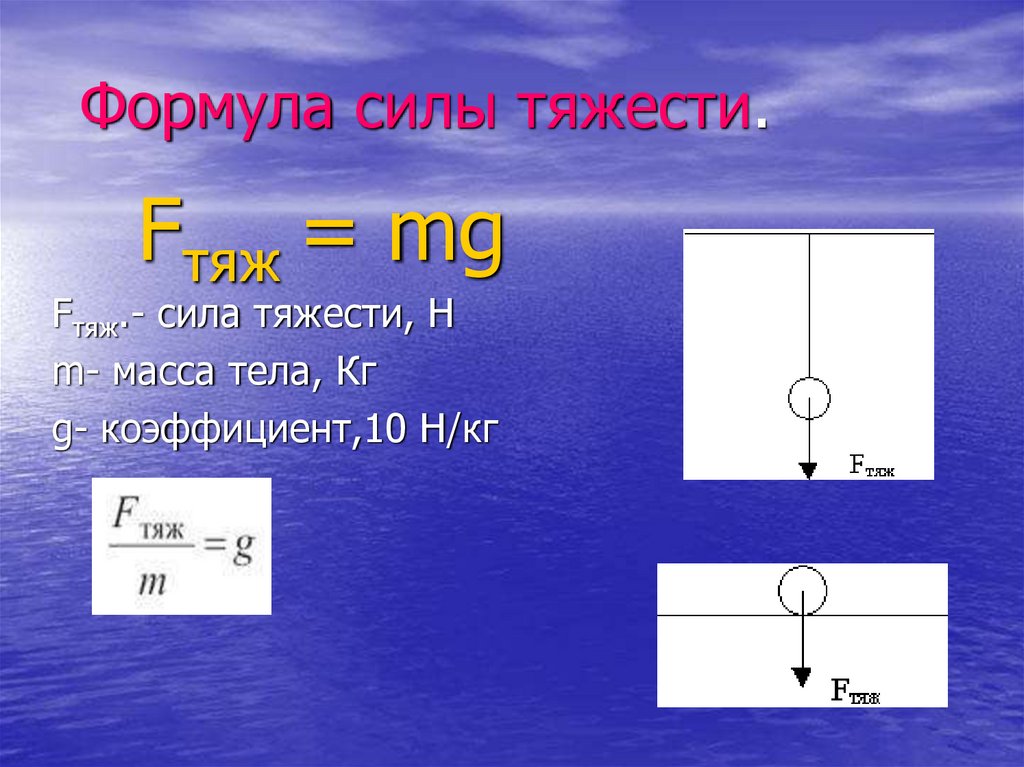
 onesample <- rbind(d, d0, d1) # объединение наборов данных
# линейная модель для оценки среднего результата в зависимости от лечения и искажающих факторов
# параметры оцениваются только с использованием исходных наблюдений (interv= -1)
# оценки параметров используются для прогнозирования среднего результата для наблюдений с набором
# лечение (interv=0 и interv=1)
fit <- glm(f, data = d.onesample)
d.onesample$predicted_meanY <- прогнозировать(подходить, d.onesample)
# оценить средний результат в каждой из групп interv=-1, interv=0 и interv=1
return(mean(d.onesample$predicted_meanY[d.onesample$interv == 1]) -
среднее (d.onesample$predicted_meanY[d.onesample$interv == 0]))
}
# начальная загрузка
результаты <- загрузка (данные = nhefs, статистика = стандартизация, R = 1000)
# создание доверительных интервалов
se <- sd (результаты $ t [ 1])
означает0 <- результаты$t0
ll <- означает 0 - qнорма(0,975) *сэ
ul <- означает0 + qnorm(0,975) * se
начальная загрузка <- data.
onesample <- rbind(d, d0, d1) # объединение наборов данных
# линейная модель для оценки среднего результата в зависимости от лечения и искажающих факторов
# параметры оцениваются только с использованием исходных наблюдений (interv= -1)
# оценки параметров используются для прогнозирования среднего результата для наблюдений с набором
# лечение (interv=0 и interv=1)
fit <- glm(f, data = d.onesample)
d.onesample$predicted_meanY <- прогнозировать(подходить, d.onesample)
# оценить средний результат в каждой из групп interv=-1, interv=0 и interv=1
return(mean(d.onesample$predicted_meanY[d.onesample$interv == 1]) -
среднее (d.onesample$predicted_meanY[d.onesample$interv == 0]))
}
# начальная загрузка
результаты <- загрузка (данные = nhefs, статистика = стандартизация, R = 1000)
# создание доверительных интервалов
se <- sd (результаты $ t [ 1])
означает0 <- результаты$t0
ll <- означает 0 - qнорма(0,975) *сэ
ul <- означает0 + qnorm(0,975) * se
начальная загрузка <- data. frame(
" " = "Лечение - Без лечения",
оценка = означает 0,
стандартная ошибка = SE,
conf.low = ll,
конф.высокая = ул,
check.names = ЛОЖЬ)
bootstrap
frame(
" " = "Лечение - Без лечения",
оценка = означает 0,
стандартная ошибка = SE,
conf.low = ll,
конф.высокая = ул,
check.names = ЛОЖЬ)
bootstrap