Уравнение плоскости онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через три точки
Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы и не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M1, M2, M3 тогда и тольно тогда, когда векторы M1M2, M1M3 и компланарны. Но векторы M1M2, M1M3, M1M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов
Так как эти точки не лежат на одной прямой, векторы и не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M1, M2, M3 тогда и тольно тогда, когда векторы M1M2, M1M3 и компланарны. Но векторы M1M2, M1M3, M1M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов
Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M1, M2, M3:
Ax+By+Cz+D=0. |
Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).
Решение.
Уравнение плоскости, проходящей через точки A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3) имеет следующий вид:
Подставляя координаты точек A, B, C в (1), получим:
Упростим:
Разложим определитель по первому столбцу:
Упростим выражение:
или
Ответ:
Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:
Уравнение плоскости, проходящей через одну точку и имеющий нормаль
nПример 2. Построить плоскость, проходящую через точку M0(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).
Решение.
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) и имеющей нормаль n(A, B, C) имеет следующий вид:
Подставляя координаты векторов M0 и n в (2), получим:
или
Начертательная геометрия | CADInstructor
В электронный учебно-методический комплекс входят лекции, контрольные работы для студентов разных ВУЗов, рабочая тетрадь, презентации, опорный конспект, видеоматериалы решения типовых задач контрольных заданий. Мы рассмотрим основные теоретические положения начертательной геометрии и примеры их применения на практике:
- Методы проецирования
- Ортогональные проекции точки, прямой, плоскости
- Взаимное положение точки, прямой и плоскости
- Многогранники. Точка на поверхности многогранника, пересечение прямой, плоскости с поверхностью многогранника
- Поверхности вращения. Точка на поверхности, пересечение прямой, плоскости с поверхностью.

Электронный учебно-методический комплекс зарегистрирован в Объединенном фонде электронных ресурсов «Наука и образование» Института научной информации и мониторинга Российской академии образования. Свидетельство о регистрации №17165 от 07.06.2011. Авторы: доцент Бочков Андрей Леонидович, профессор Голдобина Любовь Александровна.
Исключительные права на опубликование, обнародование, копирование, воспроизведение, распространение, переработку, перевод, публичное использование и демонстрацию электронного учебно-методического комплекса «Начертательная геометрия» в информационных, в иных целях принадлежат авторам.
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
Структура учебно-методического комплекса
Лекции В лекциях представлены теоретические основы начертательной геометрии. Содержат текстовую информацию, большое количество иллюстраций, а также интерактивные модели для наглядного представления объектов в трехмерном пространстве. В конце каждой темы лекции расположены задачи по начертательной геометрии для самостоятельного решения для закрепления теоретического материала. 1. Методы проецирования 2. Ортогональные проекции прямой 3. Плоскость 4. Способы преобразования ортогонального чертежа 5. Метод геометрических множеств 6. Многогранники 7. Поверхности 8. Пересечение кривых поверхностей
В конце каждой темы лекции расположены задачи по начертательной геометрии для самостоятельного решения для закрепления теоретического материала. 1. Методы проецирования 2. Ортогональные проекции прямой 3. Плоскость 4. Способы преобразования ортогонального чертежа 5. Метод геометрических множеств 6. Многогранники 7. Поверхности 8. Пересечение кривых поверхностей
ПрезентацииПрезентации содержат иллюстративный материал для лекций и в основном предназначены для преподавателей при проведении занятий, а также для студентов, пропустивших лекцию.1. Ортогональные проекции точки2. Ортогональные проекции прямой3. Взаимное положение прямых4. Ортогональные проекции плоскости5. Взаимное положение плоскостей6. Способы преобразования ортогонального чертежа7. Многогранники8. Поверхности
Рабочая тетрадь В рабочей тетради представлены дополнительные задачи по начертательной геометрии, которые полезно прорешать по каждой теме лекции.1. Точка 2. Прямая 3. Плоскость 4. Взаимное положение плоскостей 5.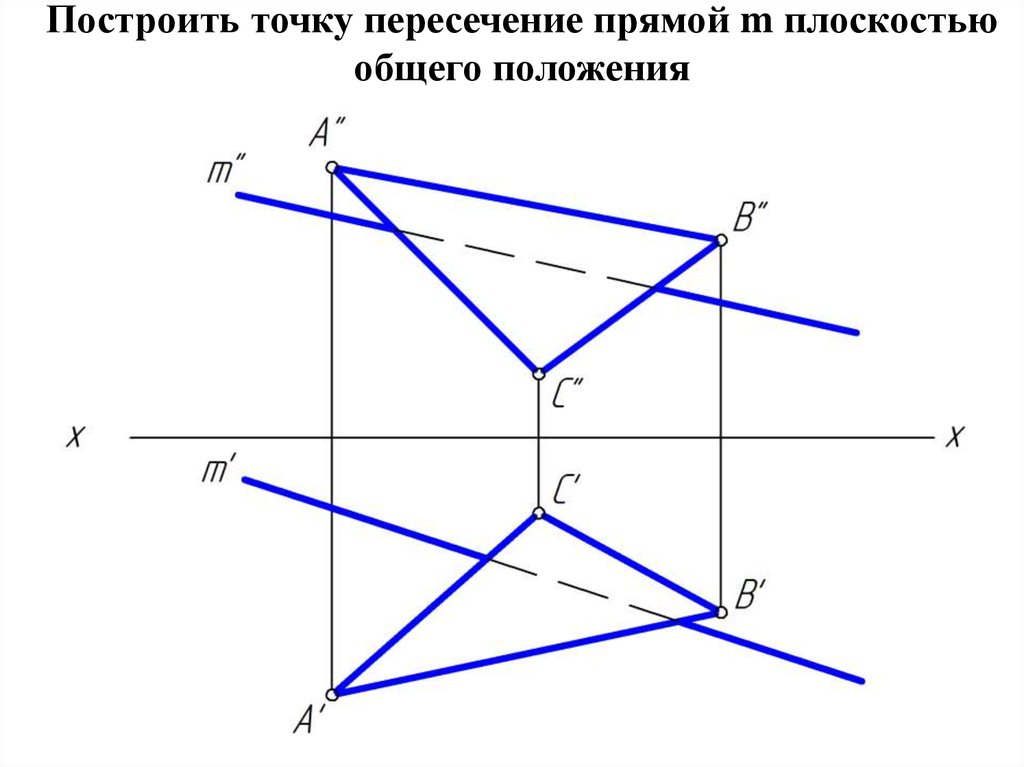 Прямая и плоскость 6. Способы преобразования ортогонального чертежа 7. Пересечение тел прямой и плоскостью 8. Взаимное пересечение поверхностей
Прямая и плоскость 6. Способы преобразования ортогонального чертежа 7. Пересечение тел прямой и плоскостью 8. Взаимное пересечение поверхностей
Опорный конспектВ опорном конспекте в сжатом графическом виде отражены все основные положения и типовые задачи начертательной геометрии. Методичку удобно использовать для самопроверки и подготовки к экзамену или зачету. Опорный конспект в виде схематических блоков учебной информации (рисунков, алгоритмов) охватывает все основные темы курса и является дополнительным пособием для изучения начертательной геометрии.Тема 1. Методы проецирования. Проекции точки, отрезка прямой Тема 2. Отрезок. Прямая, Взаимное положение прямых. Плоскость Тема 3. Пересечение плоскостей. Пересечение прямой с плоскостью Тема 4. Перпендикуляр к плоскости. Дополнительные плоскости проекций Тема 5. Способ вращения. Многогранники Тема 6. Кривые поверхностиСкачать опорный конспект одним файлом
Контрольные работы Контрольные задания (расчетно-графические работы — РГР) предназначены для домашнего выполнения и сдачи преподавателю. В описании контрольных заданий есть видеоматериалы с пошаговыми действиями решения типовых задач.Задание 1. Построение следов плоскости и определение расстояния от точки до плоскости Задание 2. Построение линии пересечения плоскостей Задание 3. Построение натурального вида сечения пирамиды плоскостью Задание 4. Построение линии пересечения поверхностейЗадание 5. Нахождения истинной формы плоской фигуры способом плоско-параллельного перемещенияЗадание 6. Построение недостающих проекций плоской фигуры, принадлежащей плоскости, заданной следамиЗадание 7. Построение точки пересечения прямой с плоскостью, заданной следамиЗадание 8. Определение расстояния между двумя прямыми способом перемены плоскостей проекций
В описании контрольных заданий есть видеоматериалы с пошаговыми действиями решения типовых задач.Задание 1. Построение следов плоскости и определение расстояния от точки до плоскости Задание 2. Построение линии пересечения плоскостей Задание 3. Построение натурального вида сечения пирамиды плоскостью Задание 4. Построение линии пересечения поверхностейЗадание 5. Нахождения истинной формы плоской фигуры способом плоско-параллельного перемещенияЗадание 6. Построение недостающих проекций плоской фигуры, принадлежащей плоскости, заданной следамиЗадание 7. Построение точки пересечения прямой с плоскостью, заданной следамиЗадание 8. Определение расстояния между двумя прямыми способом перемены плоскостей проекций
Результат обучения
- В результате прохождения курса вы научитесь видеть за плоским изображением пространственные объекты.
- Научитесь строить проекции на плоскости простейших геометрических объектов: точки, прямой, плоскости; определять их взаимное положение и размеры.

- Научитесь строить проекции пространственных объектов: многогранников, криволинейных поверхностей; решать метрические и позиционные задачи.
На кого рассчитан учебник
Электронный учебно-методический комплекс предназначен для изучения курса начертательной геометрии студентами системы заочной и дистанционной форм обучения в режиме онлайн, также может быть использован для самостоятельного изучения некоторых тем дисциплины студентами, как правило, 1 курса очной формы обучения. Преподаватели могут использовать данный комплекс для проведения занятий.
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
Создайте свою собственную плоскость эллипса
Вы можете настроить свою плоскость с помощью этого онлайн-инструмента *.
Нажмите , чтобы начать новую конфигурацию , чтобы насладиться настройкой вашего нового самолета с нуля, шаг за шагом.
* Визуализация самолета в конфигураторе носит иллюстративный характер и не отражает реальную конструкцию самолета
Запустить новую конфигурацию
Предварительно настроенный самолет в соответствии с нашими рекомендациями:
SPORT
Лучший выбор для тех, кто любит пилотировать на высокой скорости и ищет максимум удовольствия.
ПУТЕШЕСТВИЯ
Полностью оборудованный самолет для дальних и безопасных путешествий, а не только для приключений по всему миру.
CLUB
Идеальный выбор для аэроклубов, летной подготовки и обмена между пилотами.
Вернуться к итогуЦена спроса
Вас интересует цена вашего аэроплана ellipse? Не стесняйтесь обращаться к нам!
Спасибо за ваш запрос о плоскости эллипса. Мы свяжемся с вами в ближайшее время по указанным контактам.
Name and surname
Phone
Select a countryArubaAfghanistanAngolaAnguillaÅland IslandsAlbaniaAndorraUnited Arab EmiratesArgentinaArmeniaAmerican SamoaAntarcticaFrench Southern TerritoriesAntigua and BarbudaAustraliaAustriaAzerbaijanBurundiBelgiumBeninBonaire, Sint Eustatius and SabaBurkina FasoBangladeshBulgariaBahrainBahamasBosnia and HerzegovinaSaint BarthélemyBelarusBelizeBermudaBolivia (Plurinational State of)BrazilBarbadosBrunei DarussalamBhutanBouvet IslandBotswanaCentral African RepublicCanadaCocos (Keeling) IslandsSwitzerlandChileChinaCôte д’ИвуарКамерунКонго, Демократическая Республика КонгоОстрова КукаКолумбияКоморские островаКабо-ВердеКоста-РикаКубаКюрасаоОстров РождестваКаймановы островаКипрЧехияГерманияДжибутиДоминикаДанияДоминиканская РеспубликаАлжирЭквадорЕгипетЭритреяЗападная СахараИспанияЭстонияЭфиопияФинляндияФиджиФолклендские острова (Великобритания)Габонские островаФедер (Мальвинские острова)ФранцияФареры tain and Northern IrelandGeorgiaGuernseyGhanaGibraltarGuineaGuadeloupeGambiaGuinea-BissauEquatorial GuineaGreeceGrenadaGreenlandGuatemalaFrench GuianaGuamGuyanaHong KongHeard Island and McDonald IslandsHondurasCroatiaHaitiHungaryIndonesiaIsle of ManIndiaBritish Indian Ocean TerritoryIrelandIran (Islamic Republic of)IraqIcelandIsraelItalyJamaicaJerseyJordanJapanKazakhstanKenyaKyrgyzstanCambodiaKiribatiSaint Kitts and NevisKorea, Republic ofKuwaitLao People’s Democratic RepublicLebanonLiberiaLibyaSaint LuciaLiechtensteinSri LankaLesothoLithuaniaLuxembourgLatviaMacaoSaint Martin (French part)MoroccoMonacoMoldova, Republic ofMadagascarMaldivesMexicoMarshall IslandsNorth MacedoniaMaliMaltaMyanmarMontenegroMongoliaNorthern Mariana IslandsMozambiqueMauritaniaMontserratMartiniqueMauritiusMalawiMalaysiaMayotteNamibiaNew CaledoniaNigerNorfolk IslandNigeriaNicaraguaNiueNetherlandsNorwayNepalNauruNew ЗеландияОманПакистанПанамаПиткэрнПеруФилиппиныПалауПапуа-Новая ГвинеяПольшаПуэрто-РикоКорея (Демократическая ratic People’s Republic of)PortugalParaguayPalestine, State ofFrench PolynesiaQatarRéunionRomaniaRussian FederationRwandaSaudi ArabiaSudanSenegalSingaporeSouth Georgia and the South Sandwich IslandsSaint Helena, Ascension and Tristan da CunhaSvalbard and Jan MayenSolomon IslandsSierra LeoneEl SalvadorSan MarinoSomaliaSaint Pierre and MiquelonSerbiaSouth SudanSao Tome and PrincipeSurinameSlovakiaSloveniaSwedenEswatiniSint Maarten (Dutch part)SeychellesSyrian Arab RepublicTurks and Caicos IslandsChadTogoThailandTajikistanTokelauTurkmenistanTimor -LesteТонгаТринидад и ТобагоТунисТурцияТувалуТайвань, провинция КитаяТанзания, Объединенная Республика УгандаУкраинаОтдаленные малые острова СШАУругвайСоединенные Штаты АмерикиУзбекистанСвятой ПрестолСент-Винсент и ГренадиныВенесуэла (Боливарианская Республика)Виргинские острова (Британия)Виргинские острова (США)ВьетнамЮжная АфрикаЗамбиВануатуУоллис и Фут0005
Ваша конфигурация
Текст вашего сообщения
Даю согласие на обработку персональных данных на основании политики конфиденциальности.
Выбранный вариант конфликтует с предыдущим выбором.
Вы хотите удалить ?
Скопируйте этот URL-адрес, чтобы вернуться к своей конфигурации позже.
MachUp — Бесплатная онлайн-программа проектирования самолетов
от goatboy29 | 25 мая 2018 г. |
(11) Posted in How ToВы когда-нибудь хотели сконструировать свой собственный самолет? Или построили утку, а потом часами пытались понять, где должен быть центр тяжести? Или задавались вопросом, как размещение стабилизатора повлияет на устойчивость вашего самолета? Если вы можете ответить «да» на любой из этих вопросов (или «да» на любой вопрос о конструкции самолета), тогда MachUp для вас!
MachUp — это бесплатный онлайн-инструмент для аэродинамического анализа, используемый для проектирования, анализа и оптимизации самолетов. Этот инструмент был разработан аспирантами под руководством доктора Дуга Хансакера из Университета штата Юта. Я сам занимаюсь разработкой MachUp уже больше года. Моя работа конкретно связана с расчетом аэродинамики пропеллеров и моделированием того, как промывка пропеллеров может повлиять на аэродинамику подъемных поверхностей, таких как крылья. Используя этот инструмент, начинающие авиаконструкторы, практически не разбирающиеся в аэродинамике или авиационной технике, могут проектировать свои собственные самолеты. От простого летающего крыла до утки с распределенной электронной тягой, MachUp позволяет пользователям проектировать свои собственные самолеты и легко анализировать их аэродинамику.
Этот инструмент был разработан аспирантами под руководством доктора Дуга Хансакера из Университета штата Юта. Я сам занимаюсь разработкой MachUp уже больше года. Моя работа конкретно связана с расчетом аэродинамики пропеллеров и моделированием того, как промывка пропеллеров может повлиять на аэродинамику подъемных поверхностей, таких как крылья. Используя этот инструмент, начинающие авиаконструкторы, практически не разбирающиеся в аэродинамике или авиационной технике, могут проектировать свои собственные самолеты. От простого летающего крыла до утки с распределенной электронной тягой, MachUp позволяет пользователям проектировать свои собственные самолеты и легко анализировать их аэродинамику.
Целью этой статьи не является руководство пользователя для MachUp. Скорее, моя цель — познакомить вас с его потенциалом и дать вам представление о том, где вы можете найти инструменты, необходимые для начала работы.
Итак, приступим!
MachUp доступен в виде онлайн-инструмента, бесплатного и открытого для всех.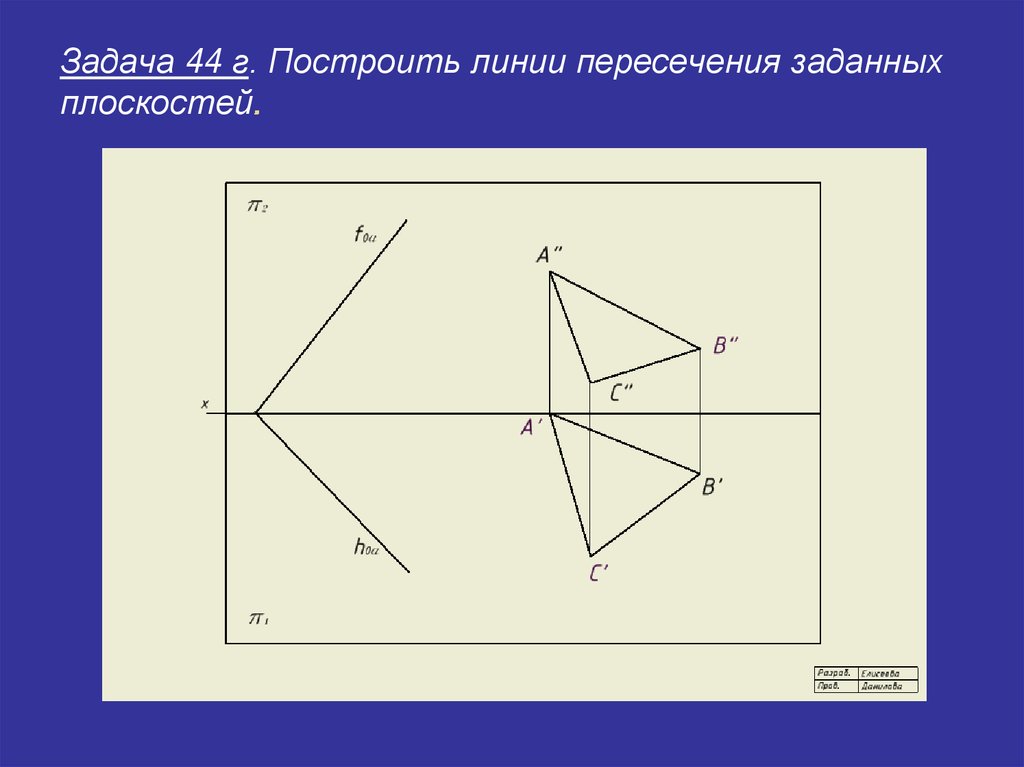 Вы можете получить доступ к нескольким различным версиям MachUp, перейдя на веб-сайт USU Aerolab. Оказавшись там, нажмите кнопку «Войти» в правом верхнем углу и либо войдите, либо зарегистрируйтесь, в зависимости от того, делаете ли вы это впервые. Регистрация очень быстрая, простая и бесплатная! Это просто помогает нам отслеживать нашу пользовательскую базу и информировать наших пользователей о важных будущих обновлениях (они происходят только один или два раза в год, поэтому мы не будем взорвать ваш почтовый ящик).
Вы можете получить доступ к нескольким различным версиям MachUp, перейдя на веб-сайт USU Aerolab. Оказавшись там, нажмите кнопку «Войти» в правом верхнем углу и либо войдите, либо зарегистрируйтесь, в зависимости от того, делаете ли вы это впервые. Регистрация очень быстрая, простая и бесплатная! Это просто помогает нам отслеживать нашу пользовательскую базу и информировать наших пользователей о важных будущих обновлениях (они происходят только один или два раза в год, поэтому мы не будем взорвать ваш почтовый ящик).
После того, как вы зарегистрируетесь и войдете в систему, вы можете выбрать доступ к двум различным версиям MachUp: MachUp 4 и MachUp 5. Они в основном одинаковы с несколькими ключевыми отличиями, а именно: MachUp4 был разработан с учетом инженеров, а MachUp5 был разработан для всех остальных. Поэтому в этой статье я сосредоточусь на MachUp5, но если у вас есть четкое представление об аэродинамике и безразмерных коэффициентах, тогда вперед и погрузитесь в MachUp4!
Как только вы войдете в MachUp, вы увидите следующее окно:
Чтобы дать вам краткий обзор, использование MachUp состоит из трех основных шагов:
- Построить самолет
- Установить условия полета
- Запустить анализ
Теперь давайте немного углубимся в каждый из этих шагов . Просто к вашему сведению: это не учебник. Я создам несколько из них позже. Моя цель прямо сейчас — просто дать вам обзор того, как работает MachUp, чтобы вы могли войти и начать играть с ним самостоятельно.
Просто к вашему сведению: это не учебник. Я создам несколько из них позже. Моя цель прямо сейчас — просто дать вам обзор того, как работает MachUp, чтобы вы могли войти и начать играть с ним самостоятельно.
Итак, первый шаг: Построить самолет .
Это делается путем добавления крыльев и/или пропеллеров в пространство 3D-проектирования. Чтобы добавить крыло, нажмите «Добавить» на верхней панели инструментов, а затем нажмите «Крыло». После добавления крыла его различные характеристики можно изменить с помощью вкладок «Объект», «Геометрия» и «Материал» с правой стороны. Эти характеристики включают в себя длину корневой и законцовочной хорды, угол стреловидности, двугранный угол, характеристики аэродинамического профиля и многое другое. Вы даже можете добавить управляющие поверхности к своим крыльям и настроить микширование для этих управляющих поверхностей, что позволит вам создавать сложные управляющие миксы, такие как элевоны, V-образные хвостовые оперения и т.
То же самое касается пропеллеров. Нажмите «Добавить», а затем выберите «Пропеллер». Теперь, когда винт выбран, вы можете изменить элементы его геометрии, включая количество лопастей, шаг, диаметр и характеристики аэродинамического профиля. Вы даже можете указать характеристики вашей системы питания, включая двигатель, регулятор скорости и аккумулятор. Затем MachUp использует эту информацию, чтобы дать вам оценку того, как пропеллер будет работать при заданных условиях полета и настройке дроссельной заслонки.
Комбинируя несколько крыльев и пропеллеров, вы сможете сконструировать целый самолет! Например, вот самолет DEP (Distributed Electric Propulsion), который я спроектировал на основе самолета вертикального взлета и посадки, созданного НАСА. Важно отметить, что, хотя я создал фюзеляж и гондолы, используя несколько других объектов, доступных в меню «Добавить», единственными объектами, которые в настоящее время используются в аэродинамическом анализе, являются крылья и пропеллеры . Таким образом, любые другие объекты, которые вы добавляете, предназначены исключительно для визуальной привлекательности и фактически не влияют на аэродинамику. В будущем мы хотели бы добавить функциональность для анализа других объектов, таких как фюзеляжи, просто мы еще не дошли до этого.
Таким образом, любые другие объекты, которые вы добавляете, предназначены исключительно для визуальной привлекательности и фактически не влияют на аэродинамику. В будущем мы хотели бы добавить функциональность для анализа других объектов, таких как фюзеляжи, просто мы еще не дошли до этого.
После того, как вы построили самолет, переходим ко второму шагу: Установите условие освещения F .
Для этого щелкните вкладку «Условие» в правом верхнем углу. На этой вкладке вы можете установить различные аспекты условий полета, включая скорость, угол атаки и любые отклонения поверхности управления. Вы также сможете установить скорость вращения или настройку дроссельной заслонки (если вы указали двигатель для всех ваших пропеллеров) пропеллеров.
Теперь обратите внимание на селектор «Единицы» вверху. В настоящее время MachUp5 настроен на использование двух разных систем измерения: английской и метрической. Если вы выберете «Английский», размеры самолета, которые вы указали при создании своего самолета, будут в футах, скорость самолета будет измеряться в футах в секунду, а силы, действующие на самолет, будут измеряться в фунтах.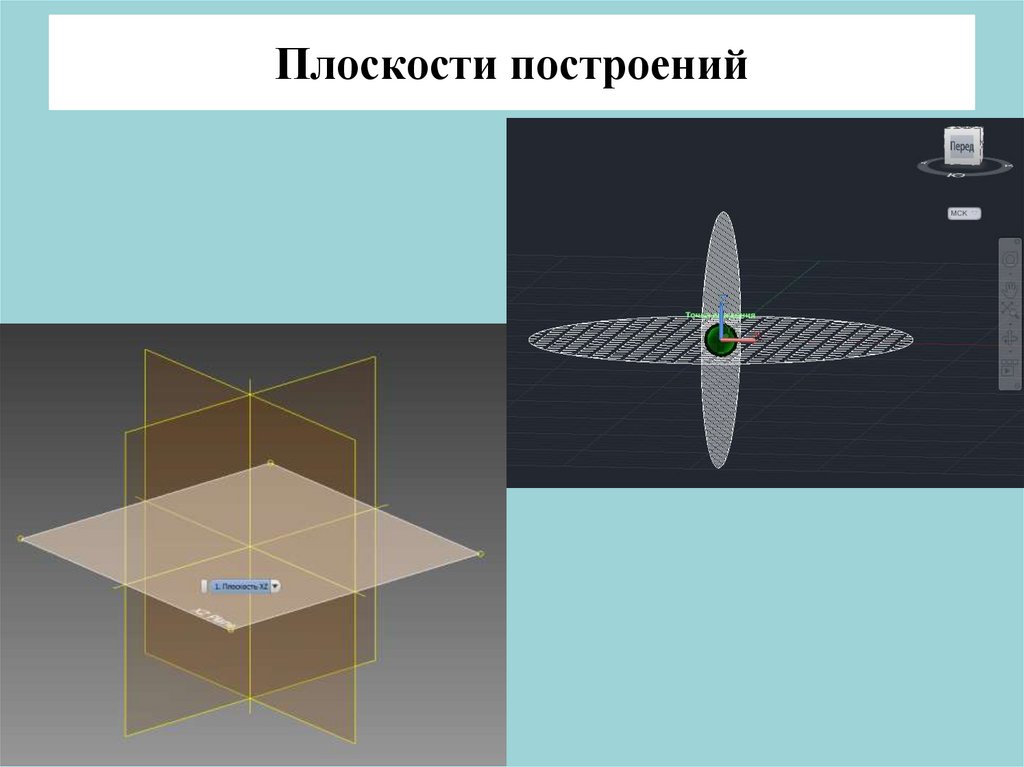 Если вы выберете «SI», размеры самолета будут в метрах, скорость самолета будет измеряться в метрах в секунду, а сила, действующая на самолет, будет измеряться в ньютонах.
Если вы выберете «SI», размеры самолета будут в метрах, скорость самолета будет измеряться в метрах в секунду, а сила, действующая на самолет, будет измеряться в ньютонах.
После того, как вы определили условия полета, вы готовы к третьему шагу: Запустите анализ.
На вкладке «Анализ» взгляните на раскрывающееся меню «Выполнить». Это меню содержит все различные анализы, которые MachUp может выполнять на вашем самолете. Чтобы запустить анализ, просто выберите нужный анализ и нажмите «Обновить результаты». Обратите внимание, что в зависимости от анализа, который вы хотите запустить, это может занять от 1 до 30 секунд, поэтому вам, возможно, придется немного набраться терпения. Если вы разочаруетесь, просто подумайте, насколько это быстрее, чем выполнение всех этих чрезвычайно сложных вычислений с использованием логарифмической линейки. Теперь, вот краткое описание всех анализов, которые вы можете запустить.
- Силы и моменты : Анализ сил и моментов на самолете для заданных условий полета.
 Результаты сначала разделяются на силы, создаваемые несущими поверхностями (крыльями) и стойками, а затем объединяются, чтобы получить общие силы на дне. FL — подъемная сила. FD — сила сопротивления. FS — боковая сила. MX, MY и MZ — моменты относительно осей x, y и z соответственно.
Результаты сначала разделяются на силы, создаваемые несущими поверхностями (крыльями) и стойками, а затем объединяются, чтобы получить общие силы на дне. FL — подъемная сила. FD — сила сопротивления. FS — боковая сила. MX, MY и MZ — моменты относительно осей x, y и z соответственно. - Производные характеристики : анализирует, как аэродинамика самолета изменяется при небольших изменениях условий полета, в частности угла атаки и угла бокового скольжения. Я напишу еще одну статью, объясняющую подробнее об этом позже, но важно вот что: Для того чтобы воздушное судно считалось стабильным, Cm,alpha < 0, Cl,beta<0 и Cn,beta>0. Если ваш анализ показывает эти результаты, небольшие нарушения условий полета не приведут к перевороту вашего самолета. Кроме того, вы хотите, чтобы статический запас был как можно ближе к 0,05 . Это мера устойчивости и маневренности самолета, и ее следует использовать для определения правильного положения центра тяжести (ЦТ).

- Аэродинамический центр : Вычисляет аэродинамический центр самолета. Аэродинамический центр — это точка, вокруг которой изменение угла атаки не влияет на момент тангажа. Это довольно важно и используется в более продвинутых аэродинамических расчетах, но может не понадобиться для того, что вы хотите сделать.
- Начало сваливания : Этот анализ берет воздушную скорость, которую вы указали в условиях полета, а затем увеличивает угол атаки до тех пор, пока какая-либо часть самолета не остановится. Затем он сообщает вам угол атаки сваливания, величину подъемной силы, которую вы можете создать при этом угле атаки и указанной воздушной скорости (прямо перед сваливанием), а также местоположение сваливания. Возможно, следующий анализ будет для вас более полезным, если он звучит интересно.
- Воздушная скорость при сваливании : Вычисляет минимальную воздушную скорость, необходимую для полета, исходя из заданного веса самолета.
 Это один из самых медленных анализов, но и один из самых полезных. По сути, после того, как вы спроектировали свой самолет, вы устанавливаете ожидаемый вес вашего самолета, и этот анализ покажет вам, с какой скоростью вам нужно двигаться, прежде чем вы сможете оторваться от земли. Также дает ту же информацию, что и анализ начала опрокидывания.
Это один из самых медленных анализов, но и один из самых полезных. По сути, после того, как вы спроектировали свой самолет, вы устанавливаете ожидаемый вес вашего самолета, и этот анализ покажет вам, с какой скоростью вам нужно двигаться, прежде чем вы сможете оторваться от земли. Также дает ту же информацию, что и анализ начала опрокидывания. - Целевая подъемная сила : Расчет угла атаки, необходимого для создания заданной подъемной силы при заданной воздушной скорости.
- Триммер по тангажу : Вычисляет угол атаки и отклонение руля высоты, необходимые для дифферентовки самолета для заданной подъемной силы и момента при заданной воздушной скорости. Чтобы выполнить этот анализ, ваш самолет должен иметь руль высоты, и вы должны спроектировать его достаточно хорошо, чтобы можно было отрегулировать его по тангажу.
- Распределения : Сохраняет текстовый файл, описывающий распределение сил и моментов на крыльях и винтах.

Теперь в заключение о проведении анализа скажу следующее: У MacUp есть ограничения. MachUp предназначен для анализа летательных аппаратов в области линейной аэродинамики. Это в основном означает ниже стойла. Итак, если вы установите угол атаки 50 градусов и создадите подъемную силу 1000 фунтов на своем 2-футовом радиоуправляемом самолете, вы не нарушите физику. Вы просто вышли за пределы диапазона, который может точно предсказать MachUp. То же самое относится и к таким вещам, как пропеллеры. Вы не можете раскачивать 3-футовый винт на FT Power Pack C, так что даже не пытайтесь. Это не даст вам точных результатов.
При этом, если вы спроектируете самолет и установите условия полета в разумных эксплуатационных пределах, MachUp даст очень точные результаты. Мы сравнили результаты, полученные с помощью MachUp, с испытаниями CFD и испытаниями в аэродинамической трубе, и MachUp дает очень точные результаты за долю времени, которое потребовалось бы для испытаний CFD или испытаний в аэродинамической трубе.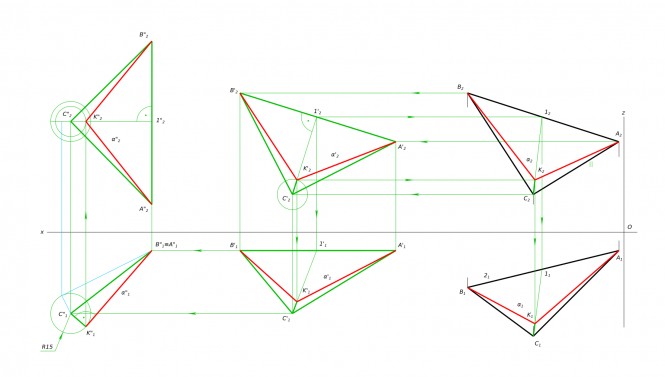

 Результаты сначала разделяются на силы, создаваемые несущими поверхностями (крыльями) и стойками, а затем объединяются, чтобы получить общие силы на дне. FL — подъемная сила. FD — сила сопротивления. FS — боковая сила. MX, MY и MZ — моменты относительно осей x, y и z соответственно.
Результаты сначала разделяются на силы, создаваемые несущими поверхностями (крыльями) и стойками, а затем объединяются, чтобы получить общие силы на дне. FL — подъемная сила. FD — сила сопротивления. FS — боковая сила. MX, MY и MZ — моменты относительно осей x, y и z соответственно.
 Это один из самых медленных анализов, но и один из самых полезных. По сути, после того, как вы спроектировали свой самолет, вы устанавливаете ожидаемый вес вашего самолета, и этот анализ покажет вам, с какой скоростью вам нужно двигаться, прежде чем вы сможете оторваться от земли. Также дает ту же информацию, что и анализ начала опрокидывания.
Это один из самых медленных анализов, но и один из самых полезных. По сути, после того, как вы спроектировали свой самолет, вы устанавливаете ожидаемый вес вашего самолета, и этот анализ покажет вам, с какой скоростью вам нужно двигаться, прежде чем вы сможете оторваться от земли. Также дает ту же информацию, что и анализ начала опрокидывания.