Построение уравнений онлайн: Построение графика функции онлайн

Построение графиков функций при решении квадратных уравнений

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Цель урока:
Применение навыков построения графиков
функций при решении квадратных уравнений
План урока
Актуализация знаний.
Новый материал: 5 способов
решения квадратных уравнений.
Практическое применение умений и навыков.
Движение графиков на плоскости.
Объяснить построение графика функции.
По графику функции написать ее уравнение

Построить график функции у aх 2 bx c
Решить уравнение х 2 2 х 3 0
у х 1
2
у ( х 2)
2
у ( х 3)
у
3
2
1
-3
-2
-1
1
2
3
х
-1
у х 3
2
-2
-3
у ( х 3) 3
2
2
у 4х 3
2
у
3
2
1
-3
-2
-1
1
-1
-2
-3
2
3
х
у 0,5( х 3)
2
у
3
2
1
-3
-2
-1
1
-1
-2
-3
2
3
х
у х 1
2
у
3
2
1
-3
-2
-1
1
-1
-2
-3
2
3
х
2
у
2
х 1
у
3
2
1
-5
-4
-3
-2
-1
1
-1
-2
-3
2
3
4
5
х
у
у 2 х 4
2
3
2
у ( х 4) 2
2
1
-5
-4
-3
-2
-1
1
-1
-2
-3
2
3
4
5
х
у
у ( х 3) 2
2
у х 1 1
3
2
1
-5
-4
-3
-2
-1
1
2
3
4
5
-1
-2
-3
у 3х 1
х
1
у
1
х 1
у
3
2
1
-5
-4
-3
-2
-1
1
-1
-2
-3
2
3
4
5
х
у х 2 2х 3
у
3
2
1
-5
-4
-3
-2
-1
1
-1
-2
Вершина параболы: (1; -4)
-3
2
3
4
5
х
I способ
II способ
у х 2 2х 3
х 2 2х 3
III способ
IV способ
( х 1) 2 4
х 3 2х
2
V способ
3
х 2
х
у
у х
7
2
у 2х 3
6
5
4
3
-2
1
-3
-2
-1
1
2
3
х
у
5
у х2 3
4
у 2х
3
2
1
-3
-2
-1
1
-1
-2
-3
2
3
х
у ( х 1)
у
2
у 4
4
3
2
1
-4
-3
-2
1
-1
-1
-2
-3
2
3
4
х
у х 2
у
3
у
х
3
2
1
-5
-4
-3
-2
-1
1
-1
-2
-3
2
3
4
5
х
Выберите способ и решите уравнение.
х 2 4х 5 0
Корней нет
х х 3 0.
2
Вывод: Графические способы красивы, но не дают
гарантии решения любого квадратного уравнения !!!

English     Русский Правила

Графер Линейных Уравнений — Mathcracker.Com

Инструкции: Используйте этот Linear Equation Grapher для построения графика любого линейного уравнения, которое вы предоставите, с отображением всех этапов. Вам нужно указать линейное уравнение, график которого вы хотите построить, в поле формы ниже.

Подробнее об этом графере линейных уравнений

Построение графиков линий является фундаментальным умением, и этот калькулятор поможет вам в этом. Для начала вам необходимо предоставить линейное уравнение вы хотите построить график.

Вы можете привести любое линейное уравнение в явном виде, например, x + 3y = 2 , или то, которое не полностью упрощено, например, x + 3y = 2/3 x.

Графические линии имеет так много применений, что это становится очень практичным навыком. Геометрически линии имеют очень простую интуицию, что облегчает построение графиков, поскольку для их задания нам не требуется много информации.

Как построить график линейных уравнений?

Вы можете использовать это графический калькулятор для построения графиков линий. Если вы решите сделать это вручную, вам нужно знать, что данный подход требует преамбулы, которая будет зависеть от типа предоставляемой информации.

Каковы этапы построения графика линии?

• Шаг 1: Определите тип предоставленной информации. Представлено ли уравнение, есть ли две точки, точка и наклон, наклон и y-интерцепт? Четко оцените, что
• Шаг 2: Независимо от полученной информации, используйте ее для нахождения двух точек, через которые проходит прямая. Для заданного уравнения решите y, например, для x = 0 и x = 1. Для наклонной и y-пересечения постройте уравнение y = a + bx и найдите две точки. Если у вас есть одна точка и наклон, определите y = y1 + b(x-x1) и вставьте его в точку x = 0
• Шаг 3: Получив две точки, через которые проходит линия, с помощью линейки проведите через них линию

Линии рисовать очень легко, просто нужно быть методичным и знать, какой информацией вы располагаете.

Даже если вы делаете это вручную, всегда приятно иметь под рукой линейку графический калькулятор онлайн чтобы проверить свои результаты.

Графические линии

Графические линии имеют очень много применений. Например, вы можете решить систему уравнений построив график соответствующих линий и посмотрев, где они пересекаются.

При использовании этого метода, когда прямые параллельны и не пересекаются, решений не будет.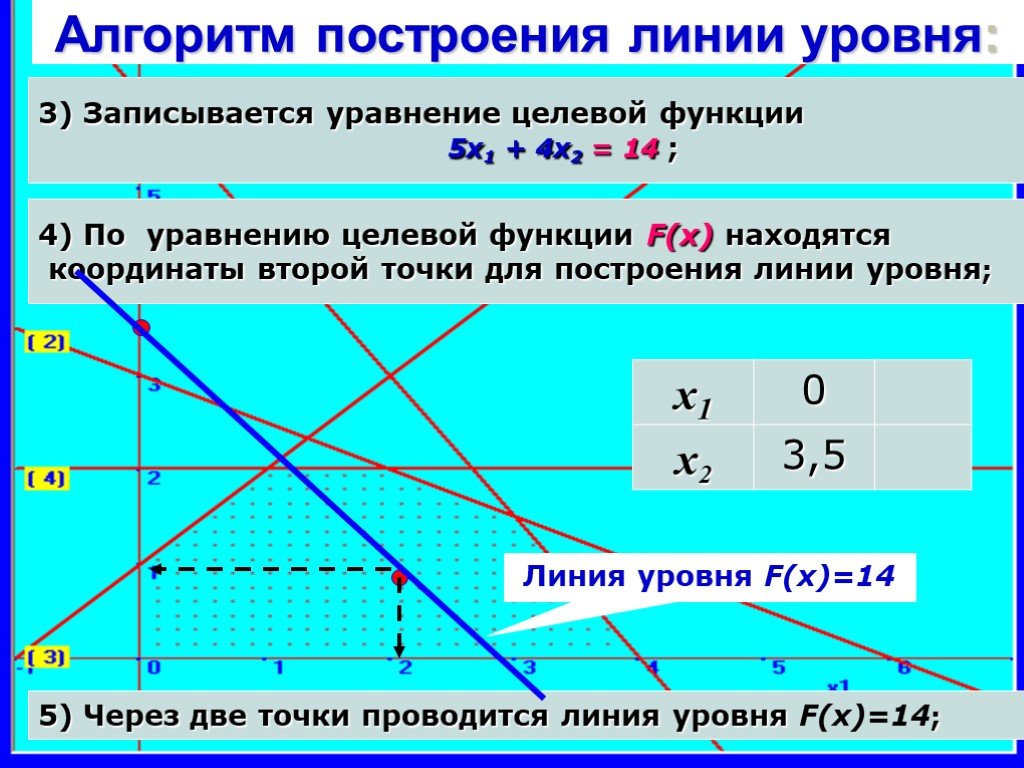

Подобно тому, как это произошло со сложением и вычитанием, деление дробей просто вытекает из умножения дробей: Чтобы разделить две дроби, нужно просто умножить первую на обратная дробь

второй (обратная дробь получается путем замены числителя на знаменатель в дроби).

Другие применения линейных графов

Линии или Линейные графики действительно присутствуют везде. линейные функции постоянно появляются в приложениях, в расчетах и оптимизации, поэтому они действительно полезны.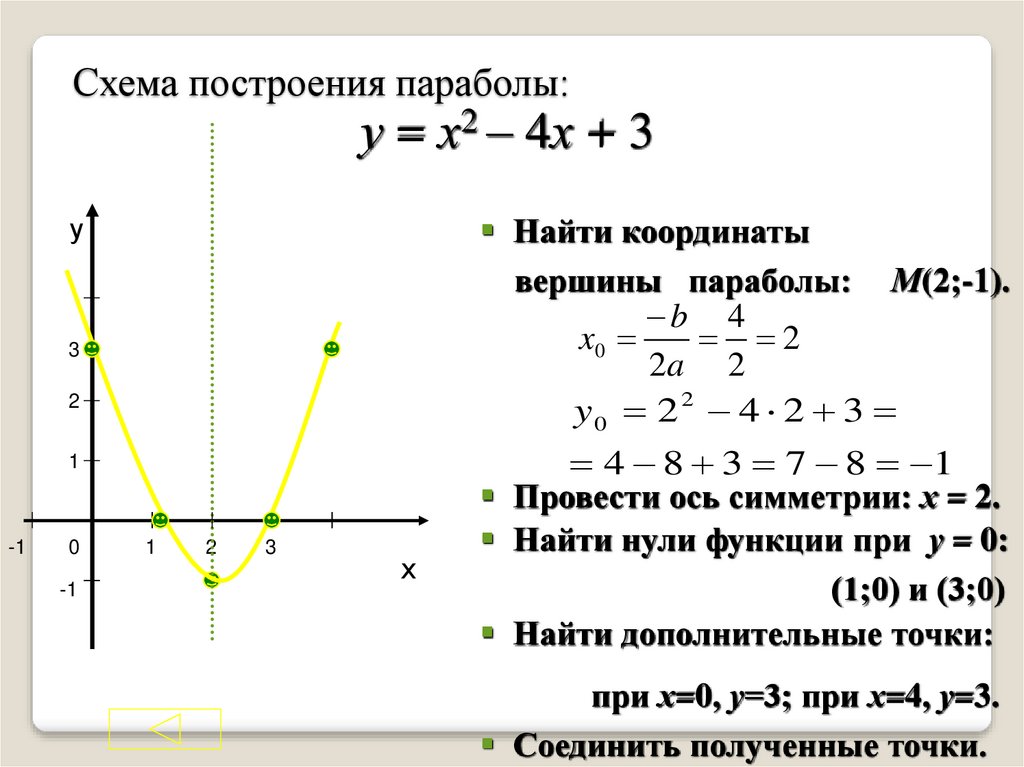

Пример: пример графера линейных уравнений

Постройте график следующих уравнений: \(\frac{1}{2}x + \frac{7}{4}y = 0\)

Отвечать: Мы должны работать со следующим уравнением:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Сначала работаем с константами:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Результат получается, если поставить (y) в левую часть, а (x) и константу — в правую:

\[\displaystyle \frac{7}{4}y = -\frac{1}{2}x \]

Затем процесс продолжается путем решения для \(y\), а затем путем деления обеих сторон уравнения на \(\frac{7}{4}\). Получаем:

\[\displaystyle y=-\frac{\frac{1}{2}}{\frac{7}{4}}x\]

и после упрощения результат будет следующим.

\[\displaystyle y=-\frac{2}{7}x\]

Вывод : На основании имеющихся данных мы приходим к выводу, что уравнение линии в форме наклон-пересечение имеет вид \(\displaystyle y=-\frac{2}{7}x\) с наклоном \(\displaystyle b = -\frac{2}{7}\) и y-пересечением \(\displaystyle n = 0\).

Следовательно, график представленной линии имеет вид

Пример: пример графера линейных уравнений

Получите строку, которая представляет: \(\frac{2}{3}x + \frac{5}{4}y = — \frac{5}{6}x + 2\)

Отвечать: Нам было предложено следующее уравнение:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Работа с константами:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Теперь, положив \(y\) в левой части, \(x\) и константу в правой части, получим

\[\displaystyle \frac{5}{4}y = \left(\frac{-5}{6}-\frac{2}{3}\right)x +2\]

Теперь член, умножающий \(y\), равен \( \frac{5}{4} — 0 = \frac{5}{4}\), а так как \( -\frac{5}{6} — \frac{2}{3} = -\frac{3}{2}\), то получается следующее

\[\displaystyle \frac{5}{4}y=-\frac{3}{2}x+2\]

Теперь, находя \(y\) путем деления обеих частей уравнения на \(\frac{5}{4}\), получается следующее

\[\displaystyle y=-\frac{\frac{3}{2}}{\frac{5}{4}}x+\frac{2}{\frac{5}{4}}\]

и упрощая окончательно получаем следующее

\[\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\]

Вывод : На основании предоставленных данных мы заключаем, что уравнение линии в форме наклона-отрезка имеет вид \(\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\), с наклоном \(\displaystyle b = -\frac{6}{5}\) и точкой пересечения по оси y \(\displaystyle n = \frac{8}{5}\).

Линейный график

Другие линейные калькуляторы

Линии настолько важны, что заслуживают собственного раздела в книге по математике. Вы можете вычислить Линейные уравнения в различных формах, в зависимости от конкретных потребностей.

Определение линий, которые в конечном итоге понадобятся две точки, через которые проходит линия , который может быть предоставлен прямо или косвенно.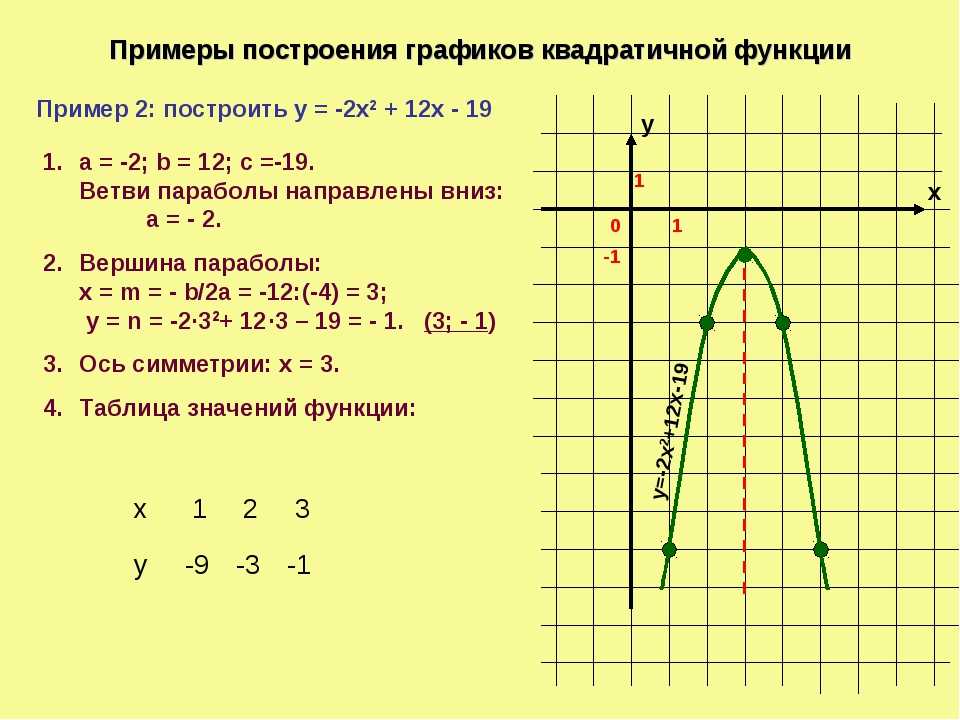

Аппроксимация функции с помощью регрессионного анализа

Проблема аппроксимации функции заключается в том, как выбрать функцию из четко определенного класса, которая точно соответствует («аппроксимирует») целевой неизвестной функции.

Этот калькулятор использует предоставленные данные таблицы целевых функций в виде точек {x, f(x)} для построения нескольких моделей регрессии, а именно: линейной регрессии, квадратичной регрессии, кубической регрессии, степенной регрессии, логарифмической регрессии, гиперболической регрессии, ab -экспоненциальная регрессия и экспоненциальная регрессия. Результаты можно сравнивать по коэффициенту корреляции, коэффициенту детерминации, средней относительной ошибке (стандартной ошибке регрессии) и визуально, на графике. Теория и формулы, как обычно, даны под калькулятором.

Аппроксимация функции с помощью регрессионного анализа

83 71 64 69 69 64 68 59 81 91 57 65 58 62

Значения X, разделенные пробелом

183 168 171 17 8 176 172 165 158 183 182 163 175 164 175

Значения Y, разделенные пробелом

Линейная регрессия

Квадратичная регрессия

Кубическая регрессия

Степенная регрессия

ab-Экспоненциальная регрессия

Логарифмическая регрессия

Hyperbo личная регрессия

Экспоненциальная регрессия

Точность вычислений

Знаки после запятой: 4

Линейная регрессия

 

Коэффициент линейной корреляции

 

Коэффициент детерминации

 

Средняя относительная ошибка, %

 

Квадратичная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя относительная ошибка, %

 

Кубическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя относительная ошибка, %

 

Регрессия мощности

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя относительная ошибка, %

 

ab-Экспоненциальная регрессия

 

Коэффициент корреляции

Коэффициент детерминации

Средняя относительная ошибка, %

Логарифмическая регрессия

Корреляция коэффициент

 

Коэффициент детерминации

 

Средняя относительная ошибка, %

 

Гиперболическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя относительная ошибка, %

 

Экспоненциальная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя относительная ошибка, %

 

Результаты

Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же формулы, что и в случае квадратичной регрессии.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же формулы, что и выше.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – то же.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — те же, что и выше.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же, что и выше.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же, что и выше.

Начнем с задачи:
Имеем неизвестную функцию y=f(x), заданную в виде табличных данных (например, таких, как полученные из экспериментов).
Требуется найти функцию с известным типом (линейная, квадратичная и т.д.) y=F(x), эти значения должны быть максимально приближены к табличным значениям в тех же точках. На практике тип функции определяют путем визуального сравнения точек таблицы с графиками известных функций.

В результате мы должны получить формулу y=F(x), называемую эмпирической формулой (уравнение регрессии, функция аппроксимации), которая позволяет вычислить y для x, не представленных в таблице. Таким образом, эмпирическая формула «сглаживает» значения y.

Мы используем метод наименьших квадратов , чтобы получить параметры F для наилучшего соответствия. Наилучшее соответствие по методу наименьших квадратов минимизирует сумму квадратов невязок, причем невязка представляет собой разницу между наблюдаемым значением и подобранным значением, предоставленным моделью.

Таким образом, когда нам нужно найти функцию F, такую ​​как сумма квадратов невязок, S будет минимальным

Опишем решение этой задачи на примере линейной регрессии F=ax+b.
Нам нужно найти наилучшее соответствие для коэффициентов a и b, таким образом, S является функцией a и b. Для нахождения минимума найдем точки экстремума, в которых частные производные равны нулю.

Используя формулу для производной комплексной функции, получим следующие уравнения:

Разложив первые формулы с частными производными, получим следующие уравнения:

Из этих уравнений можно получить формулы для a и b , что будет соответствовать приведенным выше формулам.

Базовая математика в области строительства Knowledge.net

СТРОИТЕЛЬНЫЕ ЗНАНИЯ >> ОБЩИЕ ТЕХНИЧЕСКИЕ ЗНАНИЯ >>

БАЗОВАЯ МАТЕМАТИКА

 

1. Как изменить дюймы на десятичные футы и избежать Ошибки?
2. Каковы основные формулы площади и объема?
3. Почему преобразование единиц будет одним из Самые полезные вещи, которые вы когда-либо узнаете?
4. Как изучить основы математики и алгебры?
5. Как узнать, когда сбрасывать карты в техасском холдеме?
6. Каковы 3 полезных концепции тригонометрии?
7. Секреты торговли и практические правила для базовой математики:

Как преобразовать дюймы в десятичные футы и избежать ошибок?

Бад Колдуэлл, один из лучших суперинтендантов, с которыми я когда-либо работал, научил меня ценить перемены. дюймы в десятичные футы. Мы рассматривали магазинный чертеж для предмета оборудования с большим количеством анкерных болтов, и все было в ногах, дюймов и долей дюйма. В голове он быстро преобразовал дюймы и доли дюйма в десятичные футы, поэтому мы могли легко добавить и проверить размеры. Он показал мне замечательный маленький трюк торговля, которую я использовал более 25 лет. Таблица преобразования дюймов в десятичные футы показывает информация.

Как вы знаете, большинству из нас сложно складывать дроби. Мы вероятно, в какой-то момент усвоил понятие наименьшего общего знаменателя, но трудно вспомнить, как на самом деле использовать его. Таким образом, чтобы добавить ноги и дюймы, нам приходится иметь дело с дробями и с теми 12″ в футе концепции, что означает, что мы должны добавить вручную, используя карандаш и бумагу. Имеются специальные калькуляторы для сложения футов, дюймов и долей дюймов. доступны, но они всегда казались мне трудными в использовании. Таким образом, добавление строка размеров в футах, дюймах и долях дюйма получает много легче, если мы можем просто преобразовать в десятичные футы.

Возникают многочисленные ситуации, когда эти преобразования помогают:

1. Проверка строки измерений, чтобы убедиться, что они правильно добавляют
2. Сравнение высот на чертеже площадки (обычно в десятичном формате) футы) и архитектурный чертеж (часто в футах и ​​дюймах)
3. Устройство доступных пандусов и маршрутов доступа

В качестве примера используем доступный маршрут. Скажи, что строительство закончено высота этажа составляет 401 фут — 6 1/4 дюйма, а уклон на парковочном месте 400,14 фута. На тротуаре между парковкой и входной дверью есть расстояние 30′. Теперь вы, вероятно, знаете, что доступный маршрут имеет максимальный уклон 5%, или он становится пандусом и нуждается в поручнях. Итак, 401′ — 6 1/4 дюйма преобразуется в 401,52. Затем вычтите 400,14, чтобы найти изменение уклона. 1,38′. Чтобы найти уклон, разделите изменение уклона на 1,38 фута на расстояние 30 футов, чтобы получить наклон 0,046 или 4,6%, что меньше, чем максимум 5% разрешено кодом. Так что это работает.

Каковы основные формулы A

rea и Volume?

Чтобы рассчитать, сколько бетона нужно заказать для плиты на одном уровне, необходимо знать основные формулы площади и объема. Большинство из нас понимает, что длина, умноженная на ширину, умноженная на толщину, дает нам объем. Мы можем нужно немного больше помощи, хотя, когда вещи не прямоугольные или возникают другие сложности. Давайте начнем с примера и проработаем как использовать геометрию общих форм.

Надеюсь, приведенный выше пример вам понятен и просто иллюстрирует несколько полезных концепций. Если вам нужна помощь в понимании например, вы можете просмотреть Базовая математика и алгебра ВМС США учебный класс. Этот курс дает много базовых и более продвинутых Информация для понимания математики.

Площади и объемы обычных геометрических фигур, вероятно, не нужно запоминать. Его обычно просто, чтобы знать, где легко найти формулы. К зная, как пользоваться этими формулами, вы сможете решить многие строительные проблемы, такие как:

1. Сколько земли нужно переместить? Сколько грузовиков будет реально тащить? Сколько грузовиков необходимо на объекте?
2. Сколько бетона заказать для заливки?
3. Сколько что-то весит? Что потребуется, чтобы поднять его?
4. Сколько воды будет в этом бассейне? Сколько времени потребуется, чтобы Заполните?

Эти и многие другие вопросы можно решить, зная, как рассчитать площади и объемы Общий Геометрические фигуры.

Почему преобразование единиц будет одной из самых полезных вещей, которые вы когда-либо узнаете?

Я помню, как учился переводить единицы на уроках биологии в высокие школа. Я использовал этот навык с тех пор, и это помогло мне решить много проблем (и избежать множества ошибок). Процесс преобразование единиц является простым и мощным. Секрет постоянного получение правильных ответов заключается в том, чтобы всегда перечислять единицы измерения и время отмены единиц по мере прохождения процесса. Немного примеры, показанные ниже в разделе «Преобразование Единицы — примеры», которая наглядно иллюстрирует процесс.

Научившись решать задачи с помощью простой математики проблемы, вы будете поражены тем, как много сложных вопросов вы можете понять и проблемы, которые вы можете решить. Решение проблем с хорошим отношение прогрессирует, зарабатывая больше денег и получая больше ответственности. Так найдите время, чтобы научиться решать простые математические задачи, которые помогут вам конвертировать единицы. Используйте один и тот же метод каждый раз:

1. Всегда записывайте проблему.
2. Всегда перечисляйте единицы измерения (даже если вам это кажется простым)
3. Всегда проходите и отменяйте юниты, чтобы убедиться в ответе вы получаете в правильных единицах

Этот простой прием действительно может вам помочь.

Как изучить основы

Математика и алгебра?

Способность использовать математику как инструмент может выделить вас среди многих других в строительная сфера. Так же, как плотники работают на уровне выше рабочих отчасти из-за их умения обращаться с инструментами, вы можете работать за более высокий уровень с умением формулировать и решать числовые задачи.

Базовый курс математики и алгебры ВМС США содержит инструкции, которые не предполагает никаких предварительных знаний. Вы можете использовать этот курс одним из двух способов:

1. Пройдите весь курс от начала до конца и получите твердое понимание основ.
2. Сосредоточьтесь на области, которую вам нужно понять прямо сейчас (возможно, вам непонятны проценты или как решать проблемы с дроби или, может быть, вам нужен обзор простой алгебры, чтобы знать, как найти неизвестную величину в ситуации).

Преимущество прохождения всего курса заключается в факт, что математическое знание строит на себе.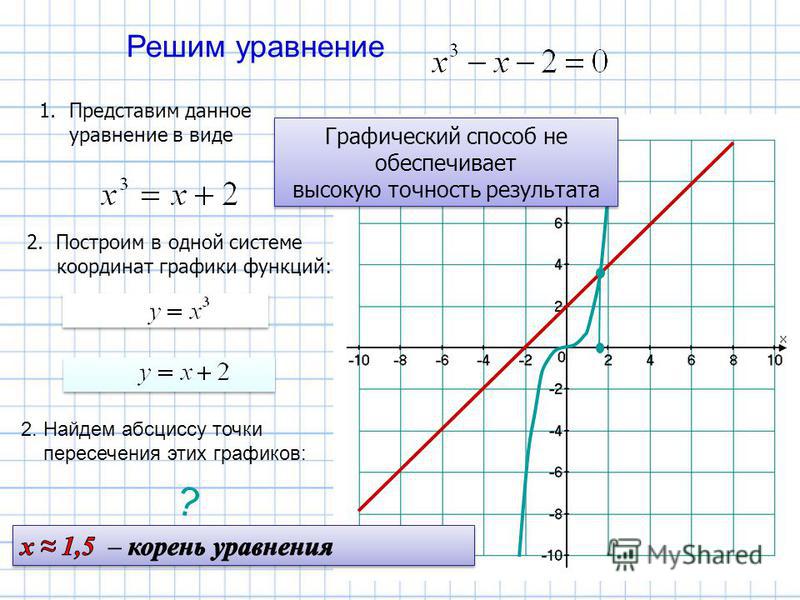 Чем яснее вы понять основные строительные блоки математики, тем лучше вы научитесь и сохранить более продвинутые концепции. Недостаток работы через весь курс — это время, которое он займет, и что вы, вероятно, узнать много вещей, которые напрямую не применимы к строительству.
 

Как мне

Знайте, когда сбрасывать их в техасском холдеме?

Вам не нужно ничего знать о вероятности и Статистика по строительству (по крайней мере, я так не думаю). Так почему я включить курсы вероятностей и статистики ВМС США? это круто знать.

Понимание основ теории вероятностей поможет вам понять жизнь. Общее представление о том, как происходят случайные события, позволит вам лучше оценить риски и выгоды. И это помогает вашей игре в покер! Ты может проверить некоторые учения о вероятности на Курс предварительного исчисления и вероятностей ВМС США.

Статистика, на с другой стороны, это математика, которая помогает вам понять большие группы информация. Мы используем статистику, чтобы принимать обоснованные решения. А строительная компания, например, может быть заинтересована в улучшении производительность для своих профессий. Поскольку различные биты информации проанализировав, возможно, они обнаружат, что прогулы по пятницам значительно выше, чем в любой другой день. Статистика может помочь понять, какая часть этого отсутствия случайна или это значительная находка. Скажем, статистика указывает на существенно более высокий прогулов по пятницам, то компания ищет причины. Работники получают зарплату по четвергам во второй половине дня. Так что теперь есть руководство выбор, который нужно сделать.

Многие строительные компании используют программы повышения качества, использовать статистику. Если компания хочет улучшить результаты, она должна понять, что на самом деле происходит в их повседневных процессах. К понять, как на самом деле работают процессы, нам нужно измерять вещи, затем попытайтесь выяснить, что важно. Статистика нам в помощь понять, что происходит на самом деле.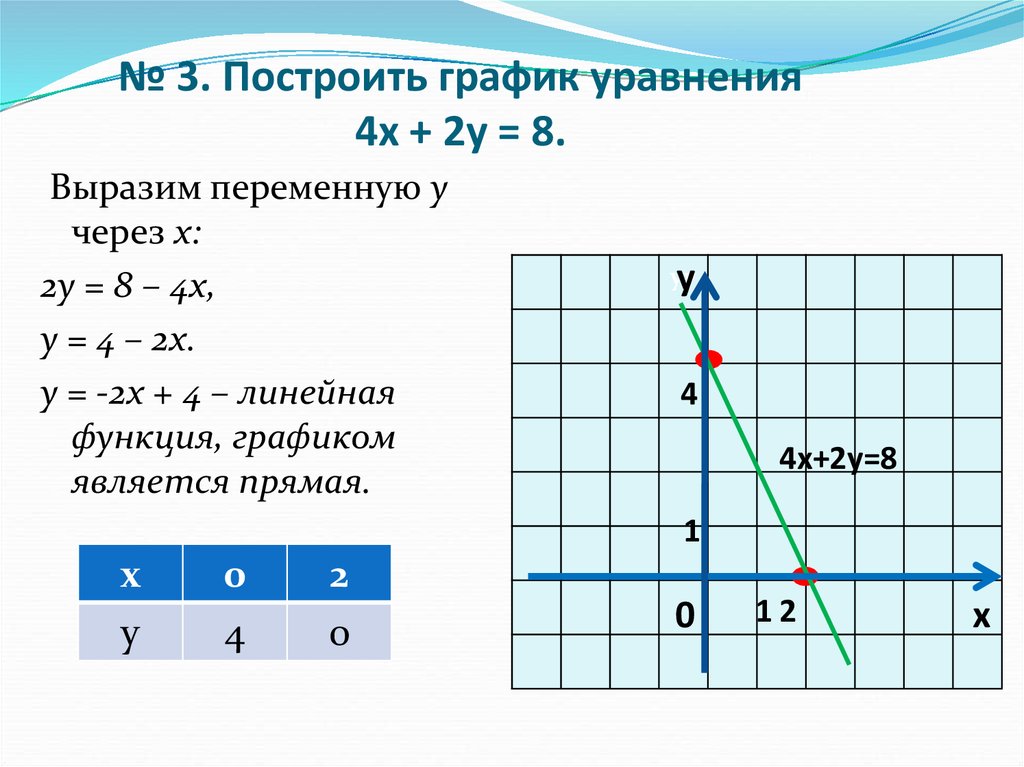 Некоторое хорошее преподавание статистики может найти в Курс «Введение в статистику ВМС США».
 

Что такое 3 U

Понятия тригонометрии?

Когда большинство людей слышит «Тригонометрия», они предполагают, что это то, что они никогда не могли понять и не использовать. На самом деле у меня никогда не было курса по тригонометрии, так что Я не эксперт, но я узнал три действительно полезных вещи самостоятельно. Синус, Косинус и тангенс помогают мне решать самые разные задачи. Если я активно участвует в создании чего-либо, я использую эти несколько простых формул. рисунок ниже поясняет концепции и дает несколько примеров.

Если вам нужна дополнительная информация о тригонометрии, см. Курс тригонометрии ВМС США.
 

Хитрости торговли и практические правила для базовой математики:

1. Преобразование футов, дюймов и долей дюйма в десятичные футы в легко складывать, вычитать и умножать.
2. При преобразовании единиц всегда записывайте единицы и отменяйте их как вы продолжаете преобразование.

   No related posts.