Y cos 2x график. Функция y=cos t, её основные свойства и график
Урок и презентация на тему: «Функция y=cos(x). Определение и график функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево.
Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1].
Это также хорошо видно из графика. - Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Это также хорошо видно из графика.Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.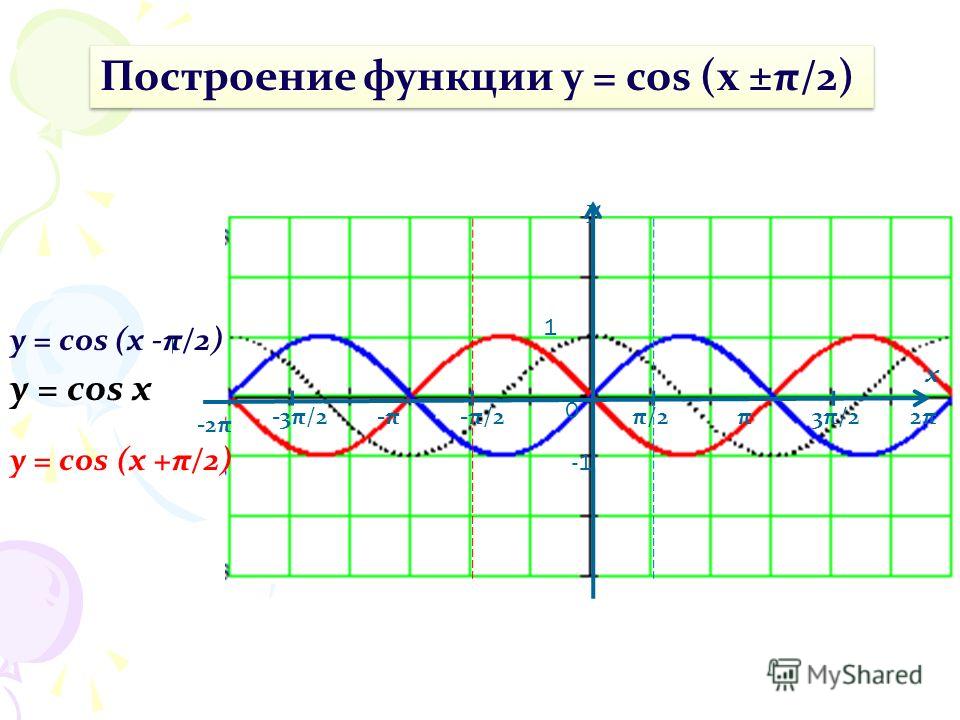
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].
На этом уроке мы подробно рассмотрим функцию у = cos х, ее основные свойства и график.В начале урока дадим определение тригонометрической функции у = cost на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции.
В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=cost, её основные свойства и график
Функцией называется закон, по которому каждому значению независимого аргумента ставится в соответствие единственное значение функции.
Вспомним определение функции Пусть t — любое действительное число. Ему соответствует единственная точка M на числовой окружности. У точки M есть единственная абсцисса. Она и называется косинусом числа t. Каждому значению аргумента t соответствует только одно значение функции (рис. 1).
Центральный угол численно равен величине дуги в радианах, т.е. числу Поэтому аргументом может быть и действительное число, и угол в радианах.
Если мы умеем для каждого значения определить то можем построить график функции
Можно получить график функции и другим способом. По формулам приведения поэтому график косинуса — это синусоида, сдвинутая по оси x на влево (рис.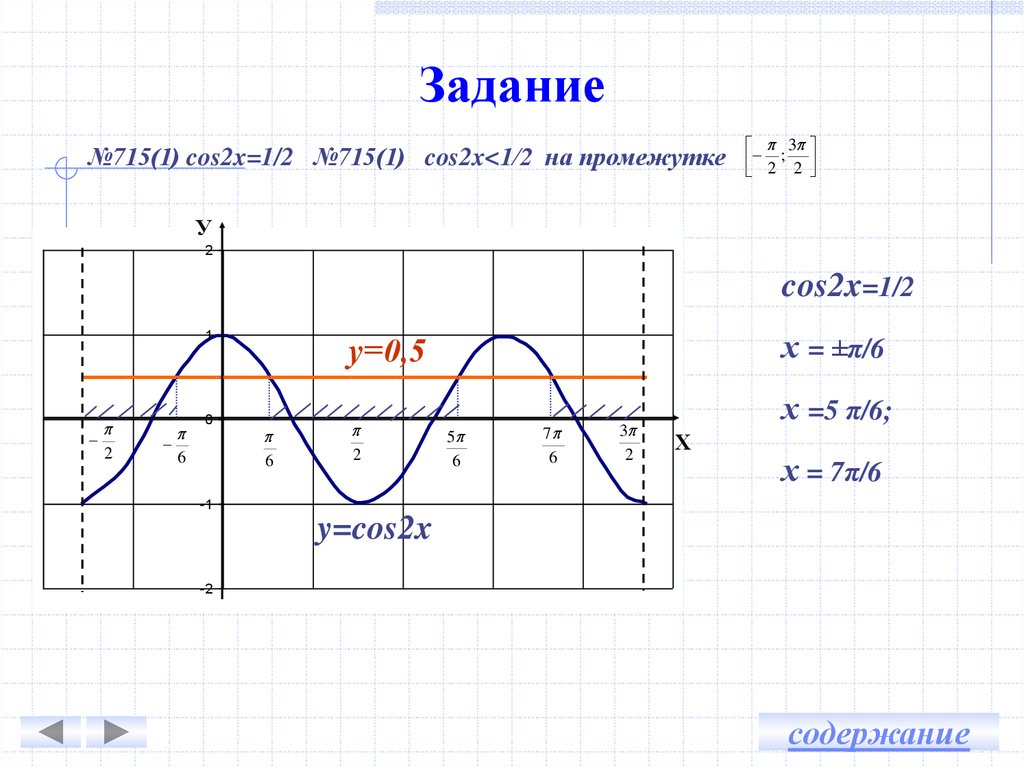
Свойства функции
1) Область определения:
2) Область значений:
3) Функция четная:
4) Наименьший положительный период:
5) Координаты точек пересечения с осью абсцисс:
6) Координаты точки пересечения с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции: .
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели основные свойства и график функции Далее они будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.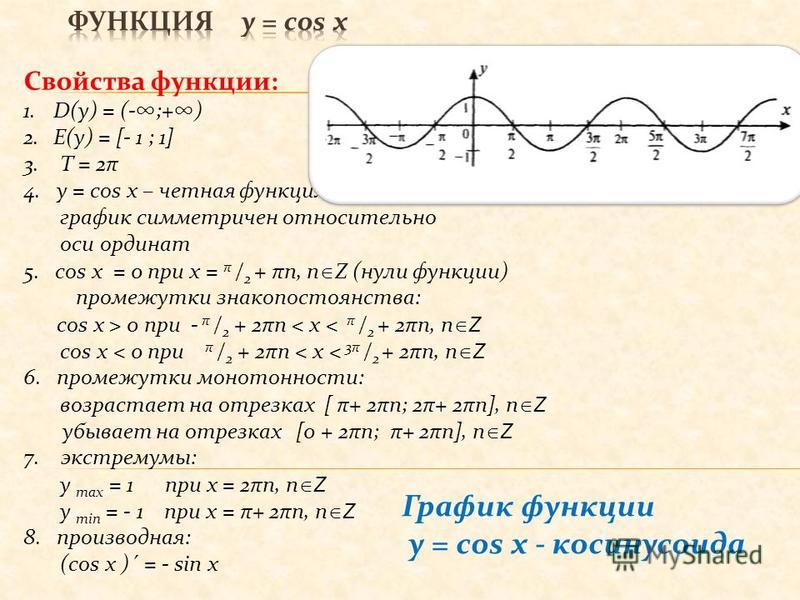
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.6, 16.7, 16.9.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная.
Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x), y=tg(x), y=ctg(x).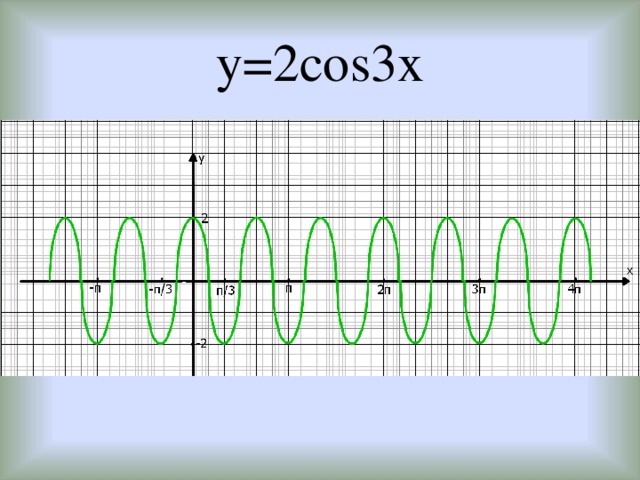
Рассмотрим каждую из них в отдельности.
Y = sin(x)
График функции y=sin(x).
Основные свойства:
3. Функция нечетная.
Y = cos(x)
График функции y=cos(x).
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений — отрезок [-1;1].
3. Функция четная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = tg(x)
График функции y=tg(x).
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k — целое.
3. Функция нечетная.
Y = ctg(x)
График функции y=ctg(x).
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k — целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
График функции cos x 2. Графики тригонометрических функций кратных углов
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево.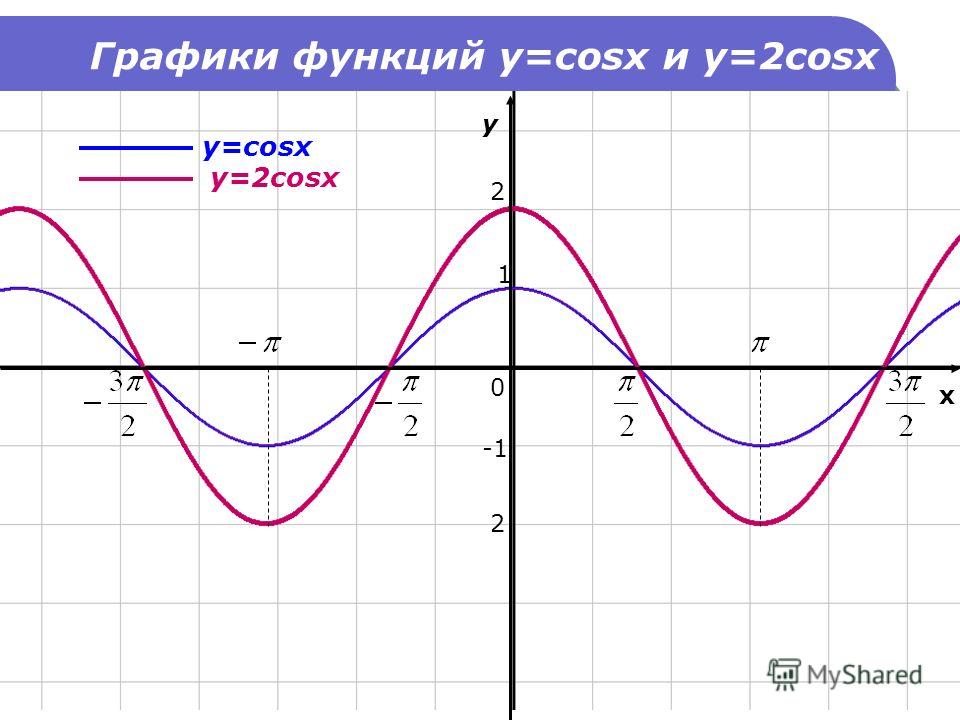
Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.
- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Это также хорошо видно из графика.Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.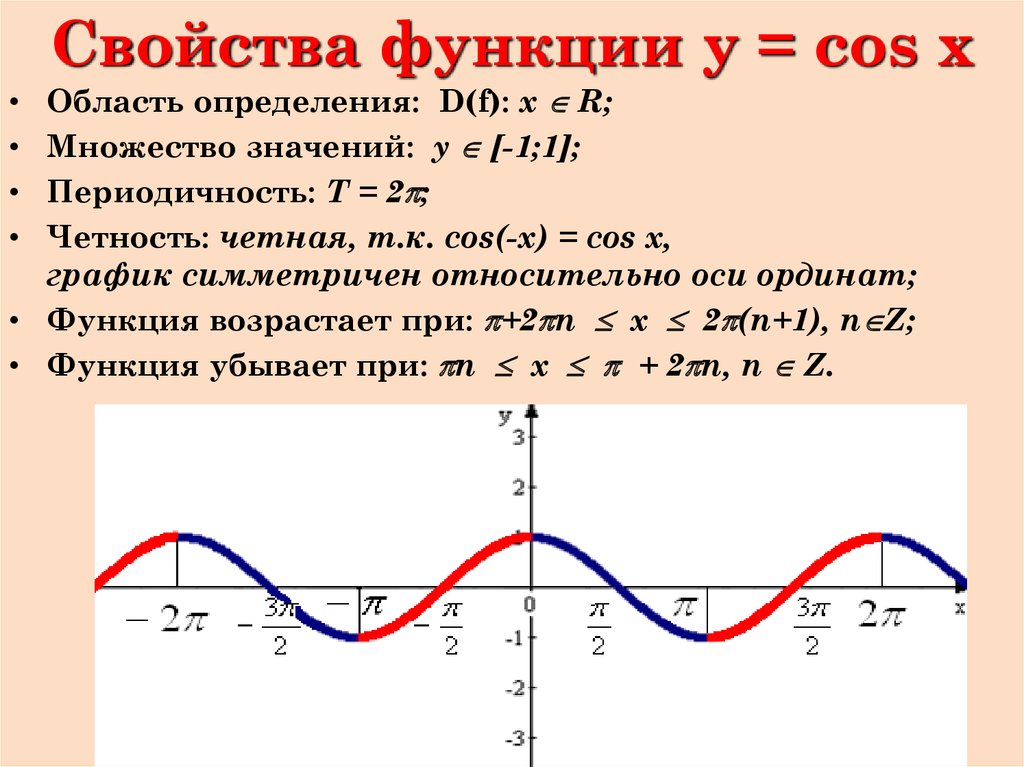
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида.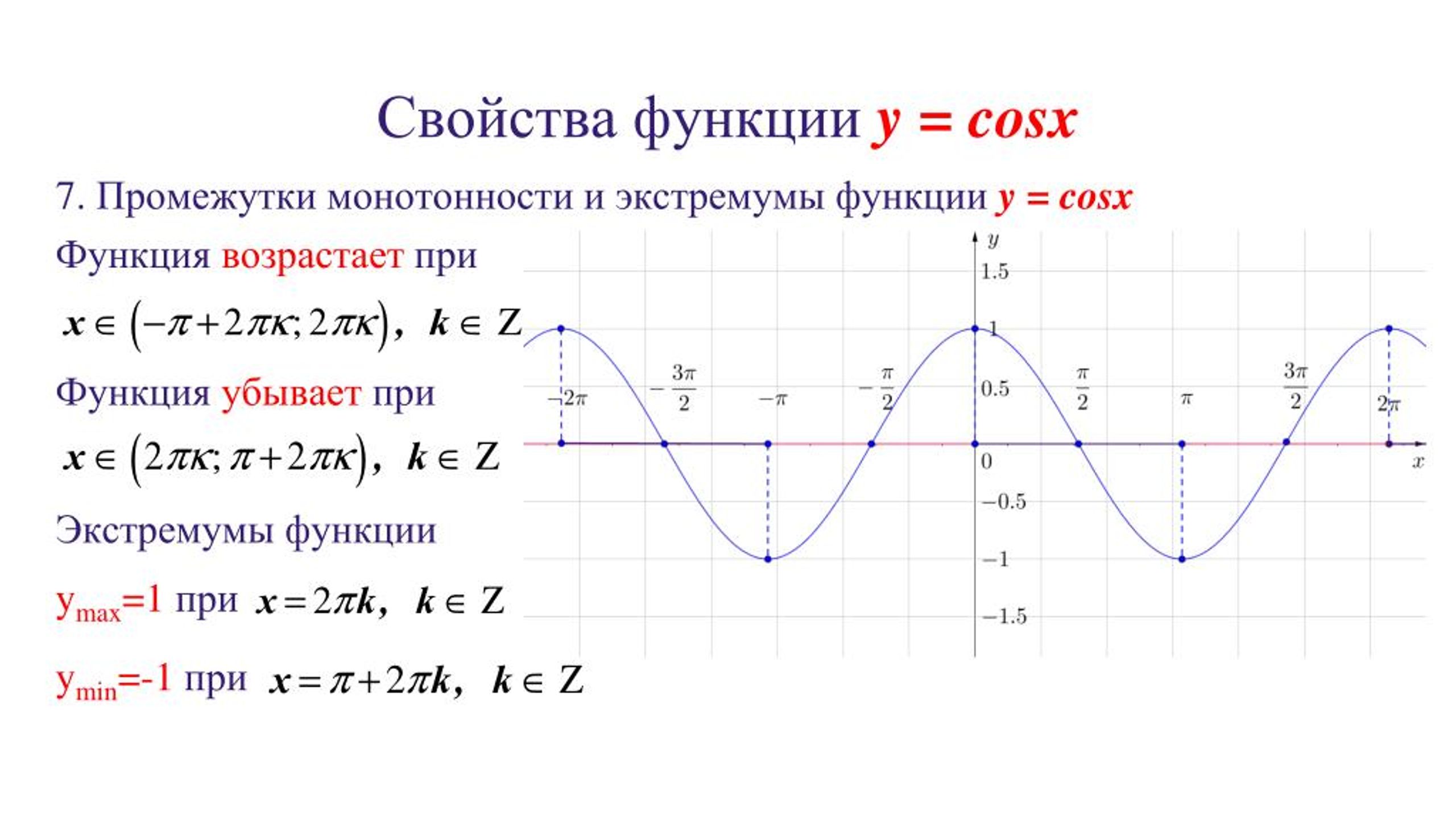
4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию.
Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом. Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.
Всего в теме 25 презентаций
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.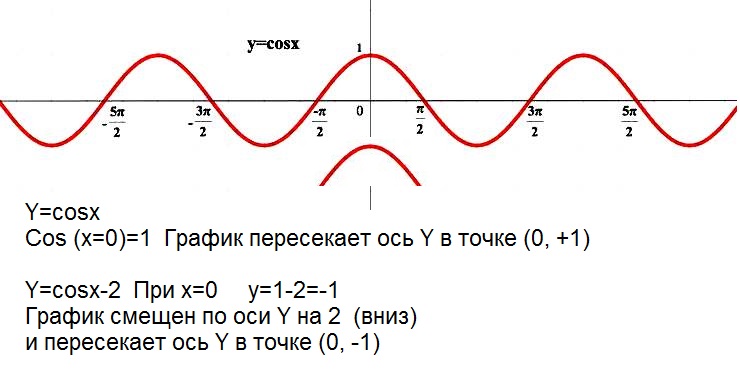
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.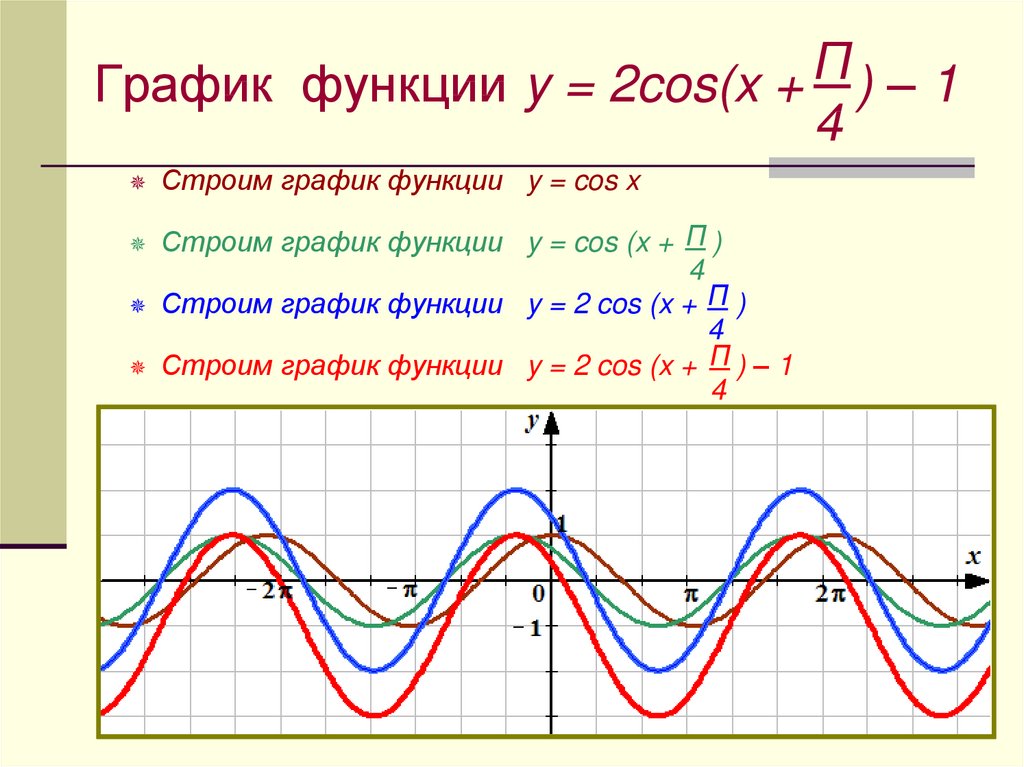
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
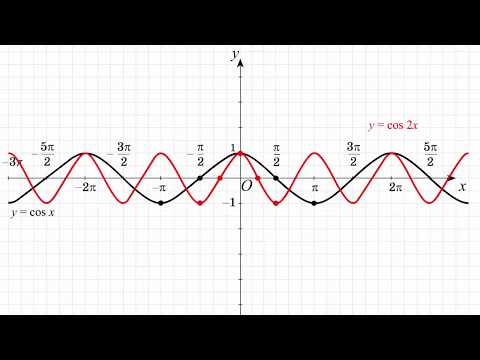
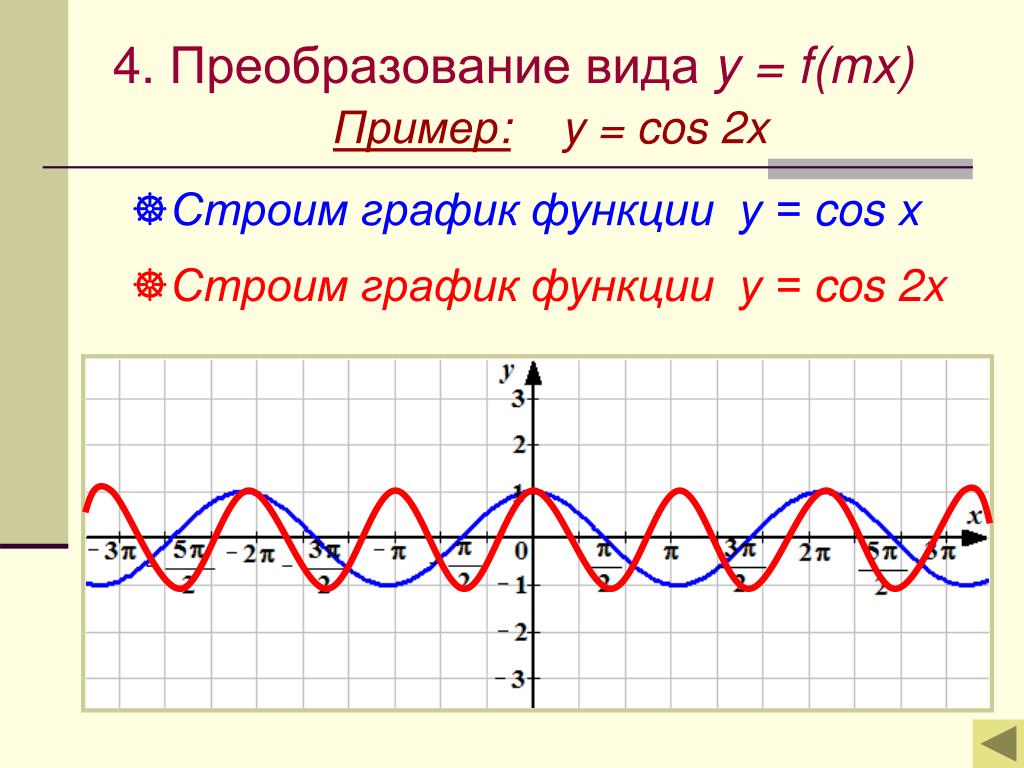
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.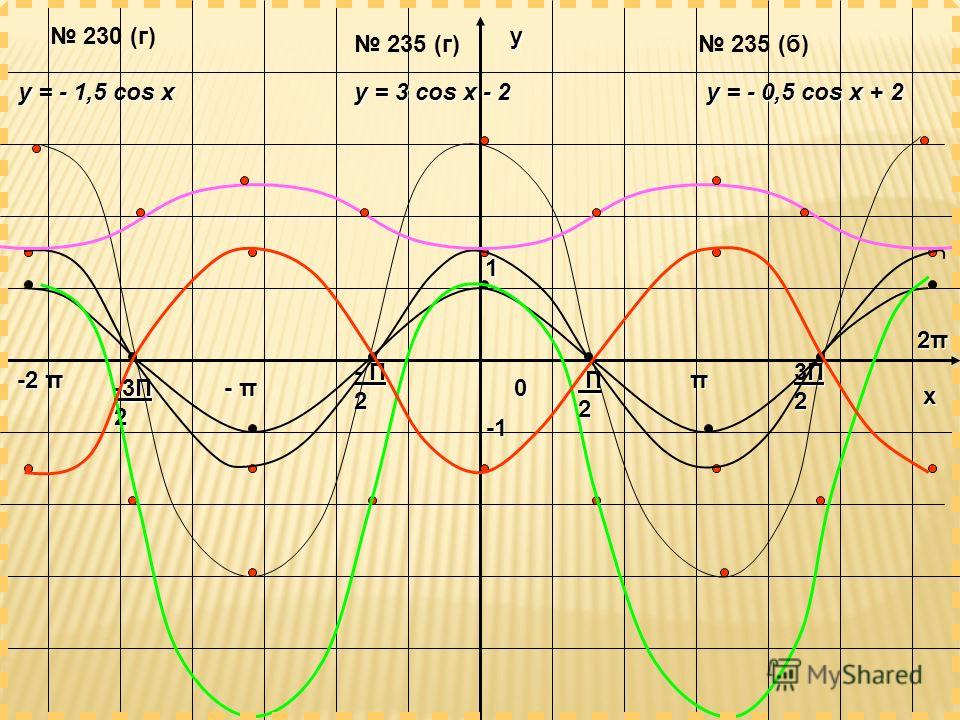
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .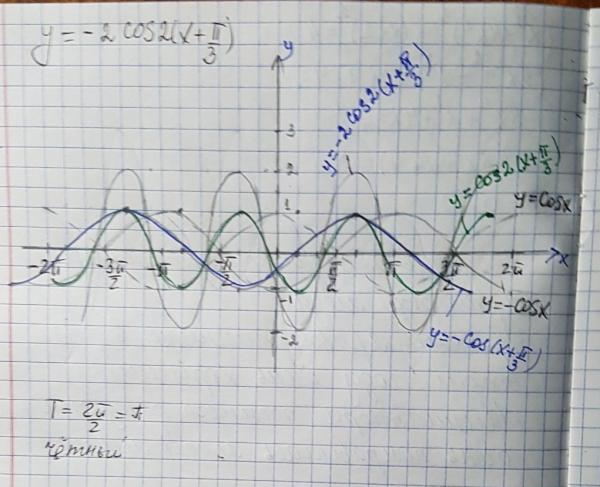
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Как построить график $y = \\cos 2x$?
Подсказка: Сначала найдите амплитуду, период, фазовый и вертикальный сдвиг для заданной периодической функции. Выберите несколько точек для построения графика. Найдите точку при $x = 0$, $x = \dfrac{\pi }{4}$, $x = \dfrac{\pi }{2}$, $x = \dfrac{{3\pi}} {4}$, $x = \pi $. Занесите точки в таблицу. Затем постройте график тригонометрической функции, используя амплитуду, период, фазовый сдвиг, вертикальный сдвиг и точки.
Используемая формула:
Период: Период идет от одного пика к другому (или от любой точки к следующей точке совпадения).
Амплитуда: Амплитуда — это высота от центральной линии до пика (или до впадины).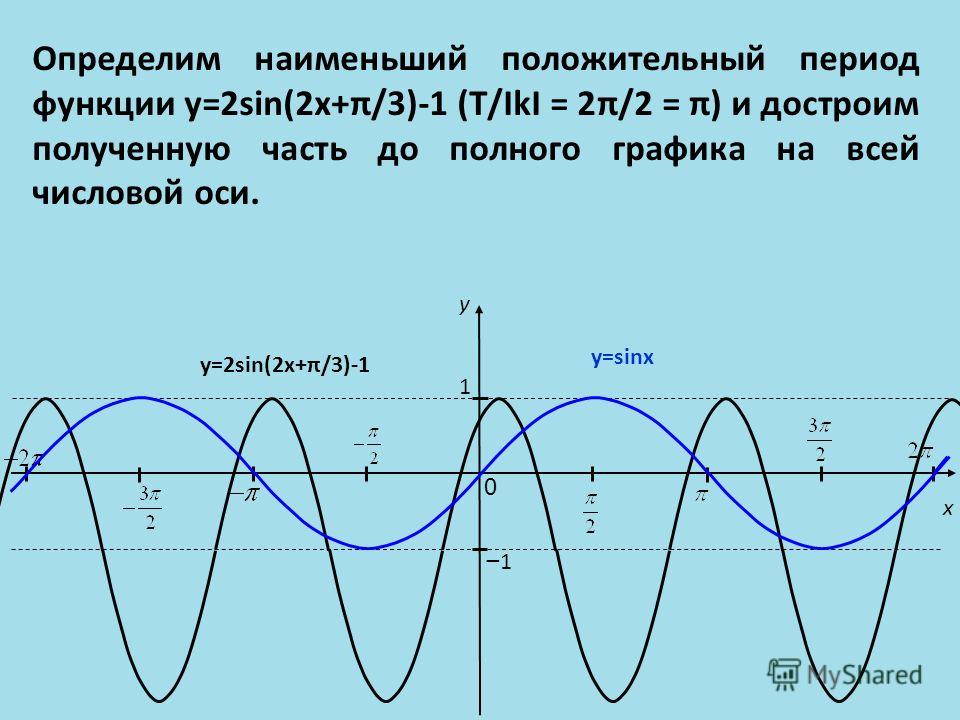
Или мы можем измерить высоту от самой высокой до самой низкой точки и разделить их на $2$.
Фазовый сдвиг: Фазовый сдвиг показывает, насколько функция смещена по горизонтали от обычного положения.
Сдвиг по вертикали: Сдвиг по вертикали показывает, насколько функция смещена по вертикали от обычного положения.
Полный пошаговый ответ:
Используйте форму $a\cos\left( {bx — c} \right) + d$, чтобы найти амплитуду, период, фазовый сдвиг и вертикальный сдвиг.
Сравните данное уравнение $y = \cos 2x$ с $a\cos \left( {bx — c} \right) + d$ и найдите переменные $a,b,c$ и $d$.
$a = 1$, $b = 2$, $c = 0$ и $d = 0$.
Найдите амплитуду $\left| а \право|$.
Здесь $a = 1$.
Амплитуда, $\left| а \право| = 1$.
Период функции можно рассчитать с помощью $\dfrac{{2\pi }}{{\left| б \право|}}$.
Период: $\dfrac{{2\pi}}{{\left| b \right|}}$
Замените $b$ на $2$ в формуле для периода.
Период: $\dfrac{{2\pi}}{{\left| 2 \справа|}}$
Абсолютное значение — это расстояние между числом и нулем.
Расстояние между $0$ и $2$ равно $2$.
Период: $\dfrac{{2\pi }}{2}$
Отменить общий множитель $2$.
Период: $\dfrac{{\not{2}\pi }}{{\not{2}}}$
Разделите $\pi $ на $1$.
Период: $\pi $
Найдите фазовый сдвиг по формуле $\dfrac{c}{b}$.
Фазовый сдвиг функции можно рассчитать по $\dfrac{c}{b}$.
Фазовый сдвиг: $\dfrac{c}{b}$
Замените значения $c$ и $b$ в уравнении для фазового сдвига.
Фазовый сдвиг: $\dfrac{0}{2}$
Разделите $0$ на $2$.
Фазовый сдвиг: $0$
Найдите сдвиг по вертикали $d$.
Сдвиг по вертикали: $0$
Теперь нам нужно составить список свойств тригонометрической функции.
Амплитуда: $1$
Период: $\pi $
Фазовый сдвиг: $0$($0$ вправо)
Вертикальный сдвиг: $0$
Также мы выбираем несколько точек для построения графика.
Найдите точку $x = 0$.
Замените в выражении переменную $x$ на $0$.
$f\влево( 0 \вправо) = \cos \влево( {2\влево( 0 \вправо)} \вправо)$
Умножить $2$ на $0$.
$f\left( 0 \right) = \cos \left( 0 \right)$
Точное значение $\cos \left( 0 \right)$ равно $1$.
$ \Rightarrow f\left( 0 \right) = 1$
Окончательный ответ: $1$.
Найдите точку $x = \dfrac{\pi }{4}$.
Замените в выражении переменную $x$ на $\dfrac{\pi }{4}$.
$ \Rightarrow f\left( {\dfrac{\pi }{4}} \right) = \cos \left( {2\left( {\dfrac{\pi }{4}} \right)} \right )$
Отмените общий делитель $2$.
Фактор $2$ из $4$.
$ \Rightarrow f\left( {\dfrac{\pi }{4}} \right) = \cos \left( {2\left( {\dfrac{\pi }{{2\left( 2 \right) }}} \right)} \right)$
Отменить общий множитель.
$ \Rightarrow f\left( {\dfrac{\pi} {4}} \right) = \cos \left( {\not{2}\left({\dfrac{\pi}}{{2 \times \ not{2}}}} \right)} \right)$
Перепишите выражение.
$ \Rightarrow f\left( {\dfrac{\pi }{4}} \right) = \cos \left( {\dfrac{\pi }{2}} \right)$
Точное значение $\ потому что \left( {\dfrac{\pi }{2}} \right)$ равно $0$.
$ \Rightarrow f\left( {\dfrac{\pi }{4}} \right) = 0$
Окончательный ответ: $0$.
Также нам нужно найти точку $x = \dfrac{\pi }{2}$.
Замените в выражении переменную $x$ на $\dfrac{\pi }{2}$.
$ \Rightarrow f\left( {\dfrac{\pi} {2}} \right) = \cos \left( {2\left({\dfrac{\pi} {2}} \right)} \right )$
Отмените общий делитель $2$.
$ \Rightarrow f\left( {\dfrac{\pi} {2}} \right) = \cos \left( {\not{2}\left( {\dfrac{\pi}}{{\not{2 }}}} \справа)} \справа)$
Перепишите выражение.
$ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = \cos \left( \pi \right)$
Примените опорный угол, найдя угол с эквивалентными тригонометрическими значениями в первом квадрант.
Сделайте выражение отрицательным, так как косинус отрицателен во втором квадранте.
$ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = — \cos \left( 0 \right)$
Точное значение $\cos \left( 0 \right)$ составляет $1$.
$ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = — 1 \times 1$
Умножить $-1$ на $1$.
$ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = — 1$
Окончательный ответ: $ — 1$.
Опять же, нам нужно найти точку $x = \dfrac{{3\pi }}{4}$.
Замените переменную $x$ на $\dfrac{{3\pi }}{4}$ в выражении.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = \cos \left( {2\left( {\dfrac{{3\pi}}}{4}} \right)} \right)$
Отмените общий делитель $2$.
$ \ Rightarrow f \ left ( {\ dfrac {{3 \ pi}} {4}} \ right) = \ cos \ left ( {2 \ left ( {\ dfrac {{3 \ pi}} {{2 \ влево( 2 \вправо)}}} \вправо)} \вправо)$
Отменить общий множитель.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = \cos \left( {\not{2}\left({\dfrac{{3\pi}} {{2 \cdot \not{2}}}} \right)} \right)$
Перепишите выражение.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = \cos \left({\dfrac{{3\pi}}{2}} \right)$
Примените опорный угол, найдя угол с эквивалентными тригонометрическими значениями в первом квадранте.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = — \cos \left({\dfrac{\pi}{2}} \right)$
Точное значение $\cos \left( {\dfrac{\pi }{2}} \right)$ равно $0$.
$ \Rightarrow f\left( {\dfrac{{3\pi}}{4}} \right) = 0$
Окончательный ответ: $0$.
Найдите точку $x = \pi $.
Замените в выражении переменную $x$ на $\pi $.
$ \Rightarrow f\left( \pi \right) = \cos \left( {2\left( \pi \right)} \right)$
$2\pi $ — это полный поворот, поэтому замените на $0$.
$ \Rightarrow f\left( \pi \right) = \cos \left( 0 \right)$
Точное значение $\cos \left( 0 \right)$ равно $1$.
$ \Rightarrow f\left( \pi \right) = 1$
Окончательный ответ: $1$.
Список точек в таблице.
| $x$ | $f\left( x \right)$ |
| $0$ | $1$pi |
| $0 $ | |
| $\dfrac{\pi }{2}$ | $ — 1$ |
| $\dfrac{{3\pi }}{4}$ | $0$ | 3 $01143 9\ пи $ | $1 $ |
График тригонометрической функции можно изобразить, используя амплитуду, период, фазовый сдвиг, вертикальный сдвиг и точки.
Амплитуда: $1$
Период: $\pi $
Фазовый сдвиг: $0$($0$ вправо)
Вертикальный сдвиг: $0$
| $x$ | $f\left( x \right ) $ | ||||||||||||
| $ 0 $ | $ 1 $ | ||||||||||||
| $ \ dfrac {\ pi} {4} $ | $ 0 $ | ||||||||||||
| $ \ DFRAC {\ PI $ | |||||||||||||
| $ \ DFRAC {\ PI {\ PI? 1$ 9Примечание: 04 $\cos 2x$ и $2\cos x$ — совершенно разные термины. $2\cos x$ равно удвоенному косинусу угла $x$. Он находится между $-2$ и $2$. $\cos 2x$ — косинус угла $2x$. Это в два раза больше угла $x$. Значение $\cos 2x$ находится между $-1$ и $1$. PinkMonkey.com-Учебное пособие по тригонометрии — 5.4 Графики тригонометрических функцийPinkMonkey.com-Учебное пособие по тригонометрии — 5.4 Графики тригонометрических функций
| |||||||||||||
