§ 21. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Е.П. Нелин, В.А. Лазарев
АЛГЕБРА
и начала математического
анализа
10 класс
Учебник для
общеобразовательных
учреждений. Базовый и
профильный уровень
Работу выполнила: Мусина В.А. студентка группы 45.3
Системы тригонометрических уравнений решаются с помощью тех же методов, что и алгебраические системы, в частности это исключение неизвестных и замена переменных. Исключить неизвестные можно с помощью одного из двух приемов:из одного уравнения выразить какое-то неизвестное (или функцию от него) и подставить его в другие или преобразовать данные уравнения и потом составить из них комбинации, в которых число неизвестных уменьшается.
Задача 1. Решите систему уравнений
Из первого уравнения находим и подставляем во второе.
Получаем
Отсюда
Замечание. Если бы для нахождения значения y мы не рассмотрели отдельно формулу (1) со знаком «+» и знаком «–», то вместе с верными решениями получили бы и посторонние решения заданной системы.
Действительно, в таком случае имеем
Тогда, например, при n = 0 получаем
Таким образом, кроме решений, которые вошли в ответ, мы имеем еще две возможности:
Но эти пары значений х и у не являются решениями заданной системы, поскольку они не удовлетворяют первому уравнению.
Поэтому следует запомнить:
Когда решение уравнения cos x = а приходится применять для дальнейших преобразований, то удобно записывать его в виде двух формул: отдельно со знаком «+» и отдельно со знаком «–».
Задача 2. Решите систему уравнений
Почленно сложим и вычтем эти уравнения. Получим равносильну систему
Получим равносильну систему
Представим последнюю систему в виде совокупности двух систем, записывая решения второго уравнения отдельно со знаком «+» и отдельно со знаком «–»:
Почленно складывая и вычитая уравнения этих систем, находим x и y:
Замечание. В запись ответа вошли два параметра n и k, которые независимо друг от друга «пробегают» множество целых чисел. Если попробовать при решении заданной системы воспользоваться только одним параметром, например n, то это приведет к потере решений. Таким образом, в каждом случае, когда система тригонометрических уравнений приводится к системе, состоящей из элементарных тригонометрических уравнений (то есть из уравнений вида sin x = a, cos x = a, tg x = a, ctg x = a), при решении каждого из этих уравнений необходимо использовать свой целочисленный параметр.
Вопросы для контроля
- Какие методы используются для решения систем тригонометрических уравнений?
- Объясните, в каком случае при формальном решении системы уравнений мы можем потерять часть решений, а в каком случае —получить посторонние решения.
 Решите эту систему.
Решите эту систему.
Упражнения
Решите систему уравнений (1–8).
Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I.  § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2.  МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ§ 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5.  СТЕПЕНЬ ДРОБИ СТЕПЕНЬ ДРОБИКонтрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2.  ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3.  ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ§ 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3.  СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК§ 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2.  ПРЕДЕЛ ФУНКЦИИ ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1.  ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Системы тригонометрических уравнений
Система тригонометрических уравнений – это система уравнений, составленная либо только из тригонометрических уравнений, либо из тригонометрических и алгебраических уравнений.
В этом разделе мы рассмотрим несколько типов систем тригонометрических уравнений с двумя переменными \(x\) и \(y\) и опишем возможные способы их решения.
Простейшие системы уравнений
Может случиться так, что одно из уравнений системы содержит тригонометрические функции относительно неизвестных x и y, а другое уравнение линейно относительно x и y. В таком случае поступаем очевидным образом: одно из неизвестных выражается из линейного уравнения и подставляется в другое уравнение системы.
В таком случае поступаем очевидным образом: одно из неизвестных выражается из линейного уравнения и подставляется в другое уравнение системы.
Пример
Решить систему:
\[\left\{ \begin{массив}{l} х + у = \ гидроразрыва {\ пи} {2} \\ \ грех х + \ грех у = 1 \конец{массив} \право..\]
Раствор.
Из первого уравнения мы выражаем \(y\) через \(x:\)
\[y = \frac{\pi}{2} — x,\]
и подставляем во второе уравнение:
\[\sin x + \sin y = 1, \Rightarrow \sin x + \sin \left({\frac{\pi}{2} — x}\right) = 1, \Rightarrow \sin x + \ потому что х = 1.\]
Мы получили линейное тригонометрическое уравнение. Решим ее методом R. Умножьте обе части уравнения на \(\frac{\sqrt{2}}{2}\) и преобразуйте выражение в левой части в одну тригонометрическую функцию:
\[\frac{\sqrt{2}}{2}\sin x + \frac{\sqrt{2}}{2}\cos x = \frac{\sqrt{2}}{2}, \Rightarrow \cos\frac{\pi}{4}\sin x + \sin\frac{\pi}{4}\cos x = \frac{\sqrt{2}}{2}, \Rightarrow \sin\left( {x + \frac{\pi}{4}}\right) = \frac{\sqrt{2}}{2}.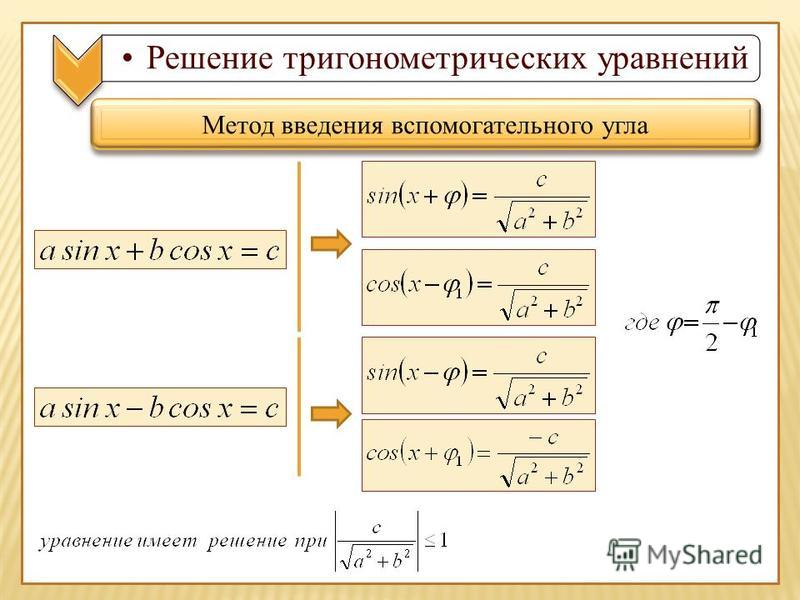 \]
\]
Решение этого уравнения записывается в виде двух ветвей:
\[x + \frac{\pi}{4} = \frac{\pi}{4} + 2\pi n, \Rightarrow x_1 = 2\pi n,\]
\[x + \frac{\pi}{4} = \frac{3\pi}{4} + 2\pi n, \Rightarrow x_2 = \frac{\pi}{2} + 2\pi n, \]
, где \(n \in \mathbb{Z}.\)
Найдите теперь соответствующие значения \(y:\)
\[y_1 = \frac{\pi}{2} — x_1 = \frac{\pi}{2} — 2\pi n,\]
\[y_2 = \frac{\pi}{2} — x_2 = \cancel{\frac{\pi}{2}} — \cancel{\frac{\pi}{2}} — 2\pi n = — 2\pi n, \;n \in \mathbb{Z}.\]
Окончательный ответ записывается как \(\left({x,y}\right)\) пар:
\[\left({2\pi n,\frac{\pi}{2} — 2\pi n}\right), \left({\frac{\pi}{2} + 2\pi n, — 2\pi n}\right),\;n\in\mathbb{Z}.\]
Приведение тригонометрической системы к алгебраической
В ряде случаев тригонометрическая система может быть сведена к системе алгебраических уравнений подходящей заменой переменных.
Пример
Решите систему: 9n\frac{\pi}{6} + \pi n,\,\pm\frac{\pi}{3} + 2\pi k}\right), \;n,k\in\mathbb{Z} . \]
\]
Сложение и вычитание уравнений
Иногда тригонометрическую систему можно упростить, добавляя или вычитая уравнения.
Пример
Решить систему:
\[\left\{ \begin{массив}{l} \sin x \cos y = \frac{1}{4}\\ \cos x \sin y = \frac{3}{4} \конец{массив} \право..\]
Раствор.
Складывая два уравнения и используя тождество сложения синусов, мы получаем
\[\sin x \cos y + \cos x \sin y = \frac{1}{4} + \frac{3}{4},\]
\[\стрелка вправо \sin \left({x + y}\right) = 1.\]
Аналогичным образом, вычитая второе уравнение из первого и используя тождество вычитания синусов, мы имеем
\[\sin x \cos y — \cos x \sin y = \frac{1}{4} — \frac{3}{4},\]
\[\стрелка вправо \sin \left({x — y}\right) = -\frac{1}{2}.\]
В результате получаем следующую эквивалентную систему уравнений:
\[\left\{ \begin{массив}{l}
\sin\left({x + y}\right) = 1\\
\sin\left({x — y}\right) = -\frac{1}{2}
\конец{массив} \право. .\]
.\]
Решение первого уравнения записывается в виде
\[x + y = \frac{\pi}{2} + 2\pi n,\;n\in\mathbb{Z}.\]
Второе уравнение имеет два семейства решений:
\[x — y = -\frac{\pi}{6} + 2\pi k,\]
\[x — y = -\frac{5\pi}{6} + 2\pi k,\;k\in\mathbb{Z}.\]
Соответственно получаем два решения:
\[\left[ \begin{массив}{l} \left\{ \begin{массив}{l} х + у = \ гидроразрыва {\ пи} {2} + 2 \ пи п \\ х — у = — \ гидроразрыва {\ пи} {6} + 2 \ пи к \end{массив} \right.\\ \left\{ \begin{массив}{l} х + у = \ гидроразрыва {\ пи} {2} + 2 \ пи п \\ x — y = -\frac{5\pi}{6} + 2\pi k \end{массив} \right. \end{массив} \right.,\]
, где \(n,k\in\mathbb{Z}.\)
Решите теперь каждую систему относительно \(x\) и \(y.\). Для этого снова сложите и вычтите уравнения:
\[\left[ \begin{массив}{l}
\left\{ \begin{массив}{l}
2x = \ frac {\ pi} {2} — \ frac {\ pi} {6} + 2 \ pi \ влево ({n + k} \ вправо) \\
2y = \frac{\pi}{2} +\frac{\pi}{6} +2\pi\left({n — k}\right)
\end{массив} \right. \\
\left\{ \begin{массив}{l}
2x = \ frac {\ pi} {2} — \ frac {5 \ pi} {6} + 2 \ pi \ влево ({n + k} \ вправо) \\
2y = \ frac {\ pi} {2} + \ frac {5 \ pi} {6} + 2 \ pi \ влево ({n — k} \ вправо)
\end{массив} \right.
\end{массив} \right., \Rightarrow \left[ \begin{массив}{l}
\left\{ \begin{массив}{l}
х = \ frac {\ pi} {6} + \ pi \ влево ({n + k} \ вправо) \\
y = \ frac {\ pi} {3} + \ pi \ влево ({n — k} \ вправо)
\end{массив} \right.\\
\left\{ \begin{массив}{l}
x = -\frac{\pi}{6} + \pi\left({n + k}\right)\\
y = \frac{2\pi}{3} + \pi\left({n — k}\right)
\end{массив} \right.
\end{массив} \right..\]
\\
\left\{ \begin{массив}{l}
2x = \ frac {\ pi} {2} — \ frac {5 \ pi} {6} + 2 \ pi \ влево ({n + k} \ вправо) \\
2y = \ frac {\ pi} {2} + \ frac {5 \ pi} {6} + 2 \ pi \ влево ({n — k} \ вправо)
\end{массив} \right.
\end{массив} \right., \Rightarrow \left[ \begin{массив}{l}
\left\{ \begin{массив}{l}
х = \ frac {\ pi} {6} + \ pi \ влево ({n + k} \ вправо) \\
y = \ frac {\ pi} {3} + \ pi \ влево ({n — k} \ вправо)
\end{массив} \right.\\
\left\{ \begin{массив}{l}
x = -\frac{\pi}{6} + \pi\left({n + k}\right)\\
y = \frac{2\pi}{3} + \pi\left({n — k}\right)
\end{массив} \right.
\end{массив} \right..\]
Ответ записывается как
\[\left({\frac{\pi}{6} + \pi\left({n + k}\right),\,\frac{\pi}{3} + \pi\left({n — k}\right)}\right),\left({-\frac{\pi}{6} + \pi\left({n + k}\right),\,\frac{2\pi}{ 3} + \pi\left({n — k}\right)}\right), \;n,k\in\mathbb{Z}.\]
Умножение и деление уравнений
Иногда можно прийти к решению, перемножив или разделив уравнения друг на друга.
Пример
Решите систему:
\[\left\{ \begin{массив}{l}
\грех х + \грех у = 1\\
\cos x — \cos y = \sqrt{3}
\конец{массив} \право. .\]
.\]
Раствор.
Используя тождества суммы и произведения, мы запишем систему как
\[\left\{ \begin{массив}{l} 2\sin\frac{x+y}{2}\cos\frac{x-y}{2} = 1\\ -2\sin\frac{x+y}{2}\sin\frac{x-y}{2} = \sqrt{3} \конец{массив} \право..\]
Обозначим \(\alpha = \frac{x+y}{2},\) \(\beta = \frac{x-y}{2}\) и перепишем систему в следующем виде:
\[\left\{ \begin{массив}{l} 2\sin\альфа\cos\бета = 1\\ -2\грех\альфа\грех\бета = \sqrt{3} \конец{массив} \право..\]
Ясно, что \(\sin\alpha \ne 0.\) Разделим второе уравнение на первое:
\[-\tan\beta = \sqrt{3}, \Rightarrow \tan\beta = -\sqrt{3}, \Rightarrow \beta = \arctan\left({-\sqrt{3}}\right) + \pi n = -\frac{\pi}{3} + \pi n, \;n\in\mathbb{Z}.\]
Угол \(\beta\) принимает два значения на единичной окружности. Представим их отдельными формулами:
\[\beta_1 = -\frac{\pi}{3} + 2\pi n,\; \beta_2 = \frac{2\pi}{3} + 2\pi n,\;n\in\mathbb{Z}.\]
Вычислить соответствующие значения \(\alpha:\)
\[\beta_1 = -\frac{\pi}{3} + 2\pi n, \Rightarrow \cos\beta_1 = \cos\left({-\frac{\pi}{3}}\right) = \frac{1}{2}, \Rightarrow 2\sin\alpha_1\cos\beta_1 = 1, \Rightarrow \sin\alpha_1 = 1, \Rightarrow \alpha_1 = \frac{\pi}{2} + 2\pi к,\;к\в\mathbb{Z}. \]
\]
\[\beta_2 = \frac{2\pi}{3} + 2\pi n, \стрелка вправо \cos\beta_2 = \cos\left({\frac{2\pi}{3}}\right) = -\frac{1}{2}, \Rightarrow 2\sin\alpha_2\cos\beta_2 = 1, \Rightarrow \sin\alpha_2 = -1, \Rightarrow \alpha_2 = -\frac{\pi}{2} + 2\pi k,\;k\in\mathbb{Z}.\]
Итак, мы получаем следующие решения для \(\alpha\) и \(\beta:\)
\[\left[ \begin{массив}{l} \left\{ \begin{массив}{l} \alpha_1 = \frac{\pi}{2} + 2\pi k\\ \beta_1 = -\frac{\pi}{3} + 2\pi n \end{массив} \right.\\ \left\{ \begin{массив}{l} \alpha_2 = -\frac{\pi}{2} + 2\pi k\\ \beta_2 = \frac{2\pi}{3} + 2\pi n \end{массив} \right. \end{массив} \right.,\;k,n\in\mathbb{Z}.\]
Следовательно,
\[\left[ \begin{массив}{l}
\left\{ \begin{массив}{l}
\ frac {x + y} {2} = \ frac {\ pi} {2} + 2 \ pi k \\
\ frac {xy} {2} = — \ frac {\ pi} {3} + 2 \ pi n
\end{массив} \right.\\
\left\{ \begin{массив}{l}
\ frac {x + y} {2} = — \ frac {\ pi} {2} + 2 \ pi k \\
\frac{x-y}{2} = \frac{2\pi}{3} + 2\pi n
\end{массив} \right.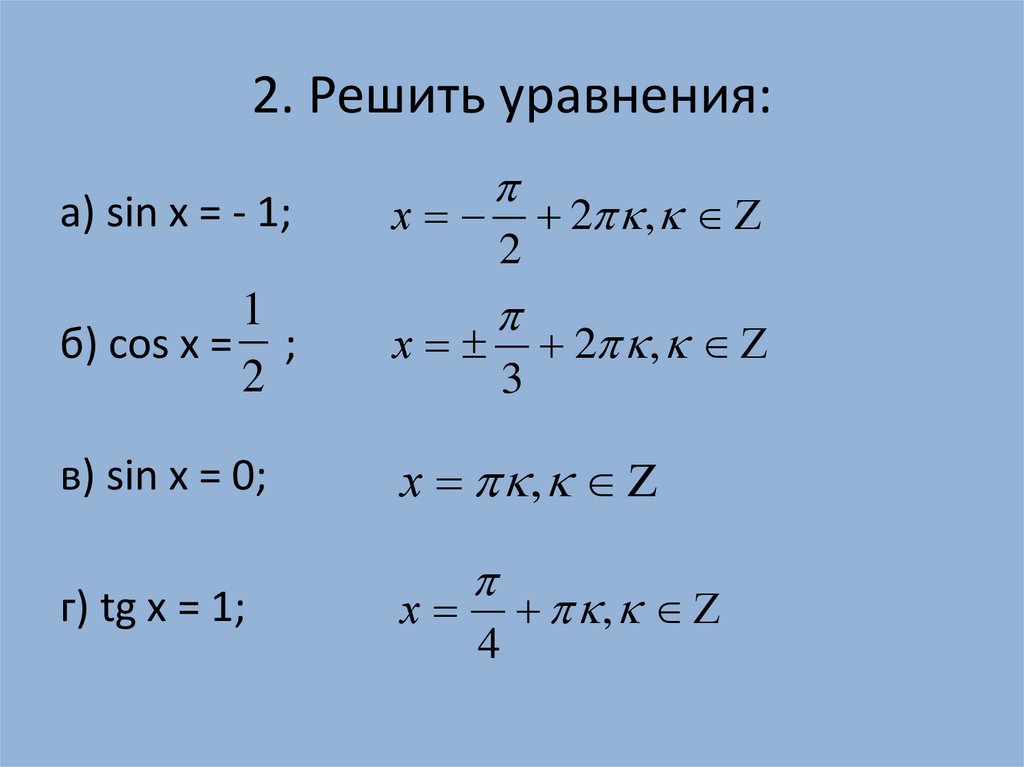 \end{массив} \right., \Rightarrow \left[ \begin{массив}{l}
\left\{ \begin{массив}{l}
x = \ frac {\ pi} {2} — \ frac {\ pi} {3} + 2 \ pi \ влево ({k + n} \ вправо) \\
y = \ frac {\ pi} {2} + \ frac {\ pi} {3} + 2 \ pi \ left ({k — n} \ right)
\end{массив} \right.\\
\left\{ \begin{массив}{l}
x = -\frac{\pi}{2} + \frac{2\pi}{3} + 2\pi\left({k + n}\right)\\
y = -\frac{\pi}{2} — \frac{2\pi}{3} + 2\pi\left({k — n}\right)
\end{массив} \right.
\end{массив} \right., \Rightarrow \left[ \begin{массив}{l}
\left\{ \begin{массив}{l}
х = \ frac {\ pi} {6} + 2 \ pi \ влево ({k + n} \ вправо) \\
y = \frac{5\pi}{6} + 2\pi\left({k — n}\right)
\end{массив} \right.\\
\left\{ \begin{массив}{l}
х = \ frac {\ pi} {6} + 2 \ pi \ влево ({k + n} \ вправо) \\
y = -\frac{7\pi}{6} + 2\pi\left({k — n}\right)
\end{массив} \right.
\end{массив} \right.,\]
\end{массив} \right., \Rightarrow \left[ \begin{массив}{l}
\left\{ \begin{массив}{l}
x = \ frac {\ pi} {2} — \ frac {\ pi} {3} + 2 \ pi \ влево ({k + n} \ вправо) \\
y = \ frac {\ pi} {2} + \ frac {\ pi} {3} + 2 \ pi \ left ({k — n} \ right)
\end{массив} \right.\\
\left\{ \begin{массив}{l}
x = -\frac{\pi}{2} + \frac{2\pi}{3} + 2\pi\left({k + n}\right)\\
y = -\frac{\pi}{2} — \frac{2\pi}{3} + 2\pi\left({k — n}\right)
\end{массив} \right.
\end{массив} \right., \Rightarrow \left[ \begin{массив}{l}
\left\{ \begin{массив}{l}
х = \ frac {\ pi} {6} + 2 \ pi \ влево ({k + n} \ вправо) \\
y = \frac{5\pi}{6} + 2\pi\left({k — n}\right)
\end{массив} \right.\\
\left\{ \begin{массив}{l}
х = \ frac {\ pi} {6} + 2 \ pi \ влево ({k + n} \ вправо) \\
y = -\frac{7\pi}{6} + 2\pi\left({k — n}\right)
\end{массив} \right.
\end{массив} \right.,\]
, где \(k,n\in\mathbb{Z}.\)
Ответ дан
\[\left({\frac{\pi}{6} + 2\pi\left({k + n}\right),\,\frac{5\pi}{6} + 2\pi\left ({k — n}\right)}\right),\left({\frac{\pi}{6} + 2\pi\left({k + n}\right),\,-\frac{7 \pi}{6} + 2\pi\left({k — n}\right)}\right), \;k,n\in\mathbb{Z}. \]
\]
тригонометрия — Решение тригонометрической системы уравнений
спросил
Изменено 9 лет, 6 месяцев назад
Просмотрено 10 тысяч раз
$\begingroup$
Я работаю репетитором по математике в местном университете и столкнулся с тригонометрической задачей, которая поставила меня в тупик. (Конечно, я уверен, что этот материал был пройден в классе моими студентами, но они тоже не знали, как его решить.) В основном задача сводится к решению следующей системы уравнений относительно $x$ и $y$ с $-\pi \leq x, y \leq \pi$:
$c_1\cos x + c_2 \cos y = 0$
$c_1\sin x + c_2 \sin y = 0$
Как решить систему тригонометрических уравнений — аналогичный вопрос, но у меня возникли трудности следуя ответу и применяя их к этой конкретной проблеме. Любые советы будут оценены.
Любые советы будут оценены.
- тригонометрия
$\endgroup$
2
$\begingroup$
Вы можете просто умножить первое уравнение на $\sin{x}$, а второе на $\cos{x}$ и вычесть, чтобы получить
$$c_2 \sin{x} \cos{y} — c_2 \cos{x} \sin{y} = c_2 \sin{(x-y)} = 0$$
Тогда $x=y$ или $ x-y = k \pi$, $k \in \mathbb{Z}$. Подставьте это обратно в любое уравнение, чтобы определить $x$ или $y$.
$\endgroup$
$\begingroup$
Случай $1:$ Если $c_1,c_2\ne0$ одинаковы, между двумя уравнениями
имеем $c_1\cos x=-c_2\cos y\ \ \ \ (1)$ и $c_1\sin x =-c_2\sin y\ \ \ \ (1=2)$
Разделите, чтобы получить $\tan x=\tan y\имеет x=n\pi+y$, где $n$ — любое целое число
Поместите значение $x$ в $(1)$ или $(2)$
Нам нужно обрабатывать четные и нечетные значения $n$ отдельно
Случай $2$: Если $c_1,c_2\ ne0$ не совпадают между двумя уравнениями
ПОДСКАЗКА:
Получить значения $\sin x,\cos x$ из $(1),(2)$
Квадрат и добавить, чтобы исключить $x$ и составить уравнение только в $y$ и решить
$\endgroup$
$\begingroup$
Запись уравнений в виде
$$\begin{выравнивание}
c_1 \cos x &= — c_2 \cos y &(1)\\
c_1 \sin x &= — c_2 \sin y &(2)
\end{выравнивание}$$
возводим в квадрат и складываем, чтобы получить
$$\begin{выравнивание}
c_1^2 \left( \cos^2 x + \sin^2 x \right ) &= \phantom{\pm} c_2^2 \left( \cos^2 y + \sin^2 y \right) \\
\ подразумевает \qquad c_1^2 &= \phantom{\pm}c_2^2 \\
\ подразумевает \qquad c_1 &= \pm c_2
\end{выравнивание}$$
Поскольку $c_1 = c_2 = 0$ приводит к исчезновению всей системы, мы предполагаем, что константы отличны от нуля, и делим уравнения системы на $c_1$, чтобы получить.

 Решите эту систему.
Решите эту систему.