Открытая Математика. Функции и Графики. Алгебраические операции над функциями
Алгебраические операции над функциями
Построение графика суммы (произведения) двух функций производится сложением (умножением) ординат точек графиков с одинаковыми абсциссами. Приведем для примера графики функций y = x + sin x и y = x sin x, являющихся соответственно суммой и произведением графиков y = x и y = sin x.
Правило построения графика функции 1f(x), если график функции f(x) уже построен.
Если x = a – вертикальная асимптота графика функции f(x), то есть limx→a+0f(x)=∞ или limx→a-0f(x)=∞, то limx→a+01f(x)=0 или соответственно limx→a-01f(x)=0.
Таким образорм, в случае, когда x = a – двусторонняя вертикальная асимптота графика функции f(x), x = a будет нулем функции 1f(x).Если у графика функции f(x) есть горизонтальная асимптота
Если у графика функции f(x) есть горизонтальная асимптота y = b при x→∞, то график функции 1f(x) будет иметь горизонтальную асимптоту y=1b.
Если график функции f(x) пересекает ось абсцисс в точке (x0; 0), то есть x0 – нуль функции f(x): f(x0)=0, то x=x0 – вертикальная асимптота графика функции y=1f(x).
Если точка (x0; y0) – точка максимума (минимума) функции f(x) и y0≠0, то (x0; 1y0) – точка минимума (максимума) функции 1f(x).
Промежуткам возрастания (убывания) графика функции f(x) соответствуют промежутки убывания (возрастания) графика функции 1f(x).
Пусть известен график y = f (x) и нужно построить график функции y = |f (x)|.
По определению,
|fx|={fxпри fx≥0,-fxпри fx<0.
Значит, часть графика, лежащую в верхней координатной полуплоскости, изменять не надо, а часть графика, лежащую в нижней координатной полуплоскости, нужно отобразить симметрично оси OX.
Пусть известен график y = f (x) и нужно построить график функции y = f (|x|). Заметим, что при x ≥ 0 f (|x|) = f (x), а функция y = f (|x|) четная. Поэтому, чтобы построить график функции y = f (|x|), нужно часть графика функции y = f (x), лежащую в левой координатной полуплоскости, отбросить, а часть графика, лежащую в правой координатной полуплоскости, отобразить симметрично относительно оси OY.
Множество точек, задаваемое уравнением |y| = f (x), рисуется следующим образом: строится график функции f (x), отбрасывается его часть, находящаяся ниже оси абсцисс, оставшаяся часть дополняется своим симметричным отражением относительно оси абсцисс.
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».
y sin x, функция синус х, функция y sin, урок и презентация
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Функция y=sin(x) (PPTX)
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
3) Функция Y=sin(X) возрастает на отрезке [0; π/2] и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
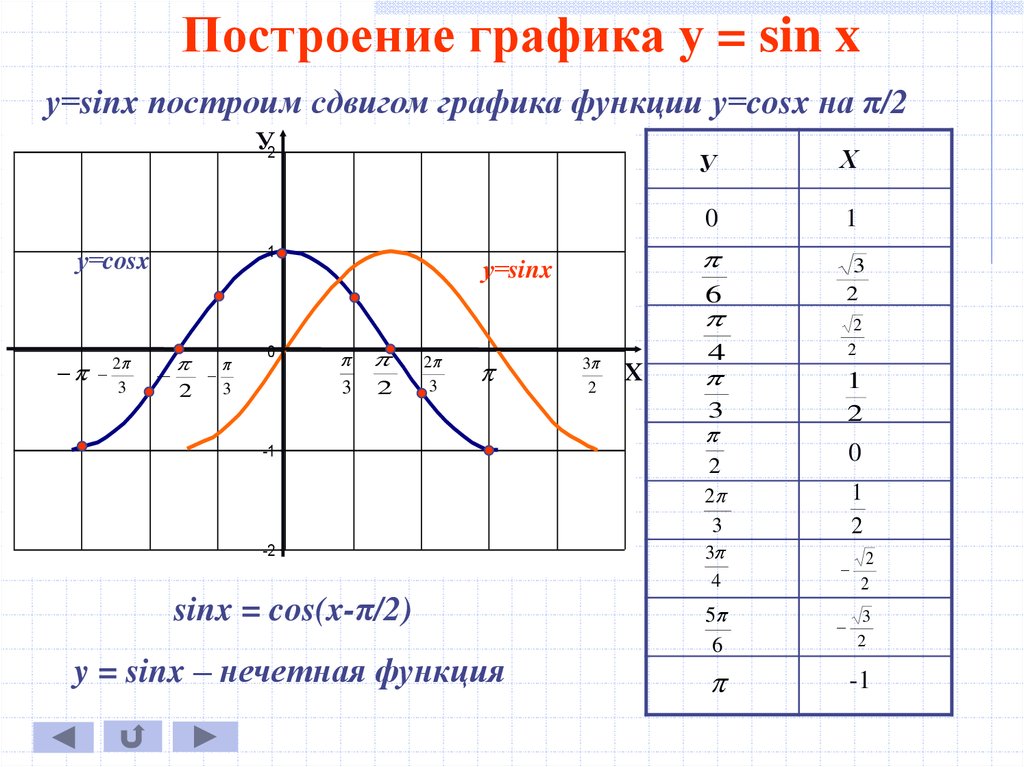
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке [0; π].
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x).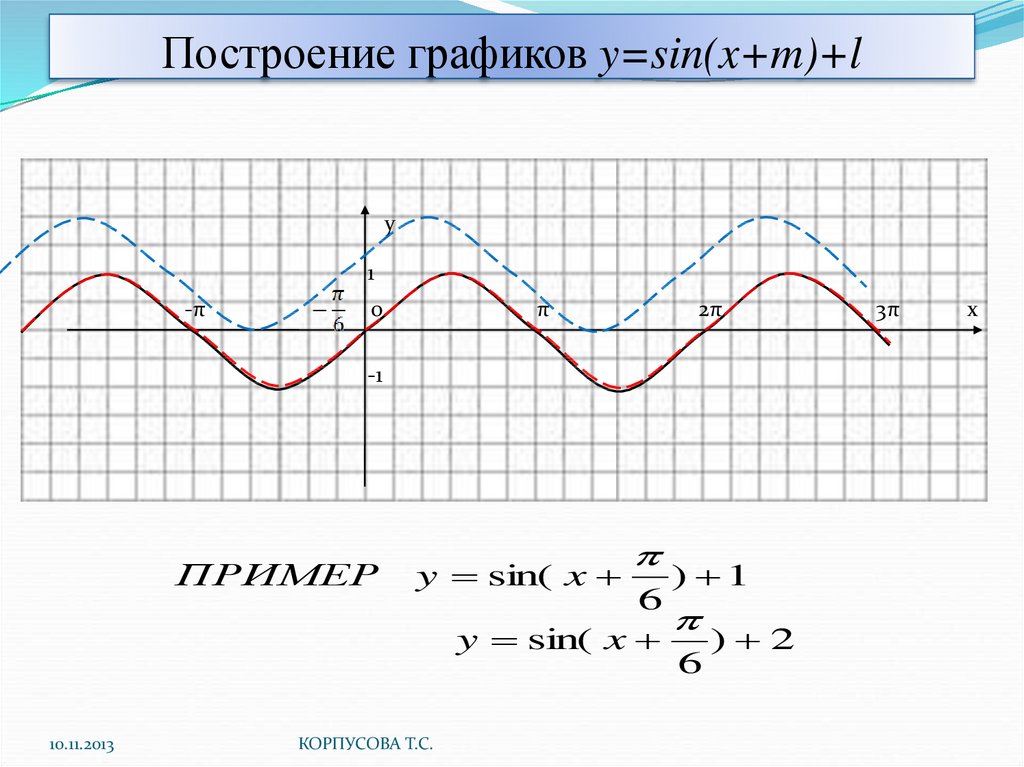
Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или [3π; 5π] или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см.
рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
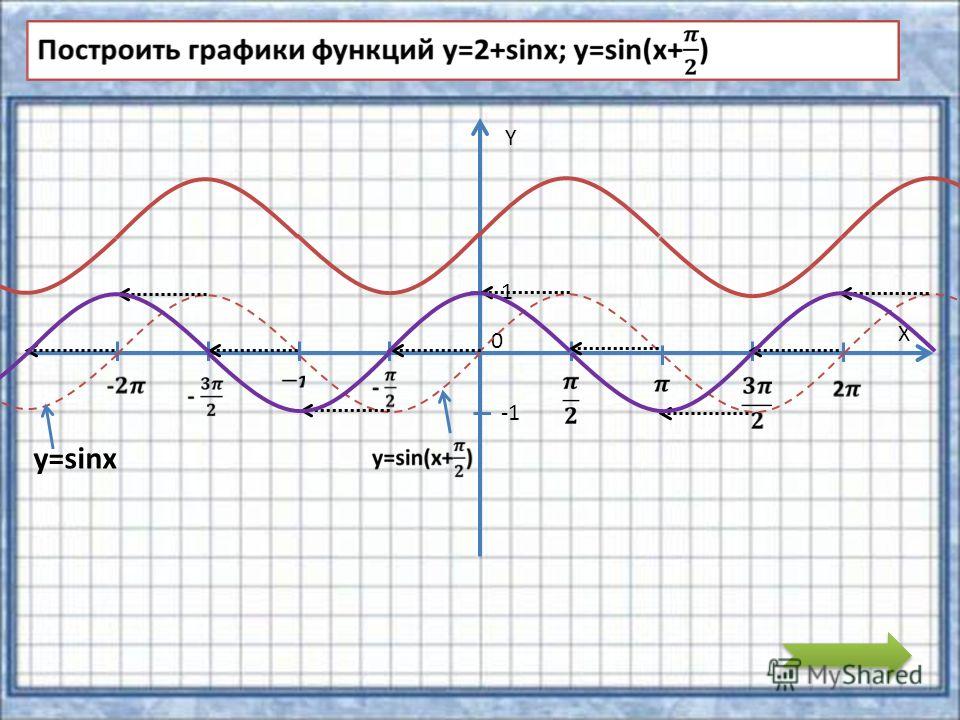
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
3. Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [π/2; 5π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [0; 4π/3]
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Python Plot Sine Wave/Function sin(x) (с Matplotlib)
В декартовой системе координат тригонометрическая функция синуса $\text{sin}(x)$ порождает правильную волнообразную кривую, проходящую через начало координат.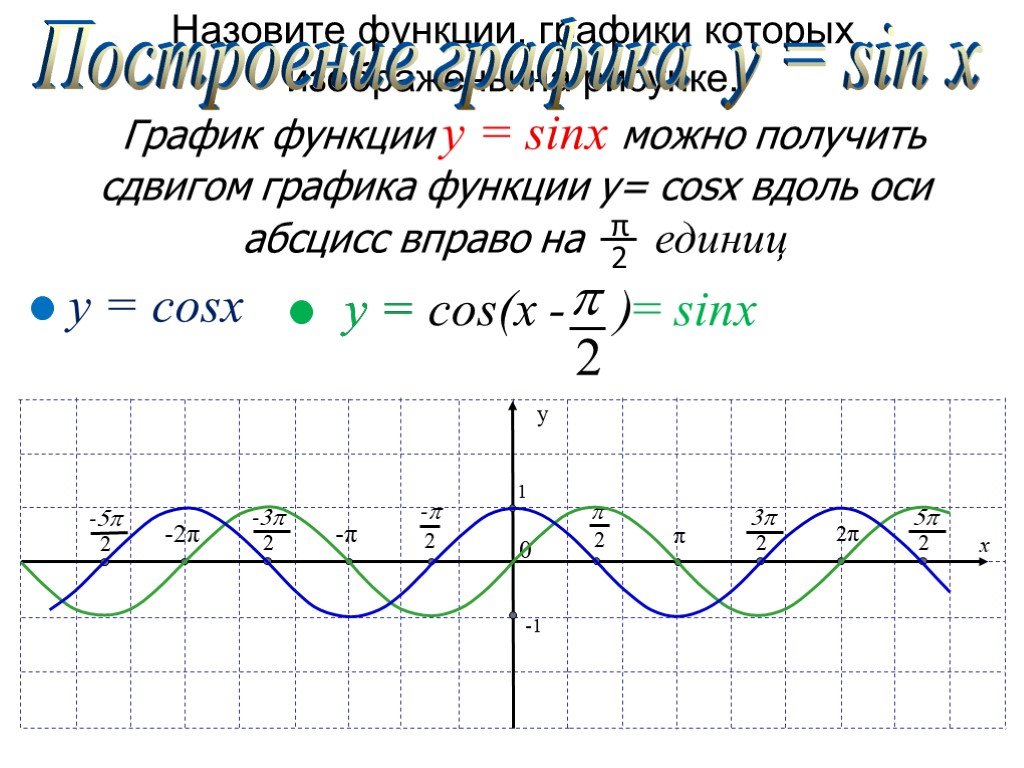
В этом уроке мы узнаем, как построить синусоиду в Python с Matplotlib. Мы будем рисовать $\text{sin}(x)$ вместе с его кратными и дольными углами между интервалами $-\pi$ и $\pi$.
Так как значения $y=\text{sin}(x)$ могут упасть ниже $-1$, ось $x$ устанавливается в центр.
Вот код для генерации синусоиды в Matplotlib. График $y=\text{sin}(x)$ для $x$ между $-\pi$ и $\pi$.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
# 100 линейно расположенных чисел
х = np.linspace(-np.pi, np.pi, 100)
# функция, которая здесь y = sin(x)
у = np.sin (х)
# установка осей в центре
рис = plt.figure()
топор = fig.add_subplot (1, 1, 1)
ax.spines['слева'].set_position('центр')
ax.spines['нижний'].set_position('центр')
ax.spines['право'].set_color('нет')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('внизу')
ax.yaxis.set_ticks_position('слева')
# построить функцию
plt. plot(x,y, 'b-')
# показать сюжет
plt.show()
Несколько углов
В этом разделе мы вместе построим графики множественных углов $y=\text{sin}(x)$, $y=\text{sin}(2x)$ и $y=\text{sin}(3x) $.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
# 100 линейно расположенных чисел
х = np.linspace(-np.pi, np.pi, 100)
p = np.sin(x) # y = sin(x)
q = np.sin(2*x) # y = sin(2x)
r = np.sin(3*x) # y = sin(3x)
# установка осей в центре
рис = plt.figure()
топор = fig.add_subplot (1, 1, 1)
ax.spines['слева'].set_position('центр')
ax.spines['нижний'].set_position('центр')
ax.spines['право'].set_color('нет')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('внизу')
ax.yaxis.set_ticks_position('слева')
# построить функции с метками
plt.plot(x,p, 'b-', метка='y=sin(x)')
plt.plot(x,q, 'c-', метка='y=sin(2x)')
plt.plot(x,r, 'm-', метка='y=sin(3x)')
plt.legend(loc='верхний левый')
# показать сюжет
plt.show()
Дольный угол
И здесь мы наносим вместе дробный угол $y=\text{sin}(\frac{x}{2})$ вместе с $y=2\text{sin}(x)$ и $y=\text{sin }(х)$.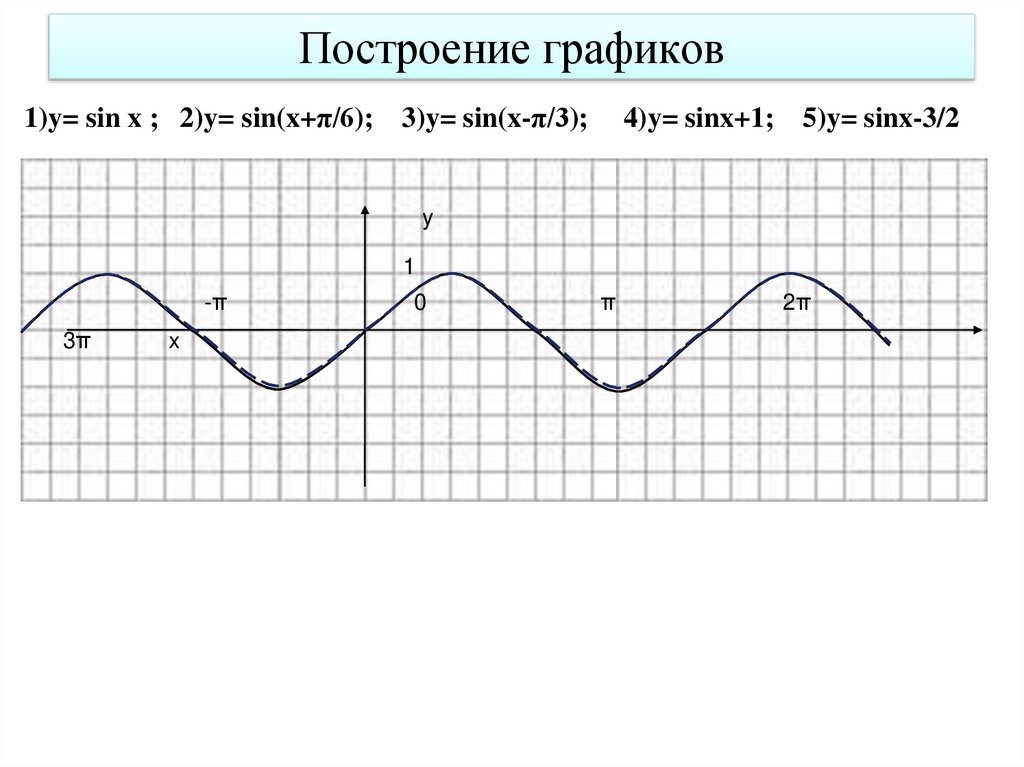
импортировать matplotlib.pyplot как plt
импортировать numpy как np
# 100 линейно расположенных чисел
х = np.linspace(-np.pi, np.pi, 100)
p = 2*np.sin(x) # y = 2sin(x)
q = np.sin(x) # y = sin(x)
r = np.sin(x/2) # y = sin(x/2)
# установка осей в центре
рис = plt.figure()
топор = fig.add_subplot (1, 1, 1)
ax.spines['слева'].set_position('центр')
ax.spines['нижний'].set_position('ноль')
ax.spines['право'].set_color('нет')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('внизу')
ax.yaxis.set_ticks_position('слева')
# построить функции с метками
plt.plot(x,p, 'b-', метка='y=2sin(x)')
plt.plot(x,q, 'c-', метка='y=sin(x)')
plt.plot(x,r, 'm-', метка='y=sin(x/2)')
plt.legend(loc='верхний левый')
# показать сюжет
plt.show()
sin(x)/x
И, наконец, иллюстрация $\text{lim}_{x \to 0} \frac{\text{sin}(x)}{x} = 1$.
импортировать matplotlib.pyplot как plt импортировать numpy как np # 100 линейно расположенных чисел х = np.
