Формулы приведения
Научись решать задачи ЕГЭ за пару минут!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2012-10-06
Формулы приведения! Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
*А тем, кто хочет набить руку решая задачи, вот здесь разобраны 22 примера от простых до самых сложных.
Перечислю лишь некоторые задачи, типы которых возможны на экзамене, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
Формулы приведения:
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение прямоугольного треугольника был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения:
Конечно, определить значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.
Данные формулы можно также выразить в табличной форме:
В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 10500, -7500, 23700 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!
Статья об этом в будущем обязательно будет, не пропустите!
Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию. На этом всё. Надеюсь, материал был вам полезен.
Получить материал статьи в формате PDF
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Формулы Теория | Как запомнитьТригонометрияФормулы
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Формулы приведения: доказательство, примеры, мнемоническое правило
Данная статья посвящена подробному изучению тригонометрических формул приведения. Дан полный список формул приведения, показаны примеры их использования, приведено доказательство верности формул. Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.
Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.
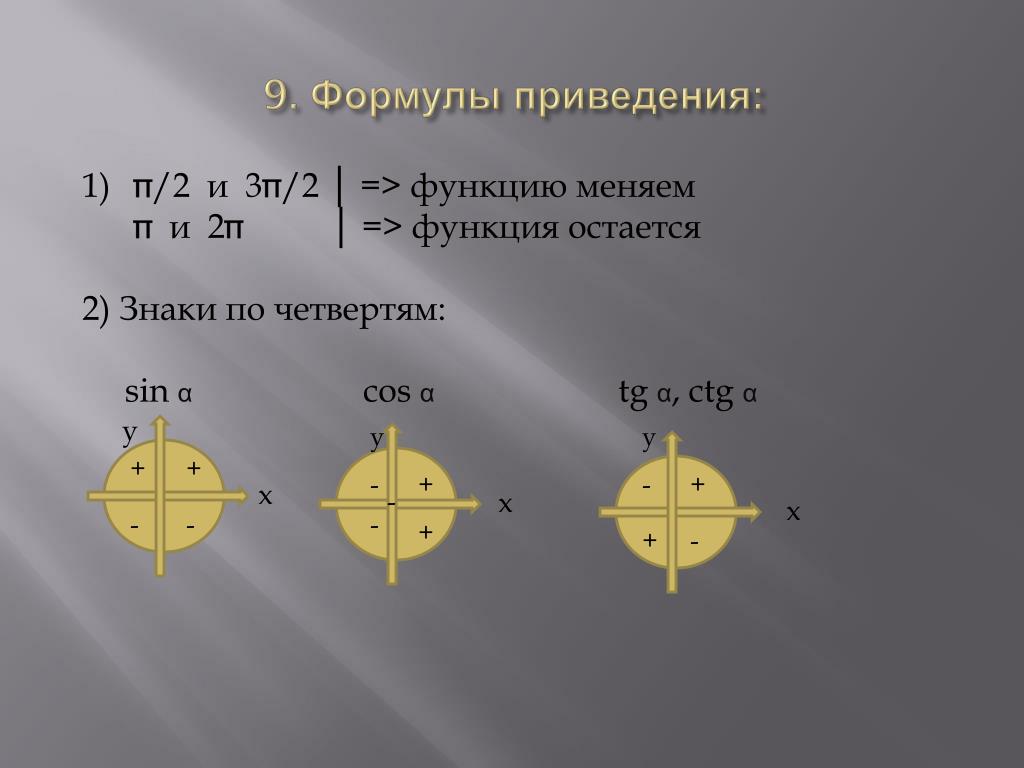
Формулы приведения. Список
Фомулы приведения позволяют приводить основные тригонометрические функции углов произвольной величины к функциям углов, лежащих в интервале от 0 до 90 градусов (от 0 до π2 радиан). Оперировать углами от 0 до 90 градусов гораздо удобнее, чем работать со сколь угодно большими значениями, поэтому формулы приведения широко применяются при решении задач тригонометрии.
Прежде, чем мы запишем сами формулы, уточним несколько важных для понимания моментов.
- Аргументами тригонометрических функций в формулах приведения являются угды вида ±α+2π·z, π2±α+2π·z, 3π2±α+2π·z. Здесь z — любое целое число, а α — произвольный угол поворота.
- Не обязательно учить все формулы приведения, количество которых довольно внушительно. Существует мнемоническое правило, которо позволяет легко вывести нужную формулу. Речь о мнемоническом правиле пойдет позже.

Теперь перейдем непосредственно к формулам приведения.
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов. запишем все формулы в виде таблицы.
Формулы приведенияsinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα
В данном случае формулы записаны с радианами. Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив π на 180 градусов.
Примеры использования формул приведения
Покажем, как пользоваться формулами приведения и как указанные формулы применяются при решении практических примеров.
Угол под знаком тригонометрической функции можно представить не одним, а множеством способов. Например, аргумент тригонометрической функции может быть представлен в видах ±α+2πz, π2±α+2πz, π±α+2πz, 3π2±α+2πz. Продемонстрируем это.
Возьмем угол α=16π3. Это угол можно записать так:
α=16π3=π+π3+2π·2α=16π3=-2π3+2π·3α=16π3=3π2-π6+2π
В зависимости от представления угла используется соответствующая формула приведения.
Возьмем тот же угол α=16π3 и вычислим его тангенс
Пример 1. Использование формул приведенияα=16π3, tg α=?
Представим угол α=16π3 в виде α=π+π3+2π·2
Этому представлению угла будет соответствовать формула приведения
tg(π+α+2πz)=tg α
Получим
tg 16π3=tgπ+π3+2π·2=tgπ3
Воспользовавшись таблицей, укажем значение тангенса
tgπ3=3
Теперь используем другое представление угла α=16π3.
Пример 2. Использование формул приведенияα=16π3, tg α=?α=-2π3+2π·3tg16π3=tg-2π3+2π·3=-tg2π3=-(-3)=3
Наконец, для третьего представления угла запишем
Пример 3. Использование формул приведения
Использование формул приведенияα=16π3=3π2-π6+2πtg3π2-α+2πz=ctg αtg α=tg (3π2-π6+2π)=ctgπ6=3
Теперь приведем пример на использование формул приведения посложнее
Пример 4. Использование формул приведенияПредставим sin 197° через синус и косинус острого угла.
Для того, чтобы можно было применять формулы приведения, нужно представить угол α=197° в одном из видов
±α+360°·z, 90°±α+360°·z, 180°±α+360°·z, 270°±α+360°·z. Согласно условию задачи, угол должен быть острым. Соответственно, у нас есть два способа для его представления:
197°=180°+17°197°=270°-73°
Получаем
sin197°=sin(180°+17°)sin197°=sin(270°-73°)
Теперь посмотрим на формулы приведения для синусов и выберем соответствующие
sin(π+α+2πz)=-sinαsin(3π2-α+2πz)=-cosαsin 197°=sin(180°+17°+360°·z)=-sin17°sin 197°=sin(270°-73°+360°·z)=-cos73°
Мнемоническое правило
Формул приведения много, и, к счастью, нет необходимости заучивать их наизусть. Существуют закономерности, по которым можно выводить формулы приведения для разных углов и тригонометрических функций. Эти закономерности называются мнемоническим правилом. Мнемоника — искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.
Эти закономерности называются мнемоническим правилом. Мнемоника — искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.
1. Аргумент исходной функции представляется в одном из видов
±α+2πzπ2±α+2πzπ±α+2πz3π2±α+2πz
Угол α должен лежать в пределах от 0 до 90 градусов.
2. Определяется знак исходной тригонометрической функции. Такой же знак будет иметь функция, записываемая в правой части формулы.
3. Для углов ±α+2πz и π±α+2πz название исходной функции остается неизменным, а для углов π2±α+2πz и 3π2±α+2πz соответственно меняется на «кофункцию». Синус — на косинус. Тангенс — на котангенс.
Чтобы пользоваться мнемоническим праилом для формул приведения нужно уметь определять знаки тригонометрических функций по четвертям единичной окружности. Разберем примеры применения мнемонического правила.
Пример 1. Использование мнемонического правилаЗапишем формулы приведения для cosπ2-α+2πz и tgπ-α+2πz.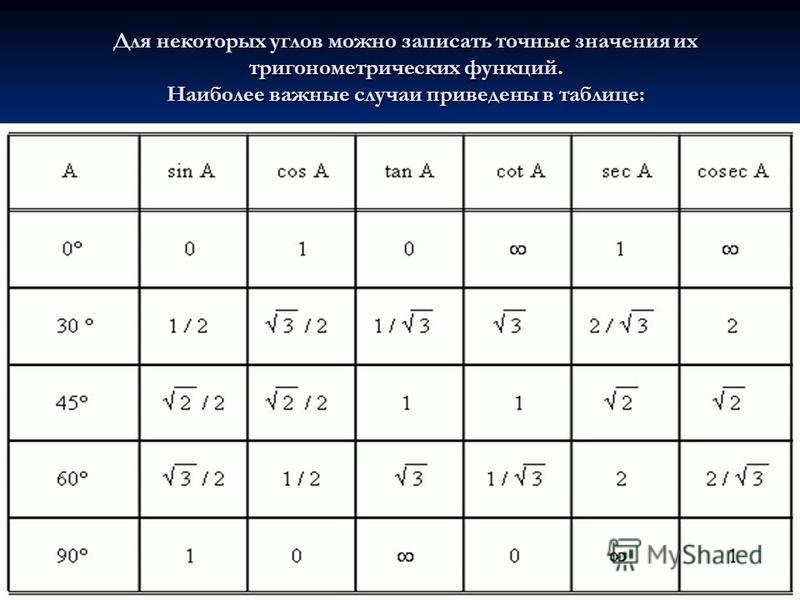 α — улог первой четверти.
α — улог первой четверти.
1. Так как по условию α — улог первой четверти, мы пропускаем первый пункт правила.
2. Определим знаки функций cosπ2-α+2πz и tgπ-α+2πz. Угол π2-α+2πz также является углом первой четверти, а угол π-α+2πz находится во второй четверти. В первой четверти функция косинуса положительна, а тангенс во второй четверти имеет знак минус. Запишем, как будут выглядеть искомые формулы на этом этапе.
cosπ2-α+2πz=+tgπ-α+2πz=-
3. Согласно третьему пункту для угла π2-α+2π название функции изменяется на конфуцию, а для угла π-α+2πz остается прежним. Запишем:
cosπ2-α+2πz=+sin αtgπ-α+2πz=-tg α
А теперь заглянем в формулы, приведенные выше, и убедимся в том, что мнемоническое правило работает.
Рассмотрим пример с конкретным углом α=777°. Приведем синус альфа к тригонометрической функции острого угла.
Пример 2. Использование мнемонического правила1. Представим углол α=777° в необходимом виде
777°=57°+360°·2777°=90°-33°+360°·2
2. Исходный угол — угол первой четверти. Значит, синус угла имеет положительный знак. В итоге имеем:
Исходный угол — угол первой четверти. Значит, синус угла имеет положительный знак. В итоге имеем:
3. sin 777°=sin(57°+360°·2)=sin 57°sin 777°=sin(90°-33°+360°·2)=cos 33°
Теперь рассмотрим пример, который показывает, как важно правильно определить знак тригонометрической функции и правильно представить угол при использовании мнемонического правила. Повторим еще раз.
Угол α должен быть острым!
Вычислим тангенс угла 5π3. Из таблицы значений основных тригонометрических функций можно сразу взять значение tg 5π3=-3, но мы применим мнемоническое правило.
Пример 3. Использование мнемонического правилаtg 5π3=?
Представим угол α=5π3 в необходимом виде и воспользуемся правилом
tg 5π3=tg3π2+π6=-ctgπ6=-3tg 5π3=tg2π-π3=-tgπ3=-3
Если же представить угол альфа в виде 5π3=π+2π3, то результат применениея мнемонического правила будет неверным.
tg 5π3=tgπ+2π3=-tg2π3=-(-3)=3
Неверный результат обусловлен тем, что угол 2π3 не явдяется острым.
Формулы приведения. Доказательство
Доказательство формул приведения основывается на свойствах периодичности и симметричности тригонометрических функций, а также на свойстве сдвига на углы π2 и 3π2. Доказательство справедливости всех формул приведения иожно проводить без учета слагаемого 2πz, так как оно обозначает изменение угла на целое число полных оборотов и как раз отражает свойство периодичности.
Первые 16 формул следуют напрямую из свойств основных тригонометрических функций: синуса, косинуса, тангенса и котанганса.
Приведем доказательство формул приведения для синусов и косинусов
sinπ2+α=cos α и cosπ2+α=-sin α
Посмотрим на единичную окружность, начальная точка которой после повоторота на угол α перешла в точку A1x, y, а после поворота на угол π2+α — в точку A2. Из обеих точек проведем перпендикуляры к оси абсцисс.
Два прямоугольных треугольника OA1h2 и OA2h3 равны по гипотенузе и прилежащим к ней углам. Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка A2 имеет координаты A2-y, x. Используя определения синуса и косинуса, запишем:
Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка A2 имеет координаты A2-y, x. Используя определения синуса и косинуса, запишем:
sin α=y, cosα=x, sinπ2+α=x, cosπ2+α=y
Отсюда
sinπ2+α=cos α, cosπ2+α=-sinα
С учетом основных тождеств тригонометрии и только что доказанного, можно записать
tgπ2+α=sinπ2+αcosπ2+α=cos α-sin α=-ctg αctgπ2+α=cosπ2+αsinπ2+α=-sin αcosα=-tg α
Для доказательства формул приведения с аргументом π2-α его необходимо представить в виде π2+(-α). Например:
cosπ2-α=cosπ2+(-α)=-sin(-α)=sinα
В доказательстве используются свойства тригонометрических функций с аргументами, противоположными по знаку.
Все остальные формулы приведения можно доказать на базе записанных выше.
Решение задач
от 1 дня / от 150 р.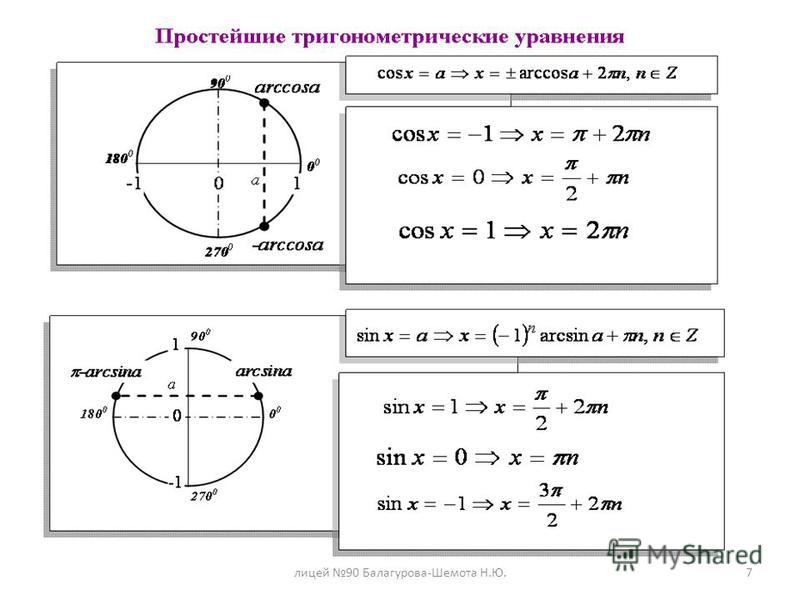
Формулы приведения в тригонометрии тригонометрических функций
Автор Ольга Андрющенко На чтение 11 мин. Просмотров 13.2k. Опубликовано
Просмотров 13.2k. Опубликовано
Формулы приведения относятся к тригонометрической функции, которая использует периодичность для преобразования тригонометрической функции с относительно большим углом в тригонометрическую функцию с относительно небольшим углом.
Содержание
Формулы взаимосвязи между углами противоположными на 360 градусов или круг
Эти формулы устанавливают связь между углами противоположными на 360 градусов или круг. Значение одной и той же тригонометрической функции для того же угла на противоположной стороне равно.
Пусть α — любой острый угол, выражение угла в радианной системе:
В градусной мере тригонометрическая функция угла будет выражаться формулами:
.
.
.
.
.
.
Формулы тригонометрической функции π + α, связанные с значением тригонометрической функции α
Эта группа устанавливает связь между значением тригонометрической функции π + α и значением тригонометрической функции α.
Пусть α — любой угол, выражение угла в радианной системе:
sin (π+α)=-sinα.
cos (π+α)=-cosα.
tg (π+α)=tgα.
ctg (π+α)=ctgα.
sec (π+α)=-secα.
cosec (π+α)=-cosecα.
В градусной мере:
sin (180°+α)=-sinα.
cos (180°+α)=-cosα.
tg (180°+α)=tgα.
ctg (180°+α)=ctgα.
sec (180°+α)=-secα.
cosec (180°+α)=-cosecα.
Связь между значением тригонометрической функции любого угла α и -α
Приведем формулы приведения, в которых устанавливается связь между значением тригонометрической функции любого угла α и угла -α:
sin (-α) = — sinα.
cos (-α) = cosα.
tg (-α) = — tgα.
ctg (-α)=ctgα.
sec (-α) = secα.
cosec (-α) = — cosecα.
Связь между значениями тригонометрических функций π-α и α
Эти формулы могут быть получены по формулам связи между значениями тригонометрических функций углов α и -α и между значением тригонометрической функции π + α и значением тригонометрической функции α :
Представление угла в радианной мере:
sin (π - α) = sinα.
cos (π - α) = — cosα.
tg (π - α) = — tgα.
ctg (π - α) = — ctgα.
sec (π - α) = — secα.
cosec (π - α) = cosecα.
Представление угла в градусной мере:
sin (180 ° -α) = sinα.
cos (180 ° -α) = — cosα.
tg (180 ° -α) = — tgα.
ctg (180 ° -α) = — ctgα.
sec(180 ° -α) = — secα.
cosec (180 ° -α) = cosecα.
Связь между значением тригонометрической функции 2π-α и α
Эти формулы могут быть получены по формулам связи тригонометрических функций аргументов противоположных на круг и угла α и угла -α :
Представление угла в радианной мере:
sin (2π - α) = — sinα.
cos (2π - α) = cosα.
tg (2π - α) = — tgα.
ctg (2π - α) = — ctgα.
sec (2π - α) = secα.
cosec (2π - α) = — cosecα.
Представление в градусной мере:
sin (360 ° -α) = — sinα.
cos (360 ° -α) = cosα.
tg (360 ° -α) = -tgα.
ctg (360 ° -α) = — ctgα.
sec(360 ° -α) = secα.
cosec (360 ° -α) = — cosecα.
Связь между значениями тригонометрических функций π/2 ± α и 3π/2 ± α и α
Связь между π / 2 + α и значением тригонометрической функции α
Представление угла в радианной мере:
sin (π / 2 + α) = cosα.
cos (π / 2 + α) = — sinα.
tg (π / 2 + α) = — ctgα.
ctg (π / 2 + α) = — tgα.
sec (π / 2 + α) = — cosecα.
cosec (π / 2 + α) = secα.
Представление угла в градусах:
sin (90 ° + α) = cosα.
cos (90 ° + α) = — sinα.
tg (90 ° + α) = -ctgα.
ctg (90 ° + α) = -tgα.
sec (90 ° + α) = -cosecα.
cosec (90 ° + α) = secα.
Связь между π / 2-α и значением тригонометрической функции α
Представление угла в радианной системе:
sin (π / 2 - α) = cosα.
cos (π / 2 - α) = sinα.
tg (π / 2 - α) = ctgα.
ctg (π / 2 - α) =tgα.
sec (π / 2 - α) = cosecα.
cosec (π / 2 - α) = secα.
Представление угла в градусах:
sin (90 ° -α) = cosα.
cos (90 ° -α) = sinα.
tg (90 ° -α) = ctgα.
ctg (90 ° -α) = tgα.
sec (90 ° -α) = cosecα.
cosec (90 ° -α) = secα.
Связь между 3π / 2 + α и значением тригонометрической функции α
Представление угла в радианах:
sin (3π / 2 + α) = — cosα.
cos (3π / 2 + α) = sinα.
tg (3π / 2 + α) = — ctgα.
ctg (3π / 2 + α) = -tgα.
sec (3π / 2 + α) = cosecα.
cosec (3π / 2 + α) = — secα.
Представление угла в градусах:
sin (270 ° + α) = — cosα.
cos (270 ° + α) = sinα.
tg (270 ° + α) = -ctgα.
ctg(270 ° + α) = -tgα.
sec (270 ° + α) = cosecα.
cosec (270 ° + α) = — secα.
Связь между 3π / 2 - α и значением тригонометрической функции α
Представление угла в радианах:
sin (3π / 2- α) = — cosα.
cos (3π / 2 -α) = — sinα.
tg (3π / 2 - α) =ctgα.
ctg (3π / 2 — α) =tgα.
sec (3π / 2 - α) = -cosecα.
cosec (3π / 2 - α) = — secα.
Представление угла в градусах:
sin (270 ° -α) = — cosα.
cos (270 ° -α) = — sinα.
tg(270 ° -α) = tgα.
ctg(270 ° -α) =tgα.
sec (270 ° -α) = -cosecα.
cosec (270 ° -α) = — secα.
Правило определения приведенной функции
Приведенные выше формулы приведения можно резюмировать так: для значения тригонометрической функции kπ / 2 ± α (k∈Z),
- Когда k — четное число, значение приведенной функции будет с тем же именем, что и приводимая функция, но для α (острый угол), то есть имя функции не изменяется
- Когда k — нечетное число, мы возьмем ко-функцию, но уже для α (острый угол), а именно sin (kπ / 2 ± α) → cosα; cos (kπ / 2 ± α) → sinα; tg (kπ / 2 ± α) → ctgα, ctg (kπ / 2 ± α) → tgα.

Запомни
Перед приведенной функцией мы должны добавить знак приводимой функции.
То есть мы получим:
(1)
(2)
Правило лошади в тригонометрии
Математики придумывают все новые и новые способы заставить ученика выучить это несложное правило, что придумали даже «кивающую лошадь». А правило, которое с ее помощью легче запомнить — это как раз вторая часть правила, когда k — нечетное число. В этом случае угол отсчитывается по вертикали. И тогда воображаемая лошадь кивает головой и функция меняется на ко-функцию. На наш взгляд абсолютно лишняя информация. Но если вам удобно — пользуйтесь.
Правило лошади в тригонометрии
Например:
sin (2π-α) = sin (4 · π/2-α), k = 4 — четное число, поэтому берется та же функция sinα.
Когда α — острый угол, 2π-α∈ (270°, 360°), sin (2π-α) <0 и поэтому перед функций мы поставим знак «-».
Итак, sin (2π-α) = — sinα.
sin (α+ π) = — sinα
youtube.com/embed/Luv3mlOkdOg?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Углы, фигурирующие во всех формулах приведения тригонометрических функций, сначала рассматриваются как острые углы, α + π — это угол в третьей четверти, а синус в третьей четверти отрицательный, поэтому конечный результат отрицательный, а π является четным кратным π/2, поэтому функция остается неизменной.
Чтобы определить знак приводимой функции, нарисуйте тригонометрический круг и вспомните знаки тригонометрических функций в координатных четвертях.
Знаки тригонометрических функций
Формулы приведения в тригонометрии таблица
Все формулы приведения тригонометрических функций можно собрать в одну таблицу.
| Угол | Функция | |||
| sinх | cosх | tgх | ctgх | |
| α | sinα | cosα | tgα | ctgα |
| -α | -sinα | cosα | -tgα | -ctgα |
| π / 2 — α | cosα | sinα | ctgα | tgα |
| π / 2 + α | cosα | -sinα | -ctgα | -tgα |
| π-α | sinα | -cosα | -tgα | -ctgα |
| π + α | -sinα | -cosα | tgα | ctgα |
| 3π / 2 -α | -cosα | -sinα | ctgα | tgα |
| 3π / 2+α | -cosα | sinα | -ctgα | -tgα |
| 2π-α | -sinα | cosα | -tgα | -ctgα |
| 2π+α | sinα | cosα | tgα | ctgα |
Формулы и правило приведения тригонометрических функций часто используются при решении тригонометрических уравнений и неравенств.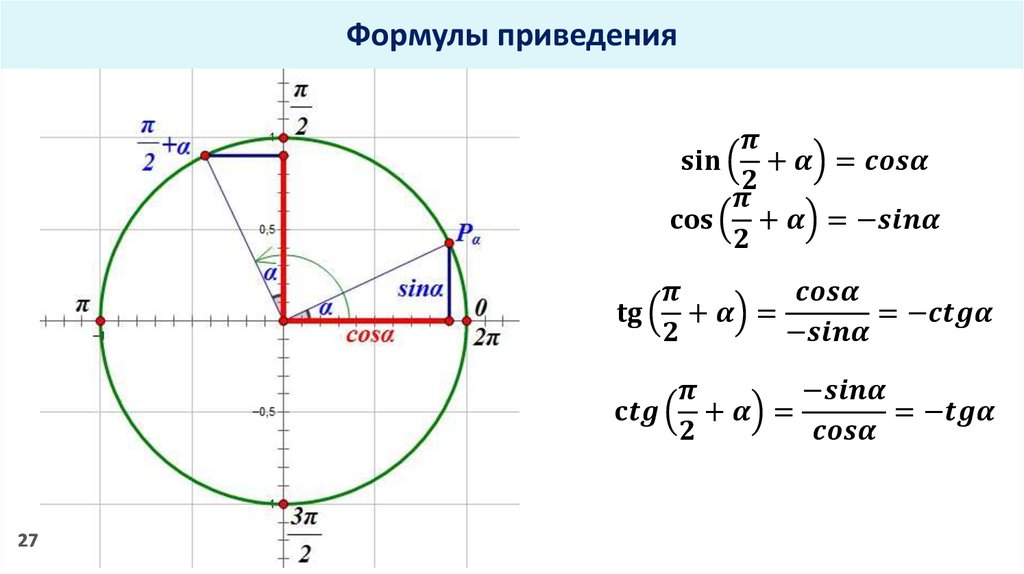
Примеры применения формул приведения
Пример 1
Вычислите .
Решение: Выделим целое количество тригонометрических кругов, каждый из которых . Получим: По формуле приведения из таблицы находим:
, подставляем .
Пример 2
Вычислите .
Решение: Представим, .
Для решения воспользуемся правилом, так как у нас получается нечетное число k и функция поменяется на ко-функцию, то есть был косинус, станет синус. Определимся со знаком, посмотрим, в какую четверть попадает — это вторая четверть, косинус во второй четверти отрицательный, значит перед синусом поставим знак минус (ставим знак приводимой функции, а приводим мы косинус):
.
Пример 3
Вычислите .
Решение: Проведем преобразования и применим правило приведения тригонометрических функций .
Пример 4
Используя формулы приведения, вычислить:
.
Решение:
Представим
Тогда,
Ответ: .
Пример 5
Упростите выражение:
.
Решение:
Приведем тригонометрические функции согласно правилу приведения, получим:
.
Ответ:
Таким образом, чтобы правильно выполнить приведение тригонометрической функции большого угла к тригонометрической функции меньшего угла вы можете использовать формулы приведения, которые нужно будет выучить наизусть, а их свыше 50, можно облегчить себе запоминание — выучив таблицу. Или же воспользоваться простым правилом (рекомендуется). Удачи на экзаменах.
Читайте также:
Формулы приведения тригонометрических функций онлайн. Формулы приведения углов в тригонометрии
Содержание
- Тригонометрические функции
- Формулы двойного угла.

- Правила преобразования формул приведения.
- Стоит ли учить формулы приведения?
- Формулы приведения. Как запомнить?
- Формулы приведения тригонометрических функций − теория, примеры и решения
- Определение для острых углов[править | править код]
- Формулы приведения: список и таблицы
- Формулы половинного угла.
- Формулы приведения для косинуса
- Тригонометрические неравенства.
- Формулы приведения в тригонометрии
- Формулы приведения для тангенса
- Формулы приведения для синуса
- Мнемоническое правило для формул приведения
- Основные тригонометрические формулы
- Формулы тройного угла.
- Тригонометрические функции суммы и разности углов
Тригонометрические функции
sin α, cos α
| tg α = | sin α | , α ≠ | π | + πn, n є Z |
| cos α | 2 |
| ctg α = | cos α | , α ≠ π + πn, n є Z |
| sin α |
| sec α = | 1 | , α ≠ | π | + πn, n є Z |
| cos α | 2 |
| cosec α = | 1 | , α ≠ π + πn, n є Z |
| sin α |
Формулы двойного угла.

cos 2α = cos² α – sin² α
cos 2α = 2cos² α – 1
cos 2α = 1 – 2sin² α
sin 2α = 2sin α · cos α
tg 2α = (2tg α) ÷ (1 – tg² α)
ctg 2α = (ctg² α – 1) ÷ (2ctg α)
Правила преобразования формул приведения.
1) Если аргумент содержит , где n – нечетное натуральное число , то функция меняется на “конфункцию”, т.е. синус на косинус, тангенс на котангенс и наоборот. Если n – четное натуральное число , то название функции не изменяется.
2) Определяем знак (“+” или “-“) значения первоначальной функции. Преобразованное выражение сохраняет знак своего родителя.
Примеры:
Стоит ли учить формулы приведения?
Вы в состоянии выучить вот такую таблицу?
А без приведения сложных аргументов тригонометрических функций к аргументам первой четверти на ЕГЭ по математике никуда.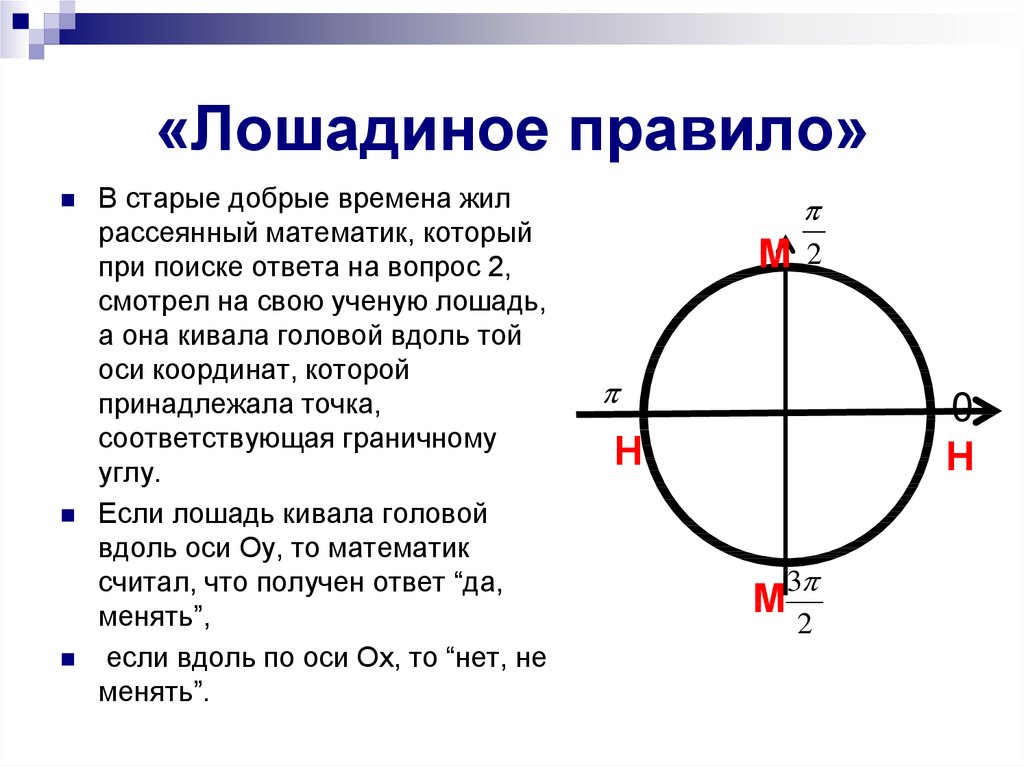
Но нет необходимости учить эту таблицу!
Нужно просто потратить немного времени и понять алгоритм применения формул приведения.
Не будем терять время! Поехали!
Формулы приведения. Как запомнить?
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
- задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.

- задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
- задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
- стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов
Формулы приведения:
Угол альфа лежит пределах от 0 до 90 градусов.
Итак, необходимо уяснить «закон», который здесь работает:
- Определите знак функции в соответствующей четверти.

Напомню их:
Запомните следующее:
- Функция изменяется на кофункцию
- Функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
- Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов.
- Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов.
- Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов.
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
В статье на решение прямоугольного треугольника был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения.
Конечно, определить значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.
В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 10500, -7500, 23700 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!
Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию. На этом всё. Надеюсь, материал был вам полезен.
Формулы приведения тригонометрических функций − теория, примеры и решения
Докажем формулы приведения тригонометрических функций для аргумента (или ) . (Здесь и далее все углы α острые т.е. меньше 90° (или меньше )). На декартовой прямоугольной системе координат проведем окружность с радиусом 1 и возьмем точки M1 и M2 так, чтобы , . Опустив перпендикуляры из точек M1 и M2 на ось OX, получим прямоугольные треугольники и (Рис.1).
Поскольку , то . Очевидно, что , так как гипотенузы этих прямоугольных треугольников равны и . Из равенства этих треугольников следует:
Из определений синуса и косинуса (о синусе и косинусе смотрите на странице Синус и косинус. Онлайн калькулятор) имеем:
или
Выведем, далее формулы приведения тригонометрических функций тангенс и котангенс для аргумента (Рис.2).
Тангенсу угла соответствует ординат точки Q, что овечает отрезку QA, взятой со знаком минус (подробнее о тангенсе и котангенсе смотрите на странице Тангенс и котангенс. Онлайн калькулятор ).
Онлайн калькулятор ).
Котангенсу угла α соответствует абсцис точки P, что отвечает отрезку BP:
Прямоугольные треугольники QAO и PBO равны, так как, , . Тогда .
Из вышеизложенного следует:
или
Котангенс угла − это абсцис точки R, т.е.
Тангенс угла α − это ординат точки S, т.е.
Прямоугольные треугольники RBO и SAO равны, т.к. , , . Тогда .
Таким образом можно вывести формулу приведения функции котангенс для угла :
или
Выведем формулы приведения тригонометрических функций синус и косинус для угла (Рис.3):
Из следует и .
Тогда
или
Аналогично, выведем формулы приведения тригонометрических функций тангенс и котангенс для угла (Рис.4):
Поскольку , следовательно . Тогда
или
Так как , следовательно . Тогда
или
Аналогично выводятся формулы приведения тригонометрический функций для углов , , .
Определение для острых углов[править | править код]
Рис. 4.
4.
Тригонометрические функции острого угла
В школьном курсе геометрии тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — прямоугольный треугольник с острым углом α. Тогда:
Построив систему координат с началом в точке , направлением оси абсцисс вдоль и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.
Данное определение имеет некоторое методическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач о тупоугольных треугольниках. (См.: теорема синусов, теорема косинусов).
Тригонометрические функции являются периодическими функциями с периодами (360°) для синуса, косинуса, секанса и косеканса, и (180°) для тангенса и котангенса. circ pm alpha`):
circ pm alpha`):
`sin(2pi — alpha)=-sin alpha;` ` sin(2pi + alpha)=sin alpha`
`cos(2pi — alpha)=cos alpha;` ` cos(2pi + alpha)=cos alpha`
`tg(2pi — alpha)=-tg alpha;` ` tg(2pi + alpha)=tg alpha`
`ctg(2pi — alpha)=-ctg alpha;` ` ctg(2pi + alpha)=ctg alpha`
Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:
Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(pi + alpha)`, достаточно найти ответ на пересечении строки ` sin beta` и столбца ` pi + alpha`. Получим ` sin(pi + alpha)=-sin alpha`.
И вторая, аналогичная таблица, где углы записаны в градусах:
Формулы половинного угла.
Синус половинного угла. Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол α/2 в левой части. Данное правило справедливо также для других формул, приведенных ниже.

Косинус половинного угла:
Тангенс половинного угла:
Котангенс половинного угла:
Выражение синуса через тангенс половинного угла:
Выражение косинуса через тангенс половинного угла:
Выражение тангенса через тангенс половинного угла:
Выражение котангенса через тангенс половинного угла:
Формулы приведения для косинуса
cos(π/2-α) = sin(α) cos(π/2+α) = -sin(α) cos(π-α) = -cos(α) cos(π+α) = -cos(α) cos(3π/2-α) = -sin(α) cos(3π/2+α) = sin(α) cos(2π-α) = cos(α) cos(2π+α) = cos(α)
Тригонометрические неравенства.
Простейшие тригонометрические неравенства:
sinx > a, sinx ≥ a, sinx < a, sinx ≤ a,
cosx > a, cosx ≥ a, cosx < a, cosx ≤ a,
tanx > a, tanx ≥ a, tanx < a, tanx ≤ a,
cotx > a, cotx ≥ a, cotx < a, cotx ≤ a.
Формулы приведения в тригонометрии
В тригонометрии, вообще, очень много разных формул. Их количество ни в коем случае не должно пугать школьника. Для того, чтобы успешно сдать ЕГЭ нужно не зубрить наизусть основные тригонометрические тождества, а понять их суть. Для многих формул разработаны даже специальные мнемонические правила, чтобы их можно было проще запомнить.
Один из самых сложных и запутанных, на взгляд ученика средней школы, раздел тригонометрических выражений – это формулы приведения. Для чего же они нужны? Отбросив вступление, скажем сразу — формулы приведения позволяют заменить функцию на кофункцию. Например, если в задании стоит синус α, его можно заменить на косинус α, и наоборот.
Функция Кофункция
| sin α | cos α |
| cos α | sin α |
| tg α | ctg α |
| ctg α | tg α |
Формулы приведения для тангенса
tg(π/2-α) = ctg(α) tg(π/2+α) = -ctg(α) tg(π-α) = -tg(α) tg(π+α) = tg(α) tg(3π/2-α) = ctg(α) tg(3π/2+α) = -ctg(α) tg(2π-α) = -tg(α) tg(2π+α) = tg(α)
Формулы приведения для синуса
sin(π/2-α) = cos(α) sin(π/2+α) = cos(α) sin(π-α) = sin(α) sin(π+α) = -sin(α) sin(3π/2-α) = -cos(α) sin(3π/2+α) = -cos(α) sin(2π-α) = -sin(α) sin(2π+α) = sin(α)
Мнемоническое правило для формул приведения
1. Задаем себе вопрос: «Меняется ли название функции на кофункцию?» (то есть синнус на косинус, косинус на синус, тангенс на котангенс и котангенс на тангенс).
Задаем себе вопрос: «Меняется ли название функции на кофункцию?» (то есть синнус на косинус, косинус на синус, тангенс на котангенс и котангенс на тангенс).
Чтобы ответить на этот вопрос нужно, не смейтесь, – подвигать головой вдоль оси, на которой располагается ключевая точка. Ключевые точки всегда располагаются здесь (см. рис.):
Например, в формулах – ключевые точки – это .
Так вот если вы мотаете головой вдоль горизонтальной прямой, потому что ключевая точка располагается на ней, то вы, как бы, отвечаете «нет» на вопрос «Меняется ли название функции на кофункцию?»
Если вы киваете головой вдоль вертикальной прямой, потому что ключевая точка располагается на ней, то вы отвечаете «да» на вопрос «Меняется ли название функции на кофункцию?».
2. Ставим справа, на выходе, тот знак, какой несет в себе левая, исходная, часть.
Данное правило еще называется «лошадиным».
Основные тригонометрические формулы
sin2 α + cos2 α = 1
tg α · ctg α = 1
| 1 + tg2 α = | 1 |
| cos2 α |
| 1 + ctg2 α = | 1 |
| sin2 α |
Формулы тройного угла.
sin 3α = 3sin α – 4sin³ α
cos 3α = 4cos³ α – 3cos α
tg 3α = (3tg α – tg³ α) ÷ (1 – 3tg² α)
ctg 3α = (3ctg α – ctg³ α) ÷ (1 – 3ctg² α)
Тригонометрические функции суммы и разности углов
sin(α + β) = sin α · cos β + cos α · sin β
sin(α – β) = sin α · cos β – cos α · sin β
cos(α + β) = cos α · cos β – sin α · sin β
cos(α – β) = cos α · cos β + sin α · sin β
| tg(α + β) = | tg α + tg β |
| 1 – tgα · tg β |
| tg(α – β) = | tg α – tg β |
| 1 + tgα · tg β |
| ctg(α + β) = | ctgα · ctg β – 1 |
| ctg β + ctg α |
| ctg(α – β) = | ctgα · ctg β + 1 |
| ctg β – ctg α |
Источники
- https://ru.
 onlinemschool.com/math/formula/trigonometry_formula/
onlinemschool.com/math/formula/trigonometry_formula/ - https://www.calc.ru/Trigonometricheskiye-Formuly.html
- https://www.calc.ru/108.html
- https://egemaximum.ru/formuly-privedeniya/
- https://rgiufa.ru/matematika-fizika-himiya/kak-zapomnit-formuly-privedeniya.html
- https://matworld.ru/trigonometry/formuly-privedenija.php
- https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B8
- https://matemonline.com/dh/%D1%82%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F/formuly-privedenija/
- https://prosto-o-slognom.ru/matematika/054-formuly_privedeniya.html
Формулы приведения 10 класс онлайн-подготовка на Ростелеком Лицей
Тема: Тригонометрические функции
Урок: Формулы приведения
1.
 Тема урока, введение
Тема урока, введение
Формулы приведения предназначены для того, чтобы привести тригонометрическую функцию произвольного угла к тригонометрической функции наименьшего из углов.
2. Суть формул приведения
Рассмотрим конкретный пример. Рассмотрим дуги в и, соответственно, (рис. 1).
как прямоугольные по гипотенузе и острому углу
Из равенства треугольников следует равенство соответствующих сторон.
Функции большего угла приведены к функциям меньшего угла. В этом суть формул приведения.
Для применения формул приведения тригонометрическую функцию любого угла нужно привести к одному из видов: .
3. Два правила формул приведения, примеры.
Формул приведения много, но все они подчиняются двум правилам:
Первое правило:
Для аргументов функция меняется на кофункцию, т.е. синус на косинус и наоборот, тангенс на котангенс и наоборот.
Для аргументов функция не меняется.
Примеры на первое правило:
Знак пока не учитываем, он определяется вторым правилом, пока важно понять, в каких случаях функция меняется на кофункцию, а в каких не меняется.
1)
2)
3)
4)
Для аргументов вида наименование функции следует изменить на кофункцию.
5)
6)
7)
8)
Для аргументов вида наименование функции не меняется.
Второе правило (для знака приведенной функции, функции угла ).
1) Считаем угол острым,
2) Определяем четверть и знак в ней приводимой функции (функции слева).
3) Ставим этот знак перед приведенной к углу функцией (функцией справа).
Примечание: Угол может быть любым, острым мы его считаем условно, для применения правила.
Примеры на второе правило:
1)
Рис. 2.
Угол находится во второй четверти. Во второй четверти , ставим знак плюс.
2)
Рис
Угол находится в третьей четверти. В третьей четверти ставим знак минус.
В третьей четверти ставим знак минус.
3)
Рис. 4.
Угол находится во второй четверти. Во второй четверти ставим знак минус.
4)
Рис. 5.
Угол находится в четвёртой четверти. В четвёртой четверти ставим знак минус.
5)
Рис. 6.
Угол находится в третьей четверти. В третьей четверти ставим знак минус.
6)
Рис. 7.
Угол находится во второй четверти, во второй четверти ставим знак минус.
7)
Рис. 8.
Угол находится во второй четверти. Во второй четверти ставим знак минус.
8)
Рис. 9.
Угол находится в четвёртой четверти. В четвёртой четверти ставим знак минус.
Итак, мы рассмотрели различные примеры применения первого и второго правил формул приведения.
4. Приемы, облегчающие запоминание формул приведени
Рассмотрим приемы, облегчающие запоминание формул приведения.
1. «Правило лошади». Глядя на числовую окружность легко ответить на вопрос, меняется ли функция на кофункцию.
Для аргументов , т.е. аргументов, отложенных от вертикальной оси, на вопрос, меняется ли функция на кофункцию, лошадь, глядя на точки , будет утвердительно кивать – функция меняется на кофункцию (рис. 10) .
Для аргументов , т.е. аргументов, отложенных от горизонтальной оси, лошадь, глядя на точки будет отрицательно мотать головой – функция не меняется (рис. 10) .
2. Используем периодичность и четность.
Вспомним, что наименьший положительный период у тангенса и котангенса равен Это значит, что
Например,
У синуса и косинуса наименьший положительный период равен
Например,
5. Задачи
Рассмотрим примеры на использование формул приведения.
1) Вычислить значения всех тригонометрических функций для
Решение (рис. 11).
Угол находится во второй четверти, синус в этой четверти положителен, косинус, тангенс и котангенс отрицательны.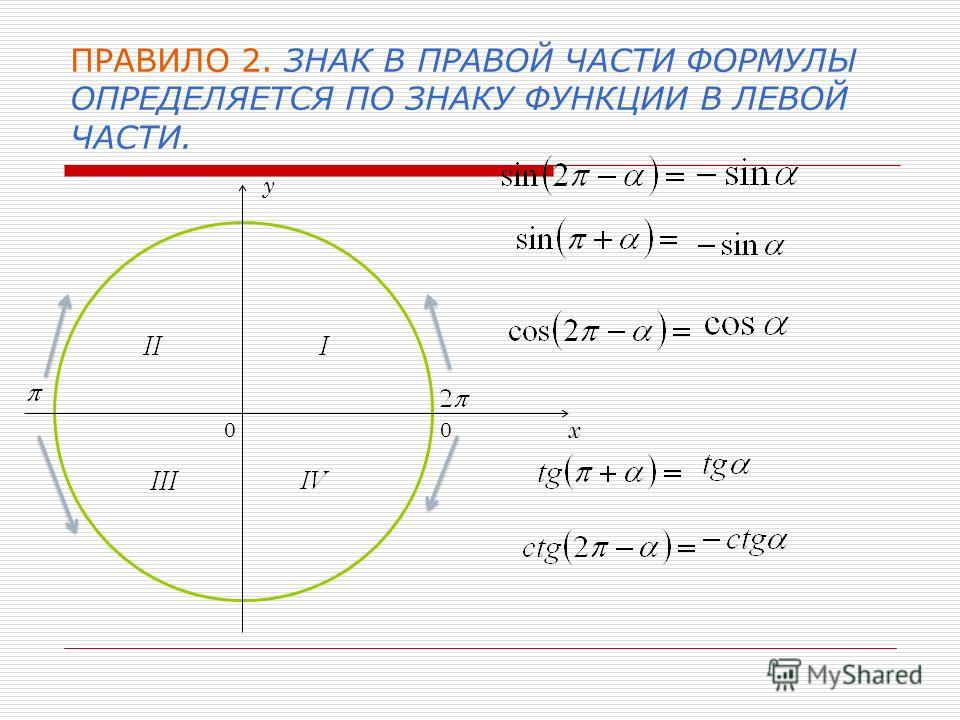
2) Вычислить значения всех тригонометрических функций угла
Решение (рис. 12).
Угол находится в третьей четверти, в третьей четверти синус и косинус отрицательны, тангенс и котангенс положительны.
6. Вывод, заключение
Мы рассмотрели формулы приведения и пояснили их на конкретных примерах. В дальнейшем мы будем активно использовать формулы приведения для преобразования тригонометрических выражений.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).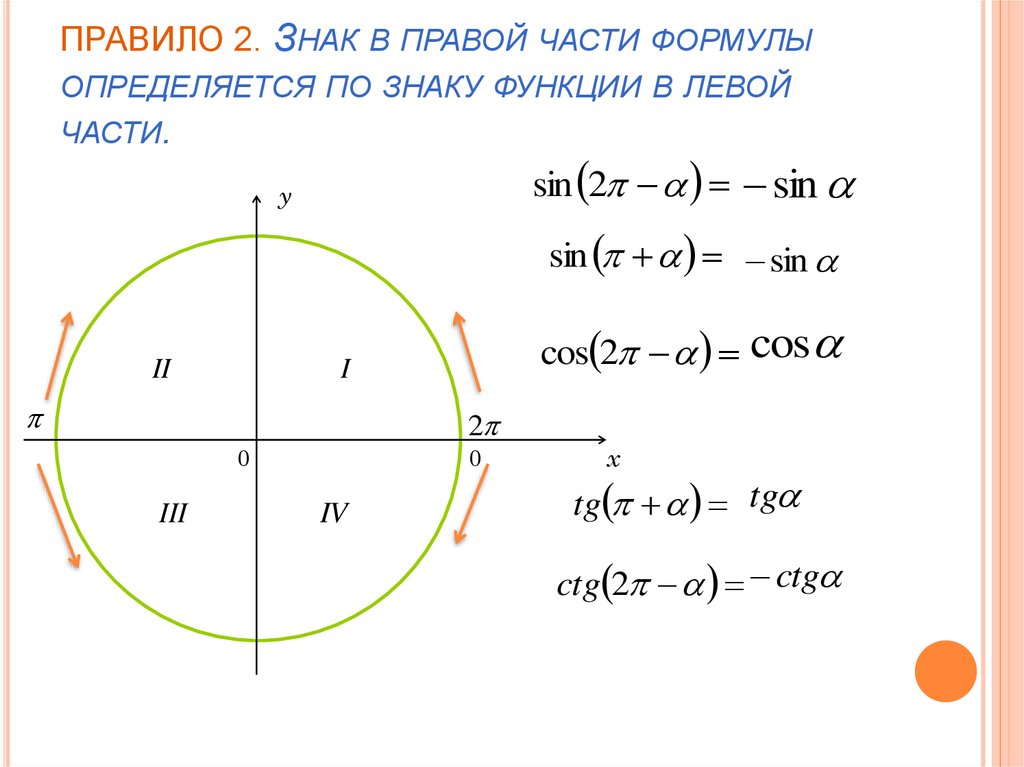 -М.: Просвещение, 1996.
-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 26.1 – 26.8.
Дополнительные веб-ресурсы
1. Математика (Источник).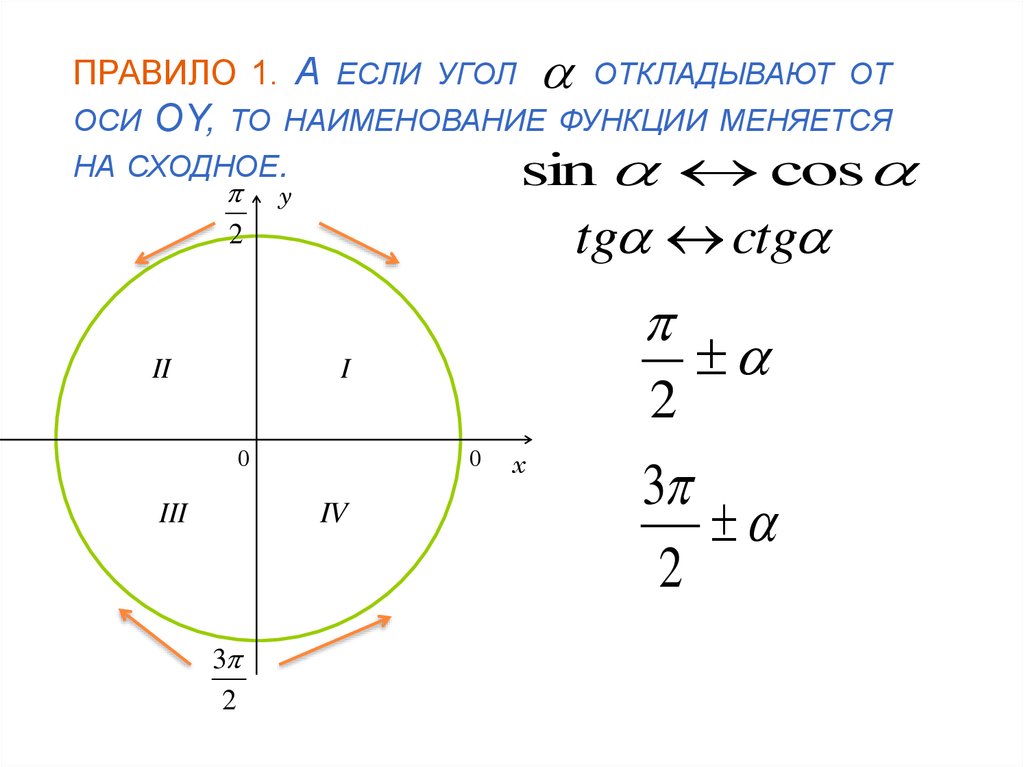
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
Как решать формулы приведения. Формулы приведения
Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента . С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Формулы приведения:
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет
2. Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Пример:
Вычислить
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен «+». Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.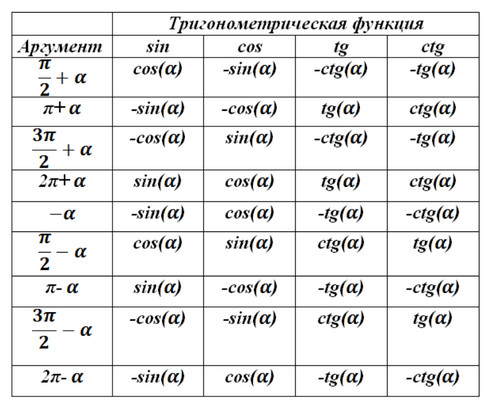
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
Данная статья посвящена подробному изучению тригонометрических формул приведения. Дан полный список формул приведения, показаны примеры их использования, приведено доказательство верности формул. Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.
Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.
Yandex.RTB R-A-339285-1
Формулы приведения. Список
Фомулы приведения позволяют приводить основные тригонометрические функции углов произвольной величины к функциям углов, лежащих в интервале от 0 до 90 градусов (от 0 до π 2 радиан). Оперировать углами от 0 до 90 градусов гораздо удобнее, чем работать со сколь угодно большими значениями, поэтому формулы приведения широко применяются при решении задач тригонометрии.
Прежде, чем мы запишем сами формулы, уточним несколько важных для понимания моментов.
- Аргументами тригонометрических функций в формулах приведения являются угды вида ± α + 2 π · z , π 2 ± α + 2 π · z , 3 π 2 ± α + 2 π · z . Здесь z — любое целое число, а α — произвольный угол поворота.
- Не обязательно учить все формулы приведения, количество которых довольно внушительно. Существует мнемоническое правило, которо позволяет легко вывести нужную формулу.
 Речь о мнемоническом правиле пойдет позже.
Речь о мнемоническом правиле пойдет позже.
Теперь перейдем непосредственно к формулам приведения.
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов. запишем все формулы в виде таблицы.
Формулы приведения
sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin — α + 2 π z = — sin α , cos — α + 2 π z = cos α t g — α + 2 π z = — t g α , c t g — α + 2 π z = — c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = — sin α t g π 2 + α + 2 π z = — c t g α , c t g π 2 + α + 2 π z = — t g α sin π 2 — α + 2 π z = cos α , cos π 2 — α + 2 π z = sin α t g π 2 — α + 2 π z = c t g α , c t g π 2 — α + 2 π z = t g α sin π + α + 2 π z = — sin α , cos π + α + 2 π z = — cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π — α + 2 π z = sin α , cos π — α + 2 π z = — cos α t g π — α + 2 π z = — t g α , c t g π — α + 2 π z = — c t g α sin 3 π 2 + α + 2 π z = — cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = — c t g α , c t g 3 π 2 + α + 2 π z = — t g α sin 3 π 2 — α + 2 π z = — cos α , cos 3 π 2 — α + 2 π z = — sin α t g 3 π 2 — α + 2 π z = c t g α , c t g 3 π 2 — α + 2 π z = t g α
В данном случае формулы записаны с радианами.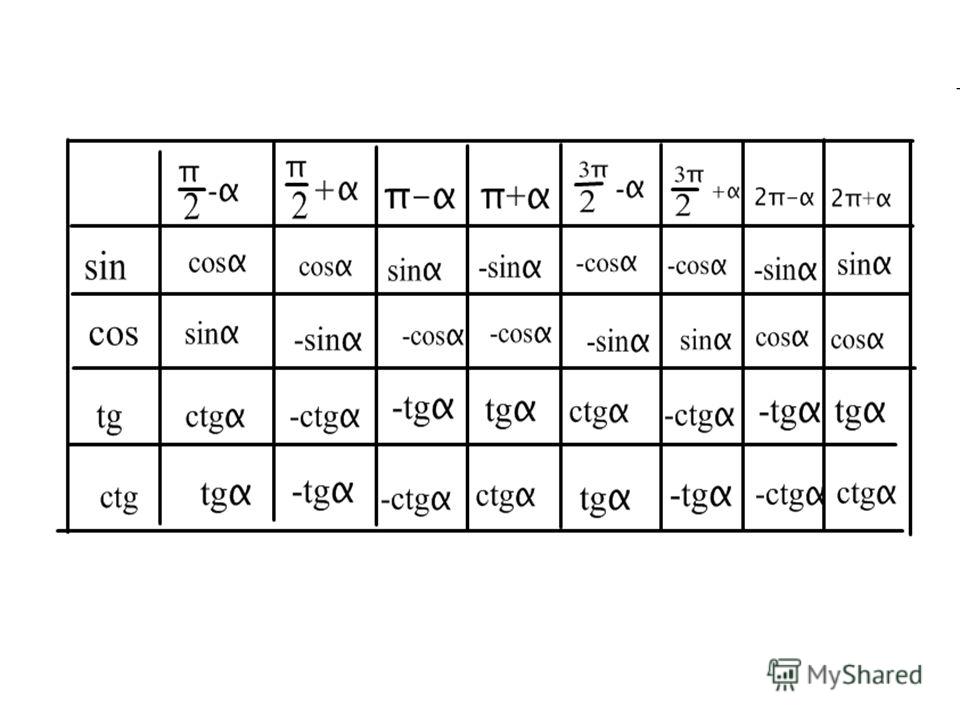 Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив π на 180 градусов.
Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив π на 180 градусов.
Примеры использования формул приведения
Покажем, как пользоваться формулами приведения и как указанные формулы применяются при решении практических примеров.
Угол под знаком тригонометрической функции можно представить не одним, а множеством способов. Например, аргумент тригонометрической функции может быть представлен в видах ± α + 2 π z , π 2 ± α + 2 π z , π ± α + 2 π z , 3 π 2 ± α + 2 π z . Продемонстрируем это.
Возьмем угол α = 16 π 3 . Это угол можно записать так:
α = 16 π 3 = π + π 3 + 2 π · 2 α = 16 π 3 = — 2 π 3 + 2 π · 3 α = 16 π 3 = 3 π 2 — π 6 + 2 π
В зависимости от представления угла используется соответствующая формула приведения.
Возьмем тот же угол α = 16 π 3 и вычислим его тангенс
Пример 1. Использование формул приведения
α = 16 π 3 , t g α = ?
Представим угол α = 16 π 3 в виде α = π + π 3 + 2 π · 2
Этому представлению угла будет соответствовать формула приведения
t g (π + α + 2 π z) = t g α
t g 16 π 3 = t g π + π 3 + 2 π · 2 = t g π 3
Воспользовавшись таблицей, укажем значение тангенса
Теперь используем другое представление угла α = 16 π 3 .
Пример 2. Использование формул приведения
α = 16 π 3 , t g α = ? α = — 2 π 3 + 2 π · 3 t g 16 π 3 = t g — 2 π 3 + 2 π · 3 = — t g 2 π 3 = — (- 3) = 3
Наконец, для третьего представления угла запишем
Пример 3. Использование формул приведения
α = 16 π 3 = 3 π 2 — π 6 + 2 π t g 3 π 2 — α + 2 π z = c t g α t g α = t g (3 π 2 — π 6 + 2 π) = c t g π 6 = 3
Теперь приведем пример на использование формул приведения посложнее
Пример 4. Использование формул приведения
Представим sin 197 ° через синус и косинус острого угла.
Для того, чтобы можно было применять формулы приведения, нужно представить угол α = 197 ° в одном из видов
± α + 360 ° · z , 90 ° ± α + 360 ° · z , 180 ° ± α + 360 ° · z , 270 ° ± α + 360 ° · z . Согласно условию задачи, угол должен быть острым. Соответственно, у нас есть два способа для его представления:
197 ° = 180 ° + 17 ° 197 ° = 270 ° — 73 °
Получаем
sin 197 ° = sin (180 ° + 17 °) sin 197 ° = sin (270 ° — 73 °)
Теперь посмотрим на формулы приведения для синусов и выберем соответствующие
sin (π + α + 2 πz) = — sinα sin (3 π 2 — α + 2 πz) = — cosα sin 197 ° = sin (180 ° + 17 ° + 360 ° · z) = — sin 17 ° sin 197 ° = sin (270 ° — 73 ° + 360 ° · z) = — cos 73 °
Мнемоническое правило
Формул приведения много, и, к счастью, нет необходимости заучивать их наизусть. Существуют закономерности, по которым можно выводить формулы приведения для разных углов и тригонометрических функций. Эти закономерности называются мнемоническим правилом. Мнемоника — искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.
Существуют закономерности, по которым можно выводить формулы приведения для разных углов и тригонометрических функций. Эти закономерности называются мнемоническим правилом. Мнемоника — искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.
Мнемоническое правило
1. Аргумент исходной функции представляется в одном из видов
± α + 2 πz π 2 ± α + 2 πz π ± α + 2 πz 3 π 2 ± α + 2 πz
Угол α должен лежать в пределах от 0 до 90 градусов.
2. Определяется знак исходной тригонометрической функции. Такой же знак будет иметь функция, записываемая в правой части формулы.
3. Для углов ± α + 2 πz и π ± α + 2 πz название исходной функции остается неизменным, а для углов π 2 ± α + 2 πz и 3 π 2 ± α + 2 πz соответственно меняется на «кофункцию». Синус — на косинус. Тангенс — на котангенс.
Чтобы пользоваться мнемоническим праилом для формул приведения нужно уметь определять знаки тригонометрических функций по четвертям единичной окружности.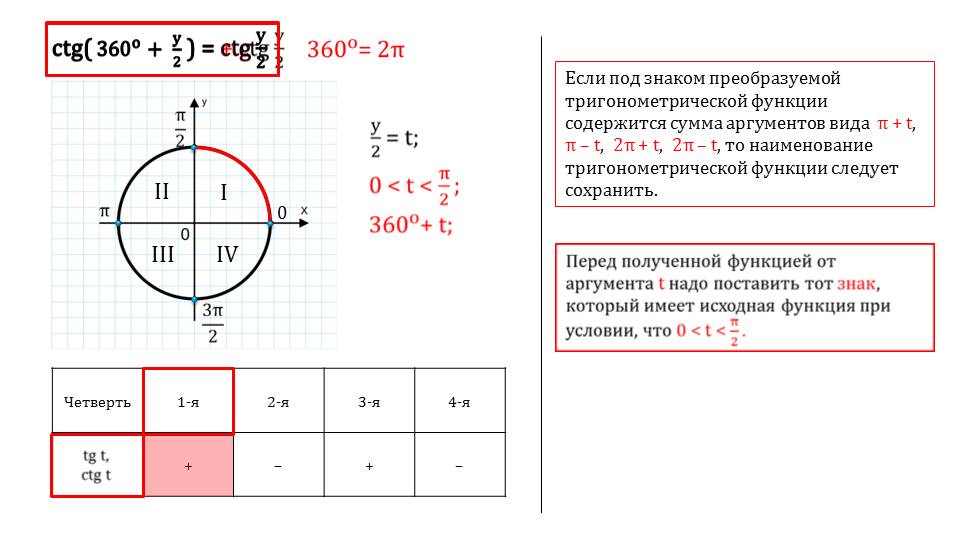 Разберем примеры применения мнемонического правила.
Разберем примеры применения мнемонического правила.
Пример 1. Использование мнемонического правила
Запишем формулы приведения для cos π 2 — α + 2 πz и t g π — α + 2 πz . α — улог первой четверти.
1. Так как по условию α — улог первой четверти, мы пропускаем первый пункт правила.
2. Определим знаки функций cos π 2 — α + 2 πz и t g π — α + 2 πz . Угол π 2 — α + 2 πz также является углом первой четверти, а угол π — α + 2 πz находится во второй четверти. В первой четверти функция косинуса положительна, а тангенс во второй четверти имеет знак минус. Запишем, как будут выглядеть искомые формулы на этом этапе.
cos π 2 — α + 2 πz = + t g π — α + 2 πz = —
3. Согласно третьему пункту для угла π 2 — α + 2 π название функции изменяется на конфуцию, а для угла π — α + 2 πz остается прежним. Запишем:
cos π 2 — α + 2 πz = + sin α t g π — α + 2 πz = — t g α
А теперь заглянем в формулы, приведенные выше, и убедимся в том, что мнемоническое правило работает.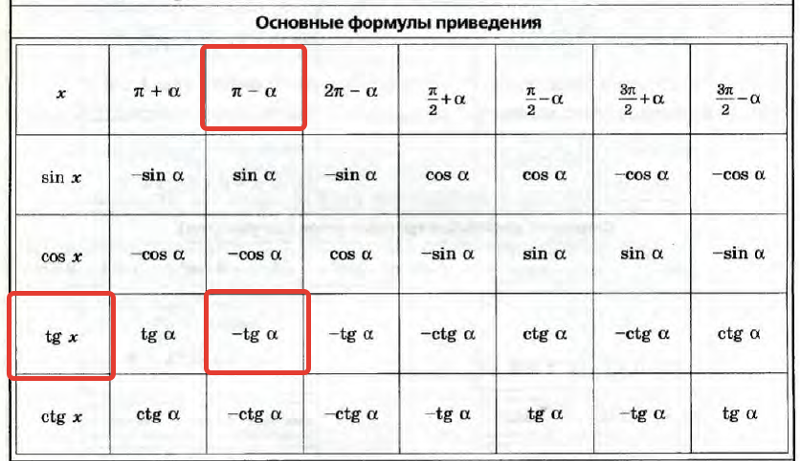
Рассмотрим пример с конкретным углом α = 777 ° . Приведем синус альфа к тригонометрической функции острого угла.
Пример 2. Использование мнемонического правила
1. Представим углол α = 777 ° в необходимом виде
777 ° = 57 ° + 360 ° · 2 777 ° = 90 ° — 33 ° + 360 ° · 2
2. Исходный угол — угол первой четверти. Значит, синус угла имеет положительный знак. В итоге имеем:
3. sin 777 ° = sin (57 ° + 360 ° · 2) = sin 57 ° sin 777 ° = sin (90 ° — 33 ° + 360 ° · 2) = cos 33 °
Теперь рассмотрим пример, который показывает, как важно правильно определить знак тригонометрической функции и правильно представить угол при использовании мнемонического правила. Повторим еще раз.
Важно!
Угол α должен быть острым!
Вычислим тангенс угла 5 π 3 . Из таблицы значений основных тригонометрических функций можно сразу взять значение t g 5 π 3 = — 3 , но мы применим мнемоническое правило.
Пример 3. Использование мнемонического правила
Представим угол α = 5 π 3 в необходимом виде и воспользуемся правилом
t g 5 π 3 = t g 3 π 2 + π 6 = — c t g π 6 = — 3 t g 5 π 3 = t g 2 π — π 3 = — t g π 3 = — 3
Если же представить угол альфа в виде 5 π 3 = π + 2 π 3 , то результат применениея мнемонического правила будет неверным.
t g 5 π 3 = t g π + 2 π 3 = — t g 2 π 3 = — (- 3) = 3
Неверный результат обусловлен тем, что угол 2 π 3 не явдяется острым.
Доказательство формул приведения основывается на свойствах периодичности и симметричности тригонометрических функций, а также на свойстве сдвига на углы π 2 и 3 π 2 . Доказательство справедливости всех формул приведения иожно проводить без учета слагаемого 2 πz , так как оно обозначает изменение угла на целое число полных оборотов и как раз отражает свойство периодичности.
Первые 16 формул следуют напрямую из свойств основных тригонометрических функций: синуса, косинуса, тангенса и котанганса.
Приведем доказательство формул приведения для синусов и косинусов
sin π 2 + α = cos α и cos π 2 + α = — sin α
Посмотрим на единичную окружность, начальная точка которой после повоторота на угол α перешла в точку A 1 x , y , а после поворота на угол π 2 + α — в точку A 2 . Из обеих точек проведем перпендикуляры к оси абсцисс.
Два прямоугольных треугольника O A 1 H 1 и O A 2 H 2 равны по гипотенузе и прилежащим к ней углам. Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка A 2 имеет координаты A 2 — y , x . Используя определения синуса и косинуса, запишем:
Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка A 2 имеет координаты A 2 — y , x . Используя определения синуса и косинуса, запишем:
sin α = y , cos α = x , sin π 2 + α = x , cos π 2 + α = y
sin π 2 + α = cos α , cos π 2 + α = — sin α
С учетом основных тождеств тригонометрии и только что доказанного, можно записать
t g π 2 + α = sin π 2 + α cos π 2 + α = cos α — sin α = — c t g α c t g π 2 + α = cos π 2 + α sin π 2 + α = — sin α cos α = — t g α
Для доказательства формул приведения с аргументом π 2 — α его необходимо представить в виде π 2 + (- α) . Например:
cos π 2 — α = cos π 2 + (- α) = — sin (- α) = sin α
В доказательстве используются свойства тригонометрических функций с аргументами, противоположными по знаку.
Все остальные формулы приведения можно доказать на базе записанных выше.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Тема урока
- Изменение синуса, косинуса и тангенса при возрастании угла.

Цели урока
- Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
- Познакомится с закономерностью изменений значений синуса косинуса и тангенса при возрастании угла.
- Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
- Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока
- Проверить знания учащихся.
План урока
- Повторение ранее изученного материала.
- Задачи на повторение.
- Изменение синуса, косинуса и тангенса при возрастании угла.
- Практическое применение.
Повторение ранее изученного материала
Начнем с самого начала и вспомним то что будет полезно освежить в памяти. Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.
Тригонометрия — это такое сложное греческое слово: тригонон — треугольник, метро — мерять. Стало быть по-гречески это означает: мерятся треугольниками.
Предмети > Математика > Математика 8 класс
Урок и презентация на тему: «Применение формул приведения при решении задач»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
1С: Школа. Интерактивные задания на построение для 7-10 классов
1С: Школа. Решаем задачи по геометрии. Интерактивные задания на построение в пространстве для 10–11 классов
Что будем изучать:
1. Немного повторим.
2. Правила для формул приведения.
3. Таблица преобразований для формул приведения.
4. Примеры.
Повторение тригонометрических функций
Ребята, с формулами привидения вы уже сталкивались, но так их еще не называли. Как думаете: где?
Как думаете: где?
Посмотрите на наши рисунки. Правильно, когда вводили определения тригонометрических функций.
Правило для формул приведения
Давайте введем основное правило: Если под знаком тригонометрической функции содержится число вида π×n/2 + t, где n – любое целое число, то нашу тригонометрическую функцию можно привести к более простому виду, которая будет содержать только аргумент t. Такие формулы и называют формулами привидения.
Вспомним некоторые формулы:
- sin(t + 2π*k) = sin(t)
- cos(t + 2π*k) = cos(t)
- sin(t + π) = -sin(t)
- cos(t + π) = -cos(t)
- sin(t + π/2) = cos(t)
- cos(t + π/2) = -sin(t)
- tg(t + π*k) = tg(x)
- ctg(t + π*k) = ctg(x)
формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения :
- Если под знаком тригонометрической функции содержатся числа вида: π + t, π — t, 2π + t и 2π — t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.

- Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 — t,
3π/2 + t и 3π/2 — t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом. - Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0
Эти правила применимы и когда аргумент функции задан в градусах!
Так же мы можем составить таблицу преобразований тригонометрических функций:
Примеры применения формул приведения
1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2
2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 sin(t + π/2) = cos(t)
3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0
4. Преобразуем ctg(270 0 + t). Наименование функции изменяется, то есть получим tg(t). Далее предположим что 0
Далее предположим что 0
Задачи с формулами приведения для самостоятельного решения
Ребята, преобразуйте самостоятельно, используя наши правила:
1) tg(π + t),
2) tg(2π — t),
3) ctg(π — t),
4) tg(π/2 — t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 — t),
9) sin(2π — t),
10) cos(2π — t),
11) cos(3π/2 + 8t),
12) cos(3π/2 — t),
13) cos(π — t).
Объяснение урока: Упрощение тригонометрических выражений
В этом объяснении мы узнаем, как упростить тригонометрическое выражение.
Эти выражения часто упрощаются при применении одного или нескольких тригонометрических тождеств, которые связывают различные тригонометрические и обратные тригонометрические функции и их аргументы. Их мотивация математическая, но они также приложения в реальных задачах.
Тригонометрические тождества имеют несколько реальных приложений в различных областях, таких как физика, инженерия, архитектура, робототехника,
теория музыки и навигация, и это лишь некоторые из них.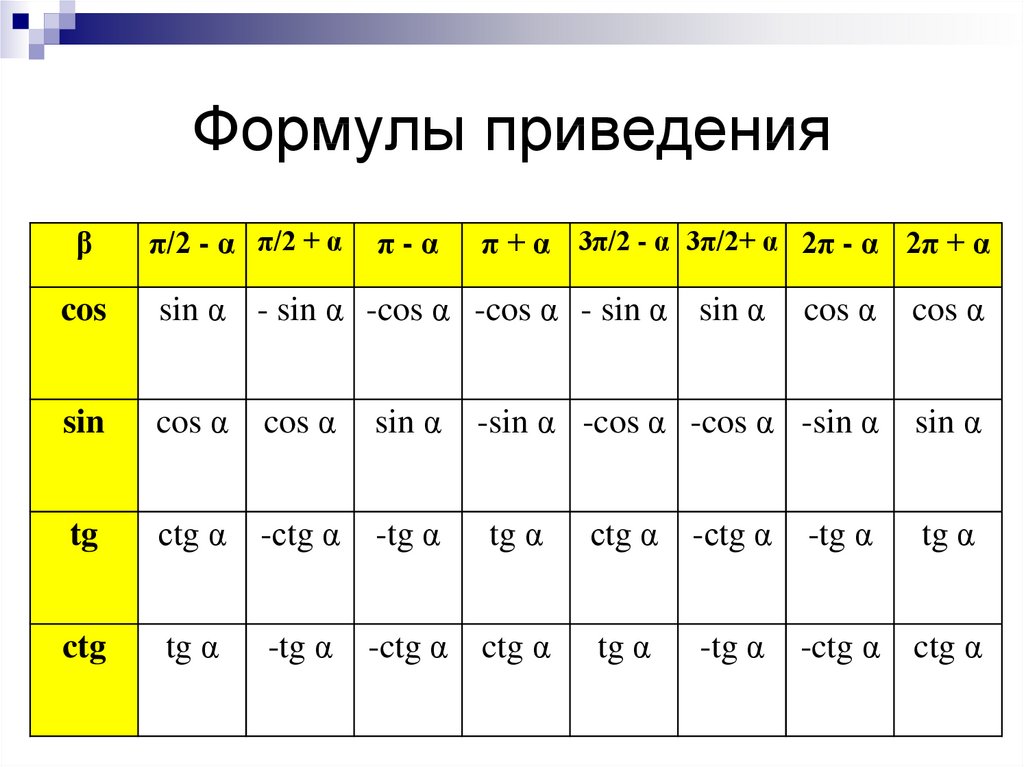 В физике их можно использовать в движении снарядов, моделируя механику
электромагнитных волн, анализируя переменные и постоянные токи и находя траекторию движения массы вокруг массивного тела под
сила тяжести.
В физике их можно использовать в движении снарядов, моделируя механику
электромагнитных волн, анализируя переменные и постоянные токи и находя траекторию движения массы вокруг массивного тела под
сила тяжести.
Начнем с напоминания о тригонометрических функциях, пифагорейские тождества которых мы рассмотрим в этом толкователе. Рассмотреть возможность следующий прямоугольный треугольник.
Тригонометрические функции могут быть выражены через отношение сторон треугольника как sinOHcosAHtanOA𝜃=,𝜃=,𝜃=.
Эти функции удовлетворяют следующему тригонометрическому тождеству: тансинкос𝜃=𝜃𝜃.
Отметим, что эти тригонометрические соотношения определены для острых углов 0𝜃90∘∘, а тригонометрические функции для всех значений 𝜃 определены на единичной окружности.
Предположим, что точка движется по единичной окружности против часовой стрелки. В определенной позиции
(𝑥,𝑦) на единичной окружности с углом 𝜃 функция синуса определяется как
𝑦=𝜃sin и функция косинуса как 𝑥=𝜃cos, как показано на диаграмме выше. Другими словами, тригонометрические функции определяются с помощью координат точки пересечения единичной окружности.
с концевой стороной 𝜃 в стандартном положении.
Другими словами, тригонометрические функции определяются с помощью координат точки пересечения единичной окружности.
с концевой стороной 𝜃 в стандартном положении.
Взаимные тригонометрические уравнения определяются в терминах стандартных тригонометрических уравнений следующим образом.
Определение: обратные тригонометрические функции
Функции косеканса, секанса и котангенса определяются как cscsinseccoscottancossin𝜃=1𝜃,𝜃=1𝜃,𝜃=1𝜃=𝜃𝜃.
Тригонометрические функции являются периодическими, что означает, что если мы добавим целое число, кратное 2𝜋, в радианы или 360∘ на угол 𝜃, значение функции остается прежней: sincoscostantan(360+𝜃)=𝜃,(360+𝜃)=𝜃,(360+𝜃)=𝜃.∘∘∘
Мы можем видеть это непосредственно из определения единичного круга тригонометрических функций. На самом деле, касательная функция периодическая по 𝜋, в радианах, или 180∘, так как у нас есть tantan(180+𝜃)=𝜃.∘
Аналогично, для обратных тригонометрических функций имеем
csccscsecseccotcot(360+𝜃)=𝜃,(360+𝜃)=𝜃,(360+𝜃)=𝜃. ∘∘∘
∘∘∘
Подобно функции тангенса, функция котангенса периодична по 𝜋, в радианы или 180∘, так как у нас есть коткот(180+𝜃)=𝜃.∘
Тригонометрические тождества, которые мы рассмотрим в этом объяснении, выполняются для любого угла 𝜃 в области функции в градусах или радианы. В частности, мы можем преобразовать угол между степени и радианах по следующему правилу: если у нас есть угол 𝜃степень, мы можем преобразовать его в радианы через 𝜃=𝜋180𝜃.radiansdegree
При работе с тригонометрическими выражениями полезно переписать обратные тригонометрические тождества в терминах синуса и косинус для упрощения.
Рассмотрим пример, в котором мы должны использовать обратные тригонометрические функции для определения значения тригонометрическое выражение.
Пример 1. Использование взаимных тождеств для вычисления тригонометрических выражений
Найдите значение 8𝜃×−5𝜃sincsc.
Ответ
В этом примере мы хотим найти значение определенного выражения, включающего тригонометрические и обратные числа. тригонометрические функции.
тригонометрические функции.
Один из способов вычисления тригонометрического выражения состоит в том, чтобы записать его в терминах функций синуса и косинуса, используя следующие определение функции косеканса, входящей в данное выражение: cscsin𝜃=1𝜃.
Следовательно, выражение можно упростить, чтобы дать 8𝜃×−5𝜃=8𝜃×−5=8𝜃×−5𝜃=−40×𝜃𝜃=−40.sincscsinsinsinsinsinsin
Теперь давайте рассмотрим пример, в котором мы упрощаем конкретное тригонометрическое выражение.
Пример 2. Упрощение тригонометрических выражений с использованием тригонометрических тождеств
Упростить coscscsin𝜃𝜃𝜃.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие
определение функции косеканса, входящей в данное выражение:
cscsin𝜃=1𝜃.
Данное тригонометрическое выражение становится coscscsincossinsincos𝜃𝜃𝜃=𝜃×1𝜃×𝜃=𝜃.
В следующем примере мы упростим тригонометрическое выражение, записав его с помощью функций синуса и косинуса.
Пример 3. Упрощение тригонометрических выражений с использованием тригонометрических тождеств
Упрощение tansinsec𝜃𝜃𝜃.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие определения для функций тангенса и секанса, которые появляются в данном выражении: тансинкоссеккос𝜃=𝜃𝜃𝜃=1𝜃.
Данное тригонометрическое выражение становится tansinsectansincossincossincossincossin𝜃𝜃𝜃=𝜃𝜃÷1𝜃=𝜃𝜃×𝜃𝜃=𝜃×𝜃𝜃=𝜃.
В следующем примере используется произведение тригонометрических и обратных тригонометрических функций, которое мы можем просто использовать, используя определение
обратных функций, а затем переписать окончательный ответ в терминах другой обратной функции.
Пример 4. Упрощение тригонометрических выражений с использованием взаимных тождеств
Simplify cosseccsc𝜃𝜃𝜃.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие определения функций косеканса и секанса, входящих в данное выражение: cscsinseccos𝜃=1𝜃,𝜃=1𝜃.
Таким образом, выражение можно упростить как cosseccsccoscossincossin𝜃𝜃𝜃=𝜃×1𝜃×1𝜃=𝜃𝜃.
Теперь, используя определение функции котангенса, коткосин𝜃=𝜃𝜃.
Данное выражение может быть выражено через функцию котангенса как cossecccscossincot𝜃𝜃𝜃=𝜃𝜃=𝜃.
Тригонометрические и обратные тригонометрические функции являются четными и нечетными функциями, поскольку они удовлетворяют свойствам
𝑓(−𝜃)=𝑓(𝜃) для четных функций и 𝑓(−𝜃)=−𝑓(𝜃) для нечетных функций. В частности, функция синуса нечетная, а функция косинуса
четно, так как они удовлетворяют
sinsincoscos(−𝜃)=−𝜃,(−𝜃)=𝜃,
для любого значения 𝜃 в градусах или
радианы. Отсюда мы также можем определить четность других
тригонометрические функции, которые определяются с их точки зрения. В частности, для касательной функции имеем
tansincossincostan(-𝜃)=(-𝜃)(-𝜃)=-𝜃𝜃=-𝜃.
В частности, функция синуса нечетная, а функция косинуса
четно, так как они удовлетворяют
sinsincoscos(−𝜃)=−𝜃,(−𝜃)=𝜃,
для любого значения 𝜃 в градусах или
радианы. Отсюда мы также можем определить четность других
тригонометрические функции, которые определяются с их точки зрения. В частности, для касательной функции имеем
tansincossincostan(-𝜃)=(-𝜃)(-𝜃)=-𝜃𝜃=-𝜃.
Таким образом, функция тангенса нечетна, и мы можем вывести четность других тригонометрических функций аналогичным образом. Мы можем обобщить их следующим образом.
Четные и нечетные тождества для тригонометрических функций
Функции косинуса и секанса четны, что означает, что для любого значения 𝜃 в соответствующих областях определения они удовлетворяют тождества coscossecsec(−𝜃)=𝜃,(−𝜃)=𝜃.
А функции синуса, тангенса, косеканса и котангенса нечетны, что означает, что они удовлетворяют следующим тождествам для любого
значение 𝜃 в соответствующих доменах:
sinsintantancsccsccotcot(-𝜃)=-𝜃,(-𝜃)=-𝜃,(-𝜃)=-𝜃,(-𝜃)=-𝜃.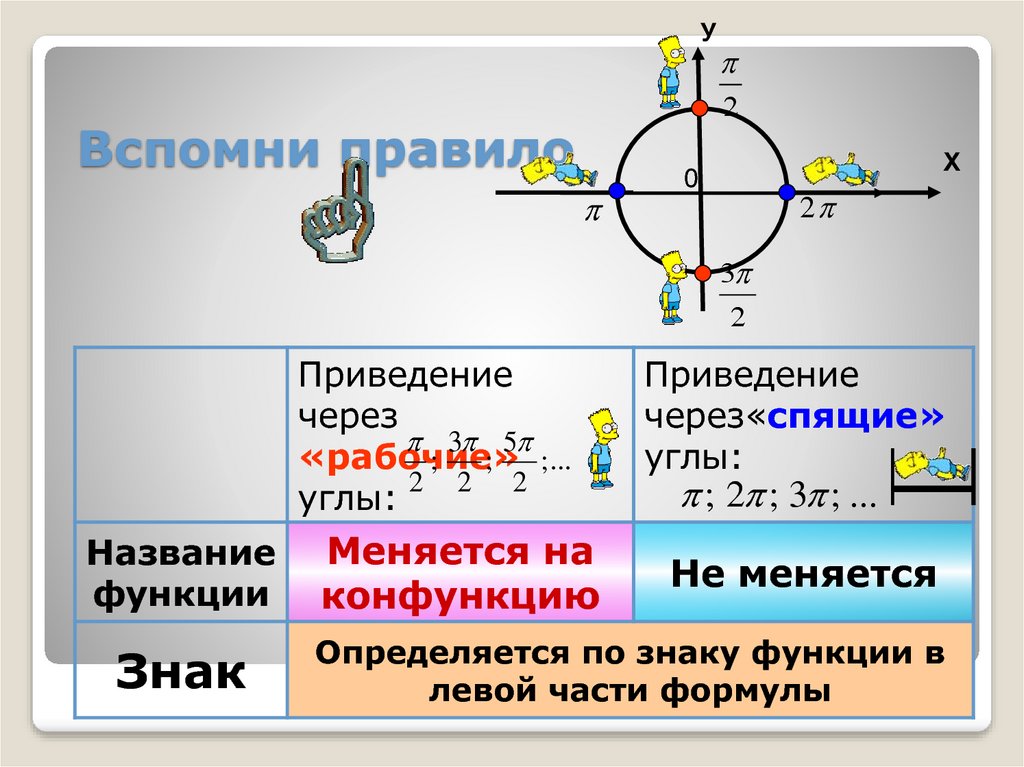
Теперь давайте рассмотрим пример, в котором мы должны применить четность тригонометрической функции, чтобы просто определить конкретную тригонометрическое выражение.
Пример 5. Упрощение тригонометрических выражений, включающих нечетные и четные тождества
Упростить tancsc(−𝜃)𝜃.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции используя четную/нечетную идентичность.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие определение функции косеканса, входящей в данное выражение: cscsin𝜃=1𝜃.
Касательная функция нечетная, поэтому тождество тантан(-𝜃)=-𝜃.
Мы можем переписать функцию тангенса, используя ее определение в терминах функций синуса и косинуса: тансинкос𝜃=𝜃𝜃.
Таким образом, выражение можно упростить как
tancsctancscsincossincos(−𝜃)𝜃=−𝜃𝜃=−𝜃𝜃×1𝜃=−1𝜃.
Наконец, мы можем переписать это выражение в терминах функции секущей, определяемой как секкос𝜃=1𝜃.
Таким образом, выражение принимает вид tancscsec(−𝜃)𝜃=−𝜃.
Функция синуса эквивалентна функции косинуса смещением на 90∘ влево, что можно визуализировать, сравнив график обеих функций.
В частности, для углов 𝜃 и 90+𝜃∘: sincoscossin(90+𝜃)=𝜃,(90+𝜃)=−𝜃.∘∘
Мы также можем проиллюстрировать их на единичной окружности, как показано.
Аналогично, заменяя 𝜃 на −𝜃, мы получаем следующие тождества кофункций для дополнительных углов 𝜃 и 90−𝜃∘: sincoscossin(90−𝜃)=𝜃,(90−𝜃)=𝜃.∘∘
Мы можем проиллюстрировать это, как показано.
На рисунке изображен прямоугольный треугольник с углом 𝐴𝑂𝐵 в стандартном положении, который пересекает единичную окружность в точке 𝐵(𝑥,𝑦) и имеет остроугольную меру 0𝜃90∘∘.
Мы можем комбинировать эти тождества и использовать их для определения тождеств для других тригонометрических функций, определенных в
функции синуса и косинуса.
Определение: тригонометрические тождества коррелированных углов
Тригонометрические функции удовлетворяют тождествам кофункций для всех 𝜃 в своих областях определения. Особенно, у нас есть sincoscossintancottancscsecseccsc(90±𝜃)=𝜃,(90±𝜃)=∓𝜃,(90±𝜃)=∓𝜃,(90±𝜃)=∓𝜃,(90±𝜃)=𝜃,(90±𝜃)= ∓𝜃.∘∘∘∘∘∘
Например, для функции касательной имеем tansincossincossincot(90±𝜃)=(90±𝜃)(90±𝜃)=𝜃∓𝜃=∓𝜃𝜃=∓𝜃.∘∘∘
Все эти тождества также выполняются в радианах, в частности, заменив 90∘ на 𝜋2 в радианы.
Теперь давайте рассмотрим пример, где мы используем это тождество вместе с четностью тригонометрической функции, чтобы упростить выражение.
Пример 6. Упрощение тригонометрических выражений с использованием коррелированных и четных тождеств
Упростить sinsec𝜋2+𝜃(−𝜃).
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее обратные тригонометрические функции.
Мы также будем использовать тождество коррелированного угла
синкос𝜋2+𝜃=𝜃
и даже тождество
сексек(−𝜃)=𝜃.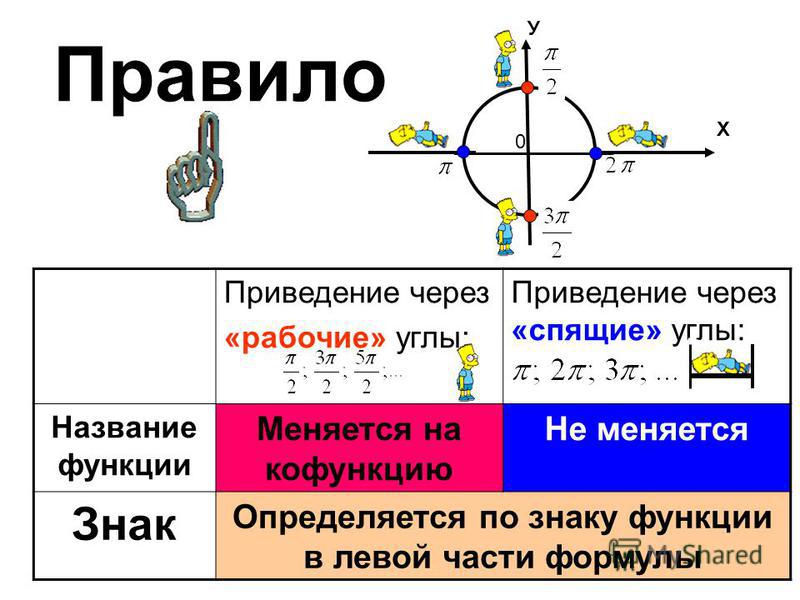
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующее определение функции секущей: секкос𝜃=1𝜃.
Используя их, выражение становится sinseccosseccoscos𝜋2+𝜃(−𝜃)=𝜃𝜃=𝜃×1𝜃=1.
Теперь предположим, что мы хотим определить sin(180−𝜃)∘. Мы можем найти это, многократно используя приведенные выше тождества. Если мы позволим 𝜃=90−𝑥∘, тогда sinsinsincos(180−𝜃)=(180−[90−𝑥])=(90+𝑥)=𝑥.∘∘∘∘
Теперь, подставляя обратно 𝑥=90−𝜃, получаем sincossin(180−𝜃)=(90−𝜃)=𝜃.∘∘
Аналогично находим coscos(180−𝜃)=−𝜃.∘
Повторно применяя эти тождества или используя единичную окружность, мы также получаем тождества для углов 𝜃 и 𝜃±180∘: sinsincoscos(180±𝜃)=∓𝜃,(180±𝜃)=−𝜃.∘∘
Для 𝜃 и 180−𝜃∘, имеем следующее.
А для 𝜃 и 180+𝜃∘ имеем следующее.
У нас также есть тождества для других тригонометрических функций, которые следуют из тождеств для функций синуса и косинуса, из их
определения:
tantancotcotcsccscsecsec(180±𝜃)=±𝜃,(180±𝜃)=±𝜃,(180±𝜃)=∓𝜃,(180±𝜃)=-𝜃. ∘∘∘∘
∘∘∘∘
В следующем примере используются определения обратных тригонометрических функций вместе с тождествами кофункций в радианах, чтобы упростить выражение.
Пример 7. Использование периодических тождеств и тождеств кофункций для упрощения тригонометрического выражения
Simplify seccot−𝜃(𝜋−𝜃)
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее обратные тригонометрические функции.
Мы также будем использовать кофункцию и коррелированные тождества: seccsccotcot𝜋2−𝜃=𝜃,(𝜋−𝜃)=−𝜃.
Один из способов упростить тригонометрическое выражение — записать его в терминах функций синуса и косинуса, используя следующие определения для функций косеканса и котангенса, которые появляются в числителе и знаменателе: cscsincotcossin𝜃=1𝜃,𝜃=𝜃𝜃.
Числитель выражения можно упростить как secscssin𝜋2−𝜃=𝜃=1𝜃.
И знаменатель как cotcotcossin(𝜋−𝜃)=−𝜃=−𝜃𝜃.
Таким образом, выражение можно упростить как
seccotsinsincoscos−𝜃(𝜋−𝜃)=−1𝜃×𝜃𝜃=−1𝜃.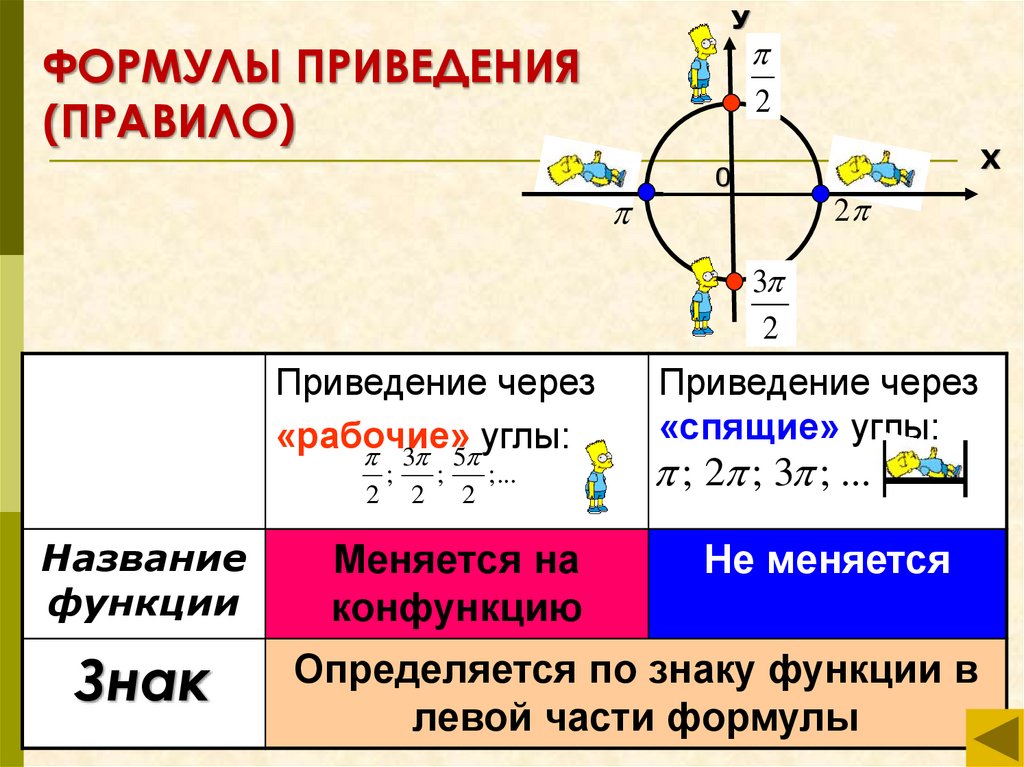
Наконец, мы можем переписать это выражение в терминах функции секущей, определяемой как секкос𝜃=1𝜃.
Таким образом, получаем seccotsec−𝜃(𝜋−𝜃)=−𝜃.
Аналогично, для углов 𝜃 и 270±𝜃∘ имеем sincoscossintancotcottancscsecseccsc(270±𝜃)=−𝜃,(270±𝜃)=±𝜃.(270±𝜃)=∓𝜃,(270±𝜃)=∓𝜃,(270±𝜃)=-𝜃,(270±𝜃 )=±𝜃.∘∘∘∘∘∘
Это можно представить следующим образом.
Используя периодичность тригонометрических функций и единичный круг, мы имеем sinsincoscostantancotcsccscsecsec(360±𝜃)=±𝜃,(360±𝜃)=𝜃,(360±𝜃)=±𝜃,(360±𝜃)=±𝜃,(360±𝜃)=±𝜃,(360±𝜃) =𝜃.∘∘∘∘∘∘
Все тождества также выполняются в радианах, заменив 360∘ на 2𝜋 в радианах. Их также можно визуализировать с помощью единичного круга, как показано на рисунке.
Все тождества с коррелированными углами можно визуализировать, используя следующее.
Теперь давайте рассмотрим несколько примеров, где мы должны применить тождества кофункций, чтобы упростить тригонометрическое выражение.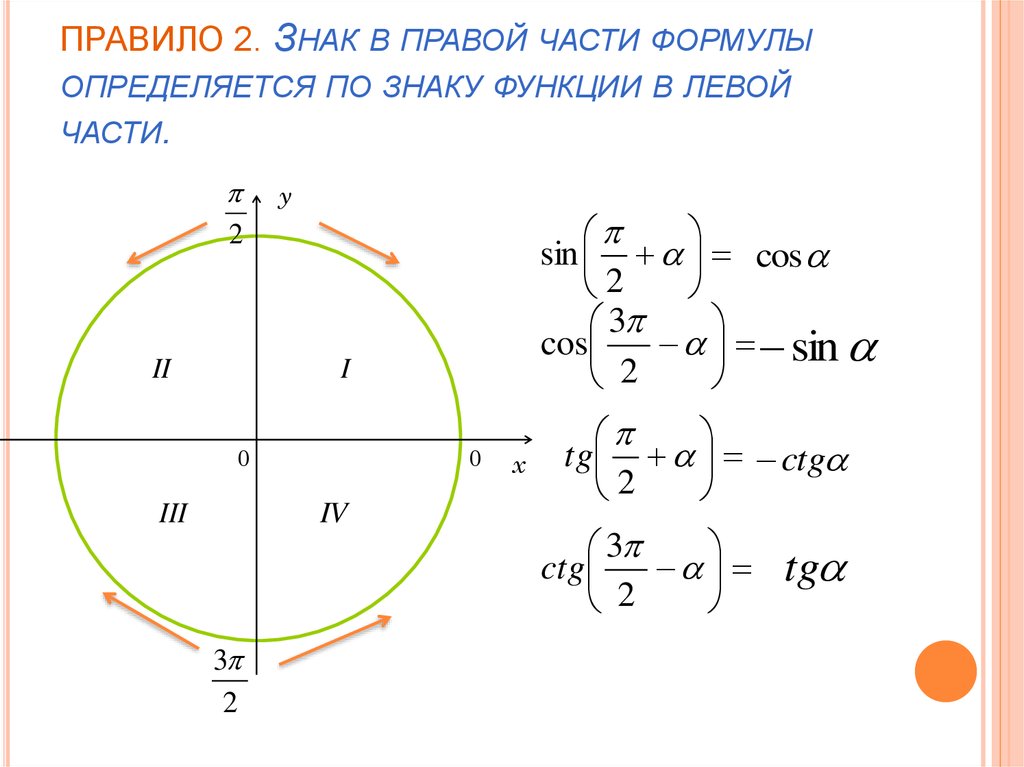 В следующем примере мы будем многократно использовать это тождество для функций косинуса и синуса, в
градусов.
В следующем примере мы будем многократно использовать это тождество для функций косинуса и синуса, в
градусов.
Пример 8. Упрощение тригонометрических выражений с использованием тождеств кофункций
Упростить sincos𝜃+(270+𝜃)∘.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические функции.
Чтобы упростить данное выражение, мы используем тождество коррелированного угла cossin(270+𝜃)=𝜃.∘
Следовательно, имеем sincossinsinsin𝜃+(270+𝜃)=𝜃+𝜃=2𝜃.∘
В последнем примере мы хотим повторно применить тождества кофункций к функциям тангенса и котангенса, в градусов, чтобы упростить тригонометрическое выражение.
Пример 9. Использование тригонометрических тождеств для упрощения тригонометрического выражения
Упрощение сектанта𝜃𝜃(270+𝜃)∘.
Ответ
В этом примере мы хотим упростить конкретное выражение, включающее тригонометрические и обратные тригонометрические функции.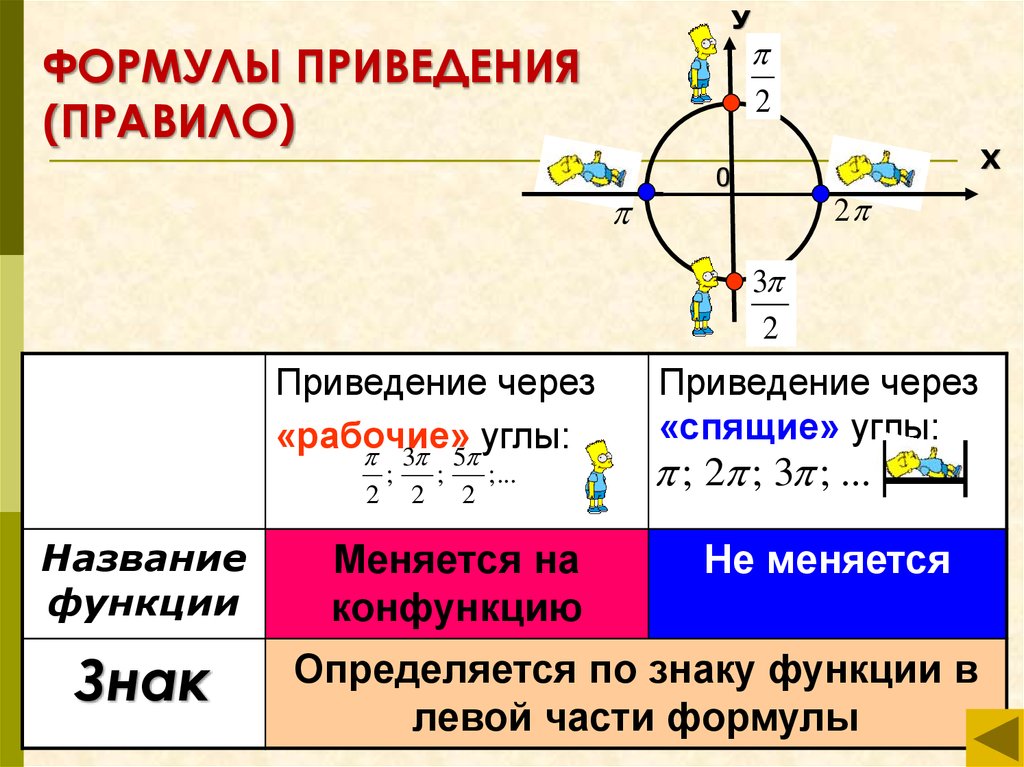
Мы также будем использовать тождество коррелированного угла tancot(270+𝜃)=−𝜃.∘
Поскольку по определению функции котангенса мы имеем хлопок𝜃=1𝜃, коррелированное тождество можно записать в терминах касательной функции как tancottan(270+𝜃)=−𝜃=−1𝜃.∘
Следовательно, выражение можно упростить как сектантансектансектансек𝜃𝜃(270+𝜃)=𝜃𝜃×−1𝜃=−𝜃×𝜃𝜃=−𝜃.∘
Давайте закончим повторением нескольких важных ключевых моментов из этого объяснения.
Ключевые моменты
- Мы можем выразить тангенс и обратные тригонометрические функции через синус и косинус как tansincoscsscsinseccoscottancossin𝜃=𝜃𝜃,𝜃=1𝜃,𝜃=1𝜃,𝜃=1𝜃=𝜃𝜃. и мы можем использовать их для упрощения тригонометрических выражений.
- Все эти тригонометрические функции либо четные, либо нечетные. В частности, для функций синуса и косинуса имеем
коскоссин(-𝜃)=𝜃,(-𝜃)=-𝜃,
и аналогично для других тригонометрических функций, следующих из определений.
 Мы можем использовать четность
тригонометрические функции, которые помогут нам упростить тригонометрические выражения.
Мы можем использовать четность
тригонометрические функции, которые помогут нам упростить тригонометрические выражения. - Единичный круг позволяет нам определить тождества коррелированных углов для синуса и косинуса.
Например, тождества кофункций (в радианах): sincoscossin𝜋2−𝜃=𝜃,𝜋2−𝜃=𝜃. Соответствующие тождества для касательной и обратной тригонометрических функций находятся по их определениям. через функции синуса и косинуса. - Нам часто приходится применять более одного тождества или типа тождества, чтобы упростить тригонометрическое выражение.
Формулы двойного угла, полуугла и приведения · Алгебра и тригонометрия
Формулы двойного угла, полуугла и приведения · Алгебра и тригонометрияВ этом разделе вы:
- Используйте формулы двойного угла, чтобы найти точные значения.
- Используйте формулы двойного угла для проверки личности.

- Используйте формулы сокращения для упрощения выражения.
- Используйте формулы половинного угла, чтобы найти точные значения.
Велосипедные рампы, изготовленные для соревнований (см. [ссылка]), должны различаться по высоте в зависимости от уровня квалификации участников. Для продвинутых участников угол, образованный рампой и землей, должен составлять θ
., так что tan θ=53.
Угол разделен пополам для новичков. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Использование формул двойного угла для нахождения точных значений
В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где α=β.
Вывод формулы двойного угла для синуса начинается с формулы суммы,
sin(α+β)=sin α cos β+cos α sin β
Если мы допустим α=β=θ,
тогда у нас
sin(θ+θ)=sin θ cos θ+cos θ sin θsin(2θ)=2sin θ cos θ
Получение двойного угла для косинуса дает нам три варианта. Во-первых, исходя из формулы суммы, cos(α+β)=cos α cos β−sin α sin β,
и пусть α=β=θ,
у нас есть
cos(θ+θ)=cos θ cos θ−sin θ sin θcos(2θ)=cos2θ−sin2θ
Используя свойства Пифагора, мы можем расширить эту формулу двойного угла для косинуса и получить еще два варианта. Первый вариант:
cos(2θ)=cos2θ−sin2θ=(1−sin2θ)−sin2θ=1−2sin2θ
Второй вариант:
cos(2θ)=cos2θ−sin2θ=cos2θ−(1−cos2θ)=2 cos2θ−1
Аналогично, чтобы вывести формулу тангенса двойного угла, заменив α=β=θ
в формуле суммы дает
tan(α+β)=tan α+tan β1−tan α tan βtan(θ+θ)=tan θ+tan θ1−tan θ tan θtan(2θ)=2tan θ1−tan2θ
Формулы двойного угла
Формулы двойного угла резюмируются следующим образом:
sin(2θ)=2 sin θ cos θ −1
tan(2θ)=2 tan θ1−tan2θ
Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение.
- Нарисуйте треугольник, чтобы отразить полученную информацию.
- Определите правильную формулу двойного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Использование формулы двойного угла для нахождения точного значения, включающего тангенс
Учитывая, что tan θ=−34
и θ
находится в квадранте II, найдите следующее:
- грех (2θ)
- cos(2θ)
- загар(2θ)
Если мы нарисуем треугольник, отражающий предоставленную информацию, мы сможем найти значения, необходимые для решения задач на изображении. Нам дано tan θ=−34,
, так что θ
находится в квадранте II. Тангенс угла равен противолежащей стороне относительно прилежащей, а так как θ
находится во втором квадранте, соседняя сторона находится на оси x и является отрицательной. Используйте Теорему Пифагора , чтобы найти длину гипотенузы:
Используйте Теорему Пифагора , чтобы найти длину гипотенузы:
(−4)2+(3)2=c216+9=c225=c2c=5
Теперь мы можем нарисовать треугольник, подобный показанному на рис. [ссылка на сайт].
- Начнем с того, что напишем формулу двойного угла для синуса.
sin(2θ)=2 sin θ cos θ
Видим, что нужно найти sin θ
и cos θ.
По [ссылке] мы видим, что гипотенуза равна 5, значит sin θ=35,
и cos θ=-45.
Подставьте эти значения в уравнение и упростите.
Таким образом,
sin(2θ)=2(35)(−45)=−2425
- Запишите формулу косинуса двойного угла.
cos(2θ)=cos2θ−sin2θ
Снова подставьте значения синуса и косинуса в уравнение и упростите.
cos(2θ)=(−45)2−(35)2=1625−925=725
- Запишите формулу тангенса двойного угла.

тангенс(2θ)=2 тангенс θ1−тангенс2θ
В этой формуле нам нужен тангенс, который мы получили как tan θ=−34.
Подставьте это значение в уравнение и упростите.
тангенс(2θ)=2(-34)1-(-34)2=-321-916=-32(167)=-247
Учитывая sin α=58,
с θ
в квадранте I, найти cos(2α).
cos(2α)=732
Использование формулы двойного угла для косинуса без точных значений
Используйте формулу двойного угла для косинуса, чтобы записать cos(6x)
через cos(3x).
cos(6x)=cos(2(3x))=2cos2(3x)−1
Анализ
Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений. В нем подчеркивается, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.
Использование формул двойного угла для проверки подлинности
Установление тождеств с помощью формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для вывода формул суммы и разности. Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной.
Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной.
Использование формул двойного угла для проверки тождества
С помощью формул двойного угла проверьте следующее тождество:
1+sin(2θ)=(sin θ+cos θ)2
знак равенства и перепишите выражение, пока оно не совпадет с левой частью. 9Анализ
Этот процесс не сложен, если вспомнить формулу идеального квадрата из алгебры:
(a±b)2=a2±2ab+b2
, где a=sin θ
и b=cos θ.
Одним из условий успеха в математике является умение распознавать закономерности. Хотя термины или символы могут меняться, алгебра остается неизменной.
Проверить тождество: cos4θ−sin4θ=cos(2θ).
cos4θ−sin4θ=(cos2θ+sin2θ)(cos2θ−sin2θ)=cos(2θ)
Проверка тождества двойного угла для касательной
Подтверждение тождества:
tan(2θ)=2cot θ−tan θ
В этом случае мы будем работать с левой частью уравнения и упростим или перепишем, пока оно не будет равно правая часть уравнения.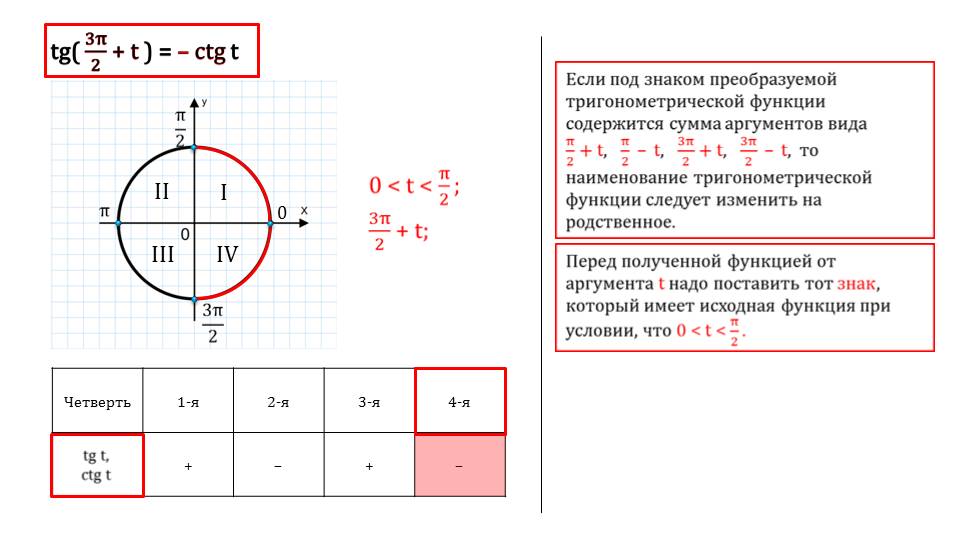
tan(2θ)=2 tan θ1−tan2θФормула двойного угла=2 tan θ(1tan θ)(1−tan2θ)(1tan θ) Умножить на член, который дает желаемый числитель.=21tan θ−tan2θ=2tan θ θ−tan θИспользовать взаимное тождество для 1tan θ.
Анализ
Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой частью. Однако, если бы мы выбрали для перезаписи левую часть, мы бы работали в обратном направлении, чтобы получить эквивалентность. Например, предположим, что мы хотели показать
2tan θ1−tan2θ=2cot θ−tan θ
Давайте работать с правой стороной.
2cot θ−tan θ=21tan θ−tan θ(tan θtan θ)=2 tan θ1tan θ(tan θ)−tan θ(tan θ)=2 tan θ1−tan2θ
При использовании тождеств для упрощения тригонометрического выражения или решения тригонометрического уравнения обычно существует несколько путей к желаемому результату. Не существует установленного правила относительно того, какой стороной следует манипулировать. Тем не менее, мы должны начать с руководящих принципов, изложенных ранее.
Проверить тождество: cos(2θ)cos θ=cos3θ−cos θ sin2θ.
cos(2θ)cos θ=(cos2θ−sin2θ)cos θ=cos3θ−cos θsin2θ
Использование формул сокращения для упрощения выражения
Формулы двойного угла можно использовать для получения формулы приведения , которые являются формулами, которые мы можем использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны в курсах математики более высокого уровня, в частности исчисления. Также называемые формулами уменьшения степени, включены три тождества, которые легко выводятся из формул двойного угла.
Мы можем использовать две из трех формул двойного угла для косинуса, чтобы вывести формулы приведения для синуса и косинуса. Начнем с cos(2θ)=1−2 sin2θ.
Решите для sin2θ:
cos(2θ)=1−2 sin2θ2 sin2θ=1−cos(2θ)sin2θ=1−cos(2θ)2
Далее используем формулу cos(2θ)=2 cos2θ−1.
Решите для cos2θ:
cos(2θ)= 2 cos2θ−11+cos(2θ)=2 cos2θ1+cos(2θ)2=cos2θ
Последняя формула приведения получается путем записи тангенса через синус и косинус:
tan2θ=sin2θcos2θ=1−cos(2θ)21+cos(2θ)2Подставить формулы редукции.=(1−cos(2θ)2)(21+cos(2θ))=1−cos(2θ)1+cos (2θ)
Формулы приведения
Формулы приведения резюмируются следующим образом:
Написание эквивалентного выражения, не содержащего степеней больше 1
Напишите эквивалентное выражение для cos4x
, которое не содержит степеней синуса или косинуса больше 1.
Мы дважды применим формулу редукции для косинуса.
cos4x=(cos2x)2=(1+cos(2x)2)2Подставьте формулу приведения вместо cos2x.=14(1+2cos(2x)+cos2(2x))=14+12 cos(2x)+14( 1+cos2(2x)2) Подставить формулу приведения вместо cos2x.=14+12 cos(2x)+18+18 cos(4x)=38+12 cos(2x)+18 cos(4x)
Анализ
Решение находится путем двойного использования формулы приведения, как уже отмечалось, и формулы полного квадрата из алгебры.
Использование формул уменьшения степени для доказательства тождества
Использование формул уменьшения степени для доказательства
sin3(2x)=[12 sin(2x)] [1−cos(4x)]
левая часть уравнения:
sin3(2x)=[sin(2x)][sin2(2x)]=sin(2x)[1−cos(4x)2]Подставьте формулу уменьшения мощности.=sin( 2x)(12)[1-cos(4x)]=12[sin(2x)][1-cos(4x)]
Анализ
Обратите внимание, что в этом примере мы заменили
1-cos(4x)2
на sin2(2x).
Формула гласит:
sin2θ=1−cos(2θ)2
Положим θ=2x,
, значит 2θ=4x.
Используйте формулы понижения мощности, чтобы доказать, что 10 cos4x=154+5 cos(2x)+54 cos(4x).
10cos4x=10(cos2x)2=10[1+cos(2x)2]2Подставьте формулу приведения вместо cos2x.=104[1+2cos(2x)+cos2(2x)]=104+102cos(2x)+104 (1+cos2(2x)2) Подставить формулу приведения вместо cos2x.=104+102cos(2x)+108+108cos(4x)=308+5cos(2x)+108cos(4x)=154+5cos(2x)+54cos (4x)
Использование формул половинного угла для нахождения точных значений
Следующим набором тождеств является набор формул половинного угла , которые могут быть получены из формул приведения и могут использоваться, когда у нас есть угол, который в два раза меньше специального угла. Если мы заменим θ
Если мы заменим θ
с α2,
Формула половинного угла для синуса находится путем упрощения уравнения и решения для sin(α2).
Обратите внимание, что формулам половинного угла предшествует a ±
9знак 0002. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором α2завершается.
Формула половинного угла для синуса получается следующим образом:
sin2θ=1−cos(2θ)2sin2(α2)=1−(cos2⋅α2)2=1−cos α2sin(α2)=±1−cos α2
Чтобы вывести формулу косинуса половины угла, мы имеем
cos2θ=1+cos(2θ)2cos2(α2)=1+cos(2⋅α2)2=1+cos α2cos(α2)=±1+cos α2
Для тождества касательной имеем
tan2θ=1−cos(2θ)1+cos(2θ)tan2(α2)=1−cos(2⋅α2)1+cos(2⋅α2)=1−cos α1+cos αtan(α2)=±1 −cos α1+cos α
Формулы полууглов
Формулы полууглов следующие: 1 -cos α1+cos α = sin α1+cos α = 1 -cos αsin α
Использование формулы половинного угла для нахождения точного значения функции синуса
Найдите sin(15°)
с помощью формулы половинного угла.
Так как 15°=30°2,
используем формулу половинного угла для синуса:
sin 30°2=1−cos30°2=1−322=2−322=2−34=2−32
Помните, что мы можем проверить ответ с помощью графического калькулятора.
Анализ
Обратите внимание, что мы использовали только положительный корень, потому что sin(15°)
является положительным.
Даны тангенс угла и квадрант, в котором находится угол, найти точные значения тригонометрических функций половины угла.
- Нарисуйте треугольник для представления данной информации.
- Определите правильную формулу половинного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Нахождение точных значений с помощью тождеств половин углов
Учитывая, что tan α=815
и α
лежит в квадранте III, найдите точное значение следующего:
- грех(α2)
- cos(α2)
- загар(α2)
Используя данную информацию, мы можем нарисовать треугольник, показанный на [ссылка]. Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sin α=−817
Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sin α=−817
и cos α=−1517.
- Прежде чем мы начнем, мы должны помнить, что если
α
находится в квадранте III, затем
180°<α<270°,, поэтому
180°2<α2<270°2.Это означает, что клеммная сторона
α2находится в квадранте II, так как
90°<α2<135°.Чтобы найти sin α2,
начнем с записи формулы половинного угла для синуса. Затем подставляем найденное значение косинуса из треугольника в [ссылка] и упрощаем.
sin α2=±1−cos α2=±1−(−1517)2=±32172=±3217⋅12=±1617=±417=41717
Выбираем положительное значение sin α2
, потому что угол заканчивается в квадранте II, а синус положителен в квадранте II.
- Найти
cos α2,
запишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника в [ссылка], и упростим.

cos α2=±1+cos α2=±1+(−1517)2=±2172=±217⋅12=±117=−1717
Выбираем отрицательное значение cos α2
, потому что угол находится в квадранте II, потому что косинус отрицателен в квадранте II.
- Найти
тангенс α2,
пишем формулу тангенса половины угла. Снова подставляем найденное значение косинуса из треугольника в [ссылка] и упрощаем.
тангенс α2=±1−cos α1+cos α=±1−(−1517)1+(−1517)=±3217217=±322=−16=−4
Выбираем отрицательное значение tan α2
потому что α2
лежит в квадранте II, а тангенс отрицателен в квадранте II.
Учитывая, что sin α=−45
и α
лежит в квадранте IV, найдите точное значение cos (α2).
−25
Нахождение измерения половинного угла
Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа построена для соревнований высокого уровня с углом θ
, образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если tan θ=53
Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если tan θ=53
для соревнований более высокого уровня, каково измерение угла для соревнований новичков?
Поскольку угол для начинающих соревнований измеряет половину крутизны угла для соревнований высокого уровня, а tan θ=53
для высоких соревнований, мы можем найти cos θ
из прямоугольного треугольника и теоремы Пифагора, так что мы можно использовать тождества половинного угла. См. [ссылка].
32+52=34c=34
Мы видим, что cos θ=334=33434.
Мы можем использовать формулу половинного угла для тангенса: tan θ2=1−cos θ1+cos θ.
Так как tan θ
находится в первом квадранте, поэтому tan θ2.
tan θ2=1−334341+33434=34−3343434+33434=34−33434+334≈0,57
Мы можем взять арктангенс, чтобы найти угол: tan−1(0,57)≈29,7°.
Таким образом, угол рампы для соревнований новичков составляет ≈29,7°.
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с формулами двойного угла, половинного угла и сокращения.
- Двухугольные удостоверения
- Полуугольные тождества
Ключевые уравнения
| Формулы двойного угла | sin(2θ)=2sin θ cos θcos(2θ)=cos2θ−sin2θ=1−2sin2θ=2cos2θ−1tan(2θ)=2tan θ1−tan2θ |
| Формулы приведения | sin2θ=1−cos(2θ)2cos2θ=1+cos(2θ)2tan2θ=1−cos(2θ)1+cos(2θ) |
| Формулы полууглов | sin α2=±1−cos α2cos α2=±1+cos α2tan α2=±1−cos α1+cos α=sin α1+cos α=1−cos αsin α |
Ключевые понятия
- Тождества двойного угла выводятся из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса. См. [ссылка], [ссылка], [ссылка] и [ссылка].
- Формулы редукции особенно полезны в математических вычислениях, поскольку они позволяют уменьшить мощность тригонометрического члена.
 См. [ссылка] и [ссылка].
См. [ссылка] и [ссылка]. - Формулы половинного угла позволяют находить значения тригонометрических функций, содержащих половинные углы, независимо от того, известен исходный угол или нет. См. [ссылка], [ссылка] и [ссылка].
Секционные упражнения
Устный
Объясните, как определить редукционные тождества из тождества двойного угла cos(2x)=cos2x−sin2x.
Используйте тождества Пифагора и изолируйте квадрат члена.
Объясните, как определить формулу двойного угла для tan(2x)
, используя формулы двойного угла для cos(2x)
и sin(2x).
Мы можем определить формулу половинного угла для tan(x2)=1−cos x1+cos x
, разделив формулу для sin(x2) на
by cos(x2).
Объясните, как определить две формулы для tan(x2)
, которые не содержат квадратных корней.
1−cos xsin x,sin x1+cos x,
, умножая верх и низ на 1−cos x
и 1+cos x,
соответственно.
Для формулы половинного угла, приведенной в предыдущем упражнении для tan(x2),
объясните, почему деление на 0 не имеет значения. (Подсказка: проверьте значения cos x
, необходимые для того, чтобы знаменатель был равен 0.)
Алгебраический
Для следующих упражнений найдите точные значения a) sin(2x),
б) cos(2x),
и в) загар(2x)
без решения x.
Если sin x=18,
и x
находится в I квадранте.
Если cos x=23,
и x
находится в квадранте I.
Если cos x=−12,
и x
находится в квадранте III.
а) 32
б) −12
в) −3
Если tan x=−8,
и x
находится в квадранте IV.
В следующих упражнениях найдите значения шести тригонометрических функций, если выполнены указанные условия.
cos(2θ)=35
и 90°≤θ≤180°
cos θ=−255,sin θ=55,tan θ=−12,csc θ=5,sec θ=−52,cot θ= −2
cos(2θ)=12
и 180°≤θ≤270°
Для следующих упражнений упростите до одного тригонометрического выражения.
2 sin(π4) 2 cos(π4)
2 sin(π2)
4 sin(π8) cos(π8)
Для следующих упражнений найдите точное значение, используя формулы половинного угла.
sin(π8)
2−22
соз(-11π12)
sin(11π12)
2−32
потому что (7π8)
тан(5π12)
2+3
тангенс (−3π12)
тангенс(−3π8)
−1−2
Для следующих упражнений найдите точные значения a) sin(x2),
б) cos(x2),
и в) загар(х2)
без решения для x,
, когда 0°≤x≤360°.
Если tan x=−43,
и x
находится в квадранте IV.
Если sin x=−1213,
и x
находится в квадранте III.
а) 31313
б) −21313
в) −32
Если csc x=7,
и x
находится в квадранте II.
Если сек x=−4,
и x
находится в квадранте II.
а) 104
б) 64
в) 153
В следующих упражнениях используйте [ссылка] для нахождения требуемых половинных и двойных углов.
Найти sin(2θ),cos(2θ),
и tan(2θ).
Найти sin(2α),cos(2α),
и tan(2α).
120169,–119169,–120119
Найти sin(θ2),cos(θ2),
и tan(θ2).
Найти sin(α2),cos(α2),
и tan(α2).
21313,31313,23
В следующих упражнениях упростите каждое выражение. Не оценивайте.
cos2(28°)−sin2(28°)
2cos2(37°)−1
cos(74°)
1−2 sin2(17°)
cos2(9x)−sin2(9x)
cos(18x)
4 sin(8x) cos(8x)
6 sin(5x) cos(5x)
3sin(10x)
Для следующих упражнений докажите данное тождество.
(sin t−cos t)2=1−sin(2t)
sin(2x)=−2 sin(−x) cos(−x)
−2 sin(−x)cos(−x)=−2(−sin(x)cos(x))=sin(2x )
детская кроватка x−tan x=2 кроватка(2x)
sin(2θ)1+cos(2θ)tan2θ=tan3 θ
sin(2θ)1+cos(2θ)tan2θ=2sin(θ)cos(θ)1+cos2θ−sin2θtan2θ=2sin(θ)cos(θ) )2cos2θtan2θ=sin(θ)cos θtan2θ=cot(θ)tan2θ=tan3 θ
Для следующих упражнений перепишите выражение с показателем степени не выше 1.
cos2(5x)
cos2(6x)
1+cos(12x)2
sin4(8x)
sin4(3x)
3+cos(12x)−4cos(6x)8
cos2x sin4x
cos4x sin2x
2+cos(2x)−2cos(4x)−cos(6x)32
загар2x sin2x
Технология
Для следующих упражнений уменьшите уравнения до степени единицы, а затем проверьте ответ графически.
tan4x
3+cos(4x)−4cos(2x)3+cos(4x)+4cos(2x)
sin2(2x)
sin2x cos2x
1−cos(4x)8
tan2x sin x
tan4x cos2x
3+cos(4x)−4cos(2x)4(cos(2x)+1)
cos2x sin(2x)
cos2(2x)sin x
(1+cos(4x))sin x2
тангенс2(х2) sin х
Для следующих упражнений алгебраически найдите эквивалентную функцию только с точки зрения sin x
и/или cos x,
, а затем проверьте ответ, построив график обеих функций.
sin(4x)
4sin xcos x(cos2x−sin2x)
cos(4x)
Расширения
Для следующих упражнений докажите тождества.
sin(2x)=2 tan x1+tan2x
2tan x1+tan2x=2sin xcos x1+sin2xcos2x=2sin xcos xcos2x+sin2xcos2x=2sin xcos x=s.cos2x1=2sin0003
cos(2α)=1−tan2α1+tan2α
tan(2x)=2 sin x cos x2cos2x−1
2sin xcos x2cos2x−1=sin(2x)cos(2x)=tan(2x)
(sin2x−1)2=cos(2x)+sin4x
sin(3x)=3 sin x cos2x−sin3x sin3x+2sin xcos2x=3sin xcos2x−sin3x
cos(3x)=cos3x−3sin2x cos x
1+cos(2t)sin(2t)−cos t=2 cos t2 sin t−1 )=2cost2sint−1
sin(16x)=16 sin x cos x cos(2x)cos(4x)cos(8x)
cos(16x)=(cos2(4x)−sin2(4x)−sin(8x))(cos2(4x)−sin2(4x)+sin(8x))
(cos2(4x)−sin2(4x) −sin(8x))(cos2(4x)−sin2(4x)+sin(8x))==(cos(8x)−sin(8x))(cos(8x)+sin(8x))=cos2(8x )−sin2(8x)=cos(16x)
Глоссарий
- формулы двойного угла
- тождеств, полученных из формул суммы синуса, косинуса и тангенса, в которых углы равны
- формулы половинного угла
- тождества, полученные из формул приведения и используемые для определения значений половинных углов тригонометрических функций
- формулы приведения 91 130 тождеств, полученных из формул двойного угла и используемых для уменьшения степени тригонометрической функции 91 131
Эта работа находится под лицензией Creative Commons Attribution 4.
 0 International License.
0 International License.Вы также можете бесплатно скачать на http://cnx.org/contents/[email protected]
Атрибуция:
- По вопросам, касающимся этой лицензии, обращайтесь по адресу [email protected].
- Если вы используете данный учебник в качестве библиографической ссылки, то цитировать его следует следующим образом: Колледж OpenStax, алгебра и тригонометрия. OpenStax CNX. http://cnx.org/contents/[email protected].
- Если вы распространяете этот учебник в печатном формате, вы должны указать на каждой физической странице следующее указание авторства: «Скачать бесплатно на http://cnx.org/contents/[email protected].»
- Если вы распространяете часть этого учебника, вы должны сохранять при каждом просмотре страницы в цифровом формате (включая, помимо прочего, EPUB, PDF и HTML) и на каждой физической печатной странице следующее указание авторства:
«Загрузите бесплатно по адресу http://cnx.
 org/contents/[email protected]».
org/contents/[email protected]».
Упрощение тригонометрических выражений
Для упрощения тригонометрических выражений необходимо знать тригонометрические тождества и алгебраические правила. Полезно следовать некоторым общим правилам:
- Если тригонометрические функции содержат разные углы, мы пытаемся свести их к функциям только одного угла, используя, например, кофункции и тождества редукции или формулы двойного угла.
- Если тригонометрическое выражение содержит большое количество функций, необходимо сократить количество функций до минимума. Для этого используются тождества приведения, тригонометрические тождества Пифагора и другие формулы.
- Если нам нужно уменьшить мощность компонента в тригонометрическом выражении, мы применяем тождества половинного угла или формулы уменьшения мощности. Только надо помнить, что при уменьшении мощности в 2 раза аргумент удваивается.
Используя эти тождества и формулы, мы можем преобразовать любое тригонометрическое выражение в рациональное выражение, содержащее только одну функцию с одним аргументом.
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Упростите тригонометрическое выражение:
\[\frac{{\sin 6\alpha}}{{\sin 2\alpha}} + \frac{{\cos \left( {6\alpha — \ pi } \right)}}{{\cos 2\alpha }}.\]
Пример 2
Упростим тригонометрическое выражение:
\[\frac{{1 — \cos \left( {8\alpha — 3\pi } \right)}}{{\tan 2\alpha — \cot 2\alpha }}.\]
Пример 3
Упростите тригонометрическое выражение:
\[\frac{{1 + \cot 2\alpha \cot \alpha }}{{\tan \alpha + \cot \alpha }}.\]
Пример 4
Упростите тригонометрическое выражение:
\[\frac{{1 — \tan \left( {\pi — 2\alpha } \right)\tan \alpha}}{{\tan \left( {\frac{{ 3\pi }}{2} — \alpha } \right) + \tan \alpha }}.\]
Пример 5 94}2\alpha .\]
Пример 6
Упрощение:
\[\frac{{\sin \left( {4\alpha + \frac{{5\pi}}}{2}} \right) }}{{1 + \cos \left( {4\alpha — \frac{{3\pi }}{2}} \right)}}.\]
Пример 7
Упрощение:
\[\ frac {{\ tan \ alpha + \ tan \ beta}} {\ tan \ left ( {\ alpha + \ beta} \ right)}} + \ frac {{\ tan \ alpha — \ tan \ beta}} { {\tan \left( {\alpha — \beta} \right)}}. \]
\]
Пример 8
Упрощение:
\[\frac{{\sin \left({\alpha — \beta} \ справа) — \ грех \ влево ( {\ бета — \ альфа} \ справа)}} {{\ соз \ влево ( {\ альфа — \ бета} \ справа) + \ соз \ влево ( {\ бета — \ альфа} \справа)}}.\]
Пример 1.
Упростим тригонометрическое выражение: \pi } \right)}}{{\cos 2\alpha}}.\]
Раствор.
Функция косинуса четная, поэтому \(\cos \left( {6\alpha — \pi } \right) = \cos \left( {\pi — 6\alpha } \right).\) Используя тождество редукции , у нас есть
\[A = \frac{{\sin 6\alpha}}{{\sin 2\alpha}} + \frac{{\cos\left({6\alpha — \pi} \right)}}{{ \cos 2\alpha}} = \frac{{\sin 6\alpha}}{{\sin 2\alpha}} + \frac{{\cos\left({\pi — 6\alpha} \right)} }{{\cos 2\alpha}} = \frac{{\sin 6\alpha}}{{\sin 2\alpha}} — \frac{{\cos 6\alpha}}}{{\cos 2\alpha }}.\]
Привести к общему знаменателю и применить формулу сложения синуса:
\[A = \frac{{\sin 6\alpha}}{{\sin 2\alpha}} — \frac{{\cos 6\alpha}}{{\cos 2\alpha}} = \frac{ {\ грех 6 \ альфа \ соз 2 \ альфа — \ соз 6 \ альфа \ грех 2 \ альфа}} {{\ грех 2 \ альфа \ соз 2 \ альфа}} = \ гидроразрыва {{\ грех \ влево ( {6 \alpha — 2\alpha} \right)}}{{\sin 2\alpha \cos 2\alpha}} = \frac{{\sin 4\alpha}}{{\sin 2\alpha \cos 2\alpha }}. \]
\]
Из двухугольного тождества получаем
\[A = \frac{{\sin 4\alpha}}}{{\sin 2\alpha \cos 2\alpha}} = \frac{{2\cancel{{\sin 2\alpha}}}\cancel{ {\cos 2\alpha}}}}{{\cancel{{\sin 2\alpha}}\cancel{{\cos 2\alpha}}}} = 2.\]
Пример 2.
Упростим тригонометрическое выражение:
\[\frac{{1 — \cos \left( {8\alpha — 3\pi } \right)}}{{\tan 2\alpha — \cot 2\альфа }}.\]
Раствор.
Напомним, что косинус — четная периодическая функция с периодом \(2\pi.\). Следовательно,
\[\cos \left( {8\alpha — 3\pi } \right) = \cos \left( {8\alpha — \pi } \right) = \cos \left( {\pi — 8\alpha } \справа).\]
Используя формулу приведения для косинуса и выражая тангенс и котангенс через синус и косинус, мы имеем 92}\alpha } \right)}}}}{{\cot \alpha }}}} = \frac{{\cot \alpha}}{2}.\]
Пример 4.
Упростим тригонометрическое выражение:
\[\frac{{1 — \tan \left( {\pi — 2\alpha } \right)\tan \alpha}}{{\tan \left( {\ frac {{3 \ pi}} {2} — \ alpha } \ right) + \ tan \ alpha }}. 2}\alpha}}.\] 92}4\альфа = \cos 8\альфа .\]
2}\alpha}}.\] 92}4\альфа = \cos 8\альфа .\]
Пример 6.
Упрощение:
\[\frac{{\sin \left( {4\alpha + \frac{{5\pi }}{2}} \right)}}{{1 + \cos \left( {4\alpha — \frac{{3\pi }}{2}} \right)}}.\]
Раствор.
Используя периодичность триггерных функций, выразим их как функции одного и того же угла:
\[\sin \left( {4\alpha + \frac{{5\pi }}{2}} \right) = \sin \left( {4\alpha + \underbrace {2\pi + \frac{ \pi }{2}}_{\frac{{5\pi}}{2}}} \right) = \sin \left( {4\alpha + \frac{\pi }{2}} \right) ,\]
\[\cos \left( {4\alpha — \frac{{3\pi }}{2}} \right) = \cos \left( {4\alpha — \frac{{3\pi }}{ 2} + 2\pi } \right) = \cos\left( {4\alpha + \frac{\pi }{2}} \right).\]
Тогда мы можем написать:
\[A = \frac{{\sin\left( {4\alpha + \frac{{5\pi}}}{2}} \right)}}{{1 + \cos \left( {4\alpha — \frac{{3\pi}}{2}} \right)}} = \frac{{\sin\left( {4\alpha + \frac{\pi}}{2}} \right)}}{ {1 + \cos\left( {4\alpha + \frac{\pi }{2}} \right)}}.\]
Теперь применить замену касательной половины угла: 92}\left( {2\alpha + \frac{\pi }{4}} \right)} \right)}}}} = \tan \left( {2\alpha + \frac{\pi }{4 }} \справа). \]
\]
Пример 7.
Упрощение:
\[\frac{{\tan \alpha + \tan \beta}}{{\tan \left( {\alpha + \beta} \right)}} + \frac{ {\ загар \ альфа — \ загар \ бета}} {\ загар \ влево ( {\ альфа — \ бета} \ вправо)}}. \]
Раствор.
Вспомните формулы сложения и вычитания для тангенса:
\[\tan \left( {\alpha + \beta} \right) = \frac{{\tan \alpha + \tan \beta}}{{1 — \tan \alpha \tan \beta}},\ ]
\[\tan \left( {\alpha — \beta} \right) = \frac{{\tan \alpha — \tan \beta}}{{1 + \tan \alpha \tan \beta}}.\ ]
Тогда имеем:
\[\ frac {{\ tan \ alpha + \ tan \ beta}} {\ tan \left( {\ alpha + \ beta } \right)}} + \ frac {{\ tan \ alpha — \ tan \ бета}}{{\tan \left({\alpha — \beta} \right)}} = \frac{{\cancel{{\tan \alpha + \tan\beta}}}}{{\frac{{ \cancel{{\tan \alpha + \tan \beta}}}}{{1 — \tan \alpha \tan \beta}}}} + \frac{{\cancel{{\tan \alpha — \tan \ бета }}}}{{\ frac {{\cancel{{\tan \alpha — \tan \beta}}}}{{1 + \tan \alpha \tan \beta}}}} = 1 — \cancel{ {\ tan \ alpha \ tan \ beta}} + 1 + \ cancel {{\ tan \ alpha \ tan \ beta}} = 2. \]
\]
Пример 8.
Упрощение:
\[\frac{{\sin \left({\alpha — \beta} \right) — \sin \left({\beta — \alpha} \right)}}{ {\ cos \ left ( {\ alpha — \ beta } \ right) + \ cos \ left ( {\ beta — \ alpha } \ right)}}. \]
Раствор.
Используя тождество суммы и произведения, числитель можно записать как
\[\ sin \left( {\alpha — \beta} \right) — \sin \left({\beta — \alpha} \right) = 2\cos \frac{{\cancel{\alpha} — \ отмена {\ бета} + \ отмена {\ бета} — \ отмена {\ альфа}}} {2} \ грех \ гидроразрыва {{\ альфа — \ бета — \ влево ({\ бета — \ альфа} \ вправо)} }{2} = 2\cos 0\sin \left( {\alpha — \beta} \right) = 2\sin \left({\alpha — \beta} \right).\]
Аналогично знаменатель представляется в виде
\[\cos \left({\alpha — \beta} \right) + \cos \left({\beta — \alpha} \right) = 2\cos \frac{{\cancel{\alpha} — \ отмена {\ бета} + \ отмена {\ бета} — \ отмена {\ альфа}}} {2} \ соз \ гидроразрыва {{\ альфа — \ бета — \ влево ({\ бета — \ альфа} \ вправо)} }{2} = 2\cos 0\cos \left( {\alpha — \beta} \right) = 2\cos \left({\alpha — \beta} \right). \]
\]
Следовательно,
\[\ frac {{\ грех \ влево ( {\ альфа — \ бета} \ вправо) — \ грех \ влево ( {\ бета — \ альфа} \ вправо)}} {{\ соз \ влево ( {\ альфа — \beta} \right) + \cos \left( {\beta — \alpha} \right)}} = \frac{{\cancel{2}\sin\left({\alpha — \beta} \right) }}{{\cancel{2}\cos\left({\alpha — \beta} \right)}} = \tan \left({\alpha — \beta} \right).\]
Дополнительные проблемы см. на стр. 2.
тригонометрических идентификаторов снижения мощности | Brilliant Math & Science Wiki
Содержание
- Личности
- Формулы половинного угла
- Примеры
Идентификаторы снижения мощности 92 \тета.\ _\квадрат \end{выровнено}21+cos(2θ)=21+cos2θ−sin2θ=2(sin2θ+cos2θ)+cos2θ−sin2θ=22cos2θ=cos2θ. □
Используя формулы приведения степени, мы можем вывести следующие формулы половинного угла :
Формулы половинного угла
Для любого угла θ\thetaθ,
cos(θ2)=±1+cosθ2sin(θ2)=±1−cosθ2tan(θ2)=±1−cosθ1+cosθ.
\begin{выровнено} \cos\left(\frac{\theta}{2} \right) &= \pm \sqrt{ \frac{1 + \cos\theta}{2} }\\ \sin \left( \frac{\theta}{2} \right) &= \pm \sqrt{ \frac{1 — \cos\theta}{2} }\\ \tan \left( \frac{\theta}{2} \right) &= \pm \sqrt{ \frac{1 — \cos\theta}{1 + \cos\theta}}. \end{align}cos(2θ)sin(2θ)tan(2θ)=±21+cosθ=±21−cosθ=±1+cosθ1−cosθ. 9{2}(2\тета)}{4}\\ &=\frac{1+2\cos(2\theta)+\frac{1+\cos(4\theta)}{2}}{4}\\ &=\frac{2+4\cos(2\theta)+1+\cos(4\theta)}{8}\\ &=\frac{1}{8}\big(\cos(4\theta)+4\cos(2\theta)+3\big).\ _\square \end{выровнено}cos4θ=(cos2θ)2=(21+cos(2θ))=41+2cos(2θ)+cos2(2θ)=41+2cos(2θ)+21+cos(4θ) =82+4cos(2θ)+1+cos(4θ)=81(cos(4θ)+4cos(2θ)+3). □
Используйте формулы половинного угла для вычисления cos(π12)\cos\left(\frac{\pi}{12} \right) cos(12π) и sin(π12).\sin\left( \frac{ \pi}{12} \right).sin(12π).
В формулах cos(θ2)±1+cosθ2\cos \left( \frac{\theta}{2} \right) \pm \sqrt{ \frac{1 + \cos\theta}{2 } }cos(2θ)±21+cosθи sin(θ2)±1−cosθ2,\sin\left(\frac{\theta}{2} \right) \pm \sqrt{ \frac {1 — \cos\theta}{2} },sin(2θ)±21−cosθ, мы заменяем θ\thetaθ на π6:\frac{\pi}{6}:6π:
cos(π12)=±1+cos(π6)2=±2+32\begin{выровнено} \cos\left(\frac{\pi}{12}\right) &=\pm\sqrt{\frac{1+\cos\left(\frac{\pi}{6}\right)}{2} } \\ & =\pm\frac{\sqrt{2+\sqrt{3}}}}{2} \end{выровнено}cos(12π)=±21+cos(6π)=±22+3
sin(π12)=±1−cos(π6)2=±2−32.
\begin{выровнено} \sin\left(\frac{\pi}{12}\right) &=\pm\sqrt{\frac{1-\cos\left(\frac{\pi}{6}\right)}{2} } \\ &=\pm\frac{\sqrt{2-\sqrt{3}}}{2}. \end{выровнено}sin(12π)=±21−cos(6π)=±22−3.
Поскольку π12\frac{\pi}{12}12π лежит в первом квадранте, мы присваиваем положительные значения sin(π12)\sin\left(\frac{\pi}{12}\right)sin(12π ) и cos(π12)\cos\left(\frac{\pi}{12}\right)cos(12π).
Следовательно, cos(π12)=2+32\cos\left(\frac{\pi}{12}\right)=\frac{\sqrt{2+\sqrt{3}}}{2}cos(12π )=22+3 и sin(π12)=2−32\sin\left(\frac{\pi}{12}\right)=\frac{\sqrt{2-\sqrt{3} }}{2}sin(12π)=22−3. □_\квадрат□
Подтвердить личность
tan(θ2)=1−cosθsinθ,tan(θ2)=sinθ1+cosθ.\tan \left(\frac{\theta}{2} \right) = \frac{ 1-\cos\theta}{\sin\theta},\quad\tan\left(\frac{\theta}{2}\right) = \frac{\sin\theta}{1+\cos\theta} .tan(2θ)=sinθ1−cosθ,tan(2θ)=1+cosθsinθ.
У нас есть
тангенс(θ2)=±1−cosθ1+cosθ.\begin{выровнено} \tan \left( \frac{\theta}{2} \right) &= \pm \sqrt{ \frac{1 — \cos\theta}{1 + \cos\theta}}.
\end{align}tan(2θ)=±1+cosθ1−cosθ. 92} }\\ &=\frac{\sin\theta}{1+\cos\theta}.\ _\квадрат \end{align}tan(2θ)=±(1+cosθ)21−cos2θ=±(1+cosθ)2sin2θ=1+cosθsinθ. □
Цитировать как: Тригонометрические тождества понижения мощности. Brilliant.org . Извлекаются из https://brilliant.org/wiki/trigonometric-power-reduction-identities/
Формула редукции — Что такое формула редукции? Примеры
Формула приведения часто используется при интегрировании для вычисления интегралов более высокого порядка. Работать с выражениями более высокой степени долго и утомительно, и здесь формулы приведения даны в виде простых выражений со степенью n для решения этих выражений более высокой степени. Эти формулы приведения были получены из базовых формул интегрирования и работают по тем же правилам интегрирования. 9{2}(2 x)+1 / 2 \ln \sec (2 x)+C\)
Часто задаваемые вопросы о формуле приведения
Что такое формула приведения?
Формула приведения часто используется при интегрировании для вычисления интегралов более высокого порядка. Работать с выражениями более высокой степени долго и утомительно, и здесь формулы приведения даны в виде простых выражений со степенью n для решения этих выражений более высокой степени. Следующие формулы приведения полезны для работы с выражениями более высокой степени, включающими алгебраические переменные, функции тригонометрии, логарифмические функции. Формулы приведения представлены здесь в виде набора из четырех формул.
Работать с выражениями более высокой степени долго и утомительно, и здесь формулы приведения даны в виде простых выражений со степенью n для решения этих выражений более высокой степени. Следующие формулы приведения полезны для работы с выражениями более высокой степени, включающими алгебраические переменные, функции тригонометрии, логарифмические функции. Формулы приведения представлены здесь в виде набора из четырех формул.
Какова цель формулы приведения?
Формула приведения используется, когда данный интеграл нельзя вычислить иначе. Повторное применение формулы редукции помогает нам вычислить данный интеграл.
Что такое формула приведения в тригонометрии?
Следующие формулы приведения полезны для работы с выражениями более высокой степени, включающими алгебраические переменные, тригонометрические функции, логарифмические функции. Любая тригонометрическая функция, аргумент которой равен 9{n — 2}x.dx\)
Проверка тригонометрических тождеств: правила и методы
Тригонометрические тождества могут иметь различные формы. Мы уже видели различные типы стандартных тождеств, такие как формулы двойного угла, сумма углов, разность углов, взаимные тождества и т. д. Это стандартные тождества, которые составляют основу для других тождеств, которые выводятся из них. Эти идентичности, которые можно разбить на фундаментальные идентичности, часто называют вторичными идентичностями.
Мы уже видели различные типы стандартных тождеств, такие как формулы двойного угла, сумма углов, разность углов, взаимные тождества и т. д. Это стандартные тождества, которые составляют основу для других тождеств, которые выводятся из них. Эти идентичности, которые можно разбить на фундаментальные идентичности, часто называют вторичными идентичностями.
На самом деле огромное количество идентичностей может быть сформировано из фундаментальных идентичностей. Чтобы проверить такие тождества, мы используем тот же тип процедуры, что и для решения различных уравнений, т. е. мы решаем для общего тождества.
Правила проверки тригонометрических тождествЕсли существует тождество, состоящее из различных тригонометрических функций, например, тождество, состоящее из тангенса и синуса, попытайтесь их разделить.
Попробуйте получить тангенс с одной стороны и синус с другой стороны уравнения, это облегчает применение основных тождеств.

Теперь самое главное — знать, какую фундаментальную идентичность нужно применить.
Преобразование уравнения в ту же функцию, т. е., например, преобразование всех тангенсов в синус или всех синусов в тангенсы.
После выполнения всех вышеперечисленных шагов, если правая часть (RHS) уравнения равна левой части (LHS), то тождество верно:
Как доказать тригонометрическое тождество Алгебраически?
Мы можем доказать тригонометрические тождества алгебраически, решая по отдельности левое и правое уравнения. Здесь сначала мы решаем комплексную часть уравнения и проверяем, равны ли как левая, так и правая стороны. Давайте рассмотрим несколько примеров.
Убедитесь, что это непротиворечивое удостоверение.
Решение:
Шаг 1: Складывая обе части уравнения, получаем
Шаг 2: Можно видеть, что это фундаментальное тождество, равное
Шаг 3: Подставляя это тождество, мы получаем
Шаг 4: Теперь мы будем использовать взаимное тождество для косеканса и возведения в квадрат обеих сторон, мы получим
Шаг 85: Подстановка2 приведенное выше тождество, мы получаем
Шаг 6: Мы уже знаем, что , и после возведения его в квадрат получается вышеуказанный шаг.
Следовательно, . Таким образом, личность подтверждается.
Проверьте удостоверение, где определено в соответствующем домене.
Решение:
Левая часть уравнения кажется немного сложной по сравнению с правой частью уравнения. Всегда проще упростить более сложную часть уравнения. Итак, давайте упростим левое положение, чтобы получить правое.
Шаг 1: Написание знаменателя отдельно, мы получаем
LHS =
Шаг 2: , используя взаимную идентичность,
Мы получаем
LHS =
9000 2LHS =
Следовательно, мы можем видеть, что .
Таким образом, тождество доказано.
Когда тригонометрическая идентичность недействительна?
Тригонометрическое тождество истинно тогда и только тогда, когда оно удовлетворяет всем значениям, для которых определена функция. Чтобы продемонстрировать это, рассмотрим тождество
Это тождество не выполняется для всех значений x в области синуса и косинуса. Это верно только для определенных значений x. Чтобы доказать, что это тождество ложно, можно алгебраически показать, что оно неверно, или привести контрпример. Здесь один контрпример
Это верно только для определенных значений x. Чтобы доказать, что это тождество ложно, можно алгебраически показать, что оно неверно, или привести контрпример. Здесь один контрпример
Где это можно увидеть.
До сих пор мы видели, как тригонометрическое тождество может быть доказано алгебраически с использованием фундаментальных тождеств. Важно отметить, что некоторые тождества могут казаться истинными, но на самом деле быть ложными. Это связано с тем, что одна функция не определена для определенного значения в домене, в то время как другая функция определена. В этом случае, когда мы делим на что-то, знаменатель может стремиться к 0, и это тождество будет ложным. Это редкий сценарий, но об этом следует знать.
Алгебраическое решение тождества — не единственный способ доказать это, альтернативный способ — графическое доказательство, давайте взглянем на него.
Как графически доказать тригонометрическое тождество?
Для графического подтверждения идентичности мы проверяем отдельно левую и правую стороны. Сначала строится график LHS, затем строится график RHS. После изучения графиков, если графики идентичны, т. е. абсолютно одинаковы для каждого значения в своей области, то мы говорим, что . Основным недостатком использования этого метода является то, что могут быть доказаны только простые тождества. Тождества с несколькими и более высокими степенями может быть очень трудно изобразить на графике. По этой причине алгебраический метод предпочтительнее этого. Давайте докажем тождество, чтобы понять этот метод.
Сначала строится график LHS, затем строится график RHS. После изучения графиков, если графики идентичны, т. е. абсолютно одинаковы для каждого значения в своей области, то мы говорим, что . Основным недостатком использования этого метода является то, что могут быть доказаны только простые тождества. Тождества с несколькими и более высокими степенями может быть очень трудно изобразить на графике. По этой причине алгебраический метод предпочтительнее этого. Давайте докажем тождество, чтобы понять этот метод.
Докажите, что .
Решение:
Шаг 1: Постройте график LHS, здесь это sinx, и его график выглядит так:
График y=sinx, StudySmarter Originals
Шаг 2: 90 график зависимости от x, который выглядит так:
График обратной величины cosecx, StudySmarter Originals
Можно видеть, что приведенные выше графики точно такие же, и, следовательно, мы делаем вывод, что .
Примеры проверки тригонометрических тождеств
Докажите, что это правильное тригонометрическое тождество.
Решение:
Шаг 1: В этом конкретном примере LHS кажется более сложным. Следовательно, мы попытаемся упростить LHS, чтобы получить RHS.
Шаг 2: Термин также может быть записан как и теперь он может быть записан как произведение двух терминов с использованием алгебраического тождества . Следовательно, мы имеем:
Шаг 3: Теперь мы можем применить тождество Пифагора, ,
Шаг 4: Применяя формулу половинного угла, получаем
, что и требуется доказать.
Таким образом, .
Действительно ли тригонометрическое тождество?
Решение:
Шаг 1: Левая сторона кажется более сложной, чем правая, поэтому давайте упростим левую сторону и проверим, достигаем ли мы правой стороны или нет.
Шаг 2: Можно видеть, что LHS можно упростить, используя алгебраическое тождество.
Применяя это тождество соответственно, мы получаем
Шаг 3: Теперь, применяя пифагорейское тождество для синуса и косинуса, мы получаем
, которое нельзя упростить дальше.
Можно заметить, что для каждого значения x. Но чтобы тождество было действительным, оно должно удовлетворять каждому значению, для которого определена функция.
Таким образом, данное тригонометрическое тождество неверно.
Проверка тригонометрических тождеств — основные выводы
- Тригонометрическое тождество истинно тогда и только тогда, когда оно удовлетворяет всем значениям, для которых определена область определения.
- Если тождество верно только для определенных значений, то эти значения называются решениями этого уравнения.
- Тригонометрическое тождество можно доказать двумя способами: алгебраически и графически.
- Чтобы доказать тождество алгебраически, упростите одну из сторон тождества, сведя ее к более простым терминам с помощью фундаментальных тождеств.


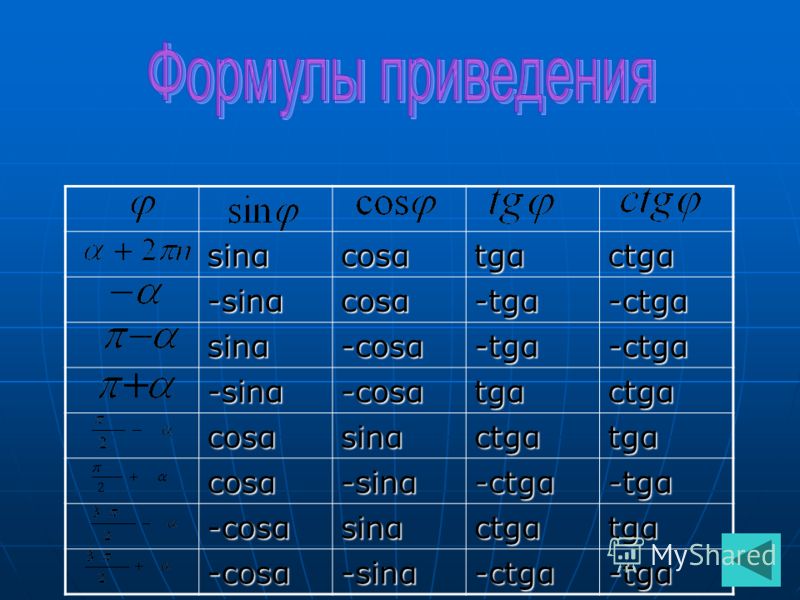





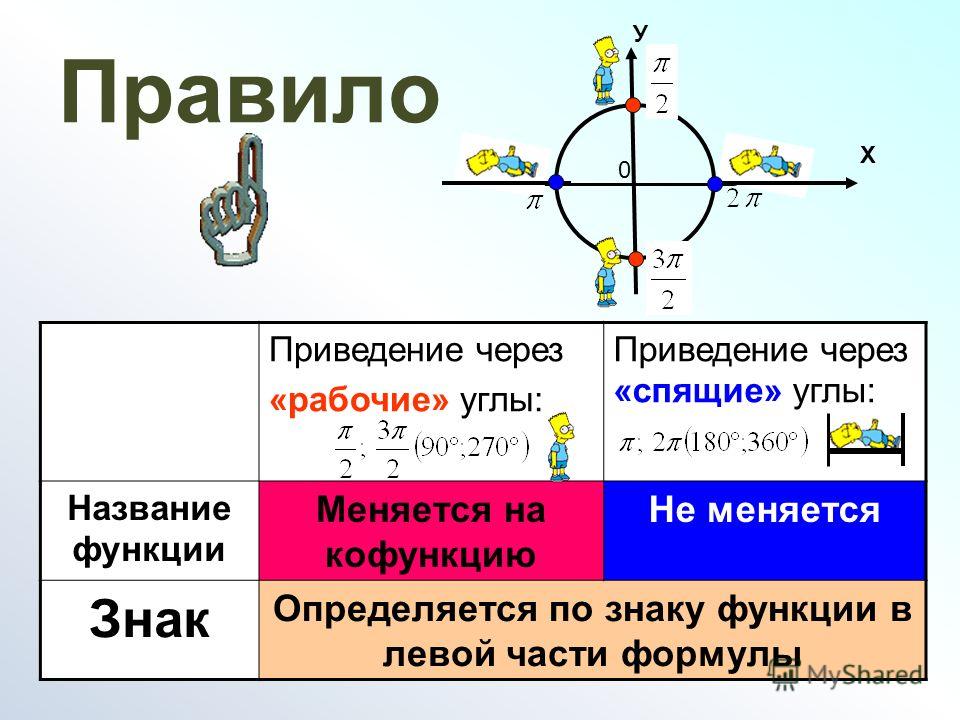 onlinemschool.com/math/formula/trigonometry_formula/
onlinemschool.com/math/formula/trigonometry_formula/
 Речь о мнемоническом правиле пойдет позже.
Речь о мнемоническом правиле пойдет позже.
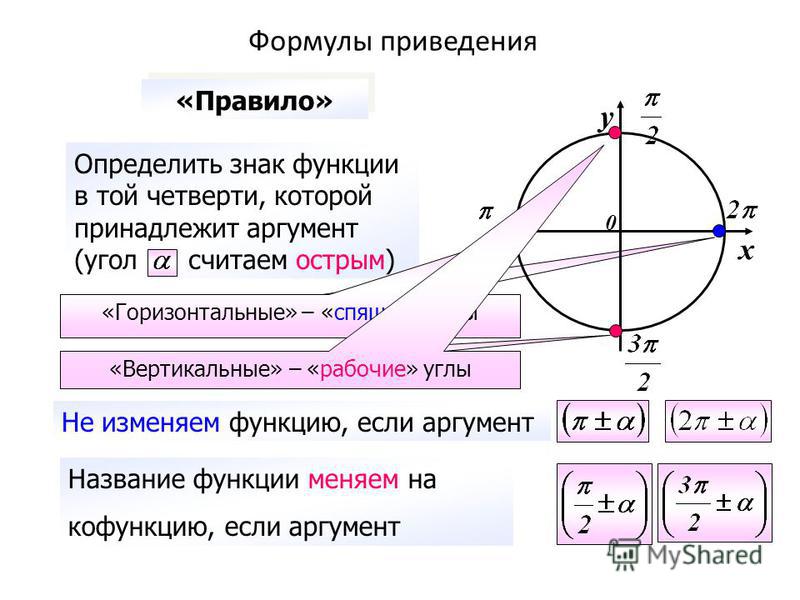
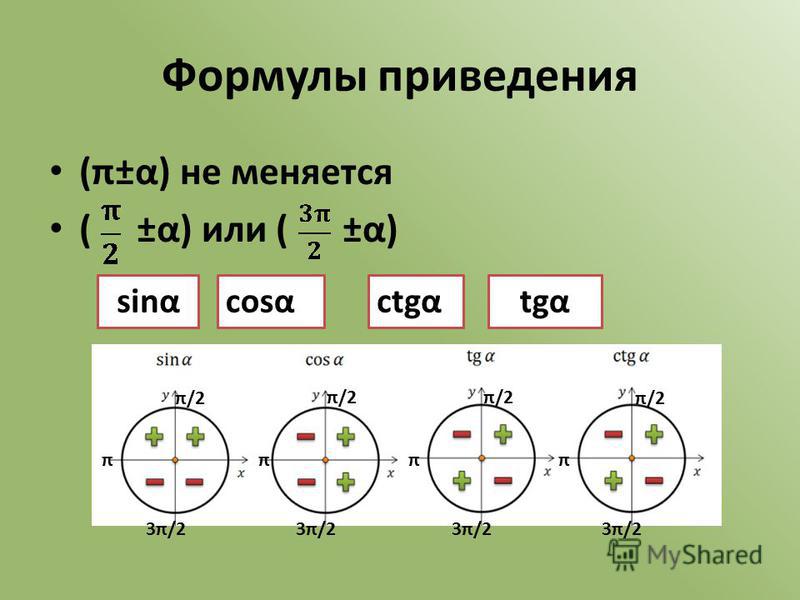 Мы можем использовать четность
тригонометрические функции, которые помогут нам упростить тригонометрические выражения.
Мы можем использовать четность
тригонометрические функции, которые помогут нам упростить тригонометрические выражения.