Презентация по алгебре 7 класса на тему» Решение задач с помощью уравнений»
Решение задач с помощью уравнений 7 КЛАСС
Сегодня на уроке
- Разминка.
- Организационный момент.
- Найди ошибку и реши правильно.
- Творческая работа.
- Самостоятельная работа.
- Физминутка.
- Как решать?
- Проверь себя!
- Подведение итогов.
Разминка
Вступительное слово учителя
Один начинающий волшебник, герой шуточной песенки,
неумело обращался с заклинаниями, в результате, вместо грозы у него получилась коза, а вместо утюга – слон.
Чтобы решать уравнения, нужно совершать ряд преобразований,
и делать это следует очень осмотрительно.
Прежде всего, надо знать правила, которые применяются при решении уравнений.
Найди ошибку!
8х+40=8(х+2)+24;
8х+40=8х+16+24;
8х-8х=16+24+40;
0х=80.
уравнение корней не имеет.
8х+40=8(х+2)+24;
8х+40=8х+16+24;
8х-8х=16+24 — 40;
0х= 0 ;
х — любое число.
Творческая работа Задача №1
Пустая коробка в 4 раза легче коробки с сахаром
Решение:
4х+4х+0,1=х+1+0,5;
4х+4х-х=1,5-0,1;
7х=1,4;
х=1,4:7;
х=0,2;
0,2(кг) — пустая коробка,
0,2 ∙ 4=0,8(кг) -коробка с сахаром,
0,8-0,2=0,6(кг) — сахар.
Ответ: 0,6кг
С
А
Х
А
р
С
А
Х
А
р
1кг
500г
100г
Сколько весит сахар?
С
Творческая работа Задача №2
Ответ:
1.
2х+2(х+4)=32;
2.(х+х+4) 2=32.
Дано: АВС D – прямоугольник,
Р(АВС D ) =32 см,
АВ ‹ ВС на 4см.
В
х+4
х
А
D
Составьте уравнение к задаче двумя способами .
Творческая работа Задача №3
Составить условие задачи по уравнению:
а) х+3х=16;
б) х +(х+2)=12.
Самостоятельная работа
Вариант 1
Часть пути в 600 км турист пролетел на самолёте, а часть проехал на автобусе.
На самолёте он проделал путь, в 9 раз больший, чем на автобусе. Сколько километров турист проехал на автобусе?
Вариант 2
Саша решил две задачи за 35 мин. Первую задачу он решал на 7 мин дольше, чем вторую. Сколько минут Саша решал вторую задачу?
ФИЗМИНУТКА
Физкультминутка
- Рисуй глазами треугольник
- Рисуй глазами треугольник.
- Теперь его переверни
- Вершиной вниз.
- И вновь глазами
- ты по периметру веди.
- Рисуй восьмерку вертикально.
- Ты головою не крути,
- А лишь глазами осторожно
- Ты вдоль по линиям води.
- И на бочок ее клади.
- Теперь следи горизонтально,
- И в центре ты остановись.
- Зажмурься крепко, не ленись.
- Глаза открываем мы, наконец.
- Зарядка окончилась.
- Ты – молодец!
Как решать?
По шоссе идут две автомашины с одной и той же скоростью.
Если первая увеличит скорость на 20 км/ч, а вторая уменьшит на 20 км/ч,
то первая за 2 ч пройдёт столько же, сколько вторая за 3 ч.
С какой скоростью идут автомашины?
Пусть х км/ч-
скорость каждой машины.
v ,км/ч t ,ч S ,км
1.
(х+20) 2 (х+20)2
2. (х-20) 3 (х-20)2
По условию задачи,
автомашины проехали одинаковое расстояние.
(х+20)2=(х-20)3;
2х-3х=-60-40;
-х=-100;
Х=100;
100 км/ч-скорость каждой автомашины.
Ответ: 100 км/ч
Задание на дом
1.Решите задачу:
Таня в школу сначала едет на автобусе, а потом идёт пешком. Вся дорога у неё занимает 30 минут. Идёт она на 10 минут дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
2.Решите уравнение:
3х-(9х-3)=3(4-2х).
Проверь себя!
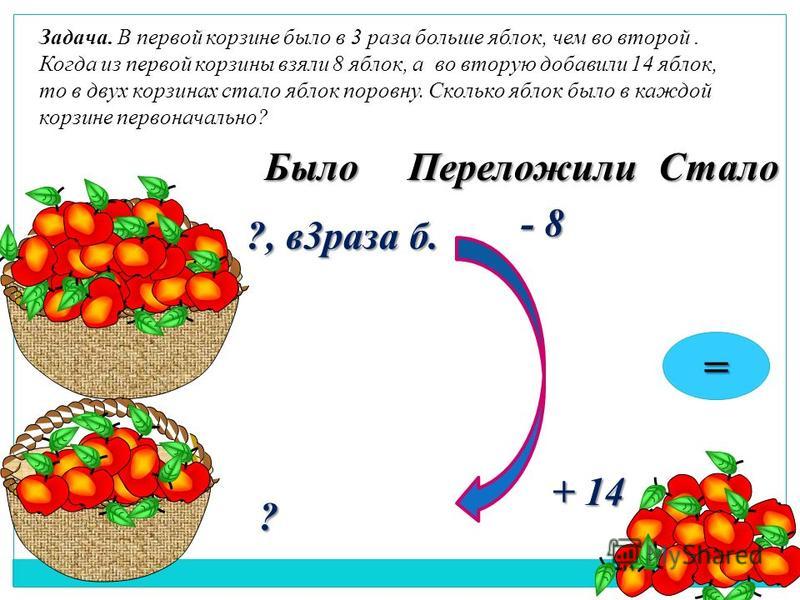
В двух сараях сложено сено, причём, в первом сарае в 3 раза больше, чем во втором. После того, как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в сараях первоначально?
Пусть х т сена было во II сарае,
тогда (3х) т сена было в I сарае, а (3х-20) т стало в I сарае,
(х+10)т стало во II сарае.
Известно, что в сараях сена стало поровну.
3х-20=х+10;
3х-х=10+20;
2х=30;
х=15; 15(т) было во II сарае;
15 ∙3=45(т) было в I сарае.
Ответ: 45 т
Дополнительные задания
Решите уравнения:
-2х=14;
3х=0;
0х=0;
0х=12;
(х-6)(х+11)=0;
Х(х+3)(х-1)=0.
Литература
- Газета «Математика».- Изд.: Первое сентября, 2000-2007.
- Звавич Л.И., Кузнецова Л.В., Суворов С.Б. Дидактические материалы по алгебре для 7 класс.- М.: Просвещение,2004.
Учащиеся не знают | |||
Правила решения уравнений, арифметический способ решения задач | алгебраический способ решения задач в два и более действий. | Деятельность учащихся | время |
1.Организационный момент Приветствие, проверка готовности к уроку. Домашнее задание Инструкция по работе с оценочными листами. 2.Актуализация знаний — Актуализация теоретических знаний и умений по теме «решение уравнений»; -мотивация к восприятию нового -целеполагание Более 5 тысяч лет назад образовалось одно из первых на земле государств. Его жители Египтяне были замечательными инженерами, они построили знаменитые пирамиды, дворцы, лабиринты. Ясно, что они обладали большим запасом знаний, в том числе и математических. Сегодня мы тоже будем строить дворец. Для фундамента у нас есть кирпичи, колонны, которые будут поддерживать крышу и сама крыша, которая будет венчать наше строение. Но что бы его построить , нам нужно вспомнить всё, что мы знаем об уравнениях, показать своё умение решать их. Итак, начнём. Блиц-опрос. Соедините стрелками понятие в левом столбике и его определение в правом (работают самостоятельно) 1 чел у доски. 1.Что называется уравнением | Найти все его корни или доказать, что корней нет | ||
2. | Равенство, содержащее переменную | ||
3. Что значит решить уравнение | Значение переменной, при котором уравнение обращается в верное числовое равенство | а-94=121 | 163-р=83 | 409 +у=511 |
138+х+52=218 | (148 +в)-58=148 | ||
37-(с+23)=0 | (124-m)+26=52 | Выполняют задания на листочках, один человек у доски. Проверяют выполнение задания, сверяясь с работой у доски. Устно решают уравнения, ответы записывают в блокноте для устного счёта, показывают учителю. Оценивают свою работу. Отвечают фронтально -Для решения задач Учиться решать задачи с помощью уравнений. -Решать задачи с помощью уравнений. Решают задачу в тетрадях. Фронтальная проверка Делятся на группы. Повторяют правила работы в группах. Работают в группе наклеивают их в нужном порядке на лист А-3, добавляют недостающий нумеруют. Работа в группах Рассказывают у доски своё решение, предлагают план Все остальные Слушают решение каждой группы, записываем в тетрадь, задают вопросы. Сверяем составленные планы с правильным:
Фронтально отвечают на вопросы | 2 мин 10мин 5мин 10 мин 10мин 5мин 3мин |
Что называется корнем уравнения
Сегодня и мы попробуем применить наши умения решать задачи с помощью уравнений для более сложных задач.
В московском музее хранятся 2 таких папируса, в музеях Лондона -5 папирусов, несколько папирусов пострадали от времени. Сколько папирусов не сохранилось, если всего было 24 папируса с задачами.
Всего было 53 литра воды
Математика, 7 класс, Алгебраическое мышление
CCSS.Math.Content.7.EE.A.1 7 класс, выражения и уравнения
Кластер: использование свойств операций для создания эквивалентных выражений
Стандарт: применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.
CCSS.Math.Content.7.EE.A.2 7 класс, выражения и уравнения
Кластер: Используйте свойства операций для создания эквивалентных выражений
Стандарт: Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины.
Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равнозначно «умножению на 1,05».
CCSS.Math.Content.7.EE.B.3 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: решение многоэтапных реальных и математических задач, связанных с положительными и отрицательными рациональными числами в любой форме (целыми числами, дробями и десятичными знаками), стратегически используя инструменты. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает повышение на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
CCSS.Math.Content.7.EE.B.4 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: использование переменных для представления величин в реальной или математической задаче и построение простых уравнений и неравенств для решения проблемы, рассуждая о количествах.
CCSS.Math.Content.7.EE.B.4a 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: решение текстовых задач, приводящих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см.
CCSS.Math.Content.7.EE.B.4b 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: решение текстовых задач, приводящих к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например, как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
CCSS.Math.Practice.MP.1 Математические практики
Кластер: Математические практики
Стандарт: Разбираться в задачах и настойчиво решать их. Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения.
CCSS.Math.Practice.MP.2 Математические практики
Кластер: Математические практики
Стандарт: Рассуждать абстрактно и количественно. Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
CCSS.Math.Practice.MP.3 Математические практики
Кластер: Математические практики
Стандарт: Придумывать жизнеспособные аргументы и критиковать рассуждения других. Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и, если в аргументе есть изъян, объяснять, в чем он заключается.
Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
CCSS.Math.Practice.MP.4 Математические практики
Кластер: Математические практики
Стандарт: Модель с математикой. Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе.
К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
CCSS.Math.Practice.MP.5 Математические практики
Кластер: Математические практики
Стандарт: Стратегическое использование соответствующих инструментов.
Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными.
Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
CCSS.Math.Practice.MP.6 Математические практики
Кластер: Математические практики
Стандарт: Следите за точностью. Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи.
2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
MCCRS.Math.Content.7.EE.A.1 7 класс
Область обучения: выражения и уравнения
Стандарт: использование свойств операций для создания эквивалентных выражений
Индикатор: применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.
MCCRS.Math.Content.7.EE.A.2 7 класс
Область обучения: выражения и уравнения
Стандарт: Используйте свойства операций для создания эквивалентных выражений
Индикатор: Поймите, что переписывание выражения в различных формах в контексте задачи может пролить свет на проблему и на то, как связаны величины в ней.
Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» — это то же самое, что «умножение на 1,05». —
MCCRS.Math.Content.7.EE.B.3 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: решение многоэтапных реальных и математических задач с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби) , используя инструменты стратегически. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает повышение на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
MCCRS.Math.Content.7.EE.B.4 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: использование переменных для представления величин в реальных или математических задачах и построение простых уравнений и неравенства для решения проблем, рассуждая о количествах.
MCCRS.Math.Content.7.EE.B.4a 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: решение текстовых задач, ведущих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см.
Его длина составляет 6 см. Какова его ширина?
MCCRS.Math.Content.7.EE.B.4b 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: решение текстовых задач, приводящих к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например, как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
MCCRS.Math.Practice.MP.1 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Разбираться в задачах и настойчиво решать их.
Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему.
Подкованные в математике учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?». Они могут понять подходы других к решению сложных задач и определить соответствие между различными подходами.
MCCRS.Math.Practice.MP.2 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Рассуждать абстрактно и количественно. Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов.
Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
MCCRS.Math.Practice.MP.3 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Придумывать обоснованные аргументы и критиковать рассуждения других. Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других.
Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и «если в аргументе есть изъян» объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
MCCRS.Math.Practice.MP.4 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Модель с математикой.
Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы.
Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
MCCRS.Math.Practice.MP.5 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Стратегически используйте соответствующие инструменты. Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения.
Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
MCCRS.Math.Practice.MP.6 Классы K-12
Область обучения: математические практики
Стандарт: математические практики
Показатель: внимание к точности. Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. В начальных классах учащиеся дают тщательно сформулированные объяснения друг другу. К тому времени, когда они переходят в старшие классы, они уже научились анализировать утверждения и явно использовать определения.
MCCRS.Math.Practice.MP.7 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Ищите и используйте структуру. Математически подкованные учащиеся внимательно смотрят, чтобы различить закономерность или структуру. Например, учащиеся младшего возраста могут заметить, что три и еще семь — это то же самое, что семь и еще три, или они могут отсортировать набор фигур по количеству сторон у фигур.
2 + 92 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
MCCRS.Math.Practice.MP.8 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Ищите и выражайте регулярность в повторяющихся рассуждениях. Подкованные в математике учащиеся замечают, повторяются ли вычисления, и ищут как общие методы, так и упрощения. Учащиеся старших классов могут заметить, что при делении 25 на 11 они повторяют одни и те же вычисления снова и снова, и прийти к выводу, что у них есть повторяющаяся десятичная дробь. Уделяя внимание вычислению наклона, постоянно проверяя, находятся ли точки на линии, проходящей через (1, 2) с наклоном 3, учащиеся средней школы могут абстрагироваться от уравнения (y — 2)/(x -1) = 3. Заметив регулярность в том, как члены сокращаются при расширении (x — 1) (x + 1), (x — 1) (x ^ 2 + x + 1) и (x — 1) (x ^ 3 + x ^ 2 + x + 1) может привести их к общей формуле суммы геометрического ряда.
Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Математика, 7 класс, Алгебраические рассуждения, Использование арифметики и уравнений для решения задач
Обзор
Учащиеся расширяют знания, полученные в 6 классе о решении уравнений. Они учатся решать уравнения, которые требуют от них использования как сложения, так и свойства умножения равенства. Они используют свои знания о решении таких уравнений, как 2 90 231 x 90 232 = 6 и 90 231 x 90 232 + 3 = 7, для решения таких уравнений, как 2 90 231 x 9.0232 + 3 = 8. Они связывают решение задач с помощью арифметики с решением задач с помощью уравнений. Они решают уравнения, содержащие как положительные, так и отрицательные рациональные числа.
- Дополнительное свойство равенства: Если a = b , то a + c = b + c .
- Свойство равенства умножения: Если a = b , то ac = bc .
- Для любого уравнения добавьте или вычтите одно и то же значение из обеих частей уравнения, и уравнение останется верным.
- Для любого уравнения умножьте или разделите обе части уравнения на одно и то же значение, и уравнение останется верным.
- На этом уроке учащиеся используют оба свойства для решения уравнений. Затем они решают уравнения, содержащие как положительные, так и отрицательные рациональные числа.
- Решите уравнения, используя свойства сложения и умножения равенства.
- Свяжите решение задач с помощью арифметики с решением задач с помощью уравнений.
- Решите уравнения, содержащие как положительные, так и отрицательные рациональные числа.
Предложите учащимся прочитать о свойствах равенства. Задайте следующие вопросы, чтобы убедиться, что учащиеся понимают свойства:
- Если x + 7 = 9, что бы вы сделали, чтобы найти x ? (Добавьте –7 к обеим частям уравнения. ) Какое свойство равенства вы используете? (дополнительное свойство равенства)
- Если 5 z = 20, что бы вы сделали, чтобы найти z ? (Умножьте обе части на 15.) Какое свойство равенства вы используете? (свойство равенства умножения)
) Какое свойство равенства вы используете? (дополнительное свойство равенства)ELL: Если учащимся трудно начать, задайте эти вопросы ELL. Убедитесь, что ваш темп адекватен, и вы предоставляете достаточно времени для обдуманного ответа. Представьте вопросы в письменном виде и позвольте учащимся использовать словари перед ответом, если в ваших вопросах есть слова, которые они не понимают.
Открытие
Прочитать и обсудить
Повторить свойства равенства.
Дополнительное свойство равенства : Если a = b , то a + c = b + c .
Свойство умножения равенства : Если a = b , то ac = bc .
Итак, для любого истинного уравнения можно сделать следующее:
- Добавьте одно и то же значение к обеим сторонам или вычтите одно и то же значение с обеих сторон, и уравнение останется верным.
- Умножьте или разделите обе части на одно и то же значение, и уравнение останется верным.
Предложите учащимся в парах прочитать информацию о шахте Ларонд. Попросите каждую пару предсказать, насколько глубоко шахтер может зайти, прежде чем температура станет опасно высокой.
Задайте следующие вопросы:
- Какая температура в градусах Фаренгейта будет опасно высокой?
- Какова была ваша стратегия при предсказании?
- Имеет ли смысл ваша стратегия?
Вскрытие
Шахта LaRonde в Квебеке, Канада, является самой глубокой шахтой в Северной Америке. В настоящее время его глубина составляет около 2,25 км (или почти 7400 футов). Когда он будет завершен, его глубина составит около 3 км (или почти 10 000 футов).
Чем глубже шахта, тем ближе она к центру Земли; так, температура в шахте повышается. На каждые 1000 футов глубины температура повышается примерно на 5ºF.
Без системы охлаждения горняки не смогли бы спуститься глубоко в шахту, не перегреваясь.
- Предскажите, как глубоко, по вашему мнению, шахтер может спуститься в шахту, прежде чем станет опасно горячим.
Обсудить математическую миссию. Студенты будут использовать свойство равенства сложения и свойство равенства умножения для решения уравнений.
Открытие
Используйте свойство сложения равенства и свойство умножения равенства для решения уравнений.
Предложите учащимся работать в парах. Задайте следующие вопросы, чтобы убедиться, что учащиеся понимают задачи:
- Когда вы спускаетесь в шахту, что происходит с температурой?
- Чем отличается температура на высоте 3000 м от температуры на высоте 100 м?
- Какое уравнение поможет вам решить задачу?
- Можно ли использовать свойства равенства для решения уравнения?
Студент не знает, как начать отвечать на вопросы о температуре в шахте.
- Какая температура на уровне земли?
- Будет ли температура в шахте выше или ниже 15°C?
- Если температура повысится на 0,010°С на глубине 1 м, насколько она повысится на глубине 2 м? 3 м? 10 м? 100 м?
Рабочее время
Предположим, что температура шахты на уровне земли составляет 15°C, и на каждый метр глубины температура повышается на 0,010°C.
- Какая температура будет на глубине 100 м?
- Какая температура будет на глубине 3000 м?
- Если температура 26°C, какова глубина в метрах?
Подсказка:
- Что происходит с температурой на каждый метр увеличения глубины?
- Будет ли температура на глубине 3000 метров больше или меньше температуры на глубине 100 метров?
- Чтобы определить глубину по температуре, подумайте, насколько увеличилась температура по сравнению с температурой на уровне земли.
Предложите учащимся поработать в парах, чтобы написать уравнение и решить его.
Математическая практика 1: Разбираться в задачах и настойчиво решать их.
Поскольку у учащихся есть возможность решить одну и ту же задачу, используя как арифметику, так и алгебру, у них есть возможность сравнить два метода и два результата и попытаться их согласовать. Если пары учащихся борются из-за того, что их результаты не совпадают, дайте им время выяснить, почему.
Студент не знает, как начать решать уравнение для определения глубины шахты.
- Ваша цель — изолировать переменную с одной стороны; то есть получить d само по себе на одной стороне уравнения.
- Попробуйте добавить или вычесть одно и то же число с обеих сторон. Какой номер следует использовать?
Учащийся не знает, как написать уравнение для определения глубины при температуре 40 °C.
- Существует ли уравнение, связывающее глубину и температуру?
- Какое число представляет температуру?
- Какое число заменить на 40?
- для решения для D : 26 = 1100D+15
26–15 = 1100D+15–15 Дополнительное свойство равенства
. равенство
1,100=d
Ответ: 1,100 м • 40=1100d+15
Чтобы решить для d :
40=1100d+15
40−15=1510 добавление свойства равенства 11000004
25 = 1100D
25–100 = 1100D порядка100 Свойства Умножения равенства
2 500 = D
Ответ: 2500 М
- Проверка: 40 = 1100 (2500)+15403+15404+15404+15404+15404+15404+15404+15404+15404+15402+
- . 1540=40
Время работы
Вы можете использовать следующее уравнение, в котором d = глубина в метрах, для определения глубины в метрах при температуре 26°C:
26=1100d+15, где d = глубина в метрах
- Покажите, как можно использовать свойства равенства для решения этого уравнения.
- Напишите уравнение, с помощью которого можно найти глубину в метрах при температуре 40°C.
- Решите уравнение.
- Используйте подстановку, чтобы проверить свое решение.
Подсказка:
- Чтобы решить уравнение типа x + 5 = 8, используйте свойство равенства сложения.
- Чтобы решить уравнение типа 1/2 x = 8, используйте свойство равенства умножения.
- Подумайте, чем эта задача отличается от проблемы, которую вы только что решили.
Ищите следующие типы ответов, чтобы поделиться ими во время обсуждения «Пути мышления»:
- Учащиеся, которые решают задачи по-разному (обратите внимание на учащихся, которые используют таблицы или диаграммы, чтобы показать изменение температуры с точки зрения спуска)
- Учащиеся, которые применяют свойства равенства для решения уравнений (обратите внимание, как учащиеся применяют свойства)
- Учащиеся, которым трудно работать с дробями
SWD: Учащиеся с ограниченными возможностями могут испытывать трудности с определением важной информации на уроках.
Предварительно просмотрите цели вместе с учащимися, чтобы помочь им определить значимость по мере прохождения инструкций и выполнения заданий.Ответ
- 59°F эквивалентно 15°C.
15=59(F-32)95(15)=59(F-32)×9527=F-3227+32=F-32+3259=F
Рабочее время
Объясните ситуацию на шахте ЛаРонд с математической точки зрения. Используйте свою работу, чтобы поддержать свое объяснение.
Связь между температурой в градусах Цельсия и градусах Фаренгейта представлена следующей формулой:
C=59(F−32)
где:
C = градусы Цельсия
F = 2239 градусов Фаренгейта Использование Эта формула позволяет определить, какая температура в градусах Фаренгейта эквивалентна 15°C. - .
1540=40
Предварительно просмотрите цели вместе с учащимися, чтобы помочь им определить значимость по мере прохождения инструкций и выполнения заданий.
Организуйте обсуждение, чтобы помочь учащимся понять математику урока в неформальной обстановке. Задайте следующие вопросы:
- Что происходит с температурой на каждом метре глубины?
- Как вы определили температуру на глубине?
- Как вы использовали свойства равенства для решения уравнения для определения глубины? Есть ли более одного способа решить уравнение?
- Объясните уравнение, которое вы использовали для определения глубины при температуре 40°C.
- Как использовать формулу для определения температуры в градусах Цельсия по температуре в градусах Фаренгейта?
- Можете ли вы сравнить решение задачи с помощью арифметики с решением задачи путем решения уравнения? Что верно в ответе? Какой ты предпочитаешь? Почему?
Performance Task
Делайте заметки о работе ваших одноклассников по решению уравнений с использованием свойств равенства.
Подсказка:
В присутствии одноклассников задайте такие вопросы, как:
- По мере того, как шахта становится глубже, почему вы прибавляете изменение температуры к температуре на уровне земли, а не вычитаете ее?
- Почему вы заменили 26 на 40 в уравнении?
- Откуда вы знаете, что ваш ответ имеет смысл?
Предложите учащимся работать индивидуально, чтобы применить то, что они узнали об использовании свойств равенства для решения уравнений. Студенты должны показать каждый шаг и указать, какие свойства они используют.
Одно свойство равенства используется для решения уравнений b и d; другие уравнения (a, c, e, f, g и h) требуют обоих свойств. Теперь учащиеся работают с уравнениями, содержащими как положительные, так и отрицательные рациональные числа. По мере того, как учащиеся будут выполнять эти упражнения, ищите учащихся, у которых могут возникнуть трудности с операциями с рациональными числами. Соедините этих студентов со студентами, которые добились успеха в использовании этих концепций.
- x = 2
- x=535
- x = −1
- x = −9
- x=1312
- x=−227
- x = −2
- х=-116
Рабочее время
Решите для x , используя свойства равенства. Используйте подстановку, чтобы проверить каждое решение.
- 4 x + 4 = 12
- −5 x = −28
- 2 x + 7 = 5
- 23x=-6
- 2 х + 8 = 35
- -7 х — 6 = 10
- -4 х + 6 = 14
- -39+2232
Пусть каждый учащийся напишет краткий обзор математики на этом уроке, а затем напишет краткий обзор класса.
Когда закончите, если вы считаете, что резюме полезно, поделитесь им с классом.Вы можете решить уравнение типа x + 5 = 13, используя свойство сложения равенства. Вы добавляете -5 к обеим частям уравнения, чтобы получить х + 5 + (-5) = 13 + (-5). Затем вы упрощаете обе стороны и получаете 90 231 x 90 232 отдельно на одной стороне: 90 231 x 90 232 = 8. 90 231 x 90 232 отдельно на одной стороне. Решение равно 8.
Вы можете решить уравнение вроде −2 x = 13, используя свойство равенства умножения. Вы умножаете обе части уравнения на -12, чтобы получить -12(-2 x )=-12 ⋅ 13. Затем вы упрощаете обе части и получаете x = -612. Решение -612.
Вы можете решить уравнение вида −2 x + 5 = 13, используя свойства сложения и умножения равенства. Вы добавляете -5 к обеим частям уравнения, чтобы получить -2 x + 5 + (-5) = 13 + (-5). Затем вы упрощаете обе части, чтобы получить -2 x = 8. Затем вы умножаете обе части уравнения на -12, чтобы получить -12(-2 x ) = -12 ⋅ 8.
Затем вы упрощаете обе части и получить х = -4. Решение -4.Формирующее оценивание
Напишите краткий обзор использования свойств равенства для решения уравнений.
Подсказка:
Проверьте свое резюме:
- Определяете ли вы свойство сложения равенства и свойство умножения равенства?
- Объясните, как можно использовать эти свойства для решения уравнений, и приведите пример? (Вы можете попробовать использовать уравнение –2 x + 5 = 13 в качестве примера.)
Пусть каждый учащийся напишет краткое размышление перед окончанием урока. Просмотрите размышления, чтобы определить уровень понимания учащимися свойств равенства.
ELL: Просьба к учащимся поразмышлять над своим обучением дает ELL возможность развить грамотность в английском языке и навыки в математике. Убедитесь, что учащиеся используют как академический, так и специализированный математический язык, размышляя о своем обучении в конце каждого занятия.
Когда закончите, если вы считаете, что резюме полезно, поделитесь им с классом.
Затем вы упрощаете обе части и получить х = -4. Решение -4.